- 1Department of Psychology, University of Chicago, Chicago, IL, United States
- 2Department of Human Development and Quantitative Methodology, University of Maryland, College Park, MD, United States
In this article, we review approaches to modeling a connection between spatial and mathematical thinking across development. We critically evaluate the strengths and weaknesses of factor analyses, meta-analyses, and experimental literatures. We examine those studies that set out to describe the nature and number of spatial and mathematical skills and specific connections between these abilities, especially those that included children as participants. We also find evidence of strong spatial-mathematical connections and transfer from spatial interventions to mathematical understanding. Finally, we map out the kinds of studies that could enhance our understanding of the mechanisms by which spatial and mathematical processing are connected and the principles by which mathematical outcomes could be enhanced through spatial training in educational settings.
Introduction
Spatial ability contributes to performance in science, technology, engineering, and mathematics (STEM) domains even controlling for verbal and mathematical abilities (Shea et al., 2001; Wai et al., 2009). In addition, spatial reasoning task performance has been found to correlate with mathematical task performance (e.g., Dehaene et al., 1999), suggesting that spatial reasoning skills overlap with, and could be necessary for, mathematical reasoning skills (Tosto et al., 2014). One correlation supported by cognitive and developmental research is between representations of numerical and spatial magnitudes. Spatial skills have been found to correlate with numerical magnitude representations across broad age ranges, from preschoolers (Gunderson et al., 2012) to adults (Sella et al., 2016). Further, spatial and numerical magnitude representations have overlapping neural representations (Piazza et al., 2007; Holloway et al., 2010). In this article, we review evidence for the connections between spatial and mathematical skills across development that has been gleaned from factor analyses, meta-analyses, and experimentation. We then suggest productive ways to elucidate spatial-mathematical connections and discuss ways that modeling could be used to improve mathematics learning.
Factor Analysis
Both spatial and mathematical ability have been investigated since the early days of psychological science using factor analytical methods that sought to map the “structure of the intellect” (Spearman, 1927; Thurstone, 1938). This research showed a connection between spatial and mathematical domains, yet the mechanisms by which training spatial thinking can promote mathematical thinking are still not well understood. Across various factor analyses of spatial skills that have been conducted in adults, the most consistent finding is that there are multiple spatial skills, such as spatial visualization (imagining transformations) and spatial relations and spatial orientation (perceiving object position and angle) (Michael et al., 1957; McGee, 1979; Lohman, 1988; Carroll, 1993). Factor analyses carried out on mathematical measures over various ages have revealed latent factors that do not appear to be specific to mathematics (e.g., deductive reasoning and adaptability to a new task among 10th grade students, Kline, 1960; abstraction, analysis, application among elementary school students Rusch, 1957). These studies are notable in that some theorists have found evidence of a spatial factor in mathematics (e.g., Kline, 1960; Werdelin, 1966) and others have argued that there is a spatial sensorimotor intelligence factor important to mathematical reasoning (Coleman, 1960; Skemp, 1961; Aiken, 1970).
Separate but Correlated Spatial and Mathematical Thinking Factors
While many studies have found evidence of connections between spatial and numerical tasks in young children, only recently have studies explored the factor structure of their spatial and mathematical skills. Mix et al. (2016, 2017a) have used factor analyses to examine the connections among a broad range of mathematical and spatial tasks in elementary school age children. Mix et al. (2016) administered a battery of tasks that had the greatest likelihood of showing spatial-mathematical connections based on the literature, including connections between (1) spatial visualization and complex mathematical relations, (2) form perception and symbolic reasoning, and (3) spatial scaling and numerical estimation (Landy and Goldstone, 2010; Slusser et al., 2013,; Thompson et al., 2013, respectively). These tasks were included in order to identify which underlying variables that connect spatial and mathematical domains in kindergarten, third and sixth grades.
Between kindergarten and sixth grade range, all spatial tasks loaded together on a distinctly spatial factor, and all mathematical tasks loaded on a distinctly mathematical factor (Mix et al., 2016, 2017a). However, there was a moderate correlation between the two factors (rs = 0.50–0.53), even when controlling for verbal ability, suggesting that although the spatial and mathematical domains are distinct, there is a significant relation between these domains. Even though verbal ability accounted for a significant portion of variance in mathematical skills in each grade tested, spatial skills accounted for a greater proportion of variance (Mix et al., 2016). Cross-loadings between the spatial and mathematical factors and tasks in the two domains also indicate specific connections. In kindergarteners, mental rotation was significantly related to the mathematical factor, whereas in sixth graders visuospatial working memory and form copying were significantly related to the mathematical factor. One possible explanation for the change in cross-loadings over development is that mathematical thinking relies at first on dynamic, object-focused spatial processes (mental rotation) and later on more static, memory-related spatial processes (visuospatial working memory and visuomotor integration).
Strengths and Limitations of Factor Analysis Evidence
Factor analysis is a useful tool for isolating the source of correlations and removing measurement error (Bollen, 1989) as well as for testing competing theories (Gerbing and Hamilton, 1996; Tomarken and Waller, 2005). However, factor analysis requires a large number of participants over a breadth of tasks in a domain to achieve a stable structure (Hair et al., 1995; MacCallum et al., 1999). The biggest limitation of factor analysis lies in the theorist; interpretation of results is a large part of proper factor analysis because the results do not uniquely point to any single interpretation of the meaning of the underlying latent variables that are revealed (Armstrong and Soelberg, 1968; Rummel, 1970). Thus, when relations do emerge from factor analysis, other methods must be used to establish mechanisms underlying these relations.
Meta-Analytic and Experimental Studies
In addition to factor analyses, researchers have tackled the question of how the domains of space and math are connected through targeted experimental studies and meta-analyses. In this section, we outline prominent theories about the divisions in each domain and evidence for correlations between spatial and mathematical skills. Understanding these theories is important because they can help us to understand which particular facet or type of spatial thinking is linked to a particular type of mathematical thinking.
One comprehensive meta-analysis of spatial skills training by Uttal et al. (2013) assumed a 2 × 2 typology supported by behavioral (Newcombe and Shipley, 2015) and neurological evidence (e.g., Chatterjee, 2008). Specifically, relations between objects are processed differently than relations of feature within an object (the extrinsic-intrinsic division). Further, spatial information conveyed by a static viewing of objects and scenes is processed differently than movements and transformations of these objects and scenes (the static-dynamic division). In their factor analysis testing the 2 × 2 typology, (Mix et al., under review) found evidence for distinct spatial factors for tasks involving within object (intrinsic) vs. between object (extrinsic) information, but did not find support for spatial tasks separating according to the static-dynamic distinction (Mix et al. under review). Echoing this finding, Kozhenikov et al. found evidence that some children process spatial information intrinsic to objects better (object visualizers) whereas others process spatial information that involves between object relationships better (spatial visualizers) but did not find that these groups of children differed in their ability to process dynamic and static imagery (Kozhevnikov et al., 2005).
The number and nature of basic mathematical skills that underlie mathematical thinking are also in question. For example, a distinction has been made between core number systems that represent exact and approximate number (Carey, 2004; Feigenson et al., 2004), between core systems for approximate number and ratio (Matthews and Hubbard, 2017), and between core approximate number system and exact number ability enabled by symbolic knowledge (e.g., Carey, 2004). However, the debate about the systems that characterize mathematical thinking has taken on a more pragmatic turn than those concerning spatial thinking. For instance, there are direct educational implications to whether core mathematical skills facilitate later symbolic mathematical understanding and achievement and how the latter might affect the former (e.g., Feigenson et al., 2013; Schneider et al., 2017) or whether mathematics is better taught through concepts or procedures (e.g., Schoenfeld, 1985), or abstractly or concretely (e.g., Kaminski et al., 2009). Researchers also debate which kinds of early mathematical skills relate to later mathematical achievement (e.g., understanding patterns, Rittle-Johnson et al., 2017; thinking symbolically, Schneider et al., 2017, or one's ordinal vs. absolute sense of number Lyons et al., 2014). These debates raise interesting questions about the connection between spatial skills, early mathematical skills, and later mathematical achievement. For example, does a particular type of spatial skill relate to children's ability to learn particular early mathematical skills more quickly, and are these the early mathematical skills that relate most strongly to later mathematical achievement?
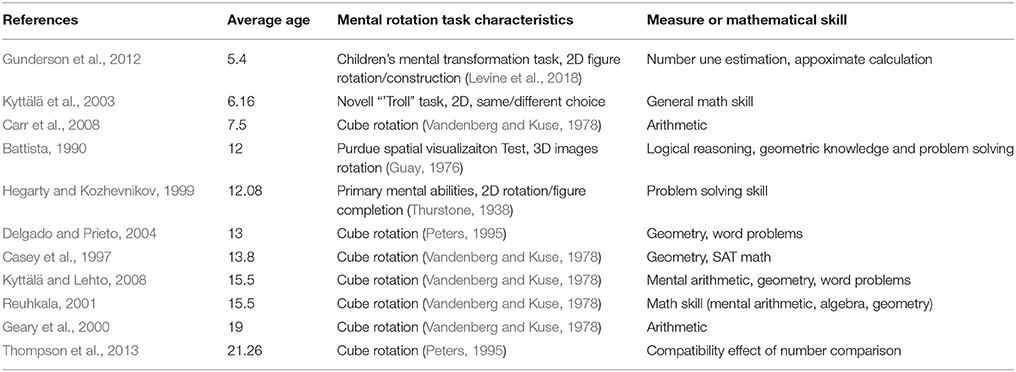
What Skills Are Used in Both Spatial and Mathematical Problems?
Certain connections between specific spatial skills and mathematical skills have been observed (e.g., visuospatial working memory and computation, Raghubar et al., 2010) whereas others have not (e.g., between disembedding shapes from scenes and parsing information in charts, Clark, 1988) with little explanation as to why this is the case (for a review of these connections see Mix and Cheng, 2012). One frequently observed connection is between mental rotation and various math skills, across age and development and with a variety of different mental rotation task characteristics (Table 1). However, little is known about the processes that account for this connection, or whether there are other spatial-mathematical connections that may be even stronger. Thus, this correlational type of evidence fails to provide support for the theory that certain specific spatial skills are particularly important for mathematics achievement nor how they enable better performance and learning of specific mathematical skills. Answers to these questions are of high importance to successfully incorporating spatial learning into mathematical curricula.
Moving beyond correlational studies, studies that have measured the impact of training mental rotation on specific mathematical skills, have not yielded consistent findings, with some finding evidence of transfer (e.g., Cheng and Mix, 2014; Lowrie et al., 2017) and some not finding such evidence (Hawes et al., 2015b; Xu and LeFevre, 2016). There is little explanation, and as of yet no meta-analysis, to compare these cross-domain training studies or determine the overall effectiveness of training any individual spatial skills to improve mathematical reasoning. In the next section, we argue that modeling and testing the processes involved in performing specific spatial and mathematical tasks can help us understand the connections between these two domains.
Cognitive Process Models
Cognitive process models provide an account of the mental processes engaged when performing a specific task. What cognitive process or processes actually drive performance on a spatial task? Answering this question would also allow us to understand the mechanism that accounts for the connection between spatial skills, like mental rotation, and performance on mathematical tasks such as missing term problems (Cheng and Mix, 2014). This in turn would inform educational efforts to improve spatial thinking in ways that would be most helpful to mathematical thinking.
What is known about the processes used for spatial skills? Various studies have supported substantive divisions between particular kinds of spatial skills, e.g., the intrinsic-extrinsic divide separating tasks such as mental rotation from perspective taking (Huttenlocher and Presson, 1973; Kozhevnikov and Hegarty, 2001). However, studies with kindergarten through sixth grade children also show a great deal of overlap among a wide range of spatial skills (Mix et al., 2016, 2017a). Further, certain spatial skills, notably mental rotation and visuospatial working memory, have been found to cross-load onto a mathematical factor at particular grade levels. An important next step is to examine process models of spatial skills and how they are manifested (or not) on mathematical tasks, as illustrated below regarding mental rotation.
A Process View of Mental Rotation
Mental rotation was first described based on the finding that time to simulate the rotation of an object was related to the angle through which the object was rotated (Shepard and Metzler, 1971). Cognitive process models, supported by empirical studies, reveal that mental rotation actually involves multiple, non-obvious sub-components. Behavior is best fit by a model that involves carrying out small, successive, variable transformations, rather than a single rotation (Provost and Heathcote, 2015) and empirical work suggests that individuals actually rotate just one part of the object rather than all parts of the whole object (Xu and Franconeri, 2015). Further, modeling shows that the type of mental rotation problem influences the process that is engaged; when rotating complex stimuli, participants tend to be slower (Bethell-Fox and Shepard, 1988; Shepard and Metzler, 1988), which has been fit by computational models of mental rotation where task relevant features of the object are focused on and task irrelevant features are ignored (Lovett and Schultheis, 2014). Participants also frequently err in problems with complex stimuli by selecting the mirror image of the correct choice that is rotated to the same degree as the correct choice (e.g., among children Hawes et al., 2015a,b), a pattern of data that is explained by a model that parameterizes “confusability” between the target and its mirror (e.g., confusing a “d” for a “b,” Kelley et al., 2000). Relatedly participants tend to use a fast flipping transformation akin to matching features for simple, 2D stimuli, which models of mental rotation have taken this into account (Kung and Hamm, 2010; Searle and Hamm, 2012). The varied components described by these models make clear that mental rotation is not a simple process, and that there are many steps needed to succeed at a mental rotation task.
Each of these modeled components of mental rotation performance has a potential role to play in the observed relationship between mental rotation and various mathematical skills over the course of development. If spatial constructs are actually based on wide-ranging processes it opens up the hypothesis space to determine the source of connections between spatial and mathematical thinking. Rather than a simple connection between two monolithic skills, there are numerous possible connections based on the components of each, and possibly even multiple ways a spatial skill can act in a single math problem. The work of figuring out which components are critical to the observed relation between spatial and mathematical skills, while daunting, is needed in order to unpack what otherwise are opaque connections.
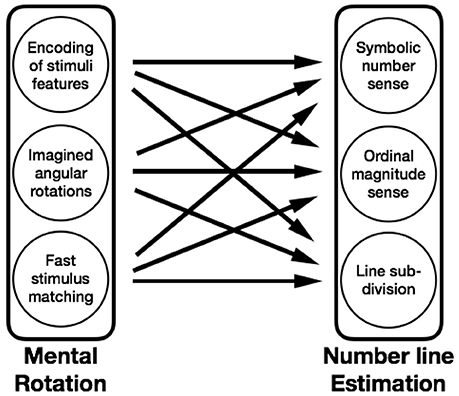
To take one example, Gunderson et al. (2012) observed a predictive relationship between young children's mental transformation skill and their number line estimation. Individual differences in mental rotation performance could have arisen as a difference in any of the components identified above: the ability to carry out rotations, to focus on relevant spatial information, or to carry out non-rotational stimulus matching. Similarly, the number line estimation task, where participants are asked to determine the position of a number along a labeled line, could be decomposed into several components as well (e.g., accessing a representation of a number's magnitude when cued by its symbol, ordering those magnitudes precisely on a continuous number line, spatially subdividing the line at salient landmarks, Siegler and Opfer, 2003). Any or all of these components might be the source of the connection between number line estimations and spatial skill (see Figure 1). By designing studies that control for and model the components of both spatial and mathematical tasks, it should be possible to identify and understand the mechanisms that explain links between spatial and mathematical thinking. This approach compliments and enriches the work focused on looking at the latent structure of skills, while not dwelling on an explanation of any one task but focusing on explaining important connections between latent skills.
Educational Implications
Meta-analyses provide strong evidence that training spatial skills in the laboratory result in significant improvements and transfer to other spatial skills (Uttal et al., 2013). However, evidence is more mixed about training spatial skills to improve mathematical skills (e.g., Cheng and Mix, 2014; Hawes et al., 2015b; Simons et al., 2016; Lowrie et al., 2017). Broader training regimes in and out of the classroom have helped to improve mathematics performance in multiple age groups (e.g., Witt, 2011; Sorby et al., 2013; Bruce and Hawes, 2015), and more generally, spatial thinking has been shown to be a significant predictor of STEM outcomes, even controlling for mathematical and verbal thinking (Wai et al., 2009).
One finding substantiated by factor analyses and interventions is that spatial skills are more closely related to novel mathematical and scientific content than to STEM skills that are more familiar (Stieff, 2013; Mix et al., 2016), suggesting that it may be particularly important to provide students with spatial scaffolding when students are learning a new mathematical concept. Another set of findings suggests that providing students with a repertoire of spatial tools, such as gesture, rich spatial language, diagrams, and spatial analogies, (Newcombe, 2010; Levine et al., 2018) can facilitate their spatial thinking. Moreover, these tools, as well as 3-D manipulatives (Mix, 2010) have been found to facilitate learning mathematical concepts (e.g., Richland et al., 2012; Verdine et al., 2014; Hawes et al., 2017; Mix et al., 2017b). An overarching principle to guide the use of spatial thinking and tools in education is that supporting spatial thinking and learning beginning early in life may result in improvements in mathematics understanding, based on the general connection between spatial and mathematical factors as well as evidence that training particular spatial skills shows some transfer to mathematics skills. A promising avenue for future work is not just to support spatial thinking in general, but to show students how they can use this kind of thinking to solve particular kinds of mathematical problems (Casey, 2004).
Conclusions
In this review, we critically evaluate the contributions of the factor analytic method to identifying and elucidating the connection between spatial and mathematical thinking across development. We highlighted a central gap in our knowledge—understanding the mechanisms connecting spatial and mathematical skills—which can be better addressed through targeted experimental studies that are informed by process models than by factor analytic studies. The findings that can emerge from this approach are important for increasing our basic understanding of why spatial and mathematical thinking are connected. They also hold promise for informing educational efforts to increase mathematical achievement by strengthening spatial thinking by training spatial skills, by encouraging the use of spatial tools, and by showing children how they can deploy these skills and tools to solve particular kind of mathematical problems.
Author Contributions
CY wrote the original draft and led efforts to refine subsequent drafts for this article. All authors worked on a related chapter; SL and KM contributed substantially to the writing and editing of this article.
Funding
This research was supported by Institute of Education Sciences Grant R305A120416 to KM and SL, as well as National Science Foundation Spatial Intelligence Learning Center Grants SBE-1041707 and SBE-0541957 to SL.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Aiken, L. R. Jr. (1970). Attitudes toward mathematics. Rev. Educ. Res. 40, 551–596. doi: 10.3102/00346543040004551
Armstrong, J. S., and Soelberg, P. (1968). On the interpretation of factor analysis. Psychol. Bull. 70:361. doi: 10.1037/h0026434
Battista, M. T. (1990). Spatial visualization and gender differences in high school geometry. J. Res. Math. Educ. e47–60.
Bethell-Fox, C. E., and Shepard, R. N. (1988). Mental rotation: effects of stimulus complexity and familiarity. J. Exp. Psychol. Hum. Percept. Perform. 14:12. doi: 10.1037/0096-1523.14.1.12
Bollen, K. A. (1989). A new incremental fit index for general structural equation models. Sociol. Methods Res. 17, 303–316. doi: 10.1177/0049124189017003004
Bruce, C. D., and Hawes, Z. (2015). The role of 2D and 3D mental rotation in mathematics for young children: what is it? Why does it matter? And what can we do about it? ZDM 47, 331–343. doi: 10.1007/s11858-014-0637-4
Carey, S. (2004). Bootstrapping and the origin of concepts. Daedalus 133, 59–68. doi: 10.1162/001152604772746701
Carr, M., Steiner, H. H., Kyser, B., and Biddlecomb, B. (2008). A comparison of predictors of early emerging gender differences in mathematics competency. Learn. Individ. Diff. 18, 61–75.
Carroll, J. B. (1993). Human Cognitive Abilities: A Survey of Factor-Analytic Studies. Cambridge University Press.
Casey, M. B., Nuttall, R. L., and Pezaris, E. (1997). Mediators of gender differences in mathematics college entrance test scores: a comparison of spatial skills with internalized beliefs and anxieties. Dev. Psychol. 33:669.
Casey, B. (2004). “Mathematics problem-solving adventures: a language-arts based supplementary series for early childhood that focuses on spatial sense,” in Engaging Young Children In Mathematics: Results of the Conference on Standards for Pre-School and Kindergarten Mathematics Education, eds D. Clements, J. Sarama, and M. A. DiBaise (Mahwah, NJ: Erlbaum Associates), 377–389.
Chatterjee, A. (2008). “The neural organization of spatial thought and language,” in Seminars in Speech and Language Vol. 29 (Thieme Medical Publishers), 226–238.
Cheng, Y. L., and Mix, K. S. (2014). Spatial training improves children's mathematics ability. J. Cogn. Dev. 15, 2–11. doi: 10.1080/15248372.2012.725186
Clark, H. T. III. (1988). “Cognitive style and competence in mathematics problem solving,” in Paper Presented at the Annual Meeting of the Eastern Educational Research Association. Miami, FL.
Coleman, R. H. (1960). An analysis of Certain Components of Mathematical Ability and an attempt to Predict Mathematical Achievement in a Specific Situation. Doctoral dissertation, Indiana University. University Microfilms, Ann Arbor.
Dehaene, S., Spelke, E., Pinel, P., Stanescu, R., and Tsivkin, S. (1999). Sources of mathematical thinking: behavioral and brain-imaging evidence. Science 284, 970–974. doi: 10.1126/science.284.5416.970
Delgado, A. R., and Prieto, G. (2004). Cognitive mediators and sex-related differences in mathematics. Intelligence 32, 25–32.
Feigenson, L., Dehaene, S., and Spelke, E. (2004). Core systems of number. Trends Cogn. Sci. 8, 307–314. doi: 10.1016/j.tics.2004.05.002
Feigenson, L., Libertus, M. E., and Halberda, J. (2013). Links between the intuitive sense of number and formal mathematics ability. Child Dev. Perspect. 7, 74–79. doi: 10.1111/cdep.12019
Geary, D. C., Saults, S. J., Liu, F., and Hoard, M. K. (2000). Sex differences in spatial cognition, computational fluency, and arithmetical reasoning. J. Exp. Child Psychol. 77, 337–353. doi: 10.1006/jecp.2000.2594
Gerbing, D. W., and Hamilton, J. G. (1996). Viability of exploratory factor analysis as a precursor to confirmatory factor analysis. Struct. Equ. Model. Mult. J. 3, 62–72. doi: 10.1080/10705519609540030
Guay, R. B. (1976). Purdue Spatial Visualization Test. West Lafayette, IN: Purdue Research Foundation.
Gunderson, E. A., Ramirez, G., Beilock, S. L., and Levine, S. C. (2012). The relation between spatial skill and early number knowledge: the role of the linear number line. Dev. Psychol. 48, 1229–1241. doi: 10.1037/a0027433
Hair, J. F. Jr., Anderson, R. E., Tatham, R. L., and William, C. (1995). Multivariate Data Analysis with Readings. Englewood Cliffs, NJ: Prentice Hall.
Hawes, Z., LeFevre, J. A., Xu, C., and Bruce, C. D. (2015a). Mental rotation with tangible three-dimensional objects: a new measure sensitive to developmental differences in 4-to 8-year-old children. Mind Brain Educ. 9, 10–18. doi: 10.1111/mbe.12051
Hawes, Z., Moss, J., Caswell, B., and Poliszczuk, D. (2015b). Effects of mental rotation training on children's spatial and mathematics performance: a randomized controlled study. Trends Neurosci. Educ. 4, 60–68. doi: 10.1016/j.tine.2015.05.001
Hawes, Z., Moss, J., Caswell, B., Naqvi, S., and MacKinnon, S. (2017). Enhancing children's spatial and numerical skills through a dynamic spatial approach to early geometry instruction: effects of a 32-week intervention. Cogn. Instr. 35, 236–264. doi: 10.1080/07370008.2017.1323902
Hegarty, M., and Kozhevnikov, M. (1999). Types of visual-spatial representations and mathematical problem solving. J. Educ. Psychol. 91:684.
Holloway, I. D., Price, G. R., and Ansari, D. (2010). Common and segregated neural pathways for the processing of symbolic and nonsymbolic numerical magnitude: an fMRI study. Neuroimage 49, 1006–1017. doi: 10.1016/j.neuroimage.2009.07.071
Huttenlocher, J., and Presson, C. C. (1973). Mental rotation and the perspective problem. Cogn. Psychol. 4, 277–299. doi: 10.1016/0010-0285(73)90015-7
Kaminski, J. A., Sloutsky, V. M., and Heckler, A. (2009). Transfer of mathematical knowledge: the portability of generic instantiations. Child Dev. Perspect. 3, 151–155. doi: 10.1111/j.1750-8606.2009.00096.x
Kelley, T. D., Lee, F. J., and Wiley, P. (2000). Developing an ACT-R Model of Spatial Manipulation (ARL Tech. Rep. No. 2179). Aberdeen, MD: Aberdeen Proving Ground.
Kline, W. E. (1960). A synthesis of Two Factor Analyses of Intermediate Algebra. Doctoral dissertation, Princeton University, University Microfilms, Ann Arbor.
Kozhevnikov, M., and Hegarty, M. (2001). A dissociation between object manipulation spatial ability and spatial orientation ability. Mem. Cogn. 29, 745–756. doi: 10.3758/BF03200477
Kozhevnikov, M., Kosslyn, S., and Shephard, J. (2005). Spatial versus object visualizers: a new characterization of visual cognitive style. Mem. Cogn. 33, 710–726. doi: 10.3758/BF03195337
Kung, E., and Hamm, J. P. (2010). A model of rotated mirror/normal letter discriminations. Mem. Cogn. 38, 206–220. doi: 10.3758/MC.38.2.206
Kyttälä, M., and Lehto, J. E. (2008). Some factors underlying mathematical performance: the role of visuospatial working memory and non-verbal intelligence. Eur. J. Psychol. Educ. 23:77. doi: 10.1007/BF03173141
Kyttälä, M., Aunio, P., Lehto, J. E., Van Luit, J., and Hautamäki, J. (2003). Visuospatial working memory and early numeracy. Educ. Child Psychol. 20, 65–76.
Landy, D., and Goldstone, R. L. (2010). Proximity and precedence in arithmetic. Quart. J. Exp. Psychol. 63, 1953–1968. doi: 10.1080/17470211003787619
Levine, S. C., Goldin-Meadow, S., Carlson, M. T., and Hemani-Lopez, N. (2018). Mental transformation skill in young children: the role of concrete and abstract motor training. Cogn. Sci. doi: 10.1111/cogs.12603. [Epub ahead of print].
Lohman, D. F. (1988). “Spatial abilities as traits, processes, and knowledge,” in Advances in the Psychology of Human Intelligence, Vol. 4, ed R. J. Sternberg (Hillsdale, NJ: Lawrence Erlbaum Associates), 181–248.
Lovett, A., and Schultheis, H. (2014). “Modeling spatial abstraction during mental rotation,” in Proceedings of the 36th Annual Meeting of the Cognitive Science Society (Quebec City, QC), 886–891.
Lowrie, T., Logan, T., and Ramful, A. (2017). Visuospatial training improves elementary students' mathematics performance. Br. J. Educ. Psychol. 87, 170–186. doi: 10.1111/bjep.12142
Lyons, I. M., Price, G. R., Vaessen, A., Blomert, L., and Ansari, D. (2014). Numerical predictors of arithmetic success in grades 1–6. Dev. Sci. 17, 714–726. doi: 10.1111/desc.12152
MacCallum, R. C., Widaman, K. F., Zhang, S., and Hong, S. (1999). Sample size in factor analysis. Psychol. Methods 4:84. doi: 10.1037/1082-989X.4.1.84
Matthews, P. G., and Hubbard, E. M. (2017). Making space for spatial proportions. J. Learn. Disabil. 50, 644–647. doi: 10.1177/0022219416679133
McGee, M. G. (1979). Human spatial abilities: Psychometric studies and environmental, genetic, hormonal, and neurological influences. Psychol. Bull. 86:889. doi: 10.1037/0033-2909.86.5.889
Michael, W. B., Guilford, J. P., Fruchter, B., and Zimmerman, W. S. (1957). The description of spatial-visualization abilities. Educ. Psychol. Meas. 17, 185–199. doi: 10.1177/001316445701700202
Mix, K. S., and Cheng, Y. L. (2012). “The relation between space and math: developmental and educational implications,” in Advances in Child Development Behavior, Vol. 42, ed J. B. Benson (New York, NY: Elsevier).
Mix, K. S., Levine, S. C., Cheng, Y. L., Young, C. J., Hambrick, D. Z., and Konstantopoulos, S. (2017a). The latent structure of spatial skills and mathematics: a replication of the two-factor model. J. Cogn. Dev. 18, 465–492. doi: 10.1080/15248372.2017.1346658
Mix, K. S., Levine, S. C., Cheng, Y. L., Young, C., Hambrick, D. Z., Ping, R., et al. (2016). Separate but correlated: the latent structure of space and mathematics across development. J. Exp. Psychol. Gen. 145, 1206–1227. doi: 10.1037/xge0000182
Mix, K. S., Smith, L. B., Stockton, J. D., and Barterian, J. A. (2017b). Grounding the symbols for place value: do concrete models help? J. Cogn. Dev. 18, 129–151. doi: 10.1080/15248372.2016.1180296
Mix, K. S. (2010). “Spatial tools for mathematical thought,” in The Spatial Foundations of Language and Cognition, eds K. S. Mix, L. B. Smith and M. Gasser (New York, NY: Oxford University Press), 41–66.
Newcombe, N. S., and Shipley, T. F. (2015). “Thinking about spatial thinking: new typology, new assessments,” in Studying Visual and Spatial Reasoning for Design Creativity, ed J. S. Gero (New York, NY: Springer), 179–192.
Newcombe, N. S. (2010). Picture this: Increasing math and science learning by improving spatial thinking. Am. Educ. 34, 29.
Peters, M. (1995). Revised Vandenberg & Kuse Mental Rotations Test: Forms MRT-A to MRT- D (Technical Report). Guelph, ON: University of Guelph, Department of Psychology.
Piazza, M., Pinel, P., Le Bihan, D., and Dehaene, S. (2007). A magnitude code common to numerosities and number symbols in human intraparietal cortex. Neuron 53, 293–305. doi: 10.1016/j.neuron.2006.11.022
Provost, A., and Heathcote, A. (2015). Titrating decision processes in the mental rotation task. Psychol. Rev. 122, 735–754. doi: 10.1037/a0039706
Raghubar, K. P., Barnes, M. A., and Hecht, S. A. (2010). Working memory and mathematics: a review of developmental, individual difference, and cognitive approaches. Learn. Individ. Differ. 20, 110–122. doi: 10.1016/j.lindif.2009.10.005
Reuhkala, M. (2001). Mathematical skills in ninth-graders: relationship with visuo-spatial abilities and working memory. Educ. Psychol. 21, 387–399.
Richland, L. E., Stigler, J. W., and Holyoak, K. J. (2012). Teaching the conceptual structure of mathematics. Educ. Psychol. 47, 189–203. doi: 10.1080/00461520.2012.667065
Rittle-Johnson, B., Fyfe, E. R., Hofer, K. G., and Farran, D. C. (2017). Early math trajectories: low-income children's mathematics knowledge from ages 4 to 11. Child Dev. 88, 1727–1742. doi: 10.1111/cdev.12662
Rusch, C. E. (1957). An Analysis of Arithmetic Achievement in Grades Four, Six, and Eight. Doctoral dissertation, University of Wisconsin University Microfilms, Ann Arbor, 57–3568.
Schneider, M., Beeres, K., Coban, L., Merz, S., Susan Schmidt, S., Stricker, J., et al. (2017). Associations of non-symbolic and symbolic numerical magnitude processing with mathematical competence: a meta-analysis. Dev. Sci. 20:e12515. doi: 10.1111/desc.12372
Searle, J. A., and Hamm, J. P. (2012). Individual differences in the mixture ratio of rotation and nonrotation trials during rotated mirror/normal letter discriminations. Mem. Cogn. 40, 594–613. doi: 10.3758/s13421-011-0172-2
Sella, F., Sader, E., Lolliot, S., and Cohen Kadosh, R. (2016). Basic and advanced numerical performances relate to mathematical expertise but are fully mediated by visuospatial skills. J. Exp. Psychol. Learn. Mem. Cogn. 42, 1458–1472. doi: 10.1037/xlm0000249
Shea, D. L., Lubinski, D., and Benbow, C. P. (2001). Importance of assessing spatial ability in intellectually talented young adolescents: a 20-year longitudinal study. J. Educ. Psychol. 93, 604–614. doi: 10.1037/0022-0663.93.3.604
Shepard, R. N., and Metzler, J. (1971). Mental rotation of three-dimensional objects. Science 171, 701–703. doi: 10.1126/science.171.3972.701
Shepard, S., and Metzler, D. (1988). Mental rotation: effects of dimensionality of objects and type of task. J. Exp. Psychol. Hum. Percept. Perform. 14:3. doi: 10.1037/0096-1523.14.1.3
Siegler, R. S., and Opfer, J. E. (2003). The development of numerical estimation: Evidence for multiple representations of numerical quantity. Psychol. Sci., 14, 237–250. doi: 10.1111/1467-9280.02438
Simons, D. J., Boot, W. R., Charness, N., Gathercole, S. E., Chabris, C. F., Hambrick, D. Z., et al. (2016). Do “brain-training” programs work?. Psychol. Sci. Pub. Inter. 17, 103–186. doi: 10.1177/1529100616661983
Skemp, R. R. (1961). Reflective intelligence and mathematics. Br. J. Educ. Psychol. 31, 45–55. doi: 10.1111/j.2044-8279.1961.tb01701.x
Slusser, E. B., Santiago, R. T., and Barth, H. C. (2013). Developmental change in numerical estimation. J. Exp. Psychol. Gen. 142, 193–208. doi: 10.1037/a0028560
Sorby, S., Casey, B., Veurink, N., and Dulaney, A. (2013). The role of spatial training in improving spatial and calculus performance in engineering students. Learn. Individ. Differ. 26, 20–29. doi: 10.1016/j.lindif.2013.03.010
Stieff, M. (2013). Sex differences in the mental rotation of chemistry representations. J. Chem. Educ. 90, 165–170. doi: 10.1021/ed300499t
Thompson, J. M., Nuerk, H. C., Moeller, K., and Kadosh, R. C. (2013). The link between mental rotation ability and basic numerical representations. Acta Psychol. 144, 324–331. doi: 10.1016/j.actpsy.2013.05.009
Tomarken, A. J., and Waller, N. G. (2005). Structural equation modeling: strengths, limitations, and misconceptions. Annu. Rev. Clin. Psychol. 1, 31–65. doi: 10.1146/annurev.clinpsy.1.102803.144239
Tosto, M. G., Hanscombe, K. B., Haworth, C. M., Davis, O. S., Petrill, S. A., Dale, P. S., et al. (2014). Why do spatial abilities predict mathematical performance?. Dev. Sci. 17, 462–470. doi: 10.1111/desc.12138
Uttal, D. H., Meadow, N. G., Tipton, E., Hand, L. L., Alden, A. R., Warren, C., et al. (2013). The malleability of spatial skills: a meta-analysis of training studies. Psychol. Bull. 139, 352–402. doi: 10.1037/a0028446
Vandenberg, S. G., and Kuse, A. R. (1978). Mental rotations, a group test of three-dimensional spatial visualization. Percept. Mot. Skills 47, 599–604.
Verdine, B. N., Irwin, C. M., Golinkoff, R. M., and Hirsh-Pasek, K. (2014). Contributions of executive function and spatial skills to preschool mathematics achievement. J. Exp. Child Psychol. 126, 37–51. doi: 10.1016/j.jecp.2014.02.012
Wai, J., Lubinski, D., and Benbow, C. P. (2009). Spatial ability for STEM domains: aligning over 50 years of cumulative psychological knowledge solidifies its importance. J. Educ. Psychol. 101, 817–835. doi: 10.1037/a0016127
Werdelin, I. (1966). A Synthesis of Two Factor Analyses of Problem Solving in Mathematics. Malmo: Malmo School of Education.
Witt, M. (2011). School based working memory training: Preliminary finding of improvement in children's mathematical performance. Adv. Cogn. Psychol. 7, 7–15. doi: 10.2478/v10053-008-0083-3
Xu, Y., and Franconeri, S. L. (2015). Capacity for visual features in mental rotation. Psychol. Sci. 26, 1241–1251. doi: 10.1177/0956797615585002
Keywords: spatial cognition, mathematical concepts, factor analysis, statistical, developmental psychology, process modeling
Citation: Young CJ, Levine SC and Mix KS (2018) The Connection Between Spatial and Mathematical Ability Across Development. Front. Psychol. 9:755. doi: 10.3389/fpsyg.2018.00755
Received: 01 February 2018; Accepted: 30 April 2018;
Published: 04 June 2018.
Edited by:
Hans-Christoph Nuerk, Universität Tübingen, GermanyReviewed by:
Robert S. Siegler, Carnegie Mellon University, United StatesZachary Hawes, University of Western Ontario, Canada
Victoria Simms, Ulster University, United Kingdom
Copyright © 2018 Young, Levine and Mix. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Christopher J. Young, eW91bmdjakB1Y2hpY2Fnby5lZHU=
 Christopher J. Young
Christopher J. Young Susan C. Levine
Susan C. Levine Kelly S. Mix
Kelly S. Mix