- 1School of Marxism, Northwestern Polytechnical University, Xi'an, China
- 2School of Marxism, Xi'an Shiyou University, Xi'an, China
- 3School of Marxism, Northwestern Polytechnical University, Xi'an, China
- 4School of Mechanics, Civil Engineering and Architecture, Northwestern Polytechnical University, Xi'an, China
The evaluation of classroom teaching quality is closely related to the development of higher education as a scientific and effective evaluation system that can provide a solid foundation for formulating educational policies. Therefore, an evaluation model of classroom teaching quality in colleges and universities is established based on the fuzzy fault tree theory with “classroom teaching failure” as the top event to effectively evaluate the reliability of college classroom teaching and optimize the teaching strategies. In consideration of the lack of availability and dynamics of classroom teaching data, fuzzy numbers are used to describe the probability of underlying events. In addition, the top event probability of the fuzzy fault tree is calculated by the double-layer Monte Carlo method (MCM), which analyzes the classroom teaching effect based on the fuzzy fault tree reasonable. In summary, the quantitative evaluation system of classroom teaching quality based on fuzzy fault trees can evaluate classroom teaching more comprehensively and dynamically and help to improve the teaching quality of higher education.
Introduction
Changes in College Classroom Teaching
The objective and effective evaluation of teaching quality is not only a key factor related to the development of students, professional development of teachers, and the quality of college education and teaching but also a basis for educational decision-making (Qiao et al., 2016), even related to the personal stress and anxiety of the undergraduates (Vilvens et al., 2021). The traditional classroom teaching evaluation methods are limited by many factors, such as technology, system, and some human factors (Lee and Mccabe, 2020) in the process of their implementation that leads to objectivity and even unfairness. The mathematical model may exclude human factors, making the evaluation more scientific, objective, and measurable (Sun, 2021). Classroom teaching can be evaluated by teacher observation form (quantitatively evaluating college classroom teaching quality), and it includes the evaluation of classroom environment, curriculum structure, implementation effect, and teaching content (Cao and Mao, 2017). Some American colleges learn about the teaching quality of teachers and the learning effect of students by the evaluation of students on classroom teaching, which not only makes the evaluation more transparent and more effective through the combination of quantitative and qualitative methods but also enlightens China to improve the learning effect of student and teaching quality of teachers by the evaluation (Dai et al., 2019).
Apply Fault Tree Analysis (FTA) to Teaching Evaluation
Nowadays, many fields have been affected by artificial intelligence (AI) (Ren et al., 2019; Tong and Sopory, 2019; Rieder et al., 2020; Vu and Lim, 2021), especially for the student-centered learning areas (Tan, 2020) and learning system (Banja, 2020; Li et al., 2020). The development of this kind of technology results in the methods of classroom teaching quality evaluation are diversified and operational, like neural network evaluation theory (Song et al., 2017), and structural equation construction (Chen, 2020). College classroom teaching is deemed as a complex system for a long time, which is not only related to the explicit educational factors, such as teaching content, teaching methods, and teaching means but also affected by such potential educational factors, such as the concentration of the students, learning consciousness, and learning initiative, and even teaching culture (Lu and Valaec, 2020). Also, the multimedia teaching system is becoming an important factor in the evaluation of teaching quality (Cheng et al., 2015). All the system engineering methods may be used to evaluate and analyze the teaching quality (Wen et al., 2019). In 1962, the Bell Telephone Laboratory proposed FTA technology that adopted a logical method for data analysis and this analysis technology become more and more popular in the engineering field, which is characterized by its simplicity, intuitiveness, systematicness, accuracy, predictability, and logicality (Sihombing and Torbol, 2018). In short, a fault tree, as an intuitive method of graphic visualization, can not only integrate possible causes of various faults but also helps to find the potential risks of the system, thereby predicting the fault of the system. Based on qualitative analysis, a fault tree can quantitatively calculate the failure probability of a complex system (Zhang et al., 2019; MacLeod et al., 2020) that may bring a big change for the teaching evaluation.
Benefits of Fuzzy Fault Tree Method Application
Today, the analysis method based on the fault tree is one of the most commonly used methods in the field of reliability analysis and risk assessment (Song and Schnieder, 2018; Hu et al., 2020; Yan et al., 2021). The traditional fault tree mainly analyzes the causes of system failure and calculates the probability of the top event caused by each bottom event (Barlow and Proschan, 1975; Reay and Andrews, 2002; Wu, 2021). The evaluation method of teaching quality based on fault tree can help teachers find out the reasons why the teaching goal is not realized completely. Besides, the weak links in the process of predicting and diagnosing the faults can be found out, so that the corresponding improvement measures are taken to realize the optimization of teaching quality. The failure of classroom teaching is the main problem to be solved, and it is the top event of the fault tree. To count the occurrence probability of the top event, the first thing is to calculate the bottom event occurrence probability by the traditional analysis, which does not apply to the analysis of classroom teaching failure. Moreover, the evaluation of classroom teaching quality involves dynamic analysis, by which bottom event probability is not obtained. In addition, the complex system itself makes it impossible to describe the relationship between its components by using the traditional FTA.
For these reasons, the fuzzy number is used to describe the bottom event occurrence probability based on the traditional fault tree, and a new fuzzy fault tree model for classroom teaching is constructed. The double-layer Monte Carlo method (MCM) is used to count the top event occurrence probability of the model, realizing the effective and quantitative reliability evaluation of college classroom teaching (Baumgärtner and Binder, 1984; Barel and Vandewalle, 2019, 2021). As a result, the fuzzy fault tree method is used to figure out the factors that influence the classroom teaching effect, quantitatively evaluating the college classroom teaching quality that made the analysis more reasonable and more feasible.
FTA Based on Fuzzy Model
Theoretical Basis of Fault Tree
Fault tree analysis refers to a process, which starts from a possible “event,” looking for the direct and indirect causes leading to the occurrence of the top event layer-by-layer from top to bottom. When tracing back to the basic events, it uses a logical diagram to show the logical relations of these events. The fault tree has two elements, one is the event and the other is the logic gate. In the process of establishing a fault tree, the occurrence of the top event, intermediate event, and the bottom event is replaced by “event,” and logical relations between each system and part are displayed by “logic gate” (Hu et al., 2020).
The mathematical description of fault tree structure-function is as follows:
Classic fault tree logic gates can be divided into two types: and-gate and or-gate. Based on the system functional logic, a system and its components are connected by logic gates to form a system FTA model, including input and output functions.
The structure-function of a fault tree under and-gate is:
The structure-function of a fault tree under or-gate is:
n is the number of bottom events, and xi(i = 1,2,…,n) is the bottom event.
Fuzzy Fault Tree
The FTA of teaching quality evaluation can help the insight of teachers into the failure of achieving teaching objectives. In addition, it can find out the weak links in the teaching process by failure prediction and diagnosis, so that the countermeasures can be taken to improve the teaching quality during the teaching process, realizing the optimization of teaching quality. Since a fault tree is a logic diagram composed of specific logic gates, it can establish a tree model and analyze qualitatively and quantitatively with the help of a computer program. FTA can not only find out the causes that influence the effect of classroom teaching but also find the ways to benefit the effect of classroom teaching in improving the effectiveness of classroom teaching and comprehensive abilities of the students.
In the research results published in 1965, Professor Zadeh, an American cybernetic expert, thought that “membership function” could be used to describe the intermediate transition in phenomenon difference, which made a breakthrough in the absolute relationship between belonging and not belonging in a group of classical set theory. This important contribution of Zadeh marks the birth of fuzzy mathematics (Shi et al., 2018). Later, fuzzy mathematics and fault tree are effectively combined, and the fuzzy FTA method comes into being (Hu et al., 2019). The traditional FTA is based on an assumption, that is, the system and its components are required to have only two states: normal or failure. The existing theory requires that the occurrence probability of the top event and the basic event of the fault tree is an accurate value, which is difficult to achieve in practice. Due to the influence of various external complex factors and equipment contingency, the failure probability of each basic event is uncertain, and it is fuzzy. The mean value of the event occurrence and its confidence interval are obtained by experience and judgment. In addition, the fuzzy number can be used to describe the occurrence of the event by carrying out an effective reliability analysis.
Fuzzy Set and Membership Function
The extension of conception can be expressed mathematically by the conception of “set.” However, many conceptions involved in daily life are often accompanied by connotative “fuzziness,” which leads to the “ambiguity” of extension, while “classic set” requires that its result must be “clear,” that is, in terms of set A and a specific object, only one of the two is true. This indicates that the extension of fuzzy conception cannot be described by a classical set and that the conception of Zadeh's fuzzy set is more accurate in practice.
Set U as a domain, the so-called fuzzy set à on U refers to ∀x ∈ U, x often belongs to à to some extent of μ(μ ∈ [0, 1]), rather than x ∈ à or x ∉ Ã. μ is called a membership function on U.
Fuzzy Number
Set à as a normal fuzzy set in the real number field R. When ∀λ ∈ [0, 1], Aλ are all closed intervals. Then, Aλ = [aλ, bλ] is obtained. à is a fuzzy real number, a fuzzy number for short. All fuzzy numbers are recorded as .
Cut Set
If à ∈ ζ(X), when λ ∈ [0, 1], then
Aλ is λ -cut set of fuzzy set Ã, or called λ -level set of Ã.
And
Aλ is strong λ -cut set of fuzzy set Ã, or called strong λ -level set of Ã; λ is the threshold value or belief level.
Aλ is a classical set, rather than a fuzzy set. Because the boundary of each set is fuzzy, different belief levels [λ(0 ≤ λ ≤ 1)] should be used to determine its membership and relationship if the fuzzy conception is to be transformed. λ -cut set is a method that can transform a fuzzy set into the classical set.
Convex Fuzzy Set
Set R as a real field. And if à ∈ ζ(R), ∀x1, x2, x3 ∈ R, and x1 > x2 > x3, the following equation is obtained:
Then à is a convex fuzzy set; if its height is 1, then it is a positive fuzzy set.
Establishment of Fault Tree Regarding “Classroom Teaching Failure”
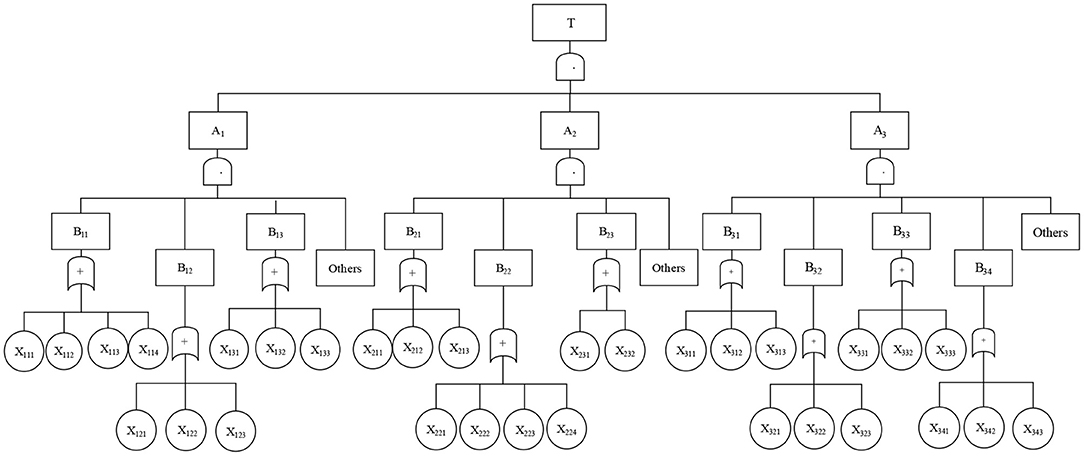
First, setting up a top event. “Classroom Teaching Failure” is taken as the top event, and the top event is analyzed layer by layer to find the causes that influence the effect of college classroom teaching. Thus, the fault tree of college classroom teaching is established.
Second, building intermediate events. The factors affecting the occurrence of classroom teaching events include not only teachers and students, but also the potential teaching environment. These three factors are regarded as composition conditions in the classroom teaching process and considered as the intermediate event of the fault tree.
Third, defining basic events. Take the factors that may affect the top event as the basic events of the fault tree. Because of the complexity of the classroom teaching environment, 10 events are involved. As for teachers, the factors concerned are teaching method, teaching speed, and charm of a teacher; in terms of students, factors concerned are learning attitude, learning motivation, and learning method; concerning teaching environment, they include teaching content, class management, exercise class, and experiment class.
Fourth, representing events. The symbols of the fault tree are used to represent these events, and the events of different levels are connected into an inverted tree with appropriate logic gates so that the logical relationship between the events of the classroom teaching effect can be described.
Classroom teaching includes intermediate events, and the lack of any party cannot make classroom teaching fully reflected. The interaction between basic events, namely, intermediate events, affects the classroom learning effect. Therefore, the three levels of events should be interconnected, and gate structure is selected, in which the top event, intermediate event, and basic event are all reflected as “•.”
When gate structure connects the bottom events, it is expressed as “+.” The reason is that the simplification of basic events makes it easier for students to answer mutually exclusive questions. After calculation, a complete fault tree diagram of “college Classroom Teaching Failure” is displayed (Lu and Valaec, 2020), as shown in Figure 1.
In Figure 1, T is a classroom teaching failure; A1 is the teacher-related intermediate event, A2 is the student-related intermediate event, and A3 is the environment-related intermediate event; B11 is teaching method, B12 is personal charm, and B13 is teaching progress; B21 is learning attitude, B22 is learning motivation, and B23 is learning method; B31 is class exercises, B32 is class experiments, B33 is teaching content, and B34 is classroom management; X111 is proficiency, X112 is vision, X113 is theory to practice, and X114 is suitable teaching; X121 is classroom atmosphere, X122 is teacher model, and X123 is teaching language; X131 is fast pace, X132 is normal pace, and X133 is slow pace; X211 is attention, X212 is homework completion, and X213 is tutoring time; X221 is subsequent courses, X222 is interests and hobbies, X223 is trouble on exam, and X224 postgraduate preparation needs; X231 is the use of preview and review and X232 is the use of answer and question methods; X311 is necessary, X312 is unnecessary, and X313 is indifferent; X321 is good effect, X322 is general effect, and X323 is normal; X331 is more than 80% relevant, X332 is more than 60% relevant, and X333 is less than 60% relevant; X341 is strict, X342 is appropriate, and X343 is loose.
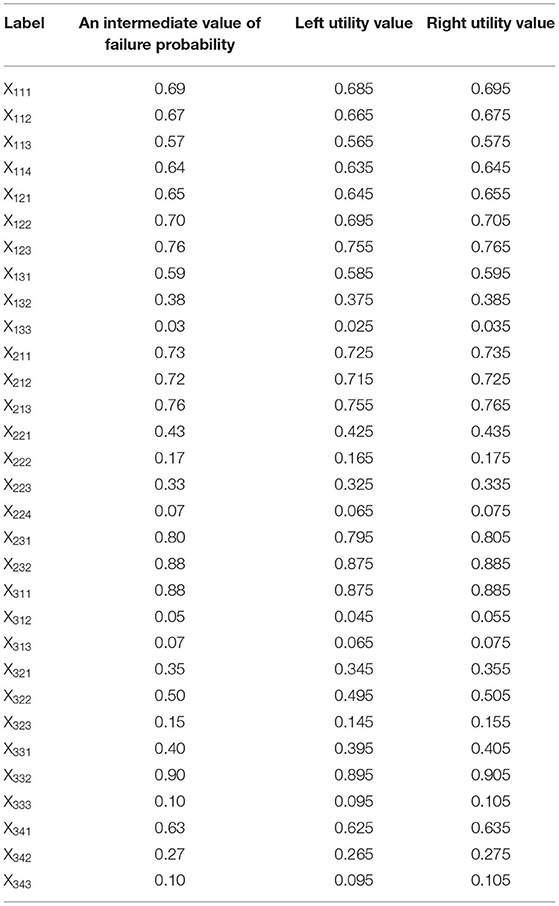
The factors that cause classroom teaching failure mainly include teachers, students, and the environment, which are regarded as the intermediate events of the fault tree. The bottom events are determined from the three aspects of teachers, students, and environments, that is, the factors that affect the top events as the basic event of the fault tree. They mainly include teaching methods of the teachers, charm of the teachers, and their teaching speed; attitudes of students toward study, their motivation for study, and their learning methods; exercises, experiments, teaching content, and classroom management. Based on the newly established fault tree model and the existing relevant information (Wen et al., 2019; Lu and Valaec, 2020), the fuzzy number of occurrence probability of each bottom event is finally determined by combining the experiences of different experts following fuzzy mathematics theory, as shown in Table 1.
Probability Analysis of Classroom Teaching Failure Under the Fuzzy Model
The theoretical basis of the MCM is the law of large numbers of probability theory and Bernoulli's theorem. Indeed, it is a kind of statistical sampling test or random simulation calculation method that can be used for relevant random variables. By estimating and describing the statistics of a function, the numerical calculation method of approximate solutions in engineering technology problems is adopted (Chong and Hu, 2020). The double-layer MCM is used for sampling (Zhang et al., 2013; Shen et al., 2019), and then the simulation method is used to solve the probability of failure of the top event.
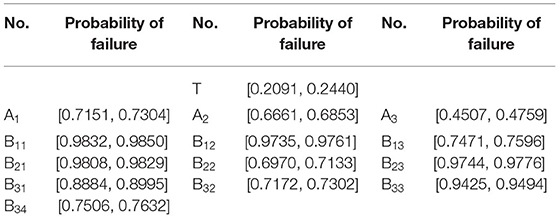
The failure transfer probability function can be obtained by analyzing the fault tree structure of the classroom teaching effect. After the membership function of the bottom, the event is determined, the upper event occurrence probability of each logic gate in the fault tree can be solved according to the system fault tree under the fuzzy model (Chen, 2018), and then the influence degree of classroom teaching effectiveness can be obtained, as shown in Table 2 below.
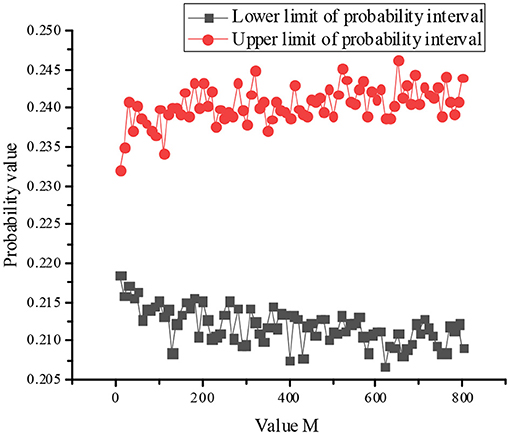
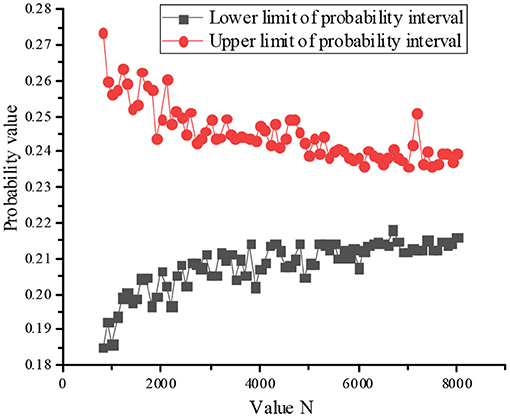
Since the convergence criterion of the MCM is used, the number of outer layer sampling is set as 800, the number of inner layer sampling as 8,000, and the probability interval value of “teaching failure” of top event calculated by double-layer MCM is [0.2091, 0.2440].
The influence of value M on the interval convergence is shown in Figure 2 as follow.
The influence of value N on probability interval convergence is shown in Figure 3 as follow.
Conclusion
The FTA method is further optimized, that is, fuzzy mathematics is introduced to describe the uncertainties of occurrence probability of the bottom event that may cause college classroom teaching failure. Then, the probability interval of teaching failure is simulated by the double-layer MCM (Chen et al., 2019). Finally, the probability interval of college classroom teaching effect is evaluated quantitatively. This study improves and innovates a traditional evaluation method for one thing, and embodies the advantages of the fuzzy FTA method for another. The probability analysis results of classroom teaching failures show that the probability of top events is [0.2091, 0.2440], which means that the students believe that the probability of classroom teaching failure is 20.91–22.4%. The representation theorem of the fuzzy set theory is used to calculate the probability of the fuzzy number of top events and the importance of bottom events. The calculation shows that the establishment of the FTA model based on fuzzy numbers provides a reference for evaluating the teaching quality of teachers in the classroom (Chen, 2019).
Comprehensiveness
Different from the single FTA, this evaluation method fully considers the uncertainties of bottom event and intermediate event into the model, so that it can comprehensively and reasonably evaluate the reliability of college classroom teaching systems (Feng et al., 2020), which makes the factors that affect the classroom teaching failure appear and provides a variety of reference factors for colleges to formulate the teaching evaluation program. It is fundamentally helpful for the improvement of college teaching quality in China.
Relevance
Educational researchers and educators can intuitively find the logical relationship between the factors that cause classroom teaching failure. When a cause (such as a bottom event and intermediate event) of classroom teaching failure occurs, the overall teaching system of classroom teaching may be traced back to its source, so that its direct and indirect causes are figured out to correct the teaching failure, which is beneficial for the improvement of classroom teaching effect (Feng and Chen, 2020).
Dynamics
The evaluation method of college classroom teaching quality is highly operational and dynamic, and the fault tree method plays an important role in computer database construction. Meanwhile, it can also improve the classroom teaching quality in a dynamic evaluation system, achieving the overall education goal of colleges (Deng et al., 2021).
Expansibility
The evaluation model has certain expansion space as well. With the change and development of the current situation of education and teaching, many non-human and pre-set factors may affect the effects of classroom teaching. For example, the COVID-19 outbreak in 2019 and other non-conventional factors may be included in the evaluation model. Thus, this model needs to be further studied and developed considering more certain and uncertain factors in the future.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Ethics Statement
The studies involving human participants were reviewed and approved by Northwestern Polytechnical University Ethics Committee. The patients/participants provided their written informed consent to participate in this study. Written informed consent was obtained from the individual(s) for the publication of any potentially identifiable images or data included in this article.
Author Contributions
LW developed the theoretical formalism, conceived of the presented idea, and wrote the manuscript with support from MF and FZ. Specially FZ fabricated the samples and performed the analytic calculations. MF supervised the project. LW and MF contributed to the final version of the manuscript. All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
Funding
This study was supported by the Shaanxi Association of higher education 2019 Higher Education Scientific Research Project (XGH19080) and Northwestern Polytechnical University Degree and Graduate Education Research Fund Project (2019–2020).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Banja, J. (2020). Obviously you, maybe you, artificial you: exploring the impact of artificial intelligence technologies on consciousness and personal identity. AJOB Neurosci. 11, 128–130. doi: 10.1080/21507740.2020.1740349
Barel, A. V., and Vandewalle, S. (2019). Robust optimization with a multilevel monte carlo method. Siam/asa J. Uncertainty Quantification 7, 174–202. doi: 10.1137/17M1155892
Barel, A. V., and Vandewalle, S. (2021). MG/OPT and multilevel monte carlo for robust optimization of PDEs. SIAM J. Optim. 31, 1850–1876. doi: 10.1137/20M1347164
Barlow, R. E., and Proschan, F. (1975). Importance of system components and fault tree events. Stochastic Processes Their Appl. 3, 153–173. doi: 10.1016/0304-4149(75)90013-7
Baumgärtner, A., and Binder, K. (1984). Applications of the Monte Carlo Method in Statistical Physics. Current Physics Book Series. Springer-Verlag (Tcphy, 36), 1–36, 145–180. doi: 10.1007/978-3-642-96788-7_5
Cao, H., and Mao, Y. (2017). Exploration and reflection of the UDOP classroom teaching quality evaluation system in the United States. Glob. Educ. Outl. 21, 79–89.
Chen, J. (2020). Construction of structural equations for the evaluation of classroom teaching quality in universities. China Continuing Med. Educ. 12, 58–61.
Chen, J., Ye, X., Chen, M., and Liang, Y. (2019), Bibliometric analysis of the papers on urban education. Library Hi Tech. 37, 894–905. doi: 10.1108/LHT-01-2019-0009
Chen, M. (2018). The research of human individual's conformity behavior in emergency situations. Library Hi Tech. 38, 593–609. doi: 10.1108/LHT-08-2018-0113
Chen, M. (2019). The impact of expatriates' cross-cultural adjustment on work stress and job involvement in the high-tech industry. Front. Psychol. 10:2228. doi: 10.3389/fpsyg.2019.02228
Cheng, K., Ren, Y., and Xu, W. (2015). Fault tree simulation analysis for improving classroom teaching effect-based on students' perspective. J. Hebei Agri. Univ. 17, 70–73.
Chong, T., and Hu, X. (2020). Mathematical modeling of security impact analysis of communication network based on Monte Carlo algorithm. Comp. Commun. 1571, 20–27. doi: 10.1016/j.comcom.2020.04.005
Dai, M., Wu, Z., Liu, Y., et al. (2019). Research on the weight of clinical teachers' classroom teaching quality evaluation index system-based on the analytic hierarchy process. Med. Educ. Res. Pract. 27, 396–399.
Deng, X., Guo, X., Wu, Y. J., and Chen, M. (2021). Perceived environmental dynamism promotes entrepreneurial team member's innovation: explanations based on the uncertainty reduction theory. Int. J. Environ. Res. Public Health. 18:2033. doi: 10.3390/ijerph18042033
Feng, B., and Chen, M. (2020). The impact of entrepreneurial passion on psychology and behavior of entrepreneurs. Front. Psychol. 11:1733. doi: 10.3389/fpsyg.2020.01733
Feng, B., Sun, K., Chen, M., and Gao, T. (2020). The impact of core technological capabilities of high-tech industry on sustainable competitive advantage. Sustainability. 12:2980. doi: 10.3390/su12072980
Hu, G., Phan, H., Ouache, R., Gandhi, H., and Sadiq, R. (2019). Fuzzy fault tree analysis of hydraulic fracturing flowback water storage failure. J. Natural Gas Sci. Eng. 72:103039. doi: 10.1016/j.jngse.2019.103039
Hu, L., Kang, R., Pan, X., and Zuo, D. (2020). Risk assessment of uncertain random system Level-1 and level-2 joint propagation of uncertainty and probability in fault tree analysis. Reliabil. Eng. Syst. Saf. 198:106874. doi: 10.1016/j.ress.2020.106874
Lee, J. J., and Mccabe, J. M. (2020). Who speaks and who listens: revisiting the chilly climate in college classrooms. Gender Soc. 35, 32–60. doi: 10.1177/0891243220977141
Li, X., Zhou, P., Wu, J., Shanthini, A., and Vadivel, T. (2020). Research on artificial intelligence learning system based on psychological knowledge to adjust anxiety and depression. Behav. Inform. Technol. 2020:1846077. doi: 10.1080/0144929X.2020.1846077
Lu, J., and Valaec, T. (2020). College multimedia teaching system devise and application evaluation. Int. J. Electr. Eng. Educ. doi: 10.1177/0020720920928477
MacLeod, J., Tan, S., and Moinuddin, K. (2020). Reliability of fire (point) detection system in office buildings in Australia-a fault tree analysis. Fire Saf. J. 115:103150. doi: 10.1016/j.firesaf.2020.103150
Qiao, R., Zhu, Q., and Luan, J. (2016). Research on classroom teaching quality evaluation based on student self-evaluation. Univ. Educ. 2016, 28–29.
Reay, K. A., and Andrews, J. D. (2002). A fault tree analysis strategy using binary decision diagrams. Reliabil. Eng. Syst. Saf. 78, 45–56. doi: 10.1016/S0951-8320(02)00107-2
Ren, J. C., Sai, H. L., Ibrahim, S., Wan, Z. W. J., and Elshafie, A. (2019). Rheological wall slip velocity prediction model based on artificial neural network. J. Exp. Theoreti. Artif. Intell. 31, 659–676. doi: 10.1080/0952813X.2019.1592235
Rieder, T. N., Hutler, B., and Mathews, D. J. H. (2020). Artificial intelligence in service of human needs: pragmatic first steps toward an ethics for semi-autonomous agents. AJOB Neurosci. 11, 120–127. doi: 10.1080/21507740.2020.1740354
Shen, C.-w., Min, C., and Wang, C.-c. (2019). Analyzing the trend of O2O commerce by bilingual text mining on social media. Comput. Hum. Behav. 101, 474–483. doi: 10.1016/j.chb.2018.09.031
Shi, S., Jiang, B., and Meng, X. (2018). Assessment of gas and dust explosion in coal mines by means of fuzzy fault tree analysis. Int. J. Min. Sci. Technol. 28, 991–998. doi: 10.1016/j.ijmst.2018.07.007
Sihombing, F., and Torbol, M. (2018). Parallel fault tree analysis for accurate reliability of complex systems. Struct. Saf. 72, 41–53. doi: 10.1016/j.strusafe.2017.12.003
Song, D., Wen, C., and Wang, X. (2017). Evaluation model of military classroom teaching quality based on BP neural network. Continuing Educ. 31, 47–49.
Song, H., and Schnieder, E. (2018). Evaluating Fault Tree by means of Colored Petri nets to analyze the railway system dependability. Saf. Sci. 110, 313–323. doi: 10.1016/j.ssci.2018.08.017
Sun, S. (2021). Quantitative methods of classroom teaching evaluation. J. Guangdong Technical Teachers Coll. 2, 46–48.
Tan, C. (2020). Digital confucius? Exploring the implications of artificial intelligence in spiritual education. Connect. Sci. 32, 280–291. doi: 10.1080/09540091.2019.1709045
Tong, S. T., and Sopory, P. (2019). Does integral affect influence intentions to use artificial intelligence for skin cancer screening? A test of the affect heuristic. Psychol. Health. 34, 828–849. doi: 10.1080/08870446.2019.1579330
Vilvens, H. L., Frame, D. L., and Owen, P. C. (2021). Promoting the inclusion of mindfulness and contemplative practices in the college classroom. Pedagogy Health Promot. 7, 148–158. doi: 10.1177/2373379920925849
Vu, H. T., and Lim, J. (2021). Effects of country and individual factors on public acceptance of artificial intelligence and robotics technologies: a multilevel SEM analysis of 28-country survey data. Behav. Inform. Technol. 2021:1884288. doi: 10.1080/0144929X.2021.1884288
Wen, S., Wang, L., and Zhang, F. (2019). Reliability evaluation of college classroom teaching based on ellipsoid model. J. High. Educ. 11, 85–87.
Wu, W. (2021). Application of fault tree analysis in LNG fire risk assessment of LNG fueled ships. Vibroeng. Proc. 36, 108–114. doi: 10.21595/vp.2021.21827
Yan, L., Zhang, T., and Gao, Y., Wang, R., Ding, S. (2021). Reliability analysis of station autonomous computer system based on fuzzy dynamic fault tree and Markov model. Eng. Rep. 2021:e12376. doi: 10.1002/eng2.12376
Zhang, F., Cheng, L., Gao, Y., Xu, X., and Wang, Y. (2019). Fault tree analysis of a hydraulic system based on the interval model using Latin hypercube sampling. J. Intell. Fuzzy Syst. 37, 8345–8355. doi: 10.3233/JIFS-190891
Keywords: college classroom, teaching evaluation, fuzzy fault tree, double-layer Monte Carlo, classroom teaching failure
Citation: Wang L, Fan M and Zhang F (2021) Applying Fuzzy Fault Tree Method to Evaluate the Reliability of College Classroom Teaching. Front. Psychol. 12:593068. doi: 10.3389/fpsyg.2021.593068
Received: 09 August 2020; Accepted: 11 August 2021;
Published: 14 September 2021.
Edited by:
Ting-Chia Hsu, National Taiwan Normal University, TaiwanReviewed by:
Shao Chen Chang, National Taiwan University of Science and Technology, TaiwanVince Zhang, Illinois Institute of Technology, United States
Amber Li, Wonkwang University, South Korea
Copyright © 2021 Wang, Fan and Zhang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Liangliang Wang, Y2VsaWF3b25nQG1haWwubndwdS5lZHUuY24=
 Liangliang Wang
Liangliang Wang Mingfang Fan3
Mingfang Fan3