- 1School of Computer Science and Artificial Intelligence, Changzhou University, Changzhou, China
- 2School of Electrical Engineering, Xi'an Jiaotong University, Xi'an, China
- 3Department of Nephrology, Affiliated Wuxi People's Hospital of Nanjing Medical University, Wuxi, China
- 4Department of Clinical Psychology, The Third Affiliated Hospital of Soochow University, Changzhou, China
The brain-computer interface (BCI) interprets the physiological information of the human brain in the process of consciousness activity. It builds a direct information transmission channel between the brain and the outside world. As the most common non-invasive BCI modality, electroencephalogram (EEG) plays an important role in the emotion recognition of BCI; however, due to the individual variability and non-stationary of EEG signals, the construction of EEG-based emotion classifiers for different subjects, different sessions, and different devices is an important research direction. Domain adaptation utilizes data or knowledge from more than one domain and focuses on transferring knowledge from the source domain (SD) to the target domain (TD), in which the EEG data may be collected from different subjects, sessions, or devices. In this study, a new domain adaptation sparse representation classifier (DASRC) is proposed to address the cross-domain EEG-based emotion classification. To reduce the differences in domain distribution, the local information preserved criterion is exploited to project the samples from SD and TD into a shared subspace. A common domain-invariant dictionary is learned in the projection subspace so that an inherent connection can be built between SD and TD. In addition, both principal component analysis (PCA) and Fisher criteria are exploited to promote the recognition ability of the learned dictionary. Besides, an optimization method is proposed to alternatively update the subspace and dictionary learning. The comparison of CSFDDL shows the feasibility and competitive performance for cross-subject and cross-dataset EEG-based emotion classification problems.
Introduction
Emotion is the attitude experience and corresponding behavior response of human beings to objective things, which has an important influence on human behavior and mental health. How to accurately identify emotions has an important significance in practical application. For example, in the medical field, emotion recognition is helpful to guide and diagnose patients with mental diseases or expression disorders, and in the education field, different teaching methods according to the emotion of the listener can improve the teaching efficiency.
Emotion recognition using a variety of modal emotion signals has now gained a lot of attention from researchers. Typically, emotions can be perceived in the form of a variety of signals. One type of visual signal can be directly observed from external behavior and characteristics, such as facial expressions, voice intonation, body movements, etc. The other type is those physiological signals, such as electroencephalography (EEG), electromyography (EMG), electrocardiogram (ECG), skin conductance, pulse, heartbeat, skin temperature, and respiratory signals; however, facial expressions, voice, and other non-physiological signals are easily restricted by environmental or social factors. The emotional information transmitted by physiological signals is more objective and can reflect the psychological emotion more reliably (Zheng et al., 2019; Doma and Pirouz, 2020; Ni et al., 2020a).
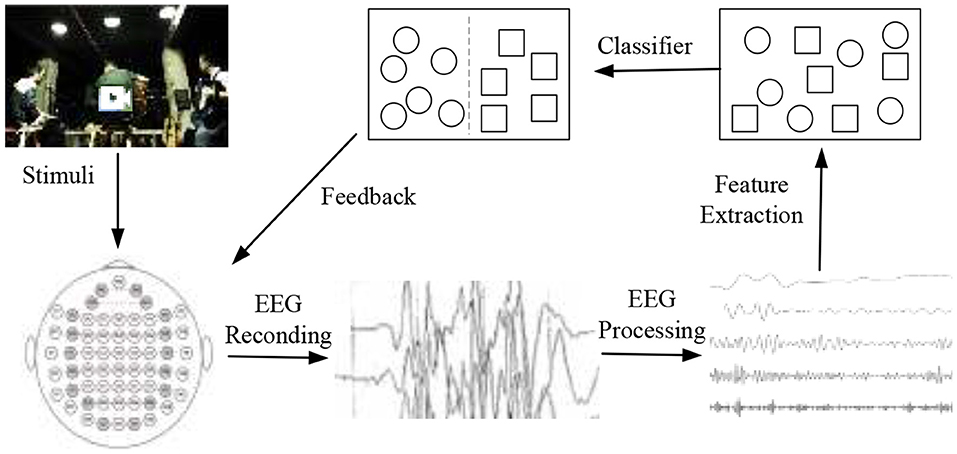
Brain-computer interface (BCI) is a human-computer interaction system that provides a communication channel for human brain interaction with the external environment and without depending on the peripheral nervous system and muscles (Zhang and Wu, 2019; Liu et al., 2020; Ni et al., 2020b). EEG plays a dominant role in emotion recognition based on physiological signals. The illustration of EEG-based emotion classification in BCI is shown in Figure 1. The operation of emotion classification begins with the presentation of stimuli to the user, which induces specific emotions. The stimuli may be music, videos, and images, etc. During the session, EEG samples are recorded by EEG devices. The next step is usually to extract features from the recorded EEG and train a classifier. The final step is to test new EEG samples to classify emotion labels (Liu et al., 2018).
The existing EEG-based emotional classification in BCI requires a large amount of label data and a lot of time in the training phase. A relatively simple and direct method is to reuse previously collected EEG data and train a new classifier, without considering differences between individuals. These classification methods are based on the assumption that training and test data are independently and identically distributed. This assumption is often difficult to hold for BCI, because EEG signals have non-stationary characteristics, and the performance of the classifier fluctuates significantly between subjects and datasets. When the same classifier is applied to EEG data of other subjects or from other datasets, the performance will be significantly reduced.
Domain adaptation learning is a fast and effective solution for developing a classifier that selectively trains a new classifier in TD using auxiliary data (source domain, SD) and less training data in the new scenario (target domain, TD) (Fahimi et al., 2019; Ni et al., 2020c). Different from multi-task learning that aims to benefit the classifier in both source and target tasks, domain adaptation learning mainly aims to benefit the classifier in TD. For example, Yang et al. (2019) proposed a support vector machine (SVM) combined with the significance test and sequential backward selection strategy for cross-subject EEG-based emotional classification. Instead of utilizing features on raw EEG signals, this method analyzed and selected features based on the significant differences between positive and negative trials. Li et al. (2020a) proposed a two-stage multi-source semi-supervised transfer learning method, in which the work of the first stage was source domain selection and the second stage was to learn style transfer mapping. This method selected the appropriate sources and projected source data to the destination via an affine mapping, so that only a few labeled data was used in the calibration sessions. Subsequently, Li et al. (2020b) developed a joint distribution adaptation method for EEG-based emotion classification in cross-subject and cross-session scenarios. The label information in the SD was used to train the model, and it also took an important part in reducing the difference of conditional distribution. This method achieves domain adaptation by combining marginal distributions and conditional distributions in the framework of neural networks. Morioka et al. (2015) also developed a cross-subject and cross-session recognition method, which learned the common spatial bases underlying both SD and TD by using unsupervised dictionary learning. The spatial transforms technology was found to be efficient in extracted common brain activities. Lan et al. (2018) developed a domain adaptation method to reduce discrepancies across datasets and inter-subject variance. This method designed a linear transformation function to adapt subspaces feature to match the marginal distributions of SD and TD.
Although domain adaptation for EEG-based emotion classification has been extensively studied, most of the studies focus on cross-subject and cross-session adaptation within the same dataset, i.e., the samples of SD and TD came from the same dataset. Domain adaptation across datasets is more challenging. Because cross-dataset domain adaptation is restricted to the different datasets, EEG signals are collected from the different devices and different stimuli, etc. (Li et al., 2018; Yang et al., 2019; Cimtay and Ekmekcioglu, 2020).
It is our opinion that although the distribution of common characters in EEG signals shows differences between subjects and datasets, it is expected that there might be some certain common knowledge that is potentially independent of the subjects and datasets. In addition, the shared common knowledge could be preserved in a shared projection subspace. Thus, we propose a domain adaptation sparse representation classifier (DASRC) to address the EEG-based emotion classification in cross-subject and cross-dataset scenarios. We consider learning the common component in both SD and TD by exploring a common dictionary in a shared subspace. Thus, we adopt the local information preserved criterion to reduce the domain distribution discrepancies in the learned subspace. We learn the common domain-invariant dictionary, which builds a connection between SD and TD. In addition, the principal component analysis (PCA) and Fisher criteria are exploited in this model to promote the recognition ability of the learned classifier.
The main contribution of the study is as follows. First, DASRC exploits the common characteristics of EEG data in SD and TD to yield a domain-invariant dictionary in the shared subspace. It takes advantage of the local data information preserved in both SD and TD. This allows enhancing the domain adaptation in subspace. Second, using PCA and Fisher criteria, the objective function of DASRC is directly related to the classification rule. This strategy can promote the recognition ability in the domain-invariant subspace. Mathematically, an alternating optimization algorithm is proposed to solve the subspace and dictionary learning problem. Third, experiments on SJTU emotion EEG dataset (SEED) (Zheng and Lu, 2015) and dataset for emotion analysis using EEG, physiological and video signals (DEAP) (Koelstra et al., 2011) demonstrate that dictionary learning in subspace is effective and DASRC outperforms the advanced methods in cross-subject and cross-dataset scenarios.
Background
Sparse representation is a data analysis method to estimate the sparse representation of measurable signals completely. It originated from neuroscience and has been used in signal processing, such as denoising and compression (Kanoga et al., 2019; Gu et al., 2020). In pattern recognition, sparse representation has also been proved to be suitable for classification. In sparse representation, the data matrix Y = [y1, y2, …, yn] can be decomposed into a linear combination of a few atoms on the dictionary,
where D is the dictionary matrix, and A is the coefficients matrix.
An adequate approximation makes DA the sparse representation as a reasonable estimation ofY. Based on this concept, Equation (1) can be rewritten as follows:
where l0 represents the sparsity constraint, ai is the sparse coefficient vector to represent yi over D. K-singular value decomposition (KSVD) algorithm is one of the most representative to solve Equation (2), in which the sparse coding and dictionary are updated alternately (Aharon et al., 2006).
Domain Adaptation Sparse Representation Classifier
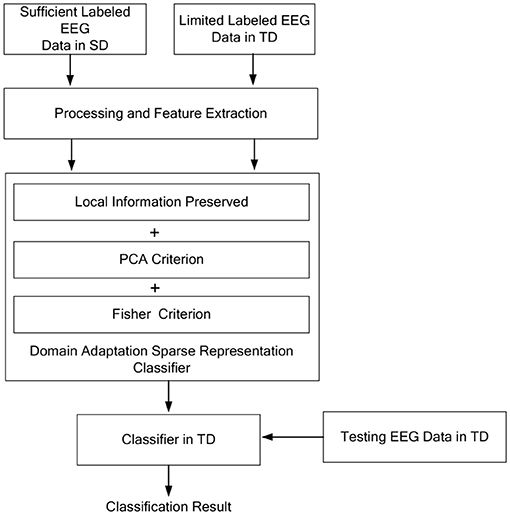
In this study, we consider the EEG data from two different domains SD and TD. The SD is with sufficient labeled samples and the TD is with limited labeled samples , such that the data distribution is P(Ys ≠ Yt) and , where and are the class label set of samples in SD and TD, respectively. The main idea of the proposed model is shown in Figure 2.
Local Information Preserved in DASRC
Because the EEG signals are collected from different domains, domain discrepancies exist between SD and TD. Usually, directly adapting the existing classifier in SD may perform poorly to new samples in TD. Domain adaptation is adopted in this study to find a latent and domain-invariant subspace and maps Ys and Yt by projection matrixes Ms and Mt, respectively. In this domain-invariant subspace, the discrepancy between SD and TD is reduced. Finally, we can train a new classifier for TD in the subspace with the help of discriminative knowledge from labeled samples in SD.
Domain adaptation method should strive to preserve the class distribution and local characteristics of training samples. Therefore, the local geometric structure of the samples is considered, so that the samples in SD and TD can be validly represented in the domain-invariant subspace. We construct the similarity matrixes Gs and Gt of SD and TD by k-nearest neighbor graphs, respectively. The elements in Gs and Gt can be computed by the following equations,
where is a set that contains k nearest neighbor samples of . The element presents the similarity between the ith and jth samples in SD. As one of the most commonly used similarity metrics in graph learning, the Gaussian kernel is adopted in Equation (3). σ is the kernel parameter. Since the number of samples in TD is insufficient, Equation (4) ensures that the limited number of samples in TD is assigned with a given one-to-one weight. Therefore, we construct the local preserved constraint to maintain the intra-domain local information.
PCA Criterion in DASRC
In addition, with the aim of classification, the discriminative knowledge of SD and TD should be enforced in subspace projection. We consider Ms and Mt are the bases of the subspaces based on the PCA criterion for SD and TD. Following Gong et al. (2019) and Ma et al. (2011), the PCA criterion is used to preserve discriminative knowledge in the subspace. To this end, we minimize the following optimization problem:
where I is the identity matrix.
The Laplacian matrixes are denoted as Ls = Gs − Ws and Lt = Gt − Wt, where Gs and Gt are diagonal matrixes whose elements in the principal diagonal are defined as and , the term J1 + J2 can be written as
where α is the regularization parameter.
Fisher Criterion in DASRC
To train the discriminative dictionary D in the projection space, where the learned dictionary can sparsely represent samples from each class in SD and TD, the representation errors of intraclass and interclass in SD and TD are required to be minimized and maximized, respectively. Inspired by the Fisher criterion (Peng et al., 2020), the ratio of intra-class scatter to inter-class scatter are minimized on the coding coefficients in SD and TD as follows:
where the function φlj() returns the coefficient vectors of the same class of yj, and the function θlj() returns the coefficient vectors of the different class of yj.
To simplify Equation (8), we denote
Equation (8) can be re-written as
when the minimization problem of J3 is solved, a shared dictionary is learned to establish an intrinsic relationship between different domains so that the discrimination information learned from SD can be transferred to TD in a cross-domain scenario.
The DASRC Model
For cross-domain EEG-based emotion classification, we take into account three objective functions J1, J2, and J3 together, joint constraints on the local information preserved, PCA and Fisher criteria to optimize the shared dictionary and domain-specific projections. Thus, the optimization problem of DASRC can be formulated as
To see all the components clearly, Equation (11) is expanded by
Let , , , , , the simplified formulation of Equation (12) can be approximately written as
Optimization of the Objective Function
Equation (13) becomes a least square problem with quadratic constraints and could be solved by many methods. The Lagrangian of the optimization problem in Equation (13) is
where β and γ are Lagrange multipliers.
We use the alternating optimization method to solve Equation (14). When fixing D, β, and γ, we take the first-order partial derivatives of Equation (14) over ,
and the optimal can be computed in the closed-form
When fixing , β, and γ, we take the first-order partial derivative of Equation (14) over D,
and the optimal D can be computed in the closed-form
When fixing , D, and γ, we take the first-order partial derivative of Equation (14) over β,
Then β can be optimized by
where λβ is the length size.
When fixing , D, and β, we take the first-order partial derivative of Equation (14) over γ,
Then γ can be optimized by,
where λγ is the length size.
The proposed DASRC model is given in Algorithm 1.
Testing
With all the optimization steps discussed above, we summarize the optimization procedure of the DASRC model in Algorithm 1. When the projection matrix and the shared dictionary D are obtained by Algorithm 1, we use the following step to recognize the new EEG signal y in TD. The sparse coefficient vector α over dictionary D can be solved as,
The sparse coefficient vector α can be obtained as
The classification label of x can be derived as
where C is the number of classes.
Experiment
Datasets and Experimental Settings
We conduct the experiments to evaluate the efficacy of the proposed classifier on two public EEG emotion datasets, SEED and DEAP. The EEG signals in the SEED dataset are recorded from 15 participants across three different sessions. Their emotions are stimulated by the Chinese file clips using an ESI NeuroScan system with 62-channel electrodes at a sampling rate of 1,000 Hz. Each film clip is related to three emotions as positive, neutral, or negative, and each emotion has five corresponding film clips. The EEG signals in the DEAP dataset are recorded from 32 participants by watching 40 videos with 32-channel electrodes. DEAP dataset labels the valence and arousal rating scores from 1 to 9, which is closely related to emotions. We manually label the valence values above 4.5 as positive and the values smaller than 4.5 as negative. For a comprehensive study, we extract four different features in terms of time analysis, frequency analysis, and non-linear analysis for each EEG channel. Time analysis includes mean absolute value (MAV) (Shim et al., 2016), frequency analysis includes power spectral density (PSD) (Jenke et al., 2014), and non-linear analysis includes fractal dimension (FD) (Li et al., 2019) and differential entropy (DE) (Zheng and Lu, 2015). The size of the extracted feature is 10 dimensions for each channel.
We evaluate the DASRC model on cross-subject and cross-dataset scenarios. We compared DASRC with two baseline methods and four domain adaptation methods. For the baseline methods, we compared the DASRC with label consistent K-SVD (LC-KSVD) (Jiang et al., 2013) and SVM (Cortes and Vapnik, 1995). For these two methods, the training data in SD and TD are combined as the input samples. The Gaussian kernel is used in SVM, and the kernel and penalty parameters are searched in the grid {10−3, 10−2,…, 103}. The number of atoms in each class is selected in {50, 60,…, 200}. We compared the DASRC model with four domain adaptation methods, including transfer component analysis (TCA) (Pan et al., 2011), adaptive subspace feature matching (ASFM) (Chai et al., 2017), maximum mean discrepancy (MMD) (Sejdinovic et al., 2013), maximum independence domain adaptation (MIDA) (Yan et al., 2018). The latent dimension in MIDA and TCA is determined by searching the grid {20, 30,…, 100}. The subspace dimension in ASFM is set as 70. The threshold parameter in ASFM was set at 0.45. In DASRC, the subspace dimension is determined by searching the grid {20, 30,…, 100}. The number of atoms in each class is selected in {10, 15, 20, 25, 30, 35}. All the algorithms are implemented in MATLAB.
Cross-Subject EEG-Based Emotion Classification
For cross-subject evaluation, one subject is left out as the test subject, and the remaining different subjects are used as training data to feed the model. In the SEED dataset, one subject contains 925 samples in each session. We randomly select 300 samples from each subject and combine them as training data. We repeat the procedure 10 times.
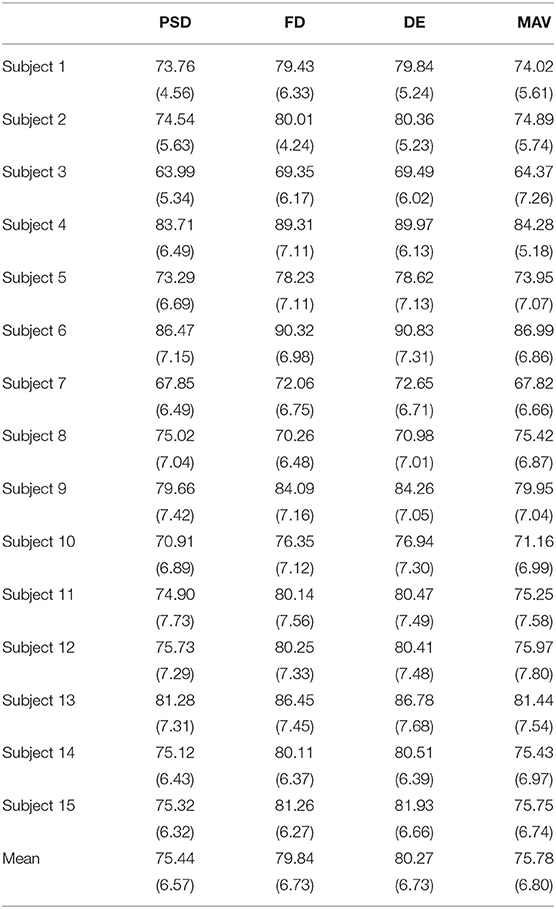
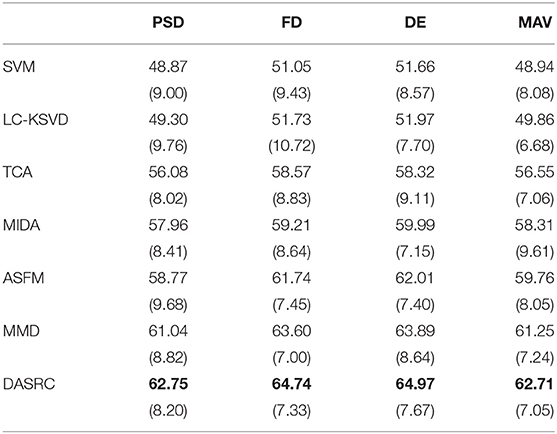
First, we evaluate how the classification accuracy of the classifier varies with the different features. For each subject, Table 1 depicts the experimental results of mean accuracies and SD on the SEED dataset. We can see that for DASRC, the classification accuracy is relatively stable, and the value of SD is acceptable. Meanwhile, the classification accuracy of some subjects is relatively high and of some subjects is relatively low. DE and FD features achieve better performance than PSD and MAV features.
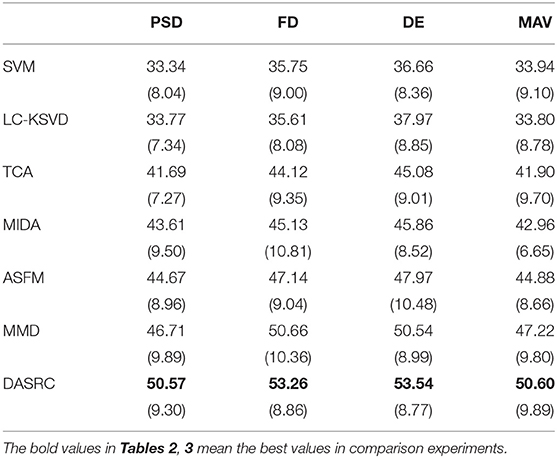
Then, DASRC is compared with two baseline methods and four domain adaptation methods. Table 2 depicts the experimental results of mean accuracies of all models using PSD, MAV, DE, and FD features. From Table 2, we can see that the classification accuracies of all methods on DE and FD features are higher than PSD and MAV features. It may suggest that non-linear analysis features may be more suitable when compared to EEG-based emotion classification. The performance of the DE feature is better than that of the FD feature, and the best results in all methods are obtained using the DE feature.
In the DEAP dataset, one subject contains 180 samples. As such, we randomly select 100 samples from each subject and the training set contains 3,100 samples. Figure 3 shows the classification accuracies of six comparison methods on the SEED dataset when four different kinds of features (PSD, MAV, DE, and FD) are used. Figure 4 shows the accuracy results of five comparison methods on the DEAP dataset for positive and negative classes. According to the experimental results, we can see that first, single-domain classification methods SVM and LC-KSVD cannot obtain satisfactory classification performance in subject-to-subject scenarios on SEED and DEAP datasets. After all, they are not proposed to address the cross-domain data scenarios. Second, among the domain adaptation methods, the proposed DASRC model based on shared dictionary and subspace learning perform better than the methods using some other shared components. The main factor is that the shared dictionary can learn more discriminative knowledge to encode the EEG signals. Third, the accuracies of all models on the DEAP dataset are lower than those obtained on the SEED dataset. It may be the reason that the labeling quality of EEG signals in DEAP is poorer.
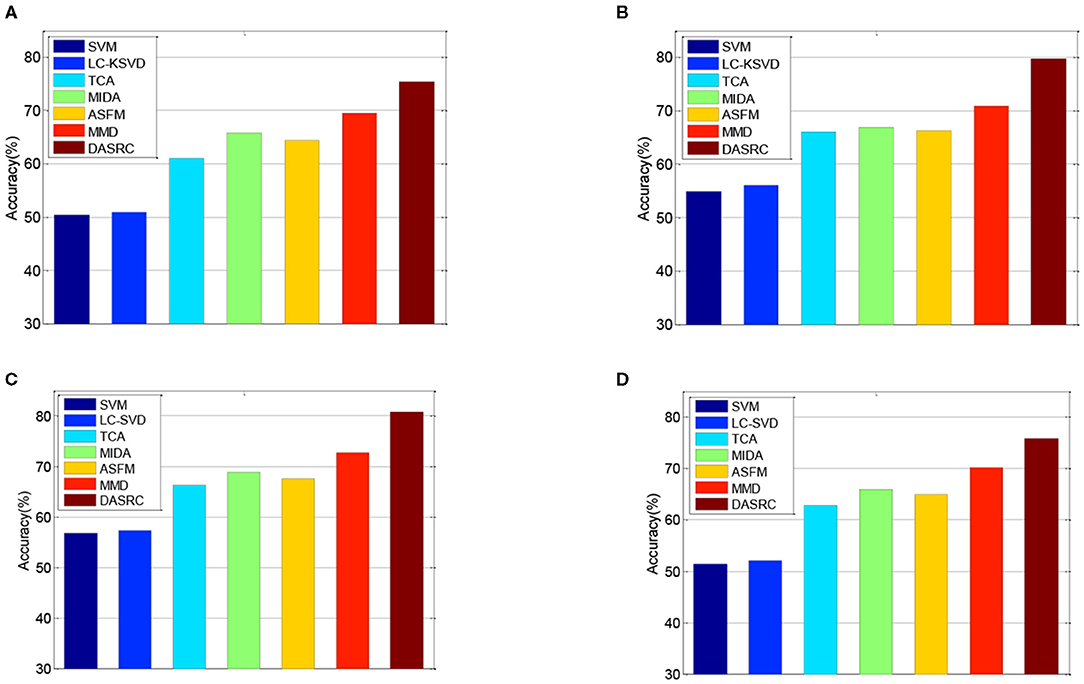
Figure 3. Cross-subject accuracy on SEED dataset with different features, (A) PSD, (B) FD, (C) DE, (D) MAV.
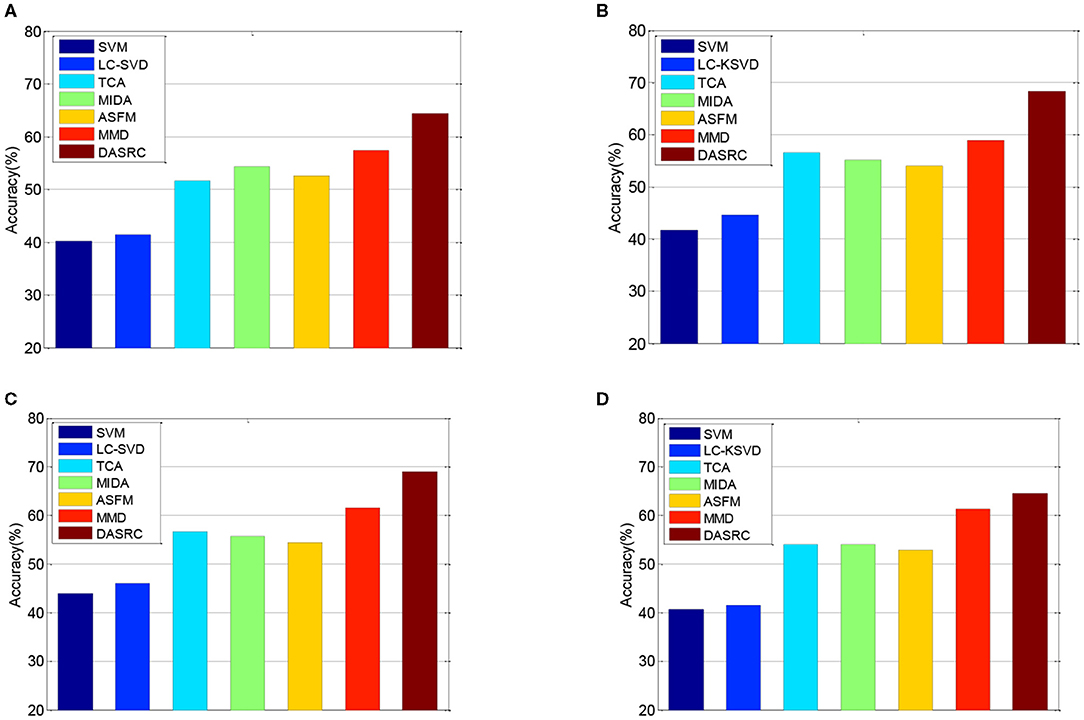
Figure 4. Cross-subject accuracy on DEAP dataset with different features, (A) PSD, (B) FD, (C) DE, (D) MAV.
Cross-Dataset EEG-Based Emotion Classification
For cross-dataset evaluation, the SD and TD are from different datasets. We perform comparison experiments across SEED and DEAP datasets. According to the given exact threshold, the samples in the DEAP dataset are divided into positive and negative classes, which correspond to the positive and negative classes of the SEED dataset. As the domain adaptation method requires the same feature space in SD and TD, we use the 32 channels shared between DEAP and SEED. In two experiments, we randomly select 3,000 samples in SD for training and 2,000 samples in TD for testing. We, then, repeat the procedure 10 times. Tables 2, 3, respectively, show the accuracy results of five comparison methods on SEED→ DEAP and DEAP→ SEED, when PSD, MAV, DE, and FD features are used. According to the experimental results, we can see that first, the performance of single-domain and domain adaptation methods exhibit evident differences, with three domain adaptation methods show significant improvements in classification accuracy. Second, DASRC is the best-performing classifier in two cross-dataset EEG emotion classifications. DASRC achieves 16.88% accuracy gains over the compared single-domain methods and 8.70% accuracy gains over the compared domain adaptation methods. The reason is that single-domain methods fail to reduce the domain shift. On the contrary, DASRC learns the shared dictionary to build the connection between SD and TD such that the discriminative knowledge from SD can be transferred to TD. In addition, besides the advantage of the cross-domain Fisher criterion and local information preserved technology, the recognition ability also promotes the classification performance of DASRC.
Parameter Analysis
In this subsection, we validate the DASRC in cross-subject and cross-dataset scenarios. The subspace dimensions, p, and size of dictionary atoms, K, are the key parameters, and they are determined by the cross-validation method. We empirically search p in {10, 20,…, 100} and K in {30, 40,…, 120}. Figure 5 plots the mean accuracy of DASRC with varying p and K, while using DE features. From Figure 5, we can see that DASRC can achieve stable performance with small p and K. The best accuracies are achieved, in general, when p is great than 60 and K is great than 80. This result indicates that the proposed DASRC can exploit the common knowledge in a relatively low dimensional subspace. Based on the results in Figure 5, the subspace dimension and dictionary size are suggested to be set to 60 and 80, respectively.
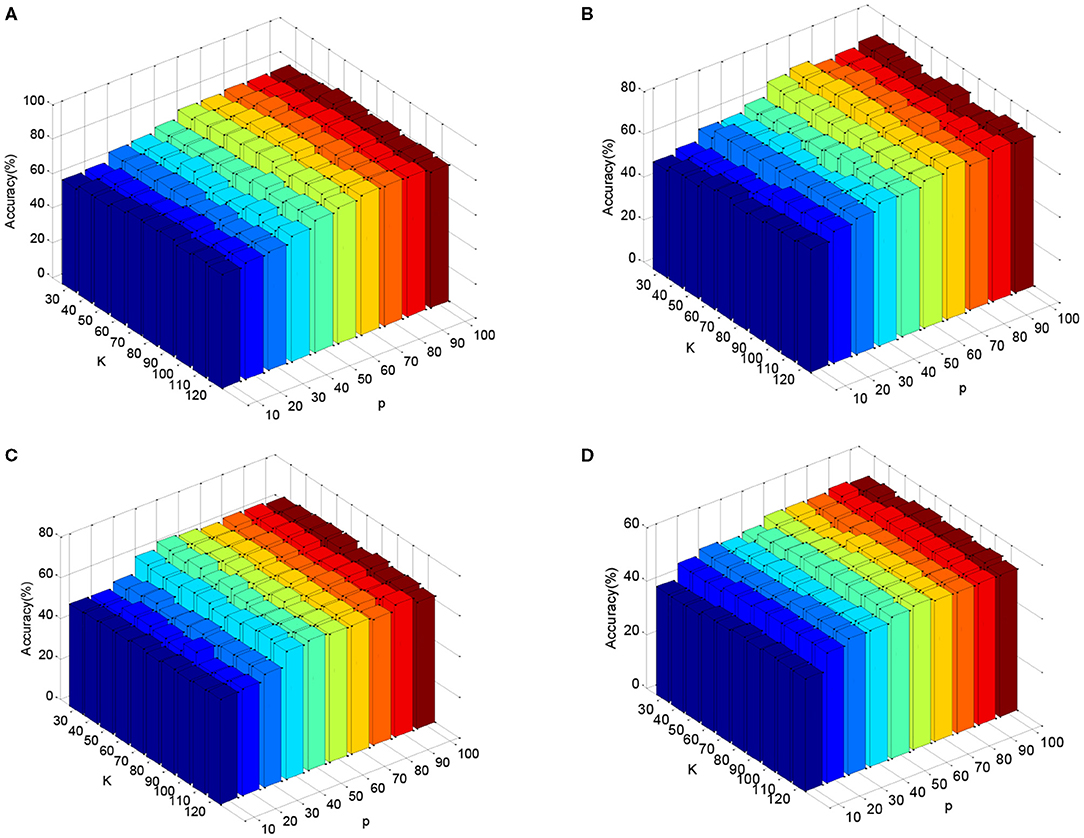
Figure 5. Cross-subject accuracy on DEAP dataset with different parameters p and K using features: (A) PSD, (B) FD, (C) DE, (D) MAV.
The domain adaptation methods often produce extra computational overhead. Figure 6 plots the convergence curves of DASRC in cross-subject and cross-dataset scenarios while using DE features. From this figure, we can see that DASRC can converge within a small number of iterations. Thus, we can set the iteration bound to 40.
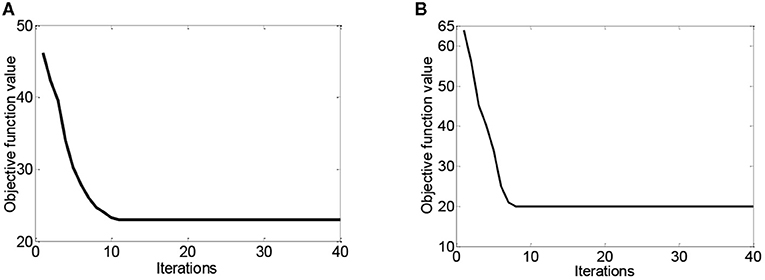
Figure 6. The convergence curves of DASRC on two scenarios, (A) cross-subject on SEED, (B) cross-dataset on DEAP→ SEED.
Conclusion
In this study, the DASRC model is proposed, which solves the EEG-based emotion classification across different subjects and datasets. Three criteria are considered to jointly learn sunspace and shared dictionary in DASRC. The local information preserved criterion is exploited to project samples in SD and TD into the shared subspace, where both PCA and Fisher criteria are exploited to transform discriminative knowledge through the shared dictionary. Experimental testing using SEED and DEAP datasets demonstrates the effectiveness of DASRC for dealing with the domain discrepancy for EEG-based emotion classification. For future work, we will explore more local preserved strategies in domain adaptation dictionary learning, such as local salience information. In addition, we will study the semi-supervised domain adaptation scenario, in which the unlabeled samples in TD rather than limited labeled samples participate in the model training. How to prevent negative transfer will also be considered in the next stage of work.
Data Availability Statement
Publicly available datasets SEED and DEAP were analyzed in this paper. These data can be found in the following links, respectively: https://bcmi.sjtu.edu.cn/home/seed/ and http://www.eecs.qmul.ac.uk/mmv/datasets/deap/.
Author Contributions
TN, JX, and SW conceived and designed the proposed model. YN and JX performed the experiment. TN and SW wrote the manuscript. All authors read and approved the manuscript.
Funding
This work was supported in part by the National Natural Science Foundation of China under Grants 61806026, the research project of maternal and child health in Jiangsu Province under Grants F202060, and the Natural Science Foundation of Jiangsu Province under Grants SBK2021022110.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Aharon, M., Elad, M., and Bruckstein, A. (2006). K-SVD: an algorithm for designing overcomplete dictionaries for sparse representation. IEEE Trans. Signal Process. 54, 4311–4322. doi: 10.1109/TSP.2006.881199
Chai, X., Wang, Q., Zhao, Y., Li, Y., Wang, Q., Liu, X., et al. (2017). A fast, efficient domain adaptation technique for cross-domain electroencephalography (EEG)-based emotion recognition. Sensors 17:1014. doi: 10.3390/s17051014
Cimtay, Y., and Ekmekcioglu, E. (2020). Investigating the use of pretrained convolutional neural network on cross-subject and cross-dataset EEG emotion recognition. Sensors 20:2034. doi: 10.3390/s20072034
Cortes, C., and Vapnik, V. (1995). Support vector machine. Mach. Learn. 20, 273–297. doi: 10.1007/BF00994018
Doma, V., and Pirouz, M. (2020). A comparative analysis of machine learning methods for emotion recognition using EEG and peripheral physiological signals. J. Big Data 7:18. doi: 10.1186/s40537-020-00289-7
Fahimi, F., Zhang, Z., Goh, W. B., Lee, T. S., Ang, K. K., and Guan, C. (2019). Inter-subject transfer learning with an end-to-end deep convolutional neural network for EEG-based BCI. J. Neural Eng. 16:026007. doi: 10.1088/1741-2552/aaf3f6
Gong, C., Zhou, P., Han, J., and Xu, D. (2019). Learning rotation-invariant and Fisher discriminative convolutional neural networks for object detection. IEEE Trans. Image Process. 28, 265–278. doi: 10.1109/TIP.2018.2867198
Gu, X., Zhang, C., and Ni, T. (2020). A hierarchical discriminative sparse representation classifier for EEG signal detection. IEEE/ACM Trans. Comput. Biol. Bioinform. doi: 10.1109/TCBB.2020.3006699. [Epub ahead of print].
Jenke, R., Peer, A., and Buss, M. (2014). Feature extraction and selection for emotion recognition from EEG. IEEE Trans. Affect. Comput. 5, 327–339. doi: 10.1109/TAFFC.2014.2339834
Jiang, Z., Lin, Z., and Davis, L. (2013). Label consistent K-SVD: learning a discriminative dictionary for recognition. IEEE Trans. Pattern Anal. Mach. Intell. 35, 2651–2664. doi: 10.1109/TPAMI.2013.88
Kanoga, S., Kanemura, A., and Asoh, H. (2019). Multi-scale dictionary learning for ocular artifact reduction from single-channel electroencephalograms. Neurocomputing 347, 240–250. doi: 10.1016/j.neucom.2019.02.060
Koelstra, S., Muhl, C., Soleymani, M., Lee, J. S., Yazdani, A., Ebrahimi, T., et al. (2011). Deap: a database for emotion analysis; using physiological signals. IEEE Trans. Affect. Comput. 3, 18–31. doi: 10.1109/T-AFFC.2011.15
Lan, Z., Olga, S., Wang, L., Reinhold, S., and Muller-Putz, G. R. (2018). Domain adaptation techniques for EEG-based emotion recognition: a comparative study on two public datasets. IEEE Trans. Cogn. Dev. Syst. 11, 85–94. doi: 10.1109/TCDS.2018.2826840
Li, J., Qiu, S., Du, C., Wang, Y., and He, H. (2020b). Domain adaptation for EEG emotion recognition based on latent representation similarity. IEEE Trans. Cogn. Dev. Syst. 12, 344–353. doi: 10.1109/TCDS.2019.2949306
Li, J., Qiu, S., Shen, Y. Y, Liu, C. L., and He, H. (2020a). Multisource transfer learning for cross-subject EEG emotion recognition. IEEE Trans. Cybern. 50, 3281–3293. doi: 10.1109/TCYB.2019.2904052
Li, X., Song, D., Zhang, P., Zhang, Y., Hou, Y., and Hu, B. (2018). Exploring EEG features in cross-subject emotion recognition. Front. Neurosci. 12:162. doi: 10.3389/fnins.2018.00162
Li, Y., Zheng, W., Cui, Z., Zong, Y., and Ge, S. (2019). EEG emotion recognition based on graph regularized sparse linear regression. Neural Process. Lett. 49, 555–571. doi: 10.1007/s11063-018-9829-1
Liu, M. J., Zhou, M. M., Zhang, T., and Xiong, N. X. (2020). Semi-supervised learning quantization algorithm with deep features for motor imagery EEG recognition in smart healthcare application. Appl. Soft Comput. 89:106071. doi: 10.1016/j.asoc.2020.106071
Liu, Y. J., Yu, M. J., Zhao, G. Z., Song, J., Ge, Y., and Shi, Y. C. (2018). Real-time movie-induced discrete emotion recognition from EEG signals. IEEE Trans. Affect. Comput. 9, 550–562. doi: 10.1109/TAFFC.2017.2660485
Ma, J., Bayram, S., Tao, P., and Svetnik, V. (2011). High-throughput ocular artifact reduction in multichannel electroencephalography (EEG) using component subspace projection. J. Neurosci. Methods 196, 131–140. doi: 10.1016/j.jneumeth.2011.01.007
Morioka, H., Kanemura, A., Hirayama, J. I., Shikauchi, M., Ogawa, T., Ikeda, S., et al. (2015). Learning a common dictionary for subject-transfer decoding with resting calibration. NeuroImage 111, 167–178. doi: 10.1016/j.neuroimage.2015.02.015
Ni, T., Gu, X., and Jiang, Y. (2020c). Transfer discriminative dictionary learning with label consistency for classification of EEG signals of epilepsy. J. Ambient Intell. Humaniz. Comput. doi: 10.1007/s12652-020-02620-9. [Epub ahead of print].
Ni, T., Gu, X., and Zhang, C. (2020b). An intelligence EEG signal recognition method via noise insensitive TSK fuzzy system based on interclass competitive learning. Front. Neurosci. 14:837. doi: 10.3389/fnins.2020.00837
Ni, T., Zhang, C., and Gu, X. (2020a). Transfer model collaborating metric learning and dictionary learning for cross-domain facial expression recognition. IEEE Trans. Comput. Soc. Syst. doi: 10.1109/TCSS.2020.3013938. [Epub ahead of print].
Pan, S. J., Tsang, I. W., Kwok, J. T., and Yang, Q. (2011). Domain adaptation via transfer component analysis. IEEE Trans. Neural Netw. 22, 199–210. doi: 10.1109/TNN.2010.2091281
Peng, Y., Liu, S., Wang, X., and Wu, X. (2020). Joint local constraint and fisher discrimination based dictionary learning for image classification. Neurocomputing 398, 505–519. doi: 10.1016/j.neucom.2019.05.103
Sejdinovic, D., Sriperumbudur, B., Gretton, A., and Fukumizu, K. (2013). Equivalence of distance-based and RKHS-based statistics in hypothesis testing. Ann. Stat. 41, 2263–2291. doi: 10.1214/13-AOS1140
Shim, H. M., An, H., Lee, S., Lee, E. H., Min, H. K., and Lee, S. (2016). EMG pattern classification by split and merge deep belief network. Symmetry 8:148. doi: 10.3390/sym8120148
Yan, K., Kou, L., and Zhang, D. (2018). Learning domain-invariant subspace using domain features and independence maximization. IEEE Trans. Cybern. 48, 288–299. doi: 10.1109/TCYB.2016.2633306
Yang, F., Zhao, X., Jiang, W., Gao, P., and Liu, G. (2019). Multi-method fusion of cross-subject emotion recognition based on high-dimensional EEG features. Front. Comput. Neurosci. 13:53. doi: 10.3389/fncom.2019.00053
Zhang, X., and Wu, D. (2019). On the vulnerability of CNN classifiers in EEG-based BCIs. IEEE Trans. Neural Syst. Rehabil. Eng. 27, 814–825. doi: 10.1109/TNSRE.2019.2908955
Zheng, W. L., and Lu, B. L. (2015). Investigating critical frequency bands and channels for EEG-based emotion recognition with deep neural networks. IEEE Trans. Auton. Ment. Dev. 7, 162–175. doi: 10.1109/TAMD.2015.2431497
Keywords: electroencephalogram, domain adaptation, emotion classification, cross-subject, cross-dataset
Citation: Ni T, Ni Y, Xue J and Wang S (2021) A Domain Adaptation Sparse Representation Classifier for Cross-Domain Electroencephalogram-Based Emotion Classification. Front. Psychol. 12:721266. doi: 10.3389/fpsyg.2021.721266
Received: 06 June 2021; Accepted: 28 June 2021;
Published: 29 July 2021.
Edited by:
Yaoru Sun, Tongji University, ChinaReviewed by:
Qin Qin, Henan Institute of Engineering, ChinaLijun Xu, Nanjing Institute of Technology (NJIT), China
Copyright © 2021 Ni, Ni, Xue and Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jing Xue, eHVlamluZ0Buam11LmVkdS5jbg==; Suhong Wang, eWFybWluZUBmb3htYWlsLmNvbQ==
 Tongguang Ni
Tongguang Ni Yuyao Ni2
Yuyao Ni2 Jing Xue
Jing Xue