- School of Mathematical Sciences, Beijing Normal University, Beijing, China
Although working memory (WM) is an important factor in mathematical problem solving (MPS), it remains unclear how well WM relates to MPS. Thus, we aimed to determine this relationship by using a meta-analysis. We searched electronic databases for studies published between 2000 and 2020 and established operational criteria. We conducted Egger’s regression tests and created funnel plots to test for publication bias. Finally, a three-level meta-analytic model analysis of data from 130 studies involving 43,938 participants and 1,355 effect sizes revealed a moderate relationship between WM and MPS (r = 0.280, 95% CI = [0.263, 0.314]). Moreover, moderator analyses showed that: (1) dressed-up word problems were more strongly tied to WM than to intra-mathematical problems; (2) the central executive function showed the strongest relation with MPS, whereas the phonological loop had the weakest; (3) gender ratio had significant moderating effects; and (4) some of the above-mentioned significant moderating effects were unique after controlling for other factors. Implications for research and practice were also discussed.
1. Introduction
Problem solving has, for some time, occupied a prominent position in education research (e.g., Lawson, 2003; Felmer et al., 2016; Priemer et al., 2020). In recent years, incorporating problem solving in school mathematics instruction has become a major area of interest within the field of mathematics education (e.g., Jitendra et al., 2005; Popham et al., 2020). From the perspective of teaching, research on the cognitive level has not been properly transferred to pedagogical issues, and remains separate from practice. Focusing on cognitive training is likely to aid in far-transferring students’ performance. However, previous studies have failed to show any stable evidence or provide impetus for teachers’ practice. Research on cognitive abilities and mathematical performance thus far has provided ideas for further exploration, and it is possible to identify the predictors for problem solving.
Working memory (WM) is frequently mentioned with regards to cognitive abilities in mathematics. Extensive studies have established that WM is related to students’ mathematical performance (e.g., Meyer et al., 2010; Ching, 2017; Wu et al., 2017; Korhonen et al., 2018; Fuchs et al., 2020). In previous studies from Baddeley and Hitch (1974) and Baddeley (1992, 2003, 2010), WM referred to a system to provide temporary storage and manipulation of the information necessary while performing complex tasks. As for mathematical problem solving (MPS), memory systems also appear to be decisive factors (Ambrus and Barczi-Veres, 2016). However, studies have yielded mixed results. For instance, Peng et al. (2016) estimated the average correlation between WM and mathematical word problem solving skills to be 0.37 while Song et al. (2011) found that students with lower WM capacity performed better on medium difficult problems than students with higher WM capacity. Solving mathematical problems appears to be complex as the process involves considerable phases (Pongsakdi et al., 2020). For mathematics, more attention should be given to “knowledge.” However, the same “knowledge” might involve different problem solving strategies and cognitive processes. For example, to calculate 8+5, a child who uses a retrieval strategy might solve it by recalling from memory, but a child who uses a decomposition strategy might break it down to 8 + (2 + 3). These are obviously different and the individual differences in memory abilities are related to individual differences in MPS. The relationship between WM and mathematics has been examined by meta-analysis (e.g., Peng et al., 2016). Although the classification divides mathematical skills (e.g., basic number knowledge, whole-number calculations, fractions, Peng et al., 2016), focusing on cognitive processes and MPS, the results are complex. For example, for geometry problem solving tasks from a standardized geometrical achievement test (Mammarella et al., 2012), children were required to calculate the area of complex figures and solve complex geometrical problems. Both calculation skills and geometry knowledge are necessary. Overall, MPS emphasizes students’ cognitive processes, providing better future direction.
In MPS, the process comprises several phases that are not necessarily performed sequentially: (1) understanding the problem information and situation; (2) translating problems into a mathematical model; (3) solving the mathematical model with mathematical skills; (4) interpreting and examining results with respect to the problem situation; and (5) communicating the results of the original problems (Pongsakdi et al., 2020). The integrity and overlapping of these processes make them difficult to break down. However, different kinds of problems might cause students varying degrees of cognitive load making it difficult to interpret students’ cognitive processes (e.g., Ayres, 2001; Jäder et al., 2017; Voica et al., 2020). In the studies of Blum et al. (2007), mathematical problems were categorized into three main types with varying focuses on cognitive processes: intra-mathematical problems, dressed-up word problems, and modeling problems. Schukajlow et al. (2012) described an intra-mathematical problem as a problem without any connection to the real world. The beginning of the cognitive process follows the mathematical model directly. Problems that appeared the most in class were dressed-up word problems (e.g., Blum, 2015). The cognitive activities involved are more complex than when solving intra-mathematical problems since the mathematical models have been dressed- up according to real-life situations. In solving modeling problems, there always exists a modeling loop and students are required to go back and forth between reality and mathematics (e.g., Herbst, 2019). Taken together, according to students’ performance on different problems, it helps to speculate and understand how cognitive factors, including WM, relate to the performance of MPS.
Furthermore, several studies have highlighted that WM relates to mathematics with the strength of these relations differing across components of WM (e.g., Costa et al., 2011; Rennie et al., 2014; Bullen et al., 2020). With their focus on knowledge and skills, previous studies do not offer an adequate explanation for the meaning between those components and the cognitive process during MPS. This article provides valuable insight for understanding the association. For instance, the central executive function might be more vital for dressed-up problems and modeling problems because students must identify what information is useful for solving the problem, plan how to apply what they know comprehensively in real life, and make decisions on how to manage the information. In solving intra-mathematical problems, the phonological loop may play a more important role in phonological awareness and coding in counting (e.g., equations, problems about a sequence of numbers). Therefore understanding the relationship between the three components and MPS is of practical significance, and will provide a fresh angle for educators to re-examine the cognitive processes in MPS. Moreover, researchers have operationalized WM and these components in a variety of ways (e.g., operation span, block span, sentence span). Previous studies have investigated the difference between MPS and WM measures based on reading and counting (Perlow and Jattuso, 2018). Clarifying these problems will also be beneficial for our understanding of the nature of MPS.
To address educators’ concerns, it is hoped that this research will contribute to a deeper understanding of students’ characteristics (e.g., grade level, gender ratio). For example, because of the changing focus of math instruction (i.e., a heavier focus on counting/calculations in primary school and at young ages, and on complex problems when the student reaches middle or high school), the role of WM may also evolve. In terms of the difficulty of the problems mentioned earlier, even when distinguished in one study, they are not comparable on a wide scale across studies. This research sought to remedy this issue by analyzing MPS by focusing more on cognitive processes rather than on the difficulty of knowledge. It is not certain whether intra-mathematical problems are easier or more difficult than dressed-up problems in different school periods. By exploring problems or cognitive processes, the results will be more general without the limitations of age or other sample types.
In summary, although studies have focused on mathematics, research has yet to systematically investigate MPS. Most studies are limited in that they may be generalizable only to mathematics knowledge, but MPS differs from mathematics in a number of important ways (e.g., understanding, comprehension, and monitoring). The aim of this study was to develop a better understanding of MPS. This paper is structured as follows: We first focus on problems that stress cognitive processes in MPS. We then discuss the components and measures of WM. This is followed by a discussion on the relationship between WM and MPS. We then explore the influence of sample type which is independent of knowledge leading to purer results. Besides, a challenge for this research is that one study may involve two types of mathematical problems or several subsystems of WM and is therefore necessary to extract more than one effect size for the same study. Common methods such as selecting only one effect size per study used in the traditional meta-analysis are unlikely to be appropriate for this study. However, by the three-level meta-analysis, all the useful effect sizes could be extracted and the heterogeneity of within-study variance was calculated to ensure independency (Ran et al., 2022). The three-level meta-analysis model has been proven to be as effective to estimate the parameters in meta-analysis as other traditional random effects approaches, with the additional advantage that multilevel models are more flexible (Van den Noortgate and Onghena, 2003; Ran et al., 2022). For example, multiple predictors can be incorporated into this model (Fernández-Castilla et al., 2020). No previous study has used the three-level meta-analysis model for analyzing the association between WM and MPS. To conclude, we answer the following two questions:
(1) What is the size of the relationship between WM and MPS?
(2) Does the relationship between WM and MPS vary as a function of (a) task type or (b) participant characteristics?
2. Methods
2.1. Data collection
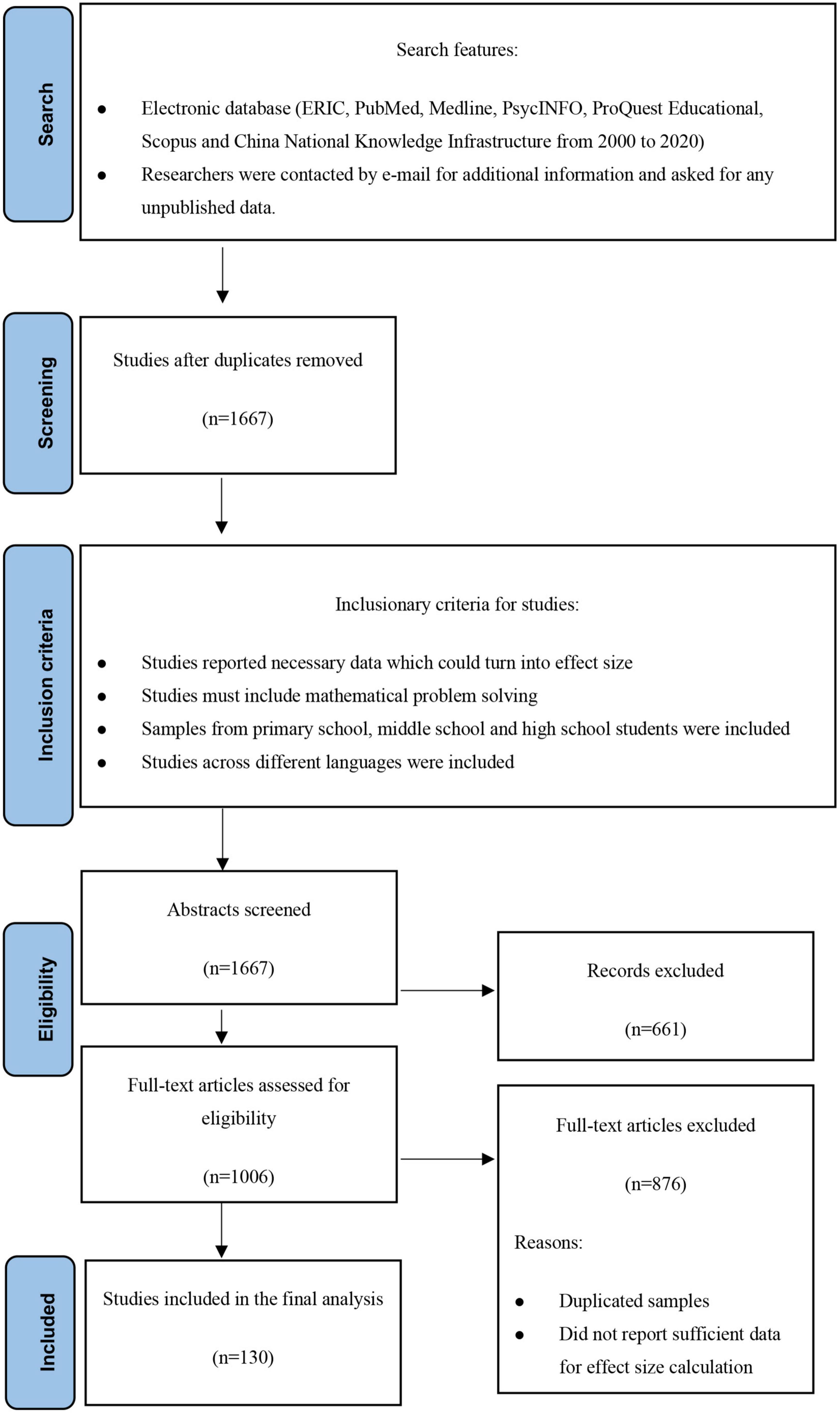
Figure 1 outlines the inclusion, search, and coding procedures. To identify studies for the three-level meta-analysis, we first searched electronic databases (i.e., ERIC, PubMed, Medline, PsycINFO, ProQuest Educational, Scopus, and the China National Knowledge Infrastructure) for studies published between 2000 and 2020. We used problem solving, math* and working memory in our search, as well as the AND command. We removed the duplicates at first and contacted authors who published studies that we could not find and asked for their papers or unpublished data.
2.2. Operational criteria for inclusion and the elimination of studies
For the target topics included in this study, we first established operational criteria to determine the indicators. We included studies that had considered WM as a whole model or measured one of the WM components (e.g., the central executive function).
Regarding MPS, we considered two kinds of outcomes (intra-mathematical problems and dressed-up word problems). As the included research focused more on young students, there was no research using modeling problems to investigate the relationship. To be considered an intra-mathematical problem, the task had to include arithmetic problems or natural operations with no relationship to reality (e.g., addition and subtraction). To be considered a dressed-up word problem, the task had to include mathematical reasoning, applied math problems, and some necessary problem situations.
Furthermore, if a dissertation was published as an article, we only considered the article itself. After applying these criteria, we identified 130 studies with sample sizes ranging from 20 to 5,234.
2.3. Coding procedures
We created an online coding form. Two researchers coded the following content of the selected studies separately: (a) participant characteristics (e.g., sample size, grade level, country/region, typically developing students vs. students with difficulties); (b) type of MPS outcome (intra-mathematical problem/dressed up word problem); (c) type of WM (unspecified WM/central executive/visuospatial sketchpad/phonological loop); (d) tool for measuring WM (inventory/operation/block/sentence/digit/spot/others).
All effect sizes were then coded. Several studies have reported more than one measure to examine the relationship between WM and MPS. According to the basic rules of the three-level meta-analysis, all relevant effect sizes from each selected study were coded without reducing the number of effect sizes in any way. To ensure the robust reliability of this study, two independent recorders double-coded all the primary studies and checked the data to ensure coding accuracy. The consensus rate (Cohen’s kappa) varied between 95 and 100%. Most differences in coding were because of the lack of effective and comprehensive information provided in several studies that described the samples and measures. After revisiting the studies, and discussing the differences, two independent recorders reached an agreement (see Supplementary Appendix A).
2.4. Moderator variables
In each study, both groups of important moderators were coded that might explain the significance of the residual within- and between-study variance.
2.4.1. Task type
We classified the WM tasks into the central executive, the visuospatial sketchpad, the phonological loop, and unspecified WM, which were unspecified in primary studies. We coded the measurement of WM to determine whether the overall effect size varied across tools. As highlighted earlier, the classification of WM tests was determined on the basis of the surface-level elements of test content. (e.g., inventory, operation, block, sentence, digit, and spot). We categorized MPS tasks into intra-mathematical and dressed-up word problems.
2.4.2. Participant characteristics
We included four participant characteristics in this study. First, we coded gender based on the ratio of males included in the samples. Second, we categorized the grade levels as follows: elementary, middle, and high school. Third, we coded the cultural environment as a category variable (1 = Eastern, 0 = Western) according to the students’ country or region reported in the study (Ran et al., 2022). Finally, we coded whether the sample included students with difficulties (e.g., math difficulties and dyslexia).
2.5. Statistical analysis
We used the metafor package for the R statistical program (Viechtbauer, 2010) and the three-level meta-analytic model tutorial (Assink and Wibbelink, 2016) for the analysis. Since three-level models assume a normal distribution of effect sizes (Van den Noortgate et al., 2013), it is necessary to transform all data into Fisher’s Z-values. We applied the Fisher Z-transformation first to conduct the meta-analysis, and then Fisher’s z-values were converted back, respectively into correlation coefficients for interpretability (Hedges and Olkin, 2014; Card, 2015). Pearson’s r value was not provided in almost 20 of the 130 studies. However, using alternative formulas from, among other sources, Lenhard and Lenhard (2016), we were able to compute the r correlation and then transformed it into Fisher’s Z-score. For instance, we used a procedure for converting standardized β to r and then r could be used directly as an effect size. We were also able to compute Cohen’s d value using the statistic about means, standard deviations and sample sizes from the treatment and control group, and the t-statistic from the group test and then transformed d into the r-value (Borenstein et al., 2009). As noted in the introduction, we used a three-level random effects model and included all effect sizes in the same study. The three-level meta-analytic model considers three variance components distributed across the model’s three levels: sampling variance of the extracted effect sizes at Level 1, variance between effect sizes from the same study at Level 2, and variance between studies at Level 3 (Assink and Wibbelink, 2016).
To establish whether the variation in the r-value between the studies was significant, we used the Q test of homogeneity (Hedges and Olkin, 2014). We also computed the 95% CI for each overall effect size to provide more information regarding the correlation. We calculated the variance at Level 1 according to Cheung’s (2014) formula and applied the log-likelihood-ratio test to examine heterogeneity at levels 2 and 3. Furthermore, we tested for significance and calculated the distribution of the overall variance.
We also explored moderator variables as potential sources of additional variance in the effect size. We used linear models to predict the study’s outcome from the moderator variables, both for the continuous (i.e., gender ratio) and categorical (i.e., school level, task type, and sample characteristics) moderators. Universal classifications were chosen as the reference category to clarify the findings between different task types (e.g., unspecified working memory in WM tasks, both in MPS tasks and others in WM tests). Furthermore, we used a multiple moderator model to scrutinize the unique effect of significant moderators in the univariate analyses and added all significant moderators to the model. We tested the degree of difference between the subsets of studies using a Q test and by comparing the correlation magnitude with CIs between the study subsets. Similarly, we investigated the variances at levels 2 and 3.
2.6. Publication bias
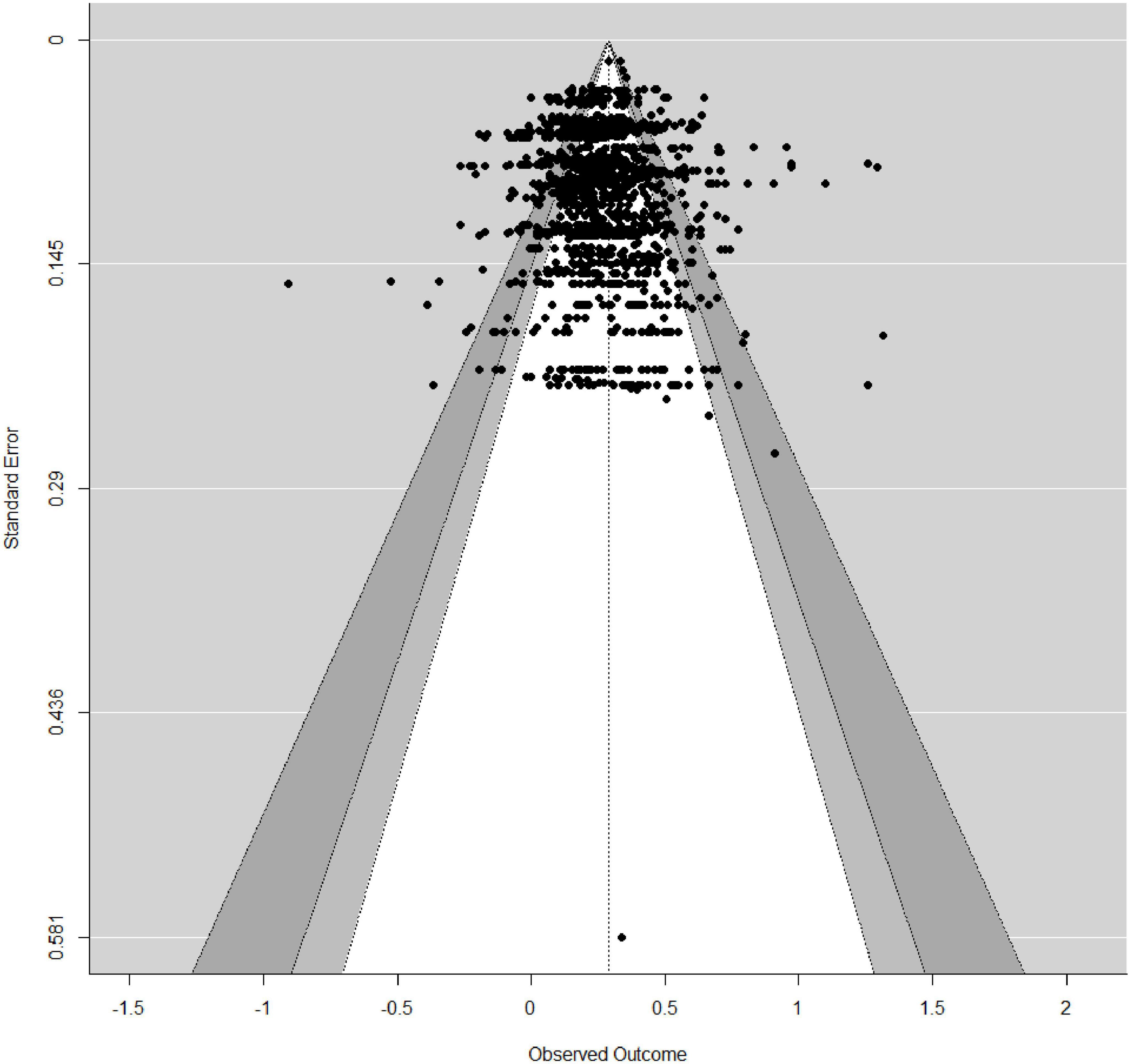
To test for publication bias, we first conducted Egger’s regression tests (Egger et al., 1997) to test the relationship between the size of the effects from each study and the associated standard error (Georgiou et al., 2020; Ran et al., 2022). If the results of the linear regression showed no significant difference, there was no publication bias. Furthermore, we created funnel plots to test for publication bias. In the funnel plot, the standard error was plotted on the y-axis and the effect size on the x-axis, and if publication bias exists, the funnel would not be symmetric (Ludwig et al., 2019; Borenstein et al., 2021).
3. Results
3.1. Study features
Of the 130 publications included in our final analysis, 24 reported results on all three components of WM, and 55 reported results on both MPS outcomes. There were 43,938 students represented, with sample sizes ranging from 20 to 5,234. Moreover, one study exclusively focused on female students. The number of effect sizes in each study ranged from 1 to 36.
3.2. Meta-analytic results
The three-level meta-analytic model demonstrated that the overall mean correlations between WM and MPS were significant (r = 0.280, p < 0.001, 95% CI = [0.263, 0.314]). Additionally, the log-likelihood-ratio test showed significant heterogeneity (p < 0.001) at the within-study variance (Level 2) and the between-study variance. Exactly 16.34% of the total variance could be attributed to variance at Level 1, 26.05% of the total variance could be attributed to the differences between the effect sizes within studies at Level 2, and 57.61% could be attributed to the between-study variance (Level 3).
3.3. Results of the moderator analyses
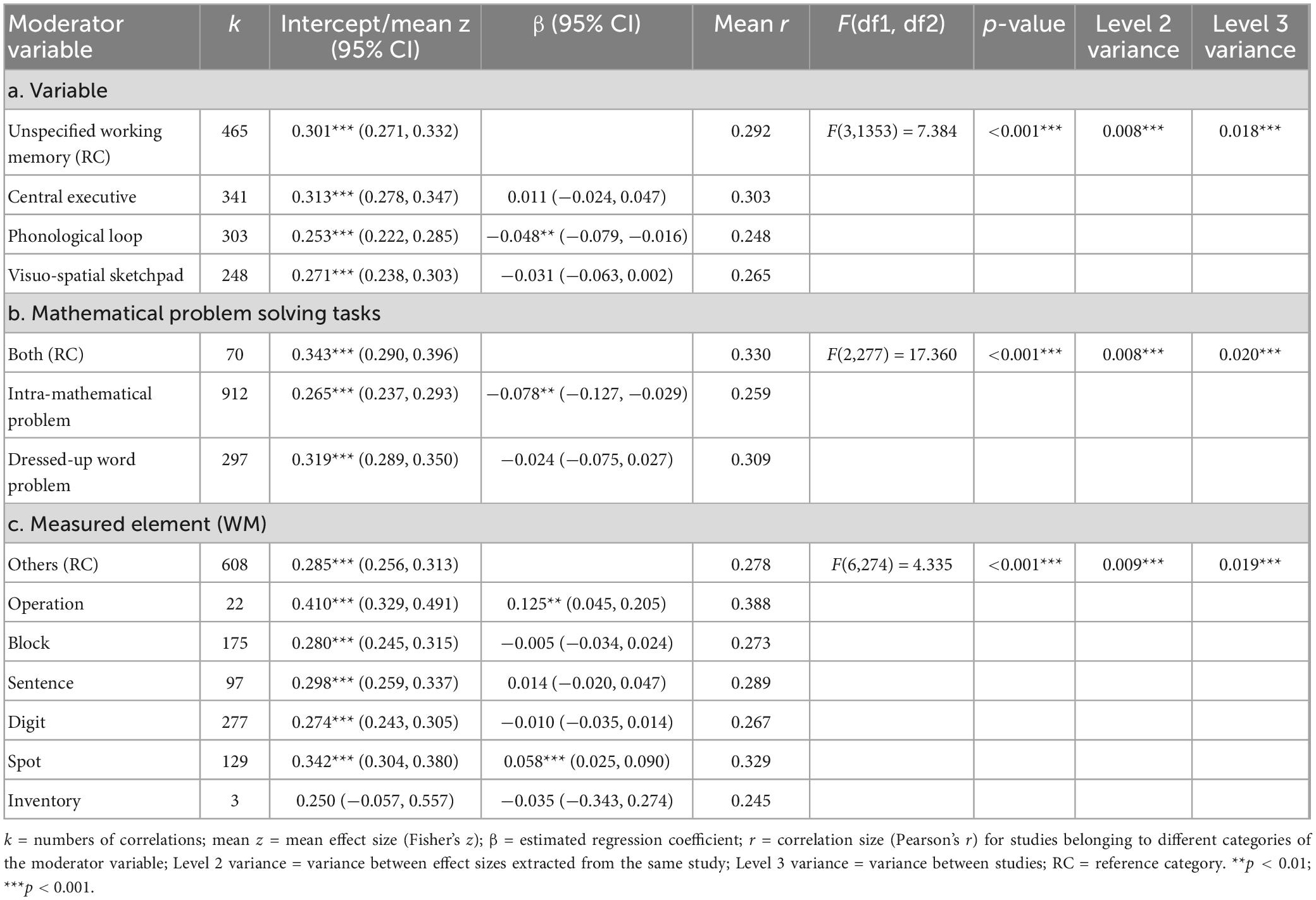
First, we delved into the role of the three components of WM, two types of MPS tasks, and the measured elements (WM) in the relationship of interest. As outlined in Table 1, they were all significant moderators. Studies testing the central executive produced significantly larger correlations than those that tested the other two components (0.303 > 0.265 > 0.248, p < 0.001). Compared with other tasks, studies using intra-mathematical problems only generated a significantly smaller correlation than those using dressed-up word problems (0.309 > 0.259, p < 0.001). Besides, measuring WM by operation showed a larger relation than any other WM tests (p < 0.001).
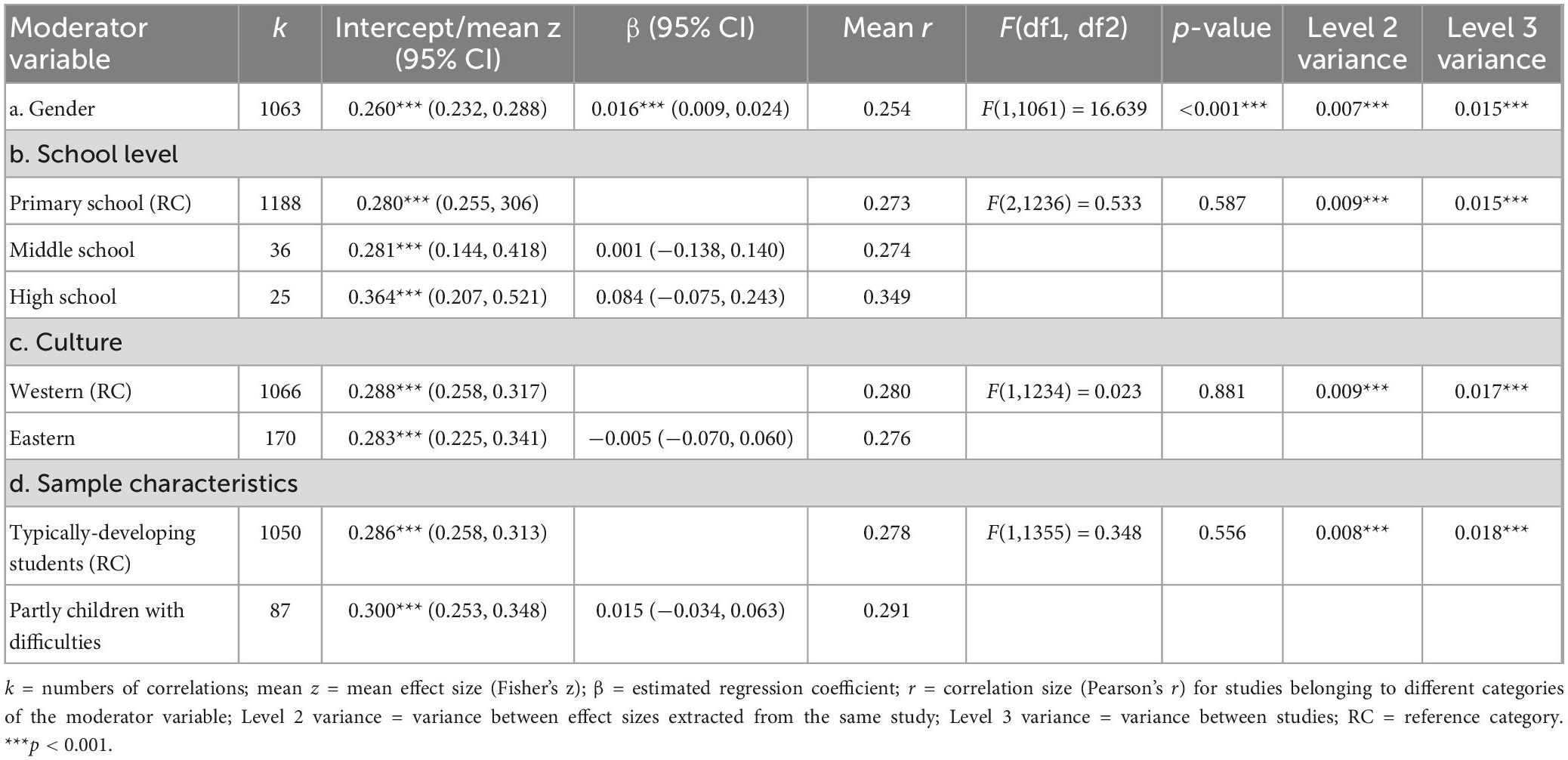
Second, we further analyzed the moderating effects of participant characteristics, including gender, school level, culture, and sample characteristics. As seen in Table 2, the gender ratio was a significant moderator. The regression coefficient was positive (β = 0.016), implying that this association was stronger in boys. Besides, the correlation between WM and MPS was stable across school level, cultural background, and unfolding situation.
Previous studies have demonstrated that moderators might be interrelated (Hox et al., 2017). Therefore, we added all the significant moderators to the multiple moderator model to examine what effects were really relevant. As mentioned earlier, we chose universal classifications as the reference category. The omnibus test showed significant results, F(12,973) = 7.676, p < 0.001, suggesting that at least one of the regression coefficients of the moderators significantly deviated from zero. Based on the findings in Table 3, we were able to assert that the components of WM, MPS tasks and measured elements for WM were not confounded by the gender ratio. These results indicated these three moderators had a uniquely moderating effect on the association.
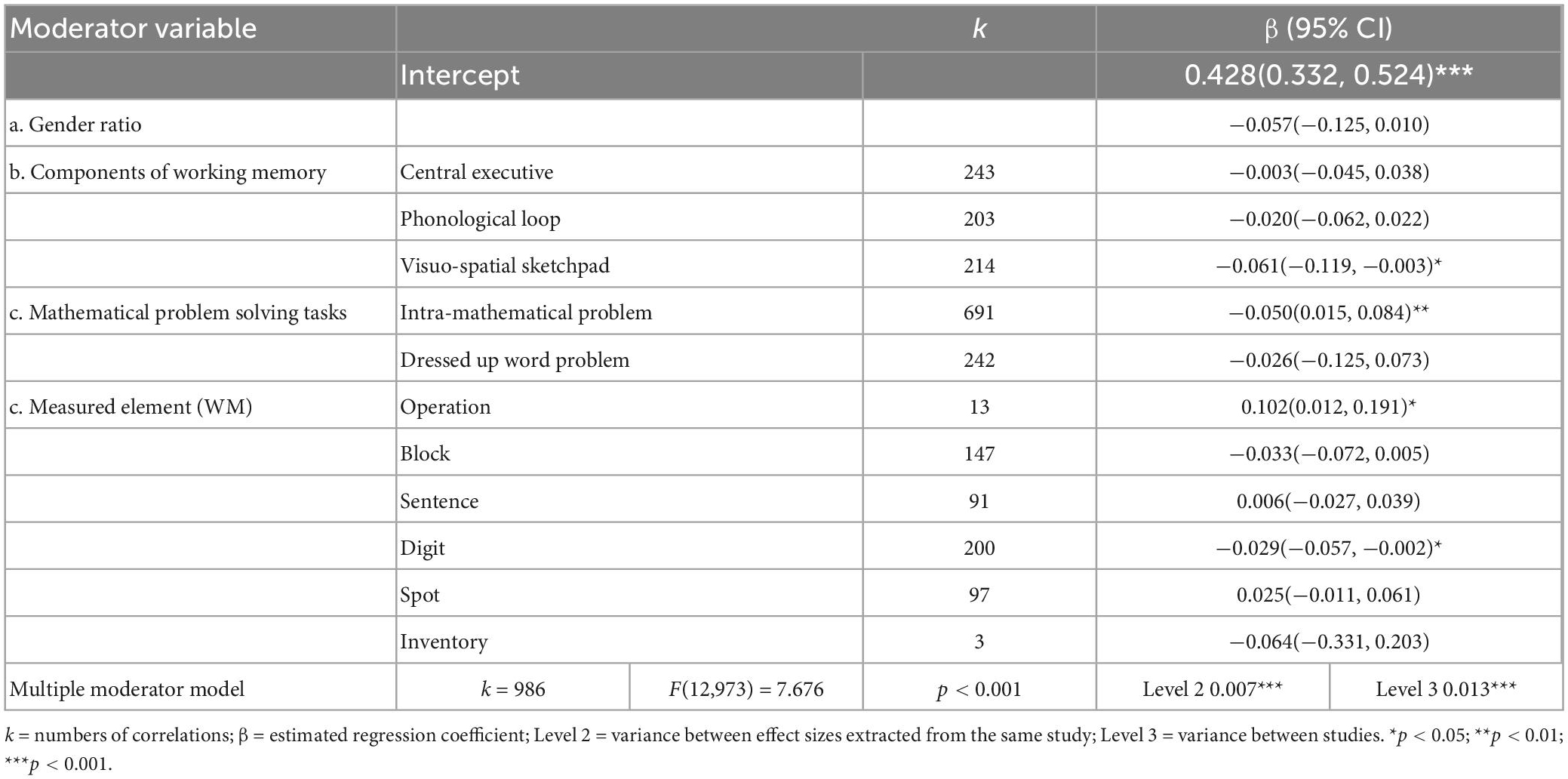
Table 3. Multiple moderator model on the relation between working memory (WM) and mathematical problem solving (MPS).
3.4. Publication bias
The results of Egger’s test suggested that publication bias should be ignored in the meta-analysis because the p-value of this test exceeded 0.05. The symmetric distribution of the funnel plot was depicted in Figure 2, which indicated that the results of our meta-analysis were stable and reliable.
4. Discussion
The purpose of this meta-analysis was to estimate the size of the relationship between WM and MPS and to determine if different factors (task type/participant characteristics) moderate their relationship. When we considered any correlation between any components of WM, we found significant links between WM and MPS (the average correlation was 0.280), which are similar to those reported in previous meta-analyses (Peng et al., 2016). Additionally, this relationship was significantly influenced by publication characteristics and task type, but not by participant characteristics. Concretely speaking, in terms of WM, all components of WM demonstrated significant ties with MPS, and the central executive showed the strongest relationship (r = 0.303). Regarding the WM tests, operation span had a strong relationship with MPS. In the field of outcomes for MPS, the connection between WM and dressed-up word problems was stronger. Furthermore, although gender ratio had significance, the results of the multiple moderator model indicated that it was not as steady as expected.
In MPS, diverse strategies and cognitive processes were identified as different types of math problems (Star and Rittle-Johnson, 2008; Hu et al., 2017; Rott et al., 2021). Since different types of problems require different cognitive abilities, we investigated this by examining the relationship between WM and intra-mathematical or dressed-up word problems (Rellensmann and Schukajlow, 2017; Krawitz and Schukajlow, 2018). In this meta-analysis, intra-mathematical problems appeared to be purely mathematical tasks and could not lead to any reality-related mental activities. In contrast, dressed-up word problems are more common in daily life and may require more cognitive resources. Students may have to identify missing or useful information, “undress” the problems, and experience the process of mathematization.
In this meta-analysis, we found that two kinds of mathematical problems were both positively related to WM and the types of MPS indeed moderated the relationship. Furthermore, dressed-up word problems showed stronger links than intra-mathematical problems (r = 0.309 for dressed-up word problems). Additionally, the results of the multiple moderator model indicated similar results. Taken together, these findings imply that cognitive processes drive the relationship between WM and MPS, and highlight their important roles. Understanding the problem situations and translating them into a mathematical model might draw upon significant WM resources. Currently, problem solving is no longer thought of as solving pure mathematical problems (Holmes et al., 2017; Priemer et al., 2020). Recent developments in science, technology, engineering, and mathematics (STEM) and project-based learning place a strong emphasis on 21st-century skills, such as solving problems in reality (Markham et al., 2003; Chen and Yang, 2019; Priemer et al., 2020). As mathematical educators, we also expect students to apply math to real-life scenarios. Students are required to practice solving more reality-related problems, such as ill-structured problems (e.g., Jäder et al., 2017), rather than intra-mathematical problems, thus they also need more regulation of cognition and experience more complex processes. Based on such a trend, WM may play a larger role in identifying valuable information, organizing, and monitoring total performance, and rethinking outcomes in real life.
Regarding WM, we found that the relationship between MPS and WM is indeed affected by components of WM, and the central executive function indicated the strongest relationship with MPS, whereas the phonological loop had the weakest relationship (r = 0.303 for the central executive, r = 0.248 for the phonological loop, and r = 0.265 for the visuospatial sketchpad). Given the variety of WM tests, we also found that each WM test-MPS relationship was well documented and the tests measuring operations showed stronger links than other types. Previous studies have demonstrated that WM tests measure both cognitive abilities and other skills (e.g., counting numbers) according to how the construct was conducted and assessors always use the tool relating best to their criterion of interest (Perlow and Jattuso, 2018). However, the results show that practitioners should pay more attention to cognitive characteristics or relationship between WM tests and other constructs. Besides, several cognitive processes of the executive system might influence WM in MPS, such as controlling, encoding, and retrieval strategies, and suppressing unnecessary information (Miyake et al., 2000; Oberauer et al., 2003). Multiple moderator model analyses also proved that the central executive function showed a stronger relationship than the other two components. Taken together, students need to better master how to organize the entire MPS process. To promote students’ performance in MPS, training the central executive function would be a powerful strategy. As mentioned earlier, because problem solving integrates information from different branches of math, students may need to have a solid command of switching strategies flexibly, and the relationship between WM and MPS should be invariant.
Although gender ratio showed significance, its moderating effects were not robust after controlling for other factors. School level and other participant characteristics did not moderate the relationship between WM and MPS either. Rooted in the idea that cognitive universals exist in this relationship, we claimed that the contributions made here have wide applicability. Additionally, although the school level had a non-significant moderation effect, students at higher school levels showed a larger relationship (0.349 > 0.274 > 0.273). Young students always rely on some basic problem solving strategies such as finger counting to solve mathematical problems at the beginning of formal schooling (Ramirez et al., 2016; Palmer and van Bommel, 2020). By practicing these strategies, they develop strong problem–answer associations. Thus, when they grow up and use more advanced problem solving strategies, they rely heavily on memory-based processes (Siegler and Shrager, 1984; Laski et al., 2013). Another possible reason is due to the different developing patterns among the three components of WM. Studies focusing on working memory have found that the central executive matures later (Palmer, 2000; Muñoz-Pradas et al., 2021), which provides a plausible explanation for our finding. However, the current research still pays insufficient attention to the relationship between WM and MPS in high school students. We recommend additional research to focus on the relationship in senior grades, and apply lab-based findings to actual situations (Cui and Guo, 2022). Clearly, our meta-analysis synthesized research from multiple sources and obtained relatively more reliable conclusions than a single study, thus to some extent making up for the current deficiencies. A greater focus on that could produce interesting findings that develop a deeper understanding of the relationships between WM and MPS.
Our study has some limitations. Although we searched for unpublished papers, this might be a problem for the current study, with a bias toward significant effects. Thus, although funnel plot analyses and Egger’s test confirmed that publication bias was probably not a major problem in this study, we may have missed studies that reported non-significant results. Besides, we acknowledge that some of the categories in the moderator analyses did not include many studies. For instance, when investigating the role of school level/grade in the relationship, we had only three students in high school and four in middle school. This may have influenced the chances of finding significant differences. Third, we did not examine the relationship between problem solving and WM. The reason for this circumstance is that primary studies rarely report on the relationship between WM and each process, such as identifying information. Hence, we strongly recommend that future empirical research about this relationship pay more attention to the specific process of MPS. This would allow researchers to further explain how WM is related to MPS. Finally, we did not control for the role of instruction in the relationship between WM and MPS. Previous studies indicate that students’ MPS competency can be improved through training and practice (Witt, 2011). Different forms of instruction can alter the cognitive processes involved in specific problems.
In summary, the present meta-analysis applied a three-level, meta-analytic model to quantitatively synthesize the overall association between WM and MPS. The manuscript, therefore, adds to a growing body of research on the role of WM (e.g., Reber and Kotovsky, 1997; Justicia-Galiano et al., 2017). Therefore, all evidence supports the significantly positive correlation between WM and MPS, suggesting that there are benefits if we develop students’ WM abilities, which are linked to mathematical performance. Subsequent moderator analyses demonstrated some significant moderators that could explain differences in the strength of the relationship, namely publication characteristics and the task type of WM, as well as MPS. These results have direct implications for instruction and interventions in programming. However, this meta-analysis also underscores areas for future research, including processes of MPS and specific populations [e.g., students with math-related disabilities, which may have significant benefits in terms of mathematical cognition (Geary et al., 2005)].
Data availability statement
The original contributions presented in this study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
KG collected and organized the data and critically reviewed and revised the manuscript. ZJ performed the statistical analysis. KG and ZJ wrote the original draft. Both authors contributed to the manuscript revision and approved the submitted version.
Funding
This study was supported by a grant from the National Social Science Fund of China (CHA180266).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fpsyg.2023.1091126/full#supplementary-material
References
Ambrus, A., and Barczi-Veres, K. (2016). “Teaching mathematical problem solving in Hungary for students who have average ability in mathematics,” in Posing and Solving Mathematical Problems. Research in Mathematics Education, eds P. Felmer, E. Pehkonen, and J. Kilpatrick (Cham: Springer), 137–156. doi: 10.1007/978-3-319-28023-3_9
*Anderisson, U. (2007). The contribution of working memory to children’s mathematical word problem solving. Appl. Cognit. Psychol. 21, 1201–1216. doi: 10.1002/acp.1317
*Andersson, U. (2008a). Mathematical competencies in children with different types of learning difficulties. J. Educ. Psychol. 100:48. doi: 10.1037/0022-0663.100.1.48
*Andersson, U. (2008b). Working memory as a predictor of written arithmetical skills in children: the importance of central executive functions. Br. J. Educ. Psychol. 78, 181–203. doi: 10.1348/000709907X209854
*Andersson, U. (2010). Skill development in different components of arithmetic and basic cognitive functions: findings from a 3-year longitudinal study of children with different types of learning difficulties. J. Educ. Psychol. 102, 115–134. doi: 10.1037/a0016838
*Andersson, U., and Lyxell, B. (2007). Working memory deficit in children with mathematical difficulties: a general or specific deficit? J. Exp. Child Psychol. 96, 197–228. doi: 10.1016/j.jecp.2006.10.001
*Aran Filippetti, V., and Cristina Richaud, M. (2017). A structural equation modeling of executive functions, IQ and mathematical skills in primary students: differential effects on number production, mental calculus and arithmetical problems. Child Neuropsychol. 23, 864–888. doi: 10.1080/09297049.2016.1199665
*Ashkenazi, S., Rosenberg-Lee, M., Metcalfe, A. W. S., Swigart, A. G., and Menon, V. (2013). Visuo-spatial working memory is an important source of domain-general vulnerability in the development of arithmetic cognition. Neuropsychologia 51, 2305–2317. doi: 10.1016/j.neuropsychologia.2013.06.031
Assink, M., and Wibbelink, C. J. (2016). Fitting three-level meta-analytic models in R: a step-by-step tutorial. Quant. Methods Psychol. 12, 154–174. doi: 10.20982/tqmp.12.3.p154
*Attout, L., and Majerus, S. (2015). Working memory deficits in developmental dyscalculia: the importance of serial order. Child Neuropsychol. 21, 432–450. doi: 10.1080/09297049.2014.922170
*Attout, L., Noel, M.-P., and Majerus, S. (2014). The relationship between working memory for serial order and numerical development: a longitudinal study. Dev. Psychol. 50, 1667–1679. doi: 10.1037/a0036496
Ayres, P. L. (2001). Systematic mathematical errors and cognitive load. Contemp. Educ. Psychol. 26, 227–248. doi: 10.1006/ceps.2000.1051
Baddeley, A. (2003). Working memory: looking back and looking forward. Nat. Rev. Neurosci. 4, 829–839. doi: 10.1038/nrn1201
Baddeley, A. D., and Hitch, G. (1974). “Working memory,” in Psychology of Learning and Motivation, Vol. 8, ed. K. Federmeier (Cambridge, MA: Academic press), 47–89. doi: 10.1016/S0079-7421(08)60452-1
*Bahar, A., and Maker, C. J. (2015). Cognitive backgrounds of problem solving: a comparison of open-ended vs. closed mathematics problems. Eurasia J. Math. Sci. Technol. Educ. 11, 1531–1546. doi: 10.12973/eurasia.2015.1410a
*Bailey, D. H., Littlefield, A., and Geary, D. C. (2012). The codevelopment of skill at and preference for use of retrieval-based processes for solving addition problems: individual and sex differences from first to sixth grades. J. Exp. Child Psychol. 113, 78–92. doi: 10.1016/j.jecp.2012.04.014
*Barnes, M. A., Raghubar, K. P., English, L., Williams, J. M., Taylor, H., and Landry, S. (2014). Longitudinal mediators of achievement in mathematics and reading in typical and atypical development. J. Exp. Child Psychol. 119, 1–16. doi: 10.1016/j.jecp.2013.09.006
*Berg, D. H. (2008). Working memory and arithmetic calculation in children: the contributory roles of processing speed, short-term memory, and reading. J. Exp. Child Psychol. 99, 288–308. doi: 10.1016/j.jecp.2007.12.002
*Bizzaro, M., Giofre, D., Girelli, L., and Cornoldi, C. (2018). Arithmetic, working memory, and visuospatial imagery abilities in children with poor geometric learning. Learn. Individ. Differ. 62, 79–88. doi: 10.1016/j.lindif.2018.01.013
Blum, W. (2015). “Quality teaching of mathematical modelling: what do we know, what can we do?,” in The Proceedings of the 12th international congress on mathematical education, (Cham: Springer), 73–96. doi: 10.1007/978-3-319-12688-3_9
Blum, W., Galbraith, P. L., Henn, H. W., and Niss, M. (2007). Modelling and Applications in Mathematics Education: The 14th ICMI Study. Boston, MA: Springer. doi: 10.1007/978-0-387-29822-1
Borenstein, M., Cooper, H., Hedges, L., and Valentine, J. (2009). Effect sizes for continuous data. Handb. Res. Synth. Meta Anal. 2, 221–235.
Borenstein, M., Hedges, L. V., Higgins, J. P., and Rothstein, H. R. (2021). Introduction to Meta-Analysis. New York, NY: John Wiley & Sons. doi: 10.1002/9781119558378
*Bresgi, L., Alexander, D. L. M., and Seabi, J. (2017). The predictive relationships between working memory skills within the spatial and verbal domains and mathematical performance of Grade 2 South African learners. Int. J. Educ. Res. 81, 1–10. doi: 10.1016/j.ijer.2016.10.004
*Bullen, J. C., Swain Lerro, L., Zajic, M., McIntyre, N., and Mundy, P. (2020). A developmental study of mathematics in children with autism spectrum disorder, symptoms of attention deficit hyperactivity disorder, or typical development. J. Autism Dev. Disord. 50, 4463–4476. doi: 10.1007/s10803-020-04500-9
*Cai, D., Georgiou, G. K., Wen, M., and Das, J. P. (2016). The role of planning in different mathematical skills. J. Cognit. Psychol. 28, 234–241. doi: 10.1080/20445911.2015.1103742
Card, N. A. (2015). Applied Meta-Analysis for Social Science Research. New York, NY: Guilford Publications.
*Caviola, S., Mammarella, I. C., Lucangeli, D., and Cornoldi, C. (2014). Working memory and domain-specific precursors predicting success in learning written subtraction problems. Learn. Individ. Differ. 36, 92–100. doi: 10.1016/j.lindif.2014.10.010
*Chan, B. M.-Y., and Ho, C. S. (2010). The cognitive profile of Chinese children with mathematics difficulties. J. Exp. Child Psychol. 107, 260–279. doi: 10.1016/j.jecp.2010.04.016
*Chan, W. W. L., and Wong, T. T.-Y. (2019). Visuospatial pathways to mathematical achievement. Learn. Instruct. 62, 11–19. doi: 10.1016/j.learninstruc.2019.03.001
Chen, C. H., and Yang, Y. C. (2019). Revisiting the effects of project-based learning on students’ academic achievement: a meta-analysis investigating moderators. Educ. Res. Rev. 26, 71–81. doi: 10.1016/j.edurev.2018.11.001
Cheung, M. W. L. (2014). Modeling dependent effect sizes with three-level meta-analyses: a structural equation modeling approach. Psychol. Methods 19:211. doi: 10.1037/a0032968
*Ching, B. H. H. (2017). Mathematics anxiety and working memory: longitudinal associations with mathematical performance in Chinese children. Contemp. Educ. Psychol. 51, 99–113. doi: 10.1016/j.cedpsych.2017.06.006
*Cormier, D. C., Bulut, O., McGrew, K. S., and Singh, D. (2017). Exploring the relations between Cattell–Horn–Carroll (CHC) cognitive abilities and mathematics achievement. Appl. Cognit. Psychol. 31, 530–538. doi: 10.1002/acp.3350
*Cornoldi, C., Carretti, B., Drusi, S., and Tencati, C. (2015). Improving problem solving in primary school students: the effect of a training programme focusing on metacognition and working memory. Br. J. Educ. Psychol. 85, 424–439. doi: 10.1111/bjep.12083
*Costa, A. J., Lopes Silva, J. B., Chagas, P. P., Krinzinger, H., Lonneman, J., Willmes, K., et al. (2011). A hand full of numbers: a role for offloading in arithmetics learning? Front. Psychol. 2:368. doi: 10.3389/fpsyg.2011.00368
Cui, X., and Guo, K. (2022). Supporting mathematics learning: a review of spatial abilities from research to practice. Curr. Opin. Behav. Sci. 46:101176. doi: 10.1016/j.cobeha.2022.101176
*De Smedt, B., Swillen, A., Devriendt, K., Fryns, J.-P., Verschaffel, L., Boets, B., et al. (2008). Cognitive correlates of mathematical disabilities in children with velo-cardio-facial syndrome. Genetic Counsel. 19, 71–94.
*De Smedt, B., Taylor, J., Archibald, L., and Ansari, D. (2010). How is phonological processing related to individual differences in children’s arithmetic skills? Dev. Sci. 13, 508–520. doi: 10.1111/j.1467-7687.2009.00897.x
*Dong, Y. (2003). Gongzuo jiyi Wenti Biaozheng Fangshi dui Xiaoxuesheng Shuxue Wenti Jiejue Yingxiang de yanjiu [Research on the influence of working memory and problem representation on pupils’ mathematical problem solving]. Changchun: Dongbei shifan daxue.
*Dube, A. K., and Robinson, K. M. (2010). Accounting for individual variability in inversion shortcut use. Learn. Individ. Differ. 20, 687–693. doi: 10.1016/j.lindif.2010.09.009
Egger, M., Smith, G. D., Schneider, M., and Minder, C. (1997). Bias in meta-analysis detected by a simple, graphical test. Bmj 315, 629–634. doi: 10.1136/bmj.315.7109.629
*Fanari, R., Meloni, C., and Massidda, D. (2019). Visual and spatial working memory abilities predict early math skills: a longitudinal study. Front. Psychol. 10:2460. doi: 10.3389/fpsyg.2019.02460
Felmer, P. L., Pehkonen, E., and Kilpatrick, J. (2016). Posing and Solving Mathematical Problems. Suiza: Springer International Publishing. doi: 10.1007/978-3-319-28023-3
Fernández-Castilla, B., Jamshidi, L., Declercq, L., Beretvas, S. N., Onghena, P., and Van den Noortgate, W. (2020). The application of meta-analytic (multi-level) models with multiple random effects: a systematic review. Behav. Res. Methods 52, 2031–2052. doi: 10.3758/s13428-020-01373-9
*Foley, A. E., Vasilyeva, M., and Laski, E. V. (2017). Children’s use of decomposition strategies mediates the visuospatial memory and arithmetic accuracy relation. Br. J. Dev. Psychol. 35, 303–309. doi: 10.1111/bjdp.12166
*Friedman, L. M., Rapport, M. D., Orban, S. A., Eckrich, S. J., and Calub, C. A. (2018). Applied problem solving in children with ADHD: the mediating roles of working memory and mathematical calculation. J. Abnormal Child Psychol. 46, 491–504. doi: 10.1007/s10802-017-0312-7
*Friedman, S. L., Scholnick, E. K., Bender, R. H., Vandergrift, N., Spieker, S., Pasek, K. H., et al. (2014). Planning in middle childhood: early predictors and later outcomes. Child Dev. 85, 1446–1460. doi: 10.1111/cdev.12221
*Fuchs, L., Fuchs, D., Compton, D., Powell, S., Seethaler, P., Capizzi, A., et al. (2006). The cognitive correlates of third-grade skill in arithmetic, algorithmic computation, and arithmetic word problems. J. Educ. Psychol. 98, 29–43. doi: 10.1037/0022-0663.98.1.29
*Fuchs, L. S., Compton, D. L., Fuchs, D., Powell, S. R., Schumacher, R. F., Hamlett, C. L., et al. (2012). Contributions of domain-general cognitive resources and different forms of arithmetic development to pre-algebraic knowledge. Dev. Psychol. 48, 1315–1326. doi: 10.1037/a0027475
*Fuchs, L. S., Fuchs, D., Compton, D. L., Hamlett, C. L., and Wang, A. Y. (2015). Is word-problem solving a form of text comprehension? Sci. Stud. Read. 19, 204–223. doi: 10.1080/10888438.2015.1005745
*Fuchs, L. S., Fuchs, D., Stuebing, K., Fletcher, J. M., Hamlett, C. L., and Lambert, W. (2008). Problem solving and computational skill: Are they shared or distinct aspects of mathematical cognition? J. Educ. Psychol. 100, 30–47. doi: 10.1037/0022-0663.100.1.30
*Fuchs, L. S., Geary, D. C., Compton, D. L., Fuchs, D., Hamlett, C. L., Seethaler, P. M., et al. (2010). Do different types of school mathematics development depend on different constellations of numerical versus general cognitive abilities? Dev. Psychol. 46, 1731–1746. doi: 10.1037/a0020662
*Fuchs, L. S., Gilbert, J. K., Fuchs, D., Seethaler, P. M., and Martin, B. N. (2018). Text comprehension and oral language as predictors of word-problem solving: insights into word-problem solving as a form of text comprehension. Sci. Stud. Read. 22, 152–166. doi: 10.1080/10888438.2017.1398259
*Fuchs, L. S., Gilbert, J. K., Powell, S. R., Cirino, P. T., Fuchs, D., Hamlett, C. L., et al. (2016). The role of cognitive processes, foundational math skill, and calculation accuracy and fluency in word-problem solving versus prealgebraic knowledge. Dev. Psychol. 52, 2085–2098. doi: 10.1037/dev0000227
*Fuchs, L. S., Powell, S. R., Fall, A. M., Roberts, G., Cirino, P., Fuchs, D., et al. (2020). Do the processes engaged during mathematical word-problem solving differ along the distribution of word-problem competence? Contemp. Educ. Psychol. 60:101811. doi: 10.1016/j.cedpsych.2019.101811
*Gathercole, S., Alloway, T., Willis, C., and Adams, A. (2006). Working memory in children with reading disabilities. J. Exp. Child Psychol. 93, 265–281. doi: 10.1016/j.jecp.2005.08.003
*Geary, D. C. (2011). Cognitive predictors of achievement growth in mathematics: a 5-year longitudinal study. Dev. Psychol. 47, 1539–1552. doi: 10.1037/a0025510
Geary, D. C., Hoard, M. K., and Campbell, J. I. D. (2005). The Handbook of Mathematical Cognition. New York, NY: Psychology Press.
Georgiou, G. K., Guo, K., Naveenkumar, N., Vieira, A. P. A., and Das, J. P. (2020). PASS theory of intelligence and academic achievement: a meta-analytic review. Intelligence 79:101431. doi: 10.1016/j.intell.2020.101431
*Giofre, D., Mammarella, I. C., and Cornoldi, C. (2014). The relationship among geometry, working memory, and intelligence in children. J. Exp. Child Psychol. 123, 112–128. doi: 10.1016/j.jecp.2014.01.002
*Greiner de Magalhaes, C., Mervis, C. B., and Cardoso-Martins, C. (2021). Cognitive predictors of arithmetic, reading, and spelling in Brazilian Portuguese-speaking children. Read. Writ. 34, 171–198. doi: 10.1007/s11145-020-10062-0
*Hajibaba, M., Farzad, R., and Hassan, A. (2013). A psychological model for mathematical problem solving based on revised bloom taxonomy for high school girl students. Res. Math. Educ. 17, 199–220. doi: 10.7468/jksmed.2013.17.3.199
*Hale, J., Fiorello, C., Bertin, M., and Sherman, R. (2003). Predicting math achievement through neuropsychological interpretation of WISC-III variance components. J. Psychoeduc. Assess. 21, 358–380. doi: 10.1177/073428290302100404
*Hecht, S., Torgesen, J., Wagner, R., and Rashotte, C. (2001). The relations between phonological processing abilities and emerging individual differences in mathematical computation skills: a longitudinal study from second to fifth grades. J. Exp. Child Psychol. 79, 192–227. doi: 10.1006/jecp.2000.2586
*Hecht, S. A., Close, L., and Santisi, M. (2003). Sources of individual differences in fraction skills. J. Exp. Child Psychol. 86, 277–302. doi: 10.1016/j.jecp.2003.08.003
Hedges, L. V., and Olkin, I. (2014). Statistical Methods for Meta-Analysis. Cambridge, MA: Academic press.
Herbst, P. (2019). “Geometric modeling tasks and opportunity to learn geometry: the ranking triangles task revisited,” in Problem Solving in Mathematics Instruction and Teacher Professional Development, eds P. Felmer, P. Liljedahl, and B. Koichu (Cham: Springer), 123–143. doi: 10.1007/978-3-030-29215-7_7
Holmes, S. D., He, Q., and Meadows, M. (2017). An investigation of construct relevant and irrelevant features of mathematics problem-solving questions using comparative judgement and Kelly’s repertory grid. Res. Math. Educ. 19, 112–129. doi: 10.1080/14794802.2017.1334576
Hox, J. J., Moerbeek, M., and Van de Schoot, R. (2017). Multilevel Analysis: Techniques and Applications. London: Routledge. doi: 10.4324/9781315650982
Hu, Y., Wu, B., and Gu, X. (2017). An eye tracking study of high-and low-performing students in solving interactive and analytical problems. J. Educ. Technol. Soc. 20, 300–311.
*Huijsmans, M. D. E., Kleemans, T., van der Ven, S. H. G., and Kroesbergen, E. H. (2020). The relevance of subtyping children with mathematical learning disabilities. Res. Dev. Disabil. 104:103704. doi: 10.1016/j.ridd.2020.103704
*Iglesias-Sarmiento, V., Carriedo Lopez, N., and Rodriguez Rodriguez, J. L. (2015). Updating executive function and performance in reading comprehension and problem solving. Anal. Psicol. 31, 298–309. doi: 10.6018/analesps.31.1.158111
*Imbo, I., and Vandierendonck, A. (2007). The development of strategy use in elementary school children: working memory and individual differences. J. Exp. Child Psychol. 96, 284–309. doi: 10.1016/j.jecp.2006.09.001
Jäder, J., Sidenvall, J., and Sumpter, L. (2017). Students’ mathematical reasoning and beliefs in non-routine task solving. Int. J. Sci. Math. Educ. 15, 759–776. doi: 10.1007/s10763-016-9712-3
*Jansen, B. R. J., De lange, E., and Van der Molen, M. J. (2013). Math practice and its influence on math skills and executive functions in adolescents with mild to borderline intellectual disability. Res. Dev. Disabil. 34, 1815–1824. doi: 10.1016/j.ridd.2013.02.022
*Jenks, K. M., van Lieshout, E. C., and de Moor, J. M. (2012). Cognitive correlates of mathematical achievement in children with cerebral palsy and typically developing children. Br. J. Educ. Psychol. 82, 120–135. doi: 10.1111/j.2044-8279.2011.02034.x
Jitendra, A. K., Sczesniak, E., and Deatline-Buchman, A. (2005). An exploratory validation of curriculum-based mathematical word problem-solving tasks as indicators of mathematics proficiency for third graders. Sch. Psychol. Rev. 34, 358–371. doi: 10.1080/02796015.2005.12086291
*Jogi, A.-L., and Kikas, E. (2016). Calculation and word problem-solving skills in primary grades—Impact of cognitive abilities and longitudinal interrelations with task-persistent behaviour. Br. J. Educ. Psychol. 86, 165–181. doi: 10.1111/bjep.12096
*Jordan, N. C., Glutting, J., and Ramineni, C. (2010). The importance of number sense to mathematics achievement in first and third grades. Learn. Individ. Differ. 20, 82–88. doi: 10.1016/j.lindif.2009.07.004
*Jordan, N. C., Hansen, N., Fuchs, L. S., Siegler, R. S., Gersten, R., and Micklos, D. (2013). Developmental predictors of fraction concepts and procedures. J. Exp. Child Psychol. 116, 45–58. doi: 10.1016/j.jecp.2013.02.001
*Justicia-Galiano, M. J., Martín-Puga, M. E., Linares, R., and Pelegrina, S. (2017). Math anxiety and math performance in children: the mediating roles of working memory and math self-concept. Br. J. Educ. Psychol. 87, 573–589. doi: 10.1111/bjep.12165
*Keeler, M., and Swanson, H. (2001). Does strategy knowledge influence working memory in children with mathematical disabilities? J. Learn. Disabil. 34, 418–434. doi: 10.1177/002221940103400504
*Khng, K. H., and Lee, K. (2009). Inhibiting interference from prior knowledge: arithmetic intrusions in algebra word problem solving. Learn. Individ. Differ. 19, 262–268. doi: 10.1016/j.lindif.2009.01.004
*Kleemans, T., Segers, E., and Verhoeven, L. (2018). Role of linguistic skills in fifth-grade mathematics. J. Exp. Child Psychol. 167, 404–413. doi: 10.1016/j.jecp.2017.11.012
*Korhonen, J., Nyroos, M., Jonsson, B., and Eklöf, H. (2018). Additive and multiplicative effects of working memory and test anxiety on mathematics performance in grade 3 students. Educ. Psychol. 38, 572–595. doi: 10.1080/01443410.2017.1356449
Krawitz, J., and Schukajlow, S. (2018). Do students value modelling problems, and are they confident they can solve such problems? Value and self-efficacy for modelling, word, and intra-mathematical problems. Zdm 50, 143–157. doi: 10.1007/s11858-017-0893-1
Laski, E. V., Casey, B. M., Yu, Q., Dulaney, A., Heyman, M., and Dearing, E. (2013). Spatial skills as a predictor of first grade girls’ use of higher level arithmetic strategies. Learn. Individ. Differ. 23, 123–130. doi: 10.1016/j.lindif.2012.08.001
Lawson, M. J. (2003). Problem solving. Netherlands: Springer, 511–524. doi: 10.1007/978-94-017-3368-7_35
*Lee, K., Ng, E. L., and Ng, S. F. (2009). The contributions of working memory and executive functioning to problem representation and solution generation in algebraic word problems. J. Educ. Psychol. 101, 373–387. doi: 10.1037/a0013843
*Lee, K., Ng, S., Ng, E., and Lim, Z. (2004). Working memory and literacy as predictors of performance on algebraic word problems. J. Exp. Child Psychol. 89, 140–158. doi: 10.1016/j.jecp.2004.07.001
*Lee, K., Ng, S. F., Bull, R., Pe, M. L., and Ho, R. H. M. (2011). Are patterns important? An investigation of the relationships between proficiencies in patterns, computation, executive functioning, and algebraic word problems. J. Educ. Psychol. 103, 269–281. doi: 10.1037/a0023068
*Lee, K., and Peh, Y. X. (2008). Differences in working memory profiles amongst children with low versus average academic performances. Int. J. Creat. Prob. Solv. 18, 21–33.
*LeFevre, J.-A., Berrigan, L., Vendetti, C., Kamawar, D., Bisanz, J., Skwarchuk, S.-L., et al. (2013). The role of executive attention in the acquisition of mathematical skills for children in Grades 2 through 4. J. Exp. Child Psychol. 114, 243–261. doi: 10.1016/j.jecp.2012.10.005
Lenhard, W., and Lenhard, A. (2016). Computation of Effect Sizes. Available online at: https://www.psychometrica.de/effect_size.html (accessed October 27, 2019).
*Li, X. D., Nie, Y. Y., Pang, A. L., and Lin, C. D. (2003). Gongzuo jiyi dui xiaoxue sannianji xuesheng jiejue bijiao wenti de yingxiang[The effects of working memory on performance of third grade solving compare problems]. Xinli Fazhan yu Jiaoyu 3, 41–45.
*Li, Y., and Geary, D. C. (2013). Developmental gains in visuospatial memory predict gains in mathematics achievement. PLoS One 8:e70160. doi: 10.1371/journal.pone.0070160
*Liu, Y. Q. (2019). Sannianji Xiaoxuesheng Zhixing Gongneng Yu Shuxue Wenti Jiejue de Guanxi Jiqi Cujin Yanjiu [The Relation between the Executive Function of the Third Grade Pupils and Mathematical Problems Solving and Promoting Research]. Baoding: Hebei University.
Ludwig, C., Guo, K., and Georgiou, G. K. (2019). Are reading interventions for English language learners effective? A meta-analysis. J. Learn. Disabil. 52, 220–231. doi: 10.1177/0022219419825855
*Lukowski, S. L., Soden, B., Hart, S. A., Thompson, L. A., Kovas, Y., and Petrill, S. A. (2014). Etiological distinction of working memory components in relation to mathematics. Intelligence 47, 54–62. doi: 10.1016/j.intell.2014.09.001
*Mabbott, D. J., and Bisanz, J. (2008). Computational skills, working memory, and conceptual knowledge in older children with mathematics learning disabilities. J. Learn. Disabil. 41, 15–28. doi: 10.1177/0022219407311003
*Maennamaa, M., Kikas, E., Peets, K., and Palu, A. (2012). Cognitive correlates of math skills in third-grade students. Educ. Psychol. 32, 21–44. doi: 10.1080/01443410.2011.621713
Mammarella, I. C., Todeschini, M., Englaro, G., and Lucangeli Cornoldi, C. (2012). Geometria test [Test of geometry]. Trento: Erickson.
Markham, T., Larmer, J., and Ravitz, J. L. (2003). Project Based Learning Handbook: A Guide to Standards-Focused Project Based Learning for Middle and High School Teachers. Novato, CA: Buck Institute for Education.
*Matejko, A. A., and Ansari, D. (2017). How do individual differences in children’s domain specific and domain general abilities relate to brain activity within the intraparietal sulcus during arithmetic? An fMRI study. Hum. Brain Mapp. 38, 3941–3956. doi: 10.1002/hbm.23640
*Metcalfe, A. W., Ashkenazi, S., Rosenberg-Lee, M., and Menon, V. (2013). Fractionating the neural correlates of individual working memory components underlying arithmetic problem solving skills in children. Dev. Cognit. Neurosci. 6, 162–175. doi: 10.1016/j.dcn.2013.10.001
*Meyer, M. L., Salimpoor, V. N., Wu, S. S., Geary, D. C., and Menon, V. (2010). Differential contribution of specific working memory components to mathematics achievement in 2nd and 3rd graders. Learn. Individ. Differ. 20, 101–109. doi: 10.1016/j.lindif.2009.08.004
Miyake, A., Friedman, N. P., Emerson, M. J., Witzki, A. H., Howerter, A., and Wager, T. D. (2000). The unity and diversity of executive functions and their contributions to complex “frontal lobe” tasks: a latent variable analysis. Cognit. Psychol. 41, 49–100. doi: 10.1006/cogp.1999.0734
Muñoz-Pradas, R., Díaz-Palacios, M., Rodriguez-Martínez, E. I., and Gómez, C. M. (2021). Order of maturation of the components of the working memory from childhood to emerging adulthood. Curr. Res. Behav. Sci. 2:100062. doi: 10.1016/j.crbeha.2021.100062
*Navarro, J. I., Aguilar, M., Alcalde, C., Ruiz, G., Marchena, E., and Menacho, I. (2011). Inhibitory processes, working memory, phonological awareness, naming speed, and early arithmetic achievement. Span. J. Psychol. 14, 580–588. doi: 10.5209/rev_SJOP.2011.v14.n2.6
*Ng, J., Lee, K., and Khng, K. H. (2017). Irrelevant information in math problems need not be inhibited: students might just need to spot them. Learn. Individ. Differ. 60, 46–55. doi: 10.1016/j.lindif.2017.09.008
*Nunes, T., Bryant, P., Barros, R., and Sylva, K. (2012). The relative importance of two different mathematical abilities to mathematical achievement. Br. J. Educ. Psychol. 82, 136–156. doi: 10.1111/j.2044-8279.2011.02033.x
Oberauer, K., Süß, H. M., Wilhelm, O., and Wittman, W. W. (2003). The multiple faces of working memory: storage, processing, supervision, and coordination. Intelligence 31, 167–193. doi: 10.1016/S0160-2896(02)00115-0
Palmer, H., and van Bommel, J. (2020). Young students posing problem-solving tasks: what does posing a similar task imply to students? Zdm Math. Educ. 52, 743–752. doi: 10.1007/s11858-020-01129-x
Palmer, S. (2000). Working memory: a developmental study of phonological recoding. Memory 8, 179–193. doi: 10.1080/096582100387597
*Passolunghi, M. C., Cargnelutti, E., and Pastore, M. (2014). The contribution of general cognitive abilities and approximate number system to early mathematics. Br. J. Educ. Psychol. 84, 631–649. doi: 10.1111/bjep.12054
*Passolunghi, M. C., Cargnelutti, E., and Pellizzoni, S. (2019). The relation between cognitive and emotional factors and arithmetic problem-solving. Educ. Stud. Math. 100, 271–290. doi: 10.1007/s10649-018-9863-y
*Passolunghi, M. C., and Mammarella, I. C. (2010). Spatial and visual working memory ability in children with difficulties in arithmetic word problem solving. Eur. J. Cognit. Psychol. 22, 944–963. doi: 10.1080/09541440903091127
*Passolunghi, M. C., Mammarella, I. C., and Altoe, G. (2008). Cognitive abilities as precursors of the early acquisition of mathematical skills during first through second grades. Dev. Neuropsychol. 33, 229–250. doi: 10.1080/87565640801982320
*Paul, J. M., Gray, S. A., Butterworth, B. L., and Reeve, R. A. (2019). Reading and math tests differentially predict number transcoding and number fact speed longitudinally: a random intercept cross-lagged panel approach. J. Educ. Psychol. 111, 299–313. doi: 10.1037/edu0000287
Peng, P., Namkung, J., Barnes, M., and Sun, C. (2016). A meta-analysis of mathematics and working memory: moderating effects of working memory domain, type of mathematics skill, and sample characteristics. J. Educ. Psychol. 108, 455–473. doi: 10.1037/edu0000079
Perlow, R., and Jattuso, M. (2018). A comparison of computation span and reading span working memory measures’ relations with problem-solving criteria. Psychol. Rep. 121, 430–444. doi: 10.1177/0033294117729183
Pongsakdi, N., Kajamies, A., Veermans, K., Lertola, K., Vauras, M., and Lehtinen, E. (2020). What makes mathematical word problem solving challenging? Exploring the roles of word problem characteristics, text comprehension, and arithmetic skills. ZDM 52, 33–44. doi: 10.1007/s11858-019-01118-9
Popham, M., Adams, S., and Hodge, J. (2020). Self-regulated strategy development to teach mathematics problem solving. Intervent. Sch. Clin. 55, 154–161. doi: 10.1177/1053451219842197
Priemer, B., Eilerts, K., Filler, A., Pinkwart, N., Rösken-Winter, B., Tiemann, R., et al. (2020). A framework to foster problem-solving in STEM and computing education. Res. Sci. Technol. Educ. 38, 105–130. doi: 10.1080/02635143.2019.1600490
*Ramirez, G., Chang, H., Maloney, E. A., Levine, S. C., and Beilock, S. L. (2016). On the relationship between math anxiety and math achievement in early elementary school: the role of problem solving strategies. J. Exp. Child Psychol. 141, 83–100. doi: 10.1016/j.jecp.2015.07.014
Ran, G., Li, J., Zhang, Q., and Niu, X. (2022). The association between social anxiety and mobile phone addiction: a three-level meta-analysis. Comput. Hum. Behav. 130:107198. doi: 10.1016/j.chb.2022.107198
Reber, P. J., and Kotovsky, K. (1997). Implicit learning in problem solving: the role of working memory capacity. J. Exp. Psychol. 126:178. doi: 10.1037/0096-3445.126.2.178
*Reeve, R. A., Gray, S. A., Butterworth, B. L., and Paul, J. M. (2018a). Variability in single digit addition problem-solving speed over time identifies typical, delay and deficit math pathways. Front. Psychol. 9:1498. doi: 10.3389/fpsyg.2018.01498
*Reeve, R. A., Reynolds, F., Paul, J., and Butterworth, B. L. (2018b). Culture-independent prerequisites for early arithmetic. Psychol. Sci. 29, 1383–1392. doi: 10.1177/0956797618769893
Rellensmann, J., and Schukajlow, S. (2017). Does students’ interest in a mathematical problem depend on the problem’s connection to reality? An analysis of students’ interest and pre-service teachers’ judgments of students’ interest in problems with and without a connection to reality. ZDM 49, 367–378. doi: 10.1007/s11858-016-0819-3
*Rennie, B., Beebe-Frankenberger, M., and Swanson, H. L. (2014). A longitudinal study of neuropsychological functioning and academic achievement in children with and without signs of attention-deficit/hyperactivity disorder. J. Clin. Exp. Neuropsychol. 36, 621–635. doi: 10.1080/13803395.2014.921284
*Resing, W. C. M., Bakker, M., Pronk, C. M. E., and Elliott, J. G. (2017). Progression paths in children’s problem solving: the influence of dynamic testing, initial variability, and working memory. J. Exp. Child Psychol. 153, 83–109. doi: 10.1016/j.jecp.2016.09.004
Rott, B., Specht, B., and Knipping, C. (2021). A descriptive phase model of problem-solving processes. ZDM Math. Educ. 53, 737–752. doi: 10.1007/s11858-021-01244-3
Schukajlow, S., Leiss, D., Pekrun, R., Blum, W., Müller, M., and Messner, R. (2012). Teaching methods for modelling problems and students’ task-specific enjoyment, value, interest and self-efficacy expectations. Educ. Stud. Math. 79, 215–237. doi: 10.1007/s10649-011-9341-2
*Siegler, R. S., Duncan, G. J., Davis-Kean, P. E., Duckworth, K., Claessens, A., Engel, M., et al. (2012). Early predictors of high school mathematics achievement. Psychol. Sci. 23, 691–697. doi: 10.1177/0956797612440101
Siegler, R. S., and Shrager, J. (1984). “Strategy choices in addition and subtraction: how do children know what to do,” in Origins of Cognitive Skills, ed. C. Sophian (Hillsdale, NJ: Lawrence Erlbaum), 229–293.
*Song, G. W., He, W. G., and Kong, W. (2011). Wenti biaozheng gongzuo jiyi dui xiaoxuesheng shuxue wenti jiejue de yingxiang [Influence of problem representation and working memory span on pupils’ mathematical problem solving]. Xinli Xuebao 11, 1283–1292.
*Spencer, M., Fuchs, L. S., and Fuchs, D. (2020). Language-related longitudinal predictors of arithmetic word problem solving: a structural equation modeling approach. Contemp. Educ. Psychol. 60:101825. doi: 10.1016/j.cedpsych.2019.101825
*St Clair-Thompson, H., and Gathercole, S. (2006). Executive functions and achievements in school: shifting, updating, inhibition, and working memory. Q. J. Exp. Psychol. 59, 745–759. doi: 10.1080/17470210500162854
Star, J. R., and Rittle-Johnson, B. (2008). Flexibility in problem solving: the case of equation solving. Learn. Instruct. 18, 565–579. doi: 10.1016/j.learninstruc.2007.09.018
*Swanson, H. (2004). Working memory and phonological processing as predictors of children’s mathematical problem solving at different ages. Mem. Cognit. 32, 648–661. doi: 10.3758/BF03195856
*Swanson, H., and Beebe-Frankenberger, M. (2004). The relationship between working memory and mathematical problem solving in children at risk and not at risk for serious math difficulties. J. Educ. Psychol. 96, 471–491. doi: 10.1037/0022-0663.96.3.471
*Swanson, H., and Sachse-Lee, C. (2001). Mathematical problem solving and working memory in children with learning disabilities: both executive and phonological processes are important. J. Exp. Child Psychol. 79, 294–321. doi: 10.1006/jecp.2000.2587
*Swanson, H. L (2006a). Cognitive processes that underlie mathematical precociousness in young children. J. Exp. Child Psychol. 93, 239–264. doi: 10.1016/j.jecp.2005.09.006
*Swanson, H. L. (2006b). Cross-sectional and incremental changes in working memory and mathematical problem solving. J. Educ. Psychol. 98, 265–281. doi: 10.1037/0022-0663.98.2.265
*Swanson, H. L., Jerman, O., and Zheng, X. (2008). Growth in working memory and mathematical problem solving in children at risk and not at risk for serious math difficulties. J. Educ. Psychol. 100:343. doi: 10.1037/0022-0663.100.2.343
*Swanson, H. L., Kong, J. E., and Petcu, S. D. (2019). Individual differences in math problem solving and executive processing among emerging bilingual children. J. Exp. Child Psychol. 187:104653. doi: 10.1016/j.jecp.2019.06.006
*Swanson, H. L., Moran, A. S., Bocian, K., Lussier, C., and Zheng, X. (2013). Generative strategies, working memory, and word problem solving accuracy in children at risk for math disabilities. Learn. Disabil. Q. 36, 203–214. doi: 10.1177/0731948712464034
*Swanson, H. L., Orosco, M. J., and Lussier, C. M. (2014). The effects of mathematics strategy instruction for children with serious problem-solving difficulties. Except. Child. 80, 149–168. doi: 10.1177/001440291408000202
*Szucs, D., Devine, A., Soltesz, F., Nobes, A., and Gabriel, F. (2014). Cognitive components of a mathematical processing network in 9-year-old children. Dev. Sci. 17, 506–524. doi: 10.1111/desc.12144
*Tam, Y. P., Wong, T. T.-Y., and Chan, W. W. L. (2019). The relation between spatial skills and mathematical abilities: the mediating role of mental number line representation. Contemp. Educ. Psychol. 56, 14–24. doi: 10.1016/j.cedpsych.2018.10.007
*Tavakoli, H. M. (2016). The relationship between accuracy of numerical magnitude comparisons and children’s arithmetic ability: a study in iranian primary school children. Eur. J. Psychol. 12, 567–583. doi: 10.5964/ejop.v12i4.1175
*Traff, U. (2013). The contribution of general cognitive abilities and number abilities to different aspects of mathematics in children. J. Exp. Child Psychol. 116, 139–156. doi: 10.1016/j.jecp.2013.04.007
*Träff, U., Olsson, L., Skagerlund, K., and Östergren, R. (2018). Cognitive mechanisms underlying third graders’ arithmetic skills: expanding the pathways to mathematics model. J. Exp. Child Psychol. 167, 369–387. doi: 10.1016/j.jecp.2017.11.010
*Träff, U., and Passolunghi, M. C. (2015). Mathematical skills in children with dyslexia. Learn. Individ. Differ. 40, 108–114. doi: 10.1016/j.lindif.2015.03.024
*Trakulphadetkrai, N. V., Courtney, L., Clenton, J., Treffers-Daller, J., and Tsakalaki, A. (2020). The contribution of general language ability, reading comprehension and working memory to mathematics achievement among children with English as additional language (EAL): an exploratory study. Int. J. Biling. Educ. Biling. 23, 473–487. doi: 10.1080/13670050.2017.1373742
*Trezise, K., and Reeve, R. A. (2014a). Working memory, worry, and algebraic ability. J. Exp. Child Psychol. 121, 120–136. doi: 10.1016/j.jecp.2013.12.001
*Trezise, K., and Reeve, R. A. (2014b). Cognition-emotion interactions: patterns of change and implications for math problem solving. Front. Psychol. 5:840. doi: 10.3389/fpsyg.2014.00840
Van den Noortgate, W., López-López, J. A., Marín-Martínez, F., and Sánchez-Meca, J. (2013). Three-level meta-analysis of dependent effect sizes. Behav. Res. Methods 45, 576–594. doi: 10.3758/s13428-012-0261-6
Van den Noortgate, W., and Onghena, P. (2003). Multilevel meta-analysis: a comparison with traditional meta-analytical procedures. Educ. Psychol. Meas. 63, 765–790. doi: 10.1177/0013164403251027
Viechtbauer, W. (2010). Conducting meta-analyses in R with the metafor package. J. Stat. Softw. 36, 1–48. doi: 10.18637/jss.v036.i03
*Villeneuve, E. F., Hajovsky, D. B., Mason, B. A., and Lewno, B. M. (2019). Cognitive ability and math computation developmental relations with math problem solving: an integrated, multigroup approach. Sch. Psychol. 34, 96–108. doi: 10.1037/spq0000267
*Viterbori, P., Traverso, L., and Usai, M. C. (2017). The role of executive function in arithmetic problem-solving processes: a study of third graders. J. Cognit. Dev. 18, 595–616. doi: 10.1080/15248372.2017.1392307
*Viterbori, P., Usai, M. C., Traverso, L., and De Franchis, V. (2015). How preschool executive functioning predicts several aspects of math achievement in Grades 1 and 3: a longitudinal study. J. Exp. Child Psychol. 140, 38–55. doi: 10.1016/j.jecp.2015.06.014
Voica, C., Singer, F. M., and Stan, E. (2020). How are motivation and self-efficacy interacting in problem-solving and problem-posing? Educ. Stud. Math. 105, 487–517. doi: 10.1007/s10649-020-10005-0
*Wang, A. Y., Fuchs, L. S., and Fuchs, D. (2016). Cognitive and linguistic predictors of mathematical word problems with and without irrelevant information. Learn. Individ. Differ. 52, 79–87. doi: 10.1016/j.lindif.2016.10.015
*Wang, F., Kuang, H., Wang, J., and Zhang, Z. H. (2010). Xiaoxue dinianji ertong shuxue yingyongti jiejue nengli yu gongzuo jiyi de guanxi yanjiu [The study on the relation between word problem solving and working memory of Lower Grade Children in Primary School]. Z. Xuexiao Weisheng 4, 471–473.
Witt, M. (2011). School based working memory training: preliminary finding of improvement in children’s mathematical performance. Adv. Cognit. Psychol. 7:7. doi: 10.2478/v10053-008-0083-3
*Wong, T. T. Y. (2018). Is conditional reasoning related to mathematical problem solving? Dev. Sci. 21:e12644. doi: 10.1111/desc.12644
*Wong, T. T.-Y., and Ho, C. S.-H. (2017). Component processes in arithmetic word-problem solving and their correlates. J. Educ. Psychol. 109, 520–531. doi: 10.1037/edu0000149
*Wu, S. S., Chen, L., Battista, C., Watts, A. K. S., Willcutt, E. G., and Menon, V. (2017). Distinct influences of affective and cognitive factors on children’s non-verbal and verbal mathematical abilities. Cognition 166, 118–129. doi: 10.1016/j.cognition.2017.05.016
*Yip, E. S. K., Wong, T. T. Y., Cheung, S. H., and Chan, K. K. W. (2020). Do children with mathematics learning disability in Hong Kong perceive word problems differently? Learn. Instruct. 68:101352. doi: 10.1016/j.learninstruc.2020.101352
*Zebec, M. S., Demetriou, A., and Kotrla-Topic, M. (2015). Changing expressions of general intelligence in development: a 2-wave longitudinal study from 7 to 18 years of age. Intelligence 49, 94–109. doi: 10.1016/j.intell.2015.01.004
*Zhang, J., Cheung, S. K., Wu, C., and Meng, Y. (2018). Cognitive and affective correlates of Chinese children’s mathematical word problem solving. Front. Psychol. 9:2357. doi: 10.3389/fpsyg.2018.02357
*Zhang, X., Rasanen, P., Koponen, T., Aunola, K., Lerkkanen, M.-K., and Nurmi, J.-E. (2017). Knowing, applying, and reasoning about arithmetic: roles of domain-general and numerical skills in multiple domains of arithmetic learning. Dev. Psychol. 53, 2304–2318. doi: 10.1037/dev0000432
*Zhao, Y. (2012). Shuxue Lingyu Zhishi Xuexi Zhong Gongzuo Jiyi yu Xueye Shuiping Dui Wenti Jiejue de Yingxiang [The Influence of Working Memory and Achievement Level on Problem-Solving in Mathematic Disciplinary Domain Knowledge]. Guangzhou: Guangzhou University.
*Zheng, X., Swanson, H. L., and Marcoulides, G. A. (2011). Working memory components as predictors of children’s mathematical word problem solving. J. Exp. Child Psychol. 110, 481–498. doi: 10.1016/j.jecp.2011.06.001
*Zhong, N. N. (2009). Xiaoxue gaonianji ertong yingyongti biaozheng shuiping gongzuo jiyi dui wenti jiejue de yingxiang [The influence of elementary school students’ representational level in math word problem and working memory on problem-solving]. Zhongguo Teshu Jiaoyu 4, 77–81.
*Zhu, M., Cai, D., and Leung, A. W. S. (2017). Number line estimation predicts mathematical skills: difference in grades 2 and 4. Front. Psychol. 8:1576. doi: 10.3389/fpsyg.2017.01576
*Zhu, X. B., Wang, J. L., and Li, X. F. (2011). Shikongjian gongzuo jiyi he feiyanyu liuti zhili zai xiaoxuesheng shuxue wenti jiejue zhong de zuoyong [A study on the effect of visuospatial working memory and non-verbal fluid intelligence on pupils’ mathematical performance]. Xinli Kexue 34, 845–851.
*Zhu, Z. J. (2013). Gongzuo Jiyi ji Tuili Nengli zai Zhongxuesheng Shuxue Wenti Jiejue Zhong de Zuoyong [The Role of Working Memory and Reasoning Ability in Middle School Students’ Mathematical Problem Solving]. Jining: Qufu Normal University. Studies preceded by an asterisk were included in the meta-analysis.
Keywords: working memory, mathematical problem solving, executive functions, word problem, three-level meta-analysis
Citation: Ji Z and Guo K (2023) The association between working memory and mathematical problem solving: A three-level meta-analysis. Front. Psychol. 14:1091126. doi: 10.3389/fpsyg.2023.1091126
Received: 06 November 2022; Accepted: 06 March 2023;
Published: 28 March 2023.
Edited by:
Xinya Liang, University of Arkansas, United StatesReviewed by:
Lang Chen, Santa Clara University, United StatesPeijie Jiang, Hunan Normal University, China
Copyright © 2023 Ji and Guo. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Kan Guo, Z3Vva2FuQGJudS5lZHUuY24=
 Zhongtian Ji
Zhongtian Ji Kan Guo
Kan Guo