Mechanical Behavior of Anisotropic Composite Materials as Micropolar Continua

Introduction

A material can be defined complex due to the presence of an internal structure and to its complex constitutive behavior. As well-known, in the description of complex materials, such as composites, the discrete, and heterogeneous nature of matter must be taken into account, because interfaces and material internal phases dominate the gross behavior. The presence of material internal structure can be accounted by direct discrete modeling, with generally high computational cost (Suzuki et al., 1991; Baggio and Trovalusci, 2000; Rapaport and Rapaport, 2004; Yang et al., 2010; Godio et al., 2017; Baraldi et al., 2018; Reccia et al., 2018) or by adopting multiscale or coarse-graining techniques for deriving homogenized continua (Budiansky, 1965; Sanchez-Palencia, 1987; Nemat-Nasser et al., 1996; Blanc et al., 2002; Curtin and Miller, 2003; Jain and Ghosh, 2009; Trovalusci and Ostoja-Starzewski, 2011; Nguyen et al., 2012; Sadowski et al., 2014; Altenbach and Sadowski, 2015; Greco et al., 2016. However, the classical Cauchy model (Grade 1) is not reliable in the presence of problems dominated by the microstructure size, both in the non-linear, such as in the case of strain localization phenomena, and linear regimes (de Borst, 1991; Sluys et al., 1993; Masiani and Trovalusci, 1996; Trovalusci and Masiani, 1999, 2003).

In the framework of a multiscale modeling aimed at deriving homogenized continua suitable for representing the material microstructure, avoiding physical inadequacies and theoretical/computational problems—such as: ill-conditioning in the field equations and mesh-dependency in numerical solutions—the “non-local” character of the description is crucial. Non-locality, by definition, implies the presence of internal lengths and spatial dispersion properties in wave propagation (Kunin, 1982), which allow to bypass the above mentioned drawbacks. Besides the so-called explicit/strong non-local theories (Eringen, 1972, 1999; Maugin, 1993), implicit/weak non-local formulations, referred to continua with extra degrees of freedom of various kind (Mindlin, 1964; Capriz, 1989; Eringen, 1999; Gurtin, 2000; Trovalusci, 2014), have been proposed in order to deal with problems in which a characteristic internal length, l (material length), is comparable to the macroscopic length, L (structural length). This continua, also named multifield continua, reveal the hidden microstructure, which affects the macroscopic mechanical properties, by means of the additional kinematic and work-conjugated dynamic descriptors (Trovalusci and Augusti, 1998; Forest, 2009; Trovalusci et al., 2010; Capecchi et al., 2011; Forest and Trinh, 2011; Trovalusci, 2014; Trovalusci and Pau, 2014). In particular, in the works (Trovalusci and Augusti, 1998; Trovalusci et al., 2010; Trovalusci, 2014) the presence of a microstructure made of different kind of inclusions (fibers, microcracks/pores) and the ability of multifield continua to represent dispersion phenomena with particular reference to microcraked bars under free and forced oscillations has been investigated.

Among this latter kind of non-local models, many papers showed the advantages of micropolar models (e.g., formulated in Nowacki, 1970; Stojanović, 1972; Eringen, 1999, and widely investigated also from the experimental point of view Lakes and Benedict, 1982; Yang and Lakes, 1982; Lakes, 1983, 1986; Bauer et al., 2012; Rueger and Lakes, 2016) for investigating problems with general heterogeneities and/or discontinuities within the context of multiscale/coarse-graining approaches, which allow to preserve memory of the original organization of materials with periodic or random microstructure (Forest and Sab, 1998; Forest et al., 1999; Stefanou et al., 2008; Trovalusci et al., 2015, 2017). Moreover, special attention to the micropolar continua with constrained rotations (Toupin, 1962; Sokolowski, 1972), always referring to multiscale descriptions (Bouyge et al., 2001; Leonetti et al., 2018) has been reserved. In particular, the micropolar modeling has been effectively adopted for solving problems wherein the solid is made of an assembly of rigid particles undergoing displacements and rotations and interacting with each other via forces and couples, as masonry-like materials or fiber-reinforced composites, both in the linear and non-linear frameworks (Masiani and Trovalusci, 1996; Trovalusci and Masiani, 1999; Sansalone et al., 2006; Pau and Trovalusci, 2012; Trovalusci and Pau, 2014).

In the present work, we want to focus on the behavior of anisotropic composite assemblies, that can be polycrystals with grain boundaries or thin interfaces as well as brick/block masonry, and in particular on material parameters with different degrees of anisotropy. To this regard, it is worth noting that the micropolar continuum, differently from the couple-stress continuum, that is a micropolar continuum with constrained rotations (Sokolowski, 1972; Masiani and Trovalusci, 1996 Appendix), and also from second gradient continuum (Bacigalupo and Gambarotta, 2011; Trovalusci and Pau, 2014), presents the peculiar strain measure of the relative rotation between the local rigid rotation (macrorotation) and the microrotation that is related to the skew symmetric part of strain and then, in terms of work expended, to the skew symmetric part of the stress, whose contribution has significant role in anisotropic media (Pau and Trovalusci, 2012; Trovalusci and Pau, 2014). It is worth noting that, the different behavior between micropolar without and with constrained rotations media, for which the relative rotation is null, is also of interest for investigating the loss of ellipticity of problems leading to strain localization phenomena (Bigoni and Gourgiotis, 2016; Gourgiotis and Bigoni, 2016). Such effects are expected to be governed by both material size (de Borst, 1991; Sluys et al., 1993) and also the degree of anisotropy.

In a recent work (Leonetti et al., 2019), by adopting the coarse-graining procedure presented in Masiani and Trovalusci (1996); Trovalusci and Masiani (1999), the behavior of orthotropic brick/block masonry panels under compressive loads at the top, described as equivalent micropolar continua, has been investigated by varying the brick size and the load footprint, showing the capability of the micropolar model to distribute the load depending on the brick size. In the present work, the effect of the degree of anisotropy of the (coarse) continuum micropolar model on the strain/stress diffusion is studied. The same coarse-graining procedure is used which can be shown to be actually dependent both on the brick size, shape and texture of the original (fine) lattice model. The simulations have been carried out for a panel under localized loads, using a standard finite element approach based on a micropolar finite element implementation, with quadratic and linear interpolation functions for the displacement and rotation fields, developed in Fantuzzi et al. (2018) following the approach in Providas and Kattis (2002) and implemented within Comsol Multiphysics© framework (Comsol, 2017). The results are presented in terms of contour plots of displacement, stress and relative rotation, the significant strain measure related to the non-symmetrical part of the strain.

The present work is structured as follows. After the introductory section, the mechanics of anisotropic micropolar continua is illustrated with particular emphasis on anisotropic composite assemblies in section Mechanics of Anisotropic Micropolar Continuum. Section Finite Element Formulation is dedicated to the finite element implementation. Section Numerical Simulations presents the numerical applications and discussions about the novel results presented in this work. Finally some conclusions and remarks are given.

Mechanics of Anisotropic Micropolar Continuum

The micropolar continuum is a well-known model equipped by theoretical, numerical, and experimental studies in the literature (Nowacki, 1970; Stojanović, 1972; Lakes and Benedict, 1982; Yang and Lakes, 1982; Lakes, 1983, 1986; Bauer et al., 2012; Rueger and Lakes, 2016). This continuum is made of particles which can undergo independent displacements and rotations and belongs to a class of generalized continua of the so-called implicit non-local type (Eringen, 1999; Trovalusci, 2014). Reducing the description to two-dimensional (2D) media, each material particle in the 2D frame has 3 degrees of freedom: the (macro) displacements components, u₁, u₂, and rotation, ϕ (micro-rotation). The local linearized kinematic compatibility relations take the form:

$\begin{array}{l}{\epsilon }_{11}=u_{1,1},{\epsilon }_{22}=u_{2,2},{\epsilon }_{12}=u_{1,2}+\varphi ,\\ {\epsilon }_{21}=u_{2,1}-\varphi ,{\chi }_{31}={\varphi }_{,1},{\chi }_{32}={\varphi }_{,2},& (1)\end{array}$

where ε_ij (i, j = 1, 2) indicate the components of the strain tensor, while χ₃₁, χ₃₂ indicate the only independent components of the curvature tensor. The term θ = (u_2,1 − u_1,2)/2 is the local rigid rotation (macro-rotation) in such a way that:

$\begin{array}{ll}{\epsilon }_{12}=u_{1,2}-\theta +\varphi ,{\epsilon }_{21}=u_{2,1}+\theta -\varphi & (2)\end{array}$

Interaction among particles is described by stresses and micro-couples as:

$\begin{array}{ll}{t}_i={\sigma }_{ij}{n}_j,m_3={\mu }_{3j}{n}_j.& (3)\end{array}$

where σ_ij and μ_ij (i, j = 1, 2) are the components of the non-symmetric stress and couple-stress tensors, respectively, n_j being the components of the outward normal to the continuum boundary. Equilibrium equations can be carried out, in the case of body micro-couple neglected, as:

$\begin{array}{ll}{\sigma }_{ij,j}+b_i=0,{\mu }_{3j,j}-e_{ij3}{\sigma }_{ij}=0,& (4)\end{array}$

b_i being the components of the body force.

Linearly anisotropic stress-strain relations of the micropolar two-dimensional continuum assume the following matrix form:

$\begin{array}{ll}\left[\begin{array}{c}{\sigma }_{11}\\ {\sigma }_{22}\\ {\sigma }_{12}\\ {\sigma }_{21}\\ {\mu }_{31}\\ {\mu }_{32}\end{array}\right]=\left[\begin{array}{cccccc}{A}_{1111}& A_{1122}& A_{1112}& A_{1121}& B_{111}& B_{112}\\ A_{2211}& A_{2222}& A_{2212}& A_{2221}& B_{221}& B_{222}\\ A_{1211}& A_{1222}& A_{1212}& A_{1221}& B_{121}& B_{122}\\ A_{2111}& A_{2122}& A_{2112}& A_{2121}& B_{211}& B_{212}\\ B_{111}& B_{122}& B_{112}& B_{121}& D_{11}& D_{12}\\ B_{211}& B_{222}& B_{212}& B_{221}& D_{21}& D_{22}\end{array}\right]\left[\begin{array}{c}{\epsilon }_{11}\\ {\epsilon }_{22}\\ {\epsilon }_{12}\\ {\epsilon }_{21}\\ {\chi }_{31}\\ {\chi }_{32}\end{array}\right].& (5)\end{array}$

By considering hyperelastic materials, the following major symmetries hold: A_ijhk = A_hkij, B_ijh = B_hij, D_ij = D_ji(i, j, h, k = 1, 2).

Finite Element FormulatioN

The two-dimensional problem of micropolar continua is solved through the finite element implementation proposed in Leonetti et al. (2019), where displacement/rotation components are ordered in the vectors $u={\left[\begin{array}{cc}{u}_1& u_2\end{array}\right]}^T$, ϕ = [ϕ], and the stress and strain components in the vectors σ = ${\left[\begin{array}{cccc}{\sigma }_{11}& {\sigma }_{22}& {\sigma }_{12}& {\sigma }_{21}\end{array}\right]}^T$, μ = ${\left[\begin{array}{cc}{\mu }_{31}& {\mu }_{32}\end{array}\right]}^T$, ε = ${\left[\begin{array}{cccc}{\epsilon }_{11}& {\epsilon }_{22}& {\epsilon }_{12}& {\epsilon }_{21}\end{array}\right]}^T$, $\chi ={\left[\begin{array}{cc}{\chi }_{31}& {\chi }_{32}\end{array}\right]}^T$.

The weak form of the present problem has to be formulated in order to carry out the finite element implementation, and, considering a domain Ω with boundary Γ_N, writes:

$\begin{array}{l}{\displaystyle \underset{\Omega }{\int }}\delta {\epsilon }^T\sigma dA+{\displaystyle \underset{\Omega }{\int }}\delta {\chi }^T\mu dA={\displaystyle \underset{\Omega }{\int }}\delta u^T\text{b}dA+{\displaystyle \underset{{\Gamma }_N}{\int }}\delta u^T\overline{t}dl+\\ \hfill {\displaystyle \underset{{\Gamma }_N}{\int }}\delta {\varphi }^T\overline{m}dl\forall \delta \text{u},\delta \varphi ,& (6)\end{array}$

with δ denoting the variation operator, b the body force vector, $\bar{t}$ and $\bar{m}$ the traction and couple-traction vectors applied on the boundary Γ_N. Note that, the curvature vector χ is due to the first-order partial derivatives of the micro-rotation, thus C⁰ finite elements are adopted.

Finite element approximation though interpolation functions N_u and N_ϕ is given by $u=N_u\tilde{u},\varphi =N_{\varphi }\tilde{\varphi },$ where the over tilde vectors indicate the kinematic parameters correspondent to in-plane displacements and rotations at the nodes. Quadratic interpolation functions for the displacements and linear ones for the rotations have been assumed, as it was introduced in Leonetti et al. (2019). Thus, displacements are modeled with nine nodes, whereas micro-rotation are related to the four corner nodes. Interpolation function vectors are given in matrix form as:

$\begin{array}{ll}{N}_u=\left[\begin{array}{cc}\begin{array}{cc}{N}_1^u& 0\\ 0& N_1^u\end{array}& \begin{array}{cc}\cdots & \begin{array}{cc}{N}_9^u& 0\\ 0& N_9^u\end{array}\end{array}\end{array}\right],N_{\varphi }=\left[\begin{array}{ccc}{N}_1^{\varphi }& \cdots & N_4^{\varphi }\end{array}\right],& (7)\end{array}$

Thus, the micropolar strains given by Equation (1) can be written as:

$\begin{array}{ll}\epsilon =Lu+M\varphi ,\chi =\nabla \varphi ,& (8)\end{array}$

where the matrix operators L and M are defined as:

$\begin{array}{ll}L={\left[\begin{array}{cccc}\frac{\partial }{\partial x_1}& 0& \frac{\partial }{\partial x_2}& 0\\ 0& \frac{\partial }{\partial x_2}& 0& \frac{\partial }{\partial x_1}\end{array}\right]}^T,M={\left[\begin{array}{cccc}0& 0& 1& -1\end{array}\right]}^T.& (9)\end{array}$

Then Equation (8) becomes:

$\begin{array}{l}\epsilon =L{N}_u\tilde{u}+M{N}_{\varphi }\tilde{\varphi }=\left[\begin{array}{cc}L{N}_u& M{N}_{\varphi }\end{array}\right]\left\{\begin{array}{c}\tilde{u}\\ \tilde{\varphi }\end{array}\right\}=B_{\epsilon }d,\chi =\nabla (N_{\varphi }\tilde{\varphi })\\ =\left[\begin{array}{cc}0& \nabla N_{\varphi }\end{array}\right]\left\{\begin{array}{c}\tilde{u}\\ \tilde{\varphi }\end{array}\right\}=B_{\chi }d,& (10)\end{array}$

Where d indicates the unknown vector of nodal displacements. The matrices B_ε and B_χ collect the derivatives of the interpolation functions matrices N_u and N_ϕ. Therefore, the constitutive relations (5) become:

$\begin{array}{ll}\sigma =D_{\epsilon \epsilon }{B}_{\epsilon }d+D_{\epsilon \chi }{B}_{\chi }d,\mu =D_{\epsilon \chi }^T{B}_{\epsilon }d+D_{\chi \chi }{B}_{\chi }d,& (11)\end{array}$

where:

$\begin{array}{l}{D}_{\epsilon \epsilon }=\left[\begin{array}{cccc}{A}_{1111}& A_{1122}& A_{1112}& A_{1121}\\ A_{2211}& A_{2222}& A_{2212}& A_{2221}\\ A_{1211}& A_{1222}& A_{1212}& A_{1221}\\ A_{2111}& A_{2122}& A_{2112}& A_{2121}\end{array}\right],\\ D_{\epsilon \chi }=\left[\begin{array}{cc}{B}_{111}& B_{112}\\ B_{221}& B_{222}\\ B_{121}& B_{122}\\ B_{211}& B_{212}\end{array}\right],D_{\chi \chi }=\left[\begin{array}{cc}{D}_{11}& D_{12}\\ D_{21}& D_{22}\end{array}\right].& (12)\end{array}$

Note that coupling between classical and micro-polar effects are considered by matrix D_εχ. Finally, the algebraic finite element problem (without body forces) reads:

$\begin{array}{l}\delta d^T{\displaystyle \underset{\mathit{\text{K}}}{{\displaystyle \underbrace{{\displaystyle \underset{\Omega }{\int }}(B_{\epsilon }^T{D}_{\epsilon \epsilon }{B}_{\epsilon }+B_{\epsilon }^T{D}_{\epsilon \chi }{B}_{\chi }+B_{\chi }^T{D}_{\epsilon \chi }^T{B}_{\epsilon }+B_{\chi }^T{D}_{\chi \chi }{B}_{\chi })dA}}}}d\\ =\delta d^T{\displaystyle \underset{\mathit{\text{F}}}{{\displaystyle \underbrace{{\displaystyle \underset{{\Gamma }_N}{\int }}\left[\begin{array}{c}{N}_u^T\bar{t}\\ N_{\varphi }^T\bar{m}\end{array}\right]dl}}}}\forall \delta d,& (13)\end{array}$

where K and F indicate the stiffness matrix and the nodal force vector of the adopted finite element for describing 2D linearly elastic anisotropic micropolar bodies. A classical Gauss-Legendre integration is considered for computing the integral terms appearing in Equation (13).

The present model has been implemented within the framework of Comsol Multiphysics^® software (Comsol, 2017).

Numerical Simulations

The present study aims at investigating the mechanical behavior of two-dimensional anisotropic micropolar media under localized loads by varying the degree of anisotropy, through the change in the material properties identified using the coarse-graining procedure described in Masiani and Trovalusci (1996), Trovalusci and Masiani (1999), considering at the (fine) micro-level anisotropic brick/block assemblies of different textures and related aspect and ratios, and at the macroscopic (coarse) level an energy equivalent micropolar continua.

It has been widely shown that homogenized micropolar models prove to be suitable of retaining memory of the behavior of the actual composite microstructure in the presence of high gradients of deformation, that occur even in the elastic range when load or geometrical singularities are present (Masiani and Trovalusci, 1996; Trovalusci and Masiani, 1999; Sansalone et al., 2006). In particular, due to the presence of the relative strain measure, it has been shown that micropolar continua perform better than classic and other generalized continua when non-symmetric shear effects have to be accounted for, as in the case of strongly orthotropic media (Pau and Trovalusci, 2012; Trovalusci and Pau, 2014).

The role of scale effects in orthotropic media under the action of a load applied on portions of variable size of the boundary of the body and the consequences in terms of strain and stress diffusion have been highlighted by the parametric analyses performed in the recent work (Leonetti et al., 2019). The present work, does not accounts for size effects but focuses on the response of anisotropic micropolar media, under localized loads, in the presence of an increasing degree of anisotropy. The strain/stress diffusion has been numerically investigated according to the constitutive relations considered, that couple the effect of normal and shear stress/strain, as well as couple stress and curvature in orthogonal direction. This study highlights aspects that, in the Authors' knowledge, have not been previously investigated in materials with anisotropies. These aspects can be also interesting in the perspective of dealing with significant problems of loss of ellipticity followed by strain localization phenomena, with folding and/or fracture for instance, that affect both classical and constrained micropolar materials (Sluys et al., 1993; Nguyen et al., 2012; Bigoni and Gourgiotis, 2016; Gourgiotis and Bigoni, 2016).

The problem numerically investigated is a square domain of width L = 4m, only fixed at the bottom edge and subjected to a top load acting on length size a/L = 0.25 (Figure 1A) and pressure q = 10MPa. Due to the symmetry of the problem only half of the domain has been analyzed and the correspondent finite element mesh is depicted in Figure 1B. Parametric analyses have been performed by increasing the coefficients representing material anisotropy according to the following three different configurations that have been selected in order to investigate separately the role of different cases of anisotropy.

FIGURE 1

Figure 1. (A) Sketch of the present problem with (B) present finite element mesh.

Table 1 reports the independent material coefficients that are considered constant in the simulations. The other coefficients increase according to a constant parameter allowing to represent four different degrees of anisotropy from a minimum (defined as Material #1) to a maximum (Material #4) value.

TABLE 1

Table 1. Constant mechanical properties used in all computations.

Configuration 1:

$\begin{array}{ll}\left[\begin{array}{l}{\sigma }_{11}\hfill \\ {\sigma }_{22}\hfill \\ {\sigma }_{12}\hfill \\ {\sigma }_{21}\hfill \\ {\mu }_{31}\hfill \\ {\mu }_{32}\hfill \end{array}\right]=\left[\begin{array}{llllll}{A}_{1111}\hfill & \hfill & \hfill & A_{1121}\hfill & \hfill & \hfill \\ \hfill & A_{2222}\hfill & A_{2222}\hfill & \hfill & \hfill & \hfill \\ \hfill & A_{1222}\hfill & A_{1212}\hfill & \hfill & \hfill & \hfill \\ A_{2111}\hfill & \hfill & \hfill & A_{2121}\hfill & \hfill & \hfill \\ \hfill & \hfill & \hfill & \hfill & D_{11}\hfill & \hfill \\ \hfill & \hfill & \hfill & \hfill & \hfill & D_{22}\hfill \end{array}\right]\left[\begin{array}{l}{\epsilon }_{11}\hfill \\ {\epsilon }_{22}\hfill \\ {\epsilon }_{12}\hfill \\ {\epsilon }_{21}\hfill \\ {\chi }_{31}\hfill \\ {\chi }_{32}\hfill \end{array}\right]& (14)\end{array}$

accounts for the increment of the constitutive elastic coefficients (reported in bold in Equation (14)) coupling the normal stresses σ₁₁, σ₂₂ with the non-symmetric shear strains ε₂₁, ε₁₂, respectively, and the non-symmetric shear stresses σ₁₂, σ₂₁ with the normal strains ε₂₂, ε₁₁, respectively: A₁₁₂₁ = A₂₁₁₁ and A₂₂₁₂ = A₁₂₂₂. The implemented values are listed in Table 2 and their values for the four materials configurations considered (ranging from Material#1, with the lower degree of anisotropy, up to Matrerial#4 with the higher degree of anisotrpoy) are obtained by considering the increase through a parameter corresponding to (A₁₂₁₂ − A₂₂₁₂)/4 and (A₂₁₂₁ − A₁₁₂₁)/4, respectively. This choice is arbitrary, but it allows us to define an increasing degree of material anisotropy obtaining plausible results, as the elastic constants on the main diagonal are generally predominant with respect to the out-of-diagonal terms, suitable to highlight the effects of interest.

TABLE 2

Table 2. Mechanical properties used in Configuration 1.

Configuration 2:

$\begin{array}{ll}\left[\begin{array}{l}{\sigma }_{11}\hfill \\ {\sigma }_{22}\hfill \\ {\sigma }_{12}\hfill \\ {\sigma }_{21}\hfill \\ {\mu }_{31}\hfill \\ {\mu }_{32}\hfill \end{array}\right]=\left[\begin{array}{llllll}{A}_{1111}\hfill & A_{1122}\hfill & \hfill & \hfill & \hfill & \hfill \\ A_{2211}\hfill & A_{2222}\hfill & \hfill & \hfill & \hfill & \hfill \\ \hfill & \hfill & A_{1212}\hfill & \hfill & \hfill & \hfill \\ \hfill & \hfill & \hfill & A_{2121}\hfill & \hfill & \hfill \\ \hfill & \hfill & \hfill & \hfill & D_{11}\hfill & D_{12}\hfill \\ \hfill & \hfill & \hfill & \hfill & D_{21}\hfill & D_{22}\hfill \end{array}\right]\left[\begin{array}{l}{\epsilon }_{11}\hfill \\ {\epsilon }_{22}\hfill \\ {\epsilon }_{12}\hfill \\ {\epsilon }_{21}\hfill \\ {\chi }_{31}\hfill \\ {\chi }_{32}\hfill \end{array}\right]& (15)\end{array}$

considers a micropolar orthotropic material, where the variable elastic coefficients (reported in bold in Equation (15)) are: A₁₁₂₂ = A₂₂₁₁ and D₁₂ = D₂₁, respectively concerns the classical “Poisson effect” and a corresponding micropolar out-of-diagonal effect in the model. The values provided are listed in Table 3. Also in this case the increase from Material#1 (with no Poisson's effect) to Material#4 (with the higher Poisson's effect) has been put constant.

TABLE 3

Table 3. Mechanical properties used in Configuration 2.

Configuration 3:

$\begin{array}{ll}\left[\begin{array}{l}{\sigma }_{11}\hfill \\ {\sigma }_{22}\hfill \\ {\sigma }_{12}\hfill \\ {\sigma }_{21}\hfill \\ {\mu }_{31}\hfill \\ {\mu }_{32}\hfill \end{array}\right]=\left[\begin{array}{llllll}{A}_{1111}\hfill & \hfill & A_{1112}\hfill & \hfill & \hfill & \hfill \\ \hfill & A_{2222}\hfill & \hfill & A_{2221}\hfill & \hfill & \hfill \\ A_{1211}\hfill & \hfill & A_{1212}\hfill & \hfill & \hfill & \hfill \\ \hfill & A_{2122}\hfill & \hfill & A_{2121}\hfill & \hfill & \hfill \\ \hfill & \hfill & \hfill & \hfill & D_{11}\hfill & \hfill \\ \hfill & \hfill & \hfill & \hfill & \hfill & D_{22}\hfill \end{array}\right]\left[\begin{array}{l}{\epsilon }_{11}\hfill \\ {\epsilon }_{22}\hfill \\ {\epsilon }_{12}\hfill \\ {\epsilon }_{21}\hfill \\ {\chi }_{31}\hfill \\ {\chi }_{32}\hfill \end{array}\right]& (16)\end{array}$

takes into account the increment of the material coefficients (reported in bold in Equation (16)) that couple the normal stresses σ₁₁, σ₂₂ with the correspondent non-symmetric shear strains ε₁₂, ε₂₁, respectively, and the non-symmetric shear stresses σ₁₂, σ₂₁ with the normal strains ε₁₁, ε₂₂, respectively: A₁₁₁₂ = A₁₂₁₁ and A₂₂₂₁ = A₂₁₂₂. The implemented values are listed in Table 4, and their values for the four materials configurations considered are obtained by considering the increase of a parameter corresponding to (A₁₂₁₂ − A₁₁₁₂)/10 and (A₂₁₂₁ − A₂₂₂₁)/10, respectively. This arbitrary choice was due on the observed strongly coupling (normal/transversal) effects on the micropolar response. As for Configuaration 1, it allows us to define an increasing degree of material anisotropy obtaining results suitable to highlight the relevant effects.

TABLE 4

Table 4. Mechanical properties used in Configuration 3.

Figures 2–4 represent the contour lines of the vertical component of displacement, u₂, the vertical stress component, σ₂₂, and relative rotation, θ − ϕ, for Configuration 1, in which the coupling material properties between normal stresses and the correspondent shear strains, and vice-versa, increase (Equation (14)) as above described. In terms of displacements (Figure 1) it can be observed that, due to the normal stress/shear strain/ coupling, the more the anisotropic degree, and the related coupling, increases, from Material#1 to Material#4, the more the load distributes affecting the panel in its bottom part. Correspondingly, in terms of vertical stresses (Figure 3) the coupling due to anisotropy increases the stress diffusion. This effect is highlighted also by the relative rotation plot (Figure 4), wherein the micropolar effect of θ − ϕ increases in Material#4 case due to the presence of a strongly anisotropy/coupling between normal and shear components.

FIGURE 2

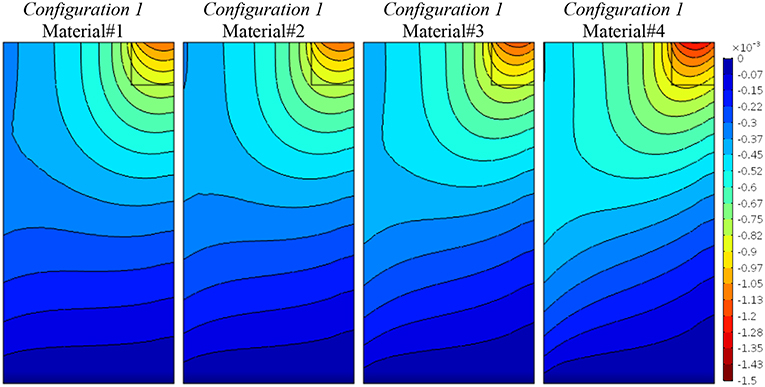
Figure 2. Configuration 1, vertical displacement component, u₂, contour plots for four material cases (Material#1/Material#4 minimum/maximum anisotropy degree).

FIGURE 3

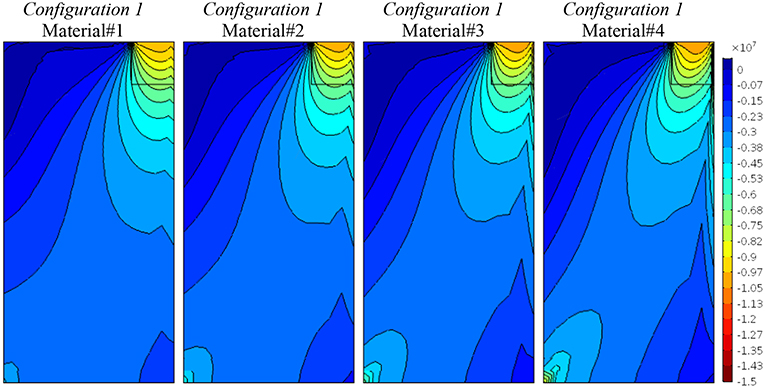
Figure 3. Configuration 1, vertical stress component, σ₂₂, contour plots for four material cases (Material#1/Material#4 minimum/maximum anisotropy degree).

FIGURE 4

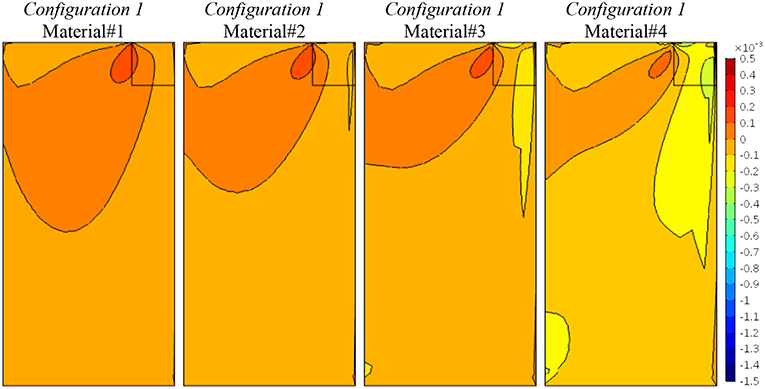
Figure 4. Configuration 1, relative rotations, θ − ϕ, contour plots for four material cases (Material#1/Material#4 minimum/maximum anisotropy degree).

Figures 5–7 show the results obtained for Configuration 2, characterized by the orthotropic material symmetry, which considers the classical and, in a sense, micropolar “Poisson's effect” through the terms A₁₁₂₂, D₁₂. The first material case (Material#1) corresponds to the one with null Poisson's effect (A₁₁₂₂ = D₁₂ = 0), whereas the others have increasing coefficients through a constant value as shown in Table 3. In Figure 5 the contour lines of the vertical component of displacement field, u₂, diffuse depending on the degree of anisotropy. Analogously, for the vertical stress component, σ₂₂, in Figure 6 we can observe the same phenomenon. In both cases the curves are more distributed in the case of higher degrees of orthotropy. Figure 7 shows that the relative rotation, θ − ϕ, map does not change, as this component is not affected by the elastic coefficients involved. For pointing out the correspondences between classical and micropolar elastic moduli the reader may refer to the work [Trovalusci and Masiani (1999), section 4].

FIGURE 5

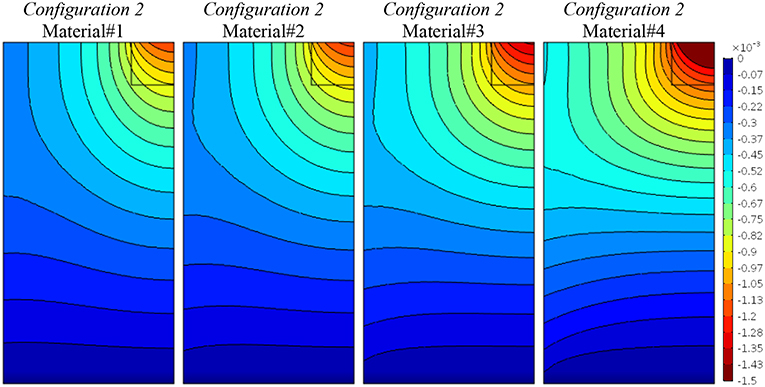
Figure 5. Configuration 2, vertical displacement component, u₂, contour plots for four material cases (Material#1/Material#4 minimum/maximum anisotropy degree).

FIGURE 6

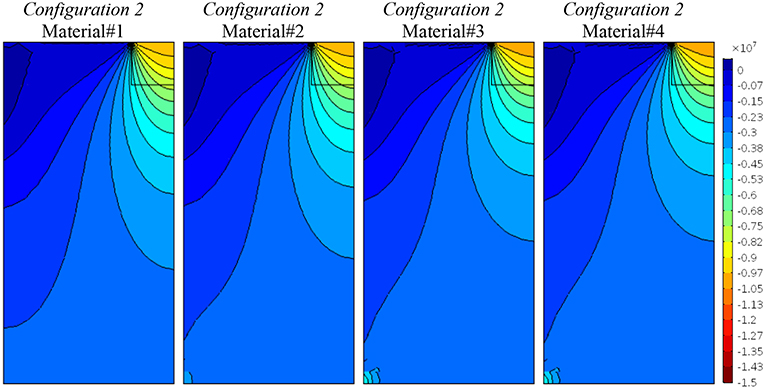
Figure 6. Configuration 2, vertical stress component, σ₂₂, contour plots for four material cases (Material#1/Material#4 minimum/maximum anisotropy degree).

FIGURE 7

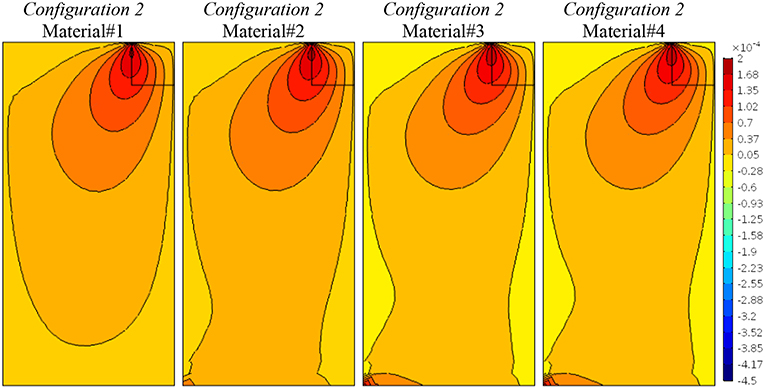
Figure 7. Configuration 2, relative rotations, θ − ϕ, contour plots for four material cases (Material#1/Material#4 minimum/maximum anisotropy degree).

Finally, Figures 8–10 are related to Configuration 3, which couples normal and shear stress/strain components as described in Equation (16). The present condition influences more the solution as it can be seen in Figure 8, where the vertical displacement component, u₂, changes homogeneously showing a wider diffusion related to the increasing of the degree of anisotropy. The same can be said for the vertical stress in Figure 9, where the reaction stresses at the bottom increases as the coupling effect increases. The most interesting representation is due to the relative rotation (Figure 10) where a strong boundary effect is shown. The field becomes distorted at the top (where the vertical load is applied) and at the bottom (even though an homogenous boundary condition has been applied) as the coupling mechanical properties are increased. The contour plot distortion at the bottom is due to the strong discontinuity between a clamped horizontal boundary condition and a free one on the left vertical edge.

FIGURE 8

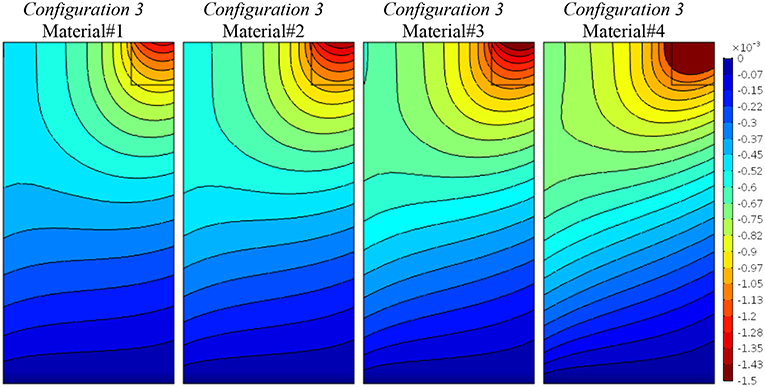
Figure 8. Configuration 3, vertical displacement component, u₂, contour plots for four material cases (Material#1/Material#4 minimum/maximum anisotropy degree).

FIGURE 9

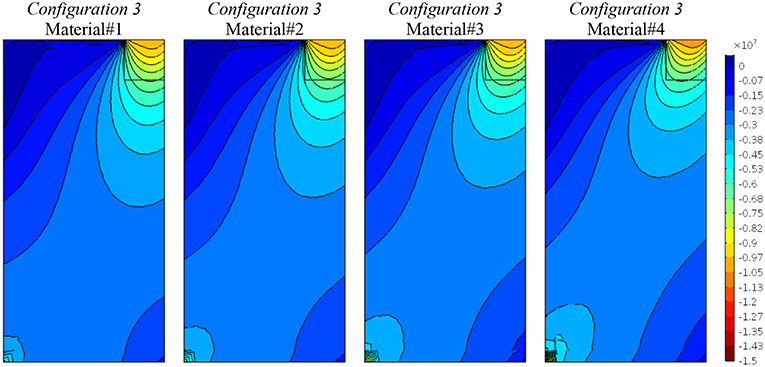
Figure 9. Configuration 3, vertical stress component, σ₂₂, contour plots for four material cases (Material#1/Material#4 minimum/maximum anisotropy degree).

FIGURE 10

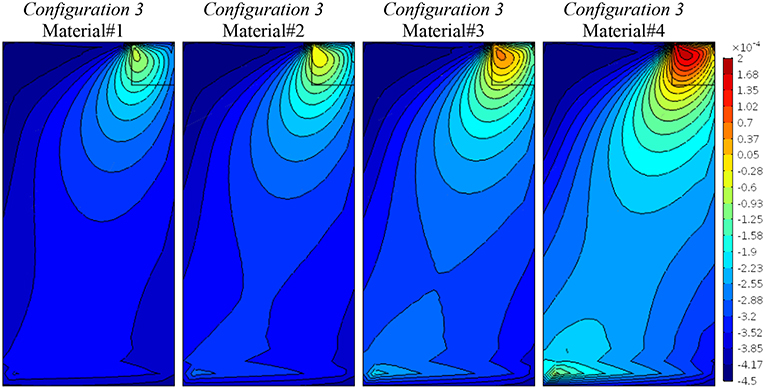
Figure 10. Configuration 3, relative rotations, θ − ϕ, contour plots for four material cases (Material#1/Material#4 minimum/maximum anisotropy degree).

Final Remarks

This work proposes a numerical finite element solution of an anisotropic micropolar panel subjected to a concentrated pressure on a small portion of the top boundary, and the effect on the mechanical behavior of this body has been investigated for particular cases of material anisotropy. The stress diffusion under concentrated load in masonry assemblies has been widely investigated also from the experimental point of view (Bigoni and Noselli, 2010). In earlier works it has been shown that while the micropolar model is able to distribute the load depending on the element size, the classical continuum lacking in material internal lengths does not entail such effect. Moreover, the micropolar model, differently from the couple stress (micropolar with microtation constrained to be equal to the local rigid rotation) and second gradient model, presents the peculiar strain measure of relative rotation suitable to take into account the non-symmetries in strain and stress that are predominant in strongly anisotropic assemblies (Pau and Trovalusci, 2012; Trovalusci, 2014; Trovalusci and Pau, 2014).

In the present work, attention has been given to the effect of different degrees of material anisotropy, not only orthotropy, for micropolar bodies subjected to localized loads, particularly focusing on the strain measure of the relative rotation. It has been highlighted that the anisotropic elastic coefficients of the micropolar continuum, which couple normal stresses with non-symmetric shear strains and vice-versa, have the effect of distributing the load according to the degree of anisotropy of the reference material. The coefficients that relate normal stress to normal strain components in the orthogonal directions, as well as the coefficients relating the couple-stress to the curvature components in the orthogonal direction, governing the classical and, in a sense, micropolar Poisson's effect, instead, does not significantly affect the response of the micropolar continuum. All the analyzed cases showed that an increasing level of anisotropy corresponds to a significant distribution of the load in terms of stresses within the continuum.

It can be concluded that when dialing with materials made of particles assembled according to strong anisotropies it is advisable to resort to micropolar theories. As further development, we expect to investigate the ability of unconstrained anisotropic micropolar models to detect strain localization phenomena.

Author Contributions

NF and PT wrote and revise the paper. SD carried out all numerical simulations.

Funding

This research was supported by the Italian Ministry of University and Research, P.R.I.N. 2015, Project 2015JW9NJT Advanced mechanical modeling of new materials and structures for the solution of 2020 Horizon challenges, Sapienza Research Unit (Grant B86J16002300001), and by Sapienza University, Grant 2016 (B82F16005920005).

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors acknowledge Dr. Lorenzo Leonetti, University of Calabria, for providing the Comsol^® framework and for implementing the model at Section Finite Element Formulation for the present investigation.

References

Altenbach, H., and Sadowski, T. (2015). Failure and Damage Analysis of Advanced Materials. Wien: Springer-Verlag.

Google Scholar

Bacigalupo, A., and Gambarotta, L. (2011). Non-local computational homogenization of periodic masonry. Int. J. Multiscale. Comput. Eng. 9, 565–578. doi: 10.1615/IntJMultCompEng.2011002017

CrossRef Full Text | Google Scholar

Baggio, C., and Trovalusci, P (2000). Collapse behaviour of three-dimensional brick-block systems using non linear programming. Struct. Eng. Mech. 10, 181–195. doi: 10.12989/sem.2000.10.2.181

CrossRef Full Text | Google Scholar

Baraldi, D., Reccia, E., and Cecchi, A. (2018). In plane loaded masonry walls: DEM and FEM/DEM models. a critical review. Meccanica 53, 1613–1628. doi: 10.1007/s11012-017-0704-3

CrossRef Full Text | Google Scholar

Bauer, S., Dettmer, W. G., Perić, D., and Schäfer, M. (2012). Micropolar hyperelasticity: constitutive model, consistent linearization and simulation of 3D scale effects. Comput. Mech. 50, 383–396. doi: 10.1007/s00466-012-0679-9

CrossRef Full Text | Google Scholar

Bigoni, D., and Gourgiotis, P. A. (2016). Folding and faulting of an elastic continuum. Proc. Royal Soc. A. 472:20160018.

PubMed Abstract | Google Scholar

Bigoni, D., and Noselli, G. (2010). Localize stress percolation through dry masonry walls. Part I – Experiments. Eur. J. Mech A/Solids. 29, 291–298. doi: 10.1016/j.euromechsol.2009.10.009

CrossRef Full Text | Google Scholar

Blanc, C., Le Bris, C., and Lions, P. L. (2002). From molecular models to continuum mechanics. Arch. Rat. Mech. Anal. 164, 341–381. doi: 10.1007/s00205-002-0218-5

CrossRef Full Text | Google Scholar

Bouyge, F., Jasiuk, I., and Ostoja-Starzewski, M. (2001). Micromechanically based couple-stress model of an elastic two-phase composite. Int. J. Solids Struct. 38, 1721–1735. doi: 10.1016/S0020-7683(00)00132-3

CrossRef Full Text | Google Scholar

Budiansky, B. (1965). On the elastic moduli of some heterogeneous materials. J. Mech. Phys. Solids 13, 223–227.

Google Scholar

Capecchi, D., Ruta, G., and Trovalusci, P. (2011). Voigt and Poincaré's mechanistic–energetic approaches to linear elasticity and suggestions for multiscale modelling. Arch. Appl. Mech. 81, 1573–1584. doi: 10.1007/s00419-010-0502-z

CrossRef Full Text | Google Scholar

Capriz, G. (1989). Continua with Microstructure. Berlin: Springer-Verlag. doi: 10.1007/978-1-4612-3584-2

CrossRef Full Text | Google Scholar

Comsol, A. B. (2017). Comsol Multiphysics Physics Builder Manual. Stockholm: Comsol.

Curtin, W. A., and Miller, R. E. (2003). Atomistic/continuum coupling in computational materials science. Model. Simul. Mater. Sci. Eng. 11, R33–R68. doi: 10.1088/0965-0393/11/3/201

CrossRef Full Text | Google Scholar

de Borst, R. (1991). Simulation of strain localization: a reappraisal of the Cosserat continuum. Eng. Comput. 8, 317–332. doi: 10.1108/eb023842

CrossRef Full Text | Google Scholar

Eringen, A. C. (1972). Linear theory of nonlocal elasticity and dispersion of plane waves. Int. J. Eng. Sci. 10, 425–435. doi: 10.1016/0020-7225(72)90050-X

CrossRef Full Text | Google Scholar

Eringen, A. C. (1999). Microcontinuum Field Theories. New York, NY: Springer-Verlag. doi: 10.1007/978-1-4612-0555-5

CrossRef Full Text | Google Scholar

Fantuzzi, N., Leonetti, L., Trovalusci, P., and Tornabene, F. (2018). Some novel numerical applications of Cosserat continua. Int. J. Comput. Meth. 15:1850054. doi: 10.1142/S0219876218500548

CrossRef Full Text | Google Scholar

Forest, S. (2009). Micromorphic approach for gradient elasticity, viscoplasticity, and damage. J. Eng. Mech. 135, 117–131. doi: 10.1061/(ASCE)0733-9399(2009)135:3(117)

CrossRef Full Text | Google Scholar

Forest, S., Dendievel, R., and Canova, G. R. (1999). Estimating the overall properties of heterogeneous Cosserat materials. Model. Simul. Mater. Sci. Eng. 7, 829–840. doi: 10.1088/0965-0393/7/5/314

CrossRef Full Text | Google Scholar

Forest, S., and Sab, K. (1998). Cosserat overall modeling of heterogeneous materials. Mech. Res. Commun. 25, 449–454. doi: 10.1016/S0093-6413(98)00059-7

CrossRef Full Text | Google Scholar

Forest, S., and Trinh, D. K. (2011). Generalised continua and the mechanics of heterogeneous material. Zeitschrift für Angewandte Mathematik und Mechanik 91, 90–109. doi: 10.1002/zamm.201000109

CrossRef Full Text

Godio, M., Stefanou, I., Sab, K., Sulem, J., and Sakji, S. (2017). A limit analysis approach based on Cosserat continuum for the evaluation of the in-plane strength of discrete media: application to masonry. Eur. J. Mech. A Solids. 66, 168–192. doi: 10.1016/j.euromechsol.2017.06.011

CrossRef Full Text | Google Scholar

Gourgiotis, P. A., and Bigoni, D. (2016). Stress channelling in extreme couple-stress materials Part I: Strong ellipticity, wave propagation, ellipticity, and discontinuity relations. J. Mech. Phys. Solids. 88, 150–168. doi: 10.1016/j.jmps.2015.09.006

CrossRef Full Text | Google Scholar

Greco, F., Leonetti, L., Luciano, R., and Nevone Blasi, P. (2016). Effects of microfracture and contact induced instabilities on the macroscopic response of finitely deformed elastic composites. Compos. Part B. Eng. 107, 233–253. doi: 10.1016/j.compositesb.2016.09.042

CrossRef Full Text | Google Scholar

Gurtin, M. E. (2000). Configurational Forces as Basis Concept of Continuum Physics. Berlin: Springer-Verlag.

Google Scholar

Jain, J. R., and Ghosh, S. (2009). Damage evolution in composites with a homogenization-based continuum damage mechanics model. Int. J. Damage Mech. 18, 533–568. doi: 10.1177/1056789508091563

CrossRef Full Text | Google Scholar

Kunin, I. A. (1982). Elastic Media with Microstructure, I-II. Berlin: Springer-Verlag.

Lakes, R. S. (1983). Size effect and micromechanics of a porous solid. J. Mat. Sci. 18, 2572–2580.

Google Scholar

Lakes, R. S. (1986). Experimental microelasticity of two porous solids. Int. J. Solids. Struct. 22, 55–63. doi: 10.1016/0020-7683(86)90103-4

CrossRef Full Text | Google Scholar

Lakes, R. S., and Benedict, R. L. (1982). Noncentrosymmetry in micropolar elasticity. Int. J. Eng. Sci. 20, 1161–1167. doi: 10.1016/0020-7225(82)90096-9

CrossRef Full Text | Google Scholar

Leonetti, L., Fantuzzi, N., Trovalusci, P., and Tornabene, F. (2019). Scale effects in orthotropic composite assemblies as micropolar continua: a comparison between weak and strong-form finite element solutions. Materials 12:758. doi: 10.3390/ma12050758

PubMed Abstract | CrossRef Full Text | Google Scholar

Leonetti, L., Greco, F., Trovalusci, P., Luciano, R., and Masiani, R. (2018). A multiscale damage analysis of periodic composites using a couple-stress/Cauchy multidomain model: application to masonry structures. Compos. Part B. Eng. 141, 50–59. doi: 10.1016/j.compositesb.2017.12.025

CrossRef Full Text | Google Scholar

Masiani, R., and Trovalusci, P. (1996). Cosserat and cauchy materials as continuum models of brick masonry. Meccanica 31, 421–432. doi: 10.1007/BF00429930

CrossRef Full Text | Google Scholar

Maugin, G. (1993). Material Inhomogeneities in Elasticity. London: Chapman and Hall. doi: 10.1007/978-1-4899-4481-8

CrossRef Full Text | Google Scholar

Mindlin, R. D. (1964). Micro-structure in linear elasticity. Arch. Ration Mech. Anal. 16, 51–78. doi: 10.1007/BF00248490

CrossRef Full Text | Google Scholar

Nemat-Nasser, S., Hori, M., and Datta, S. K. (1996). Micromechanics: overall properties of heterogeneous materials. J. Appl. Mech. 63:561. doi: 10.1115/1.2788912

CrossRef Full Text | Google Scholar

Nguyen, V. P., Lloberas-Valls, O., Stroeven, M., and Sluys, LJ. (2012). Computational homogenization for multiscale crack modelling, Implementational and computational aspects. Int. J. Numer. Meth. Engng. 89, 192–226. doi: 10.1002/nme.3237

CrossRef Full Text | Google Scholar

Nowacki, W. (1970). Theory of Micropolar Elasticity. Udine: Springer-Verlag. doi: 10.1007/978-3-7091-2720-9

CrossRef Full Text | Google Scholar

Pau, A., and Trovalusci, P. (2012). Block masonry as equivalent micropolar continua: the role of relative rotations. Acta Mech. 223, 1455–1471. doi: 10.1007/s00707-012-0662-8

CrossRef Full Text | Google Scholar

Providas, E., and Kattis, M. A. (2002). Finite element method in plane Cosserat elasticity. Comput. Struct. 80, 2059–2069. doi: 10.1016/S0045-7949(02)00262-6

CrossRef Full Text | Google Scholar

Rapaport, D. C., and Rapaport, D. C. R. (2004). The Art of Molecular Dynamics Simulation. Cambridge, UK: Cambridge University Press.

Google Scholar

Reccia, E., Leonetti, L., Trovalusci, P., and Cecchi, A (2018). A multiscale/multidomain model for the failure analysis of masonry walls: a validation with a combined FEM/DEM approach. Int. J. Mult. Comp. Eng. 16, 325–343. doi: 10.1615/IntJMultCompEng.2018026988

CrossRef Full Text | Google Scholar

Rueger, Z., and Lakes, R. S. (2016). Cosserat elasticity of negative Poisson's ratio foam: experiment. Smart Mater. Struct. 25:054004. doi: 10.1088/0964-1726/25/5/054004

CrossRef Full Text | Google Scholar

Sadowski, T., Trovalusci, P., Schrefler, B., and de Borst, R. (2014). Multi-scale and multi-physics modelling for complex materials. Meccanica 49, 2549–2550. doi: 10.1007/s11012-014-0040-9

CrossRef Full Text | Google Scholar

Sanchez-Palencia, E, and Zaoui, A. (1987). Homogenization Techniques For Composite Media. Lecture Notes In Physics. Springer.

Sansalone, V., Trovalusci, P., and Cleri, F. (2006). Multiscale modelling of materials by a multifield approach: microscopic stress and strain distribution in fiber-matrix composites. Acta Mater. 54, 3485–3492. doi: 10.1016/j.actamat.2006.03.041

CrossRef Full Text | Google Scholar

Sluys, L. J., de Borst, R., and Mühlhaus, H. B. (1993). Wave propagation, localization and dispersion in a gradient-dependent medium. Int. J. Solid. Struct. 30, 1153–1171. doi: 10.1016/0020-7683(93)90010-5

CrossRef Full Text | Google Scholar

Sokolowski, M. (1972). Theory of Couple-stresses in Bodies with Constrained Rotations, Udine: Springer-Verlag.

Google Scholar

Stefanou, I., Sulem, J., and Vardoulakis, I. (2008). Three-dimensional cosserat homogenization of masonry structures: elasticity. Acta Geotech. 3, 71–83. doi: 10.1007/s11440-007-0051-y

CrossRef Full Text | Google Scholar

Stojanović, B. (1972). Recent Developments in the Continua of Polar Elasticity. Udine: Springer-Verlag.

Suzuki, T., Takeuchi, S., and Yoshinaga, H. (1991). Dislocation Dynamics and Plasticity. Berlin: Springer-Verlag.

Google Scholar

Toupin, R. A. (1962). Elastic materials with couple-stresses. Arch Ration. Mech. Anal. 11, 385–414. doi: 10.1007/BF00253945

CrossRef Full Text | Google Scholar

Trovalusci, P. (2014). “Molecular approaches for multifield continua: origins and current developments,” in Multiscale Modeling of Complex Materials: Phenomenological, Theoretical and Computational Aspects, eds T. Sadowski, P. Trovalusci. (Berlin: Springer Int Centre for Mechanical Sciences), 211–278.

Google Scholar

Trovalusci, P., and Augusti, G. (1998). A continuum model with microstructure for materials with flaws and inclusions. J. Phys. IV. 8, 383–390.

Google Scholar

Trovalusci, P., De Bellis, M. L., and Masiani, R. (2017). A multiscale description of particle composites: From lattice microstructures to micropolar continua. Comp. Part B Eng. 128, 164–173. doi: 10.1016/j.compositesb.2017.06.015

CrossRef Full Text | Google Scholar

Trovalusci, P., and Masiani, R. (1999). Material symmetries of micropolar continua equivalent to lattices. Int. J. Solid Struct. 36, 2091–2108. doi: 10.1016/S0020-7683(98)00073-0

CrossRef Full Text | Google Scholar

Trovalusci, P., and Masiani, R. (2003). Non-linear micropolar and classical continua for anisotropic discontinuous materials. Int. J. Solid. Struct. 40, 1281–1297. doi: 10.1016/S0020-7683(02)00584-X

CrossRef Full Text | Google Scholar

Trovalusci, P., and Ostoja-Starzewski, M. (2011). Multiscale mechanical modelling of complex materials and engineering applications 2. Int. J. Mult. Comp. Eng. 9, 7–9. doi: 10.1615/IntJMultCompEng.2011002870

CrossRef Full Text | Google Scholar

Trovalusci, P., Ostoja-Starzewski, M., De Bellis, M. L., and Murrali, A. (2015). Scale-dependent homogenization of random composites as micropolar continua. Eur. J. Mech A Solids. 49, 396–407. doi: 10.1016/j.euromechsol.2014.08.010

CrossRef Full Text | Google Scholar

Trovalusci, P., and Pau, A. (2014). Derivation of microstructured continua from lattice systems via principle of virtual works: the case of masonry-like materials as micropolar, second gradient and classical continua. Acta Mech. 225, 157–177. doi: 10.1007/s00707-013-0936-9

CrossRef Full Text | Google Scholar

Trovalusci, P., Varano, V., and Rega, G. (2010). A generalized continuum formulation for composite materials and wave propagation in a microcracked bar. J. Appl. Mech. 77:061002. doi: 10.1115/1.4001639

CrossRef Full Text | Google Scholar

Yang, D., Sheng, Y., Ye, J., and Tan, Y. (2010). Discrete element modeling of the microbond test of fiber reinforced composite. Comput Mater Sci. 49, 253–259. doi: 10.1016/j.commatsci.2010.05.003

CrossRef Full Text | Google Scholar

Yang, J. F. C., and Lakes, R. S. (1982). Experimental study of micropolar and couple stress elasticity in compact bone in bending. J. Biomechanics. 15, 91–98.

PubMed Abstract | Google Scholar