- 1Beijing National Laboratory for Molecular Sciences, Institute of Chemistry, Chinese Academy of Sciences, Beijing, China
- 2School of Chemical Sciences, University of Chinese Academy of Sciences, Beijing, China
- 3Institute of Electrical Engineering, Chinese Academy of Sciences, Beijing, China
- 4National Supercomputing Center in Shenzhen, Shenzhen University Town, Shenzhen, China
The feasibility of direct laser cooling of SiH, GeH, SnH, and PbH is investigated and assessed based upon first principles. The internally contracted multi-reference configuration interaction method with the Davidson correction is applied. Very good agreement is obtained between our computed spectroscopic constants and the available experimental data. We find that the locations of crossing point between the B2Σ− and A2Δ states have the tendency of moving downwards from CH to SnH relative to the bottom of the corresponding A2Δ potential, which precludes the laser cooling of GeH, SnH, and PbH. By including the spin-orbit coupling effects and on the basis of the transition, we propose a feasible laser cooling scheme for SiH using three lasers with wavelengths varying from 400 to 500 nm, which features a very large vibrational branching ratio (0.9954) and a very short radiative lifetime (575 ns). Moreover, similar studies are extended to carbon monosulfide (CS) with a feasible laser cooling scheme proposed. The importance of electronic state crossing in molecular laser cooling is underscored, and our work suggests useful caveats to the choice of promising candidates for producing ultracold molecules.
1. Introduction
Laser cooling of diatomic molecule is an issue of great interest owing to their promising applications in many fields such as quantum computing and precision measurement (Carr et al., 2009; Hudson et al., 2011; Yan et al., 2013; Baron et al., 2014). Direct laser cooling of SrF molecules to μK level was firstly achieved with only three laser beams (Shuman et al., 2010). In addition, transverse and longitudinal laser cooling experiment was applied to YO (Hummon et al., 2013) and CaF (Zhelyazkova et al., 2014), respectively. So far only a few molecules including SrF, CaF, and YO have been cooled to the ultracold temperature experimentally, and there is an urgent need to search for more suitable molecular candidates for laser cooling. Recently, a number of theoretical efforts have been made in searching for promising molecular laser cooling candidates (Wells and Lane, 2011a; Fu et al., 2016a; Cao et al., 2019; González-Sánchez et al., 2019; Xu et al., 2019). It is generally accepted (Di Rosa, 2004; Fu et al., 2016b) that, a suitable laser-cooling candidate must meet the following three criteria: highly diagonal Franck-Condon factors (FCFs), a short lifetime, and no intermediate electronic-state interference. Here we reveal that the crossing between two electronic states may damage the cooling scheme, and may be regarded as the fourth criterion that should be checked beforehand in choosing laser-cooling candidates. We will demonstrate this point by investigating the laser cooling of group IVA hydrides.
There have been a lot of studies on SiH and GeH (Kleman and Werhagen, 1953a; Ram et al., 1998), while SnH and PbH have not been sufficiently studied (Alekseyev et al., 1996; Zhao et al., 2017). SiH radical has been attracting great interest over many years, since it plays a significant role in many industrial processes such as plasma vapor deposition (Ram et al., 1998). In 1930, the emission spectrum of SiH was observed using an arc source, and a strong transition near 410 nm was assigned to as the A2Δ→X2Π transition (Jackson, 1930). In 1969, the lifetime of the A2Δ state was measured as 700±100 ns with phase-shift technique (Smith, 1969). Later, the high-resolution spectrograms of 325 nm bands for SiH were measured with rotational analysis (Bollmark et al., 1971). In 1979, the accurate spectroscopic parameters and molecular constants of SiH were summarized and reported in the literature (Huber and Herzberg, 1979). In 1980, the emission spectroscopy of SiH in a silane glow-discharge was measured with a moderate spectrometer (Perrin and Delafosse, 1980). In 1989, the spectrum of SiH radical was observed over the laser wavelength between 426 and 430 nm by resonance-enhanced multiphoton ionization spectroscopy, and new state was tentatively assigned as 2Π state with further computer simulation (Johnson and Hudgens, 1989). Parallel to extensive studies on SiH, the spectra of GeH are well-studied in experiment, especially for the low-lying electronic states. In 1953, the spectra of A4Σ−→X2Π and A2Δ→X2Π band for GeH were first observed (Kleman and Werhagen, 1953a,b). Subsequently, the spectroscopic constants of the A2Δ state of GeH were deduced with rotational analysis (Klynning and Lindgren, 1966). In 1989, the radiative lifetime of the A2Δ state of GeH was measured as 93±10 ns with laser-induced fluorescence technique (Bauer et al., 1989). In 1938, the emission spectrum of PbH was firstly detected using arc-excitation in hydrogen atmosphere (Watson, 1938). In 2008, the near-infrared emission spectra of transitions of PbH were observed using high-resolution Fourier-transform spectrometry (Setzer et al., 2008).
Theoretically, in 1967 the first ab initio calculations on the SiH radical were performed with the Hartree-Fock method (Cade and Huo, 1967), in which the potential energy curve (PEC) of the ground-state was obtained. In 1983, the PECs of SiH were evaluated with the multi-reference double-excitation configuration interaction calculations (Lewerenz et al., 1983). In recent years, there are many calculations about spectroscopic constants of SiH (Ram et al., 1998; Kalemos et al., 2002; Shi et al., 2008, 2013; Zhang et al., 2018). In 2013, the PECs of eleven Ω states generated from seven Λ-S states of SiH radical were calculated by the internally contracted multi-reference configuration interaction method with the Davidson correction (icMRCI+Q) (Shi et al., 2013). In 2001, the X2Π and a4Σ− states of GeH were investigated with the MRCI approach and the spectroscopic parameters for the two states were reported (Bruna and Grein, 2001). In 2015, the lifetimes of A2Δ and a4Σ− states of GeH were obtained (Li et al., 2015). Some ab initio calculations on SnH and PbH were also reported (Alekseyev et al., 1996; Zhao et al., 2017).
The A2Δ→X2Π transition of CH was pointed out to be dominated by diagonal bands, making it a potential cooling candidate (Wells and Lane, 2011b). SiH is considered to be suitable for laser cooling by Zhang et al. (2018), although they ignored the SOC effects in their laser cooling schemes. In addition, they did not consider the effect of electronic state crossing. According to previous investigations (Fu et al., 2017; Xia et al., 2017), the SOC effects are important for laser cooling molecules and will be taken into account in this work. There have not been theoretical studies reported on laser cooling of GeH, SnH, and PbH. In this work, by means of highly accurate ab initio and dynamical calculations, we investigate the laser cooling of group IVA hydrides and the importance of electronic state crossing in molecular laser cooling is underscored. Additionally, based on the fourth criterion mentioned above, laser cooling of CS is investigated.
The paper is organized as follows. The theoretical methods and computational details are briefly described in section 2. The results and discussion are shown in section 3. The conclusions are given in section 4.
2. Methods and Computational Details
In this paper, all the ab initio calculations of SiH, GeH, SnH, and PbH are performed using the MOLPRO 2012.1 program package (Werner et al., 2012). For each Λ-S state, the energies are computed using the complete active space self-consistent field (CASSCF) (Werner and Knowles, 1985) approach followed by the icMRCI+Q (Langhoff and Davidson, 1974). The lowest electronic configuration of Si is (core)3s23p2 corresponding to the atomic states 3P and 1D. In combination with the 1 s function of a H atom, the lowest electronic configuration of SiH in X2Π is invariably (core)4σ25σ26σ02π1 and the next is (core)4σ25σ16σ02π2 leading to the multiplets 4Σ−, 2Δ, 2Σ−, and 2Σ+, which could be considered as involving a pσ→pπ transition within the Si atom. In asymptote region, the 5σ molecular orbital origins from the 1s on hydrogen, while the 6σ and 2π correspond to the 3p on silicon.
The choice of active space is very important in the CASSCF and MRCI+Q calculations (Liu et al., 2009; Yu and Bian, 2011, 2012). The active space of SiH used here consists of ten orbitals corresponding to Si 2p3s3p4pπ and H 1s, and is referred to as (11e, 10o), which is carefully chosen to include proper orbitals, and large enough for the present calculations. Our test calculations indicate that the full valence space is inadequate, and thus additional five orbitals are added into the active space. The inner shell orbitals are included to account for the core-valence correlation effects and the outer virtual orbitals are added to give a better description on the dissociation behavior and Rydberg character, especially for excited electronic states (Shen et al., 2017). In fact, a completely satisfactory set could neither be found by increasing the active orbital space nor by including more states (Simah et al., 1999). The best compromise we could achieve is to distribute the eleven electrons in 10 active orbitals. As for the basis set, we use the aug-cc-pV5Z basis sets for Si and H atom. In the SOC calculations, the SO eigenstates are obtained by diagonalizing Ĥel+ĤSO in the basis of eigenfunctions of Ĥel. In addition, the Ĥel and ĤSO are obtained from the icMRCI+Q calculations and icMRCI+Q waves functions, respectively. The active space for GeH in the present work is (9e, 9o), which consists of the Ge 3dπ4s4p5pπ and H 1s orbitals. The accuracy and computational performance are compromised, thus the active space of GeH includes the 3dπ orbitals, valence orbitals and 5pπ orbitals. The aug-cc-pV5Z-DK basis sets are used for GeH. Here, the active space for SnH consists of the Sn 4d5s5p and H 1s orbitals and is referred as (15e, 10o). The aug-cc-pVQZ basis sets are used for H and aug-cc-pwCVQZ-PP with ECP28MDF effective core potentials for Sn. Similarly, the active space for PbH is (15e, 10o), which consists of the Pb 5d6s6p and H 1s orbitals. We use the aug-cc-pVQZ basis sets for H and aug-cc-pwCVQZ-PP with ECP60MDF for Pb. In addition, the active space used for the study of CS is (10e, 8o) corresponding to the C 2s2p and S 3s3p, and we use the aug-cc-pV5Z basis sets for both C and S atoms.
The Einstein spontaneous emission coefficient is calculated by the following expression (Herzberg, 1950),
where is in units of s−1, ε0 is the vacuum permittivity in units of F· cm−1, M(r) is the transition dipole function in Debye unit, ν is emission frequency in units of cm−1, and Ψν, J are normalized radial wave functions, ℏ is the Planck constant and S(J′, J) is the Hönl-London rotational intensity factor. The radiative lifetime for a given vibrational level ν′ can be obtained by the following equation,
The spectroscopic parameters of group IVA hydrides, including the equilibrium bond length (Re), the harmonic vibrational constant (ωe), the rotational constant (Be), and adiabatic relative electronic energy referred to the ground state (Te) are obtained using the Le Royν′s LEVEL program (Le Roy, 2007).
3. Results and Discussion
3.1. PECs of the Λ-S States and Spectroscopic Constants
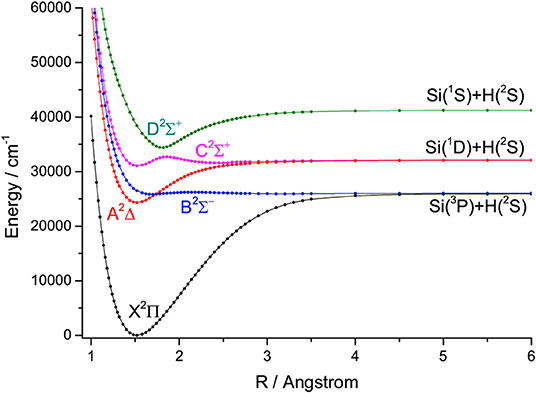
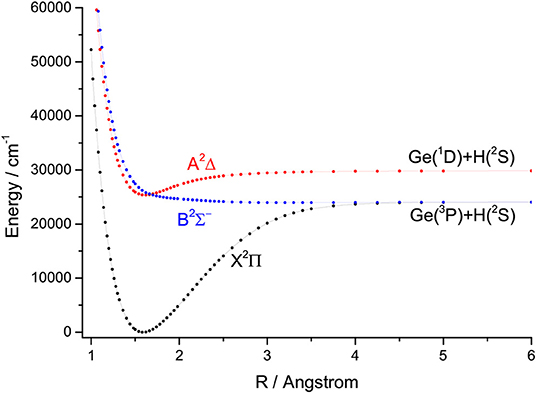
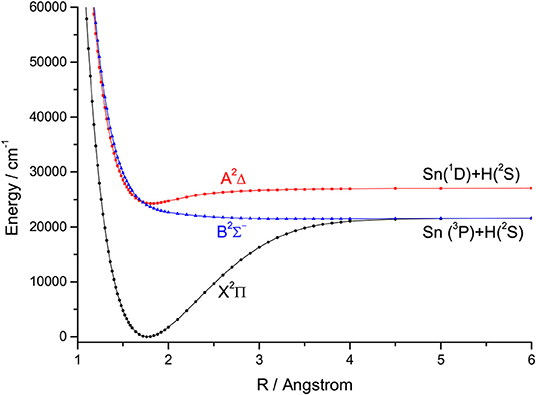
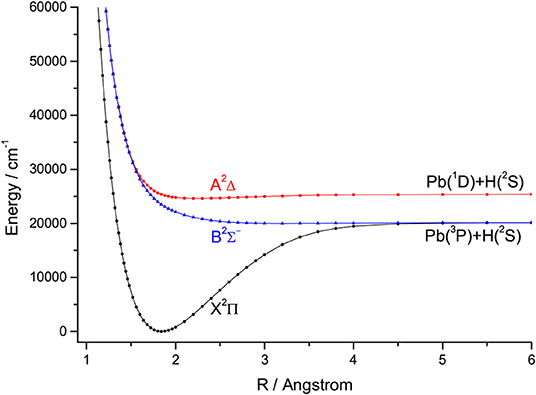
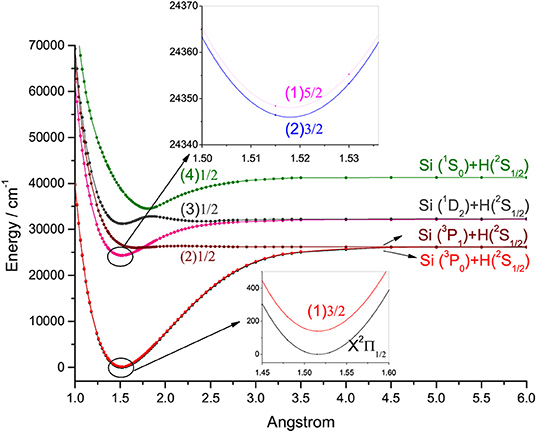
For the group IVA hydrides, the main configuration of the ground state (X2Π) is (core)4σ25σ26σ02π1. The second lowest state here is the A2Δ, whose main configuration is (core)4σ25σ16σ02π2. The PECs of SiH, GeH, SnH, and PbH computed using the icMRCI+Q method are shown in Figures 1–4, respectively. The weights of ionic configuration in the X2Π and A2Δ states decrease gradually with increasing internuclear distances. As seen in Figure 1, the five states of SiH correlate to the three dissociation limits. The X2Π and A2Δ states are the two energetically lowest lying electronic state and correlate to the neutral atomic Si(3P)+H(2S) limit and Si(1D)+H(2S) limit, respectively. From Figures 2–4, we can see that the X2Π and A2Δ states of GeH, SnH, and PbH correlate to the neutral atomic Ge/Sn/Pb(3P)+H(2S) limit and Ge/Sn/Pb(1D)+H(2S) limit, respectively. The PEC of the B2Σ− crosses with that of A2Δ will be discussed in details in section 3.2. The PECs of the B2Σ− and X2Π correlate to the same neutral atomic Si(3P)+H(2S) limit.
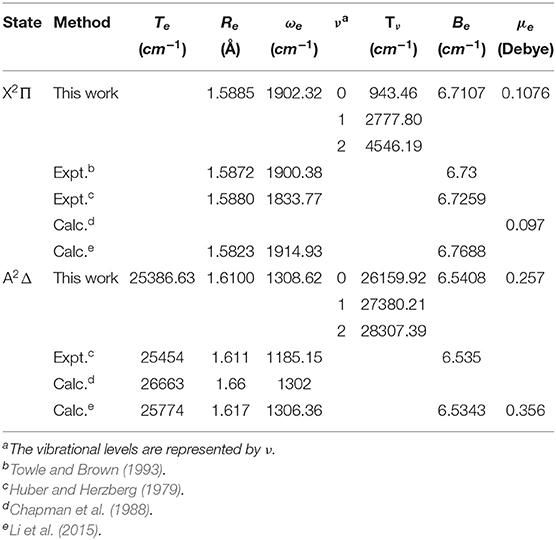
Since the spectroscopic constants of the X2Π and A2Δ states have been measured in experiment for SiH, GeH, SnH, and PbH, comparing with experimental data could provide an indicator of the reliability of our calculations. We present our calculated spectroscopic constants of SiH, GeH, and SnH in Tables 1, 2 and Table S1, together with previous theoretical and experimental values for comparison. The calculated Re and ωe of the X2Π of SiH are 1.5200 Å and 2047.71 cm−1, respectively, which are in good agreement with the corresponding experiment data (1.5201 Å and 2041.80 cm−1) (Huber and Herzberg, 1979). The contributions from non-valence orbitals to correlation energy are relatively small for the ground state, however, they become very important for the excited states and lead to noticeable differences. In particular, the experimental Te is 24300.4 cm−1 (Huber and Herzberg, 1979) and our calculated one with a better active space is 24299.20 cm−1, whereas that obtained by Zhang et al. (2018) is 25080.92 cm−1, which deviates from experimental value by about 780 cm−1. When additional virtual orbitals are taken into account by Kalemos et al. (2002), the deviation is reduced to around 200 cm−1. The spectroscopic constants of GeH obtained from the active space (9e, 9o) are shown in Table 2. The calculated Re and ωe of the X2Π of GeH are 1.5885 Å and 1902.32 cm−1, respectively, which are in very good agreement with the corresponding experiment data (1.5872 Å and 1900.38 cm−1) (Towle and Brown, 1993). The A2Δ state of GeH, the experimental Te is 25454 cm−1 (Huber and Herzberg, 1979), whereas our calculated Te is 25386.63 cm−1, which is much improvement compared with previous computational value 25774 cm−1 (Li et al., 2015).
The permanent dipole moments (PDMs) and absolute values transition dipole moments (TDMs) for the A2Δ→X2Π transition of SiH at the icMRCI+Q level are represented in Figure 5. The TDMs for the A2Δ→X2Π transition of SiH are 0.6231 D at Re and decrease with the increasing bond length. The calculated TDMs for the A2Δ→X2Π transition of GeH are given in Figure S1. The Einstein A coefficients and vibrational branching ratio of the A2Δ→X2Π transition of GeH are listed in Table S2. The calculated radiative lifetime for the A2Δ(ν′ = 0) state of SiH is 613 ns, which is in very good agreement with the experimental value (534 ± 23 ns) (Bauer et al., 1984). The FCFs of the A2Δ→X2Π transition for GeH are calculated and plotted in Figure S2. In this work, the f00 (0.995) of SiH is in excellent agreement with the value (0.994) derived from experiment (Smith and Liszt, 1971). The computational value of f00 for GeH (0.940) is in very good agreement with the experimental value 0.928 (Erman et al., 1983).
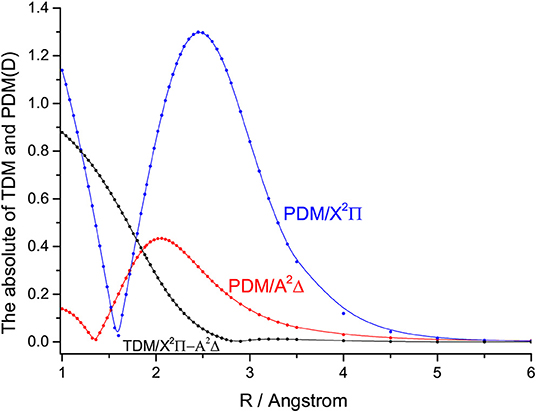
Figure 5. The permanent dipole moments (PDMs) and transition dipole moments (TDMs) for the X2Π and A2Δ states of SiH at the icMRCI+Q level.
3.2. The Comparison of the Feasibility of Laser Cooling for Group IVA Hydrides
There are some similar properties of group IVA hydrides. The inner closed-shell orbitals are occupied with 2, 10, 28, 46, and 78 electrons for CH, SiH, GeH, SnH, and PbH, respectively. The equilibrium bond length Re increases regularly from CH to PbH, while the harmonic constant ωe decreases in the order of CH>SiH>GeH>SnH>PbH (Huber and Herzberg, 1979; Alekseyev et al., 1996; Zhao et al., 2017). The comparison of the feasibility of laser cooling for group IVA hydrides is summarized here. An amplified view of crossing regions of PECs for SiH, GeH, SnH, and PbH is shown in Figure 6, we see that the dissociation energies of the A2Δ states of SiH, GeH, SnH, and PbH are 7735.89, 4465.21, 2849.26, and 798.36 cm−1, respectively. This trend is consistent when the second-row CH is included and the corresponding dissociation energy is 16641.68 cm−1 (Wells and Lane, 2011b). The depths of the A2Δ state decrease from CH to PbH, and it supports only one vibrational level for PbH. In equilibrium region, two electrons anti-parallelly are distributed on one (n/n) and two (n) sp3 hybridized orbitals for the B2Σ− and A2Δ states, respectively. The hybridized orbital effect vanishes as the internuclear distance increases to the asymptotic region. Where, n/n goes to X(3P) and n goes to X(1D). Therefore, there is a crossing point between the B2Σ− and A2Δ states of group IVA hydrides. The electronic state crossing between the B2Σ− and A2Δ states can lead to nonradiative transition (Wu et al., 2019), and may cause predissociation. This kind of electronic state crossing in a diatomic molecule will become potential energy surface intersections in the polyatomic cases involving multiple electronic states (Liu et al., 2003; Zhao et al., 2006). We find that the locations of crossing point between the B2Σ− and A2Δ states have the tendency of moving downwards from CH to SnH relative to the bottom of the corresponding A2Δ state potential. The locations of crossing point between the B2Σ− and A2Δ states of GeH and SnH are 591 and 255 cm−1 lower than the corresponding vibrational level ν′ = 0 in the A2Δ, while that of third-row SiH is 670 cm−1 higher than the vibrational level ν′ = 0 in the A2Δ. This trend is consistent when the second-row CH is included since the corresponding crossing point is 3,000 cm−1 higher (Wells and Lane, 2011b).
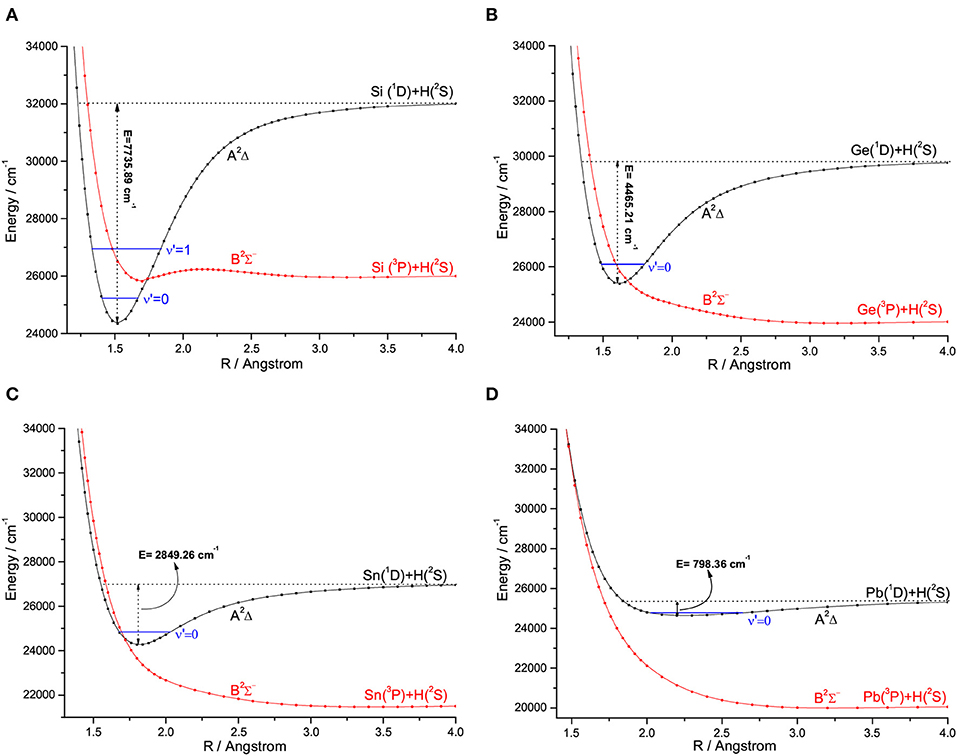
Figure 6. An amplified view of crossing regions of potential energy curves for SiH (A), GeH (B), SnH (C), and PbH (D).
The location of crossing point between the B2Σ− and A2Δ states of SiH is higher than the vibrational level ν′ = 0 in the A2Δ, indicating that laser cooling of SiH in the A2Δ→X2Π transition may not be affected by electronic state crossing. However, our results imply that the crossing between the B2Σ− and A2Δ states of GeH will lead to predissociation of all vibrational levels of the A2Δ state, which is backed up by experiments of Erman et al. (1983) using high frequency deflection technique. They reported that, 80–90% of the GeH molecules excited to the A2Δ state decay via predissociation to their ground state atomic constituents, and fewer than 20% of the molecules follow the regular decay route to the ground state. Furthermore, the A2Δ states of SnH and PbH have a similar problem to that of GeH, although there has been no relevant experimental measurements reported. It is clear that GeH and SnH can not be used for laser cooling due to the electronic state crossing. In addition, the small Franck-Condon factor f00 (0.08) of PbH also suggests that it is not suitable for laser cooling.
It seems that both CH and SiH are very good laser cooling candidates, and we make a comparison in the following. The f00 of SiH (0.995) is close to that of CH (0.9957) (Wells and Lane, 2011b). The radiative lifetimes of the A2Δ state of SiH and CH are 575 and 536 ns (Wells and Lane, 2011b), respectively. The TDoppler and Trecoil of SiH (6.65 and 3.89 μK) are also similar to that of CH (7.13 and 7.91 μK) (Wells and Lane, 2011b). The calculated pump and repump wavelengths for SiH and CH are all in the visible region. The electronic state crossing between the B2Σ− and A2Δ states of CH is higher than that of SiH, with both crossing points located above the corresponding vibrational ν′ = 0 levels in the A2Δ state. Generally speaking, a larger atomic mass difference for the diatomic candidate is desirable by experimentalists, and in this respect, SiH is better than CH. Furthermore, we will propose a scheme using two spin-orbit states for SiH in the next section, which is more feasible than the one using two Λ-S states for CH. The A2Δ→X2Π transition of CH was used to establish a laser cooling scheme, and the SOC effects were not included (Wells and Lane, 2011a). With the inclusion of the SOC effects into the icMRCI wave functions in our calculations, accurate Ω states are determined. The calculated spectroscopic constants of SiH are in very good accordance with experimental measurements. The prospect for the production of ultracold SiH molecules by means of direct laser cooling method is discussed below.
3.3. Laser Cooling Scheme for SiH
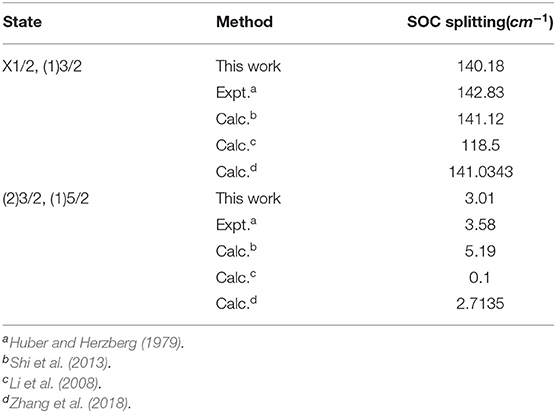
When the SOC effects are taken into account, seven Ω states, involving four states with Ω = 1/2, two states with Ω = 3/2 and one state with Ω = 5/2, are generated from the five Λ-S states of SiH. The PECs of the Ω states are depicted in Figure 7. The SOC splitting of the X2Π and A2Δ states of SiH is shown in Table 3. As seen, the energy separation of the and is 140.18 cm−1 in this work, which is in excellent agreement with the experimental value (142.83 cm−1) (Huber and Herzberg, 1979). For the and states, the energy separation is 3.01 cm−1.
We find that, the → transition is suitable for laser cooling in three possible transitions, →, →, and →. In the → transition, SiH molecules will jump from the (ν = 0) to the (ν′ = 0), then the (ν′ = 0) state will decay to the rather than according to the selection rules. The → transition can ensure a closed-loop cooling cycle, while the other two transitions can not. The three-laser cooling scheme proposed in the following using the → transition is more feasible than the one proposed by Zhang et al. (2018) without including the SOC effects. More importantly, they did not consider the effect of electronic state crossing, and proposed a laser cooling cycle for SiH involving the ν′ = 1 vibrational level of the A2Δ state, which would predissociation before the radiative transition and can not be used to establish laser cooling cycles.
The TDMs of SiH for the → transition at the icMRCI+Q level are represented in Figure 8. The TDMs of SiH is 0.6157 D at Re. The FCFs values of the → transition for SiH are computed and shown in Figure 9. As seen, the Δν = 0 transitions are significantly larger than those for the off-diagonal terms. The present value of f00 (0.9949) is so large that the spontaneous decays to ν = 1,2 vibrational levels in the are significantly restrained. Additionally, the relative strengths of the photon loss pathways are more directly related to the vibrational branching ratios than the FCFs in the laser cooling cycle (Lane, 2015). Furthermore, we calculate the Einstein A coefficients and vibrational branching ratios of the → transition for SiH. The and of the → transition are listed in Table 4. As seen in Table 4, a very large A00 (1.73 × 106 s−1) and very low scattering probabilities into off-diagonal bands (R01 = 3.61 × 10−3, R02 = 9.83 × 10−4, R03 = 9.20 × 10−8) of SiH contribute to a desirable condition for rapid and efficient laser cooling. It should be noted that R00 (0.9954) is slightly larger than f00 (0.9949), indicating that the probability of spontaneous decay to the (ν = 0) increases when the variations in transition wavelength are taken into account.
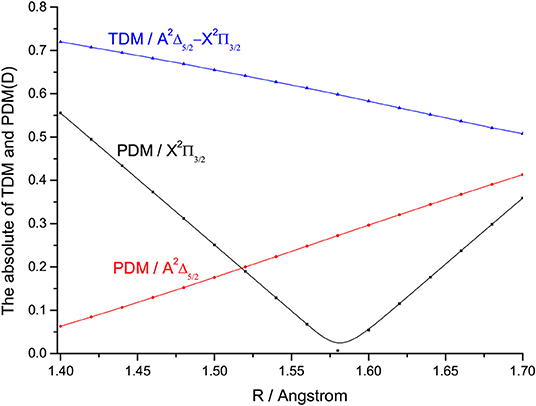
Figure 8. The permanent dipole moments (PDMs) and transition dipole moments (TDMs) for the and states of SiH at the icMRCI+Q level.
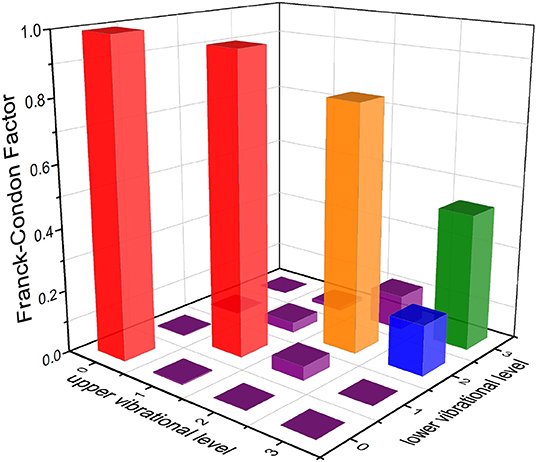
Figure 9. Franck-Condon factors of the (ν′ ≤ 3)→(ν ≤ 3) transition for SiH, calculated at the icMRCI+Q level.

Table 4. Calculated Einstein A coefficients and vibrational branching ratio of the (ν′) → transition for SiH.
The vibrational branching ratios is determined by the following expression:
Moreover, the Doppler temperature (TDoppler) is the achievable minimum temperature of translational cooling with the Doppler method, it is obtained by the following expression:
where kB and h are Boltzmann′s constant and Planck′s constant, respectively (You et al., 2016). The radiative lifetime (τ) for the (ν′ = 0) of SiH is 575 ns and TDoppler is 6.65 μK. Additionally, the recoil temperature (Trecoil) is calculated by the following expression:
and the obtained Trecoil for the transition of SiH is 3.89 μK.
The proposed scheme to facilitate the laser cooling of SiH is shown in Figure 10. The large R00 (0.9954) of SiH indicates that the transition has the largest probabilities. A desirable laser cooling cycle needs to solve the vibrational branching loss. Therefore, the off-diagonal vibrational branching ratios of SiH are calculated, and the probabilities of decay from the (ν ′ = 0) to the (ν = 1, 2) are firstly obtained (R01 = 3.61 × 10−3 and R02 = 9.83 × 10−4). Besides, the probabilities of the unwanted decay channels are also computed by using R03++R02×R13+. The negligible value of 1.0 × 10−5 means that the present scheme will allow for at least 1.0 × 105 photon absorption/emission cycles, which are sufficient enough to decelerate SiH in a cryogenic beam, in principle (Shuman et al., 2010). The laser cooling scheme takes the transition as the main pump, and as the first and second vibrational repump, respectively. Accurate Te is crucial for estimating the pump and repump wavelengths in laser cooling cycles, and our calculated Te values, which are very close to experimental ones, give confidence in the subsequent study on laser cooling, especially, for SiH. The calculated value of wavelength λ01 should be larger than λ00, however, the wavelengths λ01 obtained by Zhang et al. (2018), is 376.88 nm, which is smaller than that of their main pump. In our laser-driven cycling, the calculated pump and repump wavelengths of λ00, λ01, and λ02 are 412.6, 449.7, and 491.8 nm, respectively. The required wavelengths are all in the range of 400–500 nm and can be produced with the frequency doubled semiconductor laser, which has been used for the laser cooling experiment of the strontium atom (Wang et al., 2009). The SiH molecules will stay in the laser cooling cycle until the decay to ν≥3 ().
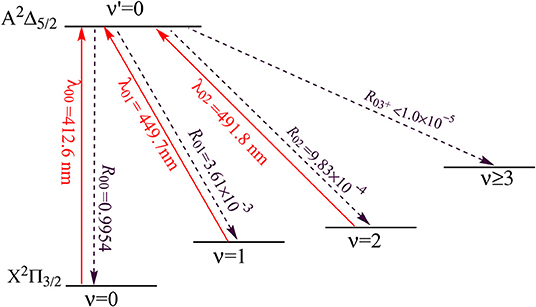
Figure 10. Proposed three-laser cooling scheme for SiH using the → transitions. Solid arrows indicate laser-driven transitions at certain wavelengths . Dashed arrows indicate spontaneous decays from the state with the calculated .
3.4. Laser Cooling Scheme for CS
We further find that CS is a promising candidate based on the criteria mentioned above. The PECs of CS, obtained at the icMRCI+Q level, is shown in Figure 11. Our calculated Re and ωe of the X1Σ+ of CS are 1.5380 Å and 1288.63 cm−1, respectively, which are in very good accordance with the corresponding experimental values (1.5349 Å and 1285.1 cm−1) (Huber and Herzberg, 1979). As for the A2Δ state of CS, our calculated Te 39175.96 cm−1 is in agreement with the experimental value 38,904 cm−1 (Huber and Herzberg, 1979). The calculated vibrational branching ratio R00 is 0.885, which is highly diagonal.
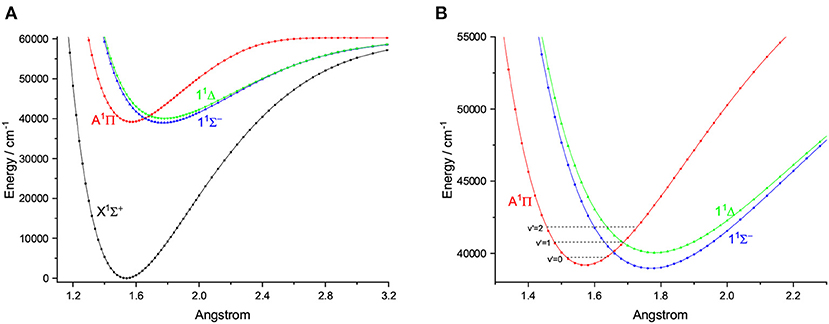
Figure 11. Potential energy curves of CS for the four Λ-S states at the icMRCI+Q level (A) and an amplified view of crossing regions of potential energy curves (B).
As shown in Figure 11, the PEC of A1Π crosses with those of two other electronic states, however, from an amplified view of the crossing regions we see that, the two crossing points are higher than the ν′ = 0 vibrational level of the A1Π state. So this kind of crossing would not affect laser cooling cycles using the A1Π(ν′ = 0)→X1Σ+(ν <3) transition. A suitable laser cooling scheme using the A1Π→X1Σ+ transition of CS is proposed and shown in Figure 12. The scheme takes the transition A1Π(ν′ = 0)→X1Σ+(ν = 0) as the main pump, A1Π(ν′ = 0)→X1Σ+(ν = 1) and A1Π(ν′ = 0)→X1Σ+(ν = 2) as the first and second vibrational repump, respectively. The radiative lifetime of the A1Π state is 70 ns, whereas the TDoppler and Trecoil of the A1Π→X1Σ+ transition are 54.61 and 6.64 μK, respectively. The large R00, short radiative lifetime and ultracold temperatures suggest CS as a promising candidate for rapid and efficient laser cooling.
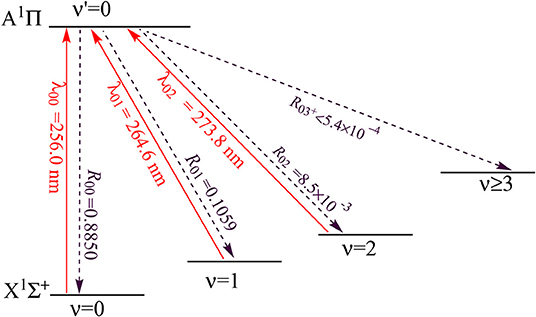
Figure 12. Proposed three-laser cooling scheme for CS using the A1Π→X1Σ+ transitions. Solid arrows indicate laser-driven transitions at certain wavelengths . Dashed arrows indicate spontaneous decays from the A1Π(ν′ = 0) state with the calculated .
4. Conclusions
The fourth criterion for molecular laser cooling is proposed in this work, that is, there is no electronic-state crossing, or the crossing point is high enough in energy. Its importance is demonstrated by investigating the laser cooling feasibility of group IVA hydrides and carbon monosulfide.
Ab initio and dynamical calculations are performed, and the calculated spectroscopic constants are in very good agreement with the available experimental data. We find that the locations of crossing point between the B2Σ− and A2Δ states have the tendency of moving downwards from CH to SnH relative to the bottom of the corresponding A2Δ potential, and this would lead to failure of cooling GeH and SnH. The potential wells of the A2Δ state of group IVA hydrides become shallower and shallower from CH to PbH, with the Franck-Condon factor decreasing, which results in a very small Franck-Condon factor for PbH. It is clear that PbH is not a suitable candidate for laser cooling either. We further propose a practical and efficient laser-cooling scheme for SiH using the → transition. The calculated excitation energy is 24299.20 cm−1, which is in perfect agreement with the experimental data (24300.4 cm−1). This allows us accurately estimate the pump and repump wavelengths in laser cooling cycles, which is shown to vary from 400 to 500 nm and are easily accessible in experiment. The Doppler temperature and recoil temperature of SiH for the → transition are 6.65 and 3.89 μK, respectively. The computed radiative lifetime is 575 ns, and the vibrational branching ratio is highly diagonally distributed with the R00 being 0.9954. Furthermore, we performed additional calculations, and find that, the carbon monosulfide (CS) is a promising candidate which meets the four criteria, and we further propose a suitable laser cooling scheme. We hope that this work will be helpful in searching for promising candidates for producing ultracold molecules.
Data Availability Statement
All datasets generated for this study are available within the article and from the corresponding author on request.
Author Contributions
DL carried out the MRCI calculations. DL, MF, HM, and WB analyzed the data and interpreted the results. ZD and CC provided computing assistance. DL, HM, and WB developed the theoretical scheme and wrote the paper. WB supervised the research and proposed the fourth criterion for molecular laser cooling.
Funding
This work was supported by the National Natural Science Foundation of China (Nos. 21773251, 21973098), the Beijing National Laboratory for Molecular Sciences and Chinese Academy of Sciences.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fchem.2020.00020/full#supplementary-material
References
Alekseyev, A. B., Liebermann, H. P., Buenker, R. J., and Hirsch, G. (1996). Ab initio study of the low-lying states of SnH. Mol. Phys. 88, 591–603. doi: 10.1080/00268979609482439
Baron, J., Campbell, W. C., Demille, D., Doyle, J. M., Gabrielse, G., Gurevich, Y. V., et al. (2014). Order of magnitude smaller limit on the electric dipole moment of the electron. Science 343, 269–272. doi: 10.1126/science.1248213
Bauer, W., Becker, K. H., Düren, R., Hubrich, C., and Meuser, R. (1984). Radiative lifetime measurements of SiH (A2Δ) by laser-induced fluorescence. Chem. Phys. Lett. 108, 560–561. doi: 10.1016/0009-2614(84)85054-X
Bauer, W., Engelhardt, B., Wiesen, P., and Becker, K. H. (1989). Lifetime measurements of GeH and CH in the A2Δ, ν′ = 0 state by laser induced fluorescence. Chem. Phys. Lett. 158, 321–324. doi: 10.1016/0009-2614(89)87344-0
Betrencourt, M., Boudjaadar, D., Chollet, P., Guelachvili, G., and Morillon-Chapey, M. (1986). Infrared emission spectrum of the radical 28SiH: observation and analysis of the rovibrational bands 1−0, 2−1, and 3−2 in the X2Π ground state. J. Chem. Phys. 84, 4121–4126. doi: 10.1063/1.450081
Bollmark, P., Klynning, L., and Pages, P. (1971). Rotational analysis of the 3250 Å bands of SiH and SiD. Phys. Scripta 185, 219–222. doi: 10.1088/0031-8949/3/5/004
Bruna, P. J., and Grein, F. (2001). Ab initio study of the X3Σ−, a1Δ, b1Σ+ states of GeH−, and electron affinity of GeH. J. Mol. Spectrosc. 599, 261–269. doi: 10.1016/S0022-2860(01)00829-8
Cade, P. E., and Huo, W. M. (1967). Electronic structure of diatomic molecules. VI.A. Hartree-Fock wavefunctions and energy quantities for the ground states of the second-row hydrides, AH. J. Chem. Phys. 47, 614–648. doi: 10.1063/1.1711938
Cao, J., Li, F., Xia, W., and Bian, W. (2019). van der Waals interactions in bimolecular reactions. Chinese J. Chem. Phys. 32, 157–166. doi: 10.1063/1674-0068/cjcp1901007
Carr, L., Demille, D., Krems, R., and Ye, J. (2009). Cold and ultracold molecules: science, technology and applications. New J. Phys. 11:055049. doi: 10.1088/1367-2630/11/5/055049
Chapman, D. A., Li, J., Balasubramanian, K., and Lin, S. H. (1988). Theoretical study of electric dipole and transition moments of GeH, SnH and PbH. J. Chem. Phys. 88, 3826–3833. doi: 10.1063/1.453883
Di Rosa, M. D. (2004). Laser-cooling molecules: concept, candidates, and supporting hyperfine-resolved measurements of rotational lines in the A-X(0,0) band of CaH. Eur. Phys. J. D 31, 395–402. doi: 10.1140/epjd/e2004-00167-2
Erman, P., Gustafsson, O., and Larsson, M. (1983). New predissociations in GeH affecting all the A2Δ state levels. Phys. Scripta 27, 256–260. doi: 10.1088/0031-8949/27/4/006
Fu, M., Cao, J., Ma, H., and Bian, W. (2016a). Laser cooling of copper monofluoride: a theoretical study including spin-orbit coupling. RSC Adv. 6, 100568–100576. doi: 10.1039/C6RA07835D
Fu, M., Ma, H., Cao, J., and Bian, W. (2016b). Extensive theoretical study on electronically excited states of calcium monochloride: molecular laser cooling and production of ultracold chlorine atoms. J. Chem. Phys. 144:184302. doi: 10.1063/1.4948631
Fu, M., Ma, H., Cao, J., and Bian, W. (2017). Laser cooling of CaBr molecules and production of ultracold Br atoms: a theoretical study including spin-orbit coupling. J. Chem. Phys. 146:134309. doi: 10.1063/1.4979566
González-Sánchez, L., Gómez-Carrasco, S., Santadaría, A., Wester, R., and Gianturco, F. (2019). Collisional quantum dynamics for MgH− (1Σ+) with He as a buffer gas: ionic state-changing reactions in cold traps. Front. Chem. 7:64. doi: 10.3389/fchem.2019.00064
Huber, K. P., and Herzberg, G. (1979). Molecular Spectra and Molecular Structure IV: Constants of Diatomic Molecules. New York, NY: Van Nostrand Reinhold.
Hudson, J. J., Kara, D. M., Smallman, I. J., Sauer, B. E., Tarbutt, M. R., and Hinds, E. A. (2011). Improved measurement of the shape of the electron. Nature 473, 493–496. doi: 10.1038/nature10104
Hummon, M. T., Yeo, M., Stuhl, B. K., Collopy, A. L., Xia, Y., and Ye, J. (2013). 2D Magneto-optical trapping of diatomic molecules. Phys. Rev. Lett. 110:143001. doi: 10.1103/PhysRevLett.110.143001
Jackson, C. V. (1930). The spectrum of silicon hydride. Proc. R. Soc. Lond. Ser. A 126, 373–405. doi: 10.1098/rspa.1930.0015
Johnson, R. D. III., and Hudgens, J. W. (1989). New electronic state of silylidyne and silylidyned radicals observed by resonance-enhance multiphoton ionization spectroscopy. J. Phys. Chem. 93, 6268–6270. doi: 10.1021/j100354a003
Kalemos, A., Mavridis, A., and Metropoulos, A. (2002). An accurate description of the ground and excited states of SiH. J. Chem. Phys. 116, 6529–6540. doi: 10.1063/1.1461817
Kleman, B., and Werhagen, E. (1953b). A4Σ−→X2Π system in germanium hydride (GeH). Arkiv Fysik 6:399.
Klynning, L., and Lindgren, B. (1966). Rotational analysis of the 2Δ→2Π band system of germanium hydride and of deuteride germanium. Arkiv Fysik 32:575.
Lane, I. C. (2015). Production of ultracold hydrogen and deuterium production via Doppler-cooled Feshbach molecules. Phys. Rev. A 92:022511. doi: 10.1103/PhysRevA.92.022511
Langhoff, S. R., and Davidson, E. R. (1974). Configuration interaction calculations on the nitrogen molecule. Int. J. Quant. Chem. 8, 61–72. doi: 10.1002/qua.560080106
Le Roy, R. J. (2007). LEVEL 8.0: A Computer Program for Solving the Radial Schrödinger Equation for Bound and Quasibound Levels, Chemical Physics Research Report CPRR-663. University of Waterloo. Available online at: http://leroy.uwaterloo.ca
Lewerenz, M., Bruna, P. J., Peyerimhoff, S. D., and Buenker, R. J. (1983). Ab initio MRD-CI study of the electronic spectrum of SiH. Mol. Phys. 49, 1–24. doi: 10.1080/00268978300101001
Li, G., Gao, T., and Zhang, Y. (2008). The splitting of low-lying or low excited states for hydride molecules (cations) of the third period under spin-orbit coupling. Chinese Phys. B 17, 2040–2047. doi: 10.1088/1674-1056/17/6/018
Li, R., Zhai, Z., Zhang, X., Jin, M., Xu, H., and Yan, B. (2015). All-electron spin-orbit configuration interaction study on the valence and low-lying Rydberg electronic states of GeH. J. Quant. Spectrosc. Radiat. Transf. 157, 42–53. doi: 10.1016/j.jqsrt.2015.02.009
Liu, C., Zhang, D., and Bian, W. (2003). Theoretical investigation of the reaction of Co+ with OCS. J. Phys. Chem. A 107, 8618–8622. doi: 10.1021/jp034693s
Liu, K., Yu, L., and Bian, W. (2009). Extensive theoretical study on various low-lying electronic states of silicon monochloride cation including spin-orbit coupling. J. Phys. Chem. A 113:1678. doi: 10.1021/jp809618y
Perrin, J., and Delafosse, E. (1980). Emission spectroscopy of SiH in a silane glow-discharge. J. Phys. D Appl. Phys. 13:759. doi: 10.1088/0022-3727/13/5/009
Ram, R. S., Engleman, R., and Bernath, P. F. (1998). Fourier transform emission spectroscopy of the A2Δ→X2Π transition of SiH and SiD. J. Mol. Spectrosc. 190, 341–352. doi: 10.1006/jmsp.1998.7582
Setzer, K. D., Borkowska-Burnecka, J., Zyrnicki, W., and Fink, E. H. (2008). High-resolution fourier-transform study of the fine structure transitions of PbH and PbD. J. Mol. Spectrosc. 252, 176–184. doi: 10.1016/j.jms.2008.08.003
Shen, Z., Ma, H., Zhang, C., Fu, M., Wu, Y., Bian, W., et al. (2017). Dynamical importance of van der Waals saddle and excited potential surface in C(1D)+D2 complex-forming reaction. Nat. Commun. 8:14094. doi: 10.1038/ncomms14094
Shi, D., Li, P., Zhu, Z., and Sun, J. (2013). Spin-orbit coupling splitting in the X2Π, A2Δ, B2Σ−, C2Σ+, D2Σ+, F2Π and a4Σ− Λ-S states of SiH radical. Spectrochim. Acta Part A 115, 259–268. doi: 10.1016/j.saa.2013.06.038
Shi, D., Zhang, J., Sun, J., Zhu, Z., Yu, B., and Liu, Y. (2008). Investigations on spectroscopic properties of SiH (X2Π) radical using coupled-cluster theory in combination with the correlation-consistent quintuple basis set. J. Mol. Struct. Theochem 851, 30–34. doi: 10.1016/j.theochem.2007.10.033
Shuman, E. S., Barry, J. F., and Demille, D. (2010). Laser cooling of a diatomic molecule. Nature 467, 820–823. doi: 10.1038/nature09443
Simah, D., Hartke, B., and Werner, H. J. (1999). Photodissociation dynamics of H2S on new coupled ab initio potential energy surfaces. J. Chem. Phys. 111, 4523–4534. doi: 10.1063/1.479214
Smith, W. H. (1969). Lifetimes and total transition probabilities for NH, SiH, and SiD. J. Chem. Phys. 51, 520–524. doi: 10.1063/1.1672027
Smith, W. H., and Liszt, H. S. (1971). Franck-Condon factors and absolute oscillator strengths for NH, SiH, S2 and SO. J. Quant. Spectrosc. Radiat. Transf. 11, 45–54. doi: 10.1016/0022-4073(71)90160-9
Towle, J. P., and Brown, J. M. (1993). The infrared spectrum of the GeH radical. Mol. Phys. 79, 249–261. doi: 10.1080/00268979300100211
Wang, S., Wang, Q., Lin, Y., Wang, M., Lin, B., Zang, E., et al. (2009). Cooling and trapping 88Sr atoms with 461 nm laser. Chinese Phys. Lett. 26:093202. doi: 10.1088/0256-307X/26/9/093202
Watson, W. W. (1938). The spectrum of lead hydride. Phys. Rev. 54, 639–642. doi: 10.1103/PhysRev.53.639
Wells, N., and Lane, I. C. (2011a). Electronic states and spin-forbidden cooling transitions of AlH and AlF. Phys. Chem. Chem. Phys. 13, 19018–19025. doi: 10.1039/c1cp21313j
Wells, N., and Lane, I. C. (2011b). Prospects for ultracold carbon via charge exchange reactions and laser cooled carbides. Phys. Chem. Chem. Phys. 13, 19036–19051. doi: 10.1039/c1cp21304k
Werner, H.-J., and Knowles, P. J. (1985). A second order multiconfiguration SCF procedure with optimum convergence. J. Chem. Phys. 82, 5053–5063. doi: 10.1063/1.448627
Werner, H.-J., Knowles, P. J., Lindh, R., Manby, F. R., Schütz, M., Celani, P., et al. (2012). Molpro, Version 2012.1, A Package of Ab Initio Programs. Available online at: http://www.molpro.net
Wu, Y., Cao, J., Ma, H., Zhang, C., Bian, W., Nunez-Reyes, D., et al. (2019). Conical intersection–regulated intermediates in bimolecular reactions: insights from C(1D) + HD dynamics. Sci. Adv. 5:eaaw0446. doi: 10.1126/sciadv.aaw0446
Xia, W., Fu, M., Ma, H., and Bian, W. (2017). A theoretical study on laser cooling of silicon monofluoride. Chem. Phys. 485–486, 29–34. doi: 10.1016/j.chemphys.2017.01.007
Xu, S., Xia, M., Yin, Y., Gu, R., Xia, Y., and Yin, J. (2019). Determination of the normal A2Π state in MgF with application to direct laser cooling of molecules. J. Chem. Phys. 150:084302. doi: 10.1063/1.5083898
Yan, B., Moses, S. A., Gadway, B., Covey, J. P., Hazzard, K. R. A., Rey, A. M., et al. (2013). Observation of dipolar spin-exchange interactions with lattice-confined polar molecules. Nature 501, 521–525. doi: 10.1038/nature12483
You, Y., Yang, C. L., Zhang, Q. Q., Wang, M. S., Ma, X. G., and Liu, W. W. (2016). Ab initio studies on the spin-forbidden cooling transitions of the LiRb molecule. Phys. Chem. Chem. Phys. 18:19838. doi: 10.1039/C6CP01618A
Yu, L., and Bian, W. (2011). Extensive theoretical study on electronically excited states and predissociation mechanisms of sulfur monoxide including spin-orbit coupling. J. Comput. Chem. 32, 1577–1588. doi: 10.1002/jcc.21737
Yu, L., and Bian, W. (2012). Electronically excited-state properties and predissociation mechanisms of phosphorus monofluoride: a theoretical study including spin-orbit coupling. J. Chem. Phys. 137:014313. doi: 10.1063/1.4731635
Zhang, Y., Dou, G., Qi, J., and Cui, J. (2018). Ab inito study on the electronic structure and laser cooling of SiH. Comput. Theor. Chem. 1134, 8–14. doi: 10.1016/j.comptc.2018.04.014
Zhao, H., Bian, W., and Liu, K. (2006). A theoretical study of the reaction of O(3P) with isobutene. J. Phys. Chem. A 110, 7858–7866. doi: 10.1021/jp060583k
Zhao, S., Li, R., Zhang, H., and Li, H. (2017). MRCI+Q calculations on spectroscopic properties of excited states of PbH including spin-orbit coupling. Chem. Phys. Lett. 671, 92–99. doi: 10.1016/j.cplett.2017.01.016
Keywords: laser cooling, ab initio, spin-orbit coupling, electronic state crossing, group IVA hydrides
Citation: Li D, Fu M, Ma H, Bian W, Du Z and Chen C (2020) A Theoretical Study on Laser Cooling Feasibility of Group IVA Hydrides XH (X = Si, Ge, Sn, and Pb): The Role of Electronic State Crossing. Front. Chem. 8:20. doi: 10.3389/fchem.2020.00020
Received: 10 October 2019; Accepted: 08 January 2020;
Published: 28 January 2020.
Edited by:
Zhuhua Zhang, Nanjing University of Aeronautics and Astronautics, ChinaReviewed by:
Jiangtan Yuan, Northwestern University, United StatesSunny Gupta, Rice University, United States
Copyright © 2020 Li, Fu, Ma, Bian, Du and Chen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Haitao Ma, bWh0QGljY2FzLmFjLmNu; Wensheng Bian, YmlhbkBpY2Nhcy5hYy5jbg==
 Donghui Li1,2
Donghui Li1,2 Mingkai Fu
Mingkai Fu Haitao Ma
Haitao Ma Wensheng Bian
Wensheng Bian