- 1Laboratoire de Chimie et Physique Quantiques, Université de Toulouse, CNRS, UPS, Toulouse, France
- 2Laboratoire de Physique Théorique, Université de Toulouse, CNRS, UPS and ETSF, Toulouse, France
Using the simple (symmetric) Hubbard dimer, we analyze some important features of the GW approximation. We show that the problem of the existence of multiple quasiparticle solutions in the (perturbative) one-shot GW method and its partially self-consistent version is solved by full self-consistency. We also analyze the neutral excitation spectrum using the Bethe-Salpeter equation (BSE) formalism within the standard GW approximation and find, in particular, that 1) some neutral excitation energies become complex when the electron-electron interaction U increases, which can be traced back to the approximate nature of the GW quasiparticle energies; 2) the BSE formalism yields accurate correlation energies over a wide range of U when the trace (or plasmon) formula is employed; 3) the trace formula is sensitive to the occurrence of complex excitation energies (especially singlet), while the expression obtained from the adiabatic-connection fluctuation-dissipation theorem (ACFDT) is more stable (yet less accurate); 4) the trace formula has the correct behavior for weak (i.e., small U) interaction, unlike the ACFDT expression.
1 Introduction
Many-body perturbation theory (MBPT) based on Green’s functions is among the standard tools in condensed matter physics for the study of ground- and excited-state properties. (Aryasetiawan and Gunnarsson, 1998; Onida et al., 2002; Martin et al., 2016; Golze et al., 2019). In particular, the GW approximation (Hedin, 1965; Golze et al., 2019) has become the method of choice for band-structure and photoemission calculations and, combined with the Bethe-Salpeter equation (BSE@GW) formalism, (Salpeter and Bethe, 1951; Strinati, 1988; Albrecht et al., 1998; Rohlfing and Louie, 1998; Benedict et al., 1998; van der Horst et al., 1999a; Blase et al., 2018, 2020), for optical spectra calculations. Thanks to efficient implementations, (Duchemin and Blase, 2019, 2020, 2021; Bruneval et al., 2016; van Setten et al., 2013; Kaplan et al., 2015, 2016; Krause and Klopper, 2017; Caruso et al., 2012, 2013b,a; Caruso, 2013; Wilhelm et al., 2018), this toolkit is acquiring increasing popularity in the traditional quantum chemistry community, (Rohlfing and Louie, 1999; van der Horst et al., 1999b; Puschnig and Ambrosch-Draxl, 2002; Tiago et al., 2003; Boulanger et al., 2014; Jacquemin et al., 2015b; Bruneval et al., 2015; Jacquemin et al., 2015a; Hirose et al., 2015; Jacquemin et al., 2017a,b; Rangel et al., 2017; Krause and Klopper, 2017; Gui et al., 2018; Blase et al., 2018; Liu et al., 2020; Blase et al., 2020; Holzer and Klopper, 2018; Holzer et al., 2018; Loos et al., 2020), partially due to the similarity of the equation structure to that of the standard Hartree-Fock (HF) (Szabo and Ostlund, 1989) or Kohn-Sham (KS) (Hohenberg and Kohn, 1964; Kohn and Sham, 1965) mean-field methods. Several studies of the performance of various flavors of GW in atomic and molecular systems are now present in the literature, (Holm and von Barth, 1998; Stan et al., 2006; Stan et al., 2009; Blase and Attaccalite, 2011; Faber et al., 2011; Bruneval, 2012; Bruneval and Marques, 2013; Bruneval et al., 2015; Karlsson and van Leeuwen, 2016; Bruneval et al., 2016; Bruneval, 2016; Boulanger et al., 2014; Blase et al., 2016; Li et al., 2017; Hung et al., 2016, 2017; van Setten et al., 2015, 2018; Ou and Subotnik, 2016, 2018; Faber, 2014), providing a clearer picture of the pros and cons of this approach. There are, however, still some open issues, such as 1) how to overcome the problem of multiple quasiparticle solutions, (van Setten et al., 2015; Maggio et al., 2017; Loos et al., 2018; Véril et al., 2018; Duchemin and Blase, 2020; Loos et al., 2020), 2) what is the best way to calculate ground-state total energies, (Casida, 2005; Huix-Rotllant et al., 2011; Caruso et al., 2013b; Casida and Huix-Rotllant, 2016; Colonna et al., 2014; Olsen and Thygesen, 2014; Hellgren et al., 2015; Holzer et al., 2018; Li et al., 2019, 2020; Loos et al., 2020), and 3) what are the limits of the BSE in the simplification commonly used in the so-called Casida equations. (Strinati, 1988; Rohlfing and Louie, 2000; Sottile et al., 2003; Myöhänen et al., 2008; Ma et al., 2009a,b; Romaniello et al., 2009b; Sangalli et al., 2011; Huix-Rotllant et al., 2011; Sakkinen et al., 2012; Zhang et al., 2013; Rebolini and Toulouse, 2016; Olevano et al., 2019; Lettmann and Rohlfing, 2019; Loos and Blase, 2020; Authier and Loos, 2020; Monino and Loos, 2021). In the present work, we address precisely these questions by using a very simple and exactly solvable model, the symmetric Hubbard dimer. Small Hubbard clusters are widely used test systems for the GW approximation (e.g. Verdozzi et al., 1995; Schindlmayr et al., 1998; Pollehn et al., 1998; Puig von Friesen et al., 2010; Romaniello et al., 2009a, 2012). Despite its simplicity, the Hubbard dimer is able to capture lots of the underlying physics observed in more realistic systems, (Romaniello et al., 2009a, 2012; Carrascal et al., 2015, 2018), such as, for example, the nature of the band-gap opening in strongly correlated systems as bulk NiO. (Di Sabatino et al., 2016). Here, we will use it to better understand some features of the GW approximation and the BSE@GW approach. Of course, care must be taken when extrapolating conclusions to realistic systems.
The paper is organized as follows. Section 2 provides the key equations employed in MBPT to calculate removal and addition energies (or charged excitations), neutral (or optical) excitation energies, and ground-state correlation energies. In Sec. 3, we present and discuss the results that we have obtained for the Hubbard dimer. We finally draw conclusions and perspectives in Sec. 4.
2 Theoretical Framework
In the following we provide the key equations of MBPT (Martin et al., 2016) and, in particular, we discuss how one can calculate ground- and excited-state properties, namely removal and addition energies, spectral function, total energies, and neutral excitation energies. We use atomic units ℏ = m = e = 1 and work at zero temperature throughout the paper.
2.1 The GW Approximation
Within MBPT a prominent role is played by the one-body Green’s function G which has the following spectral representation in the frequency domain:
where μ is the chemical potential, η is a positive infinitesimal,
The one-body Green’s function is a powerful quantity that contains a wealth of information about the physical system. In particular, as readily seen from Eq. 1, it has poles at the charged excitation energies of the system, which are proper addition/removal energies of the N-electron system. Thus, one can also access the (photoemission) fundamental gap
where
The ground-state total energy can also be extracted from G using the Galitskii-Migdal (GM) formula (Galitskii and Migdal, 1958)
where 1 ≡ (x1, t1) is a space-spin plus time composite variable and h(r) = − ∇/2 + vext(r) is the one-body Hamiltonian, vext (r) being the local external potential.
The one-body Green’s function can be obtained by solving a Dyson equation of the form G = G0 + G0ΣG, where G0 is the non-interacting Green’s function and the self-energy Σ is an effective potential which contains all the many-body effects of the system under study. In practice, Σ must be approximated and a well-known approximation is the so-called GW approximation in which the self-energy reads ΣGW = vH + iGW, where vH is the classical Hartree potential, and W = ɛ−1vc is the dynamically screened Coulomb interaction, with ɛ−1 the inverse dielectric function and vc the bare Coulomb interaction. (Hedin, 1965).
The equations stemming from the GW approximation should, in principle, be solved self-consistently, since Σ is a functional of G. (Hedin, 1965). Self-consistency, however, is computationally demanding, and one often performs a single GW correction (for example using G0 as starting point one builds W and ΣGW as ΣGW = vH + iG0W0, with vH = − ivcG0 and
Here, we choose to start from HF spatial orbitals
while the satellite (sat) peaks
where the sum runs over all the solutions of the quasiparticle equation for a given mean-field eigenstate i. Throughout this article, i, j, k, and l denote general spatial orbitals, a and b refer to occupied orbitals, r and s to unoccupied orbitals, while m labels single excitations a → r.
In eigenvalue self-consistent GW (commonly abbreviated as evGW), (Hybertsen and Louie, 1986; Shishkin and Kresse, 2007; Blase and Attaccalite, 2011; Faber et al., 2011; Rangel et al., 2016; Gui et al., 2018), one only updates the poles of G, while keeping fix the orbitals (or weights). G is then used to build ΣGW and W. At the nth iteration, the removal/addition energies are obtained from the GW quasiparticle solutions computed from Gn−1W (Gn−1) where the satellites are discarded at each iteration. Nonetheless, at the final iteration one can keep the satellite energies to get the full spectral function (Eq. 3). In fully self-consistent GW (scGW), (Caruso et al., 2012, 2013b,a; Caruso, 2013; Koval et al., 2014), one updates the poles and weights of G retaining quasiparticle and satellite energies at each iteration.
It is instructive to mention that, for a conserving approximation, the sum of the intensities corresponding to removal energies equals the number of electrons, i.e.,
2.2 Bethe-Salpeter Equation
2.2.1 Neutral Excitations
Linear response theory (Oddershede and Jorgensen, 1977; Casida, 1995; Petersilka et al., 1996) in MBPT is described by the Bethe-Salpeter equation. (Strinati, 1988). The standard BSE within the static GW approximation (referred to as BSE@GW in this work, which means the use of GW quasiparticle energies to build the independent-particle excitation energies and of the GW self-energy to build the static exchange-correlation kernel) can be recast, assuming a closed-shell reference state, as a non-Hermitian eigenvalue problem known as Casida equations:
where
and the corresponding (static) screened Coulomb potential matrix elements
the BSE matrix elements read (Maggio and Kresse, 2016).
where
In the absence of instabilities (i.e., when Aλ − Bλ is positive-definite), (Dreuw and Head-Gordon, 2005), Eq. 8 is usually transformed into an Hermitian eigenvalue problem of half the dimension
where the excitation amplitudes are
Singlet (
2.2.2 Correlation Energies
Our goal here is to compare the BSE correlation energy
The ground-state correlation energy within the trace formula is calculated as
where Aσσ′ ≡Aλ=1,σσ′ is defined in Eq.11a and Tr denotes the matrix trace. We note that the trace formula is an approximate expression of the correlation energy since it relies on the so-called quasi-boson approximation and on the killing condition on the zeroth-order Slater determinant ground state (Li et al., 2020 for more details). Note that here both sums in Eq. 14 run over all resonant (hence real- and complex-valued) excitation energies while they are usually restricted to the real-valued resonant BSE excitation energies. Thus, the Tr@BSE correlation energy is potentially a complex-valued function in the presence of singlet and/or triplet instabilities.
The ACFDT formalism, (Furche and Van Voorhis, 2005), instead, provides an in-principle exact expression for the correlation energy within time-dependent density-functional theory (TDDFT). (Runge and Gross, 1984; Petersilka et al., 1996; Ullrich, 2012). In practice, however, one always ends up with an approximate expression, which quality relies on the approximations to the exchange-correlation potential of the KS system and to the kernel of the TDDFT linear response equations. In this work, therefore, we use the ACFDT expression within the BSE formalism and we explore how well it performs and how it compares to the trace Eq. 14.
Within the ACFDT framework, only the singlet states do contribute for a closed-shell ground state, and the ground-state BSE correlation energy
is obtained via integration along the adiabatic connection path from the non-interacting system at λ = 0 to the physical system λ = 1, where
is the interaction kernel, (Angyan et al., 2011; Holzer et al., 2018; Loos et al., 2020)
is the correlation part of the two-body density matrix at interaction strength λ. Here again, the AC@BSE correlation energy might become complex-valued in the presence of singlet instabilities.
Note that the trace and ACFDT formulas yield, for any set of eigenstates, the same correlation energy at the RPA level. (Angyan et al., 2011). Moreover, in contrast to density-functional theory where the electron density is fixed along the adiabatic path, (Langreth and Perdew, 1979; Gunnarsson and Lundqvist, 1976; Zhang and Burke, 2004), at the BSE@GW level, the density is not maintained as λ varies. Therefore, an additional contribution to Eq. 15 originating from the variation of the Green’s function along the adiabatic connection should, in principle, be added. However, as commonly done within RPA (Toulouse et al., 2009, 2010; Angyan et al., 2011; Colonna et al., 2014) and BSE, (Holzer et al., 2018; Loos et al., 2020), we neglect this additional contribution.
3 Results
As discussed in Sec. 1, in this work, we consider the (symmetric) Hubbard dimer as test case, which is governed by the following Hamiltonian
Here
3.1 Quasiparticle Energies in the GW Approximation
We test different flavors of self-consistency in GW calculations: one-shot GW, evGW, partial self-consistency through the alignment of the chemical potential (pscGW), where we shift G0 or GHF in such a way that the resulting G has the same chemical potential than the shifted G0 or shifted GHF, (Schindlmayr, 1997), and scGW. In the one-shot formalism, we also test two different starting points: the truly non-interacting Green’s function G0 (U = 0) and the HF Green’s function GHF. These two schemes are respectively labeled as G0W0 and GHFWHF in the following.
The G0W0 self-energy (in the site basis) and removal/addition energies are already given in Ref. (Romaniello et al., 2012) for the Hubbard dimer at one-half filling. For completeness we report them in Supplementary Appendix S1, together with the renormalization factors, which are discussed in Sec. 3.1.1.
Starting from GHF, which reads
where I and J run over the sites, the (correlation part of the) GHFWHF self-energy is
where
to build the screened interaction W = vc + vcPW, whose only non-zero matrix elements read
due to the local nature of the electron-electron interaction. The quantities defined in Eqs 19−22 can then be transformed to the bonding (bn) and antibonding (an) basis (which is used to recast the BSE as Eq. 8) thanks to the following expressions:
Therefore, the one-shot removal/addition energies read
with the quasiparticle solutions being
and
The evGW and scGW calculations were performed numerically using the meromorphic representation of G, following Ref. (Puig von Friesen et al., 2010) with some slight modifications (Supplementary Appendix S2 for more details). At each iteration, the solution of the Dyson equations for G and W (Sec. 2.1) produces extra poles. In order to keep the number of poles under control in scGW, the poles with intensities smaller than a user-defined threshold (set from 10–4 to 10–6 depending on the ratio U/t) are discarded and the corresponding spectral weight is redistributed among the remaining poles.
In Figure 1, we present the spectral function of G (Eq. 3) for different values of the ratio U/t (U/t = 1, 5, 10, and 15) and using GHF as starting point. We consider three GW variants: GHFWHF, evGW, and scGW. For U/t ≲ 3, all the schemes considered here provide a faithful description of the quasiparticle energies. For larger U/t, GW (regardless of the level of self-consistency) tends to underestimate the fundamental gap Eg (Eq. 2), as shown in the upper left panel of Figure 2. GHFWHF and evGW give a very similar estimate of Eg, whereas the quasiparticle intensity
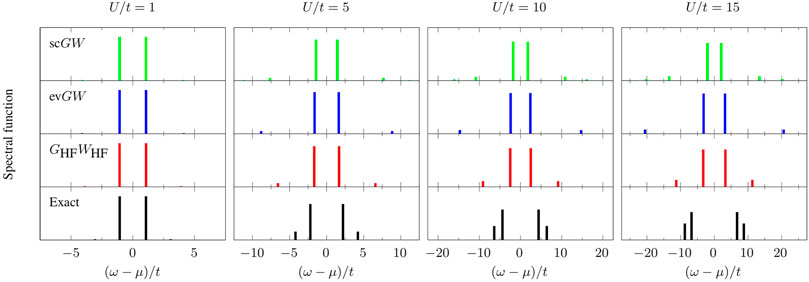
FIGURE 1. Spectral function of G (Eq. 3) as a function of (ω−μ)/t (where μ = U/2 is the chemical potential) at various values of the ratio U/t (U/t = 1, 5, 10, and 15) for different levels of theory: exact (black), GHFWHF (red), evGW (blue), and scGW (green). All approximate schemes are obtained using GHF as starting point.
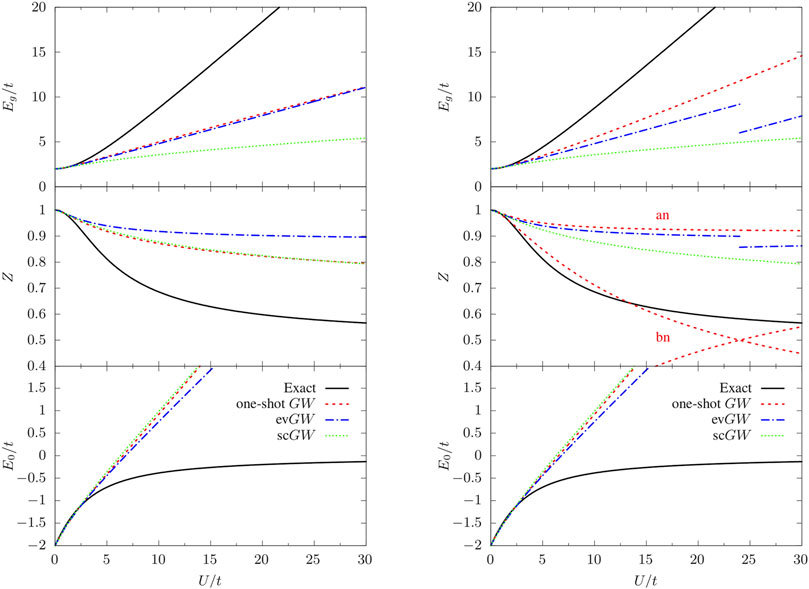
FIGURE 2. Fundamental gap (Eg), quasiparticle weight factors (
The main effects of full self-consistency are the reduction of Eg (see upper left panel of Figure 2), and the creation of extra satellites with decreasing intensity (see upper panel of Figure 1). For small U/t, the fundamental gap is similar to the one predicted by other methods while for increasing U/t the agreement worsen and Eg is grossly underestimated. The quasiparticle intensity is very similar to the one predicted by GHFWHF. Concerning the position of the satellites, we observe that the one-shot GHFWHF scheme gives the most promising results. Numerical values of quasiparticle and first satellite energies as well as their respective intensities in the spectral functions presented in Figure 1 are gathered in Table 1.

TABLE 1. Numerical values of quasiparticle energy
We notice that a similar analysis for H2 in a minimal basis has been presented in Ref. (Hellgren et al., 2015) with analogous conclusions.
For the sake of completeness, we also report in the bottom left panel of Figure 2 the total energy calculated using the Galitskii-Migdal formula (Eq. 4). Since the Galitskii-Migdal total energy is not stationary with respect to changes in G, one gets meaningful energies only at self-consistency. However, for the Hubbard dimer, we do not observe a significant impact of self-consistency, as one can see from Figure 1 by comparing the total energy at the GHFWHF, evGW, and scGW levels. For each of these schemes which correspond to a different level of self-consistency, the Galitskii-Migdal formula provides accurate total energies only for relatively small U/t (≲ 3).
If we consider GHF as starting point and we define the chemical potential as
3.1.1 G0: A Bad Starting Point
In the following we will illustrate how the starting point can influence the resulting quasiparticle energies. The Green’s function obtained from the one-shot G0W0 does not satisfy particle-hole symmetry, the fundamental gap is underestimated (top right panel of Figure 2) yet more accurate than GHFWHF (top left panel of Figure 2), the quasiparticle intensity relative to the bonding component is close to the exact result up to U/t ≈ 16 (center right panel of Figure 2), while overestimated for the antibonding components. Moreover, we note that the intensities of the two poles of the bonding component crosses at U/t = 24. This means that if we sort the quasiparticle and the satellite according to their intensity at a given U/t, the nature of the two poles is interchanged when one increases U/t, which results in a discontinuity in the QP energy. Meanwhile, the total number of particle is not conserved (N < 2). For G0W0 we found a small deviation from N = 2 for small U/t (e.g. N = 1.98828 at U = 1), which becomes larger by increasing the interaction (e.g. N = 1.55485 for U/t = 10). Instead, starting from GHF the particle number is always conserved. We checked that for the self-consistent calculations the total particle number is conserved, as it should.
Considering G0 as starting point in evGW, we encounter the problem described in Ref. (Véril et al., 2018), namely the discontinuity of various key properties (such as the fundamental gap in the top right panel of Figure 2) with respect to the interaction strength U/t. This issue is solved, for the Hubbard dimer, by considering a better starting point or using the fully self-consistent scheme scGW. Note, however, that improving the starting point does not always cure the discontinuity problem as this issue stems from the quasiparticle approximation itself. Full self-consistency, instead, avoids systematically discontinuities since no distinction is made between quasiparticle and satellites. Unfortunately, full self-consistency is much more involved from a computational point of view and, moreover, it does not give an overall improvement of the various properties of interest, at least for the Hubbard dimer, for which GHFWHF is to be preferred. For more realistic (molecular) systems, it was shown in Ref. (Berger et al., 2020). that the computationally cheaper self-consistent COHSEX scheme solves the problem of multiple quasiparticle solutions.
3.2 Bethe-Salpeter Equation
For the Hubbard dimer the matrices Aλ and Bλ in Eq. (8) are just single matrix elements and they simply read, for both spin manifolds,
while
We notice that, within the so-called Tamm-Dancoff approximation (TDA) where one neglects the coupling matrix Bλ between the resonant and anti-resonant parts of the BSE Hamiltonian (Eq. 8), BSE yields RPA with exchange (RPAx) excitation energies for the Hubbard dimer. This is the case also for approximations to the BSE kernel which are beyond GW, such as the T-matrix approximation. (Romaniello et al., 2012; Zhang et al., 2017; Li et al., 2021), and it is again related to the local nature of the electron-electron interaction. Hence, to test the effect of approximations on correlation for this model system we must go beyond the TDA.
3.2.1 Neutral Excitations
In Figure 3, we report the real part of the singlet and triplet excitation energies obtained from the solution of Eq. 8 for λ = 1. For comparison, we report also the exact excitation energies obtained as differences of the excited- and ground-state total energies of the Hubbard dimer obtained by diagonalizing the Hamiltonian (18) in the Slater determinant basis
while the unique triplet transition energy is
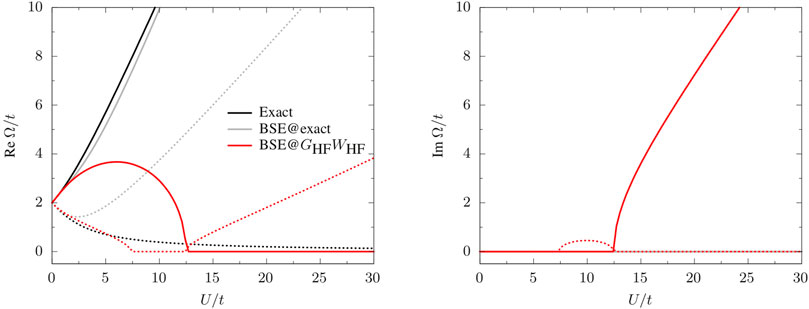
FIGURE 3. Real and imaginary parts of the singlet (solid) and triplet (dotted) neutral excitations,
Of course, one cannot access the double excitation within the static approximation of BSE, (Strinati, 1988; Romaniello et al., 2009b; Loos and Blase, 2020), so only the lowest singlet and triplet excitations,
Using one-shot GHFWHF quasiparticle energies (BSE@GHFWHF) produces complex excitation energies (see right panel of Figure 3). We find the same scenario also with other flavors of GW (not reported in the figure), such as scGW. The occurrence of complex poles and singlet/triplet instabilities at the BSE level are well documented (Holzer et al., 2018; Blase et al., 2020; Loos et al., 2020) and is not specific to the Hubbard dimer. For example, one finds complex poles also for H2 along its dissociation path, (Li and Olevano, 2021), but also for larger diatomic molecules. (Loos et al., 2020). For U/t > 12.4794, the singlet energy becomes pure imaginary, the same is observed for the triplet energy for 7.3524 < U/t < 12.4794. These two points corresponds to discontinuities in the first derivative of the excitation energies with respect to U/t (Figure 3). The BSE excitation energies are good approximations to their exact analogs only for U/t ≲ 2 for the singlet and U/t ≲ 6 for the triplet. Using exact quasiparticle energies instead produces real excitation energies, with the singlet energy in very good agreement with the exact result; the triplet energy, instead, largely overestimates the exact value. This seems to suggest that complex poles are caused by the approximate nature of the GW quasiparticle energies, although, of course, the quality of the kernel also plays a role. Indeed, setting W = 0 but using GW QP energies, BSE yields real-valued excitation energies. It would be interesting to further investigate this issue by using the exact kernel together with GW QP energies. This is left for future work.
3.2.2 Correlation Energy
For the Hubbard dimer, we have EHF = − 2t + U/2, and the correlation energy given in Eq. 15 can be calculated analytically. After a lengthy but simple derivation, one gets
Results are reported in Figure 4 and are compared with the exact correlation energy (Romaniello et al., 2009a)
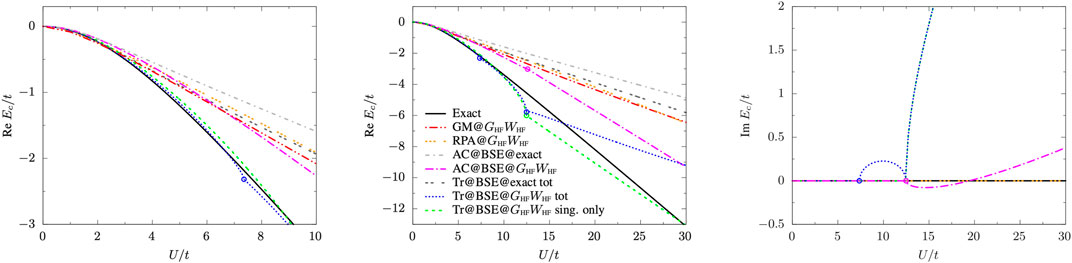
FIGURE 4. Real and imaginary parts of the BSE@GHFWHF correlation energy as a function of U/t at various levels of theory: total (dotted blue line) and singlet-only (dashed green line) Tr@BSE, AC@BSE (dot-dashed magenta line), RPA (triple-dotted orange line), GM (double-dot-dashed red line), and exact (solid black line). For comparison also the BSE@exact (Tr@BSE, double-dotted dark grey line; AC@BSE, dot-dashed light grey line) correlation energies are shown. Discontinuities in the first derivative of the energy (corresponding to the appearance of complex poles) are indicated by open circles.
The AC@BSE correlation energy does not possess the correct asymptotic behavior for small U, as Taylor expanding Eq. 29 for small U, we obtain
while the exact correlation energy behaves as
Moreover, we found that the radius of convergence of the small-U/t expansion of
In the case of the trace formula Eq. 14, the singlet and triplet contributions behave as
which guarantees the correct asymptotic behavior for the total Tr@BSE correlation energy
and cancels the cubic term (as it should).
The trace formula is strongly affected by the appearance of the imaginary excitation energies: as shown in Figure 4 where we plot the real and complex components of the BSE@GHFWHF correlation energy as functions of U/t at various levels of theory, irregularities (i.e., discontinuities in the first derivative of the energy) appear at the values of U/t for which the triplet and singlet energies become purely imaginary. The ACFDT expression, instead, is more stable over the range of U/t considered here with only a small cusp on the energy surface at the singlet instability point after which the real part of EcAC@BSE behaves linearly with respect to U/t. Overall, however, the correlation energy obtained by the trace formula is almost on top of its exact counterpart over a wide range of U/t, with a rather small contribution from the triplet component, i.e.,
4 Conclusion
In this work we have used the symmetric Hubbard dimer to better understand some features of the GW approximation and of BSE@GW. In particular, we have found that the unphysical discontinuities that may occur in quasiparticle energies computed using one-shot or partially self-consistent GW schemes disappear using full self-consistency. However, full self-consistency does not give an overall improvement in term of accuracy and, at least for the Hubbard dimer, GHFWHF is to be preferred.
We have also analyzed the performance of the BSE@GW approach for neutral excitations and correlation energies. We have found that, at any level of self-consistency, the excitation energies become complex for some critical values of U/t. This seems related to the approximate nature of the GW quasiparticle energies, since using exact quasiparticle energies (hence the exact fundamental gap) solves this issue. The BSE excitation energies are good approximations to the exact analogs only for a small range of U/t (or U/t ≲ 2 for the lowest singlet-singlet transition and U/t ≲ 6 for the singlet-triplet transition), while the strong-correlation regime remains a challenge.
The correlation energy obtained from these excitation energies using the trace (or plasmon) formula has been found to be in very good agreement with the exact results over the whole range of U/t for which these energies are real. The occurrence of complex singlet and triplet excitation energies shows up as irregularities in the correlation energy. The ACFDT formula, instead, is less sensitive to this. However, we have found that the AC@BSE correlation energy is less accurate than the one obtained using the trace formula. Both, however, perform better than the standard Galitskii-Migdal formula. Finally, we have studied the small-U expansion of the correlation energy obtained with the trace and ACFDT formulas and we found that the former, contrary to the latter, has the correct behavior when one includes both the singlet and triplet energy contributions. Our findings point out to a possible fundamental problem of the AC@BSE formalism.
Although our study is restricted to the half-filled Hubbard dimer, some of our findings are transferable to realistic (molecular) systems. In particular: 1) a fully self-consistent solution of the GW equation cures the problem of multiple QP solutions, avoiding in the process the appearance of discontinuities in key physical quantities such as total or excitation energies, ionization potentials, and electron affinities; 2) a “bad” starting point (G0 in the case of the Hubbard dimer) may result in the appearence of multiple QP solutions; 3) potential energy surfaces computed with the trace formula and within the ACFDT formalism may exhibit irregularities due to the appearence of complex BSE excitation energies; 4) for the Hubbard dimer at half-filling, the trace formula has the correct asymptotic behavior (thanks to the inclusion of singlet and triplet excitation energies) for weak interaction, contrary to its ACFDT counterpart. It would be interesting to check if it is also the case in realistic systems.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
This study has been partially supported through the EUR grant NanoX no ANR-17-EURE-0009 in the framework of the “Programme des Investissements d’Avenir” and by the CNRS through the 80|Prime program. PR and SDS also thank the ANR (project ANR-18-CE30-0025) for financial support. PFL also thanks the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement no. ∼863481) for financial support.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fchem.2021.751054/full#supplementary-material
References
Albrecht, S., Reining, L., Del Sole, R., and Onida, G. (1998). Ab InitioCalculation of Excitonic Effects in the Optical Spectra of Semiconductors. Phys. Rev. Lett. 80, 4510–4513. doi:10.1103/PhysRevLett.80.4510
Ángyán, J. G., Liu, R.-F., Toulouse, J., and Jansen, G. (2011). Correlation Energy Expressions from the Adiabatic-Connection Fluctuation-Dissipation Theorem Approach. J. Chem. Theor. Comput. 7, 3116–3130. doi:10.1021/ct200501r
Aryasetiawan, F., and Gunnarsson, O. (1998). TheGWmethod. Rep. Prog. Phys. 61, 237–312. doi:10.1088/0034-4885/61/3/002
Authier, J., and Loos, P.-F. (2020). Dynamical Kernels for Optical Excitations. J. Chem. Phys. 153, 184105. doi:10.1063/5.0028040
Benedict, L. X., Shirley, E. L., and Bohn, R. B. (1998). Optical Absorption of Insulators and the Electron-Hole Interaction: AnAb InitioCalculation. Phys. Rev. Lett. 80, 4514–4517. doi:10.1103/PhysRevLett.80.4514
Berger, J. A., Loos, P.-F., and Romaniello, P. (2020). Potential Energy Surfaces without Unphysical Discontinuities: The Coulomb Hole Plus Screened Exchange Approach. J. Chem. Theor. Comput. 17, 191–200. doi:10.1021/acs.jctc.0c00896
Blase, X., and Attaccalite, C. (2011). Charge-transfer Excitations in Molecular Donor-Acceptor Complexes within the many-body Bethe-Salpeter Approach. Appl. Phys. Lett. 99, 171909. doi:10.1063/1.3655352
Blase, X., Boulanger, P., Bruneval, F., Fernandez-Serra, M., and Duchemin, I. (2016). GW and Bethe-Salpeter Study of Small Water Clusters. J. Chem. Phys. 144, 034109. doi:10.1063/1.4940139
Blase, X., Duchemin, I., Jacquemin, D., and Loos, P.-F. (2020). The Bethe-Salpeter Equation Formalism: From Physics to Chemistry. J. Phys. Chem. Lett. 11, 7371–7382. doi:10.1021/acs.jpclett.0c01875
Blase, X., Duchemin, I., and Jacquemin, D. (2018). The Bethe-Salpeter Equation in Chemistry: Relations with TD-DFT, Applications and Challenges. Chem. Soc. Rev. 47, 1022–1043. doi:10.1039/C7CS00049A
Boulanger, P., Jacquemin, D., Duchemin, I., and Blase, X. (2014). Fast and Accurate Electronic Excitations in Cyanines with the many-body Bethe-Salpeter Approach. J. Chem. Theor. Comput. 10, 1212–1218. doi:10.1021/ct401101u
Bruneval, F., Hamed, S. M., and Neaton, J. B. (2015). A Systematic Benchmark of the ab initio Bethe-Salpeter Equation Approach for Low-Lying Optical Excitations of Small Organic Molecules. J. Chem. Phys. 142, 244101. doi:10.1063/1.4922489
Bruneval, F. (2012). Ionization Energy of Atoms Obtained from GW Self-Energy or from Random Phase Approximation Total Energies. J. Chem. Phys. 136, 194107. doi:10.1063/1.4718428
Bruneval, F., and Marques, M. A. L. (2013). Benchmarking the Starting Points of the GW Approximation for Molecules. J. Chem. Theor. Comput. 9, 324–329. doi:10.1021/ct300835h
Bruneval, F. (2016). Optimized Virtual Orbital Subspace for Faster GW Calculations in Localized Basis. J. Chem. Phys. 145, 234110. doi:10.1063/1.4972003
Bruneval, F., Rangel, T., Hamed, S. M., Shao, M., Yang, C., and Neaton, J. B. (2016). Molgw 1: Many-body Perturbation Theory Software for Atoms, Molecules, and Clusters. Computer Phys. Commun. 208, 149–161. doi:10.1016/j.cpc.2016.06.019
Carrascal, D. J., Ferrer, J., Maitra, N., and Burke, K. (2018). Linear Response Time-dependent Density Functional Theory of the Hubbard Dimer. Eur. Phys. J. B 91, 142. doi:10.1140/epjb/e2018-90114-9
Carrascal, D. J., Ferrer, J., Smith, J. C., and Burke, K. (2015). The Hubbard Dimer: A Density Functional Case Study of a many-body Problem. J. Phys. Condens. Matter 27, 393001. doi:10.1088/0953-8984/27/39/393001
Caruso, F., Rinke, P., Ren, X., Rubio, A., and Scheffler, M. (2013a). Self-consistentGW: All-Electron Implementation with Localized Basis Functions. Phys. Rev. B 88, 075105. doi:10.1103/PhysRevB.88.075105
Caruso, F., Rinke, P., Ren, X., Scheffler, M., and Rubio, A. (2012). Unified Description of Ground and Excited States of Finite Systems: The Self-consistentGWapproach. Phys. Rev. B 86, 081102. doi:10.1103/PhysRevB.86.081102
Caruso, F., Rohr, D. R., Hellgren, M., Ren, X., Rinke, P., Rubio, A., et al. (2013b). Bond Breaking and Bond Formation: How Electron Correlation Is Captured in Many-Body Perturbation Theory and Density-Functional Theory. Phys. Rev. Lett. 110, 146403. doi:10.1103/PhysRevLett.110.146403
Caruso, F. (2013). “Self-Consistent GW Approach for the Unified Description of Ground and Excited States of Finite Systems,”. PhD Thesis (Berlin, Germany: Freie Universität Berlin).
Casida, M. E. (1995). Generalization of the Optimized-Effective-Potential Model to Include Electron Correlation: A Variational Derivation of the Sham-Schlüter Equation for the Exact Exchange-Correlation Potential. Phys. Rev. A. 51, 2005–2013. doi:10.1103/PhysRevA.51.2005
Casida, M. E., and Huix-Rotllant, M. (2015). Many-body Perturbation Theory (MBPT) and Time-dependent Density-Functional Theory (TD-DFT): MBPT Insights about what Is Missing in, and Corrections to, the TD-DFT Adiabatic Approximation. Top. Curr. Chem. 368, 1–60. doi:10.1007/128_2015_632
Casida, M. E. (2005). Propagator Corrections to Adiabatic Time-dependent Density-Functional Theory Linear Response Theory. J. Chem. Phys. 122, 054111. doi:10.1063/1.1836757
Colonna, N., Hellgren, M., and de Gironcoli, S. (2014). Correlation Energy within Exact-Exchange Adiabatic Connection Fluctuation-Dissipation Theory: Systematic Development and Simple Approximations. Phys. Rev. B 90, 125150. doi:10.1103/physrevb.90.125150
Di Sabatino, S., Berger, J. A., Reining, L., and Romaniello, P. (2016). Photoemission Spectra from Reduced Density Matrices: The Band gap in Strongly Correlated Systems. Phys. Rev. B 94, 155141. doi:10.1103/PhysRevB.94.155141
Dreuw, A., and Head-Gordon, M. (2005). Single-Reference Ab Initio Methods for the Calculation of Excited States of Large Molecules. Chem. Rev. 105, 4009–4037. doi:10.1021/cr0505627
Duchemin, I., and Blase, X. (2021). Cubic-Scaling All-Electron GW Calculations with a Separable Density-Fitting Space-Time Approach. J. Chem. Theor. Comput. 17, 2383–2393. doi:10.1021/acs.jctc.1c00101
Duchemin, I., and Blase, X. (2020). Robust Analytic-Continuation Approach to many-body GW Calculations. J. Chem. Theor. Comput. 16, 1742–1756. doi:10.1021/acs.jctc.9b01235
Duchemin, I., and Blase, X. (2019). Separable Resolution-Of-The-Identity with All-Electron Gaussian Bases: Application to Cubic-Scaling Rpa. J. Chem. Phys. 150, 174120. doi:10.1063/1.5090605
Faber, C., Attaccalite, C., Olevano, V., Runge, E., and Blase, X. (2011). First-principlesGWcalculations for DNA and RNA Nucleobases. Phys. Rev. B 83, 115123. doi:10.1103/PhysRevB.83.115123
Faber, C. (2014). “Electronic, Excitonic and Polaronic Properties of Organic Systems within the Many-Body GW and Bethe-Salpeter Formalisms: Towards Organic Photovoltaics,”. PhD Thesis (Grenoble, France: Université de Grenoble).
Furche, F., and Van Voorhis, T. (2005). Fluctuation-dissipation Theorem Density-Functional Theory. J. Chem. Phys. 122, 164106. doi:10.1063/1.1884112
Galitskii, V., and Migdal, A. (1958). Applications of Quantum Field Theory to the many Body Problem. Sov. Phys. JETP 7, 96.
Golze, D., Dvorak, M., and Rinke, P. (2019). The Gw Compendium: A Practical Guide to Theoretical Photoemission Spectroscopy. Front. Chem. 7, 377. doi:10.3389/fchem.2019.00377
Gui, X., Holzer, C., and Klopper, W. (2018). Accuracy Assessment of GW Starting Points for Calculating Molecular Excitation Energies Using the Bethe-Salpeter Formalism. J. Chem. Theor. Comput. 14, 2127–2136. doi:10.1021/acs.jctc.8b00014
Gunnarsson, O., and Lundqvist, B. I. (1976). Exchange and Correlation in Atoms, Molecules, and Solids by the Spin-Density-Functional Formalism. Phys. Rev. B 13, 4274–4298. doi:10.1103/PhysRevB.13.4274
Hedin, L. (1965). New Method for Calculating the One-Particle Green's Function with Application to the Electron-Gas Problem. Phys. Rev. 139, A796–A823. doi:10.1103/physrev.139.a796
Hellgren, M., Caruso, F., Rohr, D. R., Ren, X., Rubio, A., Scheffler, M., et al. (2015). Static Correlation and Electron Localization in Molecular Dimers from the Self-Consistent RPA andGWapproximation. Phys. Rev. B 91, 165110. doi:10.1103/physrevb.91.165110
Hellgren, M., and von Barth, U. (2010). Correlation Energy Functional and Potential from Time-dependent Exact-Exchange Theory. J. Chem. Phys. 132, 044101. doi:10.1063/1.3290947
Heßelmann, A., and Görling, A. (2011). Correct Description of the Bond Dissociation Limit without Breaking Spin Symmetry by a Random-Phase-Approximation Correlation Functional. Phys. Rev. Lett. 106, 093001. doi:10.1103/PhysRevLett.106.093001
Hirose, D., Noguchi, Y., and Sugino, O. (2015). All-electronGW+Bethe-Salpeter Calculations on Small Molecules. Phys. Rev. B 91, 205111. doi:10.1103/physrevb.91.205111
Hohenberg, P., and Kohn, W. (1964). Inhomogeneous Electron Gas. Phys. Rev. 136, B864–B871. doi:10.1103/PhysRev.136.B864
Holm, B., and von Barth, U. (1998). Fully Self-consistentGWself-Energy of the Electron Gas. Phys. Rev. B 57, 2108–2117. doi:10.1103/PhysRevB.57.2108
Holzer, C., Gui, X., Harding, M. E., Kresse, G., Helgaker, T., and Klopper, W. (2018). Bethe-Salpeter Correlation Energies of Atoms and Molecules. J. Chem. Phys. 149, 144106. doi:10.1063/1.5047030
Holzer, C., and Klopper, W. (2018). Communication: A Hybrid Bethe-salpeter/time-dependent Density-Functional-Theory Approach for Excitation Energies. J. Chem. Phys. 149, 101101. doi:10.1063/1.5051028
Huix-Rotllant, M., Ipatov, A., Rubio, A., and Casida, M. E. (2011). Assessment of Dressed Time-dependent Density-Functional Theory for the Low-Lying Valence States of 28 Organic Chromophores. Chem. Phys. 391, 120–129. doi:10.1016/j.chemphys.2011.03.019
Hung, L., Bruneval, F., Baishya, K., and Öğüt, S. (2017). Benchmarking the GW Approximation and Bethe-Salpeter Equation for Groups IB and IIB Atoms and Monoxides. J. Chem. Theor. Comput. 13, 2135–2146. doi:10.1021/acs.jctc.7b00123
Hung, L., da Jornada, F. H., Souto-Casares, J., Chelikowsky, J. R., Louie, S. G., and Öğüt, S. (2016). Excitation Spectra of Aromatic Molecules within a Real-spaceGW-BSE Formalism: Role of Self-Consistency and Vertex Corrections. Phys. Rev. B 94, 085125. doi:10.1103/PhysRevB.94.085125
Hybertsen, M. S., and Louie, S. G. (1986). Electron Correlation in Semiconductors and Insulators: Band Gaps and Quasiparticle Energies. Phys. Rev. B 34, 5390–5413. doi:10.1103/PhysRevB.34.5390
Jacquemin, D., Duchemin, I., and Blase, X. (2015a). 0-0 Energies Using Hybrid Schemes: Benchmarks of TD-DFT, CIS(D), ADC(2), CC2, and BSE/GW Formalisms for 80 Real-Life Compounds. J. Chem. Theor. Comput. 11, 5340–5359. doi:10.1021/acs.jctc.5b00619
Jacquemin, D., Duchemin, I., and Blase, X. (2015b). Benchmarking the Bethe-Salpeter Formalism on a Standard Organic Molecular Set. J. Chem. Theor. Comput. 11, 3290–3304. doi:10.1021/acs.jctc.5b00304
Jacquemin, D., Duchemin, I., and Blase, X. (2017a). Is the Bethe-Salpeter Formalism Accurate for Excitation Energies? Comparisons with TD-DFT, CASPT2, and EOM-CCSD. J. Phys. Chem. Lett. 8, 1524–1529. doi:10.1021/acs.jpclett.7b00381
Jacquemin, D., Duchemin, I., Blondel, A., and Blase, X. (2017b). Benchmark of Bethe-Salpeter for Triplet Excited-States. J. Chem. Theor. Comput. 13, 767–783. doi:10.1021/acs.jctc.6b01169
Kaplan, F., Harding, M. E., Seiler, C., Weigend, F., Evers, F., and van Setten, M. J. (2016). Quasi-Particle Self-Consistent GW for Molecules. J. Chem. Theor. Comput. 12, 2528–2541. doi:10.1021/acs.jctc.5b01238
Kaplan, F., Weigend, F., Evers, F., and van Setten, M. J. (2015). Off-Diagonal Self-Energy Terms and Partially Self-Consistency in GW Calculations for Single Molecules: Efficient Implementation and Quantitative Effects on Ionization Potentials. J. Chem. Theor. Comput. 11, 5152–5160. doi:10.1021/acs.jctc.5b00394
Karlsson, D., and van Leeuwen, R. (2016). Partial Self-Consistency and Analyticity in many-body Perturbation Theory: Particle Number Conservation and a Generalized Sum Rule. Phys. Rev. B 94, 125124. doi:10.1103/PhysRevB.94.125124
Kohn, W., and Sham, L. J. (1965). Self-consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 140, A1133–A1138. doi:10.1103/PhysRev.140.A1133
Koval, P., Foerster, D., and Sánchez-Portal, D. (2014). Fully Self-consistentGWand Quasiparticle Self-consistentGWfor Molecules. Phys. Rev. B 89, 155417. doi:10.1103/PhysRevB.89.155417
Krause, K., and Klopper, W. (2017). Implementation of the Bethe−Salpeter Equation in the TURBOMOLE Program. J. Comput. Chem. 38, 383–388. doi:10.1002/jcc.24688
Langreth, D. C., and Perdew, J. P. (1979). The Gradient Approximation to the Exchange-Correlation Energy Functional: A Generalization that Works. Solid State. Commun. 31, 567–571. doi:10.1016/0038-1098(79)90254-0
Lettmann, T., and Rohlfing, M. (2019). Electronic Excitations of Polythiophene within many-body Perturbation Theory with and without the Tamm-Dancoff Approximation. J. Chem. Theor. Comput. 15, 4547–4554. doi:10.1021/acs.jctc.9b00223
Li, J., Chen, Z., and Yang, W. (2021). Renormalized Singles Green's Function in the T-Matrix Approximation for Accurate Quasiparticle Energy Calculation. J. Phys. Chem. Lett. 12, 6203–6210. doi:10.1021/acs.jpclett.1c01723
Li, J., Drummond, N. D., Schuck, P., and Olevano, V. (2019). Comparing many-body Approaches against the Helium Atom Exact Solution. Scipost Phys. 6, 040. doi:10.21468/SciPostPhys.6.4.040
Li, J., Duchemin, I., Blase, X., and Olevano, V. (2020). Ground-state Correlation Energy of Beryllium Dimer by the Bethe-Salpeter Equation. Scipost Phys. 8, 20. doi:10.21468/SciPostPhys.8.2.020
Li, J., Holzmann, M., Duchemin, I., Blase, X., and Olevano, V. (2017). Helium Atom Excitations by the GW and Bethe-Salpeter Many-Body Formalism. Phys. Rev. Lett. 118, 163001. doi:10.1103/PhysRevLett.118.163001
Li, J., and Olevano, V. (2021). Hydrogen-molecule Spectrum by the many-body Gw Approximation and the Bethe-Salpeter Equation. Phys. Rev. A. 103, 012809. doi:10.1103/PhysRevA.103.012809
Liu, C., Kloppenburg, J., Yao, Y., Ren, X., Appel, H., Kanai, Y., et al. (2020). All-electron ab initio Bethe-Salpeter Equation Approach to Neutral Excitations in Molecules with Numeric Atom-Centered Orbitals. J. Chem. Phys. 152, 044105. doi:10.1063/1.5123290
Loos, P.-F., and Blase, X. (2020). Dynamical Correction to the Bethe-Salpeter Equation beyond the Plasmon-Pole Approximation. J. Chem. Phys. 153, 114120. doi:10.1063/5.0023168
Loos, P.-F., Romaniello, P., and Berger, J. A. (2018). Green Functions and Self-Consistency: Insights from the Spherium Model. J. Chem. Theor. Comput. 14, 3071–3082. doi:10.1021/acs.jctc.8b00260
Loos, P.-F., Scemama, A., Duchemin, I., Jacquemin, D., and Blase, X. (2020). Pros and Cons of the Bethe-Salpeter Formalism for Ground-State Energies. J. Phys. Chem. Lett. 11, 3536–3545. doi:10.1021/acs.jpclett.0c00460
Ma, Y., Rohlfing, M., and Molteni, C. (2009a). Excited States of Biological Chromophores Studied Using many-body Perturbation Theory: Effects of Resonant-Antiresonant Coupling and Dynamical Screening. Phys. Rev. B 80, 241405. doi:10.1103/PhysRevB.80.241405
Ma, Y., Rohlfing, M., and Molteni, C. (2009b). Modeling the Excited States of Biological Chromophores within Many-Body Green's Function Theory. J. Chem. Theor. Comput. 6, 257–265. doi:10.1021/ct900528h
Maggio, E., and Kresse, G. (2016). Correlation Energy for the Homogeneous Electron Gas: Exact Bethe-Salpeter Solution and an Approximate Evaluation. Phys. Rev. B 93, 235113. doi:10.1103/PhysRevB.93.235113
Maggio, E., Liu, P., van Setten, M. J., and Kresse, G. (2017). GW100: A Plane Wave Perspective for Small Molecules. J. Chem. Theor. Comput. 13, 635–648. doi:10.1021/acs.jctc.6b01150
Martin, R. M., Reining, L., and Ceperley, D. (2016). Interacting Electrons: Theory and Computational Approaches. New York, NY: Cambridge University Press.
Monino, E., and Loos, P.-F. (2021). Spin-Conserved and Spin-Flip Optical Excitations from the Bethe-Salpeter Equation Formalism. J. Chem. Theor. Comput. 17, 2852–2867. doi:10.1021/acs.jctc.1c00074
Myöhänen, P., Stan, A., Stefanucci, G., and van Leeuwen, R. (2008). A many-body Approach to Quantum Transport Dynamics: Initial Correlations and Memory Effects. Europhys. Lett. 84, 67001. doi:10.1209/0295-5075/84/67001
Oddershede, J., and Jo/rgensen, P. (1977). An Order Analysis of the Particle-Hole Propagator. J. Chem. Phys. 66, 1541–1556. doi:10.1063/1.434118
Olevano, V., Toulouse, J., and Schuck, P. (2019). A Formally Exact One-Frequency-Only Bethe-salpeter-like Equation. Similarities and Differences between Gw+bse and Self-Consistent Rpa. J. Chem. Phys. 150, 084112. doi:10.1063/1.5080330
Olsen, T., and Thygesen, K. S. (2014). Static Correlation beyond the Random Phase Approximation: Dissociating H2 with the Bethe-Salpeter Equation and Time-dependent Gw. J. Chem. Phys. 140, 164116. doi:10.1063/1.4871875
Onida, G., Reining, L., and Rubio, A. (2002). Electronic Excitations: Density-Functional versus many-body green’s Function Approaches. Rev. Mod. Phys. 74, 601–659. doi:10.1103/RevModPhys.74.601
Ou, Q., and Subotnik, J. E. (2016). Comparison between GW and Wave-Function-Based Approaches: Calculating the Ionization Potential and Electron Affinity for 1D Hubbard Chains. J. Phys. Chem. A. 120, 4514–4525. doi:10.1021/acs.jpca.6b03294
Ou, Q., and Subotnik, J. E. (2018). Comparison between the Bethe–Salpeter Equation and Configuration Interaction Approaches for Solving a Quantum Chemistry Problem: Calculating the Excitation Energy for Finite 1D Hubbard Chains. J. Chem. Theor. Comput. 14, 527–542. doi:10.1021/acs.jctc.7b00246
Petersilka, M., Gossmann, U. J., and Gross, E. K. U. (1996). Excitation Energies from Time-dependent Density-Functional Theory. Phys. Rev. Lett. 76, 1212. doi:10.1103/PhysRevLett.76.1212
Pollehn, T. J., Schindlmayr, A., and Godby, R. W. (1998). Assessment of theGWapproximation Using hubbard Chains. J. Phys. Condensed Matter 10, 1273–1283. doi:10.1088/0953-8984/10/6/011
Puig von Friesen, M., Verdozzi, C., and Almbladh, C.-O. (2010). Kadanoff-baym Dynamics of hubbard Clusters: Performance of many-body Schemes, Correlation-Induced Damping and Multiple Steady and Quasi-Steady States. Phys. Rev. B 82, 155108. doi:10.1103/PhysRevB.82.155108
Puschnig, P., and Ambrosch-Draxl, C. (2002). Suppression of Electron-Hole Correlations in 3d Polymer Materials. Phys. Rev. Lett. 89, 056405. doi:10.1103/PhysRevLett.89.056405
Rangel, T., Hamed, S. M., Bruneval, F., and Neaton, J. B. (2017). An Assessment of Low-Lying Excitation Energies and Triplet Instabilities of Organic Molecules with an ab initio Bethe-Salpeter Equation Approach and the Tamm-Dancoff Approximation. J. Chem. Phys. 146, 194108. doi:10.1063/1.4983126
Rangel, T., Hamed, S. M., Bruneval, F., and Neaton, J. B. (2016). Evaluating the Gw Approximation with Ccsd(t) for Charged Excitations across the Oligoacenes. J. Chem. Theor. Comput. 12, 2834–2842. doi:10.1021/acs.jctc.6b00163
Rebolini, E., and Toulouse, J. (2016). Range-separated Time-dependent Density-Functional Theory with a Frequency-dependent Second-Order Bethe-Salpeter Correlation Kernel. J. Chem. Phys. 144, 094107. doi:10.1063/1.4943003
Rohlfing, M., and Louie, S. G. (2000). Electron-hole Excitations and Optical Spectra from First Principles. Phys. Rev. B 62, 4927–4944. doi:10.1103/PhysRevB.62.4927
Rohlfing, M., and Louie, S. G. (1998). Electron-hole Excitations in Semiconductors and Insulators. Phys. Rev. Lett. 81, 2312–2315. doi:10.1103/PhysRevLett.81.2312
Rohlfing, M., and Louie, S. G. (1999). Optical Excitations in Conjugated Polymers. Phys. Rev. Lett. 82, 1959–1962. doi:10.1103/PhysRevLett.82.1959
Romaniello, P., Bechstedt, F., and Reining, L. (2012). Beyond the G W Approximation: Combining Correlation Channels. Phys. Rev. B 85, 155131. doi:10.1103/PhysRevB.85.155131
Romaniello, P., Guyot, S., and Reining, L. (2009a). The Self-Energy beyond GW: Local and Nonlocal Vertex Corrections. J. Chem. Phys. 131, 154111. doi:10.1063/1.3249965
Romaniello, P., Sangalli, D., Berger, J. A., Sottile, F., Molinari, L. G., Reining, L., et al. (2009b). Double Excitations in Finite Systems. J. Chem. Phys. 130, 044108. doi:10.1063/1.3065669
Rowe, D. J. (1968). Methods for Calculating Ground-State Correlations of Vibrational Nuclei. Phys. Rev. 175, 1283. doi:10.1103/PhysRev.175.1283
Runge, E., and Gross, E. K. U. (1984). Density-functional Theory for Time-dependent Systems. Phys. Rev. Lett. 52, 997–1000. doi:10.1103/PhysRevLett.52.997
Sakkinen, N., Manninen, M., and van Leeuwen, R. (2012). The Kadanoff-Baym Approach to Double Excitations in Finite Systems. New J. Phys. 14, 013032. doi:10.1088/1367-2630/14/1/013032
Salpeter, E. E., and Bethe, H. A. (1951). A Relativistic Equation for Bound-State Problems. Phys. Rev. 84, 1232. doi:10.1103/PhysRev.84.1232
Sangalli, D., Romaniello, P., Onida, G., and Marini, A. (2011). Double Excitations in Correlated Systems: A many–body Approach. J. Chem. Phys. 134, 034115. doi:10.1063/1.3518705
Schindlmayr, A., Pollehn, T. J., and Godby, R. W. (1998). Spectra and Total Energies from Self-Consistent many-body Perturbation Theory. Phys. Rev. B 58, 12684–12690. doi:10.1103/PhysRevB.58.12684
Schindlmayr, A. (1997). Violation of Particle Number Conservation in the GW Approximation. Phys. Rev. B 56, 3528–3531. doi:10.1103/PhysRevB.56.3528
Shishkin, M., and Kresse, G. (2007). Self-consistent G W Calculations for Semiconductors and Insulators. Phys. Rev. B 75, 235102. doi:10.1103/PhysRevB.75.235102
Sottile, F., Olevano, V., and Reining, L. (2003). Parameter-free Calculation of Response Functions in Time-dependent Density-Functional Theory. Phys. Rev. Lett. 91, 056402. doi:10.1103/PhysRevLett.91.056402
Stan, A., Dahlen, N. E., and van Leeuwen, R. (2006). Fully Self-Consistent GW Calculations for Atoms and Molecules. Europhys. Lett. EPL 76, 298–304. doi:10.1209/epl/i2006-10266-6
Stan, A., Dahlen, N. E., and van Leeuwen, R. (2009). Levels of Self-Consistency in the Gw Approximation. J. Chem. Phys. 130, 114105. doi:10.1063/1.3089567
Strinati, G. (1988). Application of the Green’s Functions Method to the Study of the Optical Properties of Semiconductors. Riv. Nuovo Cimento 11, 1–86. doi:10.1007/BF02725962
Tiago, M. L., Northrup, J. E., and Louie, S. G. (2003). Ab Initio calculation of the Electronic and Optical Properties of Solid Pentacene. Phys. Rev. B 67, 115212. doi:10.1103/PhysRevB.67.115212
Toulouse, J., Gerber, I. C., Jansen, G., Savin, A., and Angyan, J. G. (2009). Adiabatic-connection Fluctuation-Dissipation Density-Functional Theory Based on Range Separation. Phys. Rev. Lett. 102, 096404. doi:10.1103/PhysRevLett.102.096404
Toulouse, J., Zhu, W., Angyan, J. G., and Savin, A. (2010). Range-separated Density-Functional Theory with the Random-phase Approximation: Detailed Formalism and Illustrative Applications. Phys. Rev. A. 82, 032502. doi:10.1103/PhysRevA.82.032502
Ullrich, C. (2012). Time-Dependent Density-Functional Theory: Concepts and Applications. Oxford Graduate Texts. New York: Oxford University Press.
van der Horst, J.-W., Bobbert, P. A., Michels, M. A. J., Brocks, G., and Kelly, P. J. (1999a). Ab Initio calculation of the Electronic and Optical Excitations in Polythiophene: Effects of Intra- and Interchain Screening. Phys. Rev. Lett. 83, 4413–4416. doi:10.1103/PhysRevLett.83.4413
van der Horst, J.-W., Bobbert, P. A., Michels, M. A. J., Brocks, G., and Kelly, P. J. (1999b). Ab Initio calculation of the Electronic and Optical Excitations in Polythiophene: Effects of Intra- and Interchain Screening. Phys. Rev. Lett. 83, 4413–4416. doi:10.1103/PhysRevLett.83.4413
van Setten, M. J., Caruso, F., Sharifzadeh, S., Ren, X., Scheffler, M., Liu, F., et al. (2015). GW 100: Benchmarking G0W0 for Molecular Systems. J. Chem. Theor. Comput. 11, 5665–5687. doi:10.1021/acs.jctc.5b00453
van Setten, M. J., Costa, R., Viñes, F., and Illas, F. (2018). Assessing GW Approaches for Predicting Core Level Binding Energies. J. Chem. Theor. Comput. 14, 877–883. doi:10.1021/acs.jctc.7b01192
van Setten, M. J., Weigend, F., and Evers, F. (2013). The GW -Method for Quantum Chemistry Applications: Theory and Implementation. J. Chem. Theor. Comput. 9, 232–246. doi:10.1021/ct300648t
Verdozzi, C., Godby, R. W., and Holloway, S. (1995). Evaluation of GW Approximations for the Self-Energy of a hubbard Cluster. Phys. Rev. Lett. 74, 2327–2330. doi:10.1103/PhysRevLett.74.2327
Véril, M., Romaniello, P., Berger, J. A., and Loos, P. F. (2018). Unphysical Discontinuities in Gw Methods. J. Chem. Theor. Comput. 14, 5220. doi:10.1021/acs.jctc.8b00745
von Barth, U., and Holm, B. (1996). Self-consistent GW 0 Results for the Electron Gas: Fixed Screened Potential W 0 within the Random-phase Approximation. Phys. Rev. B 54, 8411. doi:10.1103/PhysRevB.54.8411
Wilhelm, J., Golze, D., Talirz, L., Hutter, J., and Pignedoli, C. A. (2018). Toward Gw Calculations on Thousands of Atoms. J. Phy. Chem. Lett. 9, 306–312. doi:10.1021/acs.jpclett.7b02740
Zhang, D., Steinmann, S. N., and Yang, W. (2013). Dynamical Second-Order Bethe-Salpeter Equation Kernel: A Method for Electronic Excitation beyond the Adiabatic Approximation. J. Chem. Phys. 139, 154109. doi:10.1063/1.4824907
Zhang, D., Su, N. Q., and Yang, W. (2017). Accurate Quasiparticle Spectra from the T-Matrix Self-Energy and the Particle–Particle Random Phase Approximation. J. Phys. Chem. Lett. 8, 3223–3227. doi:10.1021/acs.jpclett.7b01275
Keywords: hubbard dimer, multiple quasiparticle solutions, GW, bethe-salpter equation, trace formula, adiabatic-connection fluctuation-dissipation theorem
Citation: Di Sabatino S, Loos P-F and Romaniello P (2021) Scrutinizing GW-Based Methods Using the Hubbard Dimer. Front. Chem. 9:751054. doi: 10.3389/fchem.2021.751054
Received: 31 July 2021; Accepted: 28 September 2021;
Published: 29 October 2021.
Edited by:
Patrick Rinke, Aalto University, FinlandReviewed by:
Gianluca Stefanucci, University of Rome Tor Vergata, ItalyMaria Hellgren, Sorbonne Universités, France
Copyright © 2021 Di Sabatino, Loos and Romaniello. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: S. Di Sabatino , ZGlzYWJhdGlub0BpcnNhbWMudXBzLXRsc2UuZnI=
 S. Di Sabatino
S. Di Sabatino P.-F. Loos
P.-F. Loos P. Romaniello
P. Romaniello