Ab Initio Molecular Dynamics with Quantum Monte Carlo

Luo, Ye; Sorella, Sandro

doi:10.3389/fmats.2015.00029

OPINION article

Front. Mater., 07 April 2015
Sec. Mechanics of Materials
Volume 2 - 2015 | https://doi.org/10.3389/fmats.2015.00029

Ab initio molecular dynamics with quantum Monte Carlo

Ye Luo*

Sandro Sorella

International School for Advanced Studies (SISSA) and CRS Democritos, CNR – Istituto Nazionale per la Fisica della Materia (INFM), Trieste, Italy

Quantum Monte Carlo (QMC) is one of the most accurate electronic structure methods for ab initio many-body calculations in a broad range of electronic systems. Thanks to fast evolving massively parallel computers, much larger simulations of realistic systems become affordable. We have developed an ab initio simulation scheme at finite temperature based on molecular dynamics (MD) and QMC during the past few years. In this approach, a second order Langevin MD is employed by using a statistical evaluation of the forces acting on each atom by means of QMC. Moreover, the corresponding statistical noise is also used to drive and accelerate the dynamics of ions. The accuracy and the reliability of our ab initio MD have been studied systematically and it has been already successfully applied to study the molecular and atomic phases of liquid hydrogen under pressure and liquid water at ambient conditions. Since this ab initio method provides a better resolution of the thermodynamic properties of materials, we believe that it represents a very promising tool for the most challenging applications in physics, chemistry, and biology.

Since the Car-Parrinello molecular dynamics (Car and Parrinello, 1985) was proposed three decades ago, ab initio molecular dynamics (MD) based on the density functional theory (DFT) has been widely accepted as an accurate and powerful tool to study the thermodynamic properties of systems at ambient and extreme conditions in the fields of physics, chemistry, and biology. Even though DFT is in principle exact, its accuracy, in practice, is affected by the quality of the approximation used in the exchange correlation functional term whose universal exact expression is not accessible, as the simplest approximate functionals, such as LDA, PBE, BLYP, and several other ones, so far cannot be systematically improved in a computationally efficient way. Quantum Monte Carlo (QMC) is the most promising successor of DFT in ab initio molecular dynamics. Indeed, the scaling behavior of QMC with the number of electrons is very good, from the second power (Ceperley et al., 1977) for thermodynamic properties – e.g., energy per electron, because in this case the number of samples to obtain a fixed accuracy in this quantity can be decreased when increasing the number N_e of electrons, implying $N_{e}^{3} ∕ N_{e} = N_{e}^{2}$ scaling with the standard algorithm – to the fourth power of the number of electrons when chemical accuracy in the total energy is required – in this case, instead the number of samples required for fixed accuracy has to increase with N_e, yielding $N_{e}^{3} \times N_{e} = N_{e}^{4}$ scaling. For this reason (a cost similar to DFT, albeit with a considerably larger pre-factor), QMC is also by far more efficient compared with other quantum chemistry methods based on multi-determinant expansions or many-body perturbation theory around the Hartree–Fock, such as, for instance, configuration interaction and coupled cluster theory, respectively. These methods provide a similar or even better accuracy than QMC for systems consisting of a few atoms, but they become computationally prohibitive when the system sizes increase. Another very important reason favoring the QMC algorithm is its well established efficient parallelization in current and upcoming supercomputers. QMC codes can be easily adapted to millions of CPU cores while DFT codes are still struggling with its parallel performance over several thousand cores. For the above reasons, it is probably not too far from reality to claim that QMC represents the rising star in the ab initio MD simulations.

This opinion paper focuses on the construction of the QMC-based MD by showing the key ingredients and the main recent developments of the building blocks necessary for the efficient implementation of this method. There are four main components: the basics of QMC, the wavefunction optimization, the evaluation of forces, and the molecular dynamics scheme. The last three ingredients were efficiently developed within only 10 years, with substantial contribution given also by us (Casula et al., 2004; Sorella et al., 2007; Umrigar et al., 2007; Attaccalite and Sorella, 2008; Sorella and Capriotti, 2010; Luo et al., 2014; Mazzola et al., 2014; Zen et al., 2014). Thus, the QMC-based MD is no longer a dream.

Basics of QMC

In QMC, the wavefunction ansatz is of fundamental importance for the efficiency, reliability, and accuracy of both variational and diffusion Monte Carlo calculations (VMC/DMC), namely the two most popular methods in QMC, the latter being more accurate and based on an approximate evaluation of the ground state properties with the restriction of having the same phases of the best reference VMC wavefunction – i.e., the so-called fixed-node approximation (Anderson, 1976; Ceperley and Alder, 1984; Umrigar et al., 1993), which is unavoidable for fermionic systems. The repeated evaluation of the wavefunction with also its gradients and Laplacian is one of the most consuming parts of the computation; the optimal wavefunction ansatz for MD should be also compact. The most popular choice is the Jastrow factor (Jastrow, 1955) correlated Slater determinant, which is simple and generally accurate. Pseudopotentials (Trail and Needs, 2005; Burkatzki et al., 2007) are often employed like in DFT to replace chemically in-active core electrons and keep only the valence electrons in QMC calculations.

Wavefunction Optimization

In the MD simulation, after each ionic move, the parameters in the VMC wavefunction need to be optimized in order to satisfy the Born–Oppenheimer approximation. Efficient optimization methods ensure that the energy converges to the right minimum within a sufficient accuracy in just a few steps. At present, the variance minimization method (Umrigar et al., 1988) has been recently abandoned because sometimes it failed to yield the best possible wavefunction (Snajdr and Rothstein, 2000; Bressanini et al., 2002). This method has been replaced by much more efficient and robust energy minimization methods. In our previous works, we introduced an energy minimization method, called stochastic reconfiguration (SR), which is based only on energy first derivatives, and allows a much more efficient optimization compared with other more conventional methods of this type, such as the steepest decent. In addition, the trial step length can be automatically determined by the SR with the Hessian accelerator (SRH) (Sorella, 2005) method, which makes use of the second derivatives of the energy. This method can be further improved by the recently introduced “linear method” (Umrigar and Filippi, 2005; Umrigar et al., 2007), which provides a better sampling of the Hessian matrix and represents at present the state of the art for the QMC optimization of wavefunction in realistic systems. For the application of the above techniques, to large systems, it is important to perform in a very efficient way the expensive inversion operation of a big matrix with its leading dimension (10⁴ is possible on current supercomputers) equal to the number of variational parameters (Sorella et al., 2007; Neuscamman et al., 2012).

Evaluation of Forces

In order to study thermodynamic properties, classical Monte Carlo and molecular dynamics are both widely used simulation methods. The former has a significant advantage that it does not necessarily require the computation of forces. Unfortunately, it is not straightforward to combine classical Monte Carlo and quantum Monte Carlo because all the quantities evaluated by QMC, including the energy, carry statistical errors that are very expensive to eliminate.¹ In order to move the ions according to the QMC energy and sample the canonical ensemble correctly, the penalty method (Ceperley and Dewing, 1999) was introduced to remove the bias due to the statistical uncertainty in the knowledge of the energy by rejecting the proposed moves more frequently than the standard Metropolis algorithm. For this reason, this method is very expensive, particularly in the low temperature regime, because of too many rejected moves, and so far applications have been limited to hydrogen with up to 54 protons in this regime (Pierleoni and Ceperley, 2006; Morales et al., 2010a,b).

Generally speaking, it is clear that, when the computational cost for the calculation of the nuclear forces is comparable to that of the energy, MD should be more efficient, because with the same cost all the atoms are moved without any rejection. For instance, in DFT, where the forces are obtained almost for free by applying the Hellmann–Feynman theorem, MD is a common practice to sample the canonical distribution, and, to our knowledge, only hybrid methods based on Monte Carlo and molecular dynamics (Rossky et al., 1978; Duane et al., 1987) can be competitive.

Unfortunately, computing forces with QMC is substantially more demanding than DFT. To obtain the forces in an accurate and efficient way within the VMC framework, several very important improvements have been done, concerning both theories and algorithms. The correlated sampling (Filippi and Umrigar, 2000) method allows the computation of the energy derivatives with errors much smaller than those obtained with a straightforward finite difference method. Together with the space warp coordinate transformation (Umrigar, 1989), forces computed by QMC were used for structural optimization (Casula et al., 2004). Another recent and important development in QMC was the solutions (Assaraf and Caffarel, 2000, 2003; Attaccalite and Sorella, 2008; Sorella and Capriotti, 2010; Zen et al., 2013) of the intrinsic infinite variance problem occurring in the calculation of nuclear forces in the simplest VMC scheme. Moreover, thanks to the algorithmic differentiation algorithm (Sorella and Capriotti, 2010), the cost of computing all the force components in a system can be afforded with a computational time at most a factor four larger than the one corresponding to the energy. This progress has led to several works, where structural optimization and highly accurate evaluations of the equilibrium configurations as well as related properties were possible even for quite large systems (Barborini and Guidoni, 2012; Coccia et al., 2013, 2014; Guareschi and Filippi, 2013; Zen et al., 2013).

Molecular Dynamics with QMC

Even though the efficient wavefunction optimization and fast evaluation of forces are achieved, the application of QMC for MD simulation of materials remains challenging due to the theoretical difficulties in applying the Newton’s equations of motion when the forces are given with a statistical uncertainty. For instance, the basic law of energy conservation cannot be met at all, when the forces are not exactly given at each step. Since it is prohibitive to eliminate the statistical error (for the same reason, see footnote 1), MD methods that allow the presence of random noise in the force components are certainly more suitable for QMC.

In our works, we have adopted a second order Langevin dynamics (SLD) for the sampling of the ionic configurations within the ground state Born–Oppenheimer approach. In this scheme, the statistical noise corresponding to the forces, is used to drive the dynamics at finite temperature by means of an appropriate generalized Langevin dynamics (Attaccalite and Sorella, 2008), while, during the dynamics, a noise correction is added to compensate the extra energy pumped into the system by the noise of the QMC forces. Later works also introduced two integration methods (Luo et al., 2014; Mazzola et al., 2014), which allowed us to work with noisy forces and large time steps, thus reducing the computational cost by a substantial fraction. The price to pay is the limitation of this approach to the evaluation of static quantities at finite temperature, because dynamical quantities, such as the diffusion constant, cannot be evaluated with the above stochastic implementation of SLD. Similar approaches (Krajewski and Parrinello, 2006; Kühne et al., 2007) have been proposed where an SLD algorithm has been devised also at the DFT level.

Last but not least, our proposed MD scheme with QMC also includes an automatic optimal tuning for the damping of the slow and the fast modes, which greatly improves the efficiency of the sampling. In the SLD equations, the damping coefficients matrix can be arbitrarily chosen to speed up the sampling, provided the fluctuation–dissipation theorem is satisfied by adding appropriate correlated noise to the force components. In our scheme, we have defined this correlation matrix in terms of the one corresponding to the noisy forces obtained with QMC. This is because we have empirically verified that the latter matrix is almost proportional to the dynamical matrix (see Figure 1). Therefore, the energy modes with higher frequency vibrations can be systematically damped much more than the slow modes, and this clearly allows a faster propagation with larger time steps.

FIGURE 1

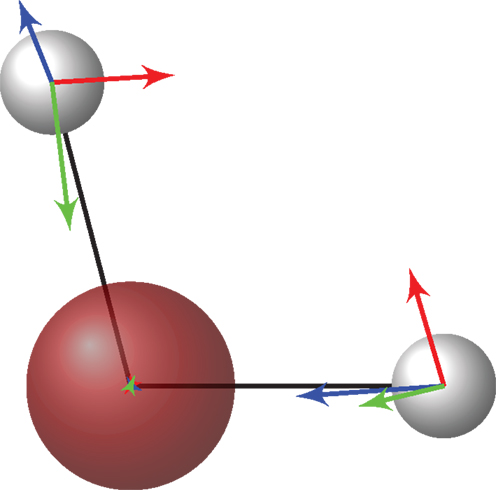
Figure 1. The eigenvectors of the covariance matrix obtained with the noisy force components evaluated by VMC. These eigenvectors correspond to the three vibrational modes of the water monomer: bending (red), symmetrical (green), and asymmetrical (blue) stretching. The smallest eigenvalue corresponds to the lowest frequency vibrational mode (red).

The VMC-based MD has been successfully applied to various systems from small molecules (Luo et al., 2014) to liquids, for instance, the liquid hydrogen at high pressure (Attaccalite and Sorella, 2008; Mazzola et al., 2014) and the liquid water at ambient conditions (Zen et al., 2014) for the properties of vibrational frequencies (Luo et al., 2014), atomic structures (Zen et al., 2014), and phase diagrams (Mazzola et al., 2014). It is implemented in the TurboRVB QMC package (Sorella, 2015) with a hybrid MPI and OpenMP paradigm and its performance in the production run reaches peta-scale, as it has been successfully tested up to 33K cores on BG/Q and 264K cores on the K-computer.

Conclusion and Outlooks

From the high performance computing perspective, the four main components that we have briefly reviewed in this work show different features in computational intensity and communications. The statistical calculation for the energy and its derivatives required by the optimization and forces puts very heavy loads on the CPU but only needs very little communication at the end of a big piece of work, which is an ideal pattern for the parallelization. In addition, each optimization step involves inversion operations of big matrices. It can be a potential bottleneck if it is solved in parallel on a network with high latency. The computational and communication cost of updating ion positions is negligible compared to the other three parts for tens and hundreds of atoms.

In conclusion, we have briefly described the main computational achievements that have allowed recently the first ab initio simulations of realistic materials with an efficient molecular dynamics based on accurate QMC forces. We believe that our work represents a first step toward an efficient tool for ab initio simulations of material properties much more reliable than DFT. Indeed, our evaluation of forces is limited to the VMC approach, and we expect some progress can be done by adopting the more reliable DMC method. Similarly, it should be possible to extend the method to more accurate wavefunctions, containing, for instance, many-body and backflow correlations, as well as implicit multi-determinant wavefunctions, such as the antisymmetrized geminal power (AGP) and the Pfaffian wavefunction. For all the above reasons, we remark once again our belief that QMC should be considered as the raising star for ab initio simulations of materials.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Footnote

^The statistical error decays as $1 ∕ \sqrt{N}$ , where N is the number of uncorrelated samples.

References

Anderson, J. B. (1976). Quantum chemistry by random walk. J. Chem. Phys. 65, 4121–4127. doi: 10.1063/1.432868