A Novel Approach to the Description of Constitutive Relations

Recent advances in the development of implicit constitutive relations to describe the response of both solids and fluids have greatly increased the repertoire of the modeler in his ability to describe natural phenomena more faithfully than hitherto possible. It would not be an exaggeration to claim that such constitutive relations have the potential to lead to breakthroughs in mechanics as they provide very promising novel means to study two of the most important and ill-understood problems in mechanics, that of fracturing of solids and of turbulence in fluids, in addition to providing a means to describe a plethora of phenomena that have eluded explanation in biomechanics, response of colloids, and mixtures, etc. In this article, we describe these recent developments within the context of both fluid and solid mechanics.

1. Introduction

Within a purely mechanical context bodies deform due to the application of surface and body forces. Their deformation is governed by the balance of mass and the balance of linear momentum, which comprise four scalar equations for the unknowns, the density ρ, velocity $\underset{¯}{\text{v}}$, and stress $\underset{¯}{\text{T}}$, namely ten scalar variables, leading to a system of equations that is not well posed with regard to the determination of the unknowns. This lack of a well posed system of equations stems from our not having provided information concerning the make-up of the body that essentially determines how it responds to the forces. This lacuna is filled by providing what is referred to as constitutive relations. A discussion of the salient aspects in the development of non-linear mechanics can be found in the article by Truesdell (1952). The usual approach to the description of the response of bodies, whether they are lumped parameter systems or solid or fluid continua, is to provide an expression for the force or stress in terms of appropriate kinematic variables. Though in linearized elasticity and viscoelasticity the stress is expressed in terms of the strain or vice-versa, when it comes to the development of governing equations, one substitutes the expression for the stress in terms of the appropriate kinematic variable, the strain for a solid, or the symmetric part of the velocity gradient for the fluid, and obtains an equation for the displacement or velocity. Such a procedure leads to a simple mathematical structure in that we have to solve a partial differential or an integro-differential equation for the density and displacement or velocity. However, this procedure is philosophically unsound as will become obvious from the discussion that follows. In fact, the procedure of prescribing a constitutive expression for the stress in terms of the kinematics in order to obtain a mathematically amenable system is an example of what Schwartz (1962) refers to as the “pernicious influence of mathematics on science.”

There are several shortcomings with respect to the manner in which constitutive relations are usually specified currently, both from a philosophical standpoint and more pragmatic considerations. From the philosophical standpoint, expressing the stress in terms of kinematical variables turns causality on its head, as forces and stresses are the causes, and the kinematics is the effect. It makes much more sense to describe kinematics in terms of the stresses and/or their derivatives [we refer the reader to Rajagopal (2003, 2007) for a detailed discussion of this issue]. However, it might not be possible to prescribe the kinematics in terms of the stress explicitly, and the best that one can do is to prescribe an implicit relation for the stress and the kinematical quantity. From a pragmatic standpoint, prescribing an expression for the stress and substituting the same into the balance of linear momentum increases the order of the governing equations thereby creating the need for the specification of additional boundary conditions, greater regularity of the solution, and other complications with regard to computational issues. Moreover, the classical approach of prescribing an expression for the stress is not possible for numerous bodies.

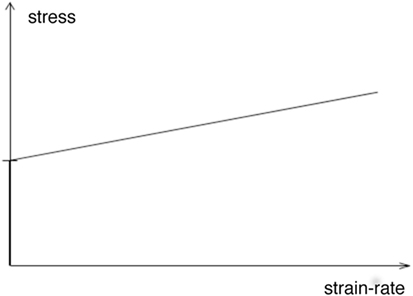
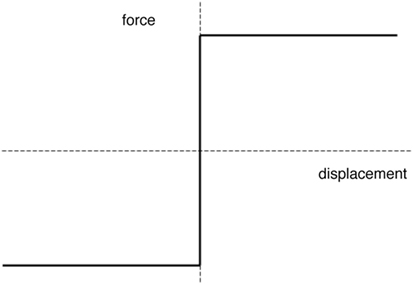
Simple examples of systems that cannot be described by providing an expression for the stress in terms of the kinematic variables are illustrated in Figures 1–3. In Figure 1A, we have a system wherein we have a spring in parallel to an inextensible string. The response of such a system is depicted in Figure 1B, and it is obvious that the force cannot be expressed in terms of the elongation, while the elongation can be expressed in terms of the force. In Figure 2, the response of a Bingham fluid, a popular model among rheologists, is depicted. We once again notice that the stress cannot be expressed as a function of the shear rate; however, the shear rate can be expressed in terms of the stress. Figure 3 displays the response associated with Coulomb friction and such a response cannot be described by expressing the force in terms of the displacement or the displacement in terms of force, and we truly need an implicit relationship. A similar situation presents itself if we try to describe elastic–plastic response.

FIGURE 1

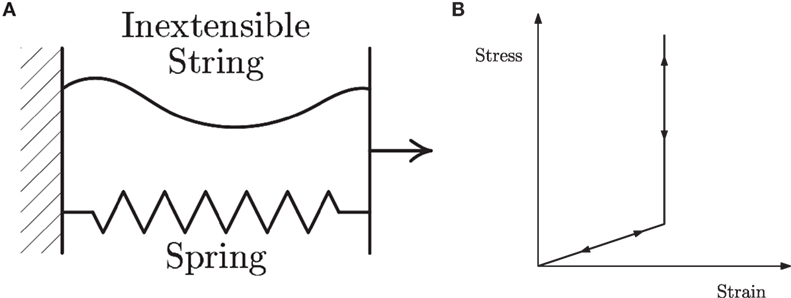
Figure 1. Mechanical analog and non-dissipative response. (A) A linear spring and an inextensible rope in parallel. The spring need not be a linear spring. (B) Non-dissipative response wherein the stress cannot be expressed explicitly as a function.

FIGURE 2

Figure 2. The response of a Bingham like mass-dashpot system.

FIGURE 3

Figure 3. Coulomb friction.

Very interesting examples of the need for implicit constitutive relations are provided by the response of biological fluids and colloidal solutions. In Figure 4, the experimental results of Boltenhagen et al. (1997) for the relationship between the shear stress and shear rate is portrayed for Tris (2-hydroxyethyl) tallowalkyl ammonium acetate (TTAA) surfactant dissolved in water containing sodium salicylate (NaSal). The apparent viscosity versus shear rate (which of course assumes a specific constitutive model) from the same set of experiments by Boltenhagen et al. (1997) is depicted in Figure 5, while in Figure 6, corroboration of the experimental results of Boltenhagen et al. (1997) using an implicit model by Perlácová and Prŭša (2015) is documented. With regard to the experimental data of Boltenhagen et al. (1997) and a lot of other experimental data for colloids, constitutive specifications wherein one has an expression for the stress in terms of the history of the deformation gradient cannot be used for the data reduction. We need an implicit constitutive relation to describe the same [see Perlácová and Prŭša (2015)].

FIGURE 4

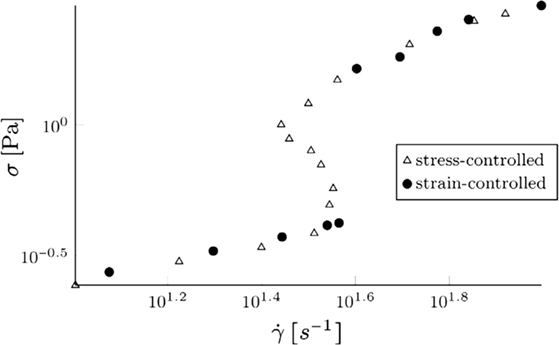
Figure 4. Shear stress versus shear rate in the experiments by Boltenhagen et al. (1997) for Tris(2-hydroxyethyl) tallowalkyl ammonium acetate (TTAA) surfactant dissolved in water containing sodium salicylate (NaSal).

FIGURE 5

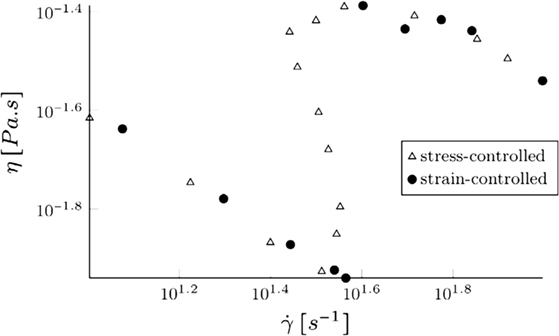
Figure 5. Variation of apparent viscosity with shear rate in the experiment by Boltenhagen et al. (1997).

FIGURE 6

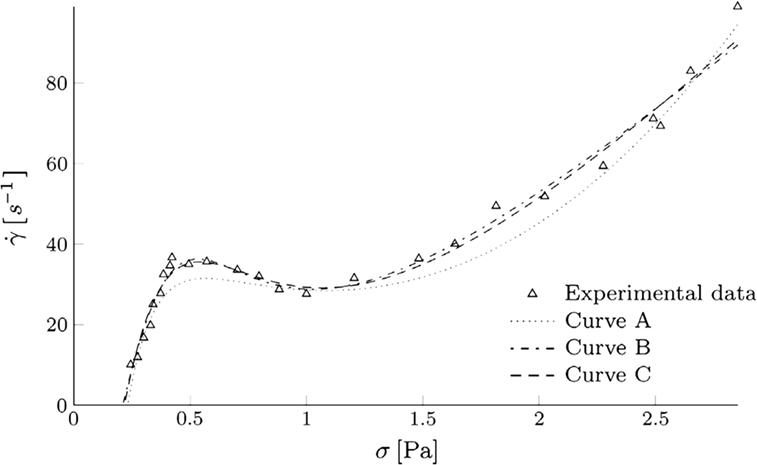
Figure 6. Fit of experimental data of by Boltenhagen et al. (1997) by Perlácová and Prŭša (2015). The qualitative nature of the curve belongs to precisely the same class of models introduced by Le Roux and Rajagopal (2013).

Implicit constitutive relations are the natural class of response relations to describe a very large class of materials, polymeric fluids, which exhibit pressure¹ dependent material properties [see Singh and Nolle (1959) and McKinney and Belcher (1963)], geological materials, biological solid matter, such as DNA and collagenous material [see Freed and Einstein (2013); Freed (2014); Freed et al. (2014); Freed and Rajagopal (2016)], elastomeric solids whose material moduli depend on the mean normal stress [see the discussion in Rajagopal and Saccomandi (2009)], magneto–elastic bodies [see Bustamante and Rajagopal (2015)], and electro–elastic bodies [see Bustamante and Rajagopal (2012, 2013)], to name some of them.

An interesting class of problems that the classical Cauchy theory of elasticity is impotent to describe is the non-linear relationship that is observed between the strain and the stress, when the strains are so small that it is in the linearized range, that is, when the squares and higher powers of the strain are negligible in comparison to the strain. Such is indeed the case of many alloys, such as Gum metal [also see the experimental works of Saito et al. (2003) and Figure 7], and the implicit theory leads to models, which when linearized can describe such response with ease. The recent paper by Rajagopal (2014) provides one such example wherein the linearization, based on the assumption that the displacement gradient is small, with regard to an implicit model fits the non-linear relationship between the linearized strain and the stress, exceptionally well. The ability to model the non-linear relationship between the stress and the strain, in the small strain range where the classical linearized theory is supposed to hold, cannot be overemphasized as such response cannot be described within the framework of linearization of the classical elasticity theory and as there are many metallic alloys as well as geomaterials and construction materials that exhibit such response. In Figure 7, we present the experimental results of Saito et al. (2003) for Gum metal, and in Figure 8, we present the experimental results of Grasley et al. (2015). Both the figures clearly show a non-linear relationship between the strain and the stress at small strains.

FIGURE 7

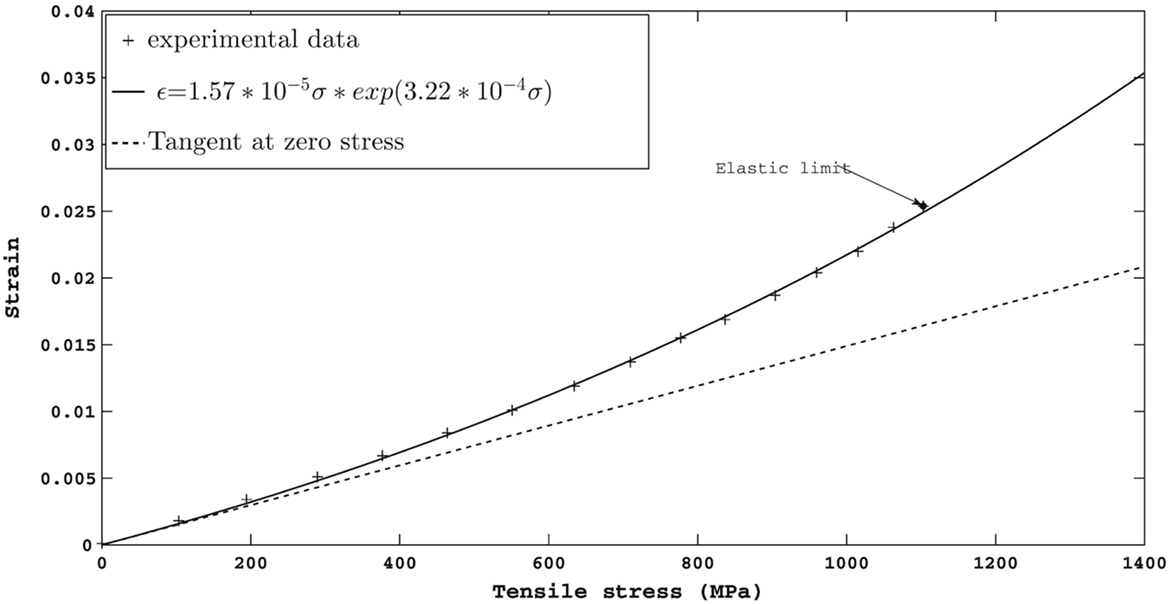
Figure 7. Non-linear relationship between the strain and stress in the small strain range for a Gum metal alloy [figure is taken from the paper by Saito et al. (2003)].

FIGURE 8

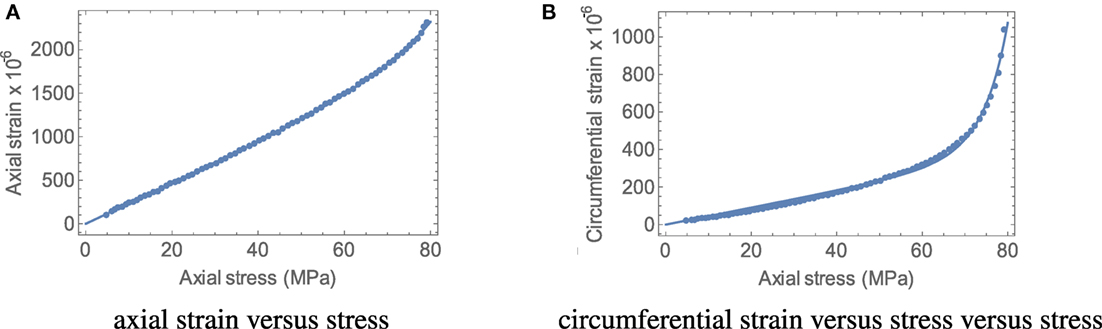
Figure 8. Non-linear relation between the stress and strain in the small strain range for concrete. Dots represent experimental data and the full line the theoretical fit based on a model belonging to the class equation (32). Data shown are for a concrete cylinder M10B1C2. Figures are taken from Grasley et al. (2015). (A) Axial strain versus stress. (B) Circumferential strain versus stress.

A few remarks concerning the ability of implicit constitutive models to describe phenomena hitherto described in an ad hoc manner are warranted. One of the most important class of problems with regard to the response of solids is the problem of the development and movement of cracks. The classical linearized theory of elasticity and non-linear theories of elasticity predict singularities that are physically unacceptable, and in the case of the classical linearized theory of elasticity self-contradictory, near and at the crack tip. Totally ad hoc procedures have been proposed to get around the problem. The newly developed implicit theory allows one to describe the response near crack tips in a rational and consistent manner.

The new class of implicit models also provides a clean and simple way for developing theories to describe limiting strain behavior that is observed in a large class of biological and geological materials. Moreover, it allows one to describe materials whose moduli depend on both the invariants of the stress, such as pressure dependence of the shear modulus and relaxation time that has been observed in polymeric materials.

In the case of fluids, implicit theories present a new approach to the modeling of turbulence where one can take into consideration the fluctuations in both the stresses and the velocities and its gradients in the modeling. It allows one to model the non-monotone relationship between the stress and the shear rate that has been observed in experiments involving colloids. And as in the case of solids, it allows one to incorporate the effect of the invariants of the stresses as well as the relevant kinematical quantities in the material properties, which cannot be done in models wherein the stress is defined explicitly in terms of kinematical quantities. The above are but a few of the many advantages that the new class of implicit models offer.

Implicit models also have numerous other important applications in fluid mechanics. For example, the field of elastohydrodynamics is built around the notion that the material properties of the lubricant are a function of the mean normal stress of the fluid. When one recognizes that most lubricants have also shear rate dependent properties, we are naturally led to models that are implicit [see Rajagopal and Szeri (2003)]. When one deals with a generalization of the Navier–Stokes fluid with a pressure dependent viscosity (usually referred to in the literature as a piezoviscous fluid), one cannot express the stress explicitly in terms of the velocity gradient, but one can express the velocity gradient as a non-linear function of the stress. Such fluids are special cases of the more general implicit fluid model and have been studied in detail in a variety of applications [see Dowson et al. (1983); Tran and Suslov (2009); Saccomandi and Vergori (2010); Szeri (2011); Rajagopal et al. (2012)].

Within the context of lumped parameter systems, the governing equations for the components of the system given in terms of implicit constitutive relations reduce to a system of differential-algebraic systems and lead to interesting and challenging mathematical problems. The development of implicit relationships to describe the components of lumped parameter systems was first introduced in Darbha et al. (2010) and Rajagopal (2010). Later, Pražák and Rajagopal (2012, 2016) studied mathematical questions concerning existence and uniqueness for some special lumped parameter system when the components are described by implicit relations. Recently, Málek et al. (2016) studied the bifurcation of solution of the differential-algebraic system for lumped parameter systems described by implicit constitutive relations. They also carried out classical studies concerning Lyapunov exponents and Poincare’ surface sections and recurrence analysis on the trajectories obtained. Yuan et al. (2015) have found numerical solutions to a system of differential-algebraic equations that correspond to a mass that is attached to spring that has limited extensibility.

While traditionally implicit constitutive relations that involve higher derivatives of either the stress or kinematical quantities, or both, have been used to describe viscoelastic and inelastic materials, they have not been used to describe purely elastic materials or fluids, which are not viscoelastic. Nor has there been a systematic attempt to study such response. A fluid whose viscosity depends on both the mean value of the stress and the shear rate seems to be a reasonable model to describe the response of fluids that are subject to a wide range of pressures. The model developed by Maxwell (1867) to describe viscoelastic fluid response is not an implicit model, though the rate equation that he provides has been misconstrued as being one; in the case of this model, the symmetric part of the velocity gradient can be expressed in terms of the stress and its material time derivative. The one-dimensional model developed by Burgers (1935) to describe the response of viscoelastic fluids seems to be the first implicit relationship to describe the response of viscoelastic fluids.² Later, Oldroyd (1950) systematically developed properly invariant rate type models to describe viscoelastic fluid response. Implicit models to describe inelastic behavior, primarily the yield surface, can be traced to Prandtl (1935) and Reuss (1930). Implicit models arise as the appropriate class of models to describe a variety of materials, as mentioned earlier examples are polymeric fluids that have pressure-dependent viscosity [see Singh and Nolle (1959) and McKinney and Belcher (1963)], geological materials, which are viscoelastic fluids whose material moduli depend on the mean normal stress [see the discussion and references in Karra et al. (2011)], several biological elastic solids [see the discussion in Freed and Einstein (2013); Freed (2014); Freed et al. (2014)], and elastomeric solids whose material moduli depend on the mean normal stress [see the discussion in Rajagopal and Saccomandi (2009)].

Rajagopal (2003) started investigation of implicit models by considering relationships between the stress and deformation gradient in the case of elastic solid bodies, and the stress and the symmetric part of the velocity gradient in case of fluids. These relationships did not involve higher derivatives of the stresses or the kinematical variables and hence can be viewed as a purely algebraic relationship between the variables involved. Recently, Prŭša and Rajagopal (2011) introduced an implicit relationship between the history of the stress, density, and the deformation gradient. Many of the classical constitutive relations that are used to describe the response of fluids are special subclasses of such a general implicit relationship. They also used a generalization of the procedure used by Coleman and Noll (1960) to find approximations within the context of retarded motion that have the same form as those of several popular non-Newtonian fluid models. However, it is important to bear in mind that these approximations only hold in these retarded motions, and the procedure does not lead to models that can be used to describe general flows of the fluids under consideration [see Dunn and Rajagopal (1995)].

Implicit elastic bodies can also be used to describe phenomena concerning wave propagation problems that cannot be described within the classical construct. For instance, while within the purview of classical theories, one attributes the change in the stress wave shape to dissipation, it can be shown that such changes of shape can take place within a purely non-dissipative elastic framework within the context of bodies described by implicit constitutive relations [see Kannan et al. (2014)]. Recently, wave propagation problems have been studied within the context of both elastic solids described by implicit constitutive relations (Kannan et al., 2014; Rajagopal and Saccomandi, 2014) and fluids described by implicit constitutive relations (Kambapalli et al., 2014).

From the mathematical perspective, implicit constitutive relations lead to exceedingly interesting issues in the analysis of partial differential equations [see Bulíček et al. (2009, 2012a,b)]. Even simple one-dimensional problems involving certain implicit constitutive equations do not even admit solutions in the sense of distributions, and one has to consider solutions within the context of much more general structures, such as Colombeau algebras [see Prŭša and Rajagopal (2011)], for a discussion of generalized solutions within the context of flows of a pressure dependent Burgers fluid [see Colombeau (1984, 1985) and Rosinger (1987) for a discussion of generalized solutions to partial differential equations, such as Colombeau algebras, and their generalizations].

2. Kinematics

We provide a minimal discussion of the kinematics that is required for the following discussion. A detailed discussion of the kinematics of continua can be found in Truesdell and Noll (1965) and Truesdell (1977).

Let $\underset{¯}{\text{x}}$ denote the current position of a particle that is at $\underset{¯}{\text{X}}$ in a stress-free configuration.³ Let $\underset{¯}{\text{x}}={\chi }_{{\kappa }_R}(\underset{¯}{\text{X}},t)$ denote the motion of a particle, and let us denote the displacement by:

$\underset{¯}{\text{u}}:=\underset{¯}{\text{x}}-\underset{¯}{\text{X}}$ (1)

The displacement gradients $\frac{\partial \underset{¯}{\text{u}}}{\partial \underset{¯}{\text{X}}}$ and $\frac{\partial \underset{¯}{\text{u}}}{\partial \underset{¯}{\text{x}}}$ are given by:

$\frac{\partial \underset{¯}{\text{u}}}{\partial \underset{¯}{\text{X}}}={\nabla }_{\underset{¯}{\text{X}}}\underset{¯}{\text{u}}=\underset{¯}{\text{F}}-\underset{¯}{\text{I}},$ (2)

and

$\frac{\partial \underset{¯}{\text{u}}}{\partial \underset{¯}{\text{x}}}={\nabla }_{\underset{¯}{\text{x}}}\underset{¯}{\text{u}}=\underset{¯}{\text{I}}-{\underset{¯}{\text{F}}}^{-1},$ (3)

where $\underset{¯}{\text{F}}$ is the deformation gradient defined through

$\underset{¯}{\text{F}}=\frac{\partial \chi }{\partial \underset{¯}{\text{X}}}.$ (4)

The velocity is defined through

$\underset{¯}{\text{v}}=\frac{\partial \chi }{\partial t}.$ (5)

and, the velocity gradient $\underset{¯}{\text{L}}$, and its symmetric part $\underset{¯}{\text{D}}$ and its skew part $\underset{¯}{\text{W}}$ through

$\underset{¯}{\text{L}}:=\frac{\partial \underset{¯}{\text{v}}}{\partial \underset{¯}{\text{x}}},\underset{¯}{\text{D}}:=\frac{1}{2}(\underset{¯}{\text{L}}+{\underset{¯}{\text{L}}}^T),\underset{¯}{\text{W}}:=\frac{1}{2}(\underset{¯}{\text{L}}-{\underset{¯}{\text{L}}}^T).$ (6)

The Cauchy–Green tensors $\underset{¯}{\text{B}}$ and $\underset{¯}{\text{C}}$ are defined through

$\underset{¯}{\text{B}}:=\underset{¯}{\text{F}}{\underset{¯}{\text{F}}}^T,\underset{¯}{\text{C}}:={\underset{¯}{\text{F}}}^T\underset{¯}{\text{F}}.$ (7)

The Green–St. Venant strain $\underset{¯}{\text{E}}$ and the Almansi–Hamel strain $\underset{¯}{\text{e}}$ are defined through

$\underset{¯}{\text{E}}:=\frac{1}{2}\left[\underset{¯}{\text{C}}-\underset{¯}{\text{I}}\right],\underset{¯}{\text{e}}:=\frac{1}{2}\left[\underset{¯}{\text{I}}-{\underset{¯}{\text{B}}}^{-1}\right]$ (8)

3. Implicit Models to Describe Viscous Fluid Response

The classical Navier–Stokes fluid is described by the following relationship between the stress and the symmetric part of the velocity gradient

$\underset{¯}{\text{T}}=-p(\rho )\underset{¯}{1}+\lambda (\rho )\text{tr}(\underset{¯}{\text{D}})\underset{¯}{1}+2\mu (\rho )\underset{¯}{\text{D}}$ (9)

where λ(ρ) and μ(ρ) are the bulk and shear viscosities, and ρ is the density. The original derivation by Navier (1827) had only one of the viscosities, the other being given in terms of the first. However, Poisson (1831) developed the full model that appears in with both the viscosities. The later derivation, on phenomenological grounds, by Saint-Venant (1843) also had one of the viscosities being given in terms of the other. In Stokes phenomenological development [see Stokes (1845)], the full model shown in equation (9) above, with both the viscosities, is derived. However, Stokes suggests the simplification that (3λ + 2μ = 0) only to have second thoughts and disown the relationship at a later date [see Stokes (1851)]. A discussion as to why the Stokes assumption is inapt can be found in the recent paper by Rajagopal (2013). Such an assumption would never have been even considered as a possibility had not an expression been given for the Cauchy stress in terms of the symmetric part of the velocity gradient. If one started with the more appropriate expression:

$\underset{¯}{\text{D}}=\alpha (\rho )\underset{¯}{\text{I}}+\beta (\rho )(\text{tr}\underset{¯}{\text{T}})\underset{¯}{\text{I}}+\gamma (\rho )\underset{¯}{\text{T}},$ (10)

one would not have arrived at such an erroneous possibility [see Rajagopal (2013)]. In the case of an incompressible Navier–Stokes fluid, the stress is usually expressed as

$\underset{¯}{\text{T}}=-p\underset{¯}{1}+2\mu \underset{¯}{\text{D}}$ (11)

where $p=-\frac{1}{3}\text{tr}\underset{¯}{\text{T}}$ is the mean normal stress but once again the more appropriate expression is the form:

$\underset{¯}{\text{D}}=\alpha \left[\underset{¯}{\text{T}}-\frac{1}{3}\text{tr}\underset{¯}{\text{T}}\right].$ (12)

We notice that such a constitutive expression automatically satisfies the requirement that the fluid be capable of undergoing only isochoric motions.

If we were to suppose that in a generalization of the above incompressible fluid the shear viscosity is a function of the mean value of the stress and shear rate (given through the second invariant of the symmetric part of the velocity gradient), then the stress in such a fluid would be given through the relation

$\underset{¯}{\text{T}}=-p\underset{¯}{\text{I}}+\mu (\text{tr}\underset{¯}{\text{T}},\text{tr}{\underset{¯}{\text{D}}}^2)\underset{¯}{\text{D}}$ (13)

which is in general an implicit relation of the form

$f(\underset{¯}{\text{T}},\underset{¯}{\text{D}})=0.$ (14)

Since f is an isotropic function in the case of an isotropic fluid, it has to meet

$\underset{¯}{\text{Q}}f(\underset{¯}{\text{T}},\underset{¯}{\text{D}}){\underset{¯}{\text{Q}}}^T=f(\underset{¯}{\text{Q}}\underset{¯}{\text{T}}{\underset{¯}{\text{Q}}}^T,\underset{¯}{\text{Q}}\underset{¯}{\text{D}}{\underset{¯}{\text{Q}}}^T)\forall \underset{¯}{\text{Q}}\in \mathcal{O}$ (15)

where 𝒪 denotes the set of all orthogonal transformations. It then follows that [see Spencer (1975)]:

$\begin{array}{l}{\alpha }_0\underset{¯}{\text{I}}+{\alpha }_1\underset{¯}{\text{T}}+{\alpha }_2\underset{¯}{\text{D}}+{\alpha }_3{\underset{¯}{\text{T}}}^2+{\alpha }_4{\underset{¯}{\text{D}}}^2+{\alpha }_5(\underset{¯}{\text{T}}\underset{¯}{\text{D}}+\underset{¯}{\text{D}}\underset{¯}{\text{T}})\\ +{\alpha }_6({\underset{¯}{\text{T}}}^2\underset{¯}{\text{D}}+{\underset{¯}{\text{D}}}^2\underset{¯}{\text{T}})+{\alpha }_7(\underset{¯}{\text{T}}{\underset{¯}{\text{D}}}^2+\underset{¯}{\text{D}}{\underset{¯}{\text{T}}}^2)+{\alpha }_8({\underset{¯}{\text{T}}}^2{\underset{¯}{\text{D}}}^2+{\underset{¯}{\text{D}}}^2{\underset{¯}{\text{T}}}^2)=\underset{¯}{0}\end{array}$ (16)

where the material functions α_i, i = 0, …, 8 depend on the invariants

$\text{tr}\underset{¯}{\text{T}},\text{tr}\underset{¯}{\text{D}},\text{tr}{\underset{¯}{\text{T}}}^2,\text{tr}{\underset{¯}{\text{D}}}^2,\text{tr}{\underset{¯}{\text{T}}}^3,\text{tr}{\underset{¯}{\text{D}}}^3,\text{tr}(\underset{¯}{\text{T}}\underset{¯}{\text{D}}),\text{tr}({\underset{¯}{\text{T}}}^2\underset{¯}{\text{D}}),\text{tr}({\underset{¯}{\text{D}}}^2\underset{¯}{\text{T}}),\text{tr}({\underset{¯}{\text{D}}}^2{\underset{¯}{\text{T}}}^2).$ (17)

The above class of models includes as a special subclass the models given by

$\underset{¯}{\text{T}}={\lambda }_0\underset{¯}{\text{I}}+{\lambda }_1\underset{¯}{\text{D}}+{\lambda }_2{\underset{¯}{\text{D}}}^2$ (18)

and the new sub-class of the form

$\underset{¯}{\text{D}}={\gamma }_0\underset{¯}{\text{I}}+{\gamma }_1\underset{¯}{\text{T}}+{\gamma }_2{\underset{¯}{\text{T}}}^2.$ (19)

A special subclass that has been studied recently consist in the stress power-law models wherein the Cauchy stress is given by

$\underset{¯}{\text{D}}=\alpha \left[1+(\text{tr}{({\underset{¯}{\text{T}}}_d)}^2\right]{\underset{¯}{\text{T}}}_d,$ (20)

where

${\underset{¯}{\text{T}}}_d=\underset{¯}{\text{T}}-\frac{1}{3}(\underset{¯}{\text{T}})\underset{¯}{\text{I}}.$ (21)

This model allows for describing phenomena that are not possible in a classical power-law fluid [see Málek et al. (2010); Le Roux and Rajagopal (2013); Perlácová and Prŭša (2015)]. The recent paper by Perlácová and Prŭša (2015) shows that such models can be used to describe the flows of biological liquids that have DNA coils suspended in them. They can also be used to describe the flow of colloidal solutions. The response exhibited by colloids are such that they cannot be described adequately by the constitutive relations that are currently used, and implicit constitutive relations provide the arsenal with which to do so, as shown by Perlácová and Prŭša (2015). Narayan and Rajagopal (2013) have studied wave propagation in fluids modeled by equations (20) and (21) and show that they exhibit characteristics that are quite different from those exhibited by classical power-law fluids.

4. Implicit Models to Describe Elastic Response

Until recently, by elastic bodies, one meant Cauchy elastic bodies or some the special subclass of Cauchy elastic bodies, namely Green elastic bodies, wherein the stress in derivable from a potential. When such models are linearized within the context of small displacement gradients, the models reduce to the classical linearized elastic model. However, there are many intermetallic alloys that exhibit non-linear response between the strain and the stress in the small strain range. We shall now show that implicit theories allow one to have a non-linear relationship between the strain and the stress, in the small strain range. Furthermore, we shall also show that implicit constitutive theories lead to meaningful models to describe the state of strain and stress near a crack tip. Before getting into a discussion of fully implicit constitutive theories for elastic solids, let us consider the class of materials defined through

$\underset{¯}{\text{F}}=\underset{¯}{\text{g}}(\rho ,\underset{¯}{\text{T}})$ (22)

which, due to the restrictions imposed by frame-indifference, reduces to

$\underset{¯}{\text{C}}=f(\rho ,\underset{¯}{\text{T}})$ (23)

If the material is isotropic, it follows that

$\underset{¯}{\text{B}}=f(\rho ,\underset{¯}{\text{T}})$ (24)

Then, one can use standard representation theorems to express the Cauchy–Green tensor $\underset{¯}{\text{B}}$ in terms of the stress, which when linearized under the assumption that the displacement gradient is small leads to a model that has a non-linear relationship between the linearized strain and the stress.

Next, we shall consider a more general class of models wherein the relationship between the stress and the deformation gradient is implicit. Rajagopal (2003) introduced implicit relations of the form

$f(\rho ,\underset{¯}{\text{T}},\underset{¯}{\text{F}})=0,$ (25)

where $\underset{¯}{\text{F}}$ is the deformation gradient. The classical definition of a Cauchy elastic body is a special subclass of the above class. In the case of isotropic bodies,⁴ the relationship reduces to the consideration of implicit relations of the form

$f(\rho ,\underset{¯}{\text{T}},\underset{¯}{\text{B}})=0,$ (26)

and since the body is isotropic, it has to satisfy the invariance

$f(\rho ,\underset{¯}{\text{Q}}\underset{¯}{\text{T}}{\underset{¯}{\text{Q}}}^T,\underset{¯}{\text{Q}}\underset{¯}{\text{B}}{\underset{¯}{\text{Q}}}^T)=\underset{¯}{\text{Q}}f(\rho ,\underset{¯}{\text{T}},\underset{¯}{\text{B}}){\underset{¯}{\text{Q}}}^T\forall \underset{¯}{\text{Q}}\in \mathcal{O}$ (27)

where 𝒪 denotes the orthogonal group. It then follows that [see Spencer (1975)]

$\begin{array}{l}{\alpha }_0\underset{¯}{\text{I}}+{\alpha }_1\underset{¯}{\text{T}}+{\alpha }_2\underset{¯}{\text{B}}+{\alpha }_3{\underset{¯}{\text{T}}}^2+{\alpha }_4{\underset{¯}{\text{B}}}^2+{\alpha }_5(\underset{¯}{\text{T}}\underset{¯}{\text{B}}+\underset{¯}{\text{B}}\underset{¯}{\text{T}})\\ +{\alpha }_6({\underset{¯}{\text{T}}}^2\underset{¯}{\text{B}}+{\underset{¯}{\text{B}}}^2\underset{¯}{\text{T}})+{\alpha }_7(\underset{¯}{\text{T}}{\underset{¯}{\text{B}}}^2+\underset{¯}{\text{B}}{\underset{¯}{\text{T}}}^2)+{\alpha }_8({\underset{¯}{\text{T}}}^2{\underset{¯}{\text{B}}}^2+{\underset{¯}{\text{B}}}^2{\underset{¯}{\text{T}}}^2)=\underset{¯}{0}\end{array}$ (28)

where the material moduli α_i, i = 0, …, 8 depend upon

$\rho ,\text{tr}\underset{¯}{\text{T}},\text{tr}\underset{¯}{\text{B}},\text{tr}{\underset{¯}{\text{T}}}^2,\text{tr}{\underset{¯}{\text{B}}}^2,\text{tr}{\underset{¯}{\text{T}}}^3,\text{tr}{\underset{¯}{\text{B}}}^3,\text{tr}(\underset{¯}{\text{T}}\underset{¯}{\text{B}}),\text{tr}({\underset{¯}{\text{T}}}^2\underset{¯}{\text{B}}),\text{tr}({\underset{¯}{\text{B}}}^2\underset{¯}{\text{T}}),\text{tr}({\underset{¯}{\text{B}}}^2{\underset{¯}{\text{T}}}^2).$

We immediately notice that the classical Cauchy constitutive expression

$\underset{¯}{\text{T}}={\nu }_0\underset{¯}{\text{I}}+{\nu }_1\underset{¯}{\text{B}}+{\nu }_2{\underset{¯}{\text{B}}}^2,$ (29)

where the ν_i, i = 0, 1, 2 are functions of ρ and the principal invariants of $\underset{¯}{\text{B}}$, as well as the constitutive expression

$\underset{¯}{\text{B}}={\alpha }_0\underset{¯}{\text{I}}+{\alpha }_1\underset{¯}{\text{T}}+{\alpha }_2{\underset{¯}{\text{T}}}^2,$ (30)

where the α_i, i = 0, 1, 2 are functions of ρ and the principal invariants of $\underset{¯}{\text{T}}$ are both subsets of equation (28). Let us now linearize equation (30) under the assumption that

$\underset{X\in \kappa (B),t\in R}{\max }\Vert {\nabla }_{x}u\Vert =O(\delta ),\delta <<1,$ (31)

where ||.|| stands for the trace norm, induced through the scalar product. Then, equation (30) reduces to

$ϵ={\beta }_0\underset{¯}{\text{I}}+{\beta }_1\underset{¯}{\text{T}}+{\beta }_2{\underset{¯}{\text{T}}}^2,$ (32)

allowing for a non-linear relationship between the linearized strain and the stress. Such a relationship can be gainfully exploited to describe a variety of phenomena that have been observed. For instance, the non-linear relationship observed in Gum metal and several metallic alloys can be described through such a relationship (Rajagopal, 2003). Also, the relationship allows one to describe the state of strain adjacent to a crack [see Rajagopal and Walton (2011) and Gou et al. (2015)] and the strain adjacent to blunt and sharp notches [see Zappalorto et al. (2016), also see Kulvait et al. (2013)] in a meaningful manner.

For elastic bodies, one could also consider rate type equations, such as (Rajagopal, 2007)

$\underset{¯}{\text{A}}(\underset{¯}{\text{S}},\underset{¯}{\text{E}})(\text{d}\underset{¯}{\text{S}}/\text{dt})+\underset{¯}{\text{B}}(\underset{¯}{\text{S}},\underset{¯}{\text{E}})(\text{d}\underset{¯}{\text{E}}/\text{dt})=0,$ (33)

which are not equivalent to the class of equations defined by (25). We shall not discuss such models here but refer the reader to Rajagopal (2007).

5. Concluding Remarks

As implicit models include explicit representations for the stress in terms of the kinematics or kinematics in terms of stress, as special subclasses, and since the converse is not true, one can use implicit constitutive relations to describe a much larger class of material response. Some new models have been recently developed to describe the complex response exhibited by some materials using the new general class of implicit constitutive relations with elastic bodies as the backbone, for both viscoelastic and inelastic response (Alagappan et al., 2014; Rajagopal and Srinivasa, 2015, 2016). We shall not discuss these models here. The aim of this note was to highlight the inherent potential of implicit models, and toward this purpose, an overview of elastic solids and viscous fluids is sufficient.

Another important goal of this note is to hope to establish a change of perspective. The theory of explicit constitutive equations, as for example the theory of simple materials á la Noll, is too narrow to give a complete description of the mechanical behavior of materials. The problem is that everybody learns only the mechanics of materials described through constitutive relations in an explicit manner. To appreciate the generality and the power of implicit theories, we have to change our mind set, and if we do so, we discover that an axiomatic approach to mechanics that is much more promising and deep that allows us to view the great work of Cauchy and the other Savants within a proper perspective.

Author Contributions

All authors listed have made substantial, direct, and intellectual contribution to the work and approved it for publication.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The research of GS is partially supported by GNFM of italian Istituto Nazionale di Alta Matematica. KRR was supported by ONR Grant Number C12-00292.

Footnotes

1. ^The terminology pressure is used to denote so many different quantities that one ought to the be very careful with regard to the sense in which it is being employed [see Rajagopal (2015b) for a detailed discussion of the same].
2. ^However, the generalization of the Maxwell model, wherein the viscosity and the relaxation time depend upon the second invariant of the symmetric part of the velocity gradient, would be an implicit model.
3. ^We are making the tacit assumption that there exists a stress-free state in which the body can exist.
4. ^Recently, Rajagopal (2015a) has defined what is meant by the symmetry group for bodies described by implicit constitutive relations.

References

Alagappan, P., Rajagopal, K. R., and Srinivasa, A. (2014). Wave propagation due to impact through layered polymer composites. Compos. Struct. 115, 1–11. doi:10.1016/j.compstruct.2014.03.037

CrossRef Full Text | Google Scholar

Boltenhagen, P., Hu, Y., Matthys, E., and Pine, D. (1997). Observation of bulk phase separation and coexistence in a sheared micellar solution. Phys. Rev. Lett. 79, 2359. doi:10.1103/PhysRevLett.79.2359

CrossRef Full Text | Google Scholar

Bulíček, M., Gwiazda, P., Málek, J., and Świerczewska-Gwiazda, A. (2009). On steady flows of incompressible fluids with implicit power-law-like rheology. Adv. Calc. Var. 2, 109–136.

Google Scholar

Bulíček, M., Gwiazda, P., Málek, J., and Swierczewska-Gwiazda, A. (2012a). On unsteady flows of implicitly constituted incompressible fluids. SIAM J. Math. Anal. 44, 2756–2801. doi:10.1137/110830289

CrossRef Full Text | Google Scholar

Bulíček, M., Gwiazda, P., Málek, J., Swierczewska-Gwiazda, A., and Rajagopal, K. (2012b). “On flows of fluids described by an implicit constitutive equation characterized by a maximal monotone graph,” in Mathematical Aspects of Fluid Mechanics (London Math. Soc. Lecture Note Ser), Vol. 402, 23–51.

Google Scholar

Burgers, J. M. (1935). “Mechanical considerations model systems phenomenological theories of relaxation and of viscosity (chapter 1),” in First Report on Viscosity and Plasticity (New York: Nordemann Publishing Company), 5–67.

Google Scholar

Bustamante, R., and Rajagopal, K. R. (2015). Implicit constitutive relations for nonlinear magnetoelastic bodies. Proc. R. Soc. A 471, 20140959. doi:10.1098/rspa.2014.0959

PubMed Abstract | CrossRef Full Text | Google Scholar

Bustamante, R., and Rajagopal, K. R. (2012). On a new class of electroelastic bodies. I. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 469. doi:10.1098/rspa.2012.0521

CrossRef Full Text | Google Scholar

Bustamante, R., and Rajagopal, K. R. (2013). On a new class of electro-elastic bodies. II. Boundary value problems. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 469. doi:10.1098/rspa.2013.0106

CrossRef Full Text | Google Scholar

Coleman, B. D., and Noll, W. (1960). An approximation theorem for functionals, with applications in continuum mechanics. Arch. Ration. Mech. Anal. 6, 355–370. doi:10.1007/BF00276168

CrossRef Full Text | Google Scholar

Colombeau, J. F. (1984). New Generalized Functions and Multiplication of Distributions (North-Holland Mathematics Studies). Amsterdam: North-Holland Publishing Co., 84.

Google Scholar

Colombeau, J. F. (1985). Elementary Introduction to New Generalized Functions (North-Holland Mathematics Studies). Amsterdam: North-Holland Publishing Co., 113.

Google Scholar

Darbha, S., Nakshatrala, K. R., and Rajagopal, K. R. (2010). On the vibrations of lumped parameter systems governed by differential-algebraic equations. J. Franklin Inst. 347, 87–101. doi:10.1016/j.jfranklin.2009.11.005

CrossRef Full Text | Google Scholar

Dowson, D., Dunn, J., and Taylor, C. (1983). The piezo-viscous fluid, rigid solid regime of lubrication. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 197, 43–52. doi:10.1243/PIME_PROC_1983_197_075_02

CrossRef Full Text | Google Scholar

Dunn, J., and Rajagopal, K. R. (1995). Fluids of differential type: critical review and thermodynamic analysis. Int. J. Eng. Sci. 33, 689–729. doi:10.1016/0020-7225(94)00078-X

CrossRef Full Text | Google Scholar

Freed, A. (2014). Soft Solids: A Primer to the Theoretical Mechanics of Materials. Heidelberg: Springer Science & Business Media.

Google Scholar

Freed, A. D., and Einstein, D. R. (2013). An implicit elastic theory for lung parenchyma. Int. J. Eng. Sci. 62, 31–47. doi:10.1016/j.ijengsci.2012.08.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Freed, A. D., Liao, J., and Einstein, D. R. (2014). A membrane model from implicit elasticity theory: application to visceral pleura. Biomech. Model. Mechanobiol. 13, 871–881. doi:10.1007/s10237-013-0542-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Freed, A. D., and Rajagopal, K. R. (2016). A promising approach for modeling biological fibers. Acta Mech. 1–11. doi:10.1007/s00707-016-1583-8

CrossRef Full Text | Google Scholar

Gou, K., Mallikarjuna, M., Rajagopal, K. R., and Walton, J. (2015). Modeling fracture in the context of a strain-limiting theory of elasticity: a single plane-strain crack. Int. J. Eng. Sci. 88, 73–82. doi:10.1016/j.ijengsci.2014.04.018

CrossRef Full Text | Google Scholar

Grasley, Z., El-Helou, R., DAmbrosia, M., Mokarem, D., Moen, C., and Rajagopal, K. (2015). Model of infinitesimal nonlinear elastic response of concrete subjected to uniaxial compression. J. Eng. Mech. 141, 04015008. doi:10.1061/(ASCE)EM.1943-7889.0000938

CrossRef Full Text | Google Scholar

Kambapalli, M., Kannan, K., and Rajagopal, K. R. (2014). Circumferential stress waves in a non-linear cylindrical annulus in a new class of elastic materials. Q. J. Mech. Appl. Math. 67, 193–203. doi:10.1093/qjmam/hbu003

CrossRef Full Text | Google Scholar

Kannan, K., Rajagopal, K. R., and Saccomandi, G. (2014). Unsteady motions of a new class of elastic solids. Wave Motion 51, 833–843. doi:10.1016/j.wavemoti.2014.02.004

CrossRef Full Text | Google Scholar

Karra, S., Prŭša, V., and Rajagopal, K. R. (2011). On Maxwell fluids with relaxation time and viscosity depending on the pressure. Int. J. Non Linear Mech. 46, 819–827. doi:10.1016/j.ijnonlinmec.2011.02.013

CrossRef Full Text | Google Scholar

Kulvait, V., Málek, J., and Rajagopal, K. R. (2013). Anti-plane stress state of a plate with a v-notch for a new class of elastic solids. Int. J. Fract. 179, 59–73. doi:10.1007/s10704-012-9772-5

CrossRef Full Text | Google Scholar

Le Roux, C., and Rajagopal, K. R. (2013). Shear flows of a new class of power-law fluids. Appl. Math. 58, 153. doi:10.1007/s10492-013-0008-4

CrossRef Full Text | Google Scholar

Málek, J., Prŭša, V., and Rajagopal, K. R. (2010). Generalizations of the Navier–Stokes fluid from a new perspective. Int. J. Eng. Sci. 48, 1907–1924. doi:10.1016/j.ijengsci.2010.06.013

CrossRef Full Text | Google Scholar

Málek, J., Rajagopal, K. R., and Suková, P. (2016). Response of a class of mechanical oscillators described by a novel system of differential-algebraic equations. Appl. Math. 61, 79–102. doi:10.1007/s10492-016-0123-0

CrossRef Full Text | Google Scholar

Maxwell, J. C. (1867). On the dynamical theory of gases. Philos. Trans. R. Soc. Lond. 157, 49–88. doi:10.1098/rstl.1867.0004

CrossRef Full Text | Google Scholar

McKinney, J. E., and Belcher, H. V. (1963). Dynamic compressibility of polyvinylacetate and its relation to free volume. J. Res. Nat. Bur. Stand. Sect. A. Phys. Chem. A 67, 43–53. doi:10.6028/jres.067A.007

CrossRef Full Text | Google Scholar

Narayan, S. A., and Rajagopal, K. R. (2013). Unsteady flows of a class of novel generalizations of the Navier–Stokes fluid. Appl. Math. Comput. 219, 9935–9946. doi:10.1016/j.amc.2013.03.049

CrossRef Full Text | Google Scholar

Navier, C. (1827). Memoire sur le lois de lequilibre at du mouvement des corps solideselastiques. Mem. Acad. Sci. Inst. France 7, 375–393.

Google Scholar

Oldroyd, J. (1950). On the formulation of rheological equations of state. Proc. R. Soc. A 200, 523–541. doi:10.1098/rspa.1950.0035

CrossRef Full Text | Google Scholar

Perlácová, T., and Prŭša, V. (2015). Tensorial implicit constitutive relations in mechanics of incompressible non-Newtonian fluids. J. Nonnewton Fluid Mech. 216, 13–21. doi:10.1016/j.jnnfm.2014.12.006

CrossRef Full Text | Google Scholar

Poisson, S. (1831). Memorie sur les equations generales de lequilibre et du mouvements des corps solides, elastiques et uides. J. de lEcole Polytechnique 13, 1–174.

Google Scholar

Prandtl, L. (1935). “Spannungsverteilung in plastischen Korpen (chapter 1),” in Proceeding of the First Int. Congr. Appl. Mech (Delft), 43–54.

Google Scholar

Pražák, D., and Rajagopal, K. R. (2012). Mechanical oscillators described by a system of differential-algebraic equations. Appl. Math. 57, 129–142. doi:10.1007/s10492-012-0009-8

CrossRef Full Text | Google Scholar

Pražák, D., and Rajagopal, K. R. (2016). Mechanical oscillators with dampers given by implicit constitutive equation. Comm. Math. Univ. Carolin. 57, 51–61.

Google Scholar

Prŭša, V., and Rajagopal, K. R. (2011). Jump conditions in stress relaxation and creep experiments of burgers type fluids: a study in the application of Colombeau algebra of generalized functions. Zeitschrift für angewandte Mathematik und Physik 62, 707–740. doi:10.1007/s00033-010-0109-9

CrossRef Full Text | Google Scholar

Rajagopal, K. R. (2007). The elasticity of elasticity. Zeitschrift für angewandte Mathematik und Physik 58, 309–317. doi:10.1007/s00033-006-6084-5

CrossRef Full Text | Google Scholar

Rajagopal, K. R. (2010). A generalized framework for studying the vibrations of lumped parameter systems. Mech. Res. Commun. 17, 463–466.

Google Scholar

Rajagopal, K. R. (2013). A new development and interpretation of the Navier–Stokes fluid which reveals why the stokes assumption is inapt. Int. J. Non Linear Mech. 50, 141–151. doi:10.1016/j.ijnonlinmec.2012.10.007

CrossRef Full Text | Google Scholar

Rajagopal, K. R. (2014). On the nonlinear elastic response of bodies in the small strain range. Acta Mech. 225, 1545–1553. doi:10.1007/s00707-013-1015-y

CrossRef Full Text | Google Scholar

Rajagopal, K. R. (2015a). A note on the classification of anisotropy of bodies defined by implicit constitutive relations. Mech. Res. Commun. 64, 38–41. doi:10.1016/j.mechrescom.2014.11.005

CrossRef Full Text | Google Scholar

Rajagopal, K. R. (2015b). Remarks on the notion of pressure. Int. J. Non Linear Mech. 71, 165–172. doi:10.1016/j.ijnonlinmec.2014.11.031

CrossRef Full Text | Google Scholar

Rajagopal, K. R., and Saccomandi, G. (2009). The mechanics and mathematics of the effect of pressure on the shear modulus of elastomers. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 465, 3859–3874. doi:10.1098/rspa.2009.0416

CrossRef Full Text | Google Scholar

Rajagopal, K. R., and Saccomandi, G. (2014). Circularly polarized wave propagation in a class of bodies defined by a new class of implicit constitutive relations. Zeitschrift für angewandte Mathematik und Physik 65, 1003–1010. doi:10.1007/s00033-013-0362-9

CrossRef Full Text | Google Scholar

Rajagopal, K. R., Saccomandi, G., and Vergori, L. (2012). Flow of fluids with pressure-and shear-dependent viscosity down an inclined plane. J. Fluid Mech. 706, 173–189. doi:10.1017/jfm.2012.244

CrossRef Full Text | Google Scholar

Rajagopal, K. R., and Srinivasa, A. (2015). Inelastic response of solids described by implicit constitutive relations with nonlinear small strain elastic response. Int. J. Plasticity 71, 1–9. doi:10.1016/j.ijplas.2015.02.007

CrossRef Full Text | Google Scholar

Rajagopal, K. R., and Srinivasa, A. (2016). An implicit three dimensional model for describing the inelastic response of solids undergoing finite deformation. Zeitschrift fur Angewandte Mathematik und Physik. doi:10.1007/s00033-016-0671-x

CrossRef Full Text | Google Scholar

Rajagopal, K. R., and Szeri, A. (2003). On an inconsistency in the derivation of the equations of elastohydrodynamic lubrication. Proc. R. Soc. A Math. Phys. Eng. Sci. 459, 2771–2786. doi:10.1098/rspa.2003.1145

CrossRef Full Text | Google Scholar

Rajagopal, K. R., and Walton, J. (2011). Modeling fracture in the context of a strain-limiting theory of elasticity: a single anti-plane shear crack. Int. J. Fract. 169, 39–48. doi:10.1007/s10704-010-9581-7

CrossRef Full Text | Google Scholar

Rajagopal, K. R. (2003). On implicit constitutive theories. Appl. Math. 48, 279–319. doi:10.1023/A:1026062615145

CrossRef Full Text | Google Scholar

Reuss, A. (1930). Berücksichtigung der elastischen formänderung in der plastizitätstheorie. ZAMM J. Appl. Math. Mech./Zeitschrift für Angewandte Mathematik und Mechanik 10, 266–274. doi:10.1002/zamm.19300100308

CrossRef Full Text | Google Scholar

Rosinger, E. E. (1987). Generalized Solutions of Nonlinear Partial Differential Equations (North-Holland Mathematics Studies). Amsterdam: North-Holland Publishing Co., 146.

Google Scholar

Saccomandi, G., and Vergori, L. (2010). Piezo-viscous flows over an inclined surface. Q. Appl. Math. 68, 747–763. doi:10.1090/S0033-569X-2010-01202-2

CrossRef Full Text | Google Scholar

Saint-Venant, J. (1843). Not a joindre au memoire sur la dynamique des uids. Comptes Rendus 17, 1240–1224.

Google Scholar

Saito, T., Furuta, T., Hwang, J.-H., Kuramoto, S., Nishino, K., Suzuki, N., et al. (2003). Multifunctional alloys obtained via a dislocation-free plastic deformation mechanism. Science 300, 464–467. doi:10.1126/science.1081957

PubMed Abstract | CrossRef Full Text | Google Scholar

Schwartz, J. (1962). “The pernicious influence of mathematics on science,” in Logic, Methodology and Philosophy of Science, 356–360.

Google Scholar

Singh, H., and Nolle, A. (1959). Pressure dependence of the viscoelastic behavior of polyisobutylene. J. Appl. Phys. 30, 337–341. doi:10.1063/1.1735164

CrossRef Full Text | Google Scholar

Spencer, A. J. M. (1975). Continuum Physics, Vol. 2, Part 111, ed. A. C. Eringen (New York: Academic Press), 239–353.

Google Scholar

Stokes, G. (1845). On the theories of the internal friction of fluids in motion, and of the equilibrium and motion of elastic solids. Trans. Camb. Phil. Soc. 8, 287–305.

Google Scholar

Stokes, G. (1851). On the effect of internal friction of fluids on the motion pendulums. Trans. Camb. Phil. Soc. 9, 8106.

Google Scholar

Szeri, A. Z. (2011). Fluid Film Lubrication: Theory and Design. Cambridge: Cambridge University Press.

Google Scholar

Tran, T. D., and Suslov, S. A. (2009). Stability of plane poiseuillecouette flows of a piezo-viscous fluid. J. Nonnewton Fluid Mech. 156, 139–149. doi:10.1016/j.jnnfm.2008.07.009

CrossRef Full Text | Google Scholar

Truesdell, C. (1952). Mechanical foundations of elasticity and fluid dynamics. J. Ration Mech. Anal. 1, 125–300.

Google Scholar

Truesdell, C., and Noll, W. (1965). The Non-Linear Field Theories of Mechanics. Handbuch der Physik III/3. Berlin: Springer.

Google Scholar

Truesdell, C. A. (1977). A First Course in Rational Continuum Mechanics. New York: Academic Press, 1.

Google Scholar

Yuan, Z., Prusa, V., Rajagopal, K. R., and Srinivasa, A. (2015). Vibrations of a lumped parameter mass–spring–dashpot system wherein the spring is described by a non-invertible elongation-force constitutive function. Int. J. Non Linear Mech. 76, 154–163. doi:10.1016/j.ijnonlinmec.2015.06.009

CrossRef Full Text | Google Scholar

Zappalorto, M., Berto, F., and Rajagopal, K. R. (2016). On the anti-plane state of stress near pointed or sharply radiused notches in strain limiting elastic materials: closed form solution and implications for fracture assessements. Int. J. Fract. 199, 169–184. doi:10.1007/s10704-016-0102-1

CrossRef Full Text | Google Scholar