Depth-Dependent Three-Layer Model for the Surface Second-Harmonic Generation Yield

1. Introduction

Surface second-harmonic generation (SSHG) has been shown to be an effective, non-destructive, and non-invasive probe to study surface and interface properties (Chen et al., 1981; Shen, 1989; McGilp et al., 1994; Bloembergen, 1999; Lüpke, 1999; McGilp, 1999; Downer et al., 2001a,b). SSHG spectroscopy is now very cost-effective and popular because it is an efficient method for characterizing the properties of buried interfaces and nanostructures. The high surface sensitivity of SSHG spectroscopy is due to the fact that within the dipole approximation, the bulk second-harmonic generation (SHG) in centrosymmetric materials is identically zero. The SHG process can occur only at the surface where the inversion symmetry is broken. SSHG has useful applications for studying thick thermal oxides on semiconductor surfaces (Hasselt et al., 1995; Kolthammer et al., 2005) and thin films (Yeganeh et al., 1992). The accurate determination of these studies is highly dependent on multiple reflections of both the SH and fundamental waves in the surface region. These considerations have been taken into account to study thin films (Hase et al., 1992; Buinitskaya et al., 2002, 2003) and, using the Maker-fringe technique (Maker et al., 1962), other materials (Tellier and Boisrobert, 2007; Abe et al., 2008).

Bloembergen and Pershan (1962) were the first to consider multiple reflections in their treatment of SHG in a non-linear slab. However, they only considered the second-harmonic (SH) fields and derived results for a dielectric with a small linear reflectance. They also neglected the multiple reflections of the fundamental waves inside the media. Surface effects were modeled by taking the limit of a thin slab with a thickness much smaller than the wavelength of the incoming light. Dick et al. (1985) used this methodology to determine the components of the non-linear optical susceptibility tensor, χ(−2ω; ω, ω), of a fluorescent dye over fused silica. Later works (Sipe et al., 1987; Mizrahi and Sipe, 1988) developed a simplified method using phenomenological models in which the surface is treated as an infinitesimally thin dipole sheet. The inclusion of multiple reflections is necessary for both the SH radiation and the incoming fundamental fields; this was experimentally verified in the study by Morita et al. (1988), where they show that the lineshape of the SSHG radiation is composed of resonances from both the SH and fundamental waves. Recent studies in amorphous silicon thin (and thick) films (Kessels et al., 2004; Aarts et al., 2006; Lettieri et al., 2007) have had success in characterizing the polarization and angular dependence of the SH signal produced from within the film. A very comprehensive review of SHG from films and substrate systems can be found in the study by Gielis et al. (2008).

As mentioned above, SSHG is particularly useful for studying the surfaces of centrosymmetric materials. From the theoretical point of view, the calculation of χ(−2ω; ω, ω) proceeds as follows. To mimic the semi-infinite system, we construct a supercell consisting of a finite slab of material plus a vacuum region. Both the size of the slab and the vacuum region should be such that the value of χ(−2ω; ω, ω) is well converged. A cut function is used to decouple the two halves of the supercell to obtain the value of χ(−2ω; ω, ω) for either half. If the supercell is itself centrosymmetric, the value χ(−2ω; ω, ω) for the full supercell is identically zero. Therefore, the cut function is of paramount importance to obtain a finite value for χ(−2ω; ω, ω) for either side of the slab (Reining et al., 1994; Anderson et al., 2015, 2016). The cut function can be generalized to one that is capable of obtaining the value of χ(−2ω; ω, ω) for any part of the slab. We can easily obtain the depth within the slab for which χ(−2ω; ω, ω) is non-zero; conversely, we can verify that it goes to zero toward the middle of the slab, where the centrosymmetry of the material is restored (Mejía et al., 2004). Therefore, for the surface of any centrosymmetric material, we can find the thickness of the layer where χ(−2ω; ω, ω) is finite.

On the basis of this approach for the calculation of χ(−2ω; ω, ω), in this article, we generalize the “three-layer model” for the SH radiation from the surface of a centrosymmetric material (Anderson and Mendoza, 2016). This model considers that the SH conversion takes place in a thin layer just below the surface of the material that lies under the vacuum region and above the bulk of the material. It is the three-layer model that allows us to integrate the effects of multiple reflections for both the SH and fundamental fields into the SSHG yield. As we show in this article, this treatment can be generalized to take into account the depth dependence of χ(−2ω; ω, ω) perpendicular to the surface. As shown in the study by Anderson and Mendoza (2016), the inclusion of these effects is necessary to accurately model the SSHG radiation.

This article is organized as follows. In Section 2, we present the relevant equations and theory that describe the SSHG yield that includes the depth dependence of χ(−2ω; ω, ω). In Section 3, we present calculated spectra for the Si(111)(1 × 1):H surface as a test case and contrast against experimental data. Finally, we list our conclusions and final remarks in Section 4.

2. The Three-Layer Model for the SSHG Yield

In this section, we will generalize the results from our previous publication (Anderson and Mendoza, 2016) to allow for the depth dependence of χ(−2ω; ω, ω). The three-layer model proposed in the aforementioned reference considers that the surface is represented by three regions or layers. The first layer is the vacuum region (denoted by v) with a dielectric function ϵ_v(ω) = 1, from where the fundamental electric field E_v(ω) impinges on the material. The second layer is a thin layer (denoted by ℓ) of thickness d characterized by a dielectric function ϵ_ℓ(ω); it is in this layer where the SHG process takes place. The third layer is the bulk region denoted by b and characterized by ϵ_b(ω). Throughout this work, we take μ = 1. Both the vacuum and bulk layers are semi-infinite (see Figure 1). The non-linear polarization responsible for the SHG is immersed in the thin layer ℓ and is given by

${\mathcal{P}}_{\ell }^{\text{a}}\left(z;\mathrm{2\omega }\right)={\mathrm{ϵ}}_0{\mathrm{\chi }}^{\text{abc}}\left(z;-\mathrm{2\omega };\mathrm{\omega },\mathrm{\omega }\right)E_{\ell }^{\text{b}}\left(z;\mathrm{\omega }\right)E_{\ell }^{\text{c}}\left(z;\mathrm{\omega }\right),$ (1)

where χ(z; −2ω; ω, ω) is the dipolar surface non-linear depth-dependent susceptibility tensor, and the Cartesian superscripts (a, b, and c) are summed over if repeated. For ease of notation, we simply use χ(z). Also, χ^abc(z) = χ^acb(z) due to the intrinsic permutation symmetry, since SHG is degenerate in $E_{\ell }^{\text{b}}\left(z;\mathrm{\omega }\right)$ and $E_{\ell }^{\text{c}}\left(z;\mathrm{\omega }\right)$. We first approximate that the linear field E(z; ω) is independent of the z position. The calculation of the position dependence of the linear field is a complicated problem worth pursuing; Tancogne-Dejean et al. (2015) present a promising method for tackling this issue, which is a rather involved, non-trivial calculation. After following the method outlined in the study by Anderson and Mendoza (2016), we define the linear reflection coefficient $r_{\text{i}}^M$ as

$r_{\text{i}}^M\equiv \frac{r_{\text{i}}^{\mathrm{\ell b}}{e}^{i\mathrm{\phi }}}{1+r_{\text{i}}^{\mathrm{v\ell }}{r}_{\text{i}}^{\mathrm{\ell b}}{e}^{i\mathrm{\phi }}},\text{i}=s,p,$ (2)

with

$r_{\text{i}}^{M\pm }=1\pm r_{\text{i}}^M,\text{i}=s,p.$ (3)

FIGURE 1

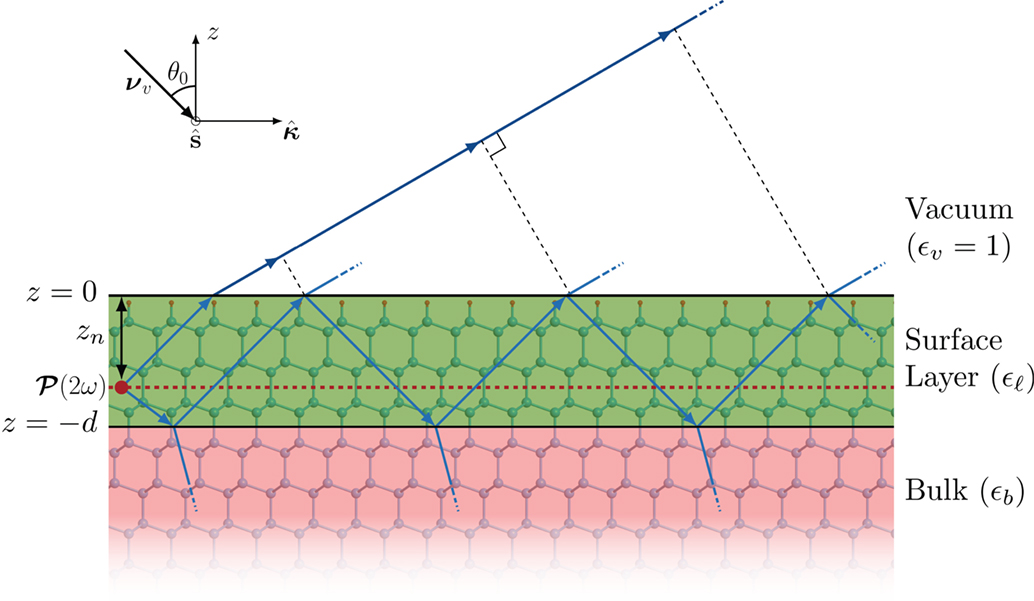
Figure 1. Sketch of the three-layer model for SHG. The vacuum region (v) is on top with ϵ_v = 1; the layer ℓ of thickness d is characterized by ϵ_ℓ(ω), and it is where the SH polarization sheet ${\mathcal{P}}_{\ell }\left(\text{2}\mathrm{\omega }\right)$ is located at a distance z_n. The bulk b is described by ϵ_b(ω). The blue lines within the slab represent the SH multiple reflections. The Si(111)(1 × 1):H surface used in this work is represented by the ball and stick model (H: small spheres, Si: large spheres) in the background. The red dotted line is the one of the many possible z_n positions.

This coefficient accounts for the multiple (M) reflections of the fundamental field that depends on the thickness d of the layer ℓ included in the phase φ = 4π(d/λ₀)w_ℓ(ω), where λ₀ is the wavelength of the incoming light, w_ℓ(ω) = (ϵ_ℓ(ω)−sin²θ₀)^1/2, θ₀ is the angle of incidence, and n_ℓ = (ϵ_ℓ(ω))^1/2. The Fresnel factors $t_{\text{i}}^{\mathit{ij}}$ and $r_{\text{i}}^{\mathit{ij}}$ for the vacuum-layer (ij = vℓ) and layer-bulk (ij = ℓb) interfaces are defined in equations (13) and (14) of the same reference.

2.1. Depth Dependence

The calculation of χ(z) using the layer-by-layer method has been developed in detail in the study by Anderson et al. (2015). Indeed, we calculate χ(z_n) at fixed positions z_n, where n = 1, 2, 3, …, N/2 denotes the atomic layer within the slab and N is the total number of atomic layers used in the supercell method, as described in the introduction. We take n = 1 as the topmost atomic layer and n = N/2 as the middle atomic layer, where it is expected that χ(z_N/2) = 0 due to the centrosymmetric environment at the center of the supercell (Anderson et al., 2015). To obtain the SH-radiated field induced by the non-linear polarization of equation (1), we generalize equation (35) from the study by Anderson and Mendoza (2016) as

$E_{\ell }\left(z_n;\mathrm{2\omega }\right)=\frac{i\mathrm{\omega }}{c\text{cos}{\mathrm{\theta }}_0}{\mathbf{\text{e}}}_{\ell }^{\mathrm{2\omega },\mathrm{F}}\left(z_n\right)\cdot \mathrm{\chi }\left(z_n\right):{\mathbf{\text{e}}}_{\ell }^{\mathrm{\omega },\mathrm{i}}{\mathbf{\text{e}}}_{\ell }^{\mathrm{\omega },\mathrm{i}},$ (4)

which is the non-linear field radiated from depth z_n as induced by χ(z_n). In this expression, i = s, p denotes the incoming polarization of the incident field, and ${\mathbf{\text{e}}}_{\ell }^{\mathrm{\omega },\text{i}}{\mathbf{\text{e}}}_{\ell }^{\mathrm{\omega },\text{i}}$ are given in equations (42) and (43) of the aforementioned reference. We must include the depth dependence for the 2ω Fresnel vector and obtain the following results for ${\mathbf{\text{e}}}_{\ell }^{\mathrm{2\omega },\text{F}}\left(z_n\right)$,

$\begin{array}{llll}\hfill {\mathbf{\text{e}}}_{\ell }^{\mathrm{2\omega },P}\left(z_n\right)& =\frac{T_p^{\mathrm{v\ell }}}{N_{\ell }}\left(\text{sin}{\mathrm{\theta }}_0{R}_p^{M+}\left(z_n\right)\widehat{\mathbf{\text{z}}}-W_{\ell }{R}_p^{M-}\left(z_n\right)\text{cos}\mathrm{\varphi }\widehat{\mathbf{\text{x}}}\right.& \hfill & \\ \hfill & \left.-W_{\ell }{R}_p^{M-}\left(z_n\right)\text{sin}\mathrm{\varphi }\widehat{\mathbf{\text{y}}}\right),\end{array}$ (5)

for F = P outgoing polarization, and

${\mathbf{\text{e}}}_{\ell }^{\mathrm{2\omega },S}=T_s^{\mathrm{v\ell }}{R}_s^{M+}\left(z_n\right)\left(-\text{sin}\mathrm{\varphi }\widehat{\mathbf{\text{x}}}+\text{cos}\mathrm{\varphi }\widehat{\mathbf{\text{y}}}\right).$ (6)

for F = S outgoing polarization. Here,

$R_{\mathrm{i}}^{M\pm }\left(z_n\right)=1\pm R_{\mathrm{i}}^M\left(z_n\right),$ (7)

and

$R_{\mathrm{i}}^M\left(z_n\right)\equiv \frac{R_{\mathrm{i}}^{\mathrm{\ell b}}}{1+R_{\mathrm{i}}^{\mathrm{v\ell }}{R}_{\mathrm{i}}^{\mathrm{\ell b}}{e}^{i\mathrm{\delta }}}{e}^{i\mathrm{8\pi }{W}_{\ell }\left(z_n∕{\mathrm{\lambda }}_0\right)},\mathrm{i}=s,p,$ (8)

is the reflection coefficient that takes into account the multiple reflections of the SH field within the layer ℓ, with δ = 8π(d/λ₀)W_ℓ. The remaining terms are the 2ω equivalents of those described below equation (3). Finally, the SSHG yield can be expressed as

${\mathcal{R}}_{\mathrm{iF}}\left(\mathrm{2\omega }\right)=\frac{{\mathrm{\omega }}^2}{2{\mathrm{ϵ}}_0{c}^3{\text{cos}}^2{\mathrm{\theta }}_0}{\left|\frac{1}{n_{\ell }}\frac{1}{N∕2}{\displaystyle \sum _{n=1}^{N∕2}}{\Upsilon }_{\mathrm{iF}}\left(z_n\right)\right|}^2,$ (9)

where

${\Upsilon }_{\mathrm{iF}}\left(z_n\right)={\mathbf{\text{e}}}_{\ell }^{\mathrm{2\omega },\mathrm{F}}\left(z_n\right)\cdot \mathrm{\chi }\left(z_n\right):{\mathbf{\text{e}}}_{\ell }^{\mathrm{\omega },\mathrm{i}}{\mathbf{\text{e}}}_{\ell }^{\mathrm{\omega },\mathrm{i}}.$ (10)

Note that χ(z_n) is given in square meters per volt since it is a surface second-order non-linear susceptibility and ${\mathcal{R}}_{\text{iF}}\left(\mathrm{2\omega }\right)$ is given in square meters per watt. The SSHG yield, ${\mathcal{R}}_{\text{iF}}$, can be derived for the usual combinations of pP, pS, sP, and sS incoming and outgoing polarizations for different surface symmetries. The interested reader can refer to the study by Anderson and Mendoza (2016), where these derivations are included in full.

3. Results: Layer-By-Layer Analysis and SSHG Yield for a Si Surface

To better view the effects of the z-dependence of χ(z_n) on the SHG yield, we will apply our formulation on a test surface. We choose the Si(111)1 × 1:H surface, since the (111) symmetry relations has only four non-zero components, and we can directly compare our theoretical calculations with experimental data available in the study by Mejía et al. (2002). We only present results for the p-in P-out $\left({\mathcal{R}}_{\mathit{pP}}\right)$ polarization case since it has the strongest yield and thus the best signal-to-noise ratio for the measured data. The (111) surface has only the following non-zero components of χ(z_n): χ^zzz(z_n), χ^zxx(z_n) = χ^zyy(z_n), χ^xxz(z_n) = χ^yyz(z_n), and χ^xxx(z_n) = −χ^xyy(z_n) = −χ^yyx(z_n), so we can easily work out that

$\begin{array}{llll}\hfill {\Upsilon }_{\mathit{pP}}\left(z_n\right)& =\frac{T_p^{\mathrm{v\ell }}}{N_{\ell }}{\left(\frac{t_p^{\mathrm{v\ell }}}{n_{\ell }}\right)}^2\left(\text{sin}{\mathrm{\theta }}_0\left[{\left(r_p^{M+}\right)}^2{\text{sin}}^2{\mathrm{\theta }}_0{R}_p^{M+}\left(z_n\right){\mathrm{\chi }}^{\mathit{zzz}}\left(z_n\right)\right.\right.& \hfill & \\ \hfill & \left.+{\left(r_p^{M-}\right)}^2{w}_{\ell }^2{R}_p^{M+}\left(z_n\right){\mathrm{\chi }}^{\mathit{zxx}}\left(z_n\right)\right]& \hfill & \\ \hfill & -w_{\ell }{W}_{\ell }\left[2r_p^{M+}{r}_p^{M-}\text{sin}{\mathrm{\theta }}_0{R}_p^{M-}\left(z_n\right){\mathrm{\chi }}^{\mathit{xxz}}\left(z_n\right)\right.& \hfill & \\ \hfill & \left.\left.+{\left(r_p^{M-}\right)}^2{w}_{\ell }{R}_p^{M-}\left(z_n\right){\mathrm{\chi }}^{\mathit{xxx}}\left(z_n\right)\text{cos}\mathrm{3\varphi }\right]\right),\end{array}$ (11)

where the threefold azimuthal symmetry of the SHG signal that is typical of the C_3v symmetry group is seen in the 3ϕ argument of the cosine function.

We consider that the Si(111)(1 × 1):H surface is an excellent case to test the versatility of the three-layer model; in particular, to study the effect that the z-dependence of χ^abc(z_n) and the multiple reflections will have on the SSHG yield. This surface is experimentally well characterized (Mitchell et al., 2001; Mejía et al., 2002; Bergfeld et al., 2004), and we have had success in reproducing these experimental results using the three-layer model with and without multiple reflections in our previous publications (Anderson and Mendoza, 2016; Anderson et al., 2016). The details of the ab initio calculation of χ^abc are discussed in the study by Anderson et al. (2016). We note that we apply a scissors shift of 0.7 eV to the theoretical spectra to include the effects of the electronic many-body interactions within the independent particle approach of our ab initio calculation. This 0.7 eV value allows the SH resonant peaks to acquire their corresponding energy positions and is obtained from a G₀W₀ calculation (Li and Galli, 2010; Anderson et al., 2016).

The number of layers N for which χ^abc converges is a compromise between accuracy and the expenditure of computational time and resources. We found that N = 50, which includes 2 layers of H and 48 layers of Si, is an excellent compromise. Recall that the slab used in the calculation is centrosymmetric and that only half of the atomic layers of the slab is what actually contributes to χ^abc. In Figure 2, we show the largest component that contributes to ${\mathcal{R}}_{\mathit{pP}}$, χ^xxz(z_n), for several choices of z_n. z₁ is the layer that corresponds to the H layer. To recover the centrosymmetric environment of the (111) surface, we must add pairs of atomic Si layers, so that they include a vertical and a slanted bond of the tetrahedral unit cell corresponding to this face. This is described in detail in the study by Mejía et al. (2004). As we move from the surface toward the bulk of the system, χ^abc will decrease steadily. In the same figure, we show χ^xxz(z₂) + χ^xxz(z₃), which corresponds to the sum of the responses from the first and second Si layers. Likewise, we also include χ^xxz(z₂₄) + χ^xxz(z₂₅), which corresponds to the last two Si layers of the half-slab. We can see that the contribution from the H layer (z₁) is considerably smaller than that of the first two Si layers, as expected from the fact that the H atoms saturate the dangling bonds of the topmost Si, quenching the response (Mejía et al., 2002). The contribution from the deepest Si layers (z₂₄ and z₂₅) is quite small compared to the topmost layers. It is logical to assume that their contribution should be zero, as the slab regains its intrinsic centrosymmetry toward the center. This is not exactly the case, however, as the relatively small size of the slab yields a correct qualitative result for this regime. Figure 2 also presents two insets with the individual responses for the mentioned Si layers. The left inset depicts the spectra for the first two Si layers, at z₂ and z₃; both have a similar line shape with matching signs and thus interfere constructively creating an overall enhancement of the final intensity. On the other hand, the right inset depicts the equivalent spectra for the Si layers at z₂₄ and z₂₅. These two have a very similar line shape but with opposite signs and therefore interfere destructively and contribute very little to the total response.

FIGURE 2

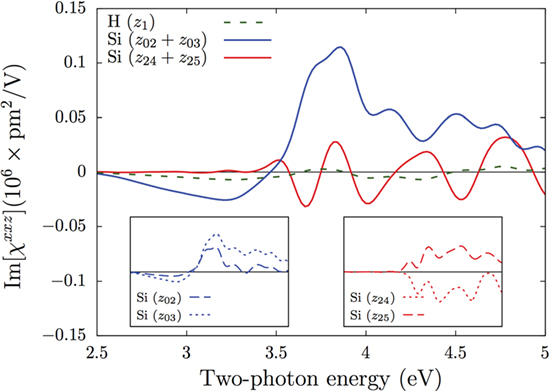
Figure 2. Main plot: imaginary part of χ^xxz(z_n) for the H layer (z₁), the sum of the two topmost Si layers (z₂ + z₃), and the sum of the bottom-most Si layers (z₂₄ + z₂₅) for the 25-layer half-slab used in this work. Left inset: the first two Si layers at z₂ and z₃. Note how the spectra are almost identical in line shape, thus enhancing the overall component intensity. Right inset: the last two Si layers at z₂₄ and z₂₅. The individual spectra are almost opposite in sign, thus producing a much smaller contribution.

For this slab, we find that

${\displaystyle \sum _{n=1}^{23}}{\mathrm{\chi }}^{\mathrm{abc}}\left(z_n\right)>>{\mathrm{\chi }}^{\mathrm{abc}}\left(z_{24}\right)+{\mathrm{\chi }}^{\mathrm{abc}}\left(z_{25}\right),$ (12)

and thus χ^abc is well converged. We present this comparison in Figure 3, contrasted against ${\mathrm{\chi }}_{\text{hs}}^{\mathit{xxz}}$, which is the total response from all 25 layers of the half-slab. The sum of the layer responses from z₁ to z₂₃ is quite close to the total half-slab response. As before, layers z₂₄ and z₂₅ contribute very little to the overall SH spectrum. From these findings, we can establish that the thickness of the layer ℓ, where the SHG takes place is around d = 3.6 nm for N/2 = 25 active layers of SHG. These results prompt us to propose the following plausible scenario. We could use a larger value for d to achieve χ^abc(z_N/2−1) + χ^abc(z_N/2) = 0, for which we need to go to increasingly larger slabs. But to keep the computational burden reasonable, we choose N = 50 and only change the value of z_n such that d = ∑_nz_n gives the new chosen value of d. In view of equation (12), we can keep the same value for each of the χ^abc(z_n) components already calculated for N = 50. This would be equivalent to say that from equation (9),

${\displaystyle \sum _{n=1}^{23}}{\Upsilon }_{\mathrm{iF}}\left(z_n\right)>>{\Upsilon }_{\mathrm{iF}}\left(z_{24}\right)+{\Upsilon }_{\mathrm{iF}}\left(z_{25}\right),$ (13)

regardless of the actual value of z_n. We will refer to this plausible scenario as “Stretched z_n” below, where a factor of 2.7 is used to stretch z_n such that d = 2.7 × 3.6 ≈ 10 nm.

FIGURE 3

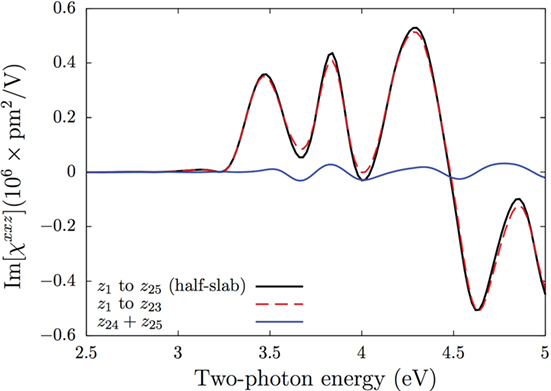
Figure 3. Imaginary part of χ^xxz(z_n) from different layer sums. The solid black line is the sum of all 25 layers (1 H + 24 Si) that comprise the half-slab $\left({\mathrm{\chi }}_{\text{hs}}^{\mathit{\text{xxz}}}\right)$; the dashed blue line is the sum of the first 23 layers, and the solid red line is the sum of the last two layers (z₂₄ + z₂₅). Note the consistency with equation (12), since the last two layers have a relatively small contribution to the overall spectrum.

In Figure 4, we compare the theoretical results for the SSHG yield for p-in P-out, ${\mathcal{R}}_{\mathit{pP}}$, with the experimental results from the study by Mejía et al. (2002) that were taken over a SH energy range of 2.5–5 eV. We use θ = 65°, ϕ = 30°, and a broadening of σ = 0.075 eV. With ϕ = 30°, the contribution of χ^xxx from equation (11) is completely eliminated. The following scenarios are presented in the figure. First, “Nominal z_n” (solid blue line) is the layer-by-layer calculation for a layer thickness of d = 3.6 nm. This is the thickness of N/2 = 25 atomic layers with the different z_n positions obtained directly from the slab used in the full ab initio calculation. Second, “Stretched z_n” is the scenario proposed in the previous paragraph, where the z_n positions are now stretched by a factor of 2.7, but the same χ^abc(z_n) of the layered ab initio calculation are used. Finally, two “Average” curves are presented for d = 3.6 (dashed green line) and d = 10 nm (dashed yellow line) that use

${\mathrm{\chi }}_{\mathrm{hs}}^{\mathrm{abc}}={\displaystyle \sum _{n=1}^{N∕2}}{\mathrm{\chi }}^{\mathrm{abc}}\left(z_n\right),$ (14)

which is the total response for the complete half-slab of 25 layers, along with the average value of equation (8), as proposed in the study by Anderson and Mendoza (2016),

${\overline{R}}_{\mathrm{i}}^M\equiv \frac{1}{d}{\int }_0^d{R}_{\mathrm{i}}^M\left(z\right)\mathit{dz}=\frac{R_{\mathrm{i}}^{\mathrm{\ell b}}{e}^{i\mathrm{\delta }∕2}}{1+R_{\mathrm{i}}^{\mathrm{v\ell }}{R}_{\mathrm{i}}^{\mathrm{\ell b}}{e}^{i\mathrm{\delta }}}\mathrm{sinc}\left(\mathrm{\delta }∕2\right).$ (15)

FIGURE 4

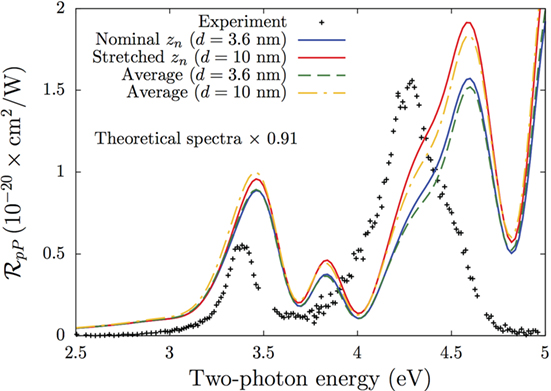
Figure 4. ${\mathcal{R}}_{\mathit{\text{pP}}}$ for z_n as given by the slab (Nominal, red line), with z_n stretched by 2.7 (Stretched, blue line), and using the half-slab value of ${\mathrm{\chi }}_{\mathrm{hs}}^{\mathrm{abc}}$ for d = 3.6 (Average, dashed green line) and d = 10 nm (Average, dashed yellow line), see text for details. The experimental data are from the study by Mejía et al. (2002). We use θ = 65°, ϕ = 30°, and a broadening of σ = 0.075 eV. Both the Nominal and Stretched results are ab initio, while the Average spectra are not; the Average (d = 10 nm) spectrum is the primary result of the study by Anderson and Mendoza (2016).

This choice is very similar to placing χ^abc(z_n) at z_n → d/2 in equation (8), which can be interpreted as placing the non-linear polarization sheet in the middle of the thin layer ℓ. These last curves are neither depth dependent nor ab initio, since the value of d = 10 nm does not come naturally from the calculation of χ^abc(z_n). Indeed, the Average spectrum for d = 10 nm is the primary result from the study by Anderson and Mendoza (2016). On the other hand, the Nominal (d = 3.6 nm) result calculated from the theory developed in this work is completely ab initio.

The experimental spectrum shows two very well-defined resonances, which come from electronic transitions from the valence to the conduction bands around the known E₁ ~ 3.4 eV and E₂ ~ 4.3 eV critical points of bulk Si (Yu and Cardona, 2005). The theoretical results reproduce the features of the spectrum, although we see that the E₂ peak is blueshifted by around 0.3 eV. We postulate that this discrepancy is mainly due to three factors. First, the ${\mathcal{R}}_{\mathit{pP}}$ spectrum tends to redshift as temperature increases (Dadap et al., 1997). Since this experiment was conducted at room temperature, our theoretical results (which consider that T = 0 K) will be blueshifted to some degree. Of course, the experimental temperature at which the spectra are measured should be taken into account in a more complete formulation. Second, equation (11) shows that ${\mathcal{R}}_{\mathit{pP}}$ includes all four non-zero components of χ(z_n). In particular, χ^zzz and χ^xxz include out-of-plane incoming fields that are affected by local field effects (Tancogne-Dejean, 2015); these reveal material inhomogeneities that are far more prevalent perpendicular to the surface than in the surface plane. Therefore, we expect that these out-of-plane components will be more sensitive to the inclusion of these local field effects. As mentioned earlier, these effects are quite challenging to compute (Tancogne-Dejean et al., 2015) and are beyond the scope of this article. Third, GW transition energies are needed to accurately predict the SSHG spectrum. A Bethe–Salpeter calculation will improve the position and the amplitude of the peaks, but is far beyond our current computing capabilities. The included ab initio scissors correction produces an E₁ peak position that is similar to experiment, and we have checked there is no single scissors value that can reproduce the energy positions of both the E₁ and E₂ peaks. We consider that ${\mathcal{R}}_{\mathit{pP}}$ requires the proper treatment of all three of these factors to improve the calculated spectrum.

We can clearly see that ${\mathcal{R}}_{\mathit{pP}}$ for the layered calculation using d = 3.6 nm (the value from the slab) differs from the one with the stretched values of z_n that lead to d = 10 nm. These enhancements are larger for E₂ than for E₁. This can be understood from the fact that the corresponding λ₀ for E₁ is larger than that of E₂. From equations (2) and (8), we see that the phase shifts are larger for E₂ than for E₁, producing a larger enhancement of the SSHG yield at E₂ from the multiple reflections. As the phase shifts grow with d, so does the enhancement caused by the multiple reflections. We have also verified that the effects of the multiple reflections from the linear field are significantly smaller than those of the SH field. This is clear since the phase shift of equation (8) is not only a factor of 2 smaller than that of equation (2) but also w_ℓ <W_ℓ. For larger energies, such as E₂, λ₀ becomes smaller, and the multiple reflection effects become more noticeable. The selected value for d < < λ₀, which comes naturally from the ab initio calculation of χ^abc, is thus very reasonable to model a thin surface layer below the vacuum region where the non-linear SH conversion takes place. Moreover, choosing a larger value d improves the peak ratio E₂/E₁ from 1.8 (d = 3.6 nm) to 2.0 (d = 10 nm), which is closer to the experimental value of 2.8 (Anderson and Mendoza, 2016). Note that the average values obtained by using ${\overline{R}}_p^M$ with d = 3.6 and d = 10 nm are very similar to the depth-dependent results for the corresponding value of d. In general, this means that using ${\mathrm{\chi }}_{\text{hs}}^{\text{abc}}$ in combination with ${\overline{R}}_i^M$ is a reasonable first approximation of the SSHG yield.

We remark that there is a significant dielectric contrast between the thin layer ℓ and the bulk region b. As discussed in Figure 6 of the study by Mendoza et al. (2006), the layer-by-layer ϵ_ℓ(z_n;ω) of a Si(100) surface begins to resemble the bulk dielectric function as we go deeper toward the bulk of the system. However, for the atomic layers of the thin layer, ℓ, ϵ_ℓ(z_n;ω) differs substantially from ϵ_b(ω). We have carried out a similar analysis for the Si(111)1 × 1:H surface used in this work and obtained equivalent results. As ${\mathrm{ϵ}}_{\ell }\left(\mathrm{\omega }\right)={\sum }_{n=1}^{N∕2}{\mathrm{ϵ}}_{\ell }\left(z_n;\mathrm{\omega }\right)\ne {\mathrm{ϵ}}_b\left(\mathrm{\omega }\right)$, it follows that there are sizeable reflections from the layer–bulk interface. It is tempting to use ϵ_ℓ(z_n;ω) instead of ϵ_ℓ(ω) in the theory developed in Section 2; however, this is related to the calculation of E(z; ω), as mentioned above, is outside the scope of this work.

SSHG is a powerful tool for characterizing film/substrate systems, and we consider that the flexibility of the three-layer model provides a good theoretical foundation for calculating the SH spectra at an ab initio level. On the one hand, this revised model does away with all adjustable parameters; namely, the depth of the film d is now determined exactly from the size of the slab. This approach differs from our previous work (Anderson and Mendoza, 2016), which considered d as an adjustable parameter that can be varied to match the experimental resonance intensity. Our new ab initio formulation allows us to readily simulate the effect of film thickness on the spectrum. Calculation time will increase rapidly with the slab size, but can be computed for any film thickness with sufficient computational resources. On the other hand, we must remember that χ(z_n) is strictly a surface quantity that can be calculated on a layer-by-layer basis. Thus, it is independent of the dielectric properties that conform the bulk material (substrate). These properties obviously play an important role in the calculation of the SSHG yield, in the form of the bulk dielectric function ϵ_b(ω). If that quantity is known, then we can effectively calculate the SHG spectra of any crystalline film over any bulk substrate. Indeed, our formulation properly accounts for both the exterior surface (vacuum layer) and interior interface (layer bulk) contributions to the overall SH signal. Our model is agnostic to any surface symmetries and can effectively model passivated (like the Si(111)1 × 1:H example used here) or clean surfaces with dangling bonds. The layer-by-layer approach will even provide us with the SH contribution from the layer that includes the passivation or the dangling bonds. With these elements, we consider that the depth-dependent three-layer model with multiple reflections is a robust, versatile, and computationally efficient method that is well suited for characterizing thin/thick film systems.

4. Conclusions

We have derived a formalism to calculate the SSHG yield based on the three-layer model that accurately describes the radiating system. This treatment includes the effects of multiple reflections inside the material from both the SH and fundamental fields and also takes into account the depth variation of the second-order non-linear susceptibility χ^abc(z_n). We applied this theoretical development to calculate the p-in and P-out SSHG yield of the Si(111)(1 × 1):H surface. Our depth-dependent three-layer model reproduces key spectral features and also yields an intensity very close to experiment. We consider it an upgrade over our previous model featured in the study by Anderson and Mendoza (2016), since the thickness d of the layer in which the SHG takes place can be directly determined for the calculation and requires no other free parameters.

Author Contributions

SA: literature review, programming, and calculations. BM: mathematical framework and general theory. Both: manuscript preparation.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Funding

This work was funded by the Consejo Nacional de Ciencia y Tecnología, México, via scholarship #349278 and partial support from grant #153930.

References

Aarts, I. M. P., Gielis, J. J. H., van de Sanden, M. C. M., and Kessels, W. M. M. (2006). Probing hydrogenated amorphous silicon surface states by spectroscopic and real-time second-harmonic generation. Phys. Rev. B Condens. Matter Mater. Phys. 73, 045327. doi: 10.1103/PhysRevB.73.045327

CrossRef Full Text | Google Scholar

Abe, M., Shoji, I., Suda, J., and Kondo, T. (2008). Comprehensive analysis of multiple-reflection effects on rotational Maker-fringe experiments. J. Opt. Soc. Am. B 25, 1616. doi:10.1364/JOSAB.25.001616

CrossRef Full Text | Google Scholar

Anderson, S. M., and Mendoza, B. S. (2016). Three-layer model for the surface second-harmonic generation yield including multiple reflections. Phys. Rev. B Condens. Matter Mater. Phys. 94, 115314. doi:10.1103/PhysRevB.94.115314

CrossRef Full Text | Google Scholar

Anderson, S. M., Tancogne-Dejean, N., Mendoza, B. S., and Véniard, V. (2015). Theory of surface second-harmonic generation for semiconductors including effects of nonlocal operators. Phys. Rev. B Condens. Matter Mater. Phys. 91, 075302. doi:10.1103/PhysRevB.91.075302

CrossRef Full Text | Google Scholar

Anderson, S. M., Tancogne-Dejean, N., Mendoza, B. S., and Vé-niard, V. (2016). Improved ab initio calculation of surface second-harmonic generation from si(111)(1×1)h. Phys. Rev. B Condens. Matter Mater. Phys. 93, 235304. doi:10.1103/PhysRevB.93.235304

CrossRef Full Text | Google Scholar

Bergfeld, S., Braunschweig, B., and Daum, W. (2004). Nonlinear optical spectroscopy of suboxides at oxidized Si(111) interfaces. Phys. Rev. Lett. 93, 097402. doi:10.1103/PhysRevLett.93.097402

PubMed Abstract | CrossRef Full Text | Google Scholar

Bloembergen, N. (1999). Surface nonlinear optics: a historical overview. Appl. Phys. B 68, 289–293. doi:10.1007/s003400050621

CrossRef Full Text | Google Scholar

Bloembergen, N., and Pershan, P. S. (1962). Light waves at the boundary of nonlinear media. Phys. Rev. 128, 606–622. doi:10.1103/PhysRev.128.606

CrossRef Full Text | Google Scholar

Buinitskaya, G., Kravetsky, I., Kulyuk, L., Mirovitskii, V., and Rusu, E. (2002). Optical second harmonic generation in ZnO film: multiple-reflection effects. Moldavian J. Phys. Sci. 1, 77–81.

Google Scholar

Buinitskaya, G., Kravetsky, I., Kulyuk, L., Mirovitskii, V., and Rusu, E. (2003). “Characterization of thin ZnO film by optical second harmonic generation: experiment and theory,” in CAS 2003 International Semiconductor Conference, Vol. 2. Sinaia, 322. doi:10.1109/SMICND.2003.1252444

CrossRef Full Text | Google Scholar

Chen, C. K., de Castro, A. R. B., and Shen, Y. R. (1981). Surface-enhanced second-harmonic generation. Phys. Rev. Lett. 46, 145–148. doi:10.1103/PhysRevLett.46.145

CrossRef Full Text | Google Scholar

Dadap, J. I., Xu, Z., Hu, X. F., Downer, M. C., Russell, N. M., Ekerdt, J. G., et al. (1997). Second-harmonic spectroscopy of a Si (001) surface during calibrated variations in temperature and hydrogen coverage. Phys. Rev. B Condens. Matter Mater. Phys. 56, 13367. doi:10.1103/PhysRevB.56.13367

CrossRef Full Text | Google Scholar

Dick, B., Gierulski, A., Marowsky, G., and Reider, G. A. (1985). Determination of the nonlinear optical susceptibility χ⁽²⁾ of surface layers by sum and difference frequency generation in reflection and transmission. Appl. Phys. B 38, 107–116. doi:10.1007/BF00697449

CrossRef Full Text | Google Scholar

Downer, M. C., Jiang, Y., Lim, D., Mantese, L., Wilson, P. T., Mendoza, B. S., et al. (2001a). Optical second harmonic spectroscopy of silicon surfaces, interfaces and nanocrystals. Phys. Status Solidi A 188, 1371–1381. doi:10.1002/1521-396X(200112)188:4<1371:AID-PSSA1371>3.0.CO;2-U

CrossRef Full Text | Google Scholar

Downer, M. C., Mendoza, B. S., and Gavrilenko, V. I. (2001b). Optical second harmonic spectroscopy of semiconductor surfaces: advances in microscopic understanding. Surf. Interface Anal. 31, 966–986. doi:10.1002/sia.1133

CrossRef Full Text | Google Scholar

Gielis, J. J. H., Gevers, P. M., Aarts, I. M. P., van de Sanden, M. C. M., and Kessels, W. M. M. (2008). Optical second-harmonic generation in thin film systems. J. Vac. Sci. Technol. A 26, 1519–1537. doi:10.1116/1.2990854

CrossRef Full Text | Google Scholar

Hase, Y., Kumata, K., Kano, S. S., Ohashi, M., Kondo, T., Ito, R., et al. (1992). New method for determining the nonlinear optical coefficients of thin films. Appl. Phys. Lett. 61, 145–146. doi:10.1063/1.108199

CrossRef Full Text | Google Scholar

Hasselt, C. W. V., Devillers, M. A. C., Rasing, T., and Aktsipetrov, O. A. (1995). Second-harmonic generation from thick thermal oxides on Si(111): the influence of multiple reflections. J. Opt. Soc. Am. B 12, 33. doi:10.1364/JOSAB.12.000033

CrossRef Full Text | Google Scholar

Kessels, W. M. M., Gielis, J. J. H., Aarts, I. M. P., Leewis, C. M., and van de Sanden, M. C. M. (2004). Spectroscopic second harmonic generation measured on plasma-deposited hydrogenated amorphous silicon thin films. Appl. Phys. Lett. 85, 4049–4051. doi:10.1063/1.1812836

CrossRef Full Text | Google Scholar

Kolthammer, W. S., Barnard, D., Carlson, N., Edens, A. D., Miller, N. A., and Saeta, P. N. (2005). Harmonic generation in thin films and multilayers. Phys. Rev. B Condens. Matter Mater. Phys. 72, 045446. doi:10.1103/PhysRevB.72.045446

CrossRef Full Text | Google Scholar

Lettieri, S., Merola, F., Maddalena, P., Ricciardi, C., and Giorgis, F. (2007). Second harmonic generation analysis in hydrogenated amorphous silicon nitride thin films. Appl. Phys. Lett. 90, 021919. doi:10.1063/1.2424661

CrossRef Full Text | Google Scholar

Li, Y., and Galli, G. (2010). Electronic and spectroscopic properties of the hydrogen-terminated Si(111) surface from ab initio calculations. Phys. Rev. B Condens. Matter Mater. Phys. 82, 045321. doi:10.1103/PhysRevB.82.045321

CrossRef Full Text | Google Scholar

Lüpke, G. (1999). Characterization of semiconductor interfaces by second-harmonic generation. Surf. Sci. Rep. 35, 75–161. doi:10.1016/S0167-5729(99)00007-2

CrossRef Full Text | Google Scholar

Maker, P. D., Terhune, R. W., Nisenoff, M., and Savage, C. M. (1962). Effects of dispersion and focusing on the production of optical harmonics. Phys. Rev. Lett. 8, 21–22. doi:10.1103/PhysRevLett.8.21

CrossRef Full Text | Google Scholar

McGilp, J. F. (1999). Second-harmonic generation at semiconductor and metal surfaces. Surf. Rev. Lett. 6, 529–558. doi:10.1142/S0218625X99000494

CrossRef Full Text | Google Scholar

McGilp, J. F., Cavanagh, M., Power, J. R., and O’Mahony, J. D. (1994). Probing semiconductor interfaces using nonlinear optical spectroscopy. Opt. Eng. 33, 3895–3900. doi:10.1117/12.186373

CrossRef Full Text | Google Scholar

Mejía, J. E., Mendoza, B. S., Palummo, M., Onida, G., Del Sole, R., Bergfeld, S., et al. (2002). Surface second-harmonic generation from si (111)(1x1) h: theory versus experiment. Phys. Rev. B Condens. Matter Mater. Phys. 66, 195329. doi:10.1103/PhysRevB.66.195329

CrossRef Full Text | Google Scholar

Mejía, J. E., Mendoza, B. S., and Salazar, C. (2004). Layer-by-layer analysis of second harmonic generation at a simple surface. Revista Mexicana de Física 50, 134–139.

Google Scholar

Mendoza, B. S., Nastos, F., Arzate, N., and Sipe, J. (2006). Layer-by-layer analysis of the linear optical response of clean and hydrogenated si(100) surfaces. Phys. Rev. B Condens. Matter Mater. Phys. 74, 075318. doi:10.1103/PhysRevB.74.075318

CrossRef Full Text | Google Scholar

Mitchell, S. A., Mehendale, M., Villeneuve, D. M., and Boukherroub, R. (2001). Second harmonic generation spectroscopy of chemically modified Si(1 1 1) surfaces. Surf. Sci. 488, 367–378. doi:10.1016/S0039-6028(01)01161-X

CrossRef Full Text | Google Scholar

Mizrahi, V., and Sipe, J. E. (1988). Phenomenological treatment of surface second-harmonic generation. J. Opt. Soc. Am. B 5, 660–667. doi:10.1364/JOSAB.5.000660

CrossRef Full Text | Google Scholar

Morita, R., Kondo, T., Kaneda, Y., Sugihashi, A., Ogasawara, N., Umegaki, S., et al. (1988). Multiple-reflection effects in optical second-harmonic generation. Jpn. J. Appl. Phys. 27, L1134–L1136. doi:10.1143/JJAP.27.L1134

CrossRef Full Text | Google Scholar

Reining, L., Del Sole, R., Cini, M., and Ping, J. G. (1994). Microscopic calculation of second-harmonic generation at semiconductor surfaces: As/Si(111) as a test case. Phys. Rev. B Condens. Matter Mater. Phys. 50, 8411–8422. doi:10.1103/PhysRevB.50.8411

CrossRef Full Text | Google Scholar

Shen, Y. R. (1989). Surface properties probed by second-harmonic and sum-frequency generation. Nature 337, 519–525. doi:10.1038/337519a0

CrossRef Full Text | Google Scholar

Sipe, J. E., Moss, D. J., and van Driel, H. M. (1987). Phenomenological theory of optical second- and third-harmonic generation from cubic centrosymmetric crystals. Phys. Rev. B Condens. Matter Mater. Phys. 35, 1129–1141. doi:10.1103/PhysRevB.35.1129

CrossRef Full Text | Google Scholar

Tancogne-Dejean, N. (2015). Ab Initio Description of Second-Harmonic Generation from Crystal Surfaces. Ph.D. thesis, Ecole polytechnique, Palaiseau.

Google Scholar

Tancogne-Dejean, N., Giorgetti, C., and Véniard, V. (2015). Optical properties of surfaces with supercell ab initio calculations: local-field effects. Phys. Rev. B Condens. Matter Mater. Phys. 92, 245308. doi:10.1103/PhysRevB.92.245308

CrossRef Full Text | Google Scholar

Tellier, G., and Boisrobert, C. (2007). Second harmonic generation: effects of the multiple reflections of the fundamental and the second harmonic waves on the Maker fringes. Opt. Commun. 279, 183–195. doi:10.1016/j.optcom.2007.06.048

CrossRef Full Text | Google Scholar

Yeganeh, M. S., Qi, J., Culver, J. P., Yodh, A. G., and Tamargo, M. C. (1992). Interference in reflected second-harmonic generation from thin nonlinear films. Phys. Rev. B Condens. Matter Mater. Phys. 46, 1603–1610. doi:10.1103/PhysRevB.46.1603

CrossRef Full Text | Google Scholar

Yu, P., and Cardona, M. (2005). Fundamentals of Semiconductors: Physics and Materials Properties, 3rd Edn. Berlin: Springer Science & Business Media.

Google Scholar