Perspectives on the Theory of Defects

1. Introduction

A general definition of “defect” is any localized disruption to the perfect crystalline order. Thus, even the surface of the material is a defect because this disruption is localized in the direction normal to the surface. Few people study all the defects that satisfy this broad definition (Stoneham, 2001). Researchers tend to specialize in impurities and other point defects, dislocations, surfaces, or other categories.

Historically, defects have played critical roles because they affect the properties of materials in important ways. This is detrimental when a pure material is desired but beneficial when new material properties are sought. In antiquity for example, making a mirror involved polishing the purest possible copper plate. On the other hand, the production of bronze required adding a few percent of tin into the melt. The result is a metal which has a lower melting temperature than pure copper (making it easier to melt) and a lower viscosity at the melting point (making it easier to cast). More importantly, after cooling, bronze is much harder than pure copper, and can be used to make tools, weapons, and shields. Later, it was realized that the manufacture of specialized metals required new techniques: Hammering, peening, and forging were developed for shaping and hardening metallic tools. Metalsmiths learned how to introduce dislocations and then pin them to other defects in order to improve the mechanical properties of the material.

The Bronze Age revolution around the dawn of civilization in the 4th Millennium BCE is but one example of the importance of defects. The Egyptians knew how to control the optical properties of glass with impurities: adding trace amounts of metals into silica glass produces beads of sharply different colors: a little Au for red, traces of Co for blue… Such beads were just as valuable as an actual ruby or sapphire. In this example, adding impurities was a good thing. On the other hand, the production of “cristallo”—the first truly transparent glass—during the Italian Renaissance required removing as many impurities as possible. This was accomplished by using pure source materials in combination with temperature control during a slow cool-down. For centuries, achieving purity was also the main issue in iron-based alloys. People tried to lower the C content or get rid of unwanted elements such as Si, Mn, S, and P which make iron brittle. To do so, processes were developed to “burn away” these elements and refine the material, usually by forcing air to flow onto the heated or molten metal in order to induce oxidation processes.

In any case, controlling material properties by adding or removing specific impurities or defects is a useful and ancient skill. So why these negative-sounding words: “defect” (as in defective) and “impurity” (as in impure)?

In the early years of the twentieth century, condensed-matter physicists wanted to describe the fundamental properties of pure materials using the new concepts and tools of quantum mechanics. These problems attracted some of the greatest minds of the time (Planck et al., 1914). The emphasis was squarely on defect-free periodic crystals. The impact of defects on many fundamental material properties was not fully recognized.

When Peierls wrote his seminal paper on the thermal transport properties of solids (Peierls, 1929), he did include a short section on the role of “lattice perturbations.” He knew that they hindered the flow of “lattice waves.” But his discussion remained qualitative. Peierls himself was curious about the impact of defects on the flow of heat and electricity, and even drafted a manuscript on this topic. But his efforts were strongly rebuffed by none other than Pauli, a member of his PhD committee. Pauli opposed the publication of Peierls's manuscript and wrote (Pauli, 1931) “the residual resistivity is caused by dirt and one should not dwell in dirt” (ist der Restwiderstand ein Dreckeffect und im Dreck soll man nicht wühlen). Further down, Pauli added “you should find more sensible questions to be answered; I find that you recently have concerned yourself too much with small issues” (sollten Sie doch vernűnftigere Fragestellungen haben als solche kleinen Problemchen; ich finde, Sie verzetteln sich in letzter Zeit zu sehr in Kleinigkeiten). The content of the draft manuscript that Peierls shared with Pauli is not known. But it is surprising to see one of the fathers of modern science argue that some subjects should not be studied, almost as a matter of principle. The study of defects was considered undignified at the time.

The situation changed during World War II with the advent of semiconductors. Suddenly, controlling the electrical properties of Ge and then Si crystals became very important. This involved introducing atoms from a different column of the Periodic Table than the host-crystal atoms: replacing a few Si atoms with B in one region of the crystal generates positive charge carriers (holes) while P atoms added to an adjacent region generate negative charge carriers (electrons). The result is a p-n junction (a diode, or a solar cell). The B and P atoms added to Si were labeled “dopants” to distinguish these useful impurities from undesirable ones. The idea was to start with a very pure crystalline material and then implant dopants at precise locations. Crystals of ultra-pure Ge could be grown early on (Haller, 2006), but Ge has two problems. First, its fundamental bandgap is too small (0.66 eV) for optimal applications near room temperature. Second, exposing Ge to oxygen (air, water vapor…) does not lead to the formation of a stable insulating oxide layer. Thus, Si emerged as the semiconductor of choice: it has a 1.12 eV band gap and a great affinity for O because of the remarkable strength of the Si-O bond.

In the early days, Si could not be grown nearly as pure as Ge: it contained a lot of interstitial oxygen (from the quartz crucible), substitutional C (from the graphite heating elements), significant concentrations of transition metals such as Fe (mostly from the source material), and smaller amounts of many other impurities. Another important class of defects were vacancies, self-interstitials, and their precipitates. They result from less-than-optimal growth conditions, the growth of surface layers (insulating oxide, anti-reflection coating…), as well as implantation and irradiation—something feared by the military at the onset of the Atomic Age.

And then, thermal annealing causes impurities to diffuse. Impurities and native defects interact with each other, resulting in the formation of pairs, small clusters and aggregates. Self-interstitials expel substitutional impurities turning them into interstitials—which completely changes their properties. Vacancies trap interstitial impurities. Impurities precipitate at grain boundaries or dislocations. And the list goes on. Each of the resulting defects affects the concentration and lifetime of charge carriers in different ways. These properties had to be understood. The study of defects in semiconductors, especially Si, became very important for several decades, keeping experimentalists and theorists quite busy at universities, national laboratories, and research centers such as Bell Labs or IBM.

As for metals and metallic alloys, the scientific progress achieved in the twentieth and twenty first centuries is impressive. Scientists have learned how to tailor the properties of iron for a wide range of applications by alloying and processing it in a plethora of ways. Dozens of classes of steels were developed for different applications: adding Cr increases its hardness and corrosion resistance; Co and Mn make steel wear-resistant; Mo increases its tensile strength; Nb and V lead to much increased elasticity; W makes steel more resistant to heat; etc. The Register of European Steels lists some 2,500 different grades of steel—over 2,000 of which have been developed in the twenty first century.

Over the decades, many defect centers have been identified and characterized. Most of this understanding has resulted from the interplay between theory and experiment. We now know that defects affect much more than just the electrical properties of semiconductors and the mechanical properties of metals. In Si for example, interstitial O locks dislocations thus enhancing the mechanical strength of wafers and allowing them to be processed without breaking; H removes the unwanted electrical activity of many defects; the ~1.5μm photoluminescence associated with the Er ion in Si is useful for optical applications; magnetic ions such as Mn in GaAs allow the spin of charge carriers (e⁻) to be controlled; ongoing research aims at controlling the flow of heat in semiconductors using interfaces, etc.

Theoretical studies of defects combined with the huge database of experimental results (mostly in Si) have allowed theorists to refine their tools and test a wide range of approximations (Chelikowsky, 2002a,b). These tools are now applied to understand and predict the properties of new materials, such as nanostructures, for which far less experimental information is available. The mass production of (very) smart phones is just one testimony to the amount of knowledge that has been gained about using impurities to manipulate the properties of materials.

Where do we stand today? The variety of materials available appears to be quasi-infinite, ranging from man-made composites to many types of nanostructures. Bulk Si is still the basis of most integrated circuits. It can be obtained in extremely pure form, such as thin Silicon-On-Insulator (SOI) layers, but only sub-micron-size areas are involved in the active region of devices. With the exception of Si photovoltaics, there are few applications today that require bulk (periodic) semiconductors. In the case of metals, instead of adding small quantities of some alloying element(s) to a base material, alloys are produced with four or more elements in similar concentrations, resulting in one particular phase becoming stable in an unexpected way. The resulting material can exhibit extraordinary properties, for example in terms of fracture toughness and yield strength.

Some categories of defects in semiconductors are always unwanted. For example, the dislocations that result from growing GaN on imperfect substrates are always a problem, as are the transition-metal precipitates at grain boundaries or stacking faults in Si solar cells. In metals, however, ductility relies on the low formation energy and high mobility of dislocations.

In nanostructures, one rarely thinks in terms of “impurities” since every atom has been placed at a specific location to play a specific role. There is no underlying periodicity, no k-space, and no Brillouin zone. Instead, one deals with nearby surfaces, interfaces or δ-layers, all of which profoundly affect the properties of the material. These are intentionally constructed structures rather than defects in an otherwise pure host crystal. Our original definition of “defect” has become obsolete.

In this article, we present an overview of the theory and summarize the key ongoing developments. This cannot be a comprehensive review of all the work done and all the defects studied. Further, recent technical reviews are available (Drabold and Estreicher, 2007; Freysoldt et al., 2014). Examples of previous studies, including our own, were selected for this review.

2. Theory of Defects in Semiconductors

2.1. Assumptions and Approximations

Systematic theoretical studies of impurities and defects in semiconductors (McCluskey and Haller, 2012) begun after World War II with the emergence of the fundamental components of solid-state electronics, in particular the transistor (Bardeen and Brattain, 1948, 1949; Shockley, 1949). This device involves adjacent regions of the host material that are heavily doped with different impurities. Understanding how doping works was a key issue.

For theorists, the starting point was the perfect material. It was taken for granted that impurities—often present in concentrations of the order of parts per million or less—are little more than perturbations and that the impurity-related states can be adequately described in the basis set of perfect-crystal states. Effective-mass theory (Pantelides, 1978; Stoneham, 2001) explained qualitatively how dopants contribute conduction electrons (or holes) to the conduction (or valence) band of the host crystal. These shallow-level impurities introduce a series of hydrogen-like levels within the fundamental energy gap (“gap”). The deepest level is a few dozen meV's below the minimum of the conduction band (or above the maximum of the valence band). The ionization of the dopant occurs far below room temperature as the electron (or hole) hops from level to level toward the nearest band. The associated wavefunctions extend over dozens (sometimes hundreds) of Å around the impurity. Describing such states in the basis set of delocalized host-crystal states could indeed be justified.

The interest soon shifted from shallow dopants to defects characterized by much more strongly localized states. Such defects often introduce gap levels that are much farther away from the band edges (“deep centers”) (Pantelides, 1986). Instead of contributing charge carriers, they are recombination centers for electrons and holes. Examples include vacancies (introduced by a range of energetic processes and surface treatments) and most transition-metal impurities (often present in the as-grown material or introduced during the deposition of contacts). These defects are not perturbations to the perfect crystal and cannot be described in the basis set of the delocalized states of the perfect material. New theoretical approaches were required.

Here lies the fundamental importance of crystalline silicon in the development of theory (Chelikowsky, 2002b): experimentalists have accumulated a vast amount of electrical, structural, optical, and magnetic data for a wide range of defects in Si: the gap levels of a defect are typically measured within 0.01eV using electrical techniques such as Deep-Level Transient Spectroscopy (DLTS); optical tools such as Fourier-Transform Infra-Red (FTIR) absorption or Raman spectroscopy provide quantitative information on the local vibrational modes (LVMs) associated with light impurities; Electron Paramagnetic Resonance (EPR) maps spin-densities; and the list goes on. Such techniques are often combined with annealing studies, isotope substitutions, exposure to band-gap light, hydrogenation etc., all of which provide additional data that can also be calculated. Theory provides defect configurations, formation and binding energies, electrical activity, migration paths and activation energies, charge and spin densities, vibrational spectra and other quantities that can be directly compared to the measured data. Sometimes, the theoretical predictions precede the measurements or challenge some measured value (Woon et al., 1992; Istratov et al., 1998). The interplay between experiment and theory is the key reason why theory has become such a reliable and necessary partner in today's materials science research. But it took some effort before theory became quantitatively useful.

Solving the full quantum mechanical problem is not possible. Indeed, if r_i and R_α represent the electronic (i = 1, …, n) and nuclear (α = 1, …, N) coordinates, respectively, the Schrödinger equation

$\begin{array}{l}\text{i}\hslash \frac{\partial }{\partial \text{t}}\Psi (\left\{{\text{r}}_{\text{i}}\right\},\left\{{\text{R}}_{\alpha }\right\},\text{t})=\text{H}\Psi (\left\{{\text{r}}_{\text{i}}\right\},\left\{{\text{R}}_{\alpha }\right\},\text{t})\end{array}$

involves a huge number of particles. Further, the full Hamiltonian H must contain all the interactions: Coulomb, electron exchange and correlation, spin terms (including spin-orbit coupling), electron-phonon interactions, and so on. Almost a century ago, Dirac recognized that this problem requires “approximate, practical methods” (Dirac, 1929). But making approximations requires being able to test the limit(s) of their validity. Such testing must be done against experimental data.

2.1.1. Born-Oppenheimer Approximation

This involves decoupling the electronic and nuclear degrees of freedom. Since the electrons are very light, they should adjust instantaneously to the motion of the much heavier nuclei. Thus, one can solve the electronic problem in a field of fixed nuclei, an enormous simplification. This works very well but is not universally valid. One example involves the tricky issue of orbital degeneracies and the Jahn-Teller theorem (Jahn and Teller, 1937). An orbitally-degenerate electronic state couples to the surrounding nuclei leading to a symmetry-lowering distortion, thus splitting the multiplet until the degeneracy is lifted. The vibronic (vibrational-electronic) states involve electron-phonon coupling: the electronic and nuclear coordinates cannot be separated and the Born-Oppenheimer approximation fails. This issue has been a point of debate (DeLeo et al., 1988; Pantelides et al., 1988; Nieminen, 2007) when describing defects such as the vacancy or divacancy in Si (Watkins, 1995). Another example where the Born-Oppenheimer approximation cannot be used involves the calculation of Seebeck coefficients, which also involves electron-phonon coupling (Giustino, 2017)¹.

2.1.2. Ignore Nuclear Quantum Effects

While the electrons are of course treated quantum-mechanically, the much more massive nuclei are assumed to behave classically and follow Newton's laws of motion. This works very well in almost all situations, but fails when nuclear tunneling occurs. There are examples of proton tunneling in semiconductors (Muro and Sievers, 1986). Another nuclear quantum effect involves zero-point vibrational energies. This affects the calculation of migration barriers, especially for light impurities. Zero-point energy corrections can be included by hand if the dynamical matrix is known at the minimum and the saddle point of the potential energy. But the impact of zero-point motion can be more subtle. For example, the vibrational lifetimes of high-frequency (impurity-related) excitations has been measured as a function of temperature by transient bleaching spectroscopy (Luepke et al., 2003). If T increases, the vibrational amplitudes and anharmonic coupling increase, and the lifetimes become shorter. But if T decreases, the measured lifetimes become constant below some critical temperature T_c. This occurs when all the receiving modes drop to their zero-point energy state and then, the anharmonic couplings no longer change. The value of T_c depends on the defect (more specifically: on the receiving modes) but is typically of the order of 50–75 K. Theory describes classical oscillators and all the modes become harmonic at low T: they no longer couple and the lifetimes become infinite instead of reaching a constant value (West and Estreicher, 2006).

2.1.3. Describe the Host Crystal

One approach is to start with the perfect crystal using Green's functions which, in principle, produce exact results. The eigenvalues give the band structure of the crystal and the eigenvectors are Bloch or Wannier functions (Koster and Slater, 1954a,b). But introducing the defect presents challenges. It is not obvious that the defect can be described with the same basis set of periodic functions used to describe the perfect crystal. Further, defining the defect potential can be tricky, especially if lattice relaxations and distortions are included. Embedding techniques (Baraff and Schlüter, 1983; Gunnarsson et al., 1983) can be used to match a perturbed defect region to the known Green's function of the host material. Green's functions have been used to study isolated impurities such as transition-metals in Si (Katayama-Yoshida and Zunger, 1985; Beeler et al., 1990; Overhof and Weihrich, 1997).

The extreme opposite approach is to ignore the perfect crystal and focus on the defect and its immediate surroundings. The periodic background is lost but the chemistry and the strongly localized features of the defect can be studied. This type of modeling started with small molecular clusters surrounding a vacancy in Si. The electronic structure was described using extended Hückel theory (Messmer and Watkins, 1970). Small and large clusters were later used in conjunction with a range of quantum-chemical tools to study defect problems (Estreicher, 1995). This approach produces a highly intuitive, molecular-orbital-based description of defects, and the geometry around them can be approximately optimized (Estle et al., 1986, 1987).

However, clusters have serious drawbacks. Since the underlying periodicity of the crystal is lost, so is the entire band structure. Placing defect levels within the gap is not possible. Further, clusters have surfaces and the dangling bonds must be saturated (usually with H atoms). The surface of the cluster is polarized because of the difference in electron affinity between the host crystal atoms and the element that saturates the dangling bonds. And then, charging the defect by adding or removing one electron to the cluster results in most of that charge accumulating on the surface of the cluster instead of remaining associated with the defect: describing charged defects becomes meaningless.

Born-von-Karman boundary conditions have been applied to clusters in order to eliminate the surface (“cyclic clusters”). This approach has only been used in conjunction with semiempirical Hartree-Fock (HF) methods because applying these boundary conditions to three- and four-center integrals proved to be very difficult (Miro et al., 1997).

The best option to approximate the host crystal containing a localized defect involves periodic supercells (Nieminen, 2007), in which periodic boundary conditions are applied to a large unit cell (Messmer and Watkins, 1973; Zunger and Katzir, 1975). Converged energies require a summation over k-points in the Brillouin zone of the supercell. The usual selection of k points involves a Monkhorst-Pack uniform mesh (Monkhorst and Pack, 1976) (usually 2 × 2 × 2 or 3 × 3 × 3) but this choice is not unique (Makov et al., 1996).

When using supercells, the underlying periodicity of the crystal is preserved, there is no surface, and charged defects can be calculated with a neutralizing background charge (Van de Walle et al., 1988). But the defect itself becomes periodic. Further, the strain field and the charge associated with the defect are artificially confined to the supercell. Charging the defect gives rise to a fictitious Madelung energy contribution. A number of authors have proposed corrections to account for this term (Leslie and Gillan, 1985; Makov and Payne, 1995; Jarvis et al., 1997; Schultz, 1999; Lany and Zunger, 2008; Freysoldt et al., 2009; Wu et al., 2017). The corrections can be substantial in small supercells (16 or 32-atoms supercells were common two decades ago) and diminish as the supercell size increases. Today, supercells containing hundreds and sometimes up to 1,000 atoms are routinely used at the first-principles level. These issues are discussed in Freysoldt et al. (2014).

2.1.4. Solve the Electronic Problem

The core regions are often removed from the calculations with pseudopotentials. The use of empirical potentials can be traced back to 1934 (Fermi, 1934; Phillips and Kleinman, 1959), but ab-initio pseudopotentials (Hamann et al., 1979; Bachelet et al., 1982; Kleinman and Bylander, 1982; Vanderbilt, 1990) are now common. They reproduce the results of all-electron ab-initio calculations and contain no parameters fitted to experimental data. However, there is still user input: one has to decide which type of pseudopotentials should be used (depending on the type of basis set: atomic-like vs. plane waves), the value of the core radii, the semi-core states, etc. Ab-initio pseudopotentials are not an exact science. All-electron calculations can also be performed (Blum et al., 2009). Since core electrons are often relativistic, this involves solving the Dirac equation.

What remains is to solve the electronic problem in the valence regions. In the early days, semi-empirical methods have been used in clusters: Estreicher (1995) Xα-scattering wave (DeLeo et al., 1981, 1982) and approximate HF methods such as CNDO, MNDO, MINDO, or PRDDO. The “-NDO” techniques ignore all three- and four-center integrals (see below) and involve many adjustable parameters, while PRDDO includes all the three-center integrals and uses an orthogonalization procedure that minimizes the value of the four-center integrals which are ignored. As computing power increased, fully ab-initio HF calculations were performed, sometimes complemented by limited post-HF corrections such as Møller-Plesset expansions (Roberson and Estreicher, 1994). They introduce some electron correlation at a substantial computational cost.

HF methods typically use atomic basis sets for the electronic states. The many-electron wavefunction is a Slater determinant of molecular orbitals which themselves are linear combinations of (optimized and tabulated) atomic orbitals. The interpretation of the results in terms of hydrogenic orbitals is highly intuitive. Electron correlation is ignored but electron exchange is calculated exactly. This involves evaluating some N⁴/8 four-center integrals of the type $\langle {\psi }_{\text{i}}(1),{\psi }_{\text{j}}(1)|\frac{1}{{\text{r}}_{12}}|{\psi }_{\text{k}}(2),{\psi }_{\ell }(2)\rangle$ where N is the number of orbitals (which is much larger than the number of atoms). A HF calculation is called “ab-initio” if all the four-center integrals are computed for a given basis set. Such calculations are computationally expensive which limits the size of the clusters that can be used. Further, electron correlation is ignored, unless even more expensive post-HF tools are used. HF provides good geometries and chemical intuition, but the band gap is hopelessly large and the location of defect-related gap levels is unreliable. Further, the frequencies of the defect-related vibrational modes are highly inaccurate. For these reasons, HF techniques have been largely abandoned in the study of defects in semiconductors.

Density-functional theory (DFT) (Kohn, 1999; Jones, 2015) in conjunction with periodic supercells is a far superior approach (Mattsson et al., 2004; Freysoldt et al., 2014). It is usually referred to as “first-principles” because no parameter adjusted to an experimental database is involved. Within DFT, one solves the Kohn-Sham equation for non-interacting effective particles whose total density matches the exact electronic ground state density provided that the exchange-correlation potential V_xc is known. This potential is of course not known. It is usually described in terms of the local density (Local-Density Approximation or LDA Kohn and Sham, 1965) and its gradients (Generalized-Gradient Approximation or GGA Perdew et al., 1996a). The latter exists with dozens of revisions and corrections: RPBE, RevPBE, PBESOL, LYP, AM05, DRSLL, KBM, LMKLL, etc. Theorists must decide which functional to use for a specific defect problem. There is no ab-initio recipe for making this decision, and some results are sensitive to the choice of V_xc (see e.g., Pacchioni et al., 2000; Estreicher et al., 2011). The true interactions between electrons are of course non local and any local approximation is bound to be incomplete. One consequence is that the DFT bandgaps are typically half the measured values. At the LDA level, the calculated (measured) gaps are 2.89 eV (5.50) for diamond, 0.79 eV (1.12) for Si, and 0.01 eV (0.66) for Ge. One popular correction involves the use of hybrid functionals which includes some exact HF exchange (Perdew et al., 1996b; Lucero et al., 2012): ${\text{E}}_{\text{xc}}^{\text{hyb}}={\text{E}}_{\text{xc}}^{\text{DFT}}+\text{α}({\text{E}}_{\text{x}}^{\text{HF}}-{\text{E}}_{\text{x}}^{\text{DFT}})$. This introduces a mixing coefficient α which is usually taken to be 0.25. Quasi-particle theories such as GW (see Ergönenc et al., 2018 for a recent example) and the Monte-Carlo approach are discussed elsewhere in this series of reviews. A list of DFT software packages can be found at https://dft.sandia.gov/codes_list.html and a quantitative discussion of the accuracy of some of them is in Lejaeghere et al. (2013).

Typical defect calculations begin with the selection of the appropriate supercell and electronic-structure tools (size and type of basis set, exchange-correlation potential, and k-point sampling). As a first step, we always optimize the lattice constant of the perfect cell in the negative, neutral, and zero charge state. The lattice constant of the defect-free supercell (that is: the size of the box that contains it) must be optimized as it varies with supercell size and DFT input parameters. In small supercells, the lattice constant also varies a little with the charge state. This effect, which is of particular importance if vibrational frequencies should be calculated, can be understood by the following consideration. In quantum chemistry, the “bond index” is the difference in the population of the bonding and anti-bonding orbitals. In a small molecule such as H₂, the bond strength and stretch-mode frequency are substantially affected by the charge state: ${\text{H}}_2^{-}$ and ${\text{H}}_2^{+}$ both have a longer bond length and lower frequency than ${\text{H}}_2^0$, while ${\text{H}}_2^{2-}$ as well as ${\text{H}}_2^{2+}$ dissociate (bond index = 0). A smaller effect occurs for larger molecules and in supercells. The charge does affect the bond lengths and strengths and that small change has an impact on the total energies and vibrational frequencies. This should be taken into account when accurate calculations are desired, in particular when the dynamical matrix is needed.

Then, the impurity or defect is introduced into the supercell and the geometry around it is optimized in various charge states by minimizing the inter-atomic forces for a number of a priori possible configurations of the defect. Typical conjugate-gradient geometry optimizations are considered to have converged when the maximum force component drops below 0.03(eV/Å) or so. For the calculation of the Hessian, it is desirable to lower this value to 0.003(eV/Å) in order to minimize the number of negative eigenvalues.

Once the various configurations and total energies of the defect in the various allowed charged states are known, other properties of the defect can be calculated (Zhang and Northrup, 1991; Van de Walle et al., 1993; Nieminen, 2007; Freysoldt et al., 2014). These include formation energies as a function of the Fermi level which gives the thermodynamic transition (or ionization) levels. The binding energies are always of interest when dealing with defects consisting of several elements. This is the energy gained by forming a complex starting with isolated components. For example, the binding energy E_b of the substitutional boron—interstitial hydrogen pair in the Si₅₁₂ supercell would be ${\text{E}}_{\text{b}}=\left\{\text{E}(\text{S}{\text{i}}_{511}{\text{B}}^{-})+\text{E}(\text{S}{\text{i}}_{512}{\text{H}}_{\text{bc}}^{+})\right\}-\left\{\text{E}(\text{S}{\text{i}}_{511}\text{B}{\text{H}}^0)+\text{E}(\text{S}{\text{i}}_{512})\right\}$, where ${\text{H}}_{\text{bc}}^{+}$ stands for isolated bond-centered hydrogen in Si. Note that at non-zero temperatures, one should consider free energies and the most important entropy contribution for such defects is the configurational term which can be of the order of 0.1–0.2 eV at room temperature (Estreicher et al., 2004). An experimental situation where this configurational entropy was seen at work involves the H₂ molecule trapped near interstitial O in Si (see section 1.2.2). Various activation energies may also be needed, such as reorientation barriers between equivalent sites or migration barriers. These barriers are best obtained using the nudged-elastic-band (NEB) method (Henkelman and Jonsson, 2000; Henkelman et al., 2000). It is computationally expensive, even in small supercells. However, the NEB method provides the correct migration path (Estreicher et al., 2011) and converges toward the true saddle point of the potential-energy surface. Many of these issues have been discussed in a recent review (Freysoldt et al., 2014). There is neither need nor room to repeat this here. However, this review did not discuss the vibrational properties of defects.

2.2. Vibrational Dynamics of Defects

FTIR and Raman spectra of light impurities in semiconductors have produced a large volume of vibrational data, which often include isotope shifts. Sometimes, the symmetry of the defect was obtained from uniaxial-stress experiments while annealing studies provided estimates for the binding energies. Numerous examples and details of the experimental techniques are in Pearton et al. (1992) and Shimura (1994). The combination vibrational spectroscopy and first-principles studies has led to the identification of many defect centers in semiconductors. The story of H₂ molecules in Si (Kissinger and Pizzini, 2015) should at least be mentioned here, as it involved many puzzling twists and turns. For example, the trapping of H₂ near interstitial O resulted in the observation of the molecule's ortho/para splitting in the IR line of O (but not that of H₂) as well as in a measurement of the configurational entropy (Chen et al., 2002). Further, a range of excited ro-vibrational states of H₂, HD, and D₂ were measured by delicate annealing studies (Stavola et al., 2003). The example of H₂ in Si alone illustrates the amazing range of detailed experimental information that can be extracted from such optical studies.

The vibrational lifetimes of many impurity-related modes were measured in situ by transient-bleaching spectroscopy (Luepke et al., 2003). One unexpected feature of the data was that very similar Si−H stretch modes sometimes exhibit lifetimes that differ by as much as two orders of magnitude. They also show some truly gigantic isotope effects (Gibbons et al., 2013). The calculations of the lifetimes and decay channels of such high-frequency stretch modes involved the use of the eigenvectors of the dynamical matrix (West and Estreicher, 2006, 2007). It soon became clear that the lifetimes of excited impurity-related modes are not related to their frequency but to the nature of the receiving modes. For example, changing the isotope of a receiving mode may result in a two-phonon decay becoming a three-phonon one, and thus substantially increase the vibrational lifetime.

Calculations of the vibrational properties of defects begins with the Hessian. It can be obtained without displacing any host atom using linear-response theory (Pruneda et al., 2002). This produces purely harmonic modes. The more common “frozen-phonon” method involves displacing atoms by small amounts to evaluate the second derivatives of the energy relative to atomic coordinates ${\partial }^2\text{E}/\partial {\text{R}}_{\alpha \text{i}}\partial {\text{R}}_{\beta \text{j}}$ (where α, β = 1…, N number the atoms and i, j are Cartesian indices). The dynamical matrix itself is obtained by dividing the Hessian matrix elements by the square roots of the nuclear masses of the atoms involved. The dynamical matrix can also be obtained at non-zero temperatures directly from molecular-dynamics (MD) simulations by mapping the calculated forces at every time step onto the elements of the matrix (Hellman et al., 2013).

The eigenvalues of the dynamical matrix are the square of the normal-mode frequencies while its eigenvectors allow the calculation of the relative displacements of all the atoms for each mode. For periodic supercells, there are three translational (but no rotational) modes with zero frequency. All the other eigenvalues should of course be positive, but this is not always the case. The geometries need to be optimized very carefully (we use F_max,i < 0.003eV/Å) in order to minimize the number of negative eigenvalues, often referred to as “imaginary modes.” No such mode really exists: negative eigenvalues indicate that one has not reached the minimum of the 3N-dimensional potential-energy surface (N is the number of atoms) since the curvature of the energy is negative along some direction(s).

Depending on the details of this surface, it can be challenging to reach the minimum. One problem is that conjugate-gradient geometry optimizations involve Cartesian coordinates, and the Cartesian displacement of an atom always corresponds to a linear combination of many normal modes. However, a system of N atoms has 3N Cartesian coordinates as well as 3N ortho-normal vibrational modes. The latter can be used to fine-tune the geometry. One can get rid of a few residual negative eigenvalues by displacing the atoms not along Cartesian coordinates but along the normal vibrational mode coordinates associated with the negative eigenvalues (Kang and Estreicher, 2014).

2.3. Non-equilibrium Molecular Dynamics Without Thermostat

The nuclear dynamics are obtained from classical MD simulations. The nuclei follow Newton's laws of motion with inter-atomic forces calculated using DFT. The energy calculated at the time t is used to calculate the velocities and positions of all the nuclei at the time t + Δt, where Δt is 1/30th to 1/40th of the shortest period of oscillation in the system. Since the energy of the oscillator is on the average half kinetic and half potential, the temperature T of the system of N nuclei is related to the total kinetic energy via $\sum _{\text{i}}^{\text{N}}\frac{1}{2}{\text{m}}_{\text{i}}{\text{v}}_{\text{i}}^2=\frac{3}{2}\text{N}{\text{k}}_{\text{B}}\text{T}$, where k_B is the Boltzmann constant.

There are various types of approaches to MD using empirical forces, the Born-Oppenheimer approach, as well as the Sankey and Car-Parrinello methods. These are not discussed here. Instead, we focus on how to prepare the system at the time t = 0 in such a way that neither thermostat nor thermalization runs are needed. The supercell preparation technique can be used with any level of MD.

The conventional way to initiate MD simulations at the temperature T involves a Maxwell-Boltzmann distribution of nuclear velocities corresponding to the temperature T while all the nuclei are in their equilibrium location. This does produce the desired temperature, but the MD run begins with all the vibrational modes exactly in phase (zero potential energy), an unphysical situation. And then, at the beginning of the MD run, all the nuclei lose and gain kinetic energy together, and the initial temperature fluctuations are very large (comparable to T). The amplitude of these fluctuations must be reduced with a thermostat, a subroutine that cuts-off excessive kinetic energy and renormalizes the temperature. Extensive thermalization runs are required until the system reaches a reasonable steady-state. This situation makes it impossible to study the coupling between the various modes while the system is far from equilibrium. Indeed, the temperature fluctuations are larger than many phonon energies and the vibrational modes couple to the thermostat much faster (every few MD time steps) than to each other. The need for thermostats and long thermalization runs entirely originates from the fact that all the vibrational modes are in phase at t = 0.

In the “supercell preparation” technique (Gibbons et al., 2015), the system is initiated in a linear combination of normal modes with random phases and energies that produce the desired initial distribution of temperatures. The key ingredient is the dynamical matrix. The orthonormal eigenvectors ${\text{e}}_{\alpha \text{i}}^{\text{s}}$ allow us to calculate the relative displacement of atom α along i = x, y, z for each mode s. These eigenvectors are related to the Cartesian nuclear coordinates R_αi via the normal-mode coordinate q_s:

$\begin{array}{l}{\text{R}}_{\alpha \text{i}}(\text{T},\text{t})={\displaystyle \sum _{\text{s}}}{\text{e}}_{\alpha \text{i}}^{\text{s}}{\text{q}}_{\text{s}}(\text{T},\text{t})/\sqrt{{\text{m}}_{\alpha }},\end{array}$

where T is the temperature and t the time. Even though the MD runs are fully anharmonic with forces obtained from the total energies, the conversion between Cartesian and normal-mode coordinates involves the harmonic assumption for the unknown q_s, namely

$\begin{array}{l}{\text{q}}_{\text{s}}(\text{T},\text{t})={\text{A}}_{\text{s}}(\text{T})cos({\omega }_{\text{s}}\text{t}+{\phi }_{\text{s}}).\end{array}$

This introduces a random distribution of phases at the time t = 0. The amplitudes A_s(T) are obtained from the condition that, in thermal equilibrium, the average energy per mode is k_BT. This remains a good approximation even when the system is prepared away from equilibrium. The randomized Boltzmann distribution of energies βexp{−βE_s}, where β = 1/k_BT produces the average energy k_BT per mode. Using the inverse-transform method for generating distributions, the cumulative distribution function

$\begin{array}{l}{\zeta }_{\text{s}}={\displaystyle {\int }_0^{{\text{E}}_{\text{s}}}}\beta {\text{e}}^{-\beta \text{E}}\text{dE}\end{array}$

gives

$\begin{array}{l}{\text{E}}_{\text{s}}=-{\text{k}}_{\text{B}}\text{T}ln(1-{\zeta }_{\text{s}}),\end{array}$

where ζ_s is a random number between 0 and 1. Equating this to the energy ${\text{E}}_{\text{s}}=\frac{1}{2}{\text{A}}_{\text{s}}^2{\omega }_{\text{s}}^2$, one gets

$\begin{array}{l}{\text{A}}_{\text{s}}^2(\text{T})=-2{\text{k}}_{\text{B}}\text{T}ln(1-{\zeta }_{\text{s}})/{\omega }_{\text{s}}^2.\end{array}$

Each set of random mode phases and energies produces an initial microstate. No thermostat is used and the magnitude of the T fluctuations is considerably smaller from the very beginning than those resulting from the “conventional” MD runs (above) even after thermalization runs. Since there is an infinite number of initial microstates corresponding to the same macrostate, it is necessary to average over many microstates. This involves averaging the results of n MD runs, each starting with different random distributions of initial mode phases and energies, all of which corresponds to the same initial temperature distribution. Increasing n is equivalent to increasing the size of the supercell, and the amplitude of the temperature fluctuations is sharply reduced as shown in Figure 1. As discussed in Gibbons et al. (2015), supercell preparation produces runs in which the temperature fluctuations are independent of time starting with MD step one and sharply decrease in magnitude after averaging over n initial microstates. At 125 K, the standard deviations of the fluctuations with n initial microstates are ΔT = ± 0.91, 0.52, 0.32, and 0.15K for n = 30, 100, 300, and 1,000, respectively. Thus, for a supercell of some 200 atoms, averaging over n=30 runs produces time-independent T fluctuations of the order of just 1% (!) of the background temperature (Gibbons et al., 2015) from the beginning of the run. Of course, large supercells require less averaging than small ones. Thus, the supercell preparation technique allows the coupling between normal vibrational modes to be studied while the system is truly away from equilibrium (where “truly” means not in a steady-state situation).

FIGURE 1

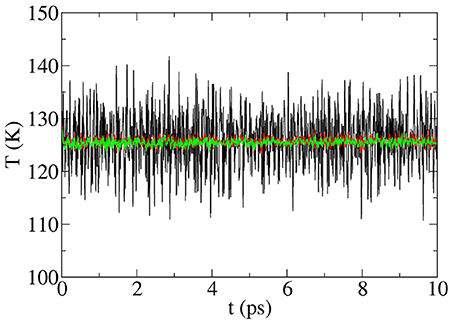
Figure 1. Total temperature of the Si₂₀₀H₃₂ supercell vs. time without averaging (black line) and after averaging over n = 50 (red line) and n = 100 (green line) initial microstates (see text). The non-equilibrium MD run includes a nanowire prepared at 100 K with a hot slice at 180 K. No thermostat is used and no thermalization run was done. The figure shows the temperatures vs. time starting with the first MD step. The time step is 1.0 fs.

To study heat flow, a small region of the supercell is prepared at the temperature T₁ while the rest of the system is at T₀. The modes are kept in phase at the T₁/T₀ interface by preparing the entire supercell at T₀ and then increasing (or decreasing) the mode amplitudes until the atoms in the hot region are at T₁. Appending the positions and velocities of the atoms in the 0 and 1 regions produces the desired initial gradient.

To calculate the lifetime (West and Estreicher, 2006, 2007) of a vibrational mode with frequency ω > k_BT/ℏ, the system is prepared at temperature T for all the modes except the one of interest which is assigned the potential energy 3ℏω/2 (zero-point energy plus one phonon). This classical oscillator now has the same initial amplitude as the quantum-mechanical one, and therefore the same amount of anharmonic coupling. During the MD run, the Cartesian coordinates at every time step are converted into normal-mode coordinates, which allows the monitoring of the energy and amplitude of all the modes vs. time. Note that the purely potential energy of the excited mode at t = 0 shifts the temperature from T to T_cell since 3Nk_BT_cell = (3N − 1)k_BT + 3ℏω/2, where N is the number of atoms.

2.4. Heat Flow and Defects

Material containing defects exhibits two types of vibrational modes (Estreicher et al., 2015). Those associated with the host crystal (bulk modes) are delocalized in space and have very short vibrational lifetimes, typically one period of oscillation. Since these modes come in near-continuous bands, the coupling between them involves very fast one-phonon processes (~0.2 − 0.3ps). On the other hand, the defect-related modes are localized at or near the defect and exhibit long vibrational lifetimes: dozens or even hundreds of periods of oscillation, a phenomenon called “phonon trapping.” Defect-related modes are “Spatially-Localized Modes” (SLMs). They do not couple easily to delocalized ones, even when they have the same frequency. Their lifetimes are characteristic of two- (~5−8ps) or even three-(over 50ps) phonon processes (Sun et al., 2006). Thus, defects in the path of a heat front act like “thermal sponges”: they absorb small amounts of energy in SLMs for meaningful lengths of time, thus reducing the flow of heat. The decay of these trapped phonons depends on the availability of receiving modes, not on the origin of the excitation. The optical analogy is fluorescence where photons are trapped for a long time and then released in directions uncorrelated to where they originated.

Defect-related SLMs are critical to understanding the interactions between thermal phonons and defects. When a heat front at the temperature T_hf encounters a defect (initially at the background temperature T₀), the SLMs with frequencies in the range k_BT₀/ℏ < ω < k_BT_hf/ℏ become resonantly excited. If there are no SLMs in this range, one has to wait for two- (or more) phonon processes to occur in order for higher-frequency SLMs to get excited. Thus, the outcome of heat-flow – defect interactions depends on the temperature window [T₀, T_hf].

This is of particular importance when the defect is the interface between two materials A and B. The defect is the A/B interface. The heat generated in the A region propagates via the coupling of A-A vibrational modes. Once the heat front reaches the interface, it traps in A-B SLMs. And then, the decay of the trapped phonons depends on the number of receiving modes on both sides of the interface. If the A region has heavier atoms than the B region, then the A side contains many more low-frequency modes than the B sides: most of the phonons trapped at the A/B interface decay back to the A side. The net result is that heat accumulates on the A side of the interface and a large temperature discontinuity (interface or Kapitza resistance) appears. On the other hand, if material A is lighter than material B, then there are many more receiving modes on the B side than on the A side and most of the phonons trapped in SLMs at the A/B interface decay toward the B side and heat easily moves forward into the B layer: the temperature discontinuity at the interface (and the Kapitza resistance) is small. Thus, the Kapitza resistance depends on the temperature window and the direction of heat flow. Stanley and Estreicher (2018) This explanation for the atomistic origin of the Kapitza resistance differs from the models (Swartz and Pohl, 1989) that include only the mismatch between the phonon densities of states of the two materials but do not include the localized vibrational modes associated with the interface. Note that the first-principles calculations performed so far involved systems too small to include the low-frequency (long-wavelength) phonons.

Finally, the reduction in the thermal conductivity associated with the surface of the material is also associated with the surface SLMs. In the case of a H-saturated Si nanowire (Kang and Estreicher, 2014), the surface SLMs are the Si-H stretch and wag modes. The former are too high in frequency (over 2, 000 cm⁻¹) to be thermally excited at moderate temperatures, but some of the latter (~900 cm⁻¹) become excited in the hot region of the nanowire when a T gradient is set-up. Since these modes are higher in frequency than any Si-Si mode, they require two-phonon processes to interact in any way with the bulk modes. The surface Si-H wag modes couple resonantly to each other much faster than they can decay into (or be excited by) Si-Si modes. The result is that heat propagates independently in the bulk and on the surface. Thus, the surface reduces the heat flow because one must wait for its contribution to arrive before the system achieves thermal equilibrium. There is precious little interaction between bulk and surface oscillators: the frequencies are too far apart.

3. Theory of Defects in Metals and Metallic Compounds

Defects are ubiquitous in metals and metallic alloys, since the creation of single point defects (such as substitutional impurities or vacancies) often costs only moderate amounts of energy in these systems. Therefore, point defects are present under virtually all technologically relevant conditions. In pure metals, typical vacancy concentrations (Kittel, 2005) at room temperature are around 10⁻⁵ (meaning that one in 10⁵ sites is a vacancy), while close to the melting point they range from 10⁻³ (low-melting-point) to 10⁻² (high-melting-point) (Kraftmakher, 1998). Larger vacancy concentrations are found in alloys than in pure metals (Mosig et al., 1992).

In addition to vacancies, which are intrinsically present due to thermodynamics, different types of defects are found in metals for various reasons. First, impurities are present in the source materials and cannot be completely removed during large-scale technological processes. Second, alloying elements are added to improve the materials properties. The effects of alloying may be unpredictable: Tungsten-rhenium, e.g., shows an anomalous dependence of the thermal expansion on the Re content (Dengg et al., 2017) with a local minimum at around 12% Re. Third, crystallographic defects such as dislocations are introduced by mechanical treatment. They play an important role in determining the mechanical properties of the material. It is very important to know the thermal and mechanical processing history of a metallic sample. Depending on that history, different samples with the same macroscopic composition can be completely different on the micrometer and at the atomic scale: New phases may appear, the grain size may change, precipitates can form, while defects can segregate and trap at grain boundaries, dislocations, etc. Theorists need detailed information about the processing history and the microstucture of a sample in order to create an atomistic model for realistic computer simulations.

3.1. Vacancies in Simple Metals and Intermetallic Compounds

Vacancies are among the most important defects in any metal. A series of techniques are employed to extract vacancy formation energies from experiment. Most prominently, they can be extracted from the nonlinear increase in the specific heat, the residual resistivity of quenched samples, positron annihilation experiments, or a simultaneous measurement of the macroscopic thermal expansion and changes in the lattice parameter at high temperatures (Kraftmakher, 1998). These experiments all produce different results. In addition, sample preparation, measurement conditions, and other external factors differ from experiment to experiment. As a result, defect formation energies extracted from measurements show a rather large scatter. In the case of Al for example, Pochapsky (1953) extracted a vacancy formation enthalpy of 1.17 eV from heat capacity and electrical resistance measurements, while Triftshäuser (1975) obtained 0.66 eV from positron annihilation experiments. The equilibrium vacancy concentrations at the melting point are 5 × 10⁻⁷ in the former case and 3 × 10⁻⁴ in the latter one. These numbers differ by almost a factor of 1000.

In this situation, theoretical estimates of the vacancy formation energy have become an increasingly attractive alternative. The early theoretical attempts were based on purely elastic considerations (Kornblit, 1981; Krause et al., 1989; Ghorai, 1991) or on calculations based on empirical interatomic potentials (Harder and Bacon, 1986; Ackland et al., 1987; Rosato et al., 1989). In the early 1990's, ab-initio codes based on density-functional theory became powerful enough to allow electronic structure calculations of vacancy formation energies in simple metals such as Al and Li (Beuerle et al., 1991; Mehl and Klein, 1991; Benedek et al., 1992). A few years later, the first ab-initio calculations of vacancies in transition metals were published. In 1999, Korzhavyi et al. calculated the vacancy formation energy of all the transition elements, including different variants in terms of crystal structures and magnetic state (Korzhavyi et al., 1999) (blue line² in Figure 2). At this point, such calculations had reached a sufficient level of accuracy to serve as a benchmark, especially when comparing vacancy formation energies in different metals, since they were done in a consistent way with reasonable predictive power. From these systematic calculations, trends in vacancy formation energy can be seen: their values range from 1 to 3 eV, and they roughly follow a parabolic trend along each row of the Periodic Table, with a maximum in the middle and the lowest values in the beginning and at the end. Interestingly, the ratio between the melting temperature (in units of k_BT_m, where T_m is the melting temperature and k_B the Boltzmann constant) and the vacancy formation energy is in the range 8 to 13 for virtually all metals, as pointed out by Grimvall (1999).

FIGURE 2

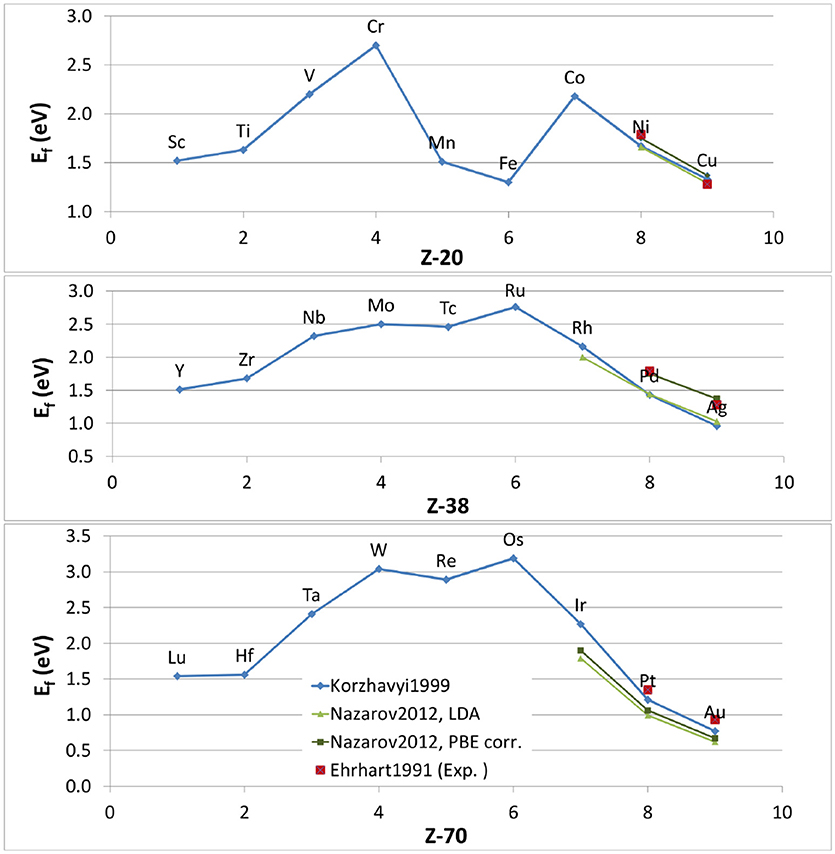
Figure 2. Vacancy formation energies of 3d (upper panel), 4d (central panel) and 5d (lower panel) transition metals as a function of atomic number (Z) as obtained from theory. The blue diamonds are taken from Korzhavyi et al. (1999), the light green triangles are data obtained with LDA from Nazarov et al. (2012), the dark green squares are from the same reference, but include a correction for describing the vacancy internal surface. The experimental values for some late transition metals (Ehrhart et al., 1991) (red squares) are included.

Korzhavyi et al. (1999) provided a reasonable description of the electronic structure and took into account volume relaxation effects. However, a few limitations were still there: (i) Local atomic relaxations were not taken into account; (ii) the local density approximation (LDA) was used for the exchange-correlation potential. This systematically overestimates binding energies and is suspected to have shortcomings for the region surrounding the vacancy where the electron density varies sharply (this is comparable to a surface effect Carling et al., 2000); (iii) the formation energies were obtained at T = 0 K. Nazarov et al. (2012) calculated these energies but included the local atomic relaxations and a special correction to overcome the shortcomings of (semi-)local exchange correlation functionals and to give correct results for the internal surface around a vacancy, in the spirit of Carling et al. (2000). Figure 2 shows their results obtained with LDA and the generalized-gradient approximations (GGA) as parameterized by Perdew et al. (1996a) (PBE). Surprisingly, GGA, (expected to perform better than LDA for strong charge density variations) seems to perform worse when no special correction is applied. But after applying the special correction, GGA performs slightly better than LDA, especially for the 4d transition metal series. It appears that LDA calculations benefit from an error cancellation which leads to surprisingly good results for vacancy formation energies, even though LDA was originally designed for systems with slowly-varying electron density. This is one of the reasons why the results by Korzhavyi et al. (1999) are so good. In addition, the results from Figure 2 show that the effect of local lattice relaxations are really small for vacancies in transition metals, as already assumed by Korzhavyi et al. based on previous work (Meyer and Fähnle, 1997; Papanikolaou et al., 1997).

The last feature missing in the results discussed so far is the effect of temperature. When finite temperature comes into play, one must go beyond the so-called total energy as resulting from a DFT run. Instead, the free energy of a system must be determined which, for an elemental solid, is

$\begin{array}{l}F(V,T)=F^{\mathrm{el}}(V,T)+F^{\mathrm{vib}}(V,T)+F^{\mathrm{vac}}(V,T).\end{array}$

Here, F^el(V, T) represents the electronic free energy, which is the sum of the total energy E(V) and the entropy term TS^el, F^el(V, T) = E(V, T) − TS^el(T). F^vib(V, T) is the vibrational free energy due to harmonic and anharmonic lattice vibrations. F^vac(V, T), finally, is the free energy due to the creation of defects. The explicit treatment of temperature in ab-initio calculations inlcuding all of these terms was introduced rather recently. Grabowski et al. (2009) provided a comprehensive description of the thermodynamic properties of Al up to the melting point, where they explicitly included all the entropy contributions (electronic, quasiharmonic, anharmonic, configurational) in addition to the electronic energy to determine the free energy of vacancies as a function of temperature. They showed that the total entropy contributions are about 2k_B and therefore substantial. At the melting point, the addition of entropy results in a 6 times larger vacancy concentration, bringing the one deduced from the GGA results in very close agreement to the positron annihilation data of Hehenkamp (1994).

In a recent paper (Bochkarev et al., 2016b), Bochkarev et al. added a new aspect to this discussion. They calculated the free energy of a vacancy using two different approaches: In the first, for each temperature, they first optimized the volume of the supercell without vacancy and then introduced a vacancy keeping the volume fixed (single-volume approach). These results were compared to the ones obtained in a second approach where the volume of the supercell including the vacancy was optimized for each temperature. It turned out that the single-volume approach leads to considerable errors both in the vacancy formation entropy S_f as well as the formation enthalpy H_f, but that the two errors almost cancel out. Thus, the single-volume results for the Gibbs free energy as a function of temperature are very close to the ones obtained in the single-volume approach. This means that at a given temperature one can obtain decent results for the Gibbs free energy of a vacancy using the optimized volume of a defect-free cell, which saves considerable computing time.

In 2014, Glensk et al. (2014) presented an ab-initio study on the temperature dependence of the Gibbs free energy of vacancy formation in Al and Cu from 0K up to the melting temperature, fully taking into account the anharmonic contributions. Their GGA-PBE results are in very good agreement with experiment in the temperature range where experimental data were available, T ≥ 500K (Simmons and Balluffi, 1960; Hehenkamp, 1994). However, at low temperatures, they found a trend in the Gibbs free energy strongly deviating from the Arrhenius behavior, which could be explained by a linear dependence of the entropy on the temperature. They concluded that an Arrhenius-like description of the Gibbs free energy was not appropriate for intermediate to lower temperatures. This would imply that the vacancy formation energies extracted from experiments which assume an Arrhenius-like behavior could contain substantial errors. As an alternative, they proposed to interpret experiments using a formalism they call local Grüneisen theory which contains the correct linear dependence of the entropy on the temperature. When re-assessing the experimental data for Cu and Al using their local Grüneisen theory, they obtained agreement within 0.02 eV with the results obtained directly from GGA-PBE without applying any surface correction. Thus, there is a fruitful discussion going on between ab-initio predictions, experimental data, and their interpretation in terms of vacancy formation energy.

So far, we have only discussed single vacancies in metals. What about the role of vacancy clusters? Kraftmakher (1998), (p. 90) states that divacancies are the only defects whose equilibrium concentrations at high temperatures may become comparable with those of monovacancies. This is surely the case for pure metals, and to some extent for random alloys, but the situation changes when going to intermetallics or metallic compounds. Metallic compounds are of high technical relevance both as structural and functional materials. Prominent members are cementite Fe₃C, an (often unwanted) phase appearing in steel, cast iron, WC, TiC (very hard materials often used as coatings for tools), and TiN (a hard metallic material used e.g., as diffusion barrier in microelectronics). Metallic compounds are often very hard and brittle, but metallic in the physical sense, i.e., they have a non-vanishing density of states at the Fermi level. As a consequence, defects in these materials are not electrically charged (as in semiconductors or insulators) and unbalanced numbers of metal and C (or N) atoms do not lead to large electrostatic interactions. In fact, in experimentally-synthesized samples, off-stoichiometry can be huge: Under normal conditions, cubic M − X_y carbides and nitrides (M = Ti, Zr, Hf, V, Nb, Ta; X = C, N) may contain up to ~30 − 50 at.% of structural vacancies in the nonmetal sublattice (Gusev, 2014).

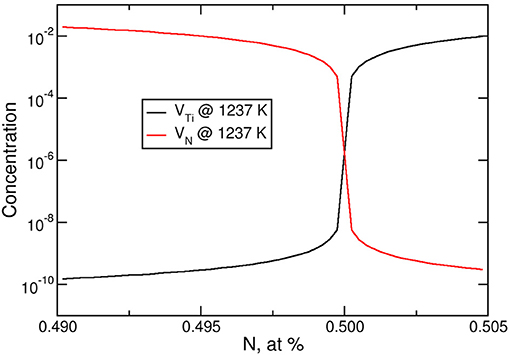
Let us have a closer look at the atomic structure of intermetallics. By default, different species of atoms sit on different sublattices. Consider TiN: In the perfect Ti_0.5N_0.5 structure, one sublattice is fully occupied with Ti and the other one with N atoms. Due to synthesis conditions, however, the concentrations may deviate from 50:50 and an excess or deficiency of one species may occur. The effective formation energies of vacancies and, as a consequence, their concentrations critically depend on this balance (Mühlbacher et al., 2015). Using the dilute solution model it is possible to predict the concentrations of vacancies as a function of stoichiometry and temperature on the basis of DFT calculations (Woodward et al., 2001; Hong et al., 2015). Figure 3 shows the concentrations of vacancies in TiN as a function of stoichiometry and temperature, based on the effective vacancy formation energies reported in Mühlbacher et al. (2015). For 1273 K, a slight 0.5% excess of Ti would lead to a concentration of Ti vacancies (V_Ti) as small 3 × 10⁻¹⁰, while a 0.5% deficiency would increase their concentration to as much as 10⁻². The concentration of N vacancies, V_N, behaves the opposite way. This has a strong impact on diffusion. TiN is a prominent diffusion barrier against Cu in microelectronic devices. The diffusion of Cu is mediated by vacancies, since the formation of interstitial Cu costs a large amount of energy (Mühlbacher et al., 2015). In this situation, the knowledge of the vacancy concentration as a function of stoichiometry and temperature is of great importance, since it directly enters the diffusion coefficient. Based on DFT calculations, the vacancy concentrations and diffusion coefficient for Cu through bulk TiN for different compositions have been determined (Bochkarev et al., 2016a): At 1,250 K, it is 0.5 × 10⁻²¹m²/s in the stoichiometric case, while for nitrogen deficient TiN_0.96, it is about 10⁻¹⁸m²/s, which is more than 3 orders of magnitude larger.

FIGURE 3

Figure 3. Concentration of vacancies in TiN as a function of stoichiometry at 1,273 K.

Razumovskiy et al. (2013) have shown that in ZrC and TiC, vacancy clusters are energetically very favorable: While single-metal vacancies have large formation energies of ~8 eV, the removal of C atoms close to the metal vacancy reduces the formation energy. A minimum occurs when all the C atoms in the first coordination shell are removed. The resulting vacancy cluster of one metal vacancy surrounded by six C vacancies has a formation energy of only 3 eV, i.e., 5eV lower than for the isolated metal vacancy. In a later study they also investigated HfC and TiN, ZrN and HfN (Razumovskiy et al., 2015). They showed that all the carbides—but none of the nitrides—tend to form vacancy clusters.

3.2. Vacancies in Random Alloys

In random alloys, the local atomic environment changes from site to site. Take for example a random alloy of atoms A and B on an fcc lattice where each site has 12 nearest neighbors. In the first coordination shell of a given site, anywhere from 0 to 12 A atoms can be present. Consequently, there is not just one vacancy formation energy but a range of these energies, depending on the local environment. A good example is the random alloy Cu_0.5Ni_0.5 investigated in Ruban (2016) and Zhang and Sluiter (2015). Depending on the number of Ni atoms in the nearest-neighbor shell, the vacancy formation energies range from 1.4eV (no Ni in the first coordination shell) to 2.4eV (only Ni in the first coordination shell) (Ruban, 2016): vacancies prefer to be surrounded by Cu atoms.

Dealing with such a wide range of vacancy formation energies means that a proper statistical model is needed (Zhang and Sluiter, 2015; Ruban, 2016). The reason is the following: At 0K, vacancies are created only at the lowest-energy sites. But at finite temperature, entropy causes vacancies to be created at higher-energy sites. A proper thermodynamic description of vacancies in random alloys must include the contribution of the configurational entropy. Ruban (2016) has shown that it has a substantial impact on the calculated vacancy concentrations. In an equiatomic binary alloy, the configurational entropy reduces the concentration of vacancies by a factor of 2 compared to a pure metal, while in a 4-component equi-atomic alloy (often called “high-entropy alloy”), the reduction is by a factor of 4. In Ruban (2016), an effective vacancy formation energy Ē was calculated. It connects the free energy of the system with the concentration of vacancies in a phenomenological way. Ē increases with temperature, but always remains lower than the average vacancy formation energy. This means that using just an average formation energy for describing the thermodynamics of vacancies introduces a considerable error.

Technically, there are 2 main ways to deal with vacancies in random alloys. The first way is to use a cluster expansion approach (Sanchez et al., 1984; Fontaine, 1994), as used e.g., in Van der Ven and Ceder (2005), Muzyk et al. (2011), and Zhang and Sluiter (2015). In this approach, the energetics of an alloy is mapped on an Ising-like Hamiltonian containing the so called effective cluster interactions (ECIs). The ECIs are obtained by fitting the Hamiltonian to a set of ab-initio calculations, typically between 40 and 100. Once the effective cluster interactions are known, the energetics of any kind of local environment can directly be determined. The second way is to describe a random alloy in the single-site mean field approximation, as conveniently done by a Green's function based DFT approach (Peil et al., 2012; Ruban, 2016). In this context, the “Exact-muffin-tin orbital Locally Self-consistent Green's Function” (ELSGF) method is especially useful: It explicitly deals with a cluster of neighboring atoms lying within a local interaction zone, embedded into an effective medium. The ELSGF method allows for calculating random alloys with a proper treatment of local environment effects in a more consistent way compared to the cluster-expansion technique. The cluster expansion, in turn, has the advantage that local lattice relaxations and the vibrational entropy can be included. However it must be handled with care due to its theoretical limitations and certain pitfalls in its practical applications (Ruban and Abrikosov, 2008; Sanchez, 2010).

3.3. Dislocations

The plastic behavior of materials is of fundamental interest for material scientists and engineers. The microscopic mechanism for plasticity is the creation and motion of dislocations in the crystal (Orowan, 1934; Polanyi, 1934; Taylor, 1934). Thus, investigation of the atomistic structure, energetics and mobility of dislocations are of key interest. Dislocations are present in almost all materials since they are the first mechanism to accommodate stress due to mechanical load or temperature changes. They can also be a consequence of material synthesis. Nevertheless, their detailed structure, energetics and mobility are hardly accessible by experiment. So they were naturally a subject of computational materials science since its beginnings 50 years ago, long before electronic structure calculations were feasible for extended unit cells. Simple interatomic potentials have provided important atomistic insight into the possible behavior of extended defects (Vitek, 1968). Over time, the interatomic potentials have become more sophisticated and simulations more complex. But the outcome often depends on the individual potential chosen, making it difficult to draw clear conclusions.

Around the year 2000, the ab-initio methodology and the computer power had reached a level that allowed treating unit cells of hundreds of atoms, leading to the first DFT results on edge (Hartford et al., 1998) and screw dislocations in Mo and Ta (Ismail-Beigi and Arias, 2000; Woodward and Rao, 2001). They latter showed that—in contrast to earlier calculations based on empirical interatomic potentials—these two refractory metals have compact and symmetric bcc screw dislocation cores. This result is in much better agreement with experimental data on the critical stress required to move dislocations.

However, the stress field around a dislocation is long ranged. It is proportional to the inverse of the distance to the dislocation core. Different approaches have emerged to deal with this issue:

The first-principles Green's function boundary condition method (Woodward and Rao, 2002) self-consistently couples the local strain field of the dislocation core to the long-range elastic field, where the local strain field is treated using DFT. This approach has the advantage to treat isolated dislocations with a quantum-mechanical description of the dislocation core. However, the method is complicated and the coupling between different regions tricky to handle.

An easier-to-use alternative is the periodic dipole approach. Supercells containing 2 dislocations running in opposite directions are constructed with no net dislocation dipole moment (Cai et al., 2001). There are two possible setups (Ventelon et al., 2013) of the supercell. The first leads to a triangular (Frederiksen and Jacobsen, 2003) and the second to a quadrupolar (Ismail-Beigi and Arias, 2000; Wang et al., 2003; Li et al., 2004) periodic array of dislocation dipoles. The former strictly preserves the 3-fold symmetry of the bcc lattice, while the latter leads to zero stress at any dislocation center thanks to the resulting square-like superposition of the elastic stress fields (Cai et al., 2003; Clouet et al., 2009). The periodic dipole approach makes the computation of the displacement field and the interaction energy well defined and simple. The approach also allows to calculate directly the Peierls stress. It is the stress required to move a dislocation away from its original place. Within the periodic dipole approach the Peierls stress is obtained by straining the supercell until the dislocation moves (Ventelon and Willaime, 2007; Romaner et al., 2010). Due to its straightforward use and the good results obtained with reasonable supercell sizes (typically one to a few hundred atoms Romaner et al., 2010; Li et al., 2012; Ventelon et al., 2013), this approach is probably the one most widely used today. Care must only be taken if the core is extended, a rather rare situation.

A third alternative is the use of the Peierls-Nabarro model to calculate the dislocation structure and energetics. Using a generalized stacking fault surface obtained from DFT as an input, it has good predictive power (Hartford et al., 1998; Lu et al., 2000).

Finally, there is the atomic row model based on atomic-row displacement energies, originally proposed by Takeuchi (1979). In this approach, the interaction between rows of atoms is the key ingredient. By rigidly shifting atomic rows and evaluating the corresponding changes in total energy, an “interatomic-row” potential can be calculated. Accurate total energies are obtained from first-principles calculations (Medvedeva et al., 2005; Li et al., 2012). The inter-row potential reliably determines the dislocation core structure and symmetry by relaxing the position of each atomic row. The model is interesting from a computational perspective. Indeed, small supercells (8–48 atoms) suffice to fit the inter-atomic row potential (Medvedeva et al., 2005; Gilbert and Dudarev, 2010; Li et al., 2012), while the supercell size for the direct calculation of a dislocation dipole is at least 5 times larger. Ventelon et al. (2013), Romaner et al. (2010), and Li et al. (2012). Since DFT calculations scale as the cube of the number of atoms, this is a substantial savings. However, the interatomic-row potentials are not suitable to calculate the Peierls stress of dislocations.

4. Discussion

The few examples we have discussed here illustrate the many roles of impurities and defects in various materials. Measurements of defect properties can be challenging and produce a rather large scatter in the result. Take the formation energy of a vacancy in metals for example. It depends on the history of the sample and on the experimental technique applied. In this situation, systematic first-principles calculations can deliver results for perfectly defined conditions. This becomes an important complement to experiment.

Today's theory can handle many more issues than just a few years ago, as abundantly illustrated in the other articles in this series. Fueled by the steady increase in computational power, theory can now treat extended defects in supercells containing up to thousands of atoms with first-principles methods, and include the effects of temperature. The early development of theory involved many healthy discussions involving theorists as well as experimentalists about the best way to represent the host crystal, the details of the electronic structure method, the basis set, geometry optimizations, etc. At every step, it is the abundance of experimental data (especially in Si) that has made it possible to reach a consensus and point to specific theoretical failures which needed to be addressed. The possibility to verify many different theoretical results (formation and binding energies, electrical activity, migration paths, vibrational spectra …) with measured data has enabled theorists to sharpen their tools and has fostered new theoretical developments. The interplay between experiment and theory is one key reason why theory has become such a reliable and necessary partner in today's materials science research.

But the world is changing. The materials of interest are no longer bulk Si and wrought iron. Instead, they range from a rapidly increasing number of nanostructures to custom alloys; from Q-bits to thermoelectrics. In some cases miniaturization and control of materials properties on the atomic scale allows to parallel an experiment with a 1:1 atomistic model, treated with the full predictive power of quantum mechanics.

Theorists now have to be concerned with much more than simple total energies and electronic properties at T = 0 K. They have to take into account electron-phonon coupling, various entropy contributions (vibrational, configurational, magnetic, electronic), excited states, and even quantum entanglement. The theory of defects is exciting.

Author Contributions

SKE wrote the section on Theory of defects in semiconductors. JS wrote the section on Theory of defects in metals and metallic compounds. Both authors have contributed to the Introduction and Discussion and reviewed the full manuscript.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

JS gratefully acknowledges the financial support from the Austrian Science Fund (FWF) Project Number P29731, and the COMET program within the K2 Center Integrated Computational Material, Process and Product Engineering (IC-MPPE) (Project No 859480). This program is supported by the Austrian Federal Ministries for Transport, Innovation and Technology (BMVIT) and for Digital and Economic Affairs (BMDW), represented by the Austrian research funding association (FFG), and the federal states of Styria, Upper Austria and Tyrol. Moreover, JS thanks A. Ruban, L. Romaner, and M. Popov for valuable discussions.

Footnotes

1. ^Nuclear Dynamics in Solid Materials: How Phonons and Electron-Phonon Coupling Affect Macroscopic Material Properties by C. Carbogno an R. Ramprasad (to be published in this Research Topic).

2. ^In Korzhavyi et al. (1999), results for all transition metals both in the fcc and bcc structure are presented; moreover, for the magnetic metals (Cr, Mn, Fe, Co, Ni) results for different magnetic states (ferromagnetic, antiferromagnetic, paramagnetic) are reported. The data included in the figure are chosen as follows: for metals which exhibit different crystallographic phases, the results for the phase stable just below the melting point is chosen; for metals with hexagonal structure, the vacancy formation energy of the face-centered-cubic (fcc) phase is used since this phase is very similar to the hexagonal one; for magnetic systems, the result obtained in the paramagnetic phase is taken.

References

Ackland, G. J., Tichy, G., Vitek, V., and Finnis, M. W. (1987). Simple n-body potentials for the noble metals and nickel. Phil. Mag. A 56, 735–756. doi: 10.1080/01418618708204485

CrossRef Full Text | Google Scholar

Bachelet, G. D., Hamann, D. R., and Schlüter, M. (1982). Pseudopotentials that work: From H to Pu. Phys. Rev. B 26, 4199–4228. doi: 10.1103/PhysRevB.26.4199

CrossRef Full Text | Google Scholar

Baraff, G. A., and Schlüter, M. (1983). Total energy of isolated point defects in solids. Phys. Rev. B 28, 2296–2298. doi: 10.1103/PhysRevB.28.2296

CrossRef Full Text | Google Scholar

Bardeen, J., and Brattain, W. H. (1948). The transistor, a semi-conductor triode. Phys. Rev. 74, 230–231. doi: 10.1103/PhysRev.74.230

CrossRef Full Text | Google Scholar

Bardeen, J., and Brattain, W. H. (1949). Physical principles involved in transistor action. Phys. Rev. 75, 1208–1226. doi: 10.1103/PhysRev.75.1208

CrossRef Full Text | Google Scholar

Beeler, F., Andersen, O. K., and Scheffler, M. (1990). Electronic and magnetic structure of 3d–transition-metal point defects in silicon calculated from first principles. Phys. Rev. B 41, 1603–1624. doi: 10.1103/PhysRevB.41.1603

PubMed Abstract | CrossRef Full Text | Google Scholar

Benedek, R., Yang, L. H., Woodward, C., and Min, B. I. (1992). Formation energy and lattice relaxation for point defects in Li and Al. Phys. Rev. B 45, 2607–2612. doi: 10.1103/PhysRevB.45.2607

PubMed Abstract | CrossRef Full Text | Google Scholar

Beuerle, T., Pawellek, P., Elsässer, C., and Elsässer, M. (1991). The influence of the atomic-sphere approximation on the calculation of the vacancy formation energy of Li. J. Phys. 3:1957.

Google Scholar

Blum, V., Gehrke, R., Hanke, F., Havu, P., Havu, V., Ren, X., et al. (2009). Ab initio molecular simulations with numeric atom- centered orbitals. Comp. Phys. Comm. 180, 2175–2196. doi: 10.1016/j.cpc.2009.06.022

CrossRef Full Text | Google Scholar

Bochkarev, A. S., Popov, M. N., Razumovskiy, V. I., Spitaler, J., and Puschnig, P. (2016a). Ab initio study of cu impurity diffusion in bulk tin. Phys. Rev. B 94:104303. doi: 10.1103/PhysRevB.94.104303

CrossRef Full Text | Google Scholar

Bochkarev, A. S., Zamulko, S. O., Gorbatov, O. I., Sidorenko, S. I., Puschnig, P., and Ruban, A. V. (2016b). A single-volume approach for vacancy formation thermodynamics calculations. Europhys. Lett. 116:16001. doi: 10.1209/0295-5075/116/16001

CrossRef Full Text | Google Scholar

Cai, W., Bulatob, V. V., Chang, J., Li, J., and Yip, S. (2003). Periodic image effects in dislocation modelling. Phil. Mag. 83, 539–567. doi: 10.1080/0141861021000051109

CrossRef Full Text | Google Scholar

Cai, W., Bulatov, V. V., Chang, J., Li, J., and Yip, S. (2001). Anisotropic elastic interactions of a periodic dislocation array. Phys. Rev. Lett. 86:5727. doi: 10.1103/PhysRevLett.86.5727

PubMed Abstract | CrossRef Full Text | Google Scholar

Carling, K., Wahnstrom, G., Mattsson, T. R., Mattsson, A, E., Sandberg, N., and Grimvall, G. (2000). Vacancies in metals: from first-principles calculations to experimental data. Phys. Rev. Lett. 85, 3862–3865. doi: 10.1103/PhysRevLett.85.3862

PubMed Abstract | CrossRef Full Text | Google Scholar

Chelikowsky, J. (2002a). Silicon in all its forms. MRS Bull. 27, 951–960. doi: 10.1557/mrs2002.301

CrossRef Full Text | Google Scholar

Chelikowsky, J. (2002b). Why silicon is the benchmark. Mater. Today 5:64. doi: 10.1016/S1369-7021(02)00664-8

CrossRef Full Text | Google Scholar

Chen, E. E., Stavola, M., and Beall Fowler, W. (2002). Ortho- and para- O-H₂ complexes in Si. Phys. Rev. B 65:245208. doi: 10.1103/PhysRevB.65.245208

CrossRef Full Text | Google Scholar

Clouet, E., Ventelon, L., and Willaime, F. (2009). Dislocation core energies and core fields from first principles. Phys. Rev. Lett 102:055502. doi: 10.1103/PhysRevLett.102.055502

PubMed Abstract | CrossRef Full Text | Google Scholar

DeLeo, G. G., Watkins, G. D., and Beall Fowler, W. (1982). Level positions of interstitial transition-metal impurities in silicon. Phys. Rev. B 25, 4972–4980. doi: 10.1103/PhysRevB.25.4972

CrossRef Full Text | Google Scholar

DeLeo, G. G., Watkins, G. D., and Beall Fowler, W. (1988). Relationship between the pseudo-jahn-teller effect and chemical rebonding. Phys. Rev. B 37, 1013–1015. doi: 10.1103/PhysRevB.37.1013

PubMed Abstract | CrossRef Full Text | Google Scholar

DeLeo, G. G., Watkins, G. D., and Beall Fowler, W. B. (1981). Theory of interstitial transition-metal impurities in silicon. Phys. Rev. B 23, 1851–1858. doi: 10.1103/PhysRevB.23.1851

CrossRef Full Text | Google Scholar

Dengg, T., Razumovskiy, V., Romaner, L., Kresse, G., Puschnig, P., and Spitaler, J. (2017). Thermal expansion coefficient of WRe alloys from first principles. Phys. Rev. B 96:035148. doi: 10.1103/PhysRevB.96.035148

CrossRef Full Text | Google Scholar

Dirac, P. A. M. (1929). Quantum mechanics of many-electron systems. Proc. R. Soc. Lond. A 123, 714–733. doi: 10.1098/rspa.1929.0094

CrossRef Full Text | Google Scholar

Drabold, D. A., and Estreicher, S. K. (ed.). (2007). Theory of Defects in Semiconductors. Berlin: Springer.

Google Scholar

Ehrhart, P., Jung, P., and Schultz, H. (1991). Atomic Defects in Metals / Atomare Fehlstellen in Metallen, Vol. 25. Berlin: Springer.

Ergönenc, Z., Kim, B., Liu, P., Kresse, G., and Franchini, C. (2018). Converged GW quasiparticle energies for transition metal oxide perovskites. Phys. Rev. Mat. 2:024601. doi: 10.1103/PhysRevMaterials.2.024601

CrossRef Full Text | Google Scholar

Estle, T. L., Estreicher, S. K., and Marynick, D. S. (1986). Preliminary calculations confirming that anomalous muonium in diamond and silicon is bond-centered interstitial muonium. Hyp. Inter. 32, 637–639. doi: 10.1007/BF02394968

CrossRef Full Text | Google Scholar

Estle, T. L., Estreicher, S. K., and Marynick, D. S. (1987). Bond-centered hydrogen or muonium in diamond: the explanation for anomalous muonium and an example of metastability. Phys. Rev. Lett. 58, 1547–1550. doi: 10.1103/PhysRevLett.58.1547

PubMed Abstract | CrossRef Full Text | Google Scholar

Estreicher, S. K. (1995). Hydrogen-related defects in crystalline semiconductors: a theorist's perspective. Mater. Sci. Engr. R 14:319. doi: 10.1016/0927-796X(95)00178-6

CrossRef Full Text | Google Scholar

Estreicher, S. K., Backlund, D. J., Carbogno, C., and Scheffler, M. (2011). Activation energies for diffusion of defects in silicon: the role of the exchange-correlation functional. Angew. Chem. 50, 10221–10225. doi: 10.1002/anie.201100733

PubMed Abstract | CrossRef Full Text | Google Scholar

Estreicher, S. K., Gibbons, T. M., and Bebek, M. B. (2015). Thermal phonons and defects in semiconductors: the physical reason why defects reduce heat flow, and how to control it. J. Appl. Phys. 117:112801. doi: 10.1063/1.4913826

CrossRef Full Text | Google Scholar

Estreicher, S. K., Sanati, M., West, D., and Ruymgaart, F. (2004). Thermodynamics of impurities in semiconductors. Phys. Rev. B 70:125209. doi: 10.1103/PhysRevB.70.125209

CrossRef Full Text | Google Scholar

Fermi, E. (1934). Sopra lo spostamento per pressione delle righe elevate delle serie spettrali. Il Nuovo Cim. (1924-1942), 11:157. doi: 10.1007/BF02959829

CrossRef Full Text | Google Scholar

Fontaine, D. D. (1994). “Cluster approach to order-disorder transformations in alloys,” in Solid State Physics, 47, 33–176.

Google Scholar

Frederiksen, S. L., and Jacobsen, K. W. (2003). Density functional theory studies of screw dislocation core structures in bcc metals. Phil. Mag. 83:365. doi: 10.1080/0141861021000034568

CrossRef Full Text | Google Scholar

Freysoldt, C., Grabowski, B., Hickel, T., Neugebauer, J., Kresse, G., Janotti, A., et al. (2014). First-principles calculations for point defects in solids. Rev. Mod. Phys. 86, 253–305. doi: 10.1103/RevModPhys.86.253

CrossRef Full Text | Google Scholar

Freysoldt, C., Neugebauer, J., and Van de Walle, C. G. (2009). Fully ab initio finite-size corrections for charged-defect supercell calculations. Phys. Rev. Lett. 102:016402. doi: 10.1103/PhysRevLett.102.016402

PubMed Abstract | CrossRef Full Text | Google Scholar

Ghorai, A. (1991). Calculation of some defect parameters in fcc metals. Phys. Stat. Sol. B 167, 551–560. doi: 10.1002/pssb.2221670217

CrossRef Full Text | Google Scholar

Gibbons, T. M., Bebek, M. B., Kang, B., Stanley, C. M., and Estreicher, S. K. (2015). Phonon-phonon interactions: first principles theory. J. Appl. Phys. 118:085103. doi: 10.1063/1.4929452

CrossRef Full Text | Google Scholar

Gibbons, T. M., Estreicher, S. K., Potter, K., Bekisli, F., and Stavola, M. (2013). Huge isotope effect on the vibrational lifetime of an H₂*(C) defect in si. Phys. Rev. B 87:115207. doi: 10.1103/PhysRevB.87.115207

CrossRef Full Text | Google Scholar

Gilbert, M. R., and Dudarev, S. L. (2010). Ab initio multi-string Frenkel-Kontorova model for a b = a/2[111] screw dislocation in bcc iron. Phil. Mag. 90:1035. doi: 10.1080/14786430903049104

CrossRef Full Text | Google Scholar

Giustino, F. (2017). Electron-phonon interactions from first principles. Rev. Mod. Phys. 89:015003. doi: 10.1103/RevModPhys.89.015003

CrossRef Full Text | Google Scholar

Glensk, A., Grabowski, B., Hickel, T., and Neugebauer, J. (2014). Breakdown of the Arrhenius law in describing vacancy formation energies: the importance of local anharmonicity revealed by ab initio thermodynamics. Phys. Rev. X 4:011018. doi: 10.1103/PhysRevX.4.011018

CrossRef Full Text | Google Scholar

Grabowski, B., Ismer, L., Hickel, T., and Neugebauer, J. (2009). Ab initio up to the melting point: anharmonicity and vacancies in aluminum. Phys. Rev. B 79:134106. doi: 10.1103/PhysRevB.79.134106

CrossRef Full Text | Google Scholar

Grimvall, G. (1999). Thermophysical Properties of Materials. Amsterdam: Elsevier Science B.V.

Google Scholar

Gunnarsson, O., Jepsen, O., and Andersen, O. K. (1983). Self-consistent impurity calculations in the atomic-spheres approximation. Phys. Rev. B 27, 7144–7168. doi: 10.1103/PhysRevB.27.7144

CrossRef Full Text | Google Scholar

Gusev, A. I. (2014). Nonstoichiometry and superstructures. Phys. Uspekhi 57:839. doi: 10.3367/UFNe.0184.201409a.0905

CrossRef Full Text | Google Scholar

Haller, E. E. (2006). Germanium: from its discovery to SiGe devices. Mater. Sci. Semiconduct. Process. 9, 408–422. doi: 10.1016/j.mssp.2006.08.063

CrossRef Full Text | Google Scholar

Hamann, D. R., Schlüter, M., and Chiang, C. (1979). Norm-conserving pseudopotentials. Phys. Rev. Lett. 43, 1494–1497. doi: 10.1103/PhysRevLett.43.1494

CrossRef Full Text | Google Scholar

Harder, J. M., and Bacon, D. J. (1986). Point-defect and stacking-fault properties in body-centred-cubic metals with n-body interatomic potentials. Phil. Mag. A 54, 651–661. doi: 10.1080/01418618608244024

CrossRef Full Text | Google Scholar

Hartford, J., von Sydow, B., Wahnstrom, G., and Lundqvist, B. I. (1998). Peierls barriers and stresses for edge dislocations in Pd and Al calculated from first principles. Phys. Rev. B 58, 2487–2496. doi: 10.1103/PhysRevB.58.2487

CrossRef Full Text | Google Scholar

Hehenkamp, T. (1994). Absolute vacancy concentrations in noble metals and some of their alloys. J. Phys. Chem. Sol. 55, 907–915. doi: 10.1016/0022-3697(94)90110-4

CrossRef Full Text | Google Scholar

Hellman, O., Steneteg, P., Abrikosov, I. A., and Simak, S. I. (2013). Temperature dependent effective potential method for accurate free energy calculations of solids. Phys. Rev. B 87:104111. doi: 10.1103/PhysRevB.87.104111

CrossRef Full Text | Google Scholar

Henkelman, G., and Jonsson, H. (2000). Improved tangent estimate in the nudged elastic band method for finding minimum energy paths and saddle points. J. Chem. Phys. 113, 9978–9985. doi: 10.1063/1.1323224

CrossRef Full Text | Google Scholar

Henkelman, G., Uberuaga, B. P., and Jonsson, H. (2000). A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J. Chem. Phys. 113, 9901–9904. doi: 10.1063/1.1329672

CrossRef Full Text | Google Scholar

Hong, D., Bharat, M., Wei, C., Persson, K. A., Haranczyk, M., and Asta, M. (2015). PyDII: a python framework for computing equilibrium intrinsic point defect concentrations and extrinsic solute site preferences in intermetallic compounds. Comp. Phys. Commun. 193, 118–123. doi: 10.1016/j.cpc.2015.03.015

CrossRef Full Text | Google Scholar

Ismail-Beigi, S., and Arias, T. A. (2000). Ab initio study of screw dislocations in Mo and Ta: a new picture of plasticity in bcc transition metals. Phys. Rev. Lett. 84, 1499–1502. doi: 10.1103/PhysRevLett.84.1499

PubMed Abstract | CrossRef Full Text | Google Scholar

Istratov, A. A., Flink, C., Hieslmair, H., Weber, E. R., and Heiser, T. (1998). Intrinsic diffusion coefficient of interstitial copper in silicon. Phys. Rev. Lett. 81, 1243–1246. doi: 10.1103/PhysRevLett.81.1243

CrossRef Full Text | Google Scholar

Jahn, H. A., and Teller, E. (1937). Stability of polyatomic molecules in degenerate electronic states. I. orbital degeneracy. Proc. R. Soc. Lond. A 161, 220–235. doi: 10.1098/rspa.1937.0142

CrossRef Full Text | Google Scholar

Jarvis, M. R., White, I. D., Godby, R. W., and Payne, M. C. (1997). Supercell technique for total-energy calculations of finite charged and polar systems. Phys. Rev. B 56, 14972–14978. doi: 10.1103/PhysRevB.56.14972

CrossRef Full Text | Google Scholar

Jones, R. O. (2015). Density functional theory: Its origins, rise to prominence, and future. Rev. Mod. Phys. 87, 897–923. doi: 10.1103/RevModPhys.87.897

CrossRef Full Text | Google Scholar

Kang, B., and Estreicher, S. K. (2014). Thermal conductivity of Si nanowires: a first-principles analysis of the role of defects. Phys. Rev. B 89:155409. doi: 10.1103/PhysRevB.89.155409

CrossRef Full Text | Google Scholar

Katayama-Yoshida, H., and Zunger, A. (1985). Chemical trends in ground- and excited-state properties of interstitial 3d impurities in silicon. Phys. Rev. B 31, 8317–8320. doi: 10.1103/PhysRevB.31.8317

PubMed Abstract | CrossRef Full Text | Google Scholar

Kissinger, G., and Pizzini, S. (ed.). (2015). Silicon, Germanium, and Their Alloys: Growth, Defects, Impurities, and Nanocrystals. Boca Raton, FL: CRC Press.

Google Scholar

Kittel, C. (2005). Introduction to Solid State Physics, 8th Edn. Hoboken, NJ: Wiley.

Kleinman, L., and Bylander, D. M. (1982). Efficacious form for model pseudopotentials. Phys. Rev. Lett. 48, 1425–1428. doi: 10.1103/PhysRevLett.48.1425

CrossRef Full Text | Google Scholar

Kohn, W. (1999). Electronic structure of matter: wave functions and density functionals. Rev. Mod. Phys. 71, 1253–1266. doi: 10.1103/RevModPhys.71.1253

CrossRef Full Text | Google Scholar

Kohn, W., and Sham, L. J. (1965). Self-consistent equations including exchange and correlation effects. Phys. Rev. 140, A1133–A1138. doi: 10.1103/PhysRev.140.A1133

CrossRef Full Text | Google Scholar

Kornblit, L. (1981). Single vacancy formation energies in bcc metals. Physica B+C 106, 351–355. doi: 10.1016/0378-4363(81)90064-4

CrossRef Full Text | Google Scholar

Korzhavyi, P. A., Abrikosov, I. A., Johansson, B., Ruban, A. V., and Skriver, H. L. (1999). First-principles calculations of the vacancy formation energy in transition and noble metals. Phys. Rev. B 59:11693. doi: 10.1103/PhysRevB.59.11693

CrossRef Full Text | Google Scholar

Koster, G. F., and Slater, J. C. (1954a). Simplified impurity calculation. Phys. Rev. 96, 1208–1223. doi: 10.1103/PhysRev.96.1208

CrossRef Full Text | Google Scholar

Koster, G. F., and Slater, J. C. (1954b). Wave functions for impurity levels. Phys. Rev. 95, 1167–1176. doi: 10.1103/PhysRev.95.1167

CrossRef Full Text | Google Scholar

Kraftmakher, Y. (1998). Equilibrium vacancies and thermophysical properties of metals. Phys. Rep. 299, 79–188. doi: 10.1016/S0370-1573(97)00082-3

CrossRef Full Text | Google Scholar

Krause, U., Kuska, J. P., and Wedell, R. (1989). Monovacancy formation energies in cubic crystals. Phys. Stat. Sol. B 151, 479–494. doi: 10.1002/pssb.2221510208

CrossRef Full Text | Google Scholar

Lany, S., and Zunger, A. (2008). Assessment of correction methods for the band-gap problem and for finite-size effects in supercell defect calculations: case studies for ZnO and GaAs. Phys. Rev. B 78:235104. doi: 10.1103/PhysRevB.78.235104

CrossRef Full Text | Google Scholar

Lejaeghere, K., V. Van Speybroeck, V., Van Oost, G., and Cottenier, S. (2013). Error estimates for solid-state density-functional theory predictions: an overview by means of the ground-state elemental crystals. Crit. Rev. Solid State Mater. Sci. 39, 1–24. doi: 10.1080/10408436.2013.772503

CrossRef Full Text | Google Scholar

Leslie, M., and Gillan, N. J. (1985). The energy and elastic dipole tensor of defects in ionic crystals calculated by the supercell method. J. Phys. C 18:973.

Google Scholar

Li, H., Wurster, S., Motz, C., Romaner, L., Ambrosch-Draxl, C., and Pippan, R. (2012). Dislocation-core symmetry and slip planes in tungsten alloys: Ab initio calculations and microcantilever bending experiments. Acta Mater. 60:748. doi: 10.1016/j.actamat.2011.10.031

CrossRef Full Text | Google Scholar

Li, J., Wang, C. Z., Chang, J. P., Cai, W., Bulatov, V. V., Ho, K. M., et al. (2004). Core energy and Peierls stress of a screw dislocation in bcc molybdenum: a periodic-cell tight-binding study. Phys. Rev. B 70:104113. doi: 10.1103/PhysRevB.70.104113

CrossRef Full Text | Google Scholar

Lu, G., Kioussis, N., Bulatov, V. V., and Kaxiras, E. (2000). Generalized-stacking-fault energy surface and dislocation properties of aluminum. Phys. Rev. B 62, 3099–3108. doi: 10.1103/PhysRevB.62.3099

CrossRef Full Text | Google Scholar

Lucero, M. J., Henderson, T. M., and Scuseria, G. E. (2012). Improved semiconductor lattice parameters and band gaps from a middle-range screened hybrid exchange functional. J. Phys. 24:145504. doi: 10.1088/0953-8984/24/14/145504

PubMed Abstract | CrossRef Full Text | Google Scholar

Luepke, G., Tolk, N. H., and Feldman, L. C. (2003). Vibrational lifetimes of hydrogen in silicon. J. Appl. Phys. 93, 2317–2336. doi: 10.1063/1.1517166

CrossRef Full Text | Google Scholar

Makov, G., and Payne, M. C. (1995). Periodic boundary conditions in ab initio calculations. Phys. Rev. B 51, 4014–4022. doi: 10.1103/PhysRevB.51.4014

PubMed Abstract | CrossRef Full Text | Google Scholar

Makov, G., Shah, R., and Payne, M. C. (1996). Periodic boundary conditions in ab initio calculations. II. Brillouin-zone sampling for aperiodic systems. Phys. Rev. B 53, 15513–15517. doi: 10.1103/PhysRevB.53.15513

PubMed Abstract | CrossRef Full Text | Google Scholar

Mattsson, A. E., Schultz, P. A., Desjarlais, M. P., Mattsson, T. R., and Leung, K. (2004). Designing meaningful density functional theory calculations in materials science: a primer. Model. Simul. Mat. Sci. Engr. 13, R1–R31. doi: 10.1088/0965-0393/13/1/R01

CrossRef Full Text | Google Scholar

McCluskey, M. D., and Haller, E. E. (2012). Dopants and Defects in Semiconductors. Boca Raton, FL: CRC Press.

Google Scholar

Medvedeva, N. I., Gornostyrev, Y. N., and Freeman, A. J. (2005). Solid solution softening in bcc Mo alloys: effect of transition-metal additions on dislocation structure and mobility. Phys. Rev. B 72:134107. doi: 10.1103/PhysRevB.72.134107

CrossRef Full Text | Google Scholar

Mehl, M. J., and Klein, B. M. (1991). All-electron first-principles supercell total-energy calculation of the vacancy formation energy in aluminium. Physica B 172, 211–215. doi: 10.1016/0921-4526(91)90433-F

CrossRef Full Text | Google Scholar

Messmer, R. P., and Watkins, G. D. (1970). Linear combination of atomic orbital-molecular orbital treatment of the deep defect level in a semiconductor: nitrogen in diamond. Phys. Rev. Lett. 25, 656–659. doi: 10.1103/PhysRevLett.25.656

CrossRef Full Text | Google Scholar

Messmer, R. P., and Watkins, G. D. (1973). Calculations of Defects in the Diamond Lattice. London: IoP Press.

Meyer, B., and Fähnle, M. (1997). Ab initio calculation of the formation energy and the formation volume of monovacancies in Mo. Phys. Rev. B 56:13595. doi: 10.1103/PhysRevB.56.13595

CrossRef Full Text | Google Scholar

Miro, J., Deak, P., Ewels, C. P., and Jones, R. (1997). Cyclic cluster model for calculating defects in solids using the local density approximation. J. Phys. 9:9555.

Google Scholar

Monkhorst, H. J., and Pack, D. J. (1976). Special points for brillouin-zone integrations. Phys. Rev. B 13, 5188–5192. doi: 10.1103/PhysRevB.13.5188

CrossRef Full Text | Google Scholar

Mosig, K., Wolff, J., Kluin, J.-E., and Hehenkamp, T. (1992). Investigation of the equilibrium concentration of lattice vacancies in silver and dilute silver-tin alloys with a differential dilatometer. J. Phys. 4:1447.

Google Scholar

Mühlbacher, M., Bochkarev, A. S., Mendez-Martin, F., Sartory, B., Chitu, L., Popov, M. N., et al. (2015). Cu diffusion in single-crystal and polycrystalline TiN barrier layers: a high-resolution experimental study supported by first-principles calculations. J. Appl. Phys. 118:085307. doi: 10.1063/1.4929446

CrossRef Full Text | Google Scholar

Muro, K., and Sievers, A. J. (1986). Proton tunneling with millielectrovolt energies at the Be-H acceptor complex in silicon. Phys. Rev. Lett. 57, 897–900. doi: 10.1103/PhysRevLett.57.897

PubMed Abstract | CrossRef Full Text | Google Scholar

Muzyk, M., Nguyen-Manh, D., Kurzydłowski, K. J., Baluc, N. L., and Dudarev, S. L. (2011). Phase stability, point defects, and elastic properties of W-V and W-Ta alloys. Phys. Rev. B 84:104115. doi: 10.1103/PhysRevB.84.104115

CrossRef Full Text | Google Scholar

Nazarov, R., Hickel, T., and Neugebauer, J. (2012). Vacancy formation energies in fcc metals: influence of exchange-correlation functionals and correction schemes. Phys. Rev. B 85:144118. doi: 10.1103/PhysRevB.85.144118

CrossRef Full Text | Google Scholar

Nieminen, N. M. (2007). “Supercell methods for defect calculations,” in Theory of Defects in Semiconductors, eds D. A. Drabold and S. K. Estreicher (Berlin: Springer), 29–68.

Google Scholar

Orowan, E. (1934). Zur kristallplastizität. i. Zeitschrift für Physik 89, 605–613. doi: 10.1007/BF01341478

CrossRef Full Text | Google Scholar

Overhof, H., and Weihrich, H. (1997). Ab initio total-energy calculations for iron-acceptor pairs in silicon. Phys. Rev. B 55, 10508–10514. doi: 10.1103/PhysRevB.55.10508

CrossRef Full Text | Google Scholar

Pacchioni, G., Frigoli, F., Ricci, D., and Weil, J. A. (2000). Theoretical description of hole localization in a quartz Al center: the importance of exact electron exchange. Phys. Rev. B 63:054102. doi: 10.1103/PhysRevB.63.054102

CrossRef Full Text | Google Scholar

Pantelides, S. T. (1978). The electronic structure of impurities and other point defects in semiconductors. Rev. Mod. Phys. 50, 797–858. doi: 10.1103/RevModPhys.50.797

CrossRef Full Text | Google Scholar

Pantelides, S. T. (ed.). (1986). Deep Centers in Semiconductors. New York, NY: Gordon and Breach.

Google Scholar

Pantelides, S. T., Harrison, W. A., and Yndurain, F. (1988). Pseudo-jahn-teller effect and chemical rebonding: two distinct physical phenomena. Phys. Rev. B 37, 1016–1018. doi: 10.1103/PhysRevB.37.1016

PubMed Abstract | CrossRef Full Text | Google Scholar

Papanikolaou, N., Zeller, R., Dederichs, P. H., and Stefanou, N. (1997). Lattice distortion in Cu-based dilute alloys: a first-principles study by the KKR Green-function method. Phys. Rev. B 55:4157. doi: 10.1103/PhysRevB.55.4157

CrossRef Full Text | Google Scholar

Pauli, W. (1931). Letter to Peierls. Ann Arbor, MI.

Pearton, S. J., Corbett, J. W., and Stavola, M. (1992). Hydrogen in Crystalline Semiconductors. Berlin: Springer-Verlag.

Google Scholar

Peierls, R. (1929). Zur kinetischen Theorie der Wärmeleitung in Kristallen. Annalen der Physik 395, 1055–1101. doi: 10.1002/andp.19293950803

CrossRef Full Text | Google Scholar

Peil, O. E., Ruban, A. V., and Johansson, B. (2012). Self-consistent supercell approach to alloys with local environment effects. Phys. Rev. B 85:165140. doi: 10.1103/PhysRevB.85.165140

CrossRef Full Text | Google Scholar

Perdew, J. P., Burke, K., and Ernzerhof, M. (1996a). Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868. doi: 10.1103/PhysRevLett.77.3865

PubMed Abstract | CrossRef Full Text | Google Scholar

Perdew, J. P., Ernzerhof, M., and Burke, K. (1996b). Rationale for mixing exact exchange with density functional approximations. J. Chem. Phys. 105, 9982–9985. doi: 10.1063/1.472933

CrossRef Full Text | Google Scholar

Phillips, J. C., and Kleinman, L. (1959). New method for calculating wave functions in crystals and molecules. Phys. Rev. 116, 287–294. doi: 10.1103/PhysRev.116.287

CrossRef Full Text | Google Scholar

Planck, M., Debye, P. J. W., Nernst, W., Smoluchowski, M., Sommerfeld, A., and Lorentz, H. A. (1914). Vorträge über die kinetische Theorie der Materie und der Elektrizität. Leipzig: Teubner.

Pochapsky, T. E. (1953). Heat capacity and resistance measurements for aluminum and lead wires. Acta Metallurgica 1, 747–751. doi: 10.1016/0001-6160(53)90034-0

CrossRef Full Text | Google Scholar

Polanyi, M. (1934). Über eine art gitterstörung, die einen kristall plastisch machen könnte. Zeitschrift für Physik 89, 660–664. doi: 10.1007/BF01341481

CrossRef Full Text | Google Scholar

Pruneda, J. M., Estreicher, S. K., Junquera, J., Ferrer, J., and Ordejón, P. (2002). Ab initio local vibrational modes of light impurities in silicon. Phys. Rev. B 65:075210. doi: 10.1103/PhysRevB.65.075210

CrossRef Full Text | Google Scholar

Razumovskiy, V. I., Popov, M. N., Ding, H., and Odqvist, J. (2015). Formation and interaction of point defects in group {IVb} transition metal carbides and nitrides. Comp. Mat. Sci. 104, 147–154. doi: 10.1016/j.commatsci.2015.03.042

CrossRef Full Text | Google Scholar

Razumovskiy, V. I., Ruban, A. V., Odqvist, J., and Korzhavyi, P. A. (2013). Vacancy-cluster mechanism of metal-atom diffusion in substoichiometric carbides. Phys. Rev. B 87:054203. doi: 10.1103/PhysRevB.87.054203

CrossRef Full Text | Google Scholar

Roberson, M. A., and Estreicher, S. K. (1994). Vacancy and vacancy-hydrogen complexes in silicon. Phys. Rev. B 49, 17040–17049. doi: 10.1103/PhysRevB.49.17040

PubMed Abstract | CrossRef Full Text | Google Scholar

Romaner, L., Ambrosch-Draxl, C., and Pippan, R. (2010). Effect of rhenium on the dislocation core structure in tungsten. Phys. Rev. Lett. 104:195503. doi: 10.1103/PhysRevLett.104.195503

PubMed Abstract | CrossRef Full Text | Google Scholar

Rosato, V., Guillope, M., and Legrand, B. (1989). Thermodynamical and structural properties of fcc transition metals using a simple tight-binding model. Phil. Mag. A 59, 321–336. doi: 10.1080/01418618908205062

CrossRef Full Text | Google Scholar

Ruban, A. V. (2016). Thermal vacancies in random alloys in the single-site mean-field approximation. Phys. Rev. B 93:134115. doi: 10.1103/PhysRevB.93.134115

CrossRef Full Text | Google Scholar

Ruban, A. V., and Abrikosov, I. A. (2008). Configurational thermodynamics of alloys from first-principles: effective cluster interactions. Rep. Prog. Phys. 71:046501. doi: 10.1088/0034-4885/71/4/046501

CrossRef Full Text | Google Scholar

Sanchez, J. M. (2010). Cluster expansion and the configurational theory of alloys. Phys. Rev. B 81:224202. doi: 10.1103/PhysRevB.81.224202

CrossRef Full Text | Google Scholar

Sanchez, J. M., Ducastelle, F., and Gratias, D. (1984). Generalized cluster description of multicomponent systems. Physica A 128, 334–350. doi: 10.1016/0378-4371(84)90096-7

CrossRef Full Text | Google Scholar

Schultz, P. A. (1999). Local electrostatic moments and periodic boundary conditions. Phys. Rev. B 60, 1551–1554. doi: 10.1103/PhysRevB.60.1551

CrossRef Full Text | Google Scholar

Shimura, F. (ed.). (1994). Oxygen in Silicon. Boston, MA: Academic.

Google Scholar

Shockley, W. (1949). The theory of p-n junctions in semiconductors and p-n junction transistors. Bell Sys. Techn. J. 28, 453–489. doi: 10.1002/j.1538-7305.1949.tb03645.x

CrossRef Full Text

Simmons, R. O., and Balluffi, R. W. (1960). Measurements of equilibrium vacancy concentrations in aluminum. Phys. Rev. 117, 52–61. doi: 10.1103/PhysRev.117.52

CrossRef Full Text | Google Scholar

Stanley, C. M., and Estreicher, S. K. (2018). Phonon dynamics at an oxide layer in silicon: heat flow and Kapitza resistance. Phys. Stat. Sol. A. doi: 10.1002/pssa.201800428. [Epub a head of print].

CrossRef Full Text | Google Scholar

Stavola, M., Chen, E. E., Beall Fowler, W., and Chi, G. A. (2003). Interstitial H₂ in Si: are all the problems solved? Physica B 340–342:58. doi: 10.1016/j.physb.2003.09.002

CrossRef Full Text | Google Scholar

Stoneham, A. M. (2001). Theory of Defects in Solids: Electronic Structure of Defects in Insulators and Semiconductors. Oxford classic texts in the physical sciences. Oxford: Clarendon Press.

Google Scholar

Sun, B., Shi, G. A., Nageswara Rao, S. V. S., Stavola, M., Tolk, N. H., Dixit, S. K., et al. (2006). Vibrational lifetimes and frequency-gap law of hydrogen bending modes in semiconductors. Phys. Rev. Lett. 96:035501. doi: 10.1103/PhysRevLett.96.035501

PubMed Abstract | CrossRef Full Text | Google Scholar

Swartz, E. T., and Pohl, R. O. (1989). Thermal boundary resistance. Rev. Mod. Phys. 61, 605–668. doi: 10.1103/RevModPhys.61.605

CrossRef Full Text | Google Scholar

Takeuchi, S. (1979). Core structure of a screw dislocation in the b.c.c lattice and its relation to slip behaviour of α iron. Phil. Mag. A 39:661. doi: 10.1080/01418617908239296

CrossRef Full Text | Google Scholar

Taylor, G. I. (1934). The mechanism of plastic deformation of crystals. part I. Theoretical. Proc. R. Soc. Lond. A 145, 362–387. doi: 10.1098/rspa.1934.0106

CrossRef Full Text | Google Scholar

Triftshäuser, W. (1975). Positron trapping in solid and liquid metals. Phys. Rev. B 12, 4634–4639. doi: 10.1103/PhysRevB.12.4634

CrossRef Full Text | Google Scholar

Van de Walle, C., Bar-Yam, Y., and Pantelides, S. T. (1988). Theory of hydrogen diffusion and reactions in crystalline silicon. Phys. Rev. Lett. 60, 2761–2764. doi: 10.1103/PhysRevLett.60.2761

PubMed Abstract | CrossRef Full Text | Google Scholar

Van de Walle, C. G., Laks, D. B., Neumark, G. F., and Pantelides, S. T. (1993). First-principles calculations of solubilities and doping limits: Li, Na, and N in ZnSe. Phys. Rev. B 47, 9425–9434. doi: 10.1103/PhysRevB.47.9425

PubMed Abstract | CrossRef Full Text | Google Scholar

Van der Ven, A., and Ceder, G. (2005). Vacancies in ordered and disordered binary alloys treated with the cluster expansion. Phys. Rev. B 71:054102. doi: 10.1103/PhysRevB.71.054102

CrossRef Full Text | Google Scholar

Vanderbilt, D. (1990). Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B 41, 7892–7895. doi: 10.1103/PhysRevB.41.7892

PubMed Abstract | CrossRef Full Text | Google Scholar

Ventelon, L., and Willaime, F. (2007). Core structure and Peierls potential of screw dislocations in α-Fe from first principles: cluster versus dipole approaches. J. Computer-Aided Mater. Des. 14:85. doi: 10.1007/s10820-007-9064-y

CrossRef Full Text | Google Scholar

Ventelon, L., Willaime, F., Clouet, E., and Rodney, D. (2013). Ab initio investigation of the peierls potential of screw dislocations in bcc Fe and W. Acta Mater. 61, 3973–3985. doi: 10.1016/j.actamat.2013.03.012

CrossRef Full Text | Google Scholar

Vitek, V. (1968). Intrinsic stacking faults in body-centred cubic crystals. Phil. Mag. 18, 773–786. doi: 10.1080/14786436808227500

CrossRef Full Text | Google Scholar

Wang, G., Strachan, A., Çagın, T., and Goddard, W. A. (2003). Role of core polarization curvature of screw dislocations in determining the peierls stress in bcc Ta: a criterion for designing high-performance materials. Phys. Rev. B 67:140101(R). doi: 10.1103/PhysRevB.67.140101

CrossRef Full Text | Google Scholar

Watkins, G. D. (1995). Comment on “resonant bonds in symmetry-lowering distortion around a silicon divacancy”. Phys. Rev. Lett. 74, 4353–4353. doi: 10.1103/PhysRevLett.74.4353

PubMed Abstract | CrossRef Full Text | Google Scholar

West, D., and Estreicher, S. K. (2006). First-principles calculations of vibrational lifetimes and decay channels: hydrogen-related modes in Si. Phys. Rev. Lett. 96:115504. doi: 10.1103/PhysRevLett.96.115504

PubMed Abstract | CrossRef Full Text | Google Scholar

West, D., and Estreicher, S. K. (2007). Isotope dependence of the vibrational lifetimes of light impurities in Si from first principles. Phys. Rev. B 75:075206. doi: 10.1103/PhysRevB.75.075206

CrossRef Full Text | Google Scholar

Woodward, C., Asta, M., Kresse, G., and Hafner, J. (2001). Density of constitutional and thermal point defects in L1₂ Al₃Sc. Phys. Rev. B 63:094103. doi: 10.1103/PhysRevB.63.094103

CrossRef Full Text | Google Scholar

Woodward, C., and Rao, S. I. (2001). Ab-initio simulation of isolated screw dislocations in bcc Mo and Ta. Phil. Mag. A 81:1305. doi: 10.1080/01418610108214442

CrossRef Full Text | Google Scholar

Woodward, C., and Rao, S. I. (2002). Flexible ab initio boundary conditions: simulating isolated dislocations in bcc Mo and Ta. Phys. Rev. Lett. 88:216402. doi: 10.1103/PhysRevLett.88.216402

PubMed Abstract | CrossRef Full Text | Google Scholar

Woon, D. E., Marynick, D. S., and Estreicher, S. K. (1992). Titanium and copper in Si: barriers for diffusion and interactions with hydrogen. Phys. Rev. B 45, 13383–13389. doi: 10.1103/PhysRevB.45.13383

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, Y. N., Zhang, X. G., and Pantelides, S. T. (2017). Fundamental resolution of difficulties in the theory of charged point defects in semiconductors. Phys. Rev. Lett. 119:105501. doi: 10.1103/PhysRevLett.119.105501

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, S. B., and Northrup, J. E. (1991). Chemical potential dependence of defect formation energies in GaAs: application to ga self-diffusion. Phys. Rev. Lett. 67, 2339–2342. doi: 10.1103/PhysRevLett.67.2339

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, X., and Sluiter, M. H. F. (2015). Ab initio prediction of vacancy properties in concentrated alloys: the case of fcc Cu-Ni. Phys. Rev. B 91:174107. doi: 10.1103/PhysRevB.91.174107

CrossRef Full Text | Google Scholar

Zunger, A., and Katzir, A. (1975). Point defects in hexagonal boron nitride. II. Theoretical studies. Phys. Rev. B 11, 2378–2390. doi: 10.1103/PhysRevB.11.2378

CrossRef Full Text | Google Scholar