- 1Department of Mechanical Engineering, Korea Advanced Institute of Science and Technology (KAIST), Daejeon, South Korea
- 2Department of Mathematical Sciences, Korea Advanced Institute of Science and Technology (KAIST), Daejeon, South Korea
Micromechanics-based homogenization has been employed extensively to predict the effective properties of technologically important composites. In this review article, we address its application to various physical phenomena, including elasticity, thermal and electrical conduction, electric, and magnetic polarization, as well as multi-physics phenomena governed by coupled equations such as piezoelectricity and thermoelectricity. Especially, for this special issue, we introduce several research works published recently from our research group that consider the anisotropy of the matrix and interfacial imperfections in obtaining various effective physical properties. We begin with a brief review of the concept of the Eshelby tensor with regard to the elasticity and mean-field homogenization of the effective stiffness tensor of a composite with a perfect interface between the matrix and inclusions. We then discuss the extension of the theory in two aspects. First, we discuss the mathematical analogy among steady-state equations describing the aforementioned physical phenomena and explain how the Eshelby tensor can be used to obtain various effective properties. Afterwards, we describe how the anisotropy of the matrix and interfacial imperfections, which exist in actual composites, can be accounted for. In the last section, we provide a summary and outlook considering future challenges.
Introduction
Composites, typically referred to materials consisting of reinforcements and a matrix, offer many advantages that cannot be gained solely with only one of its constituents to improve various materials properties, such as resistance to chemicals (Jawaid et al., 2011; Taurino et al., 2016), a high strength-to-weight ratio (Walther et al., 2010), electrical (Allaoui et al., 2002; Gojny et al., 2005; Tuncer et al., 2007) or thermal insulation properties (Wei et al., 2011; Li et al., 2016), and/or combinations of these properties (Flahaut et al., 2000; Park et al., 2012). Most advanced materials in many engineering applications are composites, such as anti-corrosion composites in the marine industry (Mouritz et al., 2001), lightweight structural carbon composites in the car (Obradovic et al., 2012; Friedrich and Almajid, 2013) and airplane industries (Immarigeon et al., 1995; EL-Dessouky and Lawrence, 2013), and electric or thermal shielding composites (Imai et al., 2006; Zheng et al., 2009) as used in relation to electric wire and heat pipe technology.
In addition to manmade synthetic composites, nature has exploited the advantages of composites to meet certain requirements related to survival and sustained living conditions, even with the limited resources and building blocks available in nature (Gibson et al., 1995; Wegst and Ashby, 2004; Launey et al., 2009; Sen and Buehler, 2011). For example, the combined high toughness and high strength levels of nacre, bone, and cone shells are attributed to their unique hierarchical composite structures ranging from the nano to macro scale, and significant effort has been expended to understand and mimic the natural composites (Tang et al., 2003; Ji and Gao, 2004; Li et al., 2012; Hu et al., 2013; Das et al., 2015; Shao and Keten, 2015; Gao et al., 2017). For the facile design and application of various composites, it is of paramount importance to understand and predict the effective properties of composites as a function of their shape, volume fraction, and spatial distribution of the reinforcements used in them.
Numerical modeling based on finite element analyses has been widely used to predict the effective properties of composites, including the mechanical, thermal, electrical, piezoelectric, thermoelectric properties (Pan et al., 2008; Wang et al., 2011; Miled et al., 2013; Lu et al., 2014; Doghri et al., 2016; Lee et al., 2019, 2018a). However, to obtain statistically meaningful results, finite element analyses require multiple evaluations of large simulation cells involving a large number of fillers, thus necessitating a much fine mesh near the boundary to serve as representative volumes and leading to the requirement of computationally expensive and time-consuming calculations (Xu and Yagi, 2004; Marcos-Gomez et al., 2010; Lee et al., 2019, 2018a). Such extensive numerical calculations are feasible for predictions of the effective properties of systems in the linear response regime. However, it becomes a formidable task numerically to predict the behavior of composites in the nonlinear response regime, where multiple linearization and convergence tasks are required (Miled et al., 2013; Doghri et al., 2016).
When composites have relatively periodic and regular arrangements, they can be modeled reasonably well by an analytic model focusing on the load transfer mechanism of a unit cell. Typical examples include synthetic composites with very long fiber reinforcements (Suh, 2005) and natural staggered platelet structures (Gao, 2006; Kim et al., 2018). In contrast, composites involving random arrangements of short-fiber fillers or spherical reinforcements must be studied via homogenization schemes, as it is infeasible directly to model the interaction among randomly/aperiodically distributed reinforcements and load transfer mechanisms in detail.
The mechanical properties of such short-fiber-reinforced composites and multicomponent alloys can be deduced by computing the strain fields in the reinforcements and the matrix (Mura, 1982). Especially for composites including well-dispersed low-volume-fraction reinforcements (below 20%), the influence of other reinforcements can be taken into account via a mean-field approach by approximating the surrounding area of each reinforcement as the matrix subjected to local strain that is identical to the average strain of the matrix within the entire specimen (Benveniste, 1987) (Mori-Tanaka method) or using a medium with the effective stiffness of the composite (Hill, 1965) (self-consistent method). In this regime, where mean-field approximation is valid, a solution to the single-inhomogeneity problem can be applied to model the effective properties while taking into account multiple reinforcements. Once such homogenization scheme has been established for the linear response regime, and it can be extended to model the non-linear response of composites based on various linear approximation schemes such as the incremental tangent method (Castaneda and Tiberio, 2000; Idiart et al., 2006; Doghri et al., 2016), the incremental secant method (Wu et al., 2013), variational approaches (Castaneda, 1991; Lahellec and Suquet, 2007a; Brassart et al., 2011), and others (Nemat-Nasser, 1999; Lahellec and Suquet, 2007b).
Although extensive efforts have been devoted to determine various effective properties of composites, relatively less attention has been paid to the modeling of the effects of imperfect matrix-reinforcement interfaces and anisotropic matrices. Moreover, while the governing equations of various phenomena are mathematically analogous, the connections among them have not been discussed in detail in the literature. Hence, in this paper, we present research which considers interfacial imperfections and anisotropy effects for the predictions of various effective physical properties and suggest a universal formalism and numerical recipe based on a mathematical analogy. Especially, for this special issue, we introduce several papers published recently from our group on this issue.
The paper is structured as follows. In section Eshelby tensor and its application to effective stiffness calculations in elasticity, we provide a brief overview on the concept of the Eshelby tensor of isotropic materials in elasticity and its application to the computation of the effective stiffness of composites. In section Mathematical analogy between governing equations in various physical phenomena, we discuss the mathematical analogy among the steady-state equations governing various physical phenomena and how the Eshelby tensor and homogenization concept can be applied to predict various effective physical properties. Section Interfacial imperfections and anisotropy of the matrix describes how anisotropy of the matrix and interfacial imperfections, present in most realistic composites, can be accounted for. In the last section, we summarize the discussion and provide our perspective on future challenges.
Eshelby Tensor and Its Application to Effective Stiffness Calculations in Elasticity
Single Inclusion Problem
We can deduce the mechanical properties of fiber-reinforced composites by considering the strain field in inclusions and in inhomogeneities. An inclusion refers to an embedded material with an elastic stiffness tensor Lpqrs identical to that of the matrix, while an inhomogeneity refers to an embedded material with a different stiffness . Eshelby showed that the strain field inside an ellipsoidal inclusion embedded in an infinite matrix is uniform when the inclusion is subject to uniform eigenstrain (Eshelby, 1957, 1959). Eigenstrain indicates the stress-free deformation strain associated with thermal expansion (Jun and Korsunsky, 2010), initial strain (Chiu, 1977), or phase transformation (George and Dvorak, 1992; Tirry and Schryvers, 2009). The Eshelby tensor is defined as the fourth-order tensor Sijrs which links the constrained strain within the inclusion to the eigenstrain , as (Eshelby, 1957; Mura, 1982). In this section, we discuss (i) the key concept of the Eshelby tensor, (ii) how an ellipsoidal inhomogeneity subjected to an external load can be transformed into the equivalent Eshelby inclusion problem, and (iii) the mean-field method used to predict the effective stiffness of a composite based on the average theorem, considering an isotropic matrix in the absence of interfacial damage.
We begin the discussion by introducing the governing equation for Green's function Gij(x − y) in elastostatics, which indicates the displacement in the ith direction at point x by the unit body force in the jth direction at point y, in an infinite elastic medium:
Here, Lijkl is the fourth-order elastic stiffness tensor, and the repeated indices represent the summation over all values from 1 to 3. For an isotropic material, Lijkl can be represented by two independent elastic constants (Section Interfacial imperfections and anisotropy of the matrix includes a discussion of anisotropy). Green's function for the isotropic material is available in a closed form (Mura, 1982), as follows,
where μ and ν are the shear modulus and the Poisson's ratio of the material, respectively, and |x − y| denotes the standard norm of vector x − y.
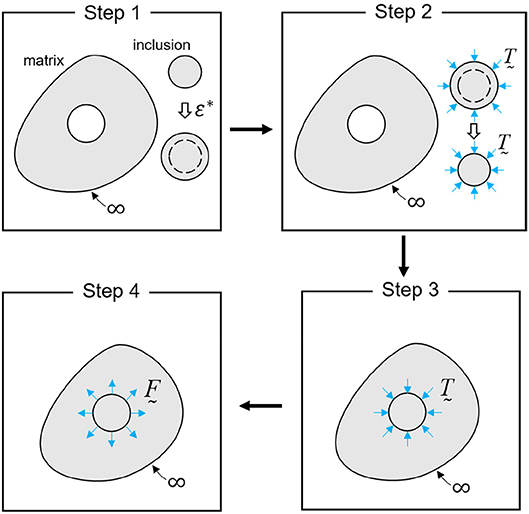
The schematic for the single inclusion problem is depicted in Figure 1, which is solved with a four-step procedure. We assume that the inclusion can deform by the eigenstrain ε* when there is no external displacement or load (step 1). In order to maintain the original shape, the load T is applied to the inclusion (step 2). The inclusion is then plugged into a hole having the original shape and size within an infinite matrix (step 3). After removing the applied load (T), the inclusion exerts traction of F = −T on the matrix (step 4). Due to the constraining effect of the matrix, the inclusion deforms by the constrained strain εc, which is different from the eigenstrain ε*. The constrained strain field can be expressed by employing Green's function, as follows:
Because the eigenstrain and constrained strain are symmetric, the Eshelby tensor has minor symmetry (Sijkl = Sjikl = Sijlk) but no major symmetry (Sijkl ≠ Sklij). In an isotropic medium, for an ellipsoidal inclusion with three different semi-axes a1, a2, and a3, the expression is given in terms of standard elliptic integrals (Mura, 1982; Qu and Cherkaoui, 2007). For isotropic material having an axi-symmetric ellipsoidal inclusion (a1 ≠ a2 = a3), all components of the Eshelby tensor can be obtained in a closed form, as shown in Appendix A (Mura, 1982; Lee and Ryu, 2018). The orientation average of a randomly distributed ellipsoidal inclusion was considered in one of our studies (Lee and Ryu, 2018). For a spherical inclusion, the Eshelby tensor can be compactly expressed as
We note that the Eshelby tensor for the spherical inclusion does not depend on the radius. In general, the Eshelby tensor does not depend on the absolute size of the inclusion because there is no characteristic length scale in elasticity. In contrast, in the presence of an interfacial imperfection, the modified Eshelby tensor depends on the absolute size of the inclusion, which will be discussed in Section Interfacial imperfections and anisotropy of the matrix. We will also describe the Eshelby tensor for an anisotropic medium in Section Interfacial imperfections and anisotropy of the matrix.
Single Inhomogeneity Problem
Having introduced the concept of the Eshelby tensor, we discuss how an ellipsoidal inhomogeneity subjected to a uniform external load (external strain for the following example) can be transformed into the equivalent Eshelby inclusion problem. In the presence of a uniform external load (either stress or strain), the total strain field of the aforementioned Eshelby inclusion problem becomes , and the stress field becomes . When the total strain field and stress field of an inhomogeneity subjected to an identical applied load are identical to those of the Eshelby inclusion, is referred to as an equivalent eigenstrain. Therefore, from the total strain and stress equality conditions, or equivalently and , we obtain the following expression for the equivalent eigenstrain:
In a tensor expression,
where : and []−1 refer to the double contraction and inverse operator, respectively. The double contraction and inverse operation of fourth-order tensors can be facilitated by adopting the Mandel notation (Helnwein, 2001), which converts all tensor operations into conventional 6 × 6 matrix operations (Lee et al., 2019, 2018b).
In the Mandel notation, the strain vector , stress vector , stiffness matrix 〈L〉, and Eshelby matrix 〈S〉 are defined as follows:
The prefactors and 2 ensure that the matrix-matrix product and the inverse coincide with the double contraction and the inverse of the fourth-order tensors, respectively. Hence, if A, B denote a fourth-order tensor with minor symmetry (Aijkl = Ajikl = Aijlk), and 〈A〉, 〈B〉 represent the corresponding 6 × 6 matrix following the Mandel notation, we can calculate the double contraction and inverse from the 6 × 6 matrix multiplication and inverse, respectively, as
Mean-Field Homogenization of the Effective Stiffness
For the problem involving multiple inhomogeneities, the Mori-Tanaka method has been widely used for predicting the effective stiffness by considering the interaction among the inhomogeneities (see Figure 2). Each inhomogeneity is assumed to be embedded effectively in the matrix subjected to a spatial average strain of the matrix over the entire specimen, which is why the technique is referred to as the mean-field homogenisation method. Because the interaction between the inhomogeneities becomes intense at a high volume fraction of inhomogeneities, the Mori–Tanaka method is known to be reliable at a relatively low volume fraction of inhomogeneities (<20%). In this mean-field homogenization scheme, the average strain fields in the matrix, inhomogeneity, and composite ( and , respectively) are related as follows:
where (where ) is the strain concentration tensor for the Mori-Tanaka method. A converges to the strain concentration tensor for the single inhomogeneity problem, T, in the limit of very small inhomogeneity volume fraction, c1. The effective stiffness can be obtained from the relationship between the volume-averaged stress and strain within the composite ( and , respectively) as follows:
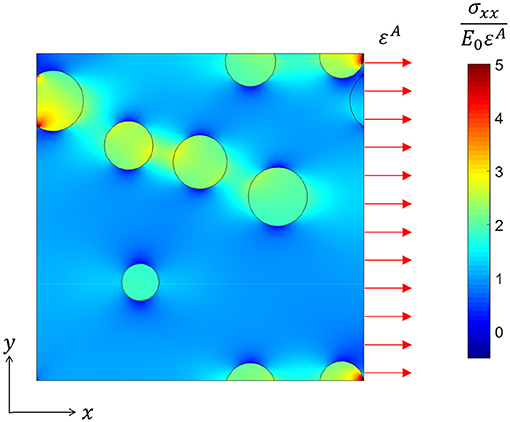
Figure 2. Non-uniform σxx field under uniform applied strain in the x direction within a cross-section in a three-dimensional volume simulation. The material properties used for this figure are E1 = 10E0and ν1 = ν0 = 0.25 and the volume fraction is 10%.
There is another class of homogenization method called the self-consistent method, where the surrounding area is approximated as a medium with the effective stiffness of the composite. However, we omit the discussion of the self-consistent method here because the effective stiffness cannot be solved explicitly (Hill, 1965; Qu and Cherkaoui, 2007). Instead, it requires an iterative numerical solution.
Mathematical Analogy Between Governing Equations in Various Physical Phenomena
Mathematical Analogy Discussion
Having introduced the key concepts of the Eshelby tensor and the mean-field homogenization scheme, we turn our attention to the predictions of various physical phenomena via a mathematical analogy. We consider two representative classes of steady-state equations governing different physics: conduction/dielectric-related equations and coupled multi-physics equations. An extensive discussion can be found in the literature (Milton, 2002).
For the first class of the equations, referred to as conductivity/dielectric-related equations, the governing equation under a steady state at any point x in a medium in the absence of an internal source can be written using the following equations,
which appear in physical problems concerning the conductivity of dielectrics, such as those linked to the concepts of electrical conductivity, dielectric phenomena, magnetism, thermal conduction, diffusion, and flows in porous media. In each field, the vector fields j(x), e(x) and, the second-order tensor K(x) have the physical interpretations given in Table 1. We note that the governing equations for these phenomena in a dynamic regime differ from each other; equations pertaining to dissipative transport phenomena use a first-order derivative with respect to time, leading to a homogeneous distribution of the temperature or concentration in an infinite time limit if an external driving force is not present, whereas equations pertaining to non-dissipative transport phenomena use a second-order derivative with respect to time, leading to electro-magnetic or acoustic wave propagation (Kreyszig, 1972). Because the steady-state equations are identical in terms of their mathematical descriptions, the homogenization scheme obtained for one of these equations can be applied directly to any of the other equations in Table 1 to obtain the effective electrical and thermal conductivities, the effective dielectric and magnetic permittivities, the effective diffusivity, and the effective fluid permeability.

Table 1. Interpretation of conductivity/dielectric-related equations under a steady state, as governed by a single class of PDE.
As examples of the second class of equations, we consider piezoelectric and thermoelectric equations. The aforementioned conductivity/dielectric-related equations describe idealized cases. In practice, lattice distortion can cause electric polarization in some classes of anisotropic materials, and vice versa (Fu and Cohen, 2000). Moreover, conducting electrons can carry some heat with them and thus causes coupling between thermal and electric phenomena (Zhao et al., 2014). The former is referred to as piezoelectricity and the latter is termed thermoelectricity.
The constitutive equations of piezoelectricity are given as
where Di is the electrical displacement vector, En is the electric field vector, is the second rank tensor of the dielectric permittivity constants under constant strain with ϵmk = ϵkm, and is the third rank tensor of the piezoelectric constants under constant stress σij with dkij = dkji. We can express Equation (12) as a simplified form of a linear equation, similar to the constitutive equations of elasticity, thermal conduction and electrical conduction using the notation introduced by Barnett and Lothe (1975). This notation is identical to the conventional notation, except that the repeated capital index implies summation from 1 to 4. With this notation, we can express the elastic strain and electric field as
where ZMn is obtained by the differentiate UM, which is given by
In a similar manner, we can simplify the stress and electric displacement to one matrix using the notation
Then, the electroelastic moduli and constitutive equation are obtained using the equations below.
On the other hand, for a thermoelectric material, similarly, the constitutive equation is arranged in tensor form, as follows:
By using the notation introduced for a piezoelectric material (Jung et al., 2018), the expression is as follows,
where
Here, JE is the electrical current density, JS(= q/T) is the entropy flux, q is the heat flux, T is the temperature, σe is the electrical conductivity, α is the Seebeck coefficient, γ(= κ+Tα·σe·α) is the heat conductivity under a zero electric field, and κ is the heat conductivity at zero current. As shown in Equation (21), PJiMn contains T, which depends on the position x and therefore does not have mathematical similarity with other physics in general. For a small temperature difference across the hot and cool sides (TH − TL = ΔT ≈ 0), we can assume that the temperature variable T in the constitutive equation is a constant average temperature , allowing us to obtain a linear constitutive equation. The validity of this assumption has been studied for wide range of ΔT by comparing theoretical predictions with finite element analysis outcomes (Jung et al., 2018).
Eshelby Tensor for Various Physical Phenomena
Due to the mathematical analogy, the Eshelby tensor can be expressed in a similar form. In the most general case of a medium with arbitrary anisotropy and an ellipsoidal inclusion with three different semi-axes a1, a2, and a3, by simplifying Equation (3), the elastic Eshelby tensor can be expressed as Mura (1982),
where . Here, Z(ξ)=[(L · ξ) ·ξ]−1 and ξ are Green's function and a vector in the Fourier space, respectively. Because Zij(ξ) is a homogeneous function of degree −2, ξkξlZij(ξ) is identical to where is a normalized vector. Equation (22) can be evaluated by using the integral variables and θ; thus, , , given the semi-axes of an ellipsoidal inclusion (ai). Similarly, by adding three more degrees of freedom from electric polarization and its coupling with lattice distortion, the pizeoelectric Eshelby tensor is derived as follows (Dunn and Taya, 1993),
Here, where . Because the piezoelectric coefficients are zero for all centrosymmetric crystals, the piezoelectric Eshelby tensor for an isotropic medium does not exist.
For the conduction or dielectric phenomena described by Equation (11) and physical property tensor K in Table 1, the Eshelby tensor is obtained from
Unlike the Green's function in elasticity, the Green's function in the conduction or dielectric phenomena for a medium with arbitrary symmetry has been derived in a closed form as follows:
The second-order Eshelby tensor can be further simplified for an arbitrary ellipsoidal inclusion as an integral having one variable (Giordano and Palla, 2008; Lee et al., 2018a):
Or it can be written in an integral involving two variables:
where . For a spherical inclusion in an isotropic matrix, the Eshelby tensor can be simplified as . For a thermoelectric material, with the coupling of electrical and heat conduction, the Eshelby tensor can be written as follows Jung et al. (2018),
where . The Eshelby tensor for a spherical inclusion in an isotropic matrix becomes . We note that the Eshelby tensor expressions for the conduction/dielectric and thermoelectric phenomena are simpler than those for elasticity and piezoelectricity, because the Green's functions for the latter consider a vector field (displacement) whereas the Green's functions for the former only involve scalar fields (such as temperature and electrical potential).
Examples of Numerical Calculations and FEA Validation
We now turn our attention to predict the effective properties of composites based on a mathematically analogous formula. In Mandel notation represented by p = Xq, where X is a N × N matrix and the input (output) field q (p) has N components, the linear operator in elasticity Lijmn, conduction (or dielectric) κin, piezoelectricity CiJMn, and thermoelectricity PJiMn become 6 × 6, 3 × 3, 9 × 9, and 6 × 6 symmetric matrices, respectively. Although most existing studies (Dunn and Taya, 1993; Huang and Kuo, 1996; Odegard, 2004; Duschlbauer et al., 2006; Martinez-Ayuso et al., 2017) utilize the Voigt notation, we adapt the Mandel notation here. For example, if we use the Voigt notation for a piezoelectric case, the linear operator matrix (which corresponds to the material properties) and the Eshelby matrix can be expressed as Equations (29, 30), respectively:
As shown by Equations (29, 30), the coefficients in the transformed matrix are different for the two set of matrices. In contrast, with the Mandel notation, the two matrices can be expressed as
and
where the same coefficients are multiplied in the two matrixes. It is important to note that the Eshelby matrix of a piezoelectric and thermoelectric material has dimensions with N/C and V/K in the coupling term. In a piezoelectric material, instead of using SI units for all physical parameters, we can use 1nC = 10−9C for the charge to avoid numerical problems due to the very large order of the magnitude difference between the elastic constant (~109N/m2) and the coupling constant (~C/N).
For the physical phenomena represented by matrix equation p = Xq in the Mandel notion, the effective property can be obtained by , where and S is the N × N matrix representation of the corresponding Eshelby tensor. We then compare the effective property prediction based on the Mori-Tanaka method with a FEA analysis for the simple case involving spherical inhomogeneities embedded in a transversely isotropic medium for piezoelectric and isotropic media for others, as shown in Figure 3.
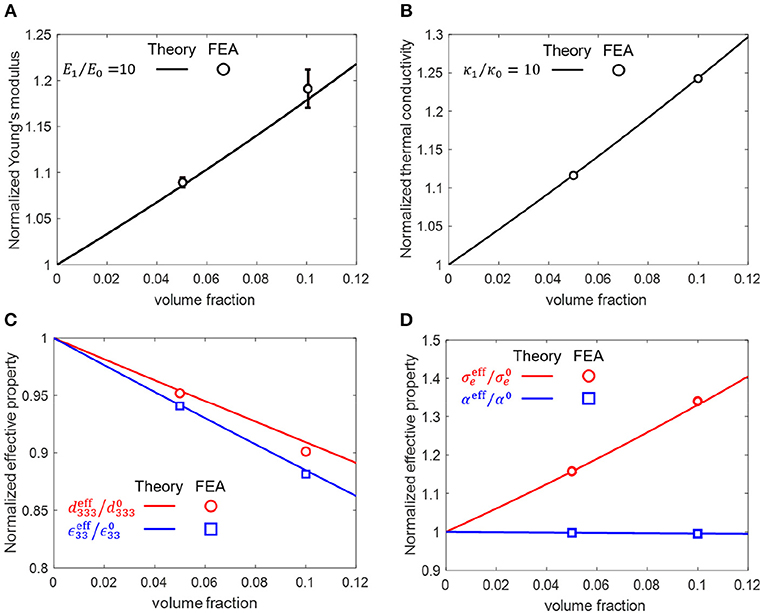
Figure 3. (A) Normalized Young's modulus of a particle-reinforced composite. The Poisson's ratios (ν) of two phases are identical at 0.25. (B) Effective heat conductivity of the composite. (C) Normalized effective piezoelectric properties of composites. The matrix and reinforcement are PZT-7A and SiC particles, respectively. (D) The effective thermoelectric properties of a Cu-reinforced Bi2Te3 composite at 300 K. All properties are normalized with respect to the properties of the matrix. We use the material properties for the piezoelectricity (Odegard, 2004) and the thermoelectricity (Jung et al., 2018) presented in the literature.
Interfacial Imperfections and Anisotropy of the Matrix
Effects of Anisotropy of the Matrix in Various Physical Problems
As mentioned in the previous chapters, we can obtain the effective properties from the Mori-Tanaka method because the expression is applicable to any arbitrarily anisotropic matrix if the Eshelby tensor is known. The Eshelby tensor for anisotropic medium in various physical problems has been extensively studied in the literature (Mura, 1982; Yu et al., 1994; Huang and Kuo, 1996; Dunn and Wienecke, 1997; Qu and Cherkaoui, 2007; Quang et al., 2011; Martinez-Ayuso et al., 2017; Lee et al., 2018b) and the Eshelby tensors for an ellipsoidal inclusion embedded in an arbitrarily anisotropic medium for elasticity, piezoelectricity, conduction/dielectric phenomena, and thermoelectricity can be obtained numerically from Equations (22, 23, 27, 28), respectively.
Although the Eshelby tensor can be obtained numerically, significant efforts have been devoted to derive the explicit expressions (either closed-form or analytical expression) for the facile application of the homogenization method and to provide better insight into the nature of the tensor. In elasticity, analytic expressions for ellipsoidal shape given in terms of a few integrals are available for spheroidal inclusion in transversely isotropic solids involving five independent elastic constants (or any medium with higher symmetry, i.e., less number of independent elastic constants) (Mura, 1982; Yu et al., 1994). In conduction/dielectric phenomena, analytic solutions have been derived for spheroidal inclusion in isotropic material (Hatta and Taya, 1986) and spherical inclusion in orthotropic and transversely isotropic material (Lee et al., 2018a). For piezoelectricity, Huang and Kuo (1996) suggested the Eshelby tensor expression of spheroidal inclusion in transversely isotropic material with a few integrals. However, for thermoelectricity, to the best of our knowledge, analytic solutions have not been obtained for an anisotropic medium.
Definition of Interfacial Imperfections
In actual composites, the interface between the matrix and an inclusion often has imperfections originating from the manufacturing process or from an inherent lattice mismatch (People and Bean, 1985; Habas et al., 2007). An interfacial imperfection in elasticity refers to debonding or slippage, i.e., a displacement jump (Qu, 1993; Lee and Ryu, 2018; Lee et al., 2019, 2018b), and an interfacial imperfection under thermal conduction (or Kapitza resistance) refers to an abrupt change in the temperature, i.e., a temperature jump (Quang et al., 2011; Lee et al., 2018a). An interfacial imperfection in electrical conduction (i.e., the electrical contact resistance) refers to an abrupt change in the electrical voltage across the interface (Giordano and Palla, 2008). The interfacial imperfection in piezoelectricity considers both displacement jump and the electric potential jump (Wang et al., 2014a,b). Similarly, the interfacial imperfection in thermoelectricity considers the abrupt discontinuities of both temperature and electric potential (Jung et al., 2018).
Out of a few characteristic methods used to describe an interfacial imperfection in elasticity (Qiu and Weng, 1991; Duan et al., 2005), in this work, we consider the interfacial spring model (Qu, 1993) owing to its (i) mathematical simplicity and (ii) mathematical analogy with the interfacial thermal (electrical) resistance in thermal (electrical) conduction. As will be shown later, due to the mathematical similarity, the expressions of the effective stiffness and effective conductivity in the presence of an interfacial imperfection are nearly identical to each other.
It is noteworthy that the interfacial imperfection can be well-treated only for a spherical inclusion, because an ellipsoidal inclusion (even with slight deviation from a sphere) introduces significantly non-uniform interior field (Qu, 1993; Qu and Cherkaoui, 2007; Lee et al., 2019, 2018a,b). In problems involving the elastic deformation, the equality between the normal and tangential interfacial compliances is additionally required to ensure the uniform field inside the inclusion (which is critical for the applicability of the Eshelby tensor and the mean field homogenization). Unfortunately, there exist several studies employing the Mori-Tanaka method to obtain effective physical properties of a composite involving ellipsoidal inhomogeneities in the presence of different normal and tangential compliances (Yang et al., 2013b; Wang et al., 2014a,b; Lee and Ryu, 2018).
Another common mistake in mean-field homogenization studies considering the interfacial damage is the application of the effective physical property expression and by simply replacing the Eshelby tensor S with a modified Eshelby tensor SM accounting for the interfacial imperfection (Qu, 1993; Barai and Weng, 2011; Yanase and Ju, 2012; Pan et al., 2013; Wang et al., 2014a,b; Shokrieh et al., 2016; Lee and Ryu, 2018). However, in addition to the Eshelby tensor, different expressions for XEff and T should be used because the derivation in Section Single inhomogeneity problem and Mean-field homogenization of the effective stiffness (where the problem is solved with the superposition of two sub-problems involving applied and constrained fields, respectively) does not account for the additional contribution from the interface imperfection. We will discuss these issues in detail in the next section.
Prediction of Effective Physical Properties in the Presence of Interfacial Imperfections
We adopt the interface spring model to consider the interfacial damage, as depicted in Figure 4. A displacement jump occurs at the interface due to the spring layer having a vanishing thickness between the infinite matrix and the single inclusion. The spring compliance(η) is represented by α and β for the tangential and normal directions, respectively, and is expressed by Equation (33) in the form of a second-order tensor, as follows:
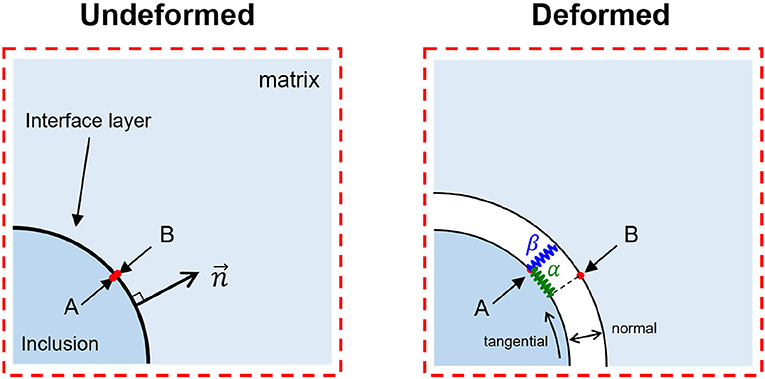
Figure 4. Schematic of an interface spring model in elasticity. To visualize the interface spring in two directions, we compare undeformed and deformed states.
The constitutive equations and traction(ti) equilibrium equation at the interface are expressed as follows,
where (∂Ω+) and (∂Ω−) denote the interface on the matrix and the inclusion side, respectively. Formulating the Eshelby inclusion problem by adopting the interfacial condition in Equation (34), the constrained strain is written as Othmani et al. (2011) and Lee et al. (2018b, 2019)
Equation (35) is shown to reproduce the perfect interface case with zero spring compliance; i.e., ηij = 0.
Because Equation (35) is an implicit integral equation involving the constrained strain , it is difficult to determine the relationship between and , i.e., the modified Eshelby tensor. Zhong and Meguid (1997) showed that, when α = β ≡ γs and the inclusion shape is a perfect sphere, the strain field inside the spherical inclusion is uniform, as in the case of a perfect interface. Hence, for this special case, the integral equation can be decomposed as follows,
where the fourth-order tensor Γijkl in Equation (36) is defined by
The constrained strain field then can be expressed by a tensor algebraic equation as follows Othmani et al. (2011) and Lee et al. (2018b),
where SM is the modified Eshelby tensor. Related to this, in an earlier work by the authors, we proved that for materials with an arbitrary elastic anisotropy, the Γ tensor can be written in terms of the Eshelby tensor for a perfect interface and an elastic stiffness tensor as Lee et al. (2018b)
where R is the radius of the inclusion. Therefore, it is proven that the modified Eshelby The tensor SM can be written as follows:
The numerical validation against a finite element analysis on a triclinic single crystal material (NaAlSi3O8) with 21 independent elastic constants (and 36 independent Eshelby tensor components) is presented in Figure 5. This leads to the simplified expression of the modified T tensor (TM) in the Mori-Tanaka method when the matrix modulus is L0 and the inhomogeneity modulus is L1:
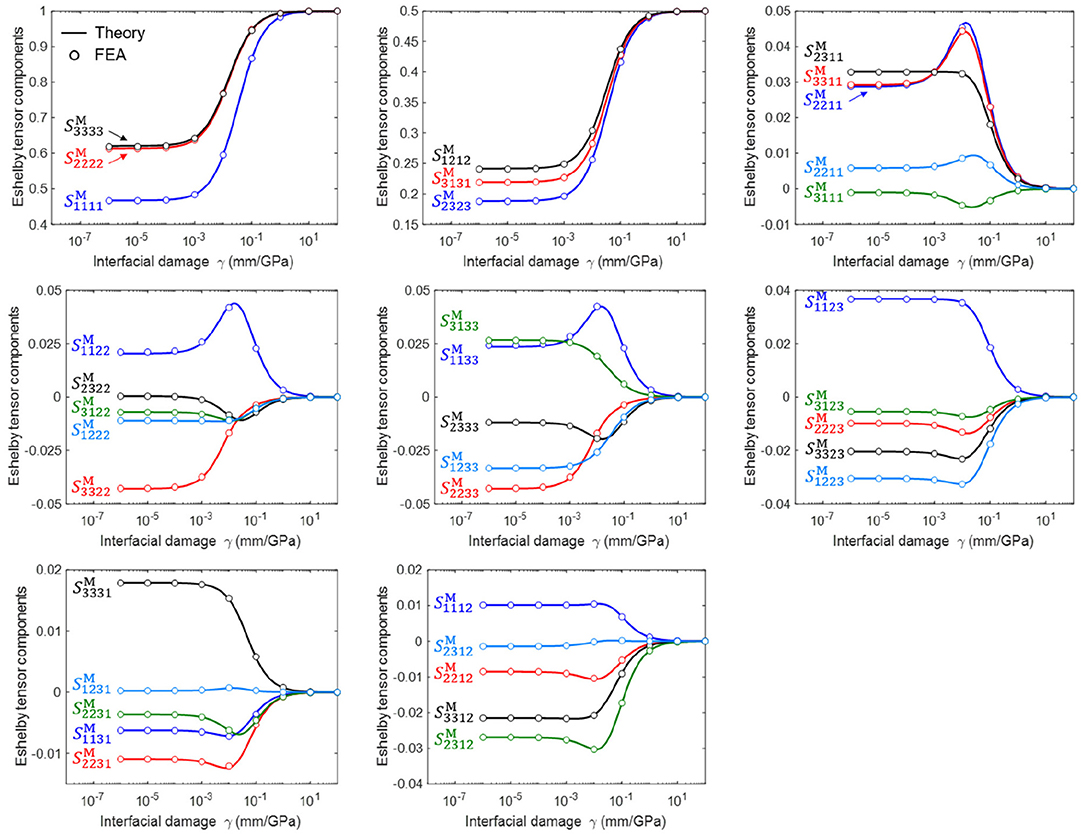
Figure 5. Thirty-six independent components of a modified Eshelby tensor for a wide range of interfacial damage. The triclinic material used for this calculation is NaAlSi3O8 (Lee et al., 2018b).
We derive the effective modulus (LEff) of the composite as follows Lee et al. (2019):
To confirm the validity of Equation (42), we compare the theoretical prediction with the effective Young's modulus of a composite for a wide range of interface damage as obtained by a FEA (See Figure 6). The equation can also be formulated in terms of the effective inclusion, and we concisely summarize the formulation in Appendix B. We note that many previous studies (Qu, 1993; Barai and Weng, 2011; Yanase and Ju, 2012; Yang et al., 2012; Pan et al., 2013; Shokrieh et al., 2016; Lee and Ryu, 2018) employing the effective stiffness equation in the presence of an interfacial imperfection employ a few incorrect expressions derived by violating Fubini's theorem and relying on inappropriate superposition. A detailed discussion of this issue can be found in work by Dogri's group (Othmani et al., 2011) and by our group (Lee et al., 2018b).
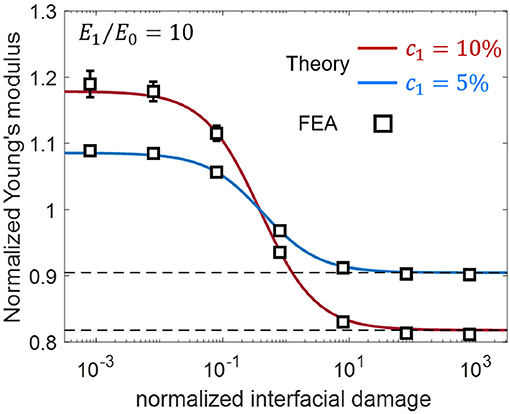
Figure 6. Effective Young's modulus of a composite with respect to the normalized interface damage parameter (μ0γ/R). The Poisson's ratio of the two phases is 0.25 (Lee et al., 2019).
We now turn our attention to other physical phenomena where interfacial imperfections play an important role, specifically the conduction problem. The interfacial thermal resistance αK (or the Kapitza resistance) is defined as Kapitza (1941) and Quang et al. (2011)
where Tout and Tin refer to the temperatures on the outer and inner surfaces of the interface, respectively, and q is the heat flux at the interface (see Figure 7). The SI unit of the interfacial thermal resistance αK is [m2K/W]. The interfacial resistance augments an additional surface integration term in the eigen-intensity problem (which corresponds to the eigenstrain problem in elasticity), as follows Quang et al. (2011) and Lee et al. (2018a),
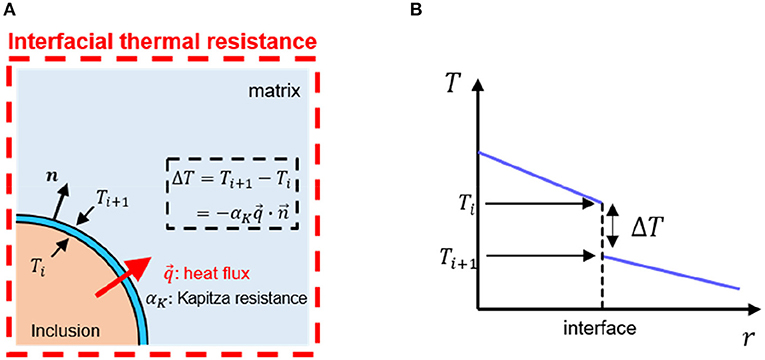
Figure 7. (A) Schematic of the Kapitza resistance at the interface, and (B) temperature jump across the interface.
It has been found that the heat flux within a spherical inclusion is uniform in the presence of interfacial thermal resistance. In an earlier work of ours, we proved that the modified Eshelby tensor for a matrix with arbitrary anisotropy can be written as follows Lee et al. (2018a),
which is similar to the modified Eshelby tensor in elasticity except that the double contraction for the fourth-order tensor is replaced with matrix multiplication for the second-order tensor. Here, I is the second-order identity tensor and S is the Eshelby tensor for the thermal conduction problem. This leads to the simplified expression of the modified concentration tensor (subjected to the constant temperature boundary condition) in the Mori-Tanaka method when the matrix and inhomogeneity thermal conductivity tensors are given as κ0 and κ1, respectively:
We can also obtain the modified localization tensor (subjected to the constant flux boundary condition (q0)) as
where q1 is the heat flux within a single inhomogeneity and ; subsequently, we compare the equation with the FEA results for the anisotropic matrix case (see Figure 8; the FEA with the flux boundary condition is more convenient to perform). Based on the modified concentration tensor, we derive the effective conductivity (κeff) of the composite as follows Quang et al. (2011) and Lee et al. (2018a),
and the theoretical predictions are well-matched with the FEA results (see Figure 9).
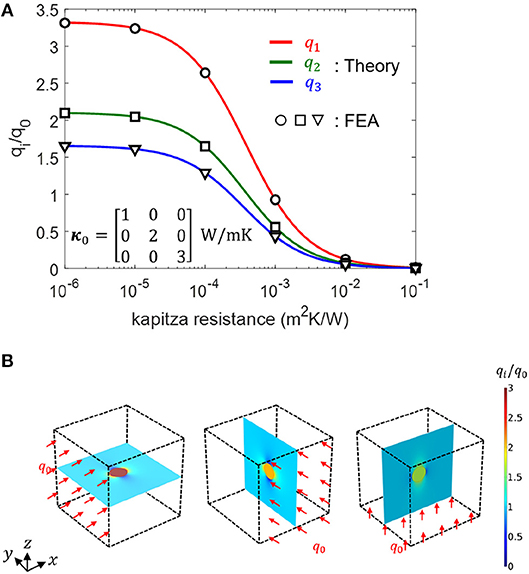
Figure 8. (A) Normalized heat flux within an inhomogeneity with respect to the interfacial thermal resistance in a single inhomogeneity problem. The inhomogeneity is an isotropic material for which (B) Heat flux distribution within a matrix and an inhomogeneity on the x, y, and z planes for three different heat flux directions (Lee et al., 2018a).
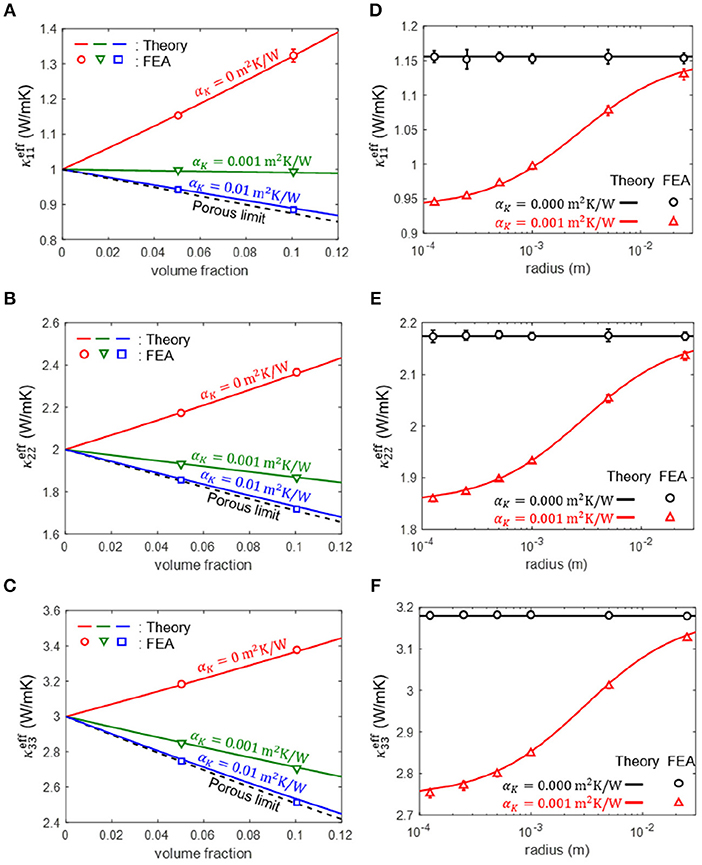
Figure 9. Effective thermal conductivity values [(A), (B) and (C)] of a particle-reinforced composite with different interfacial thermal resistances. The material properties of the matrix and particle are (W/mK), respectively. The radius of the particle used in (A–C) is 1 (mm). The effective thermal conductivity [(D), (E), and (F)] as a function of the radius of the particle under a fixed volume fraction of 5% is also shown (Lee et al., 2018a).
For a thermoelectric composite, we refer to our work on micromechanics homogenization considering both the interfacial thermal and electrical resistance (Jung et al., 2018) where mathematical solutions were obtained for the modified Eshelby tensor, the modified concentration tensor, and the effective thermoelectric properties. Our homogenization study provides new insight on the effect of interfacial thermal and electrical resistance on the thermoelectric properties. In piezoelectricity, the modified Eshelby tensor has been derived by violating the Fubini's theorem by changing integral order (Wang et al., 2014a,b). Hence, the effective piezoelectric property has not been obtained correctly in the presence of interfacial imperfections considering both displacement jump and electric potential jump. With the adaptation of Mandel notation and the careful mathematical derivation, the expression for the effective piezoelectric property is expected to be similar to that of the effective thermoelectric property (Jung et al., 2018). We close the section by providing numerically obtained interior field inside ellipsoidal reinforcement (Figure 10), which clearly demonstrate the limited applicability of the homogenization method in the presence of interfacial imperfection.
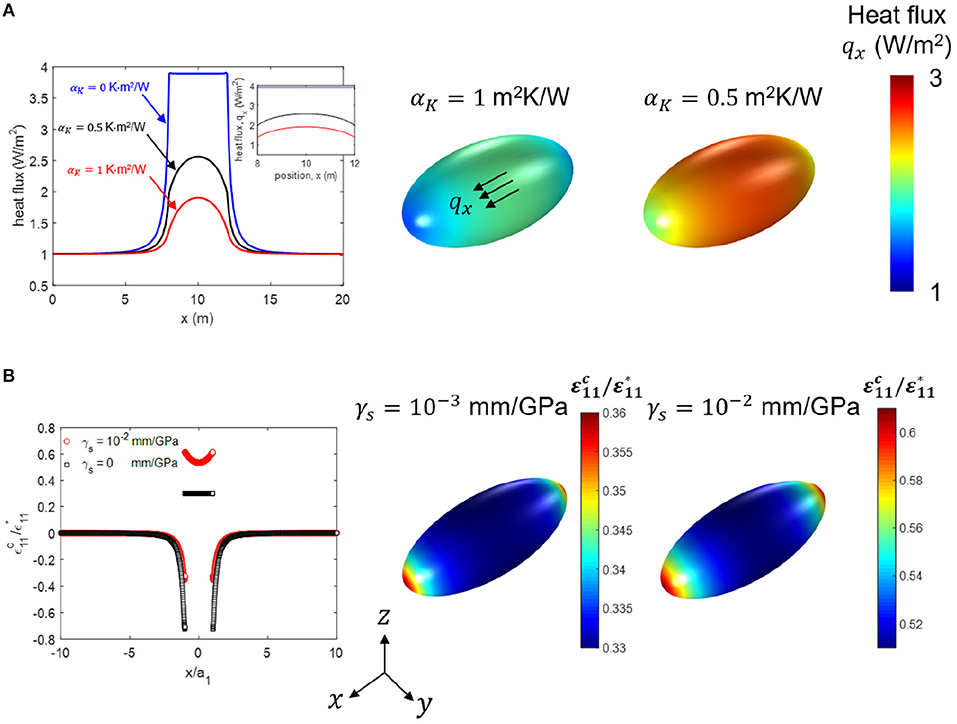
Figure 10. (A) Heat flux within an ellipsoidal inhomogeneity and (B) strain field within an ellipsoidal inclusion (ax/ay = ax/az = 2). The material properties used for the calculations are (A) κ0 = 1, κ1 = 10 (W/mK) (Lee et al., 2018a), and (B) E0 = 200GPa, ν0 = 0.25 (Lee et al., 2018b).
Summary and Outlook
In this paper, we introduce a series of recent studies which attempted to obtain the effective physical properties of composites by taking into account the interfacial damage and anisotropy of the matrix, providing a universal formulation for different physical phenomena based on their mathematical analogies. First, with the specific example of elasticity, we introduced the concept of the Eshelby tensor and discussed a how single-inclusion problem can be related to a single inhomogeneity problem, which ultimately is applied to mean-field homogenization to predict the effective properties of composites. Second, based on a mathematical analogy, we show that mean-field homogenization equations for different physical phenomena can be represented by linear equations involving symmetric matrices with different dimensions by adapting Mandel's notation. Third, we extend our discussion by taking into account two common issues in realistic applications: imperfections in a matrix-inhomogeneity interface and anisotropy of the matrix.
Although we have discussed the homogenization method while covering a wide range of issues, there remain a few issues requiring further developments. We categorize the advanced issues of homogenization theory into the six problems of (i) various physical phenomena, (ii) anisotropy of the matrix, (iii) matrix-filler interfacial imperfections, (iv) nonlinear responses, (v) time-dependent responses, and (vi) high volume fractions of reinforcements. Although issues (i)-(iii) have been investigated extensively, we nonetheless cannot take into account important non-spherical reinforcement materials (including ellipsoidal types) such as carbon nanotubes and graphene in the presence of interfacial imperfections due to the non-uniform interior field. Although there have been many scaling up attempts to couple micro/nanoscale simulations and homogenization theory to predict the properties of nanocomposites (Yang et al., 2012, 2013a, 2014; Pan et al., 2013; Shin et al., 2013; Shokrieh et al., 2016), they either rely on an incorrect solution stemming from effective stiffness expressions derived from a few problematic bases, such as violations of Fubini's theorem or inappropriate superpositions, or do not recognize the non-uniform interior field (Barai and Weng, 2011; Yang et al., 2012, 2013b; Pan et al., 2013; Shokrieh et al., 2016). There are a few studies of composites showing highly nonlinear (such as hyperelastic) and time-dependent (such as viscoelastic) responses (Friebel et al., 2006; Miled et al., 2011, 2013; Brassart et al., 2012; Doghri et al., 2016), but most lack consideration of interfacial imperfections, which can play an important role on the macroscale composites during repeated cyclic loading and/or in nanocomposites including nanoscale reinforcements with large interfacial fractions. Lastly, to account for the high reinforcement volume fraction regime where the interaction among reinforcements becomes important, several heuristic methods have been developed, such as differential schemes (Hashin, 1988) and/or matrix-filler inversion schemes (Friebel et al., 2006) as well as studies of the lower and upper bounds of the effective properties (Hashin and Shtrikman, 1961), leaving room, however, for further improvements. Studies to overcome aforementioned challenges are underway in our research group with the formation of an international collaborative research network.
Author Contributions
SR designed the structure of the review paper. SR and SL wrote the manuscript. SR and SL. contributed the sections on the micromechanics review and the treatment of anisotropy and interfacial imperfections. SR, SL, and JJ contributed to the summary of theoretical derivations, prepared figures, and discussed the mathematical analogy among different physical problems. JL contributed the theoretical derivations. YK contributed the effective inclusion method section.
Funding
This work is supported by the National Research Foundation of Korea (NRF) funded by the Ministry of Science and ICT (2016M3D1A1900038, 2016R1C1B2011979, and 2018K2A9A2A12000223).
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2019.00021/full#supplementary-material
References
Allaoui, A., Bai, S., Cheng, H. M., and Bai, J. B. (2002). Mechanical and electrical properties of a MWNT/epoxy composite. Composites Sci. Technol. 62, 1993–1998. doi: 10.1016/S0266-3538(02)00129-X
Barai, P., and Weng, G. J. (2011). A theory of plasticity for carbon nanotube reinforced composites. Int. J. Plast. 27, 539–559. doi: 10.1016/j.ijplas.2010.08.006
Barnett, D. M., and Lothe, J. (1975). Dislocations and line charges in anisotropic piezoelectric insulators. Physica Status Solidi 67, 105–111. doi: 10.1002/pssb.2220670108
Benveniste, Y. (1987). A new approach to the application of mori-tanaka theory in composite-materials. Mech. Mater.6, 147–157. doi: 10.1016/0167-6636(87)90005-6
Brassart, L., Stainier, L., Doghri, I., and Delannay, L. (2011). A variational formulation for the incremental homogenization of elasto-plastic composites. J. Mech. Phys. Solids 59, 2455–2475. doi: 10.1016/j.jmps.2011.09.004
Brassart, L., Stainier, L., Doghri, I., and Delannay, L. (2012). Homogenization of elasto-(visco) plastic composites based on an incremental variational principle. Int. J. Plast. 36, 86–112. doi: 10.1016/j.ijplas.2012.03.010
Castaneda, P. P. (1991). The effective mechanical-properties of nonlinear isotropic composites. J. Mech. Phys. Solids 39, 45–71. doi: 10.1016/0022-5096(91)90030-R
Castaneda, P. P., and Tiberio, E. (2000). A second-order homogenization method in finite elasticity and applications to black-filled elastomers. J. Mech. Phys. Solids 48, 1389–1411. doi: 10.1016/S0022-5096(99)00087-3
Chiu, Y. P. (1977). On the stress field due to initial strains in a cuboid surrounded by an infinite elastic space. J. Appl. Mech. 44, 587–590. doi: 10.1115/1.3424140
Das, P., Malho, J. M., Rahimi, K., Schacher, F. H., Wang, B. C., Demco, D. E., et al. (2015). Nacre-mimetics with synthetic nanoclays up to ultrahigh aspect ratios. Nat. Commun.6:6967. doi: 10.1038/ncomms6967
Doghri, I., El Ghezal, M. I., and Adam, L. (2016). Finite strain mean-field homogenization of composite materials with hyperelastic-plastic constituents. Int. J. Plast. 81, 40–62. doi: 10.1016/j.ijplas.2016.01.009
Duan, H. L., Wang, J., Huang, Z. P., and Luo, Z. Y. (2005). Stress concentration tensors of inhomogeneities with interface effects. Mech. Mater. 37, 723–736. doi: 10.1016/j.mechmat.2004.07.004
Dunn, M. L., and Taya, M. (1993). Micromechanics predictions of the effective electroelastic moduli of piezoelectric composites. Int. J. Solids Struct. 30, 161–175. doi: 10.1016/0020-7683(93)90058-F
Dunn, M. L., and Wienecke, H. A. (1997). Inclusions and inhomogeneities in transversely isotropic piezoelectric solids. Int. J. Solids Struct. 34, 3571–3582. doi: 10.1016/S0020-7683(96)00209-0
Duschlbauer, D., Bohm, H. J., and Pettermann, H. E. (2006). Computational simulation of composites reinforced by planar random fibers: homogenization and localization by unit cell and mean field approaches. J. Compos. Mater. 40, 2217–2234. doi: 10.1177/,0021998306062317
EL-Dessouky, H. M., and Lawrence, C. A. (2013). Ultra-lightweight carbon fibre/thermoplastic composite material using spread tow technology. Compos. Part B Eng. 50, 91–97. doi: 10.1016/j.compositesb.2013.01.026
Eshelby, J. D. (1957). The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proc. R. Soc. Lond. A 241, 376–396. doi: 10.1098/rspa.1957.0133
Eshelby, J. D. (1959). The elastic field outside an ellipsoidal inclusion. Proc. R. Soc. Lond. A 252, 561–569. doi: 10.1098/rspa.1959.0173
Flahaut, E., Peigney, A., Laurent, C., Marliere, C., Chastel, F., and Rousset, A. (2000). Carbon nanotube-metal-oxide nanocomposites: microstructure, electrical conductivity and mechanical properties. Acta Mater. 48, 3803–3812. doi: 10.1016/S1359-6454(00)00147-6
Friebel, C., Doghri, I., and Legat, V. (2006). General mean-field homogenization schemes for viscoelastic composites containing multiple phases of coated inclusions. Int. J. Solids Struct. 43, 2513–2541. doi: 10.1016/j.ijsolstr.2005.06.035
Friedrich, K., and Almajid, A. A. (2013). Manufacturing aspects of advanced polymer composites for automotive applications. Appl. Compos. Mater. 20, 107–128. doi: 10.1007/s10443-012-9258-7
Fu, H., and Cohen, R. E. (2000). Polarization rotation mechanism for ultrahigh electromechanical response in single-crystal piezoelectrics. Nature 403, 281–283. doi: 10.1038/35002022
Gao, H. J. (2006). Application of fracture mechanics concepts to hierarchical biomechanics of bone and bone-like materials. Int. J. Fracture 138, 101–137. doi: 10.1007/s10704-006-7156-4
Gao, H. L., Chen, S. M., Mao, L. B., Song, Z. Q., Yao, H. B., Cölfen, H., et al. (2017). Mass production of bulk artificial nacre with excellent mechanical properties. Nat. Commun. 8:287. doi: 10.1038/s41467-017-00392-z
George, J., and Dvorak, Y. B. (1992). On transformation strains and uniform fields in multiphase elastic media. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 437:291. doi: 10.1098/rspa.1992.0062
Gibson, L. J., Ashby, M. F., Karam, G. N., Wegst, U., and Shercliff, H. R. (1995). The mechanical-properties of natural materials.2. Microstructures for mechanical efficiency. Proc. R. Soc. Math. Phys. Sci. 450, 141–162. doi: 10.1098/rspa.1995.0076
Giordano, S., and Palla, P. L. (2008). Dielectric behavior of anisotropic inhomogeneities: interior and exterior point Eshelby tensors. J. Phys. A Math. Theor. 41:415205. doi: 10.1088/1751-8113/41/41/415205
Gojny, F. H., Wichmann, M. H. G., Fiedler, B., Bauhofer, W., and Schulte, K. (2005). Influence of nano-modification on the mechanical and electrical properties of conventional fibre-reinforced composites. Compos. Part A Appl. Sci. Manuf. 36, 1525–1535. doi: 10.1016/j.compositesa.2005.02.007
Habas, S. E., Lee, H., Radmilovic, V., Somorjai, G. A., and Yang, P. (2007). Shaping binary metal nanocrystals through epitaxial seeded growth. Nat. Mater. 6, 692–697. doi: 10.1038/nmat1957
Hashin, Z. (1988). The differential scheme and its application to cracked materials. J. Mech. Phys. Solids 36, 719–734. doi: 10.1016/0022-5096(88)90005-1
Hashin, Z., and Shtrikman, S. (1961). Note on a variational approach to the theory of composite elastic materials. J. Franklin Inst. 271, 336–341. doi: 10.1016/0016-0032(61)90032-1
Hatta, H., and Taya, M. (1986). Equivalent inclusion method for steady-state heat-conduction in composites. Int. J. Eng. Sci. 24, 1159–1172. doi: 10.1016/0020-7225(86)90011-X
Helnwein, P. (2001). Some remarks on the compressed matrix representation of symmetric second-order and fourth-order tensors. Comput. Methods Appl. Mech. Eng. 190, 2753–2770. doi: 10.1016/S0045-7825(00)00263-2
Hill, R. (1965). A self-consistent mechanics of composite materials. J. Mech. Phys. Solids 13, 213–222. doi: 10.1016/0022-5096(65)90010-4
Hu, X., Xu, Z., Liu, Z., and Gao, C. (2013). Liquid crystal self-templating approach to ultrastrong and tough biomimic composites. Sci. Rep. 3:02374. doi: 10.1038/srep02374
Huang, J. H., and Kuo, W. S. (1996). Micromechanics determination of the effective properties of piezoelectric composites containing spatially oriented short fibers. Acta Mater. 44, 4889–4898. doi: 10.1016/S1359-6454(96)00090-0
Idiart, M. I., Danas, K., and Castaneda, P. P. (2006). Second-order theory for nonlinear composites and application to isotropic constituents. Comptes Rendus Mecanique 334, 575–581. doi: 10.1016/j.crme.2006.06.006
Imai, T., Sawa, F., Nakano, T., Ozaki, T., Shimizu, T., Kozako, M., et al. (2006). Effects of nano- and micro-filler mixture on electrical insulation properties of epoxy based composites. IEEE Trans. Dielectr. Electr. Insulat. 13, 319–326. doi: 10.1109/TDEI.2006.1624276
Immarigeon, J. P., Holt, R. T., Koul, A. K., Zhao, L., Wallace, W., and Beddoes, J. C. (1995). Lightweight materials for aircraft applications. Mater. Chara. 35, 41–67. doi: 10.1016/1044-5803(95)00066-6
Jawaid, M., Khalil, H. P. S. A., Abu Bakar, A., and Khanam, P. N. (2011). Chemical resistance, void content and tensile properties of oil palm/jute fibre reinforced polymer hybrid composites. Mater. Des. 32, 1014–1019. doi: 10.1016/j.matdes.2010.07.033
Ji, B. H., and Gao, H. J. (2004). Mechanical properties of nanostructure of biological materials. J. Mech. Phys. Solids 52, 1963–1990. doi: 10.1016/j.jmps.2004.03.006
Jun, T. S., and Korsunsky, A. M. (2010). Evaluation of residual stresses and strains using the Eigenstrain Reconstruction Method. Int. J. Solids Struct. 47, 1678–1686. doi: 10.1016/j.ijsolstr.2010.03.002
Jung, J., Lee, S., Ryu, B., and Ryu, S. (2018). Effective thermoelectric properties of a composite with interfacial resistance using a micromechanics-based homogenization. eprint arXiv:1811.11340.
Kapitza, P. L. (1941). Heat transfer and superfluidity of helium II. Phys. Rev. 60, 354–355. doi: 10.1103/PhysRev.60.354
Kim, Y., Kim, Y., Lee, T. I., Kim, T. S., and Ryu, S. (2018). An extended analytic model for the elastic properties of platelet-staggered composites and its application to 3D printed structures. Compos. Struct. 189, 27–36. doi: 10.1016/j.compstruct.2018.01.038
Lahellec, N., and Suquet, P. (2007a). On the effective behavior of nonlinear inelastic composites: I. Incremental variational principles. J. Mech. Phys. Solids 55, 1932–1963. doi: 10.1016/j.jmps.2007.02.003
Lahellec, N., and Suquet, P. (2007b). On the effective behavior of nonlinear inelastic composites: II - a second-order procedure. J. Mech. Phys. Solids 55, 1964–1992. doi: 10.1016/j.jmps.2007.02.004
Launey, M. E., Munch, E., Alsem, D. H., Barth, H. B., Saiz, E., Tomsia, A. P., et al. (2009). Designing highly toughened hybrid composites through nature-inspired hierarchical complexity. Acta Mater. 57, 2919–2932. doi: 10.1016/j.actamat.2009.03.003
Lee, S., Kim, Y., Lee, J., and Ryu, S. (2019). Applicability of the interface spring model for micromechanical analyses with interfacial imperfections to predict the modified exterior Eshelby tensor and effective modulus. eprint arXiv:1811.03411. doi: 10.1177/1081286519826343
Lee, S., Lee, J., Ryu, B., and Ryu, S. (2018a). A micromechanics-based analytical solution for the effective thermal conductivity of composites with orthotropic matrices and interfacial thermal resistance. Sci. Rep. 8:7266. doi: 10.1038/s41598-018-25379-8
Lee, S., Lee, J., and Ryu, S. (2018b). Modified Eshelby tensor for an anisotropic matrix with interfacial damage. Math. Mech. Solids. doi: 10.1177/1081286518805521
Lee, S., and Ryu, S. (2018). Theoretical study of the effective modulus of a composite considering the orientation distribution of the fillers and the interfacial damage. Euro. J. Mech. a-Solids 72, 79–87. doi: 10.1016/j.euromechsol.2018.02.008
Li, T., Zhu, M. W., Yang, Z., Song, J. W., Dai, J. Q., Yao, Y. G., et al. (2016). Wood composite as an energy efficient building material: guided sunlight transmittance and effective thermal insulation. Adv. Energy Mater. 6:1601122. doi: 10.1002/aenm.201601122
Li, Y. Q., Yu, T., Yang, T. Y., Zheng, L. X., and Liao, K. (2012). Bio-inspired nacre-like composite films based on graphene with superior mechanical, electrical, and biocompatible properties. Adv. Mater. 24, 3426–3431. doi: 10.1002/adma.201200452
Lu, Z. X., Yuan, Z. S., and Liu, Q. (2014). 3D numerical simulation for the elastic properties of random fiber composites with a wide range of fiber aspect ratios. Comput. Mater. Sci. 90, 123–129. doi: 10.1016/j.commatsci.2014.04.007
Marcos-Gomez, D., Ching-Lloyd, J., Elizalde, M. R., Clegg, W. J., and Molina-Aldareguia, J. M. (2010). Predicting the thermal conductivity of composite materials with imperfect interfaces. Compos. Sci. Technol. 70, 2276–2283. doi: 10.1016/j.compscitech.2010.05.027
Martinez-Ayuso, G., Friswell, M. I., Adhikari, S., Khodaparast, H. H., and Berger, H. (2017). Homogenization of porous piezoelectric materials. Int. J. Solids Struct. 113, 218–229. doi: 10.1016/j.ijsolstr.2017.03.003
Miled, B., Doghri, I., Brassart, L., and Delannay, L. (2013). Micromechanical modeling of coupled viscoelastic-viscoplastic composites based on an incrementally affine formulation. Int. J. Solids Struct. 50, 1755–1769. doi: 10.1016/j.ijsolstr.2013.02.004
Miled, B., Doghri, I., and Delannay, L. (2011). Coupled viscoelastic-viscoplastic modeling of homogeneous and isotropic polymers: numerical algorithm and analytical solutions. Comput. Methods Appl. Mech. Eng. 200, 3381–3394. doi: 10.1016/j.cma.2011.08.015
Milton, G. W. (2002). The theory of composites. The Theory of Composites, by Graeme W. Milton. Cambridge, UK: Cambridge University Press, 748. doi: 10.1017/CBO9780511613357
Mouritz, A. P., Gellert, E., Burchill, P., and Challis, K. (2001). Review of advanced composite structures for naval ships and submarines. Compos. Struct. 53, 21–41. doi: 10.1016/S0263-8223(00)00175-6
Mura, T. (1982). Micromechanics of Defects in Solids. Netherlands: Kluwer Academic Publishers. doi: 10.1007/978-94-011-9306-1
Nemat-Nasser, S. (1999). Averaging theorems in finite deformation plasticity. Mech. Mater. 31, 493–523. doi: 10.1016/S0167-6636(98)00073-8
Obradovic, J., Boria, S., and Belingardi, G. (2012). Lightweight design and crash analysis of composite frontal impact energy absorbing structures. Compos. Struct. 94, 423–430. doi: 10.1016/j.compstruct.2011.08.005
Odegard, G. M. (2004). Constitutive modeling of piezoelectric polymer composites. Acta Mater. 52, 5315–5330. doi: 10.1016/j.actamat.2004.07.037
Othmani, Y., Delannay, L., and Doghri, I. (2011). Equivalent inclusion solution adapted to particle debonding with a non-linear cohesive law. Int. J. Solids Struct. 48, 3326–3335. doi: 10.1016/j.ijsolstr.2011.08.002
Pan, Y., Iorga, L., and Pelegri, A. A. (2008). Numerical generation of a random chopped fiber composite RVE and its elastic properties. Compos. Sci. Technol. 68, 2792–2798. doi: 10.1016/j.compscitech.2008.06.007
Pan, Y., Weng, G. J., Meguid, S. A., Bao, W. S., Zhu, Z. H., and Hamouda, A. M. S. (2013). Interface effects on the viscoelastic characteristics of carbon nanotube polymer matrix composites. Mech. Mater. 58, 1–11. doi: 10.1016/j.mechmat.2012.10.015
Park, M., Im, J., Shin, M., Min, Y., Park, J., Cho, H., et al. (2012). Highly stretchable electric circuits from a composite material of silver nanoparticles and elastomeric fibres. Nat. Nanotechnol. 7, 803–809. doi: 10.1038/nnano.2012.206
People, R., and Bean, J. C. (1985). Calculation of critical layer thickness versus lattice mismatch for Gexsi1-X/Si strained-layer heterostructures. Appl. Phys. Lett. 47, 322–324. doi: 10.1063/1.96206
Qiu, Y. P., and Weng, G. J. (1991). Elastic-moduli of thickly coated particle and fiber-reinforced composites. J. Appl. Mech. Trans. Asme 58, 388–398. doi: 10.1115/1.2897198
Qu, J., and Cherkaoui, M. (2007). Fundamentals of Micromechanics of Solidss. Hoboken, NJ: John Wiley and Sons, Inc.
Qu, J. M. (1993). The effect of slightly weakened interfaces on the overall elastic properties of composite-materials. Mech. Mater. 14, 269–281. doi: 10.1016/0167-6636(93)90082-3
Quang, H. L., He, Q. C., and Bonnet, G. (2011). Eshelby's tensor fields and effective conductivity of composites made of anisotropic phases with Kapitza's interface thermal resistance. Philos. Mag. 91, 3358–3392. doi: 10.1080/14786435.2011.580286
Sen, D., and Buehler, M. J. (2011). Structural hierarchies define toughness and defect-tolerance despite simple and mechanically inferior brittle building blocks. Sci. Rep. 1:35. doi: 10.1038/srep00035
Shao, C., and Keten, S. (2015). Stiffness enhancement in nacre-inspired nanocomposites due to nanoconfinement. Sci. Rep. 5:16452. doi: 10.1038/srep16452
Shin, H., Yang, S., Chang, S., Yu, S., and Cho, M. (2013). Multiscale homogenization modeling for thermal transport properties of polymer nanocomposites with Kapitza thermal resistance. Polymer 54, 1543–1554. doi: 10.1016/j.polymer.2013.01.020
Shokrieh, M. M., Ghajar, R., and Shajari, A. R. (2016). The effect of time-dependent slightly weakened interface on the viscoelastic properties of CNT/polymer nanocomposites. Compos. Struct. 146, 122–131. doi: 10.1016/j.compstruct.2016.03.022
Suh, N. P. (2005). Axiomatic Design and Fabrication of Composite Structures: Applications in Robots, Machine Tools, and Automobiles. New York, NY: Oxford University Press.
Tang, Z., Kotov, N. A., Magonov, S., and Ozturk, B. (2003). Nanostructured artificial nacre. Nat. Mater. 2, 413–U418. doi: 10.1038/nmat906
Taurino, R., Lancellotti, I., Tatano, F., Carchesio, M., and Pozzi, P. (2016). Mechanical and chemical resistance of composite materials with addition of anaerobic digestate. Compos. Part B Eng. 92, 259–264. doi: 10.1016/j.compositesb.2016.02.012
Tirry, W., and Schryvers, D. (2009). Linking a completely three-dimensional nanostrain to a structural transformation eigenstrain. Nat. Mater. 8, 752–757. doi: 10.1038/nmat2488
Tuncer, E., Sauers, I., James, D. R., Ellis, A. R., Paranthaman, M. P., Aytug, T., et al. (2007). Electrical properties of epoxy resin based nano-composites. Nanotechnology 18:025703. doi: 10.1088/0957-4484/18/2/025703
Walther, A., Bjurhager, I., Malho, J. M., Pere, J., Ruokolainen, J., Berglund, L. A., et al. (2010). Large-area, lightweight and thick biomimetic composites with superior material properties via fast, economic, and green pathways. Nano Lett. 10, 2742–2748. doi: 10.1021/nl1003224
Wang, H. W., Zhou, H. W., Peng, R. D., and Mishnaevsky, L. (2011). Nanoreinforced polymer composites: 3D FEM modeling with effective interface concept. Compos. Sci. Technol. 71, 980–988. doi: 10.1016/j.compscitech.2011.03.003
Wang, Z., Zhu, J., Chen, W. Q., Jin, X. Y., and Zhang, C. Z. (2014a). Modified Eshelby tensor for an ellipsoidal inclusion imperfectly embedded in an infinite piezoelectric medium. Mech. Mater. 74, 56–66. doi: 10.1016/j.mechmat.2014.03.005
Wang, Z., Zhu, J., Jin, X. Y., Chen, W. Q., and Zhang, C. (2014b). Effective moduli of ellipsoidal particle reinforced piezoelectric composites with imperfect interfaces. J. Mech. Phys. Solids 65, 138–156. doi: 10.1016/j.jmps.2013.12.007
Wegst, U. G. K., and Ashby, M. F. (2004). The mechanical efficiency of natural materials. Philos. Mag. 84, 2167–2181. doi: 10.1080/14786430410001680935
Wei, G. S., Liu, Y. S., Zhang, X. X., Yu, F., and Du, X. Z. (2011). Thermal conductivities study on silica aerogel and its composite insulation materials. Int. J. Heat Mass Transf. 54, 2355–2366. doi: 10.1016/j.ijheatmasstransfer.2011.02.026
Wu, L., Noels, L., Adam, L., and Doghri, I. (2013). A combined incremental-secant mean-field homogenization scheme with per-phase residual strains for elasto-plastic composites. Int. J. Plast. 51, 80–102. doi: 10.1016/j.ijplas.2013.06.006
Xu, Y. B., and Yagi, K. (2004). Automatic FEM model generation for evaluating thermal conductivity of composite with random materials arrangement. Comput. Mater. Sci. 30, 242–250. doi: 10.1016/j.commatsci.2004.03.011
Yanase, K., and Ju, J. W. (2012). Effective elastic moduli of spherical particle reinforced composites containing imperfect interfaces. Int. J. Damage Mech. 21, 97–127. doi: 10.1177/1056789510397076
Yang, B. J., Shin, H., Kim, H., and Lee, H. K. (2014). Strain rate and adhesive energy dependent viscoplastic damage modeling for nanoparticulate composites: Molecular dynamics and micromechanical simulations. Appl. Phys. Lett. 104, 101901–101904. doi: 10.1063/1.4868034
Yang, B. J., Shin, H., Lee, H. K., and Kim, H. (2013a). A combined molecular dynamics/micromechanics/finite element approach for multiscale constitutive modeling of nanocomposites with interface effects. Appl. Phys. Lett. 103:241903. doi: 10.1063/1.4819383
Yang, S., Yu, S., Kyoung, W., Han, D. S., and Cho, M. (2012). Multiscale modeling of size-dependent elastic properties of carbon nanotube/polymer nanocomposites with interfacial imperfections. Polymer (Guildf). 53, 623–633. doi: 10.1016/j.polymer.2011.11.052
Yang, S., Yu, S., Ryu, J., Cho, J. M., Kyoung, W., Han, D. S., et al. (2013b). Nonlinear multiscale modeling approach to characterize elastoplastic behavior of CNT/polymer nanocomposites considering the interphase and interfacial imperfection. Int. J. Plast. 41, 124–146. doi: 10.1016/j.ijplas.2012.09.010
Yu, H. Y., Sanday, S. C., and Chang, C. I. (1994). Elastic inclusions and inhomogeneities in transversely isotropic solids. Proc. R. Soc. Math. Phys. Sci. 444, 239–252. doi: 10.1098/rspa.1994.0014
Zhao, L. D., Lo, S. H., Zhang, Y., Sun, H., Tan, G. J., Uher, C., et al. (2014). Ultralow thermal conductivity and high thermoelectric figure of merit in SnSe crystals. Nature 508, 373-+. doi: 10.1038/nature13184
Zheng, Y., Chonung, K., Wang, G. L., Wei, P., and Jiang, P. K. (2009). Epoxy/nano-silica composites: curing kinetics, glass transition temperatures, dielectric, and thermal-mechanical performances. J. Appl. Polym. Sci. 111, 917–927. doi: 10.1002/app.28875
Keywords: homogenization, micromechanics, anisotropy, interfacial imperfection, effective properties
Citation: Ryu S, Lee S, Jung J, Lee J and Kim Y (2019) Micromechanics-Based Homogenization of the Effective Physical Properties of Composites With an Anisotropic Matrix and Interfacial Imperfections. Front. Mater. 6:21. doi: 10.3389/fmats.2019.00021
Received: 30 November 2018; Accepted: 04 February 2019;
Published: 01 March 2019.
Edited by:
Nicola Maria Pugno, University of Trento, ItalyReviewed by:
Pasquale Vena, Polytechnic University of Milan, ItalyStefano Mariani, Polytechnic University of Milan, Italy
Copyright © 2019 Ryu, Lee, Jung, Lee and Kim. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Seunghwa Ryu, cnl1c2hAa2Fpc3QuYWMua3I=
†These authors have contributed equally to this work
 Seunghwa Ryu
Seunghwa Ryu Sangryun Lee
Sangryun Lee Jiyoung Jung
Jiyoung Jung Jinyeop Lee
Jinyeop Lee Youngsoo Kim
Youngsoo Kim