- Applied Mathematics and Structural Mechanics Lab (LiMES), Department of Architecture, RomaTre University, Rome, Italy
The paper presents a nonlinear buckling analysis of single-layer graphene sheets using a molecular mechanics model which accounts for binary, ternary, and quaternary interactions between the atoms. They are described using a geometrically exact setting and by the introduction of Morse and cosine potential functions, equipped with an appropriate set of parameters. We examine the critical and post-critical behaviors of graphene, under compression in the zigzag and in the armchair directions, and shear. Our findings show the suitability of standard thin-plates theory for the prediction of simple critical behaviors under various edge constraint conditions.
1. Introduction
Graphene is a two-dimensional hexagonal lattice of carbon atoms with unique physical and mechanical properties (Young et al., 2012), such as high room-temperature carrier mobility, high thermal conductivity, high tensile strength and stiffness and weak optical absorptivity. Owing to these remarkable properties, graphene has attracted considerable attention for applications in many fields (Choi et al., 2010; Li et al., 2014; Aïssa et al., 2015; Sun et al., 2015; Nguyen and Nguyen, 2016; Kumar et al., 2018; Mohan et al., 2018), including energy generation and storage (e.g., photovoltaic cells, hydrogen storage, supercapacitors), sensoring and actuating systems (e.g., gas sensors), electronics (e.g., conductive inks and flexible films), biotechnologies (e.g., membranes for water filtration, gas separation, DNA sequencing), composites.
The understanding and the control of the mechanical behaviors of graphene are crucial issues (Young et al., 2012; Akinwande et al., 2017) for many applications such as composites, membranes for water filtration, hydrogen storage and electronic devices. In this regard, it is worth emphasizing also that chemical-physical properties of any material at the nanoscale depend on the relative atomic positions. Tuning these properties in specific devices through deformation control is therefore possible, in principle.
The importance for these applications has motivated continuously increasing research efforts to understand the details of the mechanical response of graphene.
However, the technical difficulties and the costs of nanoscale experiments combine to make theoretical modeling approaches preferable. Among them, ab-initio simulations (Kudin et al., 2001; Baumeier et al., 2007; Liu et al., 2007) are the most accurate tools available to investigate the behavior of nanomaterials, including their mechanics, but they demand a lot of computer power and so they are not always feasible for systems with very many atoms. For this reason, increasing attention has been given to molecular dynamics/statics formulations (Liew et al., 2004; Lu et al., 2009; Xiao et al., 2009; Zhao et al., 2009; Georgantzinos et al., 2012; Silvestre et al., 2012; Berinskii and Borodich, 2013; Davini, 2014; Theodosiou and Saravanos, 2014; Gamboa et al., 2015; Korobeynikov et al., 2015, 2018; Budarapu et al., 2017; Davini et al., 2017; Genoese et al., 2017, 2018a,b, 2019; Hossain et al., 2018; Sgouros et al., 2018; Singh and Patel, 2018b) or their structural-mechanical approximations (e.g., nanoscale equivalent beam and truss models; Sakhaee-Pour, 2009a,b; Georgantzinos et al., 2010; Alzebdeh, 2012; Giannopoulos, 2012; Tserpes, 2012; Firouz-Abadi et al., 2016; Rafiee and Eskandariyun, 2017; Savvas and Stefanou, 2018) and to continuum models (Chang, 2010; Aminpour and Rizzi, 2016; Ghaffari et al., 2018; Singh and Patel, 2018a; Zhang et al., 2018).
Most of the research on graphene has focused on its rigidities, the frequencies of free vibration, and tensile failure properties and this has produced also a refinement of the parameters of simple bonding potentials (Genoese et al., 2017; Hossain et al., 2018; Korobeynikov et al., 2018), such as the DREIDING, the Stillinger-Weber or the modified Morse potentials. Currently, molecular statics formulations based on these potentials are considered to be the best compromise at the atomistic scale in non-linear contexts, where the simplicity of the models is a major requirement. Nevertheless, studies on out-of-plane buckling behaviors of graphene are not numerous (Sakhaee-Pour, 2009a; Duan et al., 2011; Giannopoulos, 2012; Korobeynikov et al., 2015; Firouz-Abadi et al., 2016; Sgouros et al., 2018). Duan (Duan et al., 2011) has investigated the development of wrinkles in rectangular graphene sheets under increasing in-plane shear displacements using the COMPASS potential. Modes jump phenomena have been reported, with sudden changes of the number of wrinkles as the displacements increase. Similar trends have been observed by Huang and Han (2017) through molecular dynamics simulations performed using the AIREBO potential. Sakhaee-Pour (2009a), Giannopoulos (2012), and Firouz-Abadi et al. (2016) have studied the linearised buckling of compressed graphene sheets and ribbons described as assemblages of Bernoulli-like beams and truss elements. Korobeynikov et al. (2015) have studied the buckling and the initial post-buckling of compressed graphene using the DREIDING potential. Very recently, Sgouros et al. (2018) have investigated compressed ribbons under various temperatures via molecular dynamics simulations incorporating the LCBOP potential.
In the present study, we propose a buckling analysis of single-layer graphene sheets through a molecular mechanics model which extends those used in our previous works (Genoese et al., 2017, 2018a,b, 2019) in order to account for binary, ternary and quaternary interactions between the atoms. They are described using a geometrically exact setting and introducing Morse and cosine potential functions, equipped with a proper set of parameters. To this regard, following the reasoning already proposed in Genoese et al. (2017, 2018a, 2019), a constitutive problem is solved only for purposes of giving a new parametrization of the dihedral potential. Then, by solving the equilibrium equations of the atomistic system through the arc-length strategy, we obtain the critical and post-critical behaviors of graphene under compression in the zigzag and in the armchair directions and shear. Case by case, the equilibrium paths are shown and the critical behaviors are discussed in comparison with available solutions for thin-plates (Timoshenko and Gere, 1963).
2. Materials, Model, and Methods
2.1. The Molecular Mechanics Model
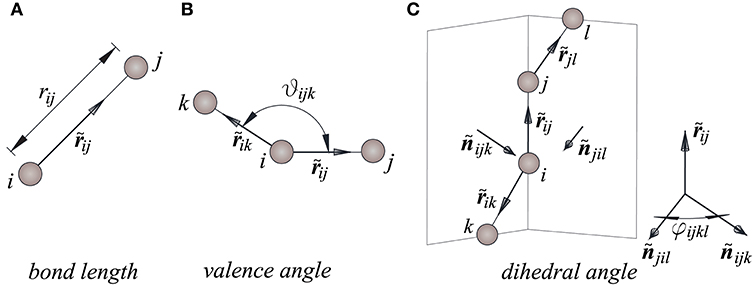
We assume that the reference configuration of the sheet is planar and stress free and that the atoms are point-particles in Euclidean space. Their interactions are usually separated into bonding interactions and long-range ones. Long-range interactions are considered to be negligible with respect to the bonding ones. In turn, bonding interactions are usually distinguished between binary, ternary and quaternary interactions, measured in terms of the bond length rij, valence angle θijk and dihedral angle φijkl (see Figure 1). The bonding interactions are derived from a potential U, here expressed in the additive form
where , , and are the energy contributions related to the bth bond length, to the ath valence angle and to the dth dihedral angle, respectively. In this paper, we use Morse and cosine energy functions (Mayo et al., 1990), which are defined to be
In Equations (2), nm, and , are the length and angles in the resting configuration, Ū is the bond breaking energy, β, C and V are parameters which we define below and p = 2.
We denote by xn and un the initial position vector of the nth atom and its displacement vector. Then, its current position vector is given by rn = xn + un. Similarly, xij = xj − xi, rij = rj − ri, and uij = uj − ui are the relative position vectors and the relative displacement vector of the atom j with respect to the atom i. Vector rij can be expressed as rij = xij + uij.
The bond length is given by
For what follows, is the direction vector defined by a pair of atoms i-j. In addition, and are, respectively, the unit vectors perpendicular to the plane determined by the current positions of the atoms i, j and k and to the plane determined by the current positions of the atoms j, l and i, given by:
The valence angle and the dihedral angle are defined as follows:
This said, the variations of rij, cosθijk and φijkl are given by
where
We refer to Blondel and Karplus (1996), Korobeynikov et al. (2015), and Genoese et al. (2019) for more details. The equilibrium configurations of the system are sought through the stationarity condition of its total potential energy
where U, defined in Equations (1, 2), is a function of the displacements of the atoms by means of Equations (3–5), and pn is the force applied to the nth atom. Recalling Equation (6), the variation of the potential U is
where
are the binary, ternary and quaternary interatomic force vectors. Finally, the equilibrium equations assume the following form
for any δun.
2.2. Nanoscale Material Parameters
The potential functions given in Equation (2) are characterized by four parameters, Ū,β, C and V. In this work, we use β = 21.671 1/nm, Ū = 0.79 aJ, and C = 1.893 aJ, which provide the force constants kr = 742 nN/nm and kθ = 1.42 aJ, since these values have shown to well describe the in-plane strength and rigidity of graphene (Genoese et al., 2017). In order to properly define V, we associate the potential related to the dihedral angle to that of a plate with thickness tending to zero in linearized elasticity. By doing this, it can be shown that the following equality holds1:
where D is the bending stiffness of the plate. Then, V is calculated from the ab-initio result D = 0.234 aJ in Kudin et al. (2001), and it results to be V = 0.029 aJ. Last but not least, we obtain the value of the corresponding force constant kφ, given by
2.3. Numerical Methods
The model has been implemented in the MATLAB” language. By using FEM standard assembly procedures the equilibrium equations are recast in the global form
where u collects all the kinematic variables, s is the inner force vector and p collects all the external loads which we express in the form , λ being a scalar load multiplier and the nominal loads vector. The pairs (u, λ) that satisfy Equation (13) define the equilibrium path of the graphene sheet. In this work it is obtained through the Riks arc-length method (Riks, 1979, 1984).
As opposed to the traditional step-by-step procedures based on a parametrization of the equilibrium path in terms of the load multiplier λ or of any displacement variable, the arc-length method describes the equilibrium path in terms of the variable ξ related to the arc-length. This implies adding a new constraint equation ξ = g[u, λ]. The equilibrium points of the path are then obtained by solving a non-linear extended system, using the Modified Newton-Raphson method and condensing the constraint equation in order to assemble and decompose only the stiffness matrix . The modified set of equations become singular only at a bifurcation point that, however, can be transformed into a simple fold by introducing small imperfection loads spending work on the critical direction.
The numerical analysis becomes more complex when multiple simultaneous or nearly simultaneous modes are found on the fundamental equilibrium path. Using a step-by-step numerical algorithm based on Riks arc-length strategy, the presence of simultaneous or nearly simultaneous modes manifests itself in the form of abrupt changes of the equilibrium configurations, named as mode jumping in the literature (Duan et al., 2011). In these cases, the prior knowledge of such critical modes is necessary in order to understand which of these directions (or linear combination thereof) are actually reachable in post-critical analysis and which, instead, are geometrical loci of secondary bifurcations. For this purpose, any step of the analysis has been accompanied by the updating of the tangent stiffness matrix and determination of its kernel, by eigenvalue analysis, at very close values of the load parameter λ.
3. Results
Numerical benchmark examples regarding graphene sheets under compression and shear are solved.
3.1. Square Graphene Under Compression and Shear
Figure 2 shows the geometrical configuration of a nearly square graphene sheet (a = 10.508 nm and b = 10.084 nm) and, in some detail, the loading conditions for the compression tests, in both zigzag and armchair directions, and for the pure shear test. The compression tests are carried out considering constraint conditions of simple support for the only loaded sides and for all the sides. The shear test is carried out considering conditions of simple support for all the sides. In all cases, N = 1 nN/nm is assumed. In addition, small imperfection forces, perpendicular to the plane of the sheet, are applied in correspondence to the atoms evidenced in red that are assumed to be control points to give the equilibrium paths.
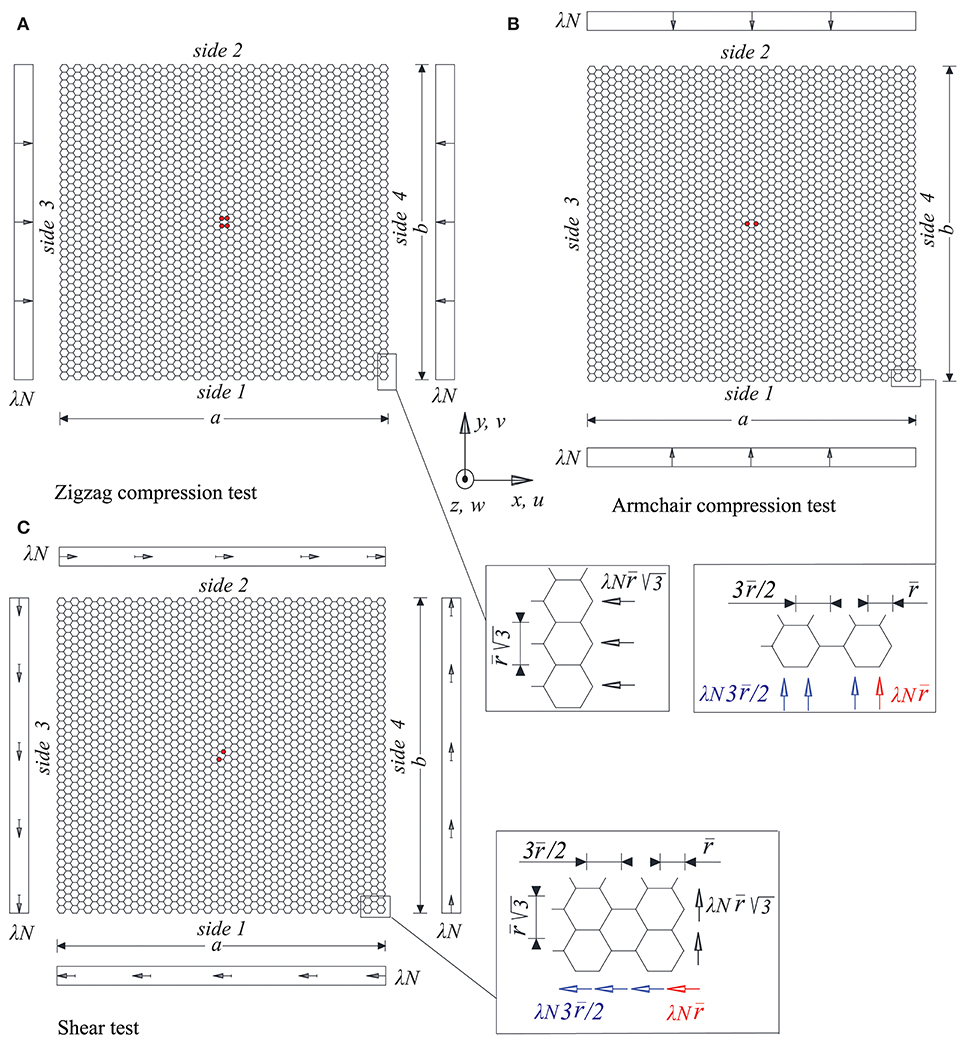
Figure 2. Schemes of the compression and shear tests of the nearly square graphene sheet: (A,B) geometry and details of the applied loads for the compression tests in the zigzag and in the armchair directions, (C) geometry, and details of the applied loads for the shear test.
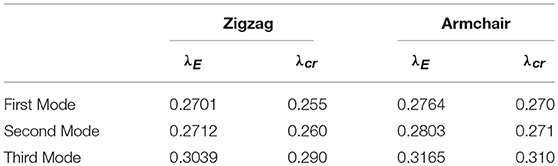
In Figures 3, 4 the results of the compression tests in the case of two supported edges are shown. The equilibrium paths, very far beyond the first critical point, and the deformed configurations, at the points A and B, respectively, are depicted, revealing a typical stable behavior from Euler compressed rods. The comparison between critical multiplier values λcr and those obtained analytically by the Eulerian formula for the zigzag case, and for the armchair case is shown in Table 1 which, on one hand, shows a good agreement between numerical and analytical results and, on the other hand, highlights the very low influence of chirality in the out-of plane nonlinear behavior of these nanostructures as already noticed in Sgouros et al. (2018). The small numerical differences found in the values calculated for zigzag and armchair cases are mostly related to the different values of a and b.
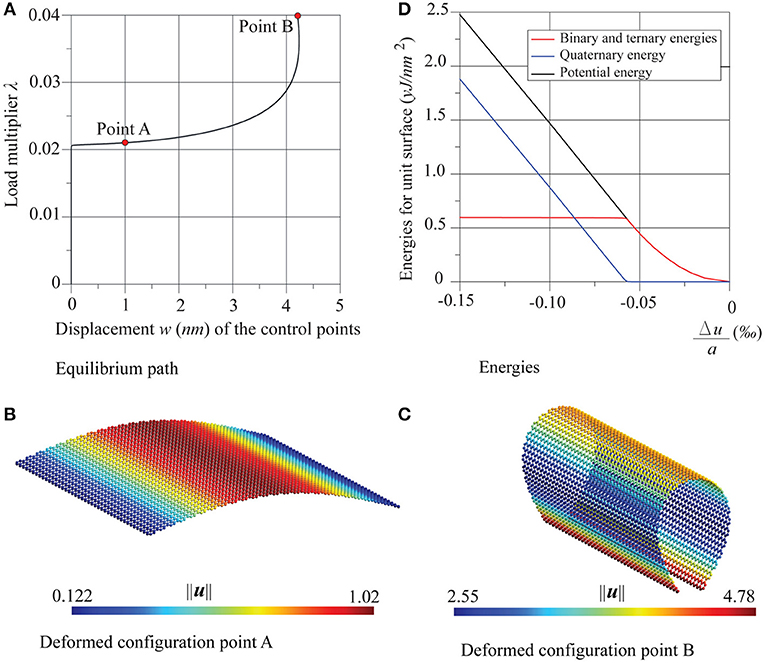
Figure 3. Graphene sheet with two supported edges under compression in the zigzag direction: (A) equilibrium path, (B,C) deformed configurations at the points A and B, and (D) energies trends.
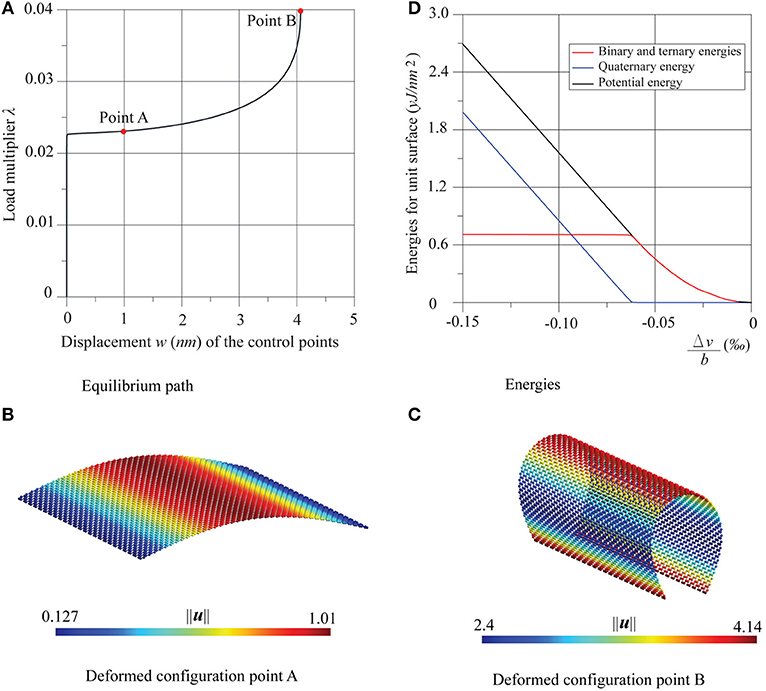
Figure 4. Graphene sheet with two supported edges under compression in the armchair direction: (A) equilibrium path, (B,C) deformed configurations at the points A and B, and (D) energies trends.
In the same Figures 3, 4 the trends of the potential energy of the sheet are shown, in the range of the equilibrium path between the initial undeformed configuration and that immediately successive to the critical one. Also, the energy contributions are shown as decoupled, separating the contribution due to membrane deformation, that is, the sum of binary and ternary energies, from the quaternary contribution, which is inherently flexural. All the energies are measured with respect to the resting state of the sheet and divided by its reference surface a × b, while the deformation of the sheet is given in terms of the non-dimensional relative displacements Δu/a = (ū4 − ū3)/a and , ūk and being the mean values of the displacements along x and y on the side k.
Diagrams show that in these two cases pre-critical behavior employs purely membranal energy, while post-critical behavior uses bending energy. Moreover, it is worth noting that energy is quadratic in the pre-critical behavior, which coincides with what was reported in the literature (Liew et al., 2004; Silvestre et al., 2012) for compressed carbon nanotubes.
In Figures 5, 6 the results of the compression tests in the case of four supported edges are shown. The equilibrium paths and the deformed configurations, in the points A, B, and C are reported. The sheet presents a similar behavior, both with regard to the equilibrium path and the deformed configurations regardless of the direction of the compression. After an initial stable post-critical behavior (point A), the equilibrium paths present a limit load configuration (point B), followed by an unstable branch. The deformed configurations are similar, corresponding to the three points A, B, and C, which turn out first bubble-shaped and then increasingly wrapped.
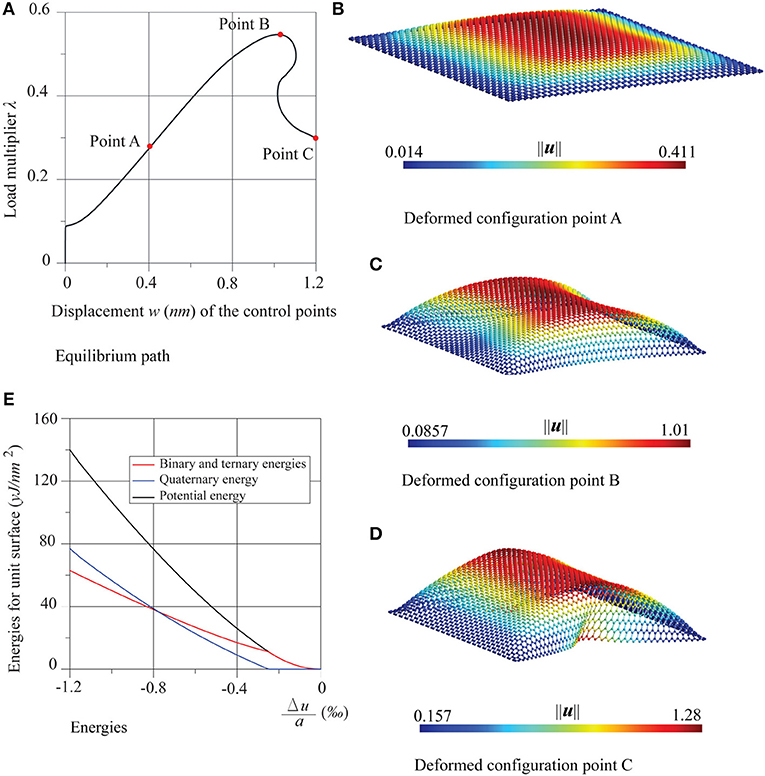
Figure 5. Graphene sheet with four supported edges under compression in the zigzag direction: (A) equilibrium path, (B–D) deformed configurations at the points A, B and C, and (E) energies trends.
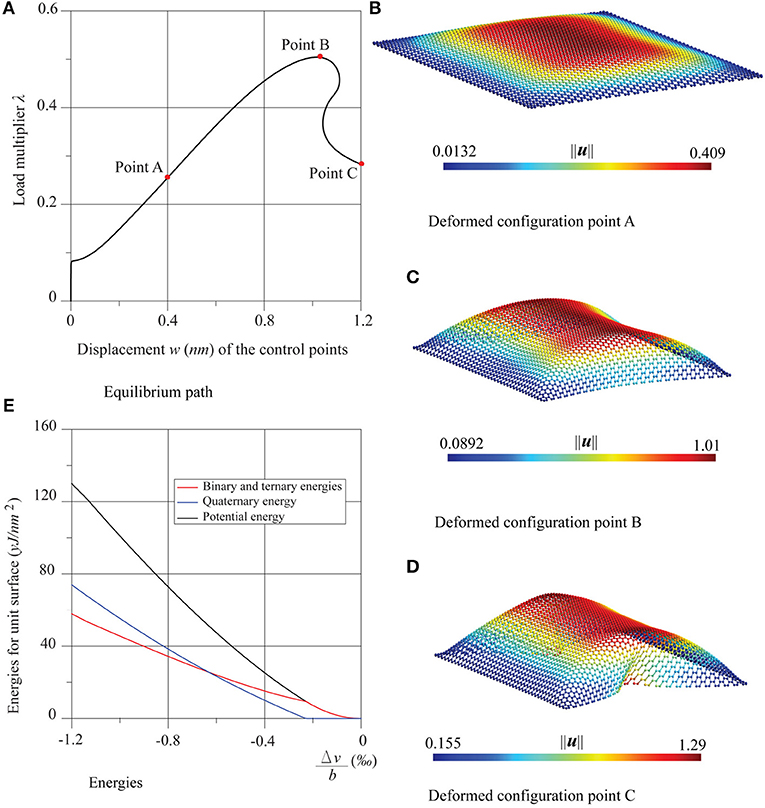
Figure 6. Graphene sheet with four supported edges under compression in the armchair direction: (A) equilibrium path, (B–D) deformed configurations at the points A, B and C, and (E) energies trends.
Once again, the comparison is positive between the numerical critical multiplier values λcr, and those obtained analytically by the formulas of buckling of Timoshenko (Timoshenko and Gere, 1963) for fully supported thin plates, namely for the zigzag case and for the armchair case, with k = 4. The comparison is given in Table 2, which highlights the very low influence of chirality in the nonlinear behavior of these nanostructures. In the same Figures 5, 6, the energy diagrams reveal that the pre-critical behavior of the sheets is likewise purely membranal and characterized by a linear behavior. However, unlike in the previous examples, in the post-critical behavior, membranal and flexural energies coexist. The same considerations can be made for the shear test, whose results are shown in Figure 7, where Δu = ū2 − ū1 and .
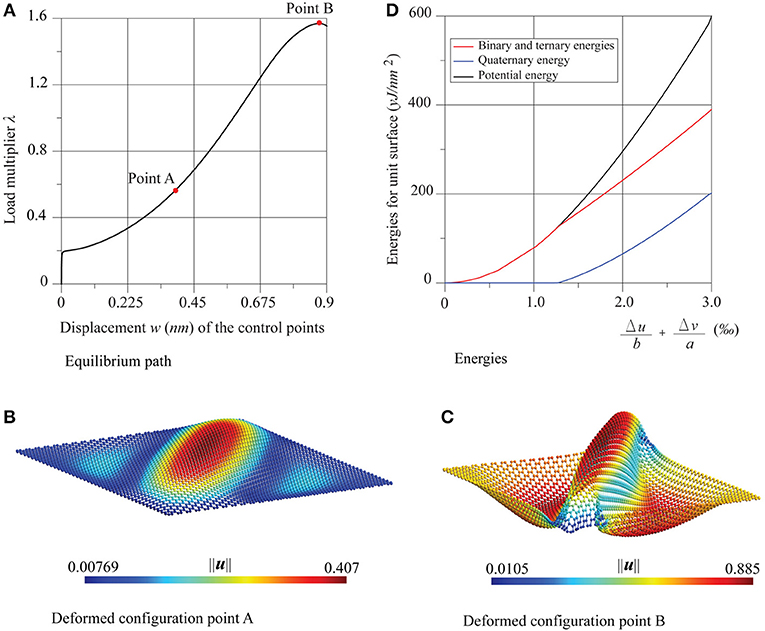
Figure 7. Graphene sheet under shear: (A) equilibrium path, (B,C) deformed configurations at the points A and B, and (D) energies trends.
The equilibrium path, after an initial stable post-critical behavior (point A), presents a limit load (point B). The critical multiplier estimated numerically λcr agrees well with the analytical value predicted by the theory of Timoshenko (Timoshenko and Gere, 1963) for thin plates subjected to shear, that is where k = 5.35 + 4(b/a)2 = 9.0337. The comparison is as follows:
The initial post-critical configuration (point A) has the shape of a bubble elongated toward the direction of the principal traction, already highlighted in the literature (Huang and Han, 2017). At the limit load configuration (point B) the deformation is accentuated and, in addition to the diagonal crest, two lateral troughs arise.
3.2. Graphene Strips Under Compression
Figure 8 shows the geometry and the nodal loads of the strips under compression in the zigzag (a = 20.306 nm and b = 5.91 nm) and in the armchair (a = 19.676 nm and b = 5.822 nm) directions. In both cases only conditions of simple support for the entire boundary are imposed and N = 1 nN/nm is assumed. The analyses have turned out to be more complex than in the case of the nearly square sheet, due to the presence of nearly simultaneous modes.
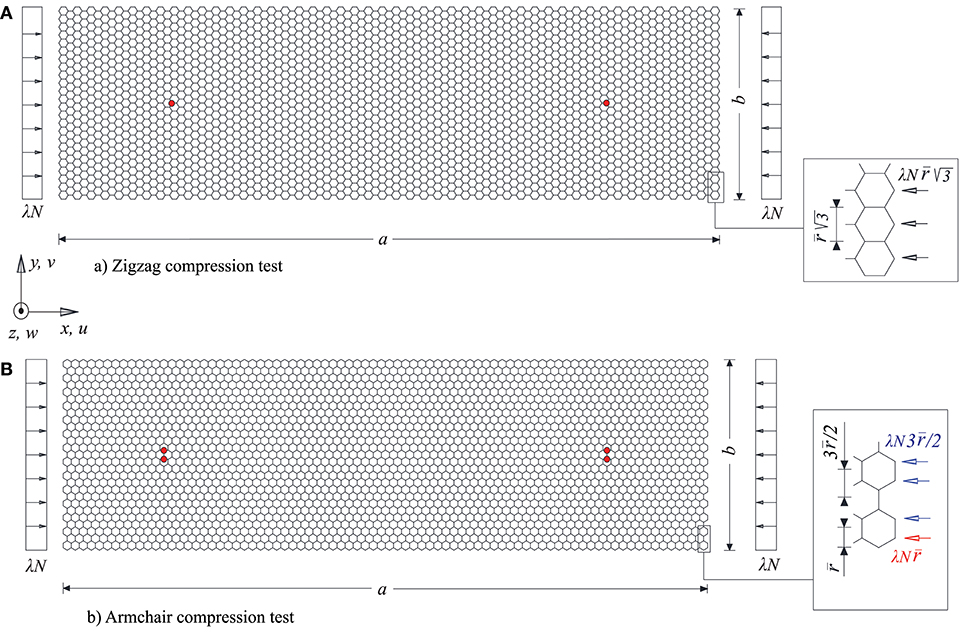
Figure 8. Schemes of the compression tests of the graphene strips: (A) geometry and details of the applied loads for the compression test in the zigzag direction, (B) geometry, and details of the applied loads for the compression test in the armchair direction.
In that regard, Figures 9, 11 show that in both cases, the fundamental equilibrium path presents three nearly simultaneous modes, two of them almost coincident and the third one at a small distance from the first two. The critical multipliers determined by numerical analyses λcr show a good agreement with the analytical solution provided by Timoshenko for the first three critical modes for the same problem, whose expressions are , where k = (mb/a + a/(bm))2, m is the number of the half-waves of the critical mode. The comparison between numerical and analytical results is shown in Table 3.
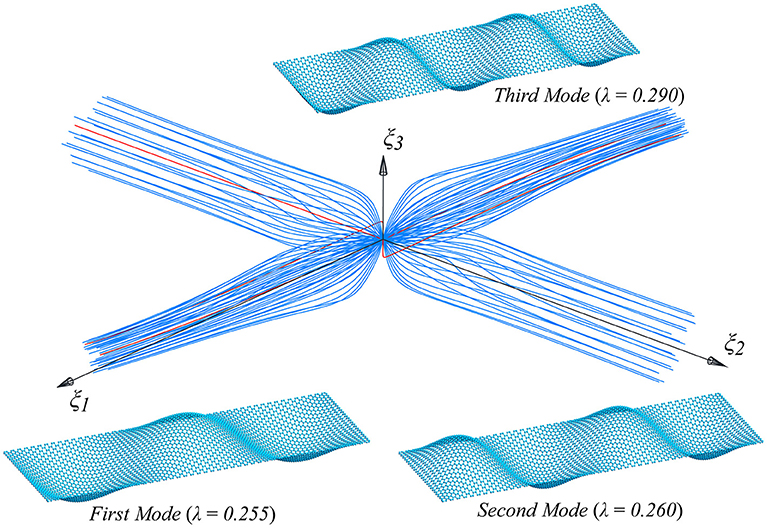
Figure 9. Supported graphene strips under compression in the zigzag direction: first three buckling modes and their interaction.
As can be seen in Figures 9, 11 many post-critical equilibrium paths are obtained when small imperfection loads are added, which are chosen to be a linear combination of the critical modes, and are projected onto the modal subspace (ξ1, ξ2, ξ3) (Salerno and Casciaro, 1997). The number of overall analysis is 114, and each of them is characterized by a different shape (or direction) of the imperfection. In agreement with the literature (Salerno and Casciaro, 1997), the 114 equilibrium paths cluster around only two directions, the first two modes, whichever is the initial imperfection to which the path is initially pushed, creating the typical zone of post-critical attractiveness, with sudden post-critical bifurcations, shown in Figures 9, 11, when moving in the direction of the third mode, which are usually called mode jumping.
That said, if we focus our attention just on the imperfection in the direction of the first mode, we get only one equilibrium path, characterized by the smallest limit load value, by the parity of the norm of the additional imperfection.
Figures 10, 12 show the paths relative to this imperfection with reference to the zigzag and the armchair case, respectively. In both cases, the displacement in abscissa is the transversal one of the control points evidenced in red in Figure 8. The paths share the same features: after an initial stable bifurcation, a limit load point is reached, followed by an unstable behavior. For both cases three successive configurations, in the points A, B, and C of the equilibrium path, are depicted. After an initial configuration characterized by three half-waves (point A), similarly to the selected critical mode, the successive configurations (points B and C) take a more wrapped form, also characterized by an approach of the edges of the strip left free to move horizontally. Both in terms of equilibrium path and of deformed configurations, the chirality has very little influence.
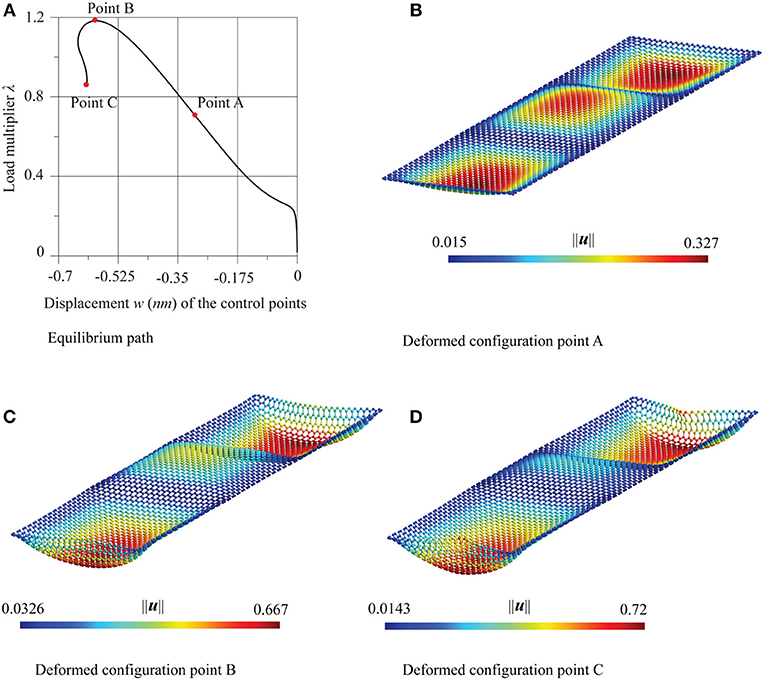
Figure 10. Supported graphene strips under compression in the zigzag direction: (A) equilibrium path and (B–D) deformed configurations at the points A, B, and C.
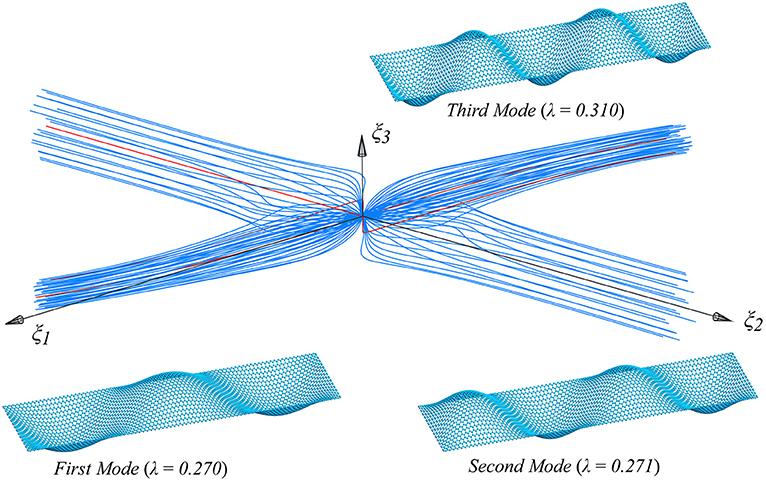
Figure 11. Supported graphene strips under compression in the armchair direction: first three buckling modes and their interaction.
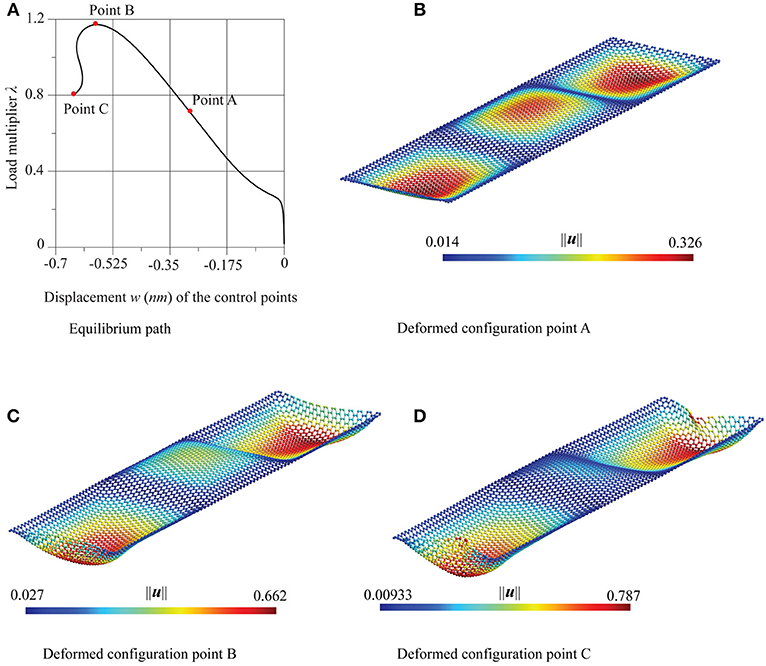
Figure 12. Supported graphene strips under compression in the armchair direction: (A) equilibrium path and (B–D) deformed configurations at the points A, B, and C.
4. Conclusions
In the present paper, the critical and post-critical behaviors of graphene, under compression in the zigzag and in the armchair directions, and shear have been investigated. A molecular mechanics model that takes into account binary, ternary and quaternary interactions has been implemented extending our previous works (Genoese et al., 2017, 2018a,b, 2019) in which only the in-plane behavior of graphene has been addressed. A geometrically exact setting and Morse and cosine potential functions, equipped with a proper set of parameters have been used to model the interatomic interactions and, at the same time, a new parametrization of the dihedral potential has been given. For each case study, the equilibrium path has been reconstructed in the advanced post-critical behavior through the arc-length strategy and some deformed configurations, deemed to be the most significant, have been displayed. This adds significantly to the existing literature, as this type of behavior has so far been little investigated. Our findings show the suitability of standard thin-plates theories to predict simple critical behaviors both for nearby square sheets, under various edge constraint conditions, and strips. Moreover, they highlight the very low influence of chirality in the nonlinear behavior of these nanostructures. The research work carried out in this paper could be the first step toward investigating the nonlinear behavior of 2D nanomaterials other than graphene or of more complex 3-dimensional nanostructures, such as tubes.
Author Contributions
ALG and ANG developed the formulation and the implementation of the molecular mechanics model under the supervision of GS and NR. All the authors collaborated on the writing of the manuscript.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We are very grateful to the University Roma Tre for cofunding the research contracts of Ph.D. ALG and ANG.
Footnotes
1. ^Analytical developments will be given in a forthcoming paper.
References
Aïssa, B., Memon, N. K., Ali, A., and Khraisheh, M. K. (2015). Recent progress in the growth and applications of graphene as a smart material: a review. Front. Mater. 2:58. doi: 10.3389/fmats.2015.00058
Akinwande, D., Brennan, C. J., Bunch, J. S., Egberts, P., Felts, J. R., and Gao, H. (2017). A review on mechanics and mechanical properties of 2D materials-graphene and beyond. Extreme Mech. Lett. 13, 42–72. doi: 10.1016/j.eml.2017.01.008
Alzebdeh, K. (2012). Evaluation of the in-plane effective elastic moduli of single-layered graphene sheet. Int. J. Mech. Mater. Des. 8, 269–278. doi: 10.1007/s10999-012-9193-7
Aminpour, H., and Rizzi, N. (2016). A one-dimensional continuum with microstructure for single-wall carbon nanotubes bifurcation analysis. Math. Mech. Solids 21, 168–181. doi: 10.1177/1081286515577037
Baumeier, B., Krüger, P., and Pollmann, J. (2007). Structural, elastic, and electronic properties of SiC, BN, and BeO nanotubes. Phys. Rev. B 76:085407. doi: 10.1103/PhysRevB.76.085407
Berinskii, I. E., and Borodich, F. M. (2013). Elastic in-plane properties of 2D linearized models of graphene. Mech. Mater. 62, 60–68. doi: 10.1016/j.mechmat.2013.03.004
Blondel, A., and Karplus, M. (1996). New formulation for derivatives of torsion angles and improper torsion angles in molecular mechanics: Elimination of singularities. J. Comput. Chem. 17, 1132–1141.
Budarapu, P. R., Javvaji, B., Sutrakar, V. K., Mahapatra, D. R., Paggi, M., Zi, G., et al. (2017). Lattice orientation and crack size effect on the mechanical properties of Graphene. Int. J. Fract. 203, 81–98. doi: 10.1007/s10704-016-0115-9
Chang, T. (2010). A molecular based anisotropic shell model for single-walled carbon nanotubes. J. Mech. Phys. Solids 58, 1422–1433. doi: 10.1016/j.jmps.2010.05.004
Choi, W., Lahiri, I., Seelaboyina, R., and Kang, Y. S. (2010). Synthesis of graphene and its applications: a review. Crit. Rev. Solid State Mater. Sci. 35, 52–71. doi: 10.1080/10408430903505036
Davini, C. (2014). Homogenization of a graphene sheet. Continuum Mech. Thermodyn. 26, 95–113. doi: 10.1007/s00161-013-0292-y
Davini, C., Favata, A., and Paroni, R. (2017). The Gaussian stiffness of graphene deduced from a continuum model based on Molecular Dynamics potentials. J. Mech. Phys. Solids 104, 96–114. doi: 10.1016/j.jmps.2017.04.003
Duan, W. H., Gong, K., and Wang, Q. (2011). Controlling the formation of wrinkles in a single-layer graphene sheet subjected to in-plane shear. Carbon 49, 3107–3112. doi: 10.1016/j.carbon.2011.03.033
Firouz-Abadi, R. D., Moshrefzadeh-Sany, H., Mohammadkhani, H., and Sarmadi, M. (2016). A modified molecular structural mechanics model for the buckling analysis of single layer graphene sheet. Solid State Commun. 225, 12–16. doi: 10.1016/j.ssc.2015.10.009
Gamboa, A., Vignoles, G. L., and Leyssale, J.-M. (2015). On the prediction of graphene's elastic properties with reactive empirical bond order potential. Carbon 89, 176–187. doi: 10.1016/j.carbon.2015.03.035
Genoese, A., Genoese, A., and Rizzi, N. L. G S (2017). On the derivation of the elastic properties of lattice nanostructures: the case of graphene sheets. Compos B Eng. 115, 316–329. doi: 10.1016/j.compositesb.2016.09.064
Genoese, A., Genoese, A., Rizzi, N. L., and Salerno, G. (2018a). Force constants of BN, SiC, AlN and GaN sheets through discrete homogenization. Meccanica 53, 593–611. doi: 10.1007/s11012-017-0686-1
Genoese, A., Genoese, A., and Salerno, G. (2018b). Elastic constants of achiral single-wall CNTs: analytical expressions and a focus on size and small scale effects. Compos B Eng. 147, 207–226. doi: 10.1016/j.compositesb.2018.04.016
Genoese, A., Genoese, A., and Salerno, G. (2019). On the nanoscale behaviour of single-wall C, BN and SiC nanotubes. Acta Mech. doi: 10.1007/s00707-018-2336-7 [Epubh ahead of print].
Georgantzinos, S. K., Giannopoulos, G. I., and Anifantis, N. K. (2010). Numerical investigation of elastic mechanical properties of graphene structures. Mater. Des. 31, 4646–4654. doi: 10.1016/j.matdes.2010.05.036
Georgantzinos, S. K., Katsareas, D. E., and Anifantis, N. K. (2012). Limit load analysis of graphene with pinhole defects: a nonlinear structural mechanics approach. Int. J. Mech. Sci. 55, 85–94. doi: 10.1016/j.ijmecsci.2011.12.006
Ghaffari, R., Duong, T. X., and Sauer, R. A. (2018). A new shell formulation for graphene structures based on existing ab-initio data. Int. J. Solids Struct. 135, 37–60. doi: 10.1016/j.ijsolstr.2017.11.008
Giannopoulos, G. I. (2012). Elastic buckling and flexural rigidity of graphene nanoribbons by using a unique translational spring element per interatomic interaction. Comput. Mater. Sci. 53, 338–395. doi: 10.1016/j.commatsci.2011.08.027
Hossain, M. Z., Hao, T., and Silverman, B. (2018). Stillinger-Weber potential for elastic and fracture properties in graphene and carbon nanotubes. J. Phys. Condens Matter 30:055901. doi: 10.1088/1361-648X/aaa3cc
Huang, J., and Han, Q. (2017). A molecular dynamic study on wrinkles in graphene with simply supported boundary under in-plane shear. J. Nanomater. 2017:1326790. doi: 10.1155/2017/1326790
Korobeynikov, S. N., Alyokhin, V. V., Annin, B. D., and Babichev, A. V. (2015). Quasi-static buckling simulation of single-layer graphene sheets by the molecular mechanics method. Math. Mech. Solids 20, 836–870. doi: 10.1177/1081286514554353
Korobeynikov, S. N., Alyokhin, V. V., and Babichev, A. V. (2018). Simulation of mechanical parameters of graphene using the DREIDING force field. Acta Mech. 229, 2343–2378. doi: 10.1007/s00707-018-2115-5
Kudin, K. N., Scuseria, G. E., and Yakobson, B. I. (2001). C2F, BN, and C nanoshell elasticity from ab initio computations. Phys. Rev. B 64:235406. doi: 10.1103/PhysRevB.64.235406
Kumar, R., Singh, R., Hui, D., Feo, L., and Fraternali, F. (2018). Graphene as biomedical sensing element: state of art review and potential engineering applications. Compos B Eng. 134, 193–206. doi: 10.1016/j.compositesb.2017.09.049
Li, P., Chen, C., Zhang, J., Li, S., Sun, B., and Bao, Q. (2014). Graphene-based transparent electrodes for hybrid solar cells. Front. Mater. 1:26. doi: 10.3389/fmats.2014.00026
Liew, K. M., Wong, C. H., He, X. Q., Tan, M. J., and Meguid, S. A. (2004). Nanomechanics of single and multiwalled carbon nanotubes. Phys. Rev. B 69:115429. doi: 10.1103/PhysRevB.69.115429
Liu, F., Ming, P., and Li, J. (2007). Ab initio calculation of ideal strength and phonon instability of graphene under tension. Phys. Rev. B 76:064120. doi: 10.1103/PhysRevB.76.064120
Lu, Q., Arroyo, M., and Huang, R. (2009). Elastic bending modulus of monolayer graphene. J. Phys. D Appl. Phys. 42:102002. doi: 10.1088/0022-3727/42/10/102002
Mayo, S. L., Olafson, B. D., and Goddard III, W. A. (1990). DREIDING: A generic force field for molecular simulations. J. Phys. Chem. 94, 8897–8909. doi: 10.1021/j100389a010
Mohan, V. B., Lau, K.-T., Hui, D., and Bhattacharyy, D. (2018). Graphene-based materials and their composites: a review on production, applications and product limitations. Compos B Eng. 142, 200–220. doi: 10.1016/j.compositesb.2018.01.013
Nguyen, B. H., and Nguyen, V. H. (2016). Promising applications of graphene and graphene-based nanostructures. Adv. Nat. Sci. 7:023002. doi: 10.1088/2043-6262/7/2/023002
Rafiee, R., and Eskandariyun, A. (2017). Comparative study on predicting Young's modulus of graphene sheets using nano- scale continuum mechanics approach. Physica E 90, 42–48. doi: 10.1016/j.physe.2017.03.006
Riks, E. (1979). An incremental approach to the solution of snapping and buckling problems. Int. J. Solids Struct. 15, 529–551. doi: 10.1016/0020-7683(79)90081-7
Riks, E. (1984). Some computational aspects of the stability analysis of nonlinear structures. Comput. Methods Appl. Mech. Engrgy 47, 219–259. doi: 10.1016/0045-7825(84)90078-1
Sakhaee-Pour, A. (2009a). Elastic buckling of single-layered graphene sheet. Comput. Mater. Sci. 45, 266–270. doi: 10.1016/j.commatsci.2008.09.024
Sakhaee-Pour, A. (2009b). Elastic properties of single-layered graphene sheet. Solid State Commun. 149, 91–95. doi: 10.1016/j.ssc.2008.09.050
Salerno, G., and Casciaro, R. (1997). Mode jumping and attrative paths in multimode elastic buckling. Int. J. Numer. Methods Eng. 40, 833–861.
Savvas, D., and Stefanou, G. (2018). Determination of random material properties of graphene sheets with different types of defects. Compos B Eng. 143, 47–54. doi: 10.1016/j.compositesb.2018.01.008
Sgouros, A. P., Kalosakas, G., Papagelis, K., and Galiotis, C. (2018). Compressive response and buckling of graphene nanoribbons. Sci. Rep. 8:9593. doi: 10.1038/s41598-018-27808-0
Silvestre, N., Faria, B., and Canongia Lopes, J. (2012). A molecular dynamics study on the thickness and post-critical strength of carbon nanotubes. Compos Struct. 94, 1352–1358. doi: 10.1016/j.compstruct.2011.10.029
Singh, S., and Patel, B. P. (2018a). A computationally efficient multiscale finite element formulation for dynamic and postbuckling analyses of carbon nanotubes. Comput. Struct. 195, 126–144. doi: 10.1016/j.compstruc.2017.10.003
Singh, S., and Patel, B. P. (2018b). Nonlinear elastic properties of graphene sheet using MM3 potential under finite deformation. Compos B Eng. 136, 81–91. doi: 10.1016/j.compositesb.2017.10.024
Sun, C., Wen, B., and Bai, B. (2015). Recent advances in nanoporous graphene membrane for gas separation and water purification. Sci. Bull. 60, 1807–1823. doi: 10.1007/s11434-015-0914-9
Theodosiou, T. C., and Saravanos, D. A. (2014). Numerical simulation of graphene fracture using molecular mechanics based nonlinear finite elements. Comput. Mater. Sci. 82, 56–65. doi: 10.1016/j.commatsci.2013.09.032
Tserpes, K. I. (2012). Strength of graphenes containing randomly dispersed vacancies. Acta Mech. 223, 669–678. doi: 10.1007/s00707-011-0594-8
Xiao, J. R., Staniszewski, J., and Gillespie Jr., J. (2009). Fracture and progressive failure of defective graphene sheets and carbon nanotubes. Compos Struct. 88, 602–609. doi: 10.1016/j.compstruct.2008.06.008
Young, R. J., Kinloch, I. A., Gong, L., and Novoselov, K. S. (2012). The mechanics of graphene nanocomposites: a review. Compos Sci. Technol. 72, 1459–1476. doi: 10.1016/j.compscitech.2012.05.005
Zhang, Y., Liew, K. M., and Hui, D. (2018). Characterizing nonlinear vibration behavior of bilayer graphene thin films. Compos B Eng. 145, 197–205. doi: 10.1016/j.compositesb.2018.03.004
Keywords: graphene, molecular mechanics, out-of-plane buckling, DREIDING potential, arc-length strategy
Citation: Genoese A, Genoese A, Rizzi NL and Salerno G (2019) Buckling Analysis of Single-Layer Graphene Sheets Using Molecular Mechanics. Front. Mater. 6:26. doi: 10.3389/fmats.2019.00026
Received: 30 November 2018; Accepted: 08 February 2019;
Published: 27 February 2019.
Edited by:
Fernando Fraternali, University of Salerno, ItalyReviewed by:
Nicholas Fantuzzi, University of Bologna, ItalyGiuseppe Zurlo, National University of Ireland Galway, Ireland
Copyright © 2019 Genoese, Genoese, Rizzi and Salerno. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Andrea Genoese, YW5kcmVhZ2Vub2VzZV84M0Bob3RtYWlsLml0
 Alessandra Genoese
Alessandra Genoese Andrea Genoese
Andrea Genoese Nicola L. Rizzi
Nicola L. Rizzi Ginevra Salerno
Ginevra Salerno