- 1Laboratory for Adaptive Structures and Intelligent Systems, Department of Vehicle Engineering, Hefei University of Technology, Hefei, China
- 2GAC Automotive Research and Development Center, Guangzhou Automobile Group Co., Ltd., Guangzhou, China
In this paper, hysteresis of magnetorheological (MR) fluids is identified from experimental tests following the mechanism of rate-independence and further studied to explore the hysteresis mechanism. The theoretical analysis based on the dipole model is provided to reveal the hysteresis mechanism of MR fluids. Specifically, the performance tests of a self-developed double-rod MR damper under different excitations show that instead of the typical force-velocity plot, the relationship between the force and displacement meets the requirements of rate-independence of the hysteresis well. A critical concept of “yield displacement” is defined and analyzed in the force-displacement plot to illustrate the hysteresis characteristics. In addition, the relationship of the normalized restoring force vs. strain is derived for a single chain from the dipole model. Then a stress-strain curve is developed for the multi-chain structure with an assumption of the dynamic equilibrium between the rupture and reconstruction of the chains. Sequentially, the hysteresis mechanism is established based on the force-displacement characteristics under reciprocating excitations. The consistency between the yield displacement in experiment and yield strain in theory verifies the effectiveness of the hypothetical hysteresis mechanism. The analysis results provide a guideline for the structural design of MR devices to enhance/reduce the hysteresis effect. The hysteresis mechanism-based further extension for the stress-strain properties of MR elastomers and the response time of MR fluids are provided as well.
Introduction
Magnetorheological (MR) fluids are a smart material with magnetic field-dependent rheological properties (De Vicente et al., 2011). Hysteresis is an inherent property of MR fluids and MR fluid-based actuators. Such hysteretic non-linearity increases the control complexity of MR actuators, which in turn limits the MR applications. Understanding the working mechanism of the hysteresis characteristics of MR fluids is significant for studying the hysteresis characteristics of MR actuators and implementing high-efficiency control for MR semi-active systems.
At present, the research on MR hysteresis characteristics mainly focuses on the mechanical properties of MR actuators (Wang and Liao, 2011; Bai et al., 2013, 2015; Sapinski et al., 2017; Yu et al., 2017; Chen et al., 2018; Shou et al., 2018), such as MR dampers and MR clutches/brakes. Experimental tests of MR dampers in valve or shear mode show that the hysteresis only occurs around the direction-change points under sinusoidal displacement excitations (Wang and Liao, 2011; Bai et al., 2015). Coincidentally, the associated velocities in this area are relatively small, and the hysteresis displays more distinctly in the force-velocity plot. However, from a view of rate-independence of hysteresis (Visintin, 2013; Chen et al., 2018), the experimental results (Wang and Liao, 2011; Bai et al., 2015; Sapinski et al., 2017; Yu et al., 2017; Shou et al., 2018) show that the hysteresis behaviors of MR fluids occur in force-displacement plot while not in the typical force-velocity plot. The “rate-independence” concept is defined by the path of the couple [with the input z(t) and the output F(t) of the system] that is invariant with respect to any increasing time, i.e., the output is not dependent on the derivative of the input z (Visintin, 2013). It should be noted that the hysteresis loops are not regarded as an essential feature of hysteresis (Visintin, 2013). The rate-independence, as the critical property of the hysteresis, provides an index to identify the input/output in any hysteresis phenomenon. In addition, the modeling analysis of MR fluids operated in squeeze mode indicates that the hysteresis in squeeze mode cannot be described by the normal force-velocity plot-based hysteresis models, but can be well-described by the force-displacement relation-based model–Bouc-Wen model (Chen et al., 2017a) and resistor-capacitor (RC) operator-based models (Chen et al., 2018; Bai et al., 2019). Similarly, as a derivative of MR fluids, the macroscopic mechanical properties of MR elastomers can also be modeled by the Bouc-Wen model or RC operator-based models. It indicates that MR fluids have the similar hysteresis characteristics to MR elastomers (Behrooz et al., 2014). Based on the rate-independence property of hysteresis, the macroscopic mechanical properties of MR actuators are actually a coupling of Duhem-type hysteresis and viscous properties which is rate-dependent (Visintin, 2013; Chen et al., 2018).
Compared with the experimental investigations of the hysteresis characteristics of MR actuators, the research on its working mechanism is rare to be found. Theoretical and experimental studies show that the compressibility of MR fluids and the compressibility of the accumulator (if exists) can be effectively used to establish the mechanical model of the hysteresis characteristics of MR dampers in valve mode (Wang and Gordaninejad, 2007; Guo et al., 2014). However, the compressibility of MR fluids fails to explain the inherent hysteresis of MR fluid- and elastomer-based actuators (Weber, 2013; Behrooz et al., 2014) working in shear mode.
Dipole model can be used to theoretically explain the working mechanism of the controllable mechanical properties of MR fluids and MR elastomers from the microscopic level. Based on the simply dipole model, researchers have deduced the enhanced dipole model considering the magnetic interaction, the local magnetic field interaction and the magnetic chain interaction in the whole chain (Jolly et al., 1996; Furst and Gast, 2000; Xu et al., 2016). A corresponding stress-strain curve is derived under the assumption that all chains maintain consistent deformation.
The main contribution and work of this paper is to theoretically analyze the experimental performance of MR dampers and explain the hysteresis mechanism of MR fluids. In order to avoid the influence of the compressibility of the accumulator and viscous damping on the hysteresis characteristics, a self-developed double-rod MR damper will be tested under triangle displacement excitations. Applying normalization method, the expression of hysteresis of MR fluids in force-displacement plot is studied. Yield displacement concept is proposed to quantitatively analyze the experimental results. Theoretically, using the dipole model, under the assumption of the dynamic equilibrium between the rupture and reconstruction, the expression of hysteresis of MR fluids via the stress-strain curve will be derived.
Experimental Tests of Hysteresis Characteristics of MR Fluids
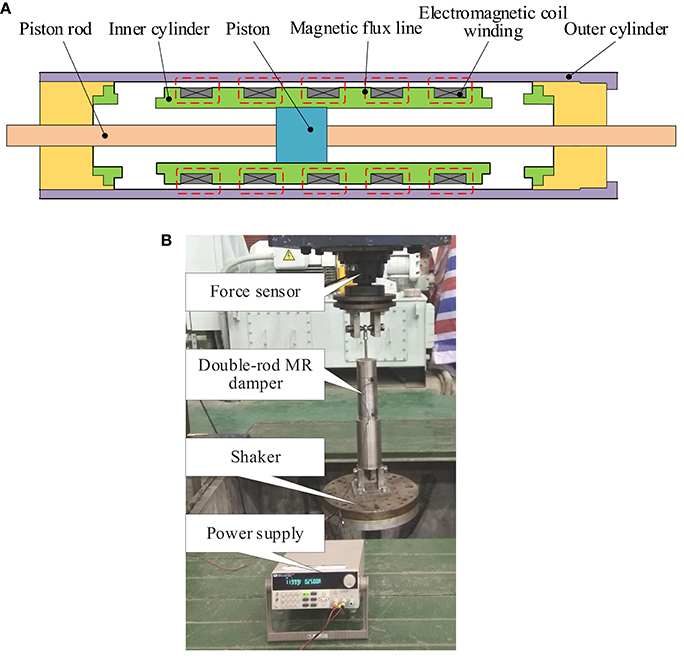
The hysteresis characteristics of MR fluids are tested on a self-developed double-rod MR damper (Bai et al., 2013, 2018a,b), as shown in Figure 1A, using the servo-hydraulic testing system (Type: LFH-LFV3068, SAGINOMIYA Inc.), as shown in Figure 1B. Observing Figure 1B, the experimental setup is composed of the servo-hydraulic testing system, the MR damper, and a power supply (Type: IT6861A, from ITECH Company). The servo-hydraulic testing system is integrated with a shaker actuator driven by a servo-hydraulic system, data acquisition and processing system with force sensors and displacement sensors, and a controller (i.e., a host computer, not shown in the figure). In order to avoid the influence from viscosity characteristics under different excitation velocities, the mechanical behaviors of the MR damper are tested under triangle displacement excitations provided by the servo-hydraulic testing system. The force and displacement signals are acquired by the data acquisition and processing system with a sample rate of 1 kHz. The geometrical dimensions and parameters of the self-developed double-rod MR damper are listed in Table 1. Such specifically developed double-rod MR damper will effectively eliminate the influence from the compressibility of the accumulator. As a reference, the experimental results of a commercial MR damper with an accumulator are provided in Appendix A.
Figure 2 presents the test results of the MR damper under a triangle displacement excitation with a frequency of 1 Hz and an amplitude of 25 mm. As shown in the figure, the damping force of the MR damper changes rapidly and converges to a stable value in a region where the excitation direction changes and the excitation velocity is constant. Moreover, the tendency of the damping forces under different currents shows a good consistency in this region.
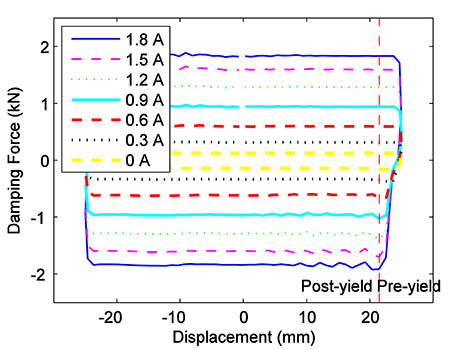
Figure 2. Mechanical behavior of the MR damper with different currents under triangle displacement excitation with a frequency of 1 Hz and an amplitude of 25 mm.
Figure 3 presents the force-displacement plot of the MR damper under different excitation frequencies to further verify the rate-independence of the hysteresis characteristics. As seen from Figure 3, the force-displacement plots also show a very good consistency. Combining Figures 2, 3, the force-displacement hysteresis characteristics of the MR damper/fluids are verified. Such phenomenon of the hysteresis being presented by the force-displacement plot is also consistent with the pre-yield and post-yield definitions of the stress-strain curve of MR fluids (De Vicente et al., 2011). Sequentially, the pre-yield and post-yield regions are defined in Figures 2, 3. As known, the unavoidable friction for the MR damper shown in Figure 1 also behaves as a kind of Duhem hysteresis. The macroscopic mechanical characteristics of MR damper are the coupling of the hysteresis characteristics of the MR fluids and the hysteresis characteristics of friction. As seen from Figure 2, in field-off state (i.e., 0 A, where only the friction shows the hysteresis characteristics), the length of pre-yield is significantly different from that in field-on states. It indicates that the hysteresis characteristics of MR fluids is an important factor for the hysteresis of the MR damper, while not the friction. In addition, in Figures 2, 3, the consistence of the pre-yield lengths under different currents provides a clue for the study of the hysteresis mechanism.
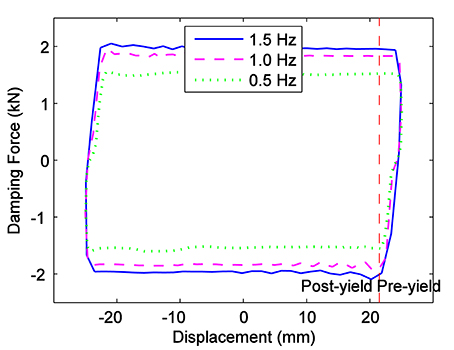
Figure 3. Mechanical behavior of the MR damper with 1.8 A current under triangle displacement excitations with different frequencies and an amplitude of 25 mm.
To study the hysteresis characteristics of MR fluids, a concept of normalized damping force is defined as
where FI,i is the damping force of the MR damper with current of I at displacement i when under triangle displacement excitation; FI,0 is the damping force when under forward excitation and the displacement excitation at position zero; F0,i and F0,0 are the damping force of the MR damper with no current at displacement i and the damping force of the MR damper with no current at the position zero, respectively; is the normalized damping force.
On one hand, the influence of the friction on the hysteresis characteristics of the MR damper (i.e., FI,i−F0,i) can be effectively excluded by using the normalization concept. On the other hand, it is convenient to study the commonality of the hysteresis characteristics of MR fluids with different currents (magnetic fields). Figure 4 presents the normalized force-displacement plot of the MR damper with different currents under triangle displacement excitation with a frequency of 1 Hz and an amplitude of 25 mm. As seen from Figure 4, the normalized force-displacement plots under different currents show a very good consistence. The distance from the displacement turning point to the convergence point of the damping force is defined as the yield displacement in this study. The yield displacements of the MR damper are nearly equal to each other under different currents, as seen from Figure 4. The yield displacement increases little with the increase of the current, due to the compressibility of the MR fluids. In other words, the compressibility of the MR fluids is not the essential factor for the hysteresis characteristics of MR actuators/fluids.
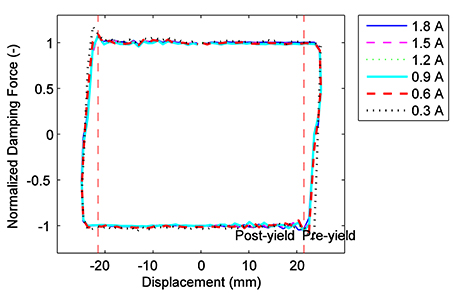
Figure 4. Normalized force-displacement plot of the MR damper with different currents under triangle displacement excitation with a frequency of 1 Hz and an amplitude of 25 mm.
Theoretical Analysis of Hysteresis Characteristics of MR Fluids
Test results and analysis have shown that the friction is only a very limited part of the hysteresis characteristics of the MR damper, and the compressibility of the MR fluids cannot fully explain the hysteresis characteristics of the MR damper. We will try to theoretically explain the hysteresis characteristics of MR damper/fluids via a theoretical perspective with the magnetic interaction of ferromagnetic particles.
Structural Evolution of Chain Clusters of MR Fluids
Dipole model can be used to essentially explain the MR effect in microscopic point. Based on the dipole model, the deformation of the chains or columns of MR fluids leads to the restoring force in the presence of the magnetic field. Further, the expression of the restoring force between two particles is derived with relation to the particle distance and the polar angle between the line of centers and the direction of the magnetic field (Klingenberg et al., 1990). This model can be applied to analyze the yield stress of MR fluids in shear mode (Bossis and Lemaire, 1991; Jolly et al., 1996). Following this idea, modified dipole models that account for the particle interaction along a single chain have been proposed (Furst and Gast, 2000; Tao, 2001; Si et al., 2008). In such models, the chains are assumed to deform in shear mode, Chen et al. proved that the restoring force would be varied with different kinds of structural evolution and the deformation of the chains would be affected by the hydraulic inaction when under valve or squeeze mode (Chen et al., 2017b).
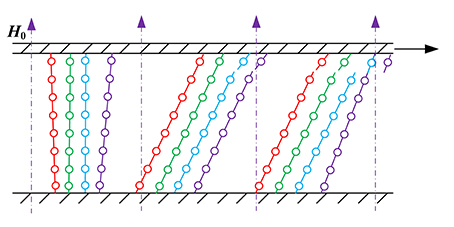
The deformation of chains in shear mode is the focus of this study, so the hydraulic interaction is neglected. A schematic of the deformation of a single chain is presented in Figure 5. With the magnetic field, the identical spherical particles dispersed in the carrier oil align themselves in the direction of the magnetic field. According to the minimum energy principle, the field energy would be minimized when d = 2R, where d is the vertical distance between the centers of the adjacent particles and R is the radius of the particle. We assume that there is no relative motion between the particles and the carrier oil, and then the chain would be stretched and deviates an angle θ from the direction of the magnetic field. Meanwhile, the minimum energy principle would allow a uniform distance between the two adjacent particles. Under magnetic field, only the interaction between the two adjacent particles would be considered, and then the restoring force FH induced by the deformation of a chain can be calculated by taking the derivative of the energy with respect to the displacement. It can be expressed as
where m=|m| and m (= 3μfμ0βVH0) is the dipole moment when a particle is placed in the magnetic field H0. , μp and μf are the relative permeabilities of the particles and medium, respectively, μ0 is the vacuum permeability, V () is the volume of a particle and γ is the shear strain. is defined as the normalized restoring force to study the relationship between the chain restoring force and shear strain under different magnetic fields.
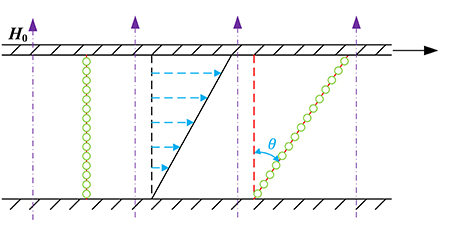
Figure 5. Schematic of the deformation of a single chain of MR fluids in shear mode under magnetic field.
Figure 6 shows the relationship between the normalized restoring force and shear strain of a single chain of MR fluids. As seen from the figure, in the initial deformation stage, as the strain increases, quickly reaches the peak. The corresponding strain is defined as the yield strain. gradually decreases to zero after the yield strain. It should be noted that the yield strain is a constant value independent of the magnetic field.
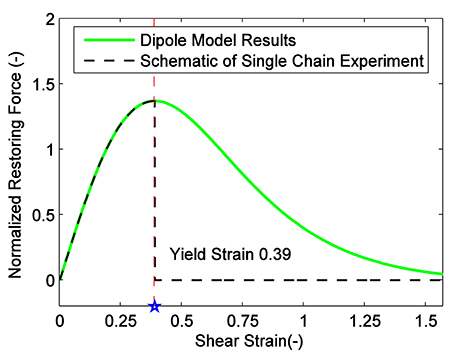
Figure 6. Response of the normalized restoring force vs. shear strain for a single chain of MR fluids.
In addition, Figure 6 presents the schematic of the test results of the restoring force vs. strain of a single chain (Furst and Gast, 2000). It is seen from Figure 6, the yield strain based on the magnetic dipole model is in good agreement with the test results, but after the yield strain, the chain of the MR fluids ruptures and the corresponding restoring force drops to zero sharply. Therefore, it is unreasonable to derive the yield stress of MR fluids based on the assumption of consistent deformation of the chain clusters (i.e., the deformation of all chains of MR fluids is consistent). The yield strain in the dipole model is derived from the derivation of the yield stress. The relationship between the restoring force and strain before the yield strain provides clues for the deformation of the chain clusters.
An assumption is made here during the expansion of a single chain to the entire chain clusters: under magnetic fields, the structural evolution of the chain clusters of MR fluids in the shearing motion is in dynamic equilibrium state from the micro deformation of chain to rupture and reconstruction. Specifically, as seen from the structural evolution of the chain clusters in Figure 7, the ferromagnetic particles are polarized into chains in a static state, and the chains of MR fluids are not in an absolute parallel with the magnetic field direction. There are slight differences between the chains. As seen from Figure 7, under the shearing motion, the inclination angle of the chains gradually increases, and due to the difference of the initial inclination angle, part of the chains reach the yield strain and then rupture occurs. As the shearing motion advances, more chains rupture to yield stress and the previously ruptured chains reconstruct and form new chains with the adjacent broken chains. The rupture and reconstruction of the chains reach a dynamic equilibrium under the steady-state conditions. In other words, the number of chains ruptured at a certain instant is equal to the amount of chains reconstructed. Thus, it exhibits a stable mechanical property. The non-absolute parallel hypothesis in the static state is verified with the results of MR fluids under electron microscope (De Vicente et al., 2011). Also, the shear tests of a single chain of MR fluids show that the restoring force of the MR fluids abruptly decreases to zero (Furst and Gast, 2000), which indicates that the structural evolution of the chain clusters of MR fluids is not consistent. Therefore, the assumption of a dynamic equilibrium of the chain clusters of MR fluids is reasonable. Based on such assumption and the dipole model of the single chain of MR fluids [i.e., equation (2)], Figure 8 shows the stress-strain relationship of MR fluids under shearing motion. As seen from Figure 8, before the yield strain, the stress increases rapidly to the peak with the increase of the overall strain of the chain clusters. When reaches the dynamic equilibrium of the rupture and reconstruction, MR fluids exhibit stable stress characteristics. Consistent with the normalized restoring force-strain plot of a single chain of MR fluids, the yield stress under the evolution of the chain clusters structure is also a magnetic field-independent constant. It should be noted that the yield stress and also the corresponding yield strain of MR fluids and the stable stress are not consistent in numerical values.
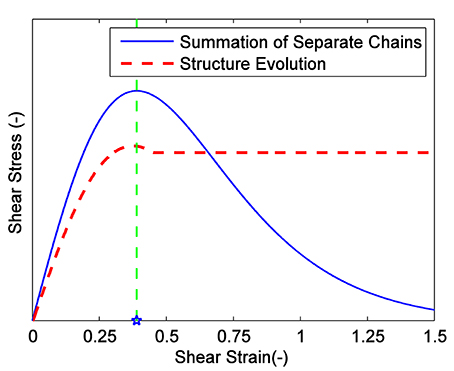
Figure 8. Schematic of the stress vs. strain for multi-chain of MR fluids under dynamic equilibrium state.
Hysteresis Mechanism of MR Fluids Under Reciprocating Displacement Excitation
Based on the stress-strain plot of the chain clusters of MR fluids obtained in Figure 8, under the reciprocating displacement excitations, the MR fluids stress increases rapidly and gradually reaches the stable. When the displacement excitation direction changes, the transient shear rate of the MR fluids can be seen as zero. Then the chain ruptured at the previous moment maintains the trend to the parallel direction of the magnetic field, while the unruptured chains maintain the previous shear strain. Therefore, when a new shearing motion starts (i.e., the shear direction changes), the restoring force of part of the chains is opposite to the shear rate, and part of the chains begin to undergo new deformation. Thus, the overall stress direction is opposite to the shear rate. As the shearing motion progresses, the stress of MR fluids gradually approaches a new stability until the new shear strain direction-change point.
Figures 9A,B provide the dipole model-based hysteresis characteristics of MR fluids under reciprocating displacement excitations with large and small amplitudes, respectively. As shown in Figure 9A, the simulation results with coupled viscous properties of MR fluids are also provided for comparison. Consistent with Figures 6, 8, the distance from the strain direction-change point to the stress stable point is a magnetic field-independent quantification. It is numerically twice of the yield strain. This agrees with the test results of the hysteresis of MR fluids. However, in the hysteresis characteristics tests of MR fluids, the macroscopic mechanical performance is affected by the friction and compressibility of MR fluids. The yield strain converted from yield displacement is not identical with the theoretical value.
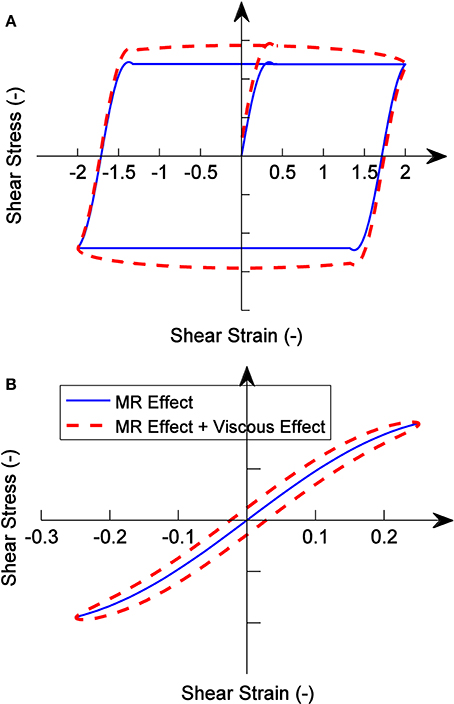
Figure 9. Dipole model-based hysteresis characteristics of MR fluids under reciprocating displacement excitations: (A) large amplitude and (B) small amplitude.
As seen from Figure 9B, when the excitation amplitude is small, the excitation strain is insufficient to reach the yield strain, and majority of the chains of MR fluids are not ruptured. The stress generated by the MR effect maintains good coincidence during the reciprocating processes, and its energy consuming characteristics are mainly reflected by the viscosity characteristics of MR fluids. This phenomenon is in good agreement with the results of MR elastomers tests. Under low shear strain amplitudes, the influence of MR effect on the macroscopic properties of MR elastomers is mainly manifested in the stiffness characteristics (Li et al., 2013). The energy consumption characteristics is influence by the MR effect (Lopez-Lopez et al., 2016), so the damping characteristics of MR elastomers is also affected by the excitation amplitudes.
Further Extensions
Hysteresis in MR Elastomers
The experimental tests and macroscopic modeling analysis indicate that the hysteresis also happened in MR elastomers where the corresponding strain is very small (Tian et al., 2011; Li et al., 2013) and it can be effectively modeled by Bouc-Wen model (Yang et al., 2013; Behrooz et al., 2014). Fortunately, the particles in MR elastomers are fixed in the rubber matrix, and especially for the anisotropic one, the deformation of the chains can be reasonably predicted. Then two properties of the proposed theoretical model can be experimentally verified: (i) the similarity in Figure 9B would be checked under quasi-static tests, and (ii) as shown in Figure 10, the yield strain can be directly measured in MR elastomers (Tian et al., 2011). Then the comparison of the yield strain would be done between experiment and theory. In MR fluids, it is not easy to measure the yield strain. The yield displacement is a vague value in the force-displacement plot, and the mixed air or the machining error would be amplified on the value of the yield strain.
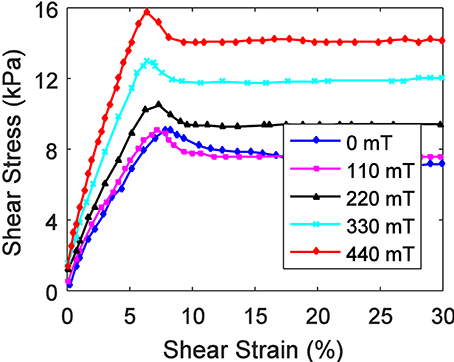
Figure 10. Measured stress-strain curve of MR elastomers (Tian et al., 2011).
Response Time of MR Fluids
Researchers believe that the response time of MR actuators has three main sources: response time of MR fluids, inductance of coil, and eddy current in the coil bobbin (Bai et al., 2018b). Under a fixed applied current, the response time from inductance of MR damper coil and eddy current in the coil bobbin would be a constant value regardless of the excitation velocity. The measured results of response time vs. excitation velocity (Koo et al., 2006) shown in Figure 11 indicate that with increasing velocity, the response time sharply decreases before the convergence. If we take the stable value as the constant value from inductance of MR actuator coil and eddy current in the coil bobbin, the response time from MR fluids seems to be inverse proportion to the excitation velocity. Hence, we can make a conjecture that instead of the response time, the response displacement is more suitable to interpret the zero-stare response of MR actuators and it would be a constant value. This conjecture is consistent with the constant yield displacement or strain in the hysteresis, which also provides another way to the measurement of the yield strain.
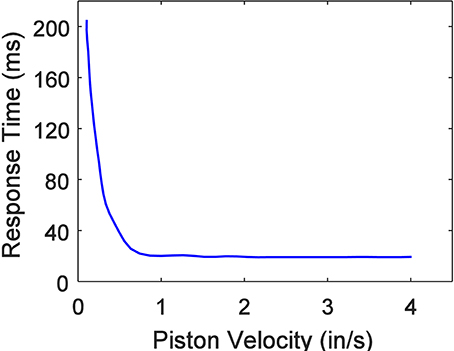
Figure 11. Response time of MR damper in field-on state as a function of piston velocity (Koo et al., 2006).
Yield Strain in Theory of Dipole Model
The yield strain in shear mode is derived with the simple dipole model, and it should be noted that the yield strain would be different if another dipole model is used. Figure 12 presents the comparison of the normalized restoring force response between simple dipole model and local field dipole model (Zhang et al., 2004). Ignoring the difference of the maximum restoring force, the corresponding yield strain is different. In addition, the yield strain is also different related with the working mode (Chen et al., 2017b). The comparison/difference between shear mode and valve mode is presented in Figure 13.
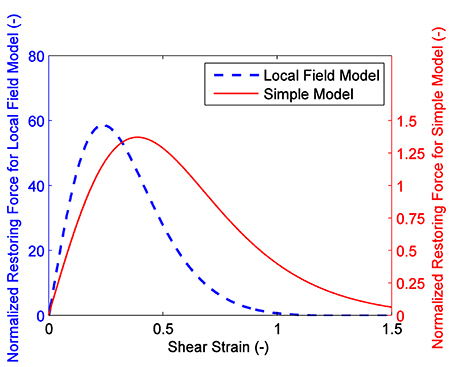
Figure 12. Comparison of normalized restoring force response between simple dipole model and local field dipole model.
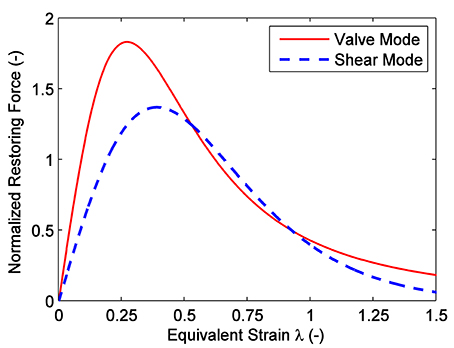
Figure 13. Comparison of normalized restoring force response between shear mode and valve mode (Chen et al., 2017b).
Discussion
The comparison between the experimental tests (refer to Figures 2–4 and Figures A1,A2 in Appendix A) and the theoretical results (Figure 9A) indicates that the hysteresis in force-displacement plot is consistent with each other and satisfies the requirement of rate-independence of hysteresis and the invariance of the experimental yield displacements under different currents and theoretical yield strain under different fields. It is also noted that (i) in the case of the double-rod MR damper, the yield displacement is almost current-dependent, and (ii) in theory, the distance between the direction-change point and yield point is approximately twice of yield strain. Hence, the tested yield displacement can be easily converted to a sort of strain, and the direct comparison of its value with the yield strain from theory would strongly prove the proposed theory. In addition, the tested stable damping force would be converted to a kind of stress, and the comparison with stable stress would provide a clue to the dynamic equilibrium of multi-chain structural evolution. We can realize the precise prediction of the hysteresis of MR fluids and MR fluid-based actuators before experimental tests, as long as we figure out the above.
Conclusions
Aiming at understanding the hysteresis mechanism of MR fluids, a self-developed double-rod MR damper was tested and the hysteresis mechanism of MR fluids using a dipole model was theoretically analyzed and explained. The double-rod MR damper under triangle displacement excitations were tested and a normalization concept was applied, to eliminate the compressibility of the accumulator and the influence of the viscous damping on macroscopic hysteresis characteristics. Test results, especially the uniformity of yield displacements under different excitation conditions, indicate that the hysteresis characteristics of MR fluids are mainly reflected in the force-displacement plot. Based on the theory of the dipole model and the dynamic equilibrium hypothesis of chain clusters rupture and reconstruction, the hysteresis mechanism of MR fluids under different excitation amplitudes was derived. Consistent with the experimental results, the theoretically derived yield strain is also independent of the excitation conditions. The theoretically derived yield strain shows difference in the magnitude of the strain corresponding to the yield displacement, due to the influence of other factors in the tests of the hysteresis characteristics of MR fluids. But the consistent rate-independence characteristics provide fundamentals for the further work on the MR effect mechanism. The reasonable deductions on the response time of MR fluids as well as the stress-strain properties of MR elastomers are helpful for the related research or applications.
From the view of future research on the MR effect mechanism, three significant issues are worthy of in-depth study. (i) Detailed physical process for portraying and explaining the MR effect mechanism should be mathematically formulated to in full-scale verify the deduction of this work, which was using only a preliminary analytical model. (ii) Tests of the yield displacements of MR fluids when filled in gaps with different widths but an identical cross-sectional area can be conducted to verify the deduction of this work: smaller gap width, smaller yield displacement. (iii) Tests of the yield strain of MR elastomers, especially the anisotropic ones, can be done to verify the deduction on the MR elastomers in this work.
Data Availability
The datasets generated for this study are available on request to the corresponding author.
Author Contributions
X-XB conceived the conception, investigated the technical background, and coordinated the study, and revised the manuscript. PC carried out the modeling and computation work, and drafted the manuscript.
Conflict of Interest Statement
PC is employed by the company Guangzhou Automobile Group, China.
The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors wish to acknowledge the Key Research and Development Projects of Anhui Province (Grant No. 1704E1002211) for its support of this research.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2019.00036/full#supplementary-material
References
Bai, X. X., Cai, F. L., and Chen, P. (2019). Resistor-capacitor (RC) operator-based hysteresis model for magnetorheological (MR) dampers. Mech. Syst. Signal Process. 117, 157–169. doi: 10.1016/j.ymssp.2018.07.050
Bai, X. X., Chen, P., and Qian, L. J. (2015). Principle and validation of modified hysteretic models for magnetorheological dampers. Smart Mater. Struct. 24:085014. doi: 10.1088/0964-1726/24/8/085014
Bai, X. X., Deng, X. C., and Shen, S. (2018b). Controllability of magnetorheological shock absorber: II. Testing and analysis. Smart Mater. Struct. 28:015023. doi: 10.1088/1361-665X/aaf099
Bai, X. X., Hu, W., and Wereley, N. M. (2013). Magnetorheological damper utilizing an inner bypass for ground vehicle suspensions. IEEE Trans. Magn. 49, 3422–3425. doi: 10.1109/TMAG.2013.2241402
Bai, X. X., Shen, S., Wereley, N. M., and Wang, D. H. (2018a). Controllability of magnetorheological shock absorber: I. insights, modeling and simulation. Smart Mater. Struct. 28:015022. doi: 10.1088/1361-665X/aaf072
Behrooz, M., Wang, X., and Gordaninejad, F. (2014). Modeling of a new semi-active/passive magnetorheological elastomer isolator. Smart Mater. Struct. 23:045013. doi: 10.1088/0964-1726/23/4/045013
Bossis, G., and Lemaire, E. (1991). Yield stresses in magnetic suspensions. J. Rheol. 35, 1345–1354. doi: 10.1122/1.550234
Chen, P., Bai, X. X., Qian, L. J., and Choi, S. B. (2017a). A new hysteresis model based on force–displacement characteristics of magnetorheological fluid actuators subjected to squeeze mode operation. Smart Mater. Struct. 26:06LT01. doi: 10.1088/1361-665X/aa6ec8
Chen, P., Bai, X. X., Qian, L. J., and Choi, S. B. (2018). An approach for hysteresis modeling based on shape function and memory mechanism. IEEE/ASME Trans. Mechatr. 23, 1270–1278. doi: 10.1109/TMECH.2018.2833459
Chen, P., Qian, L. J., Bai, X. X., and Choi, S. B. (2017b). Velocity-dependent characteristics of magnetorheological fluids in squeeze mode considering the hydrodynamic and the magnetic field interactions. J. Rheol. 61, 455–465. doi: 10.1122/1.4978594
De Vicente, J., Klingenberg, D. J., and Hidalgo-Alvarez, R. (2011). Magnetorheological fluids: a review. Soft Matter 7, 3701–3710. doi: 10.1039/c0sm01221a
Furst, E. M., and Gast, A. P. (2000). Micromechanics of magnetorheological suspensions. Phys. Rev. E 61, 6732–6739. doi: 10.1103/PhysRevE.61.6732
Guo, P., Guan, X., and Ou, J. (2014). Physical modeling and design method of the hysteretic behavior of magnetorheological dampers. J. Intell. Mater. Syst. Struct. 25, 680–696. doi: 10.1177/1045389X13500576
Jolly, M. R., Carlson, J. D., and Munoz, B. C. (1996). A model of the behaviour of magnetorheological materials. Smart Mater. Struct. 5:607. doi: 10.1088/0964-1726/5/5/009
Klingenberg, D. J., and Zukoski, I. V., C. F. (1990). Studies on the steady-shear behavior of electrorheological suspensions. Langmuir 6, 15–24. doi: 10.1021/la00091a003
Koo, J. H., Goncalves, F. D., and Ahmadian, M. (2006). A comprehensive analysis of the response time of MR dampers. Smart Mater. Struct. 15:351. doi: 10.1088/0964-1726/15/2/015
Li, Y., Li, J., Li, W., and Samali, B. (2013). Development and characterization of a magnetorheological elastomer based adaptive seismic isolator. Smart Mater. Struct. 22:035005. doi: 10.1088/0964-1726/22/3/035005
Lopez-Lopez, M. T., Rodriguez-Arco, L., Zubarev, A., Kuzhir, P., Iskakova, L., and Gonzalez-Caballero, F. (2016). N-like rheograms of concentrated suspensions of magnetic particles. J. Rheol. 60, 267–274. doi: 10.1122/1.4942232
Sapinski, B., Rosół, M., Jastrzebski, Ł., and Gołdasz, J. (2017). Outlook on the dynamic behavior of an magnetorheological squeeze-mode damper prototype. J. Intell. Mater. Syst. Struct. 28, 3025–3038. doi: 10.1177/1045389X17704919
Shou, M., Liao, C., Zhang, H., Li, Z., and Xie, L. (2018). Modeling and testing of magnetorheological energy absorbers considering inertia effect with non-averaged acceleration under impact conditions. Smart Mater. Struct. 27:115028. doi: 10.1088/1361-665X/aae6a0
Si, H., Peng, X., and Li, X. (2008). A micromechanical model for magnetorheological fluids. J. Intell. Mater. Syst. Struct. 19, 19–23. doi: 10.1177/1045389X06072488
Tao, R. (2001). Super-strong magnetorheological fluids. J. Phys. 13:R979. doi: 10.1088/0953-8984/13/50/202
Tian, T. F., Li, W. H., Alici, G., Du, H., and Deng, Y. M. (2011). Microstructure and magnetorheology of graphite-based MR elastomers. Rheol. Acta 50, 825–836. doi: 10.1007/s00397-011-0567-9
Visintin, A. (2013). Differential Models of Hysteresis (Vol. 111). Berlin: Springer Science & Business Media.
Wang, D. H., and Liao, W. H. (2011). Magnetorheological fluid dampers: a review of parametric modelling. Smart Mater. Struct. 20:023001. doi: 10.1088/0964-1726/20/2/023001
Wang, X., and Gordaninejad, F. (2007). Flow analysis and modeling of field-controllable, electro-and magneto-rheological fluid dampers. J. Appl. Mech. 74, 13–22. doi: 10.1115/1.2166649
Weber, F. (2013). Bouc–Wen model-based real-time force tracking scheme for MR dampers. Smart Mater. Struct. 22:045012. doi: 10.1088/0964-1726/22/4/045012
Xu, F. H., Xu, Z. D., Zhang, X. C., Guo, Y. Q., and Lu, Y. (2016). A compact experimentally validated model of magnetorheological fluids. J. Vib. Acoust. 138:011017. doi: 10.1115/1.4031757
Yang, J., Du, H., Li, W., Li, Y., Li, J., Sun, S., et al. (2013). Experimental study and modeling of a novel magnetorheological elastomer isolator. Smart Mater. Struct. 22:117001. doi: 10.1088/0964-1726/22/11/117001
Yu, J., Dong, X., and Zhang, Z. (2017). A novel model of magnetorheological damper with hysteresis division. Smart Mater. Struct. 26:105042. doi: 10.1088/1361-665X/aa87d6
Keywords: hysteresis, magnetorheological (MR) fluids, force-displacement characteristics, yield displacement, dipole model, yield strain
Citation: Bai X-X and Chen P (2019) On the Hysteresis Mechanism of Magnetorheological Fluids. Front. Mater. 6:36. doi: 10.3389/fmats.2019.00036
Received: 11 January 2019; Accepted: 18 February 2019;
Published: 12 March 2019.
Edited by:
Seung-Bok Choi, Inha University, South KoreaReviewed by:
Yang Yu, University of Technology Sydney, AustraliaXuan Shouhu, University of Science and Technology of China, China
U. Ubaidillah, Sebelas Maret University, Indonesia
Fitrian Imaduddin, Faculty of Engineering, Sebelas Maret University, Indonesia
Copyright © 2019 Bai and Chen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xian-Xu Bai, YmFpQGhmdXQuZWR1LmNu; www.lasiser.com
 Xian-Xu Bai
Xian-Xu Bai Peng Chen
Peng Chen