Microstructure and Size Effects on the Mechanics of Two Dimensional, High Aspect Ratio Nanoparticle Assemblies

Introduction

Nature achieves impressive mechanical properties in its uniaxial nanocomposite structures through highly regular ordering of hard and soft phases. Many biological systems exhibit high stiffness, strength, and toughness with their compliant matrices only occupying ~5% of the total material volume (Jackson et al., 1988). These structures are common across biology, from nacre in sea shells (Wang et al., 2012) to bone (Jäger and Fratzl, 2000). They possess stiffnesses and strengths on the order of their hard constituents, while, at the same time, displaying ductilities and fracture toughnesses several orders of magnitude higher than would be expected from pure hard constituent materials (Jackson et al., 1988; Jäger and Fratzl, 2000; Kamat et al., 2000; Menig et al., 2000). The small strain, elastic mechanical responses of these materials with high mechanical mismatches between phases are primarily governed by the shear deformation of the matrix phase, which is initiated by the stiff constituents sliding relative to each other during deformation. While significantly contributing to small strain behaviors, these interfaces also provide robust toughening mechanisms through stable energy dissipation (Mayer, 2005; Barthelat et al., 2012). The multiple hierarchical levels found in many biological composites further improve their mechanical responses and failure properties (Zhang Z. et al., 2010; Wei et al., 2015; Gao et al., 2016; Henry and Pimenta, 2018). It has been shown that hierarchal microstructures provide improved resiliency to stress concentrations near inclusions (Gorbatikh et al., 2010) and enhanced damage dispersion (Ritchie, 2011; Dutta and Tekalur, 2014; Mirzaeifar et al., 2015; Henry and Pimenta, 2018). These observations are part of a large and ever growing body of work establishing that staggered microstructures tend to be the most favorable architectures for simultaneously producing stiffness, strength, and toughness in thin, macroscopic materials (Espinosa et al., 2009; Zhang Z. Q. et al., 2010; Barthelat and Zhu, 2011; Dutta et al., 2013; Barthelat, 2014; Ni et al., 2015; Pro et al., 2015; Qwamizadeh et al., 2015, 2017a,b; Abid et al., 2018).

The outstanding mechanical properties of natural uniaxial nanocomposites have inspired the use of staggered architectures in engineered materials. These materials have been fabricated using techniques like freeze casting (Munch et al., 2008), coextrusion (Wilkerson et al., 2018), rapid prototyping (Gu et al., 2016), and laser cutting (Henry and Pimenta, 2018). While these synthetic materials have shown impressive combinations of stiffness, strength, and toughness (Podsiadlo et al., 2007; Bonderer et al., 2008; Wang et al., 2012; de Obaldia et al., 2015; Valashani and Barthelat, 2015; Zhang et al., 2015; Gu et al., 2017; Kim et al., 2018), attempts at reconstructing the mechanical properties of natural materials often fall short of theoretical predictions (Espinosa et al., 2009; Wei et al., 2012). This deficiency has spurred myriad studies hoping to inform the design of optimal nanocomposites built from ordered, uniaxial members embedded in relatively compliant matrices. While there have been many efforts to investigate the mechanics of these brick and mortar systems in two dimensions, they often rely on continuum (Arzt et al., 2003; Ji and Gao, 2004; Zhang Z. Q. et al., 2010; Dutta et al., 2013; Barthelat, 2014; Sakhavand and Shahsavari, 2015; Zhang et al., 2015; Ghazlan et al., 2018; Henry and Pimenta, 2018) or micromechanical (Begley et al., 2012; Abid et al., 2018; Chandler and Cheng, 2018) descriptions. Despite these constitutive and microstructural simplifications, these theoretical works have helped to elucidate many important deformation mechanisms in staggered composites. In particular, how they can achieve simultaneously high strength and toughness through features like crack bridging and deflection (Jackson et al., 1988; Shao et al., 2012; Dutta and Tekalur, 2014; Gu et al., 2017).

Understanding and designing materials adopted from Nature is further complicated by the fact that Nature is not perfect. Nearly all naturally occurring brick and mortar materials exhibit some degree of randomness in their microstructures (Barthelat et al., 2007), as do their synthetic counterparts (Bonderer et al., 2008; Munch et al., 2008; Wilkerson et al., 2018). In particular, the staggered arrangement of hard phase particles may not be adequately represented by idealization of a perfect brick wall, where the overlap between each brick relative to its neighbors is specified. The length scales over which this randomness occurs is important for determining the elastic response of these materials, as well as how efficiently energy is dissipated during yield and failure. This is especially true if matrix shear is the primary mechanism of load transfer (Zhang Z. Q. et al., 2010). Theoretical studies have indicated that randomness in the overlaps between adjacent stiff bricks can substantially and simultaneously decrease the stiffnesses, strengths, and toughnesses of brick and mortar materials (Zhang Z. Q. et al., 2010; Barthelat, 2014; Ni et al., 2015; Pro et al., 2015; Abid et al., 2018). However, boundary cases, like staggered microstructures with relatively strong matrix phases and relatively long, stiff members much greater than the critical length for shear load transfer, have yet to be fully explored.

In addition to the potential challenges manifesting from the constitutive and structural representations of materials with staggered microstructures in predictive material design, a systematic evaluation of the size scaling behaviors of these materials is severely lacking. What limited information exists on the subject is primarily used as validation of model convergence (Abid et al., 2018). However, quasibrittle materials, like many natural and synthetic microstructurally staggered materials, exhibit strong size effects, which are both statistical and deterministic (Bažant et al., 2009; Luo and Bažant, 2017a). This means that test specimen size can have a tremendous effect on the apparent mechanical properties of a material, particularly as the length scale of the material changes by orders of magnitude (Chen et al., 2006; Mathur and Erlebacher, 2007).

Previous studies have also pre-dominately focused on ordered structures with two distinct material phases; however, neat films are another important class of materials that display hierarchical ordering. One such example of this type of material is cellulose nanopaper. Cellulose nanopapers, derived from cellulose nanocrystals (CNCs), have emerged as a promising candidate for applying the outstanding properties of CNCs at the macroscale (Henriksson et al., 2008; Eichhorn, 2011; Dumanli et al., 2014; Natarajan et al., 2018). CNCs are an abundant and renewable material that can be extracted from many biological sources, including plants, bacteria, and tunicates (Moon et al., 2011; Sinko et al., 2015), as well as the by-products of the timber, paper, and pulp industries (Fratzl and Weinkamer, 2007). CNCs also readily self-assemble chiral nematic thin films with emergent photonic features (Lagerwall et al., 2014) and highly modifiable surface chemistries (Habibi et al., 2010; Moon et al., 2011; Wei et al., 2018).

Despite the successes of materials like cellulose nanopapers, much regarding the relationship between constituent structure and macroscale mechanical properties in neat, ordered uniaxial nanocomposites remains elusive. While continuum models have been useful in predicting optimal mechanical properties in matrix containing, ordered uniaxial composites, they may lack the necessary nanoscopic details required to accurately predict the mechanical performance of neat films. They tend to rely on phenomenological descriptions of deformation and interfacial physics, which is why molecular dynamics (MD) simulations have proved useful in establishing structure-property relationships for many topological and composite materials (Ostanin et al., 2013; Koh et al., 2015; Hansoge et al., 2018). In particular, MD simulations have been used in a number of recent studies to describe deformation non-uniformity and discrete failure in both stiff and soft domains of staggered, two dimensional nanocomposite materials (Mathiazhagan and Anup, 2016a,b,c, 2018). However, MD simulations, particularly at the atomic scale, are computationally expensive, minimizing their capacity as predictive material design tools for large scale materials. Between atomistic MD and continuum models lie mesoscopic, or coarse-gained (CG), MD models. These models have been highly successful at describing the mechanical properties of all CNC materials, both during quasi-static (Qin et al., 2017; Natarajan et al., 2018) and dynamic (Qin et al., 2019) deformation processes. Furthermore, MD simulations do not require explicit failure criteria and can capture discrete and non-affine deformation events, like bond breakage and molecular sliding.

The goal of this work is to analyze the effects of system size and microstructural randomness on mechanical properties of staggered, high aspect ratio nanoparticle assemblies, taking CNCs as a model structural building block. Specifically, an atomistically-informed CG MD model of CNCs is used to explore the effects of fiber geometry, arrangement, and system size on the mesoscopic mechanical properties of thin and neat, two dimensional CNC nanopapers. First, the mechanical properties of neat CNC films with various fiber lengths and regular structures (i.e., no randomness) are investigated and compared to established brick and mortar theories. Next, randomness is introduced in the ordering of CNC films to assess the resiliency of their mechanical properties to misalignment. Finally, the sizes of simulated CNC assemblies are systemically increased to evaluate the relationship between system size and observed mechanics.

Methods

The two dimensional, neat CNC films used in this study were constructed using a previously validated CG model (Qin et al., 2017). Briefly, this CG framework is a bead-spring, mesoscopic model of CNCs that is characteristic of cellulose I with a Iβ crystal structure. Each bead in the CG model represents all 4,536 atoms contained within three repeat-units of a CNC with a 36 chain internal structure and exposing (110) surfaces. Detailed atomistic mechanical assessments (uniaxial extension, three point bending, etc.) were performed to inform the CG force field parameters following the strain energy conservation principle (Qin et al., 2017). Intra-CNC bonds with local strains >5% engineering strain were deemed failed and removed from the simulation (Wu et al., 2014; Qin et al., 2017). More information on the specifics of the CG model form, its validation, or potential applications can be found in previous work (Qin et al., 2017, 2019; Natarajan et al., 2018).

Individual CNCs were assembled into close packed configurations to investigate the effects of CNC fiber length (L) and in-plane ordering on the mechanical properties of neat, thin films. Figure 1 shows representative CNC films with various in-plane orderings. The blue beads in Figure 1 represent the starts, or first CG bead, in a given CNC fiber, with the subsequent gray beads corresponding to the remainder of the fiber. This means that the total fiber length (L) is equivalent to the spacing between axially adjacent blue CG beads. Fiber in-plane orderings or arrangements refer to the spatial distribution of chain starts, which are represented by blue CG beads throughout this work. In particular, both regular (Figures 1A,B) and staggered (Figure 1C) orderings were considered for L = 50, 100, 150, 220, and 300 nm.

FIGURE 1

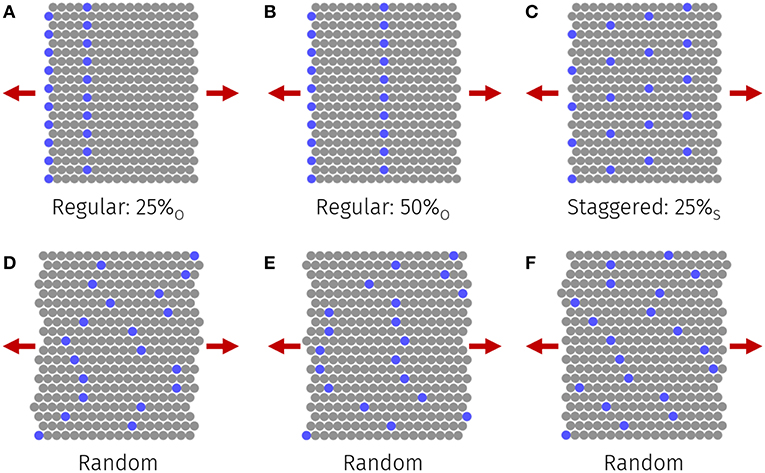
Figure 1. CNC nanopapers (L = 50 nm) with (A) 25%_O and (B) 50%_O regular and (C) 25%_S staggered offset between neighboring fibers. x%_O and x%_S refer to regular and staggered offset structures with x% offset between neighboring fibers, respectively. (D–F) Three representative realizations of CNC films (L = 50 nm) with random ordering. Red arrows indicate direction of applied load.

All CG MD simulations were conducted using LAMMPS (Plimpton, 1995), with all visualizations completed using VMD (Humphrey et al., 1996). Uniaxial tensile tests were used to determine the Young's modulus, failure strength, and toughness of each film; each uniaxial tensile test followed the same procedure. The Young's modulus was defined as the slope of the linear region (up to 0.125% nominal strain) of the stress-strain response of each CNC film. Strength was assumed to be the maximum stress supported by each CNC film prior to failure, and film toughness was calculated by directly integrating the corresponding stress-strain responses from the unloaded configuration until macroscopic film failure. Films were determined to have failed when a significant reduction (>30 MPa over a 0.00125% strain increment) in stress was observed—typically, the stress-strain responses of CNC films abruptly shifted from a loaded state to one where no effective load was measured.

Prior to each uniaxial simulation, the total energy of each CNC film was minimized using a conjugate gradient procedure until the relative difference in total energy between steps was sufficiently small (<10⁻¹⁰). Next, the energy minimized films were equilibrated at 300 K under an NVT ensemble for 20 ns. This was followed by another 50 ns of equilibration, again at 300 K, under an NPT ensemble with traction-free boundaries. Simulations were assumed to be periodic in direction of loading, as well as in the in-plane normal direction. Two dimensionality was strictly enforced by zeroing out-of-plane velocities and forces on a per atom basis. All non-bonded interactions between CG beads located at the starts and ends of individual CNCs were ignored to minimize any artificial confinement effects. After each film was equilibrated, uniaxial tension tests were conducted by deforming the simulation domain along the axial CNC direction with a constant engineering strain rate of 5 × 10⁻¹⁰ 1/fs. This strain rate was selected due to negligible strain rate and inertial effects around the specified rate (see Supplemental Material). During each uniaxial tension simulation, the total pressure acting normal and in-plane to the direction of loading was specified to be stress-free using a Berendsen barostat, while the tensile stress was assumed to be the global stress tensor, normalized by the film thickness, in the direction of loading (shown with red arrows in Figure 1). For each CNC film structure and fiber length, multiple tensile simulations were conducted to assess the expected ranges of the mechanical characterization data. Differences between mechanical responses of structurally similar films were driven by variations in the initial positions and velocities of the individual CNC atoms. All statistical comparisons between two groups of data tested a null hypothesis that there did not exist a difference between the group medians, with an alternative hypothesis of a difference between group medians using a Mann–Whitney U-test (Mann and Whitney, 1947). Statistical comparisons between groups of three or more data used a Kruskal–Wallis H-test to test a null hypothesis that all the group medians were equal, with an alternative hypothesis that at least one of the medians was different (Kruskal and Wallis, 1952).

Randomness in the structure of CNC films was introduced to determine the sensitivities of their uniaxial mechanical properties to specified in-plane ordering schemes. Figures 1D–F provides examples of three realizations of CNC films with structural randomness. In this work, film randomness was controlled by specifying the distribution of allowable offsets relative to a perfectly aligned CNC film with 50% regular offsets between neighboring fibers (see Figure 1B for an example of this baseline structure type). Uniform (U) and normal (N) offset distributions of mean 50% were considered. For each of the ranges and standard deviations of the uniform and normal distributions, respectively, specified, 16 unique CNC films were constructed. In addition to quantifying the sensitivities of films to random fiber offsets, the size scaling behavior of CNC film mechanical properties were evaluated. Figure 2 provides an illustration of how size scaling was introduced for a CNC film with L = 50 nm. Neat films with between 1 and 512 serial CNC fibers in each periodic image were simulated. The total length of the simulation box (l) depends on the number of axial fibers, as well as the individual fiber length (L).

FIGURE 2

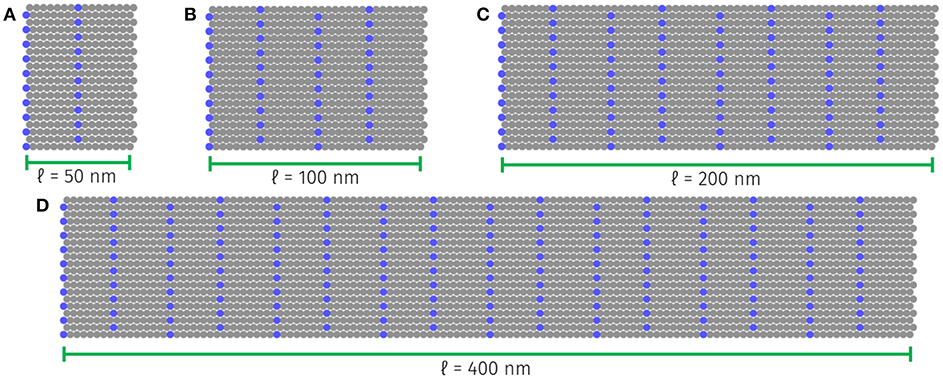
Figure 2. Size scaled initial configurations of CNC films with (A) one, (B) two, (C) four, and (D) eight serial fibers in each periodic image. In each case, the individual fibers are equally sized (L = 50 nm), but the overall simulation axial length (l) is variable.

Results

Both fiber length and the specific ordering of CNC films affected their observed mechanical properties. Figure 3 shows representative stress-strain responses of individual CNC films subjected to uniaxial tension. At short fiber lengths, the elastic responses of CNC films are highly non-linear (Figure 3A). This is particularly true as the films approach failure. No difference between the responses of films with L = 50 nm and 10 and 12.5% regular offset structures was observed because, at this fiber length, their close packed structures were identical; this is a topological limitation of the CNC bead-spring model. As the lengths of CNC fibers increases, the extent of non-linearity in the mechanical responses of the corresponding films decreases (Figures 3B,C). Additionally, the uniaxial responses of long fiber length CNC films appear more qualitatively similar compared to the responses of short fiber CNC films (Figure 3), particularly with respect to their small strain behaviors.

FIGURE 3

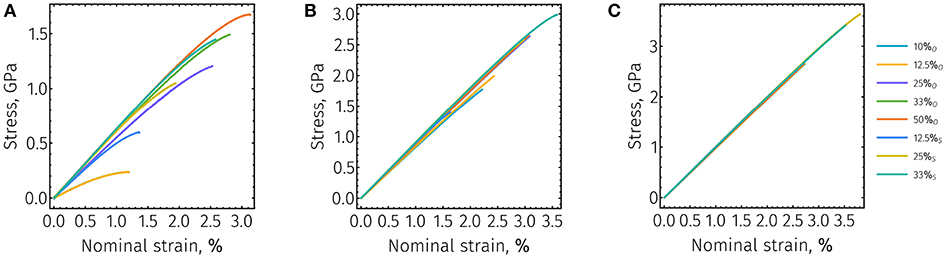
Figure 3. Stress strain responses of CNC films with approximate base fiber lengths (A) L = 50 nm, (B) L = 150 nm, and (C) L = 300 nm. Colors in each plot correspond to various fiber ordering schemes. x%_O and x%_S refer to regular and staggered offset structures with x% offset between neighboring fibers, respectively.

In all cases, significant drops in stress are observed at the transition between elasticity and failure. While short fiber films exhibited responses indicative of ductile, yield-like behavior (Figure 3A), longer fiber length films failed in a brittle manner (Figure 3C). These two distinct failure behaviors manifest from differences in the types motion present between individual CNC fibers. There exists a transition between CNC sliding (short fiber lengths) and CNC rupture (long fiber lengths), which is controlled by the critical length for shear transfer (Zhang Z. Q. et al., 2010; Wei et al., 2012; Xia et al., 2016; Qin et al., 2017). Below this critical value, individual CNC fibers freely slide during externally applied axial loads, meaning that the corresponding deformed structures do not exhibit any evidence of intra-CNC bond rupture (Figures 4A,B). Independent from their specific internal structure, all short fiber CNC films (L = 50 and L = 100 nm) failed without bond rupture. For CNC films with longer fibers (e.g., L = 300 nm), film failure occurs via catastrophic fiber failure (Figures 4E,F). For CNC films with regular offsets, this failure results from fiber rupture at the axial position of fiber junctions (Figure 4E). For staggered structures, long fiber films similarly failed by fiber rupture, except with more spatial variation (even among individual replicates of the same film structure) between their ruptures (Figure 4F). At the transition between fiber sliding and rupture, CNC films failed through a combination of the two modes (Figures 4C,D).

FIGURE 4

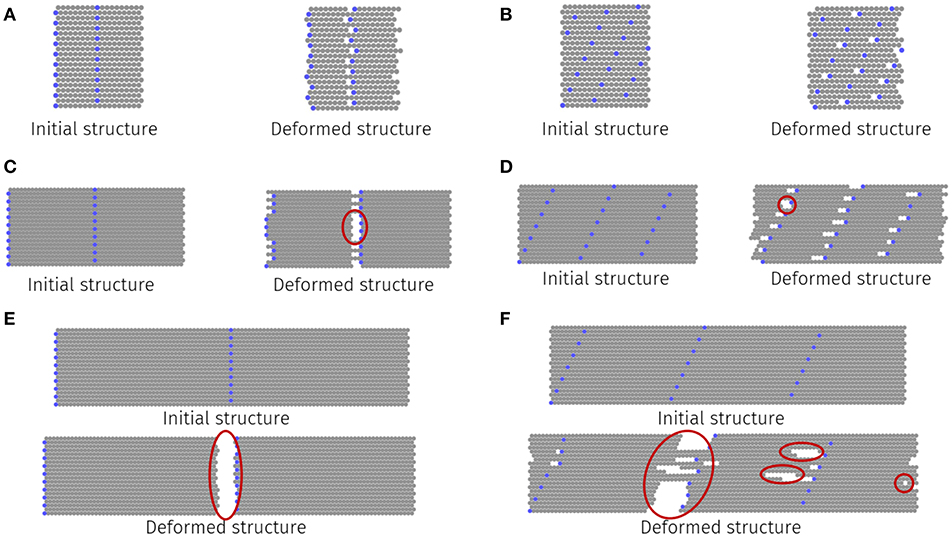
Figure 4. Initial and deformed configurations of various sized [(A,B) L = 50 nm, (C,D) L = 150 nm, and (E,F) L = 300 nm] and arranged [(A,C,E) 50% regular and (B,D,F) 33% staggered offset between neighboring fibers] two dimensional CNC films. Locations of chain rupture are indicated by red circles in deformed structures.

A more quantitative comparison between structure and fiber length can be accomplished by taking a closer look at the distributions of mechanical properties of these neat, two dimensional CNC films. Figures 5A–C show box-whisker plots of the initial, or Young's, modulus of CNC films with L = 50, 150, and 300 nm, respectively. For each specified fiber arrangement and length, 20 independent simulations were conducted to assess the expected group variation. For all fiber lengths examined, significant differences were observed among the initial moduli of the various in-plane ordering schemes (Figure 5; Kruskal–Wallis P < 0.001). For short fiber films (L = 50 nm), a substantial increase in the median initial modulus is observed as the amount of regular and staggered overlapping increases (Figure 5A). This translates to CNC films with 50% regular offsets exhibiting the highest initial modulus for L = 50 nm. In the intermediate fiber length range (L = 150 nm), increasing the shortest overlap between adjacent fibers similarly results in an increase in initial moduli (Figure 5B). However, for films of this fiber length, staggered structures tend to have higher median initial moduli compared to those with regular offsets. As the fiber length increases to L = 300 nm, the amount of variation between the initial moduli of individual film structures decreases substantially (Figure 5C). As with L = 150 nm films, L = 300 nm films with staggered structures tend to outperform regularly offset structures (Figure 5C; Mann–Whitney U between all regular and staggered structures; P < 0.001).

FIGURE 5

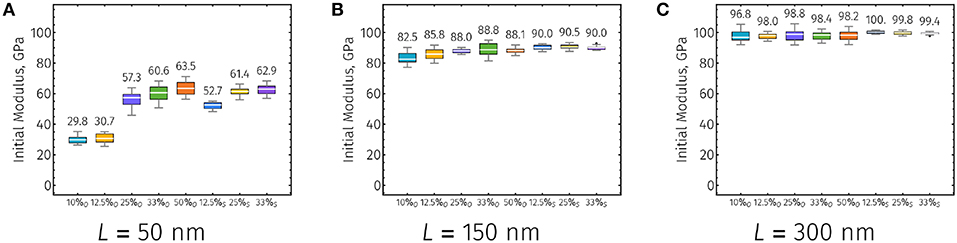
Figure 5. Initial modulus box-whisker plots (20 independent simulations for each structure) of CNC films with approximate base fiber lengths (A) L = 50 nm, (B) L = 150 nm, and (C) L = 300 nm. Colors in each plot correspond to various fiber ordering schemes. White horizontal lines, colored box, gray vertical lines, and black dots indicate the median, interquantile range (IQR) between 3rd and 1st quantiles, range (of all data within ±1.5 × IQR), and outliers (points outside the range), respectively. Numeric values of the distribution medians are listed above their respective box plots.

Much like the small strain behavior of neat, two dimensional CNC films is coupled to the specifics of their structure, so too are their failure properties. Across fiber lengths and in-plane orderings, CNC film strength distributions display substantially less relative variation between replicates compared to initial moduli distributions (Figures 5, 6). With short fibers, the trend between the strengths of CNC film structures is similar to that of initial moduli, with 50% regularly offset films demonstrating the highest strengths (Figures 5A, 6A). However, as fiber length increases, the apparent strengths of neat CNC films with regular offsets become invariant to structure and saturates (Figures 6B,C). This strength plateau is present for films with fibers longer than the critical length for shear load transfer and regular in-plane ordering, where failure occurs via fiber rupture at a particular axial location normal to the direction of loading (Figures 4C,E). For intermediate and long length fibers, the structures with the highest strengths have staggered internal orderings (Figures 6B,C and Supplemental Information). Given the nearly linear uniaxial responses of neat CNC films with fibers of these lengths (Figures 3B,C), the effect of in-plane structure on toughnesses largely follows that of strengths (see Supplemental Information). This is especially true for long fiber length films that experience purely brittle failures.

FIGURE 6

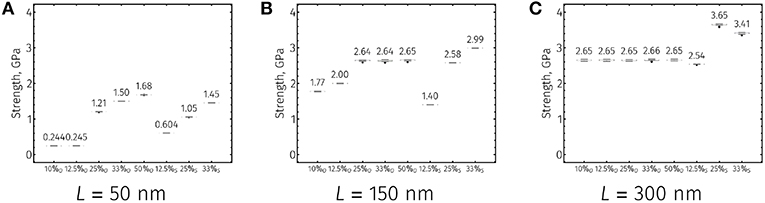
Figure 6. Strength box-whisker plots (20 independent simulations for each structure) of CNC films with approximate base fiber lengths (A) L = 50 nm, (B) L = 150 nm, and (C) L = 300 nm. Colors in each plot correspond to various fiber ordering schemes. x%_O and x%_S refer to regular and staggered offset structures with x% offset between neighboring fibers, respectively. White horizontal lines, colored box, gray vertical lines, and black dots indicate the median, interquantile range (IQR) between 3rd and 1st quantiles, range (of all data within ±1.5 × IQR), and outliers (points outside the range), respectively. Numeric values of the distribution medians are listed above their respective box plots.

The sensitivities of neat films to small variations in their internal ordering was measured by introducing increasing levels of structural randomness. Using 50% regular offset structures as baselines, normal, and uniform distributions of offsets, centered about the corresponding baseline configurations, were used to uncover any specific effects related to the particular form of the randomness within CNC films of various fiber lengths. Figures 7A,B show the distributions of expected initial moduli and strengths of neat CNC films, respectively. Each random distribution includes 16 distinct structural realizations, each with 20 independent simulations (320 simulations total). Insufficient evidence was found to reject the null hypotheses of significant differences between the initial moduli medians of ordered and random CNC films with L = 50 and L = 100 nm (Figure 7A; Kruskal–Wallis P > 0.05); however, a significant, but not substantial, difference between the initial moduli medians of ordered and random films with L = 300 nm (Figure 7A; Kruskal–Wallis P < 0.001). In terms of film strengths, there was sufficient evidence to reject the null hypotheses of no significant difference between the medians of strengths for each fiber length (Figure 7B; Kruskal–Wallis P < 0.001). Interestingly, for L = 300 nm films with N_5% random fiber offsetting, the median film strength is higher than the corresponding film with regular offsetting (Figure 7B). Similarly, the median strength of the U_55% random distribution with L = 150 nm is greater than, but not meaningfully different from, the median strength of the regularly offset structure (Figure 7B). For each fiber length, the distributions in film toughnesses followed the trends in film strengths (Figure 7B and Supplemental Information). Qualitatively, films with random offset distributions tend to have more variation in their observed mechanics, both in their elastic (Figure 7A) and failure (Figure 7B and Supplemental Information) behaviors. Specifically, CNC films with normal random offsets displayed the most variance among replicates in their mechanical properties (Figure 7 and Supplemental Information).

FIGURE 7

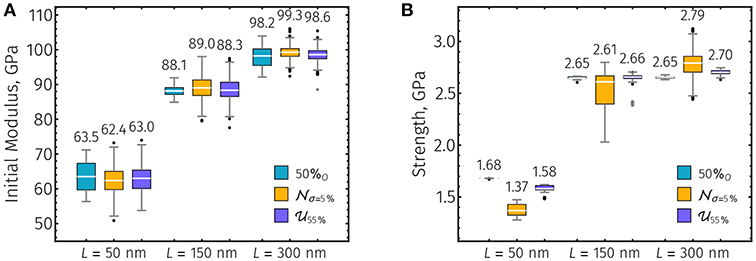
Figure 7. Box-whisker plots of (A) initial moduli and (B) strengths of CNC films with 50% regular and random orderings for L = 50, 150, and 300 nm. Random offset distributions are either normal (N_x%) or uniform (U_x%) with mean 50%, where x% indicates standard deviations and maxima of the normal and uniform distributions, respectively. The box-whisker plots for each ordered structure contains 20 independent simulations. White horizontal lines, colored box, gray vertical lines, and black dots indicate the median, interquantile range (IQR) between 3rd and 1st quantiles, range (of all data within ±1.5 × IQR), and outliers (points outside the range), respectively. Numeric values of the distribution medians are listed above their respective box-whisker plots.

In addition to assessing the sensitivity of CNC films to varying degrees of in-plane ordering randomness, the effect of system size on their observed mechanical properties was also investigated. Figure 8 shows the distributions of initial moduli for CNC films of various fiber lengths. The data in Figure 8 are equally spaced along the abscissa of their respective plots; therefore, each plot should be viewed as logarithmically transformed about system size. Independent from fiber length, the predicted initial moduli medians of neat CNC films are not significantly affected by the number of serial fibers in each periodic image (Figure 8 and Supplemental Information; Kruskal–Wallis P > 0.05). However, as the number of fibers in the simulation domain increases, the variance of the distributions of initial moduli decreases dramatically. This means that it is possible to achieve a realistic estimate of the true initial modulus median of a neat CNC film with a relatively small number of replicates if the system is sufficiently large. However, while the distribution variance does decrease with simulation size, there still exists an unavoidable statistical effect even for arbitrarily large systems.

FIGURE 8

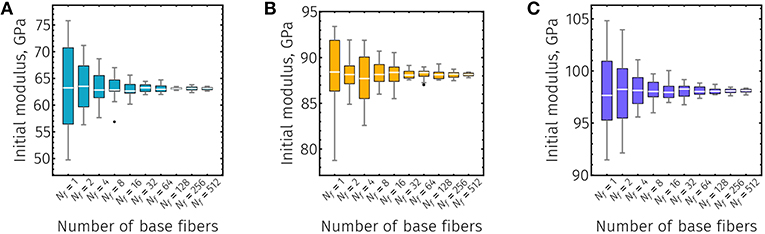
Figure 8. Initial modulus box-whisker plots (20 independent simulations for each structure size) of CNC films with approximate base fiber lengths (A) L = 50 nm, (B) L = 150 nm, and (C) L = 300 nm. Number of fibers (N_f) refers to number of CNC fibers in series within the simulation volume and scales linearly with simulation size along the direction of loading. White horizontal lines, colored box, gray vertical lines, and black dots indicate the median, interquantile range (IQR) between 3rd and 1st quantiles, range (of all data within ±1.5 × IQR), and outliers (points outside the range), respectively.

While system size did not significantly affect the small strain behaviors of neat CNC films, a pronounced effect on their failure behaviors was observed. Figures 9, 10 show the relationships between system size (number of serial fibers in each periodic images) and the predicted strength and toughness of neat CNC films of varying fiber lengths, respectively. Like Figures 8–10 are logarithmically transformed along their abscissa. Given the relatively small nominal differences between the minimum and maximum strengths of CNC films of a particular fiber length, Figure 9 may be equivalently viewed as either linearly or logarithmically transformed with respect to strength; this is also true, to a large extent, for the toughness plots shown in Figure 10. For all fiber lengths, the predicted strength and toughness medians of neat CNC films are significantly affected by the number of serial fibers in each periodic image (Figures 9, 10 and Supplemental Information; Kruskal–Wallis P < 0.001). Short fiber films (e.g., L = 50 nm) display a strongly non-linear relationship between strength and simulation size in log-log space (Figure 9A). Within the range of system sizes investigated, the effect of size on film strength for L = 50 nm films appears to essentially saturate for sufficiently large systems. This behavior is qualitatively different from that observed for intermediate (L = 150 nm) and long (L = 300 nm) fiber films, where strongly linear relationships between system size and strength in log-log space can be seen (Figures 9B,C, respectively). Moreover, the rates at which strength is affected by system size for neat CNC films with L = 150 nm and L = 300 nm are similar (i.e., the slopes of the best fit lines in log-log space between the median strengths and system sizes). The variance of predicted strengths tends to decrease with increase system size for short fiber neat CNC films (Figure 9A); however, the variance of intermediate and long fiber films is mostly invariant to system size (Figures 9B,C, respectively).

FIGURE 9

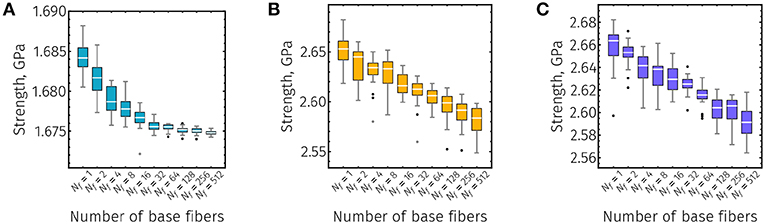
Figure 9. Strength box-whisker plots (20 independent simulations for each structure size) of CNC films with approximate base fiber lengths (A) L = 50 nm, (B) L = 150 nm, and (C) L = 300 nm. Number of fibers (N_f) refers to number of CNC fibers in series within the simulation volume and scales linearly with simulation size along the direction of loading. White horizontal lines, colored box, gray vertical lines, and black dots indicate the median, interquantile range (IQR) between 3rd and 1st quantiles, range (of all data within ±1.5 × IQR), and outliers (points outside the range), respectively.

FIGURE 10

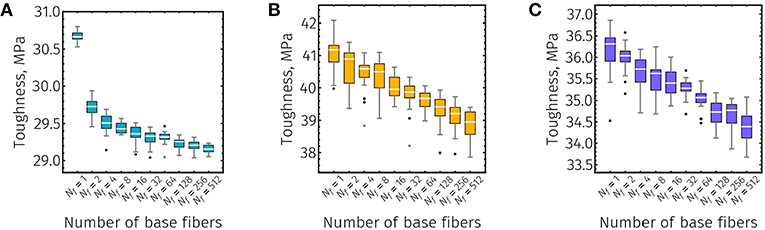
Figure 10. Toughness box-whisker plots (20 independent simulations for each structure size) of CNC films with approximate base fiber lengths (A) L = 50 nm, (B) L = 150 nm, and (C) L = 300 nm. Number of fibers (N_f) refers to number of CNC fibers in series within the simulation volume and scales linearly with simulation size along the direction of loading. White horizontal lines, colored box, gray vertical lines, and black dots indicate the median, interquantile range (IQR) between 3rd and 1st quantiles, range (of all data within ±1.5 × IQR), and outliers (points outside the range), respectively.

The effects of system size on predicted toughness were even more noticeable than those on strength. For short fiber CNC films, a qualitatively similar, non-linear relationship exists between toughness and system size (Figure 10A). While this effect appeared to saturate with respect to strength (Figure 9A), no such convergent behavior for toughness is present (Figure 10A). Additionally, across fiber lengths and contrary to the distributions of film strengths (Figure 9), there does not appear to be any substantial relationships between the variance of the toughness distribution and the system size (Figure 10). Linear relationships between toughness and system size are similarly observed for both intermediate and long fiber CNC films (Figures 10B,C, respectively), with the rates at which the median toughnesses decrease with system size being approximately equal. Compared to the size scaling behaviors of film strength, system size has a considerably larger nominal effect with respect to toughness. The predicted median toughness of a neat CNC film with L = 50 nm and 512 serial fibers was roughly 95% of the single fiber film (Figure 10A), while the median strength only decreased by 0.5% over the same system size range (Figure 9A). Similarly, over the size interval from 1 to 512 serial fibers, decreases of over 5% in film toughness can be observed for of both intermediate and long fiber length CNC films (Figures 10B,C). However, compared to short fiber films, intermediate, and long fiber films did display more consequential decreases in strength with increased system size on the order of 2.5% with respect to films with a single serial fiber (Figures 9B,C).

In addition to the quantitative effects of system size on the distributions of predicted mechanical properties, increasing the size of the simulated domain fundamentally alters the initiation and failure topologies of neat CNC films. Representative examples of neat films following failure are shown in Figure 11. Compared to films with a single CNC fiber in each periodic image (Figure 4), many-fibered films undergo more diffuse failure (Figure 11). This diffusive behavior can be readily seen in short fiber films that fail without fiber rupture (Figures 11A,B). Not only is the coordination of inter-fiber sliding and eventual surface creation of these films significantly more complex than their single fiber counterparts, there also exists evidence of heterogeneous damage far field from the primary damage site (Figures 11A,B). While long fiber films still tend to fail in a pre-dominately brittle fashion, the axial locations of the failure initiation are non-unique (Figures 11E,F). Finally, for films with intermediate length fibers, there is evidence of a combination of both brittle intra-CNC rupture and sliding events in the failed structures with many serial fibers (Figure 11D). This combination of failure modes, which is not necessarily present in every case of material failure (Figure 11C), underscores the importance of understanding how material performance may be tied to the size of the system simulated.

FIGURE 11

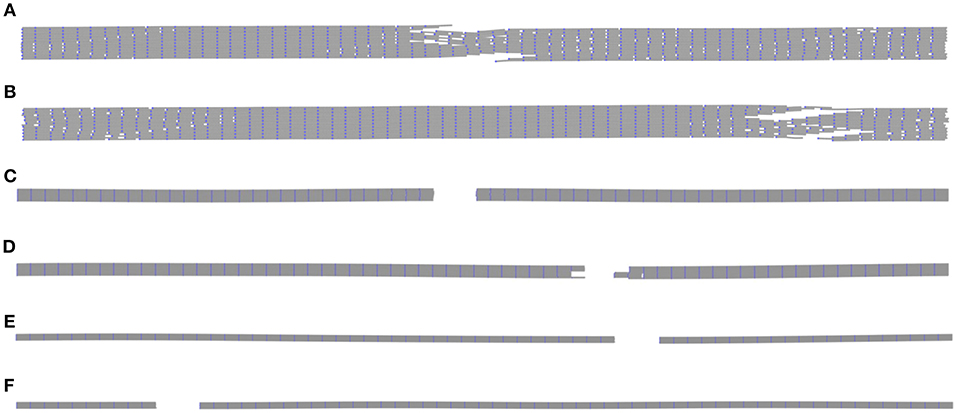
Figure 11. Deformed configurations of (A,B) L = 50 nm, (C,D) L = 150 nm, and (E,F) L = 300 nm size scaled CNC films with 32 CNC fibers in series.

Discussion

Understanding how Nature efficiently uses structural ordering in its composite materials has been the driving force behind countless theoretical and experimental investigations aimed at adopting its designs to engineered material systems (Zhang Z. Q. et al., 2010; Shao et al., 2012; Dutta et al., 2013; Barthelat, 2014; Ni et al., 2015; Wei et al., 2015; Qwamizadeh et al., 2017a; Henry and Pimenta, 2018). Yet, Nature consistently outperforms manufactured composites composed from stiff and aligned fibers embedded in low, or non-existent, volume fractions of compliant matrix material (Espinosa et al., 2009; Wei et al., 2012; Gu et al., 2016). Despite a strong theoretical understanding of how these structured materials behave, it is clear that much still remains unknown about their mechanics. In this work, many of the lessons learned from matrix-containing nanocomposites with high aspect ratio, stiff elements were put to the test in the context of quantifying the mechanical properties of neat, two-dimensional CNC films. Specifically, the initial moduli, strengths, and toughnesses of neat films of various fiber lengths and in-plane orderings were determined. The expected mechanical properties of neat film were found to be, in most cases, closely tied to their structure; therefore, the sensitivities of these mechanical property predictions were assessed to better understand the distribution of performances that might be observed for real materials that contain topological defects. Finally, simulations are often limited by their accessible length and time scales. In many situations, the size of the physical structures are orders of magnitude greater than the simulated domains. This inconsistency between the simulated and physical can have significant effects of the expected mechanics, with the neat CNC films investigated in this work showing substantial mechanical and structural effects related to simulated system size.

Structural and Fiber Length Effects

For the fiber lengths investigated in this work, the corresponding neat films exhibited, to varying degrees, non-linearity in their uniaxial stress-strain responses, and this non-linearity persisted across in-plane orderings (Figure 3). The existence of non-linearity is typically ignored in theoretical analyses of brick and mortar systems since brittle failure is assumed (Zhang Z. et al., 2010; Zhang Z. Q. et al., 2010; Dutta et al., 2013; Barthelat, 2014); however, given the apparent strain softening of these films (Figure 3), failure to consider non-linearity can potentially lead to overestimating film toughness. In short fiber length films (e.g., L = 50 nm) that tended to show the most non-linearity in their uniaxial response, assuming a linear elastic response can result in errors of over 20% compared to the true toughness (Figure 3). Errors in toughnesses calculated with the assumption of linear elasticity are less evident in films that exhibit brittle failure, with errors of <5% for intermediate and long fiber length films.

It is possible to compare many of the elastic predictions of neat CNC films to established continuum theories constructed to describe the mechanics of two phase, brick and mortar material systems. This can be accomplished by assuming the space between CG CNC fibers corresponds to the theoretical matrix material, with its mechanical properties govern by the non-bonded interactions between fibers (see Supplemental Information for details regarding the comparison of neat films to established continuum theories). Continuum theories have been successfully used to derive bounds for the initial elastic response of brick and mortar materials (Zhang Z. Q. et al., 2010; Lei et al., 2013; Qwamizadeh et al., 2017a). While short fiber CNC films qualitatively follow expected trends from relevant continuum theories (Zhang Z. Q. et al., 2010; Qwamizadeh et al., 2017a), the initial moduli of neat CNC films are consistently lower than predicted ranges (see Supplemental Information). This discrepancy may be attributed to a number of factors. First, many theories ignore the normal elastic contribution of the matrix between axial elements and its role in load transfer (Kim et al., 2018). However, accounting for the presence of pseudo-matrix material in the axial spaces between fibers of neat CNC films has only a negligible effect on the predicted initial moduli and, for the ranges of material parameters relevant to the films investigated herein, are not substantial enough to drive predictions outside the bounding cases. Another possible explanation for the discrepancy between the initial moduli of neat films and two phase continuum predictions is that continuum theories tend to assume the matrix material only supports shear loads (Ji and Gao, 2004; Zhang Z. Q. et al., 2010; Dutta et al., 2013; Lei et al., 2013; Ni et al., 2015; Wei et al., 2015; Henry and Pimenta, 2017, 2018; Qwamizadeh et al., 2017a; Abid et al., 2018; Kim et al., 2018). However, for neat films, substantial lateral expansion occurs during uniaxial extension due to the topological constraints of the CG bead-spring model. Additionally, uniformity is often assumed in the distributions of stress within both the matrix and stiff constituents, but recent simulations have suggested that the actual distributions of deformation within these domains are much more complex (Mathiazhagan and Anup, 2016c). Finally, in the context of CG bead-spring systems, as the fibers slide out of their close packed configuration during the initial film stretching, the directions of the frictional forces between fibers (the interactions that provide the effective matrix shear modulus) are not aligned with the axial fiber direction. This feature may affect the shear modulus of the region between fibers in a close packed system, as well as contribute to increased fiber deformation due topological constraints.

As fiber lengths increase, neat film initial moduli predictions start to fall within continuum ranges. With L = 150 nm and regular offsets, the initial moduli of CG MD simulations of neat CNC films are within continuum theory ranges (Zhang Z. Q. et al., 2010; Qwamizadeh et al., 2017a); however, the CG MD results of small overlap, staggered structures are more compliant than predicted by continuum theory (see Supplemental Information). The initial moduli predictions of long fiber, neat films all lie within expected ranges derived from continuum theories (see Supplemental Information). The convergent behavior between neat film and continuum theory predictions is motivated by the increased uniformity of axial stresses in stiff nanocomposite elements as their length increases (Mathiazhagan and Anup, 2016c).

Sensitivity to Structural Randomness

The sensitivities of neat CNC films to perturbations in their in-plane orderings were assessed by mechanically characterizing many independent structural replicates with different distributions of randomness. The introduction of randomness did not significantly affect the median initial moduli of neat films (Figure 7A). This result is contrary to previous work on two phase brick and mortar systems that has suggested structural randomness leads to decreased initial modulus independent from fiber geometry and mechanics (Zhang Z. Q. et al., 2010; Ni et al., 2015; Abid et al., 2018). The insensitivity to randomness in the small strain behavior of neat CNC films in this work is likely driven by the topological constraints of the CNC bead-spring model. For small deformations, it is energetically favorable for the CNC bead-spring chains to maintain their close packing. In the complimentary continuum brick and mortar theories (Zhang Z. Q. et al., 2010), this constrain is not present and the initial deformation is primarily dictated by the overlapping between neighboring stiff elements.

The strengths of brick and mortar films have also been shown to be susceptible to structural randomness, with as much as 50% reduced strength compared to pristinely ordered systems (Zhang Z. Q. et al., 2010; Ni et al., 2015; Abid et al., 2018). For many of the fiber lengths and distributions of randomness tested herein, some significant differences in strength were indeed observed. In particular, randomness reduced strength in films with short fibers (L = 50 nm; Figure 7B). This observation can be explained by the high sensitivity of short fiber length films to their structure (Figure 6A). In randomly ordered short fiber films, there exists a distribution of local, fiber-to-fiber interactions with failure behaviors that are similar to staggered films with that ordering. This means that, as films with random orderings approach failure, the local fiber-to-fiber interaction with the lowest strength will fail and, for these neat films, cause total film failure. However, as the lengths of the fibers increases, the sensitivity to structural randomness decreases and, in some cases, results in higher median film strength (Figure 7B). Looking at the distributions of film strengths for systems with intermediate fibers (Figure 6B), there is also almost no variation in strength between structures. Therefore, the presence of a distribution of local fiber-to-fiber overlaps does not tend to lead to a substantial sensitivity to randomness (Figure 7B). In the case of long fibers, there are staggered configurations that exhibit superior strengths relative to the baseline 50% regular structure (Figure 6C). This allows for certain random structural realizations of L = 300 nm films to withstand higher peak loads compared to films with a 50% regular structure. The improved strengths of long fiber films may also be aided by the admissibility of bending within and rotation about their stiff elements. Continuum theories of often neglect this contribution (Zhang Z. Q. et al., 2010; Lei et al., 2013; Qwamizadeh et al., 2017a), but it may be significant in brick and mortar systems with non-regular orderings and long fibers (Mathiazhagan and Anup, 2016c).

Size Scaling Mechanical Behavior

The small strain behavior of neat CNC films appear insensitive to simulation size. In nanoscopic materials there has been some evidence of a size dependence on the elastic properties of thin films (Miller and Shenoy, 2000; Chen et al., 2006; Mathur and Erlebacher, 2007), but also evidence that suggests minimal size influence after a critical size threshold is met (Sharpe et al., 2001). In general, the neat films studied herein are not susceptible to external factors (e.g., free surface effects, material defects, etc.) that may contribute differences in apparent initial moduli of variously sized films. As the number of serial fibers increases within the simulated domain, the variance of the initial moduli distribution decreases (Figure 8). This phenomenon may be attributed to the increased number of degrees of freedom in the system with increased system size. As the number of degrees of freedom increases, the specific mechanical outcome of the particular realization of a film tends toward the mean behavior. This central tendency is especially meaningful in the context of the random thermal motion of individual CG beads (i.e., there is a higher probability of consequential and coordinated thermal motions in smaller simulations).

While no significant variation in small strain elastic behaviors were observed for neat films of increasing system size, there were significant relationships between simulation size and failure properties. Specifically, regardless of the fiber length, as the number of serial fibers in the simulation domain increases, the measured median strength and toughness decrease (Figures 9, 10, respectively). Long fiber neat films with regular ordering tend to fail brittly via intra-CNC rupture independent from system size (Figures 4E, 11E,F). Consequently, the relationships between their failure properties (i.e., strength and toughness) are mostly linear in log-log space with respect to system size (Figures 9B,C, 10B,C). This type of behavior closely matches the size effect curve of a two dimensional material with a Weibull distribution of strengths (Bažant and Le, 2017). The modulus of a Weibull distribution of strengths can be estimated directly from the slopes of the size scaling curves in log-log space (Bažant and Le, 2017; Luo and Bažant, 2017a). Therefore, given the similarities between the slopes of the size scaling relationships for L = 150 nm and L = 300 nm films (Figures 9B,C), there is evidence to suggest that an intrinsic failure property of CNCs dictates the distribution of failure behaviors for neat films. This feature means that uniformity should be expected among the distributions of strengths of CNCs with fibers longer than the critical length for shear load transfer.

In the case of short fibers, non-linear relationships were observed in the size scaling behaviors of strength and toughness (Figures 9A, 10A, respectively). Introducing more unique opportunities for strain localization also leads to more spatially diffuse failure modes in multi-fiber short films (Figures 11A,B). These deformed configurations, in combination with the non-linear size scaling relationships (Figures 9A, 10A), are indicative of quasibrittle materials (Luo and Bažant, 2017a,b). In these types of materials, it is possible for multiple local failure events to occur prior to total material failure, providing enhanced fracture toughness and resiliency to defects. This size dependent behavior is independent from previous efforts that describe a transition from ductile to brittle failure mechanisms in nanowires with increasing length, but constant cross-sectional area (Wu et al., 2012). Future work involves extending these distributional observations of material performance to three dimensions, as well as analytic investigations to build statistical theories capable of capturing the transition between quasibrittle and brittle failure regimes of neat CNC films.

Conclusion

Taken together, the results presented herein provide reasonable evidence to suggest that many of the conclusions from matrix-containing, uniaxial nanocomposites can be applied to neat films with high aspect ratio particle assembles. Specifically, the non-bonded interactions between adjacent fibers in neat films can be well-approximated by the matrix phase of standard brick and mortar continuum theories. That being said, some important differences between two phase and neat films were observed. Namely, short fiber neat films tended to be more compliant than expected given the properties of their constituents, and this trend was consistent independent from the particular in-plane fiber arrangement. Moreover, for short fibers, CNC films with regular overlaps exhibited higher initial moduli compared to those with staggered microstructures. The differences between the initial moduli of CNC films with regular and staggered arrangements becomes less pronounced as the fiber lengths exceed the critical length for shear load transfer. However, a similar saturation trend in both strength and toughness was not observed with increasing fiber length, with staggered architectures outperforming those with regular overlaps. Additionally, neat films showed a meaningful insensitivity to randomness with respect to their in-plane fiber arrangements during elastic deformations, as well as during failure for films with sufficiently long fibers. While in-plane ordering randomness of fibers did not significantly or substantially affect the median film elastic or failure responses, a widening of the property distributions was observed. Finally, the size scaling behavior of these neat films exhibited a readily identifiable transition between quasibrittle and brittle failure modes, but an insensitivity to system size during elastic deformation.

Author Contributions

BM conducted the computation simulations and data analysis, as well as designed the statistical analyses. BM and SK contributed to the manuscript preparation and study design.

Funding

BM and SK would like to acknowledge funding from the Army Research Office (award #W911NF1710430), Office of Naval Research (PECASE Award, grant number N00014-16-1-3175), the Center for Hierarchical Materials Design (CHiMaD) funded by National Institute of Standards and Technology (award #70NANB14H012), and the Northwestern University High Performance Computing Center.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2019.00174/full#supplementary-material

References

Abid, N., Mirkhalaf, M., and Barthelat, F. (2018). Discrete-element modeling of nacre-like materials : Effects of random microstructures on strain localization and mechanical performance. J. Mech. Phys. Solids 112, 385–402. doi: 10.1016/j.jmps.2017.11.003

CrossRef Full Text | Google Scholar

Arzt, E., Fratzl, P., Gao, H., Ji, B., and Ja, I. L. (2003). Materials become insensitive to flaws at nanoscale. Proc. Natl. Acad. Sci. U.S.A. 100, 5597–5600. doi: 10.1073/pnas.0631609100

PubMed Abstract | CrossRef Full Text | Google Scholar

Barthelat, F. (2014). Designing nacre-like materials for simultaneous stiffness, strength and toughness: optimum materials, composition, microstructure and size. J. Mech. Phys. Solids 73, 22–37. doi: 10.1016/j.jmps.2014.08.008

CrossRef Full Text | Google Scholar

Barthelat, F., Rabiei, R., and Dastjerdi, A. K. (2012). Toughness amplification in natural composites. Mater. Res. Soc. Symp. Proc. 1420, 61–66. doi: 10.1557/opl.2012.714

CrossRef Full Text | Google Scholar

Barthelat, F., Tang, H., Zavattieri, P. D., Li, C. M., and Espinosa, H. D. (2007). On the mechanics of mother-of-pearl: a key feature in the material hierarchical structure. J. Mech. Phys. Solids 55, 306–337. doi: 10.1016/j.jmps.2006.07.007

CrossRef Full Text | Google Scholar

Barthelat, F., and Zhu, D. (2011). A novel biomimetic material duplicating the structure and mechanics of natural nacre. J. Mater. Res. 26, 1203–1215. doi: 10.1557/jmr.2011.65

CrossRef Full Text | Google Scholar

Bažant, Z. P., Le, J., and Bažant, M. Z. (2009). Scaling of strength and lifetime probability distributions of quasibrittle structures based on atomistic fracture mechanics. Proc. Natl. Acad. Sci. U. S. A. 106, 11484–11489. doi: 10.1115/IMECE2009-11824

PubMed Abstract | CrossRef Full Text | Google Scholar

Bažant, Z. P., and Le, J.-L. (2017). Probabilistic Mechanics of Quasibrittle Structures: Strength, Lifetime, and Size Effect, Cambridge: Cambridge University Press.

Google Scholar

Begley, M. R., Philips, N. R., Compton, B. G., Wilbrink, D. V., Ritchie, R. O., and Utz, M. (2012). Micromechanical models to guide the development of synthetic ‘brick and mortar’ composites. J. Mech. Phys. Solids 60, 1545–1560. doi: 10.1016/j.jmps.2012.03.002

CrossRef Full Text | Google Scholar

Bonderer, L. J., Studart, A. R., and Gauckler, L. J. (2008). Bioinspired design and assembly of platelet reinforced polymer films. Science 319, 1069–1074. doi: 10.1126/science.1148726

PubMed Abstract | CrossRef Full Text | Google Scholar

Chandler, M. Q., and Cheng, J. R. C. (2018). Discrete element modeling of microstructure of nacre. Comput. Part. Mech. 5, 191–201. doi: 10.1007/s40571-017-0162-7

CrossRef Full Text | Google Scholar

Chen, C. Q., Shi, Y., Zhang, Y. S., Zhu, J., and Yan, Y. J. (2006). Size dependence of Young's modulus in ZnO nanowires. Phys. Rev. Lett. 96, 1–4. doi: 10.1103/PhysRevLett.96.075505

PubMed Abstract | CrossRef Full Text | Google Scholar

de Obaldia, E. E., Jeong, C., Grunenfelder, L. K., Kisailus, D., and Zavattieri, P. (2015). Analysis of the mechanical response of biomimetic materials with highly oriented microstructures through 3D printing, mechanical testing and modeling. J. Mech. Behav. Biomed. Mater. 48, 70–85. doi: 10.1016/j.jmbbm.2015.03.026

PubMed Abstract | CrossRef Full Text | Google Scholar

Dumanli, A. G., Van Der Kooij, H. M., Kamita, G., Reisner, E., Baumberg, J. J., Steiner, U., et al. (2014). Digital color in cellulose nanocrystal films. ACS Appl. Mater. Interfaces 6, 12302–12306. doi: 10.1021/am501995e

PubMed Abstract | CrossRef Full Text | Google Scholar

Dutta, A., Arjun, S., and Miklavcic, M. (2013). Optimal overlap length in staggered architecture composites under dynamic loading conditions. J. Mech. Phys. Solids 61, 145–160. doi: 10.1016/j.jmps.2012.08.005

CrossRef Full Text | Google Scholar

Dutta, A., and Tekalur, S. A. (2014). Crack tortuousity in the nacreous layer–Topological dependence and biomimetic design guideline. Int. J. Solids Struct. 51, 325–335. doi: 10.1016/j.ijsolstr.2013.10.006

CrossRef Full Text | Google Scholar

Eichhorn, S. J. (2011). Cellulose nanowhiskers: promising materials for advanced applications. Soft Matter 7, 303–315. doi: 10.1039/C0SM00142B

CrossRef Full Text | Google Scholar

Espinosa, H. D., Rim, J. E., Barthelat, F., and Buehler, M. J. (2009). Merger of structure and material in nacre and bone – Perspectives on de novo biomimetic materials. Prog. Mater. Sci. 54, 1059–1100. doi: 10.1016/j.pmatsci.2009.05.001

CrossRef Full Text | Google Scholar

Fratzl, P., and Weinkamer, R. (2007). Nature's hierarchical materials. Prog. Mater. Sci. 52, 1263–1334. doi: 10.1016/j.pmatsci.2007.06.001

CrossRef Full Text | Google Scholar

Gao, L., Nie, G., and Zhang, T. (2016). A study of hierarchical biological composite structures via a coarse-grained molecular dynamics simulation approach. Int. J. Appl. Mech. 8:1650084. doi: 10.1142/S1758825116500848

CrossRef Full Text | Google Scholar

Ghazlan, A., Ngo, T. D., and Tran, P. (2018). Influence of geometric and material parameters on the behavior of nacreous composites under quasi-static loading. Compos. Struct. 183, 457–482. doi: 10.1016/j.compstruct.2017.05.015

CrossRef Full Text | Google Scholar

Gorbatikh, L., Lomov, S. V., and Verpoest, I. (2010). Original mechanism of failure initiation revealed through modelling of naturally occurring microstructures. J. Mech. Phys. Solids 58, 735–750. doi: 10.1016/j.jmps.2010.02.007

CrossRef Full Text | Google Scholar

Gu, G. X., Libonati, F., Wettermark, S. D., and Buehler, M. J. (2017). Printing nature: unraveling the role of nacre's mineral bridges. J. Mech. Behav. Biomed. Mater. 76, 135–144. doi: 10.1016/j.jmbbm.2017.05.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Gu, G. X., Su, I., Sharma, S., Voros, J. L., Qin, Z., and Buehler, M. J. (2016). Three-dimensional-printing of bio-inspired composites. J. Biomech. Eng. 138:021006. doi: 10.1115/1.4032423

CrossRef Full Text | Google Scholar

Habibi, Y., Lucia, L. A., and Rojas, O. J. (2010). Cellulose nanocrystals: chemistry, self-assembly, and applications. Chem. Rev. 110, 3479–3500. doi: 10.1021/cr900339w

PubMed Abstract | CrossRef Full Text | Google Scholar

Hansoge, N. K., Huang, T., Sinko, R., Xia, W., Chen, W., and Keten, S. (2018). Materials by design for stiff and tough hairy nanoparticle assemblies. ACS Nano. 12, 7946–7958. doi: 10.1021/acsnano.8b02454

PubMed Abstract | CrossRef Full Text | Google Scholar

Henriksson, M., Berglund, L. A., Isaksson, P., and Lindstro, T. (2008). Cellulose nanopaper structures of high toughness. Biomacromolecules 9, 1579–1585. doi: 10.1021/bm800038n

PubMed Abstract | CrossRef Full Text | Google Scholar

Henry, J., and Pimenta, S. (2017). Semi-analytical simulation of aligned discontinuous composites. Compos. Sci. Technol. 144, 230–244. doi: 10.1016/j.compscitech.2017.01.027

CrossRef Full Text | Google Scholar

Henry, J., and Pimenta, S. (2018). Increasing damage tolerance in composites using hierarchical brick-and-mortar microstructures. J. Mech. Phys. Solids 118, 322–340. doi: 10.1016/j.jmps.2018.06.003

CrossRef Full Text | Google Scholar

Humphrey, W., Dalke, A., and Schulten, K. (1996). VMD: visual molecular dynamics. J. Mol. Graph. 14, 33–38. doi: 10.1016/0263-7855(96)00018-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Jackson, A. P., Vincent, J. F. V., and Turner, R. M. (1988). The mechanical design of nacre. Proc. R. Soc. B. 234, 415–440. doi: 10.1098/rspb.1988.0056

CrossRef Full Text | Google Scholar

Jäger, I., and Fratzl, P. (2000). Mineralized collagen fibrils: A mechanical model with a staggered arrangement of mineral particles. Biophys. J. 79, 1737–1746. doi: 10.1016/S0006-3495(00)76426-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Ji, B., and Gao, H. (2004). Mechanical properties of nanostructure of biological materials. J. Mech. Phys. Solids 52, 1963–1990. doi: 10.1016/j.jmps.2004.03.006

CrossRef Full Text | Google Scholar

Kamat, S., Su, X., Ballarini, R., and Heuer, A. (2000). Structural basis for the fracture toughness of the shell of the conch Strombus gigas. Nature 405, 1036–1040. doi: 10.1038/35016535

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim, Y., Kim, Y., Lee, T. I., Kim, T. S., and Ryu, S. (2018). An extended analytic model for the elastic properties of platelet-staggered composites and its application to 3D printed structures. Compos. Struct. 189, 27–36. doi: 10.1016/j.compstruct.2018.01.038

CrossRef Full Text | Google Scholar

Koh, L. D., Cheng, Y., Teng, C. P., Khin, Y. W., Loh, X. J., Tee, S. Y., et al. (2015). Structures, mechanical properties and applications of silk fibroin materials. Prog. Polym. Sci. 46, 86–110. doi: 10.1016/j.progpolymsci.2015.02.001

CrossRef Full Text | Google Scholar

Kruskal, W. H., and Wallis, W. A. (1952). Use of ranks in one-criterion variance analysis. J. Am. Stat. Assoc. 47, 583–621. doi: 10.1080/01621459.1952.10483441

CrossRef Full Text | Google Scholar

Lagerwall, J. P. F., Schutz, C., Salajkova, M., Noh, J., Park, J. H., Scalia, G., et al. (2014). Cellulose nanocrystal-based materials : from liquid crystal self-assembly and glass formation to multifunctional thin films. NPG Asia Mater. 6, 1–12. doi: 10.1038/am.2013.69

CrossRef Full Text | Google Scholar

Lei, H. J., Zhang, Z. Q., Han, F., Liu, B., and Gao, H. J. (2013). Elastic bounds of bioinspired nanocomposites. J. Appl. Mech. 80:1017. doi: 10.1115/1.4023976

CrossRef Full Text | Google Scholar

Luo, W., and Bažant, Z. P. (2017a). Fishnet statistics for probabilistic strength and scaling of nacreous imbricated lamellar materials. J. Mech. Phys. Solids 109, 264–287. doi: 10.1016/j.jmps.2017.07.023

CrossRef Full Text | Google Scholar

Luo, W., and Bažant, Z. P. (2017b). Fishnet model for failure probability tail of nacre-like imbricated lamellar materials. Proc. Natl. Acad. Sci. U. S. A. 114:201714103. doi: 10.1073/pnas.1714103114

PubMed Abstract | CrossRef Full Text | Google Scholar

Mann, H. B., and Whitney, D. R. (1947). On a test of whether one of two random variables is stochastically larger than the other. Ann. Math. Stat. 18, 50–60. doi: 10.1214/aoms/1177730491

CrossRef Full Text | Google Scholar

Mathiazhagan, S., and Anup, S. (2016a). Mechanical behaviour of bio-inspired brittle-matrix nanocomposites under different strain rates using molecular dynamics. Mol. Simul. 42, 1490–1501. doi: 10.1080/08927022.2016.1205192

CrossRef Full Text | Google Scholar

Mathiazhagan, S., and Anup, S. (2016b). Investigation of deformation mechanisms of staggered nanocomposites using molecular dynamics. Phys. Lett. A 380, 2849–2853. doi: 10.1016/j.physleta.2016.06.046

CrossRef Full Text | Google Scholar

Mathiazhagan, S., and Anup, S. (2016c). Influence of platelet aspect ratio on the mechanical behaviour of bio-inspired nanocomposites using molecular dynamics. J. Mech. Behav. Biomed. 59, 21–40. doi: 10.1016/j.jmbbm.2015.12.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Mathiazhagan, S., and Anup, S. (2018). Atomistic simulations of length-scale effect of bioinspired brittle-matrix nanocomposite models. J. Eng. Mech. 144, 1–9. doi: 10.1061/(ASCE)EM.1943-7889.0001533

CrossRef Full Text | Google Scholar

Mathur, A., and Erlebacher, J. (2007). Size dependence of effective Young's modulus of nanoporous gold. Appl. Phys. Lett. 90, 2005–2008. doi: 10.1063/1.2436718

CrossRef Full Text | Google Scholar

Mayer, G. (2005). Rigid biological systems as models for synthetic composites. Science. 310, 1144–1147. doi: 10.1126/science.1116994

PubMed Abstract | CrossRef Full Text | Google Scholar

Menig, R., Meyers, M. H., Meyers, M. A., and Vecchio, K. S. (2000). Quasi-static and dynamic mechanical response of Haliotis rufescens (abalone) shells. Acta Mater. 48, 2383–2398. doi: 10.1016/S1359-6454(99)00443-7

CrossRef Full Text | Google Scholar

Miller, R. E., and Shenoy, V. B. (2000). Size-dependent elastic properties of nanosized structural elements. Nanotechnology 11, 139–147. doi: 10.1088/0957-4484/11/3/301

CrossRef Full Text | Google Scholar

Mirzaeifar, R., Dimas, L. S., Qin, Z., and Buehler, M. J. (2015). Defect-tolerant bioinspired hierarchical composites: simulation and experiment. ACS Biomater. Sci. Eng. 1, 295–304. doi: 10.1021/ab500120f

CrossRef Full Text | Google Scholar

Moon, R. J., Martini, A., Nairn, J., Youngblood, J., Martini, A., and Nairn, J. (2011). Cellulose nanomaterials review: structure, properties and nanocomposites. Chem. Soc. Rev. 40, 3941–3994. doi: 10.1039/c0cs00108b

PubMed Abstract | CrossRef Full Text | Google Scholar

Munch, E., Launey, M. E., Alsem, D. H., Saiz, E., Tomsia, A. P., and Ritchie, R. O. (2008). Tough, bio-inspired hybrid materials. Science 322, 1516–1521. doi: 10.1126/science.1164865

PubMed Abstract | CrossRef Full Text | Google Scholar

Natarajan, B., Krishnamurthy, A., Qin, X., Emiroglu, C. D., Forster, A., Foster, E. J., et al. (2018). Binary cellulose nanocrystal blends for bioinspired damage tolerant photonic films. Adv. Funct. Mater. 28, 1–11. doi: 10.1002/adfm.201800032

CrossRef Full Text | Google Scholar

Ni, Y., Song, Z., Jiang, H., Yu, S., and He, L. (2015). Optimization design of strong and tough nacreous nano- composites through tuning characteristic lengths. J. Mech. Phys. Solids 81, 41–57. doi: 10.1016/j.jmps.2015.04.013

CrossRef Full Text | Google Scholar

Ostanin, I., Ballarini, R., Potyondy, D., and Dumitric,ǎ, T. (2013). A distinct element method for large scale simulations of carbon nanotube assemblies. J. Mech. Phys. Solids 61, 762–782. doi: 10.1016/j.jmps.2012.10.016

CrossRef Full Text | Google Scholar

Plimpton, S. (1995). Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 117, 1–19. doi: 10.1006/jcph.1995.1039

CrossRef Full Text | Google Scholar

Podsiadlo, P., Kaushik, A. K., Arruda, E. M., Waas, A. M., Shim, B. S., Xu, J., et al. (2007). Ultrastrong and stiff layered polymer nanocomposites. Science 318, 1–4. doi: 10.1126/science.1143176

PubMed Abstract | CrossRef Full Text | Google Scholar

Pro, J. W., Kwei, R., Petzold, L. R., Utz, M., and Begley, M. R. (2015). The impact of stochastic microstructures on the macroscopic fracture properties of brick and mortar composites. Extrem. Mech. Lett. 5, 1–9. doi: 10.1016/j.eml.2015.09.001

CrossRef Full Text | Google Scholar

Qin, X., Feng, S., Meng, Z., and Keten, S. (2017). Optimizing the mechanical properties of cellulose nanopaper through surface energy and critical length scale considerations. Cellulose 24, 3289–3299. doi: 10.1007/s10570-017-1367-x

CrossRef Full Text | Google Scholar

Qin, X., Marchi, B. C., Meng, Z., and Keten, S. (2019). Impact resistance of nanocellulose films with bioinspired Bouligand microstructures. Nanoscale Adv. 1:1351. doi: 10.1039/C8NA00232K

CrossRef Full Text | Google Scholar

Qwamizadeh, M., Lin, M., Zhang, Z., Zhou, K., and Wei, Y. (2017a). Bounds for the dynamic modulus of unidirectional composites with bioinspired staggered distributions of platelets. Compos. Struct. 167, 152–165. doi: 10.1016/j.compstruct.2017.01.077

CrossRef Full Text | Google Scholar

Qwamizadeh, M., Zhang, Z., Zhou, K., and Wei, Y. (2015). On the relationship between the dynamic behavior and nanoscale staggered structure of the bone whole bone. J. Mech. Phys. Solids 78, 17–31. doi: 10.1016/j.jmps.2015.01.009

CrossRef Full Text | Google Scholar

Qwamizadeh, M., Zhou, K., and Zhang, Y. W. (2017b). Damping behavior investigation and optimization of the structural layout of load-bearing biological materials. Int. J. Mech. Sci. 120, 263–275. doi: 10.1016/j.ijmecsci.2016.12.003

CrossRef Full Text | Google Scholar

Ritchie, R. O. (2011). The conflicts between strength and toughness. Nat. Mater. 10, 817–822. doi: 10.1038/nmat3115

PubMed Abstract | CrossRef Full Text | Google Scholar

Sakhavand, N., and Shahsavari, R. (2015). Universal composition-structure-property maps for natural and biomimetic platelet-matrix composites and stacked heterostructures. Nat. Commun. 6:6523. doi: 10.1038/ncomms7523

PubMed Abstract | CrossRef Full Text | Google Scholar

Shao, Y., Zhao, H., Feng, X., and Gao, H. (2012). Discontinuous crack-bridging model for fracture toughness analysis of nacre. J. Mech. Phys. Solids 60, 1400–1419. doi: 10.1016/j.jmps.2012.04.011

CrossRef Full Text | Google Scholar

Sharpe, W. N., Jackson, K. M., Hemker, K. J., and Xie, Z. (2001). Effect of specimen size on young's modulus and fracture strength of polysilicon. J. Microelectromechanical Syst. 10, 317–326. doi: 10.1109/84.946774

CrossRef Full Text | Google Scholar

Sinko, R., Qin, X., and Keten, S. (2015). Interfacial mechanics of cellulose nanocrystals. MRS Bull. 40, 340–348. doi: 10.1557/mrs.2015.67

CrossRef Full Text | Google Scholar

Valashani, S. M. M., and Barthelat, F. (2015). A laser-engraved glass duplicating the structure, mechanics and performance of natural nacre. Bioinspir. Biomim. 10:026005. doi: 10.1088/1748-3190/10/2/026005

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, J., Cheng, Q., and Tang, Z. (2012). Layered nanocomposites inspired by the structure and mechanical properties of nacre. Chem. Soc. Rev. 41, 1111–1129. doi: 10.1039/C1CS15106A

PubMed Abstract | CrossRef Full Text | Google Scholar

Wei, X., Filleter, T., and Espinosa, H. D. (2015). Statistical shear lag model–unraveling the size effect in hierarchical composites. Acta Biomater. 18, 206–212. doi: 10.1016/j.actbio.2015.01.040

PubMed Abstract | CrossRef Full Text | Google Scholar

Wei, X., Naraghi, M., and Espinosa, H. D. (2012). Optimal length scales emerging from shear load transfer in natural materials: application to carbon-based nanocomposite design. ACS Nano 6, 2333–2344. doi: 10.1021/nn204506d

PubMed Abstract | CrossRef Full Text | Google Scholar

Wei, Z., Sinko, R., Keten, S., and Luijten, E. (2018). Effect of surface modification on water adsorption and interfacial mechanics of cellulose nanocrystals. ACS Appl. Mater. Interfaces 10, 8349–8358. doi: 10.1021/acsami.7b18803

CrossRef Full Text | Google Scholar

Wilkerson, R. P., Gludovatz, B., Watts, J., Tomsia, A. P., Hilmas, G. E., and Ritchie, R. O. (2018). A study of size effects in bioinspired,“nacre-like”, metal-compliant- phase (nickel-alumina) coextruded ceramics. Acta Mater. 148, 147–155. doi: 10.1016/j.actamat.2018.01.046

CrossRef Full Text | Google Scholar

Wu, X., Moon, R. J., and Martini, A. (2014). Tensile strength of I b crystalline cellulose predicted by molecular dynamics simulation. Cellulose 21, 2233–2245. doi: 10.1007/s10570-014-0325-0

CrossRef Full Text | Google Scholar

Wu, Z., Zhang, Y., Jhon, M. H., Gao, H., and Srolovitz, D. J. (2012). Nanowire failure: long = brittle and short = ductile. Nano Lett. 12, 10–14. doi: 10.1021/nl203980u

PubMed Abstract | CrossRef Full Text | Google Scholar

Xia, W., Ruiz, L., Pugno, N. M., and Keten, S. (2016). Critical length scales and strain localization govern the mechanical performance of multi-layer graphene assemblies. Nanoscale 8, 6456–6462. doi: 10.1039/C5NR08488A

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, P., Heyne, M. A., and To, A. C. (2015). Biomimetic staggered composites with highly enhanced energy dissipation : modeling, 3D printing, and testing. J. Mech. Phys. Solids 83, 285–300. doi: 10.1016/j.jmps.2015.06.015

CrossRef Full Text | Google Scholar

Zhang, Z., Zhang, Y., and Gao, H. (2010). On optimal hierarchy of load-bearing biological materials. Proc. R. Soc. B. 278, 519–525. doi: 10.1098/rspb.2010.1093

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Z. Q., Liu, B., Huang, Y., Hwang, K. C., and Gao, H. (2010). Mechanical properties of unidirectional nanocomposites with non-uniformly or randomly staggered platelet distribution. J. Mech. Phys. Solids 58, 1646–1660. doi: 10.1016/j.jmps.2010.07.004

CrossRef Full Text | Google Scholar