Glass Fracture Upon Ballistic Impact: New Insights From Peridynamics Simulations

Introduction

Glass, an archetypical brittle material, is ubiquitously used in everyday life from car wind shields to smart phone screens (Mauro, 2014; Mauro and Zanotto, 2014; Mauro et al., 2014; Wang M. et al., 2017). One of the major causes of failure in glass is the sudden load, such as impact, to which they are exposed to during the service period. These impact loads could vary from small stone pellets to bullets, resulting in a minor crack to a catastrophic failure of the glass structure, respectively (Bobaru et al., 2012; Hu et al., 2013). Understanding the role of material and geometric properties of the structure on impact-induced damage is crucial to design next generation glassware with improved impact-tolerance.

Extensive studies have been carried out in the past decades using experimental techniques on the impact-induced damage in brittle materials (Knight et al., 1977; Chaudhri and Walley, 1978; Field, 1988; Field et al., 1989; Ball and McKenzie, 1994; Bourne et al., 1995; Bless and Chen, 2010; Barefoot et al., 2013). These studies focused both on the dynamic aspects and post-mortem of cracks in typical glass-based structures subjected to impact. However, the experimental studies were limited by two major aspects. Firstly, the crack propagation and associated dynamic phenomena during impact occur at timescales barely accessible to the experiments, even with the fastest available recording devices (Tang et al., 2014). As such, most of the experimental measurements do not have a direct access to the crack propagation and energy releasing mechanisms. Secondly, a parametric study, analyzing the effect of a single material property while keeping others constant, is next to impossible using experiments. This is because, even in materials where continuous variation of compositions are possible, such as glasses or cement, properties do not vary uniformly and continuously (Krishnan et al., 2016, 2017; Bauchy et al., 2017; Li et al., 2017). This poses a fundamental challenge in critically analyzing the role of material and geometric properties on impact-induced failure through experiments.

On the other hand, in silico “numerical experiments” provide a unique means to control the initial and boundary conditions and material properties with high fidelity. Further, it provides complete access to the spatio-temporal evolution of displacement and stress fields, and energy in the structure. To study the impact-induced damage in materials, numerical simulations across the length-scales—from molecular dynamics (MD) (Samela and Nordlund, 2010; Holmström et al., 2011; Anders et al., 2012; Saiz and Gamero-Castaño, 2012) to finite element (FE) (Timmel et al., 2007; Krishnan et al., 2010; Pyttel et al., 2011; Peng et al., 2013; Doner et al., 2019)—have been carried out in the past. Although MD simulations can provide insight into the atomistic mechanisms of crack propagation (Buehler et al., 2003; Wang et al., 2016), they cannot be used to study the damage occurring at the macroscale, e.g., bullet impact. This is attributed to the fact that the system size, in MD simulations, is restricted to a few hundred nanometers, and the timescale to a few nanoseconds. In order to simulate failure at larger length scales, FE simulations are preferred. While traditional FE methods are notorious for their inability to simulate crack, advanced techniques such as extended FE methods (XFEM) (Belytschko et al., 2003; Zi and Belytschko, 2003), FE with element deletion method (Ismail et al., 2012), and cohesive-zone model (Elices et al., 2002) have been proposed as an alternative to investigate macroscopic failure in brittle materials. Each of these models carry their own deficiencies in modeling realistic crack propagations (Agwai et al., 2011; Nayak et al., 2019). The major reason for the inability of FE-based methods to predict realistic crack propagation is that the mathematical basis for these methods rely on the classical continuum mechanics. The basic assumption in continuum theory that the body remains continuous when it undergoes deformation is violated during crack initiation and propagation. This discontinuity in the displacement field, due to crack formation, renders the governing differential equations meaningless. As such, although these methods can be used to study various aspects of impact-induced failure, a start-to-end simulation of impact-induced crack propagation and failure in glasses is impeded due to the aforementioned reasons.

To address this inherent limitation in continuum mechanics, Silling et al. proposed a non-local formulation of continuum mechanics (Silling, 2000). This method, inspired from the MD-based methods (Seleson et al., 2009), proposes an alternate approach to formulate the continuum equations of motion (see the section Methodology). Thanks to the non-local integral-based formulation of peridynamics, the method has been extremely successful to simulate discontinuous phenomena, such as crack propagation (Ha and Bobaru, 2011), failure phase separated glasses (Tang et al., 2018), impact (Parks et al., 2008; Bobaru et al., 2012), blast (Fan and Li, 2017; Wang Q. et al., 2017), and other forms of extreme failures such as landslides (Lai et al., 2015) and earthquakes.

In the present work, we use peridynamic simulations to analyze the damage in glasses subjected to a projectile impact. We investigate the role of mechanical and geometric properties such as elastic modulus, fracture energy, and plate radius in determining the overall damage in the glass structure. An interesting power-law dependence is observed between the overall damage and the fracture energy of the glass plate. Through a detailed analysis on the initiation and propagation of cracks, we show that the power-law dependence is closely related to the crack-branching instability during dynamic crack propagation.

Methodology

Peridynamics

Peridynamics is a reformulation of continuum mechanics into integral equations of motion (Silling, 2000; Silling et al., 2007; Silling and Lehoucq, 2008; Le and Bobaru, 2017). This allows peridynamics to handle cracks and discontinuities inherently, as the differentiability of displacement field is not a necessary condition for the equations of motion to be valid (Silling and Askari, 2004; Foster, 2009; Agwai et al., 2011; Ha and Bobaru, 2011). In peridynamics, the continuum domain is discretized using particles or lattice points, which interact with each other based on a pair-wise force. A more generalized version of peridynamics with state-based variables has also been proposed to simulate complex material response including plasticity and viscoelasticity (Silling et al., 2007; Mitchell, 2011a,b). In peridynamics, the classical assumption of “local force” is replaced by “force acting at a distance” through the introduction of a characteristic length scale. This characteristic length scale, known as the horizon, gives the subdomain within which all particles interact with the central particle. Based on this, the peridynamics equation of motion is given by

$\begin{array}{ll}\rho \ddot{\text{u}}(\text{x};\text{ t})={\displaystyle {\int }_{H_x}f(\text{u}(\text{x}\prime ,\text{ t})-\text{u}(\text{x},\text{ t}),\text{x}\prime -\text{x})\text{dx}\prime +\text{b}(\text{x},\text{ t})}& (1)\end{array}$

where ρ is the mass density, ü is the acceleration vector field, f(.) is the pairwise force function for particles at locations x and x′, b is the body force intensity, and H_x defines the subdomain in the body, i.e., the horizon. The form of the pairwise force function depends on the material model used in the peridynamic formulation. Here, we restrict our discussion to bond-based material model, as this model has been shown to reproduce the characteristics of fracture in brittle materials successfully (Ha and Bobaru, 2011; Bobaru et al., 2012; Hu et al., 2013). For a detailed overview on peridynamics and different material models, please refer to Silling (2000); Silling et al. (2007), and Mitchell (2011a,b).

For a bond-based material, namely prototype microelastic brittle (PMB) material (Parks et al., 2008), the pairwise force is given by

$\begin{array}{ll}f\left(\eta ,\xi \right)=\{\begin{array}{cc}\frac{\xi +\eta }{\parallel \xi +\eta \parallel }\text{cs},& \parallel \xi \parallel \le \delta \\ 0,& \parallel \xi \parallel >\delta \end{array}& (2)\end{array}$

where ξ = x'–x is the relative position of the particle, η = u(x',t)—u(x,t) is its relative displacement, c(ξ) is the micromodulus function, and $s=\frac{\parallel \eta +\xi \parallel \parallel \xi \parallel }{\parallel \xi \parallel }$ gives the relative bond elongation. Using a condition for the equivalency of elastic strain energy density, the micromodulus can be derived from the bulk modulus K, and horizon δ as Ha and Bobaru (2011).

$\begin{array}{ll}c=\frac{18K}{\pi {\delta }^4}& (3)\end{array}$

Bonds between the lattice points in PMB are purely elastic with a critical stretch s₀, after which they will break. The broken bond corresponds to a local material damage and allows for the initiation and propagation of cracks in the material. The critical bond stretch s₀ is derived from the fracture energy of the material so as to represent a realistic strain-energy release rate as Ha and Ha and Bobaru (2011).

$\begin{array}{ll}{s}_0=\sqrt{\frac{5G_c}{9\text{K}\delta }}& (4)\end{array}$

where G_cis the fracture energy of the material. It should be noted that a material particle is connected to multiple particles within the horizon. To account for this while computing damage of a point, a Boolean function μ(t, η, ξ) is defined which has a value of 0 corresponding to a broken bond, and 1 otherwise. Thus, the damage at a material point x is defined as

$\begin{array}{ll}\phi (x,t)=1-\frac{{\int }_{H_x}\mu (t,\eta ,\xi )d{V}_{x^{\prime }}}{{\int }_{H_x}d{V}_{x^{\prime }}}& (5)\end{array}$

Thus, a material point with all the bonds intact will have a damage of 0, while the one with all the bonds broken have a damage of 1.

Simulation Details

Peridynamics simulations of impact damage on a glass plate are carried out using the open-source LAMMPS package (Plimpton, 1995; Parks et al., 2008, 2011). To this extent, a well-established methodology (Parks et al., 2008, 2011; Ha and Bobaru, 2011; Bobaru et al., 2012; Hu et al., 2013), which is validated against several experimental studies, is used. Figure 1 shows the geometry of the plate and the bullet setup. The plate has a radius of 37 mm and thickness of 2.5 mm. The domain is discretized using a simple cubic lattice with lattice parameter of 0.5 mm. The horizon is kept constant with a value of 2.0 mm, four times the lattice parameter. The value is chosen based on a convergence study considering three different horizons (see Supplementary Material) and is in agreement with an earlier study (Bobaru and Hu, 2012). The material properties of the plate are taken equivalent to that of a soda-lime silicate glass with an elastic modulus of 94.5 GPa and fracture energy of 4.3 J/m² (Wang et al., 2016). Note that the material properties and geometry mentioned here are chosen as the standard simulation. In other words, while investigating the effect of material properties and geometry on impact-induced damage, the constant parameters are set to the values as in the standard simulation. The values taken by the variable parameter are detailed in the relevant sections later.

FIGURE 1

Figure 1. (A) Front and (B) top view of the plate-bullet simulation setup. Note that the glass plate and bullet are colored in blue and red, respectively.

A spherical bullet with a radius of 3 mm is used in the present study. Further, to ensure the generality of results, two different bullets are considered. Both the bullets are modeled as linear-elastic materials. The first one, named as copper, has notably higher stiffness of 115 GPa and fracture energy of 2,665 J/m² than the target glass plate. This ensures that the bullet suffers close to zero damage upon impact. The second bullet has the same material properties as that of the target plate and is named as a glass bullet. It should be noted that the behavior of the first bullet may not correspond to that of a real copper bullet. This is because the effects of plasticity are not included in the model. However, the aim of the study is to ensure that the results presented herein are valid irrespective of the stiffness or fracture energy of the bullet. Both copper and glass bullets are projected with a velocity of 100 m/s in the standard case. Initially, the bullet is separated from the glass plate by a distance two times the horizon. This is to avoid any interaction between the bullet and the glass plate at the initiation of the simulation. Peridynamic equations of motion are integrated using a timestep of 10⁻⁷ s (Parks et al., 2008).

Computation of Crack Velocity

To compute the velocity with which cracks propagate, we focus on the major radial cracks. To this extent, we first plot histograms of damage with respect to angular position of all the lattice points at every timestep. In the histogram, peaks correspond to the major radial cracks and the angles at which these peaks occur correspond to the angular position of the radial crack. In other words, the cracks propagate radially outward at this angle on the glass plate. Now, around these angles at which cracks propagate, we compute the damage in the lattice points along the radial direction. Note that propagation of cracks manifests as increased damage in the lattice points. Based on previous studies, we assume that a point with damage close to 0.5 forms part of a cracked surface (Foster, 2009; Agwai et al., 2011; Bobaru and Hu, 2012). This is based on the assumption that since the “bonds” of a lattice point are uniformly distributed in three dimensions, a failure of 50% of the bonds correspond to an exposed surface. Thus, at each timestep, we compute the radial position of the cracked lattice point to obtain the crack velocity as

$\begin{array}{ll}v=\frac{r(t)-r(t-\Delta t)}{\Delta t}& (6)\end{array}$

where r(t) corresponds to the position to the maximum radial position of a lattice point with damage ≥0.5, and Δt is the timestep. It should be noted that these regions with damage greater 0.5 may not correspond to fully separated crack surfaces. It is possible that the damaged regions may still have bridging bonds left across a crack that is yet to break (Xu et al., 2018). However, we observe that the velocity of the crack is not sensitive to the cut-off 0.5 and is consistent with slightly lower and cut-offs (see Supplementary Material).

Autoregressive Modeling of Damage Evolution

To understand the nature of crack-branching and growth upon bullet impact, we model the damage evolution as a recursive time-series, namely, first order auto-regressive (AR) model (Ljung, 2001). Note that the auto-regressive model inherently suggests an exponential growth, as the value at any time t depends on the value at t-1. Thus, the values are compounded at every instant following the growth rate of the AR model. Here, the damage at any time instant t, D(t) is modeled auto-regressively, that is, evolving with respect to damage the previous time instant, D(t-1), as

$\begin{array}{ll}D(t)=\alpha (t)D(t-1)+\epsilon (t-1)& (7)\end{array}$

where, ε is the unmodeled dynamics or the noise, which follows a Gaussian distribution with zero mean and non-zero variance, and α(t) is the term governing time evolution, called as the damage growth rate. We use data sets that correspond to 5 different fracture energy levels, namely, 4.3, 15, 50, 100, 150 kJ/m²⁻ for both glass and copper bullets for performing the modeling. To exclude the effects of boundary conditions and other dynamics, we perform the fitting considering the damage evolution in the initial region.

Results

Comparison With Experiment

In order to ensure realistic simulation of impact, we compare our simulation with experiments conducted by Knight et al. (1977) on the impact of steel balls on soda-lime glass. Here, all the properties and parameters are chosen to match exactly with the ones in the experiment. As such, a spherical ball of radius 0.5 cm is projected toward a soda-lime glass plate with dimensions 10 cm × 10 cm × 5 cm, with different initial velocities varying from 30 m/s to 300 m/s, namely 30, 40, 60, 80, 100, 110, 150, 200, and 300 m/s. The Young's modulus and fracture energy of the steel ball are considered to be 200 GPa and 10,000 J/m², respectively, and that of the glass plate are 72 GPa, and 7 J/m², respectively. For the peridynamic simulations, the discretization of the glass plate and ball is carried out with lattice units of 0.1 mm and a constant horizon of 0.4 mm is maintained. The micromodulus and critical stretch are computed using Equations (3) and (4). Note that both the steel ball and the glass plate are considered to be isotropic.

First, we focus on the coefficient of restitution (C_R) of the bullet. Note that C_R, being a ratio of approaching velocities to separating velocities, essentially captures the energy dissipated in the impact process. Thus, C_R ranges from 0 to 1, the former representing a perfectly plastic collision with complete energy dissipated in crack formation and the latter representing a perfectly elastic collision with no energy dissipation. Figure 2A shows the variation of C_R with respect to initial velocity of the bullet. For low velocities of the bullet (<100 m/s), C_R remains constant and close to 1, suggesting an elastic collision for this velocity range. For higher velocities (>100 m/s), C_R reduces drastically suggesting energy dissipation in the collision, almost following a power-law with respect to the initial velocity. This is consistent with the experiments (Knight et al., 1977), where C_R is observed to be close to 1 for velocities lower than 100 m/s with little damage on the glass plate. Figures 2B,C show the cross-sectional view of the glass plate subjected to impact in experiment (Knight et al., 1977) and simulation, respectively, at the same time (4 μs). We note that the depth of the damage observed in both the simulation and experiment is similar. Further, both the simulation and experiment produce debris upon impact, which is flying away from the surface. However, we observe that the peridynamic simulation over-estimate the pulverization behavior in the glass plate in comparison to the experiment. This could be due to the inherent deficiency of particle-based methods, which exhibits an increased tendency for particle separation. Note that the damage pattern simulated by peridynamics exhibits an asymmetry (see Figure 2), which could be ascribed to the following reasons. (i) The bullet atom is not perfectly spherical due to the discretization used in peridynamics. (ii) A slight perturbation is provided for the lattice points used in the discretization to avoid the formation of perfectly symmetric crack patterns. As such, the impact on the glass plate may result in an asymmetrical damage pattern. Overall, we observe that the peridynamic simulations exhibit a reasonable match with respect to experiments in predicting impact induced damage.

FIGURE 2

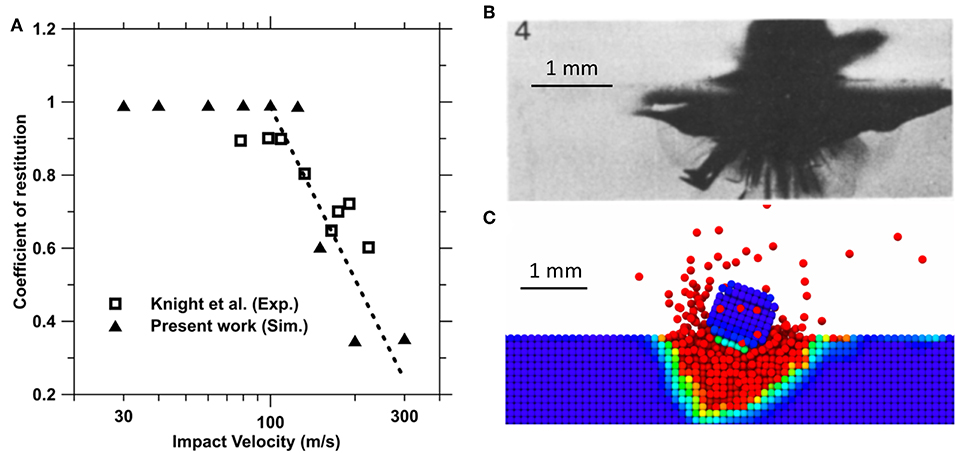
Figure 2. (A) Simulated coefficient of restitution (filled triangles) of the impact compared with the previous experiments by Knight et al. (1977) (empty squares). The dotted line is a guide to eye. (B) Impact of steel sphere on soda-lime glass with an impact velocity of 200 m/s by Knight et al. (1977). (C) Simulation of the impact experiment by Knight et al. (1977) using peridynamics. Red color represents damaged particles.

Crack Formation Under Ballistic Impact

Now, we focus on the crack formation behavior when a bullet impact occurs on a brittle glass plate. The glass plate has a radius of 0.037 mm, thickness of 0.0025 m, elastic modulus of 94.5 GPa, and fracture energy of 4.3 J/m², and is subjected to the impact of a copper bullet with a velocity of 100 m/s. The overall fraction of cracks present in the material can be quantitatively represented in the peridynamics framework by the average damage per particle. An average damage of 100% corresponds to all the lattice points broken and separated away from each other and 0% correspond to all the points intact.

Figure 3A shows the evolution of the average damage per particle and total mechanical energy in the glass plate. We observe that the average damage increases quickly upon impact and then eventually becomes constant, close to 48%, representing a saturated state. Note that the saturation of damage occurs very quickly—around 40 μs after the bullet comes into contact with the plate. Now, we focus on the evolution of the total mechanical energy gained by the plate upon impact. Note that this energy includes both the elastic energy and kinetic energy of the plate. From Figure 3A, we note that the energy initially increases, which is attributed to the elastic potential energy of the plate due to deformation and kinetic energy due to the transverse and longitudinal waves produced. Subsequently, the energy reaches a peak value, and then reduces slightly before reaching saturation. The slight decrease in energy before saturation is attributed to the release of elastic energy by the formation of a network of cracks. Note that the saturation of energy occurs concurrent to the saturation of damage. A visual representation of the bullet impact on the glass plate, followed by the crack formation, is shown in Figure 3B. The crack pattern observed is qualitatively similar to the ones observed in earlier experimental studies (Knight et al., 1977; Chaudhri and Walley, 1978), confirming the realistic nature of the simulations. We note that, upon impact, the cracks are first formed in the plate at the point where the bullet strikes (see Figure 3B). Major radial cracks then form which, while spreading outward, branch to form minor cracks. These cracks then spread to the entire glass plate forming a network of cracks in the form of radial and tangential cracks. Overall, we observe that the energy gained by glass plate upon impact is released through the formation of cracks and debris.

FIGURE 3

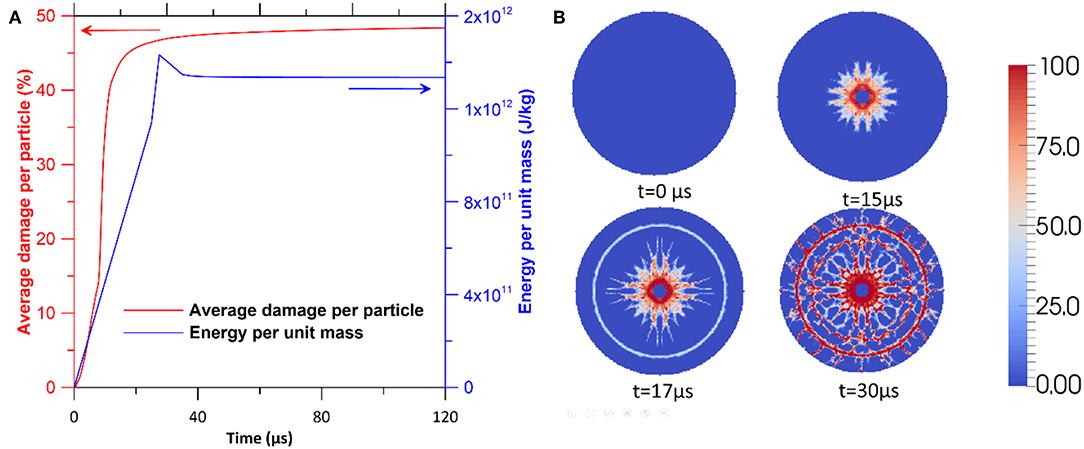
Figure 3. (A) Average damage per particle (left axis, red) and total mechanical energy (right axis, blue) of the glass plate, subjected to an impact by a copper bullet, with respect to time. Note that the results correspond to that of a glass plate with a radius of 37 mm, thickness of 0.0025 m, elastic modulus of 94.5 GPa, and fracture energy of 4.3 J/m². (B) Damage map in the glass plate subjected to impact at four different times, namely, 0, 15, 17, and 30 0 μs. The coloring scale, representing the local damage, varies from 0% (blue) to 100% (red).

Effect of Bullet Material and Velocity

In order to ensure the generality of the crack formation, we consider two different bullets—copper and glass. The copper bullet is significantly stiffer and has a fracture energy which is four orders of magnitude higher than that of the glass plate. Thus, upon impact, the copper bullet remains perfectly intact. On the contrary, the glass bullet shares the same material properties as the glass plate. During the impact, the glass bullet shatters along with the glass plate. From Figure 4A, we note that the evolution of the average damage per particle exhibits similar trend in the case of both copper and glass bullets. Overall, we note that, given the geometry and material properties of the plate remain constant, the crack formation behavior in the glass plate is similar irrespective of the bullet material.

FIGURE 4

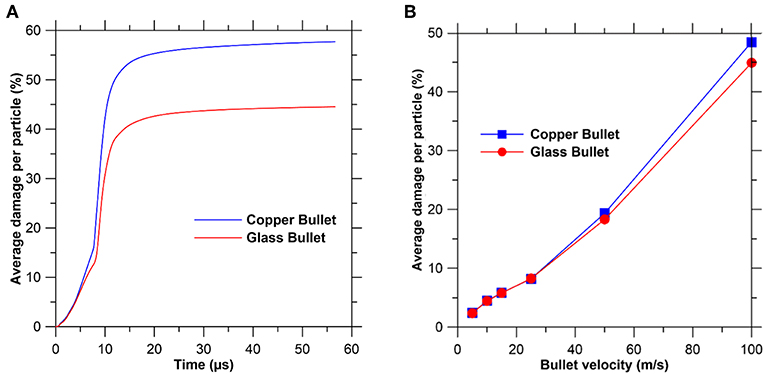
Figure 4. (A) Average damage per particle of the glass plate with respect to time upon impact with copper and glass bullets having a velocity of 100 m/s. (B) Average damage per particle, after saturation, of the glass plate with respect to bullet velocity for copper and glass bullets. Note that the results correspond to that of a glass plate with a radius of 37 mm, thickness of 2.5 mm, elastic modulus of 94.5 GPa, and fracture energy of 4.3 J/m².

Now, we focus on the effect of the bullet velocity on the overall damage on the glass plate. Figure 4B shows the maximum percentage damage of the glass plate when impacted by bullets of different velocities. To this extent, six different bullet velocities are considered, viz., 5, 10, 15, 25, 50, and 100 m/s. Note that the maximum percentage damage in each case corresponds to the saturated value of the damage after impact. We observe that the overall damage increases with the bullet velocity. While the increase is minor for lower velocities (<25 m/s), it is notably higher for higher velocities. Realistically, a velocity of 5 m/s would be similar to that of a stone striking the wind shield, while 100 m/s would be closer to that of a bullet impact. Further, we note that the velocity of 100 m/s creates maximum damage, among the selected velocities, due to high energy during impact. Therefore, we fix the bullet velocity as 100 m/s for the following studies.

Effect of Plate Radius

To investigate the effect of plate geometry, we vary the plate radius. We focus on the effect of plate radius by considering four different radii, viz., 20, 37, 50, and 100 mm. The projectile is modeled using both glass and copper bullets. Figure 5 shows the final cumulative damage (left axis) and average damage per particle (right axis) with respect to the plate radius. The cumulative damage initially increases with increasing plate radius up to 0.05 m, after which it tends to plateau. Note that a slight decrease in the cumulative damage is observed in the case of both glass and copper bullets for a radius of 0.1 m in comparison to 0.05 m. The corresponding average damage per particle is also shown in Figure 5. For a plate radius of 20 mm, ~80% final average damage is observed. Further, the average damage per particle decreases monotonically with increasing plate radius, eventually reaching ~8% for a radius of 0.1 m. The results are comparable in the case of both copper and glass bullets, although copper bullets cause slightly increased damage.

FIGURE 5

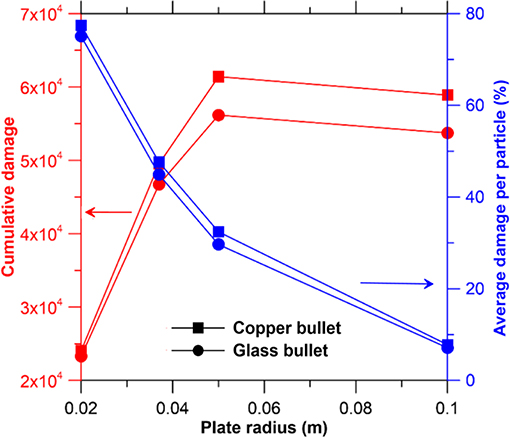
Figure 5. Cumulative damage (left axis) and average damage per particle (right axis) of the glass plate with respect to plate radius for both copper (square symbol) and glass (circle symbol) bullets.

Reconciling the cumulative and percentage damage, we note that for plate with smaller radii, the energy gained during impact is not completely dissipated by crack formation due to its smaller size. With increasing plate radius, the overall size increases, ultimately leading to the formation of more cracks, as suggested by the increasing cumulative damage. The saturated state of cumulative damage corresponds to the state, wherein the maximum area of cracks that can be formed with the impact energy has formed. In the present case, this occurs for a radius of 0.05 m. Further, with increasing plate radius, increasing kinetic energy is absorbed by the plate for dynamic motion leaving lower energies for crack formation. As such, the cumulative damage decreases slightly after the radius of 0.05 m.

Effect of Material Properties

To understand the effect of the material properties, we focus on the elastic modulus and fracture energy of the plate. First, we investigate the effect of elastic modulus by considering eight moduli values spanning over two orders of magnitude, viz., 1, 5, 10, 25, 50, 75, 100, and 150 GPa. Figure 6 shows the average damage per particle in the glass plate, with respect to the elastic modulus when impacted by glass and copper bullets. Note that all other parameters, including the plate geometry, fracture energy, and bullet velocity, are kept constant during the study. We observe that the average damage per particle remains fairly constant over the entire range of elastic moduli in the case of the copper bullet. In the case of the glass bullet, there is a slight increase in damage of the plate with increasing elastic modulus. However, the percentage damage is restricted within a range of 43 to 49% for an increase in the elastic modulus by two orders of magnitude. It should be noted that the elastic modulus is related to the fracture toughness of the material. An increase in elastic modulus would result in an increase in the fracture toughness of the material as well. This suggests that the stress required for the initiation of damage would increase with increasing elastic modulus. However, since the fracture energy of the plate—that is, the energy released upon the formation of cracks—is constant, the overall damage is not significantly affected by the variation in the elastic modulus.

FIGURE 6

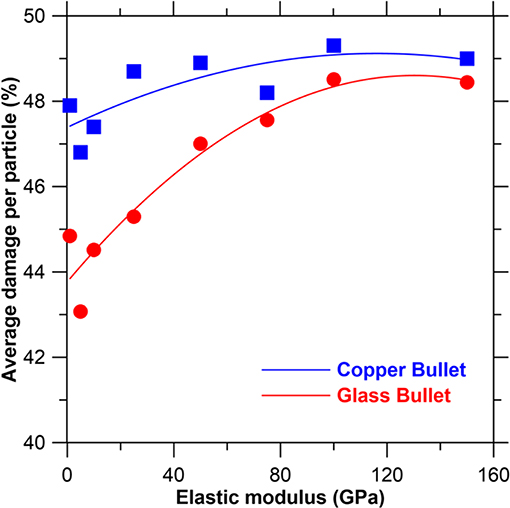
Figure 6. Average damage per particle of the glass plate with respect to the elastic modulus of the plate.

Now, we focus on the effect of the fracture energy of the glass plate. To this end, we consider five different fracture energies spanning over two orders of magnitude, viz., 4.3, 15, 50, 100, and 150 J/m². As in the case of the elastic modulus, other parameters are kept constant during the study. Figure 7 shows the final average damage per particle in the glass plate with respect to the fracture energy. Interestingly, we observe a power-law dependence of the average damage with respect to the fracture energy of the glass plate for both copper and glass bullets. It should be noted that, in peridynamics, the overall damage is proportional to the new surface area created by the cracks (Silling, 2000; Silling and Askari, 2004). Further, in the case of thin plates subjected to impact, the surface area is proportional to the overall length of the cracks, including all the major and minor crack branches. In other words, the overall damage is proportional to the total length of the cracks formed upon impact. This suggests the existence of a power-law relationship between the total crack length and the fracture energy of the material. In other words, the total crack length decreases exponentially with an increase in fracture energy. To establish the power law, we apply a logarithmic fit (see Figure 7), minimizing the least-squared error, of the form,

$\begin{array}{ll}D=a{G_c}^{-k}& (8)\end{array}$

where, D represents the percentage damage (%), a is a pre-factor, G_c is the fracture energy (J/m²), and k is the power-law exponent. The value of the power-law exponent is found to be the same, 0.526 in this case, for both glass and copper bullets. This suggests a universal nature for the relationship between total crack length and fracture energy in plates subjected to impact, which is similar to the self-affine nature of cracks in fracture (Borodich, 1997).

FIGURE 7

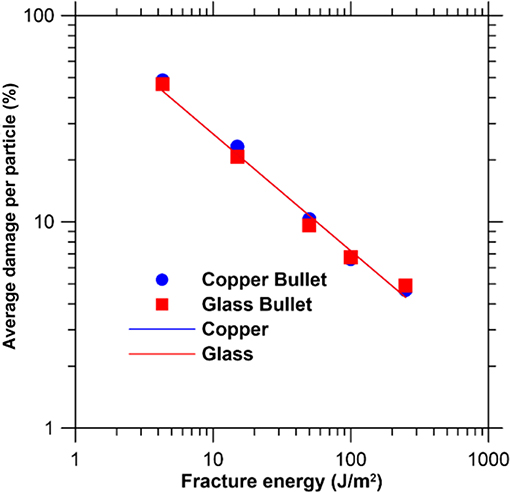
Figure 7. Final average damage per particle in the glass plate with respect to fracture energy for copper and glass bullets. The lines represent a power-law fit in the least-squared sense.

Discussion

We now discuss the power-law relationship observed between the fracture energy and crack length in the glass plate. To this extent, we focus on the radial cracks that grow from the center outwards when the bullet impacts the plate (see Figure 3B). Note that the velocity of a crack depends on the energy flowing to the crack tip and the fracture energy required to create surface. However, the maximum velocity with which the cracks can propagate is limited for any given material, which corresponds to the Rayleigh wave speed V_R of the material (Sharon and Fineberg, 1999). In brittle materials, a crack tip instability has been observed above a critical velocity v_c, that is 0.36V_R, which leads to local crack branching (Sharon et al., 1995). Such branching reduces the velocity of the cracks due to increased energy dissipation. However, as soon as one of these branches terminate, the major radial crack again accelerates leading to further branching. Thus, the crack tip velocity exhibits a cyclic behavior resulting in an increased energy dissipation (Sharon et al., 1995). Here, we suggest that two complementary mechanisms are at the origin of the power-law dependence. On the one hand, for low fracture energies, the radial cracks that propagate outwards undergo crack branching due to increased crack velocities leading to crack tip instability (Fineberg et al., 1991; Sharon et al., 1995; Sharon and Fineberg, 1999). This leads to multiplication of cracks resulting in an exponential growth of the damage with a high growth rate. On the other hand, increased fracture energy decreases the crack velocity. This reduces the crack branching and the growth rate resulting in a decreased cumulative damage.

To establish the hypothesis, we first analyze whether the crack tip velocity exhibits a cyclic behavior representative of the crack tip instability or not. To this extent, we quantify the distribution of cracks throughout the glass plate using a polar plot as shown in Figure 8A. Figure 8B shows the histogram of the angular distribution of cracks in one of the glass plates subjected to impact. The distribution of radial cracks can be obtained from the peaks of the histogram in the angular distribution. We note that the major radial cracks are represented by the taller peaks in the histogram, while the minor radial cracks and branches are represented by smaller peaks. The rest of the histogram with comparable peaks represent the axisymmetric crushing of the plate, along with some tangential cracks. Now, we compute the velocity of the major radial cracks formed during impact (see Methodology for details). Note that the intention here is to observe the relative variation in the crack tip velocity rather than the exact value itself. Therefore, we normalize the velocity values with the maximum value V_max obtained during the simulation. Figure 9A shows the normalized velocity of propagation of one of the major radial cracks in the glass plate with a fracture energy 4.3 J/m². We observe that the velocity of the crack tip exhibits an oscillatory behavior before finally going to zero, thereby confirming the existence of the microbranching instability. Moreover, the minimum value during the oscillation is fairly close to 0.36V_max. This suggests that the crack branching reduces the velocity of the crack up to 0.36V_max, after which it starts accelerating again. Figure 9B shows the maximum velocity attained by a major radial crack during the impact with respect to the fracture energy of the glass plate. We observe that the maximum velocity attained by the major radial crack decreases monotonically, thereby further affirming our hypothesis.

FIGURE 8

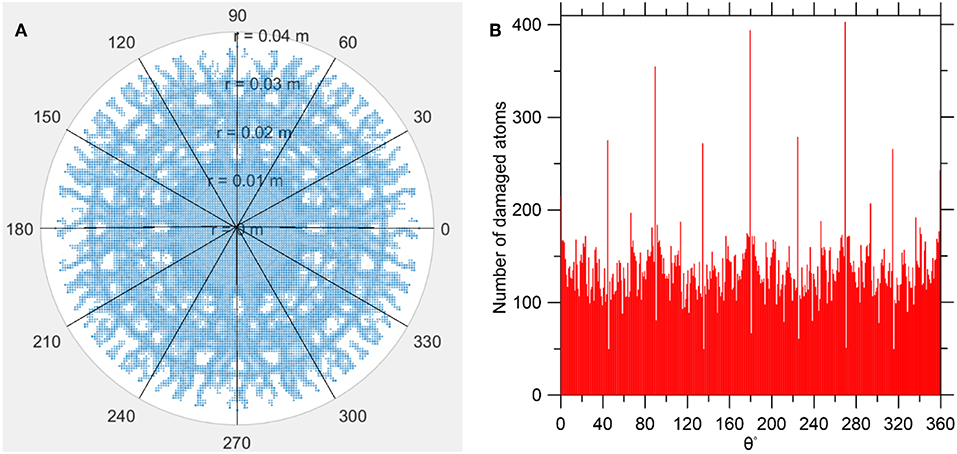
Figure 8. (A) Distribution of cracks in the glass plate in a polar coordinate system, (B) histogram of the distribution of cracks with respect to the angular position θ. Note that the peaks indicate the major radial cracks.

FIGURE 9

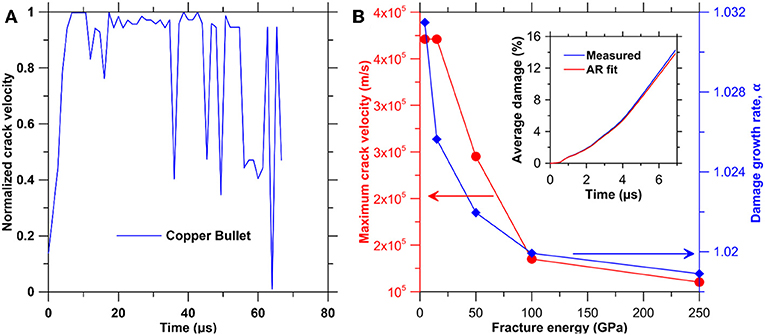
Figure 9. (A) Evolution of normalized crack velocity of a major radial crack in a glass plate with a fracture energy 4.3 J/m² for a copper bullet. Note that the crack velocity is normalized with respect to the maximum crack velocity during the propagation of the crack. (B) Maximum crack velocity (left axis) and damage growth rate (right axis) with respect to the fracture energy of the glass plate. INSET shows the AR fit compared to the measured evolution of damage in peridynamic simulation of impact on a glass plate with fracture energy 4.3 J/m².

Now, we model the damage evolution in a glass plate using an AR-based model (see Methodology). Note that an AR-based model represents a self-affine transformation essentially leading to an exponential growth of the damage. The crack branching behavior is quantified using the damage growth rate α (see Methodology). Figure 9B shows the damage growth rate with respect to the fracture energy of the glass plate. Inset shows the AR fit compared to the measured evolution of damage for a glass plate with a fracture energy of 4.3 J/m². We observe that the AR exhibits an excellent fit for the evolution of the damage confirming the exponential growth. Further, the damage growth rate monotonically decreases with an increase in fracture energy. This is qualitatively in agreement with the trend exhibited by the maximum crack velocity, which decreases monotonically with increasing fracture energy of the material. This suggests that there is a decreased tendency for crack branching with increasing fracture energy, as evident from the growth rate. Finally, Figure 10 shows the saturated damage map in the glass plates, with varying fracture energies, subjected to bullet impact. In agreement with the hypothesis, we observe visually that crack branching is increasingly suppressed with increase in fracture energy. Overall, through independent analysis of crack tip velocity, maximum crack velocity, and the AR growth rate, we corroborate that the crack branching and growth behavior is at the origin of the power-law dependence.

FIGURE 10

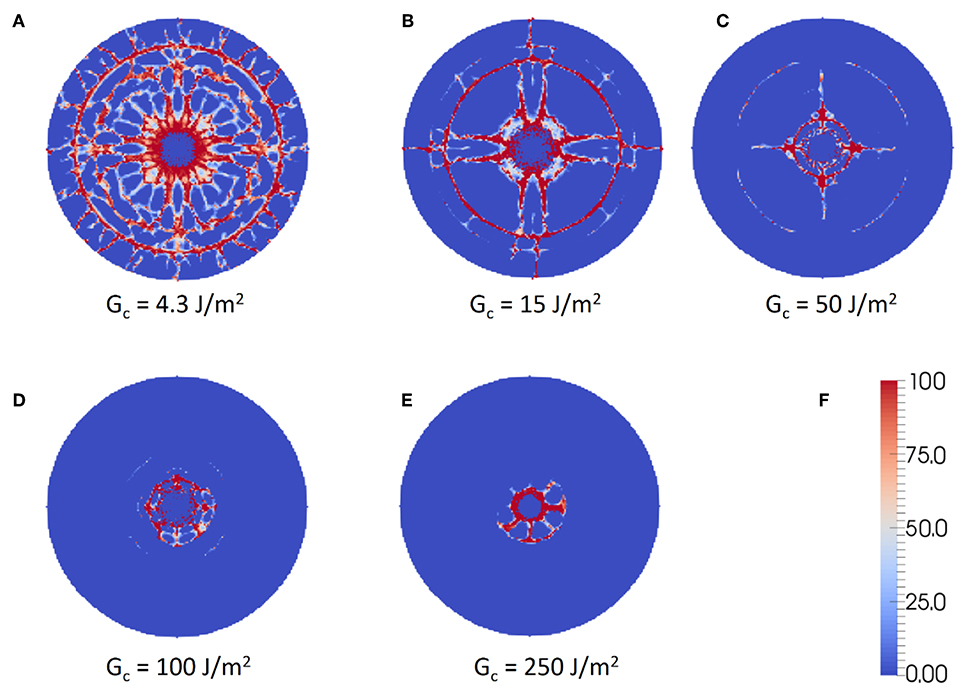
Figure 10. Damage map in the glass plates with different fracture energies, namely, (A) 4.3 J/m², (B) 15 J/m², (C) 50 J/m², (D) 100 J/m², and (E) 250 J/m², subjected to impact. (F) The coloring scheme used to denote the local damage in percent. Note that 100 corresponds to a particle with all the bonds broken, and 0 to a particle with all the bonds intact.

Conclusions

In the present study, based on peridynamic simulations, the roles of geometric and material properties on the impact-induced damage in a glass plate are explored. To this end, approximately one hundred high-throughput peridynamic simulations of bullet impact on a glass plate are performed. This methodology, validated against experimental results earlier (Ha and Bobaru, 2011; Bobaru et al., 2012; Hu et al., 2013), provides a unique way to analyze to the effect of each of the properties individually, which is otherwise impossible using experiments. We observe that the plate geometry does not play a major role in the overall damage, as long as the geometry is large enough to accommodate energy dissipation by the formation of cracks. Similarly, the elastic modulus of the material does not have a significant effect on the overall damage, although the damage tends to increase slightly with increasing values of modulus. On the contrary, the fracture energy of the glass plate directly controls the overall damage through a power-law relationship. Through a detailed analysis on crack evolution using auto-regressive model and crack-propagation velocity, we demonstrate that the power-law originates from a self-affine growth of the major radial cracks resulting from a crack tip instability. Overall, the present study suggests that peridynamics can offer new insights into the fracture behavior of glasses upon ballistic impact, which opens the door toward the development of high-performance bullet-proof glasses for applications in next generation automobile windshields to armors in ballistic applications.

Data Availability Statement

All datasets generated for this study are included in the manuscript/Supplementary Files.

Author Contributions

NK and MB conceived the problem. JR, JB, and RR carried out the simulations. All the authors analyzed the results. JR, NK, MB, and HK wrote the manuscript with the contribution from all the authors.

Funding

The authors acknowledge the financial support for this research provided by the Department of Science and Technology, India under the INSPIRE faculty scheme (DST/INSPIRE/04/2016/002774), DST SERB Early Career Award (ECR/2018/002228) and National Science Foundation under Grant Nos. 1762292 and 1826420.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors thank the UCLA Institute for Digital Research and Education's Research Technology Group and the IIT Delhi HPC facility for providing the computational and storage resources.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2019.00239/full#supplementary-material

References

Agwai, A., Guven, I., and Madenci, E. (2011). Predicting crack propagation with peridynamics: a comparative study. Int. J. Fract. 171, 65–78. doi: 10.1007/s10704-011-9628-4

CrossRef Full Text | Google Scholar

Anders, C., Bringa, E. M., Fioretti, F. D., Ziegenhain, G., and Urbassek, H. M. (2012). Crater formation caused by nanoparticle impact: a molecular dynamics study of crater volume and shape. Phys. Rev. B 85:235440. doi: 10.1103/PhysRevB.85.235440

CrossRef Full Text | Google Scholar

Ball, A., and McKenzie, H. W. (1994). On the low velocity impact behaviour of glass plates. J. Phys. IV 04, C8-783–C8-788. doi: 10.1051/jp4:19948121

CrossRef Full Text | Google Scholar

Barefoot, K. L., Dejneka, M. J., Gomez, S., Gross, T. M., and Shashidhar, N. (2013). Crack and Scratch Resistant Glass and Enclosures Made Therefrom. Available online at: http://www.google.com/patents/US8586492 (accessed September 24, 2019).

Google Scholar

Bauchy, M., Wang, M., Yu, Y., Wang, B., Krishnan, N. M. A., Masoero, E., et al. (2017). Topological control on the structural relaxation of atomic networks under stress. Phys. Rev. Lett. 119:035502. doi: 10.1103/PhysRevLett.119.035502

PubMed Abstract | CrossRef Full Text | Google Scholar

Belytschko, T., Chen, H., Xu, J., and Zi, G. (2003). Dynamic crack propagation based on loss of hyperbolicity and a new discontinuous enrichment. Int. J. Numer. Methods Eng. 58, 1873–1905. doi: 10.1002/nme.941

CrossRef Full Text | Google Scholar

Bless, S., and Chen, T. (2010). Impact damage in layered glass. Int. J. Fract. 162, 151–158. doi: 10.1007/s10704-009-9379-7

CrossRef Full Text | Google Scholar

Bobaru, F., Ha, Y. D., and Hu, W. (2012). Damage progression from impact in layered glass modeled with peridynamics. Cent. Eur. J. Eng. 2, 551–561. doi: 10.2478/s13531-012-0020-6

CrossRef Full Text | Google Scholar

Bobaru, F., and Hu, W. (2012). The meaning, selection, and use of the peridynamic horizon and its relation to crack branching in brittle materials. Int. J. Fract. 176, 215–222. doi: 10.1007/s10704-012-9725-z

CrossRef Full Text | Google Scholar

Borodich, F. M. (1997). Some fractal models of fracture. J. Mech. Phys. Solids 45, 239–259. doi: 10.1016/S0022-5096(96)00080-4

CrossRef Full Text | Google Scholar

Bourne, N. K., Rosenberg, Z., and Field, J. E. (1995). High-speed photography of compressive failure waves in glasses. J. Appl. Phys. 78, 3736–3739. doi: 10.1063/1.360709

CrossRef Full Text | Google Scholar

Buehler, M. J., Abraham, F. F., and Gao, H. (2003). Hyperelasticity governs dynamic fracture at a critical length scale. Nature 426, 141–146. doi: 10.1038/nature02096

PubMed Abstract | CrossRef Full Text | Google Scholar

Chaudhri, M. M., and Walley, S. M. (1978). Damage to glass surfaces by the impact of small glass and steel spheres. Philos. Mag. A 37, 153–165. doi: 10.1080/01418617808235430

CrossRef Full Text | Google Scholar

Doner, S., Nayak, S., Senol, K., Shukla, A., Krishnan, N. M. A., Yilmazcoban, I. K., et al. (2019). Dynamic compressive behavior of metallic particulate-reinforced cementitious composites: SHPB experiments and numerical simulations. Constr. Build. Mater. 227:116668. doi: 10.1016/j.conbuildmat.2019.08.049

CrossRef Full Text | Google Scholar

Elices, M., Guinea, G. V., Gómez, J., and Planas, J. (2002). The cohesive zone model: advantages, limitations and challenges. Eng. Fract. Mech. 69, 137–163. doi: 10.1016/S0013-7944(01)00083-2

CrossRef Full Text | Google Scholar

Fan, H., and Li, S. (2017). A Peridynamics-SPH modeling and simulation of blast fragmentation of soil under buried explosive loads. Comput. Methods Appl. Mech. Eng. 318, 349–381. doi: 10.1016/j.cma.2017.01.026

CrossRef Full Text | Google Scholar

Field, J. E. (1988). Investigation of the Impact Performance of Various Glass and Ceramic Systems. Cambridge Univ (United Kingdom) Cavendish Lab, Cambridge Univ (United Kingdom) Cavendish Lab. Available online at: http://www.dtic.mil/docs/citations/ADA202443 (accessed February 4, 2018).

Google Scholar

Field, J. E., Sun, Q., and Townsend, D. (1989). Ballistic Impact of Ceramics. IMECH-IR. Available online at: http://dspace.imech.ac.cn/handle/311007/39554 (accessed February 4, 2018).

Google Scholar

Fineberg, J., Gross, S. P., Marder, M., and Swinney, H. L. (1991). Instability in dynamic fracture. Phys. Rev. Lett. 67, 457–460. doi: 10.1103/PhysRevLett.67.457

PubMed Abstract | CrossRef Full Text | Google Scholar

Foster, J. T. (2009). Dynamic Crack Initiation Toughness: Experiments and Peridynamic Modeling. Available online at: https://search.proquest.com/docview/304990113/abstract/533CA46DCB284962PQ/1 (accessed August 14, 2017).

Google Scholar

Ha, Y. D., and Bobaru, F. (2011). Characteristics of dynamic brittle fracture captured with peridynamics. Eng. Fract. Mech. 78, 1156–1168. doi: 10.1016/j.engfracmech.2010.11.020

CrossRef Full Text | Google Scholar

Holmström, E., Samela, J., and Nordlund, K. (2011). Atomistic simulations of fracture in silica glass through hypervelocity impact. EPL Europhys. Lett. 96:16005. doi: 10.1209/0295-5075/96/16005

CrossRef Full Text | Google Scholar

Hu, W., Wang, Y., Yu, J., Yen, C. F., and Bobaru, F. (2013). Impact damage on a thin glass plate with a thin polycarbonate backing. Int. J. Impact Eng. 62, 152–165. doi: 10.1016/j.ijimpeng.2013.07.001

CrossRef Full Text | Google Scholar

Ismail, J., Zaïri, F., Naït-Abdelaziz, M., and Azari, Z. (2012). How cracks affect the contact characteristics during impact of solid particles on glass surfaces: a computational study using anisotropic continuum damage mechanics. Int. J. Impact Eng. 40–41, 10–15. doi: 10.1016/j.ijimpeng.2011.09.002

CrossRef Full Text | Google Scholar

Knight, C. G., Swain, M. V., and Chaudhri, M. M. (1977). Impact of small steel spheres on glass surfaces. J. Mater. Sci. 12, 1573–1586. doi: 10.1007/BF00542808

CrossRef Full Text | Google Scholar

Krishnan, K., Sockalingam, S., Bansal, S., and Rajan, S. D. (2010). Numerical simulation of ceramic composite armor subjected to ballistic impact. Compos. Part B Eng. 41, 583–593. doi: 10.1016/j.compositesb.2010.10.001

CrossRef Full Text | Google Scholar

Krishnan, N. M., Wang, B., Falzone, G., Le Pape, Y., Neithalath, N., Pilon, L., et al. (2016). Confined water in layered silicates: the origin of anomalous thermal expansion behavior in calcium-silicate-hydrates. ACS Appl. Mater. Interfaces 8, 35621–35627. doi: 10.1021/acsami.6b11587

PubMed Abstract | CrossRef Full Text | Google Scholar

Krishnan, N. M. A., Wang, B., Sant, G., Phillips, J. C., and Bauchy, M. (2017). Revealing the effect of irradiation on cement hydrates: evidence of a topological self-organization. ACS Appl. Mater. Interfaces 9, 32377–32385. doi: 10.1021/acsami.7b09405

PubMed Abstract | CrossRef Full Text | Google Scholar

Lai, X., Liu, L. S., Liu, Q. W., Cao, D. F., Wang, Z., and Zhai, P. C. (2015). Slope stability analysis by peridynamic theory. Appl. Mech. Mater. 744–746, 584–588. doi: 10.4028/www.scientific.net/AMM.744-746.584

CrossRef Full Text | Google Scholar

Le, Q. V., and Bobaru, F. (2017). Objectivity of state-based peridynamic models for elasticity. J. Elast. 131, 1–17. doi: 10.1007/s10659-017-9641-6

CrossRef Full Text | Google Scholar

Li, X., Song, W., Yang, K., Krishnan, N. M. A., Wang, B., Smedskjaer, M. M., et al. (2017). Cooling rate effects in sodium silicate glasses: bridging the gap between molecular dynamics simulations and experiments. J. Chem. Phys. 147:074501. doi: 10.1063/1.4998611

PubMed Abstract | CrossRef Full Text | Google Scholar

Ljung, L. (2001). “System identification,” in Wiley Encyclopedia of Electrical and Electronics Engineering, ed J. G. Webster (John Wiley & Sons, Inc.). doi: 10.1002/047134608X.W1046.pub2

CrossRef Full Text | Google Scholar

Mauro, J. C. (2014). Grand challenges in glass science. Glass Sci. 1:20. doi: 10.3389/fmats.2014.00020

CrossRef Full Text | Google Scholar

Mauro, J. C., Philip, C. S., Vaughn, D. J., and Pambianchi, M. S. (2014). Glass science in the United States: current status and future directions. Int. J. Appl. Glass Sci. 5, 2–15. doi: 10.1111/ijag.12058

CrossRef Full Text | Google Scholar

Mauro, J. C., and Zanotto, E. D. (2014). Two centuries of glass research: historical trends, current status, and grand challenges for the future. Int. J. Appl. Glass Sci. 5, 313–327. doi: 10.1111/ijag.12087

CrossRef Full Text | Google Scholar

Mitchell, J. A. (2011a). A Nonlocal Ordinary State-Based Plasticity Model for Peridynamics. Albuquerque, NM: Sandia National Laboratories (SNL-NM). Available online at: https://www.osti.gov/scitech/servlets/purl/1106734 (accessed August 15, 2017).

Google Scholar

Mitchell, J. A. (2011b). A non-local, ordinary-state-based viscoelasticity model for peridynamics. Sandia Natl. Lab Rep. 8064, 1–28. doi: 10.2172/1029821

CrossRef Full Text | Google Scholar

Nayak, S., Krishnan, N. M. A., and Das, S. (2019). Fracture response of metallic particulate-reinforced cementitious composites: insights from experiments and multiscale numerical simulations. Cem. Concr. Compos. 97, 154–165. doi: 10.1016/j.cemconcomp.2018.12.026

CrossRef Full Text | Google Scholar

Parks, M. L., Lehoucq, R. B., Plimpton, S. J., and Silling, S. A. (2008). Implementing peridynamics within a molecular dynamics code. Comput. Phys. Commun. 179, 777–783. doi: 10.1016/j.cpc.2008.06.011

CrossRef Full Text | Google Scholar

Parks, M. L., Seleson, P., Plimpton, S. J., Silling, S. A., and Lehoucq, R. B. (2011). Peridynamics with LAMMPS: A User Guide, v0. 3 Beta. Sandia Rep. 2011–8253. Available online at: http://prod.sandia.gov/techlib/access-control.cgi/2011/118523.pdf (accessed August 15, 2017).

Google Scholar

Peng, Y., Yang, J., Deck, C., and Willinger, R. (2013). Finite element modeling of crash test behavior for windshield laminated glass. Int. J. Impact Eng. 57, 27–35. doi: 10.1016/j.ijimpeng.2013.01.010

CrossRef Full Text | Google Scholar

Plimpton, S. (1995). Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 117, 1–19. doi: 10.1006/jcph.1995.1039

CrossRef Full Text | Google Scholar

Pyttel, T., Liebertz, H., and Cai, J. (2011). Failure criterion for laminated glass under impact loading and its application in finite element simulation. Int. J. Impact Eng. 38, 252–263. doi: 10.1016/j.ijimpeng.2010.10.035

CrossRef Full Text | Google Scholar

Saiz, F., and Gamero-Castaño, M. (2012). Amorphization of silicon induced by nanodroplet impact: a molecular dynamics study. J. Appl. Phys. 112:054302. doi: 10.1063/1.4748177

CrossRef Full Text | Google Scholar

Samela, J., and Nordlund, K. (2010). Classical molecular dynamics simulations of hypervelocity nanoparticle impacts on amorphous silica. Phys. Rev. B 81:054108. doi: 10.1103/PhysRevB.81.054108

CrossRef Full Text | Google Scholar

Seleson, P., Parks, M., Gunzburger, M., and Lehoucq, R. (2009). Peridynamics as an upscaling of molecular dynamics. Multiscale Model. Simul. 8, 204–227. doi: 10.1137/09074807X

CrossRef Full Text | Google Scholar

Sharon, E., and Fineberg, J. (1999). Confirming the continuum theory of dynamic brittle fracture for fast cracks. Nature 397, 333–335. doi: 10.1038/16891

CrossRef Full Text | Google Scholar

Sharon, E., Gross, S. P., and Fineberg, J. (1995). Local crack branching as a mechanism for instability in dynamic fracture. Phys. Rev. Lett. 74, 5096–5099. doi: 10.1103/PhysRevLett.74.5096

PubMed Abstract | CrossRef Full Text | Google Scholar

Silling, S. A. (2000). Reformulation of elasticity theory for discontinuities and long-range forces. J. Mech. Phys. Solids 48, 175–209. doi: 10.1016/S0022-5096(99)00029-0

CrossRef Full Text | Google Scholar

Silling, S. A., and Askari, E. (2004). Peridynamic modeling of impact damage. PVP 489, 197–205. doi: 10.1115/PVP2004-3049

CrossRef Full Text | Google Scholar

Silling, S. A., Epton, M., Weckner, O., Xu, J., and Askari, E. (2007). Peridynamic states and constitutive modeling. J. Elast. 88, 151–184. doi: 10.1007/s10659-007-9125-1

CrossRef Full Text | Google Scholar

Silling, S. A., and Lehoucq, R. B. (2008). Convergence of peridynamics to classical elasticity theory. J. Elast. 93, 13–37. doi: 10.1007/s10659-008-9163-3

CrossRef Full Text | Google Scholar

Tang, L., Krishnan, N. M. A., Berjikian, J., Rivera, J., Smedskjaer, M. M., Mauro, J. C., et al. (2018). Effect of nanoscale phase separation on the fracture behavior of glasses: toward tough, yet transparent glasses. Phys. Rev. Mater. 2:113602. doi: 10.1103/PhysRevMaterials.2.113602

CrossRef Full Text | Google Scholar

Tang, Z., Abrams, M. B., Mauro, J. C., Zoeller, L. R., Venkataraman, N., and Hu, G. (2014). High-speed camera study of Stage III crack propagation in chemically strengthened glass. Appl. Phys. A 116, 471–477. doi: 10.1007/s00339-014-8370-y

CrossRef Full Text | Google Scholar

Timmel, M., Kolling, S., Osterrieder, P., and Du Bois, P. A. (2007). A finite element model for impact simulation with laminated glass. Int. J. Impact Eng. 34, 1465–1478. doi: 10.1016/j.ijimpeng.2006.07.008

CrossRef Full Text | Google Scholar

Wang, B., Yu, Y., Wang, M., Mauro, J. C., and Bauchy, M. (2016). Nanoductility in silicate glasses is driven by topological heterogeneity. Phys. Rev. B 93:064202. doi: 10.1103/PhysRevB.93.064202

CrossRef Full Text | Google Scholar

Wang, M., Wang, B., Krishnan, N. M. A., Yu, Y., Smedskjaer, M. M., Mauro, J. C., et al. (2017). Ion exchange strengthening and thermal expansion of glasses: common origin and critical role of network connectivity. J. Non-Cryst. Solids 455, 70–74. doi: 10.1016/j.jnoncrysol.2016.10.027

CrossRef Full Text | Google Scholar

Wang, Q., Wang, Y., Zan, Y., Lu, W., Bai, X., and Guo, J. (2017). Peridynamics simulation of the fragmentation of ice cover by blast loads of an underwater explosion. J. Mar. Sci. Technol. 23, 1–15. doi: 10.1007/s00773-017-0454-x

CrossRef Full Text | Google Scholar

Xu, Z., Zhang, G., Chen, Z., and Bobaru, F. (2018). Elastic vortices and thermally-driven cracks in brittle materials with peridynamics. Int. J. Fract. 209, 203–222. doi: 10.1007/s10704-017-0256-5

CrossRef Full Text | Google Scholar

Zi, G., and Belytschko, T. (2003). New crack-tip elements for XFEM and applications to cohesive cracks. Int. J. Numer. Methods Eng. 57, 2221–2240. doi: 10.1002/nme.849

CrossRef Full Text | Google Scholar