On Strength of Brittle Nanomaterials: Confinement Effect on Weibull Distributions

Introduction

Thermodynamic potentials and free energies of elastically-deformed solid bodies explicitly depend on the strains or stresses (Kittel and McEuen, 1996; Gilman, 2003). This fact, in principle, offers a unique opportunity for materials engineers to tune and optimize many physical and chemical properties of functional materials by externally imposing elastic strains (Zhu and Li, 2010; Li et al., 2014). One necessary condition to take the utmost benefit from this strategy is large elastic deformability while suppressing failure by inelastic deformation or fracture so as to maximize the accessible domains in materials' design parameter space. This condition is only marginally fulfilled for conventional hard materials, for their strain values at yield or fracture are typically <1% (Pelleg, 2014; Anderson, 2017). On the other hand, recent studies on nanomechanics revealed that both yield (Jang and Greer, 2010; Wang et al., 2013) and fracture (Suresh and Li, 2008; Jang et al., 2013) strengths of many hard nanomaterials drastically increase, up to a significant fraction of their ideal strengths, and accordingly the elasticity limits increase as well, when the sample sizes decrease down to below a few 100 nanometers. This strengthening effect is the purely size-induced one without involving any microstructural modification and therefore gives us the additional possibility to broadly adopt the method of strain engineering as long as we can manage to keep their dimensions at the nanoscale.

In most practical cases, fabrication of a specimen entirely free from defects and flaws is almost unachievable, and its strength and elastic limit decrease substantially due to those imperfections (Anderson, 2017). In this regard, it is of great importance to properly understand and reliably predict the occurrence of an inelastic failure in the presence of pre-existing flaws in order to fully utilize elastic strain engineering for hard materials. In general, under the scheme of linear elastic fracture mechanics (LEFM), Weibull analysis based on the weakest link theory well-describes the strength and failure of brittle materials (Weibull, 1951; Quinn and Quinn, 2010). In this approach, the fracture strength depends on the sample volume following the inverse power-law relationship whose exponent is usually called Weibull modulus (Quinn and Quinn, 2010). Its linkage to the weakest link theory is easily understandable once we consider the fact that larger specimens likely contain more imperfections than smaller ones and hence have a higher probability of including more fatal flaws, which is the largest according to LEFM (Anderson, 2017). However, without restricting the upper bound for the flaw sizes to be, this theory, in its original form, has some limitations to be directly used for tiny samples in which the method of strain engineering is likely to work most efficiently. Conventional Weibull theory assumes sufficiently small flaws in comparison with the size of specimen to ensure the statistical equivalence of a randomly-chosen sub-sample, i.e., an arbitrarily small volume defined as a part of the entire sample, but this condition becomes intractable for nanomaterials as their external dimensions decrease approaching the typical flaw sizes existing in the material. Alternatively, there have been several attempts to establish theoretical foundations for the statistical determination of fracture strength of nanomaterials. For example, taking the effects from the temperature and strain rate into account, Sun et al. and Taloni et al. modified the conventional Weibull model to incorporate with plasticity in some nanomaterials (Sun et al., 2012; Taloni et al., 2018). Pugno and Ruoff recognized the discreteness of flaw characteristics at the atomic scale and developed a theory explaining the size-independent fracture strength in nearly defect-free nanomaterials containing only a few atomic vacancies (Pugno and Ruoff, 2006). Treating the contributions from the surface (2D) and the interior (3D) of the samples separately, several researchers regarded some nanomaterials as effectively having the non-integer dimensions and proposed the fractal dimensional dependency (Carpinteri and Pugno, 2004, 2005; Pugno and Ruoff, 2006) for the quantized crack propagation (Pugno and Ruoff, 2004) and fractal size effects (Carpinteri, 1994). On the other hand, there are other studies focused on the quasi-brittle nature of nano-sized samples because their comparable fracture process zone size becomes non-negligible even for macroscopically brittle (Pang et al., 2008; Le and BaŽant, 2012). However, none of the aforementioned theories have integrated the variation of the fundamental statistical characteristics affected by the volumetric confinement in the tiny nano-scaled specimens. In this study, we derived an integrated equation describing the influence of size on the fracture strength of brittle nanomaterials, based on conventional Weibull statistics but further considering confinement effects on the flaw size distribution set up by the external dimensions. We confirmed the validity of this approach by comparing our predictions with the experimental data collected from the literature (Hoffmann et al., 2007; Richter et al., 2009; Xu et al., 2010; He and Zhu, 2011). We expect that this theoretical study offers a new guideline to design the enhanced strain engineered system composed of brittle nanomaterials.

Extreme Value Distributions for Flaw Sizes and Fracture Strengths of Brittle Materials

According to LEFM, the fracture strength of brittle materials σ_f, inversely scales with the square root of the existing flaw size a (Anderson, 2017):

$\begin{array}{ll}{\sigma }_f=\frac{K_{IC}}{\sqrt{\pi a}}F(\phi )& (1)\end{array}$

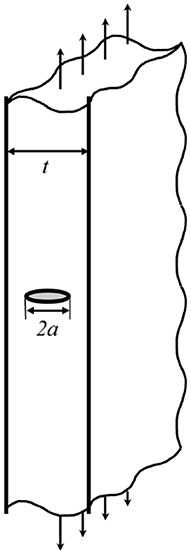
where K_IC is the fracture toughness, and F(ϕ) is a correction factor taking finite sample size effects into account and given as a function of relative flaw size with respect to the sample dimension (ϕ = a/t, see the schematics in Figure 1). This LEFM formalism clearly indicates the explicit dependence of the fracture strength on the flaw size for a given K_IC, following an inverse square-root relationship, i.e., the larger the flaw is, the weaker the material becomes. In reality, a number of flaws with different sizes exist within the material, out of which the largest one determines the actual strength of the sample in a constant stress field because fracture initiates there at the lowest far-field load. In this sense, the strength of a brittle material is not an intrinsic property but rather stochastically determined by the statistical nature of flaw sizes. Because it is the largest flaw that matters for the fracture strength, but the smaller ones are of little interest, a statistical model expressed in terms of extreme values (Coles et al., 2001; Quinn and Quinn, 2010) is required.

FIGURE 1

Figure 1. Schematic illustration of a cracked plate under uniaxial tensile load.

One of such formalism, called Weibull statistics, is well-recognized as an appropriate model for the fracture strength of brittle materials due to its functional simplicity, the physical requirement to be able to predict zero strength, and most importantly excellent agreement with experimental data (Quinn and Quinn, 2010). In his seminal work (Weibull, 1951), Weibull established the extreme value formulation of fracture strength, in which the statistical random variable is parameterized by flaw strength σ_a, the conceptual value associated with individual flaw by Equation (1). Then, considering a brittle solid as being divided into many statistically-equivalent sub-samples of uniform volume V₀ (see Figure 2A), the probability P_V0, for this volume element containing n discrete flaws not to fail under a given far-field stress of σ is (Chawla and Meyers, 1999):

$\begin{array}{l}{P}_{V0}\left(\sigma ;{\sigma }_0,m\right)=\text{Pr }\left\{{\sigma }_{\min }>\sigma \right\}=1-\text{Pr }\left\{{\sigma }_{\min }\le \sigma \right\}\\ =\text{exp}\left[-{\left(\frac{\sigma }{{\sigma }_0}\right)}^m\right]& (2)\end{array}$

where Pr stands for the probability for the condition in the curly bracket to be true, σ_min is the minimum value out of all n flaw strengths σ_a, each of which is affiliated with the individual flaw present in the sub-sample of V₀, m is a positive-valued parameter called shape parameter or Weibull modulus and σ₀ is a constant called scale parameter. Due to the one-to-one correspondence between the strength and flaw size given in Equation (1), the cumulative distribution function (CDF) in Equation (2) can now be reformulated into a form having the maximum flaw size a_max as the independent variable:

$\begin{array}{ll}{F}_{V0}(a;a_0,m)=Pr\left\{a_{max}\le a\right\}=exp\left[-{\left(\frac{a}{a_0}\right)}^{-\frac{m}{2}}\right]& (3)\end{array}$

where a₀ is the scale parameter for the flaw size distribution. Equation (3) gives the probability of the largest flaw in V₋₀ to be smaller than a certain value a. As illustrated in Figure 2A, the entire specimen with the finite volume V can now be thought of as the juxtaposition of N (=V/V₀) such sub-samples, all statistically equivalent, and its statistical characteristics can easily be built from that of the sub-sample using the max-stable nature of the extreme value distribution (Coles et al., 2001). Namely, in order for the whole specimen to survive under a given far-field stress, all of the sub-samples should remain intact simultaneously, and therefore the probability for it to occur becomes (Chawla and Meyers, 1999):

$\begin{array}{l}{P}_V\left(\sigma ;{\sigma }_0,m\right)=P_{V0}{\left(\sigma ;{\sigma }_0,m\right)}^N={\left\{\text{exp}\left[-{\left(\frac{\sigma }{{\sigma }_0}\right)}^m\right]\right\}}^{\frac{V}{V_0}}\\ =\text{exp}\left[-\frac{V}{V_0}{\left(\frac{\sigma }{{\sigma }_0}\right)}^m\right]& (4)\end{array}$

FIGURE 2

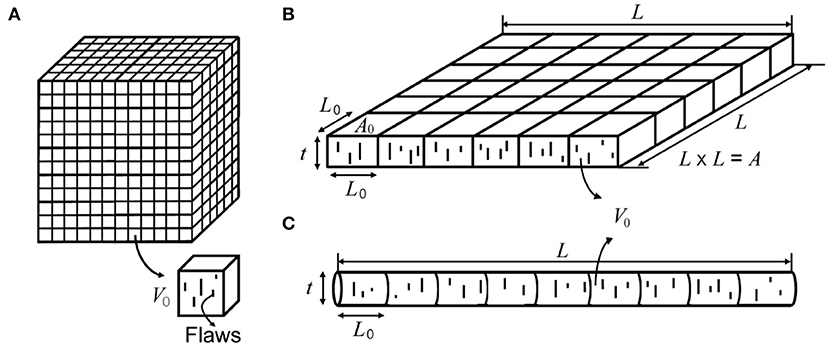
Figure 2. Schematic illustration for sub-sample division of (A) conventional bulk sample, (B) nano-plate, and (C) nano-wire into V₀.

The condition for two different specimens to have the same survival probability leads to the well-known Weibull scaling law:

$\begin{array}{ll}\frac{{\sigma }_1}{{\sigma }_2}={\left(\frac{V_2}{V_1}\right)}^{\frac{1}{m}}& (5)\end{array}$

where σ₁ and σ₂ are the strengths of each sample with volumes V₁ and V₂, respectively.

Confinement Effects on Extreme Value Distributions in Brittle Nano-samples

From the perspective of weakest link theory, the conventional Weibull scaling law given in Equation (5) emerges as a consequence of the fact that a larger specimen contains more flaws than a smaller one and therefore has a higher probability for its weakest flaw, i.e., the largest due to LEFM, to be weaker than the one in the smaller. Here, one important condition to obtain such scaling relationship is the existence of the common reference sub-sample of V₀ ensuring the statistical equivalence across different specimens in a variety of external dimensions, because Weibull equation is built upon the statistical distribution formulated as the N-power of the CDF of a single sub-sample as in Equation (4). Some requirements to keep such condition satisfactory may include (i) materials synthesis in a mutually comparable way between the different specimens so as for the fabrication processes not to affect the fundamental statistics and (ii) more importantly, sufficiently small flaws compared with the whole specimen sizes so as to warrant the presence of the statistically-uniform sub-samples not influenced by the external dimensions of materials. However, the latter condition gets gradually intractable if the size of a specimen decreases close to typical flaw sizes, as is the case for nanomaterials. In that case, the universal reference sub-sample applicable to all specimens regardless of their external dimensions becomes hard to define. Instead, the coupling of fundamental statistics and the characteristic length, e.g., the thickness of nano-plates or diameter of nano-wires as in Figures 2B,C, needs to be taken into account, further requiring the modification of parameters for flaw size distributions, such as the one presented in Equation (3).

The correlation between the flaw size distribution and characteristic length could be inferred by looking into two different statistical representations formulated with different random variables, i.e., one with the actual and the other with maximum flaw size in a sample. When sufficiently many flaws exist in a material, the probability for a flaw in a sub-sample of V₀ to have a certain size is usually given by a continuous probability density function (PDF), e.g., the Gaussian distribution. On the other hand, when expressed in terms of the size of the largest flaw determined in the sub-sample of V₀ i.e., by the extreme value formulation, the statistical distribution follows the large-end tail of the parent distribution as shown in Figure 3A (Kotz and Nadarajah, 2000). As long as the specimen is much larger than the width of the parent distribution, the statistical nature of the flaw size remains independent of the external dimensions of the material and the conventional Weibull scaling law still works satisfactorily. However, provided that any flaw can never be larger than the whole body itself, the characteristic length of the sample must bound the width of the parent distribution as it becomes comparable to the flaw sizes (Figure 3B), resulting in a mutual correlation of the former with the latter. Consequently, the extreme value distribution for the maximum flaw sizes should also be coupled with the characteristic length of the specimen, as schematically illustrated in Figure 3B. In this study, in order to incorporate this coupling effect into a statistical formulation, we assume that the scale factor a₀ in Equation (3) is linearly proportional to the characteristic length t, i.e., a₀ = αt, where α is the proportionality constant. Replacing the scale parameter a₀ by the length-dependent term αt in Equation (3) and taking the derivative, the probability density function prescribing the largest flaw in the whole sample f _v(a, t; m) becomes:

$\begin{array}{l}{f}_V\left(a,t;m\right)=\frac{d}{da}\left\{\text{exp}\left[-\frac{V}{V_0}{\left(\frac{a}{\alpha t}\right)}^{-\frac{m}{2}}\right]\right\}\\ =\frac{m}{2\alpha t}\left(\frac{V}{V_0}\right){\left(\frac{a}{\alpha t}\right)}^{-\left(\frac{m}{2}+1\right)}\exp \left[-\frac{V}{V_0}{\left(\frac{a}{\alpha t}\right)}^{-\frac{m}{2}}\right]& (6)\end{array}$

FIGURE 3

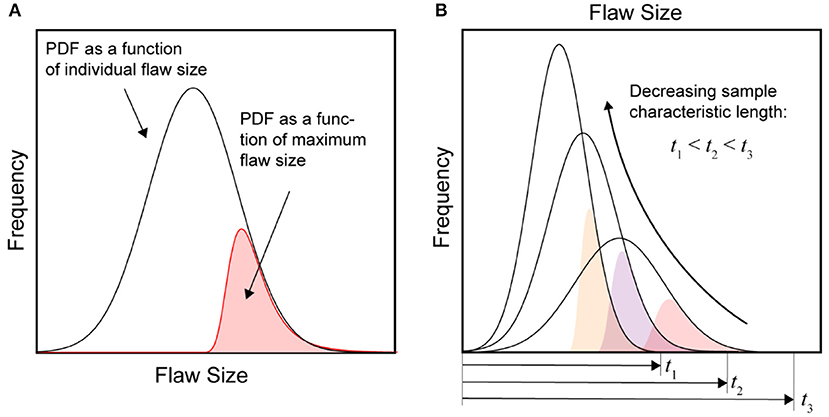
Figure 3. (A) Probability density distribution as a function of the maximum flaw size and its association with that of individual flaw size. (B) Schematic illustration showing the sample size confinement effects on the parent and maximum flaw size distributions.

The expectation value for the largest flaw size in V, $\overline{a}$, can be derived as follows:

$\begin{array}{ll}\overline{a}={\displaystyle {\int }_0^{\infty }a{f}_V(a,t;m)da}=\alpha t{\left(\frac{V}{V_0}\right)}^{\frac{2}{m}}\Gamma \left(1-\frac{2}{m}\right)& (7)\end{array}$

where Γ is the gamma function. Furthermore, plugging the maximum flaw size obtained in Equation (7) into the LEFM strength equation given in Equation (1), the expected value for the strength $\overline{\sigma }$ of a brittle nanomaterial with volume V is:

$\begin{array}{ll}\overline{\sigma }=\frac{K_{IC}}{\sqrt{\pi \overline{a}}}F(\overline{\phi })=\frac{G(\beta ,v)F(\overline{\phi })}{\sqrt{\alpha \Gamma (1-\frac{2}{m})}}{\frac{K_{IC}}{\sqrt{\pi t}}\left(\frac{V_0}{V}\right)}^{\frac{1}{m}}& (8)\end{array}$

where $\overline{\phi }=\frac{\overline{a}}{t}=\alpha {(V/V_0)}^{\frac{2}{m}}\Gamma (1-2/m)$, and G(β,ν) is the geometric factor expressed as a function of the Poisson's ratio ν, and the inclination angle of the flaw with respect to the loading axis β which varies between 0 and π/2. When an isotropically-distributed flaw orientation is assumed, G(β,ν) becomes 2/π with ν ~ 0.25 (Jayatilaka and Trustrum, 1977; Trustrum and Jayatilaka, 1983). Here, it is noteworthy that the inverse-square-root dependence of the fracture strength on the characteristic length of the specimen, t, newly appears as the result of confinement effect on the flaw size distribution in addition to the conventional Weibull scaling term (V₀/V)^1/m. The approach presented in this study is applicable to any homogeneous brittle nanomaterial whose failure is governed by the LEFM-based Griffith fracture criterion (Griffith, 1921). The exact length scale below which the confinement effect on the Weibull distribution becomes non-negligible will vary, depending on the type of material and quality of the synthesis process. In the following section, we will confirm the good agreement of our model with experimental data collected from samples under a few 100 nanometers (Hoffmann et al., 2007; Richter et al., 2009; Xu et al., 2010; He and Zhu, 2011).

Case of 1D and 2D Nanomaterials

The equation for the fracture strength shown in Equation (8) can be further developed for the 1D and 2D nanomaterials having simple geometry, such as nano-wires or nano-plates. With the help of illustrations given in Figures 2B,C the V₀/V term that appears in Equation (8) can be simplified into L₀/L and A₀/A for nano-wires and nano-plates, respectively, where L and L₀ are the lengths of the whole and a sub-sample of the nano-wires, A and A₀ are the areas of the whole and a sub-sample of the nano-plates, respectively. Then, according to Equation (8) the mean strengths for each type of material under uniaxial tensile loading becomes:

$\begin{array}{ll}\{\begin{array}{l}{\overline{\sigma }}_{1D}\left(t,L;m\right)=\frac{G\left(\beta ,\nu \right)F(\overline{\phi }(L;m))}{\sqrt{\alpha \Gamma \left(1-\frac{2}{m}\right)}}\frac{K_{IC}}{\sqrt{\text{π}t}}{\left(\frac{L_0}{L}\right)}^{\frac{1}{m}},\\ {\overline{\sigma }}_{2D}\left(t,A;m\right)=\frac{G\left(\beta ,\nu \right)F(\overline{\phi }(A;m))}{\sqrt{\alpha \Gamma \left(1-\frac{2}{m}\right)}}\frac{K_{IC}}{\sqrt{\text{π}t}}{\left(\frac{A_0}{A}\right)}^{\frac{1}{m}}.\end{array}& (9)\end{array}$

Furthermore, if we restrict our interest to the set of samples whose axial lengths (L for nano-wires) or areas (A for nano-plates) remain constant, but only the characteristic lengths (t), i.e., the diameter (nano-wires) or the thickness (nano-plates), vary, the mean strength depends on t, following the reciprocal square-root relation, i.e., σ ∞ t^−1/2. This result is, in principle, equivalent with the scaling law offered by Gao et al. for brittle nano-plates (Gao et al., 2003). The equations derived in this work are applicable only to the nanomaterials satisfying the following conditions: (i) failure of materials in different sizes should predominantly be governed by the same type of flaw. This condition may require the specimens to be prepared by the same fabrication procedure. (ii) The volume of the specimens should be large enough to include sufficiently many sub-samples to ensure the statistical consistency. Simultaneously, the critical dimension of the sample should be small enough, approximately a few tens to a few 100 nanometers, so as for the volumetric confinement effect to emerge. The uniaxial fracture strengths from a set of brittle nanowires or nanoplates differing in their sizes but with identical microstructural features would be an ideal example with which to verify the model presented in this work. To the best of our knowledge, there exist only a limited number of experimental data available until now. Nonetheless, in Figure 4, we present some examples of actual experimental data collected from the literature that reports the uniaxial tensile strengths of brittle nano-whiskers made of ZnO (Hoffmann et al., 2007; Xu et al., 2010; He and Zhu, 2011) and single crystalline Cu (Richter et al., 2009). Two important features are noteworthy here: (i) clear demonstration of the reciprocal square-root relation between the diameter t and fracture strength and (ii) large scatter in the data. The former serves as the strong evidence for our work, and the latter indicates that the statistical fluctuation originated from the large Weibull modulus is still dominant in this regime.

FIGURE 4

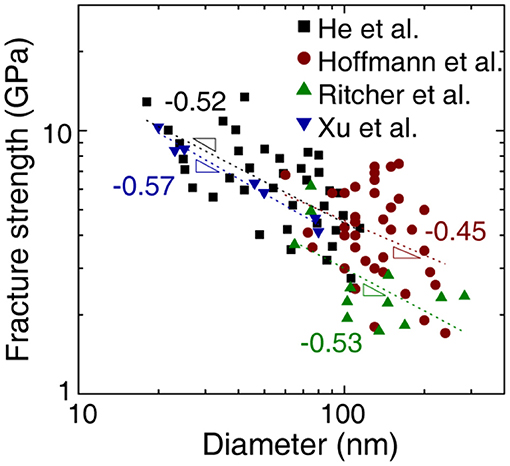
Figure 4. Fracture strength vs. diameter plots from tensile experiments on the brittle ZnO (Hoffmann et al., 2007; Xu et al., 2010; He and Zhu, 2011) and Cu (Richter et al., 2009) nanowires.

Conclusions

In conclusion, we suggest a new theoretical framework for fracture strength of brittle nanomaterials combining the confinement effect on maximum flaw size distribution into the conventional Weibull statistics. By modifying the scale factor of the maximum crack size distribution function to be proportional to the characteristic length of the specimen, we successfully derive the integrated formula of fracture strength for nanomaterials which contains both the conventional Weibull and newly-added confinement terms in its scaling relationship. We further verified the validity of our equation in the range where the characteristic length is smaller than 300 nm by fitting it to actual experimental data collected for brittle nano-whiskers. This theoretical approach offers a foundation for the design of strain engineering and enables brittle nanomaterials to be more reliable and stable for their practical applications.

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here: doi: 10.1007/s12274-010-1030-4, doi: 10.1103/PhysRevB.83.161302, doi: 10.1021/nl9015107, doi: 10.1088/0957-4484/18/20/205503.

Author Contributions

All authors conceived the research, formulated the theory, discussed the results, and wrote the manuscript.

Funding

The authors acknowledge financial support from National Research Foundation of Korea (NRF-2019M2D2A1A02038972).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Anderson, T. L. (2017). Fracture Mechanics: Fundamentals and Applications. New York, NY: CRC Press.

Google Scholar

Carpinteri, A. (1994). Scaling laws and renormalization groups for strength and toughness of disordered materials. Int. J. Solids Struct. 31, 291–302. doi: 10.1016/0020-7683(94)90107-4

CrossRef Full Text | Google Scholar

Carpinteri, A., and Pugno, N. M. (2004). Scale-effects on mean and standard deviation of the mechanical properties of condensed matter: an energy-based unified approach. Int. J. Fract. 128, 253–261. doi: 10.1023/B:FRAC.0000040988.61253.05

CrossRef Full Text | Google Scholar

Carpinteri, A., and Pugno, N. M. (2005). Are scaling laws on strength of solids related to mechanics or to geometry. Nat. Mater. 4, 421–423. doi: 10.1038/nmat1408

CrossRef Full Text | Google Scholar

Chawla, K. K., and Meyers, M. (1999). Mechanical Behavior of Materials. New York, NY: Prentice Hall Upper Saddle River.

Google Scholar

Coles, S., Bawa, J., Trenner, L., and Dorazio, P. (2001). An Introduction to Statistical Modeling of Extreme Values, Vol. 208. London: Springer.

Google Scholar

Gao, H., Ji, B., Jäger, I. L., Arzt, E., and Fratzl, P. (2003). Materials become insensitive to flaws at nanoscale: lessons from nature. Proc. Natl. Acad. Sci. U.S.A. 100, 5597–5600. doi: 10.1073/pnas.0631609100

PubMed Abstract | CrossRef Full Text | Google Scholar

Gilman, J. J. (2003). Electronic Basis of the Strength of Materials. New York, NY: Cambridge University Press.

Google Scholar

Griffith, A. A. (1921). The phenomena of rupture and flow in solids. Phil. Trans. R. Soc. Lond. A 221, 163–198. doi: 10.1098/rsta.1921.0006

CrossRef Full Text | Google Scholar

He, M.-R., and Zhu, J. (2011). Defect-dominated diameter dependence of fracture strength in single-crystalline ZnO nanowires: in situ experiments. Phy. Rev. B. 83:161302. doi: 10.1103/PhysRevB.83.161302

CrossRef Full Text | Google Scholar

Hoffmann, S., Östlund, F., Michler, J., Fan, H. J., Zacharias, M., Christiansen, S. H., and Ballif, C. (2007). Fracture strength and Young's modulus of ZnO nanowires. Nanotechnology. 18, 1–6. doi: 10.1088/0957-4484/18/20/205503

CrossRef Full Text | Google Scholar

Jang, D., and Greer, J. R. (2010). Transition from a strong-yet-brittle to a stronger-and-ductile state by size reduction of metallic glasses. Nat. Mater. 9, 215–219. doi: 10.1038/nmat2622

PubMed Abstract | CrossRef Full Text | Google Scholar

Jang, D., Meza, L. R., Greer, F., and Greer, J. R. (2013). Fabrication and deformation of three-dimensional hollow ceramic nanostructures. Nat. Mater. 12, 893–898. doi: 10.1038/nmat3738

PubMed Abstract | CrossRef Full Text | Google Scholar

Jayatilaka, A. D. S., and Trustrum, K. (1977). Statistical approach to brittle fracture. J. Mater. Sci. 12, 1426–1430. doi: 10.1007/BF00540858

CrossRef Full Text | Google Scholar

Kittel, C., and McEuen, P. (1996). Introduction to Solid State Physics, Vol. 8. New York, NY: Wiley.

Google Scholar

Kotz, S., and Nadarajah, S. (2000). Extreme Value Distributions: Theory and Applications. London: World Scientific.

Google Scholar

Le, J. L., and BaŽant, Z. P. (2012). Scaling of static fracture of quasi-brittle structures: strength, lifetime, and fracture kinetics. J. Appl. Mech. 79:031006. doi: 10.1115/1.4005881

CrossRef Full Text | Google Scholar

Li, J., Shan, Z., and Ma, E. (2014). Elastic strain engineering for unprecedented materials properties. MRS Bull. 39, 108–114. doi: 10.1557/mrs.2014.3

CrossRef Full Text | Google Scholar

Pang, S. D., BaŽant, Z. P., and Le, J. L. (2008). Statistics of strength of ceramics: finite weakest-link model and necessity of zero threshold. Int. J. Fract. 154, 131–145. doi: 10.1007/s10704-009-9317-8

CrossRef Full Text | Google Scholar

Pelleg, J. (2014). Mechanical Properties of Ceramics, Vol. 213. Cham: Springer Science & Business.

Google Scholar

Pugno, N. M., and Ruoff, R. S. (2004). Quantized fracture mechanics. Philosoph. Mag. 84, 2829–2845. doi: 10.1080/14786430412331280382

CrossRef Full Text | Google Scholar

Pugno, N. M., and Ruoff, R. S. (2006). Nanoscale Weibull statistics. J. Appl. Phys. 99:024301. doi: 10.1063/1.2158491

CrossRef Full Text | Google Scholar

Quinn, J. B., and Quinn, G. D. (2010). A practical and systematic review of Weibull statistics for reporting strengths of dental materials. Dent. Mater. 26, 135–147. doi: 10.1016/j.dental.2009.09.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Richter, G., Hillerich, K., Gianola, D. S., Monig, R., Kraft, O., and Volkert, C. A. (2009). Ultrahigh strength single crystalline nanowhiskers grown by physical vapor deposition. Nano Lett. 9, 3048–3052. doi: 10.1021/nl9015107

PubMed Abstract | CrossRef Full Text | Google Scholar

Sun, G., Pang, J. H. L, Zhou, J., Zhang, Y., Zhan, Z., and Zheng, L. (2012). A modified Weibull model for tensile strength distribution of carbon nanotube fibers with strain rate and size effects. Appl. Phys. Lett. 101:131905. doi: 10.1063/1.4754709

CrossRef Full Text | Google Scholar

Suresh, S., and Li, J. (2008). Materials science: deformation of the ultra-strong, Nature 456, 716–717. doi: 10.1038/456716a

PubMed Abstract | CrossRef Full Text | Google Scholar

Taloni, A., Vodret, M., Costantini, G., and Zapperi, S. (2018). Size effects on the fracture of microscale and nanoscale materials. Nat. Rev. Mater. 3, 211–224. doi: 10.1038/s41578-018-0029-4

CrossRef Full Text | Google Scholar

Trustrum, K., and Jayatilaka, A. D. S. (1983). Applicability of Weibull analysis for brittle materials. J. Mater. Sci. 18, 2765–2770. doi: 10.1007/BF00547593

CrossRef Full Text | Google Scholar

Wang, J., Sansoz, F., Huang, J., Liu, Y., Sun, S., Zhang, Z., et al. (2013). Near-ideal theoretical strength in gold nanowires containing angstrom scale twins. Nat. Commun. 4:1742. doi: 10.1038/ncomms2768

PubMed Abstract | CrossRef Full Text | Google Scholar

Weibull, W. (1951). A statistical distribution function of wide applicability. J. Appl. Mech. 103, 293–297.

Google Scholar

Xu, F., Qin, Q., Mishra, A., Gu, Y., and Zhu, Y. (2010). Mechanical properties of ZnO nanowires under different loading modes. Nano Res. 3, 271–280. doi: 10.1007/s12274-010-1030-4

CrossRef Full Text | Google Scholar

Zhu, T., and Li, J. (2010). Ultra-strength materials. Prog. Mater. Sci. 55, 710–757. doi: 10.1016/j.pmatsci.2010.04.001

CrossRef Full Text | Google Scholar