Field Strength of Network-Modifying Cation Dictates the Structure of (Na-Mg) Aluminosilicate Glasses

GRAPHICAL ABSTRACT

Graphical Abstract | Field strength of network-modifying cation dictates the structure of (Na-Mg) aluminosilicate glasses.

Introduction

Aluminosilicate glasses are important materials with a wide range of technological applications, and the study of their structure holds significant scientific interest. Due to their desirable refractory, mechanical, dielectric, chemical, and optical properties, they are commercially used as refractory glass-ceramics (Baker et al., 2006; Beall, 2009; Wu et al., 2018), bioactive glass-ceramics (Verné et al., 2000; Duminis et al., 2017; Nakane and Kawamoto, 2017), container glasses (Mallick and Holland, 2005), liquid crystal display (LCD) substrates (Lamberson, 2016), optical and laser materials (Gorni et al., 2017; Peng et al., 2019), and as host matrices for nuclear wastes (Frankel et al., 2018; Piovesan et al., 2018). In the field of geo-chemistry, they can be considered as frozen model systems for mantle melts and thus, their study can provide significant insights into magmatic processes and the thermal evolution of the earth’s mantle (Lee et al., 2016; Genova et al., 2017; Losq et al., 2017; Nakane and Kawamoto, 2017). Recently, there has been a growing interest in the use of aluminosilicate glass materials as supplementary cementitious materials with the advantage that they result in lower CO₂ emissions when compared to the use of ordinary Portland cement (OPC) (Moesgaard et al., 2012; Tashima et al., 2016; Newlands and Macphee, 2017; Kinnunen et al., 2019). However, to ensure enough level of strength development of these blended cements to achieve performance characteristics comparable with OPC, there is a need to focus on the assessment and enhancement of reactivity (particularly the tendency toward aqueous dissolution) of aluminosilicate glasses. One of the important parameters affecting the dissolution of aluminosilicate glasses is the type of network-modifying cations present in the glass (Snellings, 2013; Newlands and Macphee, 2017; Schöler et al., 2017; Kucharczyk et al., 2018).

In most practical cases, aluminosilicate glasses contain more than one type of network-modifying cation. In those glasses, the cation field of the network-modifying cation can dictate the structure of the glass (cation field strength = Z/r², where Z = cation charge, r = cation radius in Å). Hence, there is a need to understand how the cation field strength of network-modifying cations influence the structure of aluminosilicate glasses. Quaternary aluminosilicate glasses (such as Mg-Na aluminosilicate glass with two types of network-modifying cations) form a useful starting point for this kind of studies.

The structure of a quaternary aluminosilicate glass, for the sake of simplicity, may be visualized to have evolved from that of an amorphous silica melt in a progressive manner, as shown in Figure 1. An amorphous silica melt has a three-dimensional network structure consisting of fully polymerized silicate (SiO₄) tetrahedral units with all oxygen atoms performing the bridging role. Here, all the silicon species are depicted in Q⁴ form; in Qⁿ notation, n (0 ≤ n ≤ 4) represents the number of bridging oxygen atoms around the silicon atom as the nearest neighbor. With the addition of a network modifying cation such as sodium, the bond between silicon and bridging oxygen (BO) is broken with the creation of non-bridging oxygen (NBO) sites, thereby causing network depolymerization that leads to the creation of depolymerized silicon species Q³, Q², Q¹, and Q⁰. When the amount of modifier added is high, a portion of the cation can exist as a free oxide (Mysen et al., 1982).

FIGURE 1

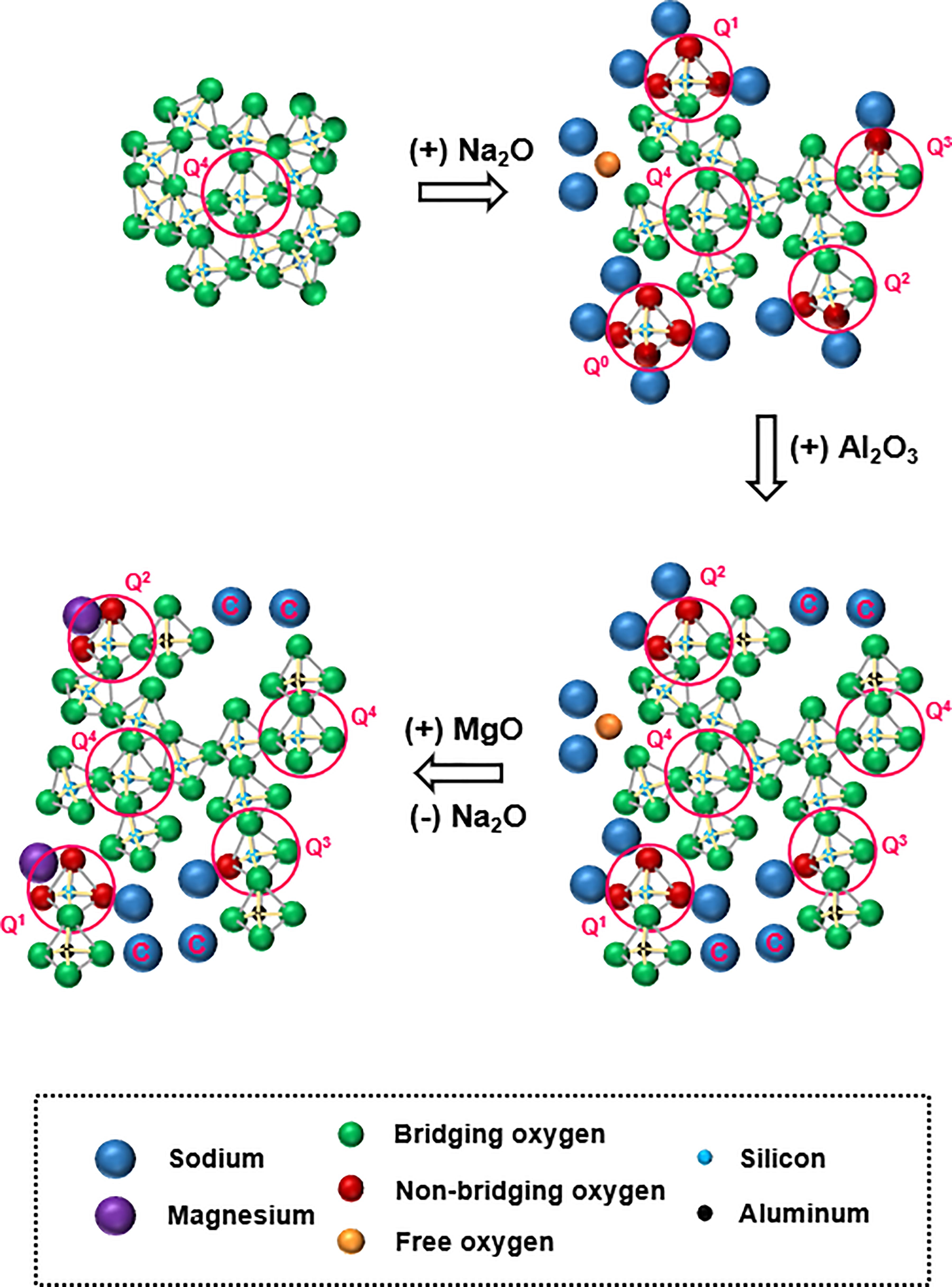
Figure 1. Simplified schematic representation of evolution of a quaternary aluminosilicate glass from silica melt. Roles of network-modifying cations (sodium and magnesium) are as follows: those acting as charge compensator are labeled “C”; those in the immediate vicinity of non-bridging oxygen atoms act as network modifier; those in the immediate vicinity of free oxygen exist as free oxide.

The addition of aluminum introduces another level of complexity. Aluminum forms tetrahedral aluminate (AlO₄) units with apical oxygen atoms (which are preferentially BO rather than NBO; Thompson and Stebbins, 2012) possessing electrical charge deficit. As a result, a portion of the sodium ions originally present in the system as network modifiers, must now act as charge compensators for the electrical charge deficit. The introduction of tetrahedral aluminate units, along with the depletion of network modifier cations, will promote polymerization of the network. Between the dual roles of sodium, the charge compensation role is always given preference over the network modifying role in the presence of aluminum (Le Losq and Neuville, 2013). The addition of magnesium brings the next level of complexity in structure. Like sodium, magnesium can also perform as either a charge compensator or network modifier. The question now is how the charge compensator and network modifying roles are distributed among co-existing sodium and magnesium cations. This distribution will have a decisive role in the glass structure, and will be dictated by the respective cation field strengths of sodium and magnesium (0.46 Å^–2 for Mg, compared to 0.18 Å^–2 for Na; Quintas et al., 2009).

In this work, the structure of a series of quaternary aluminosilicate glasses [(Na₂O)_1–x(MgO)_x (Al₂O₃)₀.₅(SiO₂)₁.₂₅; 1 ≥ x ≥ 0] are studied. The objective is to understand how the structure of aluminosilicate glass is influenced by the cation field strength of the network-modifying cation. The characterization techniques used for studying the glasses include X-ray diffraction (XRD), X-ray Photoelectron Spectroscopy (XPS), ²⁹Si Magic Angle Spinning Nuclear Magnetic Resonance spectroscopy (²⁹Si MAS NMR) and scanning electron microscopy (SEM).

Materials and Methods

Materials

Precursors used for the synthesis of glasses (original glasses and reference glasses) included silicon oxide (Alfa Aesar; purity 99.5%), aluminum oxide (Sigma-Aldrich; purity 99.5%), sodium carbonate (Sigma-Aldrich; purity 99.0%), and magnesium oxide (Sigma-Aldrich: purity 99.0%). Reference compounds for XPS analysis included magnesium carbonate (Sigma-Aldrich; 40.0–43.5% as MgO), magnesium hydroxide (Sigma-Aldrich: purity 99.0%), sodium carbonate (Sigma-Aldrich; purity 99.0%), and magnesium oxide (Sigma-Aldrich: purity 99.0%).

Glass Preparation

A series of 10 aluminosilicate glasses with fixed compositions [(Na₂O)_1–x(MgO)_x(Al₂O₃)₀.₂₅ (SiO₂)₁.₂₅; 1 ≥ x ≥ 0] were prepared. The nominal compositions and NBO/Si values of the glasses are shown in Table 1. For the sake of simplicity, glasses are represented as Gx. The precursors were mixed in the required proportions and milled in a vibratory disc mill (Retsch RS 200) at 1500 rpm for 3 min. The mixture (50 g batch size) was transferred to a platinum crucible which was subsequently placed in a Nabertherm high temperature furnace (HT 08/18). The mixture was heated at 20°C/min to 1600°C, then held for 90 min. The melt was rapidly quenched by pouring it into water at room temperature. The glass pieces were collected and dried at 60°C for 2 days. The dried glass pieces were subjected to a second melting process to ensure homogeneity. The dried glass pieces were milled in a vibratory disc mill (1–5 min, 1000 rpm) to obtain an average particle size between 1 and 10 μm before further characterization.

TABLE 1

Table 1. Nominal compositions and NBO/Si values of synthetic glasses.

Reference glasses for XPS and NMR analysis were also prepared in a similar manner as those stated above. The compositions of reference glasses included Na₀.₇₅Si₂.₅₀Al₀.₇₅O₆.₅₀, Na₁.₀₀Si₂.₅₀Al₁.₀₀O₇.₀₀, Na₁.₀₀Si₁.₀₀O₂.₅₀, Na₂.₀₀Si₁.₀₀O₃.₀₀, Mg₀.₂₅Si₂.₅₀Al₀.₅₀O₆.₀₀, Mg₀.₅₀Si₂.₅₀Al₁.₀₀O₇.₀₀, Mg₀.₅₀Si₁.₀₀O₂.₅₀, Mg₁.₀₀Si₁.₀₀O₃.₀₀, Na₂.₀₀Si₁.₀₀O₃.₀₀, Na₁.₀₀Al₁.₀₀Si₂.₅₀O₇.₀₀, Mg₁.₀₀Si₁.₀₀O₃.₀₀, and Mg₀.₅₀Al₁.₀₀Si₂.₅₀O₇.₀₀.

Characterization Techniques

X-ray diffraction (XRD) patterns were recorded with a Rigaku SmartLab 9 kW XRD machine. The following parameters were used during the analysis: Co Kα radiation (Kα1 = 1.78892 Å; Kα2 = 1.79278 Å; Kα1/Kα2 = 0.5), a scan rate of 3°/min between 5°and 85° 2θ, and 0.02°/step. Phase identification was performed with the help of “X’pert HighScore Plus” (PANalytical software). The ²⁹Si MAS NMR spectra were also recorded on a Bruker Avance III 300 spectrometer, operating at 59.65 MHz. The samples were packed inside 7 mm zirconia rotors, a rotation frequency of 7 kHz was employed, and 8192 scans were performed with a repetition rate of 3 s. Chemical shifts were referenced to tetramethylsilane as an external standard, at 0 ppm. The ²⁹Si MAS-NMR spectra were deconvoluted into Gaussian components using Origin software. During deconvolution, peak position, intensity, and FWHM were varied independently while χ² minimization principal was followed. X-ray photoelectron spectroscopy (XPS) analysis was conducted using a Thermo Fisher Scientific XPS System (ESCALAB 250Xi). The binding energies of various elements were referenced to the binding energy of adventitious carbon (C1s, 284.6 eV). For scanning electron microscopic (SEM) imaging, a Zeiss Ultra Plus field emission scanning electron microscope (FESEM) equipped with an Oxford energy-dispersive X-ray spectroscopy (EDS) detector was used. Elemental mapping was carried out employing the Aztec software. During the preparation of samples, glass powder was impregnated in epoxy resin. After the hardening of the resin, the surface of the sample was polished with diamond (0.25 μm) paste to obtain a smooth surface. The polished surface of the sample was then sputter coated with carbon to create a conductive layer.

Results and Discussion

XRD Analysis of the Glasses

The sodium endmember of the glass systems (G0.00) shows two distinct amorphous regions along with a crystalline component (Figure 2). The first amorphous region (Am1) extends from 17.0° to 32.0°, while the second amorphous region (Am2) starts at 32.0° and ends at 45.0°. The crystalline component corresponds to sodium carbonate. This indicates that a portion of the sodium in the glass systems exist in the free oxide form, which is rapidly carbonated by atmospheric CO₂ and forms sodium carbonate. The free oxide form of network-modifying cation can occur in glasses when the NBO/Si ratio is high (Mysen et al., 1982).

FIGURE 2

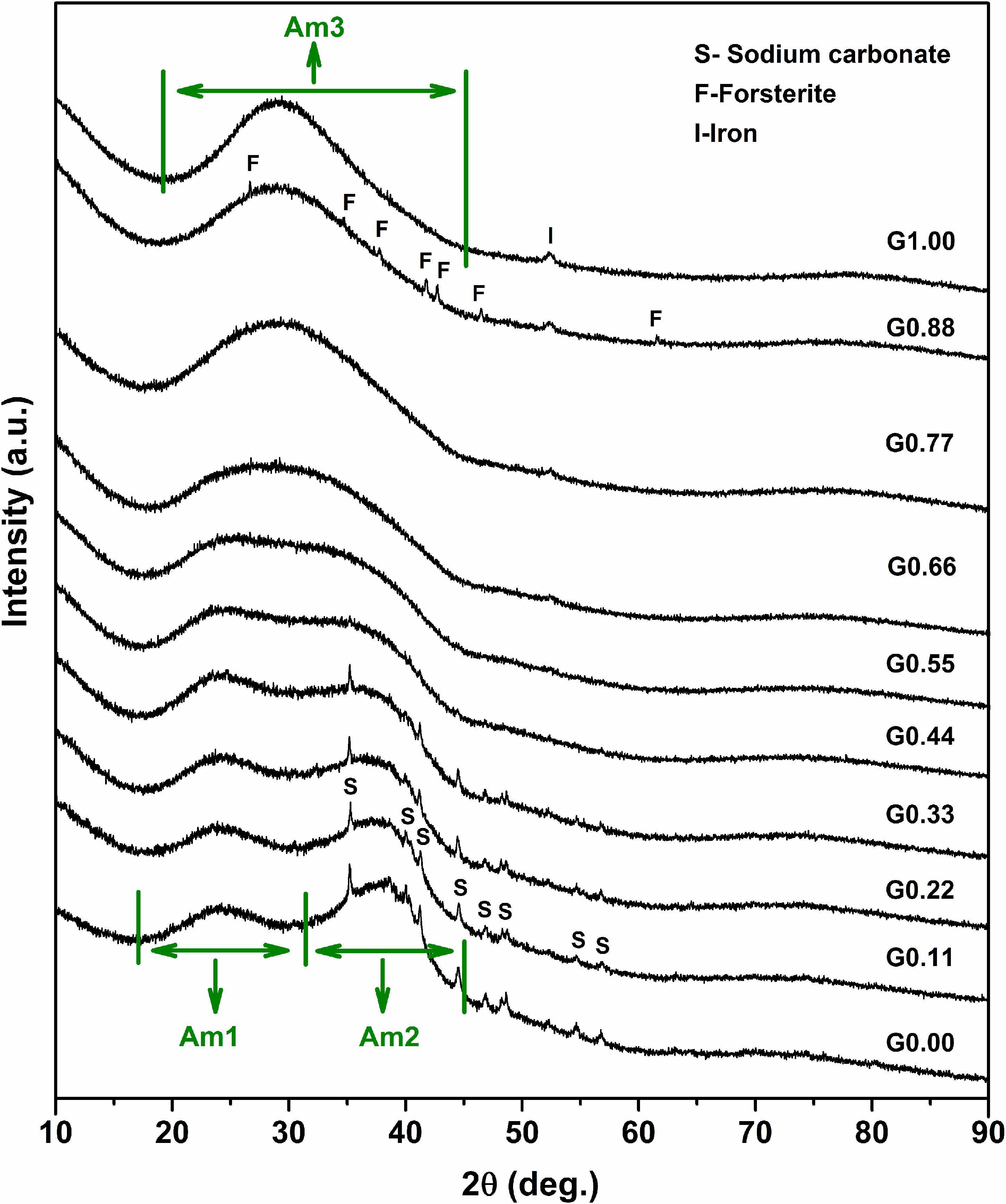
Figure 2. Results of the XRD analysis of [(Na₂O)_1–x(MgO)_x(Al₂O₃)_0.25(SiO₂)_1.25] glasses. Note that in G0.77, G0.88, and G1.00, a small XRD signal is visible at around 52.30°. This corresponds to iron metal which originates from the steel grinding equipment used for pulverizing the glass samples.

With the introduction of magnesium in the sodium endmember (starting from G0.11), Am1 remains intact in the beginning. There is no noticeable change in Am1 in glass samples from G0.00 to G0.77. However, on moving from G0.77 to G1.00, there is a slight shift of Am1 to the higher angle side by around 2° (refer Supplementary Material S1 for better details). In the case of Am2, as magnesium is introduced in the sodium endmember, there is a clear decrease in intensity. Growth of a new amorphous region is slowly underway. Finally, Am2 merges with Am1 and forms a new amorphous region (Am3) toward the magnesium endmember.

With the addition of magnesium in the sodium endmember, there is a gradual reduction in the intensity of sodium carbonate. The crystalline peaks of sodium carbonate disappear from glass samples starting from G0.44. Toward the magnesium endmember, one of the glasses (G0.88) shows the precipitation of crystalline forsterite (Mg₂SiO₄). It has been reported that the forsterite composition is difficult to vitrify (Nasikas et al., 2011). The existence of forsterite also indicates the presence of Q⁰ species. Both free network-modifying cations and highly depolymerized species such as Q⁰ can occur in glasses when the NBO/Si ratio is high (Mysen et al., 1982).

Understanding Phase Separation in Glasses Through SEM

Phase separation is a chemical disorder in glasses, which occurs when framework/network-modifying cations are not distributed in the glass network in a completely random order. This phenomenon stems from the occurrence of liquid immiscibility and positive mixing enthalpy among various oxide components of glasses (Hervig and Navrotsky, 1985; Lee, 2005). An important factor known to cause phase separation in silicate glasses is the nature of network-modifying cations. One of the earliest works in this direction was performed by Kracek (1930) who investigated the influence of network-modifying cations on liquid immiscibility of binary silicate systems by analyzing the shape of their liquidus curves. One group of cations (Cs, Rb, and K) formed binary silicates in which the shape of liquidus curve is linear. The liquidus curve of binary silicates of another group of cations (Na, Li, and Ba) followed S-shape. In the case of the binary silicates of the third group of cations (Sr, Ca, Mg), the liquidus curve is characterized by plateau. Another study by Warren and Pincus (1940) concluded that miscibility in glasses is favored by the tendency of framework cations to form bond with all available oxygens in the glass system, while immiscibility is favored when network-modifying cations are not properly surrounded by unsaturated oxygens. They suggested that ionic potential (Z/r, where Z and r represents cation charge and radius, respectively) has a critical influence on the immiscibility. Higher ionic potential of the network-modifying cations leads to greater immiscibility. Block and Levin (1957) studied the immiscibility of binary silicate systems with a focus on geometrical considerations. They suggested that the electrostatic bond strength (Z/C_n, where Z and C_n represent cation charge and coordination number respectively) of the network-modifying cations influences the shape of liquidus curve and the immiscibility. Galakhov and Varshal (1973) proposed that cationic field strength (Z/r²) is the significant factor controlling phase separation in simple silicate systems. The network-modifying cations with higher field strength produces greater phase separation. McGahay and Tomozawa (1989) used the concept of ionic interaction to study the phase separation in binary silicate systems. They found that the application of Debye–Hückel electrolyte theory in binary alkali and alkaline earth silicate systems can produce accurate predictions of critical temperatures. The study also found that immiscibility gap size is inversely proportional to the cube of the distance between cation and anion. Hess (1995) proposed that phase separation arises when non-framework cations are not sufficiently shielded from one another’s influence by the surrounding Si-O medium. Hence, strong coulombic repulsion between network-modifying cations can drive phase separation. Hudon and Baker (2002) made an exhaustive review focusing on the phase separate tendencies of 41 binary silicate glasses. Based on ionic radius (r) and coordination number (C_n), they grouped network-modifying cations into three categories. In the case of the first category (r > 87.2 pm; C_n ≥ 5) of network-modifying cations, the immiscibility gap size of the binary silicates is linearly proportional to the ionic potential (Z/r) of the network-modifying cations. For the second category (26 pm < r < 87.2 pm; C_n = 4 or 5) of cations, the immiscibility gap size has a non-linear (curve) correlation with ionic potential. The third category (r = variable; C_n = variable) formed silicates where the immiscibility gape size is larger than what is expected with network-modifying cations with similar ionic radii. They concluded that phase separation in silicate systems originates from coulombic repulsions between poorly screened network-modifying cation bounded by BO (which is strongly polarized toward Si) and by NBO. Most of the studies focusing on the influence of network-modifying cations on phase separation are performed on binary silicate systems investigates the phase separation between framework cations and network-modifying cations. Hence, it is interesting to see how network-modifying cations (like Na and Mg) can influence phase separation among framework cations (like Si and Al) in complex quaternary glass systems like Na-Mg aluminosilicate systems.

Scanning electron microscopy (SEM) along with energy dispersive X-ray analysis (EDX) allowing elemental mapping can be used to understand how the nature of network-modifying cations (Na/Mg) can cause phase separation (of Si and Al) in glasses at microstructural level. The microscopic images of glasses (Figure 3) indicates that G0.00 and G0.55 have uniform distributions of both Si and Al, although G0.00 shows some segregation of Na, which indicates the presence of the free form of Na as sodium carbonate. The last two glasses toward Mg endmember show some extent of phase separation (refer Supplementary Material S2 for some area-specific analysis). There is slight Si phase separation evident in G0.88. In G1.00, both Si and Al phase separation are observable to greater extent. It has been reported that Mg shows higher phase separation tendencies than Na in silicate systems (Galakhov and Varshal, 1973; Kreidl, 1991; Hudon and Baker, 2002). This can explain the phase separation observed in compositions close to magnesium endmember.

FIGURE 3

Figure 3. Scanning electron microscope images along with overlay of EDX elemental mapping for G0.00, G0.55, G0.88, and G1.00.

An idea about excitation volume in case of the SEM analysis can be obtained by calculating the depth of X-ray generation (Friel and Lyman, 2006). $R_x(\mathrm{\mu }m)=0.064(E_0^{1.68}-E_c^{1.68})/\mathrm{\rho }$, where E_o refers to accelerating voltage (keV), E_c represents critical excitation voltage (keV), and ρ is the mean specimen density (g/cm³). The average spatial resolution for the SEM analysis is around 2.27 μm

Insights From XPS Into the Role of Network-Modifying Cations

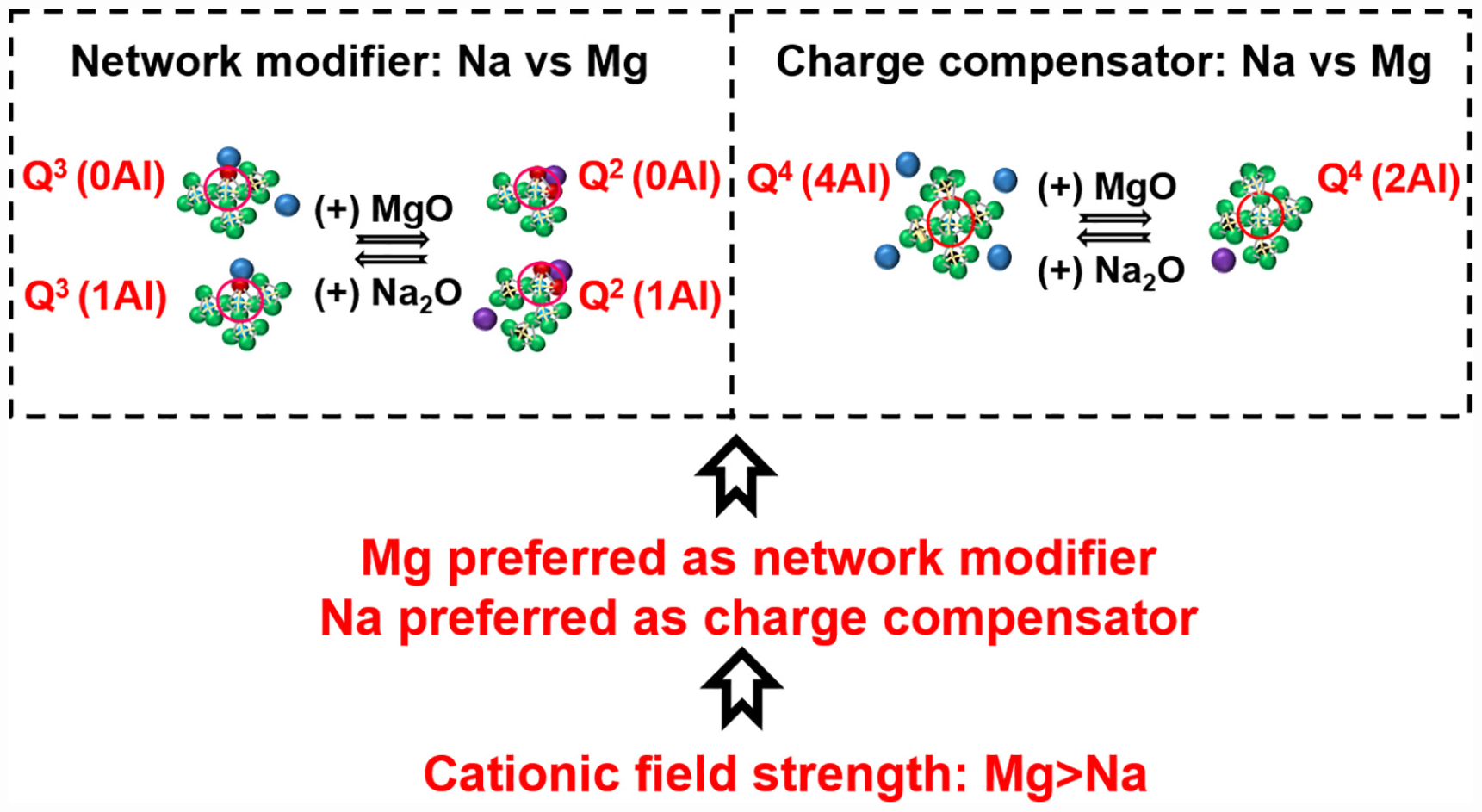
For the purpose of understanding the role of sodium in aluminosilicate glasses, Na 1s binding energies in original glasses as well as some reference compounds have been analyzed (Figure 4A). The reference compounds chosen included compounds in which sodium exists solely as charge compensator or network modifier or in free-oxide form. The following trend in binding energy has been observed in case of reference compounds: charge compensator > network modifier > free form. In the case of the original glasses, the binding energy in sodium endmember lies in the region between network modifier and free form. As the MgO/(MgO + Na₂O) ratio increases, there is a progressive increase in binding energy, and it reaches close to the charge compensator regime toward the magnesium endmember. This trend in the binding energy of sodium indicates that as magnesium is introduced into the system, it initially replaces sodium in the network modifier regime and, finally, replaces sodium in the charge compensator regime toward the magnesium endmember.

FIGURE 4

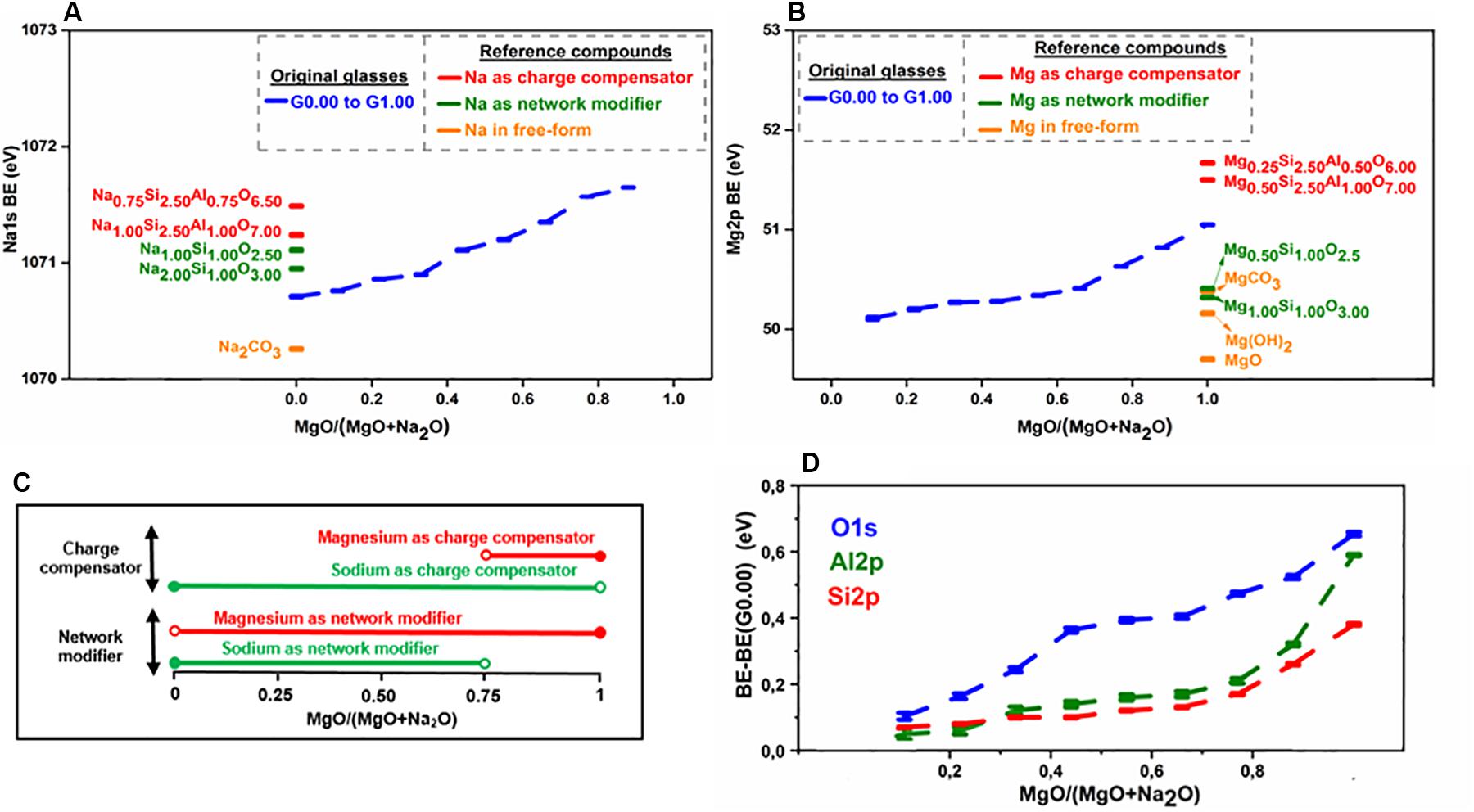
Figure 4. Results of XPS analysis of glasses. (A) Binding energy plot for sodium. (B) Binding energy plot for magnesium. (C) Role of network-modifying cations (sodium and magnesium) as indicated by XPS analysis. (D) Binding energy plots for oxygen, silicon, and aluminum.

The binding energy of magnesium (Mg 2p) in original glasses as well as some reference compounds (where magnesium exists solely as charge compensator or network modifier or in free-oxide form) has been analyzed (Figure 4B). In the case of reference compounds, it has been observed that the binding energy of magnesium is higher when it acts as charge compensator rather than network modifier [the free form of magnesium may occur as MgO, Mg(OH)₂, and/or MgCO₃, in which magnesium has different binding energies]. As the MgO/(MgO + Na₂O) ratio increases, there is a progressive increase in magnesium binding energy, and it reaches close to the charge compensator regime toward the magnesium endmember. This trend in the binding energy of magnesium indicates that as magnesium is introduced in the system, it initially performs the network modifier role and finally, performs the role of charge compensator toward the magnesium endmember.

Combining the results from the analysis of sodium and magnesium binding energies, it can be deduced that when both magnesium and sodium coexist in a glass system, sodium is preferred for charge compensation while magnesium is preferred for network modification. Figure 4C shows the role of network-modifying cations as indicated by XPS analysis.

Cation field strength can be used to explain the role preference among network-modifying cations as concluded from XPS analysis. Mg with high cation strength will have a higher concentration of positive charge than sodium with low field strength. So, magnesium needs to be surrounded by a higher concentration of negative charge to ensure neutrality of the structure. An NBO atom carries more negative charge than the apical oxygen atom (BO) of the negatively aluminum tetrahedral unit. Hence, magnesium prefers to be associated with NBO as network modifier. Similarly, preference of sodium for charge compensation (association with BO) can be explained.

The results of the XPS analysis indicate that the O 1s binding energy increases as sodium is replaced by magnesium in the aluminosilicate glasses (Figure 4D). This is because the Na-O bond has a more ionic nature than the Mg-O bond (Gibbs et al., 2006) and hence, the O 1s binding energy is higher in Mg-O bonds than Na-O bonds (refer Supplementary Material S4.4 for better details). The binding energy of the electrons of silicon increases gradually with the replacement of sodium by magnesium (Figure 4D), and steeply when approaching the magnesium endmember. As the Si-O bond is brought into closer proximity to a less-ionic Mg-O bond, according to the interjection rule (Barr, 1990), the binding energy of silicon should increase. The aluminum binding energy increases also gradually with the replacement of sodium by magnesium (Figure 4D), and the explanation given for the silicon binding energy increase holds here also.

Understanding Silicon Speciation Through ²⁹Si MAS NMR

Under normal conditions of pressure and temperature, silicon exists almost exclusively in tetrahedral form in aluminosilicate glasses (Kelsey et al., 2009). Thus, the local environments of silicon in glasses can be conveniently represented by Qⁿ (mAl), where n (4 ≥ n ≥ 0) represents the number of BO atoms surrounding the silicon atom, and m (n ≥ m ≥ 0) represents the number of the next-nearest neighbor sites, connected through these BO atoms, that are occupied by aluminum. Theoretically, this means that there can be up to 15 different local environments for silicon in aluminosilicate glasses. The quantification of these environments may be possible through credible deconvolution of spectra obtained through ²⁹Si NMR (Mysen et al., 2003; Walkley and Provis, 2019).

Much of the work in the literature on quantification of Qⁿ species in aluminosilicate glasses through ²⁹Si NMR spectral deconvolution has been focused on fully polymerized systems. In fully polymerized systems, the quantity of network-modifying cations present is just enough to balance the electrical charge deficit introduced by tetrahedral aluminum species and hence, there is no depolymerization of the network structure. In such cases, silicon can exist in only five states-Q⁴(0Al), Q⁴(1Al), Q⁴(2Al), Q⁴(3Al), and Q⁴(4Al). The spectral deconvolution is possible in a satisfactory manner as there are less overlapping among components. However, in depolymerized aluminosilicate systems (when network-modifying cations are present in a higher quantity than what is needed for charge compensation), credible deconvolution of spectra is a challenge due to overlapping among up to 15 components. Thus, there has been less work done in this area. One of the note-worthy attempts in this area had been made by Mysen et al. (2003) who deconvoluted the ²⁹Si NMR spectrum in a meaningful manner up to 10 components, excluding highly depolymerized components (Q⁰, Q¹). However, in our work, we have accounted for contributions from highly depolymerized components as our systems have higher proportions of network-modifying cations and XRD analysis indicates direct evidence of the presence of Q⁰ species.

For the purpose of determining the chemical shifts to apply for sub-peaks in the ²⁹Si MAS NMR spectra of the main series of glass samples, deconvolutions of the spectra of some simplified reference glasses were performed (refer Supplementary Material S3 for more details). Na₂.₀₀Si₁.₀₀O₃.₀₀ and Mg₁.₀₀Si₁.₀₀ O₃.₀₀ were chosen to obtain information about the chemical shifts of Q⁰–Q³ species in sodium silicate and magnesium silicate respectively. Na₁.₀₀Al₁.₀₀Si₂.₅₀O₇.₀₀ and Mg₀.₅₀Al₁.₀₀Si₂.₅₀O₇.₀₀ were chosen for obtaining information about the chemical shifts of Q⁴(mAl) species in sodium aluminosilicate and magnesium aluminosilicate, respectively.

Considering the complexity of the deconvolution procedure, we ensured the credibility of the deconvolution procedure (for the main series of glass samples) by the following three ways: (1) Choosing meaningful values for chemical shifts, and width for each spectral component, by consulting literature (Mahler and Sebald, 1995; Lee and Stebbins, 1999; Schneider et al., 2000; Mysen et al., 2003) as well as by performing spectral deconvolution for some simplified reference glasses as stated before (refer Supplementary Material S3 for better details); (2) comparing the overall Si: Al ratio obtained through spectral deconvolution (experimental) to the bulk (theoretical) value; and (3) comparing the experimental NBO/Si ratio to the theoretical ratio. The full details of the spectral deconvolutions are provided in Supplementary Material S2. In spite of the rigorous method followed, there can be major uncertainties associated with the deconvolution procedure. This uncertainty originates mainly from two sources: (1) uncertainty arising due to chemical shift variation; (2) uncertainty arising from FWHM variation. Hence, these two uncertainties were assed independently. The total uncertainty was obtained by the addition of these two uncertainties. Detailed procedure followed for uncertainty calculation has been provided in Supplementary Material S3.

Each of the spectra obtained through ²⁹Si NMR measurement of the glasses was deconvoluted into 11 components, representing the known site environments in these glasses. Deconvolution for the case of G0.00 is shown in Figures 5A,B, while those of the remaining glasses are provided in Supplementary Material S3. The experimental and theoretical values for the Si:Al ratio are close to each other in all glasses, except in those close to the magnesium endmember where experimental values are higher than theoretical values (Figure 5C). This may be due to the phase separation toward the magnesium endmember (as observed in SEM analysis). Experimental values for the NBO:Si ratio are lower than the theoretical values for glasses close to the sodium endmember, while toward the magnesium endmember the values are in good agreement (Figure 5D). According to the XRD analysis of the glasses, in glasses close to the sodium endmember, a portion of sodium exist as free form (observable as sodium carbonate). This means that the total amount of sodium available to act as network modifier or charge compensator is lower than the bulk value. This explains the lower experimental values for NBO:Si in glasses close to the sodium endmember.

FIGURE 5

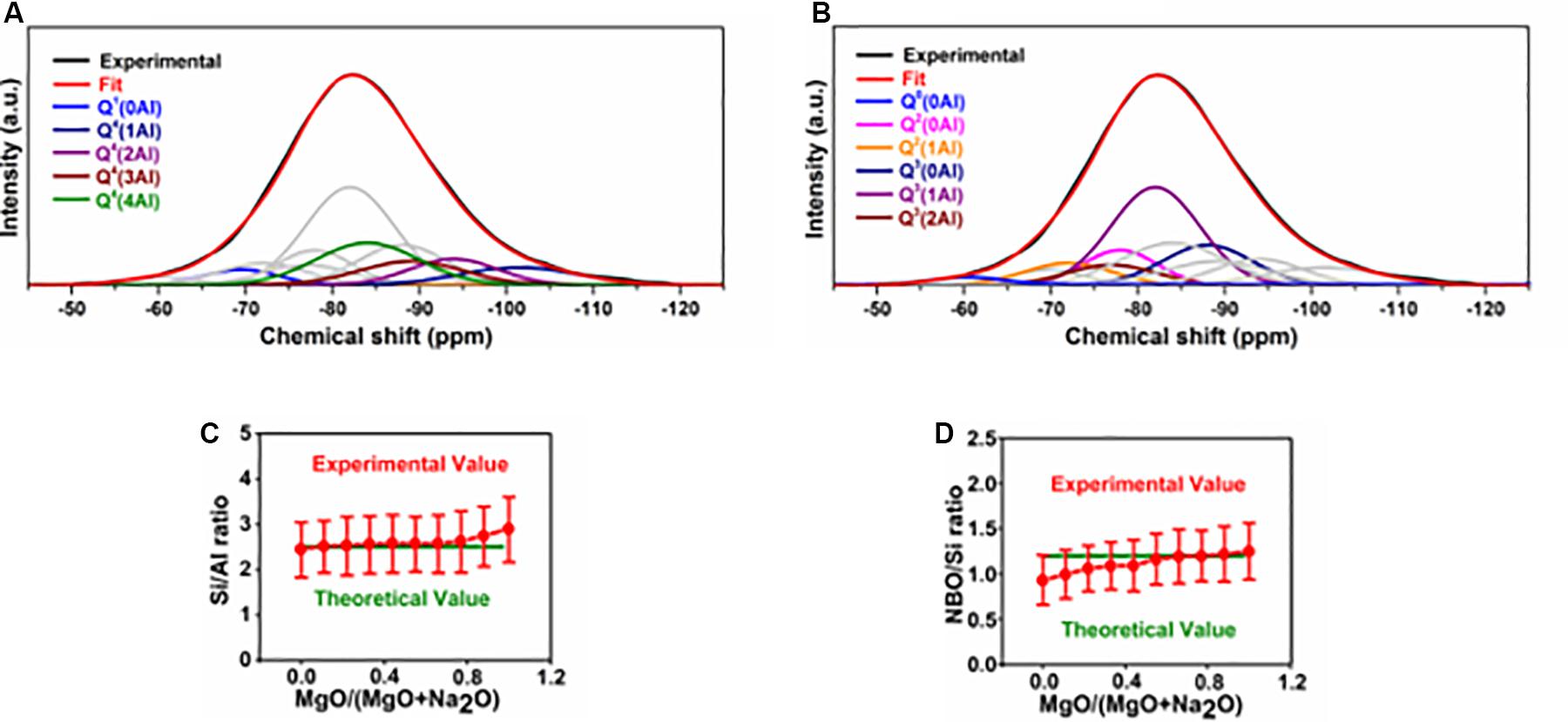
Figure 5. Results of deconvolution of ²⁹Si MAS NMR spectra of glasses. (A,B) Deconvolution of the ²⁹Si MAS NMR spectrum of G0.00. (C) Comparison of theoretical (based on bulk composition) and experimental (based on deconvolution of ²⁹Si spectra) values of Si/Al. (D) Comparison of theoretical and experimental values for NBO/Si ratio.

The results of the deconvolution (Figure 6A) indicate that sodium endmember (G0.00) is dominated by Q³ (45%) and Q⁴ (35%) species, followed by Q² (15%) species. Highly depolymerized species such as Q¹ and Q⁰ are present in relatively smaller proportions (2 and 4%, respectively). With the introduction of magnesium into the sodium endmember, as the MgO/(MgO + Na₂O) ratio increases from 0 to 0.75, there are changes in the proportions of Q³ and Q² species (associated with network modifier cations), while Q⁴ remains nearly the same, and the small fractions of Q¹ and Q⁰ also do not change significantly. This agrees with the observation above that magnesium added to the sodium endmember prefers to take on the role of network modifier rather than charge compensator (according to XPS analysis). Regarding the changes in Q³ and Q² species, there is a decrease in the proportions of Q³(0Al), Q³(1Al), and Q³(2Al) species, while the proportions of Q²(0Al) and Q²(1Al) increases (Figure 6B). The observed trends in Qⁿ speciation remain the same as the MgO/(MgO + Na₂O) ratio increases from 0 to 0.75. However, as this ratio increases beyond 0.75, there are major changes in the Q⁴ species. While the overall proportion of Q⁴ species remains nearly the same (Figure 6C), there is a decrease in the proportion of the aluminum-rich Q⁴ species [Q⁴(4Al) and Q⁴(3Al)], and a corresponding increase in aluminum-deficient Q⁴ species [Q⁴(2Al) and Q⁴(1Al)]. There is also a slight increase in the proportions of depolymerized Q¹ and Q⁰ species (This agrees with the XRD analysis, which indicated presence of forsterite (MgSiO₄), with Q⁰ silicate sites, in compositions close to the magnesium endmember).

FIGURE 6

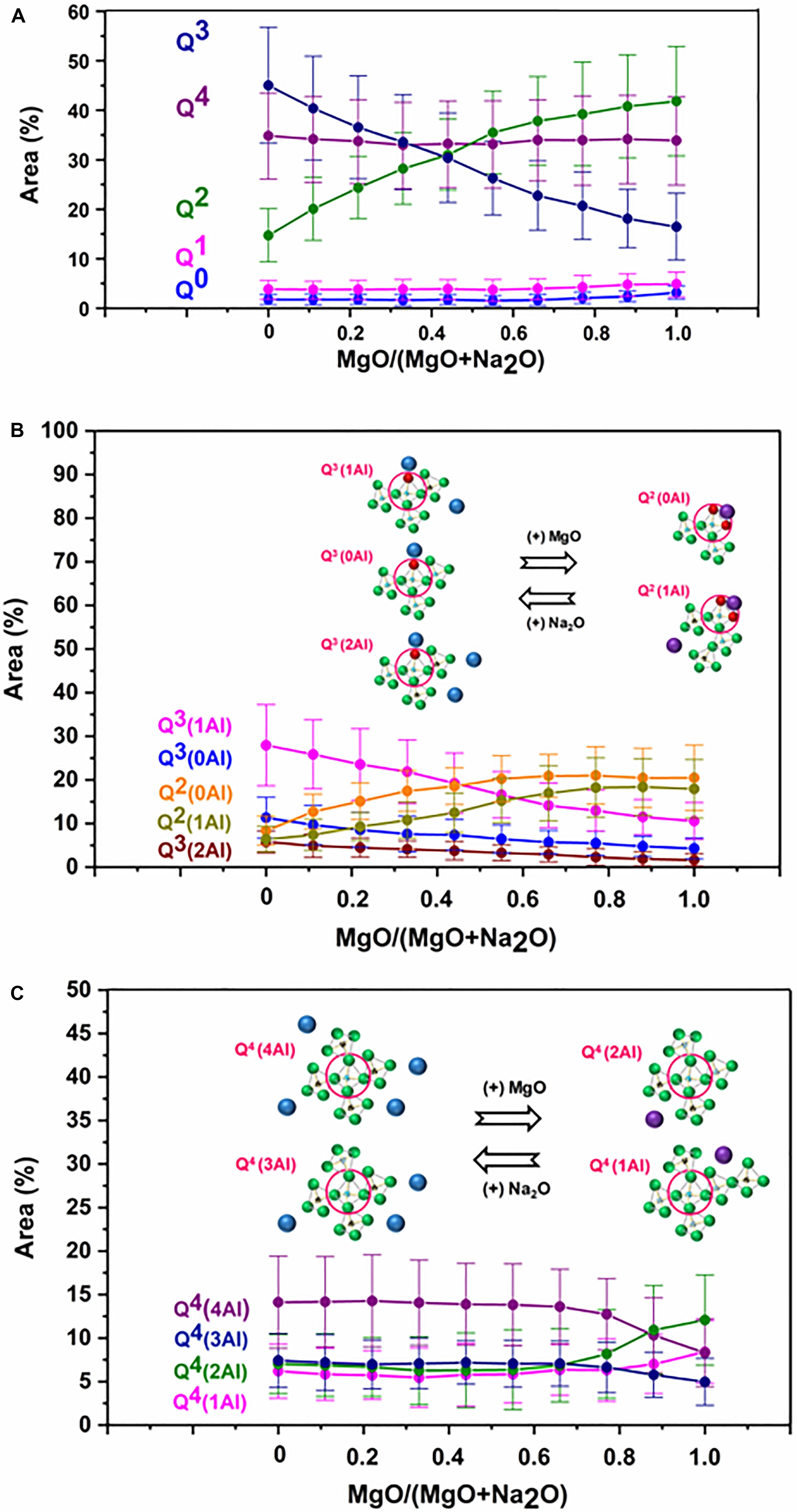
Figure 6. Results of Qⁿ speciation from ²⁹Si MAS NMR analysis of glasses. (A) Overall Qⁿ speciation in glasses. (B) Detailed Q² and Q³ speciation in glasses. (C) Detailed Q⁴ speciation in glasses.

The analysis of the Qⁿ speciation of glasses agree with the previous studies. One of the major trends in Qⁿ speciation is the reduction in Q³ species and increase in Q² species as Na is replaced by Mg in Na-Mg aluminosilicate glasses. Jones et al. (2001) investigated the structure of Ca/Na silicate glasses by ²⁹Si MAS NMR spectroscopy and observed that Ca preferably associates with Q² species, while Na associates with Q³ species (Ca has cation field strength of 0.36 Å^–2, while Na has 0.18 Å^–2 (Quintas et al., 2009). Hence, the behavior of Mg in Na-Mg silicate glasses can be compared to that of Ca in Na-Ca silicate glasses). Structural investigation of Na/Ca silicate glasses by Raman spectroscopy found that as Na is replaced with Ca, the Q³/Q² ratio decreases (Neuville, 2006). Schneider et al. (2000) studied the structure of Na/Ca silicate glasses with the help of ²⁹Si MAS NMR spectroscopy and observed that Q³ species decreases, while Q² species increases as Na content of glasses decreases. A structural investigation of Na/Ca silicaphosphate glasses by ²⁹Si MAS NMR spectroscopy concluded that Ca preferentially associates with Q² species, while Na shows more affinity for with Q³ species (Lockyer et al., 1995). Structural studies of Na/Ca aluminosilicate glasses by ²⁷Al and ²⁹Si MAS and MQMAS spectroscopies indicated that Ca occurs more near Q¹ and Q² species, while Na is more localized around Q³ and Q⁴ species (Gambuzzi et al., 2014). The other major trend in Qⁿ speciation observed in our study is that there is a reduction in the proportion of the aluminum-rich Q⁴ species [Q⁴(4Al) and Q⁴(3Al)], and a corresponding increase in aluminum-deficient Q⁴ species [Q⁴(2Al) and Q⁴(1Al)] as Na is replaced by Mg in the charge compensator regime. This is in agreement with the previous studies on aluminosilicate glasses with a similar Si:Al ratio. A structural study of Na aluminosilicate glasses using ²⁹Si MAS NMR spectroscopy revealed that Q⁴ species are mostly dominated by Q⁴(4Al) and Q⁴(3Al) species when compared to Q⁴(2Al), Q⁴(1Al), and Q⁴(0Al) species (Mysen et al., 2003). Another structural investigation of Ca aluminosilicate glasses using ²⁹Si MAS NMR spectroscopy indicated that Q⁴(2Al) and Q⁴(1Al) species dominates among Q⁴ species (Lee and Stebbins, 1999).

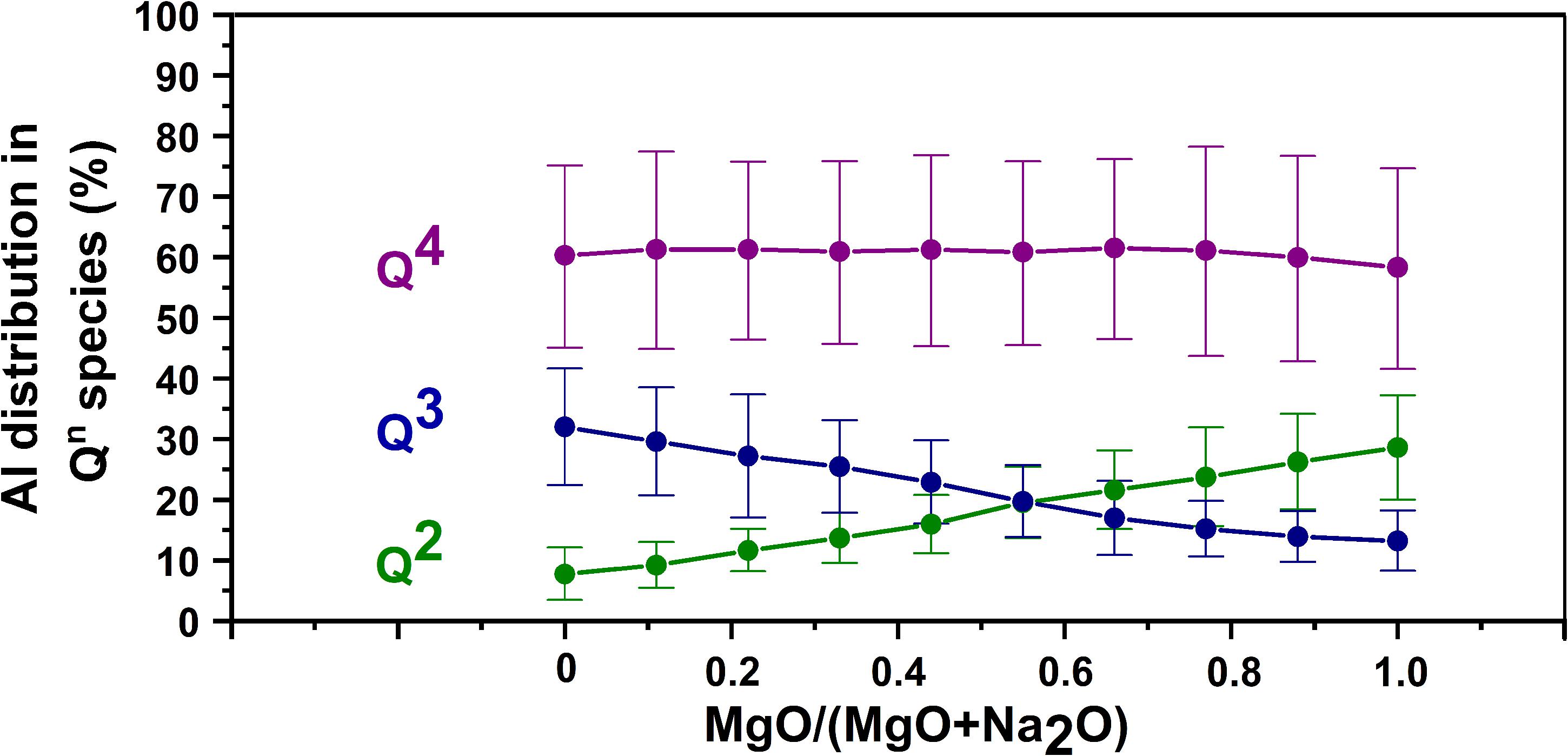
One important structural aspect of aluminosilicate glasses is the connectivity of framework units. It is related to the extent of mixing among framework cations and is known to have significant influence on many properties of the aluminosilicate glasses (Lee, 2005). An insight into the framework connectivity in the aluminosilicate glasses is possible through the estimation of Al distribution in various Qⁿ species (this can indicate if a particular Qⁿ species exhibit preference to form Si-O-Al bridges than Si-O-Si bridges).

It has been found that Al preferably associates with Q⁴ species when compared to other Qⁿ species (Figure 7). Irrespective of the nature of network-modifying cations present, all the glasses exhibit around 60% of total aluminum in Q⁴ species (There is a slight drop toward the Mg endmember, which is due the reduction in aluminum-rich Q⁴ species as discussed before). Significant Al reside in Q³ and Q² species also. In the sodium endmember, roughly 32% of the Al is associated with Q³ species, while 8% of the Al is confined to Q² species. Unlike the case of Q⁴ species, Al distribution in Q² and Q³ species is influenced by the type of network-modifying cation present. As Mg is introduced into the Na endmember, Al association with Q³ species decreases, while Al association with Q² species increases. The Mg endmember has roughly 13% of the Al associated with Q³ species, while 28% of the Al is confined to Q² species.

FIGURE 7

Figure 7. Aluminum distribution in various Qⁿ species.

The preference of Al for Q⁴ species (as discussed above) has been reported in previous studies of aluminosilicate glasses. Structural investigation of Ca/Na aluminosilicate glasses by ²⁷Al and ²⁹Si MAS and MQMAS spectroscopies revealed that Al prefers association with Q⁴ species, followed by Q³ and Q² species (Gambuzzi et al., 2014). Neuville et al. (2004) studied the structure of Ca aluminosilicate glasses by ²⁷Al MQ-MAS NMR and XANES spectroscopies and observed that Al is mainly associated with Q⁴ species. The ²⁹Si MAS NMR spectroscopic analysis of Na aluminosilicate glasses revealed that as much as 70% of the total Al is associated with Q⁴ species (Mysen et al., 2003). Raman spectroscopic studies on Na/Ca aluminosilicate glasses concluded the preference of Al for Q⁴ species (Mysen et al., 1981; Mysen, 1999). Maekawa et al. (1991) studied the structure of Na aluminosilicate glasses by ²⁹Si MAS NMR spectroscopy and found that Al has strong affinity for Q⁴ species. Due to the longer bridging Al-O bonds (when compared to bridging Si-O bonds) and larger average Si-O-Al bond angles (when compared to Si-O-Si bond angles), alumina tetrahedra can be accommodated with Q⁴ species with less energy penalty than depolymerized Qⁿ species (Mysen et al., 2003).

Cation field strength can be used to explain the trends observed in the ²⁹Si MAS NMR analysis. The major change that happens as magnesium replaces sodium in the network modifier region is the conversion of Q³ species to Q² species. Q² species (with 2 NBO) have more negative charge than Q³ species (with 1 NBO). So, it is natural that magnesium, with a high cation field strength, prefers to associate with Q² than Q³ species. As magnesium enters a charge compensation role when it is present in much larger quantities than sodium, there is a decrease in the proportion of Q⁴(4Al) and Q⁴(3Al) sites, and an increase in Q⁴(2Al) and Q⁴(1Al) sites. Q⁴(4Al) and Q⁴(3Al) sites (which are associated with 2 and 1.5 units of Mg²⁺) experience more distortion due to the high cation field strength of magnesium when compared to Q⁴(2Al) and Q⁴(1Al) sites (which are associated with 1 and 0.5 units of Mg²⁺). Hence, when magnesium acts as charge compensator, Q⁴(4Al) and Q⁴(3Al) sites are less favored when compared to Q⁴(2Al) and Q⁴(1Al) sites. This explains the observed trend within Q⁴ species.

Conclusion

It can be concluded that magnesium prefers the role of network modifier, while sodium preferably acts as charge compensator, when both network-modifying cations coexist in an aluminosilicate glass. This is since Mg with a high cation field strength prefers association with non-bridging oxygen, carrying more negative charge, for better charge stabilization. When magnesium replaces sodium as a network modifier, Q³ species are converted into Q² species. Replacement of sodium with magnesium as charge compensator leads to the following changes: (1) the proportion of aluminum-rich Q⁴ species [Q⁴(4Al) and Q⁴(3Al)] decreases, while the proportion of aluminum-deficient Q⁴ species [Q⁴(2Al) and Q⁴(1Al)] increases; and (2) there is an increased tendency for phase separation between silica-rich and alumina-rich glasses.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

HS: formal analysis, investigation, methodology, visualization, writing – original draft, and writing – review and editing. PK: conceptualization, methodology, formal analysis, investigation, funding acquisition, supervision visualization, and writing – review and editing. EA: formal analysis, investigation, visualization, and writing – review and editing. MP: formal analysis, validation, investigation, and writing – review and editing. AK and V-VT: formal analysis, validation, funding acquisition, and writing – review and editing. MH: investigation, validation, and writing – review and editing. WC: formal analysis, validation, visualization, supervision, and writing – review and editing. JP: formal analysis, validation, methodology, visualization, supervision, and writing – review and editing. MI: formal analysis, validation, writing – review and editing, supervision, and funding acquisition. All authors contributed to the article and approved the submitted version.

Funding

We gratefully acknowledge the financial support received from European Union’s Horizon 2020 Research and Innovation Programme under the Marie Skłodowska-Curie COFUND Grant Agreement No. 713606 (I4Future MSC-COFUND). AK and V-VT acknowledge the financial support from Kvantum Institute (University of Oulu) and Academy of Finland (Grants #289649 and 294027). PK acknowledges financial support from Academy of Finland (Grants #322085, #326291, and #329477).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We would like to thank Marcin Selent for his help with XRD measurement, Santtu Heinilehto with XPS measurements and Tommi Kokkonen with glass synthesis. This work/part of the work was carried out with the support of the Centre for Material Analysis, University of Oulu, Finland.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2020.00267/full#supplementary-material

References

Baker, T. J., Zimba, J., Akpan, E. T., Bashir, I., Watola, C. T., and Soboyejo, W. O. (2006). Viscoelastic toughening of aluminosilicate refractory ceramics. Acta Mater. 54, 2665–2675. doi: 10.1016/j.actamat.2006.02.009

CrossRef Full Text | Google Scholar

Barr, T. L. (1990). The nature of the relative bonding chemistry in zeolites: an XPS study. Zeolites 10, 760–765. doi: 10.1016/0144-2449(90)90058-Y

CrossRef Full Text | Google Scholar

Beall, G. H. (2009). Refractory glass-ceramics based on alkaline earth aluminosilicates. J. Eur. Ceram. Soc. 29, 1211–1219. doi: 10.1016/j.jeurceramsoc.2008.08.010

CrossRef Full Text | Google Scholar

Block, S., and Levin, E. M. (1957). Structural interpretation of immiscibility in oxide systems: II, coordination principles applied to immiscibility. J. Am. Ceram. Soc. 40, 113–118. doi: 10.1111/j.1151-2916.1957.tb12586.x

CrossRef Full Text | Google Scholar

Duminis, T., Shahid, S., and Hill, R. G. (2017). Apatite glass-ceramics: a review. Front. Mater. 3:59. doi: 10.3389/fmats.2016.00059

CrossRef Full Text | Google Scholar

Frankel, G. S., Vienna, J. D., Lian, J., Scully, J. R., Gin, S., Ryan, J. V., et al. (2018). A comparative review of the aqueous corrosion of glasses, crystalline ceramics, and metals. NPJ Mater. Degrad. 2, 1–17. doi: 10.1038/s41529-018-0037-2

CrossRef Full Text | Google Scholar

Friel, J. J., and Lyman, C. E. (2006). Tutorial review: x-ray mapping in electron-beam instruments. Microsc. Microanal. 12, 2–25. doi: 10.1017/S1431927606060211

PubMed Abstract | CrossRef Full Text | Google Scholar

Galakhov, F. Y. A., and Varshal, B. G. (1973). “Causes of phase separation in simple silicate systems. Phase-separation phenomena in glasses,” in Likvatsionnye Yavleniya v Steklakh ликвационные явления в стеклах The Structure Of Glass/Stekloobraznoe Sostoyanie/стеклооьразное состояние,. ed E. A. Porai-Koshits (Boston, MA: Springer), 7–11. doi: 10.1007/978-1-4757-0157-9_2

CrossRef Full Text | Google Scholar

Gambuzzi, E., Pedone, A., Menziani, M. C., Angeli, F., Caurant, D., and Charpentier, T. (2014). Probing silicon and aluminium chemical environments in silicate and aluminosilicate glasses by solid state NMR spectroscopy and accurate first-principles calculations. Geochim. Cosmochim. Acta 125, 170–185. doi: 10.1016/j.gca.2013.10.025

CrossRef Full Text | Google Scholar

Genova, D. D., Kolzenburg, S., Wiesmaier, S., Dallanave, E., Neuville, D. R., Hess, K. U., et al. (2017). A compositional tipping point governing the mobilization and eruption style of rhyolitic magma. Nature 552, 235–238. doi: 10.1038/nature24488

PubMed Abstract | CrossRef Full Text | Google Scholar

Gibbs, G. V., Cox, D. F., Crawford, T. D., Rosso, K. M., Ross, N. L., and Downs, R. T. (2006). Classification of metal-oxide bonded interactions based on local potential- and kinetic-energy densities. J. Chem. Phys. 124:084704. doi: 10.1063/1.2161425

CrossRef Full Text | Google Scholar

Gorni, G., Cosci, A., Pelli, S., Pascual, L., Durán, A., and Pascual, M. J. (2017). Transparent oxyfluoride nano-glass ceramics doped with Pr3+ and Pr3+-Yb3+ for NIR emission. Front. Mater. 3:58. doi: 10.3389/fmats.2016.00058

CrossRef Full Text | Google Scholar

Hervig, R. L., and Navrotsky, A. (1985). Thermochemistry of sodium borosilicate glasses. J. Am. Ceram. Soc. 68, 314–319. doi: 10.1111/j.1151-2916.1985.tb15232.x

CrossRef Full Text | Google Scholar

Hess, P. C. (1995). “Thermodynamic mixing properties and the structure of silicate melts,” in Structure, Dynamics, And Properties Of Silicate Melts Pages, eds J. F. Stebbins, P. F. McMillan, and D. B. Dingwell (Berlin: De Gruyter), 145–190. doi: 10.1515/9781501509384-008

CrossRef Full Text | Google Scholar

Hudon, P., and Baker, D. R. (2002). The nature of phase separation in binary oxide melts and glasses. I. silicate systems. J. Non Cryst. Solids 303, 299–345. doi: 10.1016/S0022-3093(02)01043-8

CrossRef Full Text | Google Scholar

Jones, A. R., Winter, R., Greaves, G. N., and Smith, I. H. (2001). MAS NMR study of soda-lime-silicate glasses with variable degree of polymerisation. J. Non Cryst. Solids 293–295, 87–92. doi: 10.1016/S0022-3093(01)00656-1

CrossRef Full Text | Google Scholar

Kelsey, K. E., Stebbins, J. F., Mosenfelder, J. L., and Asimow, P. D. (2009). Simultaneous aluminum, silicon, and sodium coordination changes in 6 GPa sodium aluminosilicate glasses. Am. Mineral. 94, 1205–1215. doi: 10.2138/am.2009.3177

CrossRef Full Text | Google Scholar

Kinnunen, P., Sreenivasan, H., Cheeseman, C. R., and Illikainen, M. (2019). Phase separation in alumina-rich glasses to increase glass reactivity for low-CO₂ alkali-activated cements. J. Clean. Prod. 213, 126–133. doi: 10.1016/j.jclepro.2018.12.123

CrossRef Full Text | Google Scholar

Kracek, F. C. (1930). The cristobalite liquidus in the alkali oxide-silica systems and the heat of fusion of cristobalite. J. Am. Chem. Soc. 52, 1436–1442. doi: 10.1021/ja01367a021

CrossRef Full Text | Google Scholar

Kreidl, N. (1991). Phase separation in glasses. J. Non Cryst. Solids 129, 1–11. doi: 10.1016/0022-3093(91)90074-G

CrossRef Full Text | Google Scholar

Kucharczyk, S., Sitarz, M., Zajac, M., and Deja, J. (2018). The effect of CaO/SiO2 molar ratio of CaO-Al2O3 -SiO2 glasses on their structure and reactivity in alkali activated system. Spectrochim. Acta A Mol. Biomol. Spectrosc. 194, 163–171. doi: 10.1016/j.saa.2018.01.018

PubMed Abstract | CrossRef Full Text | Google Scholar

Lamberson, L. (2016). Influence of Atomic Structure On Plastic Deformation In Tectosilicate Calcium-Aluminosilicate, Magnesium-Aluminosilicate, And Calcium-Galliosilicate Glasses. Dissertation. Cornell University, Ithaca, NY.

Google Scholar

Le Losq, C., and Neuville, D. R. (2013). Effect of the Na/K mixing on the structure and the rheology of tectosilicate silica-rich melts. Chem. Geol. 346, 57–71. doi: 10.1016/j.chemgeo.2012.09.009

CrossRef Full Text | Google Scholar

Lee, S. K. (2005). Microscopic origins of macroscopic properties of silicate melts and glasses at ambient and high pressure: Implications for melt generation and dynamics. Geochim. Cosmochim. Acta 69, 3695–3710. doi: 10.1016/j.gca.2005.03.011

CrossRef Full Text | Google Scholar

Lee, S. K., Kim, H.-I., Kim, E. J., Mun, K. Y., and Ryu, S. (2016). Extent of disorder in magnesium aluminosilicate glasses: Insights from 27Al and 17O NMR. J. Phys. Chem. C 120, 737–749. doi: 10.1021/acs.jpcc.5b10799

CrossRef Full Text | Google Scholar

Lee, S. K., and Stebbins, J. F. (1999). The degree of aluminum avoidance in aluminosilicate glasses. Am. Mineral. 84, 937–945. doi: 10.2138/am-1999-5-631

CrossRef Full Text | Google Scholar

Lockyer, M. W. G., Holland, D., and Dupree, R. (1995). NMR investigation of the structure of some bioactive and related glasses. J. Non Cryst. Solids 188, 207–219. doi: 10.1016/0022-3093(95)00188-3

CrossRef Full Text | Google Scholar

Losq, C. L., Neuville, D. R., Chen, W., Florian, P., Massiot, D., Zhou, Z., et al. (2017). Percolation channels: a universal idea to describe the atomic structure and dynamics of glasses and melts. Sci. Rep. 7, 1–12. doi: 10.1038/s41598-017-16741-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Maekawa, H., Maekawa, T., Kawamura, K., and Yokokawa, T. (1991). Silicon-29 MAS NMR investigation of the sodium oxide-alumina-silica glasses. J. Phys. Chem. 95, 6822–6827. doi: 10.1021/j100171a016

CrossRef Full Text | Google Scholar

Mahler, J., and Sebald, A. (1995). Deconvolution of 29Si magic-angle spinning nuclear magnetic resonance spectra of silicate glasses revisited - some critical comments. Solid State Nucl. Magn. Reson. 5, 63–78. doi: 10.1016/0926-2040(95)00027-N

CrossRef Full Text | Google Scholar

Mallick, K. K., and Holland, D. (2005). Strengthening of container glasses by ion-exchange dip coating. J. Non Cryst. Solids 351, 2524–2536. doi: 10.1016/j.jnoncrysol.2005.06.040

CrossRef Full Text | Google Scholar

McGahay, V., and Tomozawa, M. (1989). The origin of phase separation in silicate melts and glasses. J. Non Cryst. Solids 109, 27–34. doi: 10.1016/0022-3093(89)90437-7

CrossRef Full Text | Google Scholar

Moesgaard, M., Poulsen, S. L., Herfort, D., Steenberg, M., Kirkegaard, L. F., Skibsted, J., et al. (2012). Hydration of blended Portland cements containing calcium-aluminosilicate glass powder and limestone. J. Am. Ceram. Soc. 95, 403–409. doi: 10.1111/j.1551-2916.2011.04902.x

CrossRef Full Text | Google Scholar

Mysen, B. O. (1999). Structure and properties of magmatic liquids: from haplobasalt to haploandesite. Geochim. Cosmochim. Acta 63, 95–112. doi: 10.1016/S0016-7037(98)00273-7

CrossRef Full Text | Google Scholar

Mysen, B. O., Lucier, A., and Cody, G. D. (2003). The structural behavior of Al3+ in peralkaline melts and glasses in the system Na2O-Al2O3-SiO2. Am. Mineral. 88, 1668–1678. doi: 10.2138/am-2003-11-1206

CrossRef Full Text | Google Scholar

Mysen, B. O., Virgo, D., and Kushiro, I. (1981). The structural role of aluminum in silicate melts-a Raman spectroscopic study at 1 atmosphere. Am. Mineral. 66, 678–701.

Google Scholar

Mysen, B. O., Virgo, D., and Seifert, F. A. (1982). The structure of silicate melts: implications for chemical and physical properties of natural magma. Rev. Geophys. 20, 353–383. doi: 10.1029/RG020i003p00353

CrossRef Full Text | Google Scholar

Nakane, S., and Kawamoto, K. (2017). Coloration mechanism of Fe ions in β-Quartz s.s. glass-ceramics with TiO2 and ZrO2 as nucleation Agents. Front. Mater. 4:7. doi: 10.3389/fmats.2017.00007

CrossRef Full Text | Google Scholar

Nasikas, N. K., Chrissanthopoulos, A., Bouropoulos, N., Sen, S., and Papatheodorou, G. N. (2011). Silicate glasses at the ionic limit: alkaline-earth sub-orthosilicates. Chem. Mater. 23, 3692–3697. doi: 10.1021/cm2012582

CrossRef Full Text | Google Scholar

Neuville, D. R. (2006). Viscosity, structure and mixing in (Ca, Na) silicate melts. Chem. Geol. 229, 28–41. doi: 10.1016/j.chemgeo.2006.01.008

CrossRef Full Text | Google Scholar

Neuville, D. R., Cormier, L., and Massiot, D. (2004). Al environment in tectosilicate and peraluminous glasses: a 27Al MQ-MAS NMR, Raman, and XANES investigation. Geochim. Cosmochim. Acta 68, 5071–5079. doi: 10.1016/j.gca.2004.05.048

CrossRef Full Text | Google Scholar

Newlands, K. C., and Macphee, D. E. (2017). The reactivity of aluminosilicate glasses in cements - effects of Ca content on dissolution characteristics and surface precipitation. Adv. Appl. Ceram. 116, 216–224. doi: 10.1080/17436753.2017.1299986

CrossRef Full Text | Google Scholar

Peng, Y., Zhong, J., Li, X., Chen, J., Zhao, J., Qiao, X., et al. (2019). Controllable competitive nanocrystallization of La3+-based fluorides in aluminosilicate glasses and optical spectroscopy. J. Eur. Ceram. Soc. 39, 1420–1427. doi: 10.1016/j.jeurceramsoc.2018.12.036

CrossRef Full Text | Google Scholar

Piovesan, V., Bardez-Giboire, I., Fournier, M., Frugier, P., Jollivet, P., Montouillout, V., et al. (2018). Chemical durability of peraluminous glasses for nuclear waste conditioning. NPJ Mater. Degrad. 2, 1–10. doi: 10.1038/s41529-018-0028-3

CrossRef Full Text | Google Scholar

Quintas, A., Caurant, D., Majérus, O., Charpentier, T., and Dussossoy, J.-L. (2009). Effect of the nature of alkali and alkaline-earth oxides on the structure and crystallization of an aluminoborosilicate glass developed to immobilize highly concentrated nuclear waste solutions. International conference atalante 2008. nuclear fuel cycles for a sustainable future, Montpellier: France (2008). arXiv [Preprint], Available online at: http://arxiv.org/abs/0912.1576 (accessed February 19, 2020).

Google Scholar

Schneider, J., Mastelaro, V. R., Panepucci, H., and Zanotto, E. D. (2000). 29Si MAS-NMR studies of Qn structural units in metasilicate glasses and their nucleating ability. J. Non Cryst. Solids 273, 8–18. doi: 10.1016/S0022-3093(00)00139-3

CrossRef Full Text | Google Scholar

Schöler, A., Winnefeld, F., Haha, M. B., and Lothenbach, B. (2017). The effect of glass composition on the reactivity of synthetic glasses. J. Am. Ceram. Soc. 100, 2553–2567. doi: 10.1111/jace.14759

CrossRef Full Text | Google Scholar

Snellings, R. (2013). Solution-controlled dissolution of supplementary cementitious material glasses at pH 13: the effect of solution composition on glass dissolution rates. J. Am. Ceram. Soc. 96, 2467–2475. doi: 10.1111/jace.12480

CrossRef Full Text | Google Scholar

Tashima, M. M., Soriano, L., Payá, J., Monzó, J., and Borrachero, M. V. (2016). Assessment of pozzolanic/hydraulic reactivity of vitreous calcium aluminosilicate (VCAS). Mater. Des. 96, 424–430. doi: 10.1016/j.matdes.2016.02.036

CrossRef Full Text | Google Scholar

Thompson, L. M., and Stebbins, J. F. (2012). Non-stoichiometric non-bridging oxygens and five-coordinated aluminum in alkaline earth aluminosilicate glasses: effect of modifier cation size. J. Non Cryst. Solids 358, 1783–1789. doi: 10.1016/j.jnoncrysol.2012.05.022

CrossRef Full Text | Google Scholar

Verné, E., Vitale Brovarone, C., Moisescu, C., Ghisolfi, E., and Marmo, E. (2000). Coatings on Al2O3 by bioactive glass-ceramics. Acta Mater. 48, 4667–4671. doi: 10.1016/S1359-6454(00)00255-X

CrossRef Full Text | Google Scholar

Walkley, B., and Provis, J. L. (2019). Solid-state nuclear magnetic resonance spectroscopy of cements. Mater. Today Adv. 1:100007. doi: 10.1016/j.mtadv.2019.100007

CrossRef Full Text | Google Scholar

Warren, B. E., and Pincus, A. G. (1940). Atomic consideration of immiscibility in glass systems. J. Am. Ceram. Soc. 23, 301–304. doi: 10.1111/j.1151-2916.1940.tb14194.x

CrossRef Full Text | Google Scholar

Wu, S., Xia, L., Shi, B., and Wen, G. (2018). Microscopic scale evidence of phase transformation process in barium aluminosilicate glass-ceramic. J. Eur. Ceram. Soc. 38, 727–733. doi: 10.1016/j.jeurceramsoc.2017.09.025

CrossRef Full Text | Google Scholar