Screening Out Reactivity-Promoting Candidates for γ-Ca2SiO4 Carbonation by First-Principles Calculations

γ-Ca₂SiO₄ as a promising carbonation-activated cementitious material features an attractive capacity of carbon sequestration. Improving the carbonation reactivity of γ-Ca₂SiO₄ is of great significance for its practical application. In this paper, first-principles calculations are performed to single out the potential candidates for carbonation activation from a series of dopants. Electronic structure analyses reveal that the carbonation reactivity is related to the reactive site distribution and the binding strength of γ-Ca₂SiO₄ crystal. Ba, P, and F elements are found to decrease the overall binding strength of γ-Ca₂SiO₄ crystal, which benefits the dissolution of ions from the crystal to take part in the carbonation reactions. The theoretical conjectures are validated by designed and previous experiments, which confirms the first-principles-based method to effectively guide our experimental investigation.

Introduction

Exploiting effective ways to suppress the carbon dioxide level of the atmosphere is one of the most important scientific issues, which mainly includes two aspects: reducing carbon dioxide emissions and capturing carbon dioxide. Regarding the former, taking the cement industry as an example, the production of cement contributes about 7% of anthropogenic carbon dioxide emissions (Liu et al., 2015), mainly derived from the calcination and decomposition of limestone (one of the main raw minerals). The two main components of ordinary Portland cement clinker are β-dicalcium silicate (β-Ca₂SiO₄, also belite) and tricalcium silicate (Ca₃SiO₅, also alite). Belite has a lower Ca/Si ratio than alite and requires a lower calcination temperature, which means manufacturing belite causes less energy consumption and carbon dioxide emissions. Thus, in recent years, experts in the cement field have been pushing the use of high belite content cement (compared to the composition of ordinary Portland cement clinker) (Ludwig and Zhang, 2015). However, belite has a much lower hydration reactivity than alite leading to slower development of the early strength of concrete (Scrivener et al., 2015), making it difficult to meet the needs of most practical projects.

On the other hand, regarding capturing carbon dioxide, the use of geological minerals to sequestrate carbon dioxide has long been an attractive topic in geological science (Olajire, 2013). Olivine minerals such as fayalite (Fe₂SiO₄), forsterite (Mg₂SiO₄), etc. are widely investigated as the candidates for carbon sequestration (Olsson et al., 2012; Todd Schaef et al., 2012). The Fe and Mg ions in olivine can be substituted by Ca ions without destroying the symmetry of the crystal. The olivine Ca₂SiO₄ that belongs to the orthorhombic crystal system is also one of the polymorphs of belite (β-Ca₂SiO₄), known as γ-dicalcium silicate (γ-Ca₂SiO₄) (Naa et al., 2015). Previous studies have shown that among common olivine minerals, γ-Ca₂SiO₄ has a significantly dominant surface water absorption capacity (Kerisit et al., 2013), suggesting the potentially high carbonation reactivity. Besides, compared with the polymorph β-Ca₂SiO₄, γ-Ca₂SiO₄ also showed much higher carbonation reactivity (Chang et al., 2016). Mu et al. (2019) found that the γ-Ca₂SiO₄ samples exposed to a 100% carbon dioxide environment under high pressure achieved mechanical properties in hours equivalent to that of the hydration product of a cement clinker hydrated for days, which provides a perspective of using carbonation-activated cementitious materials to reduce the dependence on alite- and belite-based cementitious materials. Theoretically, the use of γ-Ca₂SiO₄ carbonation instead of cement clinker hydration not only reduces the carbon dioxide emissions from clinker production but also sequestrates the released carbon dioxide in a natural way, i.e., mineralization (Ashraf, 2016). However, the trace amount of carbon dioxide in the air does not allow γ-Ca₂SiO₄ to achieve a high degree of carbonation in a short time. Apart from the pre-carbonation process under carbon dioxide-rich conditions (Mu et al., 2018), the carbonation reactivity of γ-Ca₂SiO₄ needs to be improved. To this end, this article aims to select dopant ions that can theoretically increase the carbonation reactivity of γ-Ca₂SiO₄ through first-principles calculations.

Previous researches tried to reveal the carbonation mechanism of olivine minerals from the perspective of surface reactions. For example, Watson et al. (1997) studied the stability of seven low-index surfaces of forsterite and found that the (1 0 0) surface was the most stable one. De Leeuw et al. (2000) computed the associative and dissociative adsorption of water on the low-index surfaces of forsterite. They found that all surfaces, except the non-dipolar (1 0 0), were favorable for dissociative adsorption while the (1 0 0) surface was preferable for associative adsorption. Kerisit et al. (2013) revealed that calico-olivine (γ-Ca₂SiO₄) featured the largest adsorption energy (absolute value) among five olivine minerals, namely, forsterite, calico-olivine, tephroite, fayalite, and Co-olivine. These thermodynamic computations regarding the surface adsorption, dissolution, nucleation, and so on are conducive to understanding some steps of the carbonation process of olivine. However, they did not give a general indicator to predict the carbonation reactivity, and the performed thermodynamic calculations (like dissolution energy barrier) (Morrow et al., 2009) are too sophisticated to be used as indicators for singling out reactivity-promoting candidates from numerous dopant species. Herein, we are trying to find a simplified way to roughly give hints to our experiments for searching reactivity-promoting candidates for γ-Ca₂SiO₄ carbonation, which is actually like the machine learning using simple indicators to screen out potential materials for desirable properties. We first analyzed the electronic structures of γ-Ca₂SiO₄ to reveal the latent relationship between electronic structures and carbonation reactivity, based on which the potential influence of 10 kinds of doping ions on γ-Ca₂SiO₄ was estimated. Promising doping candidates were singled out, and the theoretical conjectures were verified by experiments.

Materials and Methods

The pristine γ-Ca₂SiO₄ crystal structure (Udagawa et al., 1980) was obtained from the inorganic crystal structure database (ICSD). The primary cell of γ-Ca₂SiO₄ contains 28 atoms (8 Ca, 4 Si, and 16 O atoms). To reduce the concentration of doped ions, a supercell of 2 × 1 × 2 was adopted as the matrix of doping models. We selected 10 common impurity ions of olivine as substituent ions: Mg, Sr, Ba, Al, Fe, Zn, P, F, Cl, and Br. As shown in Figure 1, according to the similarity of chemical properties, the anions F, Cl, and Br are supposed to replace the O ions in γ-Ca₂SiO₄, whereas the cations replace the Ca ions (Mg, Sr, Ba, Zn) or Si atoms (P). Since the Fe and Al ions can replace both the Ca ions and Si atoms as reported in previous researches (Manzano et al., 2011; Durgun et al., 2012), we calculated the two substitution methods for Fe and Al doping.

FIGURE 1

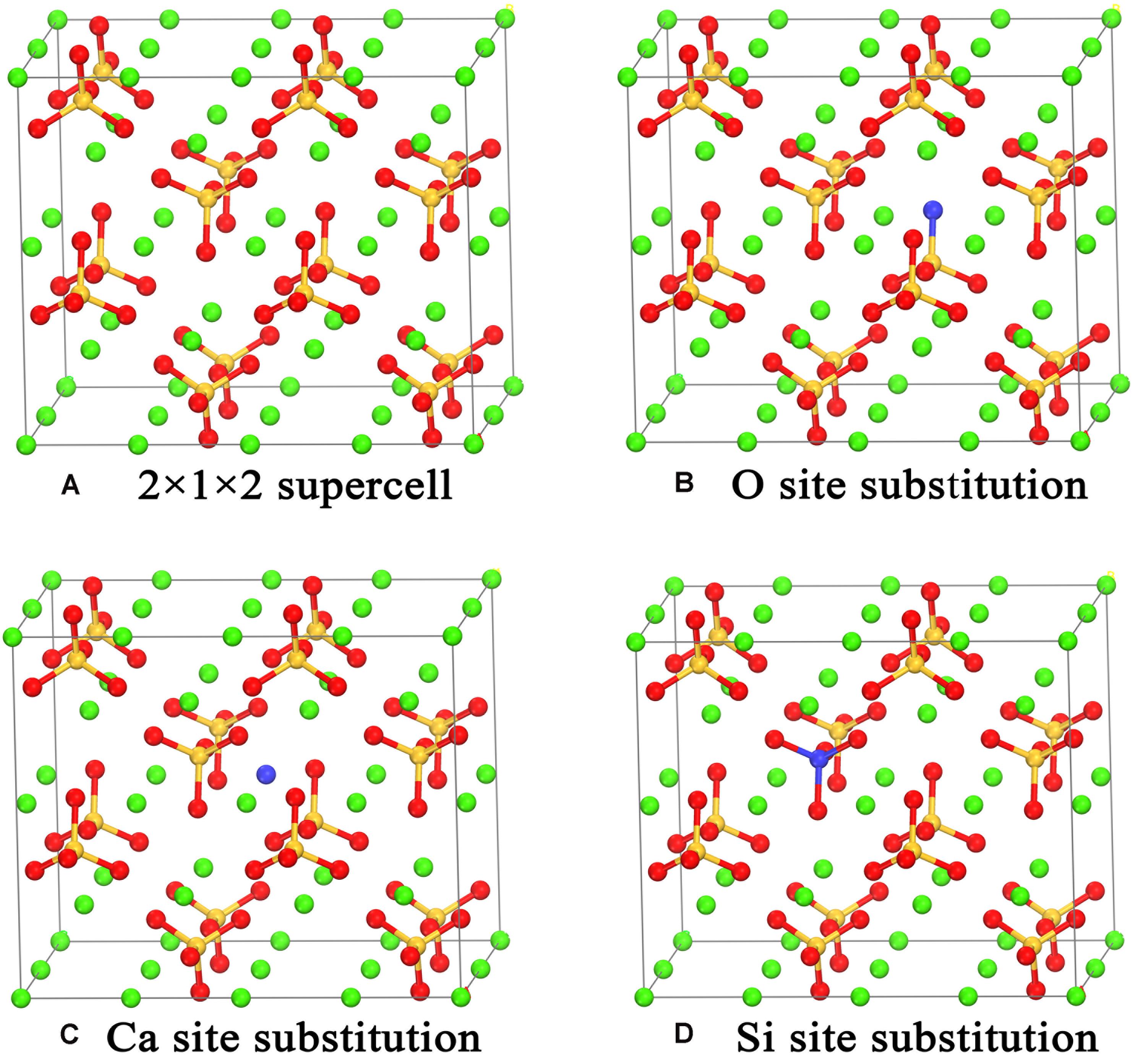
Figure 1. Crystal models of the pristine (A), O site substituted (B), Ca site substituted (C), and Si site substituted (D) γ-Ca₂SiO₄. The green, orange, and red spheres are Ca, Si, and O atoms, respectively. The blue spheres indicate the atom sites for different types of substitution.

The Vienna Ab initio Simulation Package (VASP) (Kresse and Furthmüller, 1996; Kresse, 1999) was used to optimize the crystal structure through energy minimization with the conjugate gradient method. The constructed models were continuously optimized until the energy differences and the force differences were less than 10^–5 eV/atom and 0.005 eV/Å, respectively. Then, the electronic structures were calculated and analyzed by the Cambridge Sequential Total Energy Package (CASTEP) (Clark et al., 2005). The exchange-correlation potential was estimated by the Perdew–Burke–Ernzerhof (PBE) method (Blöchl, 1994; Perdew et al., 1994) for both the VASP and CASTEP calculations. In addition, the projector augmented plane wave (PAW) method was implemented in the VASP calculation. A kinetic energy cutoff of 580 eV was adopted based on multiple tests as posted in the Supplementary Material S1. More computational details can be found in our previous studies (Tao et al., 2018a, 2019a).

To verify the doping effects on carbonation reactivity, corresponding experiments were implemented. γ-Ca₂SiO₄ was synthesized at 1400°C using the analytical reagent Ca(OH)₂ and SiO₂. Cationic dopants (Mg²⁺, Al³⁺, Ba²⁺, P⁵⁺) were introduced into the raw mix in the form of oxides while anionic dopant F^– was in the form of CaF₂. The dopant dosage was 2 mol% relative to the molar content of γ-Ca₂SiO₄ in the reference (undoped) group. The fabricated pure and doped specimens were ground into powders with a particle size smaller than 74 μm. For each group to be carbonated, 10 g of γ-Ca₂SiO₄ powder was mixed with 1.5 g water and compacted into cylindrical tablets, which were put into the carbon dioxide atmosphere (purity = 99.9%) for 3 days without extra pressure. We use the degree of carbonation (DOC) of γ-Ca₂SiO₄ to indicate the carbonation reactivity of different doping models. DOC was defined as

$$\text{DOC}=\frac{m_{real}}{m_{theo}}\times 100\%$$

where m_theo and m_real are the theoretically maximal and real uptake of CO₂ respectively. m_theo can be estimated by the carbonation reaction equation as follows:

$$C{a}_{2}Si{O}_4+2C{O}_2\stackrel{H_{2}O}{\to }2CaC{O}_3+Si{O}_2(gel)$$

The details about the materials preparation and testing procedures can be attained by consulting our previous study (Mu et al., 2018, 2019).

Results and Discussion

Electronic Structures of Pristine γ-Ca₂SiO₄

To understand the effects of doped ions on the carbonation reactivity of γ-Ca₂SiO₄, we first need to uncover the relationship between the electronic structures of the pure γ-Ca₂SiO₄ phase and its carbonation reactivity. Previous studies indicate that the carbonation reaction of γ-Ca₂SiO₄ requires water and involves the dissolution and migration of Ca ions from the crystal. Hence, mapping the reactive sites in the γ-Ca₂SiO₄ crystal and measuring the strength of the chemical bonds are essential for the analysis of carbonation reactivity. We calculated the energy band edge structures and bonding structures of γ-Ca₂SiO₄ as illustrated in Figures 2, 3. Figure 2A is the partial density of states (PDOS) and the total density of states (TDOS) of γ-Ca₂SiO₄. The dashed line locates the highest occupied molecule orbital of the system (known as the valence band maximum or VBM), which is also set as the position of relative Fermi level. The closest TDOS peak above the Fermi level implies the lowest unoccupied molecule orbital of the system (known as the conduction band minimum or CBM) (Parr and Yang, 1984; Chattaraj, 2009). The VBM and CBM are separated by a large energy band gap (about 4.2 eV) because the pure γ-Ca₂SiO₄ crystal is a typical insulator. The VBM is the most vulnerable part of the system to lose electrons. Therefore, those species whose atomic energy level contributes to the VBM are the areas in the system that are most vulnerable to an electrophilic attack, i.e., electrophilic reactive sites. Correspondingly, the CBM is the most vulnerable part of the system to accept electrons, pointing to the nucleophilic reactive sites of the system (Manzano et al., 2009; Wang et al., 2015). Figures 2B,C visualize the local charge density (LCD) distributions of pure γ-Ca₂SiO₄ at the VBM and CBM, respectively. The blue translucent electron clouds indicate the electrophilic and nucleophilic reactive sites of the system, respectively. The electrophilic reactive sites are almost entirely on O atoms, which is consistent with the result of the PDOS (left inset of Figure 2A) as the VBM is predominantly contributed by the O 2p state. In contrast, the nucleophilic reactive sites are the regions surrounded by Ca ions, which is also understandable because the CBM is mainly contributed by the 4s and 3d states of Ca atoms (right inset of Figure 2A).

FIGURE 2

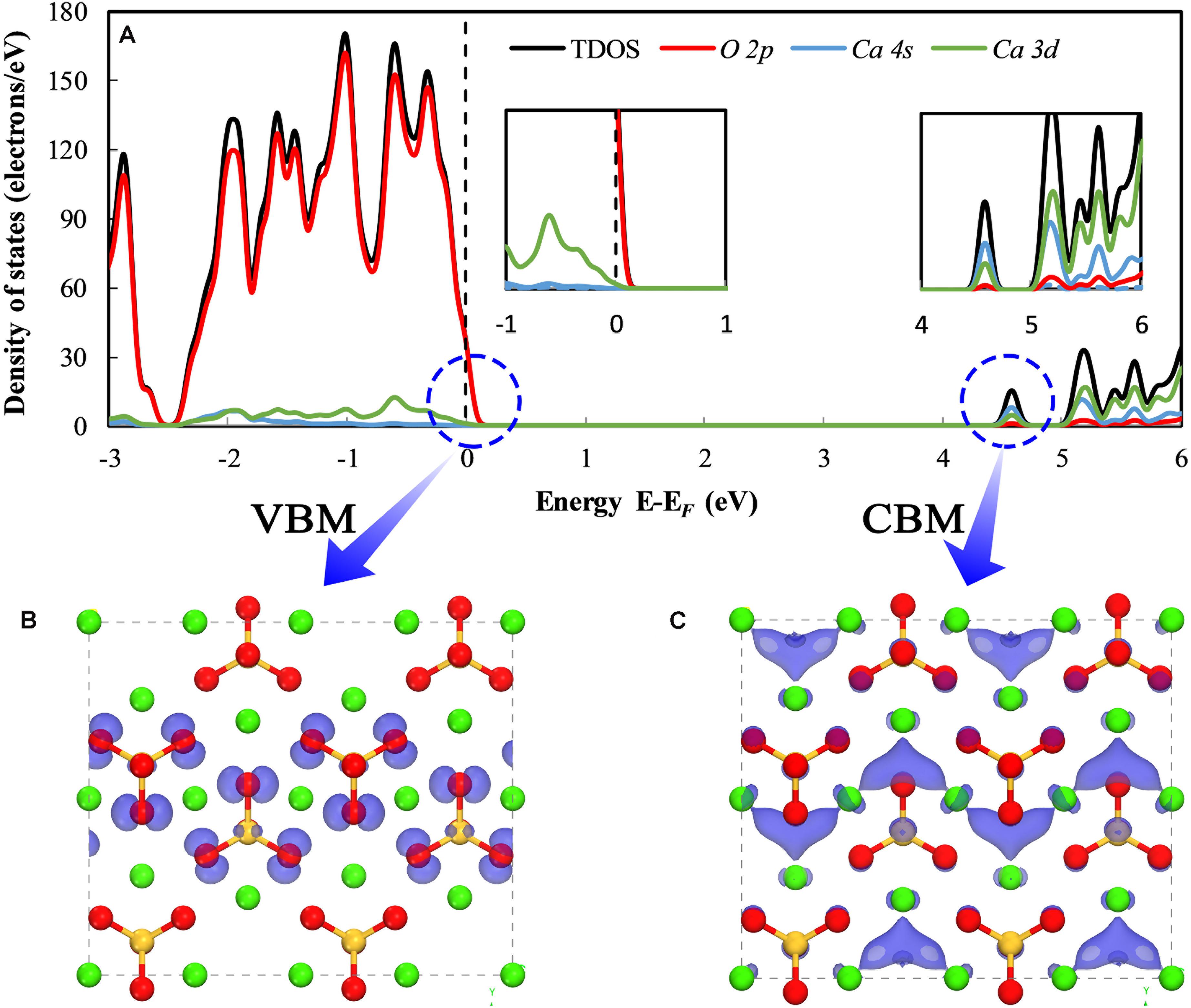
Figure 2. The density of states (A) and local charge density distribution of the valence band maximum (B) and conduction band minimum (C) of pure γ-Ca₂SiO₄. The green, orange, and red spheres are Ca, Si, and O atoms, respectively. The blue translucent electron clouds represent the orbitals of energy band edges.

FIGURE 3

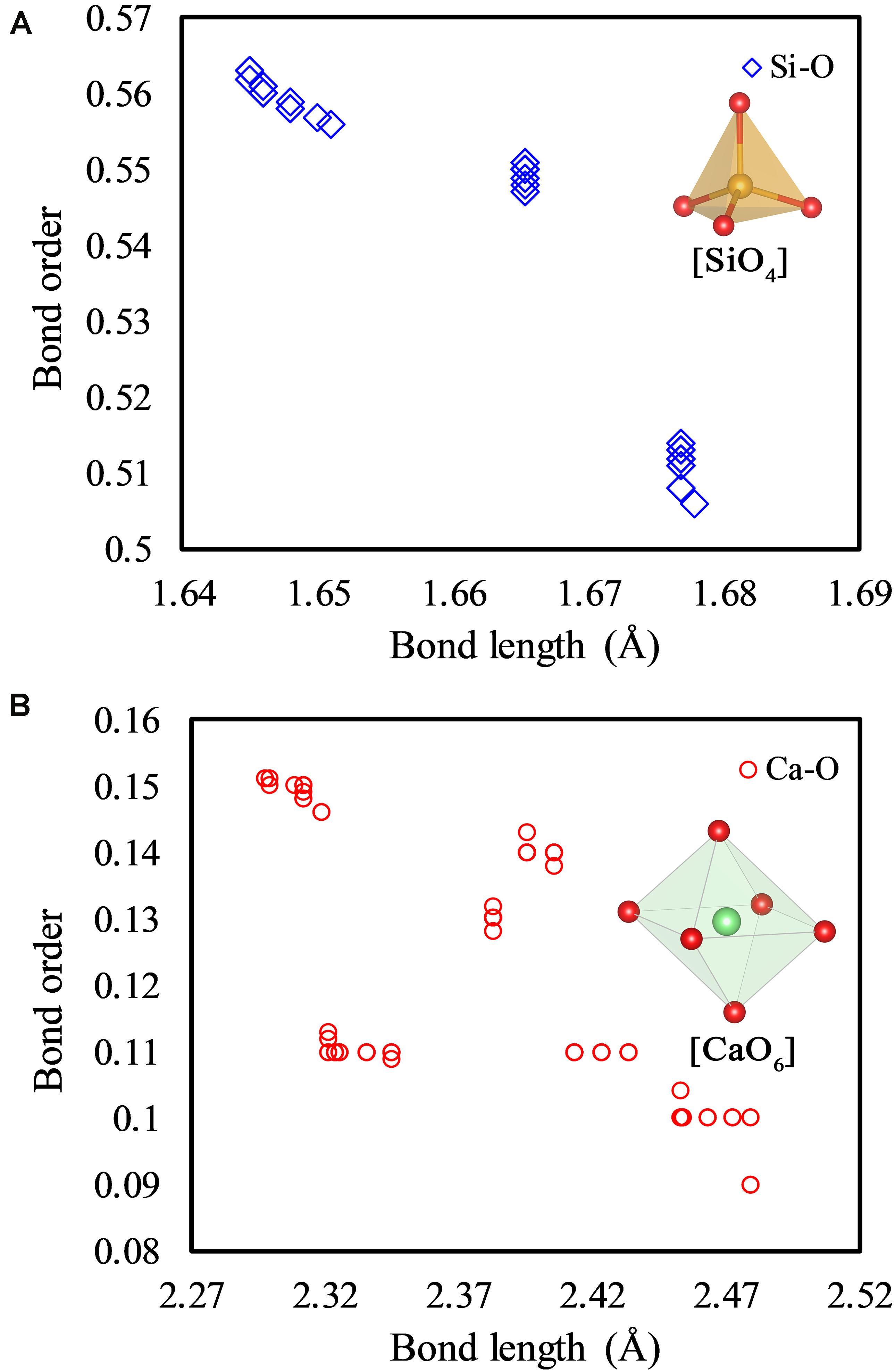
Figure 3. Bond order-bond length distribution of Si-O bonds (A) and Ca-O bonds (B) of the pure γ-Ca₂SiO₄ crystal. The coordination structures of the Si atom and Ca ion are illustrated in plots (A) and (B) respectively.

The local charge density distribution of the energy band edges (VBM and CBM) qualitatively visualized the reactive sites of the pure γ-Ca₂SiO₄ crystal, while the binding strength of ions in the system can be quantitatively estimated by the bond length (BL)–bond order (BO) analysis (Figure 3). The BO is obtained by calculating the degree of overlap of the electron cloud between two bonding atoms, which directly reflects the strength of the bond: the larger the BO, the stronger the bond (Dharmawardhana et al., 2013; Tao et al., 2018b). Therefore, the BO quantifies the difficulty of extracting ions from the crystal, which is related to the carbonation reactivity. It should be noted that there are a variety of methods of calculating the BO, and the Mulliken scheme (Mulliken, 1955) is adopted here. Although the absolute values of the BO calculated by different methods are different, it is reasonable to compare the relative magnitude of the BO calculated from the same system with the uniform method. The BL also indirectly maps the strength of chemical bonds, that is, the larger the bond length, the weaker the bond. Compared to the correlation of the BO and bond strength, the BL and bond strength are not strictly correlated. As shown in Figure 3A, the Si–O bonds in [SiO₄] tetrahedra are almost equal in length (around 1.66 Å), while their BO is clearly distinguished. The BL of Ca–O bonds varies widely from 2.31 to 2.48 Å, whereas their BO is around 0.12 (Figure 3B). Therefore, the BO is an effective indicator for measuring the binding strength of ions in a crystal, suggesting the difficulty of dissolving them from the crystal.

Reactivity Modification by Doping

Having revealed the correlation between the carbonation reactivity of pure γ-Ca₂SiO₄ and its electronic structures, we now can evaluate the doping effect on the carbonation reactivity by monitoring the changes in the electronic structures of the doped γ-Ca₂SiO₄. Figures 4, 5 depict the changes of LCD distribution of the VBM and CBM, indicating the electrophilic and nucleophilic reactive sites, respectively, as aforementioned. Compared with the undoped γ-Ca₂SiO₄ in Figures 2B,C, the anionic substitution (F, Cl, Br) significantly changes the electrophilic reactive site distribution (VBM). It is mainly because the substitution of F, Cl, or Br for O changes the effective charge of O ions, causing the shift of the original electrophilic reactive sites from O ions. For the Fe doping, both the electrophilic and nucleophilic reactive sites shifted from O ions and the Ca-blocked regions to the vicinity of Fe impurity. Previous studies have explained that this is due to the strong delocalization of the Fe 3d electron shell, almost spanning the Fermi level, which can lose or accept electrons easily (Tao et al., 2019b). Therefore, Fe ions become the new electrophilic and nucleophilic reactive center of the system. The substitution of Mg, Sr, and Ba for Ca causes less influence on the reactive sites as they come from the same family, namely the IIA group, sharing a similar valence electron structure. Compared with the diffuse distribution of reactive sites in the pure γ-Ca₂SiO₄, a slight local enhancement of some reactive sites (forming reactive center) is conducive to improving the overall reactivity. However, too strong localization of the reactive sites results in a significant decrease in the number of reactive sites, thereby reducing the overall reactivity. The difficulty lies in how to quantitatively measure the weight of these two aspects.

FIGURE 4

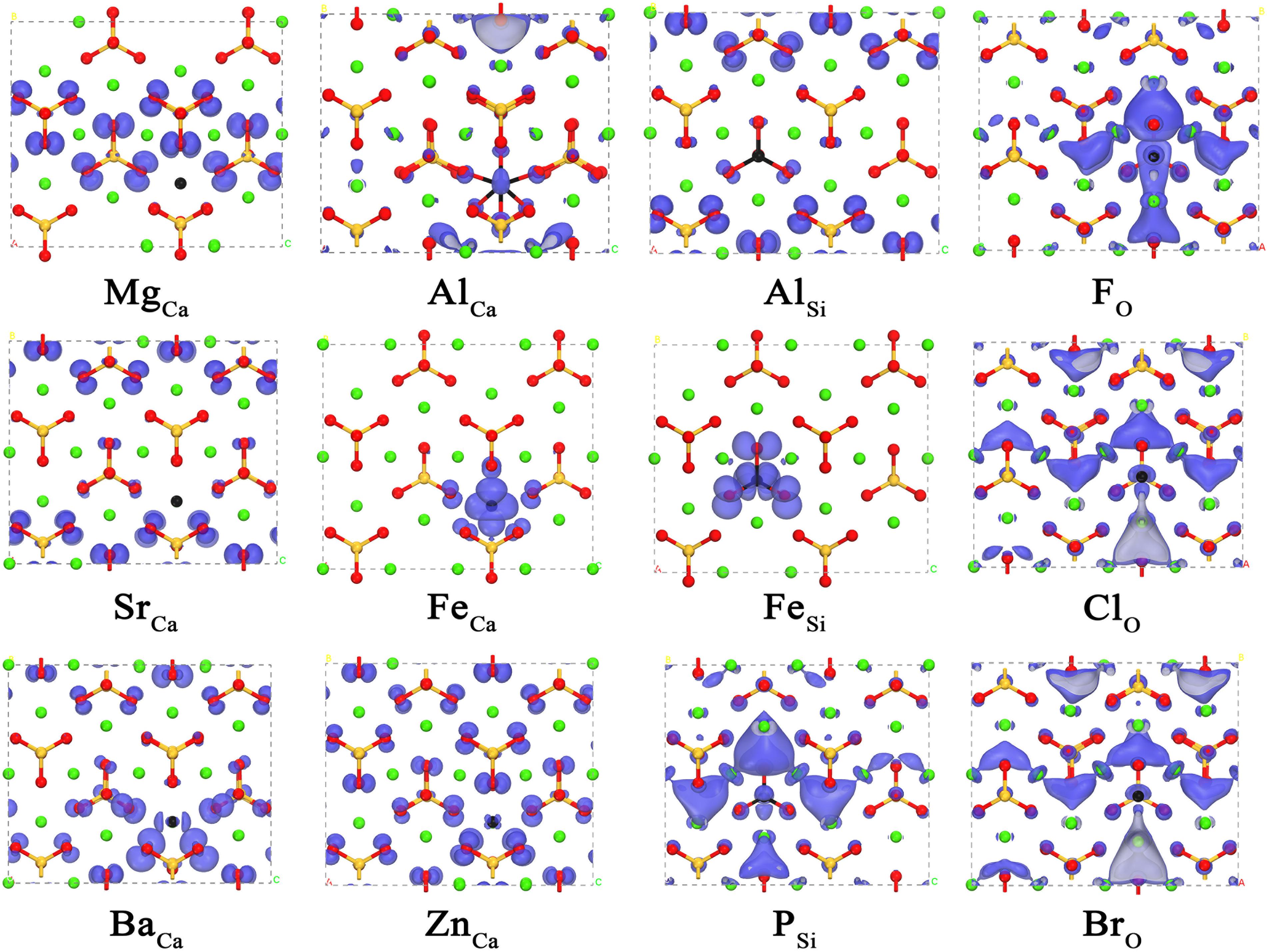
Figure 4. The local charge density distribution of the valence band maximum of doped γ-Ca₂SiO₄ crystals. The green, orange, red, and black spheres are Ca, Si, O, and dopant atoms, respectively.

FIGURE 5

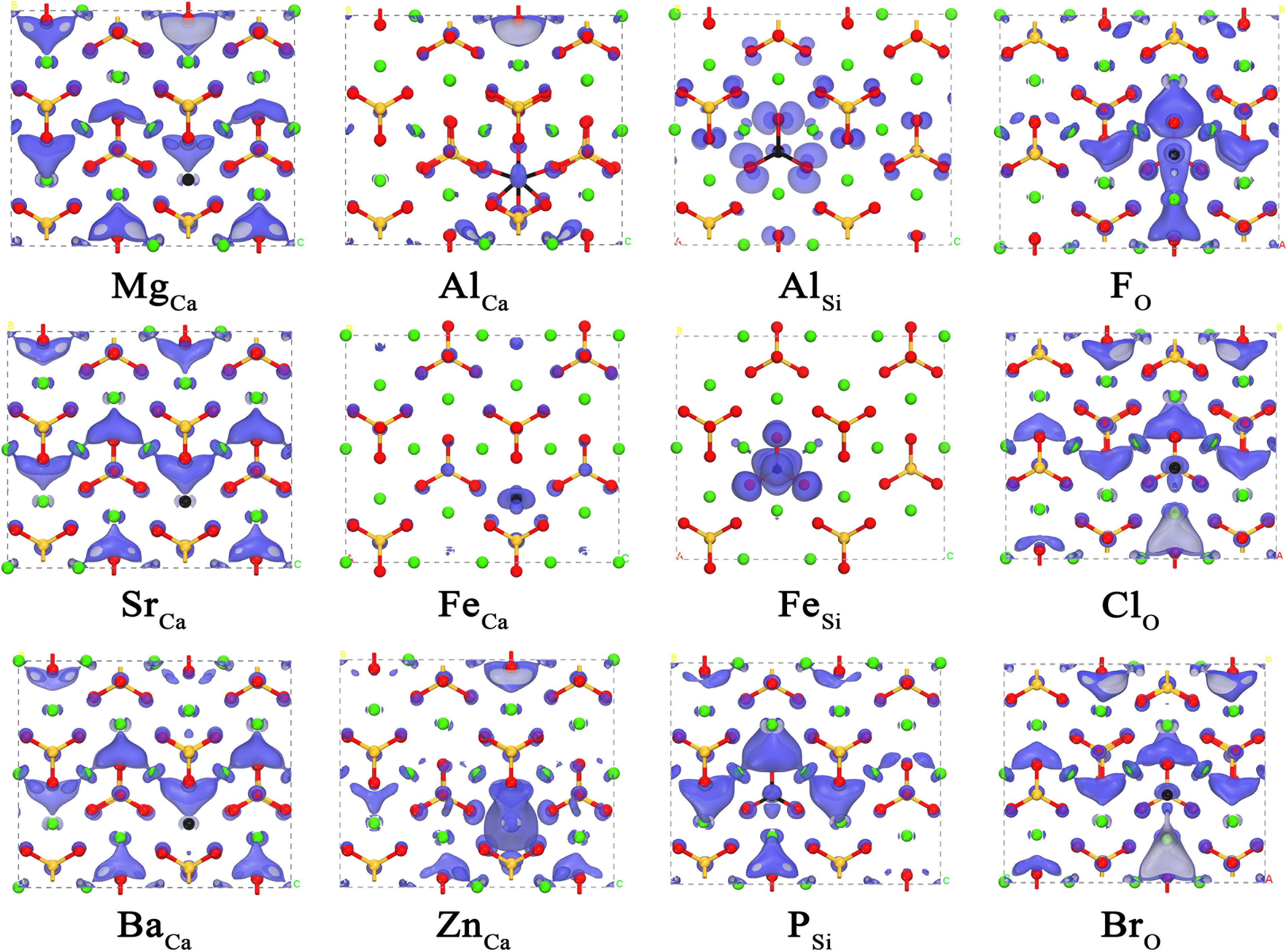
Figure 5. The local charge density distribution of the conduction band minimum of doped γ-Ca₂SiO₄ crystals. The green, orange, red, and black spheres are Ca, Si, O, and dopant atoms, respectively.

As discussed in the analysis of pure γ-Ca₂SiO₄, the BO can map the potential reactivity of ions from the perspective of their binding strength in the system, which is an easy method to quantify. Therefore, we calculated the BO of Si–O and Ca–O bonds for different doping models and used the changes in the total bond order density (TBOD) to evaluate the doping effect (Dharmawardhana et al., 2016):

$$TBOD=\sum _i^{N}B(i)/V$$

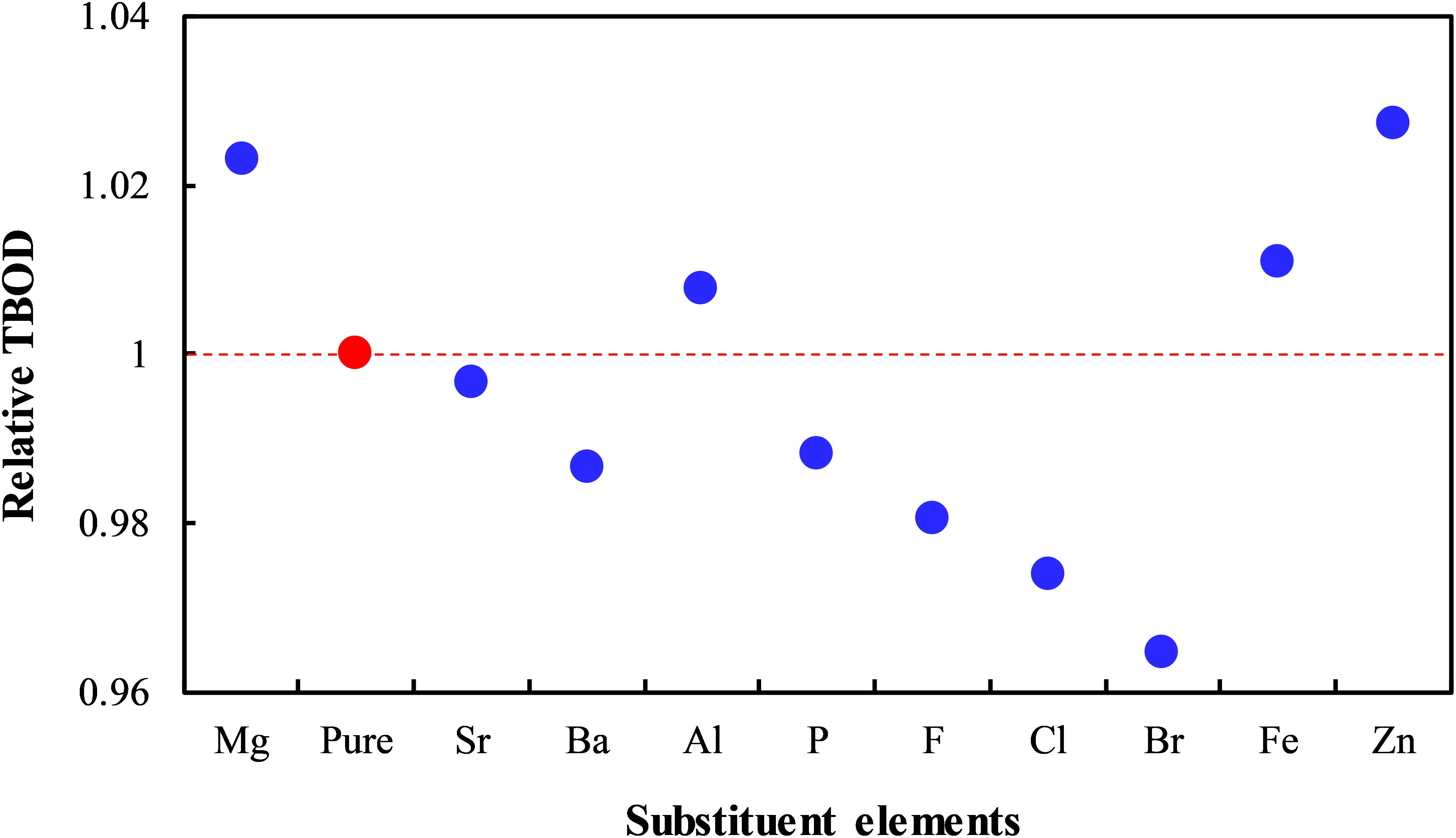
where N is the number of bonds in the model and B(i) is the bond order of the i^th bond. V is the crystal volume. Figure 6 shows the changes in the TBOD for different doped systems compared to the pure γ-Ca₂SiO₄. The TBOD of pure γ-Ca₂SiO₄ as a reference (set to unity) is marked in red in the figure. The tabulated data of the TBOD can be found in Supplementary Material S2. It should be noted that for the Al and Fe doping, the TBOD is an average of the two substitution schemes, that is, an arithmetic average of the TBOD of Ca site and Si site substitutions. The TBOD comprehensively considers the doping effect on Si–O and Ca–O bonds and the crystal volume. The smaller the TBOD, the weaker the overall binding strength of the system, and the more likely the crystal is to decompose by ion attacks, implying the potentially high carbonation reactivity. In this regard, it can be observed that some ion doping (Ba, P, F, Cl, Br) is conducive to improving the reactivity of γ-Ca₂SiO₄, whereas some ions (Mg, Al, Fe, Zn) induce the opposite effect, and the rest (Sr) causes negligible influence. The theoretical reasoning is tested by experiments discussed in the following section.

FIGURE 6

Figure 6. Total bond order density of the doped γ-Ca₂SiO₄ crystals relative to the pure γ-Ca₂SiO₄.

Experimental Verification

In order to verify the theoretical prediction of the doping effect based on the TBOD analysis, we experimentally tested the carbonation reactivity of different ion-doped systems. Due to the limitation of experimental conditions, here we only conducted tests for some representative ions: Mg, Al, Ba, P, and F. Figure 7 compares the carbonation degree of γ-Ca₂SiO₄ with five different ion-doping schemes. Comparing Figure 7 with Figure 6, our theoretical predictions are generally consistent with the experimental results. The theoretically predicted reactivity promoting ions Ba, P, and F indeed accelerated the γ-Ca₂SiO₄ carbonation, and the predicted reactivity inhibiting ions Mg and Al retarded the carbonation reaction. Moreover, Mu et al. (2018) studied in detail the Ba doping effect on the carbonation reactivity of γ-Ca₂SiO₄. They found that Ba doping significantly increased the carbonation degree of γ-Ca₂SiO₄. Although Mu and colleagues speculated from the macroscopic point of view that Ba doping modifies the surface structure, which improves carbon dioxide penetration, our calculations provide a different perspective from the electronic structure modification: Ba doping reduces the overall binding strength of γ-Ca₂SiO₄ crystal, making ions easier to dissolve and participate in the carbonation reaction. Therefore, based on our and previous experimental verifications, the theoretical method we proposed is effective to give qualitatively reliable results, which expedites exploring the activation methods of γ-Ca₂SiO₄ carbonation.

FIGURE 7

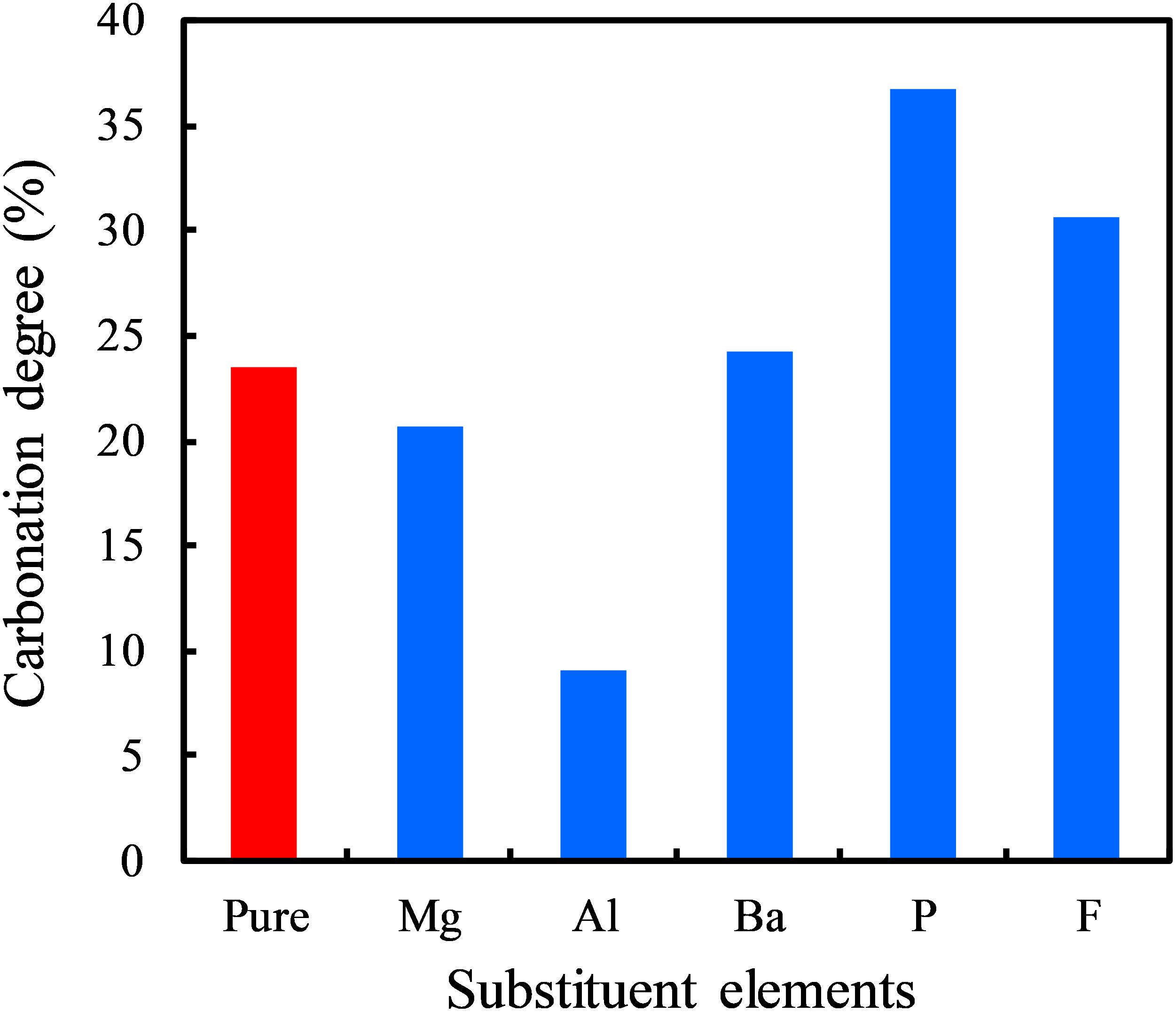
Figure 7. Carbonation degree of γ-Ca₂SiO₄ specimens in 3 days under normal pressure with different doping schemes.

Conclusion

In this paper, the potential relationship between the carbonation reactivity of γ-Ca₂SiO₄ and its electronic structures is investigated by the first-principles calculations. By monitoring the changes in the electronic structures of γ-Ca₂SiO₄ by different doping schemes, the candidates for reactivity promotion are screened out and validated by experiments. If the carbonation reaction of γ-Ca₂SiO₄ is regarded as a typical ion attack reaction, the electrophilic reactive sites of γ-Ca₂SiO₄ are the O ions while the nucleophilic reactive sites are the Ca-blocked regions. Anionic doping strikingly changes the electrophilic reactive sites, whereas the ionic substitutions that happened within the same main group scarcely modify the reactive site distribution. Doping also changes the binding strength of ions in γ-Ca₂SiO₄ crystals, which affects the dissolution rate of ions in the carbonation reactions. For this reason, the total bond order density was proposed as an indicator to estimate the changes in binding strength to further predict the effect of different ion doping on the γ-Ca₂SiO₄ carbonation reactivity. This theoretical study provides novel perspectives of the carbonation reactivity of γ-Ca₂SiO₄ and accelerates the experimental modification of γ-Ca₂SiO₄.

Data Availability Statement

All datasets generated for this study are included in the article/Supplementary Material.

Author Contributions

YT designed and performed the research and wrote the manuscript. YM performed the experimental part of the research. WZ and FW discussed and analyzed the data. All authors contributed to the article and approved the submitted version.

Funding

This research was supported by the National Key R&D Program of China (grant number 2016YFB0303501); National Natural Science Foundation of China (grant number 51872216); and China Scholarship Council (201906950033).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2020.00299/full#supplementary-material

References

Ashraf, W. (2016). Carbonation of cement-based materials: challenges and opportunities. Constr. Build. Mater. 120, 558–570. doi: 10.1016/j.conbuildmat.2016.05.080

CrossRef Full Text | Google Scholar

Blöchl, P. E. (1994). Projector augmented-wave method. Phys. Rev. B 50, 17953–17979. doi: 10.1103/physrevb.50.17953

PubMed Abstract | CrossRef Full Text | Google Scholar

Chang, J., Fang, Y., and Shang, X. (2016). The role of β-C2S and γ-C2S in carbon capture and strength development. Mater. Struct. 49, 4417–4424. doi: 10.1617/s11527-016-0797-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Chattaraj, P. K. (2009). Chemical Reactivity Theory: A Density Functional View, 1st Edn. Boca Raton: CRC Press.

Google Scholar

Clark, S. J., Segall, M. D., Pickard, C. J., Hasnip, P. J., Probert, M. I. J., Refson, K., et al. (2005). First principles methods using CASTEP. Z. Krist. 220, 567–570.

Google Scholar

De Leeuw, N., Parker, S., Catlow, C., and Price, G. (2000). Modelling the effect of water on the surface structure and stability of forsterite. Phys. Chem. Miner. 27, 332–341. doi: 10.1007/s002690050262

CrossRef Full Text | Google Scholar

Dharmawardhana, C., Bakare, M., Misra, A., and Ching, W.-Y. (2016). Nature of interatomic bonding in controlling the mechanical properties of calcium silicate hydrates. J. Am. Ceram Soc. 99, 2120–2130. doi: 10.1111/jace.14214

CrossRef Full Text | Google Scholar

Dharmawardhana, C. C., Misra, A., Aryal, S., Rulis, P., and Ching, W. Y. (2013). Role of interatomic bonding in the mechanical anisotropy and interlayer cohesion of CSH crystals. Cem. Concr. Res. 52, 123–130. doi: 10.1016/j.cemconres.2013.05.009

CrossRef Full Text | Google Scholar

Durgun, E., Manzano, H., Pellenq, R. J. M., and Grossman, J. C. (2012). Understanding and controlling the reactivity of the calcium silicate phases from first principles. Chem. Mater. 24, 1262–1267. doi: 10.1021/cm203127m

CrossRef Full Text | Google Scholar

Kerisit, S., Bylaska, E. J., and Felmy, A. R. (2013). Water and carbon dioxide adsorption at olivine surfaces. Chem. Geol. 59, 81–89. doi: 10.1016/j.chemgeo.2013.10.004

CrossRef Full Text | Google Scholar

Kresse, G. (1999). From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775. doi: 10.1103/physrevb.59.1758

CrossRef Full Text | Google Scholar

Kresse, G., and Furthmüller, J. (1996). Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50. doi: 10.1016/0927-0256(96)00008-0

CrossRef Full Text | Google Scholar

Liu, Z., Guan, D., Wei, W., Davis, S. J., Ciais, P., Bai, J., et al. (2015). Reduced carbon emission estimates from fossil fuel combustion and cement production in China. Nature 524, 335–338. doi: 10.1038/nature14677

PubMed Abstract | CrossRef Full Text | Google Scholar

Ludwig, H.-M., and Zhang, W. (2015). Research review of cement clinker chemistry. Cem. Concr. Res. 8, 24–37. doi: 10.1016/j.cemconres.2015.05.018

CrossRef Full Text | Google Scholar

Manzano, H., Dolado, J. S., and Ayuela, A. (2009). Structural, mechanical, and reactivity properties of tricalcium aluminate using first-principles calculations. J. Am. Ceram Soc. 92, 897–902. doi: 10.1111/j.1551-2916.2009.02963.x

CrossRef Full Text | Google Scholar

Manzano, H., Durgun, E., Abdolhosseine Qomi, M. J., Ulm, F.-J., Pellenq, R. J. M., and Grossman, J. C. (2011). Impact of chemical impurities on the crystalline cement clinker phases determined by atomistic simulations. Cryst. Growth Des. 11, 2964–2972. doi: 10.1021/cg200212c

CrossRef Full Text | Google Scholar

Morrow, C. P., Kubicki, J. D., Mueller, K. T., and Cole, D. R. (2009). Description of Mg2+ release from forsterite using Ab initio Methods†. J. Phys. Chem. C 114, 5417–5428. doi: 10.1021/jp9057719

CrossRef Full Text | Google Scholar

Mu, Y., Liu, Z., and Wang, F. (2019). Comparative study on the carbonation-activated calcium silicates as sustainable binders: reactivity, mechanical performance, and microstructure. ACS Sust. Chem. Eng. 7, 7058–7070. doi: 10.1021/acssuschemeng.8b06841

CrossRef Full Text | Google Scholar

Mu, Y., Liu, Z., Wang, F., and Huang, X. (2018). Effect of barium doping on carbonation behavior of γ-C2S. J. CO2 Utiliz. 27, 405–413. doi: 10.1016/j.jcou.2018.08.018

CrossRef Full Text | Google Scholar

Mulliken, R. S. (1955). Electronic population analysis on LCAO–MO molecular wave functions. I. J. Chem. Phys. 23, 1833–1840. doi: 10.1063/1.1740588

CrossRef Full Text | Google Scholar

Naa, S., Kangb, S., Leeb, S., and Songa, M. (2015). Gamma-C2S synthesis from Fly ash of fluidize-bed boiler for CO2 capture. Acta Phys. Polon. A 127, 1282–1285. doi: 10.12693/aphyspola.127.1282

CrossRef Full Text | Google Scholar

Olajire, A. A. (2013). A review of mineral carbonation technology in sequestration of CO2. J. Petrol. Sci. Eng. 109, 364–392. doi: 10.1016/j.petrol.2013.03.013

CrossRef Full Text | Google Scholar

Olsson, J., Bovet, N., Makovicky, E., Bechgaard, K., Balogh, Z., and Stipp, S. L. S. (2012). Olivine reactivity with CO2 and H2O on a microscale: Implications for carbon sequestration. Geochim. Cosmochim. Acta 77, 86–97. doi: 10.1016/j.gca.2011.11.001

CrossRef Full Text | Google Scholar

Parr, R. G., and Yang, W. (1984). Density functional approach to the frontier-electron theory of chemical reactivity. J. Am. Chem. Soc. 106, 4049–4050. doi: 10.1021/ja00326a036

CrossRef Full Text | Google Scholar

Perdew, J. P., Burke, K., and Ernzerhof, M. (1994). Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868. doi: 10.1103/physrevlett.77.3865

PubMed Abstract | CrossRef Full Text | Google Scholar

Scrivener, K. L., Juilland, P., and Monteiro, P. J. M. (2015). Advances in understanding hydration of portland cement. Cem. Concr. Res. 78, 38–56. doi: 10.1016/j.cemconres.2015.05.025

CrossRef Full Text | Google Scholar

Tao, Y., Li, N., Zhang, W., Wang, F., and Hu, S. (2019a). Understanding the zinc incorporation into silicate clinker during waste co-disposal of cement kiln: a density functional theory study. J. Cleaner Prod. 232, 329–336. doi: 10.1016/j.jclepro.2019.05.078

CrossRef Full Text | Google Scholar

Tao, Y., Zhang, W., Li, N., Wang, F., and Hu, S. (2019b). Predicting hydration reactivity of Cu-doped clinker crystals by capturing electronic structure modification. ACS Sust. Chem. Eng. 7, 6412–6421. doi: 10.1021/acssuschemeng.9b00327

CrossRef Full Text | Google Scholar

Tao, Y., Zhang, W., Li, N., Shang, D., Xia, Z., and Wang, F. (2018a). Fundamental principles that govern the copper doping behavior in complex clinker system. J. Am. Ceram Soc. 101, 2527–2536. doi: 10.1111/jace.15393

CrossRef Full Text | Google Scholar

Tao, Y., Zhang, W., Shang, D., Xia, Z., Li, N., Ching, W.-Y., et al. (2018b). Comprehending the occupying preference of manganese substitution in crystalline cement clinker phases: a theoretical study. Cem. Concr. Res. 109, 19–29. doi: 10.1016/j.cemconres.2018.04.003

CrossRef Full Text | Google Scholar

Todd Schaef, H., McGrail, B. P., Loring, J. L., Bowden, M. E., Arey, B. W., and Rosso, K. M. (2012). Forsterite [Mg2SiO4)] carbonation in wet supercritical CO2: an in situ high-pressure X-ray diffraction study. Environ. Sci. Technol. 47, 174–181. doi: 10.1021/es301126f

PubMed Abstract | CrossRef Full Text | Google Scholar

Udagawa, S., Urabe, K., Natsume, M., and Yano, T. (1980). Refinement of the crystal structure of γ-Ca2SiO4. Cem. Concr. Res. 10, 139–144. doi: 10.1016/0008-8846(80)90070-8

CrossRef Full Text | Google Scholar

Wang, Q., Manzano, H., Guo, Y., Lopez-Arbeloa, I., and Shen, X. (2015). Hydration mechanism of reactive and passive dicalcium silicate polymorphs from molecular simulations. J. Phys. Chem. C 119, 19869–19875. doi: 10.1021/acs.jpcc.5b05257

CrossRef Full Text | Google Scholar

Watson, G., Oliver, P., and Parker, S. (1997). Computer simulation of the structure and stability of forsterite surfaces. Phys. Chem. Miner. 25, 70–78. doi: 10.1007/s002690050088

CrossRef Full Text | Google Scholar