Internal Damage Identification of Sandwich Panels With Truss Core Through Dynamic Properties and Deep Learning

Introduction

Structural safety and integrity cannot be overemphasized because a catastrophic structural failure may result in a significant loss of human life and wealth. Also, a more complicated service environment may bring about additional problems (Lai, 2019; Lai et al., 2019a,b). Sandwich structures with truss core (SPTCs) have been increasingly applied in industrial sectors, such as in ships, aircraft, civil engineering, and aerospace engineering (Hg, 1969; Chiras et al., 2002; Wadley et al., 2003). The lightweight cellular core can be in the form of a stochastic foam, a periodic honeycomb, a corrugated sheet, or a lattice truss (He et al., 2014; Liu et al., 2014). During the manufacturing process or during service, damage or defects are inevitable, such as buckling of the panel (Yuan et al., 2014, 2015), breakage of the truss, burn-through of the face sheets, or truss nodes that are not bound to the face sheet. Different damage features (style, extent, and location) have different influences on the structural vibration properties (Lou et al., 2014). Compared with traditional structure styles, such as beams or plates, internal damage identification of SPTCs is more difficult:

1) Internal damage, such as unbound nodes, is shielded by the face sheets, which hinders direct visible inspection, so a vibration-based identification method may be an important choice.

2) There is a wealth of damage features that vary in damage type, location, extent, and their combinations; these can, in turn, affect the structural vibration behavior.

3) Damage identification can be classified into inversion problems, and the solutions may be non-unique.

4) The final process of damage identification relies on human judgment, which is time-consuming and subjective.

In the literature, some methods have been proposed for the detection and localization of damage in sandwich structures. For surface cracks in composite laminates, Hu et al. (2006) proposed a strain-energy method to identify the surface crack location. The results revealed that the method could identify the location of the damage successfully. For honeycomb sandwich plates, Andrzej (2014) proposed a vibration-based non-destructive testing method with a post-processing algorithm based on wavelet analysis. The results revealed that different types of damage could be detected and localized accurately. For composite SPTCs, Li et al. (2015) proposed a baseline-free damage localization method based on uniform load surface curvature, a gapped smoothing method, and the Teager energy operator to detect truss bar damage. Lu et al. (2017a) proposed a damage identification method based on a flexural matrix of metallic SPTCs. Subsequently, an improved method was also developed to identify damage to unbounded nodes (Lu et al., 2017b). Seguel and Meruane (2018) proposed four damage indices, including mode shape curvatures, uniform load surface, modal strain energy, and gapped smoothing, to evaluate the debonding damage of an aluminum honeycomb sandwich panel. Sikdar et al. (2018) proposed an acoustic emission-based real-time health monitoring framework to efficiently identify the probable damage in sandwich composite structures. Zhu et al. (2016) proposed a torsional guided wave method to detect debonding damage in honeycomb sandwich beams. Klepka et al. (2013) used non-linear acoustics to detect impact damage in a composite chiral sandwich panel. High-frequency ultrasonic excitation and low-frequency model excitation were used to observe non-linear modulations in ultrasonic waves due to structural damage.

Most of these studies could detect and locate the damage accurately, but fewer studies have discussed quantification of the extent of damage (Kumar et al., 2009; Zhu et al., 2014; Khan et al., 2019). To detect the extent of damage more accurately, some intelligent techniques, such as a genetic algorithm (GA) or convolutional neural networks (CNNs), have been combined with traditional vibration-based methods or other methods (Zhu et al., 2014; Khan et al., 2019). In these studies, damage at different locations and of different extents are considered. Kumar et al. (2009) presented a model strain-energy two-step method for a composite sandwich beam. This method can identify both the location and extent of damage in the faces and the core. Using the frequency response function (FRF), Zhu et al. (2014) proposed a non-destructive evaluation method to identify debonding in a honeycomb sandwich beam. By combining this with a GA, the method could determine both damage location and size. When detecting damage in large structures, the method cannot effectively identify small debonding, which has little influence on the low-frequency range of an FRF. Khan et al. (2019) proposed a CNN-based approach for the classification and prediction of various types of in-plane and through-the-thickness delamination in smart composite laminates by using structural vibration information.

With the capacity of massive data processing, data mining, and fast training through the deep architecture of neural networks, machine learning gives an objective solution with quantitative accuracy. Chen and Jahanshahi (2018) proposed a deep learning (DL) framework to analyze individual video frames for crack detection. The proposed framework achieves a 98.3% hit rate. Cha et al. (2017) proposed a vision-based method by using the deep architecture of a CNN for detecting cracks in concrete. The trained CNN was combined with a sliding window technique to scan any image size. The results indicate that the proposed method performs well in finding cracks in concrete in realistic situations. Zhang et al. (2016) used deep CNN to detect cracks in roads. The training images were obtained by means of a low-cost smart mobile phone, demonstrating that DL has the potential to be applied in practical damage identification. Pathirage et al. (2018) proposed an autoencoder-based framework for damage identification, which could support deep neural networks and which could be used to obtain optimal solutions for pattern recognition problems of a highly non-linear nature. The method was applied on steel-frame structures. Guo et al. (2020) presented a DL-based method that extracts the damage features from mode shapes without utilizing any hand-engineered feature or prior knowledge. Datasets based on numerical simulations, along with two datasets based on laboratory measurements, were used. Zhang et al. (2020) used machine vision and DL for structural health monitoring by focusing on detecting bolt loosening. A dataset that contains 300 images was used. Huang et al. (2020) proposed a CNN-based method for detection of surface damage to a steel wire rope (SWR). In this work, only two different types of SWR surface defects were investigated. In this study, the authors mentioned that it is necessary to combine the method with other imaging techniques to detect SWR inner damage. Liu et al. (2020) reported that a novel damage identification framework was established in this study by integrating massive datasets constructed by structural transmissibility functions and a DL strategy based on one-dimensional convolutional neural networks (1D-CNNs). Avci et al. (2017) used 1D-CNNs to automatically extract damage-sensitive features from the raw acceleration signals and presented the preliminary experiments that were conducted to verify the proposed method.

Previous studies often dealt with damage to the structural surface that could be captured by a camera or that used the structural raw displacement or acceleration data captured in experiments directly as the input data. However, for SPTCs, the weakest part is the low-density truss core, and the inside damage is covered by the face sheets and cannot be directly detected in photographs. Also, compared with plates or beams, SPTCs consist of two face sheets and a truss core, meaning that the raw response data hardly reflect the structural damage information. Therefore, vibration-based methods, which involve many forms of damage indices that could reflect both the surface and internal damage, could be used in combination with DL for structural damage identification in SPTCs.

This work incorporates a DL technique with a vibration-based method to detect internal damage to SPTCs. Unlike previous studies, which used surface photographs or raw data as the DL training dataset, we construct a dataset by using damage indices instead of raw data. An analytical model is then used to obtain massive raw structural data, which are verified by experiments. Then two damage indices, one with a baseline and the other without a baseline, are used to construct the input to the neural networks. The effectiveness of the method is evaluated according to the accuracy of damage location and extent identification.

Construction of the Dataset

Outline of the Construction Process

Obtaining more data is always the best way to make a neural network model generalize better, although the amount of data is usually limited in practice. In this study, a vibration analytical model with random damage features, described previously by the authors (Lu et al., 2017c), was used to generate the raw data. Experiments were carried out to verify the proposed model. Two damage indices were applied to extract the internal damage features. Finally, the input dataset, including massive and diverse samples, was built.

SPTC Specimens

A sketch of the pyramidal SPTC model being simulated is provided in Figure 1. The SPTC is made of stainless steel. The boundary condition for the SPTC is fully clamped (CCCC). The unit cell of the pyramidal truss is shown in Figure 1B. The thickness of the face sheets is 1 mm. Parameter L_x is equal to L_y, which is 11.312 mm. There are 15 cells along the x- and y-directions, respectively. The details of the model are given in Table 1.

FIGURE 1

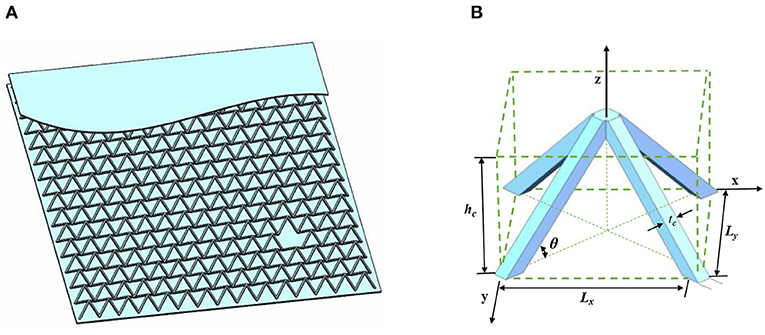
Figure 1. Model information of sandwich panel with truss core (SPTC). (A) A damaged SPTC model. (B) A unit cell of a pyramidal truss.

TABLE 1

Table 1. Material properties and geometrical information.

In the damage identification process, three types of damage features are considered, including damage location, damage style, and damage extent, denoted as D_L, D_S, and D_E, respectively. In this study, D_S, that is, cell missing damage, is used to simulate structural damage, which is a typical form of damage for SPTCs. Four D_E values are considered, including half-cell missing (HCM), one cell missing (OCM), two cells missing (TCM), and four cells missing (FCM). To consider all possible damage distributions, the parameter D_L is set as a random number, with its position inside the sandwich panels.

Analytical Models With Random Damage Features

The training dataset is often obtained through real videos or images. However, information from videos or images is normally very limited and cannot cover all possible damage features. In addition, for SPTCs, only the surface information can be obtained by videos or images, which does not reflect the internal damage features of SPTCs. Therefore, in this study, analytical models with random damage features, verified by experiments, are used as they are able to consider all possible damage features.

Analytical Models

To build the rich dataset, two kinds of analytical models are presented. For single-damage cases, a step-by-step analytical model is proposed. In the model, for a given D_E and D_S, D_L moves step by step until all possible D_L values are used, as shown in Figure 2A. For multiple-damage cases, an analytical model with random damage features is used. In the analytical model, the parameters D_L, D_S, and D_E are set as variables. By setting the values of D_L, D_S, and D_E, the damage features can be given randomly. D_E includes HCM, OCM, TCM, and FCM, and the corresponding parameter D_E is set to 1, 2, 3, and 4, respectively. D_L is the starting location of the damage, including D_LX, D_LY. The procedure used by the analytical model is shown in Figure 2B.

FIGURE 2

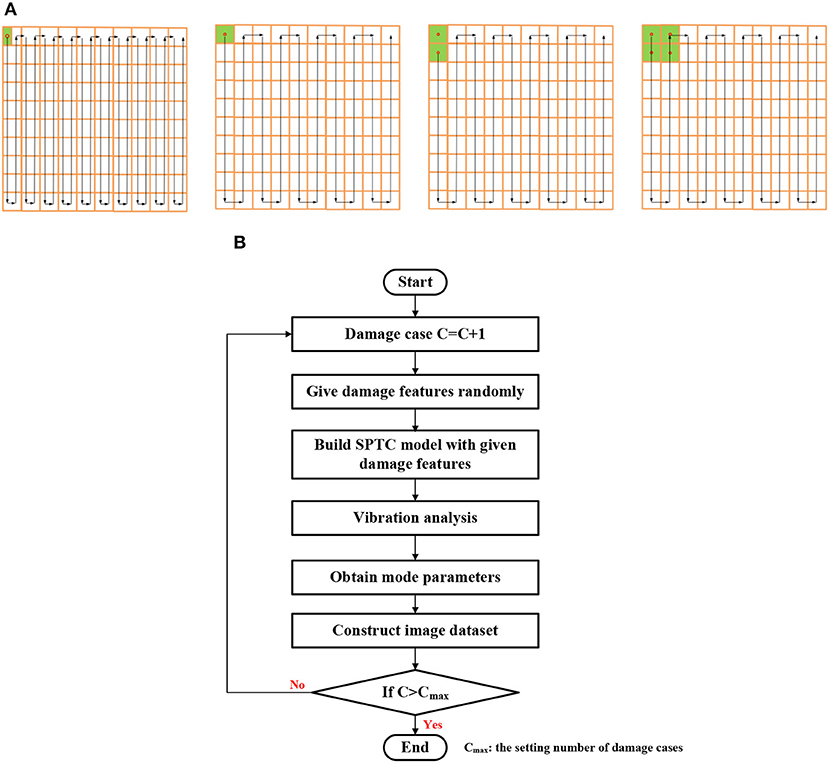
Figure 2. Vibration analytical models of sandwich structure with truss core (SPTC). (A) Single-damage case. (B) Multiple-damage case.

Experimental Validation

To verify the proposed analytical model, experiments were carried out in which pyramidal SPTCs (Figure 3A) were used. The relative density of the truss core was about 3%. The thicknesses of the face sheets and the truss core were 0.9 and 7 mm, respectively. The dimensions of the metallic SPTC specimen were 250 × 250 mm.

FIGURE 3

Figure 3. Experimental information. (A) Damaged specimen (SD1). (B) Experimental set-up.

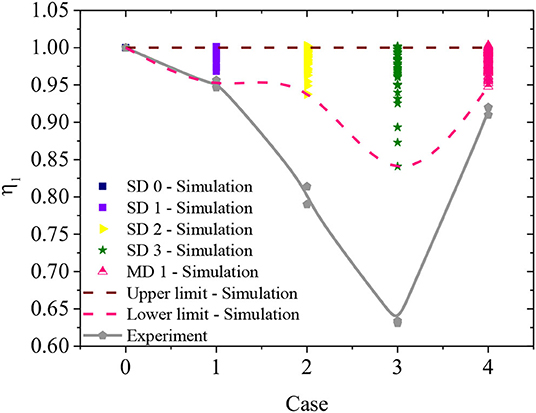
In the experiments, specimens with a single area of damage and multiple areas of damage were considered. For specimens with a single area of damage, three cases were used: SD1, SD2, and SD3. The corresponding D_E values were 2 × 3, 3 × 4, and 4 × 5, where x × y represents the D_E and x and y are the numbers of the missing cells by row and column, respectively. The defined single area of damage is in the center of the specimens. For specimens with areas of multiple damage, a specimen comprising two areas of damage at D_E 2 × 3 and 3 × 5, respectively (MD1), was used. The healthy specimen is denoted by SD0. For each damage case, repeated experiments of specimens with the same damage extent were conducted to verify the model.

The experimental set-up is shown in Figure 3B. The specimens were excited by a JZK-50 shaker. Two edges of the specimens were clamped. A laser Doppler vibrometer (Polytec, PSV-400) generated the excitation signal and measured the structural response. The structural modal information was obtained by analyzing the excitation and structural response signal.

Numerical models of the same dimensions as the experimental specimens were built to verify the analytical model. In contrast to the experimental specimens, in which the damage zone was prefabricated, the numerical model could simulate various cases with randomly distributed damage. The number of random damage cases C_max was set as 80.

To compare the numerical and experimental results, parameter η_i is defined as

$\begin{array}{ll}{\eta }_i={\omega }_i^D/{\omega }_i^U& (1)\end{array}$

where ${\omega }_i^D$ and ${\omega }_i^U$ are the i-th natural frequency of the damaged and undamaged specimens, respectively.

In the experiment, only the 1st order of mode is selected and i is set as 1. According to the results for η₁ shown in Figure 4, it can be seen that the trend of η₁ of simulation is in accordance with the experimental results as the D_E increases from 0 to 4 × 5. For a given D_E, D_L has a significant influence on the structural vibration properties. Taking SD3 for example, the largest η₁ is almost 1, and the smallest η₁ is 0.84, because the D_L is different. Therefore, in structural damage identification, various damage cases using different D_E and D_L values must be considered. When the damage case changes from SD3 to MD1, the trend of η₁ of simulation is also in accordance with experimental results. Although there are two areas of damage in the case of MD1, the effect of MD1 on the structural vibration properties is smaller than that of SD3, demonstrating that a number of areas of damage, D_L, D_E, and D_S, couple together and influence the structural vibration properties. This demonstrates that small changes in damage features may cause large variations in the structural properties. However, it is impractical to obtain massive data merely from experiments. Therefore, a simulation or numerical model is a very important way to obtain the data.

FIGURE 4

Figure 4. Numerical and experimental results.

Damage Indices

Because of the difficulty in identifying internal damage in sandwich panels (as mentioned in section introduction), damage indices are used to extract damage features. Then, by combining these with a DL technique, the identification of damage features is more accurate.

Vibration-based damage indices are used to extract the internal damage features according to information gained from the face sheet. Two damage indices are used (Li et al., 2015; Le et al., 2019) and compared; these are denoted DI-1 and DI-2.

DI-1 is proposed for filled SPTCs, and needs information from a healthy structure as the baseline. When a specimen is damaged, its stiffness or mass changes. Therefore, the vibration characteristics (natural frequencies and mode shapes) change. According to the variations in the vibration characteristics, the damage features can be identified. The damage index DIT_r(k) is defined as:

$\begin{array}{ll}DI{T}_r(k)=|DI{1}_r^2(k)-DI{1}_r(k-1)DI{1}_r(k+1)|& (2)\end{array}$

where DI-1_r is calculated according to the natural frequencies and mode shapes, expressed in Equation (3); k is the number of the selected node; and r is the weight coefficient.

$\begin{array}{ll}DI{1}_r=\sqrt{{\displaystyle \sum _{p=P_1}^{P_2}}\frac{{\omega }_p^r}{{\displaystyle \sum _{p=P_1}^{P_2}}{\omega }_p^r}{\left({\left[F_p·I\right]}_D-{\left[F_p·I\right]}_U\right)}^2}& (3)\end{array}$

$\begin{array}{ll}{F}_p=\frac{{\Phi }_p{\Phi }_p^T}{{\omega }_p^2}& (4)\end{array}$

where ω_p and Φ_p are the p-th natural frequency and mode shape, respectively; I is {1,…,1}T_1×n; P₁ and P₂ are the beginning and ending order modes, respectively, in the practical case; and D and U denote the damaged and undamaged model, respectively. Parameter r is used to define the weight of low- and high-order modes in the damage index DI-1. Different damage features have different influences on different order modes: some damage has a great influence on low-order modes and some damage has a great influence on high-order modes.

However, in practice, it is hard to obtain information on a healthy status. Therefore, a baseline-free damage index DI-2 was also used in this study. A gapped smoothing method (GSM) was used to construct a baseline. If there was no damage in the structure, the mode shapes were smooth and continuous. When there was damage in the structure, the mode shapes at the damage were not smooth. We used a GSM to construct a baseline. By comparing the information before and after the GSM, the damage features could be extracted. DI-2 is expressed as:

$\begin{array}{ll}D{I}_m^{*}(n)=T(DI{2}_m(n))=DI{2}_m^2(n)-DI{2}_m(n+1)DI{2}_m(n-1)& (5)\end{array}$

where DI-2 is defined in Equation (6), n is the number of the selected node, and m is the weight coefficient.

$\begin{array}{ll}DI{\text{2}}_m(x_i,y_j)={\displaystyle \sum _{p=P_1}^{P_2}}{\alpha }_p^m\frac{{(MD{C}_p(x_i,y_j)-MD{C}_p(x_i,y_j){}^{\prime })}^2}{{\displaystyle \sum _{i=1}^E}{\displaystyle \sum _{j=1}^F}{(MD{C}_p(x_i,y_j)-MD{C}_p(x_i,y_j){}^{\prime })}^2}& (6)\end{array}$

$\begin{array}{ll}{\alpha }_p^m{=}^{{\omega }_p^m}{/}_{{\displaystyle \sum _{p=K_1}^{K_2}}{\omega }_p^m}& (7)\end{array}$

where E and F are the numbers of the columns and rows of the measuring points; P₁ and P₂ are the beginning and ending order modes, respectively, in the practical case; and ${\alpha }_p^m$ is defined as the weight coefficient of the p-th component and is expressed in Equation (7). The details of DI-2 can be found in our previous work (Le et al., 2019).

Dataset Building

Based on the proposed analytical models and the two damage indices, data in the cases of single and multiple damage are obtained. Some samples are shown in Figure 5. To detect damage of a different orientation and to increase the variety of the dataset, data enhancement was applied to increase the number of samples.

FIGURE 5

Figure 5. Samples of datasets based on (A) DI-1 and (B) DI-2. HCM, half-cell missing; OCM, one cell missing; TCM, two cells missing; FCM, four cells missing.

Comparing the first line of results for DI-1 (Figure 5A) and DI-2 (Figure 5B), it can be seen that the results for HCM or OCM identified by DI-1 are better than those identified by DI-2 because the influence of small areas of damage on the structural vibration properties is small; however, when D_E becomes significant, DI-2 also shows very good performance.

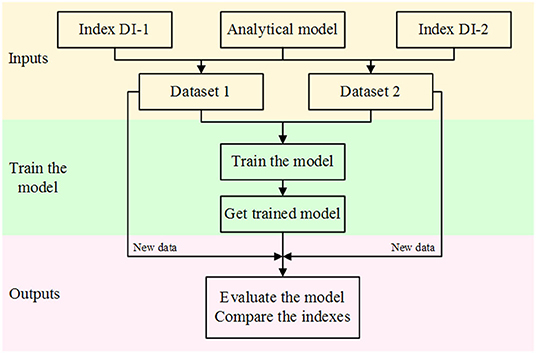
DL Framework for Internal Damage Identification in SPTCs

In this study, Faster RCNN (Ren et al., 2015), a framework for target recognition, is combined with a vibration-based method (section construction of the dataset) to identify internal damage features of SPTCs. The flowchart of the identification process is provided in Figure 6. The method can be summarized in four steps:

Step 1 Build dataset according to the damage indices and analytical model.

Step 2 Set the dataset as input and train the Faster RCNN model.

Step 3 Obtain the trained Faster RCNN model.

Step 4 Input the new data and evaluate the trained model.

FIGURE 6

Figure 6. Flowchart of the identification process.

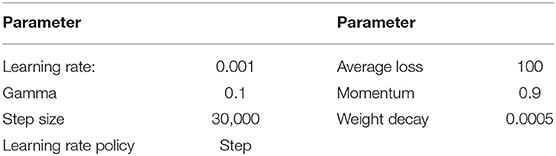
In this study, a Zend Framework (ZF) CNN was selected. Before the training process, all images were normalized to 1,491 × 1,501 pixels. To detect damage of different orientations and increase the variety of the dataset, data enhancement was applied to increase the number of samples. Of the 2018 samples obtained, 50% were set as the training set and 50% were set as the testing set. The parameters of the Faster RCNN are shown in Table 2.

TABLE 2

Table 2. Parameters of faster RCNN.

Caffe, a DL framework, was used to conduct the training process as it has been widely applied in DL and machine learning, such as computer vision, speech recognition, image feature coding, and information retrieval. The computing platform was Ubuntu 16.04, and all the codes were run on a server equipped with 12 Intel Core i7-6800K CPUs (3.40 GHz) and an NVIDIA GeForce GTX 1080 Ti with 11 GB of memory.

Results and Discussion

As is well-known, in damage identification, the effectiveness of different damage indices for the same damage feature is different. Even for the same damage, one index could identify it and another one may not. Therefore, in this section, comparisons between DI-1 and DI-2 are conducted to investigate the capability and applications of the indices.

There are two steps in damage identification: first, detect if there is any damage in the structures and identify the D_L; second, identify the D_E and D_S. Compared with D_L, it is more difficult to identify the D_E and D_S. Most of the previous studies have focused on the identification of D_L, and few studies could identify all three damage features. In this study, only one D_S (truss core missing) is considered. Therefore, in section 4.1, the capacity of the proposed method to determine the D_L and D_E is discussed.

D_L and D_E Identification

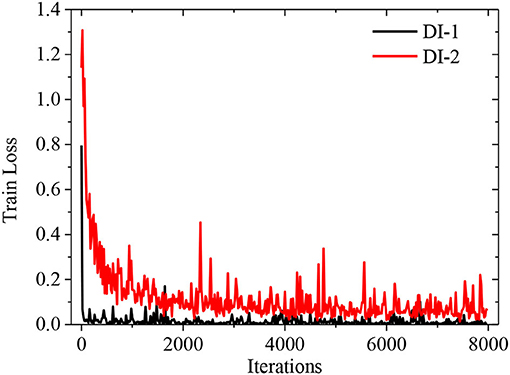
Figure 7 shows the training loss results of DI-1 and DI-2. For DI-1, the loss value becomes stable very quickly. For DI-2, it can be seen that the loss value tends to be stable when the iteration is around 1,000 times, and the final loss value is stable at around 0.1. Because the proposed damage indices have extracted the damage feature effectively, the loss value becomes stable more quickly.

FIGURE 7

Figure 7. The training loss curves of DI-1 and DI-2.

Figure 8 provides some identification results of DI-1 and DI-2. From Figure 8, it can be seen that the accuracy of damage feature identification is high, no matter whether the D_E is HCM, OCM, TCM, or FCM or whether the D_L is in the center of the model or on the boundary edge. From the middle and right-hand panels in Figure 8A, it can be seen that the features of HCM and OCM are similar; it is difficult for humans to identify the D_E accurately, but the DL-based method could identify the location and extent accurately.

FIGURE 8

Figure 8. Examples of the identified results. (A) DI-1 and (B) DI-2.

To evaluate the proposed method, 100 figures were used to test the trained network, and the statistical results are provided in Figure 9. In Figures 9A,B, the x-axis is the D_E results identified by the trained network and the y-axis is the real D_E. When using the trained network to identify the damage, five cases may occur. Taking HCM as an example, the five cases are listed in Table 3. Cases 3–5 demonstrate that the damage location is identified accurately, but the damage extent could not be detected accurately. Case 2 shows the best result, with both the location and extent identified.

FIGURE 9

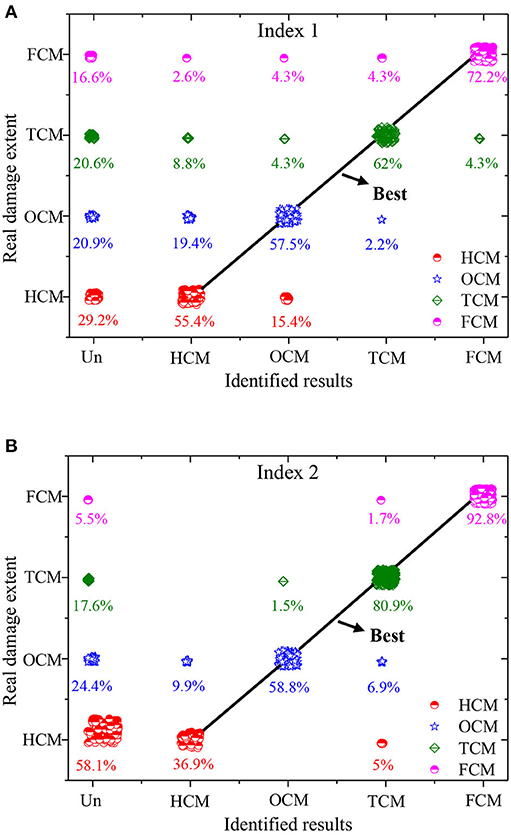
Figure 9. The statistical results. (A) DI-1 and (B) DI-2. HCM, half-cell missing; OCM, one cell missing; TCM, two cells missing; FCM, four cells missing.

TABLE 3

Table 3. Five cases for HCM identification.

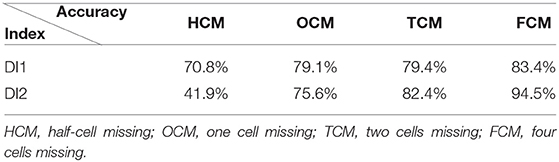
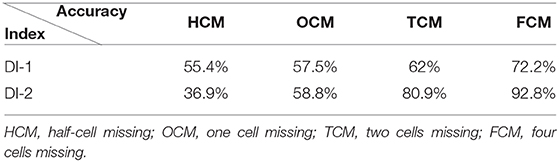
The accuracies of damage location and extent identification based on DI-1 and DI-2 are listed in Tables 4 and 5, respectively. It can be seen that the identification accuracy increases as the D_E increases because the damaged feature identified by the indices becomes more obvious as the D_E increases.

TABLE 4

Table 4. Accuracy of damage location identification according to the statistical results.

TABLE 5

Table 5. Accuracy of damage extent identification according to the statistical results.

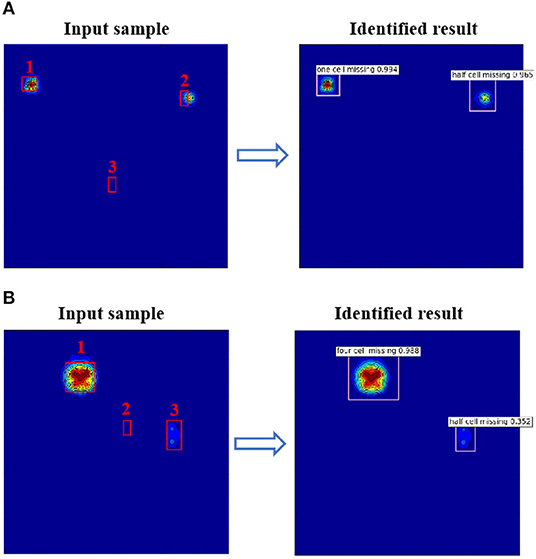
From Figure 10A, it can be seen that there are three areas of damage in the SPTC, including one OCM and two HCMs. However, after identifying the network, only damage areas 1 and 2 are identified because the effects of damage area 3 on the structure vibration properties are hidden by those of damage areas 1 and 2. This demonstrates that the sensitivity of the damage index to the damage feature plays a very important role in D_L identification. This conclusion is in accordance with previous studies. From Figure 10B, there are three areas of damage, including FCM, TCM, and HCM. The trained network could only identify damage areas 1 and 3. The reason for damage area 2 in Figure 10B not being identified is that the D_E for damage area 2 is smaller than that for the other two damage areas. Damage area 3 (TCM) is identified as HCM, and the corresponding accuracy is about 0.352, meaning that the trained network could identify that there is damage at this location but the probability of identifying it as HCM is not high.

FIGURE 10

Figure 10. Examples of DI-1. (A) Case 1 and (B) case 2.

In conclusion, according to the results in Figure 10, it can be seen that the damage can be located if the damage can be characterized in the figure, and the damage cannot be located if the damage cannot be characterized. When there are multiple areas of damage in SPTCs, damage feature identification is more difficult. The small D_E value is easily covered by large D_E values, meaning that the small D_E values could not be identified or that the damage is mis-identified, as in cases 3, 4, or 5. Therefore, to identify the damage with small D_E values, it is better to combine more effective indices that are sensitive to the small D_E values.

Comparison of DI-1 and DI-2

In this study, a dataset based on two damage indices is used; this dataset has a significant influence on the effectiveness of the proposed method. Therefore, the effectiveness of the two damage indices is compared. Comparing Figure 5A with Figure 5B, it can be seen that the extracted feature based on DI-1 is more obvious than that based on DI-2 when D_E is small (HCM and OCM). When D_E is small, the identification of damage features is easily affected by other factors, such as the boundary condition or singularity caused by contact points, especially in the baseline-free damage identification process.

When the extent of the damage is small (HCM), the accuracy of damage feature identification based on DI-1 is higher than that based on DI-2, as shown in Tables 4 and 5. When the extent of the damage increases, the accuracy of damage feature identification based on DI-1 is smaller than that based on DI-2. From Figure 5A, it can be seen that the HCM feature is very obvious based on index 1. However, based on index 2, it shows that HCM tends to be covered by an influencing factor (in Figure 5B), such as the singularity caused by the contact nodes. Therefore, when the D_E is small, DI-1 is more effective than DI-2.

However, as the D_E increases from HCM to TCM or FCM, the accuracy based on DI-2 is better than the accuracy based on DI-1, as shown in Tables 4 and 5. From Figure 5A, when the D_E increases from HCM to TCM or FCM, the characteristics of the identified damage, such as the color gradient or area, change a little, especially for HCM, OCM, or FCM. When the trained network identifies the D_E, it is easy for the framework to identify one D_E as another D_E. But, for DI-2, it can be seen that the characteristics of the identified damage change a lot as the D_E increases from HCM to FCM. As the D_E increases, DI-2 performs better than DI-1.

According to the accuracy results in Table 5, it can be seen that DI-2 performs better than DI-1. Therefore, for identification of internal damage in sandwich panels, the proposed method based on DI-2 is better and more effective, as it is more successful in extracting internal damage features.

Conclusions

This paper proposed a method for identifying internal damage to sandwich panels by integrating a DL technique with a vibration-based method for internal damage in sandwich panels with a truss core. Instead of using the photographs or raw structural responses, two damage indices were used to extract the damage features and construct the dataset. According to the statistical results, the proposed method can identify the internal damage features D_L and D_E. As the D_E increases, the accuracy of identification increases. The statistical results also reveal that damage indices play a very important role in the identification process. Considering massive damage features, it is better to combine the two indices to improve their accuracy. When D_E is small, DI-1 is better than DI-2. When D_E is large, DI-2 is better than DI-1. According to the characteristics of the damage identified by the indices, we can choose suitable indices to identify as many damage features as possible.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

LL: methodology, writing—original draft preparation, and funding acquisition. YW, JB, and LL: software. YW and CL: validation. LL and CL: formal analysis. LL and HS: writing—review and editing. CH: project administration. All authors contributed to the article and approved the submitted version.

Funding

This research was supported by the National Natural Science Foundation of China (grant nos. 11472276, 11972033, and 11332011) and the Strategic Priority Research Program of the Chinese Academy of Sciences (grant no. XDA22000000).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Andrzej, K. (2014). Vibration-based spatial damage identification in honeycomb-core sandwich composite structures using wavelet analysis. Compos. Struct. 118, 385–391. doi: 10.1016/j.compstruct.2014.08.010

CrossRef Full Text | Google Scholar

Avci, O., Abdeljaber, O., Kiranyaz, S., and Inman, D. (2017). “Structural damage detection in real-time: implementation of 1D convolutional neural networks for SHM applications,” in Structural Health Monitoring and Damage Detection, Volume 7: Proceedings of the 35th IMAC, A Conference and Exposition on Structural Dynamics. (Garden Grove, CA), 2191–5644. doi: 10.1007/978-3-319-54109-9_6

CrossRef Full Text | Google Scholar

Cha, Y. J., Choi, W., and Buyukozturk, O. (2017). Deep Learing-based crack damage detection using convolutional neural networks. Comput-aided Civ. Inf. 32, 361–378. doi: 10.1111/mice.12263

CrossRef Full Text | Google Scholar

Chen, F. C., and Jahanshahi, M. R. (2018). NB-CNN: deep learning based crack detection using convolutional neural network and naïve bayes data fusion. IEEE Trans. Indus. Electr. 65, 4392–4400. doi: 10.1109/TIE.2017.2764844

CrossRef Full Text | Google Scholar

Chiras, S., Mumm, D. R., Evans, A. G., Wicks, N., Hutchinson, J. W., Dharmasena, K., et al. (2002). The structural performance of near-optimized truss core panels. Int. J. Solids Struct. 39, 4093–4115. doi: 10.1016/S0020-7683(02)00241-X

CrossRef Full Text | Google Scholar

Guo, T., Wu, L. P., Wang, C. J., and Xu, Z. L. (2020). Damage detection in a novel deep-learning framework: a robust method for feature extraction. Struct. Health Monit. 19, 424–442. doi: 10.1177/1475921719846051

CrossRef Full Text | Google Scholar

He, Y. Z., Tian, G. Y., Pan, M. C., and Chen, D. X. (2014). Non-destructive test of low-energy impact in CFRP laminates and interior defects in honeycomb sandwich using scanning pulsed eddy current. Compos B-Eng. 59, 196–203. doi: 10.1016/j.compositesb.2013.12.005

CrossRef Full Text | Google Scholar

Hg, A. (1969). Analysis and Design of Structural Sandwich Panels. Oxford: Pergamon Press.

Hu, H. W., Wang, B. T., Lee, C. H., and Su, J. S. (2006). Damage detection of surface cracks in composite laminates using modal analysis and strain energy method. Compos. Struct. 74, 399–405. doi: 10.1016/j.compstruct.2005.04.020

CrossRef Full Text | Google Scholar

Huang, X. Y., Liu, Z. L., Zhang, X. Y., Kang, J. L., Zhang, M., and Guo, Y. L. (2020). Surface damage detection for steel wire ropes using deep learning and computer vision techniques. Measurement 161:107843. doi: 10.1016/j.measurement.2020.107843

CrossRef Full Text | Google Scholar

Khan, A., Ko, D. K., Lim, S. C., and Kim, H. S. (2019). Structural vibration-based classification and prediction of delamination in smart composite laminates using deep learning neural network. Compos. B-Eng. 161, 586–594. doi: 10.1016/j.compositesb.2018.12.118

PubMed Abstract | CrossRef Full Text | Google Scholar

Klepka, A., Staszewski, W. J., Maio, D. D., and Scarpa, F. (2013). Impact damage detection in composite chiral sandwich panels using nonlinear vibro-acoustic modulations. Smart Mater. Struct. 22, 1–11. doi: 10.1088/0964-1726/22/8/084011

CrossRef Full Text | Google Scholar

Kumar, M., Shenoi, R. A., and Cox, S. J. (2009). Experimental validation of modal strain energies based damage identification method for a composite sandwich beam. Compos. Sci. Technol. 69, 1635–1643. doi: 10.1016/j.compscitech.2009.03.019

CrossRef Full Text | Google Scholar

Lai, J. (2019). Analysis on streamwise fluidelastic instability of rotated triangular tube arrays subjected to two-phase flow. Mech. Syst. Signal Pr. 123, 192–205. doi: 10.1016/j.ymssp.2019.01.010

CrossRef Full Text | Google Scholar

Lai, J., Sun, L., and Li, P. Z. (2019b). Two-phase flow-induced instability and nonlinear dynamics of a single tube in tube bundles in the transverse direction. Eur. J. Mech. A-Solid. 78:10. doi: 10.1016/j.euromechsol.2019.103858

CrossRef Full Text | Google Scholar

Lai, J., Sun, L., Li, P. Z., Tan, T. C., Gao, L. X., Xi, Z. D., et al. (2019a). Eigenvalue analysis on fluidelastic instability of a rotated triangular tube array considering the effects of two-phase flow. J. Sound Vib. 439, 194–207. doi: 10.1016/j.jsv.2018.09.060

CrossRef Full Text | Google Scholar

Le, J., Lu, L. L., Wang, Y. B., Song, H. W., Xing, X. D., and Huang, C. G. (2019). Damage identification of low-density material-filled sandwich panels with truss core based on vibration properties. Struct. Health Monit. 18, 1711–1721. doi: 10.1177/1475921718820100

CrossRef Full Text | Google Scholar

Li, B., Li, Z., Zhou, J., Ye, L., and Li, E. (2015). Damage localization in composite lattice truss core sandwich structures based on vibration characteristics. Compos. Struct. 126, 34–51. doi: 10.1016/j.compstruct.2015.02.046

CrossRef Full Text | Google Scholar

Liu, J. Y., Zhu, X., Zhou, Z. G., Wu, L. Z., and Ma, L. (2014). Effects of thermal exposure on mechanical behavior of carbon fiber composite pyramidal truss core sandwich panel. Compos. B-Eng. 60, 82–90. doi: 10.1016/j.compositesb.2013.12.059

CrossRef Full Text | Google Scholar

Liu, T. W., Xu, H., Ragulskis, M., Cao, M. S., and Ostachowicz, W. (2020). A data-driven damage identification framework based on transmissibility function datasets and one-dimensional convolutional neural networks: verification on a structural health monitoring benchmark structure. Sensors 20, 1–25. doi: 10.3390/s20041059

PubMed Abstract | CrossRef Full Text | Google Scholar

Lou, J., Wu, L. Z., Ma, L., Xiong, J., and Wang, B. (2014). Effects of local damage on vibration characteristics of composite pyramidal truss core sandwich structure. Compos, B. 62, 73–87. doi: 10.1016/j.compositesb.2014.02.012

CrossRef Full Text | Google Scholar

Lu, L. L., Song, H. W., and Huang, C. G. (2017b). Experimental investigation of unbound nodes identification for metallic sandwich panels with truss core. Compos. Struct. 163, 248–256. doi: 10.1016/j.compstruct.2016.12.028

CrossRef Full Text | Google Scholar

Lu, L. L., Song, H. W., and Huang, C. G. (2017c). Effects of random damages on dynamic behavior of metallic sandwich panel with truss core. Compos. B-Eng. 116, 278–290. doi: 10.1016/j.compositesb.2016.10.051

CrossRef Full Text | Google Scholar

Lu, L. L., Song, H. W., Yuan, W., and Huang, C. G. (2017a). Baseline-free damage identification of metallic sandwich panels with truss core based on vibration characteristics. Struct. Health Monit. 16, 24–38. doi: 10.1177/1475921716660055

CrossRef Full Text | Google Scholar

Pathirage, C. S. N., Li, J., Li, L., Hao, H., Liu, W. Q., and Ni, P. H. (2018). Structural damage identification based on autoencoder neural networks and deep learning. Eng. Struct. 172, 13–28. doi: 10.1016/j.engstruct.2018.05.109

CrossRef Full Text | Google Scholar

Ren, S., He, K., Girshick, R., and Sun, J. (2015). Faster R-CNN: towards real time object detection with region proposal networks. IEEE Trans. Pattern Anal. Machine Intelligence 39, 1137–1149. doi: 10.1109/TPAMI.2016.2577031

PubMed Abstract | CrossRef Full Text | Google Scholar

Seguel, F., and Meruane, V. (2018). Damage assessment in a sandwich panel based on full-field vibration measurements. J. Sound Vib. 417, 1–18. doi: 10.1016/j.jsv.2017.11.048

CrossRef Full Text | Google Scholar

Sikdar, S., Ostachowicz, W., and Pal, J. (2018). Damage-induced acoustic emission source identification in an advanced sandwich composite structure. Compos. Struct. 202, 860–866. doi: 10.1016/j.compstruct.2018.04.051

CrossRef Full Text | Google Scholar

Wadley, H. N. G., Fleck, N. A., and Evans, A. G. (2003). Fabrication and structural performance of periodic cellular metal sandwich structures. Compos. Sci. Technol. 63, 2331–2343. doi: 10.1016/S0266-3538(03)00266-5

CrossRef Full Text | Google Scholar

Yuan, W., Song, H. W., Wang, X., and Huang, C. G. (2015). Experimental investigation on thermal buckling behavior of fully-clamped truss-core sandwich panels. AIAA J. 53, 948–957. doi: 10.2514/1.J053246

CrossRef Full Text | Google Scholar

Yuan, W., Wang, X., Song, H. W., and Huang, C. G. (2014). A theoretical analysis on the thermal buckling behavior of fully-clamped sandwich panels with truss cores. J. Thermal Stresses 37, 1433–1448. doi: 10.1080/01495739.2014.937263

CrossRef Full Text | Google Scholar

Zhang, L., Yang, F., Zhang, Y. D., and Zhu, Y. J. (2016). “Road crack detection using deep convolutional neural network,” in IEEE International Conference on Image Processing. (Phoenix, AZ), 3708–3712. doi: 10.1109/ICIP.2016.7533052

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Y., Sun, X. W., Loh, K. J., Su, W. S., Xue, Z. G., and Zhao, X. F. (2020). Autonomous bolt loosening detection using deep learning. Struct. Health Monit. 19, 105–122. doi: 10.1177/1475921719837509

CrossRef Full Text | Google Scholar

Zhu, K. G., Chen, M. J., Lu, Q. H., Wang, B., and Fang, D. N. (2014). Debonding detection of honeycomb sandwich structures using frequency response functions. J. Sound Vib. 333, 5299–5311. doi: 10.1016/j.jsv.2014.05.023

CrossRef Full Text | Google Scholar

Zhu, K. G., Qing, X. L. P., and Liu, P. (2016). Torional guided wave-based debonding detection in honeycomb sandwich beams. Smart Mater. Struct. 25, 1–11. doi: 10.1088/0964-1726/25/11/115048

CrossRef Full Text | Google Scholar