Mechanical Properties of Glassy Nanopillars: A Comparative, Computational Study of Size Effects in Nanoglasses and Homogeneous Bulk Glasses

1Introduction

Nanoglasses (NGs) are glassy materials with microstructural features on the nanoscale, which consist of glassy grains connected by glass–glass interfaces (Ivanisenko et al., 2018). These interfaces are characterized by an excess volume (Jing et al., 1989; Şopu et al., 2009), a defective short-range order (SRO) (Ritter et al., 2011), and a different composition as compared with the glassy grains (Adjaoud and Albe, 2016; Wang et al., 2016a; Adjaoud and Albe, 2018). NGs can be synthesized by cold compaction of nanometer-sized metallic glassy particles obtained via inert gas condensation (Jing et al., 1989; Weissmüller et al., 1992; Gleiter, 2008; Fang et al., 2012; Gleiter, 2013; Gleiter et al., 2014; Gleiter, 2016; Nandam et al., 2017; Ivanisenko et al., 2018). Microcompression test revealed considerable plasticity in an Sc₇₅Fe₂₅ NG, while the homogeneous glass (HG) with identical composition fails in a brittle manner (Fang et al., 2012). When reducing the sample size to the nanoscale, 15% plastic strain was observed in a 400 nm Sc₇₅Fe₂₅ NG nanopillar using in situ tensile tests in a transmission electron microscope (Wang et al., 2015). Moreover, a systematic study of nanosized and microsized Sc₇₅Fe₂₅ HG and NG pillars by means of compression tests showed that both, yield strength and deformation mode, are size-dependent in HG pillars. These properties, however, are size-independent in the NG pillars (Wang et al., 2016b), which was attributed to the microstructural features present in the NG. Indeed, molecular dynamic (MD) simulations revealed that glass–glass interfaces in NGs act as nucleation sites for shear transformation zones (STZs) and prevent strain localization, which leads to the more homogeneous deformation of NGs as compared with HGs (Şopu et al., 2011; Adibi et al., 2013; Albe et al., 2013; Adibi et al., 2014; Şopu and Albe, 2015; Adjaoud and Albe, 2019; Cheng and Trelewicz, 2019b).

MD simulations were also used in the past to investigate the effect of grain size on the deformation behavior of a 50 nm Cu₆₄Zr₃₆ NG nanopillar (Adibi et al., 2015a; Adibi et al., 2016). In these studies, the nanopillar was prepared by cutting a cylinder from an NG produced from an HG using the Poisson–Voronoi tessellation method (Brostow et al., 1978; Finney, 1979; Tanemura et al., 1983). However, this model of an NG underestimates the volume fraction of the interfaces as compared with the NGs prepared by consolidation of nanoparticles (Adjaoud and Albe, 2018; Cheng and Trelewicz, 2019a; Cheng and Trelewicz, 2019b; Adjaoud and Albe, 2019) which is more consistent with the experiment (Fang et al., 2012; Wang et al., 2015; Wang et al., 2016b).

In this work, we report the results of a systematic study on the influence of nanopillar diameter on the mechanical properties of NG and HG nanopillars with various diameters by means of MD simulations. The NG nanopillars were cut from NGs prepared by nanoparticle consolidation (Adjaoud and Albe, 2018). We first investigate the influence of nanopillar diameter on the deformation behavior and strain localization. Then, we examine the effects of nanopillar diameter on Young’s modulus and yield stress of NG and HG nanopillars. We finally use the obtained mechanical properties to derive a deformation map for NG and HG nanopillars. In order to see whether the mechanical properties of NG and HG nanopillars depend on the chemical composition, all simulations were done for two different types of NGs and HGs, namely, Cu₆₄Zr₃₆ and Pd₈₀Si₂₀.

2Methodology

MD simulations were carried out using the LAMMPS simulation package (Plimpton, 1995).The interatomic interactions are described by the Finnis–Sinclair-modified-type potential for Cu–Zr (Mendelev et al., 2009) and the embedded atom model potential for Pd–Si (Ding et al., 2012). These potentials have been optimized to predict accurately the structure of liquid and amorphous Cu–Zr and Pd–Si alloys and were successfully applied to Cu–Zr and Pd–Si glasses (Cheng et al., 2013; An et al., 2016; Tang et al., 2018; Adjaoud and Albe, 2019).

First, Cu₆₄Zr₃₆ and Pd₈₀Si₂₀HGs were obtained by quenching a melt, which was already equilibrated at 2,000 K, to a temperature of about 50 K at a quenching rate of 0.01 K ps⁻¹ (Ritter et al., 2011). Next, we prepared Cu₆₄Zr₃₆ and Pd₈₀Si₂₀ NGs by cold compaction of several glassy spheres with diameters ranging from 6 to 8 nm as described by Adjaoud and Albe, 2018. The resulting NGs have dimensions of about 18 nm $\times$ 18 nm $\times$ 18 nm, and their microstructure consists of glassy regions connected by glass–glass interfaces. These interfaces are characterized by a defective SRO in a zone with a width of at least 2 nm (Adjaoud and Albe, 2018; Cheng and Trelewicz, 2019a). The resulting Cu₆₄Zr₃₆ NG also exhibits locally varying compositions with copper-poor glassy bulk regions (Cu₆₁Zr₃₉) and copper-rich interfaces (Cu₇₂Zr₂₈) extending over about 1 nm. Similarly, the Pd₈₀Si₂₀ NG is made up of Pd_78.6Si_21.4 glassy regions and Pd_82.7Si_17.3 interfaces.

The NGs and HGs were replicated and relaxed in order to construct larger samples. After that, the nanopillars were prepared by cutting a cylinder followed by structural relaxation. The diameters of the nanopillars are ranging from D = 4.5–54 nm, which corresponds to 17 million atoms at maximum. The HG nanopillars have a homogeneous microstructure, while the NG nanopillars have an inhomogeneous microstructure (see Supplementary Figure S1). All nanopillars have an aspect ratio (length-to-diameter) of 2, except the nanopillars with D = 4.5 nm which have an aspect ratio of 4. The later aspect ratio is chosen in order to still keep the periodicity in the direction of the axis of the NG nanopillar.

In order to characterize the mechanical properties of NG and HG nanopillars, a series of tensile deformation simulations were performed. The uniaxial tensile load was applied along the axis of the nanopillars, which was chosen in the z-direction, with a constant strain rate of 4.10⁷ s⁻¹ at 50 K. The atomic scale deformation mechanisms were analyzed in terms of the local atomic von Mizes shear strain calculated with the OVITO analysis and visualization software (Stukowski, 2010).

3Results

3.1Deformation Behavior and Strain Localization

In NG nanopillars, the glass–glass interfaces as well as the free surface can act as nucleation sites for shear events (Albe et al., 2013). Figures 1A,B present the stress–strain curves for Cu₆₄Zr₃₆ and Pd₈₀Si₂₀ NG nanopillars with an average grain size of d = 7 nm and diameters ranging from D = 4.5–54 nm. It can be seen that the maximum stress, ${\sigma }_{max}$, is higher for Pd₈₀Si₂₀ NG nanopillars than for Cu₆₄Zr₃₆ NG nanopillars, which is essentially a modulus effect. Apart from ${\sigma }_{max}$, stress–strain curves of Cu₆₄Zr₃₆ are similar to those of Pd₈₀Si₂₀ with the same nanopillar diameter; both types of NG nanopillars do not show a stress drop upon yielding.

FIGURE 1

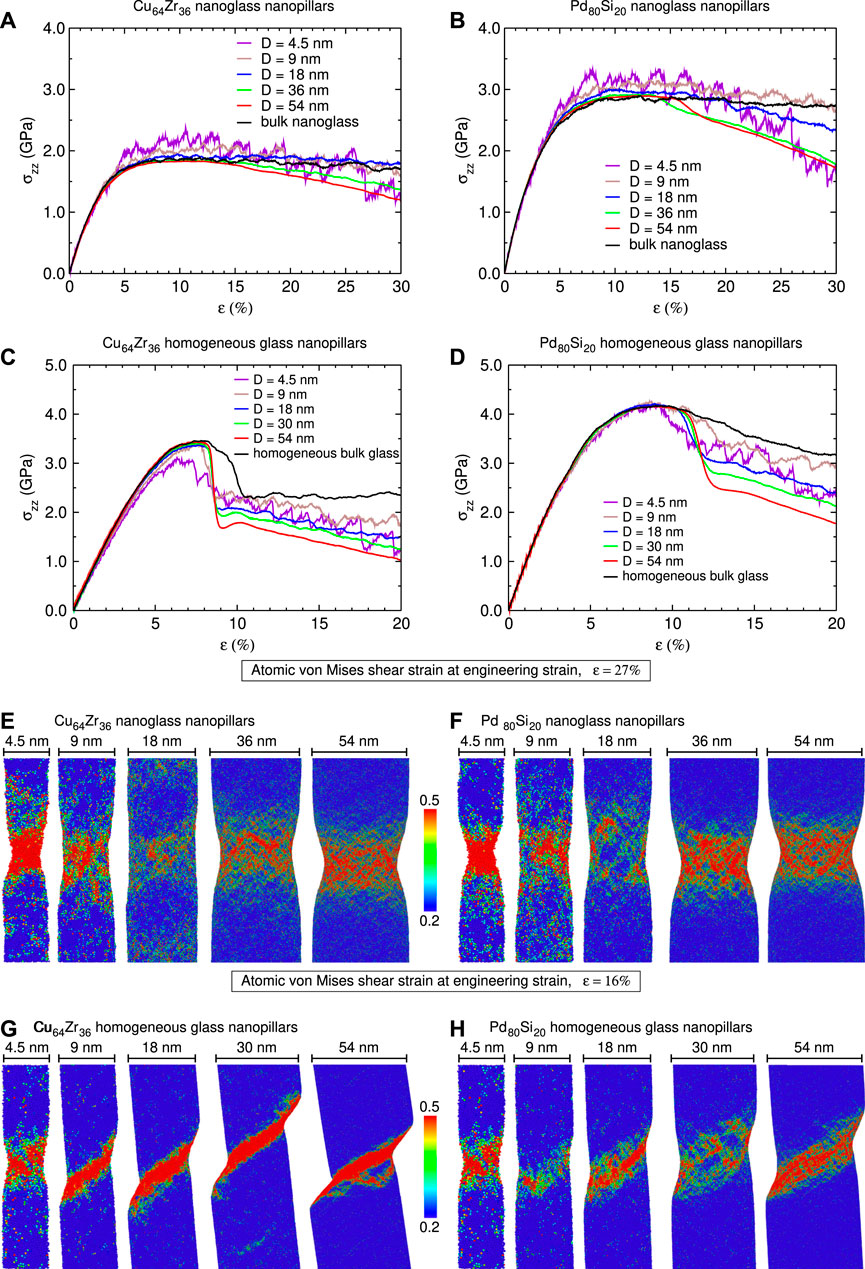
FIGURE 1. Tensile test of Cu₆₄Zr₃₆ and Pd₈₀Si₂₀ nanoglass (NG) and homogeneous glass (HG) nanopillars with an average grain size of d = 7 nm and diameters ranging from D = 4.5–54 nm. (A,B) Engineering stress–strain curves for NG nanopillars. (C,D) Engineering stress–strain curves for HG nanopillars. (E,F) Local von Mises shear strain at 27% total strain, showing strain localization in the NG nanopillars. (G,H) Local von Mises shear strain at 16% total strain, showing strain localization in the HG nanopillars. Engineering stress–strain curves for HG and NG bulk samples are added for reference; those for Cu₆₄Zr₃₆ bulk samples are taken from reference (Adjaoud and Albe, 2019).

Nanopillars with a diameter smaller than the average grain size (d = 7 nm) exhibit the highest ${\sigma }_{max}$. When D $\ge$9 nm, the stress–strain curves exhibit pronounced strain softening. The onset of strain softening occurs earlier in the large nanopillars: the stress of 36 and 54 nm NG nanopillars starts decreasing at an engineering strain of about 13–15%, in agreement with experimental results on a 400 nm Sc₇₅Fe₂₅ NG nanopillar showing about 15% plastic strain (Wang et al., 2015).

Figures 1C,D show the engineering stress–strain curves for the Cu₆₄Zr₃₆ and Pd₈₀Si₂₀ HG nanopillars with diameters ranging from 4.5 up to 54 nm. The Cu₆₄Zr₃₆ and Pd₈₀Si₂₀HGs are shown for comparison. It can be seen that the Cu₆₄Zr₃₆ HG exhibits a stress drop after the maximum stress, indicating the formation of a critical shear band (Adjaoud and Albe, 2019). The Pd₈₀Si₂₀ HG, in contrast, does not show a stress drop, suggesting that the Pd₈₀Si₂₀ HG is more ductile than the Cu₆₄Zr₃₆ HG. This is in agreement with the bending experiment and compression test on Pd–Si glasses (Yao et al., 2006; An et al., 2016). The nanopillars with smaller diameters, 4.5 nm for Cu₆₄Zr₃₆ and up to 9 nm for Pd₈₀Si₂₀, show strain softening upon yielding. Nanopillars with larger diameters, D $\ge$ 9 nm for Cu₆₄Zr₃₆ and D $\ge$ 18 nm for Pd₈₀Si₂₀, exhibit a pronounced stress drop and strain softening, while the magnitude of the stress drop is increasing with increasing nanopillar diameter. This size dependence can be understood in terms of the elastic energy release right after the stress drop, which is proportional to $D^2$ (Liu et al., 2011). In the case of Cu₆₄Zr₃₆ HG nanopillars, strain hardening occurs right after the stress drop at about 9% engineering strain, which is most pronounced in the 30 and 54 nm HG nanopillars. This effect can be explained by the structural relaxation which occurs after the elastic energy release (Ritter and Albe, 2012).

Next, we inspect the strain localization in NG nanopillars. By analyzing von Mises strains, three deformation modes can be defined: (1) pure necking, when the deformation plane is perpendicular to the deformation axis; (2) pure shear banding, when the angle between the deformation plane and the deformation axis is about 40°–60°; and (3) if a nanopillar is not long enough to allow strain localization to occur in a form of necking or shear banding, then von Mises strain distributes over the whole nanopillar which exhibits homogeneous deformation.

Figures 1E,F show the atomic von Mises shear strain at 27% engineering strain for Cu₆₄Zr₃₆ and Pd₈₀Si₂₀ NG nanopillars. It can be seen that the 4.5 nm nanopillars deform by necking. This necking deformation mode can be explained by the large surface-to-volume fraction which leads to the nucleation of a high number of STZs at the surface of the nanopillar (Albe et al., 2013). The 9 and 18 nm NG nanopillars, where the diameter is about or twice the average grain size, exhibit nearly homogeneous deformation, confirming the weak strain softening observed in the stress–strain curves (see Figures 1A,B). When the nanopillar diameter is significantly larger than the average grain size, as in the case of the 36 and 54 nm NG nanopillars, the nanopillars deform again by necking. This is consistent with the strain softening occurring in the stress–train curves. By comparing the Cu₆₄Zr₃₆ and Pd₈₀Si₂₀ NG nanopillars, it can be seen that the deformation behavior is similar and thus does not depend on the type of the NG nanopillars. Moreover, even after deformation, the interfaces are still characterized by compositional variation (see Supplementary Figure S2).

Recent MD studies (Adjaoud and Albe, 2019; Cheng and Trelewicz, 2019b) revealed that the mechanical properties of bulk NG samples are rather independent of the grain size which was attributed to the constant volume fraction of interfaces for NGs with different grain sizes because of the varying interfaces’ width. Based on those results, one could expect that the deformation behavior of the NG nanopillars in the present study is grain-size independent as their bulk NGs counterparts. It is interesting to note that a different result was obtained for bulk NGs and NG nanopillars produced by the Poisson–Voronoi tessellation method, which exhibits a grain-size-dependent deformation behavior because the glass–glass interfaces are assumed to have a constant width of 1 nm independent of the grain size (Adibi et al., 2013; Adibi et al., 2015a).

If we compare the NG nanopillars and bulk NG samples of both glasses, we see that bulk NG samples show no strain softening and a homogeneous deformation behavior (Adjaoud and Albe, 2019; Cheng and Trelewicz, 2019b) similar to the 9 nm NG nanopillars (see Figures 1A,B).

In order to see whether the necking deformation mode, which is observed in the Cu₆₄Zr₃₆ and Pd₈₀Si₂₀ NG nanopillars, is related to the presence of glass–glass interfaces or free surface, we inspected the atomic von Mises shear strain in the HG nanopillars which is shown in Figures 1G,H at 16% engineering strain. It can be seen that, with smaller diameters, the nanopillars deform by necking, while strain localization in the nanopillars with larger diameters occurs in the form of a shear band. This is in line with previous MD simulation results (Adibi et al., 2015b). Again, because of the large surface-to-volume fraction, the 4.5 nm HG nanopillars deform by necking independent of the chemical composition, similar to the 4.5 nm NG nanopillars. Previous atomistic simulations on Cu₆₄Zr₃₆ HGs have shown that a sample thickness of at least 5 nm is needed for shear band formation (Cheng and Ma, 2011).

Comparing the Cu₆₄Zr₃₆ HG nanopillars with the Pd₈₀Si₂₀ HG nanopillars, we find that the stress drop is steeper and strain localization is more pronounced in the Cu₆₄Zr₃₆ HG nanopillars. Moreover, ${\sigma }_{max}$ is higher for the Pd₈₀Si₂₀ HG nanopillars than for the Cu₆₄Zr₃₆ HG nanopillars, similar to NG nanopillars. This difference in the mechanical properties of Cu₆₄Zr₃₆ and Pd₈₀Si₂₀ HG nanopillars might be attributed to the difference in the chemical and topological SRO. In fact, recent bending experiments and MD simulations have shown that Pd₈₂Si₁₈ HG is significantly tougher than Cu₄₆Zr₅₄ HG; the higher toughness of the Pd₈₂Si₁₈ HG is related to its topological SRO (An et al. 2016). Moreover, our results reveal that the shear-band thickness in the Pd₈₀Si₂₀ HG nanopillars is larger than in the Cu₆₄Zr₃₆ HG nanopillars (see Figures 1H,G). This is consistent with previous experimental and simulation studies which have shown that the shear-band thickness is ranging from 5 to 20 nm or even 200 nm depending on the chemical composition of the metallic glass (Zhang and Greer, 2006; Cao et al., 2009; Murali et al., 2012; Shao et al., 2013; Liu et al., 2017).

Our results show that the main differences between the NG nanopillars and HG nanopillars are maximum stress ${\sigma }_{max}$ and the deformation mode: strain localization in the HG nanopillars occurs in the form of a shear band, whereas the NG nanopillars deform by necking or homogeneously, depending on the nanopillar diameter. These results are in agreement with a recent experimental study on the mechanical properties of Sc₇₅Fe₂₅ NG and HG nanopillars with diameter of 400 nm using in situ tensile tests in a transmission electron microscope (Wang et al. 2015).

3.2Stress Overshoot during Cyclic Loading

It is known that cyclic loading may significantly affect the deformation behavior of materials. Cyclic loading is usually performed in the elastic regime (Sha et al., 2015;Sha et al., 2017) or in the plastic regime (Zhu et al., 2017; Tang et al., 2018). The cyclic loading of metallic glasses in the plastic regime leads usually to the phenomenon of stress overshoot (Maaß et al., 2012).

In order to investigate the stress overshoot and the remaining plastic deformation in the NG nanopillars in more detail, we performed cyclic loading on the 18 nm Cu₆₄Zr₃₆ and Pd₈₀Si₂₀ NG nanopillars by unloading them from 15% engineering strain and then reloading them. Figures 2A,B present the corresponding stress–strain curves during the cyclic loading. In both glasses, the cyclic loading leads to a slight increase of flow stress after reloading caused by structural relaxation: the fractions of the Cu-centered icosahedra in the Cu₆₄Zr₃₆ NG nanopillar, including full icosahedra (index [0,12,0,0]) and disordered icosahedra (indexes [0,2,8,2] and [0,3,6,3]) and the most prominent Voronoipolyhedra Si[0,3,6,0] in the Pd₈₀Si₂₀ NG nanopillar, significantly increase after the first loading stage (see Figures 2C,D), which indicates that defective interfacial areas are relaxed during the initial stage of plastic deformation.

FIGURE 2

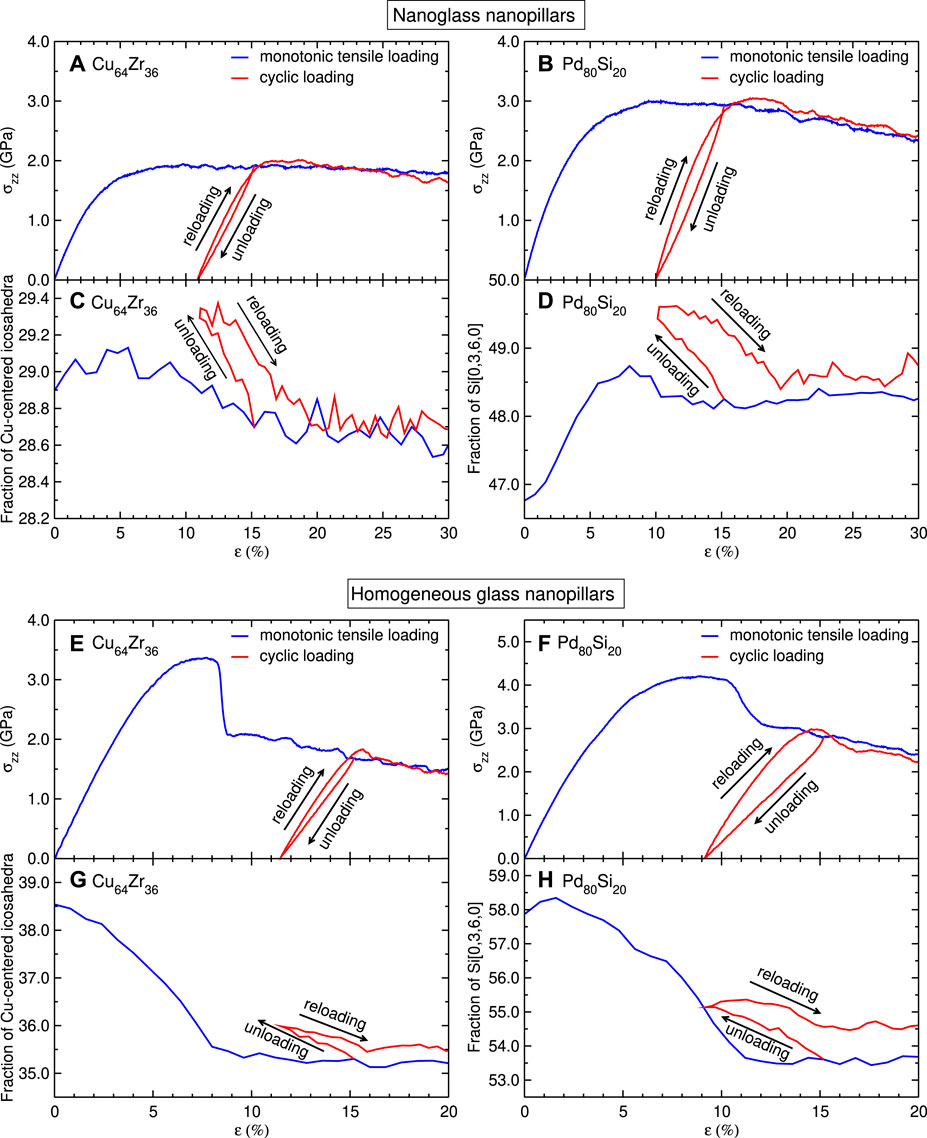
FIGURE 2. Cu₆₄Zr₃₆ and Pd₈₀Si₂₀ nanoglass (NG) and homogeneous glass (HG) nanopillars with a diameter of 18 nm under cyclic loading. (A,B) Engineering stress–strain curves for NG nanopillars. (C) Variation of Cu-centered icosahedra in the Cu₆₄Zr₃₆ NG nanopillars, including full icosahedra (index [0,12,0,0]) and disordered icosahedra (indexes [0,2,8,2] and [0,3,6,3]) as a function of the engineering strain. (D) Variation of the most prominent Voronoipolyhedra in the Pd₈₀Si₂₀ NG nanopillar, Si[0,3,6,0], as a function of the engineering strain. (E,F) Engineering stress–strain curves for HG nanopillars. (G) Variation of Cu-centered icosahedra in the Cu₆₄Zr₃₆ HG nanopillars as a function of the engineering strain. (H) Variation of the most prominent Voronoipolyhedra in the Pd₈₀Si₂₀ HG nanopillar, Si[0,3,6,0], as a function of the engineering strain. The engineering stress–strain curves for the monotonic loading of 18 nm Cu₆₄Zr₃₆ and Pd₈₀Si₂₀ NG and HG nanopillars are reproduced for reference.

The correlation between the increase of flow stress and structural relaxation is also observed in the HG nanopillars (see Figures 2E–H). However, in the HG nanopillars, the stress increases only in a small region of engineering strains as compared with the NG nanopillars: after the initial stress increases, the stresses of the monotonic tensile loading and the cyclic loading merge together in the Cu₆₄Zr₃₆ HG nanopillar, while in the Pd₈₀Si₂₀ HG nanopillar, the stress of the cyclic loading is slightly lower than that of the monotonic tensile loading. Moreover, the fractions of the Cu-centered icosahedra in the Cu₆₄Zr₃₆ HG nanopillar and the Voronoipolyhedra Si[0,3,6,0] in the Pd₈₀Si₂₀ HG nanopillar for the cyclic loading remain higher than those for the monotonic tensile loading after the stress overshoot, indicating the recovery of the local order upon unloading.

These results are in agreement with recent MD simulation results which showed that a cyclic loading after the formation of a shear band in a Cu₅₀Zr₅₀ HG leads to structural relaxation, and consequently, a stress increase occurs in the stress–strain curve (Tang et al., 2018). Experiments and theoretical models have shown that this phenomenon depends on temperature, strain rate, and structural relaxation (Kawamura et al., 1997; Lu et al., 2003; Maaß et al., 2012; Jiang et al., 2015; Yang et al., 2019).

3.3Size Effects on Young’s Modulus and Yield Strength

We, next, explore the effect of nanopillar diameter on Young’s modulus and yield strength. We obtained Young’s modulus from the slope of stress–strain curves at the small strain where the stress is proportional to the strain. We used 0.2% offset strain to calculate the yield strength. Figures 3A,B show the calculated Young’s moduli as a function of the nanopillar diameter for Cu₆₄Zr₃₆ and Pd₈₀Si₂₀ NG and HG nanopillars. The HG and NG bulk samples are shown for comparison.

FIGURE 3

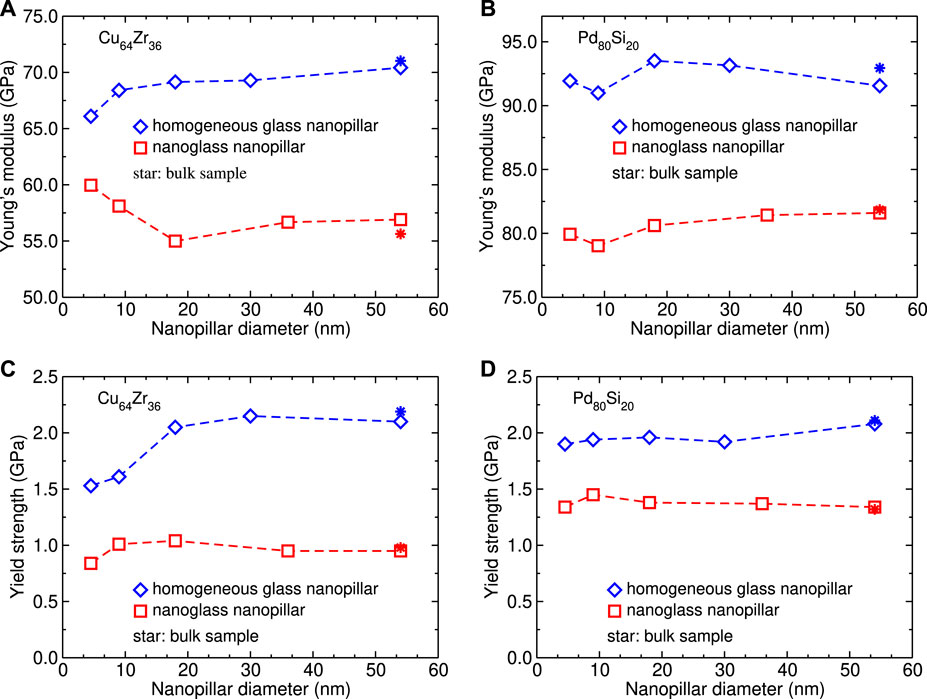
FIGURE 3. Effect of size on Young’s modulus and yield strength of homogeneous glass (HG) and nanoglass (NG) nanopillars. (A,B) Young’s modulus as a function of the nanopillar diameter for Cu₆₄Zr₃₆ and Pd₈₀Si₂₀ NG and HG nanopillars. (C,D) Yield strength as a function of the nanopillar diameter for Cu₆₄Zr₃₆ and Pd₈₀Si₂₀ NG and HG nanopillars. The HG and NG bulk samples are added for comparison.

The calculated Young’s moduli for Cu₆₄Zr₃₆ and Pd₈₀Si₂₀ HGs are in agreement with the experimental data which are about 67 GPa for Cu₆₄Zr₃₆ (Mendelev et al., 2008) and 94 Gpa for Pd₈₀Si₂₀ (Mizubayashi et al., 1998). It can be seen that Young’s modulus depends slightly on the nanopillar diameter when D$\le$9 nm. However, in the HG, surface stresses are the dominant contribution to this size effect, and the elastic softening of the NG is due to the different elastic contributions of the glass–glass interfaces and the action of surface stresses, which are counteracting. However, the nanopillars with D $\ge$ 18 nm show about the same Young’s modulus which is close to the value of the bulk samples. Similar behavior is observed for yield strength, see Figures 3C,D. Moreover, Young’s moduli and the yield strengths of NG nanopillars are clearly lower than those of HG nanopillars. This can be explained by the existence of the glass–glass interfaces in NGs, which act as a source for STZs (Albe et al., 2013). Recently, Wang et al. (2015) investigated the mechanical properties of Sc₇₅Fe₂₅ NG and HG nanopillars by using in situ tensile tests in a transmission electron microscope and found a similar trend in yield strength: the yield strength of the NG nanopillar is lower than that of the HG nanopillar with identical chemical composition. Strength softening was also observed in Ni₇₈P₂₂ NG pillars prepared by the electrodeposition technique (Li et al., 2018).

3.4Critical Stress

In order to further investigate the difference in deformation modes between the NG and HG nanopillars, we calculated the critical stress required for SB formation (Volkert et al., 2008), $\sigma =\sqrt{2^{3/2}\text{Γ}E/AD}$, where E is Young’s modulus, $\text{Γ}$ is the SB energy per unit area, A is the aspect ratio, and D is the diameter of the nanopillar. The values for E are reported in Figure 3. For $\text{Γ}$, we used a value of $1.30\text{ J}/{\text{m}}^2$ for Cu–Zr determined in a previous study (Adjaoud and Albe, 2018) and a value of $2.34\text{ J}/{\text{m}}^2$ for Pd–Si. We calculated $\text{Γ}$ for Pd–Si from the stress–strain curve of the 18 nm Pd₈₀Si₂₀ HG nanopillar, using the same method as that for Cu–Zr (Adjaoud and Albe, 2018). Our values for $\text{Γ}$ are close to $0.98\pm 0.04\text{ J}/{\text{m}}^2$ reported in tensile simulation for a Cu₅₀Zr₅₀ metallic glass film (Zhong et al., 2015) and $0.56\text{ J}/{\text{m}}^2$ reported in uniaxial compression experiments for Cu-based and Zr-based metallic glasses (Chen et al., 2010). On the other hand, our calculated $\text{Γ}$ values are much smaller than $10\text{ J}/{\text{m}}^2$ for a Pd-based metallic glass (Volkert et al., 2008) and $9\text{ J}/{\text{m}}^2$ for a Zr-based metallic glass (Dubach et al., 2009) reported in uniaxial compression experiments. This suggests that the energy $\text{Γ}$ depends on the composition of metallic glasses and their processing route.

The predicted critical stress values for the homogeneous glasses (HGs) match very well with the observed deformation modes as shown in Figure4. The only exception is the Cu–Zr nanopillar with D = 9 nm. In case of the NG nanopillars, the data fall in the homogeneous regime. The only clear exceptions are the data for the nanopillars with D $\ge$ 54 nm. Interestingly, the Cu–Zr and Pd–Si NG nanopillars have the same critical stress values. This is consistent with the results in Figures 1E,F which show that the deformation modes for the Cu–Zr and Pd–Si NG nanopillars are similar. The relative good agreement with the model prediction is implying that the more homogeneous deformation of NGs can also be understood as a mere modulus effect.

FIGURE 4

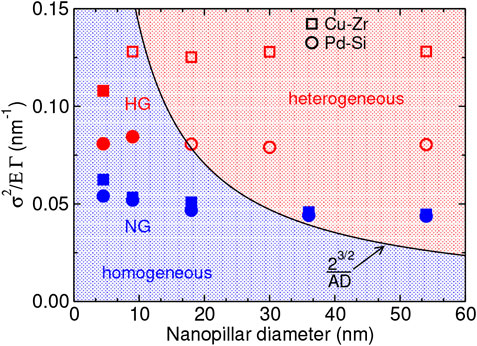
FIGURE 4. Flow stress normalized by Young’s modulus and shear band energy per unit area as a function of the nanopillar diameter at 5% total strain. Red squares and red circles represent Cu₆₄Zr₃₆ and Pd₈₀Si₂₀ homogeneous glass (HG) nanopillars, respectively. Blue squares and blue circles represent Cu₆₄Zr₃₆ and Pd₈₀Si₂₀nanoglass (NG) nanopillars, respectively. Open symbols indicate the occurrence of a shear band.

4Discussion

The results presented above are for nanopillars with diameters up to 54 nm. This size is much smaller than that used in experiment which is about 400 nm (Wang et al., 2015). Sample preparation and mechanical testing in experiments make it difficult to prepare nanopillars with diameters below 100 nm (Shi, 2019). On the other hand, the increase of the nanopillar size in MD simulation leads to the increase of the number of atoms, and this becomes computationally expensive. Although the sample size mismatched between MD simulation and experiment, MD simulation is useful to understand experimental observations (Liontas et al., 2016). From the present MD results, one can see that, for both systems, Cu–Zr and Pd–Si, the 36 and 54 nm NG nanopillars exhibit a similar mechanical behavior. This may be attributed to the small surface-to-volume fraction which leads to the deformation to be dominated by the interfaces rather than by the surface. Indeed, a recent MD simulation study on HG nanopillars has shown that the surface stress becomes less significant when the nanopillar diameter is larger than 30 nm (Zhang et al., 2015). Thus, one could expect that NG nanopillars with diameters larger than 54 nm should show a similar mechanical behavior as the 36 and 54 nm nanopillars.

Present MD simulation results on HG nanopillars show that the transition from necking to shear banding occurs at a diameter between 10 and 20 nm. These results are in agreement with previous MD simulation results which reported that size-independent shear banding until their dimensions approach the shear-band thickness which is about 5–20 nm (Adibi et al., 2016; Liontas et al., 2016; Shi, 2019). This transition appears in experiments at a lager sample diameter, between 100 and 400 nm, as compared with MD simulations (Tian et al., 2016). This difference in the sample size on the change of the deformation mode between experiments and simulations can be related to the different processing and testing conditions (Shi, 2019).

Simulations of NG nanopillars reveal no shear banding: NG nanopillars exhibit necking or homogeneous deformation. Homogeneous deformation occurs in the 9 and 18 nm NG nanopillars, where their length is not long enough to allow strain localization to form necking. Necking deformation mode was also reported in previous MD simulations on the Cu₆₄Zr₃₆ NG nanopillars with a diameter of 50 nm (Adibi et al., 2015a; Adibi et al., 2016).

The NG nanopillars studied in the present study are cut from an as-prepared NG. Structural relaxation due to the high compaction rate used in simulation during the preparation of the NG may change the deformation mode. Indeed, a recent study on the compression test of Pd–Si NG nanopillar with a diameter of 36 nm showed a change in the deformation mode from homogeneous deformation to shear banding when the nanopillar is cut from an annealed NG (Nandam et al., 2020). The effect of annealing on the change of the deformation mode was also reported in a recent experiment and simulation study on Zr–Ni–Al nanosized metallic glasses (Liontas et al., 2016).

5Conclusions

We have investigated the influence of structure size on the mechanical properties of NG and HG nanopillars with 7 nm grain size and diameters ranging from 4.5 up to 54 nm by means of MD simulations. Simulations were done for two different glasses, namely, Cu₆₄Zr₃₆ and Pd₈₀Si₂₀, as representatives of metal–metal and metal–metalloid systems, respectively. Different from previous studies, the NGs were produced by consolidation rather than Voronoi tessellation and thus have a more realistic microstructure.

Our results show a clear difference in the deformation mode between NG and HG for the 36 and 54 nm nanopillars, independent of the glass type. While HG nanopillars exhibit a stress drop and strain localization developing in a shear band, NG nanopillars show ductile deformation behavior with softening at larger engineering strains and deformation by necking. The tensile ductility of about 13–15% found in our simulations is in agreement with 15% plastic strain observed for a 400 nm Sc₇₅Fe₂₅ NG nanopillar using in situ tensile tests in a transmission electron microscope (Wang et al., 2015). HG and NG nanopillars with D = 4.5 nm, where the pillar diameter is smaller than the average grain size d = 7 nm of the NG, deform by necking since the nucleation of STZs on the surface is dominating. In the HG nanopillars with D = 9 and 18 nm, shear banding is more obvious in Cu₆₄Zr₃₆ than in Pd₈₀Si₂₀. When reducing the NG nanopillar diameter to near or double the average grain size, strain softening appears at the larger engineering strain (>20%). Moreover, structural relaxation after a cyclic loading leads to local recovery, and the stress increases upon reloading.

We determined Young’s modulus and yield strengths from stress–strain curves of tensile deformations. We find that both properties are smaller in the NG nanopillars as compared with their homogeneous counterparts in both glasses. From Young’s modulus values and the shear band energy, the critical stress for shear band formation is estimated. We find that the predicted critical stress values are quite consistent with the observed deformation modes.

Data Availability Statement

All datasets generated for this study are included in the article and Supplementary Material.

Author Contributions

OA and KA contributed equally to the conception and design of this study; OA set up and ran the simulations, performed the analysis, and wrote the first draft of the manuscript; KA supervised the work and reviewed and edited the manuscript.

Funding

The authors acknowledge the financial support of the Deutsche Forschungsgemeinschaft (DFG) through project no. AL 578/15–2.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors gratefully acknowledge the Gauss Centre for Supercomputing e.V. (www.gauss-centre.eu) for funding this project by providing computing time through the John von Neumann Institute for Computing (NIC) on the GCS Supercomputer JUWELS at Jülich Supercomputing Centre (JSC). Computational time was also made available by the Lichtenberg High Performance Computer Cluster at TU Darmstadt.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2020.544660/full#supplementary-material.

References

Adibi, S., Branicio, P. S., and Ballarini, R. (2016). Compromising high strength and ductility in nanoglass-metallic glass nanolaminates. RSC Adv. 6, 13548–13553. doi:10.1039/C5RA24715B

CrossRef Full Text | Google Scholar

Adibi, S., Branicio, P. S., and Joshi, S. P. (2015a). Suppression of shear banding and transition to necking and homogeneous flow in nanoglass nanopillars. Sci. Rep. 5, 15611. doi:10.1038/srep15611

CrossRef Full Text | Google Scholar

Adibi, S., Branicio, P. S., Liontas, R., Chen, D. Z., Greer, J. R., Srolovitz, D. J., et al. (2015b). Surface roughness imparts tensile ductility to nanoscale metallic glasses. Extreme Mech. Lett. 5, 88–95. doi:10.1016/j.eml.2015.08.004

CrossRef Full Text | Google Scholar

Adibi, S., Branicio, P. S., Zhang, Y.-W., and Joshi, S. P. (2014). Composition and grain size effects on the structural and mechanical properties of CuZr nanoglasses. J. Appl. Phys. 116, 043522. doi:10.1063/1.4891450

CrossRef Full Text | Google Scholar

Adibi, S., Sha, Z.-D., Branicio, P. S., Joshi, S. P., Liu, Z.-S., and Zhang, Y.-W. (2013). A transition from localized shear banding to homogeneous superplastic flow in nanoglass. Appl. Phys. Lett. 103, 211905. doi:10.1063/1.4833018

CrossRef Full Text | Google Scholar

Adjaoud, O., and Albe, K. (2016). Interfaces and interphases in nanoglasses: surface segregation effects and their implications on structural properties. Acta Mater. 113, 284. doi:10.1016/j.actamat.2016.05.002

CrossRef Full Text | Google Scholar

Adjaoud, O., and Albe, K. (2018). Microstructure formation of metallic nanoglasses: insights from molecular dynamics simulations. Acta Mater. 145, 322–330. doi:10.1016/j.actamat.2017.12.014

CrossRef Full Text | Google Scholar

Adjaoud, O., and Albe, K. (2019). Influence of microstructural features on the plastic deformation behavior of metallic nanoglasses. Acta Mater. 168, 393–400. doi:10.1016/j.actamat.2019.02.033

CrossRef Full Text | Google Scholar

Albe, K., Ritter, Y., and Şopu, D. (2013). Enhancing the plasticity of metallic glasses: shear band formation, nanocomposites and nanoglasses investigated by molecular dynamics simulations. Mech. Mater. 67, 94–103. doi:10.1016/j.mechmat.2013.06.004

CrossRef Full Text | Google Scholar

An, Q., Samwer, K., Demetriou, M. D., Floyd, M. C., Duggins, D. O., Johnson, W. L., et al. (2016). How the toughness in metallic glasses depends on topological and chemical heterogeneity. Proc. Natl. Acad. Sci. U. S. A. 113, 7053–7058. doi:10.1073/pnas.1607506113

CrossRef Full Text | Google Scholar

Brostow, W., Dussault, J.-P., and Fox, B. L. (1978). Construction of voronoi polyhedra. J. Comput. Phys. 29, 81–92. doi:10.1016/0021-9991(78)90110-9

CrossRef Full Text | Google Scholar

Cao, A. J., Cheng, Y. Q., and Ma, E. (2009). Structural processes that initiate shear localization in metallic glass. Acta Mater. 57, 5146 – 5155.

10.1016/j.actamat.2009.07.016CrossRef Full Text | Google Scholar

Chen, C. Q., Pei, Y. T., and De Hosson, J. T. M. (2010). Effects of size on the mechanical response of metallic glasses investigated through in situ TEM bending and compression experiments. Acta Mater. 58, 189–200. doi:10.1016/j.actamat.2009.08.070

CrossRef Full Text | Google Scholar

Cheng, B., and Trelewicz, J. R. (2019a). Controlling interface structure in nanoglasses produced through hydrostatic compression of amorphous nanoparticles. Phys. Rev. Materials. 3, 035602. doi:10.1103/PhysRevMaterials.3.035602

CrossRef Full Text | Google Scholar

Cheng, B., and Trelewicz, J. R. (2019b). Interfacial plasticity governs strain delocalization in metallic nanoglasses. J. Mater. Res. 34, 2325–2336. doi:10.1557/jmr.2019.101

CrossRef Full Text | Google Scholar

Cheng, Y. Q., Ding, J., and Ma, E. (2013). Local Topologyvs.Atomic-level stresses as a measure of disorder: correlating structural indicators for metallic glasses. Mater. Res. Lett. 1, 3–12. doi:10.1080/21663831.2012.722759

CrossRef Full Text | Google Scholar

Cheng, Y. Q., and Ma, E. (2011). Intrinsic shear strength of metallic glass. Acta Mater. 59, 1800–1807.

10.1016/j.actamat.2010.11.046CrossRef Full Text | Google Scholar

Ding, J., Cheng, Y.-Q., Sheng, H., and Ma, E. (2012). Short-range structural signature of excess specific heat and fragility of metallic-glass-forming supercooled liquids. Phys. Rev. B 85, 060201. doi:0.1103/PhysRevB.85.060201

CrossRef Full Text | Google Scholar

Dubach, A., Raghavan, R., Loffler, J., Michler, J., and Ramamurty, U. (2009). Micropillar compression studies on a bulk metallic glass in different structural states. Scripta Mater. 60, 567–570. doi:10.1016/j.scriptamat.2008.12.013

CrossRef Full Text | Google Scholar

Fang, J. X., Vainio, U., Puff, W., Würschum, R., Wang, X. L., Wang, D., et al. (2012). Atomic structure and structural stability of Sc75Fe25 nanoglasses. Nano Lett. 12, 458–463. doi:10.1021/nl2038216

CrossRef Full Text | Google Scholar

Finney, J. L.. (1979). A procedure for the construction of voronoi polyhedra. J. Comput. Phys. 32, 137–143.

10.1016/0021-9991(79)90146-3CrossRef Full Text | Google Scholar

Gleiter, H. (2008). Our thoughts are ours, their ends none of our own: are there ways to synthesize materials beyond the limitations of today? Acta Mater. 56, 5875–5893. doi:10.1016/j.actamat.2008.08.028

CrossRef Full Text | Google Scholar

Gleiter, H. (2013). Nanoglasses: a new kind of noncrystalline materials. Beilstein J. Nanotechnol. 4, 517–533. doi:10.3762/bjnano.4.61

CrossRef Full Text | Google Scholar

Gleiter, H. (2016). Nanoglasses: a new kind of noncrystalline material and the way to an age of new technologies?. Small 12, 2225–2233. doi:10.1002/smll.201500899

CrossRef Full Text | Google Scholar

Gleiter, H., Schimmel, T., and Hahn, H. (2014). Nanostructured solids - from nano-glasses to quantum transistors. Nano Today. 9, 17–68. doi:10.1016/j.nantod.2014.02.008

CrossRef Full Text | Google Scholar

Ivanisenko, Y., Kübel, C., Nandam, S. H., Wang, C., Mu, X., Adjaoud, O., et al. (2018). Structure and properties of nanoglasses. Adv. Eng. Mater. 20, 1800404. doi:10.1002/adem.201800404

CrossRef Full Text | Google Scholar

Jiang, M. Q., Wilde, G., and Dai, L. H. (2015). Origin of stress overshoot in amorphous solids. Mech. Mater. 81, 72–83.

10.1016/j.mechmat.2014.10.002CrossRef Full Text | Google Scholar

Jing, J., Krämer, A., Birringer, R., Gleiter, H., and Gonser, U. (1989). Modified atomic structure in a Pd‐Fe‐Si nanoglass. J. Non-Cryst. Solids. 113, 167–170. doi:10.1016/0022-3093(89)90007-0

CrossRef Full Text | Google Scholar

Kawamura, Y., Shibata, T., Inoue, A., and Masumoto, T. (1997). Stress overshoot in stress-strain curves of Zr65Al10Ni10Cu15 metallic glass. Appl. Phys. Lett. 71, 779–781. doi:10.1063/1.119643

CrossRef Full Text | Google Scholar

Li, F. C., Wang, T. Y., He, Q. F., Sun, B. A., Guo, C. Y., Feng, T., et al. (2018). Micromechanical mechanism of yielding in dual nano-phase metallic glass. Scripta Mater. 154, 186–191. doi:10.1016/j.scriptamat.2018.05.050

CrossRef Full Text | Google Scholar

Liontas, R., Jafary-Zadeh, M., Zeng, Q., Zhang, Y.-W., Mao, W. L., and Greer, J. R. (2016). Substantial tensile ductility in sputtered Zr-Ni-Al nano-sized metallic glass. Acta Mater. 118, 270–285. doi:10.1016/j.actamat.2016.07.050

CrossRef Full Text | Google Scholar

Liu, C., Roddatis, V., Kenesei, P., and Maaß, R. (2017). Shear-band thickness and shear-band cavities in a zr-based metallic glass. Acta Mater. 140, 206–216.

10.1016/j.actamat.2017.08.032CrossRef Full Text | Google Scholar

Liu, Z., Li, R., Wang, G., Wu, S., Lu, X., and Zhang, T. (2011). Quasi phase transition model of shear bands in metallic glasses. Acta Mater. 59, 7416–7424.

10.1016/j.actamat.2011.08.002CrossRef Full Text | Google Scholar

Lu, J., Ravichandran, G., and Johnson, W. L. (2003). Deformation behavior of the Zr41.2Ti13.8Cu12.5Ni10Be22.5 bulk metallic glass over a wide range of strain-rates and temperatures. Acta Mater. 51, 3429–3443.

10.1016/S1359-6454(03)00164-2CrossRef Full Text | Google Scholar

Maaß, R., Klaumünzer, D., Villard, G., Derlet, P. M., and Löffler, J. F. (2012). Shear-band arrest and stress overshoots during inhomogeneous flow in a metallic glass. Appl. Phys. Lett. 100, 071904. doi:10.1063/1.3684871

CrossRef Full Text | Google Scholar

Mendelev, M. I., Kramer, M. J., Ott, R. T., Sordelet, D. J., Yagodin, D., and Popel, P. (2009). Development of suitable interatomic potentials for simulation of liquid and amorphous Cu-Zr alloys. Phil. Mag. 89, 967–987. doi:10.1080/14786430902832773

CrossRef Full Text | Google Scholar

Mendelev, M. I., Ott, R. T., Heggen, M., Feuerebacher, M., Kramer, M. J., and Sordelet, D. J. (2008). Deformation behavior of an amorphous Cu64.5Zr35.5 alloy: a combined computer simulation and experimental study. J. Appl. Phys. 104, 123532. doi:10.1063/1.3043587

CrossRef Full Text | Google Scholar

Mizubayashi, H., Okamoto, T., Koyama, K., and Horiuchi, M. (1998). Dynamic anelastic response of amorphous alloys suggesting collective motions of many atoms. Acta Mater. 46, 1257–1264.

10.1016/S1359-6454(97)00283-8CrossRef Full Text | Google Scholar

Murali, P., Zhang, Y. W., and Gao, H. J. (2012). On the characteristic length scales associated with plastic deformation in metallic glasses. Appl. Phys. Lett. 100, 201901. doi:10.1063/1.4717744

CrossRef Full Text | Google Scholar

Nandam, S. H., Adjaoud, O., Schwaiger, R., Ivanisenko, Y., Chellali, M. R., Wang, D., et al. (2020). Influence of topological structure and chemical segregation on the thermal and mechanical properties of Pd-Si nanoglasses. Acta Mater. 193, 252–260. doi:10.1016/j.actamat.2020.03.021

CrossRef Full Text | Google Scholar

Nandam, S. H., Ivanisenko, Y., Schwaiger, R., Śniadecki, Z., Mu, X., Wang, D., et al. (2017). Cu-Zr nanoglasses: atomic structure, thermal stability and indentation properties. Acta Mater. 136, 181–189. doi:10.1016/j.actamat.2017.07.001

CrossRef Full Text | Google Scholar

Plimpton, S. (1995). Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 117, 1–19.

10.1006/jcph.1995.1039CrossRef Full Text | Google Scholar

Ritter, Y., and Albe, K. (2012). Chemical and topological order in shear bands of Cu64Zr36 and Cu36Zr64 glasses. J. Appl. Phys. 111, 103527. doi:10.1063/1.4717748

CrossRef Full Text | Google Scholar

Ritter, Y., Şopu, D., Gleiter, H., and Albe, K. (2011). Structure, stability and mechanical properties of internal interfaces in Cu64Zr36 nanoglasses studied by MD simulations. Acta Mater. 59, 6588–6593. doi:10.1016/j.actamat.2011.07.013

CrossRef Full Text | Google Scholar

Şopu, D., and Albe, K. (2015). Influence of grain size and composition, topology and excess free volume on the deformation behavior of Cu–Zr nanoglasses. Beilstein J. Nanotechnol. 6, 537–545. doi:10.3762/bjnano.6.56

CrossRef Full Text | Google Scholar

Şopu, D., Albe, K., Ritter, Y., and Gleiter, H. (2009). From nanoglasses to bulk massive glasses. Appl. Phys. Lett. 94, 191911. doi:10.1063/1.3130209

CrossRef Full Text | Google Scholar

Şopu, D., Ritter, Y., Gleiter, H., and Albe, K. (2011). Deformation behavior of bulk and nanostructured metallic glasses studied via molecular dynamics simulations. Phys. Rev. B 83, 100202. doi:10.1103/PhysRevB.83.100202

CrossRef Full Text | Google Scholar

Sha, Z., Wong, W. H., Pei, Q., Branicio, P. S., Liu, Z., Wang, T., et al. (2017). Atomistic origin of size effects in fatigue behavior of metallic glasses. J. Mech. Phys. Solid. 104, 84–95. doi:10.1016/j.jmps.2017.04.005

CrossRef Full Text | Google Scholar

Sha, Z. D., Qu, S. X., Liu, Z. S., Wang, T. J., and Gao, H. (2015). Cyclic deformation in metallic glasses. Nano Lett. 15, 7010–7015. doi:10.1021/acs.nanolett.5b03045

CrossRef Full Text | Google Scholar

Shao, Y., Yao, K., Li, M., and Liu, X. (2013). Two-zone heterogeneous structure within shear bands of a bulk metallic glass. Appl. Phys. Lett. 103, 171901. doi:10.1063/1.4826117

CrossRef Full Text | Google Scholar

Shi, Y. (2019). Size-dependent mechanical responses of metallic glasses. Int. Mater. Rev. 64, 163–180. doi:10.1080/09506608.2018.1476079

CrossRef Full Text | Google Scholar

Stukowski, A. (2010). Visualization and analysis of atomistic simulation data with OVITO-the Open Visualization Tool. Model. Simulat. Mater. Sci. Eng. 18, 015012. doi:10.1088/0965-0393/18/1/015012

CrossRef Full Text | Google Scholar

Tanemura, M., Ogawa, T., and Ogita, N. (1983). A new algorithm for three-dimensional voronoi tessellation. J. Comput. Phys. 51, 191–207. doi:10.1016/0021-9991(83)90087-6

CrossRef Full Text | Google Scholar

Tang, C., Laws, K., and Ferry, M. (2018). Atomistic origin of stress overshoots and serrations in a cuzr metallic glass. Materialia 1, 121–127. doi:10.1016/j.mtla.2018.04.005

CrossRef Full Text | Google Scholar

Tian, L., Wang, X.-L., and Shan, Z.-W. (2016). Mechanical behavior of micronanoscaled metallic glasses. Mater. Res. Lett. 4, 63–74. doi:10.1080/21663831.2015.1124298

CrossRef Full Text | Google Scholar

Volkert, C. A., Donohue, A., and Spaepen, F. (2008). Effect of sample size on deformation in amorphous metals. J. Appl. Phys. 103, 083539. doi:10.1063/1.2884584

CrossRef Full Text| Google Scholar

Wang, C., Wang, D., Mu, X., Goel, S., Feng, T., Ivanisenko, Y., et al. (2016a). Surface segregation of primary glassy nanoparticles of Fe90Sc10 nanoglass. Mater. Lett. 181, 248–252. doi:10.1016/j.matlet.2016.05.189

CrossRef Full Text | Google Scholar

Wang, X., Jiang, F., Hahn, H., Li, J., Gleiter, H., Sun, J., et al. (2016b). Sample size effects on strength and deformation mechanism of Sc75Fe25 nanoglass and metallic glass. Scripta Mater. 116, 95–99. doi:10.1016/j.scriptamat.2016.01.036

CrossRef Full Text | Google Scholar

Wang, X. L., Jiang, F., Hahn, H., Li, J., Gleiter, H., Sun, J., et al. (2015). Plasticity of a scandium-based nanoglass. Scripta Mater. 98, 40–43. doi:10.1016/j.scriptamat.2014.11.010

CrossRef Full Text | Google Scholar

Weissmüller, J., Birringer, R., and Gleiter, H. (1992). Nanostructured crystalline and amorphous solids. Kemi 77-78, 161–170. doi:10.4028/www.scientific.net/kem.77-78.161

CrossRef Full Text | Google Scholar

Yang, Z.-Y., Wang, Y.-J., and Dai, L.-H. (2019). Susceptibility of shear banding to chemical short-range order in metallic glasses. Scripta Mater. 162, 141–145.

10.1016/j.scriptamat.2018.11.001CrossRef Full Text | Google Scholar

Yao, K. F., Ruan, F., Yang, Y. Q., and Chen, N. (2006). Superductile bulk metallic glass. Appl. Phys. Lett. 88, 122106. doi:10.1063/1.2187516

CrossRef Full Text | Google Scholar

Zhang, Q., Li, Q.-K., and Li, M. (2015). Internal stress and its effect on mechanical strength of metallic glass nanowires. Acta Mater. 91, 174–182. doi:10.1016/j.actamat.2015.03.029

CrossRef Full Text | Google Scholar

Zhang, Y., and Greer, A. L. (2006). Thickness of shear bands in metallic glasses. Appl. Phys. Lett. 89, 071907. doi:10.1063/1.2336598

CrossRef Full Text | Google Scholar

Zhong, C., Zhang, H., Cao, Q. P., Wang, X. D., Zhang, D. X., and Jiang, J. Z. (2015). The size-dependent non-localized deformation in a metallic alloy. Scripta Mater. 101, 48–51. doi:10.1016/j.scriptamat.2015.01.015

CrossRef Full Text | Google Scholar

Zhu, B., Huang, M., and Li, Z. (2017). Brittle to ductile transition of metallic glasses induced by embedding spherical nanovoids. J. Appl. Phys. 122, 215108. doi:10.1063/1.4997281

CrossRef Full Text | Google Scholar