- Department of Physics and Astronomy, University of Missouri-Kansas City, Kansas City, MO, United States
Binary and ternary transition metal carbides are stable ceramic crystals with outstanding mechanical properties. In recent years, multicomponent single-phase high entropy alloys enjoyed explosive growth due to many of their outstanding physical properties with its large and flexible composition space. Hence the composite between them can be advantageous in forming a new class of ceramic materials with combined superiority in their properties for many applications. On the basis of a systematic large-scale ab initio simulations using density functional theory that are specifically designed for their compositional variations, subtle differences in their structures, electronic and mechanical properties are revealed and discussed in detail. Fifteen supercell models with 512 atoms with equal composition of C and high entropy alloys occupying the sub-lattices of the rock-slat structure were constructed. These models are fully optimized, and their properties carefully characterized, compared and contrasted. By applying the novel concept of total bond order density and its partial components, the partial bond order density, we revealed many subtle variations in their properties that have not been known before. This large database can play an important and valuable role in the design and synthesis of high entropy ceramic carbides.
Introduction
Following the pioneer work less than two decades ago (Senkov et al., 2013; Zhang et al., 2014; Sun et al., 2017; Ding et al., 2018), high entropy alloys (HEAs) is now a flourishing research area in metal alloys with no insight. HEAs are complex multicomponent homogeneous single crystalline alloys (Gao et al., 2016; Lim, 2016; Ye et al., 2016; Miracle and Senkov, 2017) comprised of four, five or more principal components in near equal concentrations. They possess many outstanding physical properties including high strength and ductility (Senkov et al., 2011; Gali and George, 2013; Gludovatz et al., 2014; Lim, 2016; Ye et al., 2016; Li et al., 2016; Li et al., 2017; Tsao et al., 2017), hardness (Senkov et al., 2010; Senkov et al., 2013; Ye et al., 2016), superconductivity (Von Rohr et al., 2016) and much more. These novel alloys have high entropy of mixing thus favor the formation of single phase disordered solid solutions at higher temperatures (Zhang et al., 2014; Li et al., 2016). Although the enthalpy certainly plays a critical role in determining its composition and phase stability in the absence of long-range-order (Miracle and Senkov, 2017; Santodonato et al., 2018), uncertainty remains regarding the possible existence of short-range-orders and the nature of their origin (Li et al., 2019). Disorder do exists in HEAs during experimental synthesis when they encounter precipitation, undergo elemental segregation, and variation in chemical ordering at different temperature. The fundamental theory for the formation of HEAs is still not fully established since their inception (Senkov et al., 2013; Zhang et al., 2014; Sun et al., 2017; Ding et al., 2018) due to the complexity of their compositions, difficulties encountered in synthesis, precision in experimental measurements, and proper comparison with modeling efforts. Most of these efforts are based on different perspectives and techniques. They are quite scattered, which is one of the main reasons for HEAs to be a flourishing and highly crowded area of contemporary alloy research.
Transition metal (TM) carbides have been a significant portion of ceramic materials since early 1930s (Agte and Alterthum, 1930). They are binary or ternary crystals with well-defined crystalline structures and some of them are known for exceptionally high melting temperature e.g. Ti3C2Si and Ta4HfC5 (Agte and Alterthum, 1930). The binary TM carbides have the FCC rock-salt structure with two sub-lattices and strong TM-C bonds. It is therefore obvious that the composites formed between multicomponent HEAs and carbon can be especially advantageous in forming a new class of ceramic materials with combined superiority in their properties such as increased thermal stability, enhanced mechanical properties, corrosion and oxidation resistance for special applications especially at ultrahigh temperature (Sarker et al., 2018; Harrington et al., 2019). The term for HEA-carbide is essentially to generalize the same TM-C bond as in the respective cases in the hope of additional advantages offered by multicomponent TMs. The first successful demonstration of the HEA-ceramics is by Rost et al. (2015). This is followed by the recent work on (Hf-Ta-Zr-Nb)C by Dusza et al. (2018) and Zhou et al. (2018) on (Ti-Zr-Hf-Nb-Ta)C.
It should be pointed out that there are many recent works in which a small amount of C, usually less than 5 atomic %, are added to mostly FCC HEAs such the as the standard Canton alloy CrMnFeCoNi (Stepanov et al., 2016; Cheng et al., 2017; Wang et al., 2017; Ikeda et al., 2019) to investigate the resulting local structural variations, formation of microstructures and precipitates and potential enhancement of their properties. These works are completely different from the HEAs-carbides composites in which C constitute 50% of the lattice sites.
Computational modelling has been an important component in HEA research and more recently in HEA-C (Sarker et al., 2018; Zhang et al., 2019) and other HEA-ceramics (Yang et al., 2018). They use different method and approaches follow the accepted concept of the random solid-solution-model (RSSM) for HEAs (Tian, 2017; Widom, 2018; LaRosa et al., 2019). These theoretical and computational methods for HEAs are widely spread out and include the use of CALPHAD (Senkov et al., 2013; Miracle and Senkov, 2017; Sanchez et al., 2019), special quasi-random-structure (SQS) (Zunger et al., 1990; Curtarolo et al., 2013; Yang et al., 2018), coherent potential approximations (EMTO-CPA) (Tian et al., 2016), effective medium theory (Huang et al., 2018), and different levels of density functional theory (DFT) (Chen et al., 2018) on small-size supercells. Despite a plethora of methods used, few of them can provide a comprehensive view on their formation and the prediction of their properties. Recently, we have reported a systematic study of 13 biocompatible HEAs in BCC lattice consists of refractory TMs (Ching et al., 2020). We used large supercells of 250 atoms each and the random solid-solution-model protocol. The results include in-depth analysis of their electronic structures, interatomic bonding, and predict HEA properties based on the use of the novel quantum mechanical metric, the total bond order density (TBOD) and the partial bond order density (PBOD) resulting in many new insights. This work has special merits because of 1) using large supercells; 2) accurate and large-scale DFT calculations; and 3) detailed interpretation of the results on the subtle interactions between different metal atoms.
We now extend the above ab initio simulation on pure HEAs to HEA-carbide composites in the FCC rock salt (NaCl) structure that retain the short-range-orders in binary carbides. We specifically designed a total of 15 supercell models with 50% of C and 50% of HEA among nine different TM elements to test the data-driven concept of simulating a large number of models and identify subtle differences. In these models, TMs and C occupied different sub-lattice sites. There are two types of interatomic bonding. The nearest neighbors (NN) TM-C bonding and the second NN TM-TM bonding with larger distance separations.
It should be pointed out that we used a completely different philosophy and method from the recent work of Sarker et al. (2018) although the goals are the same. Our main conclusion is the total verification of the concept the HEA-carbides retain the same short range order as in the respectively binary carbides with new twist to adjust and improve the mechanical properties by extending to multi-component HEA of TMs. The main focus is on model m1 (Ti10Nb10Ta10Zr10Mo10C50) shown in Figure 1. Other models essentially test the compositional variations from m1. Information on the structure and properties relationship at atomic scale of HEA carbide ceramics is much less available in comparison with the conventional HEAs. A large database on DFT calculations that can be used for future predictions is very valuable. In other words, computational modelling on HEA-C materials can help in exploring and developing novel HEA ceramics.
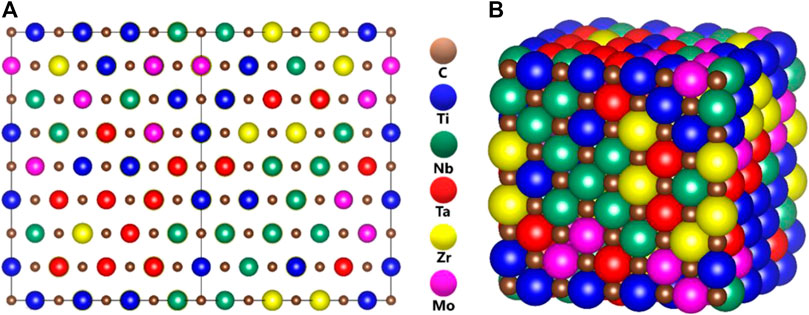
FIGURE 1. Illustration of disordered solid solution alloys of TiNbTaZrMo-C models (A) balls, and (B) space-filling.
Model Construction and Methods
The supercells are constructed from (4 × 4 × 4) of FCC rock salt (NaCl) lattice which has 512 lattice sites. The sublattice A or the 256 anion sites are fully populated by C atoms and the sub-lattice B or the 256 cation sites are randomly occupied by five TM elements in equal or nearly equal proportion. The refractory TM elements involved in these models are Ti, V, Cr, Zr, Nb, Mo, Hf, Ta, and W, They are distributed randomly in nearly equal percentage to construct two 4-component, seven 5-component, and one 6-component HEAs in the cation sub-lattice. The 4-TM component HEA-C contains 64 atoms each, the 5-TM components contains one TM with 52 and the rest with 51 atoms, and the 6-TM components contains two TMs with 42 atoms, and the other four with 43 atoms each. It is important to note that the TM components are distributed randomly in the cation sub-lattice sites of the supercell with periodic boundaries. The carbon atoms are in the other sub-lattice have different NN TMs. The supercell we constructed for the 15 HEA models differ from the quasi-random-structure SQS structure used in other studies) (Zunger et al., 1990; Curtarolo et al., 2013; Yang et al., 2018), and also claimed to be supercells but are usually much smaller in size.
In order to reveal the subtle differences due to different compositions and atomic components in these 15 models listed in Table 1, we consciously divide them into six groups (G1–G6) for specific comparison and focused discussion.
G1: (TiNbTaZrMo)50C50. This consists of a single model m1 which is central to this paper since all other models are morphed from m1 with specific modifications.
G2: 5 models with progressively reduced carbon contents from m1: (m1A–m1E).
G3: 2 models with different Ti/Mo ratios in m1: (m1F, m1G).
G4: 4 models with five TM components by replacing Mo in m1 with V, Cr, W, Hf: (m2–m5).
G5: 1 model with six components by adding V to m1: (m6).
G6: 2 models by doubling the % of Zr and Ta over the other three TMs (Ti, Nb, Mo) in m1: (m7, m8).
Structural Relaxation
The Vienna ab initio simulation package (VASP) (Kresse and Furthmüller, 1996; Kresse and Furthmuller, 2002), which is highly effective for structure optimization, was employed to relax the initial model described above. Accurate optimization of the supercells for the TM-C composites is very important since each C atom will have different TM as NN with different interatomic bond lengths and interactions. We have used the projector augmented wave method with the Perdew-Burke-Ernzerhof exchange correlation functional (Perdew et al., 1996). Perdew-Burke-Ernzerhof is one of the most popular generalized gradient approximation (GGA) potentials and is reasonably accurate for alloy systems. A relatively high energy cutoff of 500 eV and the stringent electronic convergence criterion of 10–5 eV were adopted. The force convergence criteria for ionic relaxation was set at −10–3 eV/Å. We used a single k-point calculation since our models are in the form of large supercells and a single k-point calculation at the zone center is sufficient. This has been successfully demonstrated in many of our recent studies in bio-molecular systems, organic, inorganic and metallic crystals and glasses (Poudel et al., 2015; Adhikari et al., 2016; Poudel et al., 2016; Poudel et al., 2017; San et al., 2018).
Electronic Structure and Interatomic Bonding
The electronic structure calculations use the in-house developed orthogonalized linear combination of atomic orbitals (OLCAO) method (Ching and Rulis, 2012) with the VASP-relaxed structure as input. The all-electron OLCAO method uses the atomic orbitals in the basis expansion which is far more economical than the plane-wave basis and enable us to apply it to complex HEAs using supercells. The merits of the OLCAO method is well documented. In particular, the OLCAO method can provide the effective charge (Q*) or partial charge (PC) on each atom as well as the bond order (BO) values ραβ between any pairs of atoms. They are defined as:
In the above equations,
An important concept critical to the HEAs and its composites with carbon is the TBOD and PBOD. The summation of all BO values normalized by the cell volume gives us the TBOD, which is a single metric to assess the internal cohesion in the crystal or a supercell model (Dharmawardhana et al., 2014). The TBOD can be resolved into partial components or the PBOD for the different types of atomic pairs (TM-C, TM-TM), or other structural units or compositions in the supercell. The use of TBOD and PBOD as descriptors has special merits. They are based on the quantum-mechanical calculations and avoid the use of pure geometric parameters in describing their structures and properties. It can be applied to models with different numbers of atoms and compositions, or variations in the structures. For pure HEAs, this new concept is based on understanding the nature of metallic bonding critically related to the theory of formation of HEAs. Although metallic bonding has been extensively discussed in the field of metallic glasses (MGs) (Miller and Liaw, 2007; Pelletier and Qiao, 2019), it has not been thoroughly investigated for HEAs. Metallic bonding is multi-atomic in nature, different from the covalent or ionic bonding. In comparison with the use of the total energy or enthalpy of the system, it is far much simpler and avoid the use of large samplings necessary in the Boltzmann distribution such as in the descriptor called entropy-forming-ability (EFA) (Sarker et al., 2018). Entropy-forming-ability is based on a different theoretical method called automatic flow-partial occupation which utilizes a large number of samples of different configurations.
Mechanical Properties
For the elastic and mechanical properties of the HEAs, we used the stress (σj) vs strain (εj) response analysis scheme (Nielsen and Martin, 1983; Yao et al., 2007) on the fully relaxed structure from VASP. A small strain ε (±0.5%) is applied to the supercell to obtain the elastic coefficients Cij and compliance tensor Sij (i, j = 1, 2, 3, 4, 5, 6) by solving the following set of linear equations:
From the calculated
Results and Discussion
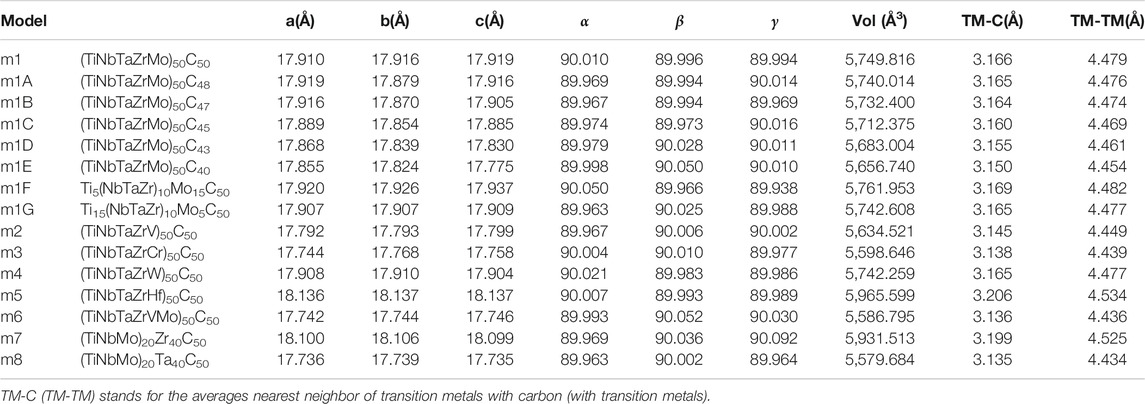
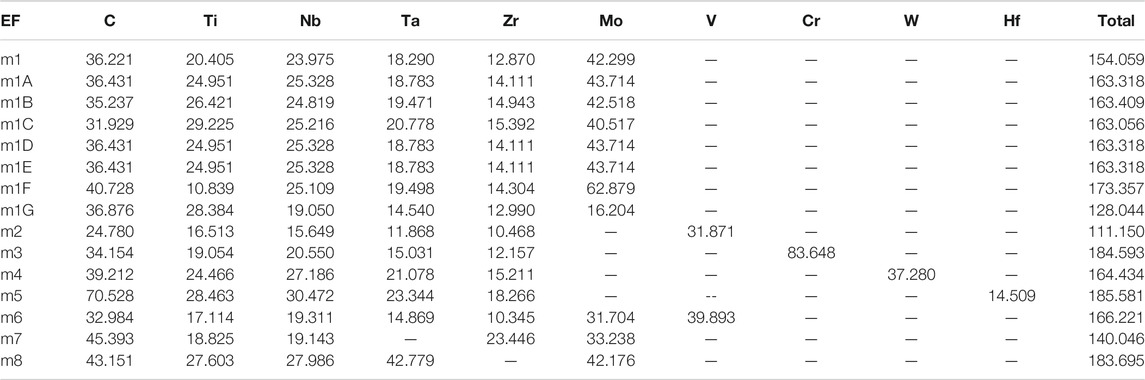
Before we specifically present and discuss the results for the six groups. We will firstly collectively present the equilibrium structure for each of the 15 models in Table 1 and their elastic and mechanical properties in Table 2 and the PC distribution on each atom in Table 3. Specific details and discussion on the electronic structures and interatomic bonding are presented below for the six groups, starting from m1, in order to facilitate the inter-comparison identify their salient features.
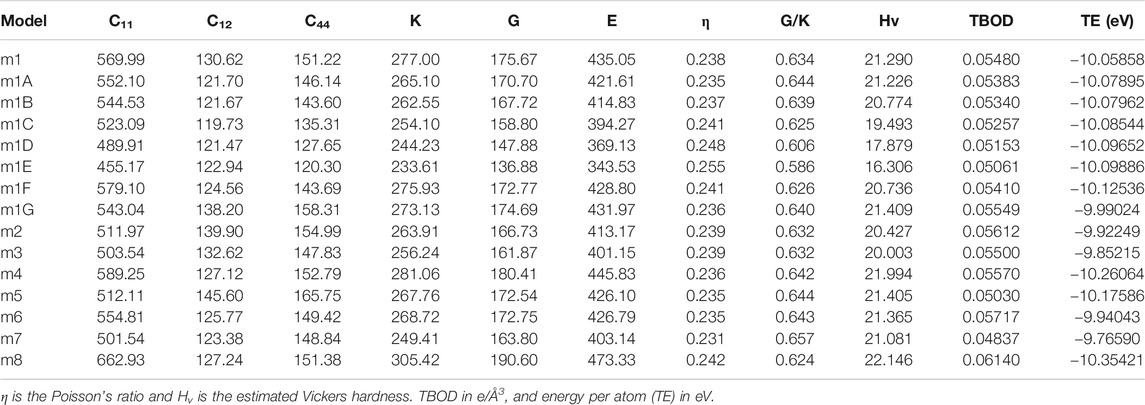
TABLE 2. Elastic coefficient Cij, bulk modulus (K), shear modulus (G) and Young’s modulus (E) in unit of GPa in 15 FCC HEAs.
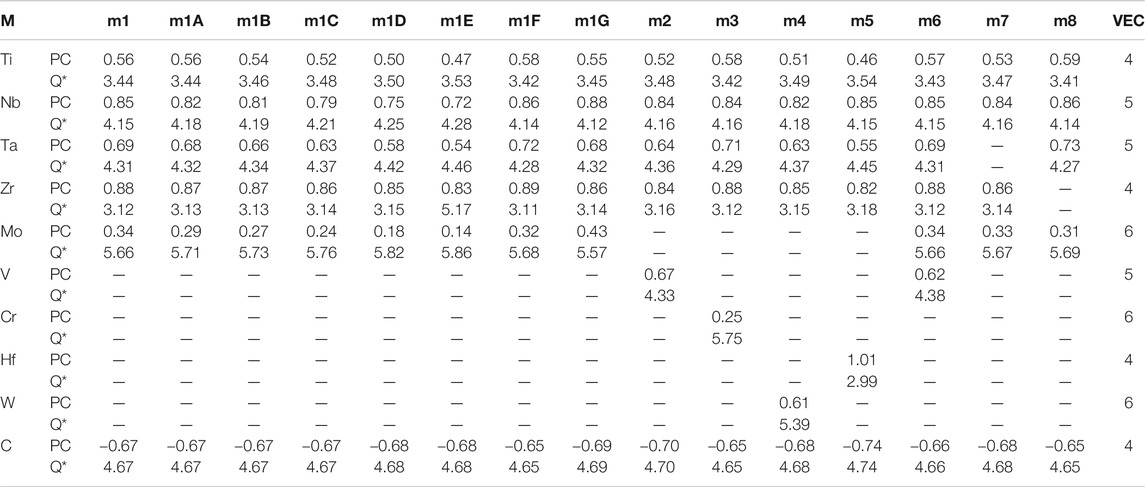
TABLE 3. Partial charge (PC) and effective charge (Q*) for each atom (in electrons) in the 15 investigated HEA models and in comparison with the standard valence electron count (VEC).
(TiNbTaZrMo)50C50, m1
Group 1 or model m1 is the main focus of HEA-carbide of the present work since other models are the derivatives of this model. It contains 50% of five TM elements Ti, Nb, Ta, Zr, Mo, and 50% of C. These five TMs in pure HEAs usually form in either FCC or BCC lattices (Todai et al., 2017; Ching et al., 2020). However, each of them, with very different atomic sizes form binary and ternary carbide with different specific properties. We choose these five refractory TMs as the most representative TM group for the study of HEA carbides (Sarker et al., 2018). As a matter of fact, the same 5-component in the pure HEAs in the BCC structure was the focus of the recently published work on 13 bio-compatible HEAs (Ching et al., 2020). In presenting the calculated results for m1, we also present the results of the 15 models collectively and discuss those results specific for each group later.
Figure 1 Shows the ball and stick illustration of model m1 in the FCC rock-slat structure of the 512-atom supercell. Similar illustrative figures of other models are not shown. Table 1 lists the equilibrium structures of these 15 models including the cell volume, the average NN TM-carbon (TM-C) and second NN (SNN) TM-TM bond length. For m1, these values are 5,749.816 (Å3), 3.166 Å, and 4.479 Å respectively. The supercells deviate only slightly from the cubic structure. No defective C-C bond or NN TM-TM bonds are identified in our simulation. Such perfect structures may not exist in real laboratory samples.
It is interesting to point out that the five refractory TM elements in m1 form pure HEA in BCC lattice [m3 in ref. (Ching et al., 2020)]. The number of TM in HEA-C is 256, very close to the 250 TM in pure HEA m3 of ref. (Ching et al., 2020). The main differences between the model TiNbTaZrMo in BCC and FCC-C lattice are all listed in Supplementary Table S1. It can be seen that the in HEA BCC lattice there is a significant lattice distortion, whereas the FCC HEA-C rock salt lattice, lattice distortion is negligible since all carbon atoms are in the anion sub-lattice. There is no TM-TM NN boning in the FCC-C model. This fundamental difference in the two models results in drastic difference in their mechanical properties. The FCC-C are significantly stronger than BCC HEA. The Vickers hardness of FCC-C is almost 10 times larger than BCC model. In addition to the comparison between FCC rock salt and BCC, the PC and effective charge of each element in these two models is quite different as shown in Supplementary Table S2.
The Calculated total DOS and atom-resolved partial DOS (PDOS) for m1 is shown in Figure 2. And those for all 15 models are shown in Supplementary Figure S1. As can been seem, the Fermi level at 0.0 eV locates very close to a local minimum in the TDOS, a signature of the stability of these TM carbides. The values of the DOS at the Fermi level or N (EF) and their atomic decomposition are listed in Table 4. For m1, N (EF) = 154.059 (States/eV) and their components are respectively 36.221, 20.405, 23.975, 18.290, 12.870, 42.299 (States/eV) for C, Ti, Nb, Ta, Zr, Mo, respectively.
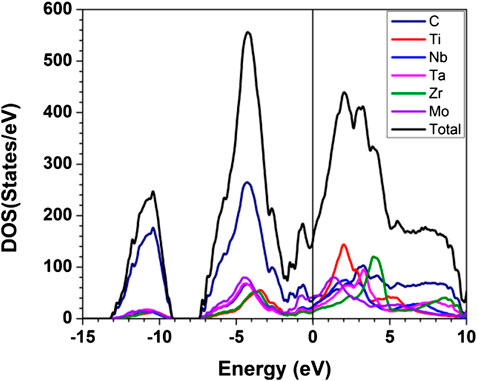
FIGURE 2. Calculated partial and total density of states for m1. The straight black line indicates the DOS at Fermi level.
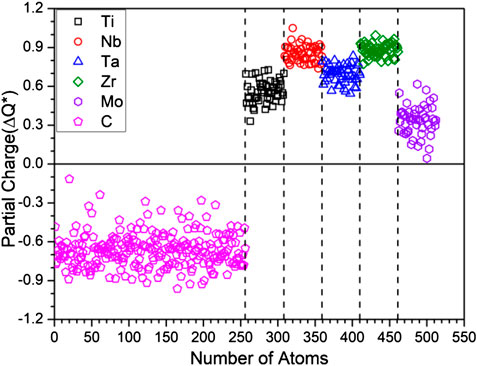
The calculated PC distribution in every atom in m1 is shown in Figure 3. Similar plots for all other models are shown in Supplementary Figure S2. Clearly, the C atoms lost charges to all TM elements. The amount of charge transfer depends on the specific TM and their local environment in the supercell. In m1, Mo receives less electrons from C, Nb and Zr receive the most with Ti and Ta in the middle. We now refer to Table 3 which list the PC, the effective charge Q* and the valence electron count (VEC) of each element in each in each model. In Supplementary Table S2, we compare the effective charges Q* and PC of same 2 models FCC-C-512 and BCC-250 in Supplementary Table S1. As can be seen, the same five TM elements Ti, Nb, Ta, Zr, Mo have very different values and trends although they have same VEC. This clearly demonstrate that VEC should never be used in any theory or explanations for HEAs or their composites.
In Figure 4, we display BO-BL for NN TM-C bonds and SNN TM-TM bonds. Similar plots for all other models are shown in Supplementary Figure S3. It can be seen that for the TM-C bonds, the data are somewhat clustered depending on the TM with the general trend of longer the BL, less the BO. The same trends also shown in the TM-TM they are more scattered. In particular, Mo-Mo bonds tend to have smaller BL and higher BO values than other pairs. Such trend can be seen much easier in the Figure 5, where the data in Figure 4 are further break down into specific atomic pairs.
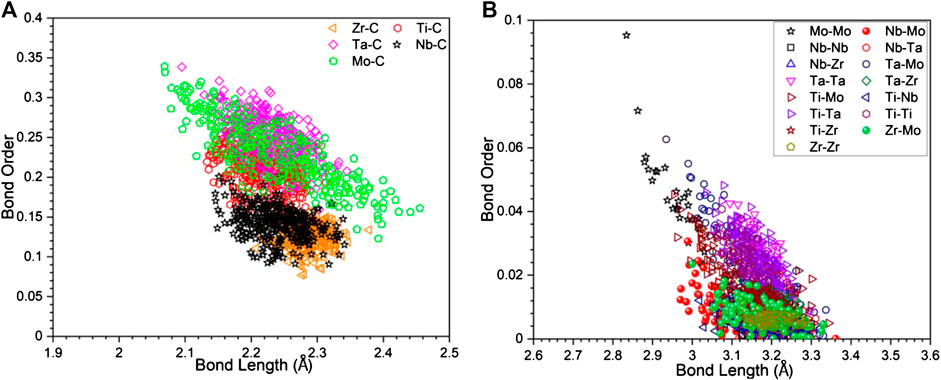
FIGURE 4. The scatter plot of bond order vs. bond length of (A) transition metal with carbon, and (B) transition metal components with itself.
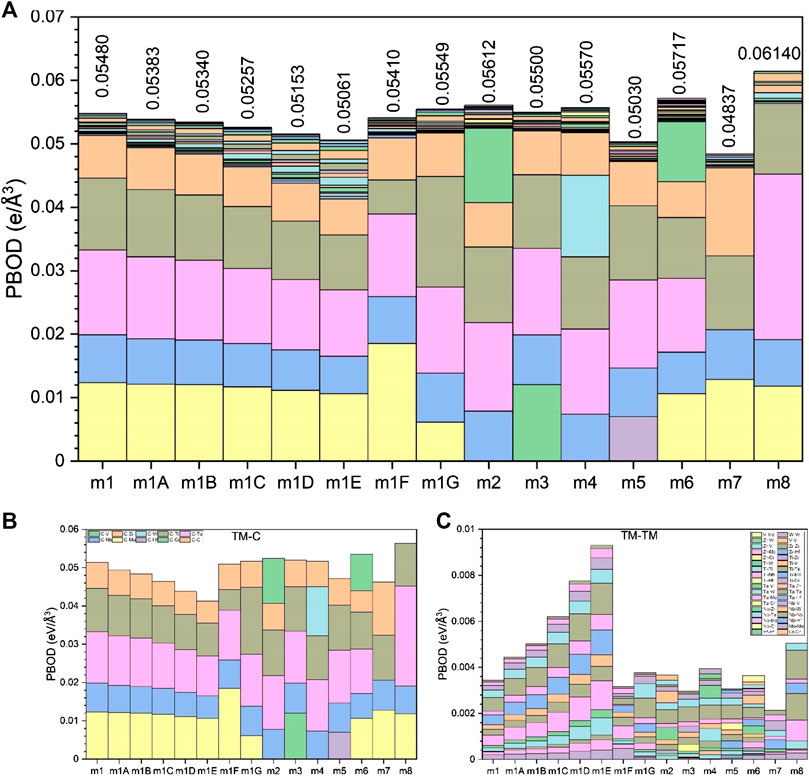
FIGURE 5. (A) TBOD and PBOD in histogram form for all 15 models. (B) TBOD and PBOD between TMs and C in the 15 models. (C) TBOD and PBOD among TMs for the 15 models.
From the sum of all the BO values, we can obtain the TBOD and the PBOD when normalized by the cell volume. These are shown in Figure 5 for the 15 models in six groups including m1. The highest TBOD is in m8 [0.0614 e/(Å) (Zhang et al., 2014)] and the lowest TBOD is in m5 [0.0503 e/(Å) (Zhang et al., 2014)]. It is obvious that the TM-C bonds contribute far more than the TM-TM bonds to the TBOD. For m1, the contribution to TBOD follow the trend of C-Ta > C-Mo > C-Ti > C-Nb > C-Zr on the TM-C bonds and the trend of 0.01335, 0.01232, 0.01136, 0.00755, 0.00674 (States/eV). For the TM-TM bonds, the trend is Ti-Ta > Ta-Mo > Ti-Mo > Ti-Ti > Ta-Ta > Mo-Mo > Ta-Zr-Ti-Zr > Ti-Nb > Zr-Mo > Nb-Ta > Nb-Mo > Nb-Zr > Zr-Zr > Nb-Nb with corresponding values of 5.90E−04, 4.50E−04, 4.20E−04, 3.20E−04, 2.60E−04, 2.00E−04, 2.00E−04, 1.60E−04, 1.60E−04, 1.40E−04, 1.20E−04, 1.10E−04, 7.00E−05, 2.00E−05 (States/eV). Apparently, the above listed numbers show that 88% of bonding in HEA-C for m1 comes from very strong TM-C bonding, and only 12% from TM-TM bonding. The fact that carbon bonding has dominated in HEA-C means it will have better and much stronger mechanical properties.
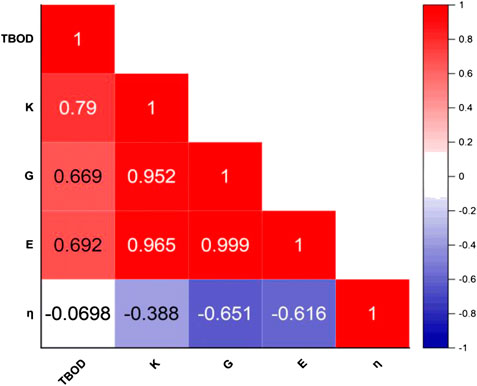
In Table 2, we listed the calculated mechanical parameters for all 15 models in six groups. These consist of the elastic coefficient C11, C12, and C14 for a cubic structure, bulk modules K, shear modulus G, and Young’s modulus E and Poisson’s ratio η. Also listed are the values for the Vickers hardness Hv, TBOD, and energy per atom since they are all intimately related to the mechanical properties. Figure 6 shows the correlation matrix between the mechanical properties among themselves and TBOD in all 15 models. The largest correlation is between Young’s and Shear modulus, and the second largest will be Bulk with Young’s and Shear moduli. These strong correlations reflect the fact that all models are related or derived from m1 with specific variations. The figure also shows that there is a negative correlation of Poison’s ratio with any other properties although Poisson’s ratio is not correlated with TBOD. It is vital to make a correlation between physical properties in models with different chemical compositions in order to reveal the subtle differences that could impact meaningful predictions in the synthesis of HEA ceramic composites with carbon.
Reduction of Carbon Contents in m1: (m1A–m1E)
The Group 2 has five models with decreasing contents of C from 256 C atoms in m1 with we designate to be 100% of C. The percentage of C atoms in the five models from m1A to m1E are reduced respectively to 96%, 94%, 90%, 85%, and 80%. In these Group 2 models the number of C atoms are randomly removed for each % of reduction. This certainly affects their structure and physical properties summarized in Tables 1–4 and part of Supplementary Figures S1–S4. Our discussion in this subsection focuses on the trend associated with the steady C reduction and in comparison with experimental data (Conclusion). Briefly, these effects can be summarized as follows: 1) Deducting carbon content causes volume decreasing since there are less atoms in the supercell. 2) The mechanical properties also decrease because of decreasing in the strong TM-C bonds. This is reflected in the reduced Vickers hardness Hv and tends to be more ductile with a decreasing G/K ratio. 3) The energy per atom is getting slightly larger since there are less strong TM-C bonds. 4) It can be observed that the PC distributions are more scattered. From m1A to m1E.
To correlate the change in mechanical properties due to C reduction, we show in Figure 7A, the plot of TBOD and the bulk modulus K against the C percentage for models m1 and m1A–m1E. Within this range, TBOD decreases in a linear fashion as expected since the reduction in C content mirrors the reduction of the strong TM-C bonds. It can also be seen that this trend is closely correlated with K as expected. There is a subtle difference at the 96% C data point where the data point for bulk modulus falls slightly below the straight line. This subtotal difference is related to the specific TM-C bonds missing due to the removal of 4% of C atoms. In Figures 7B,C, we show the similar plots for shear modulus G and Young’s modulus E vs. C%, and Poisson’s ratio η and G/K vs C% respectively. It shows that both G and E decrease with C% but not in a linear fashion as in Figure 7A but have a slight change in the slope at 96% of C content. Thus, the properties change due to reduction in C could be more complicated and will definitely affect the interpretation of experiments related to C deficiency in HEA-C composites.
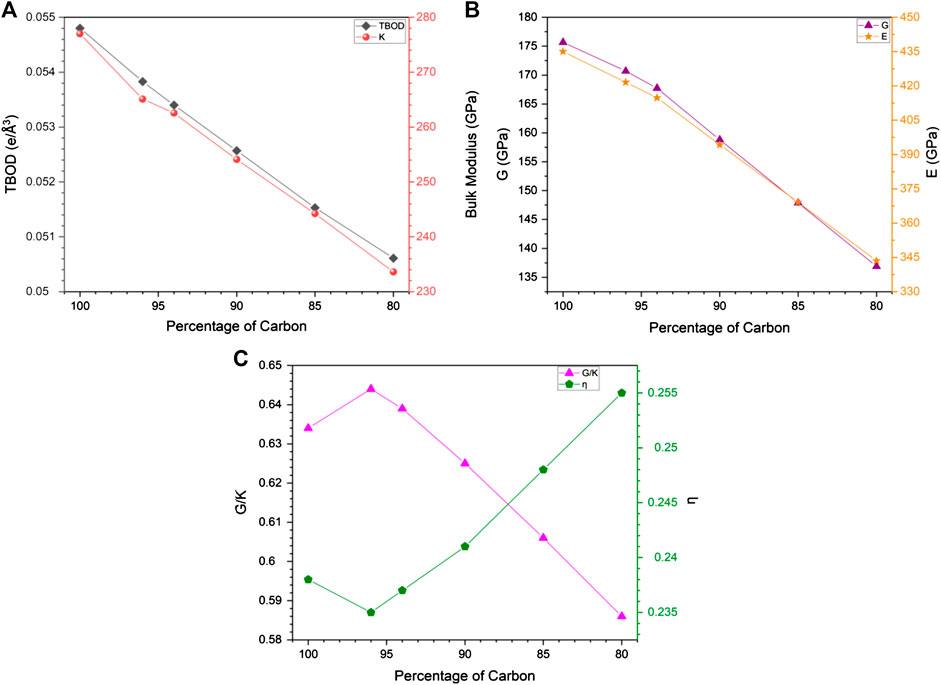
FIGURE 7. Correlation of percentage of carbon with: (A) TBOD and bulk modulus; (B) shear modules and Young’s modulus; (C) G/K and Poisson’s ratio.
Variation in Ti/Mo Ratio From m1: (m1F, m1G)
The two TM elements Ti and Mo in m1 always play some special roles in HEAs. To investigate their opposite influence on the structures and properties of TM carbides, the Group 3 compares the two models (m1F, m1G) with composition formula of Ti5(NbTaZr)10Mo15C50 and Ti15(NbTaZr)10Mo5C50 with different Ti/Mo ratios of 1–3 and 3–1 respectively. m1F has a larger cell volume than m1G because Mo is a much larger atom than Ti. This is partly reflected into the larger TBOD of m1G over m1F as well as their difference mechanical properties and Poisson’s ratio. From the PC table for all 15 models in Table 3, it can be seen that both Ti and Mo have their effective charges bellow the VEC of 4 and 6 respectively, which also make the PC in C to be less effected by different Ti/Mo ratios in m1F and m1G. On the other hand, the N (EF) values listed in Table 4 are quite different, 173.36 States/eV for m1F and 128.044 States/eV for m1G because of significantly different contribution from Ti and Mo atoms at the Fermi level. It suggests that m1F is more stable than m1G. This is quite obvious by looking into Supplementary Figure S1 that the PDOS of Ti and Mo in m1G has a deep local minimum at the Fermi level. We also observe from Supplementary Figure S4 on the BO vs BL plots that by increasing the number of Mo atoms in m1G, the bond pairs with Mo are much increased and widely distributed in the whereas the bond pairs with Ti do not change much signifying the vastly different interatomic bonding between Ti-C and Mo-C.
This group is similar to m1, but with different ratio of Ti/Mo components. The key difference between group 1 and group 3 is that the mechanical properties of G3 is lower than G1. Moreover, changing the Ti/Mo ratio from 1:3 (Ti5/Mo15), to 1:1(Ti10/Mo10), and to 3:1(Ti15/Mo5), respectively, makes the TBOD slightly higher. Thus, we can see that increasing (decreasing) number of atoms of Ti in systems, gives higher (lower) TBOD. Not only Ti is essential for the system but increasing the number of atoms of Mo is also important with a constant number of Ti (See A Six-Components High Entropy Alloy-Carbide m6: (TiNbTaZrVMo)50C50).
Comparison of Five Models With Five Transition Metals by Replacing Mo in m1 With V, Cr, W, Hf: (m1–m5)
The next group, Group 4, for us to discuss is to compare the five models with five TM components including m1 to m5 specifically identified as group 1 for in-depth study. m2–m5 replaces Mo in m1 with V, Cr, W, Hf respectively. This enables us to identify the subtle difference of changing only one TM element in TM carbides. In the nine TM involved in the 15 models for HEAs-C, Cr in m3 is the only non-refectory TM element. We observe that the PC of Cr in m3 is both gaining and losing electrons, and one C atom actually gaining an electron. Another observation is that replacing Mo with Hf makes m5 much weaker since it also does not contribute much in the bonding with C. This reveals that Mo is essential for HEAs. Also, in all 15 models Nb does not show the contribute of bonding with itself and with other elements.
We also noted that Zhang et al. (2019) also investigated the electronic structure and mechanical properties of a model similar to our m5 but with a much smaller elongated supercell of 40 atoms using a different method. Their results show a much higher total energy per atom, lower Young’s modulus and Shear modulus, and lower G/K ratio. Our results are much accurate and substantial and reflect the importance of using large supercell in the modeling of HEA-C composites.
A Six-Components High Entropy Alloy-Carbide m6: (TiNbTaZrVMo)50C50
The group 5 has only one model m6, but it is the only one with six TM components and hence a larger intrinsic entropy. The difference between this model with m1 and m2 is adding one more element, V, in m1 and replacing Mo with V in m2. Since V is a light atom, the change in properties will not be significant. For instance, the comparison of m6 with m1 shows m6 has higher TBOD. M6 also possesses lower mechanical properties than m1. On the other hand, in comparing m2 without Mo to m6 with Mo, m2 has a larger volume and lower TBOD and mechanical properties. In addition, m2 is more ductile than m6. As has been noted, Mo tends to strengthen the mechanical properties for the HEAs. This effect can be clearly seen also in pure HEAs system in BCC lattice for models m2, m3, and m5 in Ref. (Ching et al., 2020).
Two Models by Doubling the Percentage of Zr and Ta Over the Other Four Transition Metals in m1: (m7, m8)
The group 6 is the last group with 2 models m7 and m8. These two models have double percentage of Zr and Ta over the reaming four TMs again explore the subtle difference due to compositional changed concentrating on Zr and Ta, both are present in m1. It can be observed that m7 has much larger volume than m8 that related to the atomic size of Zr and Ta. This is somewhat counter intuitive since Ta atom is at the lower row in the Periodic Table with more electrons. This simply illustrate that in complex HEA-C composites, inter atomic interaction and local bonding controls the structure and properties, particularly the TBOD. m7 has the smallest TBOD and m8 has the largest TBOD among all 15 models signifying the contrasting difference between Zr and Ta. This contrasting difference between m7 and m8 can also be noticed in their PC distributions of Zr in m7 and Ta in m8 as shown in Table 3. Their deviations are much larger than the same elements in the other 13 models. The DOS value at the Fermi level N(EF) between these two models are naturally to be very different due to different electronic structure (140.05 States/eV in m7 and 183.70 States/eV in m8. Since Ta is at a higher row in the Periodic Table with 5 days electrons than Zr with 4 days electrons, it seems to bond more strongly with C than Zr-C bond. Ta-C bonds contribute 42.57% to the total bonding in m8, whereas m7 has double number of Zr-C bonds atoms contribute only 28.74% to the total bond in m7 even though the number of Zr atoms in m7 and Ta atoms m8 are the same, both twice that of the other TMs.
Conclusion
We have presented a detailed study of 15 models of TM HEA carbides using large supercells of 512 atoms each. The results are presented and discussed by dividing them into six groups for specific comparison and analysis. Detailed electronic structure, interatomic bonding, PC distributions, provide the fundamental understanding of these relatively new HEA-ceramic carbides and their mechanical properties. This unprecedented large database enables us to delineate the subtle differences in their fundamental properties that have not been revealed before or have been long ignored. Specifically, we have reached the following solid conclusions. The method and approach we developed in this paper can be extended to other more complex HEA-ceramics including oxides, nitrides, borides or silicides. The opportunity is unlimited.
(1) The TM carbides with 50/50 composition provide an ideal structure for HEA ceramics in which the NN consist of TM-C bonds and the SNN consist of TM-TM pairs. There are no C-C bonds.
(2) The rock-salt structure mimics the ideal TM-C binary alloys. However, we now have the additional advantages of having HEAs in the TM distribution, greatly expand the composition space and variety. We are able to analyse the results at a deeper level quantitatively especially in the BO vs BL plots than just using the vague argument of atomic size misfit prevailed in many published literatures.
(3) We utilize the novel concept of TBOD and PBOD to characterize the complex alloy systems in HEA-carbides which is more straightforward and easier to understand.
(4) Specific modelling for C-deficiency provide another possibility of extending HEA-ceramics with different C contents, further expand the composition space.
(5) The design of different composition of the TM elements in this work reveal many of the subtle difference due to atomic origin. These include the special insights obtained that Ta and Ti as well as Mo components make a large contribution in bonding with carbon, which enhance their strength.
(6) Our ab initio calculation in this work demonstrate that the routine use of the valence electron count for TM elements as key parameters in characterizing HEA components in untenable.
(7) The methods developed and demonstrated in this paper can be easily extended into other HEA-ceramics such as nitrides or borides. The insights gained can facilitate the design new radiation resistant HEA ceramic composites at high temperature.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
WC conceived the project. SS and WC performed the calculations, drafted the paper. Both participated in the discussion and the interpretation of the results, and proofread the final manuscript.
Funding
This research used the resources of the National Energy Research Scientific Computing Center supported by DOE under Contract No. DE-AC03-76SF00098 and the Research Computing Support Services (RCSS) of the University of Missouri System. SS was supported in part from funds provided by the University of Missouri-Kansas City, School of Graduate Studies.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This research used the resources of the National Energy Research Scientific Computing Center supported by DOE under Contract No. DE-AC03-76SF00098 and the Research Computing Support Services (RCSS) of the University of Missouri System. SS was supported in part from funds provided by the University of Missouri-Kansas City, School of Graduate Studies. WC acknowledge the fruitful discussions with Professor Yujing Wang and Dr. Lei Chen of Harbin Institute of Technology in China.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2020.575262/full#supplementary-material
References
Adhikari, P., Xiong, M., Li, N., Zhao, X., Rulis, P., and Ching, W.-Y. (2016). Structure and electronic properties of a continuous random network model of an amorphous Zeolitic Imidazolate Framework (a-ZIF). J. Phys. Chem. C 120, 15362–15368. doi:10.1021/acs.jpcc.6b06337
Agte, C., and Alterthum, H. (1930). Untersuchungen über Systeme hochschmelzender Carbide: nebst Beiträgen zum Problem der Kohlenstoffschmelzung. Z. Tech. Phy. 11, 182–191.
Chen, H.-L., Mao, H., and Chen, Q. (2018). Database development and Calphad calculations for high entropy alloys: challenges, strategies, and tips. Mater. Chem. Phys. 210, 279–290. doi:10.1016/j.matchemphys.2017.07.082
Cheng, H., Wang, H. Y., Xie, Y. C., Tang, Q. H., and Dai, P. Q. (2017). Controllable fabrication of a carbide-containing FeCoCrNiMn high-entropy alloy: microstructure and mechanical properties. Mater. Sci. Technol. 33, 2032–2039. doi:10.1080/02670836.2017.1342367
Ching, W.-Y., and Rulis, P. (2012). Electronic structure methods for complex materials: the orthogonalized linear combination of atomic orbitals. Oxford, UK: Oxford University Press.
Ching, W.-Y., San, S., Brecht, J., Sakidja, R., Zhang, M., and Liaw, P. K. (2020). Fundamental electronic structure and multiatomic bonding in 13 biocompatible high-entropy alloys. npj Comput. Mater. 6, 1–10. doi:10.1038/s41524-020-0321-x
Curtarolo, S., Hart, G. L. W., Nardelli, M. B., Mingo, N., Sanvito, S., and Levy, O. (2013). The high-throughput highway to computational materials design. Nat. Mater. 12, 191–201. doi:10.1038/nmat3568
Dharmawardhana, C., Misra, A., and Ching, W.-Y. (2014). Quantum mechanical metric for internal cohesion in cement crystals. Sci. Rep. 4, 7332. doi:10.1038/srep07332
Ding, J., Yu, Q., Asta, M., and Ritchie, R. O. (2018). Tunable stacking fault energies by tailoring local chemical order in CrCoNi medium-entropy alloys. Proc. Natl. Acad. Sci. U.S.A. 115, 8919–8924. doi:10.1073/pnas.1808660115
Dusza, J., Švec, P., Girman, V., Sedlák, R., Castle, E. G., and Csanádi, T. (2018). Microstructure of (Hf-Ta-Zr-Nb)C high-entropy carbide at micro and nano/atomic level. J. Eur. Ceram. Soc. 38, 4303–4307. doi:10.1016/j.jeurceramsoc.2018.05.006
Gali, A., and George, E. P. (2013). Tensile properties of high- and medium-entropy alloys. Intermetallics 39, 74–78. doi:10.1016/j.intermet.2013.03.018
Gao, M. C., Yeh, J.-W., Liaw, P. K., and Zhang, Y. (2016). High-entropy alloys: fundamentals and applications. Berlin, Germany: Springer.
Gludovatz, B., Hohenwarter, A., Catoor, D., Chang, E. H., George, E. P., and Ritchie, R. O. (2014). A fracture-resistant high-entropy alloy for cryogenic applications. Science 345, 1153–1158. doi:10.1126/science.1254581
Harrington, T. J., Gild, J., Sarker, P., Toher, C., Rost, C. M., and Dippo, O. F. (2019). Phase stability and mechanical properties of novel high entropy transition metal carbides. Acta Mater. 166, 271–280. doi:10.1016/j.actamat.2018.12.054
Hill, R. (1952). The elastic behaviour of a crystalline aggregate. Proc. Phys. Soc. 65, 349. doi:10.1088/0370-1298/65/5/307
Huang, S., Tian, F., and Vitos, L. (2018). Elasticity of high-entropy alloys from ab initio theory. J. Mater. Res. 33, 2938–2953. doi:10.1557/jmr.2018.237
Ikeda, Y., Tanaka, I., Neugebauer, J., and Körmann, F. (2019). Impact of interstitial C on phase stability and stacking-fault energy of the CrMnFeCoNi high-entropy alloy. Phys. Rev. Mater. 3, 113603. doi:10.1103/physrevmaterials.3.113603
Kresse, G., and Furthmüller, J. (1996). Software vasp, vienna, 1999. Phys. Rev. B 54, 169. doi:10.1103/physrevb.54.11169
Kresse, G., and Furthmuller, J. (2002). Vienna ab-initio simulation package (VASP): the guide. Wien, Austria: VASP Group, Institut fur Materialphysik, Universitat.
LaRosa, C. R., Shih, M., Varvenne, C., and Ghazisaeidi, M. (2019). Solid solution strengthening theories of high-entropy alloys. Mater. Char. 151, 310–317. doi:10.1016/j.matchar.2019.02.034
Li, Q.-J., Sheng, H., and Ma, E. (2019). Strengthening in multi-principal element alloys with local-chemical-order roughened dislocation pathways. Nat. Commun. 10, 11. doi:10.1038/s41467-019-11464-7
Li, Z., Pradeep, K. G., Deng, Y., Raabe, D., and Tasan, C. C. (2016). Metastable high-entropy dual-phase alloys overcome the strength-ductility trade-off. Nature 534, 227. doi:10.1038/nature17981
Li, Z., Tasan, C. C., Springer, H., Gault, B., and Raabe, D. (2017). Interstitial atoms enable joint twinning and transformation induced plasticity in strong and ductile high-entropy alloys. Sci. Rep. 7, 1–7. doi:10.1038/srep40704
Lim, X. (2016). Mixed-up metals make for stronger, tougher, stretchier alloys. Nature 533, 306. doi:10.1038/533306a
Miracle, D. B., and Senkov, O. N. (2017). A critical review of high entropy alloys and related concepts. Acta Mater. 122, 448–511. doi:10.1016/j.actamat.2016.08.081
Nielsen, O. H., and Martin, R. M. (1983). First-principles calculation of stress. Phys. Rev. Lett. 50, 697. doi:10.1103/physrevlett.50.697
Pelletier, J.-M., and Qiao, J. (2019). Springer handbook of glass. Berlin, Germany: Springer, 617–643.
Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865. doi:10.1103/physrevlett.77.3865
Poudel, L., Steinmetz, N. F., French, R. H., Parsegian, V. A., Podgornik, R., and Ching, W.-Y. (2016). Implication of the solvent effect, metal ions and topology in the electronic structure and hydrogen bonding of human telomeric G-quadruplex DNA. Phys. Chem. Chem. Phys. 18, 21573–21585. doi:10.1039/c6cp04357g
Poudel, L., Twarock, R., Steinmetz, N. F., Podgornik, R., and Ching, W.-Y. (2017). Impact of hydrogen bonding in the binding site between capsid protein and MS2 bacteriophage ssRNA. J. Phys. Chem. B 121, 6321–6330. doi:10.1021/acs.jpcb.7b02569
Poudel, L., Wen, A. M., French, R. H., Parsegian, V. A., Podgornik, R., Steinmetz, N. F., and Ching, W.-Y. (2015). Electronic structure and partial charge distribution of doxorubicin in different molecular environments. ChemPhysChem 16, 1451–1460. doi:10.1002/cphc.201402893
Pugh, S. F. (1954). XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. London Edinburgh Philos. Mag. J. Sci. London, Edinburgh Dublin Philos. Mag. J. Sci. 45, 823–843. doi:10.1080/14786440808520496
Reuss, A. (1929). Berechnung der Fließgrenze von Mischkristallen auf Grund der Plastizitätsbedingung für Einkristalle. Z. Angew. Math. Mech. 9, 49–58. doi:10.1002/zamm.19290090104
Rost, C. M., Sachet, E., Borman, T., Moballegh, A., Dickey, E. C., Hou, D., et al. (2015). Entropy-stabilized oxides. Nat. Commun. 6, 8485. doi:10.1038/ncomms9485
San, S., Li, N., Tao, Y., Zhang, W., and Ching, W.-Y. (2018). Understanding the atomic and electronic origin of mechanical property in thaumasite and ettringite mineral crystals. J. Am. Ceram. Soc. 101, 5177–5187. doi:10.1111/jace.15774
Sanchez, J. M., Vicario, I., Albizuri, J., Guraya, T., and Garcia, J. C. (2019). Phase prediction, microstructure and high hardness of novel light-weight high entropy alloys. J. Mater. Res. Tech. 8, 795–803. doi:10.1016/j.jmrt.2018.06.010
Santodonato, L. J., Liaw, P. K., Unocic, R. R., Bei, H., and Morris, J. R. (2018). Predictive multiphase evolution in Al-containing high-entropy alloys. Nat. Commun. 9, 4520. doi:10.1038/s41467-018-06757-2
Sarker, P., Harrington, T., Toher, C., Oses, C., Samiee, M., and Maria, J.-P. (2018). High-entropy high-hardness metal carbides discovered by entropy descriptors. Nat. Commun. 9, 4980. doi:10.1038/s41467-018-07160-7
Senkov, O. N., Senkova, S. V., Woodward, C., and Miracle, D. B. (2013). Low-density, refractory multi-principal element alloys of the Cr-Nb-Ti-V-Zr system: microstructure and phase analysis. Acta Mater. 61, 1545–1557. doi:10.1016/j.actamat.2012.11.032
Senkov, O. N., Wilks, G. B., Miracle, D. B., Chuang, C. P., and Liaw, P. K. (2010). Refractory high-entropy alloys. Intermetallics 18, 1758–1765. doi:10.1016/j.intermet.2010.05.014
Senkov, O. N., Wilks, G. B., Scott, J. M., and Miracle, D. B. (2011). Mechanical properties of Nb25Mo25Ta25W25 and V20Nb20Mo20Ta20W20 refractory high entropy alloys. Intermetallics 19, 698–706. doi:10.1016/j.intermet.2011.01.004
Stepanov, N. D., Yurchenko, N. Y., Tikhonovsky, M. A., and Salishchev, G. A. (2016). Effect of carbon content and annealing on structure and hardness of the CoCrFeNiMn-based high entropy alloys. J. Alloys Compd. 687, 59–71. doi:10.1016/j.jallcom.2016.06.103
Sun, X., Zhang, H., Lu, S., Ding, X., Wang, Y., and Vitos, L. (2017). Phase selection rule for Al-doped CrMnFeCoNi high-entropy alloys from first-principles. Acta Mater. 140, 366–374. doi:10.1016/j.actamat.2017.08.045
Tian, F. (2017). A review of solid-solution models of high-entropy alloys based on ab initio calculations. Front. Mater. 4, 36. doi:10.3389/fmats.2017.00036
Tian, F., Varga, L. K., Shen, J., and Vitos, L. (2016). Calculating elastic constants in high-entropy alloys using the coherent potential approximation: current issues and errors. Comput. Mater. Sci. 111, 350–358. doi:10.1016/j.commatsci.2015.09.058
Tian, Y. J., Xu, B., and Zhao, Z. (2012). Microscopic theory of hardness and design of novel superhard crystals. Int. J. Refract. Metals Hard Mater. 33, 93–106. doi:10.1016/j.ijrmhm.2012.02.021
Todai, M., Nagase, T., Hori, T., Matsugaki, A., Sekita, A., and Nakano, T. (2017). Novel TiNbTaZrMo high-entropy alloys for metallic biomaterials. Scripta Mater. 129, 65–68. doi:10.1016/j.scriptamat.2016.10.028
Tsao, T.-K., Yeh, A.-C., Kuo, C.-M., Kakehi, K., Murakami, H., Yeh, J., et al. (2017). The high temperature tensile and creep behaviors of high entropy superalloy. Sci. Rep. 7, 1–9. doi:10.1038/s41598-017-13026-7
Voigt, W. (1928). Lehrbuch der Kristallphysik, nachdruck, 1. Auflage, teubner. Berlin/Leipzig: B. G. Teubner.
Von Rohr, F., Winiarski, M. J., Tao, J., Klimczuk, T., and Cava, R. J. (2016). Effect of electron count and chemical complexity in the Ta-Nb-Hf-Zr-Ti high-entropy alloy superconductor. Proc. Natl. Acad. Sci. U.S.A. 113, E7144–E7150. doi:10.1073/pnas.1615926113
Wang, P., Cai, H., Zhou, S., and Xu, L. (2017). Processing, microstructure and properties of Ni1.5CoCuFeCr0.5−xVx high entropy alloys with carbon introduced from process control agent. J. Alloys Compd. 695, 462–475. doi:10.1016/j.jallcom.2016.10.288
Widom, M. (2018). Modeling the structure and thermodynamics of high-entropy alloys. J. Mater. Res. 33, 2881–2898. doi:10.1557/jmr.2018.222
Yang, Y., Wang, W., Gan, G.-Y., Shi, X.-F., and Tang, B.-Y. (2018). Structural, mechanical and electronic properties of (TaNbHfTiZr)C high entropy carbide under pressure: ab initio investigation. Phys. B Condens. Matter. 550, 163–170. doi:10.1016/j.physb.2018.09.014
Yao, H., Ouyang, L., and Ching, W.-Y. (2007). Ab initio calculation of elastic constants of ceramic crystals. J. Am. Ceram. Soc. 90, 3194–3204. doi:10.1111/j.1551-2916.2007.01931.x
Ye, Y. F., Wang, Q., Lu, J., Liu, C. T., and Yang, Y. (2016). High-entropy alloy: challenges and prospects. Mater. Today. 19, 349–362. doi:10.1016/j.mattod.2015.11.026
Zhang, F., Zhang, C., Chen, S. L., Zhu, J., Cao, W. S., and Kattner, U. R. (2014). An understanding of high entropy alloys from phase diagram calculations. Calphad 45, 1–10. doi:10.1016/j.calphad.2013.10.006
Zhang, Q., Zhang, J., Li, N., and Chen, W. (2019). Understanding the electronic structure, mechanical properties, and thermodynamic stability of (TiZrHfNbTa) C combined experiments and first-principles simulation. J. Appl. Phys. 126, 025101. doi:10.1063/1.5094580
Zhang, Y., Zuo, T. T., Tang, Z., Gao, M. C., Dahmen, K. A., Liaw, P. K., and Lu, Z. P. (2014). Microstructures and properties of high-entropy alloys. Prog. Mater. Sci. 61, 1–93. doi:10.1016/j.pmatsci.2013.10.001
Zhou, J., Zhang, J., Zhang, F., Niu, B., Lei, L., and Wang, W. (2018). High-entropy carbide: a novel class of multicomponent ceramics. Ceram. Int. 44, 22014–22018. doi:10.1016/j.ceramint.2018.08.100
Zhou, Y., Dai, F., Xiang, H., Liu, B., and Feng, Z. (2017). Shear anisotropy: tuning high temperature metal hexaborides from soft to extremely hard. J. Mater. Sci. Technol. 33, 1371–1377. doi:10.1016/j.jmst.2017.01.022
Keywords: high entropy ceramic carbides, electronic structure, interatomic bounding, mechanical properties, carbon deficiency
Citation: San S and Ching W-Y (2020) Subtle Variations of the Electronic Structure and Mechanical Properties of High Entropy Alloys With 50% Carbon Composites. Front. Mater. 7:575262. doi:10.3389/fmats.2020.575262
Received: 05 August 2020; Accepted: 06 October 2020;
Published: 10 November 2020.
Edited by:
William Yi Wang, Northwestern Polytechnical University, ChinaReviewed by:
Jin Zhao, University of Science and Technology of China, ChinaFuyang Tian, University of Science and Technology Beijing, China
Copyright © 2020 San and Ching. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Wai-Yim Ching, Y2hpbmd3QHVta2MuZWR1 Saro San
Saro San Wai-Yim Ching
Wai-Yim Ching