Design of Shape Reconfigurable, Highly Stretchable Honeycomb Lattice With Tunable Poisson’s Ratio

Introduction

Lattice structures can exhibit unusual properties by rationally arranging or adjusting their microstructures (Bertoldi et al., 2017). Among them, tunable Poisson’s ratio is of particular interest (Fozdar et al., 2011; Ai and Gao 2017; Chen et al., 2017; Khare et al., 2018; Liu and Zhang. 2018; de Jongeet al., 2019). While most naturally occurring and synthetic materials have a positive Poisson ratio, i.e., they contract transversely while elongating axially and vice versa. Some exceptions exist, including arterial endothelium (Timmins et al., 2010), cat’s skin Veronda and Westmann. (1970), cow’s teat skin Lees et al. (1991), crystalline α-cristobalite SiO₂ (Williams and Lewis, 1982; Keskar and Chelikowsky, 1992), carbon allotropes (Timmins et al., 2010), microporous polymers and laminates (Caddock and Evans, 1989; Alderson and Evans, 1992; Milton, 1992). For these materials, expansion in lateral direction and elongation in longitudinal direction occur concurrently. Due to this unusual deformation property, lattice structures with negative Poisson ratios offer superior mechanical performance compared to traditional materials, including high fracture toughness (Li et al., 2016; Saxena et al., 2016; Clayton and Knap, 2018), large energy absorption Li et al. (2018), Chetverikov et al. (2019), Guo et al. (2020), Hu et al. (2020), and strong indentation resistance (Aldeson et.al., 2000; Hu et al., 2019; Li et al., 2020). Therefore, lattices with tunable Poisson’s ratio have found applications in various areas, such as biomedical devices (Rafsanjani and Pasini, 2016; Yan et al., 2019), soft sensors (Li et al., 2016; Khan et al., 2019), Aerospace Huang and Chen (2016) and automotive engineering (Wang et al., 2016).

Another critical property of lattice structure is high stretchability (Jiang and Wang, 2016; Yiming et al., 2020). Inspired by the non-mineralized soft materials typically constructed from wavy constituents embedded in soft matrices, curved microstructures are commonly used to design lattices (Ma et al., 2016). When the lattices are subjected to external loadings, the microstructures bend, rotate and align to the loading directions and resist excessive loadings by stretching. Therefore, they generally exhibit J-shaped stress-strain curves with low initial modulus and high modulus at a large strain simultaneously, and their stretchability is significantly improved.

The development of 3D printing technologies has enabled the fabrication of complex lattice structures (Yuan et al., 2019). However, once manufactured, the mechanical behavior of the lattice structure is fixed and not reconfigurable. To overcome this problem, several methods have been proposed. One way is to use active materials to fabricate the lattice structure. Active materials have the ability to deform or change their properties under the external stimulus. Therefore, the manufactured lattice can change its shape or properties accordingly. Examples include 4D printed lattice that can deform under thermal stimulus (Yang et al., 2019), 4D printed gripper that deforms under electrical stimulus (Shao et al., 2020), 4D printed structure responding to magnetic field (Ji et al., 2017; Cao et al., 2019; Lantean et al., 2019; Testa et al., 2019; Ze et al., 2020), directly 4D printed structures (Ding et al., 2017; Ding et al., 2018), etc.

Shape memory polymer (SMP) is a class of intelligent polymer material that can maintain a temporary shape and restore its original shape in response to environmental stimuli (Lendlein and Langer, 2002). SMPs have a wide range of modulus varying from ∼MPa to ∼GPa Lendlein and Kelch (2005) and relatively fast response capability depending on actuation temperatures (Kong et al., 2021a). SMPs with various functions have been developed, such as SMP with high recovery stress reinforced by carbon fibers, self-healing SMPs (Lee et al. (2015), Kong et al. (2019) and SMP with shielding electromagnetic interference (Kong et al., 2021b). The shape-shifting behavior of the SMP has been widely used in 4D printing. Examples include self-driving structures (Bodaghi et al., 2016), reconfigurable metamaterials Ding et al. (2017), and multi-material soft actuators (Ge et al., 2016).

Despite the recent significant progress in lattice structure design, it is still a challenge to realize shape reconfigurable, highly stretchable lattice structures with tunable Poisson’s ratio. In this paper, we design a reconfigurable, highly stretchable lattice with tunable Poisson’s ratio. A hexagonal honeycomb structure is used. By replacing the straight beams in the lattice using curled microstructure, the stretchability of the lattice is significantly improved. Under a uniaxial tensile loading, the curled microstructure rotates, bends and aligns to the direction of the applied stress. Therefore, the lattice exhibits a large stretchability, comparing to the traditional hexagonal honeycomb structures. By adjusting a geometric parameter: angle α, the Poisson’s ratio can be programmed. Generally speaking, if α > 90°, the lattice exhibits a positive Poisson’s ratio. The lattice with α < 90° shows a negative Poisson’s ratio, while the Poisson’s ratio of the lattice is almost zero when α = ∼90°. The lattice is 3D printed using a shape memory polymer. Using its shape memory effect, the lattice shows the capacity to reconfigure its shapes when applying an external stimulus. A phase-evolution model is used to predict the shape reconfigurability of the lattice.

Materials and Methods

Geometric Design

The lattice structures are designed by Solidworks (3DS Dassault Systemes, France), as shown in Figure 1. The general honeycomb structures are used as the building framework (Figure 1A). An angle α is used to control the overall geometry of the lattice. To increase the lattices’ stretchability, a curled microstructure is used to replace the straight beams in the honeycomb structure (Figure 1B). The curled microstructure consists of two identical curves (Figure 1D). The parametric function of the curve is $x\left(t\right)=t^{1.5}\cos t$, $y\left(t\right)=t^{1.5}\sin t$ (t = 0 to π), as shown in Figure 1C. The geometrical parameter used are: L = 10 mm, w = 0.2 mm. The thickness of the lattice is d = 1 mm. The curve is scaled to fit the lattice structure.

FIGURE 1

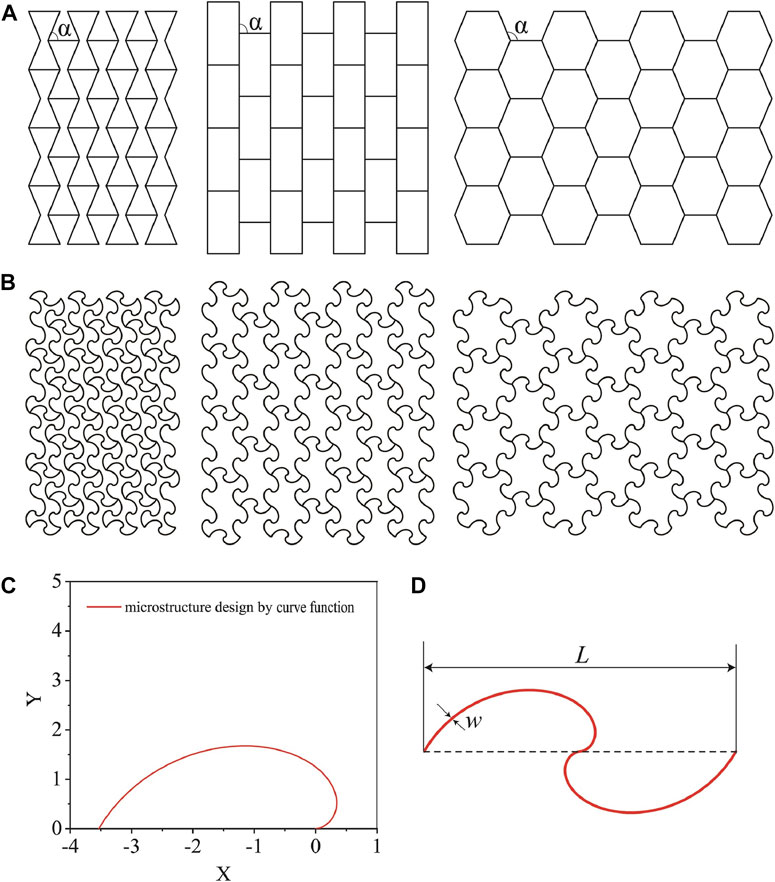
FIGURE 1. Structural design of the lattice. (A) Schematics of three different honeycomb structures. A geometric parameter α is used to control the Poisson’s ratios of the honeycomb structures. (B) By replacing the straight beam to curled microstructure, the stretchability of the lattice is significantly improved. (C) Half of a single microstructure. (D) The geometric parameters of a single microstructure.

Comparing to the straight beam, the microstructure exhibits large stretchability. The FE simulated uniaxial tensile stress-strain curves are shown in Figure 2A. The Young’s modulus of the material is set as 1.2 GPa. The corresponding shapes and the strain maps with strain = 20, 40, and 60% are shown in Figure 2B. The stress-strain curve of the microstructure shows a J-shape. Under the uniaxial loading, the microstructure bends and uncurls with a low modulus initially. When the loading force increases further, the microstructure is stretched with a higher modulus, similar as a straight beam. It can be observed that when the total strain is 60%, the maximum local strain is less than 10%. But for a straight beam, the total strain is the same as the local strain. Therefore, the microstructure exhibits a large stretchability compared to the straight beam.

FIGURE 2

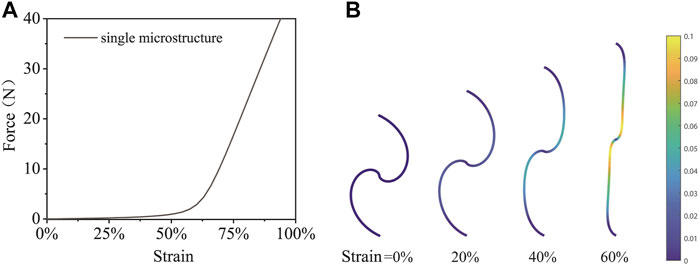
FIGURE 2. Large stretchability of the microstructure. (A) The dependence of the applied force and the axial strain of the microstructure. (B) Strain map of a single microstructure at different strains.

Next, the mechanical behaviors of the lattice structures constructed from the microstructures are investigated. The experimental uniaxial tensile curves of three lattices with a = 67.5°, 90,° and 112.5° are shown by the solid curves in Figure 3A. The lattice structures with 4*4 periodical units are used. The CAD design and the experimental snapshots are shown in Figure 3B, Supplementary Material Video S1–S3. The lattice structures are fabricated using a commercial 3D printer (Object J750, Stratasys). The shape memory polymer material Vero is used. At room temperature, the elastic modulus of Vero is ∼1.2 GPa.

FIGURE 3

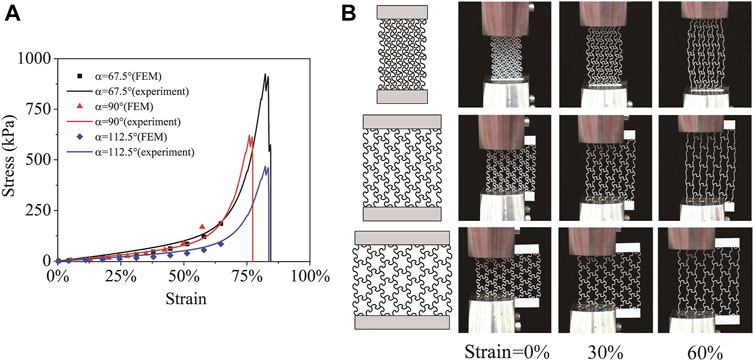
FIGURE 3. Mechanical behaviors of the lattices under uniaxial tensile loading. (A) The experimental and FE simulated curves of three lattices with α = 67.5°, 90°, and 112.5°. (B) The CAD design and the shapes at various strains are shown.

It can be seen all of the three lattice structures also show a J-shaped stress-strain curve. The failure strain of all three lattices is larger than 70%, while the Vero material’s failure strain is generally around 10% (Akbari et al., 2018). By using the microstructure, the stretchability is significantly improved. From the deformed shapes of the lattices, we can observe that: at α = 67.5°, the Poisson’s ratio is positive, i.e., the lattice expands when stretched. At α = 90°, the Poisson’s ratio of the lattice is almost zero. The lattice with α = 112.5° exhibits a negative Poisson’s ratio. Therefore, by adjusting the geometric angle α, the Poisson’s ratio can be controlled. FE simulations are conducted to simulate the mechanical behaviors of the lattice under uniaxial tensile loading. The FE simulated results are shown by the markers in Figure 3A. The finite element simulation results agree well with the experiments.

We then use the FE simulations to study the lattice’s mechanical behaviors with various α. Figure 4 shows the FE simulated uniaxial tensile results for the lattice with α changing from 63.75° to 123.75° with an interval of 3.75°. The tensile loading is applied in the y-direction. The strain in y (longitudinal strain), x (transverse strain) and the Poisson’s ratio are shown in Figure 4A–C, respectively. Each lattice structure consists of four units in both the longitudinal and transverse directions.

FIGURE 4

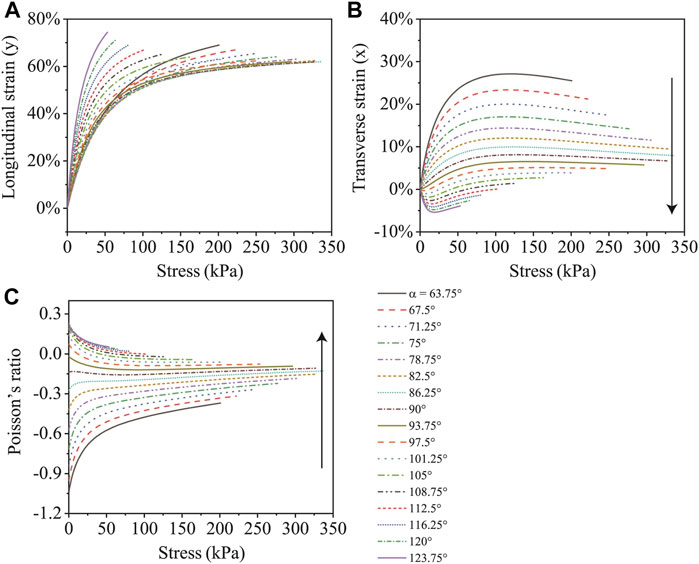
FIGURE 4. The dependences of the FE simulated (A) longitudinal strain, (B) transverse strain and (C) Poisson’s ratio on the applied stress for the highly stretchable lattices with different α.

The modulus of the designed lattice varies with α. All of positive, negative and zero Poisson’s ratios can be achieved. As α increases, Poisson’s ratio increases from a large negative value to nearly zero and then to a positive value. The Poisson’s ratio also changes with the applied stress. Generally, the magnitudes of the Poisson’s ratio decreases with the applied stress.

Shape Memory Behaviors of Vero

The material Vero used for the lattice structure is a shape memory polymer. The dependences of storage modulus E_s and tanδ on temperature T are experimentally measured using a DMA machine (TA Instruments, Model Q800), as shown by the solid black curves in Figure 5A. As the temperature increases from 0°C–100°C, the storage modulus of Vero decrease by more than two orders from ∼2 GPa (T = 0°C) to ∼8 MPa (T = 100°C). Its glassy transition temperature T_g is ∼58°C.

FIGURE 5

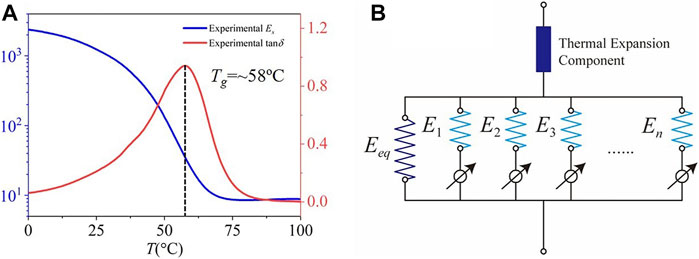
FIGURE 5. Thermomechanical behaviors of the shape memory polymer Vero. (A) The experimental storage modulus and tanδ with T. (B) The phase evolution model for the lattice.

By fabricating the lattice with the shape memory polymer Vero, the lattice can exhibit large deformation under ambient temperature. Various shapes can then be designed by applying an external stimulus. The shape memory behavior of the lattice is schematically shown in Figure 6. Here we take the lattice with α = 67.5° as an example. First, the lattice is stretched at high temperature (T > T_g) (Figure 6B). Next, the temperature is decreased to a low temperature (T < T_g), while the loading or the strain is maintained (Figure 6C). The loading is then removed at low temperature (Figure 6D). The shape of the lattice in this step is called a programmed shape. By heating the lattice, the lattice will recover to its initial shape (Figure 6E).

FIGURE 6

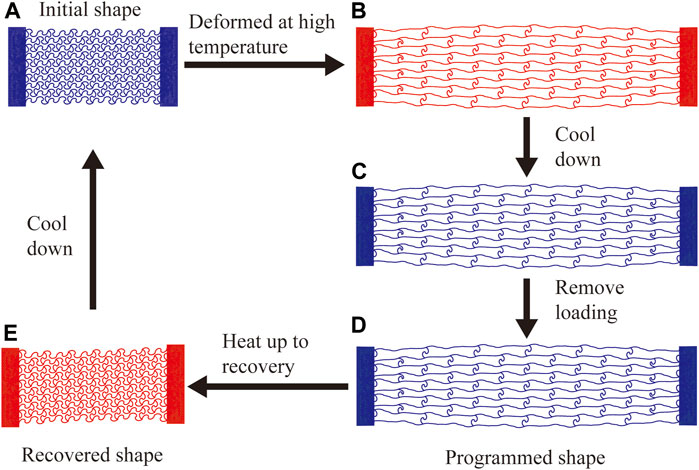
FIGURE 6. Shape memory cycle of the lattice structures. In Step 1, the lattice deforms from the initial shape (A) to (B) at high temperature. In Step 2, the lattice is cooled down from (B) to (C). In Step 3, the applied loading is removed at low temperature. In Step 4, the programmed shape (D) is recovered to shape (E) as the temperature increases.

Phase Evolution Model for Lattice

To model the shape memory behaviors of the honeycomb lattices, a phase evolution model is used (Figure 5B) (Wang et al., 2020). The total strain of the lattice is decomposed into two parts: the mechanical strain and the thermal strain. The mechanical strain is modeled by an elastic phase and several glassy phases arranged in parallel. The glassy phases gradually turn on and take effect when T decreases. Depending on the thermomechanical conditions, the glassy phases forming at different times may have different deformation history. As temperature increases, the glassy phases vanish gradually. According to the kinetic description of the heating process, the piece of glassy phase that grows at a later time vanish first. Once a small piece of glassy phase vanishes, the corresponding switch turns off and it does not carry load anymore.

The relation between the applied stress $\sigma \left(T,\epsilon \right)$ and the strain $\epsilon$ of the honeycomb lattice is assumed to be

$\sigma \left(T,\epsilon \right)=E_s\left(T\right)f\left(\epsilon \right),(1)$

in which the effects of temperature and geometric nonlinearity are decoupled. $f\left(\epsilon \right)$ represents the geometric nonlinearity due to the lattice structure. For a single solid block, $f\left(\epsilon \right)=\epsilon$. The strain comprises of two parts: the mechanical strain ${\epsilon }^M\left(T\right)$ and the thermal strain ${\epsilon }^T\left(T\right)$. The thermal strain can be written as

${\epsilon }^T\left(T\right)=\left(T-T_H\right){\alpha }_r,(2)$

where ${\alpha }_r$ is the thermal expansion coefficient. Here we set the thermal strain at a high temperature T_H as the reference state.

In Step 1, the lattice structure deformed at a high temperature T = T_H with an applied stress ${\sigma }_0$. At T = T_H, all of the glassy phases are turned off. Thus only the equilibrium phase works: $E\left(T\right)=E_e=3NkT$ where N is the crosslink density of the shape memory polymer and k is Boltzmann’s constant. Eq. 1 can then be written as:

${\sigma }_0=3Nk{T}_{H}f\left({\epsilon }^M\left(T_H\right)\right),(3)$

and the mechanical strain can be solved as:

${\epsilon }^M\left(T_H\right)=f^{-1}\left(\frac{{\sigma }_0}{3Nk{T}_H}\right)(4)$

In Step 2, the applied stress ${\sigma }_0$ is maintained. At the same time, the ambient temperature decreases from T_H to T_L. To ease the derivation, we consider the following two different cases:

1) the first glassy phase formed as T decreases.

2) the (a + 1)th glassy phase forms.

Case 1) As the ambient temperature T decreases, new glassy phases are generated. We set that the first glassy phase forms when the temperature decreases from T₀ to T₁= T₀-ΔT₁. Therefore, the applied stress can be written as the sum of the stress on the equilibrium and the first glassy phases:

${\sigma }_0=3Nk{T}_{1}f\left({\epsilon }^M\left(T_1\right)\right)+E_1\left(f\left({\epsilon }^M\left(T_1\right)\right)-f\left({\epsilon }^M\left(T_0\right)\right)\right)(5)$

Note that the modulus of the equilibrium branch decrease from 3NkT₀ to 3NkT₁. ${\epsilon }^M\left(T_0\right)$ can be obtained from Eq. 4. ${\epsilon }^M\left(T_1\right)$ is then solved as:

${\epsilon }^M\left(T_1\right)=f^{-1}\left(\frac{{\sigma }_0+E_1{\sigma }_0/3Nk{\mathit{T}}_0}{3Nk{T}_1+E_1}\right)(6)$

and the strain stored in the first glassy phase ${\epsilon }_1\left(T_1\right)$ at T₁ is then ${\epsilon }_1\left(T_1\right)={\epsilon }^M\left(T_1\right)-{\epsilon }^M\left(T_0\right)$. We use ${\epsilon }_1^0={\epsilon }^M\left(T_0\right)$ to represent the strain of the lattice structure when the first glassy branch starts to work.

Case 2) At T = T_a, the (a + 1)th glassy phase is not formed yet. The applied stress is the sum of the stress on all the currently working branches:

${\sigma }_0=3Nk{T}_{a}f\left({\epsilon }^M\left(T_a\right)\right)+{\displaystyle \sum _{i=1}^a{E}_i\left(f\left({\epsilon }^M\left(T_a\right)\right)-f\left({\epsilon }_i^0\right)\right)}(7)$

where ${\epsilon }_i^0$ represents the mechanical strain of the lattice structure when ith glassy branch starts to work.

The (a + 1)th glassy phase forms as T decreases from T_a to T_{a + 1} = T_a−ΔT_{a + 1}. As the new phases forms, the strains in all working branches increases by Δε_{a + 1}. The stress-strain relation at T = T_{a + 1} can be written as:

${\sigma }_0=3Nk{T}_{a+1}f\left({\epsilon }^M\left(T_{a+1}\right)\right)+{\displaystyle \sum _{i=1}^{a+1}{E}_i\left(f\left({\epsilon }^M\left(T_{a+1}\right)\right)-f\left({\epsilon }_i^0\right)\right)}(8)$

By comparing Eqs 7, 8, the mechanical strain can then be calculated as:

${\epsilon }^M\left(T_{a+1}\right)=f^{-1}\left(\frac{{\sigma }_0+{\displaystyle \sum _{i=1}^{a+1}{E}_{i}f\left({\epsilon }_{i0}\right)}}{3Nk{T}_{a+1}+{\displaystyle \sum _{i=1}^{a+1}{E}_i}}\right)(9)$

The strain in each phase now is ${\epsilon }_i\left(T_{a+1}\right)={\epsilon }^M\left(T_{a+1}\right)-{\epsilon }_{i0}$, i = 1 to a + 1.

The applied stress is released at T_L in step 3. Before the applied stress is released, the stress-strain relation is

${\sigma }_0=3Nk{T}_{L}f\left({\epsilon }^M\left(T_L\right)\right)+{\displaystyle \sum _{i=1}^n{E}_i\left[f\left({\epsilon }^M\left(T_L\right)\right)-f\left({\epsilon }_i^0\right)\right]}(10)$

After release, the strain in each phase increase by $\text{Δ}\epsilon$, thus

$0=3Nk{T}_{L}f\left({\epsilon }^M\left(T_L\right)+\Delta \epsilon \right)+{\displaystyle \sum _{i=1}^n{E}_i\left[f\left({\epsilon }^M\left(T_L\right)+\Delta \epsilon \right)-f\left({\epsilon }_i^0\right)\right]}(11)$

$\Delta \epsilon$ can then be calculated from Eqs 11, 12 as:

$\Delta \epsilon =f^{-1}\left(f\left({\epsilon }^M\left(T_L\right)\right)-\frac{{\sigma }_0}{3Nk{T}_L+E_g}\right)-{\epsilon }^M\left(T_L\right)(12)$

where the term $E_g={\displaystyle \sum _{i=1}^n{E}_i}$ is used.

In Step 4, the programmed shape in Step 3 recover to its initial shape when the temperature increases from T_L to T_H. At this step, the glassy phases switch off one by one, and the stored strain is released. This process is similar to step 2, except the glassy phases are disconnected.

In summary, the thermal strain is given in Eq. 2. The mechanical strain in each step is given in Eqs 4, 6, 9 and 12.

Finite Element Simulations

FE simulations are conducted using ABAQUS (3DS Dassault Systemes, France) to analyze the mechanical behaviors and the shape memory effects of the lattice structures. The multi-branch model is used to capture the thermo-mechanical behaviors of the lattices. The 3-node plane strain thermally coupled triangle element CPE3T is used.

Results and Discussion

Figure 7 presents the FE simulated shape memory cycle (solid curves) of the lattices with α = 3/8π, 1/2π, and 5/8π. The quantitative dependence of longitudinal (blue) and transverse (orange) strains on time are presented. The theoretical predicted longitudinal strain is presented by the dashed blue curves. The lattice is under stress control mode. The theoretical prediction and the FE simulated results agree well. All the three lattices demonstrate a significant recovery at T = ∼60°C. The lattice’s transverse strain with α = 3/8π is generally larger than 0, indicating a negative Poisson’s ratio. The transverse strain also decreases to around 0 when the temperature increases. The Poisson’s ratio of the lattice with α = 1/2π is almost zero in the whole shape memory cycle. The lattice with α = 5/8π always exhibits a negative transverse strain (Positive Poisson’s ratio).

FIGURE 7

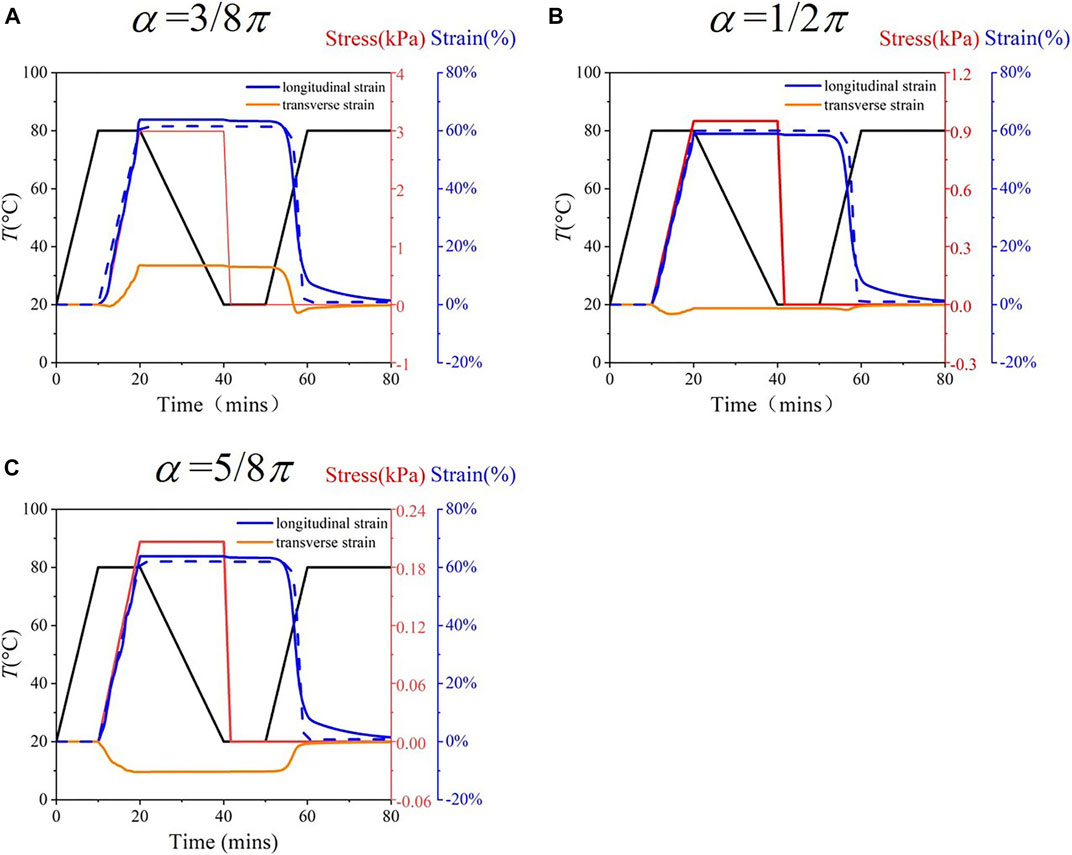
FIGURE 7. Shape memory behaviors of the lattice with different α = 3/8π, 1/2π, and 5/8π. The FE simulated longitudinal (blue solid), transverse (orange solid) strains and the theoretical predicted longitudinal strain (blue dashed) are shown.

It should be noted that there is some discrepancy between the theoretical predicted and FE simulated longitudinal strain, especially in the recovery stage. The FE simulated recovery is slower than the theoretically predicted result. In the theoretical model, the nonlinear phase is only affected by the temperature and independent of time. In the FE simulations, the dependence of the modulus on time is also taken into account. However, compared to the FE simulation's high computational cost, the theoretical results can be calculated in seconds. Therefore, the theoretical model enables the study of the effects of the geometric parameters.

In Figure 8, the dependence of the Poisson’s ratios on α is studied by the theoretical model. Three lattices with α = 82.5°, 97.5°, and 116.25° are chosen. The FE simulated stress-strain/Poisson’s ratio curves shown in Figure 4 are used as input. $f\left(\epsilon \right)$ are obtained from the FE simulated curves. The applied stress in the loading step is 1 kPa. The theoretical predicted strain and Poisson’s ratio in a shape memory cycle are shown by the red and blue curves, respectively. It can be seen that: (1) the stiffness of the three lattices are different. The stiffness of the lattice with α = 116.25° is relatively small. All of the strains and Poisson’s ratios change significantly around T_g in the heating step. The Poisson’s ratio of the lattice with α = 116.25° is always negative. For the lattice with α = 82.5°, the Poisson’s ratio changes from ∼0 to a positive value when T increases. The Poisson’s ratio of the lattice with a = 97.5° changes from negative to positive, which indicates that the lattice first expands and then shrinks when T increase. Therefore, by applying an external stimulus, not only the magnitude of the Poisson’s ratio but also its directions can be altered.

FIGURE 8

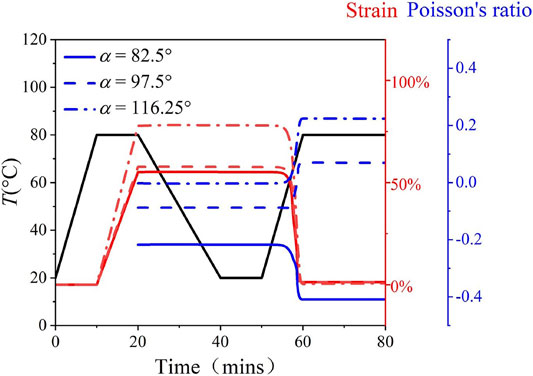
FIGURE 8. Design of the Poisson’s ratios of the lattice structures in a shape memory cycle. Theoretical predicted strains (red) and Poisson’s ratios (blue) in a shape memory cycle with α = 82.5° (solid curve), 97.5° (dashed curve), and 116.25° (dot-dashed curve) are shown.

Reliability and repeatability are important factors of structural safety. The reliability and repeatability of a lattice structure mainly depend on the geometric structure and the material. Specific lattice structures have been designed to improve the reliability with applications in areas such as energy absorption Tancogne-Dejean et al. (2016) and efficient response to impulsive loads (Imbalzano et al., 2017). The lattice structure used in this work by replacing the straight beam with microstructures can significantly reduce the local strain comparing to the traditional honeycomb Queheillalt and Wadley (2005) when the same total strain is applied. As shown in Figure 2B, the local strain is generally less than 10% when the microstructure is stretched up to 60%. The small local strain reduces the fatigue of the material and increases the repeatability of the lattice structure. The use of microstructures can also reduce sensitivity to structural defects (Yan et al., 2020). Furthermore, the material Vero has a tensile strength of around 60 MPa and strong ability to withstand bending (2.2–3.2 GPa) (Ju et al., 2014). Vero’s fracture properties have been investigated, and results show that Vero has higher tensile strength and failure strain than natural rock-like materials (Liu et al., 2020). Therefore, by combining structure design and material performance, the structure's reliability and repeatability are improved. We also note that the lattice structure's reliability and repeatability can be improved by optimizing the geometric parameters of the microstructures.

Conclusion

In this work, we designed a type of shape reconfigurable, highly stretchable honeycomb lattice structures with tunable Poisson’s ratio. Using a geometric angle α, the Poisson’s ratio of the lattice structure can be tuned to be positive, negative or zero. To increase the stretchability of the lattice structure, the straight beam in the lattice is replaced by a curled microstructure. When an external loading is applied, the microstructure bends, uncurls and rotates to aligning to the loading direction. Therefore, the stretchability of the lattice structure is significantly improved. Experiments show that the failure strain of the lattice structures is generally larger than 70%, which is seven folds larger than the failure strain of the material.

To enable the lattice’s capacity of shape reconfiguration, we use a shape memory polymer Vero to 3D print the lattice. When the ambient temperature increases, the lattice demonstrates a large shape change. To predict the shape change of lattice structure, a phase evolution model is employed. Results show that the theoretically predicted shape changes agree well with the FE simulations. Also, the theoretical model can significantly reduce the computational cost. Theoretical prediction further shows that by increasing the temperature, not only the magnitude of the lattice but also its sign can change. The shape reconfigurable, highly stretchable, Poisson’s ratio tunable lattice structures may find a broad range of applications in areas such as shock-absorbing, aerospace morphing structures, soft robotics and minimally invasive biomedical devices.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

LD, and DW conceived the idea and experimental work; LD CJ led the experiments and simulation with assistance from JW, LD, and DW contributed to data analysis and interpretation and wrote the paper. All authors provided feedback.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

DW acknowledges the support by grants from the National Natural Science Foundation of China (Grant No. 51905336) and the Shanghai Sailing Program from Shanghai Municipal Committee of Science and Technology (Grant No. 19YF1423000).

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2021.660325/full#supplementary-material

References

Ai, L., and Gao, X.-L. (2017). Micromechanical Modeling of 3D Printable Interpenetrating Phase Composites with Tailorable Effective Elastic Properties Including Negative Poisson’s Ratio. J. Micromech. Mol. Phys. 02, 1750015. doi:10.1142/s2424913017500151

CrossRef Full Text | Google Scholar

Akbari, S., Sakhaei, A. H., Kowsari, K., Yang, B., Ahmad, S., Zhang, Y., et al. (2018). Enhanced Multimaterial 4D Printing with Active Hinges. Smart Mater. Structures 27, 065027. doi:10.1088/1361-665x/aabe63

CrossRef Full Text | Google Scholar

Alderson, K. L., and Evans, K. E. (1992). The Fabrication of Microporous Polyethylene Having a Negative Poisson’s Ratio. Polymer 33, 4435–4438. doi:10.1016/0032-3861(92)90294-7

CrossRef Full Text | Google Scholar

Alderson, K. L., Fitzgerald, A., and Evans, K. E. (2000). The Strain Dependent Indentation Resilience of Auxetic Microporous Polyethylene. J. Mater. Sci. 35, 4039–4047. doi:10.1023/a:1004830103411

CrossRef Full Text | Google Scholar

Bertoldi, K., Vitelli, V., Christensen, J., and Van Hecke, M. (2017). Flexible Mechanical Metamaterials. Nat. Rev. Mater. 2, 1–11. doi:10.1038/natrevmats.2017.66

CrossRef Full Text | Google Scholar

Bodaghi, M., Damanpack, A. R., and Liao, W. H. (2016). Self-expanding/shrinking Structures by 4D Printing. Smart Mater. Struct. 25, 105034. doi:10.1088/0964-1726/25/10/105034

CrossRef Full Text | Google Scholar

Caddock, B. D., and Evans, K. E. (1989). Microporous Materials with Negative Poisson’s Ratios. I. Microstructure and Mechanical Properties. J. Phys. D: Appl. Phys. 22, 1877–1882. doi:10.1088/0022-3727/22/12/012

CrossRef Full Text | Google Scholar

Cao, C., Gao, X., and Conn, A. T. (2019). A Magnetically Coupled Dielectric Elastomer Pump for Soft Robotics. Adv. Mater. Technol. 4, 1900128. doi:10.1002/admt.201900128

CrossRef Full Text | Google Scholar

Chen, Y., Li, T., Scarpa, F., and Wang, L. (2017). Lattice Metamaterials with Mechanically Tunable Poisson’s Ratio for Vibration Control. Phys. Rev. Appl. 7, 024012. doi:10.1103/physrevapplied.7.024012

CrossRef Full Text | Google Scholar

Chetverikov, A. P., Dmitriev, S. V., Korznikova, E. A., and Sergeev, K. S. (2019). Dissipative Solitons and Crowdions in Triangular Lattice of Active Particles. J. Micromech. Mol. Phys. 04, 1850005. doi:10.1142/s2424913018500054

CrossRef Full Text | Google Scholar

Clayton, J. D., and Knap, J. (2018). Geometric Micromechanical Modeling of Structure Changes, Fracture and Grain Boundary Layers in Polycrystals. J. Micromech. Mol. Phys. 03, 1840001. doi:10.1142/s2424913018400015

CrossRef Full Text | Google Scholar

de Jonge, C., Kolken, H., Zadpoor, A., and Zadpoor, A. A. (2019). Non-Auxetic Mechanical Metamaterials. Materials 12, 635. doi:10.3390/ma12040635

CrossRef Full Text | Google Scholar

Ding, Z., Yuan, C., Peng, X., Wang, T., Qi, H. J., and Dunn, M. L. (2017). Direct 4D Printing via Active Composite Materials. Sci. Adv. 3, e1602890. doi:10.1126/sciadv.1602890

PubMed Abstract | CrossRef Full Text | Google Scholar

Ding, Z., Weeger, O., Qi, H. J., and Dunn, M. L. (2018). 4D Rods: 3D Structures via Programmable 1D Composite Rods. Mater. Des. 137, 256–265. doi:10.1016/j.matdes.2017.10.004

CrossRef Full Text | Google Scholar

Fozdar, D. Y., Soman, P., Lee, J. W., Han, L.-H., and Chen, S. (2011). Three-Dimensional Polymer Constructs Exhibiting a Tunable Negative Poisson’s Ratio. Adv. Funct. Mater. 21, 2712–2720. doi:10.1002/adfm.201002022

PubMed Abstract | CrossRef Full Text | Google Scholar

Ge, Q., Sakhaei, A. H., Lee, H., Dunn, C, and Fang, N. X (2016). Multimaterial 4D Printing with Tailorable Shape Memory Polymers. Scientific Rep. 6, 1–11. doi:10.1038/srep31110

PubMed Abstract | CrossRef Full Text | Google Scholar

Guo, Y., Zhang, J., Chen, L., Du, B., Liu, H., Chen, L., et al. (2020). Deformation Behaviors and Energy Absorption of Auxetic Lattice Cylindrical Structures under Axial Crushing Load. Aerospace Sci. Tech. 98, 105662. doi:10.1016/j.ast.2019.105662

CrossRef Full Text | Google Scholar

Hu, C., Dong, J., Luo, J., Qin, Q.-H., and Sun, G. (2020). 3D Printing of Chiral Carbon Fiber Reinforced Polylactic Acid Composites with Negative Poisson’s Ratios. Composites B: Eng. 201, 108400. doi:10.1016/j.compositesb.2020.108400

CrossRef Full Text | Google Scholar

Hu, L. L., Zhou, M. Z., and Deng, H. (2019). Dynamic Indentation of Auxetic and Non-auxetic Honeycombs under Large Deformation. Compos. Structures 207, 323–330. doi:10.1016/j.compstruct.2018.09.066

CrossRef Full Text | Google Scholar

Huang, C., and Chen, L. (2016). Negative Poisson’s Ratio in Modern Functional Materials. Adv. Mater. 28, 8079–8096. doi:10.1002/adma.201601363

PubMed Abstract | CrossRef Full Text | Google Scholar

Imbalzano, G., Tran, P., DLee, T., Lee, P. V., and Peter, T. D. (2017). Three-dimensional Modelling of Auxetic sandwich Panels for Localised Impact Resistance. Jnl Sandwich Structures Mater. 19, 291–316. doi:10.1177/1099636215618539

CrossRef Full Text | Google Scholar

Ji, Z., Yan, C., Yu, B., Wang, X., and Zhou, F. (2017). Multimaterials 3D Printing for Free Assembly Manufacturing of Magnetic Driving Soft Actuator. Adv. Mater. Inter. 4, 1700629. doi:10.1002/admi.201700629

CrossRef Full Text | Google Scholar

Jiang, Y., and Wang, Q. (2016). Highly-stretchable 3D-Architected Mechanical Metamaterials. Scientific Rep. 6, 1–11. doi:10.1038/srep34147

PubMed Abstract | CrossRef Full Text | Google Scholar

Ju, Y., Xie, H., Zheng, Z., Lu, J., Mao, L., Gao, F., et al. (2014). Visualization of the Complex Structure and Stress Field inside Rock by Means of 3D Printing Technology. Chin. Sci. Bull. 59, 5354–5365. doi:10.1007/s11434-014-0579-9

CrossRef Full Text | Google Scholar

Keskar, N. R., and Chelikowsky, J. R. (1992). Negative Poisson Ratios in Crystalline SiO2 from First-Principles Calculations. Nature 358, 222–224. doi:10.1038/358222a0

CrossRef Full Text | Google Scholar

Khan, K. A., Al-Mansoor, S., Khan, S. Z., and Khan, M. A. (2019). Piezoelectric Metamaterial with Negative and Zero Poisson’s Ratios. J. Eng. Mech. 145, 04019101. doi:10.1061/(asce)em.1943-7889.0001674

CrossRef Full Text | Google Scholar

Khare, E., Temple, S., Tomov, I., Zhang, F., and Stoyan, K. S. (2018). Low Fatigue Dynamic Auxetic Lattices with 3D Printable, Multistable, and Tuneable Unit Cells. Front. Mater. 5, 45. doi:10.3389/fmats.2018.00045

CrossRef Full Text | Google Scholar

Kong, D., Li, J., Guo, A., Yu, J., and Xiao, X. (2021a). Smart Polyimide with Recovery Stress at the Level of High Temperature Shape Memory Alloys. Smart Mater. Structures 30, 035027. doi:10.1088/1361-665x/abe182

CrossRef Full Text | Google Scholar

Kong, D., Li, J., Guo, A., and Xiao, X. (2021b). High Temperature Electromagnetic Shielding Shape Memory Polymer Composite. Chem. Eng. J. 408, 127365. doi:10.1016/j.cej.2020.127365

CrossRef Full Text | Google Scholar

Kong, D., Li, J., Guo, A., Zhang, X., and Xiao, X. (2019). Self-healing High Temperature Shape Memory Polymer. Eur. Polym. J. 120, 109279. doi:10.1016/j.eurpolymj.2019.109279

CrossRef Full Text | Google Scholar

Lantean, S., Barrera, G., Pirri, C. F., Tiberto, P., Sangermano, M., Roppolo, I., et al. (2019). 3D Printing of Magnetoresponsive Polymeric Materials with Tunable Mechanical and Magnetic Properties by Digital Light Processing. Adv. Mater. Technol. 4, 1900505. doi:10.1002/admt.201900505

CrossRef Full Text | Google Scholar

Lee, J. H., Hinchet, R., Kim, S. K., Kim, S., and Kim, S.-W. (2015). Shape Memory Polymer-Based Self-Healing Triboelectric Nanogenerator. Energy Environ. Sci. 8, 3605–3613. doi:10.1039/c5ee02711j

CrossRef Full Text | Google Scholar

Lees, C., Vincent, J. F. V., and Hillerton, J. E. (1991). Poisson’s Ratio in Skin. Bio-medical Mater. Eng. 1, 19–23. doi:10.3233/bme-1991-1104

CrossRef Full Text | Google Scholar

Lendlein, A., and Kelch, S. (2005). Shape-memory Polymers as Stimuli-Sensitive Implant Materials. Clin. Hemorheol. Microcirc. 32, 105–116.

PubMed Abstract | Google Scholar

Lendlein, A., and Langer, R. (2002). Biodegradable, Elastic Shape-Memory Polymers for Potential Biomedical Applications. Science 296, 1673–1676. doi:10.1126/science.1066102

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, S., Hassanin, H., Attallah, M. M., Adkins, N. J. E., and Essa, K. (2016). The Development of TiNi-Based Negative Poisson’s Ratio Structure Using Selective Laser Melting. Acta Materialia 105, 75–83. doi:10.1016/j.actamat.2015.12.017

CrossRef Full Text | Google Scholar

Li, T., Chen, Y., Hu, X., Li, Y., and Wang, L. (2018). Exploiting Negative Poisson’s Ratio to Design 3D-Printed Composites with Enhanced Mechanical Properties. Mater. Des. 142, 247–258. doi:10.1016/j.matdes.2018.01.034

CrossRef Full Text | Google Scholar

Li, T., Liu, F., and Wang, L. (2020). Enhancing Indentation and Impact Resistance in Auxetic Composite Materials. Composites Part B: Eng. 198, 108229. doi:10.1016/j.compositesb.2020.108229

CrossRef Full Text | Google Scholar

Li, Y., Luo, S., Yang, M.-C., Liang, R., and Zeng, C. (2016). Poisson Ratio and Piezoresistive Sensing: A New Route to High-Performance 3D Flexible and Stretchable Sensors of Multimodal Sensing Capability. Adv. Funct. Mater. 26, 2900–2908. doi:10.1002/adfm.201505070

CrossRef Full Text | Google Scholar

Liu, J., and Zhang, Y. (2018). Soft Network Materials with Isotropic Negative Poisson’s Ratios over Large Strains. Soft Matter 14, 693–703. doi:10.1039/c7sm02052j

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, P., Ju, Y., Fu, G., and Ren, Z. (2020). Visualization of Full-Field Stress Evolution during 3D Penetrated Crack Propagation through 3D Printing and Frozen Stress Techniques. Eng. Fracture Mech. 236, 107222. doi:10.1016/j.engfracmech.2020.107222

CrossRef Full Text | Google Scholar

Ma, Q., Cheng, H., Jang, K.-I., Luan, H., Hwang, K.-C., Hwang, Keh-Chih., et al. (2016). A Nonlinear Mechanics Model of Bio-Inspired Hierarchical Lattice Materials Consisting of Horseshoe Microstructures. J. Mech. Phys. Sol. 90, 179–202. doi:10.1016/j.jmps.2016.02.012In

CrossRef Full Text | Google Scholar

Milton, G. W. (1992). Composite Materials with Poisson’s Ratios Close to - 1. J. Mech. Phys. Sol. 40, 1105–1137. doi:10.1016/0022-5096(92)90063-8

CrossRef Full Text | Google Scholar

Queheillalt, D. T., and Wadley, H. N. G. (2005). Cellular Metal Lattices with Hollow Trusses. Acta Materialia 53, 303–313. doi:10.1016/j.actamat.2004.09.024

CrossRef Full Text | Google Scholar

Rafsanjani, A., and Pasini, D. (2016). Bistable Auxetic Mechanical Metamaterials Inspired by Ancient Geometric Motifs. Extreme Mech. Lett. 9, 291–296. doi:10.1016/j.eml.2016.09.001

CrossRef Full Text | Google Scholar

Saxena, K. K., Das, R., and Calius, E. P. (2016). Three Decades of Auxetics Research − Materials with Negative Poisson’s Ratio: A Review. Adv. Eng. Mater. 18, 1847–1870. doi:10.1002/adem.201600053

CrossRef Full Text | Google Scholar

Shao, L.-H., Zhao, B., Zhang, Q., Xing, Y., and Zhang, K. (2020). 4D Printing Composite with Electrically Controlled Local Deformation. Extreme Mech. Lett. 39, 100793. doi:10.1016/j.eml.2020.100793

CrossRef Full Text | Google Scholar

Tancogne-Dejean, T., Spierings, A. B., and Mohr, D. (2016). Additively-manufactured Metallic Micro-lattice Materials for High Specific Energy Absorption under Static and Dynamic Loading. Acta Materialia 116, 14–28. doi:10.1016/j.actamat.2016.05.054

CrossRef Full Text | Google Scholar

Testa, P., Style, R. W., Cui, J., Donnelly, C., Borisova, E., Derlet, P. M., et al. (2019). Magnetically Addressable Shape‐Memory and Stiffening in a Composite Elastomer. Adv. Mater. 31, 1900561. doi:10.1002/adma.201900561

PubMed Abstract | CrossRef Full Text | Google Scholar

Timmins, L. H., Wu, Q., Yeh, A. T., Moore, J. E., and Greenwald, S. E. (2010). Structural Inhomogeneity and Fiber Orientation in the Inner Arterial media. Am. J. Physiology-Heart Circulatory Physiol. 298, H1537–H1545. doi:10.1152/ajpheart.00891.2009

CrossRef Full Text | Google Scholar

Veronda, D. R., and Westmann, R. A. (1970). Mechanical Characterization of Skin-Finite Deformations. J. Biomech. 3, 111–124. doi:10.1016/0021-9290(70)90055-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, D., Xu, H., Wang, J., Jiang, C., Zhu, X., Ge, Q., et al. (2020). Design of 3D Printed Programmable Horseshoe Lattice Structures Based on a Phase-Evolution Model. ACS Appl. Mater. Inter. 12, 22146–22156. doi:10.1021/acsami.0c04097

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Y., Wang, L., Ma, Z.-d., and Wang, T. (2016). A Negative Poisson’s Ratio Suspension Jounce Bumper. Mater. Des. 103, 90–99. doi:10.1016/j.matdes.2016.04.041

CrossRef Full Text | Google Scholar

Williams, J. L., and Lewis, J. L. (1982). Properties and an Anisotropic Model of Cancellous Bone from the Proximal Tibial Epiphysis. New York: The American Society of Mechanical Engineers (ASME).

Yan, D., Chang, J., Zhang, H., Liu, J., Song, H., Xue, Z., et al. (2020). Soft Three-Dimensional Network Materials with Rational Bio-Mimetic Designs. Nat. Commun. 11, 1–11. doi:10.1038/s41467-020-14996-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Yan, Z. G., Wang, B. L., Wang, K. F., and Zhang, C. (2019). A Novel Cellular Substrate for Flexible Electronics with Negative Poisson Ratios under Large Stretching. Int. J. Mech. Sci. 151, 314–321. doi:10.1016/j.ijmecsci.2018.11.026

CrossRef Full Text | Google Scholar

Yang, C., Boorugu, M., Dopp, A., Ren, J., Martin, R., Han, D., et al. (2019). 4D Printing Reconfigurable, Deployable and Mechanically Tunable Metamaterials. Mater. Horiz. 6, 1244–1250. doi:10.1039/c9mh00302a

CrossRef Full Text | Google Scholar

Yiming, B., Wu, L., Zhang, M., Han, Z., Zhao, P., Li, T., et al. (2020). Highly Stretchable Bilayer Lattice Structures that Elongate via In‐Plane Deformation. Adv. Funct. Mater. 30, 1909473. doi:10.1002/adfm.201909473

CrossRef Full Text | Google Scholar

Yuan, C., Kowsari, K., Panjwani, S., Chen, Z., Wang, D., Zhang, B., et al. (2019). Ultrafast Three-Dimensional Printing of Optically Smooth Microlens Arrays by Oscillation-Assisted Digital Light Processing. ACS Appl. Mater. Inter. 11, 40662–40668. doi:10.1021/acsami.9b14692

PubMed Abstract | CrossRef Full Text | Google Scholar

Ze, Q., Kuang, X., Wu, S., Wong, J., Montgomery, S. M., Zhang, R., et al. (2020). Magnetic Shape Memory Polymers with Integrated Multifunctional Shape Manipulation. Adv. Mater. 32, 1906657. doi:10.1002/adma.201906657

PubMed Abstract | CrossRef Full Text | Google Scholar