- TCS Research, Tata Consulatncy Services Ltd., Pune, India
Hydrogen economy, wherein hydrogen is used as the fuel in the transport and energy sectors, holds significant promise in mitigating the deleterious effects of global warming. Photocatalytic water splitting using sunlight is perhaps the cleanest way of producing the hydrogen fuel. Among various other factors, widespread adoption of this technology has mainly been stymied by the lack of a catalyst material with high efficiency. 2D materials have shown significant promise as efficient photocatalysts for water splitting. The availability of open databases containing the “computed” properties of 2D materials and advancements in deep learning now enable us to do “inverse” design of these 2D photocatalysts for water splitting. We use one such database (Jain et al., ACS Energ. Lett. 2019, 4, 6, 1410–1411) to build a generative model for the discovery of novel 2D photocatalysts. The structures of the materials were converted into a 3D image–based representation that was used to train a cell, a basis autoencoder and a segmentation network to ascertain the lattice parameters as well as position of atoms from the images. Subsequently, the cell and basis encodings were used to train a conditional variational autoencoder (CVAE) to learn a continuous representation of the materials in a latent space. The latent space of the CVAE was then sampled to generate several new 2D materials that were likely to be efficient photocatalysts for water splitting. The bandgap of the generated materials was predicted using a graph neural network model while the band edge positions were obtained via empirical correlations. Although our generative modeling framework was used to discover novel 2D photocatalysts for water splitting reaction, it is generic in nature and can be used directly to discover novel materials for other applications as well.
Introduction
Hydrogen as an alternate fuel and energy carrier has the potential to substantially mitigate carbon emissions for a green and sustainable future (Turner, 2004). Since it is not naturally available in free form for large scale applications, hydrogen is produced synthetically through a variety of processes (Sigfusson, 2007). Photocatalytic/photoelectrochemical splitting of water using sunlight, a suitable photocatalyst, water, and renewable electricity is perhaps the environmentally most benign method to produce hydrogen at scale (Edwards et al., 2007). Ever since the demonstration of solar water splitting by Fujishima and Honda (1972) using TiO2 electrodes, enormous amount of efforts has been put in identifying new photocatalysts. Various materials, such as metal oxides, nitrides, sulfides, oxysulfides, oxynitrides, and Z-scheme materials, have been developed with enhanced efficiencies for solar water splitting. A detailed overview of these developments and the progress made in the field has been documented in several excellent review articles (Osterloh, 2008; Kudo and Miseki, 2009; Maeda and Domen, 2010; Osterloh and Parkinson, 2011; Tachibana et al., 2012; Hisatomi et al., 2014; Ahmad et al., 2015; Zou and Zhang, 2015; Moniruddin et al., 2018; Prasad, 2020). The emergence of 2D materials, heralded by the discovery of graphene (Novoselov et al., 2004), has added a new dimension in the search of efficient photocatalysts. In addition to stability and suitable electronic structure, these materials provide a large surface to volume ratio, higher charge carrier mobility, and reduced recombination rates, all of which aid in enhancing the reaction rates at the photocatalyst surface (Li et al., 2017). Various 2D materials, mostly chalcogenides such as SnS and SnSe (Sun et al., 2014), CdS (Xu et al., 2013), WS2 (Voiry et al., 2013), SnS2 (Sun et al., 2012), and MoS2 (Maitra et al., 2013) have been synthesized and shown to have enhanced photocatalytic performance.
With rapid advancements in first principles methods and computational power, in-silico design/screening of materials has emerged as a promising alternative method to narrow the search space of novel functional materials (Agrawal and Choudhary, 2016). For instance, high-throughput density functional theory (DFT) calculations have been used to identify oxynitrides (Wu et al., 2013), perovskites (Castelli et al., 2012a; Castelli et al., 2012b), and chalcogenides (Zhuang and Hennig, 2013a; Zhuang and Hennig, 2013b; Singh et al., 2015) as potential photocatalysts for water splitting. Properties of a vast number of materials computed in such high-throughput fashion using accurate first principles methods have been made openly available in repositories such as the Materials Project (MP) (Jain et al., 2013), the Open Quantum Materials Database (OQMD) (Saal et al., 2013), Automatic FLOW for materials discovery (AFLOW) (Curtarolo et al., 2012), and Novel Materials Discovery (NOMAD) (The NOMAD (Novel Materials Discovery) Center of Excellence (CoE), (2021)). While these repositories primarily contain data on bulk materials, two different datasets containing DFT-computed properties for 2D materials were also published recently (Haastrup et al., 2018; Zhou et al., 2019). Knowledge stored in these repositories has then been mined to screen materials for diverse applications (Zhang et al., 2018; Singh et al., 2019; Zhang et al., 2019). In addition, machine learning models have also been trained using data from these repositories to predict properties of novel materials (Ahmad et al., 2018; Xie and Grossman, 2018; Ye et al., 2018; Joshi et al., 2019; Liu et al., 2020). In a recent article, Sorkun et al. (2020) identified several potential 2D materials for photocatalytic water splitting, CO2 reduction, and N2 reduction by training AI models on the computational 2D materials database and using the predictions from these models to screen a vast chemical space obtained by systematic elemental substitution in 2D material prototypes.
An alternate approach to the high-throughput screening is to build unsupervised deep learning (DL) models that can learn the encodings of materials in a continuous latent space. This latent space could then be sampled to generate novel materials. When linked with one or more material property, such techniques can enable discovery of novel materials conditioned on certain properties (i.e., inverse design of functional materials). Variational autoencoder (VAE) (Kingma and Welling, 2019) and generative adversarial network (GAN) (Goodfellow et al., 2014) are two of the most widely used generative models. VAEs use concepts of variational inference to learn the representation of input data by minimizing the reconstruction loss (formally called maximizing the log likelihood of observations) as well as divergence of the learned distribution from an assumed prior distribution (formally called Kullback-Leibler divergence) (Kingma and Welling, 2019). On the other hand, GANs use concepts from game theory to adversarially train a generative and a discriminative network. While the objective of the generative network is to fool the discriminator by generating realistic samples, the discriminator aims to correctly distinguish fake samples created by the generator from true samples (Goodfellow et al., 2014). Recently, both VAEs and GANs have been used for the generation of novel inorganic materials. In their iMatGen framework, Noh et al. (2019) used an image-based representation of crystal structures and trained a VAE to generate novel phases of vanadium oxides. While their model was restricted to only two element types (V and O), Hoffmann et al. (2019) introduced a generalization of this concept via inclusion of a segmentation network, to generate novel materials containing multiple types of elements. Court et al. (2020) used these concepts to build a conditional VAE for the generation of novel binary alloys, ternary perovskites, and Heusler compounds, all in cubic symmetry. Ren et al. (2020) used an invertible representation of crystal structures by a combination of descriptors in both real and reciprocal spaces and trained a VAE to generate novel thermoelectric materials. Long et al. (2020) and Kim et al. (2020) used GANs to discover a new crystal structure of the Bi-Se and Mg-Mn-O systems, respectively.
In this study, we have developed a generative modeling framework for the discovery of novel 2D materials as photocatalysts for water splitting. In comparison to prior works, our framework does not place any restriction on the structure or the stoichiometry of the materials. The bandgap of the generated materials was predicted using the CGCNN model (Xie and Grossman, 2018) while their band edge positions were computed using empirical correlations. Using this framework, we have discovered several novel 2D materials as potentially good photocatalyst for water splitting. While we have demonstrated the discovery of 2D photocatalysts as an application, our framework is generic enough to be applied for any kind of functional material discovery.
Methods
Data Preparation and Representation
The dataset of 2D materials, to train our hierarchical generative model was obtained from the earlier published study of Jain et al. (2019). This dataset included data for all the materials that were included in earlier 2D materials’ databases such as C2DB (Haastrup et al., 2018) and 2DMatPedia (Zhou et al., 2019) as well as the materials cloud (Mounet et al., 2018). Furthermore, properties such as the bandgap and energy above hull for all the materials were reported using a uniform level of theory, thereby providing us a consistent set of data to learn from. Around 7,500 unique 2D materials were present in the dataset whose structures were provided as cif files. These structures were converted to image-based representations which were subsequently used to train all our models.
In order to represent the crystal structures as images, we followed the same concept as proposed by Noh et al. (2019) in their iMatGen framework. Just as a crystal structure is construed as a “basis” of atoms in an underlying “lattice”, each structure in our dataset was represented using a “cell” and a “basis” 3D image. Both the images had a dimension of (32 × 32 × 32). The voxel values of the cell image were obtained using a Gaussian function as:
where rijk is the Euclidean distance between the center of the lattice and (i, j, k)th voxel. The basis image was generated using an atomic number weighted Gaussian transformation as described by Hoffmann et al. (2019). Concretely, the voxel values of the basis image were obtained as follows:
where Zl is the atomic number at site “l” of the material, d[Zl, (i,,j,k)] is the Euclidean distance between the site “l” and the (i, j, k)th voxel, and “σ” is the width of the Gaussian. We used a value of σ = 1.0, consistent with earlier works by Noh et al. (2019) and Hoffmann et al. (2019), since testing with lower values of σ resulted in larger errors. In contrast, Court et al. (2020) used the ionic radius of various elements for σ instead of a constant value. Prior to generating the basis image, the atoms in a material were translated such that their center of geometry lay at the center of a cube of length 10 Å. Together with the basis image, an elements matrix was also constructed to ascertain the positions and types of atoms from the basis image. The elements matrix had the same dimensionality as the basis image (i.e., 32 × 32 × 32). The voxel values of the “elements matrix” were assigned as:
Use of a larger value for the cutoff (larger than

FIGURE 1. (A) Crystal structure of a material in our dataset, (B) its cell image, (C) its basis image, and (D) the elements matrix.
Deep Learning Model and Network Architecture
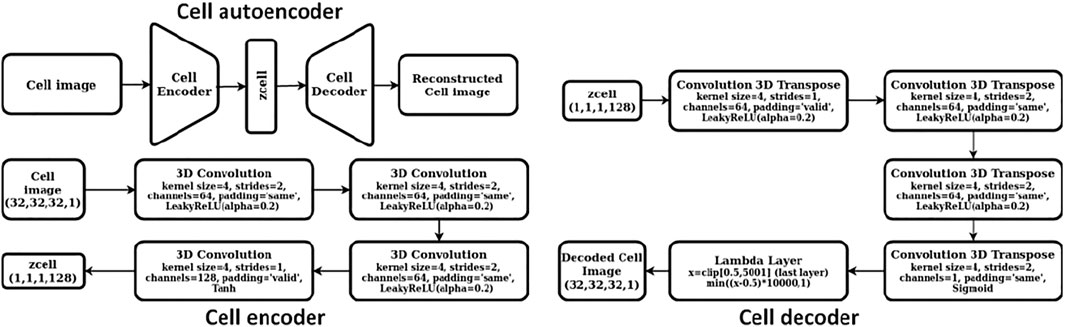
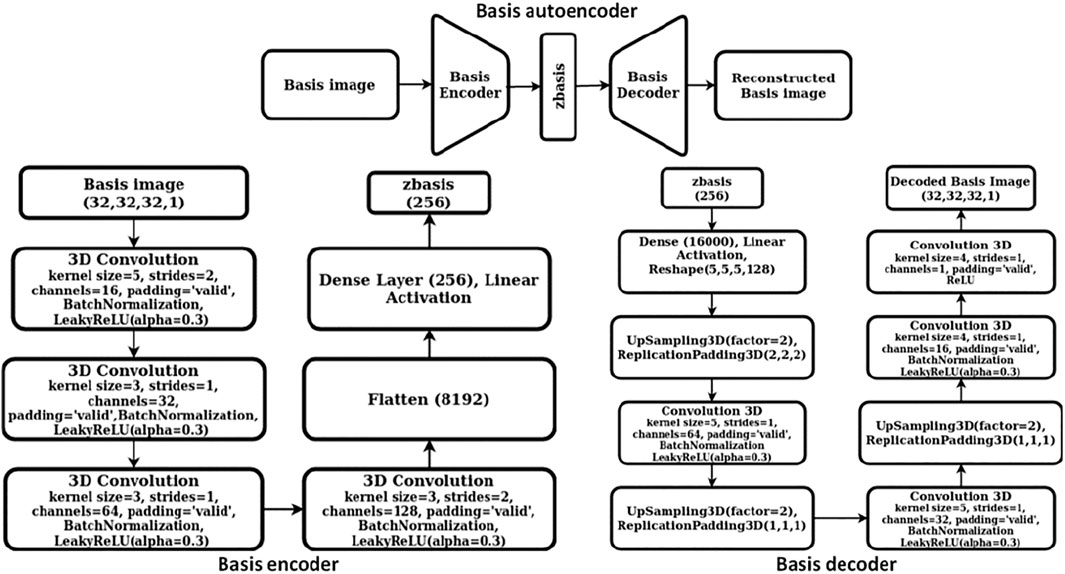
We constructed a two-step hierarchical deep learning model like the iMatGen framework (Noh et al., 2019) to learn the representations of the 2D materials in our dataset and to generate novel materials by sampling from learned continuous representations. The first step of the model consisted of training a cell and basis autoencoder as well as a segmentation network for identification of atomic positions and corresponding element types from the basis image and the elements matrix. Both the autoencoders were constructed as 3D convolutional neural networks (3D CNNs). The encoder of the cell autoencoder consisted of four 3D convolutional layers while the decoder used four 3D convolution transpose layers (i.e., a mirror image of the encoder). Similarly, the encoder of the basis autoencoder consisted of four 3D convolutional layers followed by a fully connected layer. However, the decoder used upsampling instead of 3D convolution transpose. The dimensions of cell and basis encoding vectors (i.e., the autoencoder bottleneck dimension) were 128 and 256, respectively. While training, mean squared error (MSE) was used as the loss function. The detailed architecture of cell and basis autoencoders is shown in Figures 2, 3, respectively.
After training of the basis autoencoder, the segmentation network [a 3D attention U-net model (Oktay et al., 2018)] was trained independently using the reconstructed basis images (i.e., images obtained as the output from the decoder of the basis autoencoder) to identify location and types of elements at that location as atomic clusters. This contrasts with the study of Hoffmann et al. (2019) who trained their segmentation network together with the basis autoencoder in an end-to-end fashion to identify the locations of atoms in a material. The elements matrix prepared earlier for each structure was converted into a species matrix via one hot encoding into 95 classes at each grid point. Of these 95 classes, one class represented the background (or vacuum) while the other 94 classes corresponded to different elements. If a particular element type was present at a grid point of the elements matrix, its corresponding class was set to 1 while the rest of the values of the one hot vector remained as zeros. Thus, for each material, the ground truth to train the segmentation network was a species matrix of dimension (32 × 32 × 32 × 95). The binary cross entropy (BCE) loss was used while training the segmentation network.
In the second step of our hierarchical model, we trained a generative model to obtain a continuous representation of the 2D materials that can be sampled to discover novel materials. Thermodynamic stability and the presence of a bandgap are two necessary conditions that any 2D material must satisfy to qualify as a potential photocatalyst for water splitting reaction. As a thumb rule, we considered a material in our database to be stable if its energy above the hull (e_hull) value was less than 150 meV per atom. Thus, the materials in our training dataset were classified into four categories as shown in Table 1.

TABLE 1. Classification of the 2D materials in our dataset into four different classes based on their bandgap and energy above the hull values.
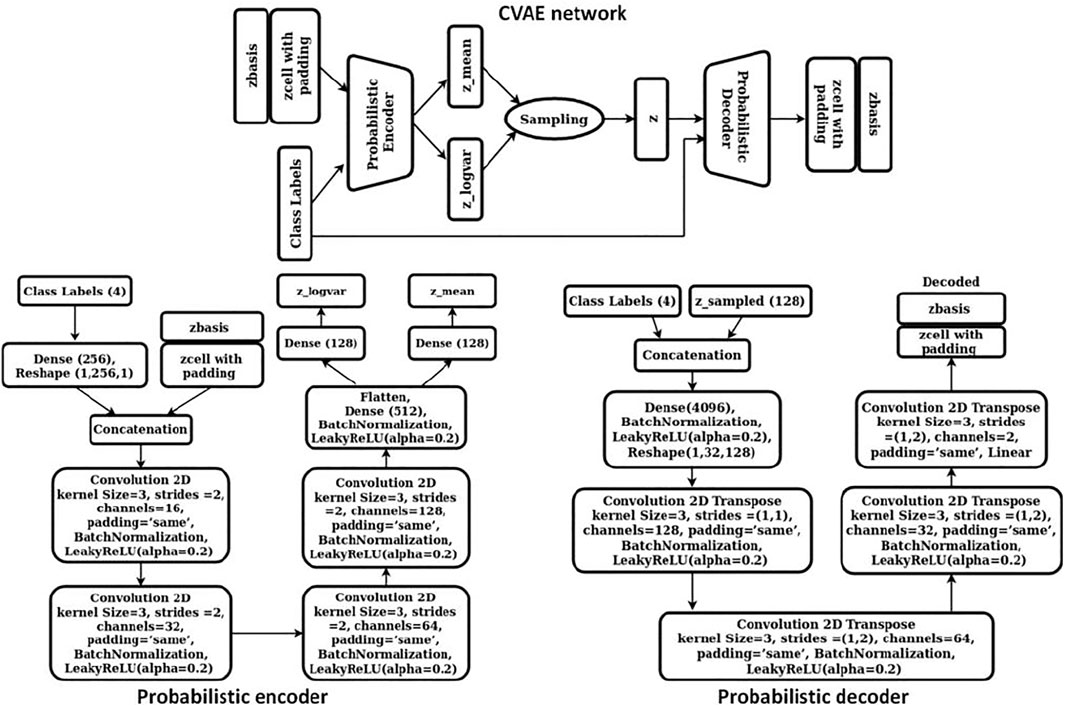
The objective of our study was to discover novel 2D materials belonging to class 1) (i.e., thermodynamically stable with a finite electronic bandgap) so that potential photocatalysts for water splitting reaction could be identified. Accordingly, a conditional variational autoencoder (CVAE) was chosen as our generative model so that, while sampling the latent space for new materials, control could be exerted over the class of material to be generated (i.e., material belonging to class 1) described above). Our CVAE model was trained using the cell and basis encodings from the previous step (step 1) together with the one hot encoded class vectors. Cell encodings were padded with zeros such that both the cell and basis encodings were 256-dimension vectors. Subsequently, these were scaled using the normal quantile transformer with 1000 quantiles. The four dimensional one-hot encoded vector was connected to a 256 dimension hidden layer so that the cell, basis, and the class encodings were all 256 dimensional vectors. These vectors were then concatenated as “channels” so that each training data was now represented by a (256 × 3) dimension image. The CVAE network comprised of a probabilistic encoder and a probabilistic decoder. We represented both the encoder and the decoder via 2D CNNs. The detailed architecture of our CVAE model is shown in Figure 4.
The probabilistic encoder encoded the input into a distribution with mean µ and standard deviation σ. A latent vector was then sampled from this distribution using the reparameterization trick, z = µ+ε*σ, where ε is a random variable from a normal distribution. This vector was passed through the probabilistic decoder to obtain the cell and basis encodings as the output. To train CVAE, we implemented optimal σ-VAE variant, a simple and effective methodology suggested by Rybkin et al. (2020), that did not require tuning the weight on the KL divergence term of the objective function as hyperparameter. The implementation automatically balances the two terms of CVAE objective function, namely, reconstruction loss (or MSE) and KL-divergence. The objective function for our CVAE network was defined as:
where D is dimensionality of the input (x), DKL is the KL divergence, q (z|x) is the encoding distribution, p(z) is the prior distribution (chosen as a normal distribution with zero mean and unit standard deviation), and σ is the weighting parameter to balance the KL-divergence and MSE terms.
Bandgap and Band Edge Positions of 2D materials
The bandgap of a material and its band edge positions must be of appropriate values for a material to be a potentially good photocatalyst for water splitting. While DFT has been the method of choice to compute these properties of a material, several DL models with good accuracy have been reported recently that are well suited for rapid screening of novel materials. We used the CGCNN model (Xie and Grossman, 2018) to predict the bandgaps of the materials obtained from our model. The weights of the CGCNN model were retrained using our 2D materials dataset. Since data augmentation of the aforementioned kind is irrelevant for graph-based models, we considered only those materials from the original dataset that had a non-zero bandgap. The bandgap predicted from the trained CGCNN model was used to compute the band edge positions using the empirical equations given below:
where ECB0 and EVB0 are the conduction and valence band edge energies, Eg is the bandgap predicted by the CGCNN model, ESHE is the absolute electrode potential of the standard hydrogen electrode (= 4.4 V), and Xi is the electronegativity of the constituent elements in a material while a,b,c..q are there number of each of these elements in the materials’ unit cell. “ω” is the geometric mean of the electronegativities of the constituent elements in a material.
Results
Deep Learning Model Training
A two-step hierarchical DL model using an image-based representation of materials was developed to discover novel 2D materials as potential photocatalysts for water splitting reaction. The first step of the model consisted of autoencoders and a segmentation network to encode the cell and basis images and ascertain the location and types of atoms from the basis images. The subsequent step used the cell and basis encodings together with a conditional property vector to obtain a continuous latent space encoding of the 2D materials using a CVAE. This latent space could be sampled to generate novel 2D materials whose bandgaps and band edge positions were predicted using a reparametrized CGCNN model and empirical correlations, respectively. While the usual practice of training these DL models initializes the weights of the networks to random values, we used a more “informed” initial guess by pretraining these networks on the data from the Materials Project (MP) database (Jain et al., 2013). Details of the dataset used for this pretraining as well as all the model hyperparameters are provided in Supplementary Tables S1, S2 of the supplementary material. We first present the training results for individual models and then present the error metrics upon execution of the entire pipeline.
Table 2 provides a summary of the test set error after training our individual DL models from the first step on the 2D materials dataset. For the cell and basis autoencoders, the MSE and MAE correspond to the error incurred in reconstructing the input images while for the segmentation network, the MAE corresponds to the error in reproducing the species matrix. Clearly, we see that the networks were able to accurately reconstruct the cell and basis images. Figure 5 compares a 2D-slice from the input 3D cell image for a material in our test set as well as the corresponding reconstructed image produced by the cell autoencoder.

TABLE 2. Test set errors in the cell and basis autoencoder and the segmentation network after training these models on the 2D materials dataset.
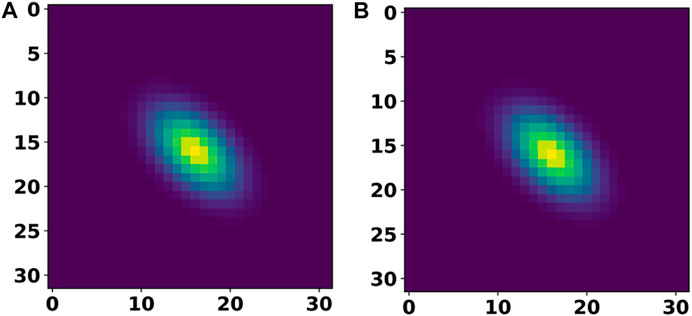
FIGURE 5. A 2D slice of the input cell image (A) and its comparison with the corresponding 2D slice from the reconstructed (output of cell autoencoder) cell image (B).
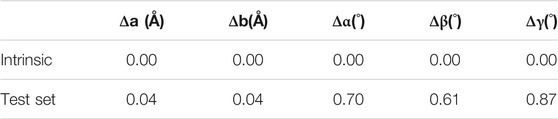
While the autoencoders learned to reconstruct the images well, the cell parameters of the materials (i.e., the cell lengths and angles) themselves were obtained from the output of the cell autoencoder (i.e., the decoded cell image) by feeding the voxel values to the inverse of the Gaussian function that was used to construct the cell images originally. Table 3 lists the reconstruction errors in the cell parameters. Firstly, we observed that the intrinsic error (i.e., the error in transforming the lattice parameters to the cell image and back calculating the lattice parameters from the constructed image) in the cell image representation was zero, suggesting that the lattice to image transformation was perfect. Secondly, we observed that the error in cell lengths and angles obtained upon inverting the output image from the cell autoencoder was also very small, suggesting that the learned cell encodings represented the cell images well.
In comparison to cell parameters, obtaining the atomic positions from the output of basis autoencoder and segmentation network required a multi-step post processing. Firstly, the output of segmentation network was converted to elements matrix using the argmax function on one-hot encoded species matrix. This assigned atomic numbers to each site in the elements matrix. Then clusters of atoms were found from the elements matrix using the skimage package (Van der Walt et al., 2014). Finally, positions of the atoms were assigned as the centroids of clusters while the type of atom at that location (i.e. the atomic number) was assigned based on majority voting among sites belonging to that cluster. The error in the atomic position was obtained by computing the distance between the predicted atom “i” in the output element matrix and the nearest true atom “j” in the original element matrix (i.e., ground truth) of that material. Figure 6A shows the test set predictions from the segmentation network as a parity plot between the predicted vs. true number of atoms while Figure 6B shows a parity plot between the predicted vs. true atom types for those materials predicted to have correct number of atoms. Clearly, from Figure 6 and the loss values mentioned in Table 2, it can be inferred that the networks were able to closely reconstruct the materials in the test set.
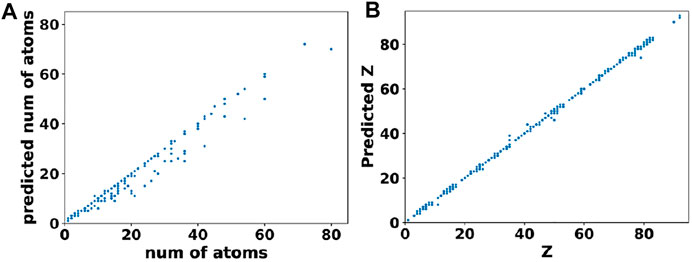
FIGURE 6. Performance of the segmentation network. (A) Predicted vs. true number of atoms in materials from the test set. (B) Predicted vs. true atomic numbers of atoms in those materials that were predicted to have the correct number of atoms.
Further analysis of these predictions revealed that for 87.7% of materials in the test set, the basis autoencoder and segmentation network was able to predict the correct number of atoms as well as material composition with a very small RMSE of 0.06 Å in the atomic positions. Such good accuracy of the basis autoencoder and segmentation network can also be gleaned from Figure 7 which shows a 2D slice of an input and reconstructed basis images of a material from the test set as well as the corresponding elements matrices.
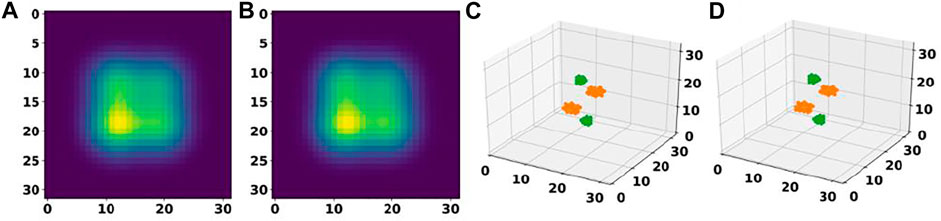
FIGURE 7. Performance of a basis autoencoder and a segmentation network. (A) and (B) panels show a 2D slice of the input and reconstructed basis images for a material from the test set, respectively. (C) and (D) panels show the corresponding input and output elements matrices, respectively.
Having trained the cell, basis autoencoders and the segmentation network, we next trained the generative model (CVAE) with the cell and basis encodings, one hot property vector as the inputs. Once again, pretrained weights from the MP dataset were taken as the initial guess for the CVAE model. The main objective of this study being the discovery of novel 2D materials for photocatalytic water splitting, it was essential that the learned latent space be smooth and continuous for generating realistic materials. The kernel density estimate (KDE) plot in Figure 8 shows that the 128-dimensional latent space was mostly smooth and continuous and approximately followed a unit Gaussian profile. This is further elucidated by the tSNE plot (Van der Maaten and Hinton, 2008) shown in Supplementary Figure S1 of the supplementary material, which shows a uniform distribution of the latent space encodings. Note that unlike conventional autoencoders, the CVAE latent space is not expected to be segregated into different regions based on the class of material since every sampling produces an instance of a material of a particular class (Atienza, 2018). The average mean and variance of the latent vectors were found to be 10−3 and 0.99, respectively. The test set KL loss was 1.97, while the reconstruction loss was 0.014.
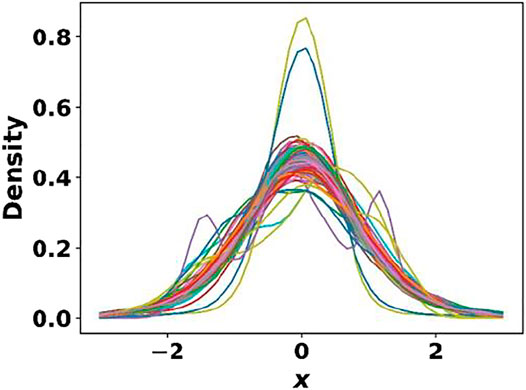
FIGURE 8. Kernel density estimate plot for the 128-dimensional CVAE latent space. The learned latent space was mostly smooth and continuous and approximately followed a unit Gaussian.
After training the individual models, we ran the entire two-step generative model pipeline to obtain the errors in our test set prediction upon end-to-end execution. The cell and basis encodings of the test set materials obtained from the respective autoencoders together with their appropriate one hot encoded property values were passed through the CVAE network. The output cell and basis encodings from the CVAE network were passed through the decoders of the respective autoencoders. The output cell images were then inverted to obtain the cell parameters, while the output basis images were segmented to obtain the positions of atoms in each material. Analysis of the results revealed that for 93.8% of the materials, the pipeline was able to predict the correct number of atoms. Among those materials predicted to have the correct number of atoms, 51% of materials were predicted to have the correct stoichiometry. For 22.4% of materials, the largest deviation in the atomic number of any atom constituting the material was within ±2. 26.6% of materials and had larger than ±2 deviation in the predicted atomic numbers. When all the test set materials were included, the errors in the lattice parameters were 0.07 Å in “a” and “b” cell lengths, 0.85̊, 0.86̊, and 1.13̊ in the α, β, and γ cell angles, respectively. These values reduced to 0.05Å and 0.06Å for “a”, “b” cell lengths and 0.73̊, 0.72̊, and 0.93̊ for α, β, and γ cell angles, respectively, when only those materials in the test set with correctly reconstructed stoichiometry were considered. While the accuracy in reconstructing the lattice and basis of the materials slightly reduced upon end-to-end execution of the pipeline, they are comparable to those reported by Hoffmann et al. (2019).
Finally, to predict the bandgap of the generated materials, we reparameterized the CGCNN model with our 2D dataset. Use of the network weights directly from the original CGCNN model resulted in a large MAE in the bandgap of 0.727 eV. To reduce the prediction error, we retrained the network beginning with the original CGCNN model weights as the initial guess. A dropout of 0.5 was introduced after the pooling layer of the model to prevent overfitting. The trained model gave a test set MAE of 0.567 eV. While this error is smaller than the original model error of 0.727 eV on our dataset, it is still larger than the CGCNN model error of 0.388 eV reported for bulk materials (Xie and Grossman, 2018). Nevertheless, owing to the generalizability of the model as well as rapid prediction of bandgaps, we used this model to predict the bandgaps of the generated materials.
Generation of Novel 2D Materials
The trained DL models were used to generate novel 2D materials by sampling from the CVAE latent space. While the latent space can be sampled in several different ways, we chose to explore the space around the encodings of the materials belonging to class 1 in our training set (i.e., thermodynamically stable and non-metal) so that the generated materials are likely to share the characteristics of the pivot material. Specifically, for each of the 1000 randomly chosen materials belonging to class 1 in our model training set, we drew 100 samples from a normal distribution of the form N(µpivot,0.1), where µpivot was the mean of the distribution learned by the CVAE for the pivot material (i.e., the material in the training set). The sample drawn from the normal distribution was then passed through the probabilistic decoder of the CVAE and subsequently through the cell and basis autoencoders to get the respective images. The lattice and atomic basis of the materials were obtained from these images as described earlier. After constructing the crystal structure, the materials were subjected to a set of post-processing steps to filter improbable structures as well as narrow our search space for photocatalysts. These steps were as follows:
1) Hydrogen atom position curation: Hydrogen atoms that were more than 1.8 Å away from atoms in the generated crystal structure were deemed “free” hydrogen atoms in vacuum, which were generated due to segmentation network errors. Such hydrogen atoms were deleted from the structure.
2) Bond distance–based filtering: Those materials in which the interatomic distance between any pair of atoms without hydrogen was less than 1.2 Å, were discarded. If an atom pair contained hydrogen atom, this distance threshold was set to 0.8 Å.
3) Number of elements–based filtering: We discarded those materials that contained more than four element types.
In all, ∼45% of the sampled materials were discarded after the above screening procedure. The crystal structure of the remaining materials was passed through the CGCNN model to obtain an estimate of their bandgap. Finally, the obtained bandgap was used in empirical equations 5–7 to obtain the position of the valence and conduction band edges. Analysis of the filtered materials firstly revealed that the sampling generated 411 materials with 73 unique compositions that were present in the test set, but not in the training set. Of these, the crystal structures of 42 materials closely matched with that in the test set. Supplementary Table S3 in the supplementary material lists these compositions as well as the absolute deviations in the predicted lattice parameters and bond lengths from their true values. The crystal structures of the predicted materials ranged from simple metal halide structures (such as MoI2, containing alternate layers of metal and halide ions) to more complicated structures containing molecular species such as carbonates (e.g., MnC2O6) and phosphates (e.g., Mo2P2O10). These results show that our model was able to generate not only realistic material compositions unseen by it during training but also closely predict their crystal structure, further emphasizing on the accuracy of model training and reliability of its predictions. In addition, the model was also able to suggest different phases (i.e., crystal structure) for a given material composition.
Having established the reliability of the trained model, we analyzed the filtered materials to search for novel 2D materials as potential water splitting catalysts. Attention was paid to those materials that were present neither in our training nor test set, so that the generated materials were truly novel. In addition to the material composition, the bandgap and the band edges of the material had to be in suitable ranges to qualify as a potential photocatalyst. Specifically, the bandgap of the material had to be between 1.6 and 3 eV, while the conduction and valence band edge had to lie below and above 0 eV and 1.23 eV, respectively. Such alignment of band edges ensures that the holes generated in the valence band upon photoexcitation are able to oxidize water [since they lie at a more positive potential than the water oxidation potential (= 1.23 V vs. SHE)] while the electrons populating the conduction band are able to reduce protons [since they lie at a more negative potential than the hydrogen evolution potential (= 0 V vs. SHE)]. Furthermore, we imposed a constraint of charge neutrality on the generated materials by assigning formal atomic charges corresponding to all the well-known oxidation states of each atom in a material. Then the charges on all the sites were summed up to ensure that at least one combination of oxidation states led to a net zero charge. Considering these aspects, our model generated about 150 new materials as potential photocatalysts for water splitting. A list of these materials, together with their bandgap, band edge positions, and lattice parameters are given in Supplementary Table S4 of the supplementary material.
To further narrow this set down to a few tens of materials, we used a CGCNN-based model to classify the materials as stable vs. unstable using a more stringent criteria for e_above_hull ≤ 50 meV/atom. As before, the CGCNN model was pretrained on the MP dataset followed by training on the 2D materials data. Details of the model training and hyperparameters are provided in Supplementary Table S5 of the supporting information. The test accuracy of the model was 0.87 while the area under the receiver operating characteristic curve (AUC curve) was 0.924. Subsequently, the ∼150 materials identified above were passed through the classification network resulting in 19 materials that had a probability of >0.99 to belong to the stable class (i.e., e_above_hull ≤ 50 meV/atom). These 19 materials are listed at the beginning of Supplementary Table S4 in bold while their structures are provided as cif files. From Supplementary Table S4 we see that all the materials generated were either halides or oxides/chalcogenides apart from Ag2PdN2, LiRhN2, and InRhN2. This stems from the fact that halides were the dominant materials in the 2D materials dataset followed by oxides and chalcogenides. Furthermore, analysis of the e_above_hull values of the materials in class 1 of the dataset revealed that the mean value was 47 meV/atom for halides while it was 69 meV/atom for oxides. Consistently, all 19 shortlisted materials were seen to be halides.
Visualization of the structure of these 19 materials revealed that they belonged to a few different structural prototypes. Ce2N2I2, Dy2S2Cl2, Lu2S2Cl2, Tm2S2Br2, and W2P2Cl2 had a BiOCl oxyhalide-like orthorhombic structure with each metal ion coordinated to 4 S/P/N atoms which were in turn coordinated to four metal ions. The halide ion occupied the hollow site above the metal ions. Other halides such as LuClI, LuSeCl, LuSCl, and RePBr adopted the 2H-MoS2-like hexagonal structure while InSCl adopted the 1T-MoS2-like structure. In both cases, each metal ion was coordinated to six anions, and each anion was coordinated to three metal ions. It must be noted that both BiOCl (Faraji et al., 2019) and MoS2 (Li et al., 2013) depicted excellent photocatalytic activity for water splitting reaction themselves. Given that these newly generated materials display favorable bandgap and band edge positions, high confidence of being thermodynamically stable and adopting a structure similar to known photocatalysts, they could perhaps be considered as new targets for synthesis and evaluation.
Ce2Se2Br4, Nb2S4Cl2, ScTiCl6¸ CeNdBr6, NdTbBr6, and PrNdCl6 had a metal trihalide-like structure, with the former three adopting a BiI3-like trigonal structure and the latter three adopting an NdBr3-like orthorhombic structure. Earlier reports have shown that metal trihalides depicted interesting magnetic behavior and could potentially be used in magnetic and spintronic applications (McGuire, 2017; Tomar et al., 2019). Thus, in addition to photocatalysts, these newly generated materials could be studied for other interesting applications as well. Finally, GaSCl adopted an HgI2-like structure with four coordinated metal ions and two coordinated anions while W2CCl2 adopted an MXene-like structure with chloride termination.
Discussion
With rapid increase in computational power and advancements in AI algorithms, applications of generative models in synthesizing realistic data has widespread appeal in various fields. Application of these techniques in materials science holds significant promise for realizing in-silico design/discovery/screening of functional materials. In this study, we have demonstrated one such generative modeling approach for the discovery of novel 2D materials as photocatalysts for water splitting. Using an image-based representation of crystal structures, our two-step model first built cell and basis autoencoders to obtain a representation of these images in a lower dimensional space. The reconstructed images from the basis autoencoder were used to train a segmentation network so that the positions and types of atoms in a material could be ascertained. Next, a CVAE model was trained using the cell and basis encodings together with a conditional one hot property vector to obtain a continuous latent space that can be sampled to generate new materials. The bandgap of the generated materials was predicted using a reparameterized CGCNN model, which was then used to obtain their band edge positions via empirical relations. Evaluation of the model showed good accuracy in reconstructing materials from the test set. The latent space was then sampled to generate novel 2D materials by exploring the region around materials from the training set. An important metric of reliability for any generative model is its ability to produce realistic samples, which in our case is the crystal structure of known materials that were previously unseen by the model. To that end, our model was able to predict 73 different compositions that were present in the test set but not in the training set. Of these, the structures of 42 compounds matched closely with their true structures. Further analysis of the sampled materials gave several novel materials as potential photocatalysts for water splitting.
Our generative modeling framework is an advancement over other related models reported in the literature. While our model is conceptually similar to the iMatGen framework (Noh et al., 2019), the latter was restricted to predicting novel phases of vanadium oxides only. The use of atomic number weighted gaussians to construct the basis image together with segmentation allowed us to generalize the model to all crystal and atom types. While Court et al. (2020) used a somewhat similar approach in their model, lack of an explicit representation of the lattice precluded the application of their model to non-orthogonal systems. Furthermore, all these generative models hold an advantage over high-throughput virtual screening approaches such as those reported by Sorkun et al. (2020), since they possess the capability to not only identify new material compositions but also new phases for known material compositions. However, this in no way undermines the importance of high-throughput screening approaches. A large amount of data is usually required to build accurate generative models. In cases where such data is absent (which often happens in materials science), building shallow models with available data and using these models in high-throughput screening is perhaps the only viable approach to identifying novel materials.
Although our generative modeling framework showed good accuracy, admittedly, there is scope for improvement. For instance, the cell and basis accuracies deteriorated upon end-to-end execution of the full model owing to the reconstruction error of the CVAE network. Better performance of the VAE network could perhaps be achieved by using deep feature consistent (DFC) VAEs (Hou et al., 2017), as was demonstrated by Court et al. (2020). Instead of minimizing the pixel-to-pixel difference between the input and reconstructed images (via MSE loss), DFC-VAEs attempt to minimize the difference in the hidden representations between the two images (called feature perceptual loss), which eventually leads to a truer (less noisy) reconstruction of the input image. Accurate reconstruction of the cell and basis encodings would then reflect in better accuracies in cell parameters, atomic positions, and element types. Furthermore, while we suggested several novel 2D photocatalysts for water splitting reaction by sampling from thermodynamically stable class of non-metals, this screening has been entirely based on bandgap and band edge positions. In addition to these necessary conditions, low aqueous solubility, small exciton binding energies and recombination rates, and favorable surface reaction kinetics are some of the other necessary conditions for a viable 2D water splitting photocatalyst (Singh et al., 2015). Our study, as also other reports based on high-throughput screening, do not currently incorporate these properties, primarily owing to the exorbitant cost associated with computing some of these quantities. Finally, any material designed in-silico gains relevance only when it is realized experimentally and displays anticipated properties. In the current era of big data, this calls for automated laboratories that could rapidly synthesize (or show otherwise) and characterize new materials. Such high-throughput experimentation when combined with data-based predictive models can significantly accelerate the discovery of novel functional materials. For instance, one could imagine a scenario in which our own generative modeling framework is trained in an active learning fashion by integrating with automated experimentation (via orchestration software such as ChemOS (Roch et al., 2018)). The generated materials could be rapidly evaluated in experiments and the outcome could be fed back to the training set so that the model can be improved iteratively. In our view, implementation of such frameworks could significantly help us move closer to realizing the vision of truly inverse design of materials.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author Contributions
SGS and AA conceptualized the idea. AA implemented the generative modeling framework. SGS and AA jointly wrote the manuscript. All authors discussed the results, their implications, and reviewed the manuscript.
Funding
This work was funded by the TCS-CTO organization under SWON number 1009292.
Conflict of Interest
AA, SGS, and BR are employed by Tata Conusultancy Services Ltd., India.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The authors wish to thank the TCS R&I infra team for providing necessary computational resources to train the deep learning models.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2021.679269/full#supplementary-material
References
Agrawal, A., and Choudhary, A. (2016). Perspective: Materials Informatics and Big Data: Realization of the “Fourth Paradigm” of Science in Materials Science. Apl Mater. 4 (5), 053208. doi:10.1063/1.4946894
Ahmad, H., Kamarudin, S. K., Minggu, L. J., and Kassim, M. (2015). Hydrogen from Photo-Catalytic Water Splitting Process: A Review. Renew. Sust. Energ. Rev. 43, 599–610. doi:10.1016/j.rser.2014.10.101
Ahmad, Z., Xie, T., Maheshwari, C., Grossman, J. C., and Viswanathan, V. (2018). Machine Learning Enabled Computational Screening of Inorganic Solid Electrolytes for Suppression of Dendrite Formation in Lithium Metal Anodes. ACS Cent. Sci. 4 (8), 996–1006. doi:10.1021/acscentsci.8b00229
Atienza, R. (2018). Advanced Deep Learning with Keras: Apply Deep Learning Techniques, Autoencoders, GANs, Variational Autoencoders, Deep Reinforcement Learning, Policy Gradients, and More. Birmingham, United kingdom: Packt Publishing Ltd.
Castelli, I. E., Landis, D. D., Thygesen, K. S., Dahl, S., Chorkendorff, I., Jaramillo, T. F., et al. (2012). New Cubic Perovskites for One- and Two-Photon Water Splitting Using the Computational Materials Repository. Energy Environ. Sci. 5 (10), 9034–9043. doi:10.1039/c2ee22341d
Castelli, I. E., Olsen, T., Datta, S., Landis, D. D., Dahl, S., Thygesen, K. S., et al. (2012). Computational Screening of Perovskite Metal Oxides for Optimal Solar Light Capture. Energ. Environ. Sci. 5 (2), 5814–5819. doi:10.1039/c1ee02717d
Court, C. J., Yildirim, B., Jain, A., and Cole, J. M. (2020). 3-D Inorganic Crystal Structure Generation and Property Prediction via Representation Learning. J. Chem. Inf. Model. 60 (10), 4518–4535. doi:10.1021/acs.jcim.0c00464
Curtarolo, S., Setyawan, W., Wang, S., Xue, J., Yang, K., Taylor, R. H., et al. (2012). AFLOWLIB.ORG: A Distributed Materials Properties Repository from High-Throughput Ab Initio Calculations. Comput. Mater. Sci. 58, 227–235. doi:10.1016/j.commatsci.2012.02.002
Edwards, P. P., Kuznetsov, V. L., and David, W. I. F. (2007). Hydrogen Energy. Phil. Trans. R. Soc. A. 365 (1853), 1043–1056. doi:10.1098/rsta.2006.1965
Faraji, M., Yousefi, M., Yousefzadeh, S., Zirak, M., Naseri, N., Jeon, T. H., et al. (2019). Two-dimensional Materials in Semiconductor Photoelectrocatalytic Systems for Water Splitting. Energ. Environ. Sci. 12 (1), 59–95. doi:10.1039/c8ee00886h
Fujishima, A., and Honda, K. (1972). Electrochemical Photolysis of Water at a Semiconductor Electrode. nature 238 (5358), 37–38. doi:10.1038/238037a0
Goodfellow, I. J., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., et al. (2014). Generative Adversarial Networks. arXiv preprint arXiv:1406.2661.
Haastrup, S., Strange, M., Pandey, M., Deilmann, T., Schmidt, P. S., Hinsche, N. F., and Thygesen, K. S. (2018). The Computational 2D Materials Database: High-Throughput Modeling and Discovery of Atomically Thin Crystals. 2D Mater. 5 (4), 042002. doi:10.1088/2053-1583/aacfc1
Hisatomi, T., Kubota, J., and Domen, K. (2014). Recent Advances in Semiconductors for Photocatalytic and Photoelectrochemical Water Splitting. Chem. Soc. Rev. 43 (22), 7520–7535. doi:10.1039/c3cs60378d
Hoffmann, J., Maestrati, L., Sawada, Y., Tang, J., Sellier, J. M., and Bengio, Y. (2019). Data-driven Approach to Encoding and Decoding 3-D crystal Structures. arXiv preprint arXiv:1909.00949.
Hou, X., Shen, L., Sun, K., and Qiu, G. (2017).Deep Feature Consistent Variational Autoencoder. in 2017 IEEE Winter Conference on Applications of Computer Vision (WACV). IEEE, Santa Rosa, CA, March 24,2017 – March 31, 2017, 1133–1141.
Jain, A., Ong, S. P., Hautier, G., Chen, W., Richards, W. D., Dacek, S., et al. (2013). Commentary: The Materials Project: A Materials Genome Approach to Accelerating Materials Innovation. APL Mater. 1 (1), 011002. doi:10.1063/1.4812323
Jain, A., Wang, Z., and Nørskov, J. K. (2019). Stable Two-Dimensional Materials for Oxygen Reduction and Oxygen Evolution Reactions. ACS Energ. Lett. 4 (6), 1410–1411. doi:10.1021/acsenergylett.9b00876
Joshi, R. P., Eickholt, J., Li, L., Fornari, M., Barone, V., and Peralta, J. E. (2019). Machine Learning the Voltage of Electrode Materials in Metal-Ion Batteries. ACS Appl. Mater. Inter. 11 (20), 18494–18503. doi:10.1021/acsami.9b04933
Kim, S., Noh, J., Gu, G. H., Aspuru-Guzik, A., and Jung, Y. (2020). Generative Adversarial Networks for crystal Structure Prediction. ACS Cent. Sci. 6 (8), 1412–1420. doi:10.1021/acscentsci.0c00426
Kingma, D. P., and Welling, M. (2019). An Introduction to Variational Autoencoders. arXiv preprint arXiv:1906.02691. doi:10.1561/9781680836233
Kudo, A., and Miseki, Y. (2009). Heterogeneous Photocatalyst Materials for Water Splitting. Chem. Soc. Rev. 38 (1), 253–278. doi:10.1039/b800489g
Li, Y., Li, Y.-L., Araujo, C. M., Luo, W., and Ahuja, R. (2013). Single-layer MoS2 as an Efficient Photocatalyst. Catal. Sci. Technol. 3 (9), 2214–2220. doi:10.1039/c3cy00207a
Li, Y., Li, Y.-L., Sa, B., and Ahuja, R. (2017). Review of Two-Dimensional Materials for Photocatalytic Water Splitting from a Theoretical Perspective. Catal. Sci. Technol. 7 (3), 545–559. doi:10.1039/c6cy02178f
Liu, H., Cheng, J., Dong, H., Feng, J., Pang, B., Tian, Z., et al. (2020). Screening Stable and Metastable ABO3 Perovskites Using Machine Learning and the Materials Project. Comput. Mater. Sci. 177, 109614. doi:10.1016/j.commatsci.2020.109614
Long, T., Fortunato, N. M., Opahle, I., Zhang, Y., Samathrakis, I., Shen, C., et al. (2020). CCDCGAN: Inverse Design of crystal Structures. arXiv preprint arXiv:2007.11228.
Maeda, K., and Domen, K. (2010). Photocatalytic Water Splitting: Recent Progress and Future Challenges. J. Phys. Chem. Lett. 1 (18), 2655–2661. doi:10.1021/jz1007966
Maitra, U., Gupta, U., De, M., Datta, R., Govindaraj, A., and Rao, C. N. R. (2013). Highly Effective Visible-Light-Induced H2Generation by Single-Layer 1T-MoS2and a Nanocomposite of Few-Layer 2H-MoS2with Heavily Nitrogenated Graphene. Angew. Chem. Int. Ed. 52 (49), 13057–13061. doi:10.1002/anie.201306918
McGuire, M. (2017). Crystal and Magnetic Structures in Layered, Transition Metal Dihalides and Trihalides. Crystals 7 (5), 121. doi:10.3390/cryst7050121
Moniruddin, M., Ilyassov, B., Zhao, X., Smith, E., Serikov, T., Ibrayev, N., et al. (2018). Recent Progress on Perovskite Materials in Photovoltaic and Water Splitting Applications. Mater. Today Energ. 7, 246–259. doi:10.1016/j.mtener.2017.10.005
Mounet, N., Gibertini, M., Schwaller, P., Campi, D., Merkys, A., Marrazzo, A., et al. (2018). Two-dimensional Materials from High-Throughput Computational Exfoliation of Experimentally Known Compounds. Nat. Nanotech 13 (3), 246–252. doi:10.1038/s41565-017-0035-5
Noh, J., Kim, J., Stein, H. S., Sanchez-Lengeling, B., Gregoire, J. M., Aspuru-Guzik, A., et al. (2019). Inverse Design of Solid-State Materials via a Continuous Representation. Matter 1 (5), 1370–1384. doi:10.1016/j.matt.2019.08.017
Novoselov, K. S., Geim, A. K., Morozov, S. V., Jiang, D., Zhang, Y., Dubonos, S. V., et al. (2004). Electric Field Effect in Atomically Thin Carbon Films. science 306 (5696), 666–669. doi:10.1126/science.1102896
Oktay, O., Schlemper, J., Folgoc, L. L., Lee, M., Heinrich, M., Misawa, K., and Rueckert, D. (2018). Attention U-Net: Learning where to Look for the Pancreas. arXiv preprint arXiv:1804.03999.
Osterloh, F. E. (2008). Inorganic Materials as Catalysts for Photochemical Splitting of Water. Chem. Mater. 20 (1), 35–54. doi:10.1021/cm7024203
Osterloh, F. E., and Parkinson, B. A. (2011). Recent Developments in Solar Water-Splitting Photocatalysis. MRS Bull. 36 (1), 17–22. doi:10.1557/mrs.2010.5
Prasad, U. (2020). BiVO4-Based Photoanodes for Photoelectrochemical Water Splitting. Clean. Energ. Mater. 1364, 137–167. doi:10.1021/bk-2020-1364.ch005
Ren, Z., Noh, J., Tian, S., Oviedo, F., Xing, G., Liang, Q., and Buonassisi, T. (2020). Inverse Design of Crystals Using Generalized Invertible Crystallographic Representation. arXiv preprint arXiv:2005.07609.
Roch, L. M., Häse, F., Kreisbeck, C., Tamayo-Mendoza, T., Yunker, L. P., Hein, J. E., et al. (2018). ChemOS: Orchestrating Autonomous Experimentation. Sci. Robotics 3 (19). doi:10.1126/scirobotics.aat5559
Rybkin, O., Daniilidis, K., and Levine, S. (2020). Simple and Effective VAE Training with Calibrated Decoders. arXiv preprint arXiv:2006.13202.
Saal, J. E., Kirklin, S., Aykol, M., Meredig, B., and Wolverton, C. (2013). Materials Design and Discovery with High-Throughput Density Functional Theory: the Open Quantum Materials Database (OQMD). Jom 65 (11), 1501–1509. doi:10.1007/s11837-013-0755-4
Sigfusson, T. I. (2007). Pathways to Hydrogen as an Energy Carrier. Phil. Trans. R. Soc. A. 365 (1853), 1025–1042. doi:10.1098/rsta.2006.1960
Singh, A. K., Mathew, K., Zhuang, H. L., and Hennig, R. G. (2015). Computational Screening of 2D Materials for Photocatalysis. J. Phys. Chem. Lett. 6 (6), 1087–1098. doi:10.1021/jz502646d
Singh, A. K., Montoya, J. H., Gregoire, J. M., and Persson, K. A. (2019). Robust and Synthesizable Photocatalysts for CO 2 Reduction: a Data-Driven Materials Discovery. Nat. Commun. 10 (1), 1–9. doi:10.1038/s41467-019-08356-1
Sorkun, M. C., Astruc, S., Koelman, J. V. A., and Er, S. (2020). An Artificial Intelligence-Aided Virtual Screening Recipe for Two-Dimensional Materials Discovery. npj Comput. Mater. 6 (1), 1–10. doi:10.1038/s41524-020-00375-7
Sun, Y., Cheng, H., Gao, S., Sun, Z., Liu, Q., Liu, Q., et al. (2012). Freestanding Tin Disulfide Single-Layers Realizing Efficient Visible-Light Water Splitting. Angew. Chem. Int. Ed. 51 (35), 8727–8731. doi:10.1002/anie.201204675
Sun, Y., Sun, Z., Gao, S., Cheng, H., Liu, Q., Lei, F., et al. (2014). All-Surface-Atomic-Metal Chalcogenide Sheets for High-Efficiency Visible-Light Photoelectrochemical Water Splitting. Adv. Energ. Mater. 4 (1), 1300611. doi:10.1002/aenm.201300611
Tachibana, Y., Vayssieres, L., and Durrant, J. R. (2012). Artificial Photosynthesis for Solar Water-Splitting. Nat. Photon 6 (8), 511–518. doi:10.1038/nphoton.2012.175
The NOMAD (Novel Materials Discovery) Center of Excellence (CoE)(2021). Available at: https://nomad-coe.eu (last Accessed March 9, 2021).
Turner, J. A. (2004). Sustainable Hydrogen Production. Science 305 (5686), 972–974. doi:10.1126/science.1103197
Van der Maaten, L., and Hinton, G. (2008). Visualizing Data Using T-SNE. J. machine Learn. Res. 9 (11). 2579–2605.
Van der Walt, S., Schönberger, J. L., Nunez-Iglesias, J., Boulogne, F., Warner, J. D., Yager, N., and Gouillart, E. (2014). Scikit-Image: Image Processing in Python. PeerJ 2, e453. doi:10.7717/peerj.453
Voiry, D., Yamaguchi, H., Li, J., Silva, R., Alves, D. C. B., Fujita, T., et al. (2013). Enhanced Catalytic Activity in Strained Chemically Exfoliated WS2 Nanosheets for Hydrogen Evolution. Nat. Mater 12 (9), 850–855. doi:10.1038/nmat3700
Wu, Y., Lazic, P., Hautier, G., Persson, K., and Ceder, G. (2013). First Principles High Throughput Screening of Oxynitrides for Water-Splitting Photocatalysts. Energ. Environ. Sci. 6 (1), 157–168. doi:10.1039/c2ee23482c
Xie, T., and Grossman, J. C. (2018). Crystal Graph Convolutional Neural Networks for an Accurate and Interpretable Prediction of Material Properties. Phys. Rev. Lett. 120 (14), 145301. doi:10.1103/physrevlett.120.145301
Xu, Y., Zhao, W., Xu, R., Shi, Y., and Zhang, B. (2013). Synthesis of Ultrathin CdS Nanosheets as Efficient Visible-Light-Driven Water Splitting Photocatalysts for Hydrogen Evolution. Chem. Commun. 49 (84), 9803–9805. doi:10.1039/c3cc46342g
Ye, W., Chen, C., Dwaraknath, S., Jain, A., Ong, S. P., and Persson, K. A. (2018). Harnessing the Materials Project for Machine-Learning and Accelerated Discovery. MRS Bull. 43 (9), 664–669. doi:10.1557/mrs.2018.202
Zhang, X., Zhang, Z., Wu, D., Zhang, X., Zhao, X., and Zhou, Z. (2018). Computational Screening of 2D Materials and Rational Design of Heterojunctions for Water Splitting Photocatalysts. Small Methods 2 (5), 1700359. doi:10.1002/smtd.201700359
Zhang, Z., Zhang, X., Zhao, X., Yao, S., Chen, A., and Zhou, Z. (2019). Computational Screening of Layered Materials for Multivalent Ion Batteries. ACS omega 4 (4), 7822–7828. doi:10.1021/acsomega.9b00482
Zhou, J., Shen, L., Costa, M. D., Persson, K. A., Ong, S. P., Huck, P., et al. (2019). 2DMatPedia, an Open Computational Database of Two-Dimensional Materials from Top-Down and Bottom-Up Approaches. Scientific data 6 (1), 1–10. doi:10.1038/s41597-019-0097-3
Zhuang, H. L., and Hennig, R. G. (2013). Single-layer Group-III Monochalcogenide Photocatalysts for Water Splitting. Chem. Mater. 25 (15), 3232–3238. doi:10.1021/cm401661x
Zhuang, H. L., and Hennig, R. G. (2013). Computational Search for Single-Layer Transition-Metal Dichalcogenide Photocatalysts. J. Phys. Chem. C 117 (40), 20440–20445. doi:10.1021/jp405808a
Zou, X., and Zhang, Y. (2015). Noble Metal-free Hydrogen Evolution Catalysts for Water Splitting. Chem. Soc. Rev. 44 (15), 5148–5180. doi:10.1039/c4cs00448e
Keywords: generative modeling, variational autoencoder, inverse design, photocatalysts, water splitting reaction
Citation: Agarwal A, Goverapet Srinivasan S and Rai B (2021) Data-Driven Discovery of 2D Materials for Solar Water Splitting. Front. Mater. 8:679269. doi: 10.3389/fmats.2021.679269
Received: 23 March 2021; Accepted: 12 July 2021;
Published: 16 September 2021.
Edited by:
Hélio Anderson Duarte, Federal University of Minas Gerais, BrazilReviewed by:
Kesong Yang, University of California, San Diego, United StatesTim Kowalczyk, Western Washington University, United States
Copyright © 2021 Agarwal, Goverapet Srinivasan and Rai. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Sriram Goverapet Srinivasan, cy5nb3ZlcmFwZXRAdGNzLmNvbQ==
 Abhishek Agarwal
Abhishek Agarwal Sriram Goverapet Srinivasan
Sriram Goverapet Srinivasan Beena Rai
Beena Rai