Analysis of Biaxial Mechanical Properties and Failure Criterion of Self-Compacting Concrete

Biaxial compression-compression, biaxial tension-compression and compression-shear tests were carried out on self-compacting concrete (SCC) using the rock true triaxial machine and compression-shear hydraulic servo machine to explore the biaxial mechanical properties of SCC. The failure modes and stress-strain curves of SCC under different loading conditions were obtained through experiment. Based on the comparison with the biaxial loading test data of ordinary concrete, the following conclusions are drawn: the failure modes and failure mechanisms under biaxial compression-compression and biaxial tension-compression are similar between SCC and ordinary concrete. Under compression-shear loading, the oblique cracks formed on the lateral surface of the specimen parallel to the shear direction gradually increased and the friction marks on the shear failure section were gradually deepened with the increase of axial compression ratio. The development trend of the stress-strain curve in the principal stress direction was not related to the lateral stress. Under the influence of lateral compressive stress, the principal compressive stress of SCC was increased by 55.78% on average; under biaxial tension-compression, the principal tensile stress of SCC had a maximum reduction of 62.79%; and under the compression-shear action, the shear stress of SCC had a maximum increase of 3.35 times. Compared with the biaxial stress test data of ordinary concrete, it can be seen that the lateral compressive stress had a more significant effect on the principal stress of SCC under biaxial loading. Subsequently, the strength criterion equations of SCC under biaxial loading were proposed based on the principal stress space and octahedral space stress respectively, which have shown good applicability in practice.

1 Introduction

Self-compacting concrete (SCC) is a type of high-fluid concrete which can be compacted in engineering applications without applying vibration. It is characterized by the advantages of good workability, high durability and strength, and ability to effectively optimize the construction environment. Particularly, for the excellent applicability in structures with difficulties in construction and pouring, SCC has shown promising research values and engineering application prospects (Zhao et al., 2015; Lazniewska-Piekarczyk, 2016; Pajak et al., 2019; Kandasamy and Kothandaraman 2020; Wang et al., 2020).

To date, the studies on SCC at home and abroad were generally carried out from the perspectives of concrete mix ratio, durability, mechanical properties and structural engineering applications. Okamura and Ozawa (1995) and Dinakar and Manu (2014) proposed the fixed sand volume method and full-calculation method for computing the mix ratio of SCC, respectively. Reiterman et al. (2019) analyzed the influence of different admixture components on the frost resistance of concrete and examined the related mechanisms. Anne-Mieke and de Schutter (2005) analyzed the creep performance of SCC and found that the environment had an important effect on the creep performance. According to Asteris and Kolovos (2019), the compressive and tensile strengths of SCC were similar to those of ordinary concrete at the same water-cement ratio, and the elastic modulus of SCC was similar to that of ordinary concrete at the same strength grade. Klaus and Yvette (2005) investigated the pull-out properties of steel fibers in SCC. Zhu et al. (2001) analyzed the structural applications of SCC and reported a high level of homogeneity. The research on the mechanical properties of SCC is usually conducted by applying conventional loading methods, i.e., compression, tension and flexural resistance. However, in actual concrete structures, concrete is often subjected to multiaxial stress states (Yu et al., 2018a; Ren et al., 2018; Xu et al., 2020). Among the studies on the multiaxial mechanical properties of concrete, the conventional triaxial loading machine is the most commonly used test method, but unfortunately, this machine cannot satisfy the loading conditions with unequal confining pressures. Therefore, the results obtained would be different from the actual engineering conditions, making it difficult to perform multiaxial tensile loading experiment. Comparatively, the true triaxial machine can satisfy multiaxial loading conditions with unequal confining pressures by eliminating the defects of the conventional triaxial machine, so that the results are more consistent with the actual engineering states (Chi et al., 2014; Shi et al., 2014; Yu et al., 2018b). By performing true triaxial experiment, Kupfer (1973) examined the biaxial mechanical properties of concrete and proposed the corresponding strength criterion equation. Fujikake et al. (2000) analyzed the multiaxial mechanical properties of concrete from the perspective of loading strain rate. Guo (1997) studied the multiaxial mechanical properties of concrete and discussed the related stress mechanism by considering different loading paths and loading methods. He and Song (2010) and Shang and Song (2013) investigated the multiaxial mechanical properties of different types of concrete by taking into account the effects of different environmental factors and proposed the corresponding strength criterion and constitutive relation respectively. The changing amplitude of multiaxial mechanical properties under the action of lateral compressive stress is mainly related to the type and composition characteristics of the concrete (Shi et al., 2014).

Since the composition and pouring method of SCC are different from those of ordinary concrete, it may have a certain impact on the changing amplitude of the principal stress of SCC under the action of lateral compressive stress. Regarding the literature on the multiaxial mechanical properties of SCC, Fantilli et al. (2011) used a conventional triaxial machine to examine the multiaxial compressive properties of SCC containing fibers and analyzed the effects of different confining pressures and fiber contents on the triaxial compressive strength and ductility. Mohamed et al. (2019) carried out an experimental study on the mechanical properties of self-compacting steel fiber concrete under biaxial loading by applying the biaxial loading technique; based on the experiment results, they proposed the biaxial failure criterion of self-compacting steel fiber concrete at different steel fiber contents. Zamri et al. (2020) investigated the multiaxial stress state of self-compacting steel fiber concrete in concrete beams and analyzed the stress mechanism of steel fiber in the multiaxial stress state. The existing research on the multiaxial mechanical properties of SCC still has deficiencies, especially when the true triaxial loading method was adopted. Moreover, concrete is not only subjected to multiaxial tension and compression in real-world structures, some structures such as concrete gravity dams, reinforced concrete deep beams and airport roads may also be subjected to multiaxial shear stress conditions. Relevant research has been conducted on the multiaxial shear stress mode of ordinary concrete, but not yet on SCC. A compressive investigation on the multiaxial mechanical properties of SCC can therefore contribute to a better understanding of its multiaxial stress characteristics, so as to facilitate the rational design and control of SCC in practical applications to avoid waste in the usage of materials or safety problems due to insufficient usage of materials. In view of this, the experimental study on the multiaxial mechanical properties of SCC has important significance and practical values.

This paper mainly aims to examine the mechanical properties of SCC under biaxial loading by considering different axial compression ratios. The true triaxial testing machine and the material compression-shear hydraulic servo machine were used to carry out biaxial compression-compression, biaxial tension-compression and compression-shear loading tests respectively. From the experiment, the failure modes and stress-strain curves under different loading conditions were obtained. Then, by extracting the characteristic values from the stress-strain curves and comparing with the biaxial loading test data of ordinary concrete, the biaxial mechanical properties of SCC were analyzed in detail and the corresponding failure criterion equations were proposed. The findings of this study are of great significance to the calculation and applications of SCC in engineering practice.

2 Experiment Program

2.1 Specimen Design

This experimental study was conducted using specimens of Grade SCC30. Of the various raw materials, the cement is ordinary Portland cement P.O 42.5; the coarse aggregates are natural gravel aggregates with the particle size ranged 4–16 mm; the fine aggregates are natural river sands with a fineness modulus of 2.5 and an apparent density of 2650 kg/m³. Considering the specific characteristics of SCC, a certain amount of fly ash powders and high-efficiency water reducer (i.e., naphthalenesulfonic acid formaldehyde condensate water reducer) were added into the concrete mixture to improve the overall performance. When the proportion of water reducer is around 1% of the cement content, the water reduction efficiency is about 20%. The mix ratio of SCC specimens was determined according to the “Technical specification for application of self-compacting concrete” (JGJ/T 283-2012). Specifically, each cubic meter of concrete contains 300 kg of cement, 123 kg of water, 865 kg of coarse aggregates, 781 kg of fine aggregates, 200 kg of fly ash and 3.20 kg of water reducer.

The pouring method of SCC in this study was different from that of ordinary concrete and was determined according to the “Technical specification for application of self-compacting concrete” (JGJ/T 283-2012) in this study. The specific process is as follows: 1) pour the cement, fine aggregates and mineral powders into the mixer according to the specified ratio for initial stirring; 2) pour water and water reducer into the mixture for the second round of stirring; 3) after stirring evenly, pour coarse aggregates into the mixture for the third round of stirring; 4) after stirring evenly, pour the mixture into mold and demold after 24 h; 5) place the specimen into the standard curing room for 28 days before the experiment.

The SCC mixture in this study was a newly prepared mixture. Its working performance was tested according to the European EFNACR2005 standard. The test results of the slump expansion and L-groove pass rate indicated that the specimens used in the experiment met the relevant requirements specified by EFNACR2005 Grade II SCC and had good working properties.

2.2 Loading Program

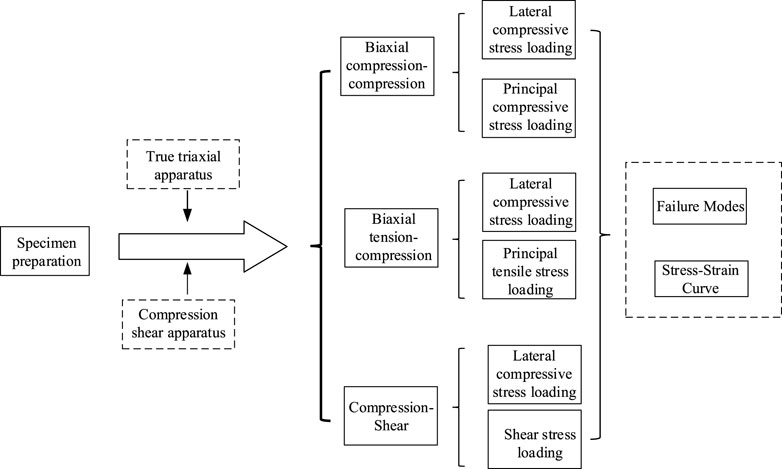
The biaxial loading program in this study mainly considered three loading methods: biaxial compression-compression, biaxial tension-compression and compression-shear. The biaxial compression-compression and biaxial tension-compression loading methods are composed of eight different lateral compressive stress values (0, 2, 4, 6, 8, 10, 12 and 14 MPa) and were applied by the constant lateral loading mode. That is, the lateral compressive stress was applied first to load the confining pressure. When the lateral stress reached the pre-specified value, the compressive stress in the principal direction (or the principal tensile stress/shear stress) was loaded until failure. The multiaxial compression-shear loading method is composed of eight different axial compression ratios (ξ) which were determined by the uniaxial compressive strength f_c of SCC in this study (0, 3, 6, 9, 12, 15, 20 and 30%f_c). Its loading process is similar to that of biaxial compression-compression and biaxial tension-compression. By referencing to the related literature (Dinakar and Manu, 2014) and the machine restrictions, the SCC specimens were designed to be 100 mm × 100 mm × 100 mm cubes in this study. The biaxial loading methods are shown in Figure 1. In view of the randomness and discreteness of concrete materials, three specimens were prepared and tested for each loading condition, and the mean values were calculated for analysis.

FIGURE 1

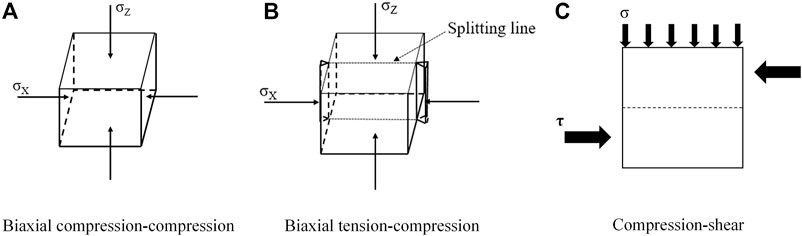
FIGURE 1. Biaxial loading schematic diagram of SCC. (A) Biaxial compression-compression. (B) Biaxial tension-compression. (C) Compression-shear.

The biaxial compression-compression loading method is shown in Figure 1A. Firstly, the lateral compressive stress was applied in the X direction to exert the confining pressure through the force control loading method at the rate of 0.05 MPa/s. After the load reached the designed confining pressure, the principal compressive stress was then applied in the Z direction through the displacement control loading method at the rate of 0.8 mm/min. The biaxial tension-compression loading method was similar to earlier related studies. Firstly, the lateral compressive stress was applied in the Z direction at the same loading rate as biaxial compression-compression. After the load reached the designed confining pressure, the split load was applied in the X direction, so as to form the tensile stress in the Y direction and eventually the biaxial tension-compression loading condition. The detailed loading method is shown in Figure 1B. The loading rate of principal tensile stress is the same as that of the principal compressive stress of biaxial compression-compression, which met the loading requirements of the experiment (Tschegg et al., 2015; Yu et al., 2019).

The multiaxial compression-shear loading method is shown in Figure 1C, and the load was applied by the constant lateral loading method. Specifically, the axial load was applied first at the loading rate of 0.05 MPa/s, and after the axial load reached the specified axial compression ratio, the shear load would be applied. The shear load was applied using the displacement control method at the rate of 0.8 mm/min until the specimen failed and the shear load became stable.

Biaxial compression-compression and biaxial tension-compression were loaded using a rock true triaxial machine (Figure 2A). This machine has three loading actuators that are perpendicular to one another, and each loading actuator is equipped with independent load sensors and a deformation measuring device. The sensitivity and error range of the load sensors meet the corresponding test requirements. The biaxial tension-compression load exerts a confining pressure in the Z direction and the split-tensile instrument exerts a split-tensile load in the X direction, so as to realize the loading program as shown in Figure 2B. In this study, the SCC biaxial compression-compression and biaxial tension-compression test methods have been evaluated according to the EN/ASTM standards. Combined with the true triaxial biaxial compression-compression and biaxial tension-compression test methods in the relevant literature, the methods adopted are able to obtain the load and deformation parameter values in the loading process to satisfy the specified research needs (Chi et al., 2014; He and Song, 2018).

FIGURE 2

FIGURE 2. Experiment equipment and loading method. (A) Rock true triaxial apparatus. (B) Split loading schematic. (C) Loading equipment.

The compression-shear loading of SCC was applied by a material compression-shear hydraulic servo machine. This machine is equipped with independent load sensors and displacement sensors in the axial direction and transverse shear direction. The error ranges of the load sensors and displacement sensors are compliant with the corresponding test requirements. The loading equipment is shown in Figure 2C. The compression-shear test equipment used in this study is able to eliminate the rotation effect and bending effect in the compression-shear testing process, so as to meet the specific test requirements (Yu et al., 2018a).

When applying the multiaxial load on the concrete specimen, it is necessary to implement anti-friction measures on the confining pressure surface, because the friction between the confining pressure surface and the contact surface of the specimen has a significant impact on the load measurement of the principal stress direction. If anti-friction measures were not taken, the obtained load results in the principal stress direction would be subjected to the friction effect and might be twice or even several times larger than the actual results. By referencing to the related literature on the biaxial compression-compression and biaxial tension-compression tests, the combination of three-layer PTFE film and mechanical butter was adopted as the anti-friction measure (i.e., an appropriate amount of mechanical butter was applied between the film layer and layer, between the film and the specimen loading surface, and between the film and the equipment loading surface) in this study to meet the test requirements (He and Song, 2010; Shang and Song, 2013). For the multiaxial compression-shear loading method, rolling balls were generally used to control the impact of friction on the test results. The experiment program aforementioned can be simplified into a flowchart as shown in Figure 3.

FIGURE 3

FIGURE 3. The biaxial loading experiment program of SCC.

3 Analysis of Test Results

3.1 Failure Mode

According to the experiment program described above, the rock true triaxial machine and the material compression-shear hydraulic servo machine were used to obtain the failure modes of SCC under different loading conditions. Then, the influences of different loading conditions on the mechanical properties of SCC were examined by analyzing the failure modes of the specimens from a macroscopic perspective. In view of space limitation, this paper chose the lateral compressive stresses of 0, 8 and 14 MPa as the examples for the analysis of biaxial compression-compression and biaxial tension-compression loading conditions, and chose the axial compression ratios of 0, 6, 15 and 30% as the examples for the analysis of the compression-shear failure mode, as shown in Figures 4–6.

FIGURE 4

FIGURE 4. SCC failure modes under biaxial loading. (A) Biaxial compression-compression. (B) Biaxial tension compression.

FIGURE 5

FIGURE 5. Shear failure modes of SCC under different axial loads. (A) 0%fcAS. (B) 6%fcAS. (C) 15%fcAS. (D) 30%fcAS.

FIGURE 6

FIGURE 6. Failure modes on the shear failure section of SCC under different axial loads. (A) 0%fcAS. (B) 6%fcAS. (C) 15%fcAS. (D) 30%fcAS.

Figure 4A shows the biaxial compression-compression failure mode of SCC. When the lateral compressive stress was 0 MPa, the specimen formed a penetrating-crack failure mode with the cracks evenly distributed on the non-loading surface. When the lateral stress was small, the biaxial compression-compression failure mode of SCC was similar to the failure mode under 0 MPa lateral stress. As the lateral compression stress increased, the specimen would gradually develop and form a flaky splitting failure mode. When the lateral compressive stress was increased to 8 MPa, the SCC specimen would begin to show a flaky failure mode. With the further increase of the lateral compressive stress, the number of flaky blocks increased continuously, and more concrete blocks would fall off from the specimen. When the lateral compressive stress was further increased to 14 MPa, the failure mode as shown in Figure 4A (0, 14 MPa) was generated. Correspondingly, there were a large amount of flaky blocks falling off from the surface of the specimen and the integrity of the specimen was weakened. The mechanism of biaxial compression-compression failure of SCC can be explained as follows. First, the axial compressive stress formed a tensile strain in the vertical direction of the non-loading surface under the action of the Poisson’s ratio effect. When the lateral compressive stress was small, the lateral loading surface was mainly subjected to tensile strain, and the specimen would eventually form the failure mode similar to that under uniaxial compression. When the lateral compressive stress was large, the vertical direction of the lateral loading surface of the specimen would form a compressive strain, and only the vertical direction of the non-loading surface would form a tensile strain. Eventually, the specimen would develop the flaky splitting failure mode. The pattern of this failure mode is similar to that of ordinary concrete under biaxial compression-compression, but the difference is that, when the lateral compressive stress is large, the flaky failure of ordinary concrete is basically vertical, while that of SCC shows an oblique development pattern. The biaxial tension-compression failure mode of SCC is shown in Figure 4B. Under different lateral compressive stresses, all the SCC specimens showed a splitting failure mode, and a penetrating and basically straight fracture line was formed. The specimens were broken into two parts after failure, and the failure mode was not related to the value of the lateral compressive stress. For the specific failure mechanism, when the splitting direction of the SCC specimen reached the ultimate tensile strain, the tensile fracture failure mode would occur. According to the relevant literature, the biaxial tension-compression failure mode of ordinary concrete showed a similar pattern and development trend to that of SCC (Guo 1997; Yu et al., 2019).

Figure 5 shows the failure modes on the specimen surfaces perpendicular to the shear loading direction and parallel to the loading direction of SCC respectively under different axial compression ratios. The failure line perpendicular to the shear direction was of a straight pattern, which was mainly caused by the loading action of the upper and lower shear boxes of the test machine. This failure mode was not affected by the axial compression ratio. The shear fracture line parallel to the shear direction showed a fluctuating pattern compared to that of the vertical loading direction. This is mainly due to the fact that the specimen would form initial cracks under the loading action of the upper and lower shear boxes. As the shear load increased, the cracks would develop along the shear direction through the weak areas in the mortar and coarse aggregates. Since these weak areas were not completely in a straight line, eventually, the failure mode as shown in Figure 5 was formed. At the same time, as the axial compression ratio increased, the number of oblique cracks on the lateral surface of the specimen that is parallel to the shear loading direction would gradually grow. This is because when shear failure occurred, oblique cracks could be easily formed on the lateral surface parallel to the shear direction affected by the shear failure section, especially when the axial load was large. With the increase of the axial load, the number of oblique cracks would gradually increase, exhibiting a more obvious damage.

Figure 6 shows the failure modes on the shear failure section of SCC under different axial compression ratios. When the axial compression ratio was 0, the failure section of the specimen was relatively flat and smooth. When the axial compression ratio began to increase, obvious friction marks would be observed on the shear failure section and a certain amount of concrete slags were generated. As the axial compression ratio increased further, the friction marks on the shear failure section became more obvious and more concrete slags would be generated along with the falling-off of some concrete blocks.

3.2 Stress-Strain Curve

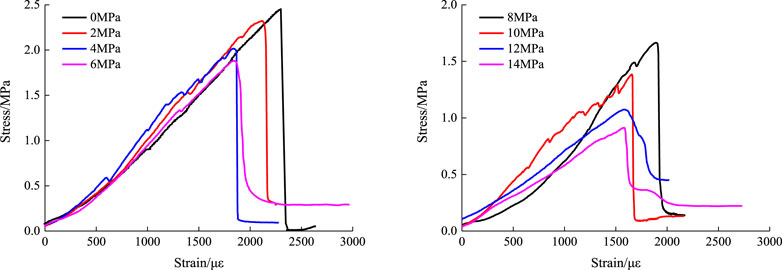
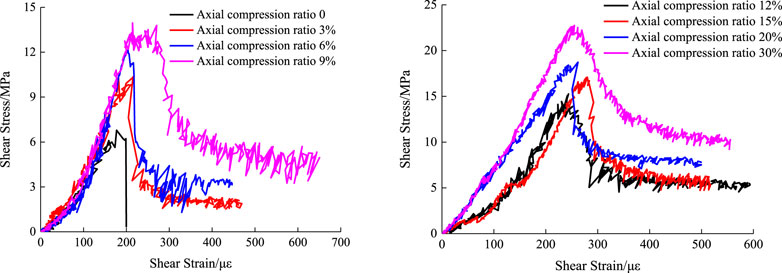
The load and deformation data was captured by the load sensors and deformation sensors of the rock true triaxial machine and the material compression-shear hydraulic servo machine. The data of biaxial compression-compression stress was determined by the ratio of the load data acquired from the load sensors to the stress area on the specimen loading surface. The strain data was determined by the ratio of the displacement data acquired from the displacement sensors to the height of the specimen in the loading direction. The data of biaxial tensile-compressive stress was calculated through the load stress conversion equation under split-tensile loading as stipulated in the “Standard for test method of mechanical properties on ordinary concrete” (GB/T 50081-2002). The strain data was determined by the ratio of the deformation data acquired from the displacement sensors in the splitting direction to the height of the specimen in the loading direction. It is noteworthy that the strain data under split-tensile loading in this paper was the nominal strain data rather than the actual tensile strain data of SCC. This paper only aims to examine and analyze the stress characteristic value and stress failure criterion, with no intention to perform quantitative analysis on the strain characteristic value. Therefore, the use of nominal strain data had little effect on the qualitative analysis of the development trend of the stress-strain curve. The shear stress-strain curves of SCC under different axial compression ratios were obtained by the compression-shear hydraulic servo machine. Shear stress refers to the ratio of the shear load to the area of the shear section, and shear strain refers to the ratio of the displacement in the shear direction to the length of the specimen parallel to the shear direction. The principal compressive stress-strain curve and tensile stress-strain curve of SCC under biaxial compression-compression and biaxial tension-compression obtained based on the aforementioned stress and strain data are shown in Figures 7–9 respectively.

FIGURE 7

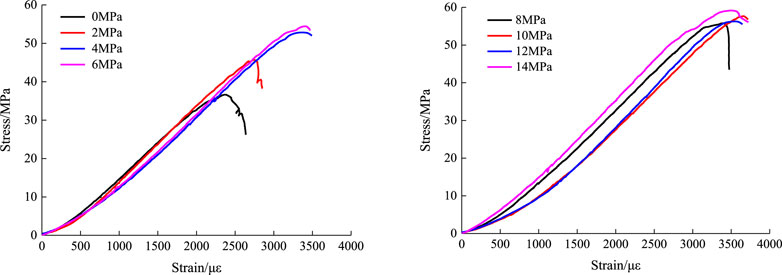
FIGURE 7. The principal compressive stress-strain curve of SCC under biaxial compression-compression.

FIGURE 8

FIGURE 8. The principal compressive stress-strain curve of SCC under biaxial tension-compression.

FIGURE 9

FIGURE 9. Shear stress-strain curves of SCC under different axial compression ratios.

It can be seen from Figure 7 that the principal compressive stress-strain curve of SCC under biaxial compression-compression had good continuity and smoothness. The development trend of the principal compressive stress-strain curve could be divided into three stages: the elastic stage (i.e., the stress of SCC increased linearly with the increase of strain), the elastoplastic stage (i.e., the stress no longer increased linearly but showed a reduced increasing amplitude with the increase of strain), and the declining stage (i.e., the strain maintained an increasing trend, but the stress began to decrease after reaching its peak value). The development trend of the principal compressive stress-strain curve had no relation with the lateral compressive stress. Compared with ordinary concrete, SCC exhibited obvious brittle failure characteristics. From the overall trend, it can be observed that the principal compressive stress of SCC under lateral compressive stress was higher than that without lateral compressive stress, indicating that the lateral compressive stress had a significant effect on the principal compressive stress. As shown in Figure 7, the biaxial compression stress-strain curve was curved to a certain extent in the initial stage. This is mainly because, in the initial stage of loading (for an extremely short period of time), there was a very small gap between the loading surface of equipment and the surface of specimen when the two were just in contact and the specimen had a very small deflection. After the gap was eliminated by compression, the stress-strain curve would show a straight pattern. This curving section of the stress-strain relation basically does not affect the accuracy of the maximum stress value of SCC under different confining pressures.

Figure 8 shows the principal tensile stress-strain curve of SCC under biaxial tension-compression. The development trend of the principal tensile stress-strain curve under biaxial tension-compression was similar to that under the uniaxial split-tension loading condition, which could be divided into two stages: the elastic stage (i.e., the stress increased linearly with the increase of deformation) and the declining stage (i.e., after the stress reached its peak value, it would decline rapidly to 0 and the specimen would exhibit obvious brittle failure characteristics). From the development trend, it can be seen that the lateral compressive stress had no effect on the principal tensile stress-strain curve. As the lateral compressive stress increased, the principal tensile stress decreased gradually.

Figure 9 shows the shear stress-strain curves of SCC under different axial compression ratios. When the axial compression ratio was 0, the shear stress-strain curve could be divided into two stages: the elastic ascending stage and the direct declining stage. When the axial compression ratio began to increase, the development trend of the shear stress-strain curve became obviously different, that is, there was an obvious stress balance stage after the elastic ascending stage and the declining stage, during which the shear stress remained basically unchanged. In the elastic ascending stage, the shear stress was mainly formed by the Van der Waals force, the chemical adhesive force and the mechanical bite force on the shear section of the concrete specimen. More specifically, in the early phase of the elastic ascending stage, the shear stress was mainly formed by the Van der Waals force and the chemical adhesive force on the shear section, while in the late phase of the elastic ascending stage, the shear stress was mainly formed by the chemical adhesive force and the mechanical bite force on the shear section. In the declining stage of the shear stress-strain curve, the shear stress was mainly caused by the mechanical bite force and the friction force on the shear section. In the stress balance stage of the shear stress-strain curve, the shear stress was mainly formed by the friction force between the shear failure sections. According to a preliminary analysis of Figure 9, it can be found that the shear stress and residual stress of SCC increased significantly with the increase of the axial compression ratio.

3.3 Analysis of Characteristic Values

3.3.1 Analysis of Stress Characteristic Values

The principal stress peak values were extracted from the principal compressive stress-strain curve under biaxial compression-compression, the principal tensile stress-strain curve under biaxial tension-compression and the stress-strain curve under compression-shear loading as shown in Figures 7–9, respectively, in order to analyze the influence of lateral compressive stress on the principal stress. Considering the discreteness of the test data and the accuracy of the analysis results, error bars were added to the principal stress data. The midpoint of the error bar was the average of the principal stress values of the three parallel SCC specimens for each loading condition. The length of the error bar was the degree of discreteness of the principal stress of each loading condition. In this study, the average discreteness percentage of the principal compressive stress under biaxial compression-compression was 3.89%, and that of the principal tensile stress under biaxial tension-compression was 6.70%. Referring to the test specifications on the concrete mechanical properties, the analysis requirements were satisfied.

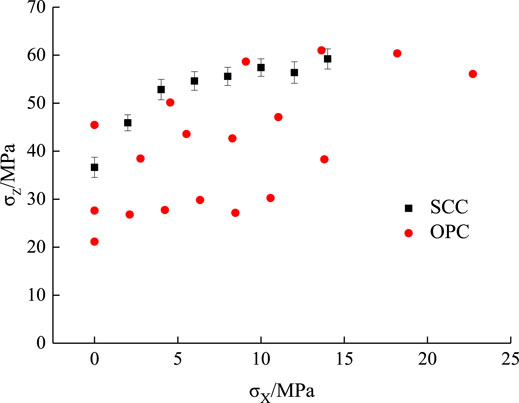
In order to compare with ordinary concrete, a comparative study was carried out between the biaxial loading test data of SCC in this study and the biaxial loading test data of three different strength grades (C30, C40 and C50) of ordinary concrete obtained from the relevant literature (Yu et al., 2019). On the basis of Figures 7, 8, the relations between the principal compressive stress under biaxial compression-compression (principal tensile stress), the shear stress under compression-shear, and the lateral compressive stress of SCC were obtained, as shown in Figures 10, 11.

FIGURE 10

FIGURE 10. The principal compressive stress and lateral compressive stress of SCC.

FIGURE 11

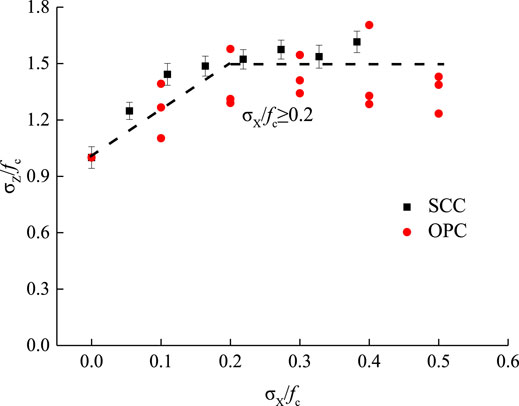
FIGURE 11. The ratio of principal compressive stress and the ratio of lateral compressive stress of SCC.

According to Figures 10, 11, the lateral compressive stress had a significant impact on the principal compressive stress of SCC under biaxial compression-compression. With the increase of the lateral compressive stress, the principal compressive stress under biaxial compression-compression showed a more significant increase than the uniaxial compressive stress. When the lateral compressive stress was 0 MPa, the principal compressive stress of SCC was 36.62 MPa. When the lateral compressive stress was increased to 14 MPa, the principal compressive stress was increased to 59.17 MPa accordingly, suggesting an average increase of 55.78% compared with the uniaxial compressive condition. This is because the mechanical bite force between mortar and coarse aggregates, and between coarse aggregates and coarse aggregates of SCC, were increased with the increase of lateral compressive stress, which eventually led to an increase in the principal compressive stress. Comparatively, under biaxial compression-compression, the average increase in the principal compressive stress of ordinary concrete C30, C40 and C50 affected by the lateral compressive stress was 32.88, 48.75 and 28.63% respectively. With respect to the overall development trend, the lateral compressive stress had a more significant impact on the principal compressive stress of SCC than on that of ordinary concrete under biaxial compression-compression. The similarities between SCC and ordinary concrete are that: when the lateral compressive stress ratio was less than 0.2, the principal compressive stress of both SCC and ordinary concrete changed significantly under the action of lateral compressive stress; when the lateral compressive stress ratio was greater than 0.2, the principal compressive stress of SCC changed stably, suggesting a similar changing trend to that of the principal compressive stress of ordinary concrete affected by the lateral compressive stress under biaxial compression-compression applied through the proportional loading mode (Guo, 1997).

According to Figure 12, when the axial compression ratio was 0, the shear stress of SCC was 6.79 MPa. As the axial compression ratio increased, the shear stress of SCC began to increase gradually. When the axial compression ratio was 9%, the corresponding shear stress was increased to 13.95 MPa, which was 2.05 times higher than that under the axial compression ratio of 0%. Comparatively, the shear stress of ordinary concrete at the axial compression ratio of 9% was increased by 2.15 times relative to the working condition of 0% axial compression ratio. There is basically a similar trend between SCC and ordinary concrete. When the axial compression ratio was 30%, the shear stress of SCC was increased to 22.75 MPa, which was 3.35 times higher than that under the working condition of 0% axial compression ratio.

FIGURE 12

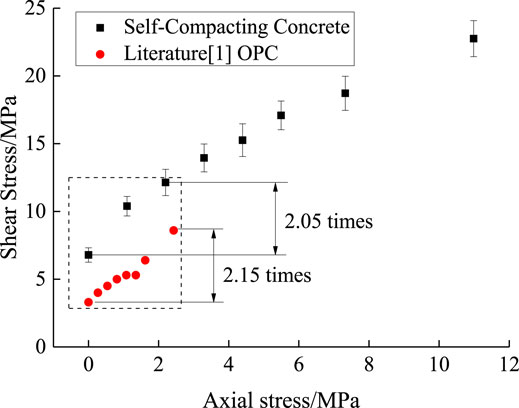
FIGURE 12. The relation between the axial action and shear action of SCC under different axial compression ratios.

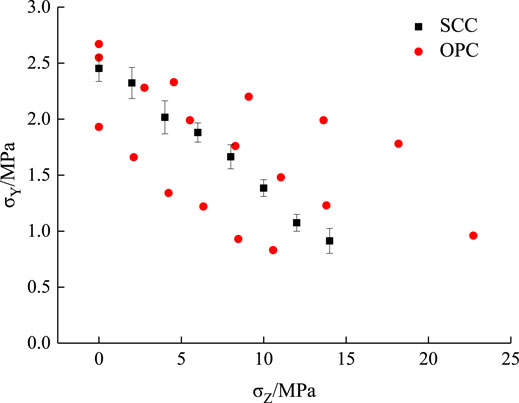
Figures 13, 14 present the changing trend of the principal tensile stress of SCC affected by the lateral compressive stress under biaxial tension-compression. As the lateral compressive stress increased, the principal tensile stress decreased gradually. When the lateral compressive stress was 0 MPa, the principal tensile stress of SCC was 2.45 MPa. When the lateral compressive stress was 14 MPa, the principal tensile stress was decreased to 0.91 MPa, suggesting a decrease of 62.79%. This is mainly because the lateral compressive stress formed a tensile strain in the principal tensile stress direction affected by the Poisson’s ratio effect. With the increase of the lateral compressive stress, the tensile strain formed in the principal tensile stress direction would increase gradually. When the principal tensile stress began to apply, the specimen would reach its ultimate tensile strain first and then gradually decrease; eventually, the principal tensile stress would decrease with the further increase of the lateral compressive stress. An earlier study (Yu et al., 2019) reported that the principal tensile stress of ordinary concrete C30, C40 and C50 under biaxial tension-compression was reduced by 51.81, 41.96 and 33.33% respectively under the influence of the lateral compressive stress. It can be seen that the lateral compressive stress had a more significant impact on the principal tensile stress of SCC than on that of ordinary concrete under biaxial tension-compression.

FIGURE 13

FIGURE 13. The principal tensile stress and lateral compressive stress of SCC.

FIGURE 14

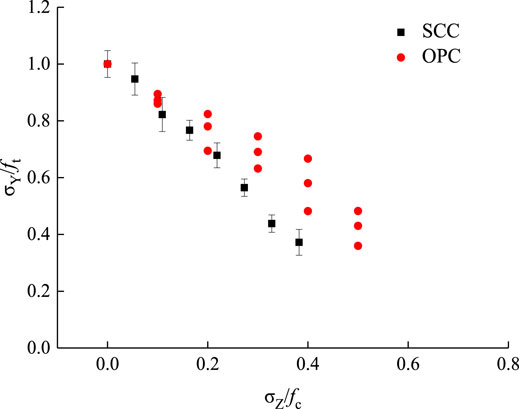
FIGURE 14. The ratio of principal tensile stress and the ratio of lateral compressive stress of SCC.

In order to eliminate the impact of different compressive strengths on the test results, the test results were preprocessed by the dimensionless method before analysis. According to Figure 15, the increase in the shear stress of SCC affected by the axial compression ratio was similar to that of ordinary concrete. As the axial compression ratio increased, the increasing amplitude of shear stress under the influence of axial compression ratio decreased gradually. This is mainly because the SCC specimen tended to enter the elastoplastic stage under a large axial load. Accordingly, the internal micro-cracks in the specimen began to expand, and the increasing amplitude of the shear stress would start decreasing at this moment. By considering the development trend of the relation between the axial compression ratio and the shear stress increase factor (τ/τ₀), the two were speculated to form a power function relation, as shown in Eq. 1.

$\frac{\tau }{{\tau }_0}=\text{a}\times {\xi }^b(1)$

FIGURE 15

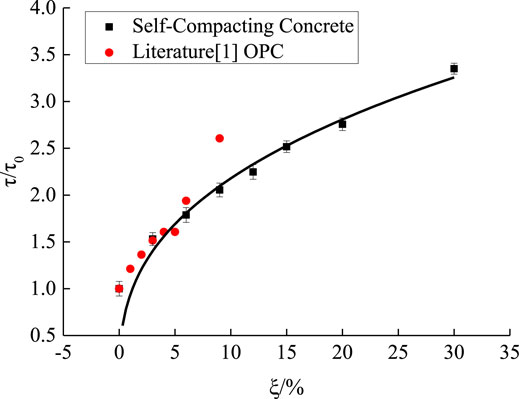
FIGURE 15. The relation between the axial action and shear action of SCC under different axial compression ratios.

According to the test data in this study, mathematical regression analysis was performed using Eq. 1 and the results are shown in Eq. 2 and Figure 15. It can be seen that the proposed equation for the relation between the axial compression ratio and the shear stress increase factor of SCC had good applicability to the quantitative stress analysis under the multiaxial compression-shear loading condition.

$\frac{\tau }{{\tau }_0}=0.93801\times {\xi }^{0.36602}{\text{R}}^2=\text{0}\text{.}9807(2)$

For the stress mechanism under multiaxial compression-shear, the axial loading effect significantly increased the mechanical bite force and friction force between the shear sections of SCC, that is, the shear load gradually increased with the increase of the axial load. When the axial load had increased to the threshold level, the increasing amplitude of shear load would begin to decline. This is because when the axial load was large, the initial internal damage of SCC would evolve greatly and the crack damage would develop rapidly. Consequently, the Van der Waals force and chemical adhesive force on the shear section would be weakened. However, since the axial load would significantly increase the mechanical bite force and friction force between the shear sections, when the axial load reached the threshold value, the increasing amplitude of shear load under the influence of axial compression ratio would start declining with the further increase of the axial load.

The residual stress is mainly formed by the mutual friction between the shear failure sections of the specimen, which can be determined by the friction coefficient between the axial load and the shear failure section. In this study, the residual stress was determined based on the shear stress-strain curve of SCC using the same method as described in the relevant literature (Yu et al., 2018a). The relations between the axial load and the residual load of SCC under different axial compression ratios were obtained as shown in Supplementary Figure S1.

Yu et al. (2018a) examined the residual stress of ordinary concrete under the multiaxial compression-shear loading condition and found that the friction coefficient between the shear failure sections of ordinary concrete was 1.46. According to the test data in this study, the relation between the axial load and residual load of SCC was obtained, as shown in Supplementary Figure S1. It can be seen that with the increase of the axial load, the residual load of SCC on the shear failure section increased gradually. Based on the test data of SCC under the multiaxial compression-shear loading condition, the friction coefficient of SCC on the shear failure section was calculated by performing mathematical regression analysis, which was 1.107, lower than that of ordinary concrete.

4 Failure Criterion

For the multiaxial compression-shear loading method, the shear stress and compressive stress were usually converted into the first principal stress, the second principal stress and the third principal stress through Eqs 3–5, in order to analyze the development trend of the multiaxial compressive-shear strength of SCC.

${\sigma }_1=\frac{\sigma }{2}+\sqrt{{\left(\frac{\sigma }{2}\right)}^2+{\tau }^2}(3)$

${\sigma }_2=0(4)$

${\sigma }_3=\frac{\sigma }{2}-\sqrt{{\left(\frac{\sigma }{2}\right)}^2+{\tau }^2}(5)$

4.1 Plane stress space

For the biaxial loading method of ordinary concrete, Kupfer (1973) put forward the biaxial compression-compression and biaxial tension-compression strength criterion equations under the proportional loading method based on regression analysis of massive experimental data and literature data, as shown in Eqs 6, 7.

${\left(\frac{{\sigma }_Z}{f_c}+\frac{{\sigma }_X}{f_c}\right)}^2-\frac{{\sigma }_Z}{f_c}-3.65\frac{{\sigma }_X}{f_c}=0(6)$

Where: σ_X and σ_Z refer to the lateral compressive stress in the X direction and the principal compressive stress in the Z direction, respectively (unit: MPa); f_c refers to the uniaxial compressive stress (unit: MPa).

$\frac{{\sigma }_Y}{f_t}+0.8\frac{{\sigma }_Z}{f_c}=1(7)$

Where: σ_Y and σ_Z refer to the principal tensile stress in the Y direction and the lateral compressive stress in the Z direction, respectively (unit: MPa); f_t refers to the uniaxial split-tensile stress (unit: MPa).

There has been extensive literature on the analysis of the biaxial stress mode of ordinary concrete under constant lateral loading. It has been argued that the Kupfer strength criterion is relatively conservative in predicting the strength relation under constant lateral loading, which is mainly attributed to the loading method itself, as different loading paths may have a significant impact on the concrete strength criterion. Based on the Kupfer strength criterion, the strength criterion equation of ordinary concrete under the constant lateral loading method was proposed, which showed good applicability to ordinary concrete structures (Yu et al., 2019). According to the analysis of the effect of lateral compressive stress on the principal compressive stress (principal tensile stress) of SCC, the biaxial compression-compression and biaxial tension-compression strength criterion equations for SCC were proposed, as shown in Eqs 8, 9. Meanwhile, a comparative analysis was performed by referring to the test data and the strength criterion of ordinary concrete under the biaxial stress loading method (Yu et al., 2019).

${\left(\frac{{\sigma }_Z}{f_c}+\frac{{\sigma }_X}{f_c}\right)}^2+a\frac{{\sigma }_Z}{f_c}+b\frac{{\sigma }_X}{f_c}=0(8)$

$\frac{{\sigma }_Y}{f_t}+\text{c}\frac{{\sigma }_Z}{f_c}=1(9)$

Based on the biaxial compression-compression and biaxial tension-compression test data of SCC related to the strength criterion equations as shown in Eqs 8, 9, the biaxial compression-compression and biaxial tension-compression strength criterion equations of SCC were established using mathematical software, as shown in Eqs 10, 11 and Supplementary Figures S2, S3.

${\left(\frac{{\sigma }_Z}{f_c}+\frac{{\sigma }_X}{f_c}\right)}^2-1.01\frac{{\sigma }_Z}{f_c}-6.43\frac{{\sigma }_X}{f_c}=0(10)$

$\frac{{\sigma }_Y}{f_t}+1.614\frac{{\sigma }_Z}{f_c}=1(11)$

From Eqs 10, 11, it can be seen that the biaxial compression-compression and biaxial tension-compression strength criterion equations of SCC proposed based on the Kupfer criterion had good applicability. In addition, according to Supplementary Figures S2, S3, the biaxial strength criterion equation of ordinary concrete under constant lateral loading appeared to be conservative in predicting the strength of SCC, that is, the lateral compressive stress had a stronger impact on the principal stress of SCC under biaxial loading than on that of ordinary concrete.

Thus, the multiaxial compression-shear test data of SCC in this paper was converted into the principal stress data using Eqs 3–5. By comparing with the multiaxial compression-shear test data of ordinary concrete (Yu et al., 2018a), the development trend of the strength of SCC in the plane stress space was obtained, as shown in Supplementary Figure S4.

It can be seen from Supplementary Figure S4 that, with the increase of the first principal stress, the third principal stress of SCC decreased gradually and showed a development trend and changing amplitude similar to those of ordinary concrete. Further, by comparing the principal stress space failure criterion of ordinary concrete under multiaxial compression-shear (Yu et al., 2018a) with the test data of SCC in this paper, the results as shown in Eq. 12 and Supplementary Figure S4 were obtained.

$\frac{{\sigma }_3}{f_c}=-0.69545\times \left(\frac{{\sigma }_1}{f_c}\right)-0.03828(12)$

According to Supplementary Figure S4, the principal stress space failure criterion proposed by Yu et al. (2018a) had deficiencies in predicting the multiaxial compression-shear strength of SCC. When the dimensionless value of the first principal stress was less than 0.4, the principal stress space failure criterion of ordinary concrete would lead to a predicted value that is higher than actual. On the contrary, when the dimensionless value of the first principal stress was higher than 0.4, the principal stress space failure criterion of ordinary concrete would lead to a conservative prediction. In view of the situation above, the multiaxial compression-shear failure criterion equation of SCC was proposed based on Eq. 11, as shown in Eq. 13.

$\frac{{\sigma }_3}{f_c}=a\times \left(\frac{{\sigma }_1}{f_c}\right)+b(13)$

The multiaxial compression-shear test data of SCC in this paper was converted into the first principal stress and the third principal stress values. Then, the failure criterion equation of SCC was obtained by performing mathematical regression analysis using Eq. 13, as shown in Eq. 14 and Supplementary Figure S4.

$\frac{{\sigma }_3}{f_c}=-0.49193\times \left(\frac{{\sigma }_1}{f_c}\right)-0.11716{\text{R}}^2=\text{0}\text{.}97845(14)$

According to Eq. 14 and Supplementary Figure S4, the multiaxial compression-shear failure criterion equation of SCC proposed based on the plane stress space had good applicability to engineering practice and could effectively demonstrate the development trend of the strength of SCC under the multiaxial compression-shear loading condition. Compared with ordinary concrete, the third principal stress of SCC showed a smoother changing curve under the influence of the first principal stress.

4.2 Octahedral Space Stress

For the examination of the multiaxial stress strength criterion of concrete, the method of using octahedral space stress expression to describe the multiaxial strength pattern has wide applicability in practice (Ottosen 1977). According to the multiaxial stress octahedral space stress of concrete, the failure criterion equation of SCC was established as shown in Eqs 15, 16.

$\frac{{\tau }_{\text{oct}}}{f_c}=a_1+b_1\frac{{\sigma }_{\text{oct}}}{f_c}(15)$

$\frac{{\tau }_{\text{oct}}}{f_c}=a_2{\left(\frac{{\sigma }_{\text{oct}}}{f_c}\right)}^2+b_2\frac{{\sigma }_{\text{oct}}}{f_c}+c_2(16)$

Where, the expression of normal stress σ_oct is shown in Eq. 17, and the expression of shear stress τ_oct is shown in Eq. 18.

${\sigma }_{\text{oct}}=\frac{{\sigma }_X+{\sigma }_Y+{\sigma }_Z}{3}(17)$

${\tau }_{\text{oct}}=\frac{1}{3}\sqrt{{\left({\sigma }_Z-{\sigma }_X\right)}^2+{\left({\sigma }_X-{\sigma }_Y\right)}^2+{\left({\sigma }_Y-{\sigma }_Z\right)}^2}(18)$

The biaxial loading test data of SCC in this paper was converted into the normal stress σ_oct and shear stress τ_oct through Eqs 17, 18 respectively. Then, the octahedral space stress strength criterion of SCC was obtained by performing mathematical regression analysis based on Eqs 15, 16 using mathematical software, as shown in Supplementary Figure S5.

Based on the octahedral stress space failure criterion equations as shown in Eqs 15, 16, the expressions of biaxial failure criterion of SCC under biaxial loading were obtained by performing mathematical regression analysis on the biaxial loading test data, as shown in Supplementary Figure S5 and Eqs 19–22.

SCC:

$\frac{{\tau }_{\text{oct}}}{f_c}=-0.94918-0.07097\frac{{\sigma }_{oct}}{f_c}{\text{R}}^2=\text{0}\text{.}96185(19)$

$\frac{{\tau }_{\text{oct}}}{f_c}=0.86531{\left(\frac{{\sigma }_{oct}}{f_c}\right)}^2-1.47159\frac{{\sigma }_{oct}}{f_c}-0.04776{\text{R}}^2=\text{0}\text{.}97778(20)$

OPC:

$\frac{{\tau }_{\text{oct}}}{f_c}=-0.05591-1.07862\frac{{\sigma }_{oct}}{f_c}{\text{R}}^2=\text{0}\text{.}9914(21)$

$\frac{{\tau }_{\text{oct}}}{f_c}=0.29666{\left(\frac{{\sigma }_{oct}}{f_c}\right)}^2-1.21882\frac{{\sigma }_{oct}}{f_c}-0.05843{\text{R}}^2=\text{0}\text{.}99422(22)$

According to the analysis on the octahedral space stress strength criterion of SCC under biaxial loading as shown in Supplementary Figure S5, the primary strength criterion equation and the secondary strength criterion equation established for octahedral space stress could effectively reflect the development trend of the strength of SCC under biaxial loading. Compared with the octahedral space stress strength criterion of ordinary concrete, the strength criterion equation of SCC had a greater similarity to that of ordinary concrete under biaxial tension-compression. Under biaxial compression-compression, the difference in the strength criterion equation between SCC and ordinary concrete gradually appeared. Meanwhile, it can be seen from Supplementary Figure S5 that the lateral compressive stress had a more significant impact on the principal stress of SCC under biaxial loading than that on ordinary concrete.

The plane stress space strength criterion and the octahedral space stress strength criterion of SCC proposed in this paper are two independent and different expressions, with different applicability in the real world. The plane stress space is a special form of expression form for the principal stress space. The principal stress space is constituted based on the first principal stress, the second principal stress and the third principal stress. Under the biaxial loading method, one of the principal stresses is zero, that is, a plane stress space is formed. The strength criterion obtained through the plane stress space has high intuitiveness, and the expression is relatively simple. Corresponding, its applicability is low and is only suitable for biaxial loading and tension/compression-shear loading conditions. For the octahedral space stress, an equal inclined plane is formed on the three principal stress axes through the space evolution of the principal stresses, and the stresses formed on this inclined plane are the normal stress and shear stress (i.e., the octahedral space stress). The failure criterion obtained in this way has high applicability, not only suitable for biaxial loading and tensile/compression shear loading, but also for triaxial loading conditions. The envelope surface of the strength criterion can be simplified by means of the meridian.

Compared with ordinary concrete, the biaxial compressive stress-strain curve of SCC shows more obvious brittleness characteristics. Meanwhile, the lateral stress has a more significant influence on the biaxial stress of SCC than that on ordinary concrete, and the failure criterion meridian of SCC is significantly higher than that of ordinary concrete. The failure criterion of SCC is obviously different from that of ordinary concrete. In the subsequent construction of the elastoplastic damage constitutive model, SCC also shows different characteristics from ordinary concrete. SCC has the advantages of high compactness, strong durability and good working performance. Its composition indicates a certain level of commonality. In this study, the lateral stress shows a more significant effect on the principal stress of SCC under biaxial loading than that on ordinary concrete. This is mainly attributed to the concrete composition, as the compactness of SCC is higher than that of ordinary concrete. Thus, it is proposed that the compactness of concrete needs to be further improved by optimizing the mix ratio design in order to achieve better multiaxial mechanical properties.

5 Conclusion

According to the test data of biaxial compression-compression, biaxial tension-compression and compression-shear in this paper, the failure modes, the principal stress-strain curves and the principal stress values of SCC under different loading conditions were obtained. Then, by comparing with the corresponding test data of ordinary concrete under biaxial loading, the following conclusions are drawn:

1) The lateral compressive stress has a significant impact on the failure mode of SCC under biaxial compression-compression. When the lateral compressive stress is small, the failure mode is similar to that of uniaxial compression. When the lateral compressive stress is large, the specimen shows an oblique flaky failure mode. The failure modes of all the specimens under biaxial tension-compression are split failure, suggesting no relationship with the lateral compressive stress. This failure pattern is basically similar to that of ordinary concrete under biaxial loading. With respect to the multiaxial compression-shear failure mode of SCC, the shear failure line of the specimen perpendicular to the direction of shear loading is of a straight pattern and is not related to the axial compression ratio. As the axial compression ratio increases, the oblique cracks on the lateral surface of the specimen that is parallel to the direction of shear loading begin to increase gradually, and meanwhile, the friction marks on the shear fracture section are gradually deepened.

2) The development trend and pattern of the principal stress-strain curve of SCC under biaxial loading are similar to those of uniaxial loading, and are not affected by the lateral compressive stress. The lateral compressive stress has a significant impact on the principal compressive stress and principal tensile stress of biaxial compression-compression and biaxial tension-compression. When a lateral compressive stress is applied, the principal compressive stress of SCC is obviously increased compared with that under uniaxial compression, while the principal tensile stress decreases gradually as the lateral compressive stress increases. Compared with the ordinary concrete under biaxial loading, the lateral compressive stress has a more significant impact on the principal stress of SCC.

3) As the axial compression ratio increases, the shear stress and residual stress of SCC increase significantly. When the axial compression ratio is large, the increasing amplitude of shear stress will slow down gradually with the further increase of the axial compression ratio. According to the analysis of residual stress, the friction coefficient of SCC on the shear failure section is lower than that of ordinary concrete.

4) Based on the plane stress space and the octahedral space stress, the strength criterion equations of SCC under biaxial loading were proposed using the data in this study. The proposed strength criterion equations are shown to have good applicability in engineering practice. In addition, according to the changing curve of the octahedral stress space strength criterion equation, it can be seen that the strength criterion equation of SCC is similar to that of ordinary concrete under biaxial tension-compression, but under biaxial compression-compression, the difference in the strength criterion equation between the two will gradually appear. The univariate quadratic failure criterion has higher applicability than the linear expression, and meanwhile, the envelope curve of the compression-shear multiaxial failure criterion of SCC is higher than that of ordinary concrete.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

JZ contributed to the conception and research method of the study. CL was responsible for testing and organizing the database. CZ performed the statistical analysis. JZ and ZZ wrote the first draft of the manuscript. All authors contributed to manuscript revision and read and approved the submitted version.

Funding

This research was funded by the General projects of natural science research in Colleges and universities of Jiangsu Province (20KJD560001). The authors gratefully acknowledge the financial support.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors would like to express sincere thanks to natural science research in Colleges and universities of Jiangsu Province.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2021.691342/full#supplementary-material

Supplementary Figure S1 | The relations between the axial load and residual load of SCC under different axial compression ratios.

Supplementary Figure S2 | Biaxial compression-compression strength criterion of SCC.

Supplementary Figure S3 | Biaxial tension-compression strength criterion of SCC.

Supplementary Figure S4 | Failure criterion of SCC in the plane stress space.

Supplementary Figure S5 | The octahedral space stress strength criterion of SCC under biaxial loading.

References

Anne-Mieke, P., and de Schutter, G. (2005). “Creep and Shrinkage of Self-Compacting concrete,” in Proceedings of 1st International Symposium on Design, Performance and Use of Self-Consolidating Concrete. Editors Z Yu, C Shi, and K Khayat (Paris: RILEM Publication SARL), 329–336.

Google Scholar

Asteris, P. G., and Kolovos, K. G. (2019). Self-Compacting Concrete Strength Prediction Using Surrogate Models. Neural Comput. Appl. 31 (1), 409–424. doi:10.1007/s00521-017-3007-7

CrossRef Full Text | Google Scholar

Chi, Y., Xu, L., Mei, G., Hu, N., and Su, J. (2014). A Unified Failure Envelope for Hybrid Fibre Reinforced concrete Subjected to True Triaxial Compression. Compos. Structures 109 (6), 31–40. doi:10.1016/j.compstruct.2013.10.054

CrossRef Full Text | Google Scholar

Dinakar, P., and Manu, S. N. (2014). Concrete Mix Design for High Strength Self-Compacting Concrete Using Metakaolin-ScienceDirect. Mater. Des. 60 (1), 661–668. doi:10.1016/j.matdes.2014.03.053

CrossRef Full Text | Google Scholar

Fantilli, A. P., Vallini, P., and Chiaia, B. (2011). Ductility of Fiber-Reinforced Self-Consolidating Concrete under Multi-Axial Compression. Cement and Concrete Composites 33 (4), 520–527. doi:10.1016/j.cemconcomp.2011.02.007

CrossRef Full Text | Google Scholar

Fujikake, K., Mori, K., Uebayashi, K., Ohno, T., and Mizuncr, J. (2000). Dynamic Properties of Concrete Materials with High Rates of Tri-Axial Compressive Loads. Structures Mater. 48, 511–522. doi:10.2495/SU000471

CrossRef Full Text | Google Scholar

Guo, Z. (1997). Strength and Deformation of concrete: Experimental Foundation and Constitutive Relationship. Beijing: Tsinghua University Press, 166–167.

Google Scholar

He, Z.-J., and Song, Y.-P. (2010). Triaxial Strength and Failure Criterion of Plain High-Strength and High-Performance concrete before and after High Temperatures. Cement Concrete Res. 40 (1), 171–178. doi:10.1016/j.cemconres.2009.08.024

CrossRef Full Text | Google Scholar

Kandasamy, S., and Kothandaraman, S. (2020). Influence of Controlled Permeable Formwork Liner on Surface Quality of Self Compacting concrete. Construction Building Mater. 260, 119756. doi:10.1016/j.conbuildmat.2020.119756

CrossRef Full Text | Google Scholar

Klaus, H., and Yvette, K. (2005). “Pull-out Behavior of Steel Fibers in Self Compacting concrete,” in Proceedings of 1st International Symposium on Design, Performance and Use of Self-Consolidating Concrete. Editors Z Yu, C Shi, and K H Khayat (Paris: RILEM Publication SARL), 523–532.

Google Scholar

Kupfer, H. B. (1973). Behavior of Concrete under Biaxial Stresses. J. Eng. Mech. Division ASCE 66 (8), 853–866. doi:10.1061/jmcea3.0001789

CrossRef Full Text | Google Scholar

Lazniewska-Piekarczyk, B. (2016). Investigations on the Relationship between Porosity and Strength of Admixtures Modified High Performance Self-Compacting Concrete. J. civil Eng. Manag. 22 (2), 520–528. doi:10.3846/13923730.2014.897978

CrossRef Full Text | Google Scholar

Mohamed, R. N., Zamri, N. F., Elliott, K. S., Rahman, A. B. A., and Bakhary, N. (2019). Steel Fibre Self-Compacting Concrete under Biaxial Loading. Construction Building Mater. 224, 255–265. doi:10.1016/j.conbuildmat.2019.07.076

CrossRef Full Text | Google Scholar

Okamura, H., and Ozawa, K. (1995). Mix Design for Self–Compacting Concrete. Concrete Libr. JSCE 25 (6), 107–120.

Google Scholar

Ottosen, N. S. (1977). A Failure Criterion for Concrete. J. Engrg. Mech. Div. 103 (4), 527–535. doi:10.1061/jmcea3.0002248

CrossRef Full Text | Google Scholar

Pajak, M., Janiszewski, J., and Kruszka, L. (2019). Laboratory Investigation on the Influence of High Compressive Strain Rates on the Hybrid Fibre Reinforced Self-Compacting Concrete. Construction Building Mater. 227 (10), 116687. doi:10.1016/j.conbuildmat.2019.116687

CrossRef Full Text | Google Scholar

Reiterman, P., Holčapek, O., Zobal, O., and Keppert, M. (2019). Freeze-thaw Resistance of Cement Screed with Various Supplementary Cementitious Materials. Rev. Adv. Mater. Sci. 58, 66–74. doi:10.1515/rams-2019-0006

CrossRef Full Text | Google Scholar

Ren, Y., Yu, Z., Huang, Q., and Ren, Z. (2018). Constitutive Model and Failure Criterions for Lightweight Aggregate Concrete: A True Triaxial Experimental Test. Construction Building Mater. 171, 759–769. doi:10.1016/j.conbuildmat.2018.03.219

CrossRef Full Text | Google Scholar

Shang, S., and Song, Y. (2013). Dynamic Biaxial Tensile–Compressive Strength and Failure Criterion of Plain Concrete. Construction Building Mater. 40 (40), 322–329. doi:10.1016/j.conbuildmat.2012.11.012

CrossRef Full Text | Google Scholar

Shi, L., Wang, L., Song, Y., and Shen, L. (2014). Dynamic Multiaxial Strength and Failure Criterion of Dam Concrete. Construction Building Mater. 66 (1), 181–191. doi:10.1016/j.conbuildmat.2014.05.076

CrossRef Full Text | Google Scholar

Tschegg, E. K., Schneemayer, A., Merta, I., and Rieder, K. A. (2015). Energy Dissipation Capacity of Fibre Reinforced Concrete under Biaxial Tension-Compression Load. Part I: Test Equipment and Work of Fracture. Cement and Concrete Composites 62, 195–203. doi:10.1016/j.cemconcomp.2015.07.002

CrossRef Full Text | Google Scholar

Wang, J., Dai, Q., Si, R., Ma, Y., and Guo, S. (2020). Fresh and Mechanical Performance and Freeze-Thaw Durability of Steel Fiber-Reinforced Rubber Self-Compacting Concrete (SRSCC). J. Clean. Prod. 277, 123180. doi:10.1016/j.jclepro.2020.123180

CrossRef Full Text | Google Scholar

Xu, D., Chen, Z., and Zhou, C. (2020). Seismic Performance of Recycled Concrete Filled Circular Steel Tube Columns. Front. Mater. 7, 612059. doi:10.3389/fmats.2020.612059

CrossRef Full Text | Google Scholar

Yu, Z., Qiao, H., Xie, X., and Lu, B. (2018b). Comparative Study on Compressive-Shear Behavior of Ordinary Concrete and Lightweight Aggregate Concrete. Mater. Rep. 32 (24), 4269–4275. doi:10.11896/j.issn.1005-023X.2018.24.011

CrossRef Full Text | Google Scholar

Yu, Z., Sun, X., and Li, F. (2019). Experimental Analysis and Failure Criterion of Plain Concrete Subjected to Biaxial Loading under Fixed Lateral Loading. Adv. Civil Eng. 2019, 7059475. doi:10.1155/2019/7059475

CrossRef Full Text | Google Scholar

Yu, Z., Huang, Q., Xie, X., and Xiao, N. (2018a). Experimental Study and Failure Criterion Analysis of Plain Concrete Under Combined Compression-Shear Stress. Construction Building Mater. 179, 198–206. doi:10.1016/j.conbuildmat.2018.05.242

CrossRef Full Text | Google Scholar

Zamri, N. F., Mohamed, R. N., and Ibrahim, I. S. (2020). The Fibre Shear Supplement of Precast Beam-Half Joints Using Steel Fibre Self-Compacting concrete. Mater. Today Proc. 39, 988–992. doi:10.1016/j.matpr.2020.04.577

CrossRef Full Text | Google Scholar

Zhao, H., Sun, W., Wu, X., and Gao, B. (2015). The Properties of the Self-Compacting Concrete with Fly Ash and Ground Granulated Blast Furnace Slag mineral Admixtures. J. Clean. Prod. 95, 66–74. doi:10.1016/j.jclepro.2015.02.050

CrossRef Full Text | Google Scholar

Zhu, W., Gibbs, J. C., and Bartos, P. J. M. (2001). Uniformity of In Situ Properties of Self-Compacting Concrete in Full-Scale Structural Elements. Cement and Concrete Composites 23 (1), 57–64. doi:10.1016/s0958-9465(00)00053-6

CrossRef Full Text | Google Scholar