Multi-Terminal Nanotube Junctions: Modeling and Structure-Property Relationship

1 Introduction

Carbon based nano-materials (graphene, nanotubes, and carbon fibers) have excellent mechanical (Chopra et al., 1995; Iijima et al., 1996), thermal (Che et al., 2000) and electrical (Bandaru, 2007) properties, yet are extremely lightweight that makes them ideal for nanoscale system design and applications (Suehiro et al., 2003; Zhang et al., 2006; Jensen et al., 2007; Mundra et al., 2014). Carbon nanotubes’ (CNTs’) -cylindrical honeycomb structures made up of Carbon atoms bonded in sp² hybridization, are popular for their high thermal conductivity, strength, modulus, and aspect ratio. They have been used for the fabrication of nano electronic devices (Yao et al., 1999; Chernozatonskii, 2003), composites (Haggenmueller et al., 2000) and cooling fins (Kordás et al., 2007). In a 3D CNT based structural forms, they are often observed as interconnecting nodes (junctions) of varying characteristics. These junctions have fascinating features that are different from the pristine CNTs (Wei and Liu, 2008) and are suitable for constructing nano-level building blocks with modulated mechanical, thermal, and electrical properties.

Recent experimental studies towards successful synthesis of nanotube based nano-porous foams (Hashim et al., 2012; Wang et al., 2013; Wang et al., 2015; Ozden et al., 2016) have motivated the scientific community on the controlled fabrication of foam structures such as ligament node, pore densities, and interconnected CNT distributions. The structure-property relationship of such junctions have been of great interest as it plays an important role in the macroscopic characteristics of designed materials and composites. Experimentally, understanding the correlation between the junction topology and micro-/macro-scropic properties is extremely difficult due to the length scales involved (∼nm), as it requires designing extremely sophisticated instrumental techniques (Yang et al., 2017) to quantitatively characterize the junction. On the other hand, computational and numerical studies can offer guidance to material processing scientists on the suitable approaches for the junction fabrication specifications to attain desired properties.

The initial step in the computational study is the construction of topologically accurate atomistic models of CNT junctions. In literature, a number of different approaches have been adopted to develop and model CNT junctions, most of which are based on molecular dynamics (MD) simulations (Menon and Srivastava, 1997; Krasheninnikov et al., 2002; Jang et al., 2004; He et al., 2009). As MD based procedures for constructing junctions require considerable computational resources as well as the use of specific force-fields that allow bond-breaking, alternative strategies are needed to develop accurate junction models. In our previous communication (Nakarmi et al., 2018), we presented an efficient methodology to create topologically accurate three terminal (3T-) junction models based on computer-aided design (CAD) based optimization and re-meshing techniques that uses dual (triangular mesh) (Patanè and Spagnuolo, 2003) of the regular hexagonal mesh. Here, we use similar procedure to create more hierarchical and complex structures including four terminal (4T-) and six terminal (6T-) nanotube junction architectures.

The structure-property relationship of the created junction models are characterized using MD simulations. Here, two key properties, i.e., thermal conductivity and mechanical strength, and their relationship with the topology of the junction are studied. The thermal conductivity of the nanostructures is determined using reverse non-equilibrium molecular dynamics simulation (RNEMD) heat bath method, whereas the tensile and compressive strengths are calculated using the traditional tensile and compression tests.

The organization of the manuscript is as follows. The methodology for the development of multi-terminal junctions are presented in Section 2. In Section 3, thermal and mechanical properties of the nanostructures in relation to the topological features are discussed. All the CAD models in this work are developed using Rhinoceros 5 by Robert McNeel and Associates (McNeel, 2012), and using Grasshopper (Version 0.9.0076) (McNeel, 2013), the algorithmic based modeler for Rhinoceros 5. The MD simulations are carried out using LAMMPS (Plimpton et al., 2007) and OVITO (Stukowski, 2010) is used for nanostructure visualization.

2 Development of Multi-Terminal Junctions

The simplest possible junction, a two terminal (2T-) junction, can be created between two CNTs when they are connected end-to-end with a single heptagon-pentagon pair of defects (Dunlap, 1994). The 2T-junctions can be categorized into metal/semiconductor, metal/metal or semiconductor/semiconductor based on the chirality of the connected CNTs. However, with only two terminals, 2T-junctions are less flexible compared to the multi-terminal devices, especially in electronics, where the third terminal can be used for switching, power gain, or current modulating properties as in nano-transistors (Chernozatonskii, 2003).

In context of multi-terminal junctions, a number of approaches, often MD simulations, have been adopted to generate atomistic models and study structure-property relationships. Menon and Srivastava (1998) created Y-shaped 3T-Junction with pentagon-octagon pairs using general tight binding molecular dynamics (TBMD) simulations. Krasheninnikov et al. (2002), Jang et al. (2004) and Piper et al. (2011) generated X-shaped 4T-junction by CNT welding using classical MD. Furthermore, 3T- and 4T-junctions have also been generated by self-assembling graphene nanoribbons (He et al., 2009) and TBMD simulations (Menon et al., 2003; Ponomareva et al., 2003; Xu et al., 2008). MD simulations require the system to be equilibrated for considerable amount of time and hence are computationally expensive. Also, it is extremely difficult to fomulate complex nanostructures like 6T-junctions and macro-scale nanotube architectures using MD simulations. An alternative approach to creating nanotube junctions is a CAD based primal/dual mesh optimization scheme, where triangular meshes of a hexagonal meshes called ‘primal/dual’ meshes are generated first (Patanè and Spagnuolo, 2003; Nakarmi et al., 2018) and was reported in our earlier communication (Nakarmi et al., 2018). A regular triangular mesh is ideal for modeling carbon nanotube systems since, the dual graph (refer Section 2.1) of the triangular mesh results in a hexagonal (honeycomb) mesh representing the sp² nature of Carbon nanostructures.

2.1 Dual Mesh

In dual graph theory, the dual of the mesh is another mesh with its vertices obtained from the centroids of the original mesh. The dual of a regular triangular mesh is a hexaongal mesh and vice versa. Mathematically, for a triangular mesh I ( f, e, v, c), where f, e, v, and c represent faces, edges, vertices and the connectivity relations respectively, the dual of I is the mesh I′(e′, v′, c′) created such that each vertex v′* in I′ corresponds to each face f * in I by the relation (Patanè and Spagnuolo, 2003):

$v\prime *(\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{p}\mathrm{o}\mathrm{n}\mathrm{d}\mathrm{i}\mathrm{n}\mathrm{g}\hspace{0.17em}\mathrm{t}\mathrm{o}\hspace{0.17em}\mathrm{f}\mathrm{a}\mathrm{c}\mathrm{e}\hspace{0.17em}{f}^{*})=\frac{1}{3}\sum _{i=1}^3{v}_{i,f^{*}}(1)$

Here, $v_{i,f^{*}}$ (i = 1, 2, 3) are the vertices of the triangular face f*. The vertices v′ are the centroid of the corresponding faces of the triangular mesh and the edges e′ are the connecting lines joining two vertices in I′ if the two corresponding faces in I have a common edge. The vertices v′ would represent the positions of the C-atoms and the edges e′ represents the C-C bonds.

There are many advantages of using triangular mesh over hexagonal mesh. Triangular meshes are easy to construct, manipulate, and optimize compared to the hexagonal meshes. Furthermore, many mesh optimization and remeshing tools are available for a triangular mesh and it is always easy to convert triangular mesh to hexagonal mesh and vice versa by the dual graph technique. Therefore, triangular meshes have been used in this work to construct complex nanotube structures like junctions. For a SWCNT model, the corresponding dual mesh is shown in Figure 1. The edges of the generated triangular mesh that will results in hexagonal CNT mesh after dual have lengths equal to $a=2\times 1.42cos(\pi /6)=2.45$Å where 1.42 Å represents C-C bond length.

FIGURE 1

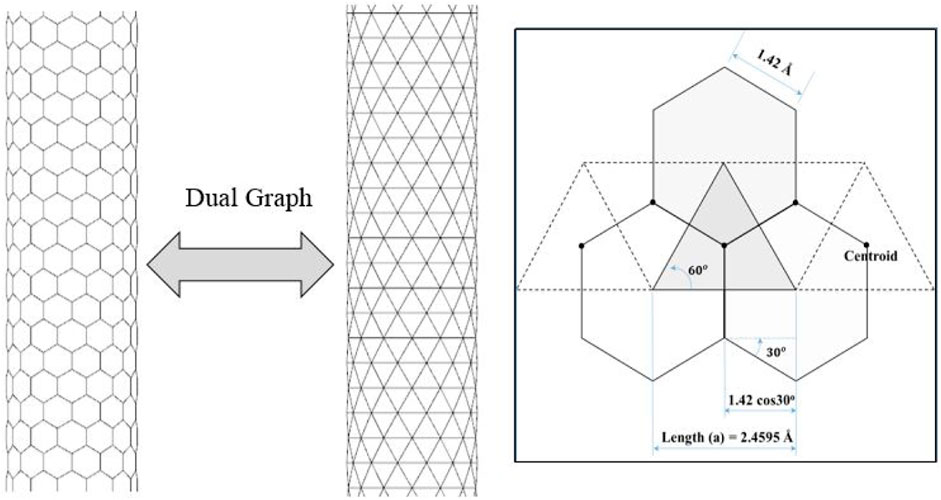
FIGURE 1. Dual mesh representation of (14,0) SWCNT. The inset figure shows the determination of the length of the regular triangular mesh.

2.2 Junction Topology

The C-C bonds in a closed convex nanostructures follow the Euler’s rule of polyhedron given by Eq. 2 (Crespi, 1998), where 2–2 G = χ is the Euler characteristic and G is the genus that relates to the number of holes in the geometry.

$Faces(F)+Vertices(V)-Edges(E)=2-2Genus(G)(2)$

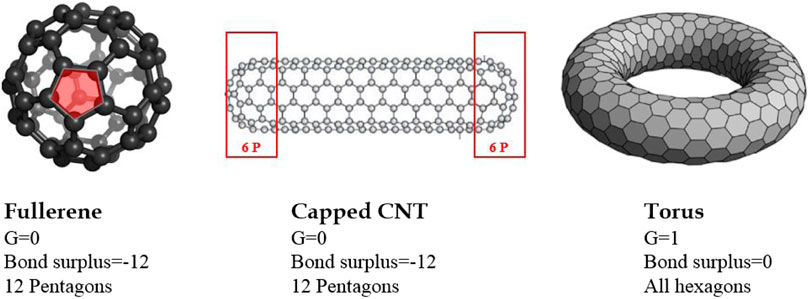
In such cases, the bond surplus in these nanostructures are indicated by 12 (G − 1) = 6 (E − F − V) (Crespi, 1998), where the bond surplus is the “net excess or deficit” of non-hexagonal defects. For example, a heptagon (or pentagon) increases (or decreases) the bond surplus by 1 and the net bond surplus of the system would depend on the total number of heptagons and pentagons at the junction. The bond surplus and the associated number of defects for some of the polyhedron nanostructures are shown in Figure 2. A single walled carbon nanotube (SWCNT) with two closed end caps has a bond surplus of −12 referring to requirement of at least 12 pentagons (6 on each end) to construct the capped SWCNT.

FIGURE 2

FIGURE 2. Bond surplus and the associated defects in the polyhedron nanostructures.

In case of multi-terminal junctions, it is difficult to determine the bond surplus directly. The combination of two 3T-junctions can form a geometrical figure with genus G = 2 as shown in (Figure 3A). Each 3T-junction shares a bond surplus of +6, hence, there are at least 6 heptagons in a 3T-junction (Crespi, 1998; Nakarmi et al., 2018). Similarly, a 4T-junction and a 6T-junction can be considered to be part of a geometry with G = 2 and G = 3, respectively. Thus, the bond surplus for 4T- and 6T-junctions are respectively +12 (Crespi, 1998; Nakarmi et al., 2018) and +24 (Figures 3B,C). The bond surplus and hence the number of defects increases dramatically with increase in the number of interconnected arms in the junction. A topologically accurate junction should satisfy the aforementioned bond surplus values.

FIGURE 3

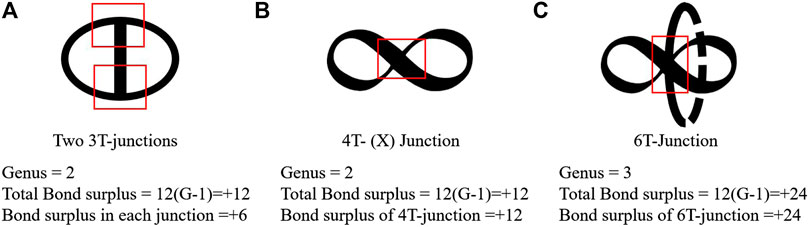
FIGURE 3. Schematic to determine the genus and bond surplus of geometrical figures of (A) 3T-junction (B) 4T-junction and (C) 6T-Junction.

2.3 Atomistic Modeling of Multi-Terminal Junctions

The methods for generating 3T-Junctions have been discussed in detail in our previous communication (Nakarmi et al., 2018). Our previous study was limited to the development of utmost 3T-junctions (Nakarmi et al., 2018) and associated configurations like staggered 4T-junctions, etc. However in the current work we are able to extend the computational procedure to develop perfect orthogonal 4T- and 6T-junctions.

The procedures involved for creating 4T-junctions are highlighted in Figure 4. The initial step involves constructing regular triangular dual meshes from SWCNT hexagonal mesh. Two of such triangular meshes are interconnected at the desired angle (90°). The nodes around the junctions which are closer than 2.45 Å are removed to ensure that the dual mesh will not have C-atoms closer than 1.42 Å. The resulting geometry is patched with a new randomly generated mesh. The remeshing and optimization strategies are adopted from Refs (Botsch and Kobbelt, 2004; Nakarmi et al., 2018). to obtain uniform triangular meshes with a target length 2.45 Å. The dual of the triangular mesh indicates the position of the C-atoms in the 4T-Junction. The junction is subjected to the molecular minimization (MM) using conjugate gradient (CG) to minimize the potential energy of the system.

FIGURE 4

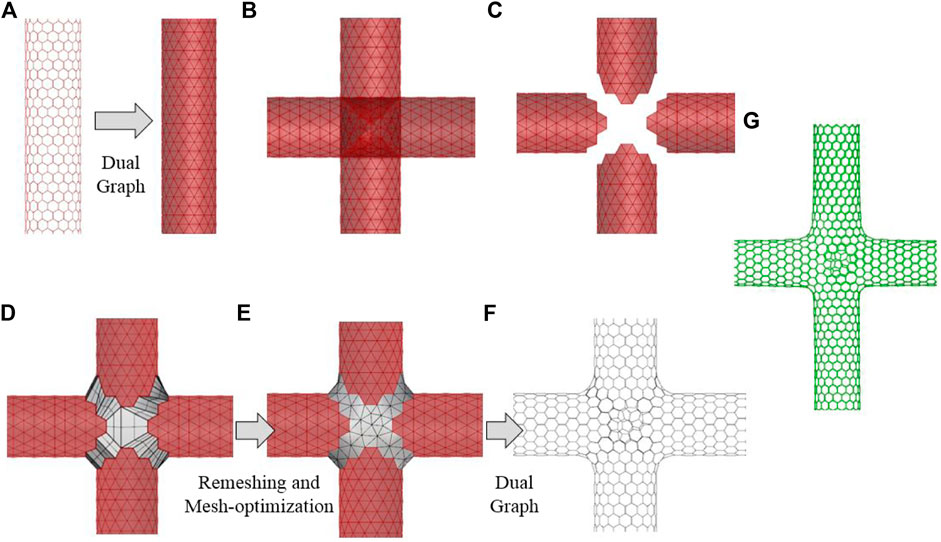
FIGURE 4. Procedure for constructing orthogonal 4T-Junction. (A) Dual triangular mesh of (16,0) nanotubes. (B) Right angle interconnection of the triangular mesh. (C) Removal of mesh vertices closer than 2.45 Å (D) Stitching the void surface with randomly generated mesh. (E) Remeshing and mesh optimization with target length 2.45 Å. (F) Dual of the final triangular mesh. (G) Atomistic model of 4T-Junction after molecular minimization (MM).

Similar methods are also used to create 6T-Junction (refer Figure 5). Here, we start with a dual triangular mesh consisting of interconnected six mutually orthogonal arms. Due to complex nature of the 6T-junction, specific region (box in Figure 5A) in the junction is chosen as a whole and re-meshing and optimization strategies are adopted in the selected region. The larger the size of the selected region, larger will be the number of defects in the junction. The dual of the optimized triangular mesh is constructed to obtain the atomistic configurations of the 6T-junction. Finally, the potential energy is minimized.

FIGURE 5

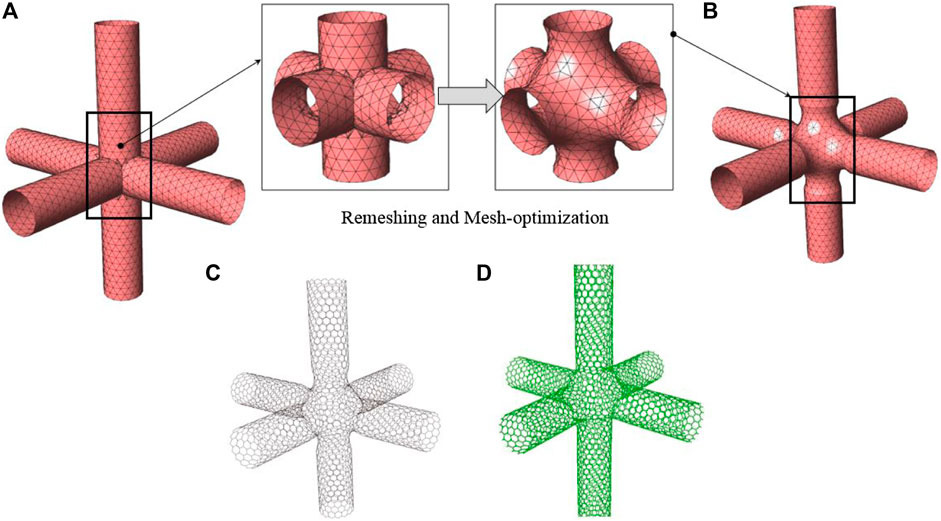
FIGURE 5. Procedure for constructing orthogonal 6T-Junction. (A) Dual triangular mesh of (16,0) nanotubes with six directly connected arms. The inset images are before and after snapshots of remeshing and mesh optimization procedures. (B) Regular triangular mesh with mesh length 2.45 Å. (C) Dual graph of the regular triangular mesh with each vertex representing position of carbon atoms. (D) Atomistic model of 6T-Junction after molecular minimization (MM).

The atomistic models of orthogonal 3T-, 4T-, and 6T-Junctions are presented in Table 1 with total number of defects and per-atom potential energies. The bond surplus of 3-, 4- and 6- Junctions are +6, +12, and +24, respectively which are valid values for the corresponding junction types based on the discussion in Section 2.2. These junctions have PE/atom comparable to pristine SWCNT (-7.7613 eV/atom) (Nakarmi et al., 2018), thereby ensuring that the created junctions are thermodynamically stable. The models of these junctions can be used in different atomistic simulations to predict their material characteristics.

TABLE 1

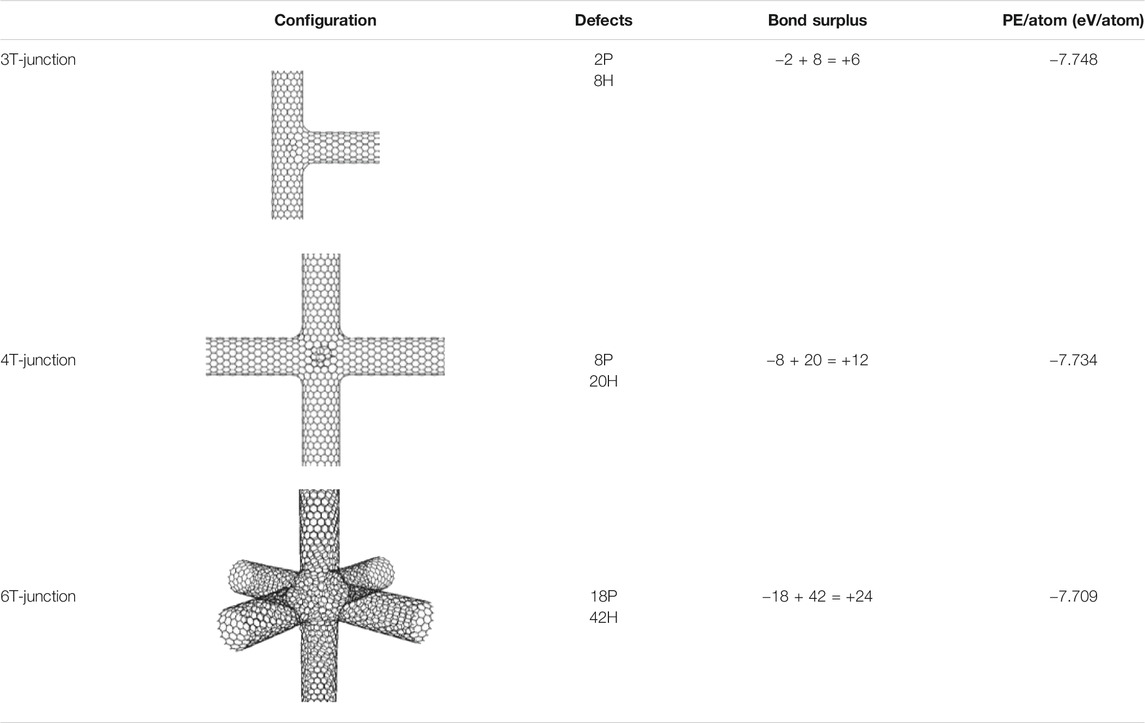
TABLE 1. Defects and PE/atom of different junction configurations. (Defects: P=Pentagon, H=Heptagons).

3 Results and Discussion

Here, the atomistic models of the multi-terminal junction configurations were used to study the structure-property relationship by determining the topological effect of the junctions on the thermal and mechanical properties.

3.1 Thermal Conductivity (k)

At the nanoscale, CNTs demonstrate a broad range of thermal conductivity (k) values, ranging from few hundreds to as high as 6,600 Wm⁻¹K⁻¹ (Berber et al., 2000). This wide variability of thermal conductivity is often attributed to the size of the CNTs (Nakarmi and Unnikrishnan, 2017), their deformation states (Nakarmi and Unnikrishnan, 2018a), temperature (Osman and Srivastava, 2001), presence of defects (Nakarmi and Unnikrishnan, 2019), and measurement methods (Salaway and Zhigilei, 2014). In multi-terminal junctions, thermal transport is expected to be governed by the number of connected arms, defects types, and their distribution around the junction, as well as the size and type of CNTs (chirality) that form the junction. A proper understanding of the effect of these parameters is critical for designing thermal management systems with desired characteristics. In this section, we are interested in characterizing the effect of defects and junction topology on the longitudinal thermal conductivity of CNT nanostructure with multi-terminal junctions.

The thermal conductivity of nanotube junction is determined using Heat Bath method (Plimpton et al., 2007; Walker, 2012) (see Figure 6), a RNEMD approach using the widely popular MD simulator LAMMPS (Plimpton et al., 2007).

FIGURE 6

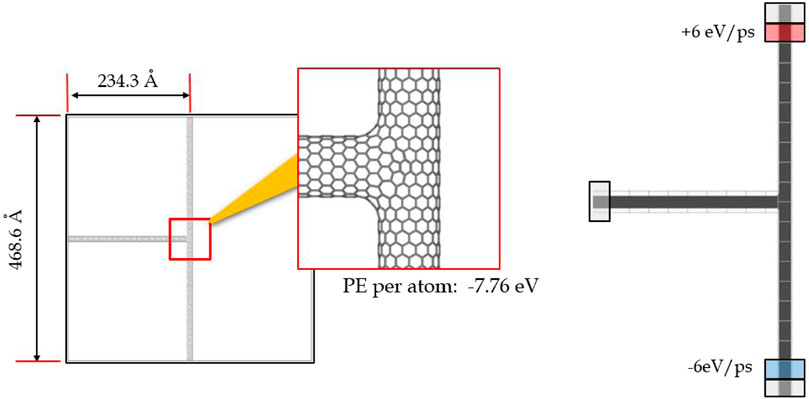
FIGURE 6. Schematic diagram showing RNEMD method for determining thermal conductivity of 3T-Junction.

AIREBO (Stuart et al., 2000) potential is used for modeling the C-C interactions. The time-step for the simulation is taken as 0.001 ps. Prior to thermal conductivity simulations, the potential energy of the system is minimized using conjugate gradient (CG) method. Then, the entire simulation setup is sub-divided into bins of size 20 Å. The end bins near the boundary are fixed such that no perturbation of the atoms are allowed, so as to ensure unidirectional heat flow within the system. Thereafter, the temperature of atoms in the remaining bins are raised to 300 K and equilibrated for 200 ps in NVT (canonical) ensemble. Once the temperature of the system is equilibrated, a pre-determined amount heat flux (q = 6 eV/ps) is added to and removed from the previously designated hot and cold regions respectively for the next 500 ps. This one-dimensional heat flow from hot to cold region creates a thermal gradient along the length of the nanostructure (refer Figure 7).

FIGURE 7

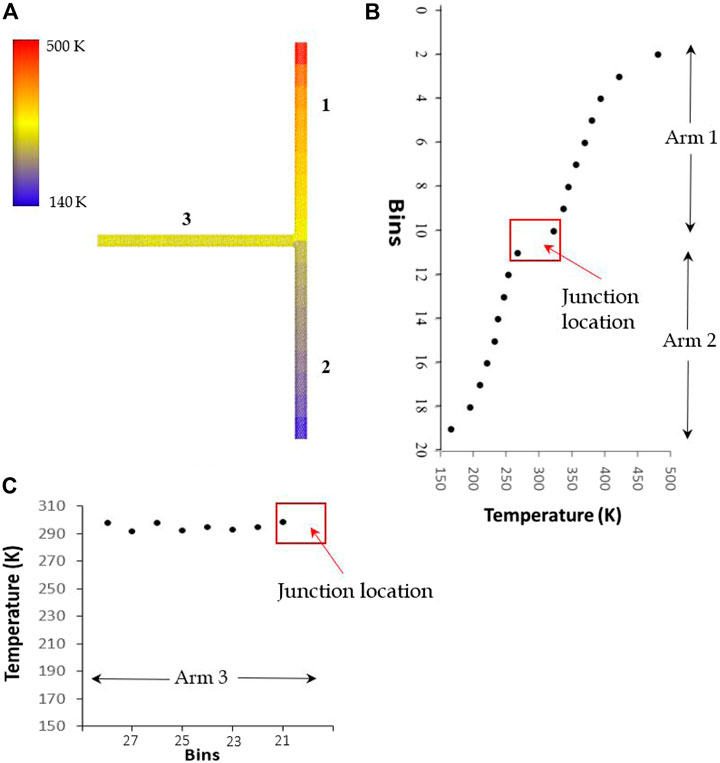
FIGURE 7. Thermal gradient in a 3T-Junction due to thermal excitation along the longitudinal direction. (A) Thermal gradient in the 3T junction represented by color scales. (B) Temperature profile along arms 1 and 2. (C) temperature profile along arm 3.

The time dependent moving average of the thermal gradient is measured for the next 500 ps monitoring the stability of the system. The longitudinal thermal conductivity k of the nanotube junction is then calculated using Fourier Law (Eq. 3).

$k=\frac{q}{A}\frac{1}{\mathrm{\Delta }\text{T}/\mathrm{\Delta }x}(3)$

Where, q, A and ΔT/Δx are the heat flow rate, cross sectional area of the tube [assuming 3.40 Å nanotube thickness (Osman and Srivastava, 2001)], and the temperature finite difference, respectively. The similar approach of determining the thermal conductivity has been used and validated for the pristine SWCNTs in our previous studies (Nakarmi and Unnikrishnan, 2017; Nakarmi et al., 2017; Nakarmi and Unnikrishnan, 2018a; Nakarmi and Unnikrishnan, 2018b; Nakarmi and Unnikrishnan, 2019; Nakarmi and Unnikrishnan, 2020). Here, the thermal conductivity determined for the 3T-junction from the thermal gradient shown in Figure 7 is 144.32 Wm⁻¹K⁻¹. It can be seen that there is 26.60% reduction in longitudinal thermal conductivity of the 3T-junction compared to pristine SWCNT of the same size (Length 468.60 Å, Diameter 10.96 Å, and k = 196.63 Wm⁻¹K⁻¹) which is attributed to the increased thermal gradient at the junction site (refer Figure 7). The presence of defects and the change in topology due to the connection of the third arm, causes the phonons to scatter at the junction, thereby contributing to the significant reduction of the thermal conductivity. Similar decrease in thermal conductivity due to other types of defect scattering along the SWCNT direction has been reported previously as well (Varshney et al., 2011). Next, we discuss the effect of number of junction and junction terminals on the longitudinal heat transfer across the junction.

3.1.1 Effect of Junction Population and Junction Terminals

Figure 8 presents the effect of number of junctions and the junction angle on longitudinal thermal conductivity of the nanostructure. Nine different cases are studied varying the junction angle (30°, 60°, and 90°) and the number of junction up to 3, and the resultant thermal conductivity values are compared with the thermal conductivity of pristine SWCNT of same length. It should reiterated that the hot and cold regions are along the main vertical arm (similar to previous discussion), whereas no heat is added to or removed from the extend side arms (as in Figure 7B). Among the cases studied (i.e., different angles), 60° junctions were observed to have least reduction in thermal conductivity and is attributed to fewest defects at the junction (refer Table 2) compared to other junction angles. In addition, with an increase in the number of junctions (thus more scattering) along the longitudinal direction, there is an increase in thermal gradient at each of the junction site, thereby further reducing the thermal conductivity as shown in Figure 8.

FIGURE 8

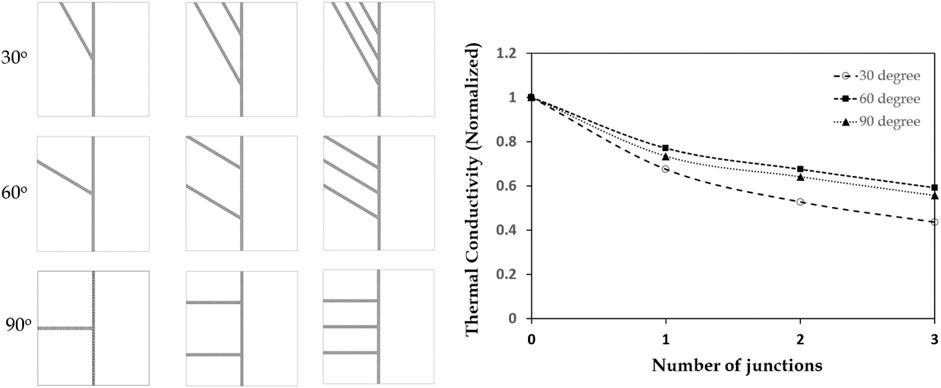
FIGURE 8. Effect of junction population on thermal transport of different angle 3T-Junctions. The figures on the left indicates nine junction configurations with rows representing 30^o, 60^o, and 90^o junctions, and columns representing one, two and three 3T-Junctions along the vertical direction. The graph on the right represents the thermal conductivity of the junction configurations normalized with respect to pristine SWCNT having the same vertical lengths.

TABLE 2

TABLE 2. Total number of defects of Junctions with different contact angles.

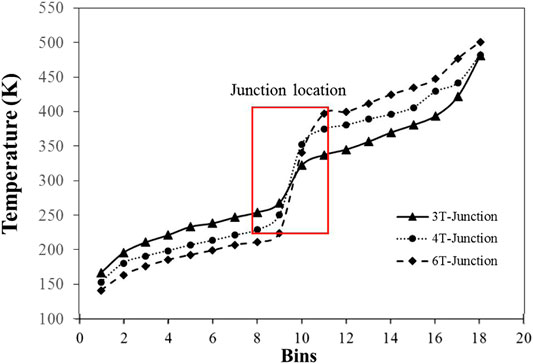
The effect of number of terminals, i.e., number of CNTs at a nodal junction on the longitudinal heat transfer is studied next via determining the thermal conductivity of a 4T- and a 6T-Junction. In this context, Figure 9 shows the thermal gradient of 3T-, 4T-, and 6T-junctions for the same value of applied heat flux (q = 6 eV/ps). At the junction (highlighted region in Figure 9), there is a sharp jump in the temperature profile, the gradient of which increases as the number of terminals increases thereby significantly reducing the overall thermal conductivity of the nanostructure.

FIGURE 9

FIGURE 9. Thermal gradient along the longitudinal direction of the junctions.

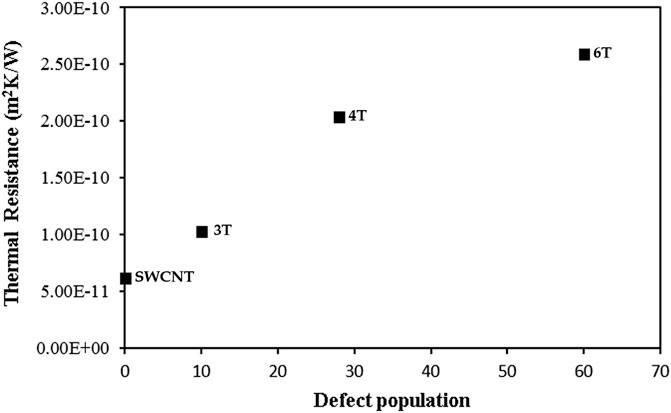
Figure 10 compares the effective thermal conductivity of different junctions with that of pristine CNT structures of the same length. It can be seen that an increase in the number of terminals results in increasing number of defects, and thereby increasing amount of phonon scattering at the junction leading to a notable decrease in thermal conductivity. To further confirm the hypothesis of increased phonon scattering, we also calculated the interface thermal resistance of different junctions (3, 4, and 6T) and are plotted in Figure 11. As can be seen from the figures, the thermal resistance at the junction interface increases notably due to presence of additional non-hexagonal defects as is also noted in Figure 10.

FIGURE 10

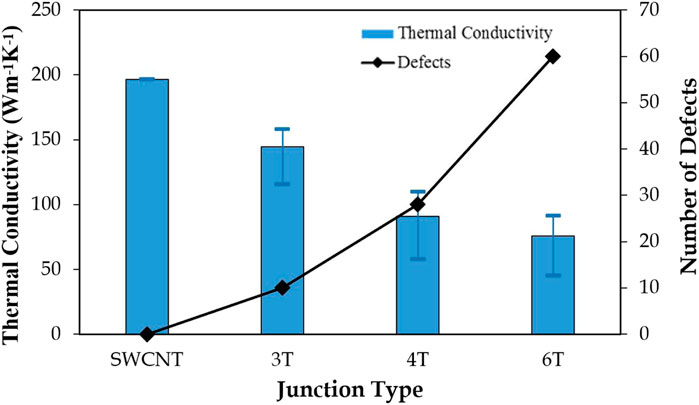
FIGURE 10. Thermal conductivity and total number of defects in different types of junctions. The bar diagram presents the mean value of the thermal conductivity k with the error bar representing k_min/k_max (number of simulations for each case = 8).

FIGURE 11

FIGURE 11. Thermal resistance and defect population in multi-terminal junctions.

3.2 Strength of Multi-Terminal Carbon Nanotubes Junction Nanostructures

Besides being highly conductive, CNT based structures have very high modulus and tensile strength. Similar to thermal conductivity, the strength and modulus of such structures are also found to be dependent upon their structural properties such as defects, junction types, etc. In this context, it is important to study and understand the inter-relationships between junction topology, defects concentration, and the corresponding change in the mechanical properties.

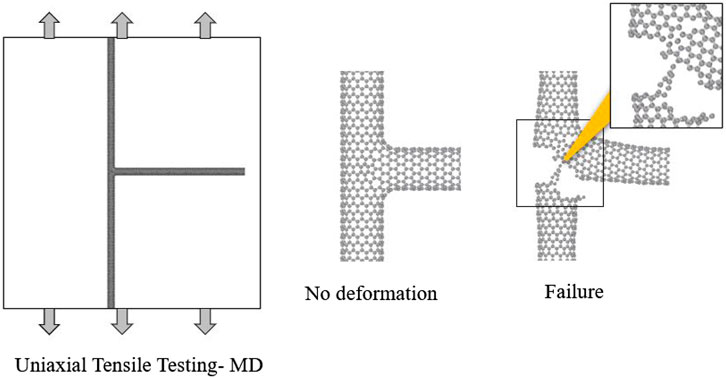
In this context, the tensile and compressive strength of the fuzed CNT nanostructures are determined from MD simulation using conventional unidirectional tension/compression tests (refer Figure 12). Here, AIREBO potential with a modified cut-off radius of 2 Å is used in the simulation in order to prevent non-physical strain hardening (Dilrukshi et al., 2015). The simulations are performed with a time-step of 0.0005 ps. Prior to tensile/compression simulations, minimized atomic configurations of the junctions are subjected to energy equilibrium for 50 ps at 1 K in NPT ensemble. Thereafter, the system is deformed at a uniform strain rate of 0.001/ps and the stress values corresponding to the deformed states are measured.

FIGURE 12

FIGURE 12. 3T-Junction under tensile loading and the tensile strain is applied until failure.

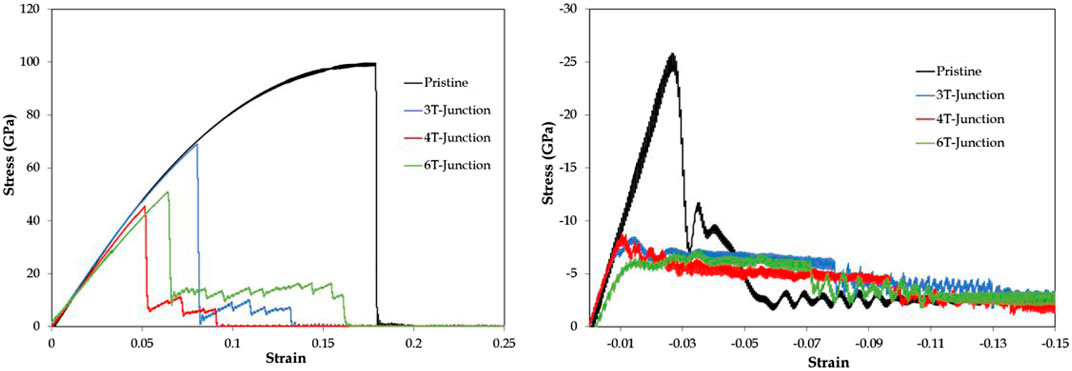
The stress-strain curves for the 3T-Junctions (60°, 90°) are presented in Figure 13 and compared with that of pristine zig-zag SWCNT. The tensile strength and the failure strain of a pristine zig-zag SWCNT as obtained from the simulation are 99.37 GPa and 17.6%, respectively. It can be seen that all studied junctions have reduced both the tensile strength and the failure strain. The respective strength of 60° and 90° junctions are 78.41 and 68.43 GPa, and the corresponding failure strains are 9.5 and 7.8%. Similar degradation in mechanical strength has been observed in nanotube-graphene junction as compared to pristine nanotubes (Yang et al., 2017) and was attributed to the topology as well as the number of defects around the junction. The lower tensile strength in a 90° junction can be attributed to the larger number of defects compared to a 60° junction. Topological defects in the structures were observed to be the locations of higher stress concentrations (refer Figure 14) initiating the localized failure that propagates through the material and thereby reducing its strength. In the 90° junction, the larger defect population along with the presence of pentagons causes high stress concentration and early failure initiation resulting in lower ultimate strengths. On the other hand, in the compressive regime, both junctions were found to have similar responses as the buckling of the structures occur at almost the same time.

FIGURE 13

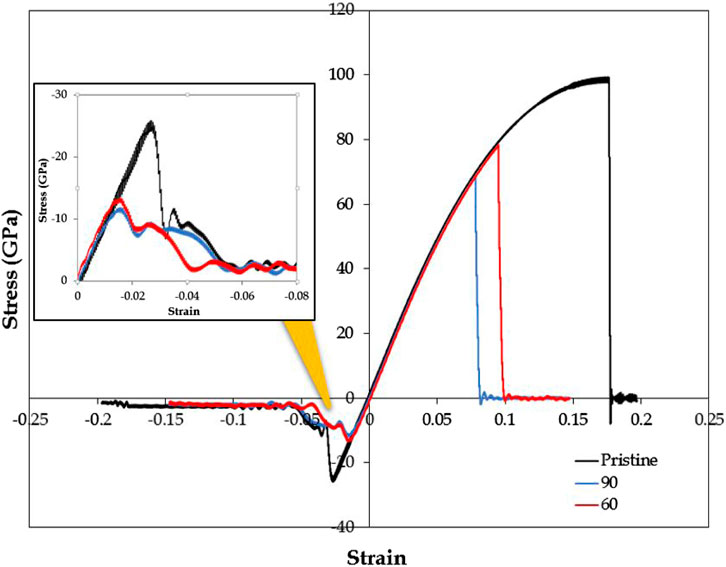
FIGURE 13. Stress-strain curve of a 3T-junction compared with the same size pristine SWCNT (at 1 K).

FIGURE 14

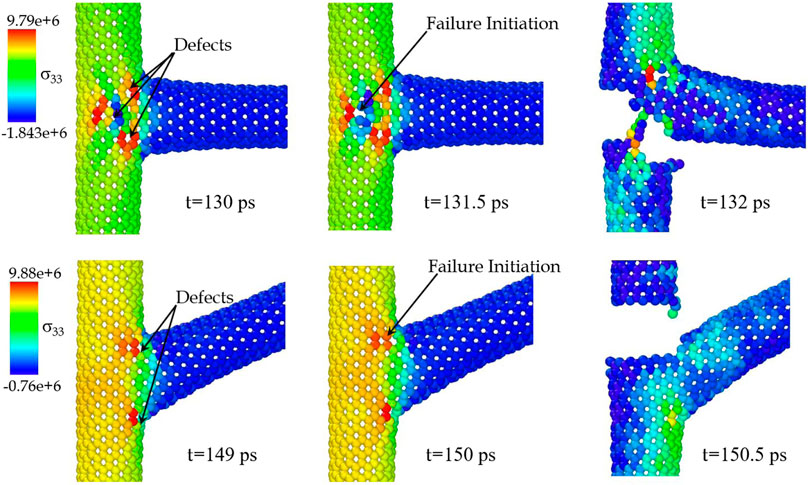
FIGURE 14. Atomic stresses in 3T-Junction during failure due to uniaxial tensile loading. The color map represents per-atom stress along vertical direction (σ₃₃, bars.ų) at 1 K temperature.

Figure 15 depicts the comparative stress-strain plots of 3T-, 4T- and 6T-junctions. The ultimate strength of 4T- and 6T-junctions are 45.50 and 50.98 GPa, respectively. Here, although 6T-junction have more defects compared to 4T-junctions, the presence of two extra arms provides enhanced rigidity resulting in higher strength. This can also be seen in Figure 16. The failure initiates early in 6T-junction (t = 95 ps) compared to 4T-junction (t = 98 ps); however, the structural stiffness of the 6T-junction prevents the propagation of the crack until t = 116 ps (t = 104.5 ps for 4T-junction). This results in slightly higher tensile strength and failure strain in 6T-junction as depicted in Figure 15.

FIGURE 15

FIGURE 15. Stress-strain curve of a multi-terminal junction.

FIGURE 16

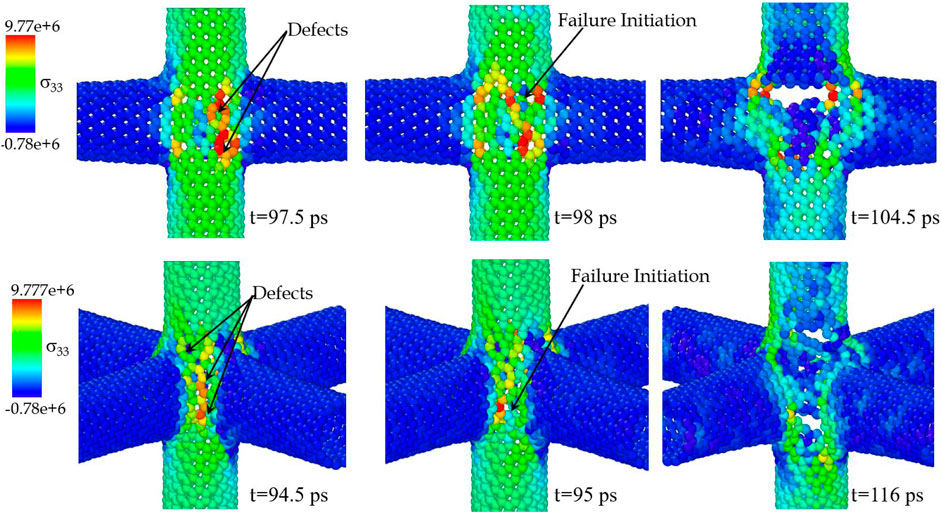
FIGURE 16. Atomic stresses in multi-terminal junctions during failure due to uniaxial tensile loading. The color map represents per-atom stress along vertical direction (σ₃₃, bars.ų) at 1 K temperature.

4 Conclusion

Efficient methods for generating highly sophisticated multi-terminal junctions are presented. The method uses CAD based optimization and remeshing of the triangular mesh, which is the dual of the hexagonal mesh representing the nanotube structures. With this method, we are able to create topologically accurate computational models of up to six terminal (6T)-junctions that can be used as building blocks to fabricate complex nano-architectures with desired thermal and mechanical characteristics. This methodology can easily be extended to more complex junctions, such as several CNTs fusing at an arbitrary angles at a single node.

Furthermore, the effect of structural features of the junction on the thermal and mechanical properties are also studied via MD simulations. A significant reduction in the thermal conductivity and mechanical strength of the nanotube junctions compared to pristine structures was observed, which is attributed to the presence and degree (abundance) of non-hexagonal defects. These defects causes discontinuity in the temperature profile around the junction, increasing phonon scattering, thereby reducing the thermal conductivity. Similarly, high stress concentration in the defects were found to be the key cause that initialized localized failure resulting in the lowering of fuzed nanostructures’ mechanical strength. We foresee that modulating the defect concentration (type and number of non-hexagonal rings) as well as their orientation (relative CNT angle) in multi-configurational CNT junctions can be used to tailor the overall thermal transport capabilities and the mechanical strengths of 3D carbon nanostructure, such as CNT based nano-porous foams (Kholmanov et al., 2015; Lu et al., 2020), nanoscale fiber reinforced composites, and light weight mechanical shock absorbers (Nakarmi et al., 2018; Nakarmi, 2020).

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

VU, VV, and AR contributed to the initial conception and SN, VU contributed to the design and analysis of this study. VV and AR contributed to the discussion, and all authors contributed to manuscript revision, read, and approved the submitted version.

Author Disclaimer

The U.S. Government is authorized to reproduce anddistribute reprints for Governmental purposes notwithstandingany copyright notation thereon. The views and conclusionscontained herein are those of the authors and should not beinterpreted as necessarily representing the official policies orendorsements, either expressed or implied, of the Air ForceResearch Laboratory or the U.S. Government.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors VU, VV, and AR acknowledge the support of Air Force Research Laboratory Minority Leaders Research Collaborative Program under agreement number FA8650-20-2-5853. VU would also like to acknowledge the support of Kilgore Research grant from West Texas A&M University. Some portions of this research were also conducted with high performance research computing resources provided by Texas A&M University (https:/hprc.tamu.edu).

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2021.692988/full#supplementary-material

References

Bandaru, P. R. (2007). Electrical Properties and Applications of Carbon Nanotube Structures. J. Nanosci. Nanotechnol. 7 (4-1), 1239–1267. doi:10.1166/jnn.2007.307

CrossRef Full Text | Google Scholar

Berber, S., Kwon, Y.-K., and Tománek, D. (2000). Unusually High thermal Conductivity of Carbon Nanotubes. Phys. Rev. Lett. 84 (20), 4613–4616. doi:10.1103/physrevlett.84.4613

PubMed Abstract | CrossRef Full Text | Google Scholar

Botsch, M., and Kobbelt, L. (2004). A Remeshing Approach to Multiresolution Modeling, Proceedings of the 2004 Eurographics/ACM SIGGRAPH symposium on Geometry processing, Nice, France, July 8-10, 2004. New York, NY: Association for Computing Machinery, 185–192.

CrossRef Full Text | Google Scholar

Che, J., Çagin, T., and Goddard, W. A. (2000). Thermal Conductivity of Carbon Nanotubes. Nanotechnology 11 (2), 65–69. doi:10.1088/0957-4484/11/2/305

CrossRef Full Text | Google Scholar

Chernozatonskii, L. (2003). Three-terminal Junctions of Carbon Nanotubes: Synthesis, Structures, Properties and Applications. J. Nanoparticle Res. 5 (5-6), 473–484. doi:10.1023/b:nano.0000006154.15176.0f

CrossRef Full Text | Google Scholar

Chopra, N. G., Benedict, L. X., Crespi, V. H., Cohen, M. L., Louie, S. G., and Zettl, A. (1995). Fully Collapsed Carbon Nanotubes. Nature 377 (6545), 135–138. doi:10.1038/377135a0

CrossRef Full Text | Google Scholar

Crespi, V. H. (1998). Relations between Global and Local Topology in Multiple Nanotube Junctions. Phys. Rev. B 58 (19), 12671. doi:10.1103/physrevb.58.12671

CrossRef Full Text | Google Scholar

Dilrukshi, K. G. S., Dewapriya, M. A. N., and Puswewala, U. G. A. (2015). Size Dependency and Potential Field Influence on Deriving Mechanical Properties of Carbon Nanotubes Using Molecular Dynamics. Theor. Appl. Mech. Lett. 5 (4), 167–172. doi:10.1016/j.taml.2015.05.005

CrossRef Full Text | Google Scholar

Dunlap, B. I. (1994). Relating Carbon Tubules. Phys. Rev. B 49 (8), 5643–5651. doi:10.1103/physrevb.49.5643

CrossRef Full Text | Google Scholar

Haggenmueller, R., Gommans, H., Rinzler, A., Fischer, J. E., and Winey, K. (2000). Aligned Single-wall Carbon Nanotubes in Composites by Melt Processing Methods. Chem. Phys. Lett. 330 (3-4), 219–225. doi:10.1016/s0009-2614(00)01013-7

CrossRef Full Text | Google Scholar

Hashim, D. P., Narayanan, N. T., Romo-Herrera, J. M., Cullen, D. A., Hahm, M. G., Lezzi, P., et al. (2012). Covalently Bonded Three-Dimensional Carbon Nanotube Solids via boron Induced Nanojunctions. Sci. Rep. 2, 363. doi:10.1038/srep00363

PubMed Abstract | CrossRef Full Text | Google Scholar

He, L., Lu, J.-Q., and Jiang, H. (2009). Controlled Carbon-Nanotube Junctions Self-Assembled from Graphene Nanoribbons. small 5 (24), 2802–2806. doi:10.1002/smll.200900911

PubMed Abstract | CrossRef Full Text | Google Scholar

Iijima, S., Brabec, C., Maiti, A., and Bernholc, J. (1996). Structural Flexibility of Carbon Nanotubes. J. Chem. Phys. 104 (5), 2089–2092. doi:10.1063/1.470966

CrossRef Full Text | Google Scholar

Jang, I., Sinnott, S. B., Danailov, D., and Keblinski, P. (2004). Molecular Dynamics Simulation Study of Carbon Nanotube Welding under Electron Beam Irradiation. Nano Lett. 4 (1), 109–114. doi:10.1021/nl034946t

CrossRef Full Text | Google Scholar

Jensen, K., Weldon, J., Garcia, H., and Zettl, A. (2007). Nanotube Radio. Nano Lett. 7 (11), 3508–3511. doi:10.1021/nl0721113

PubMed Abstract | CrossRef Full Text | Google Scholar

Kholmanov, I., Kim, J., Ou, E., Ruoff, R. S., and Shi, L. (2015). Continuous Carbon Nanotube-Ultrathin Graphite Hybrid Foams for Increased Thermal Conductivity and Suppressed Subcooling in Composite Phase Change Materials. ACS Nano 9 (12), 11699–11707. doi:10.1021/acsnano.5b02917

PubMed Abstract | CrossRef Full Text | Google Scholar

Kordás, K., Tóth, G., Moilanen, P., Kumpumäki, M., Vähäkangas, J., Uusimäki, A., et al. (2007). Chip Cooling with Integrated Carbon Nanotube Microfin Architectures. Appl. Phys. Lett. 90 (12), 123105. doi:10.1063/1.2714281

CrossRef Full Text | Google Scholar

Krasheninnikov, A. V., Nordlund, K., Keinonen, J., and Banhart, F. (2002). Ion-irradiation-induced Welding of Carbon Nanotubes. Phys. Rev. B 66 (24), 245403. doi:10.1103/physrevb.66.245403

CrossRef Full Text | Google Scholar

Lu, L., Pei, F., Abeln, T., and Pei, Y. (2020). Tailoring Three-Dimensional Interconnected Nanoporous Graphene Micro/nano-Foams for Lithium-Sulfur Batteries. Carbon 157, 437–447. doi:10.1016/j.carbon.2019.10.072

CrossRef Full Text | Google Scholar

McNeel, R. (2013). Grasshopper: Algorithmic Modeling for Rhino. Available at: http://www. grasshopper3d.com.

Google Scholar

McNeel, R. (2012). Rhinoceros, Ver., 5.0.

Google Scholar

Menon, M., Andriotis, A. N., Srivastava, D., Ponomareva, I., and Chernozatonskii, L. A. (2003). Carbon Nanotube “T Junctions”: Formation Pathways and Conductivity. Phys. Rev. Lett. 91 (14), 145501. doi:10.1103/physrevlett.91.145501

PubMed Abstract | CrossRef Full Text | Google Scholar

Menon, M., and Srivastava, D. (1997). Carbon Nanotube “T Junctions”: Nanoscale Metal-Semiconductor-Metal Contact Devices. Phys. Rev. Lett. 79 (22), 4453–4456. doi:10.1103/physrevlett.79.4453

CrossRef Full Text | Google Scholar

Menon, M., and Srivastava, D. (1998). Carbon Nanotube Based Molecular Electronic Devices. J. Mater. Res. 13 (09), 2357–2362. doi:10.1557/jmr.1998.0328

CrossRef Full Text | Google Scholar

Mundra, R. V., Wu, X., Sauer, J., Dordick, J. S., and Kane, R. S. (2014). Nanotubes in Biological Applications. Curr. Opin. Biotechnol. 28, 25–32. doi:10.1016/j.copbio.2013.10.012

PubMed Abstract | CrossRef Full Text | Google Scholar

Nakarmi, S. (2020). Atomistic Modeling and Structure-Property Relationship of Topologically Accurate Complex Nanotube junction Architectures. Ph.D. thesis. Tuscaloosa, AL: The University of Alabama.

Google Scholar

Nakarmi, S., and Unnikrishnan, V. (2018). Influence of Strain States on the thermal Transport Properties of Single and Multiwalled Carbon Nanostructures, ASME 2018 International Mechanical Engineering Congress and Exposition, Pittsburgh, PA, November 9-15, 2018. American Society of Mechanical Engineers (ASME), V009T12A043. doi:10.1115/imece2018-88620

CrossRef Full Text | Google Scholar

Nakarmi, S., and Unnikrishnan, V. (2017). Thermal Transport Properties and Interface Effects of Carbon Nanostructures, ASME 2017 International Mechanical Engineering Congress and Exposition, Tampa, FL, November 3-9, 2017. American Society of Mechanical Engineers (ASME), V009T12A058. doi:10.1115/imece2017-72475

CrossRef Full Text | Google Scholar

Nakarmi, S., and Unnikrishnan, V. U. (2019). Defect Induced Variabilities in thermal Conductivity of Nano Structures, ASME International Mechanical Engineering Congress and Exposition, Salt Lake City, UT, November 11-14, 2019, Vol. 59469. American Society of Mechanical Engineers (ASME), V009T11A036. doi:10.1115/imece2019-11654

CrossRef Full Text | Google Scholar

Nakarmi, S., and Unnikrishnan, V. U. (2020). Understanding Size and Strain Induced Variabilities in thermal Conductivity of Carbon Nanotubes: a Molecular Dynamics Study. Mech. Adv. Mater. Structures, 1–9. doi:10.1080/15376494.2020.1846232

CrossRef Full Text | Google Scholar

Nakarmi, S., Unnikrishnan, V. U., Varshney, V., and Roy, A. K. (2018). Computer-aided Design of Three Terminal (3t-) Zig-Zag Swcnt Junctions and Nanotube Architectures. Composites Sci. Techn. 166, 36–45. doi:10.1016/j.compscitech.2018.01.004

CrossRef Full Text | Google Scholar

Nakarmi, S., and Unnikrishnan, V. U. (2018). Interfacial thermal Resistance Based Effective thermal Properties of Nanocomposite Systems at Various Strain States: A Multiscale Computational Approach, in: Proceedings of the American Society for Composites—Thirty-third Technical Conference, Seattle, WA, September 24-26, 2018. doi:10.12783/asc33/26013

CrossRef Full Text | Google Scholar

Nakarmi, S., Yadav, V., and Unnikrishnan, V. U. (2017). Thermal Conductivity of Carbon Nanotubes Based on Reverse Non-equilibrium Molecular Dynamics-Size Effect, in: Proceedings of the American Society for Composites—Thirty-second Technical Conference, West Lafayette, IN, October 23-25, 2017. doi:10.12783/asc2017/15340

CrossRef Full Text | Google Scholar

Osman, M. A., and Srivastava, D. (2001). Temperature Dependence of the thermal Conductivity of Single-wall Carbon Nanotubes. Nanotechnology 12 (1), 21–24. doi:10.1088/0957-4484/12/1/305

CrossRef Full Text | Google Scholar

Ozden, S., Brunetto, G., Karthiselva, N., Galvão, D. S., Roy, A., Bakshi, S. R., et al. (2016). Controlled 3d Carbon Nanotube Structures by Plasma Welding. Adv. Mater. Inter. 3 (13). doi:10.1002/admi.201500755

CrossRef Full Text | Google Scholar

Patanè, G., and Spagnuolo, M. (2003). Triangle Mesh Duality: Reconstruction and Smoothing. Springer, 111–128. doi:10.1007/978-3-540-39422-8_9

CrossRef Full Text | Google Scholar

Piper, N., Fu, Y., Tao, J., Yang, X., and To, A. (2011). Vibration Promotes Heat Welding of Single-Walled Carbon Nanotubes. Chem. Phys. Lett. 502 (4), 231–234. doi:10.1016/j.cplett.2010.12.068

CrossRef Full Text | Google Scholar

Plimpton, S., Crozier, P., and Thompson, A. (2007). Lammps-large-scale Atomic/molecular Massively Parallel Simulator. Sandia Natl. Laboratories 18, 43. doi:10.5281/zenodo.3726416

CrossRef Full Text | Google Scholar

Ponomareva, I., Chernozatonskii, L. A., Andriotis, A. N., and Menon, M. (2003). Formation Pathways for Single-wall Carbon Nanotube Multiterminal Junctions. New J. Phys. 5 (1), 119. doi:10.1088/1367-2630/5/1/119

CrossRef Full Text | Google Scholar

Salaway, R. N., and Zhigilei, L. V. (2014). Molecular Dynamics Simulations of thermal Conductivity of Carbon Nanotubes: Resolving the Effects of Computational Parameters. Int. J. Heat Mass Transfer 70, 954–964. doi:10.1016/j.ijheatmasstransfer.2013.11.065

CrossRef Full Text | Google Scholar

Stuart, S. J., Tutein, A. B., and Harrison, J. A. (2000). A Reactive Potential for Hydrocarbons with Intermolecular Interactions. J. Chem. Phys. 112 (14), 6472–6486. doi:10.1063/1.481208

CrossRef Full Text | Google Scholar

Stukowski, A. (2010). Visualization and Analysis of Atomistic Simulation Data with OVITO-The Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 18 (1), 015012. doi:10.1088/0965-0393/18/1/015012

CrossRef Full Text | Google Scholar

Suehiro, J., Zhou, G., and Hara, M. (2003). Fabrication of a Carbon Nanotube-Based Gas Sensor Using Dielectrophoresis and its Application for Ammonia Detection by Impedance Spectroscopy. J. Phys. D: Appl. Phys. 36 (21), L109–L114. doi:10.1088/0022-3727/36/21/l01

CrossRef Full Text | Google Scholar

Varshney, V., Lee, J., Roy, A. K., and Farmer, B. L. (2011). Modeling of Interface thermal Conductance in Longitudinally Connected Carbon Nanotube Junctions. J. Appl. Phys. 109 (8), 084913. doi:10.1063/1.3560914

CrossRef Full Text | Google Scholar

Walker, E. A. (2012). Influence of Phonon Modes on the thermal Conductivity of single-wall, double-wall, and Functionalized Carbon Nanotubes. Ph.D. thesis. Nashville, Tennessee: Citeseer.

Google Scholar

Wang, C., Li, F., Qu, H., Wang, Y., Yi, X., Qiu, Y., et al. (2015). Fabrication of Three Dimensional Carbon Nanotube Foam by Direct Conversion Carbon Dioxide and its Application in Supercapacitor. Electrochimica Acta 158, 35–41. doi:10.1016/j.electacta.2015.01.112

CrossRef Full Text | Google Scholar

Wang, W., Guo, S., Penchev, M., Ruiz, I., Bozhilov, K. N., Yan, D., et al. (2013). Three Dimensional Few Layer Graphene and Carbon Nanotube Foam Architectures for High Fidelity Supercapacitors. Nano Energy 2 (2), 294–303. doi:10.1016/j.nanoen.2012.10.001

CrossRef Full Text | Google Scholar

Wei, D., and Liu, Y. (2008). The Intramolecular Junctions of Carbon Nanotubes. Adv. Mater. 20 (15), 2815–2841. doi:10.1002/adma.200800589

CrossRef Full Text | Google Scholar

Xu, L., Lin, Y., Cai, W., and Shao, X. (2008). From Multilayered Graphite Flakes to Nanostructures: A Tight-Binding Molecular Dynamics Study. J. Chem. Phys. 129 (22), 224709. doi:10.1063/1.3037212

CrossRef Full Text | Google Scholar

Yang, Y., Kim, N. D., Varshney, V., Sihn, S., Li, Y., Roy, A. K., et al. (2017). In Situ mechanical Investigation of Carbon Nanotube-Graphene junction in Three-Dimensional Carbon Nanostructures. Nanoscale 9 (8), 2916–2924. doi:10.1039/c6nr09897e

PubMed Abstract | CrossRef Full Text | Google Scholar

Yao, Z., Postma, H. W. C., Balents, L., and Dekker, C. (1999). Carbon Nanotube Intramolecular Junctions. Nature 402 (6759), 273–276. doi:10.1038/46241

CrossRef Full Text | Google Scholar

Zhang, D., Ryu, K., Liu, X., Polikarpov, E., Ly, J., Tompson, M. E., et al. (2006). Transparent, Conductive, and Flexible Carbon Nanotube Films and Their Application in Organic Light-Emitting Diodes. Nano Lett. 6 (9), 1880–1886. doi:10.1021/nl0608543

PubMed Abstract | CrossRef Full Text | Google Scholar