- 1Department of Physics, University of Central Florida, Orlando, FL, United States
- 2Idaho National Laboratory, Idaho Falls, ID, United States
- 3Theoretical Division, Los Alamos National Laboratory, Los Alamos, NM, United States
- 4Center for Integrated Nanotechnologies, Los Alamos National Laboratory, Los Alamos, NM, United States
- 5Crystal Growth Facility, Institute of Physics, École Polytechnique Fédérale de Lausanne, Lausanne, Switzerland
- 6Ames Laboratory, US Department of Energy, Ames, IA, United States
- 7Department of Physics, SUNY Buffalo State, Buffalo, NY, United States
Three-dimensional (3D) topological insulator (TI) has emerged as a unique state of quantum matter and generated enormous interests in condensed matter physics. The surfaces of a 3D TI consist of a massless Dirac cone, which is characterized by the Z2 topological invariant. Introduction of magnetism on the surface of a TI is essential to realize the quantum anomalous Hall effect and other novel magneto-electric phenomena. Here, by using a combination of first-principles calculations, magneto-transport and angle-resolved photoemission spectroscopy (ARPES), we study the electronic properties of gadolinium (Gd)-doped Sb2Te3. Our study shows that Gd doped Sb2Te3 is a spin-orbit-induced bulk band-gap material, whose surface is characterized by a single topological surface state. Our results provide a new platform to investigate the interactions between dilute magnetism and topology in magnetic doped topological materials.
1 Introduction
In topological quantum materials (TQMs), the interplay of magnetism and topology can give rise to profoundly alluring phenomena including quantum anomalous Hall effect (QAHE), topological electromagnetic dynamics, and generate new states such as magnetic Dirac and Weyl semimetals, axion insulators, etc. (Hasan and Kane, 2010; Li et al., 2010; Qi and Zhang, 2011; Hasan et al., 2015). Although multiple intrinsic magnetic TQMs have been proposed theoretically (Tang et al., 2016; Wang, 2017), their experimental realizations are rare, other than a few exceptions of magnetic Weyl, multifermionic magnetic material, and nodal-line fermionic phase compounds (Hosen et al., 2018; Belopolski et al., 2019; Kabir et al., 2019). Recently, a new magnetic topological insulator has been theoretically proposed and later experimentally realized in thin-films and single crystals of MnBi2Te4 (Chen et al., 2019; Li et al., 2019; Otrokov et al., 2019; Zhang et al., 2019). This system possesses a long-range antiferromagnetic (AFM) order and contributes a pragmatic platform to understand many compelling phenomena and phases, such as QAHE (Deng et al., 2020), axion insulator phase (Liu et al., 2020; Regmi et al., 2020), high number Chern insulator (Ge et al., 2020), and AFM TIs (Otrokov et al., 2019). Despite these recent developments, there are still several mysteries and challenges concerning the topological electronic structure and its interplay with magnetism. Specifically, there is little information on how topological properties are effected by dilute magnetism and how magnetic dopants can modify the electronic structure of a material. Time reversal symmetry in topological materials can be broken by doped magnetic impurities, yielding gap at the Dirac point (Chen et al., 2010; Katmis et al., 2016). Earlier attempts have been made to investigate the doped magnetic materials or the proximity effect in magnetic heterostructure of topological materials and magnetic insulators, in which the magnetic response is weak (Chang et al., 2013; Chang et al., 2015). Typically, increased levels of dopants may raise the exchange field, but lower the sample quality and reduce electronic mobility (Xu et al., 2012; Checkelsky et al., 2014; Li et al., 2016). Consequently, QAHE has been realized at very low temperatures in some previous experiments (Chang et al., 2013; Chang et al., 2015). These shortcomings have dragged behind the pace of the advancement of these materials for potential applications. Therefore, to generate more robust application platforms, we must find magnetic dopants that promote strong exchange fields at very low concentrations.
To date, doped TIs have been studied by doping 3d transition metals such as V, Cr, Mn, Fe, and Cu, where the doping generates various magnetic properties such as ferromagnetism, antiferromagnetism, and superconductivity (Zhou et al., 2006a; Hor et al., 2010; Haazen et al., 2012). But to realize the QAHE, very low temperatures are needed to enhance the magnetic moments and suppress bulk dissipation channels, therefore improved materials are required (Kou et al., 2014). To address this challenge, we utilize magnetism of 4f-electron elements as an alternative to 3d transition metals to dope the topological material. Due to their well-shielded 4f shell, the large moment rare earth (RE) ions (especially gadolinium) are expected to behave like localized magnetic moments in the host matrix, leading to an overall paramagnetic behavior in the doped system (Jensen and Mackintosh, 1991). However, measurements of RE-doped systems as well as pure RE metals have revealed a variety of magnetic properties, which are often complex and unpredictable (Jensen and Mackintosh, 1991). Previous studies of doped 3D TIs have indicated that the size of the Dirac gap increases with the size of the magnetic moment and increased gap size provides greater flexibility for exploring magnetic TI physics (Chen et al., 2010). Hence, large magnetic moment doping studies have already been conducted by utilizing Dy or Ho with moments 2–3 times larger than those typically observed in 3d transition metal-doped systems (Harrison et al., 2015).
Although some RE-doped systems such as Gd doped Bi2Te3 and Bi1.09Gd0.06Sb0.85Te3 have been studied by ARPES to confirm the existence of the topological surface state (TSS) (Harrison et al., 2014; Shikin et al., 2019), to date, no study of Gd doped Sb2Te3 has been performed to probe the effect of dilute magnetism in it with its basic transport or electronic properties. Therefore, we utilize ARPES, thermodynamic and magneto-transport experiments, complemented by first principle calculations to investigate both the bulk and surface states of Gd0.01Sb1.99Te3. The low-temperature electrical resistivity of Gd0.01Sb1.99Te3 reveals a subtle antiferromagnetic ordering below 2.4 K. For the first time, we report the direct observation of single Dirac cone at the
2 Crystals Growth, Crystal Structure, and Sample Characterization
The growth condition of Gd doped Sb2Te3 is similar to previously reported undoped Sb2Te3 (Sultana et al., 2018). Single crystals of Gd0.01Sb1.99Te3 were grown by melting the stoichiometric mixture of elemental Gd, Sb and Te at temperature of 1123 K for 24 h in a sealed vacuum quartz tube. The sample was then cooled down over a period of 48 h until it reaches 893 K, and was stored at this temperature for additional 96 h before quenching in liquid nitrogen. In this way, crystals of centimeter size with a shiny surface could efficiently be attained. Magnetization, electrical resistivity (four-probe method), and heat capacity measurements have been performed using a Quantum Design DynaCool-9 system equipped with a 9 T superconducting magnet and VSM, ETO, and HCP options. The phase purity of the sample was confirmed, with no observation of contaminated phases, by a powder x-ray diffraction (XRD) method (PANalytical X’Pert PRO diffractometer). The XRD pattern was well fitted with the hexagonal structure of Gd0.01Sb1.99Te3 with space group R
The trigonal crystal structure (R
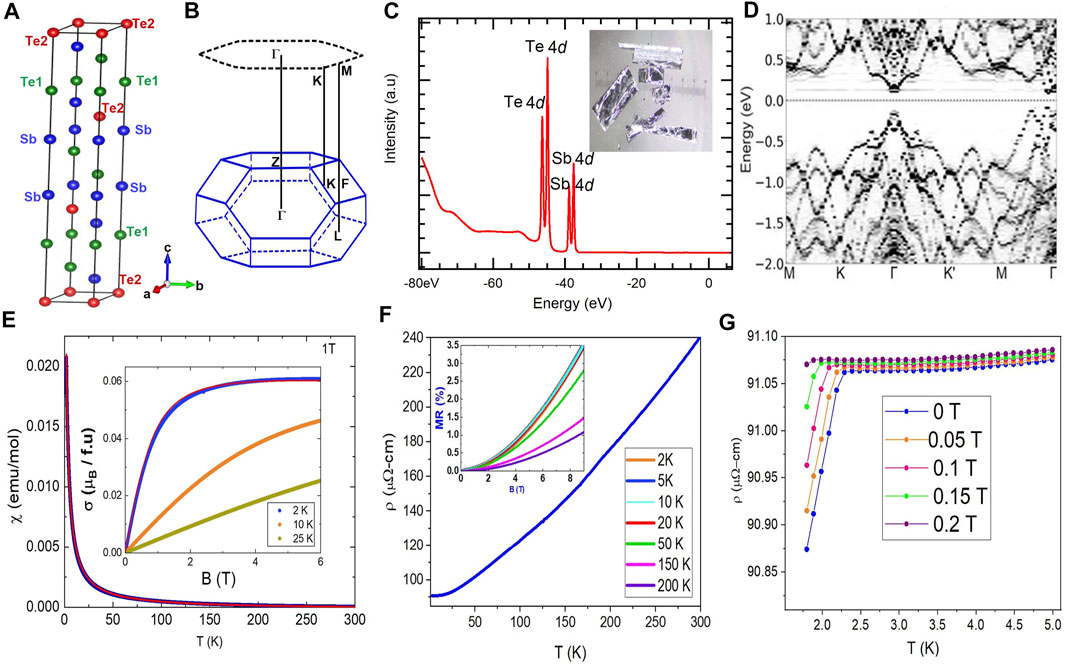
FIGURE 1. Crystal structure and sample characterization. (A) Crystal structure of Sb2Te3. (B) Projection of the 3D bulk brillouin zone onto the [001] surface, high symmetry points are labeled. (C) Core level spectrum shows the peaks for Te 4d and Sb 4d. Inset shows the picture of Gd doped Sb2Te3 crystal used in our experiment. (D) First principles calculations of the bulk band of Gd0.01Sb1.99Te3. The hole-like valence band is robust against the Gd-doping, whereas the Gd-4f impurity level is hybridized with the electron-like conduction band, to produce a small gap. (E) Magnetic susceptibility (Applied magnetic field = 1T) as a function of temperatures together with a Curie-Weiss model shown by the solid red line (see the text). Inset shows the magnetization vs. magnetic field measured at different temperatures. The solid red line is a fitting curve. (F) The electrical resistivity as a function of the temperature. Inset shows the magnetoresistance (MR) taken at various magnetic fields. (G) The resistivity at low-temperatures measured at various magnetic fields.
In order to determine the magnetic properties of Gd0.01Sb1.99Te3, we have performed a detailed magnetization and magnetic susceptibility measurements. We have also used the magnetic measurements, together with energy dispersive spectroscopy (EDS) studies (see Supplementary Figures S3 and S4 for more detail), to precisely determine the level of Gd content in our crystals. Figure 1E shows the temperature dependence of the magnetic susceptibility of Gd0.01Sb1.99Te3 single crystals with the applied magnetic field parallel to the c axis. Whilst the parent antimony telluride is itself a diamagnetic material (Van Itterbeek et al., 1966), our crystals display a characteristic Curie-Weiss magnetic susceptibility, confirming the presence of Gd in our Sb2Te3 crystals. The experimental data have been analyzed using a modified Curie-Weiss law (CW), χ(T) = C/(T − θ) + χ0, where C is the Curie constant, θ is the Weiss temperature, and χ0 is the temperature-independent contribution, most probably associated with the parent Sb2Te3. By fitting the CW law to the experimental data of our crystals yields, χ0 = −1.90 x 10−4 emu/mol, θ= −1.19 K, and the CW parameter C = 0.0664 emu K mol−1. The effective moment μeff = 0.7288 μB/f.u. is calculated with χ0 taken out. The magnitude and negative sign of χ0 agrees well with the previously obtained magnetic susceptibility values of Sb2Te3, −2.3 x 10−4 emu/ mol (Zhou et al., 2006b). Furthermore, the negative Weiss temperature, θ= −1.19 K suggests a possible tendency toward antiferromagnetic interactions among the Gd spins in this material. Assuming that the Curie term results only from localized trivalent Gd atoms,
The temperature dependence of the electrical resistivity of Gd0.01Sb1.99Te3 shows a typical metallic behavior in the whole measured temperature range (Figure 1F). Inset of Figure 1F presents the magnetoresistance (MR) of the sample, at various temperatures. As seen from the figure, the magnetoresistivity is relatively small (about 3.5%) and exhibits ∼ H2 dependence characteristic of metallic systems. Interestingly, at low temperatures, (Figure 1G), there is a weak anomaly in the ρ(T) curve at around 2.4 K. This transition is shifted by applying a magnetic field as strong as 0.2 T, in a manner typical for antiferromagnetic systems. Though the negative value of θ might suggest the presence of long-range antiferromagnetic ordering in Gd0.01Sb1.99Te3, a lack of clear anomalies in both χ(T) and Cp(T) (see Supplementary Figure S5) indicate that the magnetic ordering is not a bulk phenomena. In some doped systems, the low-temperature anomaly might originate from the formation of antiferromagnetic (due to -θ) droplets or clusters in the crystal (Kovaleva et al., 2012). Interestingly, a TI doped with magnetic impurities can exhibit a long-range magnetic order on the surface, and such ordering can be independent of a bulk magnetic ordering (Chen et al., 2010; Hor et al., 2010). Such ordering (with or without bulk magnetic order) can also lead to the breaking of TRS, that can result in a gap opening at the Dirac point making the surface state massive. More studies, however, are required to draw any firm conclusions on the nature of the low-temperature behavior in this material.
3 Electronic Structure Measurement by ARPES
Synchrotron-based ARPES measurements of the electronic structure of Gd0.01Sb1.99Te3 were performed at ALS BL 10.0.1 with a Scienta R4000 hemispherical electron analyzer. The samples were cleaved in situ in an ultra high vacuum conditions (5x10−11 Torr) at 8 K. The energy resolution was set to be better than 20 meV and the angular resolution was set to be better than 0.2° for the synchrotron measurements. The Gd0.01Sb1.99Te3 specimens were found to be very durable and did not exhibit any signs of deterioration for the typical measurement period of 20 hours. A small sample piece cut from the crystal was mounted on a copper post. We then used silver epoxy to attach a ceramic post on the top of the sample. The whole set was then loaded into the measurement chamber for in situ cleavage before the measurement.
To elucidate the electronic structure of Gd0.01Sb1.99Te3, we measure the electronic dispersion maps and the Fermi surface of our sample using high-resolution ARPES. Figure 2A reveals the Fermi surface map of Gd0.01Sb1.99Te3 in the paramagnetic state (T = 8 K), with the constant energy contours at various binding energies with photon energy of 55 eV. A star shaped Fermi pocket around the center of the BZ (
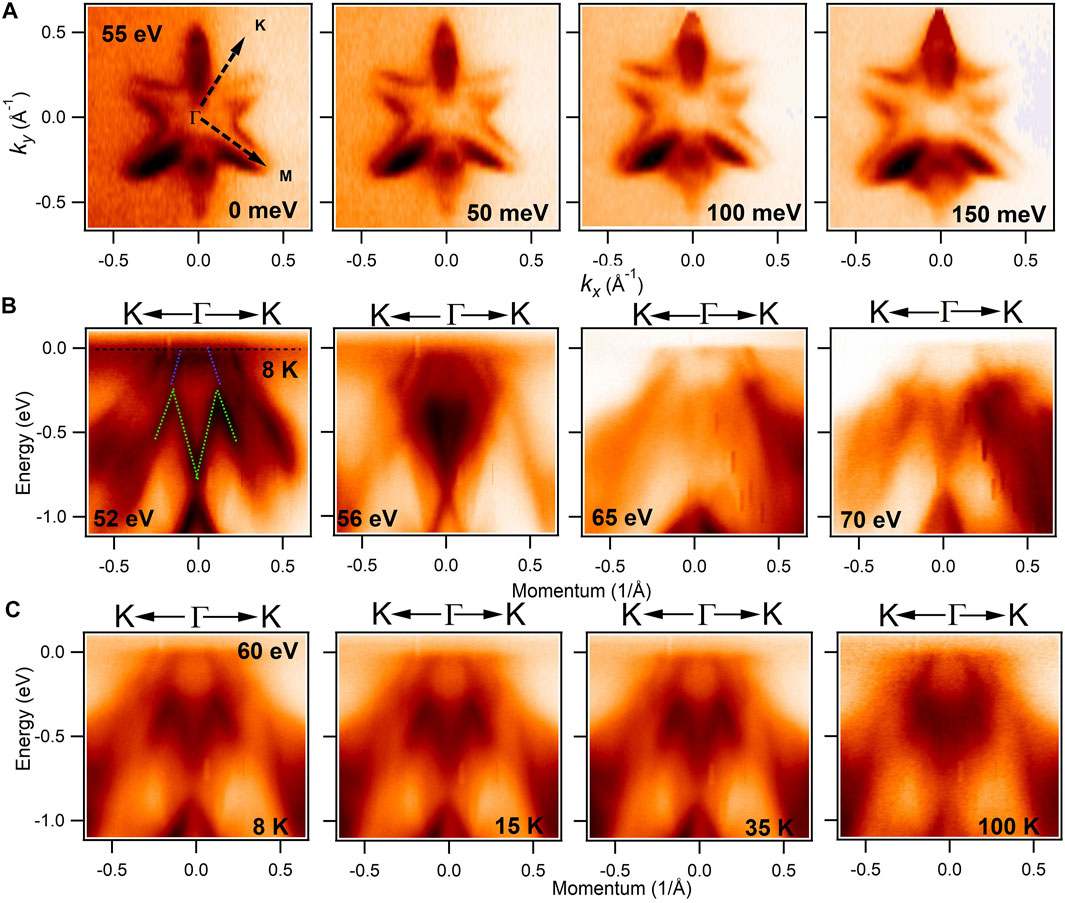
FIGURE 2. Fermi surface, constant energy contours and dispersion maps of Gd0.01Sb1.99Te3. (A) Fermi surface at photon energy of 55 eV and corresponding constant energy contour plots. High symmetry points and binding energies are noted in the plots. (B) Photon energy dependent dispersion maps along the
In order to reveal the nature of the bands along various high symmetry directions, we present photon energy and temperature dependent ARPES-measured dispersion maps in Figures 2B,C, respectfully. Where the photon energies are noted in the plots. Figure 2B shows the measured dispersion maps along the
From the linear dispersion maps presented in Figure 2B, we observe a single Dirac cone in the vicinity of the Fermi level. Now, to test the robustness of the observed surface states of Gd0.01Sb1.99Te3, we carry out a series of temperature-dependent ARPES measurements at photon energy of 60 eV. Figure 2C shows the temperature dependent dispersion maps of Gd0.01Sb1.99Te3 along the
4 Electronic Structure Calculations
First-principles calculations were carried out using the pseudopotential projected augmented wave method (Kresse and Joubert, 1999) implemented in the Vienna ab initio simulation package (Kresse and Hafner, 1993; Kresse and Furthmüller, 1996) with an energy cutoff of 420 eV for the plane-wave basis set. Exchange-correlation effects were treated using the generalized gradient approximation (GGA) (Perdew et al., 1996), where only the Γ-point was used to sample the Brillouin zone of the super cell crystal structure. A 4 × 4 × 1 super cell of Sb2Te3 was considered to achieve the dilute doping (2%) of antiferromagnetically ordered Gd impurities. A total energy tolerance of 10−6 eV was used in self-consisting the charge density. Spin orbit coupling effects were included in a self-consistent manner. To compare our super cell band dispersion to the ARPES spectra, we unfolded the bands into the primitive cell using BandUp (Medeiros et al., 2014; Medeiros et al., 2015). Further benchmarks were performed with the full-potential linearized augmented plane wave (FP-LAPW) method implemented in a WIEN2k package (Blaha et al., 2001). More details are presented in Supplementary Figure S2.
5 Observation of Single Dirac Cone
From the electronic structure measurement of Gd0.01Sb1.99Te3, we observe the surface state through static ARPES, where we extrapolate the data from momentum distribution curves (MDCs) and find the approximate position of the Dirac point above the Fermi level. More elaborately, to observe the position of Dirac point above the Fermi level, first, we focus on the dispersion map of Gd0.01Sb1.99Te3 in Figure 3A, where we observe one hole-like band crossing the Fermi level. Since we are unable to see the features above the Fermi level using standard ARPES techniques, we extrapolate the data from the MDC curve from Figure 3A in order to find out the expected position of the Dirac point shown in Figure 3B. Thus we observe the approximate position of the Dirac point around 150 meV above the Fermi level (see Supplementary Figures S9 and S10 for more detail), which is comparable with the previously observed Dirac point position for primitive Sb2Te3 (180 meV) (Zhu et al., 2015). Hence, adding small amount of Gd made the position of the Dirac point closer to the Fermi level. Now, from the theoretically obtained bulk band electronic structure for both doped and pristine Sb2Te3 compounds, (Figures 3C,D, respectively), one can see that the electron-like bands of the Gd doped system are shifted closer to the Fermi level with respect to those of the pristine system (to compare with the surface state of the pristine system, see Supplementary Figure S1C). With the hole-like bands aligned for both doped and pristine systems, we are able to identify that the band gap is narrower in the Gd-doped Sb2Te3 as compared to pristine Sb2Te3.
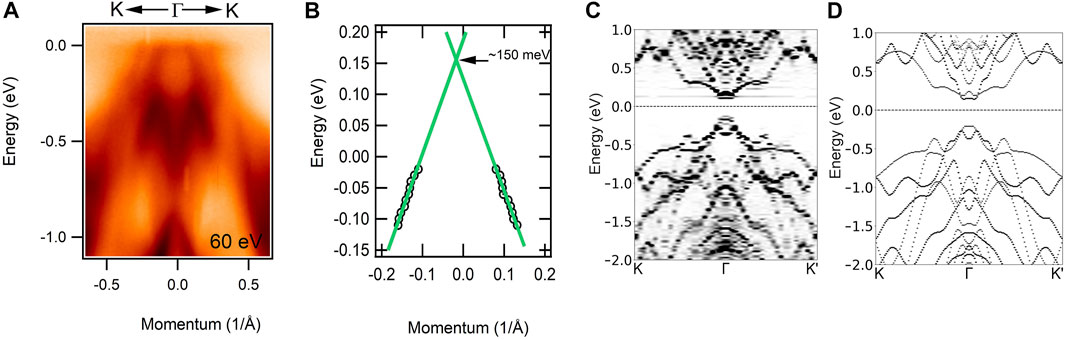
FIGURE 3. Comparison of band structure of parent Sb2Te3 and Gd0.01Sb1.99Te3. (A) Experimental band dispersion map of Gd0.01Sb1.99Te3 along the
From these bulk band structure calculations, it is clear that a small amount of added Gd in Sb2Te3 (Figure 3C) did not make a huge overall change of the bulk bands compared to the pristine Sb2Te3 (Figure 3D). The main difference of including Gd is that, the electron-like band at Γ comes closer to the Fermi level. Again, from the surface state calculation of primitive Sb2Te3 (see Supplementary Figure S1C), we already observe non trivial Dirac-like band at the
6 Summary
In summary, we use detailed magnetic, electrical transport, and ARPES measurements together with DFT calculations to study the electronic structure of the Gd-doped Sb2Te3 topological insulator. The magnetic and transport measurements show that Gd doping gives rise to local magnetism with Curie-Weiss-like behavior of the magnetic susceptibility and show some indications of possible magnetic ordering at 2.4 K. We observe the surface state from the electronic structure measurement of Gd0.01Sb1.99Te3 through static ARPES. The surface states are directly associated with the 4f-electron magnetism of gadolinium. We predict the approximate position of the Dirac point around 150 meV above the Fermi level. We show that adding a small amount of gadolinium introduces dilute magnetism into it, and that does not prevent the formation of the Dirac state in a relatively wide temperature range. Hence, our overall electronic structure reveals topological non-trivial surface state above the Fermi level in this material, which could be a promising platform to study the effect of dilute magnetism on the electronic structures and topology of similar doped materials.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
MN conceived the study; AP synthesized the samples and performed the electrical transport characterizations; YL was involved in sample preparation; XD, and KG performed the transport and magnetization measurements; FK performed the measurements with the help of MH, GD, YL, KD, CS, SR, AS, LP, JB, MC, and MN; CL and J-XZ performed the ab initio calculations; FK, CL, J-XZ, KG, and MN wrote the manuscript with the input from all authors; MN was responsible for the overall research direction, planning, and integration among the different research units.
Funding
MN is supported by the Air Force Office of Scientific Research under Award No. FA9550-17-1-0415, the Air Force Office of Scientific Research MURI (Grant No. FA9550- 20-1-0322), and the Center for Thermal Energy Transport under Irradiation, an Energy Frontier Research Center funded by the U.S. DOE, Office of Basic Energy Sciences. XD and KG acknowledge support from INL’s LDRD program (19P45-019FP) and the DOE’s Early Career Program. This work at Los Alamos was carried out under the auspices of the U.S. Department of Energy (DOE) National Nuclear Security Administration under Contract No. 89233218CNA000001 (CL and J-XZ). The work was supported, in part, by the Center for Integrated Nanotechnologies, a DOE BES user facility, in partnership with the LANL Institutional Computing Program for computational resources. MC was supported by the Air Force Office of Scientific Research under Award Nos. FA9550-16-1-0149 and FA9550-20-1-0284. Work at Ames Laboratory was supported by the Materials Sciences and Engineering Division of the Office of Basic Energy Sciences, Office of Science of U. S. Department of Energy. Ames Laboratory is operated for the U.S. DOE by Iowa State University of Science and Technology under Contract No. DE-AC02-07CH11358. AP was supported by the faculty startup fund from the Dean’s Office, School of Arts and Sciences, State University of New York (SUNY), Buffalo State.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
We thank Sung-Kwan Mo for beamline assistance at the LBNL.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2021.706658/full#supplementary-material
References
Belopolski, I., Manna, K., Sanchez, D. S., Chang, G., Ernst, B., Yin, J., et al. (2019). Discovery of Topological Weyl Fermion Lines and Drumhead Surface States in a Room Temperature Magnet. Science 365, 1278–1281. doi:10.1126/science.aav2327
Blaha, P., Schwarz, K., Madsen, G. K. H., Kvasnicka, D., and Luitz, J. (2001). WIEN2k: An Augmented Plane Wave Plus Local Orbitals Program for Calculating crystal Properties. 2nd Edition. Vienna: Vienna University of Technology.
Chang, C.-Z., Zhang, J., Feng, X., Shen, J., Zhang, Z., Guo, M., et al. (2013). Experimental Observation of the Quantum Anomalous Hall Effect in a Magnetic Topological Insulator. Science 340, 167–170. doi:10.1126/science.1234414
Chang, C.-Z., Zhao, W., Kim, D. Y., Zhang, H., Assaf, B. A., Heiman, D., et al. (2015). High-precision Realization of Robust Quantum Anomalous Hall State in a Hard Ferromagnetic Topological Insulator. Nat. Mater. 14, 473–477. doi:10.1038/nmat4204
Checkelsky, J. G., Yoshimi, R., Tsukazaki, A., Takahashi, K. S., Kozuka, Y., Falson, J., et al. (2014). Trajectory of the Anomalous Hall Effect towards the Quantized State in a Ferromagnetic Topological Insulator. Nat. Phys. 10, 731–736. doi:10.1038/nphys3053
Chen, Y. J., Xu, L. X., Li, J. H., Li, Y. W., Wang, H. Y., Zhang, C. F., et al. (2019). Topological Electronic Structure and its Temperature Evolution in Antiferromagnetic Topological Insulator MnBi2Te4. Phys. Rev. X 9, 041040. doi:10.1103/PhysRevX.9.041040
Chen, Y. L., Chu, J.-H., Analytis, J. G., Liu, Z. K., Igarashi, K., Kuo, H.-H., et al. (2010). Massive Dirac Fermion on the Surface of a Magnetically Doped Topological Insulator. Science 329, 659–662. doi:10.1126/science.1189924
Deng, Y., Yu, Y., Shi, M. Z., Guo, Z., Xu, Z., Wang, J., et al. (2020). Quantum Anomalous Hall Effect in Intrinsic Magnetic Topological Insulator MnBi2Te4. Science 367, 895–900. doi:10.1126/science.aax8156
Ge, J., Liu, Y., Li, J., Li, H., Luo, T., Wu, Y., et al. (2020). High-Chern-number and High-Temperature Quantum Hall Effect without Landau Levels. Natl. Sci. Rev. 7, 1280–1287. doi:10.1093/nsr/nwaa089
Haazen, P. P. J., Laloë, J.-B., Nummy, T. J., Swagten, H. J. M., Jarillo-Herrero, P., Heiman, D., et al. (2012). Ferromagnetism in Thin-Film Cr-Doped Topological Insulator Bi2Se3. Appl. Phys. Lett. 100, 082404. doi:10.1063/1.3688043
Harrison, S. E., Collins-McIntyre, L. J., Li, S., Baker, A. A., Shelford, L. R., Huo, Y., et al. (2014). Study of Gd-Doped Bi2Te3 Thin Films: Molecular Beam Epitaxy Growth and Magnetic Properties. J. Appl. Phys. 115, 023904. doi:10.1063/1.4861615
Harrison, S. E., Collins-McIntyre, L. J., Zhang, S.-L., Baker, A. A., Figueroa, A. I., Kellock, A. J., et al. (2015). Study of Dy-Doped Bi2Se3: Thin Film Growth and Magnetic Properties. J. Phys. Condens. Matter 27, 245602. doi:10.1088/0953-8984/27/24/245602
Hasan, M. Z., and Kane, C. L. (2010). Colloquium: Topological Insulators. Rev. Mod. Phys. 82, 3045–3067. doi:10.1103/RevModPhys.82.3045
Hasan, M. Z., Xu, S.-Y., and Neupane, M. (2015). Topological Insulators: Fundamentals and Perspectives. Editors F. Ortmann, S. Roche, and S. O. Valenzuela (New York: John Wiley & Sons). doi:10.1002/9783527681594
Hor, Y. S., Roushan, P., Beidenkopf, H., Seo, J., Qu, D., Checkelsky, J. G., et al. (2010). Development of Ferromagnetism in the Doped Topological insulator Bi2−xMnxTe3. Phys. Rev. B 81, 195203. doi:10.1103/PhysRevB.81.195203
Hosen, M. M., Dhakal, G., Dimitri, K., Maldonado, P., Aperis, A., Kabir, F., et al. (2018). Discovery of Topological Nodal-Line Fermionic Phase in a Magnetic Material GdSbTe. Sci. Rep. 8, 13283. doi:10.1038/s41598-018-31296-7
Kabir, F., Hosen, M. M., Kabeer, F. C., Aperis, A., Ding, X., Dhakal, G., et al. (2019). Observation of Multiple Dirac States in a Magnetic Topological Material EuMg2Bi2. arXiv:1912.08645.
Katmis, F., Lauter, V., Nogueira, F. S., Assaf, B. A., Jamer, M. E., Wei, P., et al. (2016). A High-Temperature Ferromagnetic Topological Insulating Phase by Proximity Coupling. Nature 533, 513–516. doi:10.1038/nature17635
Kou, X., Guo, S.-T., Fan, Y., Pan, L., Lang, M., Jiang, Y., et al. (2014). Scale-invariant Quantum Anomalous Hall Effect in Magnetic Topological Insulators beyond the Two-Dimensional Limit. Phys. Rev. Lett. 113, 137201. doi:10.1103/PhysRevLett.113.137201
Kovaleva, N. N., Kugel, K. I., Bazhenov, A. V., Fursova, T. N., Löser, W., Xu, Y., et al. (2012). Formation of Metallic Magnetic Clusters in a Kondo-Lattice Metal: Evidence from an Optical Study. Sci. Rep. 2, 890. doi:10.1038/srep00890
Kresse, G., and Furthmüller, J. (1996). Efficient Iterative Schemes Forab Initiototal-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B 54, 11169–11186. doi:10.1103/PhysRevB.54.11169
Kresse, G., and Hafner, J. (1993). Ab Initiomolecular Dynamics for Open-Shell Transition Metals. Phys. Rev. B 48, 13115–13118. doi:10.1103/physrevb.48.13115
Kresse, G., and Joubert, D. (1999). From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B 59, 1758–1775. doi:10.1103/PhysRevB.59.1758
Li, J., Li, Y., Du, S., Wang, Z., Gu, B.-L., Zhang, S.-C., et al. (2019). Intrinsic magnetic topological insulators in van der Waals layered MnBi2Te4 -family materials. Sci. Adv. 5, 9. doi:10.1126/sciadv.aaw5685
Li, R., Wang, J., Qi, X.-L., and Zhang, S.-C. (2010). Dynamical Axion Field in Topological Magnetic Insulators. Nat. Phys. 6, 284–288. doi:10.1038/nphys1534
Li, W., Claassen, M., Chang, C.-Z., Moritz, B., Jia, T., Zhang, C., et al. (2016). Origin of the Low Critical Observing Temperature of the Quantum Anomalous Hall Effect in V-Doped (Bi,Sb)2Te3 Film. Sci. Rep. 6, 32732. doi:10.1038/srep32732
Liu, C., Wang, Y., Li, H., Wu, Y., Li, Y., Li, J., et al. (2020). Robust Axion Insulator and Chern Insulator Phases in a Two-Dimensional Antiferromagnetic Topological Insulator. Nat. Mater. 19, 522–527. doi:10.1038/s41563-019-0573-3
Medeiros, P. V. C., Stafström, S., Björk, J., and Björk, J. (2014). Effects of Extrinsic and Intrinsic Perturbations on the Electronic Structure of Graphene: Retaining an Effective Primitive Cell Band Structure by Band Unfolding. Phys. Rev. B 89, 041407. doi:10.1103/PhysRevB.89.041407
Medeiros, P. V. C., Tsirkin, S. S., Stafström, S., and Björk, J. (2015). Unfolding Spinor Wave Functions and Expectation Values of General Operators: Introducing the Unfolding-Density Operator. Phys. Rev. B 91, 041116. doi:10.1103/PhysRevB.91.041116
Otrokov, M. M., Rusinov, I. P., Blanco-Rey, M., Hoffmann, M., Vyazovskaya, A. Y., Eremeev, S. V., et al. (2019). Unique Thickness-Dependent Properties of the van der Waals Interlayer Antiferromagnet MnBi2Te4 Films. Phys. Rev. Lett. 122, 107202. doi:10.1103/PhysRevLett.122.107202
Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 77, 3865–3868. doi:10.1103/PhysRevLett.77.3865
Qi, X.-L., and Zhang, S.-C. (2011). Topological Insulators and Superconductors. Rev. Mod. Phys. 83, 1057–1110. doi:10.1103/RevModPhys.83.1057
Regmi, S., Hosen, M. M., Ghosh, B., Singh, B., Dhakal, G., Sims, C., et al. (2020). Temperature-dependent Electronic Structure in a Higher-Order Topological Insulator Candidate EuIn2As2. Phys. Rev. B 102, 165153. doi:10.1103/PhysRevB.102.165153
Shikin, A. M., Estyunin, D. A., Surnin, Y. I., Koroleva, A. V., Shevchenko, E. V., Kokh, K. A., et al. (2019). Dirac gap Opening and Dirac-Fermion-Mediated Magnetic Coupling in Antiferromagnetic Gd-Doped Topological Insulators and Their Manipulation by Synchrotron Radiation. Sci. Rep. 9, 4813. doi:10.1038/s41598-019-41137-w
Sultana, R., Gahtori, B., Meena, R. S., and Awana, V. P. S. (2018). Synthesis and Structural Characterization of Bulk Sb2Te3 Single crystal. AIP. Conf. Proc. 1953, 070021. doi:10.1063/1.5032799
Tang, P., Zhou, Q., Xu, G., and Zhang, S.-C. (2016). Dirac Fermions in an Antiferromagnetic Semimetal. Nat. Phys. 12, 1100–1104. doi:10.1063/5.001532810.1038/nphys3839
Van Itterbeek, A., Van Deynse, N., and Herinckx, C. (1966). Measurements on the Magnetic Anisotropy of Single Crystals of Bi2Te3, Sb2Te3 and Compounds of Them, between Room Temperature and 1.3°K. Physica 32, 2123–2128. doi:10.1016/0031-8914(66)90173-X
Xu, S.-Y., Neupane, M., Liu, C., Zhang, D., Richardella, A., Andrew Wray, L., et al. (2012). Hedgehog Spin Texture and Berry's Phase Tuning in a Magnetic Topological Insulator. Nat. Phys. 8, 616–622. doi:10.1038/nphys2351
Zhang, D., Shi, M., ZhuXing, T. D., Xing, D., Zhang, H., and Wang, J. (2019). Topological Axion States in the Magnetic Insulator MnBi2Te4 with the Quantized Magnetoelectric Effect. Phys. Rev. Lett. 122, 206401. doi:10.1103/PhysRevLett.122.206401
Zhou, Z., Chien, Y.-J., and Uher, C. (2006). Thin Film Dilute Ferromagnetic semiconductors Sb2−xCrxTe3 with a Curie Temperature up to190K. Phys. Rev. B 74, 224418. doi:10.1103/PhysRevB.74.224418
Zhou, Z., Žabèík, M., Lošták, P., and Uher, C. (2006). Magnetic and Transport Properties of Sb2−xFexTe3 (0<x<0.02)(0<x<0.02) Single Crystals. J. Appl. Phys. 99, 043901. doi:10.1063/1.2171787
Keywords: Angle resolved photoemission spectroscopy (ARPES), magnetism, topologial insulator, gadolinium-doped, doping, Dirac state
Citation: Kabir F, Hosen MM, Ding X, Lane C, Dhakal G, Liu Y, Dimitri K, Sims C, Regmi S, Sakhya AP, Persaud L, Beetar JE, Liu Y, Chini M, Pathak AK, Zhu J-X, Gofryk K and Neupane M (2021) Effect of Dilute Magnetism in a Topological Insulator. Front. Mater. 8:706658. doi: 10.3389/fmats.2021.706658
Received: 07 May 2021; Accepted: 07 October 2021;
Published: 25 November 2021.
Edited by:
Friedrich Malte Grosche, University of Cambridge, United KingdomReviewed by:
Jie Ma, Shanghai Jiao Tong University, ChinaJiji Thomas Joseph Pulikkotil, National Physical Laboratory (CSIR), India
Copyright © 2021 Kabir, Hosen, Ding, Lane, Dhakal, Liu, Dimitri, Sims, Regmi, Sakhya, Persaud, Beetar, Liu, Chini, Pathak, Zhu, Gofryk and Neupane. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Madhab Neupane, TWFkaGFiLk5ldXBhbmVAdWNmLmVkdQ==
 Firoza Kabir
Firoza Kabir M. Mofazzel Hosen
M. Mofazzel Hosen Xiaxin Ding2
Xiaxin Ding2 Gyanendra Dhakal
Gyanendra Dhakal Sabin Regmi
Sabin Regmi Luis Persaud
Luis Persaud Jian-Xin Zhu
Jian-Xin Zhu Krzysztof Gofryk
Krzysztof Gofryk