- 1PIMM, Arts et Métiers Institute of Technology, CNRS, CNAM, HESAM University, Paris, France
- 2Safran Composites, A Platform of Safran Tech, Itteville, France
This article deals with the thermal oxidation mechanisms and kinetics of epoxy-diamine (EPO-DA) networks used as composite matrices reinforced with carbon fibers in the aeronautical field. The first part of this article is devoted to a detailed presentation of the new analytical kinetic model. The so-called “closed-loop” mechanistic scheme, developed in the last 3 decades in our laboratory in order to accurately describe the thermal oxidation kinetics of saturated hydrocarbon polymers, is recalled. Its main characteristics are also briefly recalled. Then, the system of differential equations derived from this oxidation mechanism is analytically solved without resorting to the usual simplifying assumptions that seriously degrade the reliability of all kinetic models. On the contrary, the generalization of the proportionalities observed between the steady concentrations of the different reactive species (i.e., hydroperoxides and alkyl and peroxy radicals) to the entire course of thermal oxidation gives a series of much sounder equations. From this basis, the kinetic model is completed by considering new structure/property relationships in order to predict the consequences of thermal oxidation on the thermomechanical properties, in particular on the glass transition temperature (Tg). To reach this second objective, the two main mechanisms responsible for the alteration of the macromolecular network structure are recalled: chain scissions and crosslinking. Like any other chemical species, their kinetics are directly expressed from the oxidation mechanistic scheme using the classical concepts of chemical kinetics. The second part of this article is devoted to the checking of the kinetic model reliability. It is shown that this latter accurately simulates the experimental curves of carbonyl build-up and Tg decrease versus time of exposure determined in our laboratory for three EPO-DA networks under study, exposed in a wide variety of thermal oxidative environments. The values determined by inverse solving method for the different model parameters are discussed and their temperature dependence are elucidated. Finally, an end-of-life criterion is proposed for predicting the lifetime of EPO-DA networks involving a predominant chain scission process.
Introduction
Most of the composite material structures used in the civil aeronautical sector are composed of an epoxy or polyimide matrix reinforced with carbon fibers. Since the early 1980s, many studies have clearly shown that these materials can perish by matrix embrittlement induced by thermal oxidation when used in service in their glassy state (Alston, 1980; Kerr and Haskins, 1984; Street et al., 1988; Young and Chang, 1988; Scola and Vontell, 1991; Nam and Seferis, 1992; Salin and Seferis, 1993; Bowles et al., 1994; Skontorp et al., 1995; Parvatareddy et al., 1996; Tsotsis, 1998; Tsotsis and Lee, 1998; Colin et al., 1999; Tsotsis et al., 2001; Lafarie-Frenot and Rouquie, 2004; Colin et al., 2005a; Schoeppner et al., 2007; Tandon et al., 2009; Colin et al., 2011; Tandon and Pochiraju, 2011; Colin and Verdu, 2012a; Tandon, 2012). Thermal oxidation is limited to a superficial layer due to its kinetic control by oxygen diffusion (Gillen and Clough, 1989; Audouin et al., 1994). “Spontaneous” cracks can then be initiated in this superficial layer (even in the absence of external mechanical loading) due to both the development of a tensile stress gradient and the catastrophic fall of its fracture properties (Colin et al., 2005b; Colin et al., 2011; Colin and Verdu, 2012a; Colin and Verdu, 2012b), thus allowing oxygen penetration into deeper layers (Bowles et al., 1993; Meador et al., 1996; Colin et al., 2005b). Repeating this sequential scenario is expected to allow damage to propagate until the core of the composite material (Colin et al., 2005b) and failure to occur untimely.
Since the early 1980s, different approaches used for predicting the lifetime of composite materials gave a central role to kinetic modeling (Nelson, 1983; Bowles and Meyer, 1986; Bowles and Nowak, 1988; Salin and Seferis, 1996a; Salin and Seferis, 1996b; Cunningham and McManus, 1996; McManus and Cunningham, 1997; Crews and McManus, 1997; McManus et al., 2000; Colin et al., 2001a; Colin et al., 2001b; Colin et al., 2002; Decelle et al., 2003; Colin and Verdu, 2003; Colin et al., 2005a; Colin and Verdu, 2005; Tandon and Pochiraju, 2006; Tandon et al., 2006; Olivier et al., 2008; Olivier et al., 2009; Barjasteh et al., 2009; Barjasteh et al., 2011; Pochiraju et al., 2008; Pochiraju and Tandon, 2009; Lafarie-Frenot et al., 2010; Colin et al., 2011; Tandon and Pochiraju, 2011; Pochiraju, 2012; Cinquin et al., 2016; Colin et al., 2016; Colin et al., 2020; Colin et al., 2021). Within the scientific community, it was quickly accepted that all the empirical steps had to be eradicated in kinetic models, so that these latter could be efficient as well in simulation as in extrapolation. In particular, our laboratory played a major role in contributing this objective over the past 2 decades (Colin et al., 2001a; Colin et al., 2001b; Colin et al., 2002; Decelle et al., 2003; Colin and Verdu, 2003; Colin et al., 2005a; Colin and Verdu, 2005; Lafarie-Frenot et al., 2010; Cinquin et al., 2016; Colin et al., 2016; Colin et al., 2020; Colin et al., 2021).
To date, two versions of the kinetic model are fully operational for composites materials made of diamine cross-linked epoxy (EPO-DA) matrices. The “numerical version” allows solving the complete problem under consideration with, as only assumption, the uniqueness of the oxidation site (Colin et al., 2020). In EPO-DA matrices, this site corresponds to the C−H bond located in α position of a heteroatom (O or N) in oxy-methylene (−O−CH2−), amino-methylene (>N−CH2−) and methanol groups (>CH−OH). Indeed, this latter is characterized by a lower dissociation energy (ED ≈ 376 kJ mol−1) compared to the aliphatic C−H bond in polymethylenic sequences (ED ≈ 393 kJ mol−1) and the aromatic C−H bond (ED ≈ 393 kJ mol−1) (Colin et al., 2011). It is commonly noted PH in both the oxidation mechanistic scheme and the corresponding kinetic model.
The “analytical version,” in contrast, gives access to the oxidation kinetics only at low conversion ratios, i.e., when [PH] ≈ [PH]0, because it results from the generalization of observations in the steady state regime to the entire course of thermal oxidation (Colin et al., 2021). As embrittlement due to oxidation generally occurs for very low conversion ratios in polymers and, more particularly, in EPO-DA networks (Colin et al., 2011; Colin and Verdu, 2012a; Colin and Verdu, 2012b), the use of such an analytical kinetic model seems to largely be sufficient, not only for determining the corresponding critical oxidation events, but also for fully applying the classical methodology for lifetime prediction. It should be mentioned that the reliability this analytical kinetic model was recently demonstrated for two EPO-DA matrices considered for applications of composite structures at temperatures typically between 70 and 150°C in the civil aeronautical sector (Colin et al., 2021).
This complementary article aims at starting the generalization of this new analytical kinetic model to the whole family of EPO-DA matrices. After having recalled its theoretical foundations and structure, it will be shown that this kinetic model also successfully describes the thermal oxidation kinetics of a third EPO-DA network studied over the past decade in our laboratory (Terekhina et al., 2013; Cinquin et al., 2016; Colin et al., 2016; Colin et al., 2020). It should be pointed out that these three EPO-DA networks have very different glass transition temperatures, typically ranged between 158 and 263°C, thus allowing to study the impact of the molecular mobility on the thermal oxidation kinetics. The values determined by inverse solving method for the different model parameters will be discussed and their temperature dependence will be elucidated. In addition, the kinetic model will be completed by adding new structure/property relationships in order to predict the consequences of thermal oxidation on the thermomechanical properties. Finally, a peculiar attention will be paid to a possible end-of-life criterion in order to predict the lifetime of EPO-DA networks.
Theory
Foundations of the Kinetic Model
The mechanistic scheme chosen for accurately describing the thermal oxidation of EPO-DA networks has been extensively detailed in previous publications, for instance in (Colin et al., 2020; Colin et al., 2021). It is composed of the following six reactions:
Initiation:
1b) 2POOH → P• + PO2• (k1b)
Propagation:
2) P• + O2 → PO2• (k2)
3) PO2• + PH → POOH + P• (k3)
Terminations:
4) P• + P• → Inactive products (k4)
5) P• + PO2• → Inactive products (k5)
6) PO2• + PO2• → Inactive products + O2 (k6)
Where PH, POOH, P•, and PO2• designate an oxidation site (i.e., C−H bond in oxy-methylene, amino-methylene or methanol group), an hydroperoxide, and alkyl and peroxy radicals, respectively. In addition, ki (with i = 1b, … , 6) are rate constants.
The main peculiarity of this mechanistic scheme is to produce its own initiator. Indeed, radicals are formed by the thermal decomposition (according to the bimolecular mode) of the main propagation product: the hydroperoxide group (POOH). This closed-loop character explains well the sharp auto-acceleration of the oxidation reaction at the end of the induction period (Colin et al., 2006).
Recently, it was shown that the system of differential equations derived from the closed-loop mechanism can analytically be solved by generalizing the proportionality relationships observed between the steady concentrations of the different reactive species, i.e., [POOH], [PO2•], and [P•], to the entire course of thermal oxidation (Colin et al., 2021). These simplifying (but quite realistic) assumptions allowed obtaining an analytical kinetic model much sounder than all the other developed until now. In particular, this new kinetic model is able to accurately describe the first three stages of the thermal oxidation kinetics, i.e., the induction period, the auto-acceleration of the oxidation kinetics at the end of the induction period, and the steady-state regime. Unfortunately, due to the assumption of the low conversion ratios (i.e., [PH] ≈ [PH]0 ≈ constant), it cannot allow accounting for the sudden slow-down of the oxidation kinetics at long-term. This behavioral deviation between theory and experiment typically appears when [PH] decreases by about ten percent. Then, it amplifies with exposure time.
The following solution was proposed for [POOH] (Colin et al., 2021):
with:
where [POOH]0 and [POOH]∞ are the initial and steady concentrations of hydroperoxides, respectively.
Experimental measurements show that [POOH]∞ > 10 [POOH]0 for weakly pre-oxidized polymer samples (Da Cruz et al., 2016; Huang et al., 2020). Consequently, b >> 1. Finally, the following order of magnitude (b = 10) was chosen for this study.
The following solutions were proposed for [PO2•] and [P•] (Colin et al., 2021):
with:
where [PO2•]∞ and [P•]∞ are the steady concentrations of peroxy and alkyl radicals, respectively.
In Eqs 2, 3, 7, 8, C is the oxygen concentration in the EPO-DA network under consideration, which depends on the oxygen partial pressure PO2 in the exposure environment according to the common Henry’s law:
where SO2 is the coefficient of oxygen solubility in the EPO-DA network under consideration. The different values of SO2 reported in literature for EPO-DA networks were compiled in reference (Colin et al., 2020).
Two subfamilies of EPO-DA networks were clearly put in evidence:
1) Epoxies cross-linked with an aliphatic diamine hardener (e.g., Jeffamine D230, Jeffamine D400, Ancamine 2049, or IPDA) for which SO2 ≈ 5.1 × 10−8 mol.L−1.Pa−1 whatever the temperature,
2) Epoxies cross-linked with an aromatic diamine hardener (e.g., CAF, DDM, or DDS) for which SO2 ≈ 1.45 × 10−7 mol.L−1.Pa−1 whatever the temperature.
Only the second value will be used in this study because the three EPO-DA networks under study are cross-linked by CAF or DDS. In addition, β−1 roughly corresponds to the critical oxygen concentration CC above which oxygen excess is reached:
Calculation of the Physico-Chemical Properties
Still using the classical concepts of the chemical kinetics, it is now possible to calculate, from the previous mathematical expressions of [POOH], [PO2•], and [P•], several key physico-chemical properties that can easily be checked experimentally. The mathematical expressions of some of them were already reported in reference (Colin et al., 2021). New expressions will be added at the end of this section in order to then calculate the thermomechanical properties, in particular the glass transition temperature.
Oxygen Consumption
Undoubtedly, hydroperoxide concentration [POOH] and the oxygen consumption Q are the most relevant properties because their mathematical expressions can be deduced from the closed-loop mechanism without having to use additional adjustable parameter. Both properties can thus allow accurately determining the different rate constants ki from the experimental data. The mathematical expression of Q was already reported in reference (Colin et al., 2021):
with:
where r∞ and r0 are the steady oxidation rates in the general case and in oxygen excess, respectively.
Carbonyl Groups
Another key property, also often chosen to assess the rate constants ki, is the carbonyl concentration [P=O]. In the closed-loop mechanism, these oxidation products are formed in the initiation (1b) and termination reactions (6) by specific chemical events involving radicals (e.g., β scission, disproportionation, etc.), which generally compete with many other chemical events, especially with hydrogen abstraction giving alcohols. Therefore, the calculation of [P=O] requires the use of additional adjustable parameters, namely formation yields. The mathematical expression of [P=O] was also reported in reference (Colin et al., 2021):
with:
where rCO∞ is the steady rate of carbonyl build-up, and γ1CO and γ6CO are the formation yields of carbonyls in initiation (1b) and termination (6), respectively. In a recent publication (Colin et al., 2020), it was found that γ1CO and γ6CO are increasing functions of molecular mobility. The same orders of magnitude reported for these two yields in reference (Colin et al., 2020) were kept in this study (see Table 2).
Macromolecular Changes
The last key properties that will be detailed below are the concentrations of chain scissions (S) and crosslinking events (X) because these two macromolecular changes are known to be responsible for the changes in the thermomechanical properties (Colin et al., 2011; Colin and Verdu, 2012a; Colin and Verdu, 2012b). The most famous chain scission mechanism in literature is the β scission of alkoxyl radicals, which occurs during initiation (1b) in the closed-loop mechanistic scheme. In contrast, crosslinking usually takes place in terminations (4), (5), and (6) by the coupling of the different radical species. Their respective rates can be written as follows:
where γ1S, γ4X, γ5X, and γ6X are the yields in chain scissions in initiation (1b) and crosslinking in terminations (4), (5), and (6), respectively.
In a first approximation, to avoid having too many unknown parameters compared to our identification possibilities using the inverse solving method, it was assumed that crosslinking mainly occurs in oxygen excess, thus leading to peroxide bridges. Consequently, the crosslinking events in termination (4) and (5) were neglected: γ4X ≈ γ5X ≈ 0, and Eq. 17 was simplified as:
The replacement of [POOH] and [PO2•] by their mathematical expressions in Eqs 16, 18 leads to:
The integration of Eqs 19, 20 with respect to time t gives mathematical expressions similar in form to Q and [P=O]:
with:
where rS∞ and rX∞ are the steady rates of chain scissions and crosslinking, respectively.
Calculation of the Glass Transition Temperature
In an ideal EPO-DA network (i.e., without dangling chains), the ends of the elastically active chains are connected to tri-functional nodes. Consequently, each chain scission suppresses three elastically active chains and two nodes, and create two dangling chains, whereas each crosslinking event creates two new elastically active chains and one node of higher functionality (i.e., tetra-functional). All these macromolecular changes are schematized in Figure 1.
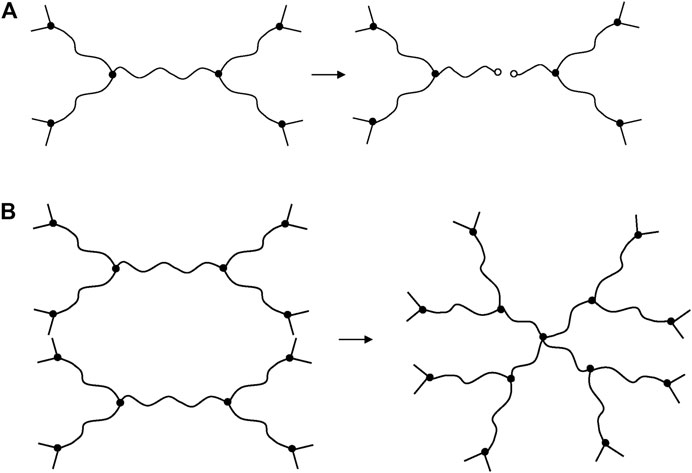
FIGURE 1. Schematization of a chain scission (A) and a crosslinking event (B) in an ideal EPO-DA network.
Thus, the concentrations of elastically active chains (ν) and nodes (n) can be written as a function of the concentrations of chain scissions (S) and crosslinking events (X) as follows:
where ν0, n0, ν and n are the concentrations of elastically active chains and nodes before and after thermal ageing, respectively.
The glass transition temperature Tg is an increasing function of n (or ν). It can thus be used to assess the impact of thermal oxidation on the macromolecular network. There is a lot of relationships between Tg and n (or ν) in literature, but to our opinion (Colin et al., 2011; Colin and Verdu, 2012a; Colin and Verbu, 2012b), the best one for polymer networks is the Di Marzio’s equation (Di Marzio, 1964):
where KDM is an universal constant (KDM ≈ 3 for tri-functional crosslink nodes), F is the flex parameter characterizing the stiffness of the elastically active chains, and Tgl is the glass transition temperature of an hypothetical linear polymer containing all the structural units of the EPO-DA network under consideration, except its crosslink nodes.
In an ideal network (i.e., without dangling chains), the concentration of nodes is simply related to the concentration of elastically active chains by:
where f is the node functionality (let us recall that f = 3 for ideal EPO-DA networks).
The introduction of Eq. 28 into Eq. 27 leads to:
which leads to:
where Tg0 and Tg are the values of the glass transition temperature before and after thermal ageing, respectively.
The introduction of Eq. 25 into Eq. 31 leads to:
Thus, as expected, chain scissions decrease Tg whereas crosslinking increases it. The introduction of Eqs 21, 22 into Eq. 32 leads finally to:
Experimental
EPO-DA Networks
The three perfect EPO-DA networks (i.e., without dangling chains) under study are characterized by quite different Tg values, typically ranged between 158 and 263°C (see Table 1), thus allowing to analyze the possible effects of molecular mobility on the oxidation kinetics over a relatively wide temperature range. They result from the reaction of common bi-functional or tri-functional epoxy monomers with an aromatic amine hardener: 9,9-bis(3-chloro-4-aminophenyl) fluorine (CAF) or 4,4’-diamino diphenyl sulfone (DDS). Over the past decade, these three networks were considered in turn as potential matrices for composite structure applications at temperatures typically between 70 and 150°C in the civil aeronautical sector.

TABLE 1. Molar mass of the repetitive constitutive unit (mCRU), density (ρ), concentration of oxidation sites ([PH]) and glass transition temperature (Tg) for the three perfect EPO-DA networks under study.
Network No. 3 was first considered in the early 2010s for potential applications at temperatures above 200°C, for which there is clearly a lack of solutions in organic matrix composites in Europe. Its thermal degradation was also the subject of a few articles, for instance (Terekhina et al., 2013; Cinquin et al., 2016; Colin et al., 2016). Networks No. 1 and 2 were only considered for applications near heat sources (i.e., aircraft engine applications) in the past 2 years. Their thermal degradation between 120 and 150°C is reported in recent articles (Colin et al., 2020; Colin et al., 2021).
The concentration in oxidation sites ([PH]) of these three perfect EPO-DA networks was directly determined from their theoretical repetitive monomer unit (see Table 1). It should then be pointed out that, when DDS is the amine hardener, the sulfonyl group protects the C−H bond of the amino-methylene group (i.e., −CH2−N<) formed during the polymerization reaction against oxidation. Indeed, the sulfonyl group is a high electron-attracting group whose inductive effect through aromatic rings leads to an increase in the strength of the C−H bond. This stabilizing effect was first demonstrated by comparing the polymerization kinetics of different epoxy-diamine mixtures (Girard-Reydet et al., 1995). This is the reason why [PH] is lower for network 3 (about 10 mol.L−1) compared to networks 1 and 2 (about 13–15 mol.L−1).
Films and plates of these three EPO-DA networks with thicknesses typically ranging between 25 μm and 1 mm were produced by compression molding, then post-cured under primary vacuum (i.e., 10−3 bar) in accordance with the recommended industrial cure cycle in order to reach the maximum crosslinking density while avoiding any undesired pre-oxidation before thermal exposure. These precautions allowed minimizing the concentration of structural defects (in particular, in hydroperoxides POOH) in the EPO-DA networks. That is the reason why, as explained in Foundations of the Kinetic Model, a high value was chosen for the model parameter b in this study (typically, b = 10).
Thermal Ageing and Physico-Chemical Analyses
The oxidation kinetics of the three EPO-DA networks was studied at 120, 150, 180, and 200°C under an oxygen partial pressure ranged between 0.21 (i.e., ambient air) and 20 bars in autoclaves.
Films of EPO-DA networks were periodically removed from the autoclaves and cooled to room temperature in a desiccator containing silica gel for preventing any moisture recovery prior to be characterized by FTIR spectrophotometry. All FTIR spectra were recorded in a transmission mode between 400 and 4,000 cm−1 with a Perkin Elmer Frontier device, after having averaged the 16 scans obtained with a minimum resolution of 4 cm−1.
As often reported in literature (Bellenger et al., 1981; Dyakonov et al., 1996; Rivaton et al., 1997; Colin et al., 2001a; Musto et al., 2001; Musto, 2003; Mailhot et al., 2005; Dao et al., 2006; Delor-Jestin et al., 2006; Longerias et al., 2007; Galant et al., 2010; Pei et al., 2011), the main structural changes were observed in the carbonyl region where two new wide absorption bands appeared and grew rapidly with exposure time: one centered around 1,690−1,670 cm−1, and the other around 1,720−1,730 cm−1. As an example, Figure 2 shows the changes over time in the FTIR spectrum for network No. 3 at 150°C under 0.21 bar of oxygen (i.e., ambient air). These two bands were assigned to amides and other types of carbonyl products, respectively.
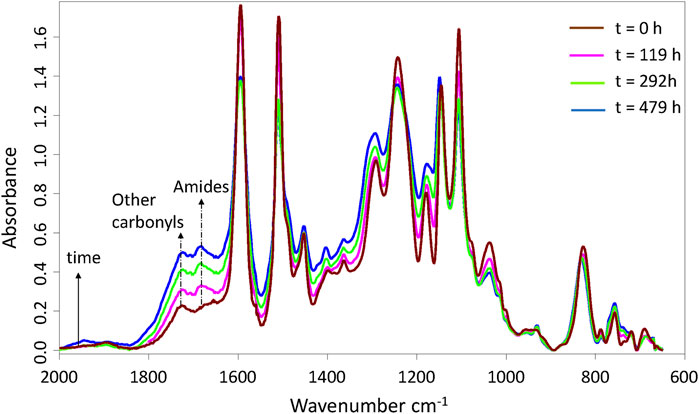
FIGURE 2. Changes in the IR spectrum of network No. 3 (Tactix 123/Tactix 742-DDS) during its thermal ageing at 150°C under 0.21 bar of oxygen (i.e., ambient air).
Unfortunately, it was not possible to precisely identify these latter products mainly resulting from oxidation induced chain scissions in the hydroxyl propyl ether segment (Bellenger and Verdu, 1985) due to their wide variety: aldehydes, carboxylic acids, phenyl formates, etc … Nevertheless, their average concentration throughout the film thickness [P=O] was determined by applying the common Beer-Lambert’s law:
where OD is the optical density of the IR absorption band centered at 1720–1730 cm−1 (dimensionless), ε is the corresponding molar extinction coefficient (expressed in L.mol−1.cm−1), and ep is the film thickness (in cm).
Typical values of ε are ranged between 150 L mol−1.cm−1 (for ketones) and 850 L mol−1.cm−1 (for carboxylic acids) (Flett, 1962; Domke and Steinke, 1986; Lacoste and Carlsson, 1992; Barth, 2007; Da Cruz et al., 2016). In a first approximation, an average value of 500 L mol−1.cm−1 was chosen for carbonyl products in this study.
Plates of EPO-DA networks were removed from the autoclaves after definite durations and cooled at room temperature according to the same procedure as for films. Parallelepipedic shaped barrels of 25 × 2 × 1 mm3 were machined from the plates in order to be analyzed by mechanical spectrometry in a tension mode between −110 and 330°C with a TA Instruments DMA Q800 device. The tests were performed with a controlled sinusoidal strain in the linear domain of the material viscoelasticity and the corresponding stress was measured. From the stress and strain values, the complex modulus E* was calculated:
where E′ is the storage (elastic component) modulus, E′′ is the loss (viscous component) modulus and
The frequency and heating rate were set at 1 Hz and 2°C min−1, respectively. The principal relaxation temperature Tα, associated to the glass transition temperature Tg, was taken at the maximum of the α dissipation band. Examples of changes in the DMA thermogram of network No. 3 (Tactix 123/Tactix 742-DDS) are reported in Supplementary Material.
It should be mentioned that the repeatability of the aging tests was only checked for specific ageing conditions because of the long durations of these tests. As an example, Figure 3 compares three different campaigns of ageing tests performed at 180°C under 0.21 bar of oxygen (i.e., ambient air). It can be seen that the three curves of carbonyl build-up only differ by the duration of their induction period, which is typically ranged between 6 and 13 h. Such a low experimental variability can be explained by small differences in the initial state of the samples (in particular, in their initial concentration of hydroperoxides) (Colin et al., 2006). In addition, at the end of the induction period, the three curves exhibit the same auto-acceleration of the oxidation kinetics.
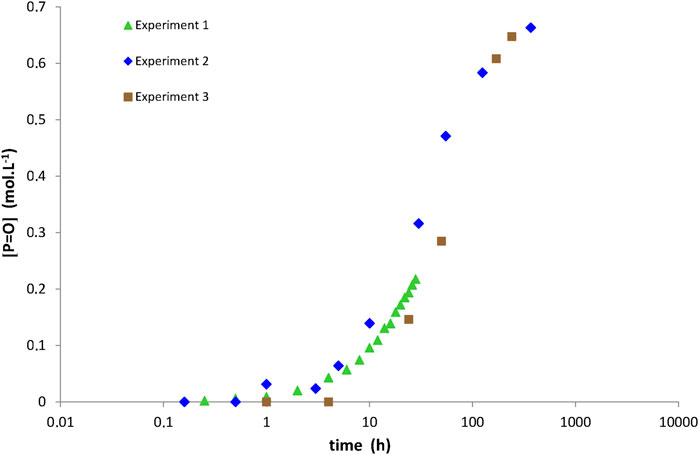
FIGURE 3. Carbonyl build-up in 100 µm thick films of network No. 3 (Tactix 123/Tactix 742-DDS) at 180°C under 0.21 bar of oxygen (i.e., ambient air). Comparison between three different campaigns of ageing tests.
Due to the high test repeatability, it was decided to group together all the experimental data obtained under the same ageing condition within a single experimental curve and no longer distinguish original from replicate data thereafter (both for [P=O] and Tg).
Results and Discussion
Determination of Model Parameters
Let us recall that the validity of the analytical kinetic model constituted by Eq. 1 to Eq. 15 was already checked in a previous article devoted to the thermal oxidation kinetics of networks No. 1 and 2 at 120 and 150°C under an oxygen partial pressure ranged between 0.21 (i.e., ambient air) and 10 bars (Colin et al., 2021). It was shown that Eq. 14 allows accurately accounting for the three first stages of the thermal oxidation kinetics, i.e., the induction period, the sharp auto-acceleration of the oxidation reaction at the end of the induction period, and the steady-state regime. However, it cannot account for the last stage, i.e., the sudden slow-down of the oxidation reaction, when the concentration of oxidation sites is vanishing, because of the starting assumption of low conversion ratios (i.e., [PH] ≈ [PH]0 ≈ constant). It was also shown that this behavioural deviation between theory and experiment appears when [PH] typically decreases by about ten percent, and it amplifies with exposure time. However, as the embrittlement of EPO-DA matrices is generally observed at low conversion ratios, i.e. during the induction period or the auto-acceleration of the oxidation reaction, it was concluded that the analytical kinetic model is largely sufficient for fully applying the classical methodology for lifetime prediction thereafter. The corresponding values of the model parameters determined for networks No. 1 and 2 by the inverse solving method are recalled in Table 2.

TABLE 2. Values of parameters used for simulating the carbonyl build-up and Tg decrease for the three EPO-DA networks under study between 120 and 200°C with Eq. 14 and Eq. 33, respectively.
Examples of simulations with Eq. 14 for network No. 3 at 150°C under an oxygen partial pressure ranged between 0.21 and 20 bars, but also between 120 and 200°C under an oxygen partial pressure of 0.21 bar (i.e., ambient air), are now reported in Figures 4, 5, respectively. The same conclusions as for networks No. 1 and 2 can now be done for network No. 3. The corresponding values of the model parameters determined for network No. 3 by the inverse solving method are also listed in Table 2. Let us recall that the order of magnitudes of γ1CO and γ6CO come from a recent publication (Colin et al., 2020).
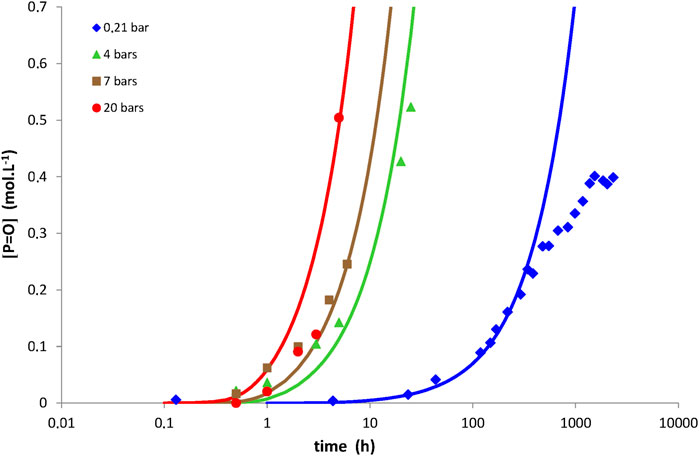
FIGURE 4. Carbonyl build-up in 100 µm thick films of network No. 3 (Tactix 123/Tactix 742-DDS) at 150°C between 0.21 bar (i.e., ambient air) and 20 bars of oxygen. Comparison between simulations with Eq. 14 (solid lines) and experimental data (points).
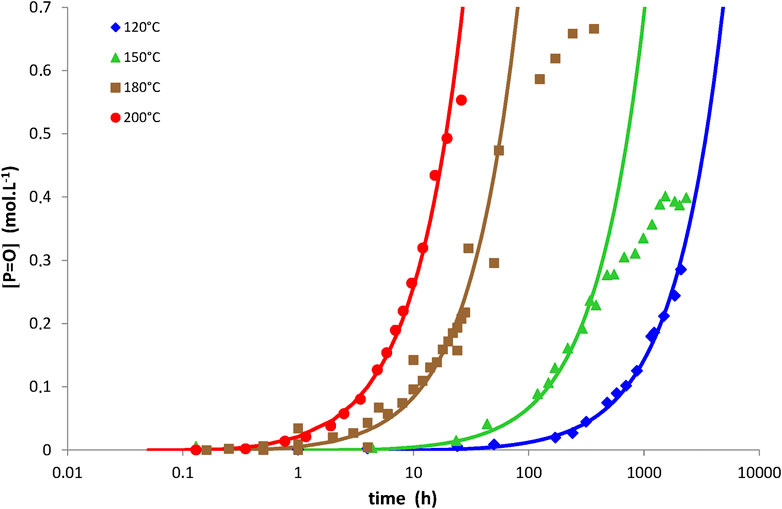
FIGURE 5. Carbonyl build-up in 100 µm thick films of network No. 3 (Tactix 123/Tactix 742-DDS) between 120 and 200°C under 0.21 bar of oxygen (i.e., ambient air). Comparison between simulations with Eq. 14 (solid lines) and experimental data (points).
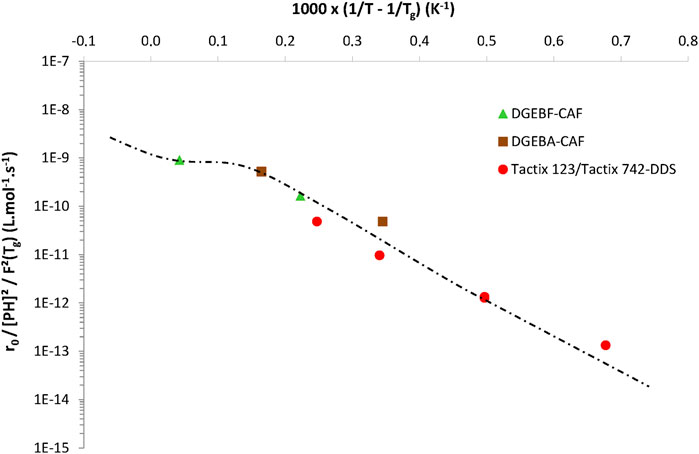
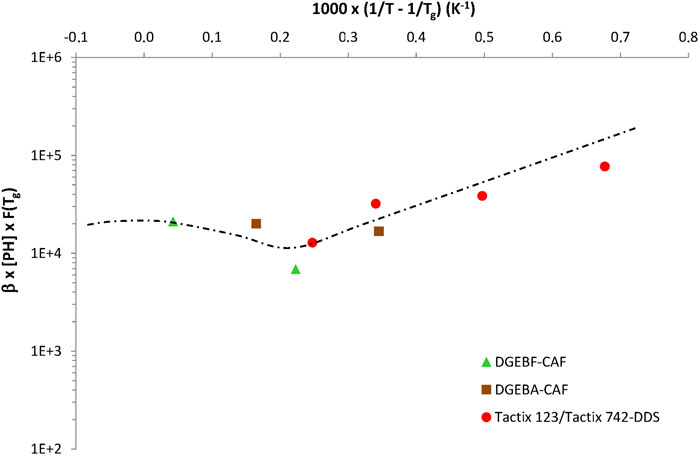
The values thus obtained for the three other model parameters (i.e., k1b, r0, and β) were plotted in Arrhenius graphs in order to elucidate their temperature dependence. The following conclusions can be drawn:
1) Eq. 14 gives almost the same values of k1b as those recently determined with the “numerical version” of the kinetic model for all EPO-DA networks (Colin et al., 2020). Thus, it is confirmed that k1b obeys the following general Arrhenius law:
As an illustration, Figure 6 reports the Arrhenius graph obtained for k1b for networks No. 1, 2, and 3.
2) In contrast, the temperature dependence of parameters r0 as β is much more complicated because they depend both on the concentration of oxidation sites (see Eqs 10, 13, respectively) and the molecular mobility (Colin et al., 2020). It is therefore necessary to correct the values determined for these two parameters by the concentration of oxidation sites [PH] and the effect of molecular mobility in order to obtain master curves in an Arrhenius diagram for all the EPO-DA networks. In a first approach, the impact of molecular mobility in EPO-DA networks was described taking a simple exponential function of Tg (Colin et al., 2020):
which leads to:
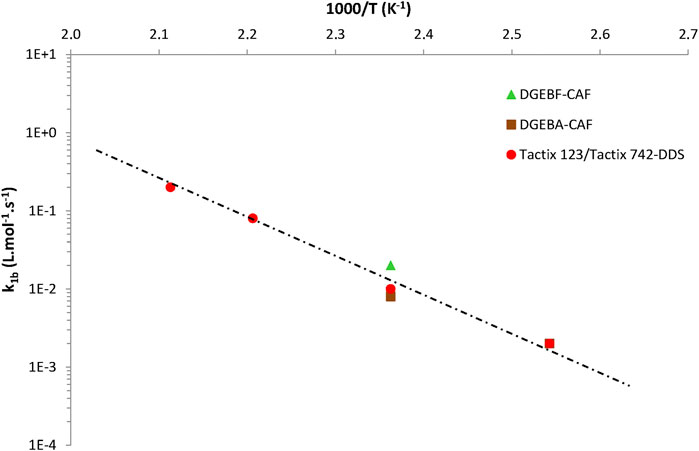
FIGURE 6. Arrhenius graph between 120 and 200°C for the rate constant k1b for the three EPO-DA networks under study.
Let us recall that β−1 roughly corresponds to the critical oxygen concentration CC above which oxygen excess is reached (see Eq. 10). Of course, the corresponding value of PO2C can be easily deduced using the common Henry’s law (Eq. 9). The values of CC and PO2C thus calculated for the three EPO-DA networks under study are reported in Table 3. In the glassy domain, it is found that CC and PO2C are both increasing functions of temperature. In the glass transition zone, typically at 150°C for network No. 1 (i.e., for DGEBF-CAF), it is found that PO2C is about 5 bars, i.e., a value often reported for several other EPO-DA networks in literature, for instance in reference (Olivier 2008).

TABLE 3. Critical values of oxygen concentration and oxygen partial pressure for the three EPO-DA networks under study between 120 and 200°C.
Prediction of Thermomechanical Properties
Then, Eq. 33 was used to predict the changes in Tg of the different EPO-DA networks under study. Fortunately, the three parameters (i.e., KDM, F, and Tgl) of the Di Marzio’s equation were already carefully determined for network No. 3 in a previous study (Terekhina et al., 2013). Their values are recalled in Table 4.

TABLE 4. Values of the parameters of the Di Marzio’s equation for network No. 3 (i.e., for Tactix 123/Tactix 742-DDS).
Examples of simulations with Eq. 33 for network No. 3 at 200°C under oxygen partial pressures of 0.21 bar (i.e., ambient air) and 10 bars are reported in Figure 9. It can be seen that Eq. 33 satisfyingly predicts the catastrophic decrease in Tg because of a predominant chain scission process. In a first approach, the crosslinking events were totally ignored and thus, their yield γ6X in the termination reactions was set to zero. It was found that a very small amount of chain scissions, calculated with a yield γ1S much lower than unity (typically, γ1S = 0.16%), allows explaining the observed changes in the thermomechanical behaviour of network No. 3.
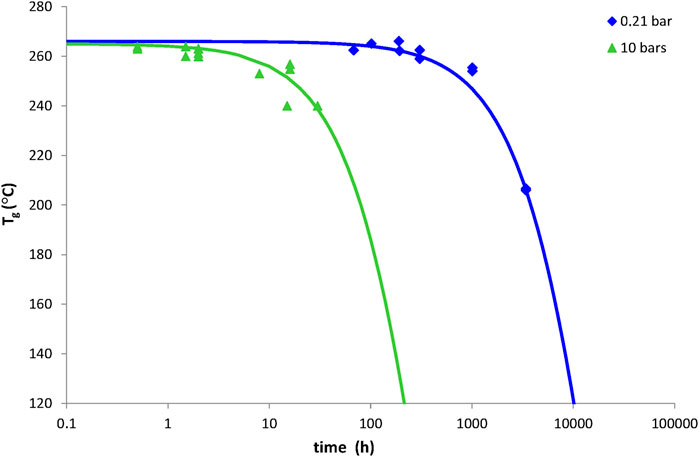
FIGURE 9. Tg decrease in 1 mm thick plates of network No. 3 (Tactix 123/Tactix 742-DDS) at 150°C under 0.21 bar (i.e., ambient air) and 10 bars of oxygen. Comparison between simulations with Eq. 33 (solid lines) and experimental data (points).
It is common to define the temperature range of use of a composite material from the Tg value of its matrix. Indeed, it is generally considered that, when the temperature dangerously approaches Tg, the mechanical properties of the composite material (in particular, its elastic properties) start to drop dramatically. In the case of network No. 3, considered for high temperature applications in the aeronautic field because of its high initial Tg value (Tg0 = 263°C), the fact that chain scissions largely predominate over crosslinking events poses a serious problem. Indeed, a too great decrease in Tg will no longer allow the composite material to fulfill its initial function of mechanical structure. From this brief analysis, it can be concluded that an end-of-life criterion for network No. 3 would be a minimum value of Tg, denoted TgF. In other words, the lifetime tF of network No. 3 could be determined from Eq. 33 as follows:
Conclusion
The analytical kinetic model developed for the thermal oxidation of two first EPO-DA networks in reference (Colin et al., 2021) was successfully generalized to an additional EPO-DA network in the present study. The model parameters were determined by inverse solving method from the experimental curves of carbonyl build-up and Tg decrease between 120 and 200°C under an oxygen partial pressure ranged between 0.21 (i.e., ambient air) and 10 bars. It was confirmed that the rate constant k1b obeys a general Arrhenius law for all the EPO-DA networks. In contrast, the temperature dependence of parameters r0 as β is much more complicated because they depend both on the concentration of oxidation sites and the molecular mobility. However, it was shown that master curves can be obtained in an Arrhenius diagram for these two parameters if their values are corrected by the concentration of oxidation sites and a relatively simple exponential function of Tg, proposed for describing the impact of molecular mobility.
In its current form, this new analytical kinetic model can be now easily implemented into commercial mechanical calculation codes for determining the consequences of thermal oxidation on the thermomechanical properties and predicting the lifetime of composite material structures. In particular, when chain scissions largely predominate over crosslinking, a minimum value of Tg can be used as end-of-life criterion.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
XC–experimental testing and results post-processing, kinetic model development and calculation, writing original manuscript. JD–experiment scheme guidance, manuscript revision. GM–manuscript revision, project coordinator.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2021.720455/full#supplementary-material
References
Alston, W. B. (1980). Characterization of PMR-15 in Thermooxidatively Exposed Graphite Fiber Composites. In Proc. 12th Nat. SAMPE Tech. Conf. Seatle, WA. 7–9.
Audouin, L., Langlois, V., Verdu, J., and De Bruijn, J. C. M. (1994). Role of Oxygen Diffusion in Polymer Ageing: Kinetic and Mechanical Aspects. J. Mater. Sci. 29, 569–583. doi:10.1007/bf00445968
Barjasteh, E., Bosze, E. J., Tsai, Y. I., and Nutt, S. R. (2009). Thermal Aging of Fiberglass/carbon-Fiber Hybrid Composites. Composites A: Appl. Sci. Manufacturing 40 (12), 2038–2045. doi:10.1016/j.compositesa.2009.09.015
Barjasteh, E., Kar, N., and Nutt, S. R. (2011). Effect of Filler on Thermal Aging of Composites for Next-Generation Power Lines. Composites Part A: Appl. Sci. Manufacturing 42 (12), 1873–1882. doi:10.1016/j.compositesa.2011.08.006
Barth, A. (2007). Infrared Spectroscopy of Proteins. Biochim. Biophys. Acta (Bba) - Bioenerg. 1767, 1073–1101. doi:10.1016/j.bbabio.2007.06.004
Bellenger, V., Bouchard, C., Claveirolle, P., and Verdu, J. (1981). Photo-Oxidation of Epoxy Resins Cured by Non-aromatic Amines. Polym. Photochem. 1 (1), 69–80. doi:10.1016/0144-2880(81)90016-6
Bellenger, V., and Verdu, J. (1985). Oxidative Skeleton Breaking in Epoxy-Amine Networks. J. Appl. Polym. Sci. 30 (1), 363–374. doi:10.1002/app.1985.070300132
Bowles, K. J., Jayne, D., Leonhardt, T. A., and Bors, D. (1994). Thermal Stability Relationships between PMR-15 Resin and its Composites. J. Adv. Mater. 26 (1), 23–32.
Bowles, K. J., Jayne, D., and Leonhardt, T. A. (1993). Isothermal Aging Effect on PMR15. SAMPE Quart 24 (2), 2–9.
Bowles, K. J., and Meyers, A. (1986).Specimen Geometry Effects on Graphite/PMR-15 Composites during Thermo-Oxidative Aging. In Proc. 31st Int. SAMPE Symp. Exhib. Los Angeles, 1285–1299.
Bowles, K. J., and Nowak, G. (1988). Thermo-Oxidative Stability Studies of Celion 6000/PMR-15 Unidirectional Composites, PMR-15 and Celion 6000 Fiber. J. Compos. Mater. 22 (6), 966. doi:10.1177/002199838802201005
Cinquin, J., Colin, X., Fayolle, B., Mille, M., Terekhina, S., Chocinski-Arnault, L., et al. (2016). Thermo-oxidation Behaviour of Organic Matrix Composite Materials at High Temperatures. Adv. aircraft spacecraft Sci. 3 (2), 171–195. doi:10.12989/aas.2016.3.2.171
Colin, X., Essatbi, F., Delozanne, J., and Moreau, G. (2021). A New Analytical Model for Predicting the Thermal Oxidation Kinetics of Composite Organic Matrices. Application to Diamine Cross-Linked Epoxy. Polym. Degrad. Stab. 186, 109513. doi:10.1016/j.polymdegradstab.2021.109513
Colin, X., Essatbi, F., Delozanne, J., and Moreau, G. (2020). Towards a General Kinetic Model for the Thermal Oxidation of Epoxy-Diamine Networks. Effect of the Molecular Mobility Around the Glass Transition Temperature. Polym. Degrad. Stab. 181, 109314. doi:10.1016/j.polymdegradstab.2020.109314
Colin, X., Fayolle, B., Audouin, L., and Verdu, J. (2006). The Classical Kinetic Model for Radical Chain Oxidation of Hydrocarbon Substrates Initiated by Bimolecular Hydroperoxide Decomposition. Int. J. Chem. Kinet. 38 (11), 666–676. doi:10.1002/kin.20201
Colin, X., Fayolle, B., and Cinquin, J. (2016). Nouvelles Avancées en Modélisation Cinétique de la Thermo-Oxydation des Matrices Epoxy-Diamine. Mater. Tech. 104 (2), 102. doi:10.1051/mattech/2016008
Colin, X., Marais, C., and Favre, J. P. (19991999). Damage/Weight Loss Relationship of Polymer Matrix Composites under Thermal Ageing. In Proc. 12th Int. Conf. Compos. Mater. Paris, France, 311.
Colin, X., Marais, C., and Verdu, J. (2001a). A New Method for Predicting the thermal Oxidation of Thermoset Matrices. Polym. Test. 20 (7), 795–803. doi:10.1016/s0142-9418(01)00021-6
Colin, X., Marais, C., and Verdu, J. (2002). Kinetic Modelling and Simulation of Gravimetric Curves: Application to the Oxidation of Bismaleimide and Epoxy Resins. Polym. Degrad. Stab. 78 (3), 545–553. doi:10.1016/s0141-3910(02)00230-6
Colin, X., Marais, C., and Verdu, J. (2005a). Kinetic Modelling of the Stabilizing Effect of Carbon Fibres on Thermal Ageing of Thermoset Matrix Composites. Composites Sci. Tech. 65, 117–127. doi:10.1016/j.compscitech.2004.06.009
Colin, X., Marais, C., and Verdu, J. (2001b). Thermal Oxidation Kinetics for a Poly(bismaleimide). J. Appl. Polym. Sci. 82 (14), 3418–3430. doi:10.1002/app.2203
Colin, X., Mavel, A., Marais, C., and Verdu, J. (2005b). Interaction between Cracking and Oxidation in Organic Matrix Composites. J. Compos. Mater. 39 (15), 1371–1389. doi:10.1177/0021998305050430
Colin, X., Teyssèdre, G., and Fois, M. (2011). “Ageing and Degradation of Multiphase Polymer Systems,” in Handbook of Multiphase Polymer Systems. Editors A. Boudenne, L. Ibos, Y. Candau, and S. Thomas (Chichester, United Kingdom: John Wiley & Sons), 797–841. doi:10.1002/9781119972020.ch21
Colin, X., and Verdu, J. (2012a). “Aging of Organic Matrix Composite Materials,” in Wiley Encyclopedia of Composites. Editors L. Nicolais, A. Borzacchielo, and S. M. Lee. 2nd edition (New York, NY: John Wiley & Sons), 35–49.
Colin, X., and Verdu, J. (2012b). “Mechanisms and Kinetics of Organic Matrix Thermal Oxidation,” in Long-Term Durability of Polymer Matrix Composites. Editors K. V. Pochiraju, G. P. Tandon, and G. A. Schoeppner (New York, NY: Springer), 311–344. doi:10.1007/978-1-4419-9308-3_8
Colin, X., and Verdu, J. (2005). Strategy for Studying Thermal Oxidation of Organic Matrix Composites. Composites Sci. Tech. 65, 411–419. doi:10.1016/j.compscitech.2004.09.011
Colin, X., and Verdu, J. (2011).Themooxidative and Thermohydrolytic Aging of Composite Organic Matrices. In Resin Composites: Properties, Production and Applications, D.B. Song. New York, NY: Nova Science Publishers, Inc, 255–297.
Colin, X., and Verdu, J. (2003). Thermal Ageing and Lifetime Prediction for Organic Matrix Composites. Plastics, Rubber and Composites 32 (8/9), 349–356. doi:10.1179/146580103225004117
Crews, L. K., and McManus, H. L. (1997). Modelling the High Temperature Degradation of Graphite/Epoxy. Proc. 12th Tech. Conf. Compos. Mater. Detroit, MI, 1123–1132.
Cunningham, J., and McManus, H. L. (1996). Editorial. Logic Jnl IGPL 4, 353. doi:10.1093/jigpal/4.3.353
Da Cruz, M., Van Schoors, L., Benzarti, K., and Colin, X. (2016). Thermo-Oxidative Degradation of Additive Free Polyethylene. Part I- Analysis of the Chemical Modifications at Molecular and Macromolecular Scales. J. Appl. Polym. Sci. 133 (18), 43287. doi:10.1002/app.43287
Dao, B., Hodgkin, J., Krstina, J., Mardel, J., and Tian, W. (2006). Accelerated Aging versus Realistic Aging in Aerospace Composite Materials. I. The Chemistry of thermal Aging in a Low-Temperature-Cure Epoxy Composite. J. Appl. Polym. Sci. 102 (5), 4291–4303. doi:10.1002/app.24862
Decelle, J., Huet, N., and Bellenger, V. (2003). Oxidation Induced Shrinkage for Thermally Aged Epoxy Networks. Polym. Degrad. Stab. 81 (2), 239–248. doi:10.1016/s0141-3910(03)00094-6
Delor-Jestin, F., Drouin, D., Cheval, P.-Y., and Lacoste, J. (2006). Thermal and Photochemical Ageing of Epoxy Resin - Influence of Curing Agents. Polym. Degrad. Stab. 91 (6), 1247–1255. doi:10.1016/j.polymdegradstab.2005.09.009
DiMarzio, E. A. (1964). On the Second-Order Transition of a Rubber. J. Res. Natl. Bur. Stan. Sect. A. 68A, 611–617. doi:10.6028/jres.068a.059
Domke, W.-D., and Steinke, H. (1986). Oxidative Structures in Polyolefins: FT-IR Method of Quantitative Determination. J. Polym. Sci. A. Polym. Chem. 24 (10), 2701–2705. doi:10.1002/pola.1986.080241024
Dyakonov, T., Mann, P. J., Chen, Y., and Stevenson, W. T. K. (1996). Thermal Analysis of Some Aromatic Amine Cured Model Epoxy Resin Systems-II: Residues of Degradation. Polym. Degrad. Stab. 54 (1), 67–83. doi:10.1016/0141-3910(96)00096-1
Flett, M. (1962). Intensities of Some Group Characteristic Infra-red Bands. Spectrochimica Acta 18, 1537–1556. doi:10.1016/s0371-1951(62)80282-3
Galant, C., Fayolle, B., Kuntz, M., and Verdu, J. (2010). Thermal and Radio-Oxidation of Epoxy Coatings. Prog. Org. Coat. 69 (4), 322–329. doi:10.1016/j.porgcoat.2010.07.005
Gillen, K. T., and Clough, R. L. (1989). “Techniques for Monitoring Heterogeneous Oxidation of Polymers,” in Handbook of Polymer Science and Technology. Editor M. P. Cheremisinoff (New York, NY: Marcel Dekker), 167–202.
Girard-Reydet, E., Riccardi, C. C., Sautereau, H., and Pascault, J. P. (1995). Epoxy-Aromatic Diamine Kinetics. Part 1. Modeling and Influence of the Diamine Structure. Macromolecules 28, 7599–7607. doi:10.1021/ma00127a003
Huang, J., Minne, W., Drozdzak, R., Recher, G., Le Gac, P. Y., and Richaud, E. (2020). Thermal Oxidation of Poly(dichloropentadiene). Decomposition Hydroperoxides. Polym. Degrad. Stab. 174, 109102. doi:10.1016/j.polymdegradstab.2020.109102
Kerr, J. R., and Haskins, J. F. (1984). Effects of 50,000 H of Thermal Aging on Graphite/Epoxy and Graphite/Polyimide Composites. AIAA J. 22 (1), 96–102. doi:10.2514/3.8345
Lacoste, J., and Carlsson, D. J. (1992). Gamma-, Photo-, and Thermally-Initiated Oxidation of Linear Low Density Polyethylene: A Quantitative Comparison of Oxidation Products. J. Polym. Sci. A. Polym. Chem. 30, 493–500. doi:10.1002/pola.1992.080300316
Lafarie-Frenot, M. C., Grandidier, J. C., Gigliotti, M., Olivier, L., Colin, X., Verdu, J., et al. (2010). Thermo-Oxidation Behaviour of Composite Materials at High Temperatures: A Review of Research Activities Carried Out within the COMEDI Program. Polym. Degrad. Stab. 95 (6), 965–974. doi:10.1016/j.polymdegradstab.2010.03.019
Lafarie-Frenot, M. C., and Rouquie, S. (2004). Influence of the Oxidative Environments on Damage in C/Epoxy Laminates Subjected to Thermal Cycling. Compos. Sci. Technol. 64 (10-11), 1725–1735. doi:10.1016/j.compscitech.2004.01.005
Longerias, N., Sebban, M., Palmas, P., Rivaton, A., and Gardette, J. L. (2007). Degradation of Epoxy Resins under High Energy Electron Beam Irradiation: Radio-Oxidation. Polym. Degrad. Stab. 92 (12), 2190–2197.
Mailhot, B., Morlat-Thérias, S., Ouahioune, M., and Gardette, J.-L. (2005). Study of the Degradation of an Epoxy/Amine Resin, 1. Macromol. Chem. Phys. 206 (5), 575–584. doi:10.1002/macp.200400395
McManus, H. L., and Cunningham, R. A. (1997). “Materials and Mechanics Analyses of Durability Tests for High-Temperature Polymer Matrix Composites,” in ASTM STP 1302: High Temperature and Environmental Effects on Polymeric Composites. Editors T. S. Gates, and A. H. Zureick (West Conshohocken, PA: ASTM), 1–17.
McManus, H. L., Foch, B. J., and Cunningham, R. A. (2000). Mechanism-Based Modeling of Long-Term Degradation. J. Compos. Technol. Res. 22 (3), 146–152.
Meador, M. A. B., Lowell, C. E., Cavano, P. J., and Herrera-Fierro, P. (1996). On the Oxidative Degradation of Nadic Endcapped Polyimides: I. Effect of Thermocycling on Weight Loss and Crack Formation. High Perform. Polym. 8, 363–379. doi:10.1088/0954-0083/8/3/003
Musto, P., Ragosta, G., Russo, P., and Mascia, L. (2001). Thermal-oxidative Degradation of Epoxy and Epoxy-Bismaleimide Networks: Kinetics and Mechanism. Macromol. Chem. Phys. 202 (18), 3445–3458. doi:10.1002/1521-3935(20011201)202:18<3445::aid-macp3445>3.0.co;2-n
Musto, P. (2003). Two-Dimensional FTIR Spectroscopy Studies on the Thermal-Oxidative Degradation of Epoxy and Epoxy−Bis(maleimide) Networks. Macromolecules 36 (9), 3210–3221. doi:10.1021/ma0214815
Nam, J. D., and Seferis, J. C. (1992). Anisotropic Thermo-Oxidative Stability of Carbon Fiber Reinforced Polymeric Composites. SAMPE Quart 24 (1), 10–18.
Nelson, J. B. (1983). “Thermal Ageing of Graphite/Polyimide Composites,” in ASTM STP-813: Long-Term Behavior of Composites. Editor T. K. O’Brien (Philidelphia, PA: ASTM), 206–221.
Olivier, L. (2008). Prévision du Vieillissement Thermo-Oxydant de Composites à Matrice Organique Dédiés à l’Aéronautique. PhD dissertation. Poitiers, France: Université de Poitiers.
Olivier, L., Baudet, C., Bertheau, D., Grandidier, J. C., and Lafarie-Frenot, M. C. (2009). Development of Experimental, Theoretical and Numerical Tools for Studying Thermo-Oxidation of CFRP Composites. Composites Part A: Appl. Sci. Manufacturing 40 (8), 1008–1016. doi:10.1016/j.compositesa.2008.04.005
Olivier, L., Ho, N. Q., Grandidier, J. C., and Lafarie-Frenot, M. C. (2008). Characterization by Ultra-micro Indentation of an Oxidized Epoxy Polymer: Correlation with the Predictions of a Kinetic Model of Oxidation. Polym. Degrad. Stab. 93 (2), 489–497. doi:10.1016/j.polymdegradstab.2007.11.012
Parvatareddy, H., Wang, J. Z., Lesko, J. J., Dillard, D. A., and Reifsnider, K. L. (1996). An Evaluation of Chemical Aging/Oxidation in High Performance Composites Using the Vickers Micro-indentation Technique. J. Compos. Mater. 30 (2), 210–230. doi:10.1177/002199839603000204
Pei, Y.-m., Wang, K., Zhan, M.-s., Xu, W., and Ding, X.-j. (2011). Thermal-oxidative Aging of DGEBA/EPN/LMPA Epoxy System: Chemical Structure and Thermal-Mechanical Properties. Polym. Degrad. Stab. 96 (7), 1179–1186. doi:10.1016/j.polymdegradstab.2011.04.019
Pochiraju, K., and Tandon, G. P. (2009). Interaction of Oxidation and Damage in High Temperature Polymeric Matrix Composites. Composites Part A: Appl. Sci. Manufacturing 40 (12), 1931–1940. doi:10.1016/j.compositesa.2009.03.010
Pochiraju, K. V. (2012). “Modeling Thermo-Oxidative Aging and Degradation of Composites,” in Long-Term Durability of Polymer Matrix Composites. Editors K. V. Pochiraju, G. P. Tandon, and G. A. Schoeppner (New York, NY: Springer), 383–425. doi:10.1007/978-1-4419-9308-3_10
Pochiraju, K. V., Tandon, G. P., and Schoeppner, G. A. (2008). Evolution of Stress and Deformations in High-Temperature Polymer Matrix Composites during Thermo-Oxidative Aging. Mech. Time-depend. Mater. 12 (1), 45–68. doi:10.1007/s11043-007-9042-5
Rivaton, A., Moreau, L., and Gardette, J.-L. (1997). Photo-oxidation of Phenoxy Resins at Long and Short Wavelengths-I. Identification of the Photoproducts. Polym. Degrad. Stab. 58 (3), 321–332. doi:10.1016/s0141-3910(97)00089-x
Salin, I. M., and Seferis, J. C. (1993). Anisotropic Effects in Thermogravimetry of Polymeric Composites. J. Polym. Sci. B Polym. Phys. 31 (8), 1019–1027. doi:10.1002/polb.1993.090310812
Salin, I., and Seferis, J. C. (1996a). Anisotropic Degradation of Polymeric Composites: From Neat Resin to Composite. Polym. Compos. 17 (3), 430–442. doi:10.1002/pc.10631
Salin, I., and Seferis, J. C. (1996b). Mass Transfer Effects in Degradation of Bismaleimide Matrix Composite. J. Appl. Polym. Sci. 62 (7), 1023–1027. doi:10.1002/(sici)1097-4628(19961114)62:7<1023::aid-app7>3.0.co;2-m
Schoeppner, G. A., Tandon, G. P., and Ripberger, E. R. (2007). Anisotropic Oxidation and Weight Loss in PMR-15 Composites. Composites Part A: Appl. Sci. Manufacturing 38, 890–904. doi:10.1016/j.compositesa.2006.07.006
Scola, D. A., and Vontell, J. H. (1991). Mechanical Properties and Mechanism of the Degradation Process of 316°C Isothermally Aged Graphite fiber/PMR-15 Composites. Polym. Eng. Sci. 31 (1), 6–13. doi:10.1002/pen.760310103
Skontorp, A., Wong, M. S., and Wang, S. S. (1995). High Temperature Anisotropic Oxidation of Carbon Fiber Reinforced Polyimide Composites: Theory and Experiments. Proc. 10th Int. Conf. Compos. Mater. Whistler B.C., Can. 1995, 375–384.
Street, K. N., Russell, A. J., and Bonsang, F. (1988). Thermal Damage Effects on Delamination Toughness of a Graphite/Epoxy Composite. Composites Sci. Tech. 32, 1–14. doi:10.1016/0266-3538(88)90026-7
Tandon, G. P. (2012). “Characterization of Thermo-Oxidation in Laminated and Textile Composites,” in Long-term Durability of Polymer Matrix Composites. Editors K. V. Pochiraju, G. P. Tandon, and G. A. Schoeppner (New York, NY: Springer), 345–382. doi:10.1007/978-1-4419-9308-3_9
Tandon, G. P., and Pochiraju, K. V. (2011). Heterogeneous Thermo-Oxidative Behavior of Multidirectional Laminated Composites. J. Compos. Mater. 45 (4), 415–435. doi:10.1177/0021998310376109
Tandon, G. P., and Pochiraju, K. V. (2006). Modeling Thermo-Oxidative Layer Growth in High-Temperature Resins. J. Eng. Mater. Technol. 128, 107–116.
Tandon, G. P., Pochiraju, K. V., and Schoeppner, G. A. (2006). Modeling of Oxidative Development in PMR-15 Resin. Polym. Degrad. Stab. 91, 1861–1869. doi:10.1016/j.polymdegradstab.2005.11.008
Tandon, G. P., Ragland, W. R., and Schoeppner, G. A. (2009). Using Optical Microscopy to Monitor Anisotropic Oxidation Growth in High-Temperature Polymer Matrix Composites. J. Compos. Mater. 43 (5), 583–603. doi:10.1177/0021998308097685
Terekhina, S., Mille, M., Fayolle, B., and Colin, X. (2013). Oxidation Induced Changes in Viscoelastic Properties of a Thermostable Epoxy Matrix. Polym. Sci. Ser. A. 55 (10), 614–624. doi:10.1134/s0965545x13090058
Tsotsis, T. K., Keller, S., Lee, K., Bardis, J., and Bish, J. (2001). Aging of Polymeric Composite Specimens for 5000 hours at Elevated Pressure and Temperature. Composites Sci. Tech. 61, 75–86. doi:10.1016/s0266-3538(00)00196-2
Tsotsis, T. K., and Lee, S. M. (1998). Long-Term Thermo-Oxidative Aging in Composite Materials: Failure Mechanisms. Compos. Sci. Technol. 58 (3-4), 355–368. doi:10.1016/s0266-3538(97)00123-1
Tsotsis, T. K. (1998). Long-Term Thermo-Oxidative Aging in Composite Materials: Experimental Methods. J. Compos. Mater. 32 (11), 1115–1135. doi:10.1177/002199839803201104
Keywords: epoxy matrix, thermal oxidation, analytical kinetic model, chain scissions, glass transition temperature, lifetime prediction
Citation: Colin X, Delozanne J and Moreau G (2021) New Advances in the Kinetic Modeling of Thermal Oxidation of Epoxy-Diamine Networks. Front. Mater. 8:720455. doi: 10.3389/fmats.2021.720455
Received: 04 June 2021; Accepted: 28 July 2021;
Published: 10 August 2021.
Edited by:
Francesca Lionetto, University of Salento, ItalyReviewed by:
Veronica Calado, Federal University of Rio de Janeiro, BrazilYan Meng, Beijing University of Chemical Technology, China
Copyright © 2021 Colin, Delozanne and Moreau. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xavier Colin, eGF2aWVyLmNvbGluQGVuc2FtLmV1
 Xavier Colin
Xavier Colin Justine Delozanne2
Justine Delozanne2 Gurvan Moreau
Gurvan Moreau