A Universal Approach for Maximizing Terahertz Wave Absorption in Graphene Cut-Wires

Graphene micro-/nanostructures and their arrays have attracted considerable attention in infrared (IR) and terahertz (THz) applications due to their strong plasmon responses. However, as too many parameters, including geometry, carrier concentration, frequency, and adjacent substrate, can affect the plasmonic behaviors of the micro-/nanostructures, the optimization of the THz-IR responses, such as absorption and reflection, of these structures and their arrays require tremendous computations on parameter scanning. Here, we propose a theoretical approach to design graphene cut-wires with maximized THz wave absorption. Analytical expression describing the THz absorption/reflection of graphene cut-wires is derived. Accordingly, a maximum THz wave absorption of the array, regardless of its operating frequencies and geometrical parameters, can be achieved by simply tuning the cut-wires duty ratio. The analytical results are further validated by numerical simulations. This intuitive design manner is of significance for the design of graphene arrays with high-efficiency THz responses as well as promoting their practical applications in THz functional devices.

Introduction

Surface plasmons (SPs) refer to the collective electron oscillations at the conductor-dielectric interface (Low and Avouris, 2014). Their outstanding capabilities of manipulating and localizing electromagnetic fields at the subwavelength scale has triggered various applications in nanophotonics in the visible spectral region (Shalaev, 2007; Luk’yanchuk et al., 2010), including photovoltaic device (Atwater and Polman, 2010), biosensing (Xu et al., 1999; Kabashin et al., 2009), integrated photonic devices, (Gramotnev and Bozhevolnyi, 2010; Schuller et al., 2010; Novotny & van Hulst, 2011), thermal radiation control, (Basov et al., 2016) etc., However, when it comes to IR and especially THz bands, SPs in noble metals experience a severe reduction in optical confinement, which hampers its practical applications (Maier, 2007). In contrast, graphene has attracted considerable attention recently as an excellent SPs materials in THz spectral regions owing to the capability of supporting highly confined THz plasmonic modes. As a two-dimensional material, graphene can in addition be electrically tuned by injecting charge carriers so that their plasmonic responses can be controlled dynamically, (Huard et al., 2007), leading to a variety of potential applications in active optoelectronic devices (Luo et al., 2013; Low and Avouris, 2014; Otsuji et al., 2014; Cui et al., 2021).

Despite its importance, the atomic thickness and low free-carrier concentration of graphene still lead to its weak interactions with electromagnetic fields in comparison with its metal counterparts. Inspired by the design concept of metamaterials and metasurfaces, enormous efforts have been devoted to pattern and shape graphene sheets into arrays for enhancing their interaction cross-sections with THz waves (Liu et al., 2012; Thongrattanasiri et al., 2012; Wang, 2012; Yan et al., 2012; Fan et al., 2013; Shen et al., 2014; Fan et al., 2015; Guo et al., 2018). Accordingly, several analytical models including sheet retrieval method (Fan et al., 2015), plasmon wave functions (PWFs), (García de Abajo, 2014; Silveiro et al., 2015; Yu et al., 2017), and coupled-mode theory (CMT) (Guo et al., 2018) have been proposed to optimize THz wave absorption of graphene. In particular, graphene cut-wire array (GCWA) has been recognized as the simplest THz plasmonic metasurface and its absorption is reported to reach the maximum value of 50% (Fan et al., 2015). However, as too many parameters including geometry, carrier concentration, wavelength, and substrate effect are involved in these models, the optimization of a specific GCWA is still case-dependent, and a numerical data bank with lengthy numerical calculations is still needed. For the efficient design of GCWA with optimized THz absorption, an intuitive understanding of their THz absorption mechanism with all parameters incorporated is strongly desired.

In this study, we propose a universal theoretical approach to design GCWAs with maximized THz wave absorption. Specifically, we combine temporal CMT with quasistatic PWFs to derive a formula for calculating THz absorption of the GCWAs. This approach, which we denote as quasistatic coupled-mode theory (QCMT), enables an efficient optimization of the GCWAs absorption by matching its absorption (Γ_abs) and radiative (Γ_rad) decay rates. When reaching the optimal condition, the maximum absorption is only determined by the substrate given by (1−r₀)/2, with r₀ the substrate reflection coefficient without the GCWA structure. In particular, we identify that this optimal condition can be fulfilled simply by tuning the duty ratio of the array, regardless of operating frequency or geometrical parameters, such as the rectangle length, width, or array period. The theoretical results are further verified numerically using finite element method (FEM) simulations. It is noted that our results can be applied throughout the entire IR and THz spectral regions, which therefore can guide the design of graphene nano-micro structure arrays for applications in high-performance optoelectronic devices.

Results and Discussion

The GCWA is schematically shown in Figure 1 (left), which is placed onto a dielectric substrate with permittivity of ε₂. Considering that our study is focused on the THz spectral region, we assume that the array period (P_x and P_y as shown in Figure 1) is much smaller than the wavelength of interest. Accordingly, only specular transmission and reflection are allowed. The excitation THz waves, which are denoted as $|s_{+}\rangle ={\left[\begin{array}{cc}{s}_{1+}& s_{2+}\end{array}\right]}^T$, illuminate perpendicularly towards the GCWA surface. Similarly, the outgoing THz waves are defined by $|s_{-}\rangle ={\left[\begin{array}{cc}{s}_{1-}& s_{2-}\end{array}\right]}^T$. Symbols s₁₊ (s₁₋) and s₂₊ (s_2-) are complex incident (outgoing) wave amplitudes at the air and the dielectric side. The time-variant mode amplitude, a, of the GCWA can be expressed according to CMT as (Haus, 1984; Fan et al., 2003):

$\{\begin{array}{c}\frac{da}{dt}=j\left({\omega }_0+j{\Gamma }_{\text{tot}}/2\right)a+\left({\langle d|}^{\ast }\right)|s_{+}\rangle \\ |s_{-}\rangle =C|s_{+}\rangle +a|d\rangle \end{array}(1)$

where Γ_tot represents the total decay rate, which is the sum of radiative decay rate Γ_rad and absorption rate Γ_abs.$|d\rangle ={\left[\begin{array}{cc}{d}_1& d_2\end{array}\right]}^T$ is the coupling vector with $\langle d|d\rangle ={\Gamma }_{\text{rad}}$. Parameter C is the background scattering matrix without the GCWA, which is stated as,

$C=\left[\begin{array}{cc}{r}_0& j{t}_0\\ j{t}_0& r_0\end{array}\right](2)$

where $r_0=\frac{\sqrt{{\epsilon }_2}-\sqrt{{\epsilon }_1}}{\sqrt{{\epsilon }_2}+\sqrt{{\epsilon }_1}}$ and $t_0=\frac{2\sqrt{{\epsilon }_1{\epsilon }_2}}{\sqrt{{\epsilon }_2}+\sqrt{{\epsilon }_1}}$ are the port reflection and transmission coefficients, respectively (Haus, 1984) ε₁ and ε₂ are permittivities of the substrate and surrounding environment (set as air in our current study), respectively. Note that from the time-reversal symmetry and conservation of energy, we have CC⁺ = I and $C{|d\rangle }^{\ast }=-|d\rangle$. Thereafter, d₁ and d₂ can be calculated as,

$\{\begin{array}{l}{d}_1=-\sqrt{\frac{{\Gamma }_{\text{rad}}\left(1-r_0\right)}{2}}\\ d_2=j\sqrt{\frac{{\Gamma }_{\text{rad}}\left(1+r_0\right)}{2}}\end{array}(3)$

FIGURE 1

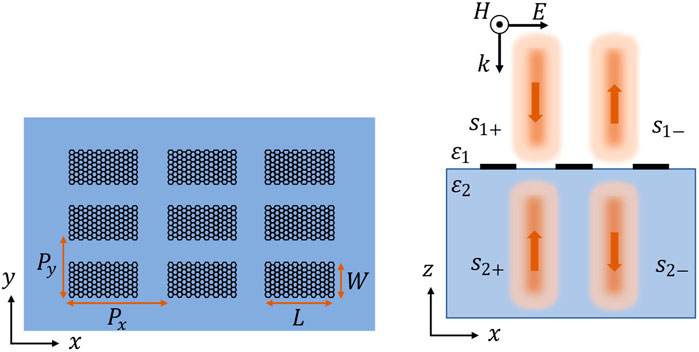
FIGURE 1. Schematic depiction of the graphene cut-wire array. The array is located on a dielectric substrate (left), where the THz wave illuminates the sample perpendicularly either from the air or dielectric side. The polarization of the THz wave is along the x-axis. The periods of the array along the x- and y-axes are denoted as P_x and P_y, respectively. Parameters L and W delegate the length and width of the cut-wire, respectively. The array can be fabricated by e-beaming lithography (Guo et al., 2018) or standard optical lithography followed by oxygen plasma etching process (Ju et al., 2011).

By solving the differential. Eqs. 1–3, one can obtain,

$a=\frac{\begin{array}{cc}\left({\langle d|}^{\ast }\right)& |s_{+}\rangle \end{array}}{j\left(\omega -{\omega }_0-j{\Gamma }_{\text{tot}}/2\right)}(4)$

When the THz wave is illuminated from the air side, i.e., $|s_{+}\rangle ={\left[\begin{array}{cc}{s}_{1+}& 0\end{array}\right]}^T$, the reflection and transmission coefficients for the GCWA can be written as,

$\{\begin{array}{l}r=\frac{s_{-1}}{s_{+1}}=r_0+\frac{{\Gamma }_{\text{rad}}\left(1-r_0\right)/2}{j\left(\omega -{\omega }_0\right)+{\Gamma }_{\text{tot}}/2}\\ t=\frac{s_{-2}}{s_{+1}}=j{t}_0-\frac{j{\Gamma }_{\text{rad}}{t}_0/2}{j\left(\omega -{\omega }_0\right)+{\Gamma }_{\text{tot}}/2}\end{array}(5)$

Consequently, the total absorption of the GCWA is given by,

$A=1-{\left|r\right|}^2-{\left|t\right|}^2=\frac{{\left|a\right|}^2{\Gamma }_{\text{abs}}}{{\left|s_{+1}\right|}^2}=\frac{{\Gamma }_{\text{abs}}{\Gamma }_{\text{rad}}\left(1-r_0\right)/2}{{\left(\omega -{\omega }_0\right)}^2+{\left({\Gamma }_{\text{tot}}/2\right)}^2}(6)$

The absorption rate of the graphene array is determined by electron scattering rates, impurity and defect densities, which can be approximated as a constant.(Jablan et al., 2009). Therefore, the maximum absorption of the GCWA can be achieved at the condition of $\partial A/\partial {\Gamma }_{\text{rad}}=0$, yielding the well-known critical coupling condition Γ_rad = Γ_abs. As a result, the theoretical maximum absorption for graphene array becomes (at oscillation frequency ω = ω₀) $A_{\max }=\left(1-r_0\right)/2$, which only depends on the reflection of the substrate. For GCWA in vacuum, the reflection coefficient r₀ is 0 and the maximum absorption rate is A_max,vac = 0.5. This result is consistent with literature where the graphene array is suspended in the air (Fan et al., 2015). When graphene array is placed onto silicon oxide substrate ($n_{Si{O}_2}=1.955$ and $r_{0,Si{O}_2}=0.323$), the maximum absorption is reduced to $A_{max,Si{O}_2}=0.338$. Specifically, if the graphene array is supported onto a perfect metal, the QCMT reduces to single port condition (r₀ = −1), and the perfect absorption A_max = 1 can be achieved (Guo et al., 2018).

In the QCMT model, ω₀, Γ_rad, and Γ_abs are phenomenological parameters that are associated with a specific structure. For the GCWA, we can deduce their explicit expressions based on quasistatic PWFs. (Garcıía de Abajo, 2013; Silveiro et al., 2015; Yu et al., 2017). Specifically, in the long-wave limit (q << k_F, k_F is Fermi wave vector) and high doping condition (E_F >> $\hslash \omega$, E_F is the Fermi energy), the surface conductivity of graphene can be approximated by Drude model, (Hanson, 2008; Low and Avouris, 2014),

$\sigma \left(\omega \right)=\frac{e^2}{\pi {\hslash }^2}\frac{j{E}_F}{\omega +j{\tau }^{-1}}(7)$

where e is the charge of an electron, $\hslash$ is the reduced Planck constant, and τ is the electron relaxation time. When the size of the graphene cut-wire is much smaller than the incidence wavelength, it is convenient to describe its response in the electrostatic limit (Fang et al., 2013; Garcıía de Abajo, 2013; García de Abajo, 2014; Silveiro et al., 2015; Yu et al., 2017) According to the quasistatic PWFs, the transmission of the GCWA can be expressed as, (García de Abajo, 2007; Abd El-Fattah et al., 2019)

$t=t_0\left(1+\frac{j\beta }{{\alpha }^{-1}-G}\right)(8)$

where $G=g/S^{3/2}+j\beta$ (g is the dimensionless parameter and for square lattice, g = 4.52), (Thongrattanasiri et al., 2012; García de Abajo, 2014) $\beta =2\pi \omega /c\overline{n}S$ is the radiation coupling term, ω is the incidence frequency, c is the speed of light in vacuum, S is the lattice area with S = P_xP_y, $\overline{n}$ is the average refractive index of the surrounding medium, $\alpha ={\zeta }_n^2\overline{\epsilon }{D}^3/\left[1/\eta \left(\omega \right)-1/{\eta }_n\right]$ is the polarizability of individual graphene cut-wire, ${\zeta }_n$ is the mode dipole moment, ${\eta }_n$ is the mode eigenvalue, $\eta \left(\omega \right)=j\sigma \left(\omega \right)/\left(\omega D\overline{\epsilon }\right)$, and n is the order of the plasmon mode. Parameter $\overline{\epsilon }=\left({\epsilon }_1+{\epsilon }_2\right)/2$ is the average dielectric constant of the surrounding medium and $D=\sqrt{LW}$ is the characteristic size of the graphene cut-wire (García de Abajo, 2014; Yu et al., 2017; Fang et al., 2013). For the lowest-order dipolar plasmon mode with electron oscillations along x-axis, n = 1, and only ${\eta }_1$ and ${\zeta }_1$ are considered in Eq. 8 (Yu et al., 2017) Eq. 8 can be further written as,

$t=t_0\left[1+\frac{j{\Gamma }_{\text{rad}}}{{\omega }_0^2/\omega -\omega -j\left({\Gamma }_{\text{rad}}+{\Gamma }_{\text{abs}}\right)}\right](9)$

where

${\omega }_0=\sqrt{\frac{e^2{E}_F}{4{\pi }^2{\epsilon }_0{\hslash }^2\left(-{\eta }_1\right)\overline{\epsilon }D}-\frac{c\overline{n}g}{2\pi \sqrt{S}\overline{\epsilon }}{\Gamma }_{\text{rad}}}(10)$

${\Gamma }_{\text{rad}}=\frac{{\zeta }_1^2{E}_F{e}^2}{2\pi {\epsilon }_{0}c\overline{n}{\hslash }^2}\frac{D^2}{S}(11)$

${\Gamma }_{\text{abs}}={\tau }^{-1}(12)$

For coupled-mode with narrow linewidth (high quality factor Q) and when ω ≈ ω₀, Eq. 9 is reduced to the same form as Eq. 5 except a universal phase factor. Therefore, Eqs. 10–12 are explicit expressions of the phenomenological parameters used in QCMT model, which can be applied to calculate the THz wave absorption of the GCWAs.

Several observations can be made from Eqs. 10–12. First, according to Eq. 10, the first term inside the square root represents the oscillation frequency of the individual graphene cut-wire, while the second term is accounted for interactions between different cut-wires in the array. Therefore, when the period of the lattice decreases, plasmon frequency undergoes a small redshift due to such interactions. Second, the absorption rate of GCWA keeps constant as Γ_abs = τ⁻¹, which is independent of the specific geometry and frequency. This is a direct consequence of electrostatic approximation. Third, the radiative decay rate Γ_rad is proportional to E_F, the duty ratio of the array $\xi =D^2/S$ and the square of the mode dipole moment ${\zeta }_1^2$. Importantly, ${\zeta }_1$ is solely determined by the shape of the cut-wire (Silveiro et al., 2015; Yu et al., 2017; Abd El-Fattah et al., 2019). As will be shown in the following discussion, ${\zeta }_1$ can be approximated as a constant for the longitudinal plasmonic dipole mode. Finally, by applying Equations (11) and (12) to the critical coupling condition (Γ_rad = Γ_abs), one can obtain,

$\xi ={\tau }^{-1}\frac{2\pi {\epsilon }_{0}c\overline{n}{\hslash }^2}{{\zeta }_1^2{E}_F{e}^2}(13)$

Eq. 13 is the central result of this work. That is, with substrate refractive index $\overline{n}$, Fermi energy E_F, and electron relaxation time τ at hand, the optimum absorption condition only depends on the duty ratio of the array, regardless of other geometrical parameters including period of the array, length and width, as well as oscillation frequency of the GCWA. Additionally, such a conclusion can be scaled throughout the entire infrared and terahertz band once the electrostatic approximation is valid.

We then carried out FEM simulations (COMSOL MULTIPHYSIC)¹ to validate the theoretical predictions. To that end, we first verify the critical coupling condition by modeling the optical response of GCWA with different duty ratios (ξ) suspended in the air (n_air = 1) and supported onto SiO₂ substrate ($n_{Si{O}_2}=1.955$). E_F and the graphene damping rate are set to 0.3 eV and τ⁻¹ = 0.249 THz as phenomenological parameters (Jablan et al., 2009). The L and W of a graphene cut-wire are 10 and 5 μm, respectively. The periods of the GCWA are $P_x=L/\sqrt{\xi }$, $P_y=W/\sqrt{\xi }$. The other geometrical parameters used in the simulations are listed in Table 1.

TABLE 1

TABLE 1. Geometrical parameters for GCWA associated with Figure 1.

The simulated reflection |r|², transmission |t|² and absorption A spectra of the two GCWAs are plotted in Figure 2A–C and Figures 2E–G. It can be seen clearly that |r|², |t|², and A are strongly dependent on the ξ of the GCWAs. In particular, there exists optimized ξ for the THz absorption of the GCWAs. This can be seen more clearly by plotting the evolution of A at the oscillation frequency of the GCWA as a function of the corresponding ξ (Figures 2D,H, orange squares and lines). Specifically, maximum A can be obtained at ξ = 0.26 and 0.38 for GCWA suspended in the air and supported onto SiO₂ substrate, respectively. The two ξ values for optimum absorption condition are exactly the same as those calculated using Eq. 13, where $\overline{n}$ is one and $1.478=\left(1+n_{{\text{SiO}}_2}\right)/2$ are employed for air and SiO₂ substrate, respectively. Furthermore, in such a circumstance, Γ_rad is equal to Γ_abs.

FIGURE 2

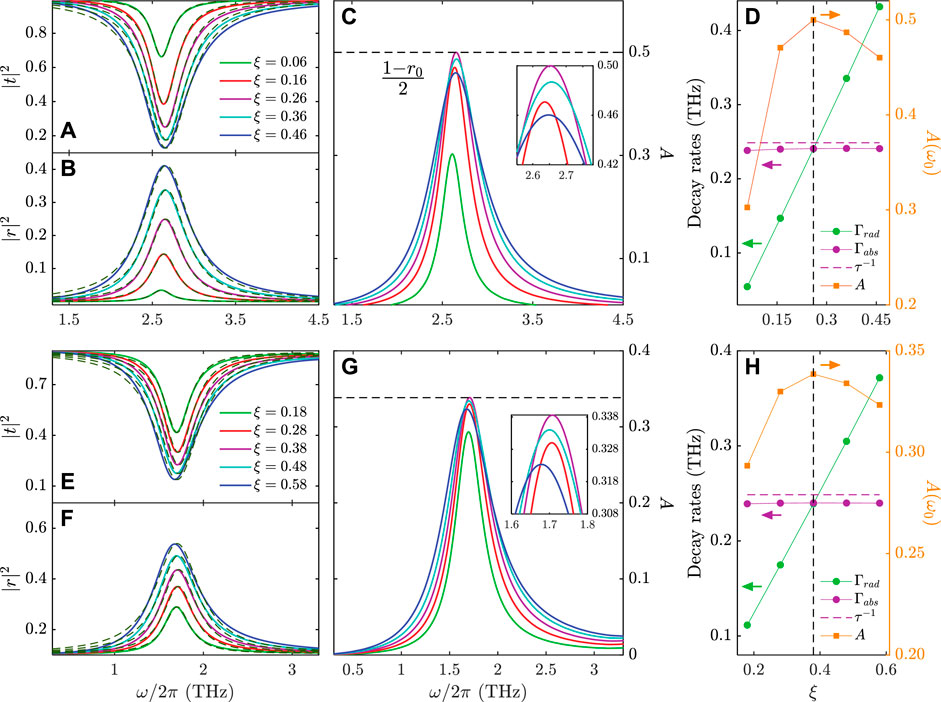
FIGURE 2. THz wave responses of GCWA with different duty ratios. (A–C) Numerical simulations of transmission (A), reflection (B), and absorption (C) spectra for GCWA suspended in the air. (E–G) The corresponding transmission (E), reflection (F), and absorption (G) spectra for GCWA supported onto SiO₂ substrate. The gray dashed curves are fittings using the QCMT model. The dashed lines in (C) and (G) are the theoretical maximum absorption calculated by A_max = (1−r₀)/2. The insets in (C) and (G) display the magnified absorption spectra near the oscillation frequencies. (D, H) Radiative decay rate Γ_rad and absorption decay rate Γ_abs of GCWA suspended in the air (G) and supported onto SiO₂ substrate (H). The decay rates are obtained from fitting the spectra shown in Figure (A, B) and (E, F) using the QCMT model. Absorption maxima, A (ω₀), extracted at different oscillation frequencies are also included. Dashed black lines shown in (D) and (H) indicate the critical coupling condition.

To further compare the simulation and QCMT model results quantitatively, Eq. 5 obtained from the QCMT model were then employed to fit the simulated spectra. As shown by the dashed lines corresponding to each $\xi$, the QCMT model corroborates with the FEM simulation very well. Figures 2D,H depict the fitted absorption rate (Γ_abs, purple) and radiative decay rate (Γ_rad, green), where the graphene damping rate τ⁻¹ is plotted as a dashed line for comparison. As expected from the QCMT model, Γ_rad is proportional to ξ, while Γ_abs remains as a constant that is close to the intrinsic damping rate of graphene (Eq. 12). At the maximum absorption, the Γ_rad coincides with Γ_abs exactly (Figures 2D,H, black dashed lines). These results indicate that as described by QCMT model, when critical coupling condition is fulfilled the GCWA will exhibit maximum absorption in response to THz wave illumination.

We proceed to validate the analytical expressions of ω₀ and Γ_rad (Equation (10) and (11)). These two parameters can be calculated based on the mode eigenvalue η₁ and dipole moment ζ₁. For graphene cut-wires, they are only determined by the aspect ratio defined as κ = L/W. We first calculated η₁ and ζ₁ associated with different κ through mode analysis on an isolated graphene cut-wire (more details on the calculations of η₁ and ζ₁ can be found in Supporting Information, Note 1). As shown in Figure 3A and 3D, η₁ decreases against κ, while ζ₁ first increases as κ increases and then keeps approximately constant when κ is larger than 1. Because the plasmonic mode is associated with electron oscillations along the x-axis, it becomes a longitudinal mode when κ > 1. Therefore, the dependence of ζ₁ on κ indicates that the effective dipole moment of the longitudinal dipole mode of the cut-wire stays unchanged. With the knowledge of η₁ and ζ₁, we then calculated Γ_rad and ω₀ using Eqations (10) and (11). Different GCWAs with L and W ranging from 5 to 15 μm and 2–8 μm, respectively, are considered. The lattice period is fixed as P_x = P_y = 24.5 μm. As shown in Figure 3B, Γ_rad increases as either L or W becomes larger. This is reasonable because the area of the cut-wire D² is equal to L×W. A larger D² means that more electrons will be driven by the external field, and consequently more energy will be radiated back to the vacuum due to the stronger electron oscillations. The dependence of working frequency ω₀ on the geometrical parameters is shown in Figure 3E. Clearly, when fixing L (W) while increasing W (L), the ω₀ increases (decreases) monotonically.

FIGURE 3

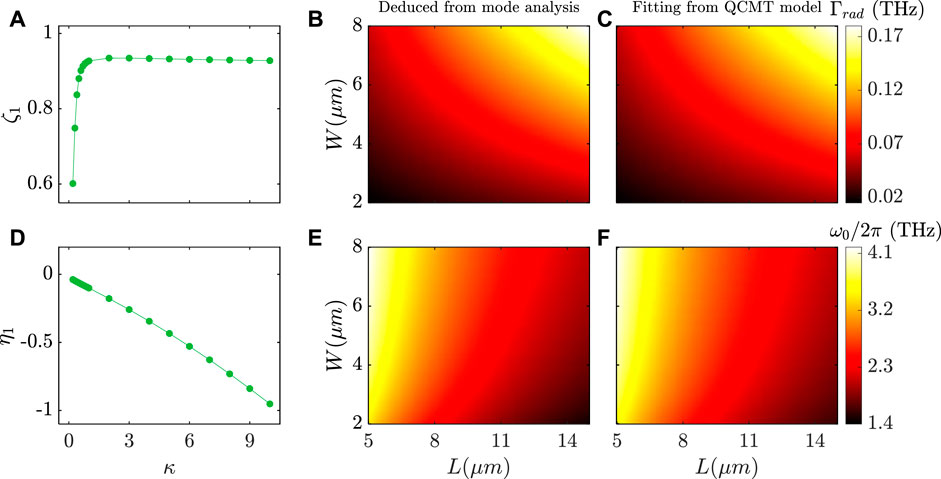
FIGURE 3. Validations of Γ_rad and ω₀ calculated from the QCMT model. (A,D) ζ₁ (A) and η₁ (D) obtained from mode analysis. The green solid lines are guides for eyes (B,C) Γ_rad as a function of L and W calculated from Eq. 11 (B) and fitted from QCMT model (C). (E,F) ω₀ as a function of L and W calculated from Eq. 10 (E) and fitted from QCMT model (F).

We further simulated the reflection and transmission spectra of the GCWAs with different L and W using the FEM. QCMT model (Equation (5) and (6)) was then employed to fit the simulated spectra and extract the corresponding Γ_rad and ω₀ (Detailed simulations and fitting results can be found in Supporting Information, Note two and Supplementary Figure S1). As shown in Figures 3C,F, the Γ_rad and ω₀ obtained from the QCMT model agree well with those deduced from Eqations (10) and (11), which unambiguously confirms the accuracy of the QCMT model we developed.

It should be emphasized that for graphene cut-wires of mico-meter scale characteristic sizes, our QCMT model and the duty ratio-oriented design can in principle cover a vast geometric space and spectral region ranging from the mid-infrared to THz frequencies, as long as the electrostatic limit is still valid. Specifically, given a dielectric substrate of refractive index n_die and a targeting ω₀, the geometrical parameters of GCWA with maximum absorption can be obtained by using Eqs 10–13 and the numerical results shown in Figures 3A,D. To simplify the discussion, we set ζ₁ = 0.925 according to Figure 3A, and consequently Eq. 13 can be simplified as,

$\xi =\alpha \frac{\overline{n}\hslash {\tau }^{-1}}{E_F}(14)$

where α = 80.13 is a dimensionless coefficient. To validate Eq. 14, we consider GCWA with E_F = 0.5 eV, $\hslash {\tau }^{-1}=1$ meV (τ⁻¹ = 0.249 THz), and substrate refractive index n = 1. The optimal $\xi$ of GCWA is calculated to be $0.165$. We have numerically simulated three types of GCWAs with different combinations of L, W, P_x, and P_y: a) fixed lattice period (P_x = 4.93 μm and P_y = 2.46 μm) and characteristic size (D = 1.414 μm), but varying graphene cut-wire aspect ratio κ; b) fixed graphene cut-wire (L = 2 μm and W = 1 μm) and lattice area (S = 12.13 μm²), but varying lattice period ratio P_x:P_y; c) varying all L, W, P_x and P_y parameters. All the GCWAs share fixed duty ratio ($\xi =0.165$) with detailed geometrical parameters are listed in Table 2–4. Their corresponding absorption spectra are depicted in Figure 4. As shown in Figure 4A, the oscillation frequency of GCWAs decreases with the increasing κ. This can be explained by the decrease in η₁ of individual graphene cut-wire (the first term in Eq. 10). In contrast, for graphene cut-wire with fixed size, the oscillation frequency of GCWA experiences a small redshift when increasing the lattice period ratio. This can be attributed to the mutual interactions between different cut-wires (the increase of g in the second term in Eq. 10 (Thongrattanasiri et al., 2012; García de Abajo, 2014)). Figure 4C shows the absorption spectra for cut-wires arrays with the different combinations of P_x:P_y and κ. Their oscillation frequencies are deliberately chosen to cover 3–28 THz. Nevertheless, all the spectra exhibit maximum absorptions in spite of the geometry diversity, confirming the applicability of the QCMT.

TABLE 2

TABLE 2. Geometrical parameters for GCWA associated with Figure 4A.

TABLE 3

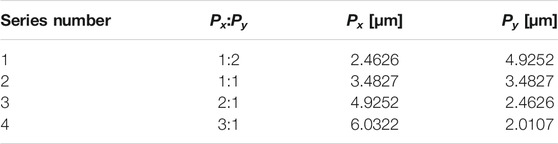
TABLE 3. Geometrical parameters for GCWA associated with Figure 4B.

TABLE 4

TABLE 4. Geometrical parameters for GCWA associated with Figure 4C.

FIGURE 4

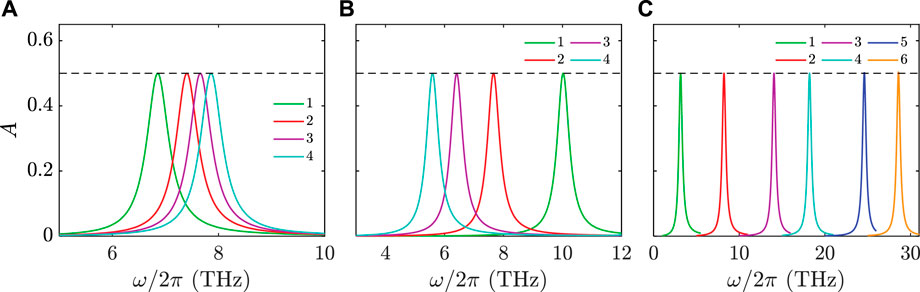
FIGURE 4. Absorption spectra of GCWA with same duty ratio but different geometric parameters. (A) Absorption spectra for GCWAs with the same P_x (4.93 μm) and P_y (2.46 μm) but different L and W. (B) Absorption spectra for GCWAs with the same L (2 μm) and W (1 μm) but different P_x and P_y. (C) Absorption spectra for GCWA with different P_x, P_y, L and W oscillating at 3–28 THz. The duty ratio of GCWAs is fixed to $\xi =0.165$. All the spectra exhibit maximum absorptions, confirming the applicability of the QCMT.

The analyses in Figures 2–4 have validated the accuracy of our developed QCMT model. This model can be employed as an effective tool to design GCWAs with optimized electromagnetic wave absorption. To demonstrate the capability of the QCMT model, we employed it to design three types of GCWAs with optimum electromagnetic wave absorptions. We consider three types of GCWAs: I) E_F = 0.4 eV, ω₀ = 30 THz, n_die = 1; II) E_F = 0.7 eV, ω₀ = 6 THz, n_die = 1.955; III) E_F = 1 eV, ω₀ = 2 THz, n_die = 3.42. The GCWAs I to III are supported in the air, onto SiO₂, and silicon substrates, respectively. In addition, we set the aspect ratios κ of all the three GCWAs to 2. Based on Equations (10) and (11), it is able to deduce the feature size of an individual graphene cut-wire to be L×W = 0.088 μm × 0.044 μm (Type I), 1.63 μm × 0.81 μm (Type II), and 7.92 μm × 3.96 μm (Type III), respectively. According to Eq. 14 the duty ratio of each GCWA can be determined as ξ = 0.2, 0.17, and 0.18, respectively. Afterwards the periods $P_x=P_y=\sqrt{LW/\xi }$ of the GCWAs can be obtained.

To validate the above designs, we numerically simulated the absorption spectra of the three types of GCWAs with different duty ratios. The GCWAs are respectively suspended in the air or supported onto SiO₂ and silicon substrates. The lengths and widths of the three types of GCWAs are employed according to the QCMT designs. As shown in Figure 5A, for the GCWA suspended in the air (Type I), a working frequency at 31.3 THz (mid-infrared regime) can be found with a duty ratio of 0.2. Additionally, such a duty ratio leads to a maximum peak absorption of 0.5, which is consistent with the QCMT calculation and previous study (Fan et al., 2015). For the GCWAs supported onto SiO₂ (Type II) and silicon (Type III) substrates, the maximum absorption occurs for duty ratios of 0.17 and 0.18, respectively (Figures 5B,C). The corresponding working frequencies are 6.23 THz and 2.02 THz, respectively. These results are all corroborated with the QCMT predictions, except for small deviations on the oscillation frequencies (the discrepancies are 4.3% for Type I, 3.8% for Type II and 1% for Type III). We attribute such discrepancies to the deviation of GCWA from quasistatic limitation as well as the high-Q approximation when reducing Equation (9) to Equation (5). Nevertheless, our results unambiguously demonstrate the effectiveness of the QCMT model in designing of GCWAs with optimum electromagnetic absorption in mid-infrared to THz spectral regime.

FIGURE 5

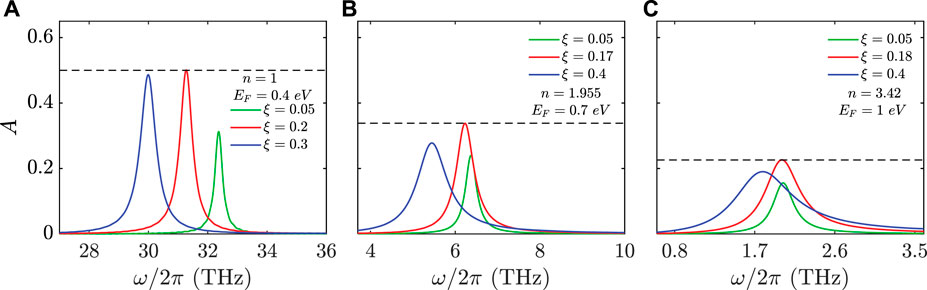
FIGURE 5. Simulated absorption spectra of the GCWAs designed by the QCMT model. The geometrical parameter for each GCWA is: (A) L = 0.088 μm, W = 0.044 μm; (B) L = 1.63 μm, W = 0.81 μm; (C) L = 7.92 μm, W = 3.96 μm. The GCWAs corresponding to (A–C) are respectively suspended in the air (A) and supported onto SiO₂ (B) and silicon (C) substrates. For better demonstration, for each array the absorption spectra corresponding to duty ratios that are not associated with the optimum absorption are included. Black dashed lines shown in (A–C) indicate the maximum absorption of each array.

Conclusion

In summary, we have developed an analytical model, i.e., the QCMT model, for designing GCWA with optimum electromagnetic wave absorption in the mid-infrared to THz spectral regime. In the QCMT model, all of the phenomenological parameters employed to calculate the electromagnetic wave reflection and transmission of a specific GCWA can be calculated analytically, which on one hand provides an intuitive physical insight on these parameters, and on the other hand can help optimize the electromagnetic wave absorption of the GCWA. As a result, by utilizing the QCMT model it is able to facilely obtain the geometrical parameters associated with maximum electromagnetic absorption of the GCWA, which otherwise requires arduous parameter securitizing by numerical simulations. We show that a maximum THz wave absorption can be achieved by choosing proper duty ratio of the GCWA, regardless of its working frequencies and other geometrical parameters. The model developed in our study can in principle generalized to other types of polaritonic 2D crystals, which therefore provide a guideline for the design of 2D micro-/nanostructure arrays operating in the long-wave regime with optimized electromagnetic wave absorption.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author Contributions

SD, ZC, and HC, conceived and supervised the study. HZ and ZC developed the analytical model and conducted the numerical simulations. The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

Funding

This work was financially supported by the National Key Basic Research Program of China (Grant Nos. 2019YFA0210203), the National Natural Science Foundation of China (Grant Nos. 91963205, 11904420, 61905290), and the Guangdong Basic and Applied Basic Research Foundation (Grant Nos. 2020A1515011329, 2019A1515011355, 202102020579). HC acknowledges the support from Changjiang Young Scholar Program. SD, ZC, and HC conceived and supervised the study. HZ, and ZC developed the analytical model and conducted the numerical simulations. The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2021.737347/full#supplementary-material

Footnotes

¹https://www.comsol.com/, accessed.

References

Abd El-Fattah, Z. M., Mkhitaryan, V., Brede, J., Fernández, L., Li, C., Guo, Q., et al. (2019). Plasmonics in Atomically Thin Crystalline Silver Films. ACS Nano 13, 7771–7779. doi:10.1021/acsnano.9b01651

PubMed Abstract | CrossRef Full Text | Google Scholar

Atwater, H. A., and Polman, A. (2010). Plasmonics for Improved Photovoltaic Devices. Nat. Mater 9, 205–213. doi:10.1038/nmat2629

PubMed Abstract | CrossRef Full Text | Google Scholar

Basov, D. N., Fogler, M. M., and García de Abajo, F. J. (2016). Polaritons in van der Waals materials. Science 354, aag1992. doi:10.1126/science.aag1992

PubMed Abstract | CrossRef Full Text | Google Scholar

Cui, L., Wang, J., and Sun, M. (2021). Graphene Plasmon for Optoelectronics. Rev. Phys. 6, 100054. doi:10.1016/j.revip.2021.100054

CrossRef Full Text | Google Scholar

Fan, S., Suh, W., and Joannopoulos, J. D. (2003). Temporal Coupled-Mode Theory for the Fano Resonance in Optical Resonators. J. Opt. Soc. Am. A. 20, 569. doi:10.1364/josaa.20.000569

PubMed Abstract | CrossRef Full Text | Google Scholar

Fan, Y., Shen, N.-H., Koschny, T., and Soukoulis, C. M. (2015). Tunable Terahertz Meta-Surface with Graphene Cut-Wires. ACS Photon. 2, 151–156. doi:10.1021/ph500366z

CrossRef Full Text | Google Scholar

Fan, Y., Wei, Z., Zhang, Z., and Li, H. (2013). Enhancing Infrared Extinction and Absorption in a Monolayer Graphene Sheet by Harvesting the Electric Dipolar Mode of Split Ring Resonators. Opt. Lett. 38, 5410. doi:10.1364/ol.38.005410

PubMed Abstract | CrossRef Full Text | Google Scholar

Fang, Z., Thongrattanasiri, S., Schlather, A., Liu, Z., Ma, L., Wang, Y., et al. (2013). Gated Tunability and Hybridization of Localized Plasmons in Nanostructured Graphene. ACS Nano 7, 2388–2395. doi:10.1021/nn3055835

PubMed Abstract | CrossRef Full Text | Google Scholar

García de Abajo, F. J. (2007). Colloquium: Light Scattering by Particle and Hole Arrays. Rev. Mod. Phys. 79, 1267–1290. doi:10.1103/revmodphys.79.1267

CrossRef Full Text | Google Scholar

García de Abajo, F. J. (2014). Graphene Plasmonics: Challenges and Opportunities. ACS Photon. 1, 135–152. doi:10.1021/ph400147y

CrossRef Full Text | Google Scholar

Garcıía de Abajo, F. J. (2013). Multiple Excitation of Confined Graphene Plasmons by Single Free Electrons. ACS Nano 7, 11409. doi:10.1021/nn405367e

PubMed Abstract

Gramotnev, D. K., and Bozhevolnyi, S. I. (2010). Plasmonics beyond the Diffraction Limit. Nat. Photon 4, 83–91. doi:10.1038/nphoton.2009.282

CrossRef Full Text | Google Scholar

Guo, C., Zhang, J., Xu, W., Liu, K., Yuan, X., Qin, S., et al. (2018). Graphene-Based Perfect Absorption Structures in the Visible to Terahertz Band and Their Optoelectronics Applications. Nanomaterials 8, 1033. doi:10.3390/nano8121033

PubMed Abstract | CrossRef Full Text | Google Scholar

Guo, Q., Yu, R., Li, C., Yuan, S., Deng, B., García de Abajo, F. J., et al. (2018). Efficient Electrical Detection of Mid-infrared Graphene Plasmons at Room Temperature. Nat. Mater 17, 986–992. doi:10.1038/s41563-018-0157-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Hanson, G. W. (2008). Dyadic Green's Functions and Guided Surface Waves for a Surface Conductivity Model of Graphene. J. Appl. Phys. 103, 064302. doi:10.1063/1.2891452

CrossRef Full Text | Google Scholar

Haus, H. (1984). Waves and fields in Optoelectronics. Englewood Cliffs, NJ, USA: Prentice-Hall.

Huard, B., Sulpizio, J. A., Stander, N., Todd, K., Yang, B., and Goldhaber-Gordon, D. (2007). Transport Measurements across a Tunable Potential Barrier in Graphene. Phys. Rev. Lett. 98, 236803. doi:10.1103/physrevlett.98.236803

PubMed Abstract | CrossRef Full Text | Google Scholar

Jablan, M., Buljan, H., and Soljačić, M. (2009). Plasmonics in Graphene at Infrared Frequencies. Phys. Rev. B 80, 245435. doi:10.1103/physrevb.80.245435

CrossRef Full Text | Google Scholar

Ju, L., Geng, B., Horng, J., Girit, C., Martin, M., Hao, Z., et al. (2011). Graphene Plasmonics for Tunable Terahertz Metamaterials. Nat. Nanotech 6, 630–634. doi:10.1038/nnano.2011.146

CrossRef Full Text | Google Scholar

Kabashin, A. V., Evans, P., Pastkovsky, S., Hendren, W., Wurtz, G. A., Atkinson, R., et al. (2009). Plasmonic Nanorod Metamaterials for Biosensing. Nat. Mater 8, 867–871. doi:10.1038/nmat2546

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, P., Cai, W., Wang, L., Zhang, X., and Xu, J. (2012). Tunable Terahertz Optical Antennas Based on Graphene Ring Structures. Appl. Phys. Lett. 100, 153111. doi:10.1063/1.3702819

CrossRef Full Text | Google Scholar

Low, T., and Avouris, P. (2014). Graphene Plasmonics for Terahertz to Mid-infrared Applications. ACS Nano 8, 1086–1101. doi:10.1021/nn406627u

PubMed Abstract | CrossRef Full Text | Google Scholar

Luk'yanchuk, B., Zheludev, N. I., Maier, S. A., Halas, N. J., Nordlander, P., Giessen, H., et al. (2010). The Fano Resonance in Plasmonic Nanostructures and Metamaterials. Nat. Mater 9, 707–715. doi:10.1038/nmat2810

PubMed Abstract | CrossRef Full Text | Google Scholar

Luo, X., Qiu, T., Lu, W., and Ni, Z. (2013). Plasmons in Graphene: Recent Progress and Applications. Mater. Sci. Eng. R: Rep. 74, 351–376. doi:10.1016/j.mser.2013.09.001

CrossRef Full Text | Google Scholar

Maier, S. A. (2007). Plasmonics: Fundamentals and Applications. Berlin, Germany: Springer Science & Business Media.

Novotny, L., and van Hulst, N. (2011). Antennas for Light. Nat. Photon 5, 83–90. doi:10.1038/nphoton.2010.237

CrossRef Full Text | Google Scholar

Otsuji, T., Popov, V., and Ryzhii, V. (2014). Active Graphene Plasmonics for Terahertz Device Applications. J. Phys. D: Appl. Phys. 47, 094006. doi:10.1088/0022-3727/47/9/094006

CrossRef Full Text | Google Scholar

Schuller, J. A., Barnard, E. S., Cai, W., Jun, Y. C., White, J. S., and Brongersma, M. L. (2010). Plasmonics for Extreme Light Concentration and Manipulation. Nat. Mater 9, 193–204. doi:10.1038/nmat2630

PubMed Abstract | CrossRef Full Text | Google Scholar

Shalaev, V. M. (2007). Optical Negative-index Metamaterials. Nat. Photon 1, 41–48. doi:10.1038/nphoton.2006.49

CrossRef Full Text | Google Scholar

Shen, N.-H., Tassin, P., Koschny, T., and Soukoulis, C. M. (2014). Comparison of Gold- and Graphene-Based Resonant Nanostructures for Terahertz Metamaterials and an Ultrathin Graphene-Based Modulator. Phys. Rev. B 90, 115437. doi:10.1103/physrevb.90.115437

CrossRef Full Text | Google Scholar

Silveiro, I., Ortega, J. M. P., and Abajo, F. J. G. d. (2015). Plasmon Wave Function of Graphene Nanoribbons. New J. Phys. 17, 083013. doi:10.1088/1367-2630/17/8/083013

CrossRef Full Text | Google Scholar

Thongrattanasiri, S., Koppens, F. H. L., and García de Abajo, F. J. (2012). Phys. Rev. Lett. 108, 047401. doi:10.1103/physrevlett.108.047401

PubMed Abstract | CrossRef Full Text

Wang, W. (2012). Plasmons and Optical Excitations in Graphene Rings. J. Phys. Condens. Matter 24, 402202. doi:10.1088/0953-8984/24/40/402202

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, H., Bjerneld, E. J., Käll, M., and Börjesson, L. (1999). Spectroscopy of Single Hemoglobin Molecules by Surface Enhanced Raman Scattering. Phys. Rev. Lett. 83, 4357–4360. doi:10.1103/physrevlett.83.4357

CrossRef Full Text | Google Scholar

Yan, H., Li, X., Chandra, B., Tulevski, G., Wu, Y., Freitag, M., et al. (2012). Tunable Infrared Plasmonic Devices Using Graphene/insulator Stacks. Nat. Nanotech 7, 330–334. doi:10.1038/nnano.2012.59

PubMed Abstract | CrossRef Full Text | Google Scholar

Yu, R., Cox, J. D., Saavedra, J. R. M., and García de Abajo, F. J. (2017). Analytical Modeling of Graphene Plasmons. ACS Photon. 4, 3106–3114. doi:10.1021/acsphotonics.7b00740

CrossRef Full Text | Google Scholar