- 1Xuchang Hengsheng Pharmaceutical Co., Ltd., Xuchang, China
- 2Guangdong Provincial Key Laboratory of Durability for Marine Civil Engineering, College of Civil and Transportation Engineering, Shenzhen University, Shenzhen, China
Chloride-induced corrosion is an important factor that affects the durability of building structures in coastal areas; it causes serious deterioration of reinforced concrete (RC) structures and leads to structural failure. However, chloride-induced corrosion is a slow process which spans the whole service life of building structures, and many factors can affect their service life, such as location, structural design, and drug management. This paper aims to predict the service life of building structures in terms of chloride-induced corrosion and through the concept of engineering vulnerability. It first investigates the model of corrosion initiation of reinforcement, along with the consequent concrete cover cracking. Second, according to the characteristics of building structure and corrosion, it determines an evaluation index system of engineering vulnerability and establishes an evaluation method of engineering vulnerability, considering that corrosion is based on the AHP method and fuzzy comprehensive evaluation. Finally, using a case study of a pharmaceutical factory structure in a coastal city, this study verifies the feasibility of the assessment method considering corrosion effects.
Introduction
A marine environment is one of the worst conditions for concrete structures, with marine concrete structures prone to durability damage due to combined physical, chemical, and mechanical factors. Among these factors, chloride attack is the main reason for reinforcement corrosion, concrete cover spalling, decreased bearing capacity, and structural concrete failure. As major building structures in coastal areas, pharmaceutical factories also suffer from chlorine-induced reinforcement corrosion, which destroy the passivation film of steel bars and thus reduce the cross-sectional area. Due to the continuous accumulation of corrosion byproducts, concrete covers will corrode and crack, leading to early damage to structures and the attenuation of their bearing capacity—structures may even be unable to meet their normal use and structural safety performance requirements of their design and use (Du et al., 2005; Jin et al., 2007; Wu and Yuan, 2008; Luo and NiuSu, 2019; Zhang et al., 2021). Chloride-induced reinforcement corrosion is one of the main factors affecting the service life of building structures, and other factors need to be considered in this light. Engineering vulnerability can fully reflect the potential impact of internal and external factors on building structures and has been widely used in recent years to guide disaster prevention and mitigation through rapid response and early prediction (Chen et al., 2020). Therefore, it is very important to correctly evaluate the service life of building structures under the influence of reinforcement corrosion based on the concept of engineering vulnerability.
Many building structures have long stood in chloride-laden environments in coastal areas. The corrosion process includes corrosion initiation of reinforcement (corrosion critical point) (Apostolopoulos et al., 2013; Wang et al., 2013) and concrete cover cracking (cracking critical point) (Reale and O’Connor, 2012; Jamali et al., 2013), which have generally been regarded as failure criteria for assessing the service life of RC structures (Bazant, 1979a; Bitaraf and Mohammadi, 2008; Matsumura et al., 2008; Pour-Ghaz et al., 2009; Jang and Oh, 2010; Leonid et al., 2010; AI-Harthy et al., 2011; Guzmán et al., 2011; Wang et al., 2018; Tian et al., 2019). Therefore, a large number of theoretical models have been investigated to predict these two important stages (Bazant, 1979a; Bazant, 1979b; Morinaga, 1990; Liu and Weyers, 1998; Wu, 2006; Maaddawy and Soudki, 2007; Tamer and Khaled, 2007; Bitaraf and Mohammadi, 2008; Matsumura et al., 2008; Wang et al., 2008; Pour-Ghaz et al., 2009; Jang and Oh, 2010; Leonid et al., 2010; Lu et al., 2010; Zhang et al., 2010; AI-Harthy et al., 2011; Guzmán et al., 2011; Jin and Zhao, 2014; Liu and Yu, 2016; Zhang et al., 2017; Wang et al., 2018; Tian et al., 2019; Lun et al., 2021). Such studies have established a strong theoretical background for the focus of this study.
The current model of the chloride penetration process is based on Fick’s second law, which is mainly affected by the diffusion coefficient of chloride ions, the critical concentration of chloride ions on the surface of reinforcement, the concentration of chloride ions on the surface of concrete, and the concrete cover depth (Bitaraf and Mohammadi, 2008; Matsumura et al., 2008; Pour-Ghaz et al., 2009; Wang et al., 2012; Wang et al., 2018; Tian et al., 2019). Among these, the diffusion coefficient of chloride ion and the critical concentration of chloride ions are greatly variable and are important factors which affect the length of the first stage. Many factors affect the diffusion coefficient of chloride ions, such as concrete hydration age, temperature, and relative humidity; the influencing factors are not independent and have a complex non-linear relationship, so it is difficult to establish a model that includes all influencing factors.
As another important corrosion stage, the various prediction models of the time for concrete cover cracking have been widely studied (Bazant, 1979a; Bazant, 1979b; Morinaga, 1990; Liu and Weyers, 1998; Wu, 2006; Maaddawy and Soudki, 2007; Tamer and Khaled, 2007; Wang et al., 2008; Jang and Oh, 2010; Leonid et al., 2010; Lu et al., 2010; Zhang et al., 2010; AI-Harthy et al., 2011; Guzmán et al., 2011; Jin and Zhao, 2014; Liu and Yu, 2016; Zhang et al., 2017; Lun et al., 2021). The theoretical models of concrete cover cracking time have been based on elastic, elastoplastic, damage, or fracture mechanics—considering the internal relationships between concrete cover cracking time and basic material parameters (e.g., elastic model, cover depth, reinforcement diameter, and pore zone thickness) and other parameters (e.g., temperature, corrosion current density, and corrosion rate of reinforcement). These models have been established on a clear mechanical theoretical basis and derivation process, which can reflect the real dynamic process of rust cracking and meet the characteristics of concrete cover cracking. However, the versatility of the prediction models based on different mechanics is still uncertain.
Over their long service, building structures are not only subject to the deterioration of concrete caused by chloride-induced reinforcement corrosion but are also affected by their location, engineering design, structural construction, and drug management, resulting in significant differences in their state, causes of change, and development trends, similar to the engineering bearing model. This paper thus introduces the concept of “engineering vulnerability” for engineering geological disaster prevention research. Engineering vulnerability is usually investigated using other evaluation methods, such as analytic hierarchy process and fuzzy comprehensive analysis (Wang et al., 2022; Wu and Tang, 2022). As a non-engineering measure, engineering vulnerability has been fully applied in the evaluation of debris flow hazard in bridge and tunnel engineering (Xu et al., 2010; Xu et al., 2014), service state evaluation of high-speed railway subgrade (Chen et al., 2020), and seismic vulnerability evaluation of concrete structures (Qiang Zhang et al., 2020; Li et al., 2021; Marasco et al., 2021; Dai et al., 2022). These have achieved important research results which can fully reflect the potential impact of internal and external factors on building structures and provide a more scientific evaluation. There are, however, few reports on the service-life evaluation of building structures that consider corrosion effects based on engineering vulnerability. Therefore, it is of engineering significance to carry out a two-stage service-life assessment of building structures based on the concept of engineering vulnerability, considering the various factors related to the corrosion of building structures.
This study, based on previous service-life assessments in building structure research, investigates the engineering vulnerability analysis method for the service life of building structures considering corrosion effects. The model of the corrosion initiation of reinforcement is proposed based on Fick’s second law, considering the various important parameters; the applicability of the existing models proposed by many scholars for predicting cover cracking time in building structures is then analyzed to select the most reasonable cracking model by experimental comparison. Based on the concept of engineering vulnerability, an evaluation index system for the service life of building structures considering corrosion effects is established, and the evaluation results of actual building structures are obtained using an analytic hierarchy process and fuzzy comprehensive analysis methods.
Research on service-life prediction of building structure
Based on previous research into building structure service life, this paper identifies two stages: corrosion initiation and cover cracking. Corrosion initiation occurs when chloride concentration on a steel surface reaches a critical value as an important dividing point, indicating that the passive film of the steel bar has just been destroyed. Concrete cover cracking is a process from the beginning of reinforcement corrosion to the concrete cover cracking, which represents the end of service life.
Model investigation for corrosion initiation
When concrete is saturated with water, the law of chloride penetration through concrete can be expressed based on Fick’s second law, as indicated by numerous studies (Bitaraf and Mohammadi, 2008; Matsumura et al., 2008; Pour-Ghaz et al., 2009; Wang et al., 2012; Wang et al., 2018):
where tin is the time of structure exposure to the chloride environment (s), C (x, tin) is the corresponding chloride concentration at depth x (m) (%/m3), D is the chloride diffusion coefficient (m2/s), Cs is chloride surface concentration (m2/s), and erf is the Gaussian error function.
Therefore, Eq. 1 can be expressed as:
However, in actual concrete structures, the microstructure of the concrete changes over time, and the effective diffusion coefficient of chloride ions is not constant but varies; thus, an improved chloride diffusion coefficient was proposed by Zhu (2017) as follows:
where K is the deterioration effect coefficient of the chloride diffusion performance of concrete; m is the damped exponential, with a value of 0.64; RD is structural defect parameters; and D0 is the chloride diffusion coefficient of concrete at hydration age of t0, which is also affected by the w/c ratio, relative humidity, and temperature (Rodriguez and Hooton, 2003; Tang and Gulikers, 2007). In order to assess the effect of these parameters on the chloride diffusion coefficient, the corresponding correction diffusion coefficient D0 is established thus:
where λRH is the correction coefficient for relative humidity RH (%), λT is the corresponding coefficient for temperature T (K), and D28 is the chloride diffusion coefficient for a specimen under standard curing (28 days) (Tang and Gulikers, 2007; Bitaraf and Mohammadi, 2008).
The parameters λRH and λT can be, respectively, expressed as
where RHc is the threshold relative humidity (RHc = 75), R is the gas constant, U is the activation energy equal to 35,000 J/mol, and T28 is the temperature for standard curing on day 28 (293 K).
Substituting Eq. 5 into Eq. 4 leads to
When the critical concentration of chloride ions is Ccr and the concrete cover depth is C, the prediction formula of chloride penetration life can be obtained as follows:
Model investigation for cover cracking
Various models for predicting a corrosion-induced cracking model
Eight empirical and theoretical models were chosen to predict the concrete cover cracking time of chloride-contaminated building structures (Morinaga, 1990; Liu and Weyers, 1998; Wu, 2006; Maaddawy and Soudki, 2007; Lu et al., 2010; Zhang et al., 2010; Liu and Yu, 2016; Lun et al., 2021). These models were chosen to check versatility because they are based on different mechanics theories which can clearly reflect the variation of concrete corrosion. For a reasonable comparison between them, each model is briefly described.
Morinaga model (1990)
Morinaga (1990) proposed an expression of cover cracking time by considering the influencing factors of concrete cover depth, reinforcement diameter, and current corrosion density based on experimental data:
where tcr is the concrete cover cracking time (d), C is the concrete cover depth (mm), d is the reinforcement diameter (mm), and icorr is the corrosion’s current density (10−4 g/cm2/year).
This model is the earliest empirical model for predicting concrete cover cracking time and is easy to compute since the parameters are readily available. It provided important parameters for later researchers to establish theoretical models. However, Morinaga did not consider the influence of the corrosion rate and the thickness of the porous zone on concrete cover cracking time and also ignored the process of corrosion byproduct filling the gap between the steel bar and concrete.
Liu and Weyers model (1998)
Based on theoretical analysis, Liu and Weyers (1998) first obtained the corrosion quality of steel bars when the concrete cover cracked and constructed the relationship between the corrosion quality of steel bars and the cracking time based on the corrosion production rate kp to express a theoretical model of concrete cracking time as:
where tcr is the concrete cover cracking time (a), Wcrit is the weight of the rust product when the concrete cover cracks (mg/mm), α is the coefficient related to the type of rust product, and icorr is the corrosion’s current density (μA/cm2).
This model is the earliest theoretical model for predicting cover cracking time and is discussed in research on the expansion process of corrosion products based on the theory of elasticity, considering the thickness of the pore area at the junction of concrete and steel bars. However, Liu and Weyers ignore the influence of the corrosion rate and cover depth on concrete cover cracking time, and the solution of Wcrit is also difficult.
Wu model (2006)
Based on the theory of elasticity and Faraday’s law of corrosion, the influence of corrosion current density proposed by Vu and Stewart (2000) on concrete cover cracking was considered by Wu (2006), who established a theoretical model of concrete cover cracking time in a natural corrosion environment as follows:
where tcr is the concrete cover cracking time (a), m is the molecular weight of rust products, z is the ionic valence, C is concrete cover (cm), d is the reinforcement diameter (cm), ρcr is the corrosion rate of the reinforcement when the concrete cover is cracked, F is Faraday’s constant (value of 96,500 (C)), and w/c is the water–cement ratio.
Wu’s model effectively combines the factors of corrosion current density with the corrosion rate of reinforcement based on elastic mechanics, which have a great influence on the cover cracking time. However, the versatility of the selected corrosion current density and the rust expansion force requires further verification.
Maaddawy and Soudki model (2007)
Based on the theory of elasticity, Maaddawy and Soudki (2007) proposed a mathematical model from corrosion initiation to cracking, in which some important parameters such as reinforcement diameter, cover depth, the thickness of the pore area, and corrosion current density are considered. The prediction model is expressed as
where tcr is the concrete cover cracking time (d); Eef is the effective modulus of elasticity of concrete, Eef = Ec/(1+φcr); φcr is the creep coefficient of concrete, with the value of 2.0; C is concrete cover (mm); ft is concrete tensile strength (MPa); d is the reinforcement diameter (mm); d0 is the thickness of the pore area (mm); icorr is corrosion current density (μA/cm2); v is Poisson’s ratio of concrete; and ψ is the representative, ψ = Y2/2C(C + Y),Y = d+2d0.
This mathematical model also uses the elastic mechanics theory of thick-walled cylinders to analyze the relationship between the cover cracking time and the material properties (Eef, d0, ft, and v), the importance of which is also considered by certain models. However, the versatility of the Maaddawy and Soudki model also needs similar verification as Wu (2006).
Lu et al. model (2010)
Lu et al. (2010) established a model based on the theory of elasticity and Faraday’s law of corrosion that, when a concrete cover cracks, the corrosion rate and the theoretical model of concrete cover cracking time considers the deformation characteristics of rust products and the entry of rust products into the crack:
where tcr is the concrete cover cracking time (h); d0 is the thickness of the pore area (mm); k is the correction factor of corrosion depth; n is the volume expansion rate of rust products; r0 is the thick-walled cylinder inner radius (mm), r0 = d/2 + d0; icorr is the corrosion current density (μA/cm2); and νc is Poisson’s ratio of concrete.
This theoretical model was developed based on the elasticity theory and Faraday’s law of corrosion, which consider the influence on concrete cover cracking time of the deformation characteristics of rust products and rust byproducts filling cracks. However, like other models based on elastic mechanics, the adaptability of the Lu et al. model needs further verification.
Zhang et al. model (2010)
Zhang et al. (2010) proposed a dynamic cracking time model in two stages—the fine cracking initiation and concrete cover cracking, considering the effect of initial defects, in which cracking time contained the solution process of the initial fracture toughness and the unstable fracture toughness of corrosion-induced cracking after considering the size effect based on fracture mechanics and double K theory.
The initiation of fine cracking time is
The concrete cover cracking time is
where tcrini, tcrun is the time to fine crack initiation and the time to concrete cover cracking (d); u1ini, u1un is the radial displacement; Wcrini, Wcrun is the mass of steel (mg/mm) per unit length of the reinforcement being consumed by the corrosion process; ρs is the mass density of reinforcing steel; α1 is the ratio of the volume of expansive corrosion byproduct to the volume of iron consumed during corrosion; and α is the ratio of the molecular weight of iron to the molecular weight of corrosion products.
Zhang et al. principally considered the coupled effect of initial micro-crack propagation, corrosion current density, the creep of concrete cover, and the softening character of concrete on the concrete cover cracking time under two concrete saturations. They adopt fracture toughness in fracture mechanics to study the whole process of cover cracking, considering the influence of the actual defect in the concrete. However, the expressions of the corrosion rate and corrosion current density are not reflected.
Liu and Yu model (2016)
Based on the elastic-plastic theory and Faraday’s law of corrosion, Liu and Yu (2016) developed a uniform rust-expansion thick-walled cylinder model and prediction model of cover cracking time, expressed as
where A can be expressed as
where tcr is the concrete cover cracking time (h); n is the volume expansion rate of rust products; Δ is the average volumetric strain in the plastic zone; α is the ratio of tensile strength to the compressive strength of concrete, and α = σt/σc; ν is Poisson’s ratio of concrete.
This model uses the double shear strength criterion and the thick-walled cylinder theory to perform an elastic–plastic analysis of the uniform cracking process of the concrete cover, providing a new research method for corrosion cracking. However, the adaptability of the model needs further verification.
Lun et al. model (2021)
Based on fracture mechanics and double K theory (Zhang et al., 2010), Lun et al. (2021) proposed a theoretical model of the natural corrosion of cover cracking and electrification acceleration which considers the initial defect shape inside the concrete and the modified corrosion rate formula of reinforcement, which can be expressed as follows:
The cracking time in a natural corrosive environment:
where H* can be expressed as
where tcr is the concrete cover cracking time (a), ρcr is the corrosion rate of reinforcement (%), Ct is concrete chloride content (kg/m3), and ρ is concrete resistivity (kohm.cm).
Electrically accelerated cracking time:
where tcr is the concrete cover cracking time (d) and a, b, c are the combination coefficients (Lun et al., 2021).
Both internal and external factors are taken into account in this model, which truly reflects the influence of corrosion current density and the initial defect shape inside the concrete on cover cracking; it is an effectively improved model for predicting the true value of the actual project, with engineering application significance.
Through the analysis of the aforementioned models, each of the cracking models are largely different and consider different parameters based on the mechanical model. However, cover depth, corrosion current density, and reinforcement diameter have a relatively large effect on concrete cover cracking time, which are considered by each predicted model. However, it should be noted that the units of concrete cover cracking time including time (years, days, or hours) and current corrosion density (μA/cm2 or 10−4 g/cm2/year) need to be calculated and unified. To more effectively compare the analysis results, the eight different concrete cover cracking time models need to be normalized regarding these two factors.
Comparison of different concrete cover cracking time models
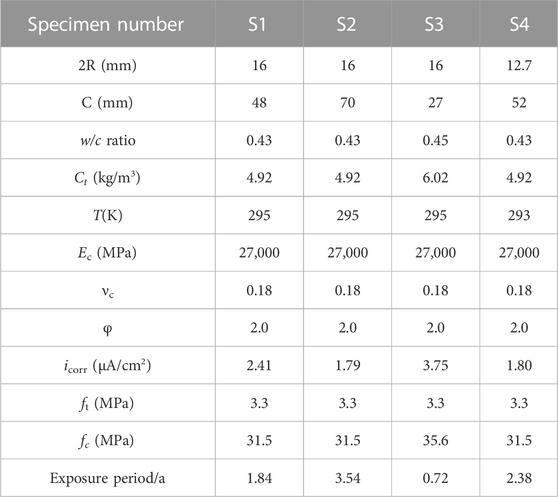
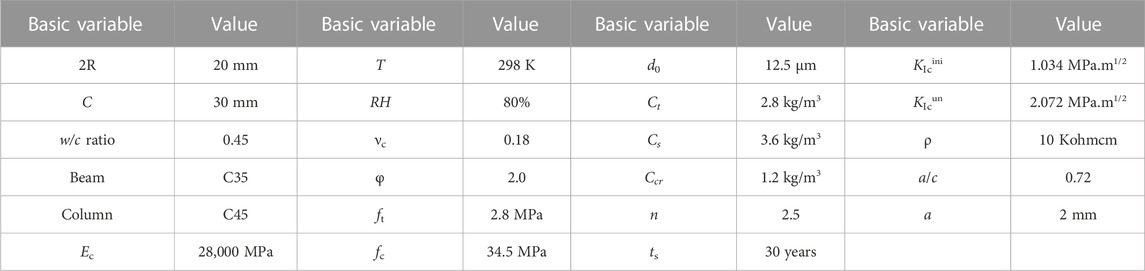
In order to quantitatively compare the differences between different models, the five-year naturally exposed experiments conducted by Liu and Weyers (1998) was used, which have very persuasive model validation. The experimental data of slabs are listed in Table 1, which illustrates the specimen numbers, chloride content (Ct), ambient temperature (T), elastic modulus (Ec), Poisson’s ratio (vc), tensile strength (ft), compressive strength (fc), and corrosion current density (icorr).
The computation parameters of the model based on fracture mechanics are the stable values of
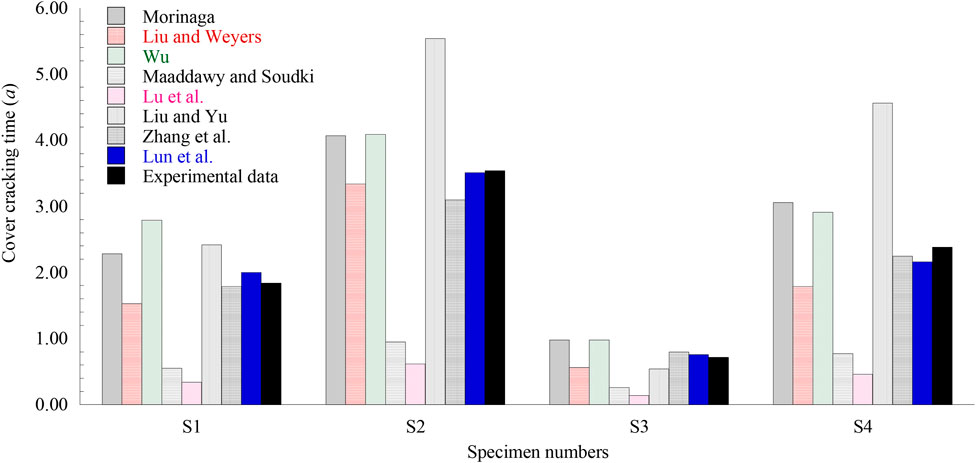
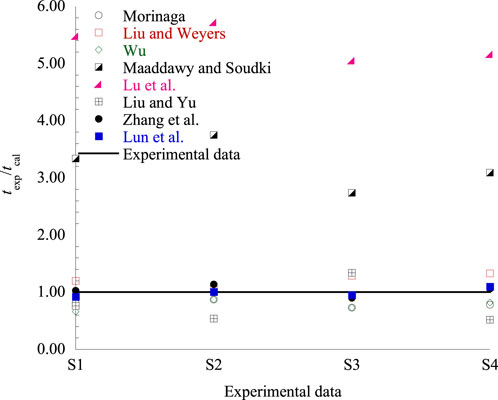
Using computational analysis, the comparison results with experimental data are shown in Figure 1, and the ratio of the experimental results and the calculated results of the different models are shown in Figure 2. The mean (M) and coefficient of variation (CV) for the different models are listed in Table 2.
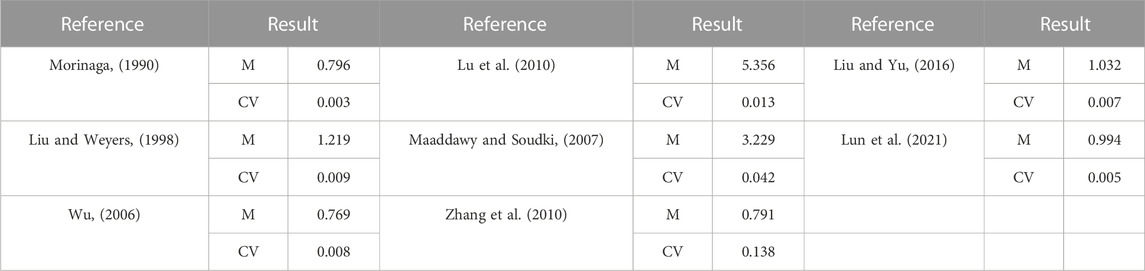
TABLE 2. Comparisons of cover cracking time obtained from experiments and the predictions of these models.
As can be seen in Figure 1, the cracking time results calculated by each cover cracking model are different. The predicted cracking time values are almost the same for the theoretical models based on fracture mechanics proposed by Zhang et al. (2010) and Lun et al. (2021). These were both close to the experimental results, indicating that the theoretical model established by fracture mechanics can accurately predict cracking time. Similarly, Liu and Weyers (1998) and Wu (2006) also reach similar conclusions and laws, which are based on elastic mechanics. However, the prediction results of Liu and Weyers (1998) are less than the experimental results, and Wu (2006) shows the opposite result; this may be related to the different parameters and modeling processes. Morinaga (1990)—an empirical model with three parameters—also agrees well with the experimental data, and the predicted results are the same as Wu (2006). The predicted results of Liu and Yu (2016) are almost the same as the experimental results (S1 and S4), but show a big difference (S2 and S4). The predicted results of Maaddawy and Soudki (2007) and Lu et al. (2010), which both considered the effective elastic model of concrete and the tensile strength of concrete, are generally much smaller than the experimental results. However, these models all show similar variation with changes in the test data.
As shown in Figure 2 and Table 2, the mean ratio similarly ranged from 0.769 (Wu) to 5.356 (Lu et al.), and the coefficient of the variation of the ratio ranged from 0.003 (Morinaga) to 0.138 (Liu and Yu). Moreover, Lun et al. (2021) proposed a theoretical model based on fracture mechanics and provided the best results, with a mean ratio of 0.994 and a coefficient of variation ratio of 0.005; Zhang et al. (2010) also provided excellent results, with a mean ratio of 1.032 and coefficient of variation ratio of 0.007. Although Morinaga provided the best results with a coefficient of variation ratio of 0.003, the mean ratio of 0.796 was poor. The mean ratio of Liu and Yu (2016) and Lu et al. (2010) is 0.791 and 5.356, respectively, and the coefficient of variation ratio is 0.138 and 0.013, which show much dispersion and difference in numbers. There are thus great differences between the calculated results of these cracking models and the experiment.
From the aforementioned findings in terms of mean and variability, Lun et al. (2021) best agree with the experimental data, which considers more comprehensive factors and the actual situation of concrete structures.
Through the previous analysis, the service lifetime t of a building structure includes two parts: corrosion initiation of reinforcement and concrete cover cracking. The equation of life prediction is
For the same building structure, the service life cycle from chloride penetration to reinforcement corrosion to concrete cover cracking is defined, which is the core content of service-life assessment.
Evaluation index system of the engineering vulnerability of structures
It is well known that, in the long-term service process of building structures in coastal areas, in addition to chloride-induced-reinforcement corrosion, they are also affected by subjective factors such as structural characteristics, engineering design, and management technology. It is necessary to adopt a more reasonable evaluation method to evaluate the service life of building structures, and such evaluation must be based on the concept of engineering vulnerability for an effective result.
Selection of evaluation factors
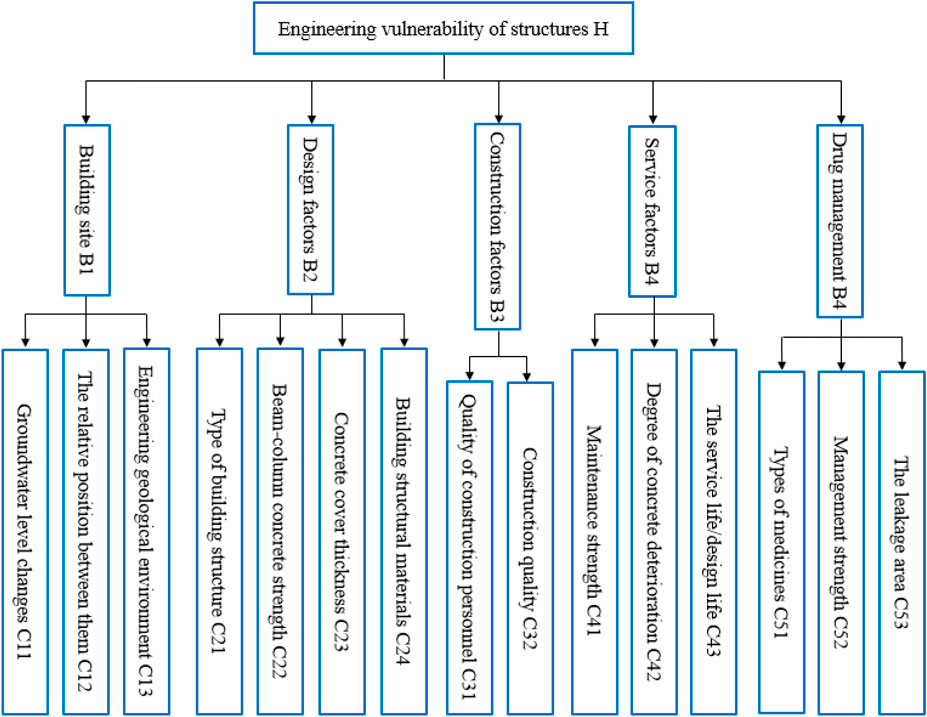
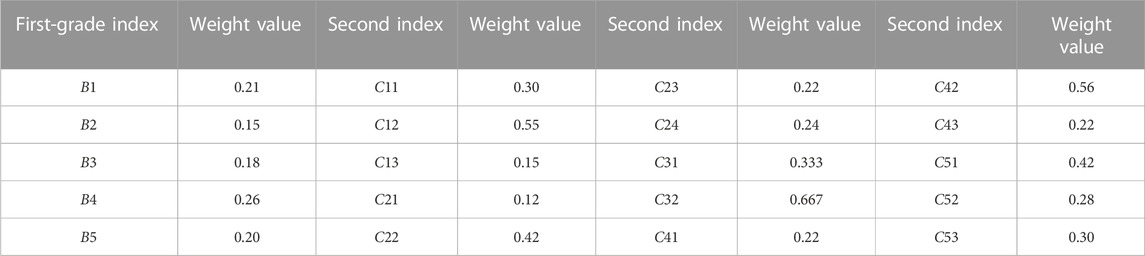
Based on the understanding that engineering vulnerability reflects the differences between the structure, materials, engineering geological conditions of the engineering body, and the potentially harmful service environment of the structure, the selection of building site B1, design factor B2, construction factor B3, service factor B4, and drug management B5 are selected as first-level evaluation factors. B1 focuses on the spatial relationship between the structure and the coastline and the impact of engineering geology at the location of the structure on the vulnerability of the project (C11∼C13); B2 focuses on the influence of factors such as structure type and concrete strength (C21∼C24); B3 focuses on the influence of factors such as the quality of construction personnel and construction quality (C31∼C32); B4 focuses on the influence of factors such as maintenance strength, concrete deterioration caused by corrosion (C41∼C43); B5 focuses on the influence of factors such as the drug leakage area and drug management strength (C51∼C53) (Table 3).
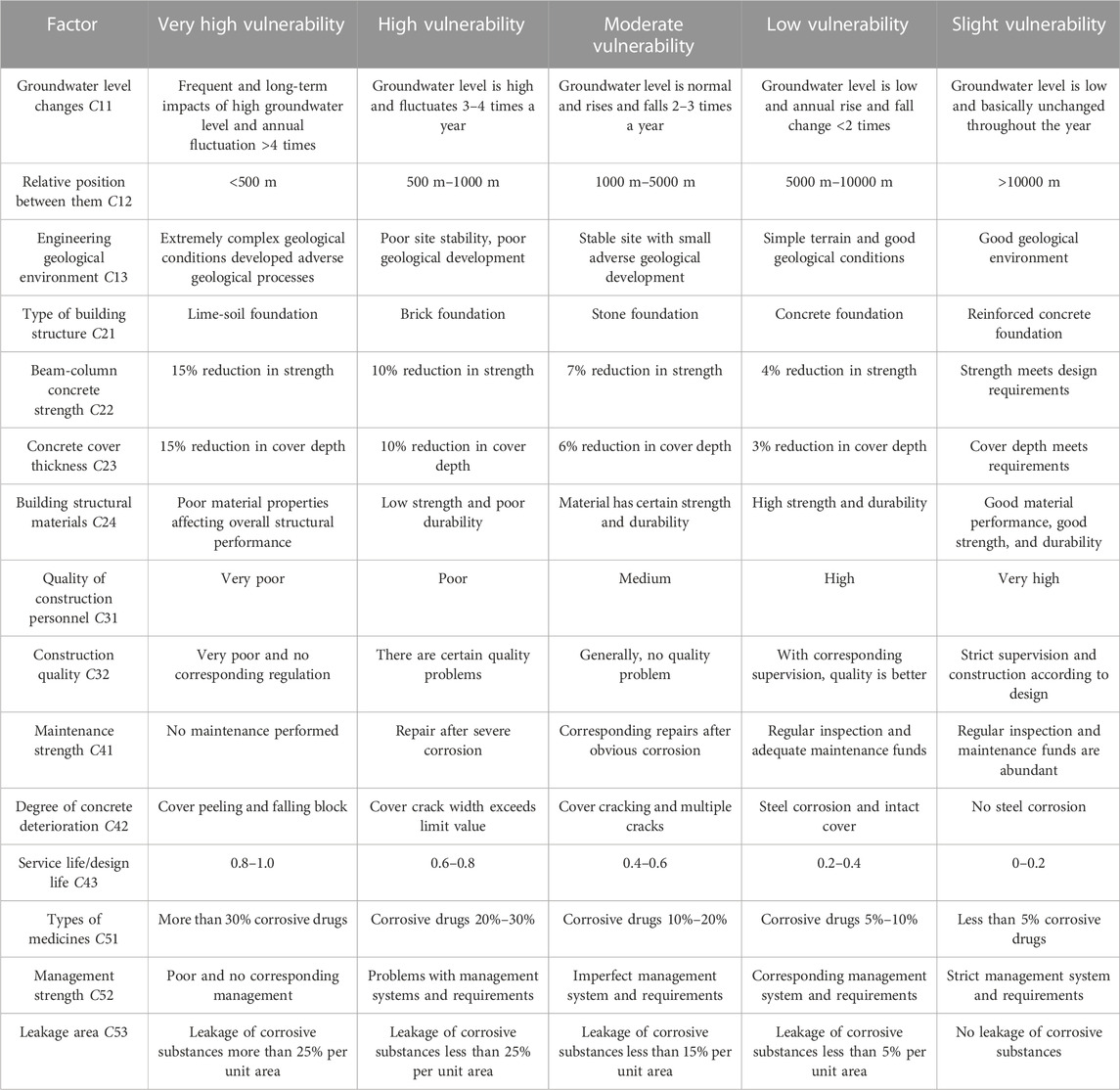
TABLE 3. Probability characteristics of modeling uncertainty parameters (Wei et al., 2008; Li, 2012; DB11∕637-2015 and Standard for structure comprehensive, 2015; Zhang and Xu, 2021; Zhang et al., 2020).
Build an evaluation index system
According to the factors and their interrelationships determined in Section 2.1, a hierarchical structure is established (Figure 3). It can be divided into three layers: target, class indicator, and basic indicator. The target layer refers to the overall vulnerability of the building structure under the action of chloride corrosion, which is the ultimate goal of the entire hierarchy analysis. The class index layer represents the structure, materials, engineering geological environment, construction and maintenance, and the corrosive environment characteristics of the structure’s engineering itself. The first-level evaluation factor of damage evaluation, which analyzes the factors affecting the first-level evaluation factor, is refined into 15 basic indicators to characterize the specific characteristics of structure and corrosion.
Determining index weight by the analytic hierarchy process
AHP can express each factor in numerical form by introducing an appropriate judgment scale, thus forming a judgment matrix to compare the importance of two factors. In this paper, the 1–9 scale method proposed by Saaty (1980) is used to grade each factor, and the discriminant matrix of the index factor is established. Under the condition that the random consistency ratio of the discriminant matrix is reasonable, the weight values of the indexes at all levels are obtained (Table 4).
Fuzzy comprehensive evaluation method of structural engineering vulnerability
Build index set and alternative set
The index set is a common set composed of various indexes that affect the object, which can be expressed as follows:
The alternative set is a collection of various total evaluation results that the evaluation object may make, with V expressed as follows:
Each element vi (i = 1,2, … ,5) represents all possible overall evaluation results. The purpose of fuzzy evaluation is to obtain the best evaluation results from the alternative set based on a comprehensive consideration of all indicators. The evaluation results of this paper are set to five levels, expressed as follows:
Determination of index membership
The fuzzy relation between the index set and the alternative set can be expressed by the fuzzy relation matrix. R represents the degree of membership of each evaluation factor to each grade standard of the alternative set, which can be calculated by the following formula to form a fuzzy matrix.
where
The fuzzy comprehensive evaluation
The secondary evaluation Cij (i,j = 1,2, … ,5) is a single factor investigation and calculation result, and the membership matrix of the secondary evaluation index can be obtained thus:
Combined with Table 2 to get the weight value of each secondary index, the final fuzzy comprehensive evaluation model can be obtained as follows:
Similarly,
According to the operation method of fuzzy sets, the membership degree can be determined by the principle of taking the largest from the smallest and of taking the largest and the normalized weighted model, and thence the vulnerability can be finally determined.
Engineering vulnerability of a coastal pharmaceutical factory
Survey of a coastal pharmaceutical factory
Topography and geomorphology
The pharmaceutical factory is located in the central part of the city to the southwest. The terrain is gentle from west to south and the topography belongs to the low platform, about 8.5 km from the coastline, which represents an elevation of 5–25 m.
Stratum lithologic
According to the geological survey report, the pharmaceutical factory is located in the southwest end of the Dashan fault zone. Regional tectonic movement is active, regional metamorphism and magmatic activity are frequent, damage to the stratum is obvious, and the continuity of the stratum is poor. In addition to the Mesozoic–Cenozoic stratum, the rocks of other strata are subject to different degrees of metamorphism.
Meteorology and hydrology
The region has subtropical marine monsoon climate characteristics, long summers and short winters, a mild climate, and abundant rainfall and sunshine. Average annual temperature is about 22.5°C, with the lowest at 0.2°C and the highest at 38.7°C; the temperature is above 25°C for half the year. Annual average relative humidity is 77%, and annual average rainfall is more than 2000 mm. The rainy season is from April to September, with a relative humidity of more than 90%. It has a more developed surface water system, high groundwater level, and belongs to the Gulf Stream System.
Data survey of service and management periods
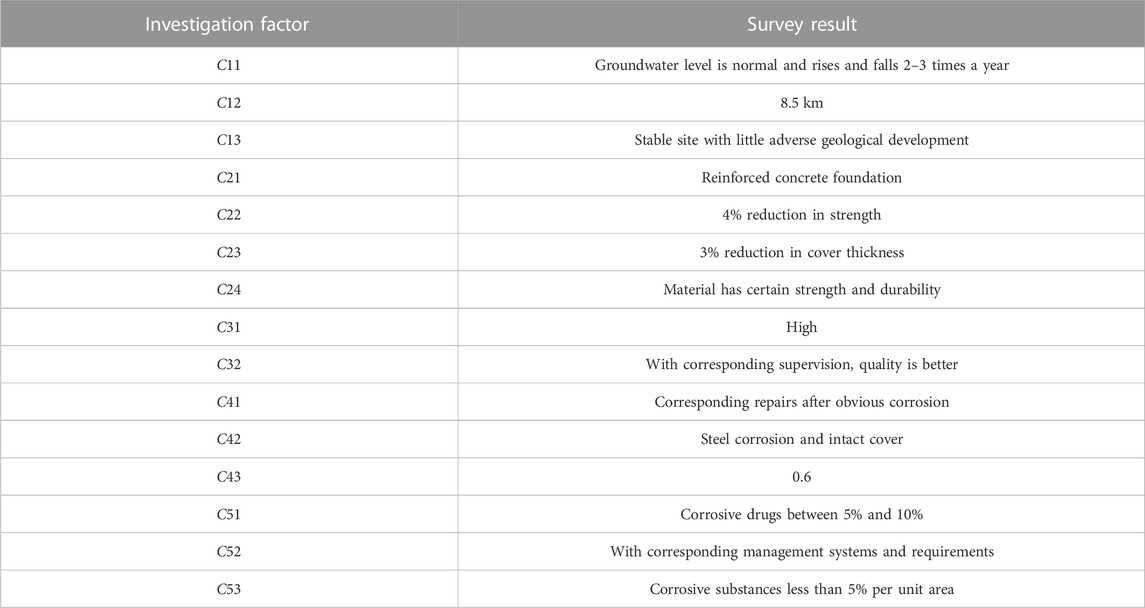
The pharmaceutical factory came into operation in 1992, with a design life of 50 years. In order to reasonably and accurately evaluate the service life of pharmaceutical factories based on the concept of engineering vulnerability, it is necessary to combine the 15 established index systems to conduct on-site investigation of building structures and equipment use to extract relevant data, such as concrete strength, cover thickness, and chloride ion content on concrete surface. However, in addition to the technical testing methods based on various non-destructive and destructive testing equipment to obtain data, technical and management mechanisms such as daily inspection statistics, maintenance data, and written records of drug types provided by the plant are also important reference materials. To this end, Tables 5, 6 show survey results for the building structure according to several basic parameters of typical beam column service state combined with basic structural parameters.
In summary, the pharmaceutical plant has been in long-term service in a marine environment with relatively high humid and annual temperatures in a relatively complex geological environment. It has adopted a standardized modern enterprise management system to manage the drugs. The types of corrosive drugs are less than 10%, and the leakage area of drugs is less than 5%. This paper investigated 15 indicators of field investigation, with the specific survey results shown in Table 6.
Engineering vulnerability calculation of building structure
Calculation of the corrosion initiation of reinforcement and concrete cover cracking
Based on the engineering parameters provided in Table 5, the time from chloride corrosion to steel corrosion initiation obtained by Eq. 11 is 28 years, and the concrete cracking time obtained by Eq. 23 is 12 years; this indicates that the service life of the building structure is 40 years. On-site steel inspection revealed that some steel bars were corroded; slight cracks were also found in some of the columns, which may be related to a combination of corrosion and loading (Zhang et al., 2022).
Engineering vulnerability calculation of building structure service life
According to the operation method of fuzzy sets, the membership vector of the building structure is calculated by Eqs 27–32 and Table 4 to be E = (0.106, 0.152, 0.227, 0.468, 0.094), and the maximum value in the membership vector is 0.468. According to Eq. 29, the engineering vulnerability of the service life of the building structure is determined to be low, and the building structure has a strong ability to resist corrosion risks. During the long-term service of the pharmaceutical factory, the investigation shows that the maintenance and management of the building structure are good, which verifies the applicability of the evaluation model.
Conclusion
This study investigated two key stages in the service prediction of building structure—corrosion initiation of reinforcement and concrete cover cracking—and evaluated the service life of a building structure based on the concept of engineering vulnerability. The following conclusions can be drawn:
1) Based on Fick’s second law, a theoretical model for corrosion initiation of reinforcement is established by considering the important parameters of the critical concentration of chloride ions, chloride ion surface concentration, and the cover depth and solution of chloride diffusion coefficient, providing a theoretical basis for predicting the process of chloride penetration in a marine environment.
2) Comparing the calculation results of eight models of concrete cover cracking time with the experimental data, a theoretical model for cover cracking time proposed by Lun et al. (2021) was chosen with consideration of the important parameters of the shape of the initial defects, cover depth, reinforcement diameter, ambient temperature, relative humidity, concrete chloride content, and corrosion rate based on the fracture mechanics theory, which are in good agreement with the experimental results and effectively predict the service life of building structures.
3) An engineering vulnerability evaluation index system for building structure was constructed. The building location, design, construction, and service factors, and drug management were selected as the first-level evaluation factors, and these were refined to obtain 15 main basic evaluation factors, with which the range of basic factors was determined. By means of AHP method and fuzzy comprehensive evaluation methodology, the assessment method of the service life engineering vulnerability of a building structure was established.
4) The evaluation method established in this paper was used to evaluate a pharmaceutical factory in a coastal area. The evaluation results show that the building structure is of low vulnerability, which is consistent with the survey results, indicating that the method is suitable for the vulnerability of building structure engineering in coastal areas.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
Data curation, YL; funding acquisition, PL; investigation, AX; resources, PL; writing—review and editing, XC.
Conflict of interest
XC, AX, and YL were employed by the company Xuchang Hengsheng Pharmaceutical Co., Ltd.
The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Ai-Harthy, A. S., Stewart, M. G., and Mullard, J. (2011). Concrete cover cracking caused by steel reinforcement corrosion. Mag. Concr. Resarch 63 (9), 655–667. doi:10.1680/macr.2011.63.9.655
Apostolopoulos, C. A., Demis, S., and Papadakis, V. G. (2013). Chloride-induced corrosion of steel reinforcement-mechanical performance and pit depth analysis. Constr. Build. Mater. 38, 139–146. doi:10.1016/j.conbuildmat.2012.07.087
Bazant, Z. P. (1979). Physical model for steel corrosion in concrete sea structures-theory. J. Struct. Div. ASCE 105 (6), 1137–1153. doi:10.1061/jsdeag.0005168
Bazant, Z. P. (1979). Physical model for steel corrosion in concrete sea structures—application. J. Struct. Div. ASCE 105 (6), 1155–1166. doi:10.1061/jsdeag.0005169
Bitaraf, M., and Mohammadi, S. (2008). Analysis of chloride diffusion in concrete structures for prediction of initiation time of corrosion using a new meshless approach. Constr. Build. Mater. 22, 546–556. doi:10.1016/j.conbuildmat.2006.11.005
Chen, S. Y., Cao, L. L., and Yao, Y. S. (2020). High-speed railway subgrade service status assessment based on hazard-affected engineering vulnerability concept. J. Railw. Sci. Eng. 7 (17), 1645–1654. doi:10.19713/j.cnki.43-1423/u.T20190978
Dai, K. Y., Yu, X. H., Li, Y. S., and Lv, D. G. (2022). Seismic fragility analysis of reinforced concrete structures considering reinforcement corrosion. J. Build. Struct. 43 (8), 20–31. doi:10.14006/j.jzjgxb.2021.0081
DB11∕637-2015, Standard for structure comprehensive safety appraisal of buildings, Beijing: Standards Press of China, (2015).
Du, Y. G., Clark, L. A., and Chan, A. H. C. (2005). Residual capacity of corroded reinforcing bars. Mag. Concr. Resarch 57 (3), 135–147. doi:10.1680/macr.2005.57.3.135
Guzmán, S., Gálvez, J. C., and Sancho, J. M. (2011). Cover cracking of reinforced concrete due to rebar corrosion induced by chloride penetration. Cem. Concr. Res. 41 (8), 893–902. doi:10.1016/j.cemconres.2011.04.008
Jamali, A., Angst, U., Adey, B., and Elsener, B. (2013). Modeling of corrosion-induced concrete cover cracking: A critical analysis. Constr. Build. Mater. 42, 225–237. doi:10.1016/j.conbuildmat.2013.01.019
Jang, B. S., and Oh, B. H. (2010). Effects of non-uniform corrosion on the cracking and service life of reinforced concrete structures. Cem. Concr. Res. 40 (9), 1441–1450. doi:10.1016/j.cemconres.2010.03.018
Jin, W. L., Lv, Q. F., and Zhao, Y. X. (2007). Research progress on the durability design and life prediction of concrete structures. J. Build. Struct. 28 (1), 7–13. doi:10.14006/j.jzjgxb.2007.01.002
Leonid, C., Dimitri, V. V., and Volokh, K. Y. (2010). Analytical modelling of concrete cover cracking caused by corrosion of reinforcement. Mater. Struct. 43, 543–556. doi:10.1617/s11527-009-9510-2
Li, M. X., Wang, G. X., Yang, X. R., and Yang, F. J. (2021). Loss assessment of wind-induced damage for residential buildings groups based on engineering vulnerability. J. Build. Eng. 42, 102435. doi:10.1016/j.jobe.2021.102435
Li, Y. S. (2012). Detection and safety appraisal of China foreign exchage trade system building theteh bund of shanghai. Tunnle Constr. 42 (S1), 612–615. doi:10.19701/j.jzjg.2012.s1.149
Liu, R. G., and Yu, M. X. (2016). Calculation model of corrosion expansion crack time for concrete cover. J. Jiangsu Univ. 37 (2), 219–224. doi:10.3969/j.issn.1671-7775.2016.02.016
Liu, Y. P., and Weyers, R. E. (1998). Modeling the time-to-corrosion cracking in chloride contaminated reinforced concrete structures. ACI Mater. J. 95 (6), 675–681.
Lu, C. H., Zhao, Y. X., and Jin, W. L. (2010). Modeling of time to corrosion-induced cover cracking in reinforced concrete structures. J. Build. Structrures 31 (2), 85–92. doi:10.14006/j.jzjgxb.2010.02.010
Lun, P. Y., Zhang, X. G., Jiang, C., Ma, Y. F., and Fu, L. (2021). Modelling of corrosion-induced concrete cover cracking due to chloride attacking. Materials 14, 1440. doi:10.3390/ma14061440
Luo, D. M., Niu, D. T., and Su, L. (2019). Research progress on durability of stressed concrete under environmental actions. Eng. Mech. 36 (1), 4–17. doi:10.6052/j.issn.1000-4750.2018.08.ST11
Maaddawy, T. E., and Soudki, K. (2007). A model for prediction of time from corrosion initiation to corrosion cracking. Cem. Concr. Compos. 29 (3), 168–175. doi:10.1016/j.cemconcomp.2006.11.004
Marasco, S., Noori, A. Z., Domaneschi, M., and Cimellaro, G. P. (2021). Seismic vulnerability assessment indices for buildings: Proposals, comparisons and methodologies at collapse limit states. Int. J. Disaster Risk Reduct. 63, 102466. doi:10.1016/j.ijdrr.2021.102466
Matsumura, T., Shirai, K., and Saegusa, T. (2008). Verification method for durability of reinforced concrete structures subjected to salt attack under high temperature conditions. Nucl. Eng. Des. 238 (5), 1181–1188. doi:10.1016/j.nucengdes.2007.03.032
Morinaga, S. (1990). “Prediction of service life of reinforced concrete buildings based on the corrosion rate of reinforcing steel, Durability of building Materials and components,” in Proceedings of 5th international conference on brighton (UK: Spon Press), 27–52.
Pour-Ghaz, M., Isgor, O. B., and Ghods, P. (2009). The effect of temperature on the corrosion of steel in concrete. Part 1: Simulated polarization resistance tests and model development. Corros. Sci. 51, 415–425. doi:10.1016/j.corsci.2008.10.034
Qiang Zhang, L., Fu, L., and Xu, A. (2020). An efficient approach for numerical simulation of concrete-filled round-ended steel tubes. Journal of Construction Steel Research 170, 106086. doi:10.1016/j.jcsr.2020.106086
Reale, T., and O’Connor, A. (2012). A review and comparative analysis of corrosion-induced time to first crack models. Constr. Build. Mater. 36, 475–483. doi:10.1016/j.conbuildmat.2012.06.033
Rodriguez, O. G., and Hooton, R. D. (2003). Influence of cracks on chloride ingress into concrete. ACI Mater. J. 100 (2), 120–126. doi:10.14359/12551
Tamer, E. M., and Khaled, S. (2007). A model for prediction of time from corrosion initiation to corrosion cracking. Cem. Concr. Compos. 29, 168–175. doi:10.1016/j.cemconcomp.2006.11.004
Tang, L. P., and Gulikers, J. (2007). On the mathematics of time-dependent apparent chloride diffusion coefficient in concrete. Cem. Concr. Res. 37 (4), 589–595. doi:10.1016/j.cemconres.2007.01.006
Tian, Y., Chen, C. C., Jin, N. G., Jin, X., Tian, Z., Yan, D., et al. (2019). An investigation on the three-dimensional transport of chloride ions in concrete based on X-ray computed tomography technology. Constr. Build. Mater. 221, 443–455. doi:10.1016/j.conbuildmat.2019.05.144
Vu, K. A. T., and Stewart, M. G. (2000). Structural reliability of concrete bridges including improved chloride-induced corrosion models. Struct. Saf. 22 (4), 313–333. doi:10.1016/s0167-4730(00)00018-7
Wang, H. L., Jin, W. L., and Sun, X. Y. (2008). Fracture model for protective layer cracking of reinforced concrete structure due to rebar corrosion. J. Hydraulic Eng. 39 (7), 863–869. doi:10.15935/j.cnki.jggcs.2012.04.014
Wang, S. L., Chen, C., Zhang, J. H., Gu, X. F., and Huang, X. D. (2022). Vulnerability assessment of urban road traffic systems based on traffic flow. Int. J. Crit. Infrastructure Prot. 38, 100536. doi:10.1016/j.ijcip.2022.100536
Wang, X. G., Zhang, W. P., Gu, X. L., and Dai, H. C. (2013). Determination of residual cross-sectional areas of corroded bars in reinforced concrete structures using easy-to-measure variables. Constr. Build. Mater. 38, 846–853. doi:10.1016/j.conbuildmat.2012.09.060
Wang, Y. D., Tang, Y. J., Chen, C., and Lin, L. D. (2012). Study on life predicting model of subsea tunnel based on chloride corrosion. Struct. Eng. 28 (4), 57–62.
Wang, Y. Z., Wu, L. J., Wang, Y. C., Liu, C. X., and Li, Q. M. (2018). Effects of coarse aggregates on chloride diffusion coefficients of concrete and interfacial transition zone under experimental drying-wetting cycles. Constr. Build. Mater. 185, 230–245. doi:10.1016/j.conbuildmat.2018.07.049
Wei, P., Chen, X. M., and Liu, L. J. (2008). Assessement on vulnerability of tunnels to earthquake loads based on holistic risk analysis approach. Tunnle Constr. 28 (3), 871–873.
Wu, Q., and Yuan, Y. S. (2008). Experimental study on the deterioration of mechanical properties of corroded steel bars. China Civ. Eng. J. 41 (12), 42–47. doi:10.3321/j.issn:1000-131X.2008.12.007
Wu, X. H. (2006). Analytical solution for cracking time of reinforced concrete structure due to corrosion expansion in marine envi-ronment. J. Shanghai Marit. Univ. 3, 22–26. doi:10.3969/j.issn.1672-9498.2006.03.005
Wu, X. L., and Tang, S. Y. (2022). Comprehensive evaluation of ecological vulnerability based on the AHP-CV method and som model: A case study of badong county, China. Ecol. Indic. 137, 108758. doi:10.1016/j.ecolind.2022.108758
Wu, Z. M., Xu, S. L., and Ding, Y. N. (2001). The double-K fracture parameter of concrete for non-standard three point bending beam spec-imens. China Enginerring Sci. 3, 76–81. doi:10.3969/j.issn.1009-1742.2001.04.014
Xu, L. R., Chen, S. Y., and Cao, L. L. (2014). Engineering vulnerability assessment for bridgeds and tunnels harmed by debris flow hazards. Rock Soil Mech. 35 (9), 2642–2650. doi:10.16285/j.rsm.2014.09.015
Xu, L. R., Wang, L., and Su, Z. M. (2010). Assessment of engineering vulnerability of tunnel suffering from debris flow. Rock Soil Mech. 31 (7), 2153–2158. doi:10.16285/j.rsm.2010.07.010
Zhang, Q., Lun, P. Y., and Li, X. (2021). A simplified approach for prediction of concrete resistivity: Experimental study and mathematic model. Mater. Struct. 54, 155. doi:10.1617/s11527-021-01688-9
Zhang, Q., and Xu, L. (2021). Evaluation of moments of performance functions based on polynomial chaos expansions. Int. J. Mech. Mater. Des. 18, 395–405. doi:10.1007/s10999-021-09585-3
Zhang, Q., Zhao, Y. G., Kolozvari, K., and Xu, L. (2022). Reliability analysis of reinforced concrete structure against progressive collapse. Reliab. Eng. Syst. Saf. 228, 108831. doi:10.1016/j.ress.2022.108831
Zhang, Q., Zhao, Y. G., Kristijan, K., and Xu, L. (2020). Simplified model for assessing progressive collapse resistance of reinforced concrete frames under an interior column loss. Eng. Struct. 215, 110688. doi:10.1016/j.engstruct.2020.110688
Zhang, X. G., Li, M. H., Tang, L. P., Memon, S. A., Ma, G., Xing, F., et al. (2017). Corrosion induced stress field and cracking time of reinforced concrete with initial defects: Analytical modeling and experimental investigation. Corros. Sci. 120, 158–170. doi:10.1016/j.corsci.2017.01.012
Zhang, X. G., Zhao, Y. G., and Lu, Z. H. (2010). Dynamic corrosion-induced cracking process of RC considering effect of initial defects. J. Asian Archit. Build. Eng. 9 (2), 439–446. doi:10.3130/jaabe.9.439
Keywords: building structure, chloride-induced corrosion, corrosion initiation, concrete cover cracking time, engineering vulnerability
Citation: Chi X, Xu A, Liu Y and Lun P (2023) Engineering vulnerability evaluation of building structures in coastal areas considering the effects of corrosion. Front. Mater. 9:1107378. doi: 10.3389/fmats.2022.1107378
Received: 24 November 2022; Accepted: 21 December 2022;
Published: 11 January 2023.
Edited by:
Chun-Xu Qu, Dalian University of Technology, ChinaCopyright © 2023 Chi, Xu, Liu and Lun. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xiaona Chi, dGlhbm41MjExQDE2My5jb20=
 Xiaona Chi
Xiaona Chi Anna Xu1
Anna Xu1