- 1Interdisciplinary Center for Quantum Information, State Key Laboratory of Modern Optical Instrumentation, ZJU-Hangzhou Global Scientic and Technological Innovation Center, Zhejiang University, Hangzhou, China
- 2School of Information and Electrical Engineering, Zhejiang University City College, Zhejiang, China
- 3International Joint Innovation Center, Key Laboratory of Advanced Micro/Nano Electronic Devices and Smart Systems of Zhejiang, The Electromagnetics Academy at Zhejiang University, Zhejiang University, Haining, China
- 4Jinhua Institute of Zhejiang University, Zhejiang University, Jinhua, China
Reconfigurable metasurfaces have been regarded as an emerging subfield of metasurfaces that can manipulate electromagnetic wave information in a smart manner. They stimulate a gradual transition in metasurface holography from passive to active elements. To date, intelligent dynamic holographic imaging schemes typically rely on iterative or data-driven methods to obtain holograms at a fixed imaging distance, which significantly hinders the development of intelligent dynamic holographic imaging in practical scenarios involving high demands for dynamic imaging distances. Herein, a computer-generated hologram algorithm with a dynamic imaging distance and a reconfigurable metasurface are proposed, which is referred to as a generator and physical diffractive network. Simulation results of time–distance division for three-dimensional imaging are provided to demonstrate the reliability and high efficiency of the proposed algorithm.
Introduction
Holography is one of the most promising three-dimensional (3D) imaging techniques that can integrally reconstruct an imaging target by recording the amplitude and phase information of electromagnetic wavefronts(Gabor, 1948) (Leith and Upatnieks, 1962). Breakthroughs in computer-generated holograms and spatial light modulators(Xu et al., 2017) have enabled the creation of holograms of virtual objects. Holography have garnered significant attention in the fields of metrology(Kreis et al., 2001; Mundt and Kreis, 2010; Desse and Picart, 2015), data storage (Hesselink et al., 2004) (Kim et al., 2009), and displays (Cem et al., 2020) (Shi et al., 2021). However, several challenges remain to be overcome. Reconstruction using bulky macroscale interference-based generation methods(Tricoles, 1987) has many physical limitations, such as narrow bandwidths, small fields of view, and multiple diffraction orders.
The emergence of metamaterials(Huang and Chen, 2011) (Chen et al., 2004) in recent years has provided novel perspectives for the modulation of light and electromagnetic waves. Metamaterials have generated tremendous attention in the field of cloak(Chen et al., 2007; Xi et al., 2009; Xu et al., 2012) etc. Metasurfaces(Allen et al., 2020; Han et al., 2021; Hu et al., 2021; Yang et al., 2016; Pfeiffer and Grbic, 2013) are ultrathin subwavelength planar metamaterials that can control electromagnetic wavefronts into almost arbitrary profiles. Metasurfaces have become an excellent solution for holograms owing to their ability to control electromagnetic waves(Wang et al., 2016a; Devlin et al., 2016; Zhang et al., 2016; Yan et al., 2021). Compared with conventional holograms, metasurface-based holograms provide unprecedented spatial resolution, high precision and low noise. The subwavelength pixel-sized unit can contribute to excellent holographic imaging owing to the elimination of undesired diffraction orders and improvements in the transmission or reflection efficiency.
Recently, reconfigurable metasurfaces(Li et al., 2020; Li et al., 2021; Wu et al., 2021; Li et al., 2022) have been proposed to realise various functionalities by integrating them with phase-changing materials. Reconfigurable metasurfaces have been used to implement holograms for dynamic control. For instance, coding metasurface holograms can be generated using a 1-bit Gerchberg-Saxton algorithm(Li et al., 2017) or a dichotomous neural network (Liu et al., 2021) (Liu et al., 2022). The iterative-based GS algorithm must satisfy the Fourier correspondence between forward and backward diffractions, which exists only in the far field. In terms of the dynamic imaging distance, an overly large solution space and phase periodicity results in a network that is difficult to converge. However, a dynamic imaging distance is required when a complex imaging environment is involved.
In this study, a holographic imaging mathematical model was constructed to analyse the inverse design problem, and the phase-generation problem of the generator and physical diffractive network (GPDN) was resolved using a two-channel method. Specifically, the structure of the GPDN was combined with a physical diffraction model to facilitate the unsupervised training of the network, including the metasurface and diffraction layers. The proposed method can rapidly generate a hologram when the target and distance are specified. A reconfigurable metasurface for 3D imaging at approximately 6 GHz was designed to validate the proposed method. Specifically, the 3D model was partitioned into imaging targets and distances at equal spacings, which generated 20 × 20 supercell holograms in real time, and the simulation results validated the efficiency and reliability of this approach.
Theory and Method
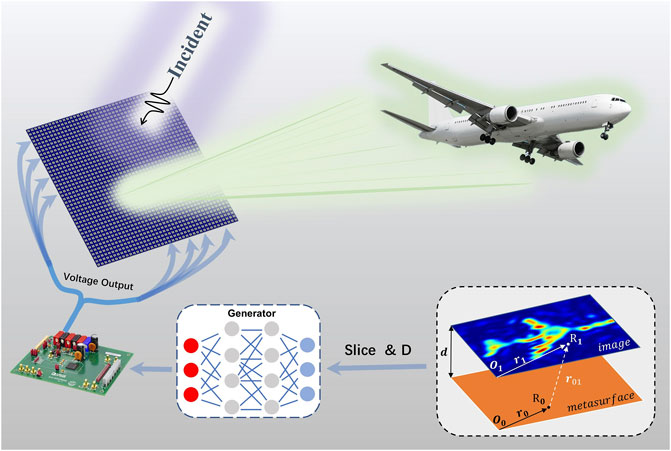
Figure 1 shows a schematic illustration of the proposed dynamic-distance holographic imaging system. The holograms are generated after inputting the image and distance of the 3D model slice to the generator of GPDN; subsequently, the reconfigurable metasurfaces yield the corresponding holograms via a voltage control module.
The Rayleigh–Sommerfeld diffraction formula (Wang et al., 2016b). is acknowledged as a forward propagation function from the phase distribution of metasurfaces to the near-field EM distribution.
where
In a two-dimensional (2D) imaging system, this expression can be decomposed into a mathematical convolution, as follows:
This formula can be calculated via the Fourier transform to reduce the computational complexity, as follows:
The effect of each pixel on the imaging is the same at a fixed imaging distance; however, the phase periodicity of each pixel causes multi-solution uncertainty. In other words, the imaging result is the same for a phase hologram and the initial phase. Furthermore, the addition of a dynamic imaging distance directly results in network convergence failure.
To suppress the corner-related scattering effect (Li et al., 2017). of reconfigurable metasurface units, 2
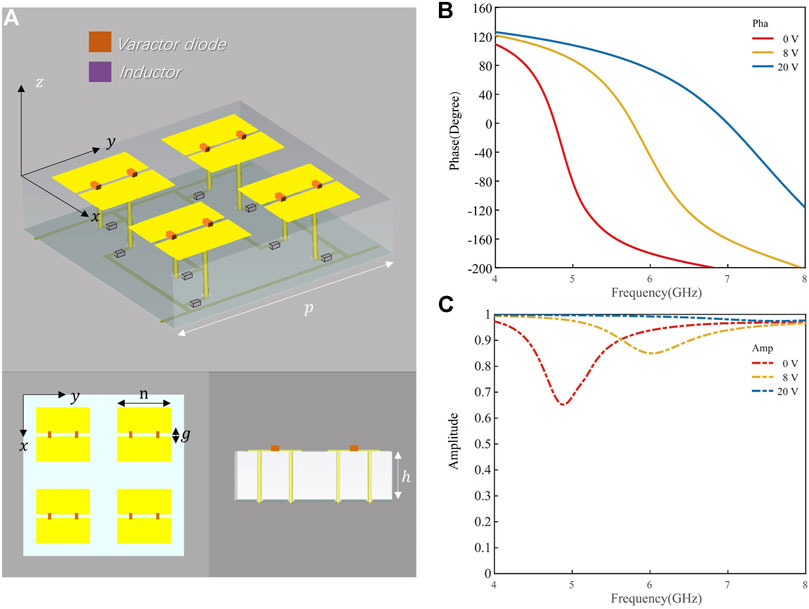
FIGURE 2. (A) Structure of supercell (B) phase responses of supercell at 0, 8, and 20 V (C) amplitude responses of supercell at 0, 8, and 20 V.
Figure 3 shows the structure of the proposed GPDN. It comprises two main modules: a generator and a physical diffraction model. The generator uses a special multi-layer perceptron (MLP) model. In particular, the 40*40 image is stretched and stiches with the distance to form the 1601*1 vector for input of the MLP. The input layer generates dual channel vector in the first hidden layer via two parallel independent weights and biases. The second hidden layer and output layer work similarly to the above. Finally, the 400*2 feature vector characterizing the real and imaginary parts is captured and then synthesizes the phase parameters ranging from ˗π to π via Atan2 function. This approach allows the generator of GPDN to uniquely output any phase, which can avoid network oscillation owing to the periodicity of the phase. The physical diffractive model comprises two layers: a metasurface layer and a diffractive layer. The metasurface layer synthesises phase parameters based on the phase response with the ground performance of the supercell, which is further compressed to -180° to 100°, and the amplitude varies with phase. This network structure of GPDN solves the physical limitations of reconfigurable metasurface units. Our GPDN can be used by re-measuring the phase compression relationship and amplitude–phase change curve for any new reconfigurable metasurface unit. Subsequently, the metasurface layer generates a 40
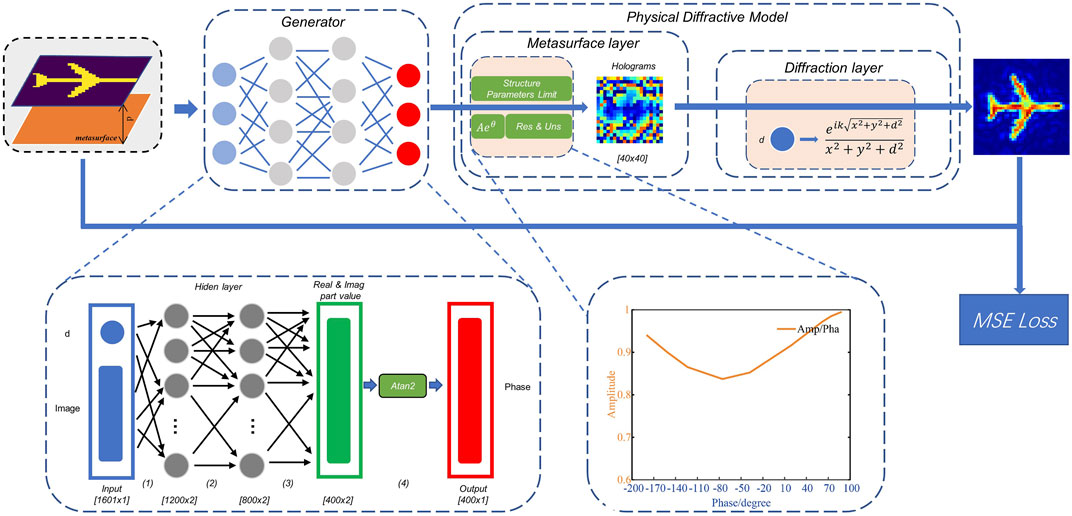
FIGURE 3. Structure of GPDN, which comprises two modules: generator and physical diffractive model. Physical diffraction model includes metasurface and diffraction layers.
The mean square error
Results and Discussions
Approximately 60,000 data points including imaging distances of 200–400 mm and random imaging targets were generated, and they supported the unsupervised training of the GPDN. The Adam optimiser was set at a learning rate of 1e-3, and the batch size was 64. A program was developed using a PyTorch deep-learning platform on a GPU (1050Ti). After approximately 1000 epochs, the

FIGURE 4. Imaging results of hologram obtained via numerical simulation based on generator inputs of d = 200, 300, and 400 mm.
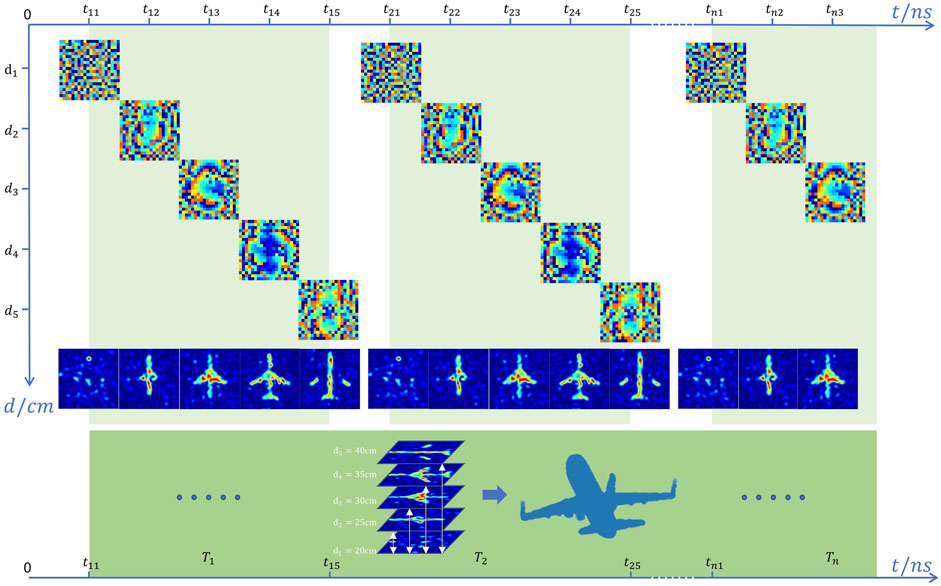
For 3D holographic imaging, an increase in the spatial dimension implies more meta units required to restore the information. Currently, partitioning a 3D target into a 2D target and the distance to reduce the complexity of the imaging system is a smart scheme. An airplane model can be segmented into slices every 5 cm along the Z-axis. The slices and corresponding imaging distances are shown in Figure 5A, which can be used to generate the target holograms by the generator, as shown in Figure 5B. Figure 5C shows the imaging numerical simulation results generated using the exact diffraction formula. To verify the effectiveness of the proposed GPDN model based on physics, we used the commercial software CST STUDIO SUITE to perform a full-wave simulation (Figure 5D), and the supercell structure was as described above. In particular, the results of the full-wave and numerical simulations were highly consistent, which is attributable to two reason. First, the metasurface and diffractive layers provide many physical constraints to the hologram, which renders the holographic imaging system similar to the practical scenario. Second, the phase holograms generated by any network are considered messy, which may destroy the periodicity of the metasurfaces and result in unit coupling. Therefore, a supercell was used in this system. Moreover, excellent performance was no longer required in the optical response of the metasurface unit, such as 2π phase coverage or amplitude uniformity. Consequently, the abovementioned GPDN structure is applicable to other imaging problems and hence can reduce difficulties in complex imaging systems.
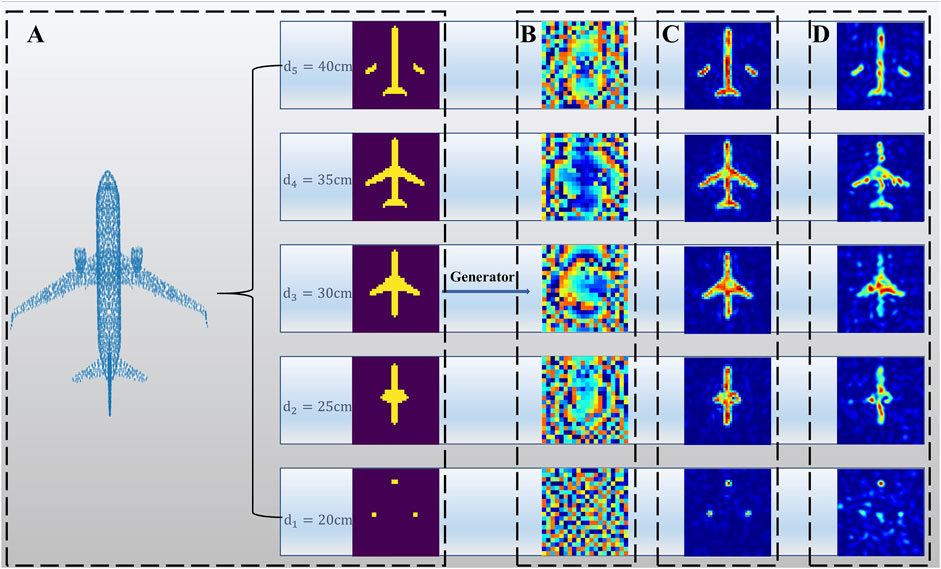
FIGURE 5. (A) Three-dimensional airplane model segregated into two-dimensional Images at five different distances (B) Holograms yielded by generator based on images and distances (C) Diffraction imaging results obtained via numerical simulation at corresponding distance (D) Full-wave simulation results based on supercell obtained via CST.
The holographic display of the 3D model can be realised using time–distance division technology. However, the cost is expressed in the time domain. Nonetheless, the reconfigurable metasurface unit can expand the time dimension. Each subholographic image can be completed by a one-time adjustment of the phase distribution, i.e. holographic imaging is not completely generated until metasurfaces traverse the phase distributions corresponding to all imaging distance points. Based on the datasheet of the varactor diode (SMV-2019), its response speed is
Conclusion
In this study, a reconfigurable metasurface holographic imaging system with adjustable distance was designed. In particular, we innovatively added a metasurface layer to the system, which allows the output of the hologram to be adjusted according to the optical response of the unit, thereby rendering the entire physical diffractive model more accurate. Consequently, the imaging system can rapidly regulate the state of the reconfigurable metasurface elements to control the distribution of near-field electromagnetic waves and display 3D holographic images. In addition, the proposed method can be easily extended to dynamic frequencies. We believe that a more comprehensive imaging system will be developed in the near future.
Data Availability Statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author Contributions
B. Z. and R. Z. conceived the idea and supervised the the research. B. Z. and R. Z. guided the theory. Y. Z. designed the algorithm framework and unit Structure. Y. Z. and L. S. performed the numerical and simulation verifications. Y. Z., B. Z., R. Z. and L. S. analyzed the data. Y. Z. and L. S. wrote the paper. All authors discussed the results and commented on the manuscript.
Funding
This work was sponsored by the National Natural Science Foundation of China under Grant Nos. 62071423 and 61905216, Natural Science Foundation of Zhejiang Province under Grant No. LQ21F050002, and Fundamental Research Funds for the Central Universities.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Allen, K. W., Dykes, D. J. P., Reid, D. R., and Lee, R. T. (2020). Multi-Objective Genetic Algorithm Optimization of Frequency Selective Metasurfaces to Engineer Ku-Passband Filter Responses. Prog. Electromagn. Res. 167, 19–30. doi:10.2528/pier19112609
Cem, A., Hedili, M. K., Ulusoy, E., and Urey, H. (2020). Foveated Near-Eye Display Using Computational Holography. Sci. Rep. 10, 14905. doi:10.1038/s41598-020-71986-9
Chen, H., Ran, L., Huangfu, J., Zhang, X., Chen, K., Grzegorczyk, T. M., et al. (2004). Left-handed Materials Composed of Only S-Shaped Resonators. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 70, 057605. doi:10.1103/PhysRevE.70.057605
Chen, H., Wu, B.-I., Zhang, B., and Kong, J. A. (2007). Erratum: Electromagnetic Wave Interactions with a Metamaterial Cloak [Phys. Rev. Lett.99, 063903 (2007)]. Phys. Rev. Lett. 99, 149901. doi:10.1103/physrevlett.99.149901
Desse, J.-M., and Picart, P. (2015). Stochastic Digital Holography for Visualizing inside Strongly Refracting Transparent Objects. Appl. Opt. 54, A1–A8. doi:10.1364/ao.54.0000a1
Devlin, R. C., Khorasaninejad, M., Chen, W. T., Oh, J., and Capasso, F. (2016). Broadband High-Efficiency Dielectric Metasurfaces for the Visible Spectrum. Proc. Natl. Acad. Sci. U.S.A. 113, 10473–10478. doi:10.1073/pnas.1611740113
Han, B., Li, S., Li, Z., Huang, G., Tian, J., and Cao, X. (2021). Asymmetric Transmission for Dual-Circularly and Linearly Polarized Waves Based on a Chiral Metasurface. Opt. Express 29, 19643–19654. doi:10.1364/oe.425787
Hesselink, L., Orlov, S. S., and Bashaw, M. C. (2004). Holographic Data Storage Systems. Proc. IEEE 92, 1231–1280. doi:10.1109/jproc.2004.831212
Hu, Z., He, N., Sun, Y., Jin, Y., and He, S. (2021). Wideband High-Reflection Chiral Dielectric Metasurface. Prog. Electromagn. Res. 172, 51–60. doi:10.2528/pier21121903
Huang, L., and Chen, H. (2011). Multi-band and Polarization Insensitive Metamaterial Absorber. Prog. Electromagn. Res. 113, 103–110. doi:10.2528/pier10122401
Kim, J. H., Yang, H., and Park, J. B. (2009). “IPI Noise Reduction by Fuzzy Rules and Data Compression Using Wavelet Transform Method in a Holographic Data Storage System,” in Optical Data Storage Topical Meeting, 55–57. doi:10.1109/ods.2009.5031752
Kreis, T. M., Aswendt, P., and Höfling, R. (2001). Hologram Reconstruction Using a Digital Micromirror Device. Opt. Eng. 40, 926–933. doi:10.1117/1.1367346
Leith, E. N., and Upatnieks, J. (1962). Reconstructed Wavefronts and Communication Theory*. J. Opt. Soc. Am. 52, 1123–1130. doi:10.1364/josa.52.001123
Li, L., Jun Cui, T., Ji, W., Liu, S., Ding, J., Wan, X., et al. (2017). Electromagnetic Reprogrammable Coding-Metasurface Holograms. Nat. Commun. 8, 197. doi:10.1038/s41467-017-00164-9
Li, S. J., Li, Y. B., Li, R. Q., Li, Z. X., Zhang, C., Guo, Z. X., et al. (2020). A Thin Self‐Feeding Janus Metasurface for Manipulating Incident Waves and Emitting Radiation Waves Simultaneously. Ann. Der Phys. 532, 2000020. doi:10.1002/andp.202000020
Li, S. J., Li, Y. B., Zhang, L., Luo, Z. J., Han, B. W., Li, R. Q., et al. (2021). Programmable Controls to Scattering Properties of a Radiation Array. Laser & Photonics Rev. 15, 2000449. doi:10.1002/lpor.202000449
Li, S., Li, Z., Han, B., Huang, G., and Liu, X. (2022). Multifunctional Coding Metasurface with Left and Right Circularly Polarized and Multiple Beams. Front. Mat. 854062. doi:10.3389/fmats.2022.854062
Liu, C., Yu, W. M., Ma, Q., Li, L., and Cui, T. J. (2021). Intelligent Coding Metasurface Holograms by Physics-Assisted Unsupervised Generative Adversarial Network. Phot. Res. 9, B159–B167. doi:10.1364/prj.416287
Liu, C., Ma, Q., Luo, Z. J., Hong, Q. R., Xiao, Q., Zhang, H. C., et al. (2022). A Programmable Diffractive Deep Neural Network Based on a Digital-Coding Metasurface Array. Nat. Electron. 5, 113–122. doi:10.1038/s41928-022-00719-9
Mundt, J., and Kreis, T. (2010). Digital Holographic Recording and Reconstruction of Large-Scale Objects for Metrology and Display. Opt. Eng. 49, 125801. doi:10.1117/1.3524238
Pfeiffer, C., and Grbic, A. (2013). Metamaterial Huygens' Surfaces: Tailoring Wave Fronts with Reflectionless Sheets. Phys. Rev. Lett. 110, 197401. doi:10.1103/physrevlett.110.197401
Shi, L., Li, B., Kim, C., Kellnhofer, P., and Matusik, W. (2021). Towards Real-Time Photorealistic 3D Holography with Deep Neural Networks. Nature 591, 234–239. doi:10.1038/s41586-020-03152-0
Tricoles, G. (1987). Computer Generated Holograms: an Historical Review. Appl. Opt. 26, 4351–4357. doi:10.1364/ao.26.004351
Wang, L., Kruk, S., Tang, H., Li, T., Kravchenko, I., Neshev, D. N., et al. (2016). Grayscale Transparent Metasurface Holograms. Optica 3, 1504–1505. doi:10.1364/optica.3.001504
Wang, Q., Zhang, X., Xu, Y., Gu, J., Li, Y., Tian, Z., et al. (2016). Broadband Metasurface Holograms: toward Complete Phase and Amplitude Engineering. Sci. Rep. 6, 32867. doi:10.1038/srep32867
Wu, N., Zhang, Y., Ma, H., Chen, H., and Qian, H. (2021). Tunable High-Q Plasmonic Metasurface with Multiple Surface Lattice Resonances (Invited). Prog. Electromagn. Res. 172, 23–32. doi:10.2528/pier21112006
Xi, S., Chen, H., Wu, B.-I., and Kong, J. A. (2009). One-directional Perfect Cloak Created with Homogeneous Material. IEEE Microw. Wirel. Compon. Lett. 19, 131–133. doi:10.1109/lmwc.2009.2013677
Xu, S., Cheng, X., Xi, S., Zhang, R., Moser, H. O., Shen, Z., et al. (2012). Experimental Demonstration of a Free-Space Cylindrical Cloak without Superluminal Propagation. Phys. Rev. Lett. 109, 223903. doi:10.1103/physrevlett.109.223903
Xu, K., Snyman, L. W., and Aharoni, H. (2017). Si Light-Emitting Device in Integrated Photonic CMOS ICs. Opt. Mater. 69, 274–282. doi:10.1016/j.optmat.2017.03.055
Yan, T., Ma, Q., Sun, S., Xiao, Q., Shahid, I., Gao, X., et al. (2021). Polarization Multiplexing Hologram Realized by Anisotropic Digital Metasurface. Adv. Theory Simul. 4, 2100046. doi:10.1002/adts.202100046
Yang, Y., Jing, L., Zheng, B., Hao, R., Yin, W., Li, E., et al. (2016). Full-polarization 3D Metasurface Cloak with Preserved Amplitude and Phase. Adv. Mat. 28, 6866–6871. doi:10.1002/adma.201600625
Zhang, X., Jin, J., Wang, Y., Pu, M., Li, X., Zhao, Z., et al. (2016). Metasurface-based Broadband Hologram with High Tolerance to Fabrication Errors. Sci. Rep. 6, 19856. doi:10.1038/srep19856
Keywords: metasurfaces, holography, imaging, deep learning, diffractive model
Citation: Zou Y, Zhu R, Shen L and Zheng B (2022) Reconfigurable Metasurface Hologram of Dynamic Distance via Deep Learning. Front. Mater. 9:907672. doi: 10.3389/fmats.2022.907672
Received: 30 March 2022; Accepted: 20 April 2022;
Published: 20 May 2022.
Edited by:
Chen Shen, Rowan University, United StatesReviewed by:
Yuxin Zhai, University of Michigan, United StatesSi Jia Li, Southeast University, China
Copyright © 2022 Zou, Zhu, Shen and Zheng. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Rongrong Zhu, cm9yb3podUB6anUuZWR1LmNu; Bin Zheng, emhlbmdiaW5Aemp1LmVkdS5jbg==
 Yijun Zou
Yijun Zou Rongrong Zhu
Rongrong Zhu Lian Shen
Lian Shen Bin Zheng
Bin Zheng