Quintuple: A Tool for Introducing Quantum Computing Into the Classroom

1. Introduction

Quantum computers can perform certain tasks more efficiently than classical computers [1, 2]. Furthermore, the results and limitations of realistic quantum computers gives us insight into the fundamentals of quantum mechanics. Quantum computation has thus attracted great interest from the research community. In 2016, IBM released access to its 5-qubit quantum computer to the scientific community under the moniker “IBM Quantum Experience” [3]. The IBM Quantum Experience provides access to a 5-qubit quantum computer with a limited set of gates described by IBM as “the worlds first quantum computing platform delivered via the IBM Cloud.” A body of research focuses on properties of 5-qubit systems [4, 5], and much of it has recently been released or updated to rely upon results running on IBM's Quantum Experience [6–13]. With IBM's release of 16- and 20- qubit systems, the study of 5-qubit systems remains ideal for the education context, in which it is large enough to illustrate foundational quantum algorithms, yet small enough to illustrate calculations on the blackboard.

Analyzing and simulating 5-qubit systems in detail can prepare students to exploit the capabilities of, and developing and debugging algorithms for deployment on experimental quantum computing infrastructure as this infrastructure scales to an increasing number of qubits in the coming decades.

Within the universal gate quantum computation paradigm, a variety of existing software toolkits are useful in quantum computation study and research, ranging from the general QuTIP [14, 15] available in Python, to more specialized toolkits available in a variety of scientific computing languages: QUBIT4MATLAB (Matlab) [16], QCMPI (Fortran 90) [17] provide rapid evaluation of quantum algorithms, including noise analysis, for a large number of qubits by exploiting parallel computing. The FEYNMAN (Maple) [18–21] program offers interactive simulations on n-qubit quantum registers without restrictions other than available memory and time resources of computation. The QDENSITY (Mathematica) [22] program provides commands to create and analyze quantum circuits. The libquantum package (C) provides the ability to simulate a variety of processes based on its implementation of a quantum register [23], Qinf (Maxima) allows the manipulation of instances of objects that appear in quantum information theory and quantum entanglement [24]. Most relevant to the IBM Quantum Experience, is the QISKit SDK [25] which is a comprehensive Python library for the Quantum Experience API. A detailed comparison between other quantum simulators is beyond the scope of this work. Those that are available use various computer languages, the majority in C/C++, and have different focuses, ranging from particular algorithms, generalisability, or scalability. A more comprehensive list of available tools for work in quantum computation is given on the Quantiki wiki [26].

This paper focuses on universal gate quantum computation, but it is useful to note the plethora of work in quantum computing focusing on quantum annealing [27–29] Of particular note in the education context is an introduction to the simulation of such quantum annealers constructed specifically for the classroom [30].

In this paper, I describe Quintuple, an open-source Python module allowing both simulation of all operations available via IBM's Quantum Experience hardware and programming for a 5-qubit quantum computer at a high level of abstraction [31]. Quintuple is available for download and updates at https://github.com/corbett/QuantumComputing. Quintuple allows the researcher, educator or student to quickly and repeatedly execute code in a simplified language compatible with execution on the IBM Quantum Experience hardware and/or in pure Python compatible with other Python code and libraries. By dialing in the focus of Quintuple on the uniquely available IBM Quantum Experience hardware, it can be deployed on the platform without additional configuration. By keeping the implementation to just those elements necessary to perform an ideal simulation of IBM's 5-qubit quantum computer, and not relying on a much larger, fuller featured toolkit, as well as by providing an open-source object-oriented implementation in a widely used high level language, Python, it is hoped this module will be useful to more novice programmers and/or those less experienced in the intricacies of quantum computation. The core of Quintuple is only 675 lines of Python code, and Quintuple additionally provides over 40 example programs with expected results, including examples of Grover's Algorithm and the Deutsch-Jozsa algorithm, for execution within Quintuple or on the IBM Quantum Experience.

In section 2 a brief overview is given of the terminology and mathematics necessary to follow the operation of Quintuple. In section 3, the Quintuple code and the APIs to design and test 5-qubit quantum algorithms in simulation and/or on IBM's hardware are introduced. In section 4, through the lens of an algorithm which swaps the state of two qubits, various modes of usage of the APIs presented in section 3 are presented. Section 5 provides a summary and outlook for potential future work.

2. Overview of Quantum Information

Here I give a brief primer on quantum information and computation necessary to describe Quintuple's implementation and assisting in understanding the IBM Quantum Experience. Knowledge of complex conjugation, basic linear algebra fluency; matrix operations including multiplication, tranpose, trace, and tensor products is assumed, among other mathematical concepts. Explicit exposition of this formalism and any explanation of the whys of quantum mechanics is beyond the scope of this limited overview of quantum information. For an detailed overview of the math and quantum mechanics of quantum information, as well as a lucid exposition of the fundamentals of quantum information in detail, an excellent resource is the canonical textbook of Nielsen and Chuang [32]. For further overview of the simulation of n-qubit systems the overview by Radtke is an excellent supplement to this more limited exposition [18].

A qubit is the quantum generalization of a classical bit. Unlike a classical bit, it can take any value corresponding to a linear superposition of its constituents: formally two orthonormal eigenstates. Our default choice of basis throughout this manuscript is

$\{|0\rangle =\left(\begin{array}{c}1\\ 0\end{array}\right),|1\rangle =\left(\begin{array}{c}0\\ 1\end{array}\right)\}$

This multi-purpose notation (〈| or |〉), used throughout this manuscript to represent a quantum state, is called bra-ket or Dirac notation and is standard in quantum mechanics. Without getting into a detailed discussion of the mathematics, one can, simplistically, think of the symbol lying between the |〉 notation as being a label for the state. Whether the notation is |symbol〉 vs. 〈symbol| indicates whether it is represented as a column or a row vector respectively, where 〈symbol| is the conjugate transpose of |symbol〉 and vice versa.

Thus a generic one-qubit state |ψ〉 is

$|\psi \rangle =a|0\rangle +b|1\rangle .(1)$

The coefficients a, b are complex numbers and these complex coefficients provide the representation of ψ in the |0〉, |1〉 basis. The probability of finding |ψ〉 in state |0〉 is |a|² = aa* where a* is the complex conjugate of a, similarly the probability of finding |ψ〉 in state |1〉 is |b|² = bb*. These two probabilities normalize to one: |a|² + |b|² = 1. A single qubit state |ψ〉 can be physically realized by a variety of mechanisms which correspond to a quantum-mechanical two-state systems, for example a two spin system, or a two level system, among many others. The Bloch sphere is a useful way to visualize the state of a single qubit on a unit sphere. Formally, in the Bloch sphere representation the qubit state is written as

$|\psi \rangle =\cos \frac{\theta }{2}|0\rangle +e^{i\varphi }\sin \frac{\theta }{2}|1\rangle ,(2)$

where θ and ϕ are the polar coordinates to describe a vector on the unit sphere.

To make use of the power of quantum computation we will in general want more than one qubit. In a classical n-bit register we can initialize each bit to 0 or 1. For example to represent the base 10 number 19 in a classical 5-bit register we can set its elements to 10011. For n qubits, to create an analogous state, a so-called quantum register we prepare the state |10011〉 = |1〉 ⊗ |0〉 ⊗ |0〉 ⊗ |1〉 ⊗ |1〉. Here ⊗ corresponds to the tensor product (also known as the direct or Kronecker product). Generically an n-bit quantum register can hold any superposition of n-qubit states.

For an n qubit state there are 2ⁿ possible values of which the n-qubit state can, in general, be a superposition of. For example for a 2-qubit state we have 2² = 4 possible states, {|00〉, |01〉, |10〉, |11〉}. For a 3-qubit state we have 2³ = 4 possible states or

$\{|000\rangle \text{},|001\rangle \text{},|010\rangle \text{},|011\rangle \text{},|100\rangle \text{},|101\rangle \text{},|110\rangle \text{},|111\rangle \}.(3)$

Numbering the states from 0 to 2ⁿ − 1, the canonical ordering used throughout this manuscript is:

${\displaystyle \sum _{m=0}^1\dots }{\displaystyle \sum _{j=0}^1{\displaystyle \sum _{i=0}^1|ij\mathrm{...}m\rangle }}\text{},(4)$

where the number of summations corresponds to the total number of qubits. Thus if we incorporate the amplitudes, the complex coefficients of these states, we can compute the probability of finding

$|\psi \rangle ={\displaystyle \sum _{m=0}^1\dots }{\displaystyle \sum _{j=0}^1{\displaystyle \sum _{i=0}^1{c}_{ij\dots m}}}|ij\mathrm{...}m\rangle \text{},(5)$

in state |ij…m〉 as the squared absolute value of c_ij…m, $|c_{ij\dots m}{|}^2=c_{ij\dots m}{c}_{ij\dots m}^{*}$.

If we can represent an n-qubit state as the tensor product of the states of individual qubits

$|q_0{q}_1\dots q_n\rangle =|q_0\rangle \otimes |q_1\rangle \otimes \dots \otimes |q_n\rangle \text{},(6)$

the state is called separable. However, due to the nature of superposition, it may be that a multi-qubit state is non-separable and individual qubits states are not well defined independent of other qubits. This non-local correlation phenomenon known as entanglement is a necessary resource to achieve the exponential speed up of quantum compared to classical computation [33]. As such, the concept of quantum registers, necessary to store multi-qubit non-separable states, will play a primary role in quantum computation simulation.

We have outlined the analogy to the classical n-bit register, the n-qubit quantum register for keeping track of quantum data. Here we will do the same with a classical gate and a quantum gate, which evolve classical and quantum states respectively. In classical computation, a classical gate operates on a classical register to evolve its state. In quantum computation, a quantum gate operates on a quantum register to evolve its state. Quantum states can be represented by matrices; the mathematics of the evolution of quantum states can unsurprisingly be represented by matrices as well. To represent quantum gates, these matrices must conform with the postulates of quantum mechanics as they multiply a state to produce an evolved state. Specifically, we know that the evolution of states must conserve probability (preserve norms); we cannot produce a state which is a superposition of states with probability greater than one.

Matrices which ensure the conservation of probability when they multiply states are called unitary. Formally, this corresponds to any matrix U which satisfies the property that its conjugate transpose U^† is also its inverse, that is U^†U = UU^† = I, where I is the identity matrix. In quantum computation, a quantum gate corresponds to a unitary matrix, and any unitary matrix corresponds to a valid quantum gate. Since unitary matrices are always invertible, quantum gates and thus computation is reversible; any operation we can do we can undo [34]. As a qubit state can be realized physically by a variety of quantum mechanical systems, so can quantum gates be physically realized by a variety of quantum mechanical mechanisms, which must necessarily depend on the system's representation of the qubit. For example, in a system where qubits are represented by ions in a quantum trap, a laser tuned to a particular frequency can induce a unitary transformation effectively acting as a quantum gate.

Gates acting on a single qubit can be applied to a quantum register of an arbitrary qubit number. For example, for a gate X if the desired qubit to act on is the 3rd qubit in a 4-qubit quantum register. X is a gate which flips the qubit it acts on from |0〉 to |1〉 or from |1〉 to |0〉. The appropriate gate is formed via X_3of4 = I ⊗ I ⊗ X ⊗ I where I is the 2 × 2 identity matrix. In general, to create a gate G_mofn to operate on the mth qubit of a register of n qubits from a gate G that operates on a single qubit, one may use

$G_{i\text{ of }n}={\displaystyle \underset{i=1}{\overset{n}{\otimes }}}\{\begin{array}{cc}I& \text{if }i\ne m\\ G& \text{if }i=m.\end{array}(7)$

Here, ${\otimes }_{i=1}^n$ is the analog of $\sum _{i=0}^n$ corresponding to the tensor product, instead of the summation operation. We can see that the application of a gate on a single qubit in this fashion doesn't generate entanglement as it never results in the expansion of the size of the quantum register it is acting on.

Specific sets of classical gates, for example the the NOT and AND gates can be used to construct all other classical logic gates and thus forms a set of universal classical gates. Other such sets exist; in fact the NAND, negative and gate alone is a universal classical gate [32]. In quantum computation, to obtain a universal gate set we will need a multi-qubit gate which applies on 2-qubits of an n-qubit register. The CNOT gate is one such gate. CNOT is the 2-qubit controlled not gate. Its first input is known as the control qubit, the second as the target qubit and the state of the target qubit is flipped on output if and only if the control qubit is |1〉. The application of CNOT can under many scenarios generate entanglement. CNOT combined with single qubit gates can approximate arbitrarily well any (unitary) operation on a quantum computer [35]. Quantum gates can be combined to form quantum circuits, the analog to classical circuits composed of logic gates connected by wires. The full set of gates that both the IBM Quantum Experience and Quintuple support, form a (non-minimal) universal quantum gate set, such that we can combine the gates in a quantum circuit to create any multi-qubit logic gate we desire.

We'll need to understand how measurement functions in quantum mechanics to understand the constraints of extracting information from a quantum register. Measurement in quantum mechanics is something which engages a lot of discussion, but its properties are straightforward to state in mathematics if not in philosophy. It is possible to perform a measurement of a single qubit with respect to any basis {|a〉, |b〉} (not just the default {|0〉, |1〉} basis) so long as this basis is orthonormal, that is that the total probability is one. It likewise is possible to measure a multi-qubit system with respect to any orthonormal basis. Earlier, we stated that the probability of finding:

$|\psi \rangle ={\displaystyle \sum _{m=0}^1\dots }{\displaystyle \sum _{j=0}^1{\displaystyle \sum _{i=0}^1{c}_{ij\dots m}}}|ij\mathrm{...}m\rangle \text{},(8)$

in state |ij…m〉 is the squared absolute value of c_ij…m, $|c_{ij\dots m}{|}^2=c_{ij\dots m}{c}_{ij\dots m}^{*}$. Here when we perform a measurement we actually do find the system in one of these states |ij…m〉 with the appropriate probability $|c_{ij\dots m}{|}^2$. After the measurement is performed, the state is collapsed and all further measurements return the same result, state |ij…m〉 with probability 1.

3. Quantum Information Tools Represented in Quintuple

Only those states and gates which are useful to interfacing with IBM's 5-qubit quantum computer are supported by Quintuple. The only external Python module Quintuple relies upon is the numpy module. The core of Quintuple is just 675 lines long.

3.1. States

States are available as static member variables of the $\text{class }\text{State}$. The following qubit states are are available

Standard (z) basis ($\text{State.zero\_state,State.one\_state}$):

$|0\rangle =\left(\begin{array}{c}1\\ 0\end{array}\right),|1\rangle =\left(\begin{array}{c}0\\ 1\end{array}\right).(9)$

Diagonal (x) basis ($\text{State.plus\_state,State.minus\_state}$):

$|+\rangle =\frac{1}{\sqrt{2}}\left(\begin{array}{c}1\\ 1\end{array}\right),|-\rangle =\frac{1}{\sqrt{2}}\left(\begin{array}{c}1\\ -1\end{array}\right).(10)$

Circular (y) basis ($\text{State.plusi\_state,State.minusi\_}$ $\text{state}$):

$|\circlearrowright \rangle =\frac{1}{\sqrt{2}}\left(\begin{array}{c}1\\ i\end{array}\right),|\circlearrowleft \rangle =\frac{1}{\sqrt{2}}\left(\begin{array}{c}1\\ -i\end{array}\right).(11)$

The $\text{class }\text{State}$ has a variety of helper methods, including those to transform to the x or y basis, to see if a multi-qubit state is simply separable into individual qubits in the set {|0〉, |1〉, |+〉, |−〉, |↻〉, |↺〉}, and to extract the nth qubit from a separable multi-qubit state. This class implements the measurement method, following the limitations of nature, and supports retrieving a state's representation on the Bloch sphere, not possible in nature but feasible in simulation. The class also has a method to create a state from binary string (e.g., “01011” corresponding to |01011〉) and return a string from a separable state. For example, we can compute the representation of the state |10011〉 in the Quintuple module numerically with

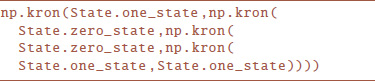
or more concicely by $\text{State.state\_from\_string(}\text{“10011”}\text{)}$.

3.2. Gates

A variety of single qubit gates are supported, as is the 2-qubit gate CNOT. Later, the $\text{class }\text{QuantumComputer}$ will use these gates as building blocks to define gates which operate on quantum registers of up to 5-qubits appropriately. In the following gate definitions the Python syntax is given in parenthesis.

H gate; Hadamard gate ($\text{Gate.H}$):

$\begin{array}{rc}H=\frac{1}{\sqrt{2}}\left(\begin{array}{cc}1& 1\\ 1& -1\end{array}\right).& (12)\end{array}$

X, Y, Z gates; Pauli gates ($\text{Gate.X,Gate.Y,Gate.Z}$):

$\begin{array}{rc}X=\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right),& (13)\end{array}$

$\begin{array}{rc}Y=\left(\begin{array}{cc}0& -i\\ i& 0\end{array}\right),& (14)\end{array}$

$\begin{array}{rc}Z=\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right).& (15)\end{array}$

I gate; Identity gate ($\text{Gate.eye}$):

$\begin{array}{rc}I=\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right).& (16)\end{array}$

S gate; Phase gate ($\text{Gate.S}$):

$\begin{array}{rc}S=\left(\begin{array}{cc}1& 0\\ 0& i\end{array}\right).& (17)\end{array}$

S^† gate ($\text{Gate.Sdagger}$):

$\begin{array}{rc}{S}^{†}=\left(\begin{array}{cc}1& 0\\ 0& -i\end{array}\right).& (18)\end{array}$

T gate; π/8 gate ($\text{Gate.T}$):

$\begin{array}{rc}T=\left(\begin{array}{cc}1& 0\\ 0& e^{\frac{i\pi }{4}}\end{array}\right).& (19)\end{array}$

T^† gate ($\text{Gate.Tdagger}$):

$\begin{array}{rc}{T}^{†}=\left(\begin{array}{cc}1& 0\\ 0& e^{-\frac{i\pi }{4}}\end{array}\right).& (20)\end{array}$

CNOT gate ($\text{Gate.CNOT2\_01}$):

$\begin{array}{rc}CNOT=\left(\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 0& 1\\ 0& 0& 1& 0\end{array}\right).& (21)\end{array}$

It can easily be checked that these gates produce the desired behavior. All other combinations of target and control qubits are available within $\text{class }\text{Gate}$ acting on quantum registers of up to 5 qubits. Here, the number appearing after the CNOT indicates the number of qubits in the register the gate is to operate on, the first subscript indicates the control qubit index in the entangled qubit register, and the second subscript indicates the target qubit index, both 0 based. For example $\text{CNOT4\_03}$ is to operate on a 4-qubit register with the 0th qubit corresponding to the control qubit and the 3rd qubit corresponding to the target qubit. The $\text{class }\text{QuantumComputer}$ helpfully supports specifying only the target and control qubits when applying the CNOT gate and automatically deploys the correct gate to achieve this based on the internal configuration of its quantum registers.

3.3. Probabilities

Several convenience methods are provided to help compute probabilities and expectation values. For a qubit residing in a quantum register representing an arbitrary number of entangled qubits, the method $\text{Probability.get\_probabilities(qubit)}$ returns an array of probabilities representing the quantum register in the canonical ordering defined in Equation (4). The method $\text{Probability.pretty\_print\_probabilities}$ prints each state and its associated probability for easy examination. For a state representing a single qubit, there are several additional methods available within $\text{class }\text{Probability}$ to help calculate the expectation of the state in the standard (z), circular (x) or diagonal bases, respectively.

3.4. QuantumRegister

To represent a possibly non-separable group of distinguishable qubits, one can treat them together in terms of a single quantum register to keep track of their ordering and their entangled state. Quintuple uses the $\text{class }\text{QuantumRegister}$ for this purpose, and the register is managed by the $\text{class }\text{QuantumComputer}$ so that it isn't necessary to follow how the qubits within $\text{class }\text{QuantumComputer}$ are internally arranged for the user to be able to perform operations and measurements. The $\text{QuantumRegister}$ object can be queried as to the number of qubits it represents, which particular qubits it represents, its state, and whether it is equal to another $\text{QuantumRegister}$ object.

The $\text{class }\text{QuantumRegister}$ has an additional method not provided in nature. Specifically a qubit is a superposition of states and when measured its state collapses to just one of these states with a probability given by the probability amplitude squared. All further measurements return the same state as the qubit is no longer in a superposition of states. The $\text{QuantumComputer}$ supports measurement in the fashion of nature, but it also for convenience of further analysis, saves the value of the full state before collapse in the $\text{QuantumRegister}$ object, which can be retrieved with the method $\text{get\_noop()}$.

3.5. QuantumRegisterCollection

The $\text{class }\text{QuantumRegisterCollection}$ is an abstraction that assists the $\text{class }\text{QuantumComputer}$ in managing its $\text{QuantumRegister}$s. This class returns the register in which a particular qubit resides, manages the merging of two $\text{QuantumRegister}$s under the hood via its $\text{entangle\_qubits}$ method, and allows easy querying as to the order of the qubits it is representing. This is useful to the $\text{class }\text{QuantumComputer}$ as it supports the user querying about the state of the qubits in any increasing order the user desires. The abstraction of the $\text{QuantumRegisterCollection}$ allows the $\text{QuantumComputer}$ to keep the qubits separately, in separate registers for as long as possible, only merging into a single register when necessary. This means that the matrix operations associated with gate action are kept smaller and that states are kept separated for clarity for as long as is possible.

3.6. QuantumComputer

The $\text{class }\text{QuantumComputer}$ manages five qubits in an arbitrary grouping of quantum registers and allows the user to apply quantum gates and measure and extract state information without having to consider how the qubits are internally represented. At creation or upon reset, the $\text{class }\text{QuantumComputer}$ prepares five qubits named “q0,” “q1,” “q2,” “q3,” “q4,” and “q5” each having state |0〉. Its two primary methods are $\text{apply\_gate}$ and $\text{apply\_two\_qubit\_gate\_CNOT}$, which allow the user to apply the respective one and two qubit quantum gates which Quintuple supports. Additionally, the $\text{execute}$ method allows the user to execute code snippets in a simplified syntax designed to be fully compatible with execution on the IBM Quantum Experience hardware, which compiles to use the appropriate pure Python methods. After the evolution code has been executed, the internal state can be easily queried and compared to expected results.

3.6.1. Applying Gates to Individual Qubits

The method $\text{apply\_gate}$ takes as arguments a gate of the $\text{class }\text{Gate}$ and the name of the qubit to act on. Under the hood, this method acts on this qubit by simply applying the gate if the qubit is the only element of its quantum register, or if the qubit is a member of a quantum register with more than one element, by creating and applying the corresponding gate to act on that qubit within the register.

3.6.2. Applying Controlled Gates to Two Qubits

The $\text{apply\_two\_qubit\_gate\_CNOT}$ method has a similar syntax, taking as an argument the name of the control and the name of the target qubit. No gate name is needed as this method handles CNOT only. The quantum register(s) containing these two qubits, potentially the same register, are found within the $\text{QuantumComputer}$'s $\text{QuantumRegisterCollection}$. If the two quantum registers the method is acting on (containing the control and the target qubit respectively) are distinct and each contain one qubit only, then a combined state corresponding to the tensor product of these two states is created and the default $\text{Gate.CNOT2\_01}$ gate is applied. If after application, the combined state is fully separable into two individual qubits in the z basis ({|0〉, |1〉}), the target qubit is alone changed and the two are not entangled. If, however, after the application the combined state is not fully separable in this fashion, they are merged into a single quantum register.

If one or both of the quantum registers given contain more than one qubit, then their states are likewise combined via a tensor product as necessary (if they don't already reside in the same quantum register). Then the appropriate CNOT matrix formulation for the combined state is applied to the combined state. The state of the relevant quantum register–the new register if one was created, otherwise the existing register which held both qubits–is set to the output of this calculation. Although Quintuple currently supports only the $\text{CNOT}$ controlled gate out of the box; additional controlled gates could be easily supported. Indeed, given that the gate set Quintuple supports is universal further controlled gates can be built out of supported components without modification.

3.6.3. Measurement

The $\text{measure}$ method of the $\text{class }\text{QuantumComputer}$ does a probabilistic measurement of the quantum register in which the desired qubit resides. The measurement is performed in the default (z) basis and collapses the state. Since we are in a simulation, we can perform the same computation repeatedly and verify that the measurement operation statistically converges to the distribution given by the probability amplitude of the state in superposition resulting from the computation. Since we are in a simulation we can also have direct access to these amplitudes. For convenience, before a measurement is performed the state in superposition is stored and is accessible later via the method $\text{get\_noop()}$ of the $\text{class }\text{QuantumRegister}$. Nature doesn't give us this information, but the Quintuple module can. This is useful for testing or later analysis. The $\text{bloch}$ method of $\text{class }\text{QuantumComputer}$ implements the capability of visualizing a single qubit on the bloch sphere. If the value of $\text{get\_noop()}$ is set, the state has been accessed and is collapsed.

3.6.4. Checking Output

Internally, $\text{class }\text{QuantumComputer}$ may be representing qubits in any combination of $\text{QuantumRegister}$s and within each $\text{QuantumRegister}$ in any order. To compare to expected outputs, we need to be able to compare the probability amplitudes or qubit states for a collection of qubits in a specified order or to compare the Bloch coordinates for a given qubit to an expected result. Thus, methods are provided so that the user can specify a qubit or group of qubits in a comma separated string, along with the expected result in their specified order and use an equality to test whether the result matches. The algorithm used to output the entangled state in the desired order is given in Appendix A (Supplementary Material). At this time the requested order must be in increasing qubit index order due to the detailed implementation of the reordering algorithm.

The $\text{probabilites\_equal}$ and $\text{qubit\_states\_equal}$ methods function similarly, the former comparing probabilities and the latter amplitudes. If one of the quantum registers contains the requested qubits in order directly, this is simply computed and returned. Otherwise, an algorithm is run to output an entangled state representing the ordered tensor product of the requested qubits, and the probability or amplitude vector representing this entangled state is compared to that specified by the user. The $\text{bloch\_coords\_equal}$ simply compares the Bloch representation of the desired qubit to that specified, if it happens to be in its own quantum register. If the desired qubit is in a quantum register with other qubits, it attempts to separate it from the quantum register in which it resides. The “easy” separation algorithm is simplistic, and only succeeds if the state is a permutation of the tensor product single-qubit states which are in the set {|0〉, |1〉, |+〉, |−〉, |↻〉, |↺〉}. Thus, just because the separation algorithm returns failure does not imply the state is fundamentally inseparable. If the desired qubit is not easily separable from others in its quantum register, the comparison method raises an exception. If it is, then the method finds the desired qubit, now in a single qubit state, and compares the result to that desired.

3.6.5. Execution of Programs in IBM's Syntax

Programs for execution on Quintuple's $\text{class }\text{QuantumComputer}$ can be written in a concise format, compatible with direct execution on the IBM Quantum Experience hardware. It is the language which is printed out to accompany the graphical setup of states, gates, and measurement operations in the IBM Quantum Experience interface. The interface also allows the user to simply copy and paste programs in this language, rather than forcing them through the graphical intermediary.

Currently, the following syntax for use in $\text{class }\text{QuantumComputer}$'s $\text{execute}$ method encompasses all that a user is able to do on the 5-qubit IBM Quantum Experience hardware:

Here {h,t,tdg,s,sdg,x,y,z,id} correspond to the Python

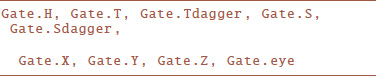
A program in this syntax it can be executed easily. Program code can be put in a Python string or equivalently read in from a file into a string. The code can be executed with the $\text{execute}$ method, and afterwards the state of the quantum computer can be probed as desired in pure Python. The following section 4 contains an explicit example of code in this syntax and its usage. For convenience, although the $\text{execute}$ method takes in a string representing the program code, for testing and keeping track of program output the $\text{class }\text{Program}$ is provided. This has the code in its $\text{code}$ variable but additionally can store an expected $\text{result\_probability}$ or $\text{bloch\_vals}$. For perusal, use, elaboration and testing, over 40 example programs are collected in the $\text{class }\text{Programs}$.

4. Quintuple Code, Exploration of Modes of Usage

In this section a variety of modes of usage of the Quintuple module are provided. For consistency and comparison, each example mode of usage executes the same algorithm, corresponding to swapping the states of two qubits. As a more detailed overview of the action of this algorithm, here the quantum computer begins with |q₁〉 = |0〉, |q₂〉 = |0〉. Then the code applies the X gate to |q2〉 which inverts it to be |q₂〉 = |1〉. Thus at the initial stage |q₁q₂〉 = |01〉. The algorithm then applies a series of CNOT and H gates such that we end up with |q₁q₂〉 = |10〉, a swapping of the states of the qubits at the initial stage.

4.1. Syntax Compatible With IBM Quantum Experience Hardware

To prepare for execution, we set the $\text{swap\_code}$ variable to the string containing the program code:

We can then execute and examine the results with:

which will print, as expected:

4.2. Swap Program in Pure Python

This same algorithm can be executed in pure python using the machinery of $\text{class }\text{QuantumComputer}$

4.3. Swap in Pure Python, Without the QuantumComputer Machinery

Equivalently this algorithm can be run using the machinery of the Quintuple module states and gates without relying on the abstraction of its $\text{class }\text{QuantumComputer}$ in the following manner:

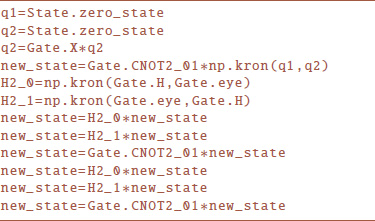
This manner of working with the module provides the most complete mathematical understanding of the operations that $\text{class }\text{QuantumComputer}$ is abstracting. Any individual state or gate can be printed, and it is clear how entanglement is represented as this is not done under the hood. This mode of execution also provides the most clear understanding of the convenience that Quintuple's $\text{class }\text{QuantumComputer}$ affords. Explicit execution in this manner requires a more complicated syntax, manual management of quantum registers, and no convience methods are available.

5. Summary and Outlook

Quintuple has been developed to aid the study and research of 5-qubit systems, with a focus on educational application. Quintuple facilitates the understanding and exploration of quantum algorithms for deployment on IBM's Quantum Experience by providing an out-of-the-box self-contained ideal simulator of IBM's 5-qubit hardware and software infrastructure. Using the widely available and open source computer language Python and its numerical module numpy, Quintuple provides full support for all operations available on the IBM Quantum Experience hardware. This quantum computer class can be used interactively or scripted, in native Python or using a simplified syntax directly compatible with that used on the IBM Quantum Experience infrastructure. Quintuple has been designed to be flexible enough to be simply extended to support further qubits, gates, syntax, and algorithmic abstractions as the IBM Quantum Experience infrastructure itself expands in functionality. These expansion endeavors would themselves integrate well into the classroom.

Several extensions of Quintuple are planned. First, as the IBM Quantum Experience evolves, whether to support additional gates, qubit number, or abstraction, Quintuple will necessarily need to be updated to keep parity. Some of these updates can and will be done in anticipation, so long as the simplicity of Quintuple is maintained and is backwards compatible with the existing IBM Quantum Experience hardware support. Second, Quintuple is an ideal quantum computer simulator, but a real quantum computer has a variety of interactions of a quantum register with its environment. Hardware designers attempt to minimize such interactions, but realistically always exist. These interactions, due to the noise of the environment, induce a non-unitary evolution component to the system, resulting in a loss of information called decoherence. The IBM Quantum Experience hardware is no exception to being susceptible to these non-ideal interactions, and it is possible to model these as well in simulation. Doing so will make Quintuple even more useful to researchers designing and implementing algorithms to run on the IBM Quantum Experience, so integrating such modeling is planned for a future update of Quintuple.

The author has successfully used Quintuple as an educational tool to introduce students to quantum computing concepts such as universal gate quantum computing, qubits, quantum registers, quantum gates, quantum circuits and quantum algorithms. Quintuple's approach allows teaching students without a firm grasp of linear algebra at a level in between the abstraction of the IBM Quantum Experience and low-level hand calculations involving more detailed mathematical understanding. Early exposure to quantum computation encourages and enables students to acquire the necessary mathematical ability as they progress in their studies. The author currently is writing a textbook companion to this classroom usage. After the publication of the codebase and the textbook a detailed study as to Quintuple's use in the classroom is planned.

Author Contributions

The author confirms being the sole contributor of this work and approved it for publication.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This paper was written while on leave from NSF AAPF grant 1501208 to conduct observations in Antarctica with the South Pole Telescope. I would like to thank Dr. Casey Handmer and Dr. Jerry M. Chow respectively for helpful comments during the preparation of this manuscript. I acknowledge use of the IBM Quantum Experience for this work. The views expressed are those of the author and do not reflect the official policy or position of IBM or the IBM Quantum Experience team.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2018.00069/full#supplementary-material

References

1. Shor PW. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM J Comput. (1997) 26:1484–09. doi: 10.1137/S0097539795293172

CrossRef Full Text

2. Bennett CH, Bernstein E, Brassard G, Vazirani U. Strengths and weaknesses of quantum computing. SIAM J Comput. (1997) 26:1510–23.

Google Scholar

3. IBM Quantum Experience (2018). Available online at: http://www.research.ibm.com/quantum/

4. Touchette D, Ali H, Hilke M. 5-Qubit Quantum Error Correction in a Charge Qubit Quantum Computer. arXiv:10103242. [Preprint]. (2010) Available online at: https://arxiv.org/abs/1010.3242

Google Scholar

5. Das R, Bhattacharyya R, Kumar A. Quantum information processing by NMR using a 5-qubit system formed by dipolar coupled spins in an oriented molecule. J Magnet Reson. (2004) 170:310–21. doi: 10.1016/j.jmr.2004.07.008

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Devitt SJ. Performing quantum computing experiments in the cloud. Phys Rev A (2016) 94:032329. doi: 10.1103/PhysRevA.94.032329

CrossRef Full Text | Google Scholar

7. Alsina D, Latorre JI. Experimental test of Mermin inequalities on a 5-qubit quantum computer. arXiv:160504220. [Preprint]. (2016). Available online at: http://arxiv.org/abs/1605.04220

Google Scholar

8. Rundle R, Tilma T, Samson JH, Everitt MJ. Quantum state reconstruction made easy: a direct method for tomography. arXiv:1605.08922 (2016).

Google Scholar

9. Berta M, Wehner S, Wilde MM. Entropic uncertainty and measurement reversibility. N J Phys. (2015) 18:073004. doi: 10.1088/1367-2630/18/7/073004

CrossRef Full Text | Google Scholar

10. Takita M, Córcoles AD, Magesan E, Abdo B, Brink M, Cross A, et al. Demonstration of weight-four parity measurements in the surface code architecture. Phys Rev Lett. (2016) 117:210505. doi: 10.1103/PhysRevLett.117.210505

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Li R, Alvarez-Rodriguez U, Lamata L, Solano E. Approximate quantum adders with genetic algorithms: an IBM quantum experience. Quant Measure Quant Metrol. (2017) 4:1–7. doi: 10.1515/qmetro-2017-0001

CrossRef Full Text | Google Scholar

12. Castelvecchi D. Quantum cloud goes commercial. Nature (2017) 543:159. doi: 10.1038/nature.2017.21585

PubMed Abstract | CrossRef Full Text

13. Deffner S. Demonstration of entanglement assisted invariance on IBM's Quantum Experience. Heliyon (2017) 3:e00444. doi: 10.1016/j.heliyon.2017.e00444

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Johansson JR, Nation PD, Nori F. QuTiP: An open-source Python framework for the dynamics of open quantum systems. Comput Phys Commun. (2012) 183:1760–72. doi: 10.1016/j.cpc.2012.02.021

CrossRef Full Text | Google Scholar

15. Johansson JR, Nation PD, Nori F. QuTiP 2: A Python framework for the dynamics of open quantum systems. Comput Phys Commun. (2013) 184:1234–40. doi: 10.1016/j.cpc.2012.11.019

CrossRef Full Text | Google Scholar

16. Tóth G. QUBIT4MATLAB V3.0: A program package for quantum information science and quantum optics for MATLAB. Comput Phys Commun. (2008) 179:430–7. doi: 10.1016/j.cpc.2008.03.007

CrossRef Full Text | Google Scholar

17. Tabakin F, Juliá-Díaz B. QCMPI: A parallel environment for quantum computing. Comput Phys Commun. (2009) 180:948–64. doi: 10.1016/j.cpc.2008.11.021

CrossRef Full Text | Google Scholar

18. Radtke T, Fritzsche S. Simulation of n-qubit quantum systems. I. Quantum registers and quantum gates. Comput Phys Commun. (2005) 173:91–113. doi: 10.1016/j.cpc.2005.07.006

CrossRef Full Text | Google Scholar

19. Radtke T, Fritzsche S. Simulation of n-qubit quantum systems. II. Separability and entanglement. Comput Phys Commun. (2006) 175:145–66. doi: 10.1016/j.cpc.2006.03.006

CrossRef Full Text | Google Scholar

20. Radtke T, Fritzsche S. Simulation of n-qubit quantum systems. III. Quantum operations. Comput Phys Commun. (2007) 176:617–33. doi: 10.1016/j.cpc.2007.02.106

CrossRef Full Text | Google Scholar

21. Radtke T, Fritzsche S. Simulation of n-qubit quantum systems. IV. Parametrizations of quantum states, matrices and probability distributions. Comput Phys Commun. (2008) 179:647–64. doi: 10.1016/j.cpc.2008.06.007

CrossRef Full Text | Google Scholar

22. Juliá-Díaz B, Burdis JM, Tabakin F. QDENSITY-A Mathematica quantum computer simulation. Comput Phys Commun. (2009) 180:474. doi: 10.1016/j.cpc.2008.10.006

CrossRef Full Text | Google Scholar

23. Butscher B, Weimer H. Libquantum (2016). Available online at: http://www.libquantum.de

24. Lapeyre J. Qinf Quantum Information and Entanglement Package for the Maxima Computer Algebra System (2016). Available online at: http://www.johnlapeyre.com/qinf/index.html

25. QISKit API: GitHub repository (2018). Available online at: https://github.com/QISKit/qiskit-api-py

26. Quantiki: List of QC simulators (2016). Available online at: https://quantiki.org/wiki/list-qc-simulators

27. Das A, Chakrabarti BK. Colloquium: quantum annealing and analog quantum computation. Rev Modern Phys. (2008) 80:1061. doi: 10.1103/RevModPhys.80.1061

CrossRef Full Text | Google Scholar

28. Albash T, Lidar DA. Adiabatic quantum computation. Rev Modern Phys. (2018) 90:015002.

Google Scholar

29. Tanaka S, Tamura R, Chakrabarti BK. Quantum Spin Glasses, Annealing and Computation. Cambridge University Press (2017).

30. Rodríguez-Laguna J, Santalla SN. Building an adiabatic quantum computer simulation in the classroom. Am J Phys. (2018) 86:360–7. doi: 10.1119/1.5021360

CrossRef Full Text | Google Scholar

31. Quintuple Source Code (2018). Available online at: https://github.com/corbett/QuantumComputing

32. Nielsen MA, Chuang IL. Quantum Computation and Quantum Information. Cambridge University Press (2010).

33. Jozsa R, Linden N. On the role of entanglement in quantum-computational speed-up. In: Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences. The Royal Society (2003). p. 2011–32.

Google Scholar

34. Bennett CH. Logical reversibility of computation. IBM J Res Dev (1973) 17:525–32.

Google Scholar

35. Barenco A, Bennett CH, Cleve R, Divincenzo DP, Margolus N, Shor P, et al. Elementary gates for quantum computation. Phys Rev A (1995) 52:3457–67. doi: 10.1103/PhysRevA.52.3457

PubMed Abstract | CrossRef Full Text | Google Scholar