- 1Center for Biomedical Imaging, Department of Radiology, NYU School of Medicine, New York, NY, United States
- 2Sackler Institute of Graduate Biomedical Sciences, Biomedical Imaging and Technology Program, NYU School of Medicine, New York, NY, United States
- 3Department of Pathology, New York University Langone Medical Center, New York, NY, United States
- 4Department of Radiology, New York University Langone Medical Center, New York, NY, United States
For many pathologies, early structural tissue changes occur at the cellular level, on the scale of micrometers or tens of micrometers. Magnetic resonance imaging (MRI) is a powerful non-invasive imaging tool used for medical diagnosis, but its clinical hardware is incapable of reaching the cellular length scale directly. In spite of this limitation, microscopic tissue changes in pathology can potentially be captured indirectly, from macroscopic imaging characteristics, by studying water diffusion. Here we focus on water diffusion and NMR relaxation in the human prostate, a highly heterogeneous organ at the cellular level. We present a physical picture of water diffusion and NMR relaxation in the prostate tissue, that is comprised of a densely-packed cellular compartment (composed of stroma and epithelium), and a luminal compartment with almost unrestricted water diffusion. Transverse NMR relaxation is used to identify fast and slow T2 components, corresponding to these tissue compartments, and to disentangle the luminal and cellular compartment contributions to the temporal evolution of the overall water diffusion coefficient. Diffusion in the luminal compartment falls into the short-time surface-to-volume (S/V) limit, indicating that only a small fraction of water molecules has time to encounter the luminal walls of healthy tissue; from the S/V ratio, the average lumen diameter averaged over three young healthy subjects is measured to be 217.7 ± 188.7 μm. Conversely, the diffusion in the cellular compartment is highly restricted and anisotropic, consistent with the fibrous character of the stromal tissue. Diffusion transverse to these fibers is well described by the random permeable barrier model (RPBM), as confirmed by the dynamical exponent ϑ = 1/2 for approaching the long-time limit of diffusion, and the corresponding structural exponent p = −1 in histology. The RPBM-derived fiber diameter and membrane permeability were 19.8 ± 8.1 μm and 0.044 ± 0.045 μm/ms, respectively, in agreement with known values from tissue histology and membrane biophysics. Lastly, we revisited 38 prostate cancer cases from a recently published study, and found the same dynamical exponent ϑ = 1/2 of diffusion in tumors and benign regions. Our results suggest that a multi-parametric MRI acquisition combined with biophysical modeling may be a powerful non-invasive complement to prostate cancer grading, reducing the need for biopsies.
Introduction
Magnetic resonance imaging (MRI) research aims to identify and validate imaging biomarkers that offer insight for diagnosing diseases and monitoring their progression. This problem is difficult, because MRI hardware limitations result in images of about 1 mm resolution in all three dimensions. This resolution is too coarse to directly observe and categorize pathologies originating, primarily, at the cellular level of ~1–100 μm. Hence, tissue characterization with MRI has generally been empirical in nature. However, recently the field of quantifying tissue microstructure with MRI has been gaining increasing attention, with the number of publications growing exponentially [1]. While not accessing the cellular-level structure directly, its overarching goal is to quantify typical microstructural tissue parameters indirectly, relying on biophysical modeling of the NMR signal acquired (i.e., averaged) over a macroscopic imaging voxel [2, 3].
The possibility of model-based microstructural mapping has spurred with the advent of diffusion MRI (dMRI) [4, 5], an imaging technique based on diffusion NMR [6–8], that measures the spatial Fourier transform Gt, q of the voxel-averaged diffusion propagator Gt, x (i.e., probability density of water molecules' displacements x (t) over time t), in each voxel. By shifting the focus from nominal hardware resolution, to the effective length scale probed by the Brownian motion of spin-carrying molecules in each voxel, dMRI becomes sensitive to the microscopic tissue structure commensurate with the diffusion length (rms molecular displacement) . The time-dependent diffusion coefficient D (t) = 〈x2(t)〉/2t ~ 1 μm2/ms, or more generally, the time-dependent diffusion tensor, characterizes the rate of effective coarse-graining [3] of the tissue structure by the diffusing molecules over the diffusion time t. This time scale, and with that, the coarse-graining window L (t), can be experimentally controlled within the range between a few to a few tens of microns, limited by the tissue NMR T1 ~ 1,000 ms time scale.
The fundamental challenge lies in interpreting the measured diffusion propagator Gt, q, or its basic characteristics [e.g., the cumulants, such as the bulk diffusion coefficient D(t)], in the context of the complex mesh of biological tissue. In physics terms, for a given tissue, one has to identify the relevant degrees of freedom of its structural complexity at the scale of L (t), that affect the bulk measurement the most, and thus can be quantified using biophysical modeling. Therefore, from the basic science standpoint, clinically-relevant dMRI research falls into the category of transport in classical disordered (random) media, a part of modern-day condensed matter physics. This establishes a somewhat unexpected yet exciting and fruitful connection [3, 9, 10] between the fundamental characterization of classical disordered transport, and the potentially clinically impactful applications in diagnostic radiology and in assessing treatment efficacy.
This study is focused on identifying the relevant degrees of freedom for dMRI within the prostate, which is a male organ that has highly heterogeneous tissue at multiple length scales Figures 1A,B [11]. While dMRI is used in clinic for prostate cancer diagnosis [12], the basic MRI-relevant characteristics of prostate microstructure have yet to be identified and validated. We will use prostate dMRI as an example to illustrate our basic physics-inspired approach for revealing and validating potential diagnostic markers of in vivo MRI.
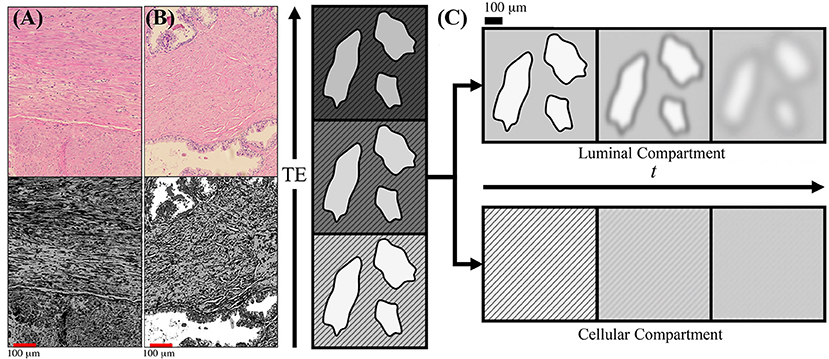
Figure 1. Schematic of prostate microstructure and coarse-graining. H&E stained cross sections are shown from a radical prostatectomy (A,B). To emphasize the structures and orientations, K-means clustering was applied onto the H&E images to emphasize the different intra-voxel compartrments and stromal orientations. In (A) we show that there is considerable structural anisotropy and local coherence in stromal cell orientation. There is an apparent directionality as certain fiber bundles of smooth muscle appear in both perpendicular and longitudinal cross sections within the a 1,000 × 784 μm2 section. In (B) we show that stroma and glandular lumen can reside very close to each other, therefore the signal contribution from a voxel will be a weighted average depending on various tissue weightings. (C) As the echo time (TE) increases, the cellular compartment (stripes) decays with a faster T2, while the luminal compartment (solids) decays with a slower T2. By modeling the T2 weighting of each compartment, the signal weighting, W, of each tissue subtype can be determined based on the diffusion-free signal, S0, cellular compartment fraction, f, and relaxation parameters T1, , and Given the compartment weights, the overall diffusion tensor may be subsequently separated into cellular-only and lumen-only tensors. Once tissue compartments are separated, the evolution of D(t) in each tissue compartment can be interpreted through the context of the underlying microstructure. Diffusing molecules “see” the compartmental microstructure through the lens of a Gaussian filter of width , which increases with t.
To give a general sense of the relevant prostate anatomy (Figure 1), signal arising from any given voxel will come from a mixture of macroscopic stroma, epithelium, and lumen contributions, usually referred to as “compartments” [13]. Here, “macroscopic” means that their sizes exceed the available range of diffusion length scales. Yet the diffusion inside each of these compartments, at the scale L (t), may be quite complex (non-Gaussian), as we will argue below. The stroma and epithelium compartments are densely packed and have comparable cellular length scales ~10 μm, which allows us, for simplicity, to lump them into a single “cellular” compartment, whereas the glandular lumen are considerably larger and biophysically distinct—reminiscent of the “lakes” of almost unrestricted water, of ~100 μm diameter in healthy tissue Figure 1B [14, 15]. (Later, we will comment on the relative roles of epithelium and stroma in the dMRI signal).
Partial-volume contributions of macroscopic compartments have been a persistent problem for model selection in dMRI. An empirical approach to intermixing compartments is by representing them with a multi-Gaussian diffusion signal expression, in which the signal is separated into components with different diffusion coefficients (or tensors), equivalent to the Laplace transform with respect to the so-called “diffusion weighting” parameter b = q2t, such that the Gaussian propagator corresponds to a monoexponential diffusion signal S ~ e−bD. A bi-exponential signal representation, with “fast” and “slow” empirical diffusion coefficients, has been shown to fit very well to signals from fresh and fixed ex-vivo prostates [16], however the biophysical origin of compartment fractions and diffusivities has remained unclear.
The parameter b does not fully characterize a measurement, since, generally speaking, signal from each tissue compartment does not have to be Gaussian, in which case one needs to specify two parameters – e.g., q and t, or, as we will do here, b and t, in adherence to existing historical conventions [5]. In fact, the time dependence of the overall diffusion coefficient D(t) necessarily means that at least one macroscopic tissue compartment n is characterized by time-dependent diffusion, in which case its propagator must be non-Gaussian [10], i.e., the Taylor expansion of should generally have time-dependent higher-order cumulant terms O(q4), O(q6), …. Recently, we found significant time-dependence of the diffusion coefficient in benign and cancerous human prostates [17], highlighting the need to re-interpret multiexponential fits. Even at fixed t, over-interpreting the bi-exponential fit of the signal in terms of genuine Gaussian diffusion compartments has been cautioned against [18, 19].
Several studies have compared various modeling approaches side-by-side to determine the “correct” model using fit quality. Unfortunately, there is still no clear consensus on the preferred biophysical model, or even the most optimal signal representation (i.e., a set of basis functions, cf. ref [1]). Some studies favor a mono-exponential [20, 21], others favor bi-exponential [16], while some suggest that including the empirical fourth-order cumulant (kurtosis) term in the overall signal provides the best fit [22]. Most importantly, each of these works agree that even the simplest mono-exponential representation of diffusion (at fixed t) already fits clinical data reasonably well. Putting their conclusions together, these works suggest that there may not be enough information to reliably select the adequate biophysical tissue model by studying diffusion (at fixed t) alone in clinically feasible acquisitions.
While identifying tissue compartments using diffusion is a challenge, separating compartments using transverse NMR relaxation, T2, has been done as early as 1987 [23]. There has been a catalog of studies [23–27], which state that there exists a fast-decaying T2 component, associated with cellular (epithelium+stromal) tissue, ms, and a slowly-decaying T2 component, associated with luminal tissue, ms. Interestingly, the luminal compartment has a small volume fraction in the average MRI voxel (<10%) [13], yet due to its much longer T2, it may notably contribute to the overall signal, as we confirm below. Meanwhile, the distinct geometry [14, 15] of cellular and luminal compartments should give rise to distinct functional forms for the time-dependent diffusion coefficients DC (t) and DL(t), respectively.
Here we introduce the following diffusion-relaxation model in the 3-dimensional parameter space: b, t, and echo time, TE (Figure 2), with the signal as a sum of (generally non-Gaussian) contributions with distinct T2 times:
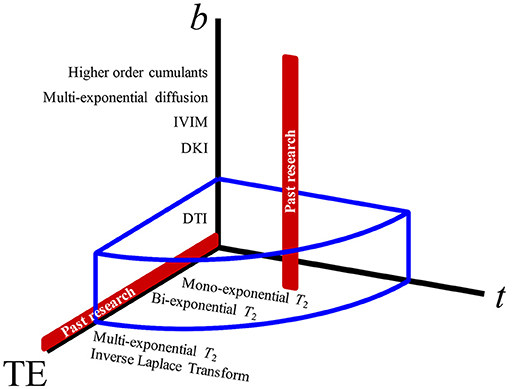
Figure 2. The parameter space of MRI experiments. Varying the b-value (that yields, progressively, diffusion tensor imaging, diffusion kurtosis imaging, intravoxel-inherent motion, multiexponential diffusion, and other signal representations) has been the most popular approach to studying diffusion weighting (red vertical line). Diffusion time, t, giving measurements regarding structural disorder, and echo time, TE, which can be used for altering the compartment weighting, have both been largely unexplored as effects on the diffusion measurements in the prostate. The blue volume surrounding the 3-axes represents the extent of parameter space covered by this study.
In this work, we limit ourselves to the two major compartments, cellular = (stroma + epithelium), with volume fraction fC ≡ f, and luminal, with fL = 1 − f. Due to the notable difference in T2 relaxation rates, the cellular compartment will lose its signal much faster than the luminal compartment with increasing echo time TE, thereby creating a large dynamic range that will facilitate the separation of tissue compartments and their diffusion properties, as schematically pointed in Figure 1C. We will keep the b-value low, to stay in the diffusion tensor regime (effectively, factoring out the q-dependence) (see Supplemental Information), and vary the mixing time TM of the stimulated echo sequence (Figure 3), thereby studying the dependence of diffusion tensors in the cellular and luminal compartments separately on the diffusion time t. The qualitatively distinct time-dependencies of DC(t) and DL(t) will be utilized for model selection in each compartment.
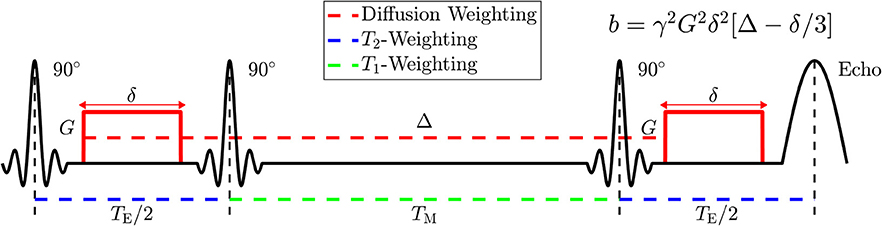
Figure 3. Diagram of the Stimulated Echo Acquisition Mode (STEAM) sequence showing how to manipulate parameters of NMR relaxometry (T2 and T1) by varying the echo time, TE, and the mixing time, TM; and how to manipulate parameters of diffusion weighting by varying the applied gradient amplitude, G, the applied gradient duration, δ, and the spacing Δ between applied gradients. The diffusion time t is approximately given by Δ; the accuracy in its definition is set by the value of δ, cf. section 2.3 of Novikov et al. [3].
Relevant Models of Time-Dependent Diffusion
Short-Time Limit: D(t) as a Probe of S/V
At short diffusion times, the time-dependence of the diffusion coefficient can be described solely by the surface-to-volume ratio (S/V) of the pore walls (e.g., cell membranes), and the unrestricted (free) diffusivity D0 [28]:
This equation assumes isotropic distribution of the restrictions to diffusion in d spatial dimensions. The advantage of this limit is that it offers a biologically relevant length scale, the inverse S/V, without too much model complexity and minimal assumptions. The disadvantage is in being sensitive only to the net amount of restrictions, rather than to their relative positions in space (i.e., structural correlations) and their permeability, as it occurs at longer times.
The range of times over which the S/V limit (2) is applicable is , where lpore is the pore characteristic length scale; this estimate was recently validated in a phantom on the same clinical scanner used in this study [29]. Assuming that glandular lumen has D0 ≈ 3 μm2/ms (free water at body temperature), and diameter lpore ~ 100 μm, the S/V limit will apply for t ≪ 500 ms. This indicates that the S/V limit would be applicable in the healthy glandular lumen over a broad t range. However, luminal diameters do shrink with tumor grade [15, 30], which will shorten the range of t over which the S/V limit is applicable in patients. The corrections to Equation (2) due to wall curvature or permeability are beyond the scope of this work, due to signal-to-noise ratio and scan time limitations.
Long-Time Limit: D(t) as a Probe of Membrane Permeability and Structural Correlations
In contrast to the luminal compartment, the cellular compartment is densely packed and contains cells with small ~10 μm diameters, which may shrink even further with increasing tumor grade [31]. Assuming D0 ~1 μm2/ms, locally in d = 2-dimensions due to fibrous geometry [13, 32] (as we will also confirm below), the range over which the S/V limit would apply is expected to be t ≤ 25 ms. For clinically accessible t, diffusion in the cellular compartment will be acquired outside of the S/V limit. Exceeding this limit, the diffusion length becomes comparable or greater than the characteristic length scale of the tissue (cell diameter), and D(t) becomes dependent on numerous tissue parameters describing both cell geometry and membrane permeability. In general, modeling diffusion in tissue geometry over a broad range of times is an unsolved problem, as it is unclear which features of tissue microarchitecture need to be included.
To identify what features of tissue complexity are most relevant for the measurement, Novikov et al. [9] showed that it is advantageous to observe time-dependent diffusion in the long time limit, approaching the bulk diffusion coefficient D∞. Time-dependence in this limit reveals the most essential footprint of the underlying structure via the dynamical exponent ϑ in the instantaneous diffusion coefficient
Here, A is the associated strength of the structural disorder, which is being effectively coarse-grained [3] by the molecules traveling over an increasing diffusion length. The exponent
is related to the statistics of the global arrangement of tissue microstructure—in our case, of stroma and epithelium cells—via the structural exponent p in d spatial dimensions. The exponent p defines the structural universality class [9] of random media. Roughly speaking, the larger the exponent p, the faster the structural fluctuations decrease at large distances, and the more ordered the medium. Formally, this exponent describes the low-k behavior of the power spectrum Γ (k) ~ Akp of the restrictions, corresponding to the decay of their density-density correlation function at large distances r. The Poissonian, and more generally, short-range disorder corresponds to p = 0, strong disorder to p < 0 (diverging fluctuations at large distances, e.g., due to spatially extended restrictions [9, 33]), and hyper-uniform disorder to p > 0 (variance of fluctuations within a volume growing slower than the volume [34]). The gradual coarse-graining of the structure embodied in Γ (r) over an increasing diffusion length L(t) ~ r results in the universal scaling, Equation (3). Note that the dimensionality d of the diffusion process has to be inferred from the shape of the diffusion tensor. In an isotropic case d = 3, whereas, for instance, for an axially symmetric diffusion tensor (e.g., in tissue fibrous geometry), d = 2 for the transverse and d = 1 for the longitudinal diffusion eigenvalues λ⊥ and λ||, correspondingly.
The universal asymptotic law (3), with the relation (4) between the structure and diffusive dynamics, is a recipe for model selection. However, dMRI measures the cumulative . Such temporal averaging limits the range of directly-measurable exponents (without differentiating noisy data), since the corresponding long-time tail in D(t) will have the exponent [9, 35]. We now outline a few relevant structural universality classes.
Structural order in any d, and hyperuniform disorder (p > 0) in d ≥ 2 dimensions all have ϑ > 1, which means that the tail in the cumulative D(t) will have exponent , masking the genuine ϑ:
Hyperuniform disorder suppresses structural fluctuations and may arise in optimal random packings [36]. In a sense, hyperuniform disorder is the closest to a perfectly periodic arrangement of the building blocks in a medium. Equation (5) tells that any such arrangement (e.g., a periodic lattice of barriers [37], or the “crystal lattice” of identical cells) would yield the asymptotic ~1/t behavior in D(t).
A similar-looking 1/t tail arises when a tissue compartment corresponds to perfectly impermeable cells of size (fully restricting cell walls), placing a hard upper bound on 〈x2(t)〉. This is, perhaps, the simplest non-Gaussian compartment model, and it has been popular in describing dMRI signal from tumors [38–42].
Short-range disorder in 2 dimensions (e.g., transverse to aligned fibers randomly packed in a bundle) yields ϑ = 1 and the corresponding ln(t/δ)/t tail in D(t), which, for the diffusion gradient pulse width δ > tc exceeding the corresponding correlation time across the packing correlation length, yields the behavior [43]
that asymptotically becomes Aln(t/δ)/t for t ≫ δ.
Extended-disorder (random membranes), e.g., random lines in d = 2 dimensions or randomly placed and oriented planes in d = 3, yields the slow power-law tail [33]
This disorder geometry was approximately described for all t by the random permeable barrier model (RPBM) based on the real-space renormalization group approach to the diffusion equation represented as a scattering problem [33]. The RPBM was subsequently found to well describe diffusion transverse to muscle fibers (d = 2) [9, 44–46], where diffusion along fibers was practically unrestricted, while the transverse diffusion coefficient strongly decreased with t.
Note a subtle yet important difference between Equations (6) and (7), as applied to the d = 2 fiber geometry: Equation (6) applies if the fibers are randomly packed in a bundle, hindering the extra-cellular water (such as a random packing of disks in the cross-section [43]), yielding Γ (k) ~ const for k → 0, i.e., p = 0, while Equation (7) applies if the cell walls appear to be locally flat (i.e., lines in the cross-section, Figure 4A) and sufficiently permeable, so that the intra- and extra-cellular spaces can be considered on an equal footing. The exponent arises due to the distinct spatial statistics of the restrictions, Figure 4A, represented by the locally flat permeable membranes (fiber walls) that extend for longer than the diffusion length, and yield the corresponding low-k divergence in Γ (k) ~ k−1; the temporal scaling (7) emerges when these membranes are traversed more than once during the diffusion time t.
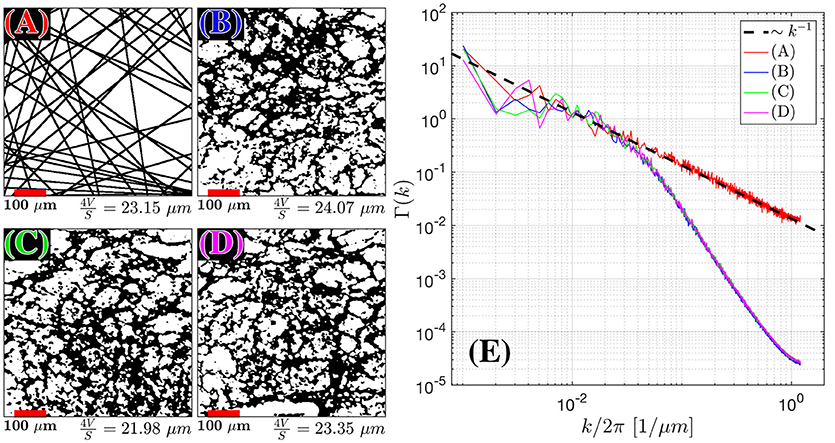
Figure 4. Structural Correlation from histopathology. H&E stained samples of benign fibromuscular stroma from a radical prostatectomy were considered. In the body of the text, we found that extended disorder geometry, related to random membranes, defined the structural disorder for . We plot 55 randomly oriented membranes in 2D (A) as an idealistic case for extended disorder and 3 samples (B–D) of segmented prostate fibromuscular stroma, which are predominantly taken through perpendicular cross sections. The segmentation was used to emphasize the cell walls as the primary sources of restriction to diffusion. The average length scale from was determined by calculating S/V = 2l/A (A) and S/V = l/A for (B–D), where l is the number of voxels found at the edge of each cell, and A is the area of the sample. The number of randomly oriented barriers in (A) was selected to match the average fiber diameter 4V/S for the histological samples. For (A–D) the Fourier transform density autocorrelation function, Γ(k) was determined by radially averaging over k-space and plotting 1,200 bins from the 1,440 × 1,440 pixel2 / 590 × 590 μm2 images (E). The dashed black line represents the fit Γ(k) = Ak−1.
We have recently shown that there is a measurable effect of a time-dependent D(t), which differs between benign and various stages of peripheral zone cancer [17]. This adds to a growing body of research that is interested in modeling D(t) for cancer applications [42]. However, at that point we have not separated the relative compartment contributions to the overall D(t). We realized that partial volume effects [47] need to be overcome, so that the microstructure of intermixing tissue can be identified. In what follows, by decomposing the dMRI signal into fast and slow T2 compartments, model selection for D(t) within cellular and luminal tissues will be performed independently, based on the above range of models of diffusion in disordered media.
We emphasize, that here we are performing model selection by inferring the distinct functional form of the measured D(t), rather than relying on goodness-of-fit metrics which can be often misleading [1]. By identifying the dynamical exponent (4), or the short-time regime (2), we are, in a way, asking the tissue to reveal its type of structure (the S/V limit, or a structural universality class), instead of imposing a particular model of restricted diffusion from the outset. Identification of the disorder class will then justify searching for the most parsimonious model within that class. This logic naturally follows the fact that the structural complexity is hierarchical; its most relevant degrees of freedom should be identified first (they define the signal's overall functional form), followed by fine-tuning the remaining microscopic details, SNR permitting.
Methods
Subjects
This study was in compliance with the Health Insurance Portability and Accountability Act guidelines and was approved by the institutional review board of New York University School of Medicine. Following written informed consent, 3 male volunteers (ages: 22, 28, 32) with no history of prostate disease were imaged on a MAGNETOM 3T Prisma system (Siemens AG, Erlangen, Germany) using the 18-channel phased array body coil.
MRI Acquisition
The major challenge in separating between the compartment diffusivities is to accurately map out the necessary parameters pertaining multi-compartment relaxation, and to measure the diffusion in a broad range of diffusion times for the model selection purpose. For these reasons, we used a stimulated echo acquisition mode (STEAM) sequence (WIP916B, Siemens), which allows us to study diffusion dependence on TE and t simultaneously (Figure 3). STEAM is the preferable pulse sequence, as it is T1-weighted and preserves more signal at long t, than the more commonly used T2-weighted pulsed gradient spin echo (PGSE) diffusion sequence.
Diffusion weighted images (DWI) were acquired in sets of 17 non-collinear directions distributed on a sphere at b = 0.5 ms/μm2 = 500 s/mm2, and 2 nominally-unweighted images (which do not, technically, correspond to b = 0, but whose b-value is calculated within the sequence). With this orientation of gradient directions, DWI were acquired with TE = [52, 115, 180] ms and t = [25.2, 40, 65, 105, 175, 280, 450, 740] ms, resulting in a total of 24 imaging series, each containing 17+2 = 19 imaging volumes. The applied gradient pulse duration, δ, was fixed to 10 ms, and the applied gradient amplitude, G, decreased with t, where the average G(t) was [56.51, 43.65, 33.66, 26.21, 20.18, 15.89, 12.51, 9.74] mT/m. STEAM allows the user to modulate the mixing time (TM), which is the spacing between the second and third RF pulses, giving rise to a variable T1 weighting (Figure 3). The mixing time is also related to t, which is the spacing between the de-phasing and re-phasing diffusion gradients in the narrow-pulse limit. Here, TM ranged from 6.38 to 719.32 ms and varied with changing TE and t.
The order of the acquisitions was randomized to avoid any potential temperature effects and aid in image registration (see next sub-section). Diffusion gradients were compensated to match the requested b-value [42, 48, 49]. As the amplitude of diffusion gradients decreased with t, the nominal b = 0 weighting increased from 3 to 102 s/mm2. The SNR, calculated via [50], at these nominal b = 0 ranged from 39.0 down to 5.3, dropping with increasing TM and TE. The repetition time, TR, was fixed to 5 s in order to minimize scan time, yet enabling practically full magnetization recovery. The imaging resolution was 2.5 × 2.5 × 5.0 mm3 over a 96 × 96 × 10 grid with a bandwidth of 1,490 Hz/pixel. To minimize the echo train length, the acquisition was under-sampled using GRAPPA parallel receive with acceleration factor 2, multiband acceleration with factor 2, and 6/8 partial Fourier. Adaptive combine was used to merge images from individual receive coils with optimal phase shifts. In order to minimize geometric distortions, diffusion images were acquired axially with slices oriented parallel to the static magnetic field rather than perpendicular to the rectal wall. Distortion was further reduced through the use of the static field correction [51] as implemented by the vendor.
Image Processing
Firstly, Gibbs ringing correction [52] was applied to all dMRI images. Outlier rejection and reduction of eddy currents was then implemented for each of the 24 series separately, using FSL's eddy [53] tool. This tool also applied rigid registration within each diffusion tensor. A separate mutual-information rigid transformation was performed [54, 55] to align the images from each series to one another. Given the wide range of TE and SNR, we found that mutual registration to TE = 180 ms would produce inconsistent results. To resolve this, the acquisition was performed in random order. The parameters for rigid (Euler) transformation calculated from higher SNR images at either TE = 52 or 115 ms were then applied to the subsequent TE = 180 ms series, acquired immediately afterwards. This assumes that the volunteers remained mostly stationary for ~3 minutes. Parametric maps of mean diffusivity (D) and fractional anisotropy (FA) were derived for each tensor acquisition using a weighted linear least squares fit [56, 57] using diffusion tensor imaging (DTI) estimation implemented in MATLAB. The region of interest (ROI) was drawn on a high resolution T2-weighted image to study the peripheral zone (PZ) of the prostate (Figure 9A). Our volunteers were much younger than a typical prostate patient, so the size of the transition zone/central gland was much smaller than that in the clinical practice. For this reason, ROI analysis focused on PZ only.
Estimation of Compartment Weights
If there are observable compartments in T2, they likely exist in T1 as well. One conference abstract [58] identified a slow T1 compartment of 2,944 ± 765 ms, which suggests that the luminal compartment is indeed nearly unbounded water. Kjaer et al. [23] have also acknowledged that a long T1 compartment likely exists, but stated that they were unable to measure it within clinical SNR and time-constraints. Since the range of TM in our experiment was <800 ms, we were unable to take advantage of this longer T1 compartment to improve our modeling estimates. For this reason, we account for mono-exponential T1 relaxation only. If we maintain a constant repetition time (TR) and assume perfect π/2 RF pulses, the signal evolution for a STEAM acquisition without diffusion weighting can be written as:
We used weighted linear least squares [57] to estimate the un-weighted S|b=0 images. S|b=0 values for the range of TM and TE were used to solve for the 5 parameters (S0, f, , , T1) in Equation (8), Figure 5. The fit of Equation (8) to the data in each voxel was reinitialized 100 times with randomized starting values over unconstrained bounds. After rejecting the trials in which the fit results were unphysical, the median of the cluster of estimated parameters with the highest prevalence was selected as the final result.
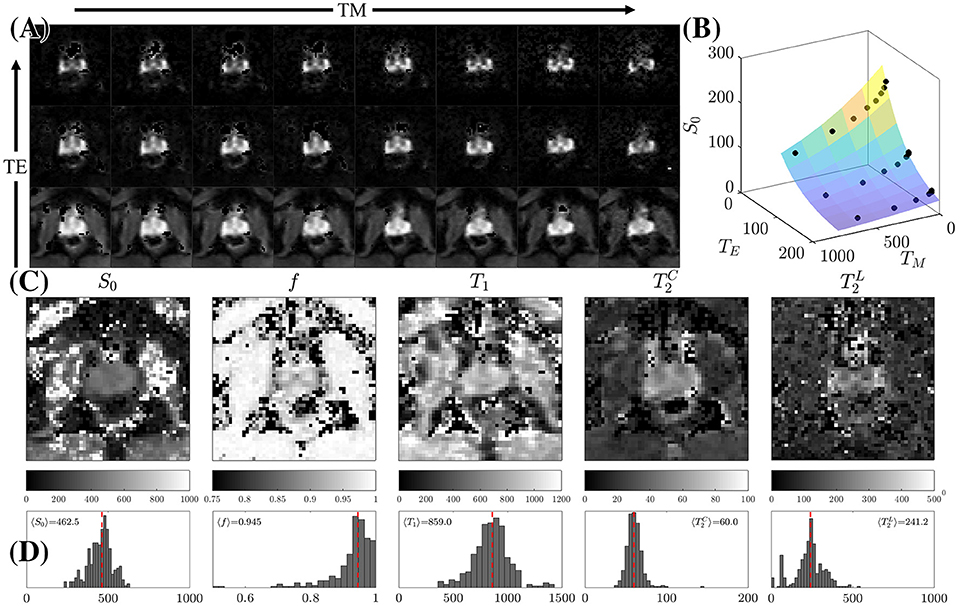
Figure 5. STEAM Relaxometry. (A) Echo time (TE) and mixing time (TM) dependence of the non-diffusion-weighted dMRI signal, S|b = 0, demonstrating the suppression of the majority of tissues at long TE. (B) Fitting Equation (8) to S|b=0 after averaging over the peripheral zone (PZ). (C) Parametric maps of the 5 fitted parameters: the proton density S0, overall T1, cellular compartment fraction, f, fast (cellular) and slow (luminal) . (D) Histograms displaying the distribution of relaxation parameters on all 3 volunteers within PZ only. The dashed line is the mean parameter derived from 〈S|b = 0〉 across all volunteers.

Table 1. The mean and standard deviation over a PZ ROI is shown for the relaxation parameters derived from S|b = 0.
Subsequently, the relative compartment weights for each TM and TE can be determined [with C and L from Equation (8)]:
The cumulant expansion [59] of the signal, Equation (1), yields
For a number N of distinct TE measurements, Equation (10) reads
Using the fact that the weights depend on TE but not on t, while the compartment diffusivities (in any given diffusion direction) depend on t but not on TE, we determine DC(t) and DL(t) (in any given direction) separately for each t using matrix pseudo-inversion W+ = (W′W)−1 W′, as
This is schematically illustrated in Figure 1. In our case, the number of different TE measurements was N = 3.
Compartment Tensor Eigenvalues and Fiber Tracking
Each set of compartment directional diffusivities [cf. Equation (11)] was processed using standard DTI methodology [5] with weights of Veraart et al. [57] to generate the diffusion tensors, the associated eigenvectors (ε1, ε2, ε3), eigenvalues (λ1, λ2, λ3), and fractional anisotropy (FA), for each compartment, over each t, Figure 6. Eigenvalues for each t were averaged to produce mean diffusivity, .
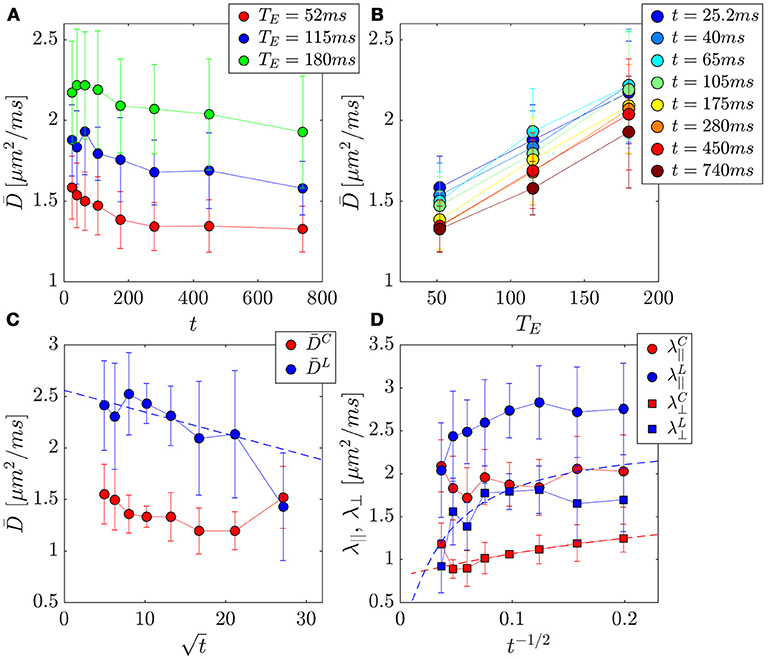
Figure 6. PZ ROI separation of prostate tissue diffusivities (A,B) into compartment contributions (C,D) in 3 healthy volunteers. Error bars indicate variance between subjects. (A) The change in the mean diffusivity, , with t was as much as ~16% for a given TE. (B) Replotting as function of TE for a given t, reveals a larger change of ~59% over this parameter. (C) Mean diffusivities from the cellular and luminal compartments plotted against , where a linear dependence be the hallmark of the short-time S/V limit. (D) Axial and radial compartment diffusivities, λ||, λ⊥ plotted against t−1/2, where a linear dependence of λ⊥ would indicate extended disorder universality class of random membranes, and justify the usage of the RPBM for calculating length scales and permeability.
FA(t) typically increases with t [17, 60], implying that the anisotropy of the diffusion tensor becomes more apparent at longer diffusion times, driven by the fact that the differences between the physics of diffusion in different directions become more apparent with coarse-graining over larger distances.
Orientation in each eigenvector, on the other hand, will be independent of t, as it is produced by the same underlying tissue anisotropy. Given this orientation redundancy, an averaged orientation of the i-th eigenvector can be derived from the mean dyadic tensor computed across t [61]:
for each of principal directions i (no summation over i is implied). The principal eigenvector associated with the dyadic tensor serves as the tissue orientation averaged over all t, where Nt = 8. The orientation and anisotropy is then visualized by creating directionally-encoded color FA (DEC-FA) maps, in which the median FA(t) is multiplied by the principal eigenvector of .
The principal eigenvectors from , , and for each compartment and the eigenvalues at t = 105 ms were used to reconstruct the corresponding diffusion-weighted images. They were subsequently used as input to perform fiber tractography in mrtrix3.0 using probabilistic streamline tractography. The fibers from the cellular compartment represent smooth muscle stroma, for which the structural anisotropy is clear on histology (Figure 1A). At each voxel, residual bootstrap was performed to obtain a unique realization of the dMRI data. The data was then resampled via trilinear interpolation at each streamline step. The diffusion tensor representation was then applied and streamlines were drawn following the orientation of the principal eigenvector.
Revisiting Clinical Data From 38 Subjects, Lemberskiy et al. [17]
In addition to the newly acquired data from 3 normal volunteers, we also revisited the dataset recently published [17], with the purpose of determining the disorder class in regions of variable Gleason score. This set of dMRI was not acquired with multiple TE, thus it cannot be used to assess cellular and luminal diffusivities separately. Instead, relaxation parameters derived from each of the 3 volunteer subjects were used to determine the signal weighting W = WC at the TE = 40.4ms of the patient data: [0.862, 0.916, 0.927]. The prostate increases in size with age, largely relating to expansion of the stroma and epithelium [62]. Given a median age in Lemberskiy et al. [17] of 64 years, we assume that the patient data was weighted more heavily by the cellular compartment (~W ≥ 0.927, fast T2, large f), with approximately less than 0.07 of the signal represented by the luminal compartment. Additionally, the luminal compartment shrinks as prostate cancer progresses [63], therefore prostate cancer ROIs are expected to have an even greater cellular compartment fraction. For these reasons, we treat D(t) from the patient cohort as samples of the cellular compartment.
Determination of the Dynamical Exponent From Diffusion
The compartmental diffusion coefficients, DC (t), and DL(t), were compared against the short-time S/V limit, Equation (2), and the associated power law tail of the long-time limit for ordered or hyperuniform restrictions, Equation (5), short-range disorder in dimension d = 2, Equation (6), and extended disorder, Equation (7). The most appropriate disorder geometry and its corresponding tissue model was selected using Pearson correlation, ρ, with the corresponding power-law tail , as an objective goodness-of-fit criterion. In addition, systematic features in the residuals were examined, Figure 7.
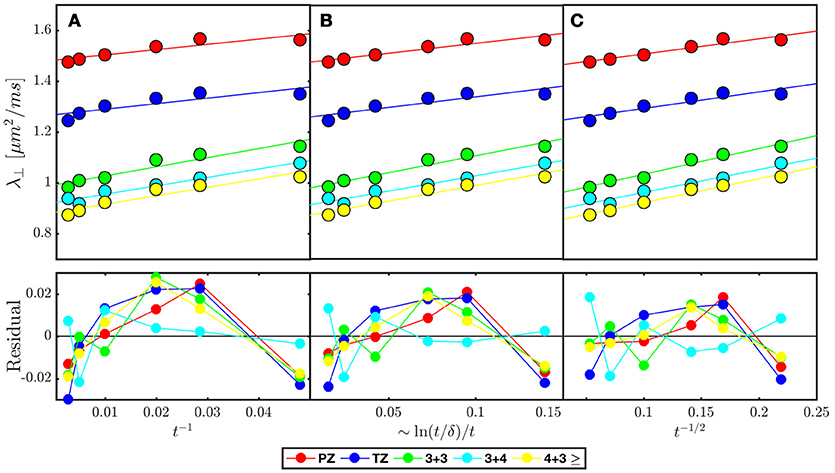
Figure 7. Model selection in prostate cancer of various Gleason Scores based on disorder class from ROI averaged across 38 patients published in Lemberskiy et al. [17] Radial diffusivity (λ⊥) is fitted (solid line over each ROI) by the associated power law tail for (A) ordered or hyper-uniform restrictions Equation (5), (B) short-range disorder in 2-dimensions Equation (6), and (C) extended-range disorder Equation (7). The residual is included to emphasize systematic differences between the tested disorder classes. λ⊥ and the residual is plotted against the corresponding power laws of t, in which a linear dependence would indicate stronger association with the given disorder class (Table 2).
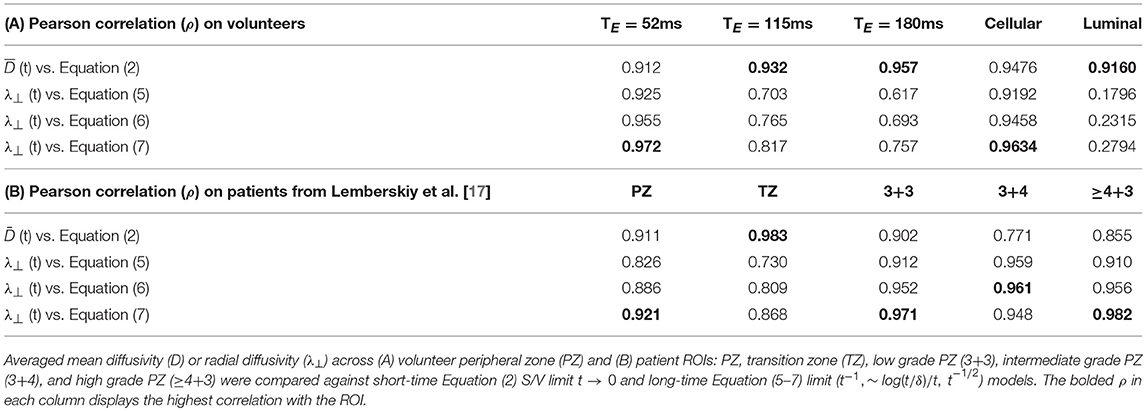
Table 2. Pearson correlation coefficient, ρ, is used as a proxy for model selection at various echo time (TE) and at separated cellular/luminal diffusion tensors.
Given the anisotropy and fiber-like geometry of the stromal contribution to the cellular compartment (Figures 8A, 9B), the long-time models were evaluated in d = 2 dimensions, perpendicular to the principal axis of diffusion, using the overall λ⊥(t, TE), and the derived and , from the compartment diffusion tensors. Conversely, given the isotropic characteristics of the luminal compartment (Figure 8A), the short-time behavior was evaluated over the mean diffusivity: the measured D (t, TE), and the derived , and . For the volunteer data, SNR became an issue for D(n) (t = 480, 740 ms) at SNR < 10, as evident on both ROI analysis, Figures 6C,D, and parametric maps, Figure 8I. The last two points were excluded from studying correlations between D(n)(t) and .

Figure 8. Compartment parameters derived from the diffusion tensor. (A) Cellular and luminal directionally-encoded color FA (DEC-FA) were derived from principle eigenvalues of the mean dyadic tensor over time and the median FA(t). (B–I) Mean diffusion over diffusion time, (t), is shown for both cellular and luminal compartments. The whole prostate ROI was drawn from the image at t = 25.2 ms and overlaid onto all parameter maps with a white outline to highlight any motion.
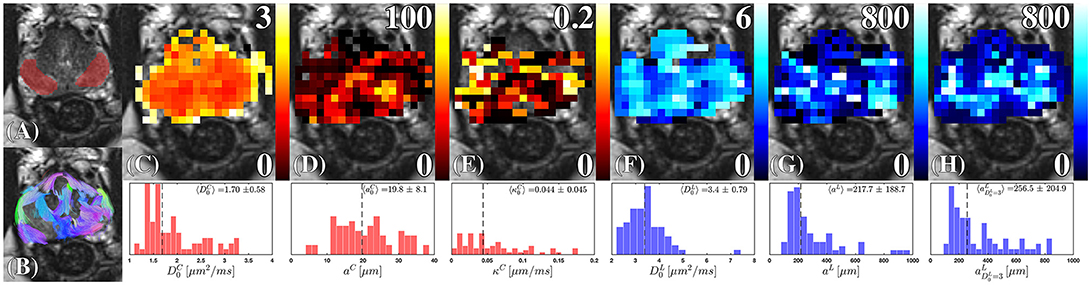
Figure 9. Cellular and luminal parameters derived from D(t). (A) The peripheral zone ROI, is overlaid onto a high-resolution T2-weighted image. (B) The probabilistic fiber tracks, derived from the cellular compartment, are color coded by their terminal endpoints. These tracks were derived from a dyadic tensor across all diffusion times. (C) Cellular diffusivity, , (D) cellular fiber diameter, aC, and (E) cellular membrane permeability, κC, were derived from the RPBM applied to the cellular diffusion tensor. The (F) luminal diffusivity, , (G) luminal diameter, aL, and (H) the luminal diameter, a, were derived by applying Equation (2) to the luminal diffusion tensor. The corresponding histograms under each parameter map, show the range and median (dashed line) of the modeled parameter under the ROI (A) combining estimates obtained from all volunteers.
For the patient data from Lemberskiy et al. [17], the diffusion tensor eigenvalues were averaged over 5 ROIs and over the cohorts taken from the set of 38 subjects: peripheral zone (PZ), transition zone (TZ), low grade PZ (3+3), intermediate grade PZ (3+4), and high grade PZ (≥4+3) tumors. The power-law tails corresponding to hyper-uniform (Equation 5), short-range (Equation 6), and extended (Equation 7) disorder classes in d = 2 dimensions were compared with the ROI-averaged data. Linear evolution of λ⊥(t) was plotted against the power-law scaling, , for each disorder class, and the Pearson correlation values as well as qualitative inspection of fit residuals were used to identify the most appropriate disorder geometry among the long-time models.
Parameter Estimation for Tissue Compartments (Healthy Controls)
As a result of model selection (see section Results), time-dependent diffusion was modeled within the PZ ROI of each subject using the RPBM in the cellular compartment and the S/V limit in the luminal compartment.
Luminal Compartment
D (t) within the luminal compartment was evaluated using the S/V limit, Equation (2). Lumen diameters were estimated from aL = 6V/S, which would be the length of one side on a 3-dimensional cube with given S/V. Alternatively, one can consider modeling aL via a 3-dimensional sphere, which would result in a factor of 2 difference in the definition of luminal diameters; given the irregular shape of the lumen, the identification of the precise pre-fractor in front of V/S is beyond the scope of this work. We also estimate with a fixed , which follows from the model assumption that the glandular lumen are lakes of largely unrestricted restricted water, where t → 0 would give the free water diffusion coefficient at body temperature [64].
Cellular Compartment
The dynamical exponent analysis (see section Results) indicated the dominance of the extended disorder geometry in 2 dimensions (Figure 7, Table 2). This suggests that the RPBM utilized previously for studying muscle fiber diameter and membrane permeability [9, 33, 44–46] can be applied to study the cellular compartment using .
The RPBM depends on 3 parameters: the free-diffusivity D0, the S/V ratio of all membranes, and the membrane permeability κ. The RPBM result for D(t) in d = 2 dimensions is given in terms of D0 and the two auxiliary parameters: the effective “volume fraction” ζ = (S/V) · (D0/4κ) of the membranes [describing the net effect of their hindrance relative to D0, as D∞ = D0/(1+ζ)], and the time-scale associated with a single membrane, [33]; see Fieremans et al. [45] for the details of fitting and practical implementation of RPBM. For improved model precision, here was fixed to , Figure 9C. These model parameters are then used to calculate cellular (fiber) diameter, which can be approximately estimated as aC = 4/(S/V), which yields ; and fiber membrane permeability .
The parameters from the RPBM: and, κC; and from the S/V limit: , and aL, were estimated (i) by applying the model to every voxel separately, and (ii) averaging the corresponding DTI eigenvalues across all PZ voxels and estimating model parameters from this average.
Determination of Structural Exponent and Fiber Diameter From Histopathology
For an independent validation of the prevailing disorder geometry, 590 × 590 μm samples with 1,440 × 1,440 pixels of benign stromal tissue in cross-section were selected by a board certified pathologist. These samples were obtained from radical prostatectomy of a 72 y/o patient with Gleason Score 4+3, which were stained with Hematoxylin and eosin (H&E). These samples were evaluated using the power spectrum approach [9, 43], determining the power-law behavior of the power spectrum at low wave-vectors k = |k|, by calculating the 2-dimensional Γ (k) = ρ (−k) ρ (k)/V, where ρ (k) is the Fourier transform of the intensity of restrictions in the histological image (Figures 4B–D), and subsequent binning of Γ(k) over 1,200 concentric shells (bins), parametrized by the shell radius k. The low-k behavior was then characterized by a structural exponent p, which can take a discrete set of values (cf. text after Equation 4).
From the H&E-stained histology image we needed to produce the contrast that depicts fiber walls in the cross-section, Figure 4. The domains with fiber bundles transverse to the histology slice were identified within a large field of view that contained many fiber orientations; these fragments of the large image were subsequently processed to emphasize the cell walls, as we now describe.
First, the red channel was isolated and filtered by a Gaussian filter with a smoothing kernel of σ = 5 pixels. The low pass filter removed salt-and-pepper spatially-uncorrelated noise that would otherwise interfere with segmentation in the subsequent steps, but did not have an impact on the low-k (large-distance) behavior which we were after. Second, K-means clustering in MATLAB was performed to isolate the three predominant clusters: extracellular space, intracellular space, and cellular nuclei. The masks of cellular nuclei and intracellular space were then combined; the remaining space was deemed mostly related to the fiber membranes (i.e., everything but cells and their organelles). The resulting membrane mask was used to determine the power spectrum Γ (k) as a function of the two-dimensional Fourier wave vector k. Last, the histological length scale was determined by calculating ahist = 4V/S, where S/V = l/A. The area, A, was determined by the total area of the membrane mask image, and the length, l, was determined by finding the total number of voxels outlining each cell from the membrane mask, i.e., counting both faces of each membrane. In the case of the simulated image with parallel lines, l was multiplied by 2 to account for the surface on both sides of the unit-thickness membrane, Figure 4A. With this definition of S/V, conventional in the field of porous media, the length scale ahist would correspond to the size of a square if the membranes were to be arranged in a perfect square lattice (a checkerboard) within the fiber cross-section.
Determination of the Luminal Fraction fL and the Luminal Diameter aL From Histology
Two larger samples taken again from the radical prostatectomy of the 72 y/o subject (Figures 10A,B) of benign peripheral zone were selected containing 1,000 × 1,400 pixels over a field of view of 2.4 × 3.4 mm2. The lumen were segmented using K-means clustering with the same approach described in the previous subsection. The luminal mask was used to determine the lumen area fraction, fL, A, over 200 × 200 non-overlapping pixel segments. In order to compare our results with MRI, we assumed cubic-shaped lumen and estimated the corresponding luminal volume fraction and the cell volume fraction:
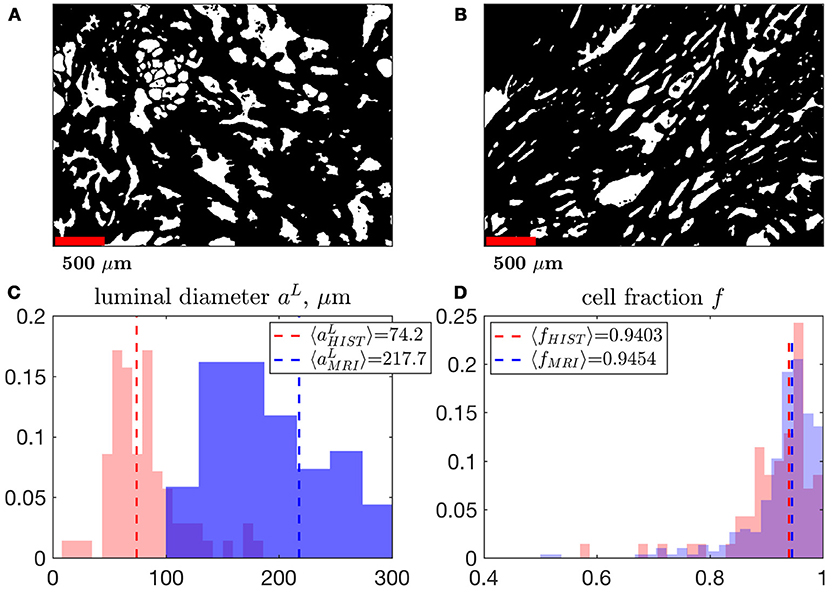
Figure 10. A comparison of MRI- and histology-derived cellular fraction, f, and luminal diameter, aL. (A,B) Two samples of benign peripheral zone containing 1,000 × 1,400 pixels over a field of view of 2.4 × 3.4 mm2 were segmented using K-means clustering. 200 × 200 non-overlapping pixel segments were sampled from these masks in order to determine the volume fraction, Equation (13), and surface-to-volume ratio, , which was then used to approximate a. The power-law exponent 3/2 was used to convert the 2-dimensional properties of histology into 3-dimensional units (in order to match the MRI results). This conversion approximately assumes a 3-dimensional cubic geometry within the luminal compartment (see section Methods). We display histograms the median of each distribution comparing aL (C) and f (D), derived from MRI and histology. Note that the histograms for MRI results are identical to distributions shown in Figure 5C, for fMRI, Figure 9G, for a.
We note that for lumen of different shape, the right-hand side of the first formula in Equation (13) would have a non-universal coefficient ~1. Therefore, our estimates are to be treated as order-of-magnitude. However, the power law exponent 3/2 in the above equation is universal, and will prove to be quite important to match MRI with histology.
To determine the luminal diameter, , from the histology, we again, for simplicity and consistency, assume the cubic-shaped lumen of size , for which case the perimeter-to-area ratio , or, equivalently, the 3-dimensional . Hence, we estimate within each histology segment, and compare our distributions with MRI-derived metrics. We can equivalently view this comparison as that between the 3-dimensional S/V ratios from MRI and from histology (re-calculated from the 2-dimensional slices).
Results
Relative Contributions of Prostate Compartments
Increasing TE led to suppression of much of the surrounding pelvic signal as shown on S|b=0(TM, TE). Surrounding tissues which are largely composed of muscle or collagen are completely dark at TE = 180 ms (Figure 5A). Unlike the surrounding tissues, the prostate retains its signal, particularly around PZ. Fitting Equation (8) to S|b = 0(TM, TE) reveals a non-linear surface, dependent on compartment fractions and NMR relaxation times (Figure 5B). On average, fit R2 > 0.92 for each subject; however, as with previous studies [23–27], our dynamic range and SNR limitations led toward larger variance on estimated (Table 1, Figures 5C,D). The range of parameters derived from Equation (8) indicate that the signal at each TE are weighted by the cellular compartment differently, W(TE=52)~0.9, whereas W(TE=180)~0.6. Additionally, model fitting suggests that the volume fraction of the cellular compartment, f, increases with age as evidenced by the f = [0.91, 0.95, 0.96], which confirms observations from histopathology [9].
We found a remarkably strong agreement between MRI and histology-derived f (Figure 10D), where Equation (13) was used to calculate the histological counterpart. The difference between the medians of the MRI distribution across voxels, and histology distribution across histology segments is 0.5%. Such degree of the quantitative agreement may be accidental because of the ~1 coefficient in Equation (13) for non-cubic glands, as well as because of comparing young healthy controls (MRI) with radical prostatectomy (benign area, histology). However, the order-of-magnitude correspondence between MRI and histology is reassuring.
Dependence of the Overall D(t) on TE
Mean diffusivity consistently increased with TE (Figures 6A,B), revealing the competing effect of cellular and luminal compartment weighting on the measured diffusion signal. The difference between D (t) at TE = 52 ms and TE = 180 ms appears to grow over the first six time points (25.2–280 ms) (ρ = 0.89, p = 0.016), with (t = 25.2 ms) increasing by 34% and (t = 280 ms) increasing by 59%. However, it begins to drop at the latest t, (t = 450 ms, 51%) and (t = 740 ms, 45%). This finding indicates that the degree of separation between compartments is also confounded by diffusion time-dependence.
Structural Universality Class and Model Selection From Diffusion Measurements
First, we consider the time-dependence of the overall D(t). The volunteer data at each TE was used to determine the most appropriate choice of tissue specific D(t) model (Table 2). Linear correlation of mean diffusivity with various models is chosen to be the criterion for evaluating the changing functional form of with TE. At the shortest TE, all models representing the long-time limit, Equations (5–7), (ρ>0.93) describe D(t) better than the S/V limit, Equation (2) (ρ = 0.92). Overall, the model with ϑ = 1/2, Equation (7), had the greatest correlation with the overall radial diffusivity λ⊥(t) at TE = 52 ms. At longer TE, the correlation with the S/V limit continued to increase: ρ(TE = 115) = 0.93, ρ(TE = 180) = 0.96; whereas the correlation with long-time limit continued to drop precipitously: ρ(TE = 115)~0.7, ρ(TE = 180)~0.6. To summarize, shorter TE is associated with diffusion through extended disorder, Equation (7), whereas longer TE is associated with the short-time S/V limit, Equation (2).
Clinical data from Lemberskiy et al. [17] was acquired with low TE=40.4 ms, suggesting W = Wc ≥ 0.927. For this reason, the diffusion-weighted signal was dominated by the cellular compartment (Table 2). Given this context, the power law scaling of the radial diffusivity λ⊥(t) can be used to determine the most appropriate tissue model for (stroma+epithelium). We find that the power-law approach of λ⊥(t) in nearly all ROIs was described best by the dynamical exponent ϑ = 1/2, Equation (7), again indicating the extended disorder (Figure 7), with the exception of (t) in the Gleason-score 3+4 ROIs, which were best described by Equation (6). Given the overall agreement of benign and malignant PZ with Equation (7), it seems appropriate to use the RPBM to study λ⊥(t) in the cellular compartment.
As for TZ, although there is a preference for Equation (7) in the ROI pertaining to TZ, it is not well described by any of the established disorder classes: R2 = [0.73, 0.81, 0.87], for Equations (5–7), respectively. If considered as a long-time limit, the corresponding ϑ appears to be closer to 0 than to 1/2, indicating that (t) in TZ is either (i) highly confounded by partial volume, or (ii) far from the long-time limit. Alternatively, comparing to the short-time S/V limit, Equation (2), revealed remarkably strong correlation with the model in TZ (ρ = 0.98).
For the volunteer data, and (Figures 6C,D, 8B–I) were best described by extended disorder, Equation (7) (ρ = 0.963), and the S/V limit, Equation (2) (ρ = 0.916), respectively. This is consistent with the above observation that shorter TE is associated with extended disorder (where DC(t) dominates), while longer TE is associated with the S/V limit, where DL(t) is dominant. Following the conclusion of extended disorder defining the cellular compartment, we find that RPBM had better correlation with the cellular λ⊥(t) (ρ = 0.986) than with the luminal λ⊥(t) (ρ = 0.551) (Figure 6D).
Quite remarkably, the 1/t scaling, Equation (5), a hallmark of either ordered/hyperuniform restrictions, or fully confined water pools (e.g., impermeable cells), never gives the best fit. Moreover, the data residuals (Figure 7B) show temporal structure, which also disfavors this scaling, and with that, the assumption of assigning compartment non-Gaussianity (i.e., time-dependence of diffusion) to fully restricted pore(s) in VERDICT [38] and RSI [39, 65] models. This means that randomly-placed, permeable and extended membranes, Figure 4A, rather than the fully restricted compartments, are most relevant for explaining the diffusion time dependence in the bulk prostate tissue (excluding lumen), and therefore are also key for biophysical modeling of non-Gaussian diffusion in its microstructure.
The DEC-FA based on the calculated diffusion tensor in each compartment provides a measurement of compartment anisotropy (Figure 8A). The cellular compartment displays highly oriented structure, with large regions within PZ colored in purple, which would be characterized by a mixture of blue (in-plane/out-plane) and green (up-down) orientation (Figure 9B). The urethra, which is at the center of the prostate, is entirely colored in blue (in-plane/out-plane orientation). In contrast, it is difficult to identify any meaningful structures from the DEC-FA of the luminal compartment, as both FA and principal eigenvector ε1 are dominated by noise (Figure 8A).
Structural Universality Class From Histology
The power spectra for the restrictions in all of the histological samples in the cellular compartment converged toward Γ~kp with exponent p = −1, where the measured p across each sample was found to be—[1.00, 1.17, 1.01 ± 0.17, 0.14, 0.13] (Figures 4B–D), indicating that the structure belongs to the extended-disorder structural universality class. This is consistent with the low-frequency/long diffusion time dependence in the stromal cross section being well described by randomly oriented barriers (RPBM), a representative of this universality class.
Between the 3 cases shown in this publication, the scale beyond which random barriers become a dominant tissue feature occur at . At the smallest k (corresponding to distances of the order of the histology cut-out), statistical fluctuations between the samples are large, and the power-law scaling becomes noisy.
The dynamical exponent ϑ = 1/2 identified above in λ⊥(t) for the cellular compartment, and the structural exponent p = −1 in d = 2 dimensions, are in agreement with the relation (4).
Cellular and Luminal Parameters From the Compartmental D(t)
Luminal Compartment
Fitting of (Figure 9F), we find its values sometimes greater than 3 μm2/ms. In the Supplementary Information we show that this is consistent with the noise propagation at the relevant SNR. As the mean of the distribution of is quite close to water diffusion coefficient at the body temperature, this result reinforces our initial assumption that the luminal compartment is composed of “lakes” of practically unrestricted water. The range of luminal diameters, aL, and (Figures 9G,H), overlap with the range of observed diameters anticipated from histology 300 ± 120 μm [14, 15, 30]. However, the lumen diameter of our healthy controls exceeds that obtained from histology of radical prostatectomy, , Figure 10C, with 65.9% difference between the means of each distribution; this is consistent with the glandular shrinkage with age. Fixing does improve the precision of over aL (Figure 9H, Supplementary Figure S4). Overall, the spread in the model parameter estimates seem to come mostly from the noise rather than from the biological variability (see Supplementary Information).
Cellular Compartment
Diffusion through the cellular compartment reveals restriction sizes of aC = 19.79 ± 8.09 μm from diffusion MRI, indicating a near perfect match with histology reported from Γ(k)|k → 0. Although the striking similarity in diameters may to some degree be a coincidence, our findings indicate that cellular diameters measured with diffusion were consistent with the length scales anticipated from the tissue (Figure 4). Moreover, aC varies over the prostate, where the largest fibers appeared closer toward the peripheral zone (Figure 9D). The distribution of cellular permeability (Figure 9E) was close to the permeability of the red blood cell membrane—perhaps, the most studied permeable biological membrane, with permeability between 0.02 and 0.09 μm/ms [66, 67]. On the other hand, voxel-wise and ROI averaged κC demonstrated substantial similarity, indicating that the range of possible permeability is much smaller than the range of possible fiber diameters.
Discussion
Specificity Toward Microstructure Arising From Dependence on Both t and TE
This study emphasizes the importance of compartment weighting on modeling prostate diffusion. Although time-dependence is apparent at individual TE, the functional form of D(t) for different TE reflects a different mixture of tissue microstructure (Table 2). This relative compartment weighting implies that the selection of the most appropriate tissue model is confounded by TE. Partial volume between cellular and luminal compartments must be resolved, before modeling D(t) could reflect tissue specific length scales. For example, when applying RPBM or S/V limit models to the overall D(t), the calculated length scale, a = 4/(S/V), increased with TE. Using compartment weighting to decompose the diffusion representation into cellular and luminal tensors reveals a unique contrast as well; the maps of appear smooth, whereas the has higher diffusivity localized around PZ, a region that is dense with glandular lumen (Figure 8).
We emphasize that it is the t-dependence, in combination with TE, that helped us identify the relevant microstructural degrees of freedom, as the time dependence provides the sensitivity to the cellular-level length scale and the spatial correlations of the restrictions. Without investigating D(t), one could only argue that there are 2 compartments with different T2, and that this has an impact on the diffusivity (Figures 6A,B). Having identified the relevant degrees of freedom for the compartmental D(t), we apply specific models to obtain corresponding length scales and membrane permeability. Good agreement with existing histopathology [14, 15, 30] for the luminal sizes (300 ± 120 μm) and myofiber diameters (19.81 ± 1.18) μm, as well as with previous measurements of T2 volume fractions (ffast>0.8 and fslow < 0.2) [13, 26], points at strong associations of compartment-specific properties with non-invasive MRI parameters.
Due to the large differences between cellular and lumen T2 values, this study focused on separation of only these tissue compartments. In principle, the “cellular” compartment which had volume fractions >0.9 was a combination of all non-luminal tissue subtypes. Since our acquisition had merely 3 TE values, modeling more than 2 compartments would be a challenge. Researchers have shown considerable interest in studying epithelium and stroma separately [13, 15, 30, 63, 68]. If this experiment were revisited with a denser sampling of TE, the “cellular” compartment would be expected to split into more granular components, such as epithelium and stroma, with potentially different microstructural degrees of freedom.
RPBM v. Fully Restricted Compartment (RSI, VERDICT)
Model selection based solely on the goodness of fit is unreliable [1]. Given how “remarkably unremarkable” [69, 70] the dMRI signal is, model selection is always a challenge. Here, we tried to reveal subtle signatures of distinct classes of structural complexity, by choosing between them on an equal footing, rather than pre-conditioning ourselves toward a particular model. For Equations (5–7), the goodness of fit at low TE or in the cellular compartment were all consistently strong, ρ > 0.9. If this work were dedicated to an individual model, the strong correlation would likely give a false sense of security about that model's success.
The previous modeling assumption of diffusion being fully restricted by impermeable barriers is a common one in the prostate [38, 39, 65], perhaps, because this is the easiest “nontrivial” model of diffusion, for which exact solutions for simple geometries (e.g., a spherical pore) have been derived decades ago [71, 72]. However, a fully restricted compartment's asymptotic D(t) behavior, Equation (5), is not preferred by the goodness-of-fit (neither in volunteers nor in the clinical population), and, more importantly, shows systematic temporal structure in the fit residuals, Figure 7. Based on our accumulated body of evidence, we conclude that the cellular compartment's time dependence is dominated by the extended disorder universality class, Equation (7).
Strictly speaking, the biophysical assumptions of, on the one hand, the RPBM, and on the other hand, an impermeable compartment at the heart of RSI and VERDICT, are mutually exclusive. If the extended disorder and the functional form of Equation (7) is indeed a correct assumption, fitting a model based on the asymptotic behavior of Equation (5) (e.g., for a fixed t by varying b) will yield biased results; moreover, because of a qualitatively different functional form, the fit results for VERDICT and RSI will depend on the chosen range of t and b, reflecting the acquisition/modeling variability challenge discussed by Novikov et al. [1]. The corresponding estimated “compartment sizes,” technically speaking, will lose their meaning.
Because we lumped fibromuscular stroma and epithelium into a single cellular compartment, in principle there could be a competition between different power law tails from different compartments. If, for instance, the epithelium compartment is described by approximately impermeable cells (VERDICT/RSI holds there), it will be practically impossible to distinguish its role in the overall “cellular” diffusivity time dependence as it will be asymptotically dominated by the smallest exponent ϑ = 1/2,
which will overshadow the effect of other compartments. To understand whether the fully restricted compartment can play a non-negligible role, one should repeat our analysis but with N = 3 compartments, provided that the separation between epithelium and stroma via their T2 values is practically achievable, and investigate the dynamical exponent of the epithelium separately.
The dynamical exponent reveals the extended nature of the restrictions and their permeability as relevant degrees of freedom for diffusion in this tissue. Furthermore, we find that the cellular compartment falls into the same disorder structural universality class as skeletal muscle. If restrictions in the cellular compartment are largely dominated by fibromuscular stroma (smooth muscle), as shown by Bourne et al. [13], then the strong agreement with Equation (7), which also best describes skeletal muscle [9, 44–46], should be anticipated. Based on our permeability estimates, the effective membrane hindrance parameter ζ~2.14 ± 1.77 is not very large, indicating that the membranes are quite leaky, which a posteriori also justifies neglecting the distinction between intra- and extra-cellular space in the RPBM. Lastly, the average standard deviation in D∞ across all measurements was ~0.03 μm2/ms, indicating that this is a highly robust parameter. These consistent findings of a finite D∞ are also incompatible [1] with the pictures of stretched-exponential diffusion signal, and anomalous diffusion in prostate [73].
Correlating MRI With Histology
In 2012, Bourne et al. [13] presented work that quantified microscopic diffusion compartmentation using high resolution MRI on a 16.4 T magnet, with 40 μm isotropic voxels. The study stated that benign prostate had an extremely small luminal compartment, with fraction of about 0.03, and a massive cellular compartment, with fraction of about 0.97. Remarkably, our estimates (Figure 10) are very close to these values. This agreement can be expected, since the experiment of Bourne et al. was directly resolving the three-dimensional volume fractions of sufficiently large glands. Other publications [27, 63, 74] correlate histology with MRI findings, which is a challenging task as histological images are in 2 dimensions whereas MRI measurements are in 3 dimensions. Sabouri et al. [27] discussed this challenge and suggests that this difference contributes to as much as 33% of the mismatch between histology and MRI. To our knowledge it is for this reason, that no previous MRI publication has been able to reproduce the volume fractions obtained from Bourne et al. [13]. In our work, the median area fraction was fL, A = 0.153 ± 0.119; however the corresponding median volume fraction estimated via Equation (13) was fL, Hist = 0.059 ± 0.734. This conversion from 2d to 3d makes the agreement between Bourne et al. [13] and the results of our histology and MRI experiment very close (Figure 10). We anticipate that this assumption would break down as the isotropic 3d geometry of the luminal compartment may gradually change with the progression of prostate cancer. The mismatch between histology and MRI for aL could suggest that the S/V greatly changes with age and/or noise propagation and modeling considerations should be refined in future work (we note, however, that MRI was performed on healthy controls, while histology was obtained from the benign area of the radical prostatectomy in a 72 yo patient). Measurements sampling multiple slices or more sophisticated modeling approaches should be considered for future histological comparisons with MRI.
Effect of Intra-Compartmental Non-Gaussian Diffusion
Previous studies have invoked the concept of multiple compartments, by empirically separating fast/slow diffusing water “pools” from an individual voxel [75, 76]. However, the estimation of the compartment fractions can be easily biased via higher-order terms in b from an individual compartment [10, 18]. Fast diffusivity derived from the bi-exponential model represents well over 40% of the signal in the prostate [16, 22]. Given that the expected luminal volume fraction is ~5%, it is clear that compartment fractions derived from the bi-exponential model cannot be easily linked toward major tissue compartments: stroma, epithelium, and lumen. A likely reason for why the bi-exponential model does not reflect any meaningful familiar tissue properties is that for the prostate in particular, the assumption of Gaussian compartments was in-validated by the observation of a time-dependent D(t) [17, 60]. Fortunately, separating compartments via T2 relaxation is “orthogonal” (Figure 2) to diffusion acquisition parameters b and t. This implies that our approach, Equation (1), can be extended further to include higher order diffusion metrics, such as kurtosis, in each compartment, by relying on the distinct T2 relaxation properties.
Chatterjee et al. [74] modeled diffusion and T2 relaxometry together, albeit assigning purely Gaussian diffusion to each of the distinct compartments. In particular, a compartment with high diffusivity and long T2 was also assigned to the lumen. However, the 3d volume fractions estimated in that paper from MRI were nearly in a 1:1 agreement with the 2d area fractions from histology. While these results were presented as a validation of the model, as we already mentioned above, the 3d volume fractions [13] have been shown to be significantly different from those measured from 2d histology [27]; in other words, a correct model should provide the lumen fraction that is notably below the histological area fraction. Hence, we suggest that the volume fractions estimated in Chatterjee et al. [74] are notably biased by the non-negligible effect of time-dependent diffusion resulting in the non-Gaussianity of the diffusion propagator at higher-b values employed in the multi-exponential dMRI fit. This strong effect of higher-order terms in b in each compartment has been precisely the reason to leave them out in this work, and to rather remain at the level of DTI.
Our multi-parametric acquisition revealed TE as a meaningful filter to separate cellular and luminal diffusivity. TE compartment weighting affecting ADC measurements in the prostate has been shown previously [77]; however, the connection to the bi-exponential T2 was not established in that publication. A recent study explored the effect of TE and t on the prostate diffusion signal ex-vivo [60], by varying both TE and t simultaneously. The effect of TE dependence was minimal on that dataset as the monotonically decreasing diffusion coefficient began to increase only at the longest t and TE. Outside of prostate applications, the value of varying TE to study diffusion to stabilize model fitting was recently demonstrated in the brain [78, 79].
Given the appropriate range of TE, estimating the NMR relaxation times via S|b=0(TM, TE) was fairly simple, i.e., we did not need to employ constraints or priors to produce robust estimates of f, . The fitting was simple mainly due to the large separation of compartmental T2 values. However, it is well established that T2 becomes shorter with increasing field strength [80]. By extension, this will have an impact on diffusion measurements: the diffusion coefficient in the brain between 1.5 and 3T systems has been reported to have a variance of ~7% [81].
Compartmental Anisotropy
Since the cellular compartment was found to be within the long-time limit, it is possible to derive a meaningful interpretation of the diffusion tensor orientation. Fiber tracking could be performed on this compartment to characterize tissue anisotropy in 3-dimensions. Many areas do not display any track information, which could mean that (1) the fiber orientation was incoherent, as an example, Figure 1A shows a histological cross section with axial and perpendicular stromal cross-sections, or (2) the dataset was unable to resolve meaningful tracts. This could be expected as prostate imaging is vulnerable to motion and distortion artifacts. While the rigid motion correction and the Siemens static distortion correction [51] have been very useful for the experiment, the image quality is still imperfect (Figures 8B–I). For this reason, the only fiber tracks shown are the ones that were generated with high confidence. The luminal compartment is far from the long-time limit, and thus no consistent orientation information is apparent (Figure 8A). This finding serves as additional confirmation that the luminal compartment for our volunteer data is indeed within the S/V limit. Note that lumen may as well be anisotropic (at sufficiently large length scales), but our acquisition would only become sensitive to this anisotropy at prohibitively long t in healthy subjects. The applicability of the S/V limit to the lumen compartment is expected to change in patient populations as glandular lumen shrinks with increasing tumor grade [15, 82]. At higher tumor grade, characterization of orientation dependence in both the cellular and gland compartments may become feasible.
Perfusion/IVIM as a Possible Confounding Factor
At low b-values, the signal dependence on b is sensitive to incoherent or multi-directional flow, attributed to a vascular compartment. Perfusion has been studied in the context of prostate cancer through the intra-vascular incoherent motion (IVIM) [20, 83], e.g., incorporated in the VERDICT parameter estimation scheme [20, 38]. However, in a recent paper, Merisaari et al. [20] performed a diffusion acquisition that has been optimized for measuring perfusion: b = 0, 2, 4, 6, 9, 12, 14, 18, 23, 28, 50, 100, 300, 500 s/mm2. After comparing multiple models using Akaike Information Criterion, the mono-exponential model prevailed as the best representation of diffusion in the prostate over b = 0–500 s/mm2 (same range as our study). Remarkably, an acquisition with 14 b-values in the optimal range was insufficient for IVIM parameters to outperform the mono-exponential diffusion. Given this finding, we doubt that perfusion would bias our results in any meaningful capacity.
As a counter-argument, one may point toward the ~10% vascular fraction, fvasc, estimated by the VERDICT model [84]. Let us now argue that this apparent vascular compartment (characterized by high diffusivity) could rather be assigned to the luminal water. For that, we recall that VERDICT models the IVIM compartment not by the signal's phase eiqvt averaged over the directions of flow velocity v, but rather via a collection of “sticks” (i.e., cylinders with zero radius) in direction n with longitudinal effective diffusion coefficient P. For the prostate, the sticks are considered to be uniformly oriented within a voxel, such that a signal in the gradient direction g averaged over sticks' orientations
looks like an isotropic diffusion signal with an effective diffusion coefficient D* = P〈 cos2θ〉 = P/3. To improve the precision for the prostate, the intrinsic diffusivity of the vascular compartment was fixed to P = 8 μm2/ms [84]; the values for P were previously estimated to range between 7 and 12 μm2/ms [38]. Hence, the effective diffusivity value for the vascular VERDICT compartment is μm2/ms. Remarkably, D* and fvasc from VERDICT are quite similar to our (free water value) and fL. Hence, VERDICT seems to be attributing the luminal contribution to the vascular compartment. If this is the case, VERDICT's fvasc encapsulates both vascular and luminal contributions. Since luminal fraction [27] is much larger than the vascular fraction [85], then fvasc ≈ fL, especially in the view of the shorter T2 of the blood than of the luminal water (T2≈180 ms for the oxygenated blood at 3T and even shorter for the deoxygenated blood [86, 87]). This suggests that the luminal contribution should dominate the vascular one in the high-diffusivity compartment.
Localization Regime as a Possible Future Avenue for Model Validation and Parameter Estimation
Since the diffusion gradient G was not fixed with t, the diffusion weighting could be confounded by spatially variable spin dephasing (with the signal suppressed less next to, e.g., lumen walls), which is an interesting albeit orthogonal avenue of microstructure investigation [88–90]. In the case of luminal diffusivities, D = 3 μm2/ms, the localization length in our experiment increased together with t, because of the decreasing gradient: [5.83, 6.36, 6.93, 7.54, 8.22, 8.90, 9.64, 10.48] μm; the diffusion length m was fixed. This indicates that our experiment was always performed in the “free-diffusion” regime [91] (LG > LD), where the “localization regime” near the walls has a relatively weak contribution toward echo decay. However, we emphasize that LG and LD are fairly close to each other; therefore, we in principle can have the choice of selecting for the free diffusion regime or the localization regime. In practice, the localization regime could be probed by varying G while setting δ~t, or by varying δ, with relatively high G, such that LD>LG.
Limitations
The study had some notable limitations that should be addressed in future research. From a theoretical perspective, we did not investigate diffusion kurtosis or higher-order terms in q-space. For a finite b, this may cause potential bias for estimated DC and DL (see Supplementary Information). Supplementary Figure S3 shows that higher-order terms may affect diffusion estimates, but does not alter the functional form of D(t) or the conclusions regarding model selection (Supplementary Table S2). This modeling limitation will be revisited in later works.
This volunteer data experiments employed only 3 TE values. More TE values potentially would enable to become sensitive to different compartments of the bulk tissue (such as stroma vs. epithelium), and produce more precise measurements, which will be investigated in future work. The patient data was not acquired with multiple TE; for this reason, model selection on D(t) was confounded by the luminal compartment. However, since the clinical dataset was acquired with smaller TE, coupled with the fact that the luminal compartment shrinks with age, we made the assumption that the signal contribution from lumen did not impact model selection too much.
Due to the acquisition length, nearly 1 h, the volunteer could move a great deal. We were able to address most of the motion using rigid registration, but there is still room for improvement as registration was impacted by SNR limitations, particularly at long TM and TE. Alternative coil designs and removing noise through data redundancy [50, 92] may alleviate concerns regarding SNR. As for the scan time, many cutting edge acceleration techniques such as parallel imaging and multiband, were already used in this experiment. Reducing the acquisition time any further would require a novel acquisition approach, similar to Sabouri et al. [26].
Finally, our histological validation had the following confounds. Although a histological image is two dimensional, a 1:1 cross section of fibromuscular stroma representing 2-dimensional diffusion may be difficult to find. Even in the samples that were selected, there is inevitably some degree of orientation dispersion that confounds Γ(k). Lastly, the H&E is not a faithful representation of restrictions to water diffusion. For example, heavily stained structures such as cellular nuclei are prominent on H&E, but are unlikely to be the primary sources of restriction to D⊥(t). The histological images had to be segmented to emphasize the borders of the cell walls, providing a more faithful representation of tissue diffusion. Nonetheless, we were reassured that the length scale beyond which the 1/k scaling is valid, estimated to be about 20 μm from histology, Figures 4A–D, is quite close to the length scale estimated from applying the RPBM onto , aC~20 μm.
Clinical Implications
According to the National Cancer Institute, roughly 11.6% of men will be diagnosed with prostate cancer (PC) within their lifetime. It is the second most common cancer among men in the United States and represents nearly 9.6% of all new cancers [93]. An estimated 26,730 individuals will die from PC in 2017; however, this represents less than 1% of the 3,085,209 individuals living with PC.
Given the indolent nature of most cases, it is valuable to be able to properly identify tumor grade before pursuing radical prostatectomy (RP). While RP entails complete surgical removal of the prostate and is effective for preventing disease progression in patients with high-grade disease, the operation is associated with considerable morbidity including erectile dysfunction and incontinence [94]. In order to maintain quality of life, there is increasing use of active surveillance (AS) for managing patients with low-risk PC. Traditionally, AS involves serial biopsies and measurements of serum prostate specific antigen (PSA), with any evidence of PC progression on such testing resulting in RP [95, 96]. The biopsy specimens are interpreted using the Gleason Score, which remains the gold standard for PC grading [97–100]. However, a primary challenge relates to incomplete sampling during biopsy [101–104], such that there may be a lack of confidence in low-risk biopsy results.
Diffusion MRI is actively used as a biomarker aiding in AS [12]. The sequence has a key role in identifying regions suspicious for clinically significant PC that can be confirmed via targeted biopsy. The so-called apparent diffusion coefficient (ADC) is utilized through a single b, t, and TE measurement. Much of the imaging and clinical community interprets ADC as a biomarker of “cellularity.” This association with cellularity relied on studies observing a strong correlation between cell density and ADC [105–107]. A more recent study recognized that the representation described earlier is insufficient and that changes in epithelium, stroma, and lumen volume fractions correlate more strongly with prostate ADC values than the cellularity [63]. This study offered histological validation that diffusion MRI is actually more sensitive to changes in prostate tissue microstructure rather than to changes in cell density. Our study builds upon this observed correlation with prostate tissue microstructure by modeling individual features that make up the prostate signal, rather than a vague concept of an aggregate cellularity. Our work suggests that the dMRI signal is specific to the individual underlying microarchitecture of distinct tissue types.
It has not escaped our notice that specific microstructural degrees of freedom, such as compartment fractions, luminal diameter, fiber diameter, and cell membrane permeability, identified by our physics-inspired model selection strategy, may serve as a foundation for objective cellular-level assessment of tumor grade and of treatment efficacy. Furthermore, our acquisition and parameter estimation is quite modest from a hardware perspective. For example, our choice of b does not require high imaging gradients, which implies that this approach can be easily ported toward lower-end scanners. Though we employed DTI for our images, our acquisition and modeling approach may be further simplified: e.g., if clinicians are mainly interested in lumen diameters, the acquisition may be accelerated even further by only studying the isotropic mean diffusion coefficient (t) derived from 3 orthogonal directions, without the need to estimate the full tensor.
Conclusions
This study identified basic building blocks for a physical picture of water diffusion in prostate tissue microstructure, relevant for in vivo diffusion MRI measurements in humans. We showed that both diffusion and transverse NMR relaxation is comprised of at least two biophysically distinct contributions, which we attribute to glandular lumen (long T2 and fast diffusion), and tissue, such as stroma, with short T2 and heavily restricted anisotropic diffusion. In both compartments, the diffusion is time-dependent, and therefore, non-Gaussian. For the luminal compartment, diffusion appears to be in the short-time S/V limit, affected by the initial restrictions by lumen walls; the corresponding time-dependent diffusion coefficient yields typical prostate lumen diameters. In the tissue compartment, diffusion is anisotropic, with the transverse diffusivity strongly decreasing with diffusion time. Its dynamical exponent reveals that the restrictions are permeable, and fall into the universality class of random permeable barriers in two spatial dimensions, most likely corresponding to the stroma fiber walls in cross-section. Applying the RPBM, we derive the fiber diameter and membrane permeability, which have good agreement with histopathology from literature and from our quantification of radical prostatectomy specimen. Our approach offers a number of objective cellular-level tissue structure parameters as candidate markers for the non-invasive diagnosis and staging of prostate cancer with MRI.
Author Contributions
GL and DN developed theory. GL and EF planned experiments. GL, DN, EF, and JV developed the parameter estimation approach. GL performed the experiments and analyzed data. AR identified zones and grades for prostate cancer lesions on MRI. FMD provided histology and identified relevant prostate regions. GL and DN wrote the manuscript. DN and EF supervised the project. All authors discussed the results, implications, and commented on the manuscript at all stages.
Conflict of Interest Statement
GL, EF and DN disclose intellectual property rights related to a pending patent. JV, FMD and ABR declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This research was supported in part by the Center of Advanced Imaging Innovation and Research (CAI2R, www.cai2r.net), a NIBIB Biomedical Technology Research Center: P41 EB017183. JV is a postdoctoral fellow of the Research Foundation - Flanders (FWO; grant number 12S1615N).
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2018.00091/full#supplementary-material
References
1. Novikov DS, Kiselev VG, Jespersen SN. On modeling. Magn Reson Med. (2018) 79:3172–93. doi: 10.1002/mrm.27101
2. Kiselev VG. Fundamentals of diffusion MRI physics. NMR Biomed. (2017) 30:e3602. doi: 10.1002/nbm.3602
3. Novikov DS, Fieremans E, Jespersen SN, Kiselev VG. Quantifying brain microstructure with diffusion MRI: Theory and parameter estimation. NMR Biomed. (2018) doi: 10.1002/nbm.3998
4. Le Bihan D, Breton E, Lallemand D, Grenier P, Cabanis E, Laval-Jeantet M. MR imaging of intravoxel incoherent motions: application to diffusion and perfusion in neurologic disorders. Radiology (1986) 161:401–7. doi: 10.1148/radiology.161.2.3763909
5. Jones DK. Diffusion MRI: Theory, Methods, and Application. Oxford, NY: Oxford University Press (2010).
7. Stejskal EO, Tanner JE. Spin diffusion measurements: spin echoes in the presence of a time-dependent field gradient. J Chem Phys. (1965) 42:288.
8. Callaghan PT. Principles of Nuclear Magnetic Resonance Microscopy. Oxford: Clarendon Press (1991).
9. Novikov DS, Jensen JH, Helpern JA, Fieremans E. Revealing mesoscopic structural universality with diffusion. Proc Natl Acad Sci USA. (2014) 111:5088–93. doi: 10.1073/pnas.1316944111
10. Novikov DS, Kiselev VG. Effective medium theory of a diffusion-weighted signal. NMR Biomed. (2010) 23:682–97. doi: 10.1002/nbm.1584
11. Bourne R, Panagiotaki E. Limitations and prospects for diffusion-weighted MRI of the prostate. Diagnostics (2016) 6:E21. doi: 10.3390/diagnostics6020021
12. Radiology ACo. MR Prostate Imaging Reporting and Data System version 2.0. Available online at: http://www.acr.org/Quality-Safety/Resources/PIRADS/ (Accessed December 2015).
13. Bourne RM, Kurniawan N, Cowin G, Stait-Gardner T, Sved P, Watson G, et al. Microscopic diffusivity compartmentation in formalin-fixed prostate tissue. Magn Reson Med. (2012) 68:614–20. doi: 10.1002/mrm.23244
14. Gorelick L, Veksler O, Gaed M, Gomez JA, Moussa M, Bauman G, et al. Prostate histopathology: learning tissue component histograms for cancer detection and classification. IEEE Trans Med Imaging (2013) 32:1804–18. doi: 10.1109/TMI.2013.2265334
15. Gilani N, Malcolm P, Johnson G. A monte carlo study of restricted diffusion: Implications for diffusion MRI of prostate cancer. Magn Reson Med. (2017) 77:1671–7. doi: 10.1002/mrm.26230
16. Bourne RM, Panagiotaki E, Bongers A, Sved P, Watson G, Alexander DC. Information theoretic ranking of four models of diffusion attenuation in fresh and fixed prostate tissue ex vivo. Magn Reson Med. (2014) 72:1418–26. doi: 10.1002/mrm.25032
17. Lemberskiy G, Rosenkrantz AB, Veraart J, Taneja SS, Novikov DS, Fieremans E. Time-dependent diffusion in prostate cancer. Invest Radiol. 2017. 52:405–11. doi: 10.1097/RLI.0000000000000356
18. Kiselev VG, Il'yasov KA. Is the “biexponential diffusion” biexponential? Magn Reson Med. (2007) 57:464–9. doi: 10.1002/mrm.21164
19. Grebenkov DS. Use, misuse, and abuse of apparent diffusion coefficients. Concepts Magn Reson Part A (2010) 36A:24–35. doi: 10.1002/cmr.a.20152
20. Merisaari H, Movahedi P, Perez IM, Toivonen J, Pesola M, Taimen P, et al. Fitting methods for intravoxel incoherent motion imaging of prostate cancer on region of interest level: Repeatability and gleason score prediction. Magn Reson Med. (2017) 77:1249–64. doi: 10.1002/mrm.26169
21. Quentin M, Blondin D, Klasen J, Lanzman RS, Miese FR, Arsov C, et al. Comparison of different mathematical models of diffusion-weighted prostate MR imaging. Magn Reson Imaging (2012) 30:1468–74. doi: 10.1016/j.mri.2012.04.025
22. Jambor I, Merisaari H, Taimen P, Bostrom P, Minn H, Pesola M, et al. Evaluation of different mathematical models for diffusion-weighted imaging of normal prostate and prostate cancer using high b-values: a repeatability study. Magn Reson Med. (2015) 73:1988–98. doi: 10.1002/mrm.25323
23. Kjaer L, Thomsen C, Iversen P, Henriksen O. In vivo estimation of relaxation processes in benign hyperplasia and carcinoma of the prostate gland by magnetic resonance imaging. Magn Reson Imaging (1987) 5:23–30. doi: 10.1016/0730-725X(87)90480-2
24. Storas TH, Gjesdal KI, Gadmar OB, Geitung JT, Klow NE. Prostate magnetic resonance imaging: multiexponential T2 decay in prostate tissue. J Magn Reson Imaging (2008) 28:1166–72. doi: 10.1002/jmri.21534
25. Gilani N, Rosenkrantz AB, Malcolm P, Johnson G. Minimization of errors in biexponential T2 measurements of the prostate. J Magn Reson Imaging (2015) 42:1072–7. doi: 10.1002/jmri.24870
26. Sabouri S, Chang SD, Savdie R, Zhang J, Jones EC, Goldenberg SL, et al. Luminal water imaging: a new mr imaging T2 mapping technique for prostate cancer diagnosis. Radiology (2017) 284:451–9. doi: 10.1148/radiol.2017161687
27. Sabouri S, Fazli L, Chang SD, Savdie R, Jones EC, Goldenberg SL, et al. MR measurement of luminal water in prostate gland: quantitative correlation between MRI and histology. J Magn Reson Imaging (2017). 46:861–9. doi: 10.1002/jmri.25624
28. Mitra PP, Sen PN, Schwartz LM. Short-time behavior of the diffusion coefficient as a geometrical probe of porous media. Phys Rev B (1993) 47:8565–74. doi: 10.1103/PhysRevB.47.8565
29. Lemberskiy G, Baete SH, Cloos MA, Novikov DS, Fieremans E. Validation of surface-to-volume ratio measurements derived from oscillating gradient spin echo on a clinical scanner using anisotropic fiber phantoms. NMR Biomed. (2017) 30:e3612. doi: 10.1002/nbm.3708
30. Gilani N, Malcolm P, Johnson G. A model describing diffusion in prostate cancer. Magn Reson Med. (2017) 78:316–26. doi: 10.1002/mrm.26340
31. Delahunt B, Grignon DJ, Samaratunga H, Srigley JR, Leite KR, Kristiansen G, et al. Prostate cancer grading: a decade after the 2005 modified gleason grading system. Arch Pathol Lab Med. (2017) 141:182–3. doi: 10.5858/arpa.2016-0300-LE
32. Bourne RM, Bongers A, Chatterjee A, Sved P, Watson G. Diffusion anisotropy in fresh and fixed prostate tissue ex vivo. Magn Reson Med. (2016) 76:626–34. doi: 10.1002/mrm.25908
33. Novikov DS, Fieremans E, Jensen JH, Helpern JA. Random walk with barriers. Nat Phys. (2011) 7:508–14. doi: 10.1038/nphys1936
34. Torquato S. Hyperuniformity and its generalizations. Phys Rev E (2016) 94:022122. doi: 10.1103/PhysRevE.94.022122
35. Papaioannou A, Novikov DS, Fieremans E, Boutis GS. Observation of structural universality in disordered systems using bulk diffusion measurement. Phys Rev E (2017) 96:61101. doi: 10.1103/PhysRevE.96.061101
36. Skoge M, Donev A, Stillinger FH, Torquato S. Packing hyperspheres in high-dimensional Euclidean spaces. Phys Rev E Stat Nonlin Soft Matter Phys. (2006) 74:041127. doi: 10.1103/PhysRevE.74.041127
37. Tanner JE. Self diffusion of water in frog muscle. Biophys J. (1979) 28:107–16. doi: 10.1016/S0006-3495(79)85162-0
38. Panagiotaki E, Walker-Samuel S, Siow B, Johnson SP, Rajkumar V, Pedley RB, et al. Noninvasive quantification of solid tumor microstructure using VERDICT MRI. Cancer Res. (2014) 74:1902–12. doi: 10.1158/0008-5472.CAN-13-2511
39. Rakow-Penner RA, White NS, Parsons JK, Choi HW, Liss MA, Kuperman JM, et al. Novel technique for characterizing prostate cancer utilizing MRI restriction spectrum imaging: proof of principle and initial clinical experience with extraprostatic extension. Prostate Cancer Prostatic Dis. (2015) 18:81–5. doi: 10.1038/pcan.2014.50
40. Reynaud O, Winters KV, Hoang DM, Wadghiri YZ, Novikov DS, Kim SG. Pulsed and oscillating gradient MRI for assessment of cell size and extracellular space (POMACE) in mouse gliomas. NMR Biomed. (2016) 29:1350–63. doi: 10.1002/nbm.3577
41. Jiang X, Li H, Xie J, McKinley ET, Zhao P, Gore JC, et al. In vivo imaging of cancer cell size and cellularity using temporal diffusion spectroscopy. Magn Reson Med. (2017) 78:156–64. doi: 10.1002/mrm.26356
42. Reynaud O. Time-dependent diffusion MRI in cancer: tissue modeling and applications. Front Phys. (2017) 5:58. doi: 10.3389/fphy.2017.00058
43. Burcaw LM, Fieremans E, Novikov DS. Mesoscopic structure of neuronal tracts from time-dependent diffusion. Neuroimage (2015) 114:18–37. doi: 10.1016/j.neuroimage.2015.03.061
44. Sigmund EE, Novikov DS, Sui D, Ukpebor O, Baete S, Babb JS, et al. Time-dependent diffusion in skeletal muscle with the random permeable barrier model (RPBM): application to normal controls and chronic exertional compartment syndrome patients. NMR Biomed. (2014) 27:519–28. doi: 10.1002/nbm.3087
45. Fieremans E, Lemberskiy G, Veraart J, Sigmund EE, Gyftopoulos S, Novikov DS. In vivo measurement of membrane permeability and myofiber size in human muscle using time-dependent diffusion tensor imaging and the random permeable barrier model. NMR Biomed. (2017) 30:e3612. doi: 10.1002/nbm.3612
46. Winters KV, Reynaud O, Novikov DS, Fieremans E, Kim SG. Quantifying myofiber integrity using diffusion MRI and random permeable barrier modeling in skeletal muscle growth and Duchenne muscular dystrophy model in mice. Magn Reson Med. (2018) 1–15. doi: 10.1002/mrm.27188
47. Langer DL, van der Kwast TH, Evans AJ, Sun L, Yaffe MJ, Trachtenberg J, Haider MA. Intermixed normal tissue within prostate cancer: effect on MR imaging measurements of apparent diffusion coefficient and T2–sparse versus dense cancers. Radiology (2008) 249:900–8. doi: 10.1148/radiol.2493080236
48. Fieremans E, Burcaw LM, Lee HH, Lemberskiy G, Veraart J, Novikov DS. In vivo observation and biophysical interpretation of time-dependent diffusion in human white matter. Neuroimage (2016) 129:414–27. doi: 10.1016/j.neuroimage.2016.01.018
49. Lundell H, Alexander DC, Dyrby TB. High angular resolution diffusion imaging with stimulated echoes: compensation and correction in experiment design and analysis. NMR Biomed. (2014) 27:918–25. doi: 10.1002/nbm.3137
50. Veraart J, Fieremans E, Novikov DS. Diffusion MRI noise mapping using random matrix theory. Magn Reson Med. (2016) 76:1582–93. doi: 10.1002/mrm.26059
51. Jezzard P, Balaban RS. Correction for geometric distortion in echo planar images from B0 field variations. Magn Reson Med. (1995) 34:65–73. doi: 10.1002/mrm.1910340111
52. Kellner E, Dhital B, Kiselev VG, Reisert M. Gibbs-ringing artifact removal based on local subvoxel-shifts. Magn Reson Med. (2016) 76:1574–81. doi: 10.1002/mrm.26054
53. Andersson JL, Sotiropoulos SN. An integrated approach to correction for off-resonance effects and subject movement in diffusion MR imaging. Neuroimage (2016) 125:1063–78. doi: 10.1016/j.neuroimage.2015.10.09
54. Klein S, Staring M, Murphy K, Viergever MA, Pluim JP. Elastix: a toolbox for intensity-based medical image registration. IEEE Trans Med Imaging (2010) 29:196–205. doi: 10.1109/TMI.2009.2035616
55. Shamonin DP, Bron EE, Lelieveldt BP, Smits M, Klein S, Staring M. Alzheimer's Disease neuroimaging i. fast parallel image registration on CPU and GPU for diagnostic classification of Alzheimer's disease. Front Neuroinform. (2013) 7:50. doi: 10.3389/fninf.2013.00050
56. Salvador R, Pena A, Menon DK, Carpenter TA, Pickard JD, Bullmore ET. Formal characterization and extension of the linearized diffusion tensor model. Hum Brain Mapp (2005) 24:144–55. doi: 10.1002/hbm.20076
57. Veraart J, Sijbers J, Sunaert S, Leemans A, Jeurissen B. Weighted linear least squares estimation of diffusion MRI parameters: strengths, limitations, and pitfalls. Neuroimage (2013) 81:335–46. doi: 10.1016/j.neuroimage.2013.05.028
58. Storaas T, Gjesdal KI. (2012). Assessment of biexponential T1 decay in prostate tissue. In: ISMRM 20th Scientific Meeting & Exhibition. Melbourne, VIC Australia (2012).
59. Kiselev VG. The cumulant expansion: an overarching mathematical framework for understanding diffusion NMR. In: Diffusion MRI: Theory, Methods, and Applications. Oxford, UK: Oxford University Press (2010). p. 152–68. Available online at: http://oxfordmedicine.com/view/10.1093/med/9780195369779.001.0001/med-9780195369779-chapter-010
60. Bourne R, Liang S, Panagiotaki E, Bongers A, Sved P, Watson G. Measurement and modeling of diffusion time dependence of apparent diffusion coefficient and fractional anisotropy in prostate tissue ex vivo. NMR Biomed. (2017) 30:e3751. doi: 10.1002/nbm.3751
61. Jones DK. Determining and visualizing uncertainty in estimates of fiber orientation from diffusion tensor MRI. Magn Reson Med. (2003) 49:7–12. doi: 10.1002/mrm.10331
62. Williams AM, Simon I, Landis PK, Moser C, Christens-Barry W, Carter HB, et al. Prostatic growth rate determined from MRI data: age-related longitudinal changes. J Androl. (1999) 20:474–80. doi: 10.1097/00005392-199904020-00155
63. Chatterjee A, Watson G, Myint E, Sved P, McEntee M, Bourne R. Changes in epithelium, stroma, and lumen space correlate more strongly with gleason pattern and are stronger predictors of prostate ADC changes than cellularity metrics. Radiology (2015) 277:751–62. doi: 10.1148/radiol.2015142414
64. Holz M, Heil SR, Sacco A. Temperature-dependent self-diffusion coefficients of water and six selected molecular liquids for calibration in accurate 1H NMR PFG measurements. Phys Chem Chem Phys. (2000) 2:4740–2. doi: 10.1039/b005319h
65. Brunsing RL, Schenker-Ahmed NM, White NS, Parsons JK, Kane C, Kuperman J, et al. Restriction spectrum imaging: an evolving imaging biomarker in prostate MRI. J Magn Reson Imaging (2017) 45:323–36. doi: 10.1002/jmri.25419
66. Benga G, Pop VI, Popescu O, Borza V. On measuring the diffusional water permeability of human red blood cells and ghosts by nuclear magnetic resonance. J Biochem Biophys Methods (1990) 21:87–102. doi: 10.1016/0165-022X(90)90057-J
67. Herbst MD, Goldstein JH. A review of water diffusion measurement by NMR in human red blood cells. Am J Physiol. (1989) 256(5 Pt 1):C1097–104.
68. Gilani N, Malcolm P, Johnson G. An improved model for prostate diffusion incorporating the results of Monte Carlo simulations of diffusion in the cellular compartment. NMR Biomed. (2017) 30:e3782. doi: 10.1002/nbm.3782
69. Ackerman JJ, Neil JJ. The use of MR-detectable reporter molecules and ions to evaluate diffusion in normal and ischemic brain. NMR Biomed. (2010) 23:725–33. doi: 10.1002/nbm.1530
70. Yablonskiy DA, Sukstanskii AL. Theoretical models of the diffusion weighted MR signal. NMR Biomed. (2010) 23:661–81. doi: 10.1002/nbm.1520
72. Murday JS, Cotts RM. Self-diffusion coefficient of liquid lithium. J Chem Phys. (1968) 48:4938–45. doi: 10.1063/1.1668160
73. Mazaheri Y, Afaq A, Rowe DB, Lu Y, Shukla-Dave A, Grover J. Diffusion-weighted magnetic resonance imaging of the prostate: improved robustness with stretched exponential modeling. J Comput Assist Tomogr. (2012) 36:695–703. doi: 10.1097/RCT.0b013e31826bdbbd
74. Chatterjee A, Bourne RM, Wang S, Devaraj A, Gallan AJ, Antic T, et al. Diagnosis of prostate cancer with noninvasive estimation of prostate tissue composition by using hybrid multidimensional MR imaging: a feasibility study. Radiology (2018) 287:864–73. doi: 10.1148/radiol.2018171130
75. White NS, Leergaard TB, D'Arceuil H, Bjaalie JG, Dale AM. Probing tissue microstructure with restriction spectrum imaging: Histological and theoretical validation. Hum Brain Mapp. (2013) 34:327–46. doi: 10.1002/hbm.21454
76. Clark CA, Le Bihan D. Water diffusion compartmentation and anisotropy at high b values in the human brain. Magn Reson Med. (2000) 44:852–9. doi: 10.1002/1522-2594(200012)44:6<852::AID-MRM5>3.0.CO;2-A
77. Wang S, Peng Y, Medved M, Yousuf AN, Ivancevic MK, Karademir I, et al. Hybrid multidimensional T(2) and diffusion-weighted MRI for prostate cancer detection. J Magn Reson Imaging (2014) 39:781–8. doi: 10.1002/jmri.24212
78. Veraart J, Novikov DS, Fieremans E. TE dependent Diffusion Imaging (TEdDI) distinguishes between compartmental T2 relaxation times. Neuroimage (2017). doi: 10.1016/j.neuroimage.2017.09.030
79. Ferizi U, Scherrer B, Schneider T, Alipoor M, Eufracio O, Fick RHJ, et al. Diffusion MRI microstructure models with in vivo human brain Connectome data: results from a multi-group comparison. NMR Biomed. (2017) 30:e3734. doi: 10.1002/nbm.3734
80. Crooks LE, Arakawa M, Hoenninger J, McCarten B, Watts J, Kaufman L. Magnetic resonance imaging: effects of magnetic field strength. Radiology (1984) 151:127–33. doi: 10.1148/radiology.151.1.6701302
81. Qin W, Yu CS, Zhang F, Du XY, Jiang H, Yan YX, et al. Effects of echo time on diffusion quantification of brain white matter at 1.5 T and 3.0 T. Magn Reson Med. (2009) 61:755–60. doi: 10.1002/mrm.21920
82. Gordetsky J, Epstein J. Grading of prostatic adenocarcinoma: current state and prognostic implications. Diagn Pathol. (2016) 11:25. doi: 10.1186/s13000-016-0478-2
83. Pang Y, Turkbey B, Bernardo M, Kruecker J, Kadoury S, Merino MJ, et al. Intravoxel incoherent motion MR imaging for prostate cancer: an evaluation of perfusion fraction and diffusion coefficient derived from different b-value combinations. Magn Reson Med. (2013) 69:553–62. doi: 10.1002/mrm.24277
84. Panagiotaki E, Chan RW, Dikaios N, Ahmed HU, O'Callaghan J, Freeman A, et al. Microstructural characterization of normal and malignant human prostate tissue with vascular, extracellular, and restricted diffusion for cytometry in tumours magnetic resonance imaging. Invest Radiol. (2015) 50:218–27. doi: 10.1097/RLI.0000000000000115
85. Bonet-Carne E, Tariq M, Pye H, Appayya M, Haider A, Bayley C, et al. Histological Validation of in-vivo VERDICT MRI for Prostate using 3D Personalised Moulds. In: (Proceedings) ISMRM 2018, International Society for Magnetic Resonance in Medicine, Paris (2018). p. 16–21.
86. Spees William M, Yablonskiy Dmitriy A, Oswood Mark C, Ackerman Joseph JH. Water proton MR properties of human blood at 1.5 Tesla: Magnetic susceptibility, T1, T2, T, and non-Lorentzian signal behavior. Magn Reson Med. (2001) 45:533–42. doi: 10.1002/mrm.1072
87. Chen Jean J, Pike GB. Human whole blood T2 relaxometry at 3 Tesla. Magn Reson Med. (2009) 61:249–54. doi: 10.1002/mrm.21858
88. Stoller SD, Happer W, Dyson FJ. Transverse spin relaxation in inhomogeneous magnetic fields. Phys Rev A (1991) 44:7459–77. doi: 10.1103/PhysRevA.44.7459
89. Axelrod S, Sen PN. Nuclear magnetic resonance spin echoes for restricted diffusion in an inhomogeneous field: methods and asymptotic regimes. J Chem Phys. (2001) 114:6878–95. doi: 10.1063/1.1356010
90. Grebenkov DS. NMR survey of reflected Brownian motion. Rev Mod Phys. (2007) 79:1077–137. doi: 10.1103/RevModPhys.79.1077
91. Hurlimann MD, Helmer KG, Deswiet TM, Sen PN. Spin echoes in a constant gradient and in the presence of simple restriction. J Magn Reson A (1995) 113:260–4. doi: 10.1006/jmra.1995.1091
92. Veraart J, Novikov DS, Christiaens D, Ades-Aron B, Sijbers J, Fieremans E. Denoising of diffusion MRI using random matrix theory. Neuroimage (2016) 142:394–406. doi: 10.1016/j.neuroimage.2016.08.016
93. Howlader, N, Noone, A, Krapcho, M, Miller, D, Bishop, K, Kosary, C, et, al,. SEER Cancer Statistics Review, 1975-2014. Bethesda, MD: National Cancer Institute. Available online at: https://seer.cancer.gov/csr/1975_2014/, based on November 2016 SEER data submission, posted to the SEER web site, April 2017.
94. Hugosson J, Stranne J, Carlsson SV. Radical retropubic prostatectomy: a review of outcomes and side-effects. Acta Oncol. (2011) 50(Supp1.):92–7. doi: 10.3109/0284186X.2010.535848
95. Klotz L. Active surveillance for prostate cancer: a review. Curr Urol Rep. (2010) 11:165–71. doi: 10.1007/s11934-010-0110-z
96. Klotz L, Zhang L, Lam A, Nam R, Mamedov A, Loblaw A. Clinical results of long-term follow-up of a large, active surveillance cohort with localized prostate cancer. J Clin Oncol. (2010) 28:126–31. doi: 10.1200/JCO.2009.24.2180
97. Epstein JI, Allsbrook WC Jr, Amin MB, Egevad LL. The 2005 International Society of Urological Pathology (ISUP) Consensus Conference on Gleason Grading of Prostatic Carcinoma. Am J Surg Pathol. (2005) 29:1228–42. doi: 10.1097/01.pas.0000173646.99337.b1
98. Epstein JI. What's new in prostate cancer disease assessment in 2006? Curr Opin Urol. (2006) 16:146–51. doi: 10.1097/01.mou.0000193389.31727.9b
99. Kattan MW, Eastham JA, Stapleton AM, Wheeler TM, Scardino PT. A preoperative nomogram for disease recurrence following radical prostatectomy for prostate cancer. J Natl Cancer Inst. (1998) 90:766–71. doi: 10.1093/jnci/90.10.766
100. Kattan MW, Wheeler TM, Scardino PT. Postoperative nomogram for disease recurrence after radical prostatectomy for prostate cancer. J Clin Oncol. (1999) 17:1499–507. doi: 10.1200/JCO.1999.17.5.1499
101. Fine SW, Epstein JI. A contemporary study correlating prostate needle biopsy and radical prostatectomy Gleason score. J Urol. (2008) 179:1335–8. doi: 10.1016/j.juro.2007.11.057
102. Mufarrij P, Sankin A, Godoy G, Lepor H. Pathologic outcomes of candidates for active surveillance undergoing radical prostatectomy. Urology (2010) 76:689–92. doi: 10.1016/j.urology.2009.12.075
103. Boccon-Gibod LM, Dumonceau O, Toublanc M, Ravery V, Boccon-Gibod LA. Micro-focal prostate cancer: a comparison of biopsy and radical prostatectomy specimen features. Eur Urol. (2005) 48:895–9. doi: 10.1016/j.eururo.2005.04.033
104. Anast JW, Andriole GL, Bismar TA, Yan Y, Humphrey PA. Relating biopsy and clinical variables to radical prostatectomy findings: can insignificant and advanced prostate cancer be predicted in a screening population? Urology (2004) 64:544–50. doi: 10.1038/aja.2011.140
105. Gibbs P, Liney GP, Pickles MD, Zelhof B, Rodrigues G, Turnbull LW. Correlation of ADC and T2 measurements with cell density in prostate cancer at 3.0 Tesla. Invest Radiol. (2009) 44:572–6. doi: 10.1097/RLI.0b013e3181b4c10e
106. Zelhof B, Pickles M, Liney G, Gibbs P, Rodrigues G, Kraus S, et al. Correlation of diffusion-weighted magnetic resonance data with cellularity in prostate cancer. BJU Int. (2009) 103:883–8. doi: 10.1111/j.1464-410X.2008.08130.x
Keywords: prostate diffusion, microstructure imaging, prostate cancer, gleason score, RPBM, diffusion tensor imaging, biophysical modeling, PIRADS
Citation: Lemberskiy G, Fieremans E, Veraart J, Deng F-M, Rosenkrantz AB and Novikov DS (2018) Characterization of Prostate Microstructure Using Water Diffusion and NMR Relaxation. Front. Phys. 6:91. doi: 10.3389/fphy.2018.00091
Received: 27 December 2017; Accepted: 26 July 2018;
Published: 25 September 2018.
Edited by:
Julien Valette, Commissariat à l'Energie Atomique et aux Energies Alternatives (CEA), FranceReviewed by:
Eleftheria Panagiotaki, University College London, United KingdomDenis Grebenkov, Centre National de la Recherche Scientifique (CNRS), France
Copyright © 2018 Lemberskiy, Fieremans, Veraart, Deng, Rosenkrantz and Novikov. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Gregory Lemberskiy, Z3JlZ29yeWxlbWJlcnNraXlAZ21haWwuY29t
 Gregory Lemberskiy
Gregory Lemberskiy Els Fieremans
Els Fieremans Jelle Veraart
Jelle Veraart Fang-Ming Deng3
Fang-Ming Deng3 Dmitry S. Novikov
Dmitry S. Novikov