- 1Laboratoire de Physique Théorique (UMR 8627), CNRS, Université Paris-Saclay, Orsay, France
- 2Laboratoire de Physique de Clermont (UMR 6533), CNRS/IN2P3, Univ. Clermont Auvergne, Aubière, France
New Physics models in which the Standard Model particle content is enlarged via the addition of sterile fermions remain among the most minimal and yet most appealing constructions, particularly since these states are present as building blocks of numerous mechanisms of neutrino mass generation. Should the new sterile states have non-negligible mixings to the active (light) neutrinos, and if they are not excessively heavy, one expects important contributions to numerous high-intensity observables, among them charged lepton flavor violating muon decays and transitions, and lepton electric dipole moments. We briefly review the prospects of these minimal SM extensions to several of the latter observables, considering both simple extensions and complete models of neutrino mass generation. We emphasise the existing synergy between different observables at the Intensity Frontier, which will be crucial in unveiling the new model at work.
1. Introduction
Several observational problems fuel the need to extend the Standard Model (SM): among them, the baryon asymmetry of the Universe (BAU), the absence of a dark matter candidate, and neutrino oscillation phenomena (i.e., neutrino masses and mixings). Many well-motivated New Physics (NP) scenarios have been proposed to overcome the observational (and theoretical) caveats of the SM: the beyond the Standard Model (BSM) constructions either rely on extending the particle content, enlarging the symmetry group, or then embedding the SM into larger frameworks. Interestingly, a common ingredient of many of the previously mentioned possibilities is the presence of additional neutral leptons, sterile states (singlets under the SM gauge group) with a mass mνs, which only interact with the active neutrinos and possibly the Higgs. Such sterile fermions can be simply added to the SM content, as is the case of right-handed (RH) neutrinos in type I seesaw mechanisms of neutrino mass generation [1–5], or emerge in association with extended gauge groups—as occurs in Left-Right (LR) symmetric models [6–8].
Additional sterile fermions have been proposed at very different scales, aiming at addressing very distinct observational problems: very light states, with a mass around the eV, have long been considered to explain the so-called “oscillation anomalies” (reactor, Gallium, and LSND); for a recent update, see [9]. Sterile fermions with masses around the keV are natural warm dark matter candidates. They are subject to stringent constraints, concerning their stability, indirect detection (via X-ray emission), phase space constraints, successful production in the early Universe, and finally, impact for structure formation. Recent reviews of the cosmological appeal of these states can be found in [10, 11]. The MeV regime opens the first window to searches at the high-intensity frontier: several observables are already sensitive to sterile fermion masses around the MeV. However, cosmological constraints remain severe, in particular those arising from Big-Bang nucleosynthesis (BBN); the latter are particularly stringent for mνs ≲ 200 MeV.
Heavy neutral leptons (HNL), with masses ranging from the GeV to the tenths of TeV are among the phenomenologically most exciting extensions of the SM, as they can give rise to numerous phenomena. Sterile fermionic states with a mass between 100 MeV and a few GeV can be produced in muon and tau decays, as well as in meson leptonic and semileptonic decays, giving rise to deviations from SM expectations, or to signatures which would otherwise be forbidden in the SM, such as violation of lepton number, of lepton flavor, or of lepton universality. These processes can be looked for in laboratory and high-intensity experiments. Provided their mass is not much larger than the electroweak (EW) scale, sterile fermions can also be present in the decays of Z and Higgs bosons, typically produced in high-energy colliders, and thus induce new experimental signatures. Finally, heavy sterile states can also be directly produced at colliders (mνs ~ a few TeV). In all cases, they can contribute to numerous processes as virtual intermediate states. In addition, sterile fermions in the GeV-TeV range also open the door to explaining the BAU via low-scale scenarios of leptogenesis (some relying on resonant mechanisms) without conflict with other cosmological observations, such as BBN, for example.
Depending not only on their mass regime but also on their couplings to the “active” neutrinos, the new neutral fermions can lead to very distinctive phenomenological features, which in turn identify the possible means to explore their presence: additional neutral leptons can be searched for in cosmology and astrophysics, in high energy colliders, or in high-intensity experiments. Concerning the latter, the fermionic singlets can be responsible for contributions to electric and magnetic leptonic dipole moments, and be responsible for numerous rare transitions and decays, including charged lepton flavor violating (cLFV), lepton number violating (LNV), and lepton flavor universality violating (LFUV) observables.
Observables involving muons offer numerous possibilities to look for imprints of the HNL; this is the case of cLFV channels (rare decays and transitions) [12, 13], and contributions to leptonic moments (electric and magnetic) [14]. The advent of very intense beams renders the muon system one of the best laboratories to look for NP states capable of contributions to the above mentioned rare decays and transitions.
The phenomenological appeal of HNL is thus manifest: their non-negligible contributions might either lead to ease some existing tensions between SM predictions and experimental data, or then render these SM extensions testable and even falsifiable. In what follows, we focus on these NP candidates, and discuss the impact that they might have for numerous observables which can be probed at the high-intensity frontier. We will consider two complementary approaches, firstly discussing the phenomenological impact of minimal SM extensions via a number nS of heavy sterile states (bottom-up approach, or “3+nS toy-models”), and subsequently consider contributions of the HNL to several observables when the latter are naturally embedded in the framework of complete models of New Physics.
This contribution is organized as follows: in section 2 we present the modified leptonic interaction Lagrangian (due to the presence of the heavy neutral leptons), and detail the contributions of the HNL to several observables; we also briefly describe the constraints that these SM extensions must comply with. Section 3 is devoted to discussing the impact of these new sterile fermionic states, first under a model-independent bottom-up approach, and then for several well-motivated New Physics models embedding them. Our final comments and discussion are collected in the Conclusions.
2. Muon High-Intensity Observables
As mentioned in the Introduction, the existence of heavy neutral leptons is a well-motivated hypothesis. The particular case of sterile fermions—i.e., SM singlets which only interact with light active neutrinos, other singlet-like states, and/or the Higgs sector—has received increasing attention in recent years, due to the extensive impact they can have, regarding both particle physics and cosmology.
2.1. Impact of HNL on Muon Observables
Depending on their masses and mixings with the light (active) neutrinos, sterile fermions have a potential impact on a number of high-intensity observables, in particular those involving the muon sector; high-intensity muon beams may thus offer a unique window to probe and to indirectly test SM extensions via HNL.
In order to address their phenomenological effects, it is convenient to consider a modified SM Lagrangian, which reflects the addition of nS sterile neutral fermions that mix with the active neutrinos. In order to simplify this first approach, we further hypothesize that:
(a) The new states are Majorana fermions;
(b) The interactions responsible for their mixing with the left-handed (active) states lead to a generic mass term of the form
which is written in the “flavor basis” (denoted with an “′” superscript); in the above, C denotes the charge conjugation matrix1. The fields have been assigned as
In the above, MνLνs is a (3 + nS) × (3 + nS) matrix, in general complex symmetric. The diagonalisation of the latter allows to identify the (3 + nS) physical (Majorana) neutrino fields,
with the corresponding basis transformations,
In the physical basis, the Lagrangian mass term of Equation (1) can be rewritten as
while the SM Lagrangian is modified (in the Feynman-'t Hooft gauge) as follows2:
in which PL,R = (1 ∓ γ5)/2, gw and θw respectively denote the weak coupling constant and weak mixing angle, and mj are the physical neutrino masses (j = 1, …, 3 + nS). We have also introduced , where U is a 3 × (3 + nS) (rectangular) matrix, which can be decomposed as
In the above, ŨPMNS is a 3 × 3 matrix and UνS is a 3 × (ns) matrix. The matrix UνS encodes the information about the mixing between the active neutrinos and the sterile singlet states (which can be often approximated, in particular in type I seesaw-like models, as ); the left-handed mixings are parameterized by a non-unitary ŨPMNS introduced in Equation (10), which can be cast as [16]
where the matrix η encodes the deviation of ŨPMNS from unitarity [17, 18], due to the presence of extra fermion states. In the limiting case of three neutrino generations (the 3 light active neutrinos), and assuming alignment of the charged lepton's weak and mass bases, U can be identified with the (unitary) PMNS matrix, UPMNS.
In summary, the presence of the additional states leads to the violation of lepton flavor in both charged and neutral current interactions. The above modified interactions are at the source of new contributions to many observables, which we proceed to discuss.
2.1.1. Lepton Dipole Moments: Muon EDM and (g−2)μ
Should the model of NP involving heavy sterile fermions further include sources of CP violation, then one expects that there will be non-negligible contributions to electric dipole moments (EDMs), which violate both T and CP conservation. Likewise, one also expects new contributions to flavor conserving observables—as for example the anomalous magnetic moment of the muon.
2.1.1.1. Electric Dipole Moments
The current bound for the muon EDM is cm (Muon g−2 [19]), and the future expected sensitivity should improve to cm (J-PARC g−2/EDM [20]). In general, the contributions of heavy leptons to the EDMs occur at the two-loop level, and call upon a minimal content of at least 2 non-degenerate sterile states [21]. As shown in [21], in the presence of nS new states, the EDM of a charged lepton ℓα can be written as
in which e is the electric charge, g2 is the SU(2) coupling constant, and mα (MW) denote the mass of the charged lepton (W boson mass). In the above are invariant quantities - respectively sensitive to Majorana and Dirac CP violating phases, defined as
and IM,D are the loop functions cast in terms of (A = i, j, α, β) (see [21]). As will be illustrated via the phenomenological analyses summarized in section 3, the “Majorana”-type contributions tend to dominate over the “Dirac”ones.
2.1.1.2. Anomalous Magnetic Moments
The muon anomalous magnetic moment induced at one-loop level by neutrinos and the W gauge boson is
in which GF is the Fermi constant, mμ the muon mass, and mi refers to the mass of the neutrinos in the loop; the loop function FM(x) is defined in the Appendix A.2, Equation (36). Subtracting the SM-like contribution from the full expression of Equation (13) (arising from one-loop diagrams, dominated by the mostly active light neutrino contribution), one obtains
where one neglects the light neutrino masses mi (i = 1, 2, 3) and Gγ(x) is also given in Appendix A.2, Equation (37). The experimental value of the muon anomalous magnetic moment has been obtained by the Muon g−2 Collaboration [22], and the discrepancy between the experimental value and the SM prediction is given by [23]. As shown in [24], the new contributions from HNL to the muon anomalous magnetic moment cannot account for the discrepancy between the experimental measured value and the SM theoretical prediction.
2.1.2. Charged Lepton Flavor Violation: The Muon Sector
Many new contributions to cLFV rare decays and transitions involving muons can be induced by the modified neutral and charged lepton currents; examples of Feynmann diagrams mediated by HNL at the origin of the cLFV transitions can be found in Figure 1. On Table 1, we summarize the experimental status (current bounds and future sensitivities) of several processes involving muons which can be studied at high-intensity frontier.

Figure 1. Examples (subset) of HNL mediated diagrams contributing to some of the cLFV decays and transitions discussed in the text: nuclear μ − e conversion and muonium oscillations. In the neutral fermion internal lines, i, j = 1, …, 3 + nS.

Table 1. Current experimental bounds and future sensitivities of cLFV processes relying on intense muon beams.
2.1.2.1. Muon Radiative Decays: μ → eγ
In a framework with a total number of 3 + nS physical neutral leptons, the contributions to the cLFV radiative decays ℓi → ℓjγ can be written as
with , (sw corresponding to the sine of the weak mixing angle), and where mℓi and Γℓi denote the mass and decay width of the decaying lepton. For the case of the muon, the latter is given by [38]
In Equation (15), denotes a composite form factor which encodes the lepton mixing angles and which is given in Appendix A.1, while the corresponding loop function, written in terms of , can be found in Appendix A.2 [see Equation (37)]. The limits for the form factors, as well as for the different loop functions, which apply in extreme regimes (e.g., x ≫ 1, or strong hierarchy in the sterile spectrum) can be found in the pioneering study of [15].
2.1.2.2. Muon 3-body Decays: μ → 3e
The full formulae, detailing the most general decay ℓi → ℓjℓkℓm in the presence of sterile states can be found in [15]; here we mostly focus on cases with same-flavor final states. The branching ratio for the decay ℓi → 3ℓj is given by
where one has included the contributions from (non-local) dipole, photon and Z penguins as well as box diagrams, corresponding to the composite form factors , , and (see Appendix A.1).
2.1.2.3. Neutrinoless Muon-Electron Conversion In Nuclei
Muonic atoms are formed when a negatively charged muon is stopped inside matter, and after cascading down in energy level becomes bound in the 1s state; in the presence of NP, the muon can be converted into an electron without neutrino emission (neutrinoless muon capture, or conversion). The observable can be defined as
the rate of the coherent conversion (spin-independent process)3 increases with the atomic number (Z) for nuclei with Z ≲ 30, being maximal for 30 ≲ Z ≲ 60 [40]. For heavier elements, one finds a reduction of the corresponding conversion rate (due to Coulomb distortion effects of the wave function).
In the framework of the SM extended by sterile neutrinos, the contributions to the muon-electron conversion rate can be written as (see, for example, [41, 42])
in which α = e2/(4π) and Γcapt(Z) is the capture rate of the nucleus (with an atomic number Z) [40], and the form factors (q = u, d) are given by
where Qq corresponds to the quark electric charge (Qu = 2/3, Qd = −1/3) and is the weak isospin (). The form factors D, V(p) and V(n) encode the relevant nuclear information. The quantities , and denote the form factors of the distinct diagrams contributing to the process (see examples in Figure 1), their expressions being given in Equations (32–35) of Appendix A.1, and those of the involved loop factors can also be found in Appendix A.2.
2.1.2.4. LNV Muon-Electron Conversion: μ−−e+, N
Should the heavy leptons be of Majorana nature, then they can induce a cLFV and LNV conversion process in the presence of nuclei, μ−+(A, Z) → e++(A, Z−2)*. Contrary to the lepton number conserving process, in this case the final state nucleus can be in a state different from the initial one (in particular, it can be either in its ground state or in an excited one—thus preventing a coherent enhancement). We will not address this process here (for model-independent recent approaches, see [43, 44]).
2.1.2.5. Coulomb Enhanced Muonic Atom Decay: μ−e−→e−e−
In the presence of NP, another cLFV channel can be studied for muonic atoms: their Coulomb enhanced decay into a pair of electrons [45, 46],
in which the initial fermions are the muon and the atomic 1s electron, bound in the Coulomb field of the nucleus. (This is a “new” observable, which has not yet been experimentally searched for; thus no experimental bounds are currently available.) In SM extensions via heavy neutral fermions, the dominant contributions arise from contact interactions, which include photon- and Z-penguins as well as box diagrams4. Neglecting the interference between contact terms (which can be sensitive to CP violating phases), the new contributions of the sterile states to the cLFV decay of a muonic atom, with an atomic number Z, can be written as
In the above, correspond to the contributions from photon- and Z-penguins (as previously introduced in Equation 19); denotes the lifetime of the muonic atom, that depends on the specific element from which it is formed (always smaller than the lifetime of free muons, τμ). The function fCoul.(Z) encodes the effects of the enhancement due to the Coulomb attraction from the nucleus (which increases the overlap of the 1s electron and muon wavefunctions); typically, , or even more than (Z−1)3 for large Z nuclei [46].
2.1.2.6. Muonium Channels: oscillation and Mu → e+e− decay
The Muonium (Mu) atom is a Coulomb bound state of an electron and an anti-muon (e−μ+) [47]; strongly resembling an hydrogen-like atom, its binding is purely electromagnetic, and thus can be well described by SM electroweak interactions, with the advantage of being free of hadronic uncertainties. The Muonium system is thus an interesting laboratory to test for the presence of new states and modified interactions. Concerning cLFV, two interesting channels can be studied: Muonium-antimuonium conversion Mu- [48], and the muonium's decay to an electron-positron pair, Mu → e+e−.
Under the assumption of (V−A) × (V−A) interactions, the Mu- transition can be described by an effective four-fermion interaction with a coupling constant ,
Searches for Mu- conversion at PSI have allowed to establish the current best bound on [37]: , at 90%C.L. [37]. In SM extensions including HNL, Mu− conversion receives contributions from four distinct types of box diagrams (mediated by Dirac and Majorana neutrinos, see [42]). In a unitary gauge, the computation of these diagrams leads to the following expression for the effective coupling [42, 49–51]:
in which and GMuonium(xi, xj) is the loop function arising from the two groups of boxes (generic and Majorana), and is given in Appendix A.2.
The presence of HNL can also be at the origin of the cLFV Muonium decays [42, 52]; the decay ratio can be written as
with Γμ the muon decay width, and where denotes the full amplitude, summed (averaged) over final (initial) spins [52]. The full expression for can be found in [42]. At present, no bounds exist on this cLFV observable, nor are there prospects for searches in the near future.
2.1.2.7. In-flight (On-Target) Conversion: μ → τ
The advent of high-intensity and sufficiently energetic muon beams (for instance at muon and future neutrino factories) allows the study of another muon cLFV observable: in-flight (elastic) conversion of muons to taus, μ + N → τ + N (with N denoting a generic nucleus) [53]. The ℓi → ℓj on-target conversion can be mediated (for example) by photon and Z boson exchanges; the differential cross sections for γ-dominated and Z-only mediation can be respectively cast as
in which Q2 is the momentum transfer, Z denotes the target atomic number, denotes the hadronic tensor and the leptonic tensors can be decomposed as , with encoding the cLFV (effective) couplings (for a complete discussion and detailed list of contributing diagrams, see [54]). In the presence of new heavy sterile fermions and can be cast (we consider the case when the target is made of nucleons) as
with the associated cLFV form factors already having been introduced for other observables.
2.2. The Several Constraints on HNL
The impact of the additional neutral leptons concerns not only potentially observable contributions to the muonic processes discussed above, but also to several other observables, possibly in conflict with current data. It is thus mandatory to evaluate the impact of these SM extensions in what concerns many available constraints obtained from high-intensity, high-energy, as well as from cosmology.
In addition to complying with neutrino data, i.e., mass differences and bounds on the PMNS mixing matrix [55, 56], sterile fermions can induce important contributions to several EW observables due to the modification of the charged and neutral currents. Other than respecting the perturbative unitarity condition [57–62], ,5 bounds from electroweak precision tests [63–66] and non-standard interactions [67–69] must also be taken into account.
The so-far negative searches for rare cLFV lepton decays and transitions (among which those discussed in the previous section), already put severe constraints on SM extensions with additional HNL [15, 18, 41, 42, 70–74]; likewise, at higher energies, searches for cLFV Higgs decays [75–80] and for neutral Z boson decays [81–84] give rise to further constraints, which must then be taken into account. Several observables associated with leptonic and semi-leptonic meson decays (cLFV, LNV, and LFUV) are also sensitive to new contributions from sterile fermions, and the corresponding bounds must thus be taken into account [66, 85–89]. Finally, and as discussed previously, there might be non-negligible contributions from Majorana HNL to CP violating observables, such as charged lepton EDMs [21, 24, 90], and to neutrinoless double beta decays (0ν2β) [91]6. The additional mixings and possible new CP-violating Majorana phases might enhance the effective mass, potentially rendering it within experimental reach, or even in conflict current bounds. Further constraints arise from peak searches in meson decays [85, 86, 93–95]; one should also apply the bounds arising from negative searches for monochromatic lines in the spectrum of muons from π± → μ±ν [87, 96], as well as those from direct searches at the LHC.
Finally, HNL are also subject to constraints of cosmological origin: a wide variety of cosmological observations [96, 97] has been shown to lead to severe bounds on heavy neutral leptons with a mass below the TeV (obtained under the assumption of a standard cosmology). Mixings between the active neutrinos and the sterile fermions can lead to radiative decays νi → νjγ, well constrained by cosmic X-ray searches; Large Scale Structure and Lyman-α data further constrain the HNL states, since these can constitute a non-negligible fraction of the dark matter of the Universe (thus impacting structure formation). Further bounds on the HNL masses and mixings with the active states can be inferred from Lyman-α limits, the existence of additional degrees of freedom at the epoch of Big Bang Nucleosynthesis, and Cosmic Microwave Background data (among others). Notice however, that in scenarios of “non-standard cosmology” (for instance, in the case of low reheating temperatures [98], or when the heavy neutral leptons couple to a dark sector [99]), all the above cosmological bounds can be evaded.
3. Phenomenological Implications of HNL for Muon Observables
Sterile neutrinos are well-motivated New Physics candidates, and their existence is considered at very different mass scales, as motivated by distinct observations. As mentioned before, heavier states, with a mass ranging from the MeV to a few TeV, are particularly appealing, as they can give rise to numerous phenomena which can be looked for in laboratory, high-energy colliders and high-intensity experiments - as the one explored in this contribution.
From a theoretical point of view, (heavy) sterile fermions play an important role in several SM extensions which include well-motivated mechanisms of neutrino mass generation; among these, one finds low-scale realisations of the seesaw mechanism (including, for example, low-scale type I and its variants, distinct realisations of the Inverse Seesaw, as well as the Linear Seesaw), and their embedding into larger frameworks, as for instance supersymmetrisations of the SM, or Left-Right symmetric models.
Before considering the contributions of these complete frameworks (which typically call upon the heavy neutral leptons as a key ingredient of the mechanism of neutrino mass generation) to the distinct high-intensity muon observables previously described, it proves convenient—and insightful—to first carry a phenomenological bottom-up approach. Without any formal assumption on the underlying mechanism of mass generation, the addition of a massive sterile state to the SM content allows to encode into a simple “toy model” the effects of a larger number of HNL states, possibly present in complete models.
3.1. Bottom-Up Approach: 3 + nS Toy Models
The “toy models” strongly rely on the assumption of having uncorrelated neutrino masses and leptonic mixings (or in other words, that one does not consider a specific mechanism of ν mass generation, for instance a seesaw). The model is described by a small set of physical parameters, which include the masses of the 3 mostly active light neutrinos, the masses of the (mostly sterile) heavy neutral leptons, and finally the mixing angles and the CP-violating phases encoded in the mixing matrix which relates the physical neutrino to the weak interaction basis; for nS additional neutral leptons, the matrix U can be parameterized by (3 + nS)(2 + nS)/2 rotation angles, (2 + nS)(1 + nS)/2 Dirac phases and 2 + nS Majorana phases7. For instance, in the simplest case where nS = 1 (the “3 + 1” model), the matrix U4 can be constructed as follows
in which the Majorana CP-violating phases are factorized in the last term. In the above, Rij is a unitary rotation matrix describing the mixing between i and j generations, parameterized in terms of the mixing angle θij and of the Dirac CP-violating phase δij. For example, R14 can be cast as
In the above, Ũ is a 4 × 4 matrix whose upper 3 × 3 block encodes the mixing among the left-handed leptons, and includes the “standard” Dirac CP phase. In the case in which the HNL decouples, this sub-matrix would correspond to the usual unitary PMNS lepton mixing matrix, UPMNS. In the case of nS = 2, the definition of U given in Equation (28) can be extended as
3.1.1. Flavor Conserving Observables
As mentioned before, if the HNL are Majorana particles, they can have an impact regarding LNV 0ν2β decays, since the new contributions to the effective mass can translate into enlarged ranges for mee. The experimental implications are striking, given that the interpretation of a future signal can no longer be associated to an inverted ordering of the light neutrino spectrum [24, 100]. Interestingly, the HNL can also be at the origin of contributions to a distinct class of (lepton flavor conserving) observables, as is the case of lepton EDMs, discussed in section 2.1.1. The contributions of the HNL to the two-loop diagrams are dominated by the terms associated with the new Majorana CP phases (the Dirac contribution being in general sub-dominant), and become important provided that there are at least two non-degenerate states, with masses in the [100 GeV, 100 TeV] range [21]; the predictions obtained in a minimal “3+2” model are displayed in Figure 2 (left). As can be inferred, in such a minimal setup, one can have at best cm, which is far below the future sensitivity of J-PARC g−2/EDM Collaboration [20], . By increasing the number of HNL (nS > 2) one could have an enhancement of a few orders of magnitude for the maximal values of |dμ|/e; however, and since the charged lepton EDMs approximately scale as [21], any future observation of ~ 10−21 cm for the muon EDM must necessarily be interpreted in the light of another new physics scenario.
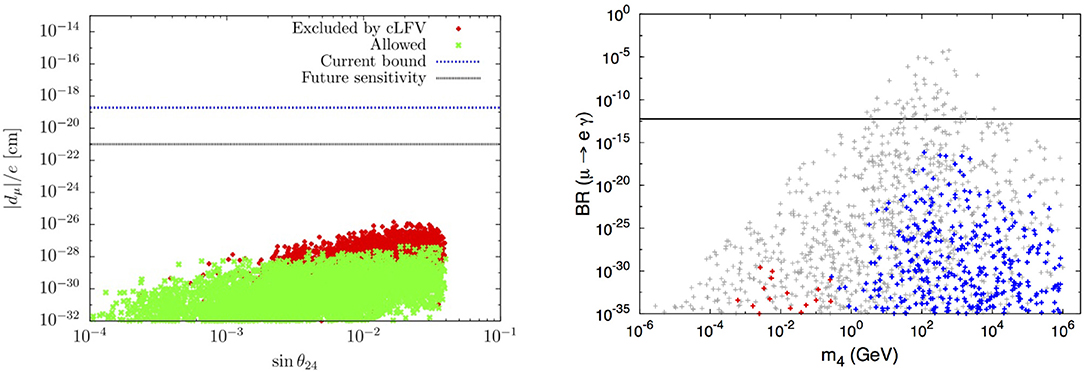
Figure 2. Contributions to the muon EDM in a “3+2” model as a function of θ24 (left panel); blue and black lines respectively denote the current upper bounds and future experimental sensitivity. From [21], reproduced with permission from the Authors. On the (right), BR(μ → eγ) as a function of m4; gray points correspond to the violation of at least one experimental bound and the horizontal line the current MEG bound.
As mentioned before, sterile states can also have an impact on other flavor-conserving observables, as is the case of the muon anomalous magnetic moment. Once all the experimental constraints discussed in section 2.2 are imposed, in generic “3 + nS” scenarios, the predicted value of the muon anomalous magnetic moment is found to be for (with i ≥ 4) [24], and thus additional contributions to the anomalous magnetic moment are still required.
3.1.2. cLFV Observables
Muon cLFV channels are in general very sensitive probes to the presence of sterile fermions, in particular HNL with masses above the electroweak scale. Beginning with radiative muon decays, the contributions to BR(μ → eγ) can be very large, well above the current bounds, as can be confirmed from the right panel of Figure 2; however, these regimes are already excluded by other experimental constraints - in particular they are in conflict with bounds arising from other cLFV muon channels, as is the case of 3-body decays and μ − e conversion in Nuclei. The contributions of the HNL (obtained in a simple “3 + 1” extension) to these two observables are displayed in the left panel of Figure 3, as a function of the mass of the heavy, mostly sterile, state, m4. Especially for m4 ≳ MZ, one can verify that the contributions are sizeable, within the sensitivity of future μ − e conversion dedicated facilities (Mu2e and COMET) and of Mu3e.
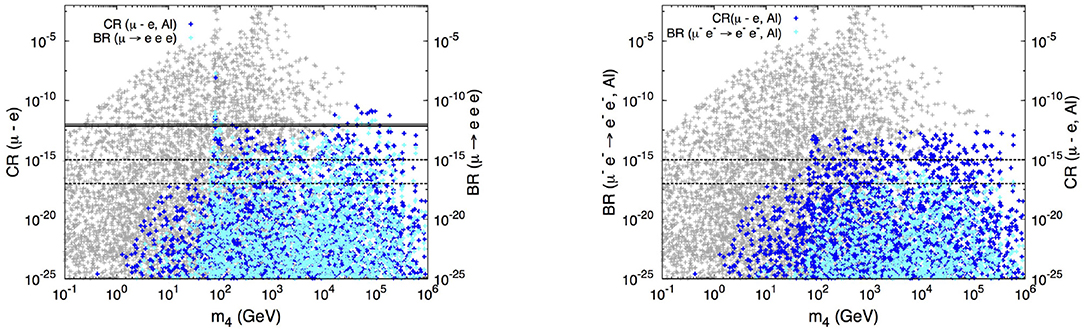
Figure 3. On the (left), predictions for CR(μ − e, Al) and BR(μ → eee) as a function of m4; the former is displayed in dark blue (left axis), while the latter is depicted in cyan (right axis). A thick (thin) solid horizontal line denotes the current experimental bound on the CR(μ − e, Au) [29] (μ → eee decays [27]), while dashed lines correspond to future sensitivities to CR(μ − e, Al) [31, 33, 34]. On the (right), BR(μ−e− → e−e−) (cyan, left axis) and CR(μ − e, Al) (dark blue, right axis) as a function of m4; dashed horizontal lines denote the (expected) future sensitivity of COMET to both observables. Both figures were obtained in the “3+1” model, and in both panels gray points correspond to the violation of at least one experimental bound (from [42], reproduced with permission from the Authors).
In the μ − e sector, neutrinoless conversion in nuclei (Aluminium) appears to be the cLFV observable offering the most promising experimental prospects; nevertheless, the Coulomb-enhanced decay of a muonic atom into a pair of electrons might prove to be also very competitive, especially for heavy target nuclei (such as Lead or Uranium), since it has been shown that the associated decay widths can be enhanced in this case [46]. Still in the framework of a minimal “3+1” model, the comparison of the expected contributions to these observables can be found in the right panel of Figure 3. For HNL states heavier than the EW scale, both observables are within reach of COMET (should the μe → ee decay be included in its Phase II programme).
It is interesting to notice that in the regime in which the mass of the HNL is heavier than the electroweak scale, the dominant contributions to processes such as μe → eee, μ − e conversion and μe → ee decays arise from Z-penguin exchange; this is at the source of a strong correlation between the corresponding cLFV decays and the lepton flavor violating decays of the Z boson, Z → μℓ. Although marginal to the present discussion, we notice that as pointed out in [82], the cLFV Z decays allow to probe μ−τ flavor violation beyond the reach of Belle II.
Heavy sterile fermions can also lead to cLFV in association with the Muonium system; the predictions for the contributions of an additional sterile state (in a minimal “3+1” model) to Mu- oscillation are displayed in the left panel of Figure 4; in view of the present experimental roadmap, it remains unclear whether or not the HNL contribution could be within future experimental reach.
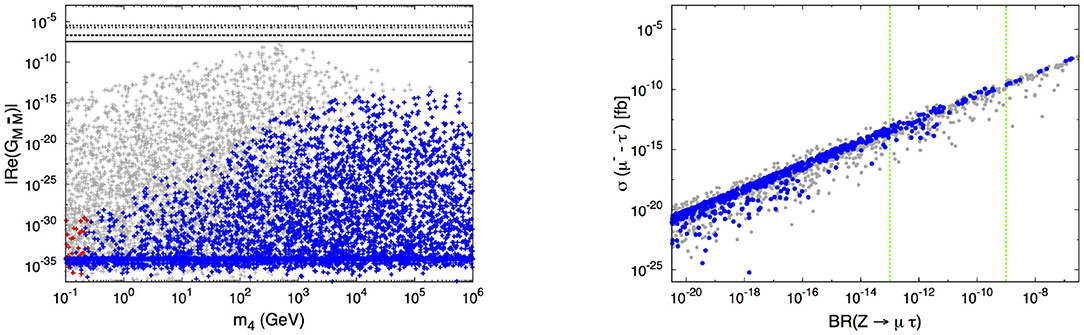
Figure 4. On the (left), effective coupling () for Mu - conversion as a function of m4 (within the framework of a simple “3+1 model”). Dark blue points are in agreement will all available bounds (the horizontal lines denote the evolution of the experimental bounds and constraints); from [42], reproduced with permission from the Authors. On the (right), correlation of cLFV in-flight σ(μ → τ) vs. BR(Z → τμ) in the “3+1 model”; blue (gray) points denote allowed (excluded) regimes, vertical green lines denote the future sensitivities; from [54], reproduced with permission from the Authors. In both panels, gray points correspond to the violation of at least one experimental bound.
Finally, we comment on the prospects for cLFV in-flight conversion of future intense muon beams, in particular focusing on the mode σ(μ → τ). Larger values of the cross-section, which could potentially be within reach of a future Muon Collider (for nominal values of 1020μ/year), are in fact already excluded, as the associated regimes (mass and mixings of the additional sterile) lead to values of BR(τ → 3μ) already in conflict with experimental bounds [54]. This is a consequence of having again dominant contributions from Z-mediated penguins in both cases; this is visible in the right panel of Figure 4, in which we illustrate the prospects of σ(μ → τ) vs. the expected contributions to BR(Z → μτ). The correlation of the observables is clear, and further serves to illustrate the probing power of flavor violating Z decays (albeit at the high energy frontier).
3.2. Complete NP Frameworks and HNL: Contributions to Muon Observables
To conclude our brief overview, we thus consider a few illustrative examples of complete SM extensions calling upon heavy neutral fermions, focusing our attention on “low-scale” (≲ TeV) NP models. Other than low-scale realisations of a type I seesaw, we will refer to many of its variations including well-motivated realisations such as the Inverse Seesaw (ISS) [17, 18, 101], the Linear Seesaw (LSS) [102, 103] and the ν-MSM [104–106]. In addition, we also briefly comment on larger frameworks also including HNL, and which have an important impact for the muon observables here addressed. When relevant, we shall also discuss how the synergy of the distinct observables might be instrumental in unveiling the NP model at work.
3.2.1. Low-Energy Variants of Type I Seesaw
The type I Seesaw relies in extending the SM content by at least two additional “heavy” right-handed neutrinos.
The light neutrino masses are given in terms of the Yukawa couplings and of the RH neutrino mass matrix by the “seesaw relation”, . The low-scale seesaw (and its different variants) consists in a realisation of a type I seesaw in which the (comparatively light) heavy mediators have non-negligible mixings with the active neutrinos, and do not decouple. Just as in the case of the simple “toy-models” described in the previous section, the modification of the leptonic currents can lead to contributions to numerous observables [41, 73]. One such example - concerning contributions to cLFV muon radiative and 3-body decays, as well as μ − e conversion in nuclei—can be found in the left panel of Figure 5, in which the contributions to the distinct observables (and the associated experimental bounds/future sensitivities) are displayed as a function of the average seesaw mediator mass.
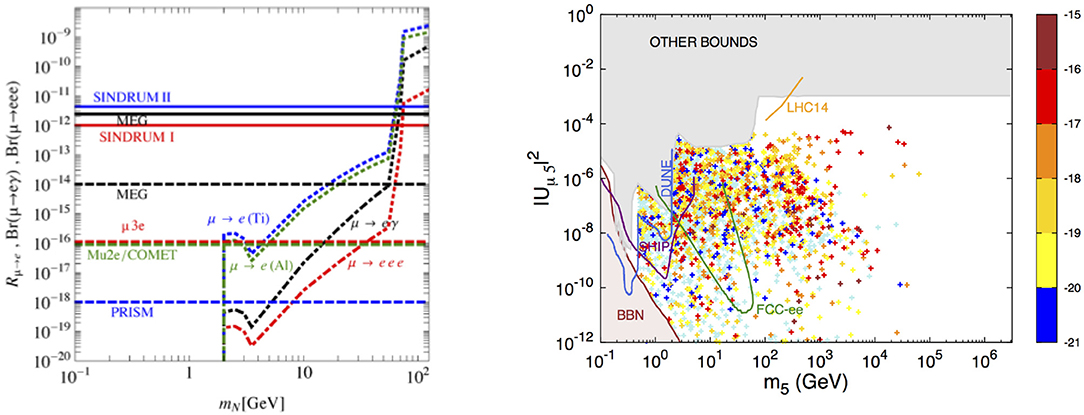
Figure 5. On the (left), maximal allowed cLFV rates compatible with current searches in a low-scale seesaw; horizontal full (dashed) lines denote present (future) experimental sensitivity. From [41], reproduced with permission from the Authors. On the (right), logarithm of BR(μ−e− → e−e−, Al), displayed on parameter space of a (3,3) ISS realisation; the shaded surfaces correspond to the exclusion from BBN (rose) or from the violation of at least one experimental bound (gray), while solid lines delimit the expected sensitivity of several facilities (from [42], reproduced with permission from the Authors).
The νMSM consists in a specific low-energy realisation of a type I seesaw, which aims at simultaneously addressing the problems of neutrino mass generation, the BAU and providing a viable dark matter candidate [104–107]. The νMSM spectrum contains the three light (mostly active) neutrinos, with masses given by a type I seesaw relation, as well as three heavy states (with masses mν4−6). In view of the model's goal to comply with the above requirements, the couplings and masses of the new states are severely constrained. In particular, and due to the smallness of the active-sterile mixings, the expected contributions of the νMSM in what concerns cLFV observables are found to lie beyond experimental sensitivity. This has been discussed in [42, 54].
Other than extending the SM by RH neutrinos, the Inverse Seesaw [17, 18, 101] calls upon the introduction of additional sterile fermion8 states, X. In the case of 3 generations of each, the spectrum of the (3,3) ISS realisation contains 6 heavy neutral fermions, which form 3 pseudo-Dirac pairs; the smallness of the light (active) neutrino masses is explained by the suppresion due to the only source of LNV in the model (μX), as given by the following modified seesaw relation: . This allows for a theoretically natural model, in which one can have sizeable Yukawa couplings for a comparatively light seesaw scale. On the right panel of Figure 5 we illustrate the (3,3) ISS contributions to a muonic atom observable: the Coulomb enhanced decay into a pair of electrons, displaying the predictions for the corresponding BR in terms of the mass of the lightest sterile state (m5) and . As can be seen, the contributions for these observables can be sizeable, well within experimental reach. Particularly interesting is the fact that these HNL states are within reach of future facilities such as DUNE, FCC-ee and SHiP. Likewise, one expects important contributions to other observables [42].
Another low-scale seesaw mechanism relying on an approximate conservation of lepton number is the Linear Seesaw [102, 103]. Similar to the case of the ISS, the Linear Seesaw also calls upon the addition of two types of fermionic singlets (RH neutrinos and other sterile states) with opposite lepton number assignments. However, in this case LNV is due to the Yukawa couplings of the sterile states to the LH neutrinos. The resulting light neutrino masses are linearly dependent on these Yukawa couplings, . The obtained spectrum in the mostly sterile sector is composed by pairs of pseudo-Dirac neutrinos (almost degenerate in mass) - a consequence of having the mass splittings determined by the small LNV couplings (), which are also responsible for the suppression of the active neutrino masses. This is similar to what occurs in the ISS scenario, with which the LSS shares many phenomenological features (notice that distinctive signatures can arise due to having two sources of flavor mixing, Yν and ).
3.2.2. Extended NP Frameworks: LR Models and SUSY
Restoring parity conservation in SM gauge interactions naturally leads to models of NP which include HNL (right-handed neutrinos). In Left-Right symmetric models [6–8], the SM gauge group is enlarged to SU(3)c×SU(2)L×SU(2)R×U(1)B−L, and the particle content now includes, in addition to the RH neutrinos, new WR and ZR bosons, as well as bi-doublet and triplet (Higgs) bosons. Not only RH neutrinos are automatically incorporated as part of an SU(2)R doublet upon realisation of the extended gauge group (and thus interacting with the heavy right-handed bosons), but a hybrid type I-II seesaw mechanism is at work in this class of models. Dirac neutrino mass terms arise from the interactions of the RH neutrinos with the lepton doublets and the Higgs bi-doublets, while Majorana mass terms are present for both left- and right-handed neutral fermions,
in which Y(′) and fL,R denote 3 × 3 complex Yukawa matrices in flavor space; κ and κ′ are the vevs of the Higgs bi-doublets, while vL(R) is the vev of the triplet ΔL(R) (notice that vR is the vev responsible for breaking SU(2)R×U(1)B−L down to U(1)Y). In the “seesaw limit” (i.e., for |mD| ≪ |MR|), block-diagonalisation of in Equation (31) leads to a light neutrino mass matrix of the form , where both seesaw contributions are visible. The new states (in particular the HNL and the right-handed gauge bosons) lead to extensive contributions to many muonic channels and, interestingly, to strong correlations between high-intensity and high-energy cLFV and LNV observables (see, e.g., [109–111]). One such example (from [110, 111]) can be found on the left panel of Figure 6, in which the rose-shaded surfaces correspond to different regimes of contributions to μ → eγ, μ → 3e, and μ − e conversion in nuclei. Future sensitivities to μ − e conversion already allow to cover most of the parameter space (here represented in mN, mWR plane), and further important information can be inferred from cLFV decays at colliders: the blue lines denote the number of events with a signature e±μ∓+2 jets (no missing energy) at the LHC run 2 (assuming nominal values of and integrated luminosity ), with dashed ones corresponding to 5σ significance (discovery) and 90% C.L. (exclusion).
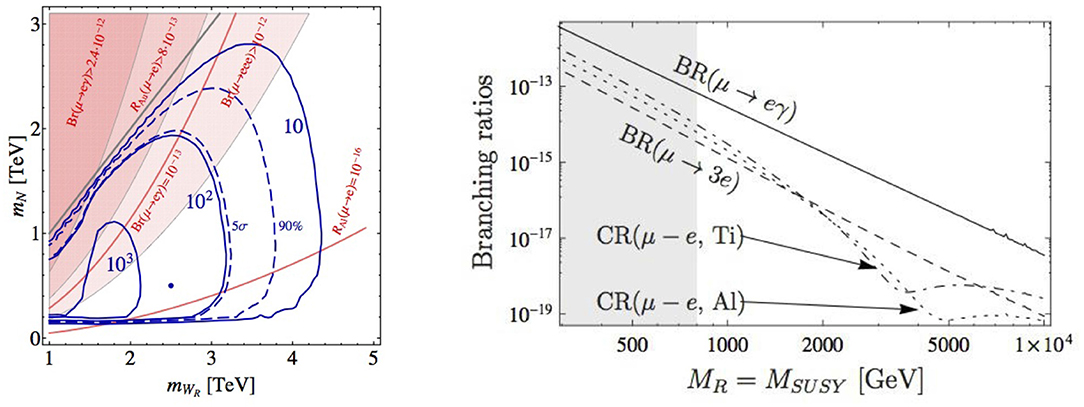
Figure 6. On the (left), muon cLFV rates in LRSM: rose-shaded areas denote the corresponding experimental regimes (exclusion and future sensitivity); solid lines denote the number of events with a signature e±μ∓ + 2 jets (no missing energy) at the LHC run 2 ( and ), while the dashed ones define regions with significances at 5σ (discovery) and 90% C.L. (exclusion). From [110], and appearing also in [111] (reproduced with permission from the Authors). On the (right), predictions for cLFV muon channels obtained in a SISS realisation: BR(μ → eγ), BR(μ → 3e), and CR(μ − e, Al,Ti) as a function of MR = MSUSY. The gray area roughly denotes regimes excluded by direct LHC searches. From Abada et al. [74], reproduced with permission from the Authors.
The seesaw (in its distinct realisations) can be embedded in the framework of supersymmetric (SUSY) extensions of the SM; in order to render less severe the so-called “SUSY CP and flavor problem”, the seesaw is embedded in otherwise flavor and CP conserving SUSY models, as is the case of the constrained Minimal SUSY SM (cMSSM). These BSM constructions offer many new contributions to cLFV observables, as in general the different scales at work allow for sizeable Yukawa couplings, and new—not excessively heavy—exotic mediators (sleptons and gauginos).
For the “standard” type I SUSY seesaw, the right-handed neutrino superfields (neutrinos and sneutrinos) are in general very heavy—with masses GeV. Interestingly, it has been emphasized that the synergy of cLFV observables (among which the muonic ones here discussed) might provide one of the best probes into the spectrum of the (extremely) heavy neutrinos (see, for example [112, 113]).
The supersymmetrisation of the ISS (in which case the HNL and their SUSY partners are significantly lighter, closer to the TeV scale)—SISS—also leads to abundant signatures in what concerns muon observables; a thorough study of several observables (for different regimes, and taking into account distinct contributions) was carried in [74]. Here, we illustrate the potential of the SISS via the contributions to several muon channels as a function of the SUSY and seesaw scales (MR), which are displayed on the right panel of Figure 6.
4. Final Remarks and Discussion
In the coming years, the High Intensity Frontier will offer many opportunities to explore particle and astroparticle physics. In addition to testing some of the SM predictions, high-intensity experiments will open unique windows to probe New Physics models. Many current tensions between the SM and observation are currently associated with the lepton sector: in addition to neutrino oscillation data, several other observables (as is the case of the muon anomalous magnetic moment) call for NP ingredients. As common ingredient to many BSM constructions, neutral leptons (such as right-handed neutrinos, or other sterile fermions) play a key role in many mechanisms of neutrino mass generation. The motivations for these states are extensive: neutral fermions with masses in the GeV-TeV range (“heavy neutral leptons”) are particularly appealing, as in addition to a possible role in light neutrino mass generation they might induce significant contributions to many high intensity observables, such as cLFV, LNV, or contributions to lepton dipole moments, which can be searched for with the advent of intense muon beams.
In this small overview, we have discussed the contributions of HNL to several observables which can be studied in high-intensity muon experiments. We have illustrated the potential of the heavy sterile states via two complementary approaches: considering ad-hoc “3 + nS” toy models and well-motivated appealing NP models (seesaw mechanisms, LR models, supersymmetric extensions of the SM, …). As seen from our discussion, the new states can easily give rise to significant contributions to many observables well within experimental sensitivity (in fact, some of the current bounds already heavily constraining the associated new degrees of freedom). Given their elusive nature, high-intensity muon observables might be a unique probe of SM extensions via additional heavy neutral leptons.
Author Contributions
AA and AT have equally contributed to the review, relying on their complementary expertise and on the results of several previous publications (many done working in collaboration).
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We acknowledge partial support from the European Union Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie: RISE InvisiblesPlus (grant agreement No 690575) and the ITN Elusives (grant agreement No 674896). We thank R. Bernstein and Y. Kuno for fruitful discussions.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2018.00142/full#supplementary-material
Footnotes
1. ^We follow the conventions under which , with CT = −C. The fields transform as , changing chirality under the action of the operator, i.e., is a left-handed field.
2. ^See, for example, [15] for a detailed derivation starting from explicit lepton mass matrices.
3. ^For a recent study of spin-dependent contributions to muon-electron conversion in nuclei, see [39].
4. ^In this class of models, and in the regimes associated with significant cLFV contributions, the “long-range” photonic interactions are typically subdominant.
5. ^Since the dominant contribution to Γνi arises from the charged current term, one can rewrite the perturbative unitarity condition as: , with U the lepton mixing matrix.
6. ^Working in the framework of the SM extended by ns sterile fermions, one must generalise the definition of the effective mass (to which the 0ν2β amplitude is proportional to) as , where p2≃−(125MeV)2 is the virtual momentum of the propagating neutrino (obtained from average estimates over different decaying nuclei) [92]. The new mixings (and the possibility of additional CP-violating Majorana phases) can have a sizeable impact on the effective mass.
7. ^In the case of a complete model of neutrino mass generation, the neutrino masses and the (3 + ns) × (3 + ns) lepton mixing matrix U3+ns would be formally derived from the diagonalisation of the full (3 + nS) × (3 + nS) neutrino mass matrix and thus be related; it is important to emphasize that in such a case the model must necessarily account for ν oscillation data.
8. ^The minimal realisations of the Inverse Seesaw mechanism have ben discussed in [108].
References
1. Minkowski P. Mu → E gamma at a rate of one out of 1-billion Muon decays? Phys Lett B (1977) 67:421–8. doi: 10.1016/0370-2693(77)90435-X
2. Gell-Mann M, Ramond P, Slansky R. Complex spinors and unified theories. In: Van Nieuwenhuizen P, Freedman DZ, editors. Supergravity. Amsterdam (1979). p. 315.
3. Yanagida T. Proceedings of the Workshop on the Unified Theory and the Baryon Number in the Universe. Tsukuba: KEK (1979). p. 95.
5. Mohapatra RN, Senjanović G. Neutrino mass and spontaneous parity nonconservation. Phys Rev Lett. (1980) 44:912.
7. Senjanovic G, Mohapatra RN. Exact left-right symmetry and spontaneous violation of parity. Phys Rev D (1975) 12:1502.
9. Gariazzo S, Giunti C, Laveder M, Li YF. Updated global 3+1 analysis of short-baseLine neutrino oscillations. arXiv:1703.00860 (2017). doi: 10.1007/JHEP06(2017)135
10. Abazajian KN, Acero MA, Agarwalla SK, Aguilar-Arevalo AA, Albright CH, Antusch S, et al. Light sterile neutrinos: a white paper. arXiv:1204.5379. Available online at: http://inspirehep.net/search?ln=en&ln=en&p=arXiv%3A1204.5379&of=hlxe&action_search=Search&sf=earliestdate&so=d&rm=&rg=25&sc=0
11. Drewes M, Lasserre T, Merle A, Mertens S, Adhikari R, Agostini M, et al. A white paper on keV sterile neutrino dark matter. arXiv:1602.04816 (2017). doi: 10.1088/1475-7516/2017/01/025
12. Kuno Y, Okada Y. Muon decay and physics beyond the standard model. Rev Mod Phys. (2001) 73:151. doi: 10.1103/RevModPhys.73.151
13. Bernstein RH, Cooper PS. Charged lepton flavor violation: an experimenter's guide. Phys Rept. (2013) 532:27–64. doi: 10.1016/j.physrep.2013.07.002
14. Raidal M, van der Schaaf A, Bigi I, Mangano ML, Semertzidis YK, Abel S, et al. Flavour physics of leptons and dipole moments. Eur Phys J C (2008) 57:13–182. doi: 10.1140/epjc/s10052-008-0715-2
15. Ilakovac A, Pilaftsis A. Flavor violating charged lepton decays in seesaw-type models. Nucl Phys B (1995) 437:491
16. Fernandez-Martinez E, Gavela MB, Lopez-Pavon J, Yasuda O. CP-violation from non-unitary leptonic mixing. Phys Lett B (2007) 649:427–35. doi: 10.1016/j.physletb.2007.03.069
18. Gronau M, Leung CN, Rosner JL. Extending limits on neutral heavy leptons. Phys. Rev. D (1984) 29:2539.
19. Bennett GW, Bousquet B, Brown HN, Bunce G, Carey RM, Cushman P, et al. An improved limit on the Muon electric dipole moment. Phys. Rev. D (2009) 80:052008. doi: 10.1103/PhysRevD.80.052008
20. Saito N. A novel precision measurement of muon g-2 and EDM at J-PARC. In: AIP Conference Proceedings (2012). p. 45. Available online at: http://inspirehep.net/search?ln=en&ln=en&p=Saito%3A2012zz&of=hb&action_search=Search&sf=earliestdate&so=d&rm=&rg=25&sc=0
21. Abada A, Toma T. Electric dipole moments of charged leptons with sterile fermions. arXiv:1511.03265 (2016). doi: 10.1007/JHEP02(2016)174
22. Bennett GW, Bousquet B, Brown HN, Bunce G, Carey RM, Cushman P, et al. Final report of the Muon E821 anomalous magnetic moment measurement at BNL. Phys Rev D (2006) 73:072003. doi: 10.1103/PhysRevD.73.072003
23. Patrignani C, Agashe K, Aielli G, Amsler C, Antonelli M, Asner DM, et al. Review of particle physics. Chin. Phys. C (2016) 40:100001. doi: 10.1103/PhysRevD.98.030001
24. Abada A, De Romeri V, Teixeira AM. Effect of steriles states on lepton magnetic moments and neutrinoless double beta decay. arXiv:1406.6978 (2014). doi: 10.1007/JHEP09(2014)074
25. Baldini AM, Bao Y, Baracchini E, Bemporad C, Berg F, Biasotti M, et al. Search for the lepton flavour violating decay μ+→e+γ with the full dataset of the MEG experiment. Eur. Phys. J. C (2016) 76:434. doi: 10.1140/epjc/s10052-016-4271-x
26. Baldini AM, Chiappini M, Gerone M, D'Onofrio A, Rutar G, Baracchini E, et al. The design of the MEG II experiment. Eur. Phys. J. C (2018) 78:380. doi: 10.1140/epjc/s10052-018-5845-6
27. Bellgardt U, Otter G, Eichler R, Felawka L, Niebuhr C, Walter HK, et al. Search for the Decay mu+ —> e+ e+ e-. Nucl. Phys. B (1988) 299:1.
28. Blondel A, Bravar A, Pohl M, Bachmann S, Berger N, Kiehn M, et al. Research proposal for an experiment to search for the decay μ → eee. arXiv:1301.6113. Available online at: http://inspirehep.net/search?ln=en&ln=en&p=arXiv%3A1301.6113&of=hlxe&action_search=Search&sf=earliestdate&so=d&rm=&rg=25&sc=0
29. Bertl WH, Rosenbaum F, Ryskulov NM, Engfer R, Hermes EA, Kurz G, et al. A search for muon to electron conversion in muonic gold. Eur. Phys. J. C (2006) 47:337–46. doi: 10.1140/epjc/s2006-02582-x
30. Nguyen TM. Search for μ – e conversion with DeeMe experiment at J-PARC MLF. Proc Sci. 248 (2015). doi: 10.22323/1.248.0060
31. Kuno Y. A search for muon-to-electron conversion at J-PARC: the COMET experiment. PTEP(2013) 2013:022C01. doi: 10.1093/ptep/pts089
32. Krikler BE. An overview of the COMET experiment and its recent progress. arXiv:1512.08564. Available online at: http://inspirehep.net/search?ln=en&ln=en&p=arXiv%3A1512.08564&of=hlxe&action_search=Search&sf=earliestdate&so=d&rm=&rg=25&sc=0
33. Bartoszek L, Barnes E, Miller JP, Mott J, Palladino A, Quirk J, et al. Mu2e technical design report. arXiv:1501.05241. Available online at: http://inspirehep.net/search?ln=en&ln=en&p=arXiv%3A1512.08564&of=hlxe&action_search=Search&sf=earliestdate&so=d&rm=&rg=25&sc=0
34. Abusalma F, Ambrose D, Artikov A, Bernstein R, Blazey GC, Bloise C, et al. Expression of interest for evolution of the Mu2e experiment. arXiv:1802.02599 (2018). Available online at: http://inspirehep.net/search?ln=en&ln=en&p=arXiv%3A1802.02599+&of=hlxe&action_search=Search&sf=earliestdate&so=d&rm=&rg=25&sc=0
35. Kuno Y. Prism/prime. Nucl Phys Proc Suppl. (2005) 149:376. doi: 10.1016/j.nuclphysbps.2005.05.073
36. Kaulard J, Dohmen C, Haan H, Honecker W, Junker D, Otter G, et al. Improved limit on the branching ratio of mu- –> e+ conversion on titanium. Phys Lett B (1998) 422:334.
37. Willmann L, Schmidt PV, Wirtz HP, Abela R, Baranov V, Bagaturia J, et al. New bounds from searching for muonium to anti-muonium conversion. Phys Rev Lett. (1999) 82:49–52. doi: 10.1103/PhysRevLett.82.49
38. Beg MAB, Sirlin A. Gauge theories of weak interactions. 2. (Circa 1981 - 82 C.e.). Phys Rep. (1982) 88:1.
39. Cirigliano V, Davidson S, Kuno Y. Spin-dependent μ → e conversion. Phys Lett B (2017) 771:242. doi: 10.1016/j.physletb.2017.05.053
40. Kitano R, Koike M, Okada Y. Detailed calculation of lepton flavor violating muon electron conversion rate for various nuclei. Phys Rev D (2002) 66:096002. doi: 10.1103/PhysRevD.66.096002
41. Alonso R, Dhen M, Gavela MB, Hambye T. Muon conversion to electron in nuclei in type-I seesaw models. arXiv:1209.2679 (2013). doi: 10.1007/JHEP01(2013)118
42. Abada A, De Romeri V, Teixeira AM. Impact of sterile neutrinos on nuclear-assisted cLFV processes. arXiv:1510.06657 (2016). doi: 10.1007/JHEP02(2016)083
43. Geib T, Merle A, Zuber K. μ−−e+ conversion in upcoming LFV experiments. Phys Lett B (2017) 764:157–62. doi: 10.1016/j.physletb.2016.11.029
44. Berryman JM, de Gouv A, Kelly KJ, Kobach A. Lepton-number-violating searches for muon to positron conversion. Phys Rev D (2017) 95:115010. doi: 10.1103/PhysRevD.95.115010
45. Koike M, Kuno Y, Sato J, Yamanaka M. A new idea to search for charged lepton flavor violation using a muonic atom. Phys Rev Lett. (2010) 105:121601. doi: 10.1103/PhysRevLett.105.121601
46. Uesaka Y, Kuno Y, Sato J, Sato T, Yamanaka M. Improved analysis for μ−e−→e−e− in muonic atoms by photonic interaction. Phys Rev D (2018) 97:015017. doi: 10.1103/PhysRevD.97.015017
49. Clark TE, Love ST. Muonium - anti-muonium oscillations and massive Majorana neutrinos. Mod Phys Lett A (2004) 19:297–306. doi: 10.1142/S0217732304013143
50. Cvetic G, Dib CO, Kim CS, Kim JD. Muonium-antimuonium conversion in models with heavy neutrinos. Phys Rev D (2005) 71:113013. doi: 10.1103/PhysRevD.71.113013
51. Liu B. Gauge invariance of the muonium-antimuonium oscillation time scale and limits on right-handed neutrino masses. Mod Phys Lett A (2009) 24:335. doi: 10.1142/S021773230903000X
52. Cvetic G, Dib CO, Kim CS, Kim J. Lepton flavor violation in muonium decay and muon colliders in models with heavy neutrinos. Phys Rev D (2006) 74:093011. doi: 10.1103/PhysRevD.74.093011
53. Gninenko SN, Kirsanov MM, Krasnikov NV, Matveev VA. Probing lepton flavor violation in muon-neutrino + N —> tau + …scattering and mu —> tau conversion on nucleons. Mod Phys Lett A (2002) 17:1407. doi: 10.1142/S0217732302007855
54. Abada A, De Romeri V, Orloff J, Teixeira AM. In-flight cLFV conversion: e−μ, e−τ and μ−τ in minimal extensions of the standard model with sterile fermions. Eur Phys J C (2017) 77:304. doi: 10.1140/epjc/s10052-017-4864-z
55. Gonzalez-Garcia MC, Maltoni M, Schwetz T. Global analyses of neutrino oscillation experiments. Nucl Phys B (2016) 908:199–217. doi: 10.1016/j.nuclphysb.2016.02.033
56. Esteban I, Gonzalez-Garcia MC, Maltoni M, Martinez-Soler I, Schwetz T. Updated fit to three neutrino mixing: exploring the accelerator-reactor complementarity. arXiv:1611.01514 (2017). doi: 10.1007/JHEP01(2017)087
57. Chanowitz MS, Furman MA, Hinchliffe I. Weak interactions of ultraheavy fermions. 2. Nucl Phys B (1979) 153:402.
58. Durand L, Johnson JM, Lopez JL. Perturbative unitarity revisited: a new upper bound on the Higgs Boson Mass. Phys Rev Lett. (1990) 64:1215.
59. Korner JG, Pilaftsis A, Schilcher K. Leptonic flavor changing Z0 decays in SU(2) x U(1) theories with right-handed neutrinos. Phys Lett B (1993) 300:381.
60. Bernabeu J, Korner JG, Pilaftsis A, Schilcher K. Universality breaking effects in leptonic Z decays. Phys Rev Lett. (1993) 71:2695.
61. Fajfer S, Ilakovac A. “Lepton flavor violation in light hadron decays. Phys Rev D (1998) 57:4219.
62. Ilakovac A. Lepton flavor violation in the standard model extended by heavy singlet Dirac neutrinos. Phys Rev D (2000) 62:036010. doi: 10.1103/PhysRevD.62.036010
63. Akhmedov E, Kartavtsev A, Lindner M, Michaels L, Smirnov J. Improving electro-weak fits with TeV-scale sterile neutrinos. arXiv:1302.1872 (2013). doi: 10.1007/JHEP05(2013)081
64. Basso L, Fischer O, van der Bij JJ. Precision tests of unitarity in leptonic mixing. Europhys Lett. (2014) 105:11001. doi: 10.1209/0295-5075/105/11001
65. Fernandez-Martinez E, Hernandez-Garcia J, Lopez-Pavon J, Lucente M. Loop level constraints on Seesaw neutrino mixing. arXiv:1508.03051 (2015). doi: 10.1007/JHEP10(2015)130
66. Abada A, Teixeira AM, Vicente A, Weiland C. Sterile neutrinos in leptonic and semileptonic decays. arXiv:1311.2830 (2014). doi: 10.1007/JHEP02(2014)091
67. Antusch S, Baumann JP, Fernandez-Martinez E. Non-standard neutrino interactions With matter from physics beyond the standard model. Nucl Phys B (2009) 810:369–388. doi: 10.1016/j.nuclphysb.2008.11.018
68. Antusch S, Fischer O. Non-unitarity of the leptonic mixing matrix: Present bounds and future sensitivities. arXiv:1407.6607 (2014). doi: 10.1007/JHEP10(2014)094
69. Blennow M, Coloma P, Fernandez-Martinez E, Hernandez-Garcia J, Lopez-Pavon J. Non-Unitarity, sterile neutrinos, and Non-Standard neutrino interactions. arXiv:1609.08637 (2017). doi: 10.1007/JHEP04(2017)153
70. Ma E, Pramudita A. Flavor changing effective neutral current couplings in the Weinberg-Salam Model. Phys Rev D (1980) 22:214.
71. Deppisch F, Valle JWF. Enhanced lepton flavor violation in the supersymmetric inverse seesaw model. Phys Rev D (2005) 72:036001. doi: 10.1103/PhysRevD.72.036001
72. Deppisch F, Kosmas TS, Valle JWF. Enhanced mu- - e- conversion in nuclei in the inverse seesaw model. Nucl Phys B (2006) 752:80. doi: 10.1016/j.nuclphysb.2006.06.032
73. Dinh DN, Ibarra A, Molinaro E, Petcov ST. The μ − e conversion in nuclei, μ → eγ, μ → 3e decays and TeV scale see-saw scenarios of neutrino mass generation. arXiv:1205.4671 (2012). doi: 10.1007/JHEP09(2013)023
74. Abada A, Krauss ME, Porod W, Staub F, Vicente A, Weiland C. Lepton flavor violation in low-scale seesaw models: SUSY and non-SUSY contributions. arXiv:1408.0138 (2014). doi: 10.1007/JHEP11(2014)048
75. Arganda E, Herrero MJ, Marcano X, Weiland C. Imprints of massive inverse seesaw model neutrinos in lepton flavor violating Higgs boson decays. Phys Rev D (2015) 91:015001. doi: 10.1103/PhysRevD.91.015001
76. Deppisch FF, Bhupal Dev PS, Pilaftsis A. Neutrinos and collider physics. N J Phys. (2015) 17:075019. doi: 10.1088/1367-2630/17/7/075019
77. Banerjee S, Dev PSB, Ibarra A, Mandal T, Mitra M. Prospects of heavy neutrino searches at future lepton colliders. Phys Rev D (2015) 92:075002. doi: 10.1103/PhysRevD.92.075002
78. Bhupal Dev PS, Franceschini R, Mohapatra RN. Bounds on TeV Seesaw models from LHC Higgs Data. Phys Rev D (2012) 86:093010. doi: 10.1103/PhysRevD.86.093010
79. Cely CG, Ibarra A, Molinaro E, Petcov ST. Higgs decays in the low scale type I See-Saw Model. Phys Lett B (2013) 718:957. doi: 10.1016/j.physletb.2012.11.026
80. Bandyopadhyay P, Chun EJ, Okada H, Park JC. Higgs signatures in inverse Seesaw Model at the LHC. arXiv:1209.4803 (2013). doi: 10.1007/JHEP01(2013)079
81. Illana JI, Riemann T. Charged lepton flavor violation from massive neutrinos in Z decays. Phys Rev D (2001) 63:053004. doi: 10.1103/PhysRevD.63.053004
82. Abada A, De Romeri V, Monteil S, Orloff J, Teixeira AM Indirect searches for sterile neutrinos at a high-luminosity Z-factory. arXiv:1412.6322 (2015). doi: 10.1007/JHEP04(2015)051
83. Abada A, Bečirević D, Lucente M, Sumensari O. Lepton flavor violating decays of vector quarkonia and of the Z Boson. Phys Rev D (2015) 91:113013. doi: 10.1103/PhysRevD.91.113013
84. De Romeri V, Herrero MJ, Marcano X, Scarcella F. Lepton flavor violating Z decays: a promising window to low scale seesaw neutrinos. Phys Rev D (2017) 95:075028. doi: 10.1103/PhysRevD.95.075028
85. Shrock RE. New tests for, and bounds on, neutrino masses and Lepton mixing. Phys Lett. (1980) 96B:159.
86. Shrock RE. General theory of weak leptonic and semileptonic decays. 1. Leptonic pseudoscalar meson decays, with associated tests for, and bounds on, neutrino masses and lepton mixing. Phys Rev D (1981) 24:1232. doi: 10.1103/PhysRevD.24.1232
87. Atre A, Han T, Pascoli S, Zhang B. The search for heavy majorana neutrinos. arXiv:0901.3589 (2009). doi: 10.1088/1126-6708/2009/05/030
88. Abada A, Das D, Teixeira AM, Vicente A, Weiland C. Tree-level lepton universality violation in the presence of sterile neutrinos: impact for RK and Rπ. arXiv:1211.3052 (2013). doi: 10.1007/JHEP02(2013)048
89. Abada A, De Romeri V, Lucente M, Teixeira AM, Toma T. Effective Majorana mass matrix from tau and pseudoscalar meson lepton number violating decays. arXiv:1712.03984 (2018). doi: 10.1007/JHEP02(2018)169
90. de Gouvea A, Gopalakrishna S. Low-energy neutrino Majorana phases and charged-lepton electric dipole moments. Phys Rev D (2005) 72:093008. doi: 10.1103/PhysRevD.72.093008
91. Deppisch FF, Hirsch M, Pas H. Neutrinoless double beta decay and physics beyond the standard model. J Phys G (2012) 39:124007. doi: 10.1088/0954-3899/39/12/124007
92. Blennow M, Fernandez-Martinez E, Lopez-Pavon J, Menendez J. Neutrinoless double beta decay in seesaw models. arXiv:1005.3240 (2010). doi: 10.1007/JHEP07(2010)096
93. Lello L, Boyanovsky D. Searching for sterile neutrinos from π and K decays. Phys Rev D (2013) 87:073017. doi: 10.1103/PhysRevD.87.073017
94. Lazzeroni C, Lurkin N, Newson F, Romano A, Ceccucci A, Danielsson H, et al. Search for heavy neutrinos in decays. Phys Lett B (2017) 772:712–8. doi: 10.1016/j.physletb.2017.07.055
95. Cortina Gil E, Minucci E, Padolski S, Petrov P, Velghe B, Kozhuharov V, et al. Search for heavy neutral lepton production in K+ decays. Phys Lett B (2018) 778:137–45. doi: 10.1016/j.physletb.2018.01.031
96. Kusenko A. Sterile neutrinos: the Dark side of the light fermions. Phys Rep. (2009) 481: 1–28. doi: 10.1016/j.physrep.2009.07.004
97. Smirnov AY, Zukanovich Funchal R. Sterile neutrinos: direct mixing effects versus induced mass matrix of active neutrinos. Phys Rev D (2006) 74:013001. doi: 10.1103/PhysRevD.74.013001
98. Gelmini G, Osoba E, Palomares-Ruiz S, Pascoli S. MeV sterile neutrinos in low reheating temperature cosmological scenarios. arXiv:0803.2735 (2008). doi: 10.1088/1475-7516/2008/10/029
99. Dasgupta B, Kopp J. A ménage à trois of eV-scale sterile neutrinos, cosmology, and structure formation. Phys Rev Lett (2014) 112:031803. doi: 10.1103/PhysRevLett.112.031803
100. Giunti C. Light sterile neutrinos: status and perspectives. Nucl Phys B (2016) 908:336–53. doi: 10.1016/j.nuclphysb.2016.01.013
101. Mohapatra RN, Valle JWF. Neutrino mass and baryon number nonconservation in superstring models. Phys Rev D (1986) 34:1642.
102. Barr SM. A different seesaw formula for neutrino masses. Phys Rev Lett. (2004) 92:101601. doi: 10.1103/PhysRevLett.92.101601
103. Malinsky M, Romao JC, Valle JWF. Novel supersymmetric SO(10) seesaw mechanism. Phys Rev Lett. (2005) 95:161801. doi: 10.1103/PhysRevLett.95.161801
104. Asaka T, Blanchet S, Shaposhnikov M. The nuMSM, dark matter and neutrino masses. Phys Lett B (2005) 631:151–6. doi: 10.1016/j.physletb.2005.09.070
105. Asaka T, Shaposhnikov M. The nuMSM, dark matter and baryon asymmetry of the universe. Phys Lett B (2005) 620:17–26. doi: 10.1016/j.physletb.2005.06.020
106. Shaposhnikov M. The nuMSM, leptonic asymmetries, and properties of singlet fermions. arXiv:0804.4542 (2008). doi: 10.1088/1126-6708/2008/08/008
107. Canetti L, Drewes M, Frossard T, Shaposhnikov M. Dark matter, baryogenesis and neutrino oscillations from right handed neutrinos. Phys Rev D (2013) 87:093006. doi: 10.1103/PhysRevD.87.093006
108. Abada A, Lucente M. Looking for the minimal inverse seesaw realisation. Nucl Phys B (2014) 885:651–678. doi: 10.1016/j.nuclphysb.2014.06.003
109. Cirigliano V, Kurylov A, Ramsey-Musolf MJ, Vogel P. Lepton flavor violation without supersymmetry. Phys Rev D (2004) 70:075007. doi: 10.1103/PhysRevD.70.075007
110. Das SP, Deppisch FF, Kittel O, Valle JWF. Heavy neutrinos and lepton flavour violation in left-right symmetric models at the LHC. Phys Rev D (2012) 86:055006. doi: 10.1103/PhysRevD.86.055006
111. Deppisch FF. Lepton flavour violation and flavour symmetries. Fortsch Phys. (2013) 61:622. doi: 10.1002/prop.201200126
112. Antusch S, Arganda E, Herrero MJ, Teixeira AM. Impact of theta(13) on lepton flavour violating processes within SUSY seesaw. JHEP (2006) 0611:90. doi: 10.1088/1126-6708/2006/11/090
Keywords: lepton-flavor violation, neutrino physics, beyond standard model physics, EDM, muon observables
Citation: Abada A and Teixeira AM (2018) Heavy Neutral Leptons and High-Intensity Observables. Front. Phys. 6:142. doi: 10.3389/fphy.2018.00142
Received: 12 September 2018; Accepted: 29 October 2018;
Published: 21 December 2018.
Edited by:
Yoshitaka Kuno, Osaka University, JapanReviewed by:
Hiroaki Sugiyama, Toyama Prefectural University, JapanMariam Tórtola, Instituto de Física Corpuscular (IFIC), Spain
Copyright © 2018 Abada and Teixeira. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ana M. Teixeira, YW5hLnRlaXhlaXJhQGNsZXJtb250LmluMnAzLmZy
 Asmaa Abada
Asmaa Abada Ana M. Teixeira
Ana M. Teixeira