Rare Third-Party Punishment Promotes Cooperation in Risk-Averse Social Learning Dynamics

1. Introduction

Cooperation is observed in various species, albeit it seems unfavorable in view of selfishness [1–3]. Among others, human cooperation is unique as they enforce themselves to cooperate by means of social norms and institutions: norm violators are punished by community members and thus cooperation is maintained [4–10]. In human cooperation, a punisher is often a third party who does not directly suffer from a norm violation. From the viewpoint of rationality, the third-party punisher has no incentive to vicariously punish the norm violator at a personal cost [7, 8]; therefore, third-party punishment is another dilemma of cooperation [6, 10–12]. Despite that, empirical studies suggest that third-party punishment is ubiquitous across humans [8, 13].

Numerous evolutionary models have been proposed to solve the dilemma of third-party punishment: group selection [14], reputation as a signal to induce the others' cooperation toward the punisher [15], social structure that localizes interactions [16, 17], conformist bias whereby a majority strategy is imitated in social learning [18], an option to opt-out of joint enterprize [12, 19], second-order punishment [20, 21], commitment to cooperation before playing a game [22], and implicated punishment in which members in the same group with a wrongdoer are also punished [23]. In all the models, punishment should be sufficiently frequent to maintain cooperation. On the other hand, laboratory studies found that participants frequently engaged in punishment did not success in comparison with those not eager for performing punishment, suggesting that punishing others too frequently is maladaptive [24, 25]. If so, how cooperation can be maintained with only occasional third-party punishment?

In this study, we propose an idea to promote cooperation even when third-party punishment is rare—risk aversion. An obvious psychological fact is that norm violation is a risky choice: it may provoke anger of community members that can lead to actual execution of punishment to the norm violator [26]. In fact, public executions were common in pre-modern societies, intended by rulers to cause fear to commit a norm violation. Moreover, experimental studies suggest that the mere threat of punishment can promote cooperation [27, 28].

To incorporate risk psychology with evolutionary game, we extend the canonical evolutionary game dynamics with a risk-sensitive utility function, which can describe risk-prone and risk-averse strategy selection. To summarize our results, risk aversion promotes cooperation with a little bit of third-party punishment.

2. Authoritative Third-Party Punishment

We first introduce a simple model of competition between cooperators and defectors in an infinite, well-mixed population, in which defectors are probabilistically punished by a third-party authority. From time to time, randomly sampled two individuals play a social dilemma game called the weak prisoner's dilemma game [29] in which players have two options: cooperation (C) and defection (D). Its payoff matrix is given by

$\begin{array}{cc}\begin{array}{l}\begin{array}{cc}\text{C}& \text{D}\end{array}\\ \begin{array}{c}\text{C}\\ \text{D}\end{array}\begin{array}{c}\left[\begin{array}{cc}1& 0\\ T& 0\end{array}\right]\end{array},\end{array}& (1)\end{array}$

where T > 1. In this game, mutual cooperation provides payoff 1 to both players, while they have temptation to enjoy one-sided defection as it provides better payoff T (> 1). However, each game is observed by an authoritative third-party punisher with probability z, and those who have selected defection are fined by an amount F (> 0). The population evolves according to replicator dynamics [30, 31].

2.1. Evolutionary Stability of Cooperators

Here, we consider evolutionary stability of a monomorphic population of cooperators against invasion by defectors. Our finding is that risk aversion of individuals lower the required frequency of observation to maintain cooperation; the authority's cost for punishment is significantly lower than the prediction by the risk-neutral theory.

The ordinary evolutionary game dynamics assume that players change strategies based on their expected payoffs. Let us consider our model on this line. In a monomorphic population of cooperators, the expected payoff of resident cooperators is 1—they mutually cooperate—and that of mutant defectors is T−zF—they enjoy one-sided defection but are punished with probability z. Therefore, the population of cooperators is evolutionarily stable against invasion by defectors, i.e., ESS, if 1> T − zF, i.e.,

$\begin{array}{cc}\begin{array}{r}z>\frac{T-1}{F}=:z_{\mathrm{\text{neutral}}}^{*}.\end{array}& (2)\end{array}$

The infimum of the required probability of observation, $z_{\mathrm{\text{neutral}}}^{*}$, is a power function of the amount of fine, F; i.e., $z_{\mathrm{\text{neutral}}}^{*}\propto F^{-1}$ (the dashed line in Figure 1). This implies that even if the authority imposes a heavy fine on defectors, for maintaining cooperation, the authority needs to punish defectors quite often; the cost to maintain cooperation should be considerable.

FIGURE 1

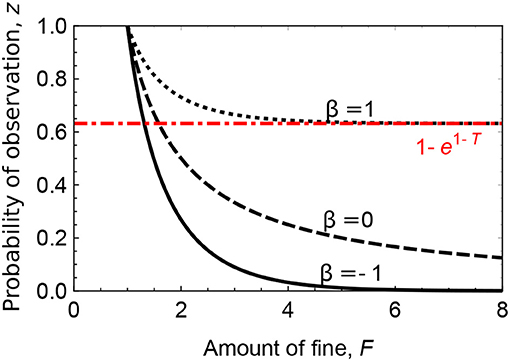
Figure 1. The infimum of the required probability of observation by an authority to maintain cooperation: individuals are risk newtral (dashed line; $z_{\mathrm{\text{neutral}}}^{*}$ where β = 0), risk averse (solid line; $z_{\mathrm{\text{biased}}}^{*}$ with β = −1), or risk prone (dotted line; $z_{\mathrm{\text{biased}}}^{*}$ with β = 1). The red dot-dashed line represents the asymptotic line to which $z_{\mathrm{\text{biased}}}^{*}$ with β = 1 converges. Parameters: T = 2.

We extend the ordinary theory by assuming that players change strategies according to their utility. Given that using strategy s results in a stochastic payoff represented by random variable R_s (the realization of R_s is $R_s^{(i)}$ with probability $p_s^{(i)}$ where i indicates each outcome), its utility is defined by

$\begin{array}{cc}\begin{array}{r}{u}_s=\frac{1}{\beta }log𝔼\left[{\text{e}}^{\beta R_s}\right],\end{array}& (3)\end{array}$

where $𝔼\left[{\text{e}}^{\beta R_s}\right]=\sum _i{p}_s^{(i)}{\text{e}}^{\beta R_s^{(i)}}$ represents the expected value of random variable ${\text{e}}^{\beta R_s}$. Equation (3) is a well-known exponential utility function developed by Pratt [32], Howard and Matheson [33], Coraluppi and Marcus [34] and Mihatsch and Neuneier [35]. It can be expanded to

$\begin{array}{cc}\begin{array}{r}𝔼\left[R_s\right]+\frac{\beta }{2}\text{Var}\left[R_s\right]+O({\beta }^2),\end{array}& (4)\end{array}$

where the first term is the expected value of the payoff and the second term is proportional to the variance of the payoff. Thus, if β = 0, the utility is equal to the expected value, implying risk-neutral utility; if β < 0, the utility is decreased by the second term, implying risk-averse utility with which an individual finds a strategy less preferable if it produces a highly variable payoff; and if β > 0, the utility is increased by the second term, implying risk-prone utility with which an individual finds a strategy more preferable if it produces a highly variable payoff.

In case of risk aversion or proneness (i.e., if β ≠ 0), the utility of being a cooperator and that of being a defector are, from Equation (3), given by

$\begin{array}{cc}\begin{array}{r}{u}_{\text{C}}=\frac{1}{\beta }log\left[1·{\text{e}}^{\beta ·1}\right]=1\end{array}& (\mathrm{5a})\end{array}$

and

$\begin{array}{cc}\begin{array}{r}{u}_{\text{D}}=\frac{1}{\beta }log\left[z{\text{e}}^{\beta (T-F)}+(1-z){\text{e}}^{\beta T}\right],\end{array}& (\mathrm{5b})\end{array}$

respectively. A straightforward calculation leads to the ESS condition corresponding to Equation (2): u_C > u_D, i.e.,

$\begin{array}{cc}\begin{array}{r}z>\frac{1-{\text{e}}^{-\beta (T-1)}}{1-{\text{e}}^{-\beta F}}=:z_{\mathrm{\text{biased}}}^{*}.\end{array}& (6)\end{array}$

Note that $\underset{\beta \to 0}{lim}{z}_{\mathrm{\text{biased}}}^{*}=z_{\mathrm{\text{neutral}}}^{*}$ holds true. If β < 0, its asymptotic form is an exponential function of F—i.e., $z_{\mathrm{\text{biased}}}^{*}\propto {\text{e}}^{\beta F}$—and it rapidly approaches 0 as F increases (the solid line in Figure 1). This implies that for maintaining cooperation among risk-averse individuals, the authority needs to punish defectors only occasionally. Compared to the ordinary theory, the cost to maintain cooperation should be significantly less expensive. If β > 0, $z_{\mathrm{\text{biased}}}^{*}$ approaches 1−e^−β(T−1) (> 0) as F increases; punishment needs to be most often (the dotted line in Figure 1).

2.2. Dimorphism of Cooperators and Defectors

If Equations (2) or (6) is violated, defectors invade the population of cooperators. After that, they may form a stable dimorphic population with cooperators. Here, we study the effect of risk attitude of individuals on such dimorphism. We find that risk aversion increases the frequency of cooperators. Moreover, we introduce three variants of punishment relevant in dimorphism: (a) to punish all defectors (most costly); (b) to punish one of them as a warning for others [less costly than variant (a)]; or (c) to punish only one-sided defectors (cheapest). We find that the first and second variants but the third achieve cooperative dimorphism. Surprisingly, the first variant can be the most cost-effective solution to maintain cooperation with a reasonably small probability of observation.

Unlike the case of monomorphism (Section 2.1) in which defection by a mutant is always toward a resident cooperator, mutual defection between two defectors is also likely in dimorphism. Consequently, a problem arises—how should the third-party authority treat mutual defection? Should the authority punish both defectors? This might be too costly. Punish only one of them as a warning for others to inhibit defection in the future? This is less costly but could be insufficient. As the two defectors obtain nothing in mutual defection, punish none of them? For this, we consider three variants that rule differently on mutual defection (Figure 2): (a) the authority punishes all defectors; (b) the authority punishes one of defectors selected at random; and (c) the authority punishes only a one-sided defector so that neither defectors are punished. Hereafter, we call them ALL, ONE, and ONE-SIDED variants, respectively.

FIGURE 2

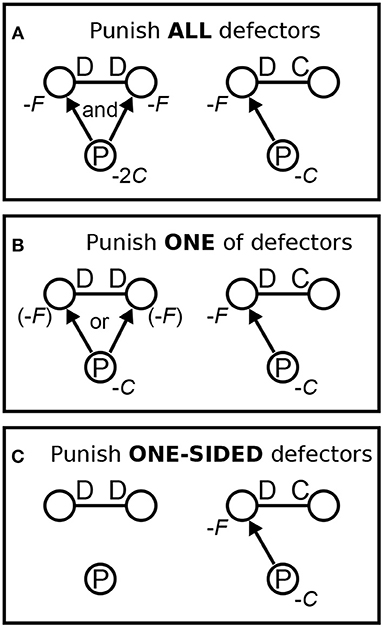
Figure 2. Three variants of third-party punishment. Blank circles represent players and those with “P” represent punishers as observers. Each line connecting blank circles, above which “D D” or “D C” is attached, represents mutual defection or one-sided defection in a game, respectively. Arrows represent that punishment is executed. (A) ALL defectors are punished: in case of mutual defection, the punisher pays cost 2C and each of the two defectors pays fine F. (B) Only ONE of defectors is punished: in case of mutual defection, the punisher pays cost C and one of the two defectors, selected at random, pays fine F. (C) Only a ONE-SIDED defector is punished: the punisher does not care about mutual defection. In all the three variants, the punisher pays cost C and the defector pays fine F in case of one-sided defection.

For each variant with different risk attitudes, we numerically find stable points of the replicator dynamics of cooperators and defectors, i.e.,

$\begin{array}{cc}\begin{array}{r}\dot{x}=x(1-x)\left[u_{\text{C}}-u_{\text{D}}\right],\end{array}& (7)\end{array}$

where x is the frequency of cooperators, u_C and u_D are the utility of being a cooperator (Equation A1) and that of being a defector (Equation A2). The ALL and ONE variants achieve stable dimorphism of cooperators and defectors (Figures 3A,B). In these variants, smaller β increases the stable frequency of cooperators more. As expected, the ALL variant achieve higher cooperation than the ONE variant. The ONE-SIDED variant does not achieve dimorphism because u_C > u_D with Equations (A1, A2c) are equivalent to Equation (6); a stable population in this variant consists of all defectors if the ESS condition (i.e., Equations 2 or 6) is violated.

FIGURE 3

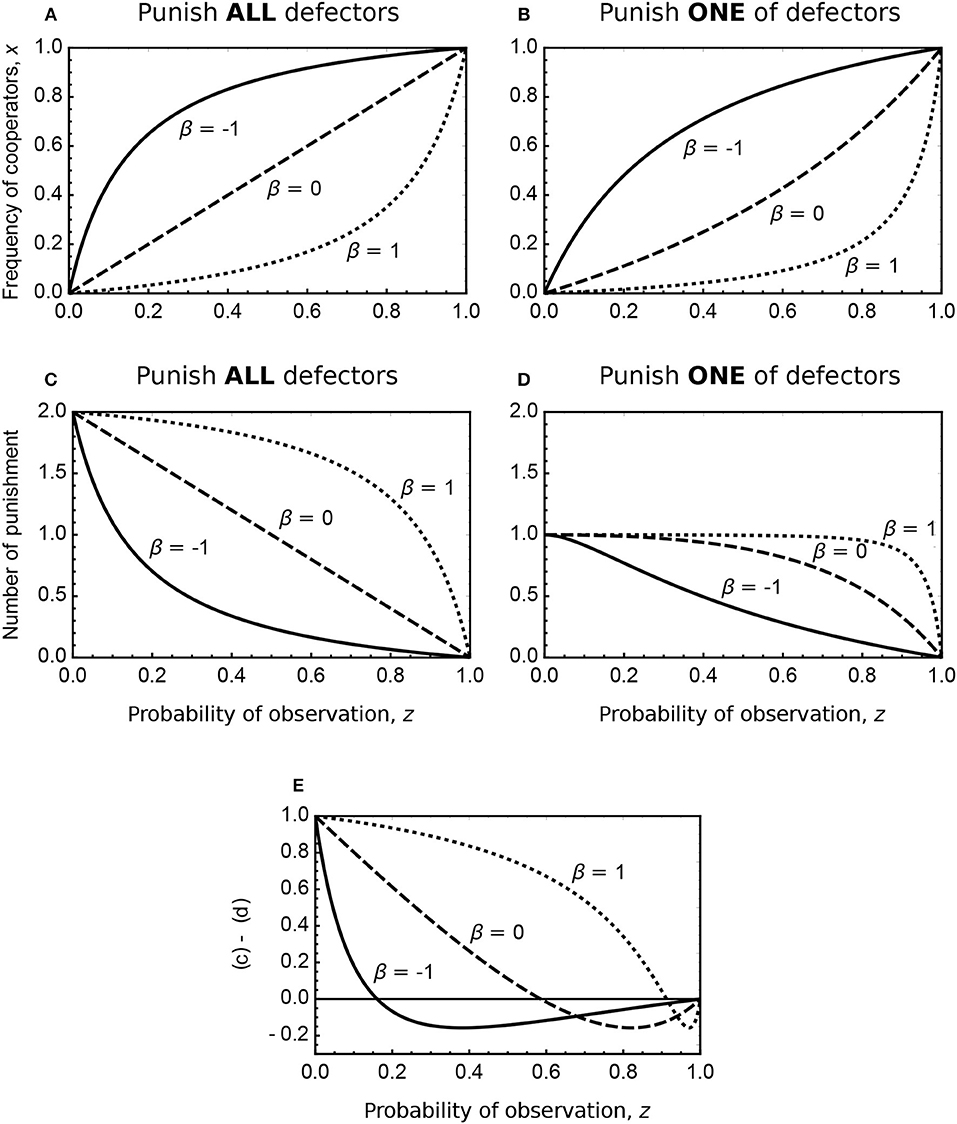
Figure 3. Stable frequency of cooperators (A,B) and the expected number of punishment per observation (C,D) in a dimorphic population of cooperators and defectors if Equations (2) or (6) is violated. (A,C) The ALL variant. (b, d) The ONE variant. (E) Shows the difference between (C,D). Individuals are risk newtral (dashed line; β = 0), risk averse (solid line; β = −1), or risk prone (dotted line; β = 1). Parameters: T = 2 and F = 1.

Although the ALL variant achieves higher cooperation than the ONE variant does, the authority might have to punish more defectors—thus pay higher cost—in the ALL variant than in the ONE variant. This concern is needless for risk-averse individuals with a sufficiently large—but reasonably small—probability of observation, z. Given that the stable frequency of cooperators is x*, the probability for the observing authority to find one-sided defection is 2x*(1−x*) and that to find mutual defection is (1−x*)². Thus, the expected number of punishment per observation in the ALL variant is 2x*(1−x*) × 1+(1−x*)²×2 = 2(1−x*) and that in the ONE variant is 2x*(1−x*) × 1+(1−x*)²×1 = 1−x*²—at first glance, the former looks larger than the latter. Since x* in the ALL variant is larger than that in the ONE variant (see Figures 3A,B), the effective number of punishment per observation in the ALL variant can be smaller than that in the ONE variant (Figures 3C,D plot them and Figure 3E shows their difference). If individuals are risk averse, a reasonably small z makes the ALL variant less expensive; i.e., the branching point at which the sign of the difference changes becomes smaller as β decreases (In Figure 3E, the branching point in case of β = −1 is located around z = 0.15).

3. Endogenous Third-Party Punishment

So far, we have assumed that the punisher is an exogenous authority that exists outside the population dynamics. Although this assumption seems reasonable for societies in which a mature institution for authoritative punishment exists, small-scale societies such as hunter-gatherers may require a different scenario. Our next question is what if without any leviathan. Our finding is that if individuals are risk averse, a few of endogenous third-party punishers—they evolve in the population dynamics—can maintain high cooperation.

Here, we consider another model of competition among cooperators, defectors, and endogenous third-party punishers. From time to time, randomly sampled three individuals participate in a situation: as well as section 2, two of them—selected at random—play the weak prisoner's dilemma game; the remaining one observes the game and can punish each defector at cost C (> 0). Again, those being punished pay fine F. Cooperators select C in a game and do nothing if being an observer; defectors select D in a game and do nothing if being an observer; and punishers select C in a game and perform punishment if being an observer (and observing defectors). The individuals change strategies according to replicator–mutator dynamics [36–38] based on their risk-sensitive utilities (Equation 3), given by

$\begin{array}{cc}\begin{array}{r}\dot{x}=x{f}_{\text{C}}(1-\mu )+y{f}_{\text{D}}\frac{\mu }{2}+z{f}_{\text{P}}\frac{\mu }{2}-x\langle f\rangle ,\end{array}& (\mathrm{8a})\end{array}$

$\begin{array}{cc}\begin{array}{r}\dot{y}=y{f}_{\text{D}}(1-\mu )+z{f}_{\text{P}}\frac{\mu }{2}+x{f}_{\text{C}}\frac{\mu }{2}-y\langle f\rangle ,\end{array}& (\mathrm{8b})\end{array}$

and

$\begin{array}{cc}\begin{array}{r}\dot{z}=z{f}_{\text{P}}(1-\mu )+x{f}_{\text{C}}\frac{\mu }{2}+y{f}_{\text{D}}\frac{\mu }{2}-z\langle f\rangle ,\end{array}& (\mathrm{8c})\end{array}$

where x, y, and z are frequencies of cooperators, defectors, and punishers,

$\begin{array}{cc}\begin{array}{r}\langle f\rangle =x{f}_{\text{C}}+y{f}_{\text{D}}+z{f}_{\text{P}}\end{array}& (9)\end{array}$

is the average fitness and

$\begin{array}{cc}\begin{array}{r}{f}_s=1-w+w{u}_s\end{array}& (10)\end{array}$

is the fitness of strategy s (= C, D, and P) where u_s is given by Equations (A3, A4). In Equation (8), μ is the probability with which an individual mutates his/her strategy to another by chance: one does not mutate his/her strategy s with probability 1−μ; otherwise, his/her strategy after mutation is one of the other strategies s′(≠ s) with probability μ/2, where 2 is the number of the other strategies. In Equation (10), w (0 ≤ w ≤ 1) is a parameter that controls intensity of selection; large (small) w implies strong (weak) selection.

As our main interest is not on their effects, we fix w = 0.1 and μ = 0.01 throughout Section 3. Our motivation to employ replicator–mutator dynamics here is (1) to avoid artificial neutral stability between cooperators and punishers when defectors are not present and (2) to incorporate more reality in the model—in social learning, humans often explore different strategies at random [39].

We numerically examine the replicator–mutator dynamics (Equation 8) for each variant with different risk attitudes. As a reference point, we choose a set of parameters (T = 2, C = 1, F = 3, w = 0.1, andμ = 0.01) with which defectors are frequent in a population of risk-neutral (i.e., β = 0) individuals (Figures 4G–I). Then, we check the effect of changing parameter β: with extreme risk aversion (β = −10), individuals achieve almost full cooperation (Figures 4A–C); on the other hand, with extreme risk proneness (β = 10), they reach almost full defection (Figures 4M–O). We can understand these two extreme cases by examining $\underset{\beta \to \pm \infty }{lim}{u}_s$ for s = C, D, and P (see Appendix B in Supplementary Material): because $\underset{\beta \to -\infty }{lim}{u}_{\text{C}}=0$, $\underset{\beta \to -\infty }{lim}{u}_{\text{D}}=-F$ (ALL and ONE variants) or T−F (ONE-SIDED variant), and $\underset{\beta \to -\infty }{lim}{u}_{\text{P}}=-2C$ (ALL variant) or −C (ONE and ONE-SIDED variants) in the interior of the state space (apply Equation B1a to Equations A3, A4), the utility of cooperators is the largest if individuals are extremely risk averse (and if T < F in the ONE-SIDED variant); similarly, because $\underset{\beta \to \infty }{lim}{u}_{\text{C}}=\underset{\beta \to \infty }{lim}{u}_{\text{P}}=1$ and $\underset{\beta \to \infty }{lim}{u}_{\text{D}}=T$ (apply Equation B1b to Equations A3, A4), the utility of defectors is the largest if individuals are extremely risk prone. With moderate risk aversion (β = −1) or risk proneness (β = 1), the outcomes are in-between (Figures 4D–F or Figures 4J–L, respectively). In case of risk aversion, a population of frequent cooperators and a few punishers establishes stable and high cooperation; as well as Section 2, the required frequency of observation—i.e., the frequency of punishers in this model—is small.

FIGURE 4

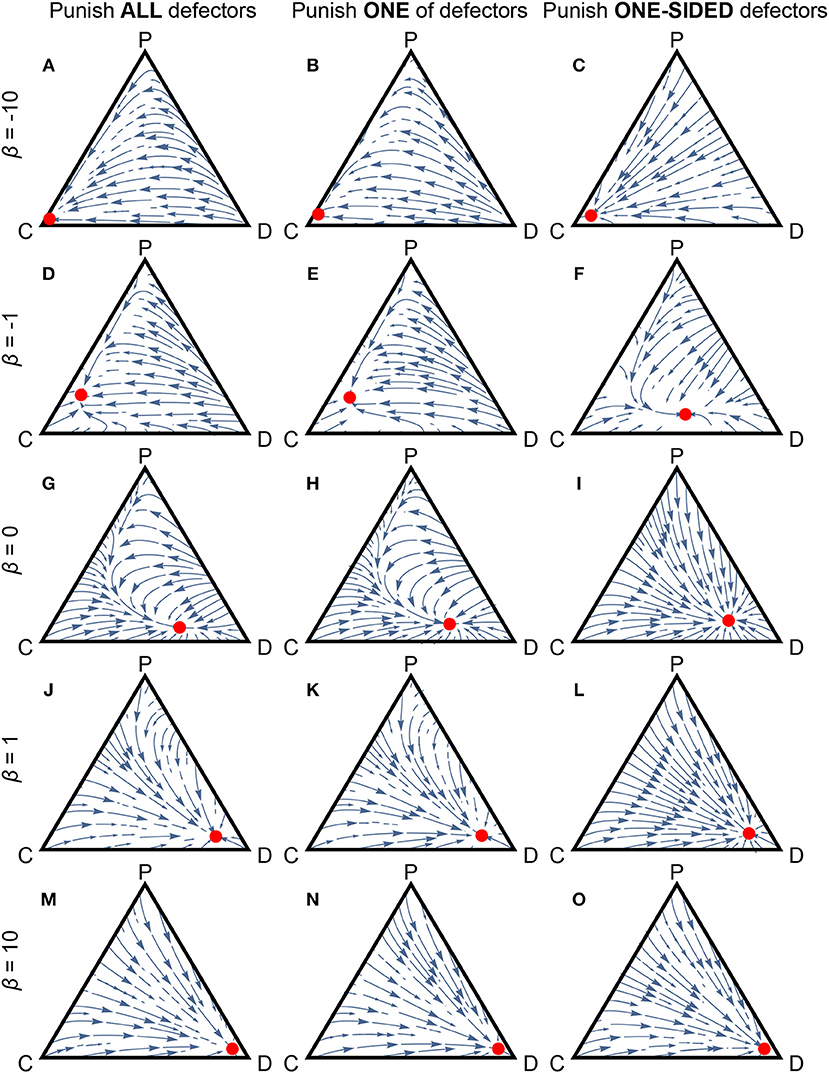
Figure 4. The replicator–mutator dynamics of cooperators (C), defectors (D), and third-party punishers (P). A population is full of one of them at the “C,” “D,” and “P” corners, respectively. Their frequencies are equal at each center of each simplex. Arrows represent trajectories starting from various initial states. Red points represent stable outcomes. (A,D,G,J,M) The ALL variant. (B,E,H,K,N) The ONE variant. (C,F,I,L,O) The ONE-SIDED variant. We set (A–C) β = −10. (D–F) β = −1. (G–I) β = 0. (J–L) β = 1. (M–O) β = 10. Parameters: T = 2, F = 3, C = 1, w = 0.1, and μ = 0.01.

FIGURE 5

Figure 5. The replicator–mutator dynamics of cooperators (C), defectors (D), and third-party punishers (P) if we assume the donation game. A population is full of one of them at the “C,” “D,” and “P” corners, respectively. Their frequencies are equal at each center of each simplex. Arrows represent trajectories starting from various initial states. Red points represent stable outcomes. (A,D,G) The ALL variant. (B,E,H) The ONE variant. (C,F,I) The ONE-SIDED variant. We set (A–C) β = −10. (D–F) β = −1. (G–I) β = 0. Parameters: c = 1, b = 2, F = 4, C = 1.5, w = 0.1, and μ = 0.01. Note that we omit the results if β>0 in which defectors win.

Comparing the three variants of punishment, the ALL and ONE variants promote cooperation more easily than the ONE-SIDED variant in the case of risk aversion (clearly observed in Figures 4D–F). This is because among the three variants, only the ONE-SIDED variant misses term e^−βF in the defector's utility (see Equations A4a, A4c, A4e). In the other two variants with sufficiently strong risk aversion, the largest term in the defector's utility is e^−βF, meaning that the defector's utility is most affected by the worst-case scenario that he/she obtains nothing from cheating but is punished. In the ONE-SIDED variant, the largest term in the defector's utility is e^β(T−F), meaning that the most dominating scenario in the utility is that the defector at least enjoys cheating but is punished. It is most difficult to promote cooperation in the ONE-SIDED variant because the defectors' worst-case scenario in this variant is milder than that in the ALL and ONE variants.

4. The Donation Game

Throughout the analyses, we have assumed that individuals play the weak prisoner's dilemma game (i.e., Equation 1). The so-called donation game, i.e., payoff matrix

$\begin{array}{cc}\begin{array}{l}\begin{array}{cc}\text{C}& \text{ D}\end{array}\\ \begin{array}{c}\text{C}\\ \text{D}\end{array}\begin{array}{c}\left[\begin{array}{cc}b-c& -c\\ b& 0\end{array}\right]\end{array},\end{array}& (11)\end{array}$

where b > c > 0, has been adopted in many studies [3, 16, 17, 24, 25]. For those interested in the difference between the two games, in Appendix C (Supplementary Material), we note the results if we assume the donation game instead of the weak prisoner's dilemma game.

The two games have similar results except for the case of authoritative third-party punishment in which observation by the authority is not sufficiently frequent to stabilize cooperation: in this case, only the weak prisoner's dilemma game with the ALL or ONE variant achieves dimorphism of cooperators and defectors (Section 2.2). This is technically because in the weak prisoner's dilemma game, one-sided cooperation (i.e., selecting C against an opponent's D) and mutual defection (i.e., selecting D against an opponent's D) have the same payoff. Consider a monomorphic population of defectors. We denote by S and P, respectively, the payoff if selecting C and the payoff if selecting D in the population. Assuming the authoritative third-party punishment of ALL or ONE variant, the utility of being a cooperator is S and that of being a defector is 1/βlog[z/ke^β(P−F)+(1−z/k)e^βP] where k = 1 in the ALL variant and k = 2 in the ONE variant. Thus, $u_{\text{C}}>u_{\text{D}}\iff z/k>(1-{\text{e}}^{\beta (S-P)})/(1-{\text{e}}^{-\beta F})$; in the case of the weak prisoner's dilemma game (i.e., if S = P), cooperators can invade the population of defectors if the authority watches individuals with any frequency (i.e., z>0); in the case of the donation game (i.e., if S−P = −c), cooperators can invade the population of defectors if $z>k{z}_{\mathrm{\text{DG}}}^{*}$ (see Equation C2).

5. Discussion

In this work, we have investigated the effect of risk attitude on social learning dynamics of third-party punishment. We studied two models: in the first model, the third-party punisher is an external authority that stands outside the competition of individuals; in the second model, those individuals endogenously perform third-party punishment so that the third-party punishers compete against non-punishers. In both models, risk-averse individuals achieved higher cooperation with a significantly lower frequency of punishment than risk-neutral or risk-prone individuals. In the first model, this means that a strong leviathan who constantly watches people and severely punishes norm violators is not needed; in the second model, it implies that not everyone needs to be an enforcer.

We also examined the effects of three variants of third-party punishment, ALL, ONE, and ONE-SIDED variants, on the social learning dynamics. In the ALL variant, all defectors are punished; in the ONE variant, only one of defectors is punished as a warning to others; and in the ONE-SIDED variant, only who actually enjoyed cheating against a cooperator is punished. We found that since the worst-case payoff of defectors in the ONE-SIDED variant is milder than that in the other two variants, it is most difficult to promote cooperation in the ONE-SIDED variant: even if cheating is toward a cheater, it should be punished for maintaining cooperation. We also found that in the case of authoritative punishment, the ALL variant can be more efficient than the ONE variant with a reasonably small frequency of observation: punishment as a warning for others is efficient only if the authority can watch people really rarely.

Risk aversion has been directly or indirectly observed in laboratory experiments of social dilemma games with punishment opportunity [27, 28, 40]. Yamagishi [27] reported that in his study, the mere existence of punishment was sufficient to promote cooperation in early trials of the social dilemma experiments. The participants might not sufficiently realize the reward structure in their early trials, so that uncertainty of punishment would increase participants' cooperation. This is in line with the present study predicting that risk aversion promotes cooperation under the existence of punishment. Qin and Wang studied the effect of probabilistic punishment. In their study, they observed an inverted U-shaped relationship between the probability of punishment and the level of cooperation, suggesting that the participants' utility function was risk averse [40]. Moreover, children seem to be risk averse under the threat of punishment [28].

A number of experimental studies reported that punishing just one, the worst contributor in a game, was enough to maintain cooperation [27, 40–44]. These observations are consistent with the present study in which the ONE variant as well as the ALL variant is effective to promote cooperation in risk averse individuals. Comparing the two variants, punishing one and punishing all, Andreoni and Gee [41] and Kamijo et al. [42] suggested that punishing one is a more efficient solution to promote cooperation. In the present study, however, the ONE variant was more effective than the ALL variant only when the frequency of watching by authority was rare. Because in their studies the amount of fine if being punished was variable depending on the amount of contribution, their study and ours are not directly comparable. More investigations to clarify this point would be required.

Finally, we mention some concerns about the assumptions in our model. One is the assumption that the risk attitude of individuals is homogenous so that they have an identical utility function of stochastic payoffs. In reality, however, people have a variety of personality and they have heterogenous attitudes toward risk [45, 46]. Risk takers might tend to be norm violators or punishers, while cautious people might tend to be non-punishing cooperators who avoid risky things. It should be interesting to incorporate such a correlation between risk attitudes and strategies into an extended model. Another concern is the assumption that the risk attitude of individuals is constant over time whereas their strategies evolve. It could be justified by thinking about the importance of risk aversion in evolutionary history. In fact, risk aversion is widely observed among animals [47], implying that it is a crucial concern across species. Risk aversion could be stressed under far stronger selection pressure than the punishment norms.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Funding

Funding This work was supported in part by Monbukagakusho grant 16H06412 to Joe Yuichiro Wakano.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We would like to thank the reviewers for their constructive comments to improve the manuscript.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2018.00156/full#supplementary-material

References

1. West SA, Griffin AS, Gardner A. Evolutionary explanations for cooperation. Curr Biol. (2007) 17:R661–72. doi: 10.1016/j.cub.2007.06.004

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Clutton-Brock T. Cooperation between non-kin in animal societies. Nature (2009) 462:51–7. doi: 10.1038/nature08366

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Rand DG, Nowak MA. Human cooperation. Trends Cogn Sci. (2013) 17:413–25. doi: 10.1016/j.tics.2013.06.003

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Axelrod R. An evolutionary approach to norms. Am Polit Sci Rev. (1986) 80:1095–111. doi: 10.2307/1960858

CrossRef Full Text | Google Scholar

5. Ostrom E. Governing the Commons: The Evolution of Institutions for Collective Action. New York, NY: Cambridge University Press (1990).

Google Scholar

6. Boyd R, Richerson P. Punishment allows the evolution of cooperation (or anything else) in sizable groups. Ethol Sociobiol. (1992) 13:171–95. doi: 10.1016/0162-3095(92)90032-Y

CrossRef Full Text | Google Scholar

7. Fehr E, Fischbacher U. Social norms and human cooperation. Trends Cogn Sci. (2004) 8:185–90. doi: 10.1016/j.tics.2004.02.007

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Fehr E, Fischbacher U. Third-party punishment and social norms. Evol Hum Behav. (2004) 25:63–87. doi: 10.1016/S1090-5138(04)00005-4

CrossRef Full Text | Google Scholar

9. Gürerk Ö, Irlenbusch B, Rockenbach B. The competitive advantage of sanctioning institutions. Science (2006) 312:108–11. doi: 10.1126/science.1123633

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Sigmund K. Punish or perish? Retaliation and collaboration among humans. Trends Ecol Evol. (2007) 22:593–600. doi: 10.1016/j.tree.2007.06.012

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Colman AM. The puzzle of cooperation. Nature (2006) 440:744–5. doi: 10.1038/440744b

CrossRef Full Text | Google Scholar

12. Hauert C, Traulsen A, Brandt H, Nowak MA, Sigmund K. Via freedom to coercion: the emergence of costly punishment. Science (2007) 316:1905–7. doi: 10.1126/science.1141588

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Henrich J, Richard M, Barr A, Ensminger J, Barrett C, Bolyanatz A, et al. Costly punishment across human societies. Science (2006) 312:1767–70. doi: 10.1126/science.1127333

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Boyd R, Gintis H, Bowles S. The evolution of altruistic punishment. Proc Natl Acad Sci USA. (2003) 100:3531–5. doi: 10.1073/pnas.0630443100

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Brandt H, Hauert C, Sigmund K. Punishment and reputation in spatial public goods games. Proc R Soc B. (2003) 270:1099–104. doi: 10.1098/rspb.2003.2336

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Nakamaru M, Iwasa Y. The evolution of altruism by costly punishment in lattice-structured populations: score-dependent viability versus score-dependent fertility. Evol Ecol Res. (2005) 7:853–70. Available online at: http://www.evolutionary-ecology.com/abstracts/v07/1864.html

Google Scholar

17. Roos P, Gelfand M, Nau D, Carr R. High strength-of-ties and low mobility enable the evolution of third-party punishment. Proc R Soc B. (2014) 281:20132661. doi: 10.1098/rspb.2013.2661

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Henrich J, Boyd R. Why people punish defectors. Weak conformist transmission can stabilize costly enforcement of norms in cooperative dilemmas. J Theor Biol. (2001) 208:79–89. doi: 10.1006/jtbi.2000.2202

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Sasaki T, Brännström Å, Dieckmann U, Sigmund K. The take-it-or-leave-it option allows small penalties to overcome social dilemmas. Proc Natl Acad Sci USA. (2012) 109:1165–9. doi: 10.1073/pnas.1115219109

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Sigmund K, Silva H, Traulsen A, Hauert C. Social learning promotes institutions for governing the commons. Nature. (2010) 466:861–3. doi: 10.1038/nature09203

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Hilbe C, Traulsen A, Röhl T, Milinski M. Democratic decisions establish stable authorities that overcome the paradox of second-order punishment. Proc Natl Acad Sci USA. (2014) 111:752–6. doi: 10.1073/pnas.1315273111

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Sasaki T, Okada I, Uchida S, Chen X. Commitment to cooperation and peer punishment: its evolution. Games (2015) 6:574–87. doi: 10.3390/g6040574

CrossRef Full Text | Google Scholar

23. Chen X, Sasaki T, Perc M. Evolution of public cooperation in a monitored society with implicated punishment and within-group enforcement. Sci Rep. (2015) 5:17050. doi: 10.1038/srep17050

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Dreber A, Rand DG, Fudenberg D, Nowak MA. Winners don't punish. Nature (2008) 452:348–52. doi: 10.1038/nature06723

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Wu JJ, Zhang BY, Zhou ZX, He QQ, Zheng XD, Cressman R, et al. Costly punishment does not always increase cooperation. Proc Natl Acad Sci USA. (2009) 106:17448–51. doi: 10.1073/pnas.0905918106

CrossRef Full Text | Google Scholar

26. Berthoz S, Armony J, Blair R, Dolan R. An fMRI study of intentional and unintentional (embarrassing) violations of social norms. Brain (2002) 125:1696–708. doi: 10.1093/brain/awf190

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Yamagishi T. The provision of a sanctioning system as a public good. J Pers Soc Psychol. (1986) 51:110–16. doi: 10.1037/0022-3514.51.1.110

CrossRef Full Text | Google Scholar

28. Lergetporer P, Angerer S, Glätzle-Rützler D, Sutter M. Third-party punishment increases cooperation in children through (misaligned) expectations and conditional cooperation. Proc Natl Acad Sci USA. (2014) 111:6916–21. doi: 10.1073/pnas.1320451111

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Rapoport A. Experiments with N-person social traps I: prisoner's dilemma, weak prisoner's dilemma, volunteer's dilemma, and largest number. J Conf Resol. (1988) 32:457–72. doi: 10.1177/0022002788032003003

CrossRef Full Text | Google Scholar

30. Hofbauer J, Sigmund K. Evolutionary Games and Population Dynamics. Cambridge : Cambridge University Press (1998).

Google Scholar

31. Taylor PD, Jonker LB. Evolutionary stable strategies and game dynamics. Math Biosci. (1978) 40:145–56. doi: 10.1016/0025-5564(78)90077-9

CrossRef Full Text | Google Scholar

32. Pratt JW. Risk aversion in the small and in the large. Econometrica. (1964) 32:122–36. doi: 10.2307/1913738

CrossRef Full Text | Google Scholar

33. Howard RA, Matheson JE. Risk sensitive Markov decision processes. Manag Sci. (1972) 18:356–69. doi: 10.1287/mnsc.18.7.356

CrossRef Full Text | Google Scholar

34. Coraluppi SP, Marcus SI. Risk-sensitive, minimax, and mixed risk-neutral/minimax control of Markov decision processes. In: McEneaney WM, Yin GG, Zhang Q, editors. Stochastic Analysis, Control, Optimization and Applications. Boston, MA: Birkhäuser (1999). p. 21–40.

Google Scholar

35. Mihatsch O, Neuneier R. Risk-sensitive reinforcement learning. Mach Learn. (2002) 49:267–90. doi: 10.1023/A:1017940631555

CrossRef Full Text | Google Scholar

36. Page K, Nowak MA. Unifying evolutionary dynamics. J Theor Biol. (2002) 219:93–8. doi: 10.1016/S0022-5193(02)93112-7

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Hadeler KP. Stable polymorphisms in a selection model with mutation. SIAM J Appl Math. (1981) 41:1–7. doi: 10.1137/0141001

CrossRef Full Text | Google Scholar

38. Bomze IM, Burger R. Stability by mutation in evolutionary games. Games Econ Behav. (1995) 11:146–72. doi: 10.1006/game.1995.1047

CrossRef Full Text | Google Scholar

39. Traulsen A, Semmann D, Sommerfeld RD, Krambeck HJ, Milinski M. Human strategy updating in evolutionary games. Proc Natl Acad Sci USA. (2010) 107:2962–6. doi: 10.1073/pnas.0912515107

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Qin X, Wang S. Using an exogenous mechanism to examine efficient probabilistic punishment. J Econ Psychol. (2013) 39:1–10. doi: 10.1016/j.joep.2013.07.002

CrossRef Full Text | Google Scholar

41. Andreoni J, Gee LK. Gun for hire: delegated enforcement and peer punishment in public goods provision. J Pub Econ. (2012) 96:1036–46. doi: 10.1016/j.jpubeco.2012.08.003

CrossRef Full Text | Google Scholar

42. Kamijo Y, Nihonsugi T, Takeuchi A, Funaki Y. Sustaining cooperation in social dilemmas: comparison of centralized punishment institutions. Games Econ Behav. (2014) 84:180–95. doi: 10.1016/j.geb.2014.01.002

CrossRef Full Text | Google Scholar

43. Wu JJ, Li C, Zhang BY, Cressman R, Tao Y. The role of institutional incentives and the exemplar in promoting cooperation. Sci Rep. (2014) 4:6421. doi: 10.1038/srep06421

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Dong Y, Zhang B, Tao Y. The dynamics of human behavior in the public goods game with institutional incentives. Sci Rep. (2016) 6:28809. doi: 10.1038/srep28809

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Filbeck G, Hatfield P, Horvath P. Risk aversion and personality type. J Behav Fin. (2005) 6:170–80. doi: 10.1207/s15427579jpfm0604_1

CrossRef Full Text | Google Scholar

46. Tom SM, Fox CR, Trepel C, Poldrack RA. The neural basis of loss aversion in decision-making under risk. Science (2007) 315:515–8. doi: 10.1126/science.1134239

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Hintze A, Olson RS, Adami C, Hertwig R. Risk sensitivity as an evolutionary adaptation. Sci Rep. (2015) 5:8242. doi: 10.1038/srep08242

PubMed Abstract | CrossRef Full Text | Google Scholar