- 1Department Biologie, Friedrich-Alexander-Universität Erlangen-Nürnberg, Erlangen, Germany
- 2Max-Planck-Zentrum für Physik und Medizin, Erlangen, Germany
- 3Institut für Physik und Astronomie, Universität Potsdam, Potsdam, Germany
In nature as well as in the context of infection and medical applications, bacteria often have to move in highly complex environments such as soil or tissues. Previous studies have shown that bacteria strongly interact with their surroundings and are often guided by confinements. Here, we investigate theoretically how the dispersal of swimming bacteria can be augmented by microfluidic environments and validate our theoretical predictions experimentally. We consider a system of bacteria performing the prototypical run-and-tumble motion inside a labyrinth with square lattice geometry. Narrow channels between the square obstacles limit the possibility of bacteria to reorient during tumbling events to an area where channels cross. Thus, by varying the geometry of the lattice it might be possible to control the dispersal of cells. We present a theoretical model quantifying diffusive spreading of a run-and-tumble random walker in a square lattice. Numerical simulations validate our theoretical predictions for the dependence of the diffusion coefficient on the lattice geometry. We show that bacteria moving in square labyrinths exhibit enhanced dispersal as compared to unconfined cells. Importantly, confinement significantly extends the duration of the phase with strongly non-Gaussian diffusion, when the geometry of channels is imprinted in the density profiles of spreading cells. Finally, in good agreement with our theoretical findings, we observe the predicted behaviors in experiments with E. coli bacteria swimming in a square lattice labyrinth created in a microfluidic device. Altogether, our comprehensive understanding of bacterial dispersal in a simple two-dimensional labyrinth makes the first step toward the analysis of more complex geometries relevant for real world applications.
1. Introduction
Bacteria are ubiquitous on our planet. They inhabit diverse environments such as soil, oceans, hot springs and the human body, where they may cause infections or serve to establish a natural flora [1]. Being adapted to such a broad spectrum of habitats, bacteria show different forms of locomotion, depending on their specific needs [2, 3]. The motility apparatus and patterns of many different bacterial species have been described and extensively analyzed [4–6]. This experimental work has also been accompanied by theoretical efforts abstracting the motion of cells to random walks or modeling it as diffusion of active particles [7–9]. A significant number of studies exists on how bacteria move, by which mechanic and hydrodynamic forces the motility is driven and what the underlying molecular mechanisms are [10–12]. However, the motion of bacteria is strongly influenced by their surroundings, which often spatially restrict their spreading in natural habitats. Therefore, the behavior of bacteria in confinement has also been investigated [13], for example bacteria moving through narrow channels [14–18] or porous media [19, 20]. For active particles moving in channel confinements [21] or obstacle lattices [22, 23] theoretical models also exist. In specific confinements, these studies reported more persistent motion of bacteria and thus an enhanced diffusion [23].
Studying bacterial behaviors in narrow channels or complex labyrinths is of great medicinal relevance. It can help to better understand the spreading of bacteria during infection, where cells have to move inside of the body through natural constrictions with narrow spacing like blood vessels or the extracellular matrix [24]. On the other hand, it can also help in the design and evaluation of new therapeutic methods like targeted treatment of cancer by genetically modified bacteria, which are used to transport the drugs to the tumor or synthesize the drug on-site [25, 26].
In general, dispersal of bacteria in a complex environment is a result of an intricate interplay of confinement geometry and cell motility pattern. Here, we study the diffusive spreading of swimming bacteria with the well-known run-and-tumble pattern in a square labyrinth. This is probably the simplest possible geometry, which allows for analytical treatment and at the same time provides interesting and nontrivial results. Results obtained from this simplified model will complement the existing literature by offering possible reasoning for previously reported properties of bacterial motion in confinement. Constituting the first step in understanding the spreading of bacteria in complex environments, these results can be applied to problems in various areas dealing with directed transport of bacteria. Microbial enhanced oil recovery, for example, relies on the ability of bacteria to penetrate porous media. To optimize the recovery process, the spreading of the bacteria through the corresponding environment has to be optimal [27, 28]. Also, in ecological sciences, more precisely in the process of bioremediation by bioaugmentation, bacteria have to pass through complex environments to remove organic contaminants from soil and ground water [29]. In medicine, furthermore, quantifying the spreading of bacteria inside the human body—a complex network of tissue as well as lymphatic and blood vessels—helps to better understand the spreading of infections [24] and also to develop new therapies [30], as for example the targeted treatment of cancer [26].
Bacteria performing run-and-tumble motion alternate phases of almost straight swimming with tumbling events, when the cell turns and reorients its swimming direction [31]. On a macroscopic scale, that leads to a random walk like behavior and diffusive spreading of cells. By putting cells in a labyrinth, we anticipate that the reorientation process may be hindered when bacteria are in the channels between the obstacles [32]. However, in the crossings, there is more room available to tumble and cells may choose a new random direction. This provides a mechanism of how the labyrinth can rectify the diffusion of bacteria, which we aim to investigate in this paper. Using theoretical estimates, simulations and experimental data, we are able to show that bacteria disperse faster inside the labyrinth than in a spatially unrestricted environment. For the spreading inside the labyrinth, the diffusion coefficient depends in a nontrivial way on the parameters of the underlying lattice structure. For small times, the bacteria show a pronounced ballistic-like, non-Gaussian dispersal. In this regime, which lasts longer than for unrestricted motion, the bacterial density keeps memory of the underlying lattice geometry. At larger times, the memory of the geometry is lost and the density of bacteria attains an isotropic Gaussian profile. Thus, the underlying geometry of the labyrinth can greatly influence the dispersal of the bacteria on experimentally relevant time scales.
The paper is organized as follows. We start by describing our model system of E. coli bacteria swimming in a labyrinth. We then introduce a theoretical model and derive the estimates for the diffusion coefficient in a labyrinth with square lattice geometry (for a detailed derivation please refer to the Supplementary Material). After validating the theoretical predictions by numerical simulations we compare our results with experimental data on E. coli swimming in microfluidic labyrinths.
2. Model Setup
2.1. Swimming Bacteria in a Labyrinth
In this work, we consider E. coli bacteria as a well studied model organism but also as a widely used model in synthetic biology and thus in applications, for example, for the on-site synthesis of anti-cancer drugs. E. coli swim in a fluid environment by means of flagella and perform the well known run-and-tumble motion. This motion consists of periods of almost straight runs, interrupted by tumbles. The times between consecutive tumbling events follow an exponential distribution [7]. During the runs, multiple flagella, rotating in the same direction, are arranged as a bundle and push the cell forward. If at least one flagellum starts to rotate in the opposite direction and dissociates from the bundle, the run is shortly interrupted and the tumbling bacterium chooses a new random direction for the next run [31, 33]. Since the flagella have the length of several cell-bodies [33], the bacterium needs enough space to enable the dissociation and rearrangement of the flagellar bundle as well as the cell reorientation. Thus, in a lattice structure with sufficiently narrow channels, the bacteria may not be able to change their direction during the tumble, but continue to swim forward [32, 34]. This behavior is illustrated in Figure 1. The lattice is defined by the parameters b, w and h, being the side length of the square obstacles, the width of the channels between two obstacles and the height of the channels, respectively. By using a sufficiently small channel width w and height h, we can potentially forbid tumble events with a change of the swimming direction inside of the channels between the obstacles and reduce the effective spreading of the bacteria to two dimensions of the x/y-plane. Thus, in theoretical considerations and simulations, we disregard the z-direction. In the model, bacteria move inside of a square lattice defined by b and w, in which they are only able to change their moving direction in the crossings of two channels. If a tumbling event happens in a crossing, the bacteria can turn right, left, backward or continue their path forward.
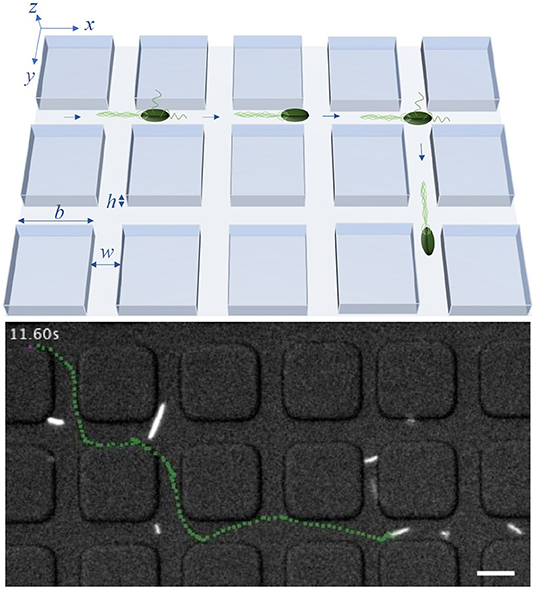
Figure 1. Model system: An illustration of the bacterial motility pattern within a lattice with channel width w, height h and side length of obstacles b (upper row) and a trajectory, marked in green, of a tracked bacterium inside a labyrinth with b = 20 μm and w = 8 μm (lower row). The scale bar in the lower row corresponds to 10 μm. In experiments, w and h are equal, restricting the effective spreading of bacteria to two dimensions. Times between consecutive tumble events follow an exponential distribution with mean τ0. In the model, tumbling events may lead to directional change only within crossings of two channels separating the squares.
2.2. Run-and-Tumble Pattern
Generally, when modeling the run-and-tumble motion, the bacteria are assumed to move in straight lines with constant velocity v0 during runs. Here, we will neglect rotational diffusion as the channel confinement naturally limits its effect (see, however, section 5). During tumbling events, the bacterium changes its direction by turning at a random angle with respect to its prior running direction. Usually, the bacteria turn left or right with equal probability and thus, the turning angle distribution considers only angles between 0° and 180° [7]. In the simplest case, the turning angle distribution is considered to be uniform. The free-swimming E. coli bacteria, however, have a tendency toward smaller turning angles ϕ, with an average ϕ0 ≈ 70° [35], resulting in a more persistent motion. The time between consecutive tumbling events is random and well approximated by an exponential distribution with the mean τ0 ≈ 1 s [36]. The duration of tumbles is one order of magnitude shorter than that of runs [35] and is usually neglected in the modeling. The run-and-tumble motion for large times, due to the exponential distribution of run times, is a memoryless random walk. Therefore, on time scales much larger than the mean run time, the mean squared displacement (MSD) of an ensemble of swimming bacteria is linearly proportional to time and can be quantified by the diffusion coefficient D. In the diffusive regime of the dispersal, the MSD 〈r(t)2〉 in two dimensions can be written as [7]
Here, 〈r2〉 is the mean squared run length and 〈τ〉 is the mean run time. As runs happen with constant velocity v0 (for freely swimming E. coli v0 ≈ 20 μm s−1), we have . Thus, the diffusion coefficient depends on the first and the second moment of the run time distribution. For the unconstrained but two-dimensional run-and-tumble motion, bacteria are assumed to move freely without spatial restrictions. If they also show no bias in the choice of the turning angle during a reorientation event, we have 〈τ〉 = τ0 and , due to the exponential distribution of run times with mean τ0. Thus, the diffusion coefficient D0 for this case becomes
When generalizing this result to the run-and-tumble motion of E. coli, the directional persistence exhibited by the bacterium has to be taken into account. This persistence can be incorporated by rescaling the average run time with the factor (see [37] and Supplementary Material for details) resulting in
Thus, the diffusion coefficient De for the dispersal of E. coli in two dimensions is
which for the above mentioned parameters results in De ≈ 300 μm2s−1. Moreover, an analytical description of the MSD, valid also for small times, can be calculated in this general case by using the Green-Kubo relation [37, 38] yielding
This result describes ballistic-like dispersal of cells for times comparable to and diffusive motion at larger times.
3. Theoretical Estimates of Diffusion Properties
3.1. Run-and-Tumble in a Lattice With Uniform Turning Angle Distribution
We now consider the movement of run-and-tumbling bacteria in a labyrinth with square lattice geometry– the two-dimensional equivalent of the system illustrated in Figure 1. Here, we assume the width of the channel between two obstacles w to be small enough to inhibit reorientation events in the channels. Therefore, the bacteria can only change their swimming direction inside of the crossings. Since bacteria swimming without spatial confinement exhibit run times following an exponential distribution with mean τ0, we can calculate the probability to tumble inside of a crossing of width w, Pw, as:
Correspondingly, the probability of not tumbling in the crossing is 1 − Pw. Thus, the probability of the first tumble to occur in the k-th crossing is given by the product of the probability not to tumble in the first k − 1 crossings and the probability to tumble in the k-th:
In the model, we assume that in each crossing only one tumbling event can occur (see below). As for the unrestricted case, we still expect the dispersal to become a diffusive process after multiple reorientation events. However, this now takes much longer time, as reorientations are only possible in the crossings.
We first consider the tumbling process with uniform turning angle distribution, where all four possible directions (forward, right, backward and left) are equally probable after a tumbling event in a crossing. To determine the diffusion coefficient D, as defined in Equation (1), the first two moments of the run time distribution have to be calculated. Since the bacteria are only able to perform reorientation events inside of the crossings and not in the channels connecting them, the relation 〈τ〉 = τ0 of the unrestricted case does not hold anymore. Assuming the bacteria to start in the middle of one crossing at t = 0 and tumbling events to occur on average also in the middle of crossings, the run times now have to be multiples of the time needed to travel from the center of one crossing to the next, , with lattice parameters b and w. Thus, the moments of the run time can be calculated as
Plugging the above expressions into Equation (1) the diffusion coefficient Dl in the labyrinth becomes
Comparing the diffusion coefficient of the spatially unrestricted walk, given in Equation (2), to our estimate of the walk inside the labyrinth in Equation (5), we see that the ratio
depends on the lattice and motility parameters. The ratio becomes larger for smaller channel width w and bigger side length of the obstacles b. This behavior is also emphasized in the approximation of the ratio for small channel widths w with w ≪ v0τ0, where . Thus, in the model, for relevant lattice and motility parameters, we get a higher diffusion coefficient in the labyrinth and consequently faster spreading.
3.2. Run-and-Tumble in a Lattice With Nonuniform Turning Angle Distribution
To consider bacteria exhibiting a nonuniform distribution of turning angles after a tumbling event, the diffusion coefficient has to be modified to include a term accounting for the nonuniformity, similarly to what was done in Equation (3) for the spatially unrestricted walk. For the motion inside the labyrinth, this can be performed as follows. By considering the walk as steps from one crossing to the next, the mean run time 〈τ〉 becomes
and . To account for the nonuniform turning angle distribution, we introduce an additional factor B to the formula of the diffusion coefficient. In the square labyrinth, the bacterium can only go in four different directions (forward, right, backward and left), therefore this factor will depend on the four corresponding probabilities pf, pr, pb and pl, determined by the turning angle distribution. The probability to go forward after a tumbling event pf, for example, will be the probability that a bacterium swimming outside the labyrinth turns in an angle between 0° and 45° after a tumble. However, as we defined the run time in a crossing-oriented way, to calculate the factor B, we need to consider the bacterial behavior in each crossing, not only in the crossings in which a tumbling event happens. Given the probabilities pf, pr, pb and pl after a tumbling event and the exponentially distributed run time, the corresponding turning probabilities defined for every passed crossing are
Assuming the probability to go right and left to be the same, as done by considering only angles between 0° and 180°, we find B to depend only on and as
With this, the diffusion coefficient Dlb can be written down:
Here too, by comparing this result to the diffusion coefficient for the unrestricted walk, Equation (3), we see that the bacteria swimming inside the lattice structure are spreading faster. We can also evaluate the effect of the nonuniformity of the turning angle distribution on the diffusion inside the labyrinth, by looking at the ratio
Here, v0, τ0 and w are the same for both systems. Thus, the ratio depends on the two probabilities pf and pb. As expected, for the case with uniform turning angle distribution, i.e., pf = pb, the ratio becomes one. For a higher probability to go forward, pf > pb, it will, in contrast, become greater than one, corresponding to facilitated diffusion through directional persistence. If pf < pb instead, the dispersal with uniform turning angle distribution is faster.
It is important to note here, that our theoretical predictions are made for the long-time asymptotics of the diffusive regime. In principle, Equation (4) could have been used with the mean of the run time calculated for the labyrinth as an approximation of the ballistic regime of the dispersal. However, it is derived under the assumption of exponentially distributed run times, which, in the case of the random walk in the labyrinth, is not fulfilled. It might give a much better agreement to the actual MSD measured in computer simulations or in the experiment for small times, but it would still not be exact. That is why, for the remaining of the paper, we will primarily focus on the asymptotic diffusive regime.
Now that we quantitatively understand the properties of the long-time diffusion, we turn to numerical simulations to test our predictions. In particular, it is interesting to see how the dispersal process occurs at shorter times and what the effect of several simplifying assumptions of the analytical approach is.
4. Simulations of 2D Bacterial Dispersal in Lattice
In the simulations, all bacteria generally start their walk at the origin (0, 0), which is located in the middle of the same crossing. However, in section 5 we will also consider random starting points. To facilitate computations we use an event-driven algorithm. At each step, a random variable representing the run time is drawn from an exponential distribution with mean τ0, which is used to determine the position of the next tumble. However, the directional change of the tumbling event happens only if the bacterium is inside of a crossing, as depicted in Figure 1. In the case of a uniform turning angle distribution, all four directions are chosen with equal probability. In contrast to the theoretical derivation, multiple tumbles in one crossing are allowed in simulations. For a quantitative evaluation of the effect of multiple tumbles on the diffusion coefficient (see Figure S2).
4.1. Diffusive Properties
The results of the simulations are summarized in Figure 2. As can be seen in Figures 2A,B, the trajectories and bacterial densities have a pronounced square outline at small times (upper row), while acquiring a circular shape at larger times (lower row). This indicates that at the beginning, the bacterial motion is greatly influenced by the geometry of the labyrinth. The clearly seen boundary of the density profile is the ballistic front determined by the constant and finite velocity of the bacteria v0 as |x| + |y| = v0T, where T is the measurement time. At a given moment in time, the total distance traveled along the x- and y-directions of the labyrinth cannot exceed the value of v0T. Trajectories which end up at the front are those where no two steps were done in opposite directions. The effect of ballistic fronts is not frequently mentioned in the context of normal diffusion. However, as this example shows (see also experimental results below), the density of diffusing particles may carry on the information about the underlying lattice for an extended period of time. This effect can be even more dramatic in the case of anomalous diffusion [39]. This behavior is also illustrated in the x-projection of the 2D density of the bacteria shown in Figure 2C. The density of the bacteria keeps memory of the underlying geometry at small times but then loses it at larger times and becomes isotropic after many reorientation events. In this diffusive regime, at large times, the bacterial density also quantitatively agrees with the analytical prediction of a Gaussian distribution, shown as red dashed line, validating the theoretical description for the long-time diffusion in the labyrinth. In Figure 2D, presenting the mean squared displacement of the bacteria as a function of time, it can be seen that the bacteria indeed exhibit nearly ballistic motion with 〈r(t)2〉 ∝ t2 at the beginning and then switch to a diffusive regime with 〈r(t)2〉 ∝ t, where the derived estimates for the diffusion coefficient are confirmed. At large times, numerical and theoretical curves for the MSD are linear with the same slope, which directly corresponds to the diffusion coefficient. We also clearly see that the slope of the MSD of the walk within the labyrinth is higher than for a walk without spatial restrictions, thus further confirming the hypothesis of facilitated diffusion in the lattice.
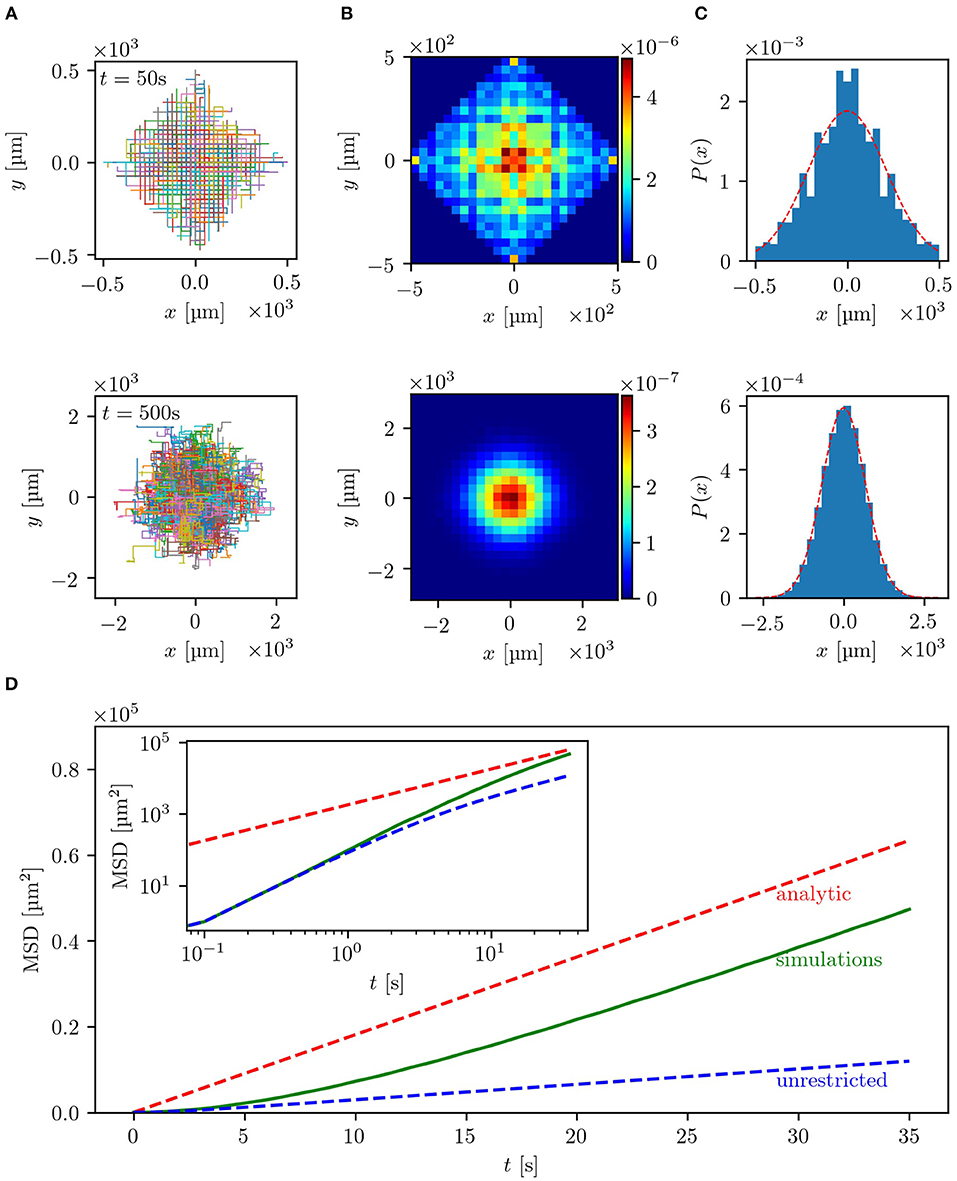
Figure 2. Results of the simulations with uniform turning angle distribution in a lattice with b = 20 μm and w = 5 μm: (A) depicts the trajectories of 500 bacteria for small times, t = 50 s (upper row), and large times, t = 500 s (lower row). In (B) the two-dimensional histograms of the particle density for the same time scales used in (A) for 105 bacteria are shown. The particle density projected on the x-axis, also for 105 bacteria, is plotted in (C) with the red dashed line representing the analytical solution . For small times the underlying geometry has strong influence on the bacterial spreading, while for large times the distribution becomes isotropic. In (D) the mean squared displacement of 105 bacteria is shown in linear scale, while the inset shows the double logarithmic plot. The red dashed line represents the theoretical estimate introduced in section 3.1 and the green line the empirical MSD of the simulated bacteria. The blue dashed line corresponds to the same random walk without spatial restrictions, which can be described by Equation (4), where ϕ0 = 90° due to the uniform turning angle distribution. The theoretical estimates match the simulated MSD for large times. Guiding the bacteria through a lattice of channels significantly enhances the dispersal as compared to an unrestricted motion.
4.2. Dependence of Diffusion Coefficient on Lattice Parameters
To further test the level of agreement between our theoretical estimates for the diffusion coefficient and the simulation results, we compared these for a range of different parameters determining the geometry of the lattice and evaluated the dependence of the diffusion coefficient on b—the side length of the obstacles—and on w—the width of the channels between two obstacles. In Figure 3A, it can be seen that for three different channel widths w the diffusion coefficient shows a linear dependence on the side length b and can be rescaled onto a single master curve (see inset) with being
As shown in the inset, the rescaled curves of the simulated diffusion coefficients all coincide with the analytical expression. Similarly, for the dependence on the channel width w, the predicted diffusion coefficient matches—as presented in Figure 3B—the simulation results for three different side lengths b and can also be rescaled to one master curve, shown as inset. Here, the scaled diffusion coefficient is defined as:
In the expression for a factor of is still included, which makes it not completely independent of the parameter b. However, for w/b ≪ 1 this term becomes small and can be neglected. Thus, with increasing b, the rescaled curves for the simulations shown in the inset of Figure 3B converge to the analytical expression, so that the curve for b = 100 μm already agrees with the theoretical prediction. This very good agreement between simulation results and analytical expressions also suggests that multiple tumbles in the crossing included in simulations but neglected in theory are not making a significant contribution for the range of tested parameters (see also Figure S2).
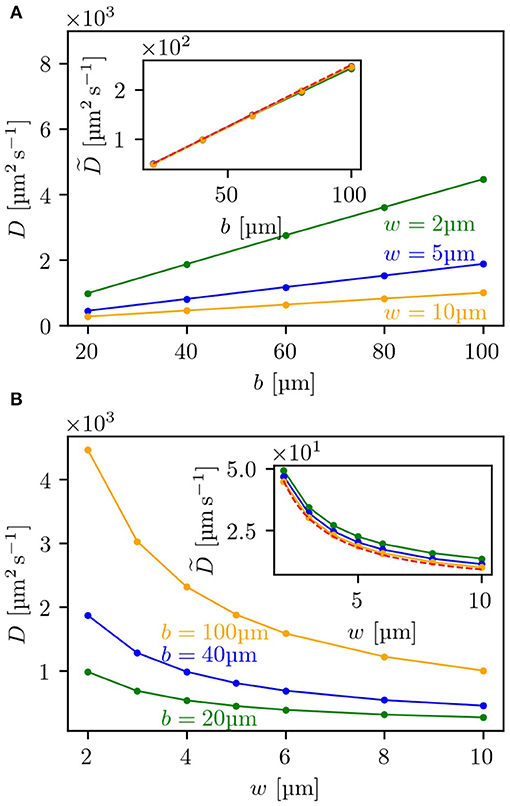
Figure 3. Dependence of the diffusion coefficient on lattice parameters: (A) depicts the dependence of the diffusion coefficient in the labyrinth Dl on the side length b of the obstacles for three different channel widths w, (B) the dependence on w for three different values of b. Both insets show the rescaled diffusion coefficients as given by Equation (10) for (A), and by Equation (11) for (B). The red dashed line shows the corresponding analytical expression. For each measurement 5,000 bacteria were each simulated to perform 2,000 tumbling events.
5. Introducing a Nonuniform Turning Angle Distribution: Comparison of Simulations and Experiments
After verifying the analytical solutions for the case with a uniform turning angle distribution during tumbles, we now switch to the system with a nonuniform turning angle distribution. To test our theory and its practical applicability we implemented the nonuniformity of the turning angle distribution after a tumbling event in a crossing in simulations and compared these results to experimental data [40].
The experiments were performed by using microfluidic devices with a lattice geometry of obstacles with a side length b = 20 μm and with two channel widths w and heights h of 5 μm and 8 μm. For these dimensions, some tumbling events of the bacteria inside the channels between two obstacles were observed. Fluorescently labeled E. coli were imaged with an inverted fluorescence microscope. Thereby, trajectories in the range of 2.5–20 s could be recorded and analyzed. An example trajectory of one E. coli bacterium swimming in a labyrinth with w = 5 μm can be seen in the Supplementary Movie. The simulation parameters were adjusted to the experimentally observed values. More precisely, the turning angle distribution after a reorientation event and the mean run time were taken from measurements of bacteria moving without geometric restrictions in the x/y-plane but with a vertical constraint at a height of h = 5 μm or h = 8 μm, respectively. This confinement to effectively two dimensions changes the motility parameters, e.g., the velocity v0 and turning angle distribution, compared to bacteria freely swimming in three dimensions. In the 5 μm channels the bacteria swim with a mean run time τ0 = 1.8 s, while in the 8 μm channels with τ0 = 1.7 s. For both channel widths a velocity v0 ≈ 10 μm s−1 was measured. By splitting the histogram of turning angles (see Supplementary Material) into the domains 0°-45°, 45°−135° and 135°−180°, we determine the turning probabilities in the labyrinth pf ≈ 0.1, pr ≈ 0.3, pl ≈ 0.3, pb ≈ 0.3. Further information on how the experiments and simulations were performed can be found in the section 7. In Figure 4, side-by-side comparisons between simulations and experiments for w = 8 μm are shown (for w = 5 μm see Figure S3). As basis for the comparisons, we chose the trajectories themselves, the MSD and the decision making behavior at the crossings. Since the longest trajectory length measured in the experiments was around 20 s, the time scale of the comparisons lies, according to our estimates, in the regime of ballistic motion with 〈r(t)2〉 ∝ t2. Contrasting both sets of trajectories, shown in Figure 4A, it can be observed that both simulations and experiments show evidence of the underlying geometry resembling a ballistic front with the typical |x| + |y| = v0T shape. In experiments, hence also in simulations, the trajectories are of different lengths and start at an arbitrary point in the labyrinth. Because of this, both the outlines of obstacles and the ballistic fronts are smeared out in comparison to Figure 2A. The distance traveled by the bacteria is quantified by the MSD and shown in double logarithmic display in Figure 4B. Here, it can be seen that the simulated curve reproduces the overall trend of the experimental curve and also quantitatively agrees with the experimental data. This becomes even more evident in the direct comparison between the simulated and experimental MSD shown in Figures S4, S5. Interestingly, in the experiments, we can track bacterial decisions at every crossing, plot the histogram of the chosen directions and compare it to simulation results, as shown in Figure 4C. Here, we see that the simulations reproduce the overall tendency of the decision distributions measured in the experiments. The smaller probability to go forward paired with the higher probability to go right or left in experiments compared to the simulations, can be attributed to smooth directional changes in the crossings due to rotational diffusion, without tumbling events happening. Thus, it would be predicted that in narrower channels the effect of rotational diffusion deflecting the cell from straight motion should be weaker. Indeed, we see that in 5 μm channels (see Figure S3), the probability to continue forward approaches the theoretical value. The otherwise good agreement between experiments and simulations suggests that by taking the angle distribution of x/y-unrestricted motion we can reproduce the behavior inside the labyrinth. Here, we should note that the numerical simulations achieve good agreement with experimental data without any fitting parameters. All values and distributions were obtained directly from experiments. Finally, we provide the results of a control experiment, comparing the dispersal of bacteria in the labyrinth and outside the labyrinth. We see a clear effect of enhanced diffusion in agreement with the predictions of the model, see Figure S5. Thus, our theoretical model of the diffusion through a square lattice of channels proves to be a reasonable simplification covering the most significant features of experimentally observed bacterial behavior inside of a microfluidic labyrinth.
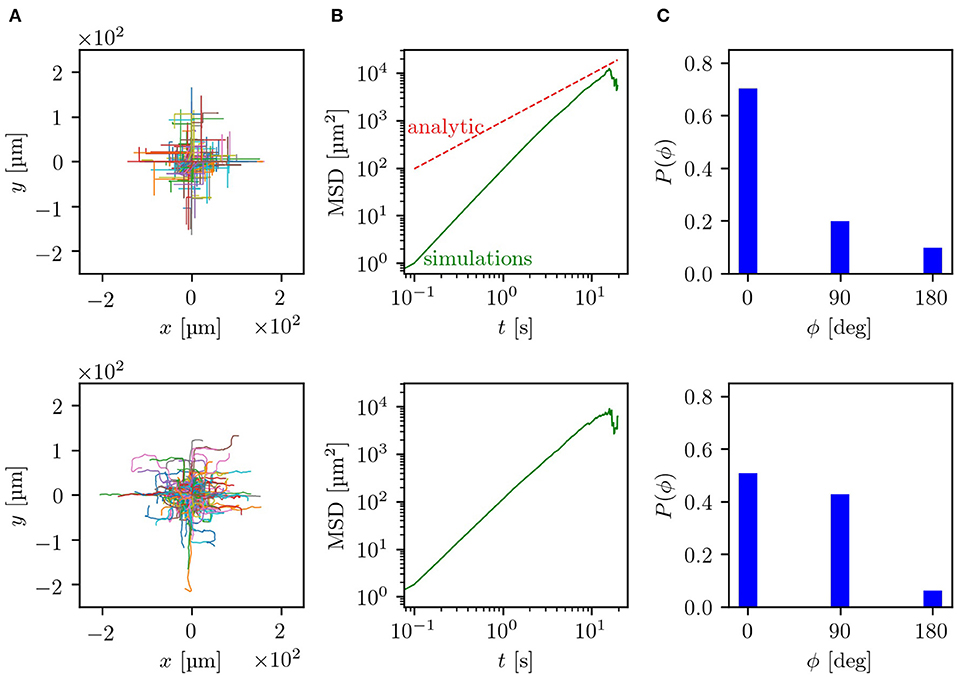
Figure 4. Comparison between simulation results (upper row) and experiments (lower row) for a lattice with b = 20 μm and w = 8 μm: (A) compares the trajectories, starting at a random position in the lattice, which are centered to the zero point. (B) Shows the mean squared displacements in double logarithmic plots, where the green line displays the simulated and measured MSD while the red dashed line corresponds to the analytical prediction. (C) Displays the probabilities for turning decisions at each crossing. Parameters of simulations are chosen to match experimental data as discussed in the section 7.
6. Discussion
We analyzed the process of bacterial dispersal in a labyrinth of channels with square geometry. Narrow channels between the obstacles guide the motion of bacteria and prevent them from changing the swimming direction. The reorientation events can, however, happen in the channel crossings. By modeling this system as a two-dimensional random walk with exponentially distributed run times we provided analytical expressions for the diffusion constants quantifying large time asymptotics of bacterial dispersal in the labyrinth. The main theoretical predictions are an enhanced diffusion constant for smaller channel widths and larger obstacle sizes and a prolonged regime of non-Gaussian diffusion where the geometry of the channels is imprinted in the density of bacteria spreading in the labyrinth. Here, we focused on the two-dimensional geometry to be able to compare our results to experiments. However, a generalization of the developed theoretical and numerical approaches to higher dimensions is rather straightforward.
To assess the practical applicability of the model we specialized it to describe the run-and-tumble motion of E. coli with a nonuniform turning angle distribution. We then compared both simulations and theory to experimental data, collected by tracking E. coli bacteria in microfluidic labyrinths with lattice geometry. Thereby, we were able to quantitatively verify our theoretical results and demonstrate that our approach can serve as an adequate model of bacterial dispersal in simple labyrinth geometries.
Our results suggest that the developed model can be used to theoretically analyze the behavior of bacteria in an environment with lattice structure. Understanding the dispersal of bacteria in these rather simple geometries can help to evaluate the usability of E. coli as a transport bacterium for on-site treatments in more complex environments as well as in other fields like ecology and industrial processes. Our future work will include the analysis of other geometries, for example a hexagonal lattice, and the evaluation of different bacteria species and motility patterns, for example the run-and-reverse pattern of Pseudomonas putida or run-reverse-flick of Vibrio alginolyticus bacteria. Another interesting task will be the analysis of the effects of different chemical landscapes, e.g., a concentration gradient of a chemoattractant, on the diffusive properties of the bacteria. Additionally, in the future, the diffusion mechanism of bacteria in lattice structures can be further extended to interpret the evolution of game strategies in square lattices [41, 42].
7. Materials and Methods
7.1. Microfluidic Experiments
7.1.1. Cell Culturing
The GFP-expressing E.coli AW405 strain was cultured overnight in rich liquid LB medium (10 g L−1 Tryptone, 5 g L−1 NaCl, 5 g L−1 Yeast Extract, pH 7.0) including 100 μg ml−1 ampicillin at 37 °C on a rotary shaker at 200 rpm. The cell suspension from the overnight culture was diluted 1:100 with fresh LB, and grown to an OD600 of 0.6. The cells were washed by centrifugation (1500 g at 20 °C for 2 min) and resuspended in motility buffer (11.2 g L−1 K2HPO4, 4.8 g L−1 KH2PO4, 3.93 g L−1 NaCl, 0.029 g L−1 EDTA and 0.5 g L−1 glucose; pH 7.0).
7.1.2. Cell Imaging and Tracking
The cells were infused into microfluidic chips (for details about the fabrication see Supplementary Material). The chips had two wide chambers connected by a maze-like mid-section (see Figure S1). This region was made of periodically arranged square structures with a side-length of 20 μm. In this study, two different chips were fabricated with different widths of the channels in the maze (5 μm and 8 μm). The cells freely swam in the wide chambers and occasionally entered the maze and explored this region as well. The GFP-expressing cells were visualized in the chips using an IX71 inverted microscope equipped with a 20X UPLFLN-PH objective (both Olympus, Japan) and an Orca Flash 4.0 CMOS camera (Hamamatsu Photonics, Japan). Two image stacks were acquired at 10 fps over 3 min for each chip. The 5 μm data set contains 45 trajectories with a total length of 409 s. The 8 μm data set consists of 346 trajectories with a total length of 2,231 s.
A custom Matlab program based on the Image Processing Toolbox (version R2015a, The MathWorks, USA) together with the open source image analysis platform Fiji were used to process the image sequences. For each image stack, the images projected into a single image by taking the median value for each pixel over stack. The median image was subtracted from each frame to eliminate non-moving objects including dead cells. A despeckle filter was then applied to correct the noise at the CMOS-sensor of the camera. Afterward, the high frequency noise in the images was filtered out by a Gaussian blur filter. The filtered images were binarized by using maximum entropy thresholding following Kapur et al. [43]. The binary images were further processed to find connected regions in the images using the built-in function bwconncomp. The regionprops function was used to determine the size and centroid of the objects. Finally, the centroid position was tracked utilizing the algorithms by Crocker and Grier [44].
7.2. Simulation
All simulations have been implemented as event-driven algorithms in Python 3.7 using the freely available packages NumPy and matplotlib. Simulations used in section 4 were performed on an unbounded domain with channels being located on the intervals with k ∈ ℤ in x- as well as in y-direction. Therein all bacteria start their walk at zero at time t = 0 positioned in the middle of the same crossing in a random direction taken from a uniform distribution. For each bacterium, N tumbling events are simulated. At each step a random variable τ is drawn from an exponential distribution with mean τ0 representing the run time until the next tumbling event. Using the constant speed v0 the new position of the bacterium is determined from its prior position as . Only if this lies inside a crossing, a new walking direction (forward, right, backward, left) is randomly drawn from a uniform distribution and used as the direction of the next step. The variable parameters are set to be equal to the experimentally determined values. These are in the two-dimensional confinement a mean run time τ0 = 1.8 s, a constant speed v0 = 10 μm s−1 and a side length b = 20 μm of the obstacles for a width w = 5 μm of the channels, and τ0 = 1.7 s, v0 = 10 μm s−1, b = 20 μm for a channel width w = 8 μm. In Section 5, instead of a uniform distribution, the experimentally determined turning angle distribution (see Figure S6) for bacterial movement with spatial restrictions only in the z-plane has been used. By taking the probability to turn in an angle between 0° and 45° in the two-dimensional unrestricted case, the probability to go forward pf is set to be pf = 0.1. For the probability to go right pr and to go left pl the relation pr = pl = 0.3 holds, being each approximately half of the probability to take an angle between 45° and 135° in the unrestricted experiments. Finally, the probability to turn backwards pb is pb = 0.3, corresponding to the probability to turn in an angle between 135° and 180°. Also, here the simulated bacteria do not start in the middle of one crossing at t = 0, but at a random place inside the lattice. To plot the trajectories—as done in Figure 4A—the trajectories were centered to the zero position. For both comparisons, i.e., for w = 5 μm and w = 8 μm, the same number of trajectories and same trajectory lengths were simulated as were tracked in experiments.
Data Availability Statement
The datasets generated and analyzed for this study can be found under the doi: 10.5281/zenodo.3367324.
Author Contributions
AW performed numerical simulations, analyzed the data, and wrote the manuscript. All coauthors contributed to the conception and design of the study and to writing the manuscript. XZ and VZ provided analytical results. MB performed the experiments. MB and ZA analyzed the experimental data. CB designed the experimental research.
Funding
MB, ZA, and CB gratefully acknowledge financial support by the research training group GRK 1558 funded by Deutsche Forschungsgemeinschaft.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank Hui-Shun Kuan and Tim Klingberg for stimulating discussions and Marius Hintsche for support with the experiments and the cell tracking algorithm.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2019.00148/full#supplementary-material
Supplementary Movie. Bacteria swimming in square labyrinth.
References
1. Turnbaugh PJ, Ley RE, Hamady M, Fraser-Liggett CM, Knight R, Gordon JI. The human microbiome project. Nature. (2007) 449:804. doi: 10.1038/nature06244
2. Mitchell JG, Kogure K. Bacterial motility: links to the environment and a driving force for microbial physics. FEMS Microbiol Ecol. (2006) 55:3–16. doi: 10.1111/j.1574-6941.2005.00003.x
3. Jarrell KF, McBride MJ. The surprisingly diverse ways that prokaryotes move. Nat Rev Microbiol. (2008) 6:466. doi: 10.1038/nrmicro1900
4. Johansen JE, Pinhassi J, Blackburn N, Zweifel UL, Hagström Å. Variability in motility characteristics among marine bacteria. Aquat Microb Ecol. (2002) 28:229–37. doi: 10.3354/ame028229
5. Bardy SL, Ng SY, Jarrell KF. Prokaryotic motility structures. Microbiology. (2003) 149:295–304. doi: 10.1099/mic.0.25948-0
6. Berg HC. The rotary motor of bacterial flagella. Annu Rev Biochem. (2003) 72:19–54. doi: 10.1146/annurev.biochem.72.121801.161737
8. Fürth R. Die brownsche Bewegung bei Berücksichtigung einer Persistenz der Bewegungsrichtung. Mit Anwendungen auf die Bewegung lebender Infusorien. Zeitschrift für Physik A Hadrons and Nuclei. (1920) 2:244–56. doi: 10.1007/BF01328731
9. Tailleur J, Cates M. Statistical mechanics of interacting run-and-tumble bacteria. Phys Rev Lett. (2008) 100:218103. doi: 10.1103/PhysRevLett.100.218103
10. Lauga E. Bacterial hydrodynamics. Annu Rev Fluid Mech. (2016) 48:105–30. doi: 10.1146/annurev-fluid−122414-034606
11. DeRosier DJ. The turn of the screw: the bacterial flagellar motor. Cell. (1998) 93:17–20. doi: 10.1016/S0092-8674(00)81141−1
13. Bechinger C, Di Leonardo R, Löwen H, Reichhardt C, Volpe G, Volpe G. Active particles in complex and crowded environments. Rev Mod Phys. (2016) 88:045006. doi: 10.1103/RevModPhys.88.045006
14. Männik J, Driessen R, Galajda P, Keymer JE, Dekker C. Bacterial growth and motility in sub-micron constrictions. Proc Natl Acad Sci USA. (2009) 106:14861–6. doi: 10.1073/pnas.0907542106
15. Libberton B, Binz M, Van Zalinge H, Nicolau DV. Efficiency of the flagellar propulsion of Escherichia coli in confined microfluidic geometries. Phys Rev E. (2019) 99:012408. doi: 10.1103/PhysRevE.99.012408
16. Wioland H, Lushi E, Goldstein RE. Directed collective motion of bacteria under channel confinement. New J Phys. (2016) 18:075002. doi: 10.1088/1367-2630/18/7/075002
17. Theves M, Taktikos J, Zaburdaev V, Stark H, Beta C. Random walk patterns of a soil bacterium in open and confined environments. Europhys Lett. (2015) 109:28007. doi: 10.1209/0295-5075/109/28007
18. Raatz M, Hintsche M, Bahrs M, Theves M, Beta C. Swimming patterns of a polarly flagellated bacterium in environments of increasing complexity. Eur Phys J Spec Top. (2015) 224:1185–98. doi: 10.1140/epjst/e2015-02454-3
19. Sosa-Hernández JE, Santillán M, Santana-Solano J. Motility of Escherichia coli in a quasi-two-dimensional porous medium. Phys Rev E. (2017) 95:032404. doi: 10.1103/PhysRevE.95.032404
20. Bhattacharjee T, Datta SS. Bacterial hopping and trapping in porous media. Nat Commun. (2019) 10:2075. doi: 10.1038/s41467-019−10115−1
21. Elgeti J, Gompper G. Run-and-tumble dynamics of self-propelled particles in confinement. Europhys Lett. (2015) 109:58003. doi: 10.1209/0295-5075/109/58003
22. Jakuszeit T, Croze OA, Bell S. Diffusion of active particles in a complex environment: role of surface scattering. Phys Rev E. (2019) 99:012610. doi: 10.1103/PhysRevE.99.012610
23. Pattanayak S, Das R, Kumar M, Mishra S. Enhanced dynamics of active Brownian particles in periodic obstacle arrays and corrugated channels. Eur Phys J E. (2019) 42:62. doi: 10.1140/epje/i2019−11826-7
24. Ribet D, Cossart P. How bacterial pathogens colonize their hosts and invade deeper tissues. Microbes Infect. (2015) 17:173–83. doi: 10.1016/j.micinf.2015.01.004
25. Forbes NS. Engineering the perfect (bacterial) cancer therapy. Nat Rev Cancer. (2010) 10:785. doi: 10.1038/nrc2934
26. Patyar S, Joshi R, Byrav DP, Prakash A, Medhi B, Das B. Bacteria in cancer therapy: a novel experimental strategy. J Biomed Sci. (2010) 17:21. doi: 10.1186/1423-0127−17-21
27. Jang LK, Chang PW, Findley JE, Yen TF. Selection of bacteria with favorable transport properties through porous rock for the application of microbial-enhanced oil recovery. Appl Environ Microbiol. (1983) 46:1066–72.
28. Al-Sulaimani H, Joshi S, Al-Wahaibi Y, Al-Bahry S, Elshafie A, Al-Bemani A. Microbial biotechnology for enhancing oil recovery: current developments and future prospects. Biotechnol Bioinf Bioeng. (2011) 1:147–58.
29. Zhong H, Liu G, Jiang Y, Yang J, Liu Y, Yang X, et al. Transport of bacteria in porous media and its enhancement by surfactants for bioaugmentation: a review. Biotechnol Adv. (2017) 35:490–504. doi: 10.1016/j.biotechadv.2017.03.009
30. Akin D, Sturgis J, Ragheb K, Sherman D, Burkholder K, Robinson JP, et al. Bacteria-mediated delivery of nanoparticles and cargo into cells. Nat Nanotechnol. (2007) 2:441. doi: 10.1038/nnano.2007.149
32. Molaei M, Barry M, Stocker R, Sheng J. Failed escape: solid surfaces prevent tumbling of Escherichia coli. Phys Rev Lett. (2014) 113:068103. doi: 10.1103/PhysRevLett.113.068103
33. Turner L, Ryu WS, Berg HC. Real-time imaging of fluorescent flagellar filaments. J Bacteriol. (2000) 182:2793–801. doi: 10.1128/JB.182.10.2793-2801.2000
34. Biondi SA, Quinn JA, Goldfine H. Random motility of swimming bacteria in restricted geometries. AIChE J. (1998) 44:1923–9. doi: 10.1002/aic.690440822
35. Berg HC, Brown DA. Chemotaxis in Escherichia coli analysed by three-dimensional tracking. Nature. (1972) 239:500. doi: 10.1038/239500a0
36. Phillips BR, Quinn JA, Goldfine H. Random motility of swimming bacteria: single cells compared to cell populations. AIChE J. (1994) 40:334–48. doi: 10.1002/aic.690400212
37. Lovely PS, Dahlquist F. Statistical measures of bacterial motility and chemotaxis. J Theor Biol. (1975) 50:477–96. doi: 10.1016/0022-5193(75)90094-6
38. Taktikos J, Stark H, Zaburdaev V. How the motility pattern of bacteria affects their dispersal and chemotaxis. PLoS ONE. (2013) 8:e81936. doi: 10.1371/journal.pone.0081936
39. Zaburdaev V, Fouxon I, Denisov S, Barkai E. Superdiffusive dispersals impart the geometry of underlying random walks. Phys Rev Lett. (2016) 117:270601. doi: 10.1103/PhysRevLett.117.270601
40. Bahrs M. Diffusive spreading of Escherichia coli and Pseudomonas putida in complex environments (Master thesis). Universität Potsdam, Potsdam, Germany (2017).
41. Chen Mh, Wang L, Wang J, Sun Sw, Xia Cy. Impact of individual response strategy on the spatial public goods game within mobile agents. Appl Math Comput. (2015) 251:192–202. doi: 10.1016/j.amc.2014.11.052
42. Chen MH, Wang L, Sun SW, Wang J, Xia CY. Evolution of cooperation in the spatial public goods game with adaptive reputation assortment. Phys Lett A. (2016) 380:40–7. doi: 10.1016/j.physleta.2015.09.047
43. Kapur JN, Sahoo PK, Wong AKC. A new method for gray-level picture thresholding using the entropy of the histogram. Comput Vis Graph. (1985) 29:273–85. doi: 10.1016/0734−189X(85)90125-2
Keywords: diffusion, rectification, random walk, bacteria, confinement
Citation: Weber A, Bahrs M, Alirezaeizanjani Z, Zhang X, Beta C and Zaburdaev V (2019) Rectification of Bacterial Diffusion in Microfluidic Labyrinths. Front. Phys. 7:148. doi: 10.3389/fphy.2019.00148
Received: 02 June 2019; Accepted: 19 September 2019;
Published: 09 October 2019.
Edited by:
Jürgen Vollmer, Universität Leipzig, GermanyReviewed by:
Chengyi Xia, Tianjin University of Technology, ChinaNuno A. M. Araújo, University of Lisbon, Portugal
Anupam Sengupta, University of Luxembourg, Luxembourg
Copyright © 2019 Weber, Bahrs, Alirezaeizanjani, Zhang, Beta and Zaburdaev. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Carsten Beta, YmV0YUB1bmktcG90c2RhbS5kZQ==; Vasily Zaburdaev, dmFzaWx5LnphYnVyZGFldkBmYXUuZGU=
 Ariane Weber
Ariane Weber Marco Bahrs3
Marco Bahrs3 Zahra Alirezaeizanjani
Zahra Alirezaeizanjani Vasily Zaburdaev
Vasily Zaburdaev