- 1Department of Physics, Jordan University of Science and Technology, Irbid, Jordan
- 2Department of Physics, The Hashemite University, Zarqa, Jordan
- 3Department of Physics, University of Nebraska at Omaha, Omaha, NE, United States
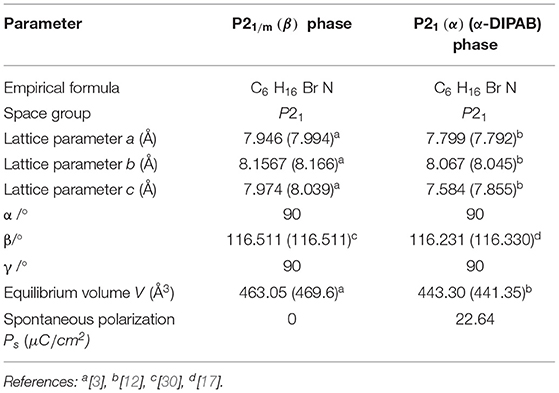
- 4Department of Physics, Khalifa University of Science and Technology, Abu Dhabi, United Arab Emirates
- 5Department of Electronic Engineering, Yarmouk University, Irbid, Jordan
We report accurate calculations of tonsorial elements of α-Diisopropylammonium bromide (α-DIPAB) molecular ferroelectric crystal. In particular, elastic, piezoelectric and dielectric tensors were computed using density functional theory (DFT)-based Vienna ab initio simulation package (VASP). The determination of above parameters allows an accurate description of the energy landscape for modeling of realistic devices at finite temperatures. We determine the major physical tensors in energy expansion of total energy per volume of un-deformed crystal to provide experimentalists with valuable information for designing and fabrication of pyroelectric detectors, capacitors, piezoelectric devices based on α-DIPAB. The spontaneous polarization Ps was calculated using Berry phase approach and found to be 22.64 μC/cm2 in agreement with reported theoretical value. Furthermore, we calculate dynamical Born effective charge tensor to get a deeper insight into the bonding network and lattice dynamic of α-DIPAB crystal. The neighboring layers of DIPA molecules were found to be strongly crenelated due to the strong short-ranged electrostatic repulsion between Br sites in the DIPAB crystal structure. The organization of species in DIPA molecular layer as well as in the bromine “stitching” layer is essential for accurate calculation of DIPAB elastic properties. Having understood the actual network bonding in α-DIPAB, we calculated the components of the elastic moduli tensor. Our results indicate that a Young's modulus of 50–150 GPa and a shear modulus of 4–26 GPa were found. Thus, α-DIPAB phase has a great potential to be a terrific candidate for flexible electronic device applications. The value of the principle component of electronic contribution to the static dielectric tensor of α-DIPAB is found to be ≈2.5, i.e., 50% smaller than that in typical perovskite-based ferroelectrics. Therefore, α-DIPAB is anticipated to exhibit creative materials' innovations. It could be potential candidate as insulating layer of polymer thick films. Its mechanical, insulating and elastic properties make it eligible for switch keys and flex-circuit applications. Furthermore, clamped-ion piezoelectric tensor is calculated. Our results indicate a reasonable piezoelectric response of this polar crystal making it a low cost attractive candidate for piezoelectric applications.
Introduction
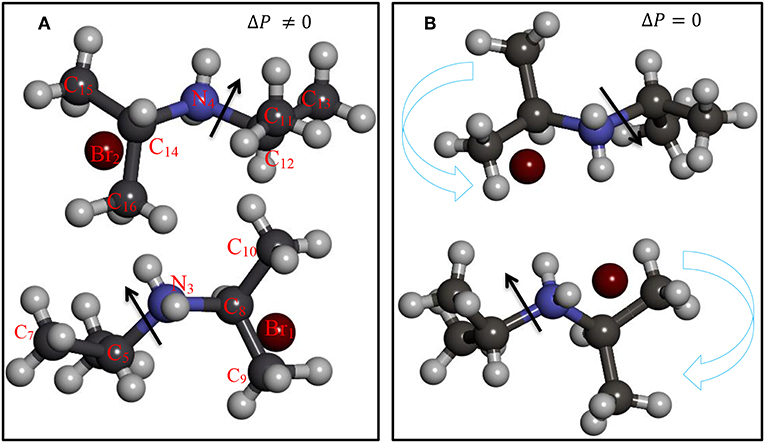
Ferroelectric materials and in particular perovskites [1, 2] are widely investigated experimentally and theoretically due to their prospective opto-electronic and piezoelectric device applications [3]. The outstanding physical and piezoelectric properties of the Lead Lanthanum Zirconate Titanate [Pb1−xLax(ZryTi1−y)O3 (PLZT)] discovered in 1971 [4, 5] have attracted much interest for synthesis of ferroelectric films. In the past 20 years, more studies were published on the structural and electrical properties of ferroelectric films [6]. Molecular ferroelectrics are highly desirable due to their lightweight, mechanical flexibility and for being friendly to environment. It was reported that diisopropylammonium chloride (DIPAC) molecule exhibits a room-temperature polar phase with spontaneous polarization of 8.2 μC/cm2 [7]. It has been reported that diisopropylammonium bromide (DIPAB) crystallizes into a room-temperature ferroelectric phase branded as P21 (α-DIPAB) and a high temperature paraelectric phase categorized as P21/m(β) [7]. X-ray diffraction (XRD) structural characterization indicates that P21 (α-DIPAB) belongs to polar point group C2 [8] illustrated schematically in Figure 1A. In contrast, at high temperature P21/m(β) has a crystal structure with a non-polar point group D2 shown schematically in Figure 1B. It has been found that polar α-DIPAB exhibits a large enhanced spontaneous polarization of 23 μC/cm2 [9]. It has also been shown that α-DIPAB exhibits good piezoelectric response. In the past few years, α-DIPAB and DIPAC have become key candidate materials for several technological applications such as, information storing, energy reaping [3], frequency-modulation devices [10, 11], polymers [12], sensors [13], and flex-circuits. Attributed to their extraordinary properties, α-DIPAB and DIPAC and other molecular ferroelectrics have overcame some weaknesses of traditional molecular ferroelectrics. Lately the effect of bromine deficiency on the lattice dynamics and dielectric properties of α-DIPAB crystals. It was found that bromine (Br) deficiency intensely affects the dielectric properties of α-DIPAB [14]. Our FT-IR and Raman vibrational spectra measurements proposed the presence of disorder in the α-DIPAB crystal. We have successfully determined major vibrational modes of α-DIPAB crystal using vdW + DF2 functional and were found to match with the experimentally determined modes [14]. We report our results on the structural and optical properties, as well as, vibrational modes of α-DIPAB [15].
Figure 1 shows the structures of the two polymorphs of DIPAB crystal. It was observed that the transformation from P21/m(β) phase to α-DIPAB phase occurs above room temperature [16]. It was observed that such transition is accompanied by a drastic change in structural, dielectric, elastic, thermal, and other properties [17, 18]. Several external factors can influence this transition such as pressure and electric field [19, 20]. It is much desired to elucidate the electronic, dielectric and optical properties of these materials in details. We perform density functional based studies of electronic properties of α-DIPAB. We obtained the basic physical quantities describing the dielectric behavior of α-DIPAB including spontaneous polarization, dynamical Born effective charges, static dielectric, clamped-ion piezoelectric, and elastic stiffness tensors. This information can be used for modeling of potential DIPAB-based devices both ordered and disordered [21, 22].
Toward achieving the goal of understanding the electronic and optical properties of the α-DIPAB, we report the detailed study of the physical properties using ab initio DFT based simulations. The main motivation of the present work is to report accurate parameterization of the vector components of the “gradient” vector A and tonsorial elements of “Hessian matrix” B of polar α-DIPAB crystal. Such parameterization is backbone of the correct depiction of the energy background for fabrication of convincing optoelectronic and piezoelectric devices at finite temperatures for large scale and massive production.
Our manuscript is structured as follows: following the above introduction, a comprehensive discussion of the computational methods is introduced in section Computational Methods. In section Results and Discussion, a detailed analysis of the calculated physical properties of α-DIPAB is presented. Particularly, we report an ab initio calculation of the spontaneous polarization, dynamical Born effective charges, static dielectric, and clamped-ion piezoelectric, and elastic stiffness tensors of polar α-DIPAB. We, finally, conclude the findings and results of this work in section Summary And Conclusions.
Computational Methods
Ab initio simulations based on DFT [23, 24] were implemented in this work to carry out all calculations. The electronic structure was calculated using the Projector Augmented Wave (PAW) method [25] as implemented in the Vienna ab initio simulation package VASP [26]. The generalized gradient approximation (GGA) [27] was used for the exchange-correlation potential. We used cut off energy of 400 eV and a 4 x 4 x 4 Monkhorst- Pack grid for integration over Brillion zone. Elastic tensors were calculated with the energy cut-off of 700 eV. The relaxed atomic locations were monitored by minimizing the total energy (i.e., as small as 10−6 eV), and the Hellmann-Feynman forces as small as 0.003 eV/Å at convergence. Electronic polarization was computed using the Berry phase approach [28]. The spontaneous polarization (Ps) of α-DIPAB crystal is defined as the difference between the polarization of the polar ferroelectric phase and the paraelectric centrosymmetric phase (P = 0). We have done the Convergence test for our investigated system. The plot of Total Energy vs. Cut-off energy shows that beyond a Cut-off energy of 400 eV, the value of Etot does not change significantly for a E Cut-off >400–500 eV (This depends on the accuracy required by the calculation). Therefore, we do not need to take a greater value of E Cut-off for our calculation since the result will be always the same. This justified the use of 400 eV as a Cut-off energy in our calculations.
While current ab initio density-functional calculations cannot adequately determine material properties at high temperature, it is possible to compute the static-lattice equation of state and elastic moduli of α-DIPAB crystal. If correlations between equilibrium properties and high-temperature properties are precisely determined, they can then be used to design the experiments to perform practical measurements. When appropriate, we mention the computation of related properties, like dielectric tensor and Born effective charges that are needed to get infrared spectra. Our results are valid for the temperatures ranging between T = 0 and T = 300 K (Room temperature).
Structural Properties
We considered two different DIPAB polymorphs formed experimentally during recrystallization from aqueous solution, one is the ferroelectric phase labeled P21(α) 1-F (α-DIPAB) and the other is the paraelectric structure mimicking P21/m (β). Figure 1A shows the orientation of N atoms relative to Br atoms leads to a lack of inversion symmetry. In This atomic arrangement, the local electric dipoles created due to the covalent bonding between nitrogen and carbon atoms are aligned to enforce the existence of finite electric polarization. Figure 1B shows that upon heating above 426 K (warm symmetry restoration), the nitrogen atoms apparently enter a disordered state resulting in a centrosymmetric (P21/m(β)) phase in which the dipole moments cancel out and leads to exactly zero spontaneous polarization. Upon cooling to room temperature (cooling symmetry breaking), the crystal goes back to polar P21(α). Thus, spontaneous polarization appears as a result of the breaking of the mirror symmetry. We used lattice constants obtained from XRD measurements as for the input structure in our ab-initio calculations [29] and then performed gradient-descent procedure to obtain the equilibrium lattice parameters of the two phases. The optimized lattice constants are presented in Table 1 found to agree fairly well with the experimental findings.
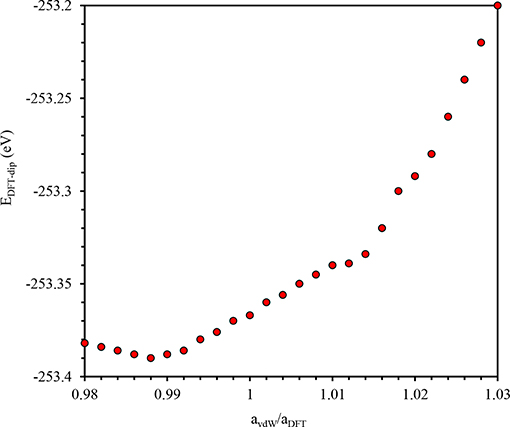
In order to calculate spontaneous polarization we perform macroscopic polarization calculations for the centrosymmetric P21/m(β) prototype phase and the experimental polar P21(α) state. The difference in total polarization between the two states is the spontaneous polarization Ps. Inclusion of Van der Waals (vdW) correction to energy performed in VASP [31, 32] using DFT-D3 method with Becke-Jonson damping yields minor changes the equilibrium lattice parameters. Figure 2 shows the computed corrected energy (EDFT−disp) as function of lattice parameter ratio (avdW/aDFT). A realistic approach to tackle this issue is to add a correction to the conventional Kohn-Sham DFT energy (EKS−DFT), EDFT−disp = EKS−DFT + Edisp, where Edisp is the correction term evaluated using DFT-D3 method [33, 34]. The lattice parameters do not differ significantly (<1% from GGA calculation) because the electrostatic attractions between molecules mediated by Br atom are strong.
Energy Per Undeformed Crystal Volume
Energy of the crystal in ground state (at zero strain and in the absence of external fields), H0, is defined as the energy per unit volume, i.e., an energy density, with units of J/m3. The energy, H, is calculated as the energy per primitive cell of the strained crystal divided by the volume of the unstrained crystal. It also has units of J/m3, as though it were an energy per unit volume, but it is really an energy per undeformed unit volume. The expansion of the energy density can be written as
Where in collective notations xα = (um, ηj, Eα) : um is the displacement of atoms from equilibrium positions, ηj is the strain in Voigt notations, and Eα is the external electric field. The “gradient” vector A and “Hessian matrix” B are:
Here F notates force computed at xα = 0, σ–stress and P–polarization. The notations in tensor B on the diagonal: K–force constant matrix, λ –elastic constant, χ-dielectric susceptibility matrices; and off-diagonal components: Λ-force response “internal strain tensor,” Z*-Born dynamical charges, and e is piezoelectric tensors (V-cell volume). For a detailed description of the formalism of the elementary response tensors [35, 36] (see [19, 20] and the references therein). The determination of above parameters allows an accurate description of the energy landscape for modeling of realistic devices at finite temperatures. Below, we determine the major physical quantities in energy expansion of total energy per volume of undeformed crystal.
Numbers of approaches have shown predictive capabilities of classical Hamiltonians based on the above parameterization [37–39]. The advantage of atomistic simulations at finite temperatures is well-established [40, 41]. However, in case of ferroelectric materials there is a need of connecting atomic positions, strains and external electric field with parameters describing polar materials such as polarization and stress. The interplay between structural, elastic and electric properties in ferroelectrics is essential for the understanding and designing of ferroelectric devices. This information is frequently missing in the studies of ferroelectrics, particularly, when studies mainly focus only on a specific selected property.
Results and Discussion
Electric Polarization of α-DIPAB
The calculated spontaneous polarization of the polar ferroelectric phases is presented in Table 1. The magnitude of spontaneous polarization is Ps = 22.64 μC/cm2 in agreement with previous theoretical data and also with the theoretical calculations using hybrid density functionals [4]. This value is comparable to the one in perovskite-based ferroelectric such as BTO. Ferroelectrics lose their intrinsic spontaneous polarization at temperatures above a transition temperature (Curie temperature Tc) and become paraelectric. We found that the energy difference between ferroelectric P21(α) phase and P21/m(β) paraelectric phase is 15.3 eV. This energy difference can be used to calculate the Curie temperature of α-DIPAB crystal [42, 43]. The details of the derivation of tonsorial elements of matrices A and B is provided in the Supplementary Information. Below we describe and calculate each of the tonsorial elements of matrices A and B.
The Static Dielectric Tensor at Constant Vanishing Strain (η= 0) of α-DIPAB
The accurate determination of the static dielectric tensor of a material is crucial for a realistic design of opto-electronic devices.
In this section, we focus on investigating the dielectric properties of α-DIPAB by calculating their response to homogeneous electric fields. It is usually difficult to handle the electric field effects within crystalline solids. Currently, density functional perturbation theory (DFPT) is considered as the appropriate approach to handle the response of molecular ferroelectrics to electric fields [18].
The elements of the static dielectric tensor are
Where E is the electric field and P is the total macroscopic polarization. The at constant vanishing strain (η = 0) is related to the susceptibility tensor χij in Equation (2). It is defined at fixed (vanishing) strain via .
In this section, we study the perturbations applied to the crystal by applying homogeneous electric fields εα. As mentioned above, can be split into an electronic contribution and a lattice contribution. The electronic contribution is manifested by the crystal ability to rearrange charges in response to external electric field considered with clamped nuclear position. The principle components of the electronic contribution to the dielectric tensor of α-DIPAB obtained by applying an external field are presented in Table 2 including the local field effects. The lattice contribution to the dielectric tensor depends on the thermal phonon response and is not considered here. Piecha et al. have shown that although the zero temperature static dielectric permittivity of DIPAB in relatively small it may reach much higher values at the maximum near the phase transition at temperature ~ 426K [29].

Table 2. The electronic contribution to the static dielectric tensor at constant vanishing strain (η = 0) of α-DIPAB including local field effects (applying external electric field) and Van der Waals forces.
The values of the principle components of the static dielectric tensor are found to be smaller than in typical perovskite-based ferroelectric. For example, it is about 50% of those of Orthorhombic KNbO3 recently reported [44] and 46% of the experimental finding [45] and 37% of the theoretical value [46] of that of BTO. Accurate parameterization of tensor at constant vanishing strain (η = 0) provides a deeper insight into understanding the origin of the dielectric properties exhibited by the crystal. The understanding of these properties is essential for proper description of the long wave lattice dynamics.
Born Effective Charge Tensor of α-DIPAB
The accurate calculation of Born effective charge tensor is crucial for understanding of crystal lattice dynamics, piezoelectric and ferroelectric properties. We computed the Born effective charge tensors of α-DIPAB using the density functional perturbation theory and from the response to finite electric fields. The Born effective charge tensor,
Where ∂Pj is the change in polarization prompted by the periodic displacement ∂ui,k or to the force Fi,k induced on atom i by the electric field Ej. Therefore, in terms of atomic displacements is given by
Where i stands for the ith atom. The j and k indices indicate the direction of the polarization component and atomic displacement, respectively.
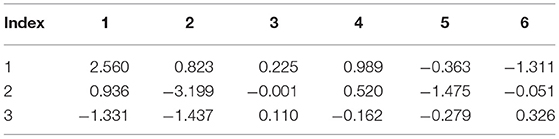
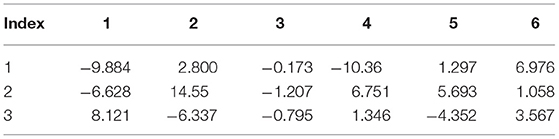
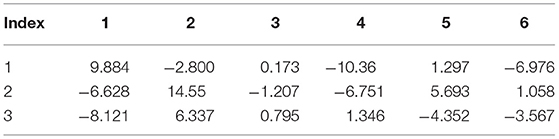
Tables 3, 4 present the Born effective charge tensor of bromine and nitrogen atoms of α-DIPAB calculated from response to a homogenous electric field and density functional perturbation theory, respectively.

Table 3. Calculated Born effective charge tensor of bromine and nitrogen atoms of α-DIPAB calculated by applying a homogenous electric field = + 0.01ŷ + 0.01ẑ eV/.

Table 4. Born effective charge tensor for Br and N ions of α-DIPAB using Density Perturbation Functional Theory (DPFT).
The complete Born effective charge tensors of all atoms of α-DIPAB are reported in Tables S1, S2. Tables 3, 4 show that the principal components of Born effective charge of the two bromine and two nitrogen atoms predicted by the two approaches are very close. It can be seen from Tables 3, 4; Tables S1, S2 that the principal components of Z*-tensor of bromine atoms is >1e and for N, C, and H atoms is <1e. We found that principle components of Born effective charge tensor of bromine and nitrogen atoms are the most prominent and the off-diagonal elements are relatively small. The acoustic-sum rule [47] ensures that the charge neutrality is also satisfied at the level of the Born effective charges. By examining Tables S1, S2, it is obvious that this sum rule is satisfied.
By examining Tables 3, 4 and Figures 3, 4A–C, we found that Born effective charges of carbon atoms covalently bonded to nitrogen atom are positive and effectively create a local dipole moments with negatively charged nitrogen site, while Br atom also has an effective negative charge. The origin of this comes from the charge transfer between molecules of DIPA and Br. We found that Br p-states are weakly hybridized to states of α-DIPAB and its p-states are located between HOMO and LUMO states of the molecules. All these states are occupied, i.e., charge is transferred from molecules to Br sites filling its 4p6 shell. Inside the α-DIPAB molecule charge transfer occurs due to the covalent bonding between C and N sites. Nitrogen is more electronegative and shifts the center of bond charge toward N. The indication of binding is seen in molecular orbital energies where hybridized MO (having contribution from N and C sites) are shifted with respect to “unmixed” carbon states (i.e., without N states contribution to wave function).
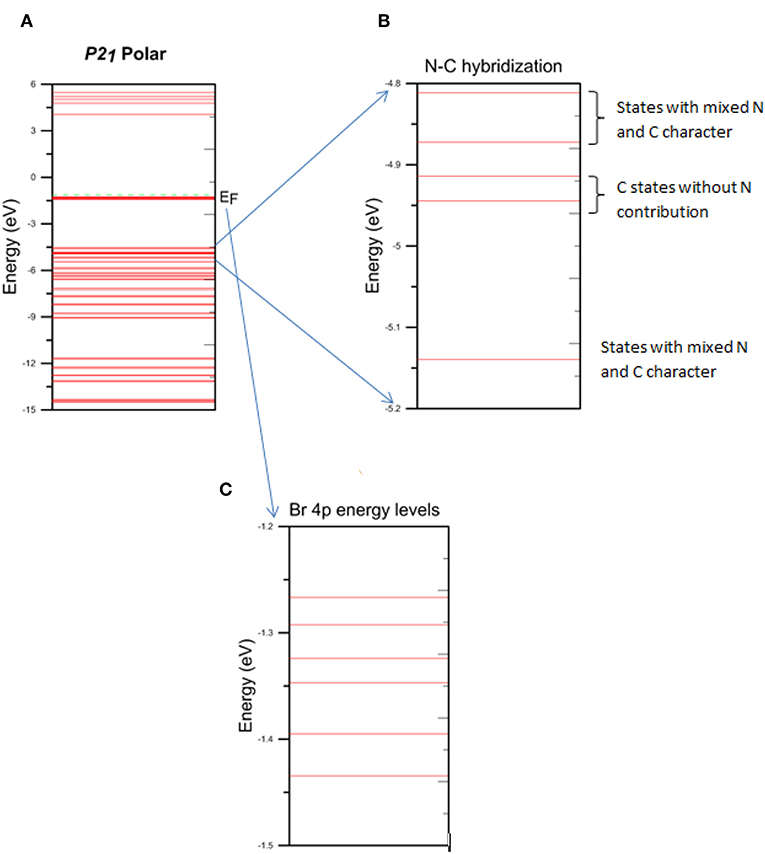
Figure 4. Energy level diagrams of α-DIPAB (A) entire energy level spectrum, (B) energy levels that represent the N-C hybridization, and (C) energy levels of Br 4p band.
The Piezoelectric Tensor of α-DIPAB
Piezoelectricity is the formation of electric polarization of certain non-conducting crystals when they are mechanically strained. As a result, piezoelectric material can yield electricity through mechanical disturbance. Piezoelectricity has been studied extensively, both experiments and theories for devices, such as sensor and controller, such as in energy harvesting.
For piezoelectric effect, the polarization change per unit area (Pi) or the magnitude of electric moment per unit volume (Ei) is related to an applied stress or strain via the piezoelectric strain coefficients (dijk) and the piezoelectric stress coefficient (eijk). This relation can be described using the third-rank tensors [48] with the following equations:
The piezoelectric eij coefficients are related to the piezoelectric dij coefficients by elastic coefficients λkj [49], where ηijk is the strain tensor and σijk is the stress tensor and the polarization changes per unit area (Pi) is defined in Equation (5).
In terms of the energy defined in Equation (1), the clamped-ion piezoelectric tensors (Voigt notation) can be written as
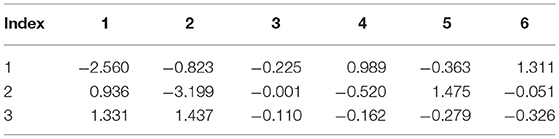
The piezoelectric response is computed by calculating all non-zero components of the piezoelectric tensor. The clamped-ion piezoelectric coefficients tensor is shown in Table 5 relates polarization to applied strain, which represented diagrammatically in Figure 4. For the monoclinic phase, the coefficient links a uniaxial strain and spontaneous polarization parallel to each other. Table 5 shows that component links a uniaxial strain applied perpendicular to the N-C bonds and the resulting polarization is smaller than . When the strain twists the N-C bonds, a large change in polarization component is expected.
For the α-DIPAB, the most significant piezoelectric coefficients are and . These coefficients indicate the quantative rotation of the electric dipole from the z-direction when η13 and η31shears are applied. The shear strain η13 twists the N-C bond causing the polarization vector to rotate along x-direction producing a large change in the electric dipole in this direction as can be clearly demonstrated from Figure 5 that shows 3D and 2D plots of the piezoelectric tensor of α-DIPAB.
As the homogenous electric field is applied to ferroelectric phase of α-DIPAB, the Br, N, C and N ions positions are displaced causing minor changes in crystal dimensions and shear strains are generated [18, 50–54]. Such shear strain induced by the application of electric fields are crucial for the functioning of actuators and sensors [54]. Therefore, strain-induced piezoelectricity in ferroelectric α-DIPAB manifested by significant values piezoelectric coefficients makes it a potential candidate for the design of non-volatile ferroelectric random-access memories (NVFRAM's) [18].
Internal Strain Tensors of α-DIPAB
Force-response internal strain tensor is defined as
The force-response internal-strain tensor Λmj must be distinguished from the displacement-response internal strain tensor where K is the force constant matrix that describes the first order displacements resulting from a first-order strain.
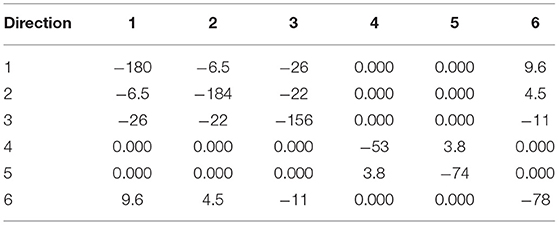
Tables 6–9 present the force response “internal strain tensor” from the displaced atoms of the bromine and nitrogen atoms. They appear in crystals missing inversion symmetry. Accurate parameterization of internal strain tensor is important for the description of crystals under stress.
The Elastic Stiffness Tensor of α-DIPAB
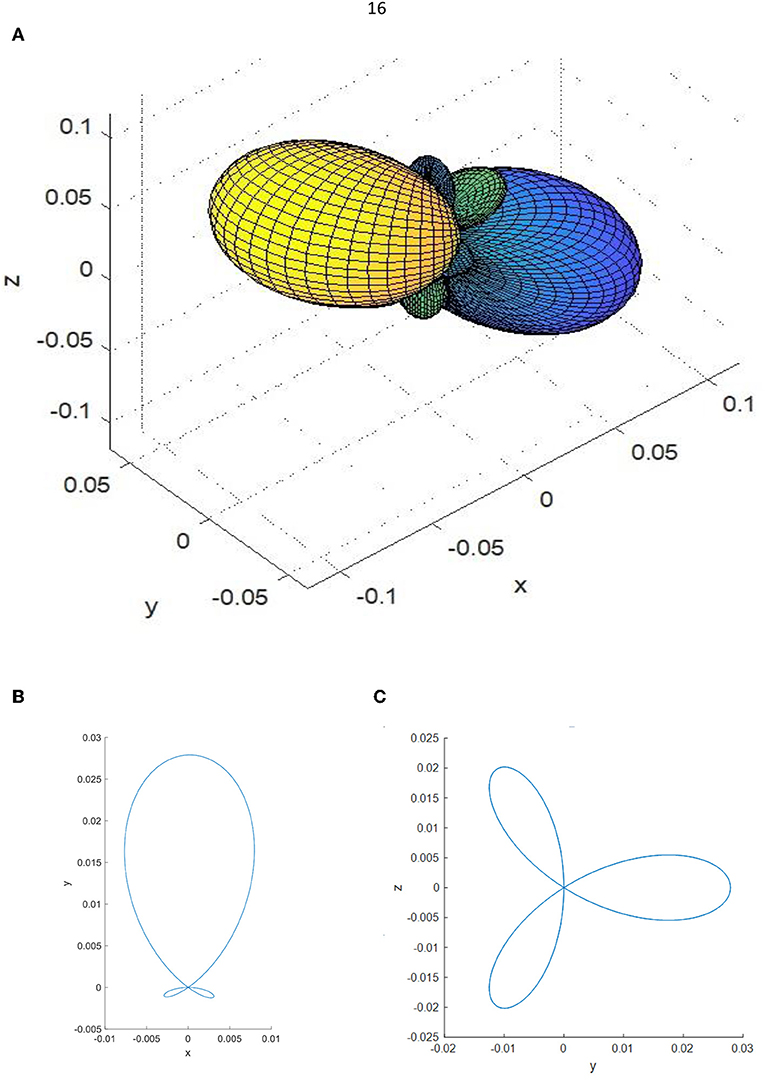
Potential applications of α-DIPAB in flexible electronic devices could benefit from detailed understanding of elastic properties of this material. Elastic moduli of materials show the connection between the strain and stress applied to the system. Equation (16) indicates the relationship of the stress and strain tensors with the elastic moduli tensor. Elastic stiffness tensor of the α-DIPAB with the simple monoclinic lattice that belongs to the space group P21 has an asymmetric form. The calculated elements of the elastic moduli contribution from ionic relaxation, lattice contribution and total elastic stiffness tensor are presented in Table 10. Figure 6 shows the two and three-dimensional surface constructions of the elastic modulus for α-DIPAB. From Figure 6, it is obvious that elastic modulus of α-DIPAB exhibits a large deviation in shape from spherical symmetry indicating a strong anisotropic behavior in different directions. The 3D contour deviates from the spherical shape laterally along the z- axis along which it exhibits the largest value. The large deviation from spherical shape along z-axis indicates that elastic modulus of α-DIPAB is highly anisotropic.
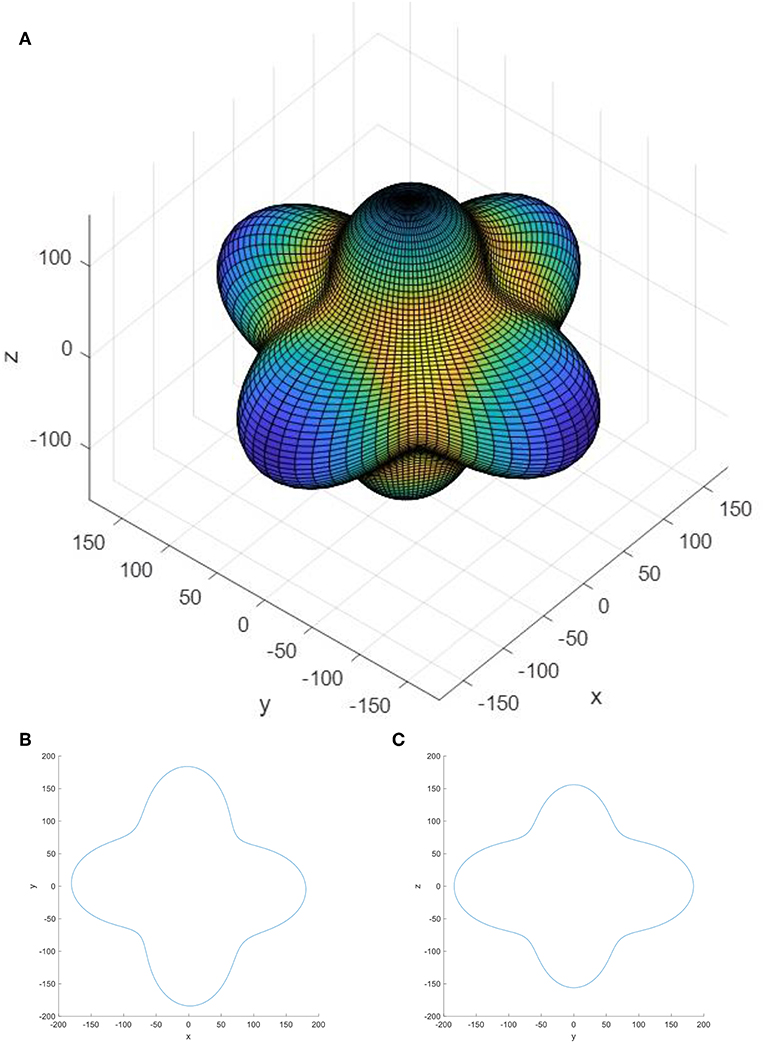
Figure 6. (A) 3D, (B) xy 2D, and (C) yz 2D representation of the elastic modulus of α-DIPAB. The contour indicates the magnitude of elastic modulus along different directions. The units along x and y-axes are GPa.
Anisotropies of mechanical properties are investigated by calculating the directional dependences of Young's modulus of α-DIPAB. We found that the Young's modulus exhibits evident anisotropy, with the largest value 150 GPa along the normal of {111} planes and the minimum value 50 GPa along the {100} planes normal.
Several previous studies has been performed to study the static and dynamic dielectric tensors, piezoelectric, and elastic characteristics of the first known ferroelectrics crystals such as Rochelle salt crystals [36, 37]. For the α-DIPAB, the elastic stiffness tensor is symmetrical obeying the relations , , , . The table shows that α-DIPAB exhibits negative diagonal elastic moduli and the magnitudes of the components indicate that the material is relatively soft. This result shows that this material has a potential to be used in flex circuits for flexible electronic applications. Flexible electronics is a technology for assembling electronic circuit by mounting electronic devices on substrates [55]. The Siegfried Bauer article “Sophisticated skin” and the related articles [56–65] presented the idea of sophisticated electronic skin for understanding the functioning of light- emitting diodes (OLEDs).
Flexible electronics is projected to provide the market with new generation of smart devices that are characterized of low cost of production, lightweight, thinner, non-breakable. Flexible electronic assemblies may be manufactured using boards conform to a desired shape. The light weight and non-toxic nature of α-DIPAB with Young's modulus of 50–150 GPa and shear modulus of 4–26 GPa make it good candidate as substrate for flex circuit boards and electronic skin.
Summary and Conclusions
In summary, ab initio computations are performed to compute all tonsorial elements of the gradient vector and Hessian matrix of α-DIPAB molecular crystal. The main theme of this work is to reveal the relationship between the accurate computation of diagonal force constant matrix, elastic constant, dielectric susceptibility matrices; and off-diagonal components: force response “internal strain tensor,” Born dynamical charges, piezoelectric tensors and the modeling of potential α-DIPAB-based devices. Accurate parameterization of all tonsorial elements is essential for the accurate description of the energy landscape for modeling of realistic optoelectronic and piezoelectric devices at finite temperatures. Furthermore, we found that α-DIPAB molecular crystal exhibits a significantly enhanced spontaneous polarization of 22.64 μC/cm2 due the stabilization of large unit-dipole canting. Interestingly, such large value of spontaneous polarization of this easy processing, Lead-free, environment friendly compound is comparable to those of traditional perovskites. Consequently, α-DIPAB crystal offers a low cost alternative for several expensive and environment unfriendly perovskites. To get a deeper insight and to reveal the actual structure of α-DIPAB crystal, it is critical to calculate the Born effective charges for each species of the crystal. We found a negative Born effective charge for nitrogen (~ −0.8e), positive for carbon atom bonded to nitrogen (~ +0.4e) and negative of more than 1e for Bromine. Such values indicate that during the growth of DIPAB, HBr molecules react with DIPA components resulting in a crystal structure that could be considered as “layered,” where bromine ions (Br−) intermediate the indirect bonding between neighboring layers of DIPA+ molecules. Exploring α-DIPAB crystal for potential dielectric applications lead us to compute the principle components of the static dielectric tensor of α-DIPAB. We found it to be (~ 2.5) comparable with that of Diisoamylene (2.4) and about 50 % of that of BTO. As a result, our findings provide substantial evidence of the importance of this crystal for potential dielectric devices. Accurate calculation of static dielectric constant is critical for the molding and design of realistic capacitors employing the dielectric properties of insulator α-DIPAB at finite temperatures. As far as piezoelectric applications of α-DIPAB are concerned, we found that α-DIPAB exhibits piezoelectric coefficients and indicating a significant piezoelectric response that makes the molecule attractive for several electro-mechanical applications such as micro-electro mechanical (MEM) switch. The total elastic moduli calculations show that α-DIPAB exhibits Young's modulus of ~ 50−180 GPa, while shear modulus of ~ 4−26 GPa. Thus, α-DIPAB has a strong potential for flexible electronic applications. Elastic properties of this material are of particular interest because of the potential application in flexible electronic and sensor applications.
Data Availability Statement
The datasets generated for this study are available on request to the corresponding author.
Author Contributions
AAl has participated in performing all calculations and analysis of results. RS has supervised Born effective charge and piezoelectric tensor calculations. AAh has participated in data analysis and writing the manuscript. IQ has performed elastic tensor calculations and participated in writing the manuscript. ZA has participated in 3D and 2D plots of piezoelectric and elastic tensors, analyzed data, and wrote the paper. NA-A has performed calculations to calculate the equilibrium structure of alpha-DIPAB. QA-B has participated in data analysis, writing the manuscript, and performed the elastic tensor calculations.
Funding
This work was supported by NSF-MRSEC (Grant No. DMR-1310542, and in partDMR-0820521) and NCMN. The University of Nebraska Holland Computing Center has provided computations resources.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
AAl is grateful to Jordan University of Science and Technology at Irbid, Jordan for providing him with the financial support to come to University of Nebraska at Omaha (UNO), USA to spend his sabbatical year. We would like to acknowledge the technical and generous financial support provided by Khalifa University of Science and Technology.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2019.00203/full#supplementary-material
References
1. King-Smith R, Vanderbilt D. Theory of polarization of crystalline solids. Phys Rev B. (1993) 47:1651. doi: 10.1103/PhysRevB.47.1651
2. Resta R, Posternak M, Baldereschi A. Towards a quantum theory of polarization in ferroelectrics: the case of KNbO 3. Phys Rev Lett. (1993) 70:1010. doi: 10.1103/PhysRevLett.70.1010
3. Scott J. Applications of modern ferroelectrics. Science. (2007) 315:954–9. doi: 10.1126/science.1129564
4. Haertling GH. Ferroelectric ceramics: history and technology. J Am Ceram Soc. (1999) 82:797–818. doi: 10.1111/j.1151-2916.1999.tb01840.x
5. Heywang W, Lubitz K, Wersing W. Piezoelectricity: Evolution and Future of a Technology. Vol. 114. New York, NY: Springer Science and Business Media (2008).
6. Tong S, Narayanan M, Ma B, Liu S, Koritala R E, Balachandran U, et al. Effect of lanthanum content and substrate strain on structural and electrical properties of lead lanthanum zirconate titanate thin films. Mater Chem Phys. (2013) 140:427–30. doi: 10.1016/j.matchemphys.2013.03.067
7. Fu DW, Zhang W, Cai H L, Ge JZ, Zhang Y, Xiong R G. Diisopropylammonium chloride: a ferroelectric organic salt with a high phase transition temperature and practical utilization level of spontaneous polarization. Adv Mater. (2011) 23:5658–62. doi: 10.1002/adma.201102938
8. Kociok-Köhn G, Lungwitz B, Filippou AC. Diisopropylammonium bromide. Acta Crystallogr C. (1996) 52:2309–11. doi: 10.1107/S010827019600354X
9. Fu D-W, Cai H-L, Liu Y, Ye Q, Zhang W, Zhang Y, et al. Diisopropylammonium bromide is a high-temperature molecular ferroelectric crystal. Science. (2013) 339:425–8. doi: 10.1126/science.1229675
10. Horiuchi S, Tokunaga Y, Giovannetti G, Picozzi S, Itoh H, Shimano R, et al. Above-room-temperature ferroelectricity in a single-component molecular crystal. Nature. (2010) 463:789–92. doi: 10.1038/nature08731
11. Veithen M, Gonze X, Ghosez P. First-principles study of the electro-optic effect in ferroelectric oxides. Phys Rev Lett. (2004) 93:187401. doi: 10.1103/PhysRevLett.93.187401
12. Lovinger AJ. Ferroelectric polymers. Science. (1983) 220:1115–21. doi: 10.1126/science.220.4602.1115
14. Alsaad A, Marin CM, Alaqtash N, Chao H-W, Chang T-H, Cheung CL, et al. Effect of bromine deficiency on the lattice dynamics and dielectric properties of alpha-phase diisopropylammonium bromide molecular crystals. J Phys Chem Solids. (2018) 113:82–5. doi: 10.1016/j.jpcs.2017.10.004
15. Alsaad A, Marin CM, Alaqtash N, Chao H-W, Chang T-H, Cheung CL, et al. Crystallographic, vibrational modes and optical properties data of α-DIPAB crystal. Data Brief. (2018) 16:667–84. doi: 10.1016/j.dib.2017.11.074
16. Fu D-W, Cai H-L, Li S-H, Ye Q, Zhou L, Zhang W, et al. 4-Methoxyanilinium perrhenate 18-crown-6: a new ferroelectric with order originating in swinglike motion slowing down. Phys Rev Lett. (2013) 110:257601. doi: 10.1103/PhysRevLett.110.257601
17. Zhang W, Xiong R-G. Ferroelectric metal–organic frameworks. Chem Rev. (2011) 112:1163–95. doi: 10.1021/cr200174w
18. Lines ME, Glass AM. Principles and Applications of Ferroelectrics and Related Materials. New York, NY: Oxford university press (2001).
19. Kadau K, Germann TC, Lomdahl PS, Holian BL. Microscopic view of structural phase transitions induced by shock waves. Science. (2002) 296:1681–4. doi: 10.1126/science.1070375
20. Collet E, Lemée-Cailleau M-H, Buron-Le Cointe M, Cailleau H, Wulff M, Luty T, et al. Laser-induced ferroelectric structural order in an organic charge-transfer crystal. Science. (2003) 300:612–5. doi: 10.1126/science.1082001
21. Tinte S, Stachiotti M, Phillpot S, Sepliarsky M, Wolf D, Migoni R. Ferroelectric properties of BaxSr1– xTiO3 solid solutions obtained by molecular dynamics simulation. J Phys Condens Matter. (2004) 16:3495. doi: 10.1088/0953-8984/16/20/019
22. Beckman S, Wang X, Rabe K M, Vanderbilt D. Ideal barriers to polarization reversal and domain-wall motion in strained ferroelectric thin films. Phys Rev B. (2009) 79:144124. doi: 10.1103/PhysRevB.79.144124
23. Giovannetti G, Ortix C, Marsman M, Capone M, Van Den Brink J, Lorenzana J. Proximity of iron pnictide superconductors to a quantum tricritical point. Nat Commun. (2011) 2:398. doi: 10.1038/ncomms1407
24. Hohenberg P, Kohn W. Inhomogeneous electron gas. Phys Rev. (1964) 136. B864. doi: 10.1103/PhysRev.136.B864
25. Perdew JP, Chevary JA, Vosko SH, Jackson KA, Pederson MR, Singh DJ, et al. Atoms, molecules, solids, and surfaces: applications of the generalized gradient approximation for exchange and correlation. Phys Rev B. (1992) 46:6671. doi: 10.1103/PhysRevB.46.6671
26. Kresse G, Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys Rev B. (1999) 59:1758. doi: 10.1103/PhysRevB.59.1758
27. Perdew JP, Burke K, Ernzerhof M. Generalized gradient approximation made simple. Phys Rev Lett. (1996) 77:3865. doi: 10.1103/PhysRevLett.77.3865
28. Kudin KN, Car R, Resta R. Berry phase approach to longitudinal dipole moments of infinite chains in electronic-structure methods with local basis sets. J Chem Phys. (2007) 126:234101. doi: 10.1063/1.2743018
29. Piecha A, Gągor A, Jakubas R, Szklarz P. Room-temperature ferroelectricity in diisopropylammonium bromide. Cryst Eng Comm. (2013) 15:940–4. doi: 10.1039/C2CE26580J
30. Lee JH, Fang L, Vlahos E, Ke X, Jung YW, Kourkoutis LF, et al. A strong ferroelectric ferromagnet created by means of spin–lattice coupling. Nature. (2010) 466:954–8. doi: 10.1038/nature09331
31. Dion M, Rydberg H, Schröder E, Langreth DC, Lundqvist BI. Van der Waals density functional for general geometries. Phys Rev Lett. (2004) 92:246401. doi: 10.1103/PhysRevLett.92.246401
32. Román-Pérez G, Soler JM. Efficient implementation of a van der Waals density functional: application to double-wall carbon nanotubes. Phys Rev Lett. (2009) 103:096102. doi: 10.1103/PhysRevLett.103.096102
33. Klimeš J, Bowler DR, Michaelides A. Van der Waals density functionals applied to solids. Phys Rev B. (2011) 83:195131. doi: 10.1103/PhysRevB.83.195131
34. Klimeš J, Bowler DR, Michaelides A. Chemical accuracy for the van der Waals density functional. J Phys Condens Matter. (2009) 22:022201. doi: 10.1088/0953-8984/22/2/022201
35. Wu X, Vanderbilt D, Hamann D. Systematic treatment of displacements, strains, and electric fields in density-functional perturbation theory. Phys Rev B. (2005) 72:035105. doi: 10.1103/PhysRevB.72.035105
36. Baroni S, Giannozzi P, Testa A. Green's-function approach to linear response in solids. Phys Rev Lett. (1987) 58:1861. doi: 10.1103/PhysRevLett.58.1861
37. Prosandeev S, Bellaiche L. Characteristics and signatures of dipole vortices in ferroelectric nanodots: first-principles-based simulations and analytical expressions. Phys Rev B. (2007) 75:094102. doi: 10.1103/PhysRevB.75.094102
38. Naumov II, Bellaiche L, Fu H. Unusual phase transitions in ferroelectric nanodisks and nanorods. Nature. (2004) 432:737–40. doi: 10.1038/nature03107
39. Akbarzadeh A, Bellaiche L, Leung K, Íñiguez J, Vanderbilt D. Atomistic simulations of the incipient ferroelectric K Ta O 3. Phys Rev B. (2004) 70:054103. doi: 10.1103/PhysRevB.70.054103
40. Li J, Porter L, Yip S. Atomistic modeling of finite-temperature properties of crystalline β-SiC: II. Thermal conductivity and effects of point defects. J Nucl Mater. (1998) 255:139–52. doi: 10.1016/S0022-3115(98)00034-8
41. Xu R, Liu B. A hybrid molecular dynamics/atomic-scale finite element method for quasi-static atomistic simulations at finite temperature. J Appl Mechan. (2014) 81:051005. doi: 10.1115/1.4025807
42. Dowben P, McIlroy D, Li D. Surface magnetism of the lanthanides. In: Handbook on the Physics and Chemistry of Rare Earths. Vol. 24. Seattle, WA: Amazon (1997). p. 1–46
43. Scott J. Phase transitions in ferroelectric thin films. Phase Transitions. (1991) 30:107–10. doi: 10.1080/01411599108207969
44. Wan L, Nishimatsu T, Beckman S. The structural, dielectric, elastic, and piezoelectric properties of KNbO3 from first-principles methods. J Appl Phys. (2012) 111:104107. doi: 10.1063/1.4712052
45. Axe J. Apparent ionic charges and vibrational eigenmodes of BaTiO3 and other perovskites. Phys Rev. (1967) 157:429. doi: 10.1103/PhysRev.157.429
46. Ghosez PSH, Gonze X, Michenaud JP. Ab initio phonon dispersion curves and interatomic force constants of barium titanate. Ferroelectrics. (1998) 206:205–17. doi: 10.1080/00150199808009159
48. Duerloo K-AN, Ong MT, Reed EJ. Intrinsic piezoelectricity in two-dimensional materials. J Phys Chem Lett. (2012) 3:2871–6. doi: 10.1021/jz3012436
49. Shimada K. First-principles determination of piezoelectric stress and strain constants of Wurtzite III–V nitrides. Jpn J Appl Phys. (2006) 45:L358. doi: 10.1143/JJAP.45.L358
50. Grundmann M, Stier O, Bimberg D. InAs/GaAs pyramidal quantum dots: strain distribution, optical phonons, and electronic structure. Phys Rev B. (1995) 52:11969. doi: 10.1103/PhysRevB.52.11969
51. Schulz S, Caro M, O'Reilly E, Marquardt O. Symmetry-adapted calculations of strain and polarization fields in (111)-oriented zinc-blende quantum dots. Phys Rev B. (2011) 84:125312. doi: 10.1103/PhysRevB.84.125312
52. Gonze X, Lee C. Dynamical matrices, Born effective charges, dielectric permittivity tensors, and interatomic force constants from density-functional perturbation theory. Phys Rev B. (1997) 55:10355. doi: 10.1103/PhysRevB.55.10355
53. Caro MA, Schulz S, O'Reilly EP. Comparison of stress and total energy methods for calculation of elastic properties of semiconductors. J Phys Condens Matter. (2012) 25:025803. doi: 10.1088/0953-8984/25/2/025803
54. Uchino K. Piezoelectric Actuators and Ultrasonic Motors. Vol. 1. New York, NY: Springer Science and Business Media (1996).
55. Park S-E, Wada S, Cross L, Shrout TR. Crystallographically engineered BaTiO3 single crystals for high-performance piezoelectrics. J Appl Phys. (1999) 86:2746–50. doi: 10.1063/1.371120
56. Auciello O, Scott JF, Ramesh R. The physics of ferroelectric memories. Phys Today. (1998) 51:22–7. doi: 10.1063/1.882324
57. Levitskii R, Zachek I, Verkholyak T, Moina A. Dielectric, piezoelectric, and elastic properties of the Rochelle salt NaKC4H4O6·4H2O: a theory. Phys Rev B. (2003) 67:174112. doi: 10.1103/PhysRevB.67.174112
58. Moina A, Levitskii R, Zachek I. Piezoelectric resonance and sound attenuation in the Rochelle salt NaKC 4 H 4 O 6· 4 H 2 O. Phys Rev B. (2005) 71:134108. doi: 10.1103/PhysRevB.71.134108
60. Wang C, Hwang D, Yu Z, Takei K, Park J, Chen T, et al. User-interactive electronic skin for instantaneous pressure visualization. Nat Mater. (2013) 12:899. doi: 10.1038/nmat3711
61. Webb RC, Bonifas AP, Behnaz A, Zhang Y, Yu KJ, Cheng H, et al. Ultrathin conformal devices for precise and continuous thermal characterization of human skin. Nat Mater. (2013) 12:938. doi: 10.1038/nmat3755
62. Suo Z. Mechanics of stretchable electronics and soft machines. Mrs Bull. (2012) 37:218–25. doi: 10.1557/mrs.2012.32
63. Wagner S, Bauer S. Materials for stretchable electronics. Mrs Bull. (2012) 37:207–13. doi: 10.1557/mrs.2012.37
64. Wang S, Li M, Wu J, Kim DH, Lu N, Su Y, et al. Mechanics of epidermal electronics. J Appl Mech. (2012) 79:031022. doi: 10.1115/1.4005963
65. Kaltenbrunner M, Sekitani T, Reeder J, Yokota T, Kuribara K, Tokuhara T, et al. An ultra-lightweight design for imperceptible plastic electronics. Nature. (2013) 499:458–63. doi: 10.1038/nature12314
66. Sutcliffe B T, Wilson S. Potential energy curves and surfaces. In: Handbook of Molecular Physics and Quantum Chemistry. London: Auris Reference Limited (2003). p. 574–87.
67. Zhigilei LV, Volkov A N, Dongare AM. Computational study of nanomaterials: from large-scale atomistic simulations to mesoscopic modeling. In: Encyclopedia of Nanotechnology. London: Auris Reference Limited (2012). p. 470–80.
68. Hagedorn GA, Joye A. Born–Oppenheimer approximations. In: Spectral Theory and Mathematical Physics: Quantum Field Theory, Statistical Mechanics, and Nonrelativistic Quantum Systems. Vol. 76. London: Auris Reference Limited (2007). p. 203.
69. Bernardini F, Fiorentini V, Vanderbilt D. Polarization-based calculation of the dielectric tensor of polar crystals. Phys Rev Lett. (1997) 79:3958. doi: 10.1103/PhysRevLett.79.3958
70. Mostofi AA, Yates JR, Lee YS, Souza I, Vanderbilt D, Marzari N. wannier90: a tool for obtaining maximally-localised Wannier functions. Comput Phys Commun. (2008) 178:685–99. doi: 10.1016/j.cpc.2007.11.016
Keywords: α-diisopropylammonium bromide, Vienna ab initio simulation package (VASP), piezoelectric and dielectric tensors, elastic and dielectric properties, molecular ferroelectrics
Citation: Alsaad A, Al-Aqtash N, Sabirianov RF, Ahmad A, Al-Bataineh QM, Qattan I and Albataineh Z (2019) First-Principles Calculation of Physical Tensors of α-Diisopropylammonium Bromide (α-DIPAB) Molecular Ferroelectric Crystal. Front. Phys. 7:203. doi: 10.3389/fphy.2019.00203
Received: 04 August 2019; Accepted: 14 November 2019;
Published: 29 November 2019.
Edited by:
Jinjin Li, Shanghai Jiao Tong University, ChinaReviewed by:
Anna Morozovska, National Academy of Sciences of Ukraine, UkraineEngin Deligoz, Aksaray University, Turkey
Chris Bowen, University of Bath, United Kingdom
Copyright © 2019 Alsaad, Al-Aqtash, Sabirianov, Ahmad, Al-Bataineh, Qattan and Albataineh. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: A. Alsaad, YWxzYWFkMTFAanVzdC5lZHUuam8=
 Ahmad Alsaad
Ahmad Alsaad Nabil Al-Aqtash2
Nabil Al-Aqtash2 Ahmad Ahmad
Ahmad Ahmad Qais M. Al-Bataineh
Qais M. Al-Bataineh Issam Qattan
Issam Qattan Zaid Albataineh
Zaid Albataineh