Feedback of Non-Local dxy Nematicity on the Magnetic Anisotropy in FeSe

We analyze theoretically the magnetic anisotropy in the nematic phase of FeSe by computing the spin and the orbital susceptibilities from the microscopic multiorbital model. In particular, we take into account both the xz/yz and the recently proposed non-local xy nematic ordering and show that the latter one could play a crucial role in reproducing the experimentally-measured temperature dependence of the magnetic anisotropy. This provides a direct fingerprint of the different nematic scenarios on the magnetic properties of FeSe.

1 Introduction

Iron-based superconductors offer the opportunity to explore the interplay between electronic nematicity, magnetism and superconductivity. While the broad studies on cuprates already provide insights into the competition between magnetism and superconductivity [1, 2], the role of the still enigmatic nematic state is of particular interest. Since anisotropy arises in crystal structure, orbital and spin degrees of freedom, it is intricate to decipher the underlying mechanism [3, 4]. In most of the iron pnictides the structural transition precedes or coincides with the magnetic transition at T_N, below which long-range antiferromagnetic order sets in [5], supporting the idea that nematicity (spin nematicity) is driven by magnetic interactions [6]. Note that the spin-nematic scenario can also lead to an effective orbital ordering once one takes the orbital content of the spin fluctuations within the so-called orbital-selective spin-fluctuation scenario into account [7–9].

Among various iron-based superconductors, FeSe with a simple crystal structure of the stacked FeSe layers has a rather unique behavior due to the presence of a marked nematic (structural) transition at T_S = 90 K and a transition to superconductivity below T_c = 9 K, while magnetic order is absent [10–15]. Consequently, orbital degrees of freedom have also been proposed as the underlying mechanism for nematic order in FeSe [16–22]. The small lattice distortion contrasts with strong in-plane anisotropy of resistivity, magnetic susceptibility, electronic structure and orbital and momentum structure of the superconducting gap [23–34]. The phase diagram of FeSe is rich and sensitive to the application of hydrostatic pressure or chemical substitution [35–38]. Furthermore, various exotic superconducting states have been recently reported in this compound [15].

Recent experiments have overcame the intricacies of the formation of orthorombic domains in FeSe by applying uniaxial strain [39–43]. Using this technique, the in-plane anisotropy of resistivity, uniform magnetic susceptibility and the Knight shift have been found to exhibit the opposite sign of the anisotropy as compared to iron-pnictides [24, 25, 44–46]. Moreover, carefully avoiding eddy-current heating, a slight suppression of the Knight shift in the superconducting state has been measured recently, while superconductivity and nematicity seem to coexist [47–49]. This agrees with direct magnetization measurements [25].

From the experimental point of view the systematic investigation of the band-structure of FeSe by means of ARPES and quantum oscillations revealed a sizeable deformation of the Fermi surface, that can be described by the interplay of the d_xz, d_yz and d_xy orbitals, their spin-orbit coupling and the nematic order [50–53]. Concerning the nematic order there is general understanding about the existence of a xz/yz splitting that changes sign in going from the Brillouin-zone center to momenta around Q_X = (π, 0) and Q_Y = (0, π) points of the 1-Fe-unit cell Brillouin Zone (BZ) (both folded onto the M-point of the folded BZ with 2-Fe ions per unit cell). This can be represented by a nematic order parameter ${\mathrm{\Phi }}^{xz/yz}=⟨d_{xz}^{†}{d}_{xz}-d_{yz}^{†}{d}_{yz}⟩$, that is positive around the Γ point and is negative around the M point of the BZ. Accounting for this nematic order is straightforward but yields rather controversial electronic structure. In particular, a large electron pocket with mixed xz and xy character is expected at the M point of the BZ, which has not been resolved in the most recent ARPES measurements in detwinned samples [40–42]. One approach to explain these experimental data and to suppress modelled contributions associated with this pocket, is to include orbital-selective quasiparticle weights [26, 44, 54, 55]. More recently an alternative scenario has been proposed [56–59], where an additional non-local nematic order parameter accounting for the splitting of the xy occupancy in the two electron pockets ${\mathrm{\Phi }}^{xy}=⟨d_{xy}^{X†}{d}_{xy}^X-d_{xy}^{Y†}{d}_{xy}^Y⟩$ [56–58] plays a crucial role. An important consequence of this scenario is a resulting occurrence of a Lifshitz transition at the M-point leaving only one electron pocket at the Fermi level.

This possibility to have a non-local nematic ordering of the d_xy states was previously outlined in the literature [60–62] but assumed to be small in the models having on-site interaction terms only. However, an inclusion of the nearest-neighbor interaction terms (such as nearest neighbor exchange or Coulomb interaction) would change this picture. Note, recent NMR [63] and ARPES [41, 42] have also suggested that the d_xy orbital may be strongly affected by the onset of the nematic state.

In this manuscript we investigate the consequences of the non-local d_xy-nematic scenario for the magnetic susceptibility taking into account spin and orbital contributions. We analyze its temperature and doping dependencies and compare the results to the available experiments. We show that the non-local nematicity is responsible for the non-monotonic temperature dependence of the susceptibility and predict how it evolves with doping in FeSe_1−xS_x. Finally we studied how the magnetic anisotropy is affected in the superconducting state.

2 Methods

We adopt the low energy model for FeSe, previously employed in Ref. [56], and fitted to the available ARPES experiments [40, 45, 64]. It is based on the generalized low-energy effective model for iron-based superconductors, formulated by Cvetkovic and Vafek [65].

2.1 Tetragonal State

In particular, to describe the tetragonal state of FeSe, we start by describing the low-energy states near the corresponding symmetry points of the BZ. In particular, near the Γ point of the BZ there are two Fermi surface pockets formed by the hybridized xz- and yz-orbitals. For completeness we also take the xy-orbital band into account which is located approximately 50 meV below the Fermi level [64]. Its inclusion allows to treat correctly the spin-orbit coupling (SOC) within the t_2g manifold. The states can be described by the spinor ${\mathrm{\Psi }}_{\mathrm{\Gamma },\mathbf{k}}^{†}=(d_{xz\uparrow }^{†},d_{yz\uparrow }^{†},d_{xy\downarrow }^{†})$, where the other (“lower”) spin part of the Hamiltonian is related by symmetry. For readability we omit the momentum index in the creation and annihilation operators here and in what follows. In particular, for each momentum k the Hamiltonian is given by

$H^{\mathrm{\Gamma }}\left(\mathbf{k}\right)=\left(\begin{array}{ccc}\hfill {ϵ}_{xz,\mathbf{k}}-\frac{b}{2}\left(k_x^2-k_y^2\right)\hfill & \hfill b{k}_x{k}_y-i\frac{{\lambda }_1}{2}\hfill & \hfill \frac{i{\lambda }_2}{2}\hfill \\ \hfill b{k}_x{k}_y+i\frac{{\lambda }_1}{2}\hfill & \hfill {ϵ}_{yz,\mathbf{k}}-\frac{b}{2}\left(k_y^2-k_x^2\right)\hfill & \hfill -\frac{{\lambda }_2}{2}\hfill \\ \hfill -\frac{i{\lambda }_2}{2}\hfill & \hfill -\frac{{\lambda }_2}{2}\hfill & \hfill {ϵ}_{xy,\mathbf{k}}\hfill \end{array}\right),(1)$

where ${ϵ}_{\mu ,\mathbf{k}}={ϵ}_{\mu ,0}-\frac{{\mathbf{k}}^2}{2m_{\mu }}-\mu$. Figure 1A shows the resulting band dispersion for the tetragonal state. The orbital weights of the bands are illustrated in the usual red-green-blue-color scheme for d_xz, d_yz and d_xy-orbitals, respectively.

FIGURE 1

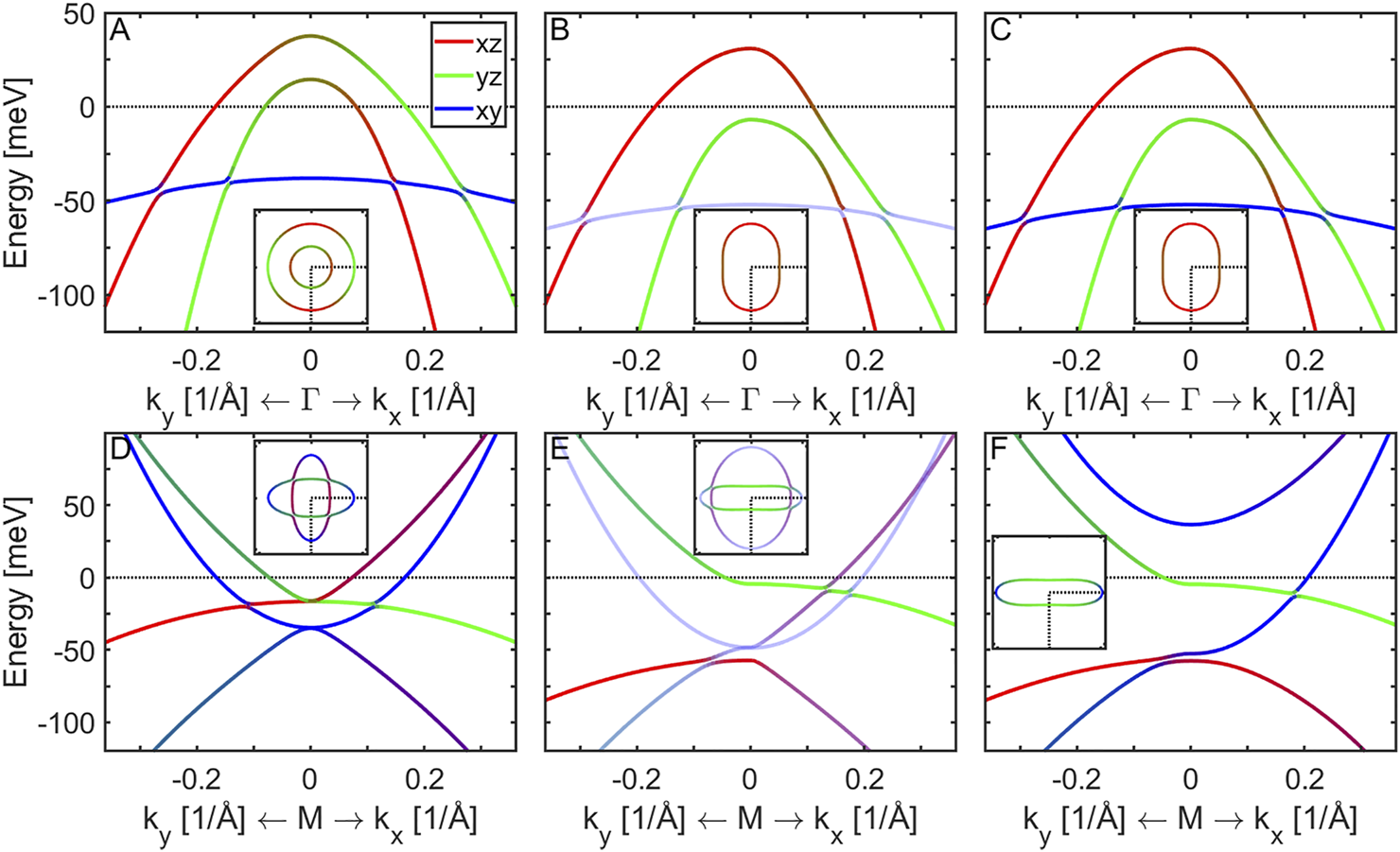
FIGURE 1. The band structure of the 2-Fe Brillouin zone around the Γ and the M point is presented comparing the tetragonal state and scenarios A and B for the nematic state in FeSe as described in the text. Panels (A)–(C) show the energy dispersion near the Γ point in the tetragonal state (A) and two nematic states without (Scenario A) (B) and with (C) non-local d_xy nematicity (Scenario B). Panels (D–F) display the corresponding band structure near the M point. Red, green and blue colors illustrate the orbital weights of the d_xz, d_yz and d_xy Fe-orbitals, respectively. The insets show the corresponding Fermi surface and demonstrate the cuts performed. Shading according to the d_xy orbital weight in panels (B) and (E) reflects the Z-factors used in [44].

To describe the electronic states near the M-point of the 2-Fe unit cell we introduce the spinors ${\mathrm{\Psi }}_{X/Y,\mathbf{k}}^{†}=(d_{yz/xz\uparrow }^{†},d_{xy\uparrow }^{†})$. The momenta are defined with respect to X/Y point of the 1-Fe unit cell, which are folded into the M-point. The Hamiltonian reads

$H^{X/Y}\left(\mathbf{k}\right)=\left(\begin{array}{cc}\hfill A_{yz/xz,\mathbf{k}}^{X/Y}\hfill & \hfill -i{V}_{\mathbf{k}}^{X/Y},\hfill \\ \hfill i{V}_{\mathbf{k}}^{X/Y}\hfill & \hfill A_{xy,\mathbf{k}}^{X/Y}.\hfill \end{array}\right).(2)$

and the elements are

$A_{\mu ,\mathbf{k}}^{X/Y}={ϵ}_{\mu ,0}-\frac{{\mathbf{k}}^2}{2m_{\mu }}\mp \frac{a_{\mu }}{2}\left(k_x^2-k_y^2\right)-\mu ,(3)$

$V^{X/Y}=\sqrt{2}v{k}_{y/x}+\frac{p_1}{\sqrt{2}}\left(k_{y/x}^3+3k_{y/x}{k}_{x/y}^2\right)\mp \frac{p_2}{\sqrt{2}}{k}_{y/x}\left(k_x^2-k_y^2\right).(4)$

The orbitals are coupled by the in-plane SOC λ₂

$H_{\text{SOC}}^M=\frac{{\lambda }_2}{2}\sum _{\mathbf{k}}\left(i_{yz\uparrow }^{X†}{d}_{xy\downarrow }^Y+d_{xy\uparrow }^{X,†}{d}_{xz\downarrow }^Y+h.c.\right).(5)$

The band dispersion for the tetragonal state near the M point is shown in the bottom panel of the Figure 1D. Note the value of SOC is taken different if the orbitals originate from the same sublattice in the 1-Fe unit cell, λ₁ = 23 meV or from the two different sublattices, λ₂ = 4 meV [66]. This agrees with the experimental ARPES observation, which measured different values of the SOC near different symmetry points of the BZ [67, 68].

2.2 Nematic State

To describe the nematic state in FeSe, which forms below the T_S = 90 K, we add the nematic order to the Hamiltonian in a phenomenological fashion. We assumed the nematic order parameters follow a mean-field temperature dependence $\mathrm{\Phi }(T)=\mathrm{\Phi }(0)\sqrt{1-T/T_S}$. As described in the Introduction we distinguish two scenarios: Scenario A containing an order parameter Φ^h,e that lifts the d_xz and d_yz degeneracy, and Scenario B in which an additional non-local d_xy-order parameter Φ_xy and a d_xy-Hatree shift Δϵ_xy are added [56].

In particular, the xz/yz nematic order parameter near the Γ point can be described as:

$H_{\text{nem}}^{\mathrm{\Gamma }}={\mathrm{\Phi }}^h\sum _{\mathbf{k},\sigma \in \left(\uparrow ,\downarrow \right)}\left(d_{xz,\sigma }^{†}{d}_{xz,\sigma }-d_{yz,\sigma }^{†}{d}_{yz,\sigma ,}\right).(6)$

For a given value of the SOC λ₁, adding a nematic order parameter yields a Lifshitz transition such that one of the Fermi surface pockets near the Γ point sinks below the Fermi level as shown in panels 1B and 1C for Φ^h(10 K) = 15 meV. Near the M point the xz/yz nematic order has opposite sign to Φ^h and we also include an additional non-local d_xy-nematic order [56]:

$H_{\text{nem}}^M=\sum _{\mathbf{k},\sigma }\left({\mathrm{\Phi }}^e\left(d_{xz,\sigma }^{Y†}{d}_{xz,\sigma }^Y-d_{yz,\sigma }^{X†}{d}_{yz,\sigma }^X\right)+\left(\mathrm{\Delta }{ϵ}_{xy}+{\mathrm{\Phi }}_{xy}\right)d_{xy,\sigma }^{Y†}{d}_{xy,\sigma }^Y+\left(\mathrm{\Delta }{ϵ}_{xy}-{\mathrm{\Phi }}_{xy}\right)d_{xy,\sigma }^{X†}{d}_{xy,\sigma }^X\right).(7)$

In the conventional scenario of nematicity (Scenario A), only Φ^e(10 K) = −26 meV is included and the resulting band structure near the M point is illustrated in Figure 1E. Observe two electron pockets at the M point, which exist for all temperatures. To connect Scenario A with experimental ARPES results in the nematic state, which do not observe the larger electron pocket, orbital-selective quasiparticle weights are introduced in various works [26, 30, 44, 54, 69], see also for a recent review Ref. [70]. Within this scenario the quasiparticle weight of the d_xy orbital is claimed to be much smaller than that of the d_yz/d_xz orbitals. This would lead to a suppression of the quasiparticle weight of the d_xy dominated bands and especially of the outer electron pocket at M point, making d_xy- rbital states invisible in the ARPES experiment. This is illustrated in panels 1B and 1E by orbital-selective shading. The idea of orbital-selective spectral weights is motivated also by the previous results of the dynamical mean-field theory calculations [71]. This scenario was claimed to be in agreement with STM measurements of the electronic structure [69], the superconducting gap properties [30], and the magnetic susceptibility measured by inelastic neutron scattering [26]. A problem of this scenario is that both in the tetragonal and the nematic state of FeSe, bands of d_xy orbital character have been identified around the M point [28]. Although d_xy orbital appears indeed to exhibit a larger effective mass renormalization than the other two orbitals, it is not sufficiently large to mask d_xy spectral weight completely in the ARPES experiments [64].

Within the Scenario B one introduces the non-local nematic order within the xy-orbital: Φ_xy(10 K) = 45 meV and Δϵ_xy(10 K) = 40 meV and the resulting band structure is shown in Figure 1F. As the band structure evolves from the tetragonal to the nematic state, an additional Lifshitz transition occurs around 70 K, leaving a single electron Fermi surface pocket at 10 K. The Scenario B assumes that the nematic ordering near the M point does not cause a minor perturbation of the electronic structure, but can lift an entire electron pocket away from the Fermi level. Its consequences for various experiments were reviewed in Ref. [59] and present an alternative description of the nematicity in FeSe. The chemical potential μ is renormalized to fulfill the Luttinger theorem and is set to zero at 10 K [56].

2.3 Superconducting State

It was argued in the past that within both the Scenario A and the Scenario B the superconducting order parameter and its angular dependence on the Fermi surface pockets can be equally well described within a microscopic description [54, 56]. This indicates that superconductivity just adopts the existing electronic structure in the nematic state without further significant feedback on the nematicity. So within Scenario B we use the microscopic description of Ref. [56]. In particular, below the superconducting transition at T_c = 8 K, we additionally include superconducting gaps in the d_xz and d_yz orbitals and use previously found values from a microscopic calculations describing an extended s-wave gap structure [56]. The values are obtained solving the gap equations at T = 0 K focusing on the bands crossing the Fermi surface. Possible d_xy contributions to the pairing interaction are neglected. To describe the temperature dependence we assume a typical BCS form ${\mathrm{\Delta }}_{\mu }(T)={\mathrm{\Delta }}_{\mu }(0\text{\hspace{0.17em}K})\tanh (1.74\sqrt{T_c/T-1})$. For the Γ point we use

$H_{\text{sc}}^{\mathrm{\Gamma }}=\sum _{\mathbf{k},\mu \in \left\{\text{xz,\hspace{0.17em}yz}\right\}}\left({\mathrm{\Delta }}_{\mu }^{\mathrm{\Gamma }}{d}_{\mu ,\uparrow ,\mathbf{k}}^{†}{d}_{\mu ,\downarrow ,-\mathbf{k}}^{†}+h.c.\right)(8)$

with ${\mathrm{\Delta }}_{xz}^{\mathrm{\Gamma }}(0\text{\hspace{0.17em}K})=-0.1$ meV and ${\mathrm{\Delta }}_{yz}^{\mathrm{\Gamma }}(0\text{\hspace{0.17em}K})=-5.3$ meV. For the M point we use

$H_{\text{sc}}^M=\sum _{\mathbf{k},\mu \in \left\{\text{yz}\left(\text{X}\right),\text{xz}\left(\text{Y}\right)\right\}}\left({\mathrm{\Delta }}_{\mu }^{X/Y}{d}_{\mu ,\uparrow ,\mathbf{k}}^{†}{d}_{\mu ,\downarrow ,-\mathbf{k}}^{†}+h.c.\right)(9)$

with ${\mathrm{\Delta }}_{xz}^Y(0\text{\hspace{0.17em}K})=3.1$ meV and ${\mathrm{\Delta }}_{yz}^X(0\text{\hspace{0.17em}K})=1.6$ meV. The resulting Bogoliubov-de Gennes Hamiltonian is diagonalized numerically.

2.4 Magnetic Susceptibility

Within random phase approximation (RPA) analysis of the magnetic susceptibility χ [72–74] the bare part of the susceptibility is given by a combination of normal and anomalous contributions (GG and FF-terms)

${\chi }_{{\eta }_1{\eta }_4}^{{\eta }_2{\eta }_3}\left(q\right)=\sum _k\left[F_{{\eta }_2{\eta }_4}\left(k\right){\bar{F}}_{{\eta }_1{\eta }_3}\left(k+q\right)-G_{{\eta }_2{\eta }_1}\left(k\right)G_{{\eta }_4{\eta }_3}\left(k+q\right)\right],(10)$

where G and F denote the single-particle normal and anomalous Green’s functions and the FF-term vanishes above T_c. We use the short hand notations k = (k, iω_n) and η = (μ, σ) denoting orbital and spin degrees of freedom. The sum of Matsubara frequencies is carried out analytically and yields a Lindhard-type expression for the bare susceptibilities. Further details can be found in the Supplementary Material S1.

Within RPA we include the local interactions from a Hubbard-Hund Hamiltonian

$\begin{array}{ll}\hfill H_{\mathit{int}}& =\frac{U}{2}\sum _{\mu \sigma \mathbf{k}{\mathbf{k}}^{\prime }\mathbf{q}}{d}_{\mu \sigma \mathbf{k}+\mathbf{q}}^{†}{d}_{\mu \bar{\sigma }{\mathbf{k}}^{\prime }-\mathbf{q}}^{†}{d}_{\mu \bar{\sigma }{\mathbf{k}}^{\prime }}{d}_{\mu \sigma \mathbf{k}}+\frac{U^{\prime }}{2}\sum _{\mu \ne \nu \sigma {\sigma }^{\prime }\mathbf{k}{\mathbf{k}}^{\prime }\mathbf{q}}{d}_{\mu \sigma \mathbf{k}+\mathbf{q}}^{†}{d}_{\nu {\sigma }^{\prime }{\mathbf{k}}^{\prime }-\mathbf{q}}^{†}{d}_{\nu {\sigma }^{\prime }{\mathbf{k}}^{\prime }}{d}_{\mu \sigma \mathbf{k}}\hfill \\ \hfill & +\frac{J}{2}\sum _{\mu \ne \nu \sigma {\sigma }^{\prime }\mathbf{k}{\mathbf{k}}^{\prime }\mathbf{q}}{d}_{\nu \sigma \mathbf{k}+\mathbf{q}}^{†}{d}_{\mu {\sigma }^{\prime }{\mathbf{k}}^{\prime }-\mathbf{q}}^{†}{d}_{\nu {\sigma }^{\prime }{\mathbf{k}}^{\prime }}{d}_{\mu \sigma \mathbf{k}}+\frac{J^{\prime }}{2}\sum _{\mu \ne \nu \sigma \mathbf{k}{\mathbf{k}}^{\prime }\mathbf{q}}{d}_{\mu \sigma \mathbf{k}+\mathbf{q}}^{†}{d}_{\mu \bar{\sigma }{\mathbf{k}}^{\prime }-\mathbf{q}}^{†}{d}_{\nu \bar{\sigma }{\mathbf{k}}^{\prime }}{d}_{\nu \sigma \mathbf{k}}.\hfill \end{array}(11)$

In what follows we set the intraorbital Coulomb repulsion interaction U = 1 eV. For the interorbital Coulomb repulsion U′, the residual Hund interaction J and the pair hopping J′ terms we use the standard spin-rotational relations U′ = U − 2J and J = J′ and set J/U = 1/6 similar to previous studies [26, 44].

The RPA treatment yields a Dyson type equation with a symbolic solution

${\chi }_{RPA}={\left[1-{\chi }_0\widehat{U}\right]}^{-1}{\chi }_0.(12)$

The interaction matrix $\widehat{U}$ results from Eq. 11 and the free spin and orbital indices are contracted with matrix elements from the magnetic operator, which is a combination of spin and angular momentum operators

${\mu }_{{\eta }_1{\eta }_4}^a=\left(\frac{g}{2}{\sigma }_{{\sigma }_1{\sigma }_4}^a{\delta }_{{\mu }_1{\mu }_4}+L_{{\mu }_1{\mu }_4}^a{\delta }_{{\sigma }_1{\sigma }_4}\right).(13)$

The magnetic susceptibility tensor component χ^ab results from the contraction of the external spin and orbital indices of the solution with the a-th and b-th component of the operator. We can separate the spin χ_spin, the orbital χ_orb and mixed χ_mix components of the susceptibility. In this manuscript we focus on the static limit of uniform susceptibility χ^ab(q → 0) and further details of the calculation can be found in the Supplementary Material S1.

3 Results

In the following we present the results for the magnetic susceptibility χ(q → 0) and its anisotropy following Scenario B. Note that within Scenario A the behavior of the magnetic susceptibility was considered in Ref. [44]. One of the main findings of this study was that in order to reproduce the correct sign of the magnetic anisotropy at low temperatures, i.e. χ^yy < χ^xx, the quasiparticle weight of various orbitals has to fulfil Z_xy < Z_xz < Z_yz. Within Scenario B this assumption is not necessary as the d_xy orbital is weakly present at the Fermi level and this should yield in principle the right sign of the magnetic anisotropy. We show in the Supplementary that further factors can affect the signs of the anisotropy as well and the situation depends on the details of the electronic structure in both Scenarios. In addition, in our case we find the dominance of the spin component of the susceptibility χ_mix < χ_orb < χ_spin, which is a consequence of the low-energy model we used. Moreover, we find that RPA primarily amplifies the spin contribution. Including the whole 3d state manifold would increase the temperature-independent orbital contribution to the susceptibility, which can be treated as a constant.

Nevertheless, one of the interesting questions is how to distinguish between both scenarios and whether one is able to identify an additional Lifshitz transition associated with the removal of the second electron pocket from the Fermi level at the M point both theoretically and experimentally. To do so we calculate the temperature dependence of the static uniform susceptibility and compare our results with experimental data of Ref. [25] where the standard notations x∥a, y∥b and z∥c are used.

The temperature dependence of the static uniform susceptibility is shown in Figure 2A. For comparison we also display the experimental data from Ref. [25] in the inset. Above the nematic transition the magnetic anisotropy is governed by the spin-orbit coupling and shows an easy-plane anisotropy χ^xx = χ^yy > χ^zz. Below T_S, one observes two characteristic features. First we find that χ^xx becomes progressively larger than χ^yy as a result of the nematic order and the splitting between them increases continuously upon decreasing temperature. At the same time all three components of the magnetic susceptibility show a non-monotonic temperature dependence characterized by a rapid decrease below T_S and a plateau-like behavior, which starts around 60 K. Both, a continuous increase of the anisotropy upon lowering temperature and the non-monotonic temperature dependence of the susceptibilities agree well with the available experimental data of Ref. [75], shown in the inset.

FIGURE 2

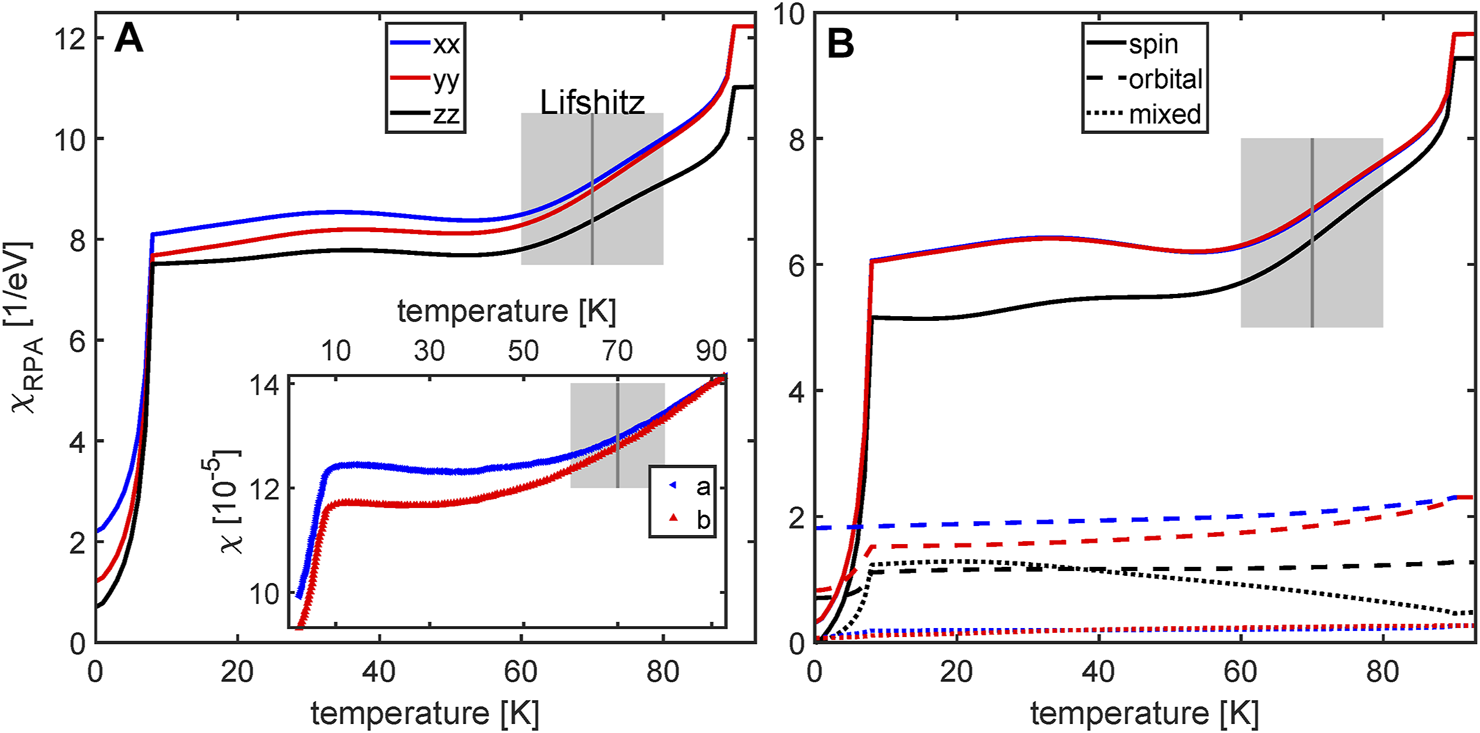
FIGURE 2. Calculated temperature dependence of the magnetic susceptibility χ(q → 0) calculated with an RPA approach. In (A) the total diagonal components χ^xx, χ^yy and χ^zz of the susceptibility calculated for scenario B are presented as blue, red and black curves, respectively. The corresponding spin, orbital and mixed contributions to the different components are shown in (B) as solid, dashed and dotted curves, respectively. The inset in (A) shows the experimental data extracted from [25] for comparison. The markers do not represent data points from the experiment. The gray boxes illustrate the decrease in susceptibility due to the Lifshitz transition of the Y-band. The boxes are centered around the Lifshitz transition temperature (dark gray line). Notice that the blue solid curve for the ${\chi }_{\text{spin}}^{xx}$ component in (B) is almost completely hidden behind the red curve for the ${\chi }_{\text{spin}}^{yy}$ component due to tiny in-plane anisotropy in the spin susceptibility.

To understand better the origin of these effects we show in Figure 2B the spin, the orbital, and the mixed susceptibilities. Note, the spin component of the magnetic susceptibility is the largest in magnitude and its non-monotonic temperature dependence is connected to the Lifshitz transition within Scenario B. In this scenario, the non-local d_xy nematic order parameter induces the shift of the larger electron pocket away from the Fermi level, which occurs in the temperature interval 60 K $<T<T_S$ and is clearly visible in the spin part of each (xx, yy and zz) component of the magnetic susceptibility. At the same time the main origin of the continuous increase of the magnetic in-plane anisotropy χ^xx > χ^yy comes from the orbital part of the magnetic susceptibility as evident from Figure 2B. The in-plane anisotropy for the spin susceptibility is three orders of magnitude smaller within our modeling, which is a consequence of the small in-plane SOC λ₂ present at the M point and of the out-of-plane SOC between xz and yz orbitals present at hole pockets only transferring out-of-plane anisotropy to the spin susceptibility. Overall the orbital susceptibility is less sensitive to the orbital content of the Fermi surface but to overall orbital structure at low energies. This indicates that not only the pockets at the Fermi level but the overall electronic structure (also away from the Fermi level) is responsible for the continuous increase of the magnetic anisotropy and its correct sign. Note that within both Scenario A and Scenario B of the nematicity in FeSe the correct sign of the magnetic in-plane anisotropy in the uniform susceptibility can be successfully reproduced. What, however, remains unclear in the Scenario A is whether the non-monotonous temperature dependence, which in Scenario B is a clear signature of a Lifshitz transition, could be reproduced in the Scenario A as well.

We also note that in the iron pnictides, where nematicity coexists with the antiferromagnetic order an in-plane anisotropy of the magnetic susceptibility would give a corresponding feedback on the magnetic order parameter and also enhance the anisotropy of the spin susceptibility below the magnetic transition temperature, see for example Ref. [76]. However, as the magnetic transition in FeSe appears only upon applying pressure and bearing in mind that the in-plane anisotropy we found is only few percent of the total magnitude of the spin susceptibility, the anisotropy of the orbital susceptibility will be the main origin of the magnetic anisotropy in FeSe.

To complete the analysis we also computed the change of the uniform superconductivity in the superconducting state. Due to the spin singlet superconducting order parameter in FeSe we see a sharp drop in the uniform susceptibility upon entering the superconducting state, see Figure 2A. This is due to the strong reduction of the spin component of the susceptibility, as evident from Figure 2B. Note the small admixture of the spin-triplet component of the superconducting gap due to the finite spin-orbit coupling does not affect much the magnetic anisotropy in the spin part. The residual contribution to the magnetic susceptibility stems largely from the orbital part of the susceptibility and corresponds to inter-orbital contributions, which is slightly affected by the onset of superconductivity. The decrease in ${\chi }_{\text{orb}}^{yy}$ yields an increase of the in-plane anisotropy and results from intra-band contributions, which appear due to hybridization of d_yz and d_xy orbitals at Fermi level (compare Figure 1F).

To make a qualitative prediction on the evolution of the uniform susceptibility and its in-plane magnetic anisotropy in Figure 3, we present our calculations for the susceptibility in the doped FeSe_1−xS_x compounds, following previous analysis of superconductivity and nematicity [56]. In particular, we show χ^xx and χ^yy for x = 0, x = 0.085 and x = 0.135 in panels 3A-3C, respectively. The doping evolution of the nematic order parameters is modeled with a mean-field dependence $\mathrm{\Phi }(x)=\mathrm{\Phi }(0)\sqrt{1-x/x_0}$. Here we estimate x₀ = 0.18, T_S(x = 0.085) = 68 K and T_S(x = 0.135) = 55 K from interpolation of the phase diagram given in [77]. The Lifshitz transition is shifted to lower (relative) temperatures with increasing doping and is expected to disappear at around x ≈ 0.13. Thus, for intermediate doping, we expect to see further the Lifshitz transition and significant changed temperature dependence for doping above x = 0.135. As the orbital part is not as sensitive to the Lifshitz transition, significant residual in-plane anisotropy is expected for all dopings.

FIGURE 3

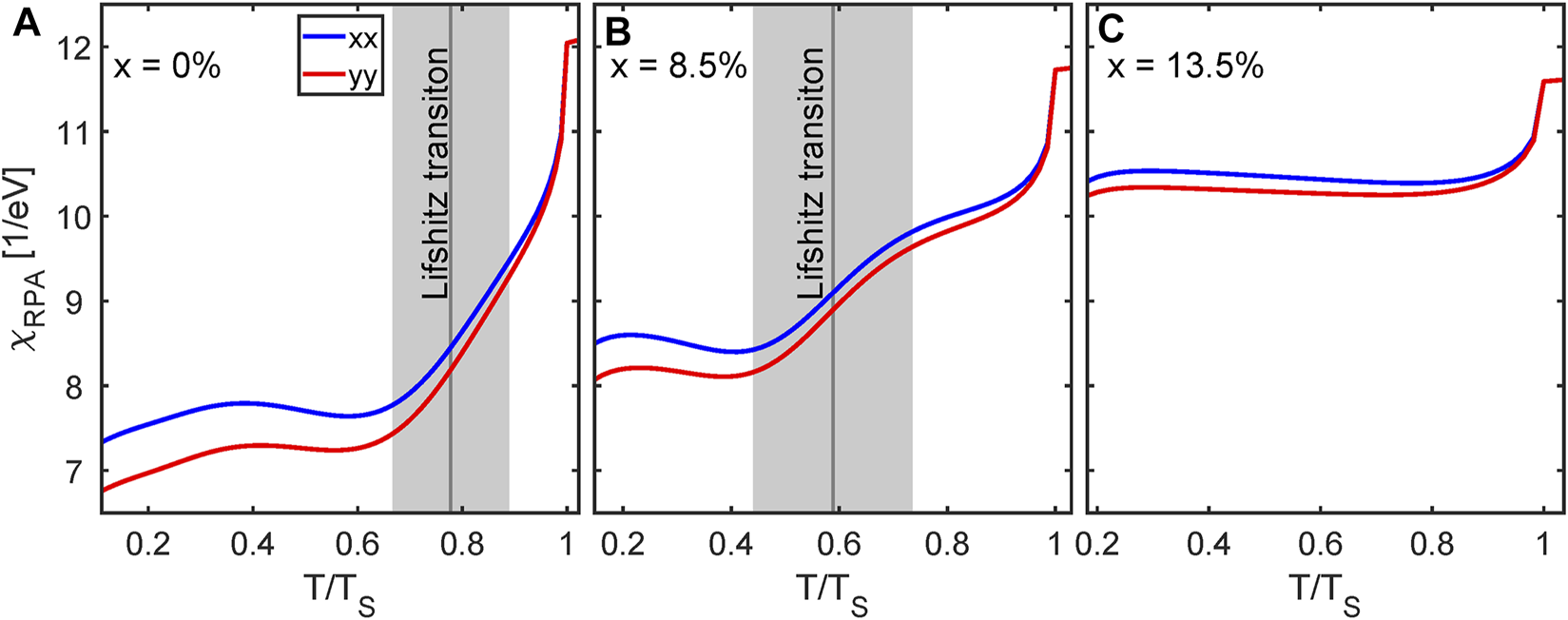
FIGURE 3. Calculated effect of sulphur doping of FeSe_1−xS_x on temperature dependence of the magnetic susceptibility χ(q → 0). The panels (A)–(C) compare the doping values x = 0, x = 0.085 and x = 0.135. As in 2, the gray boxes illustrate the Lifshitz transition region of the Y-band. For x = 13.5, the Lifshitz transition is absent.

4 Discussion and Conclusion

Our calculated results for the uniform magnetic susceptibility within the non-local d_xy nematicity agree well with experimental observations including the Knight shift measurements [16, 21, 25, 47, 48, 75]. Within this scenario there is no necessity to use orbital-selective quasiparticle weights. Furthermore, this scenario can also successfully explain the non-monotonic temperature dependence of the uniform susceptibility as resulting from the Lifshitz transition of the larger electron pocket, which rapidly shifts away from the Fermi level within 60 K $<T<T_S$ temperature interval.

Our studies suggest that both spin and orbital contributions and their temperature dependencies are important in describing the uniform magnetic susceptibility or the Knight shift. While the spin part provides the main contribution to the temperature dependence, the orbital part is crucial for a sizeable in-plane anisotropy as observed in experiments. The temperature dependence of the spin part fits very well to the scenario of a Lifshitz transition at Y-point, which appears due to the inclusion of the non-local d_xy-nematicity. The finite temperature dependence of the orbital susceptibility breaks linear relation between the bulk magnetic susceptibility and the Knight shift and naturally explains the observed Knight shift anomaly [47, 75]. We note further that the orbital contribution can be in fact larger if one includes larger energy window for the considered model. This should result in the larger in-plane anisotropy but will not affect the non-monotonic temperature dependence of the spin susceptibility.

Our results for the superconducting state also agree qualitatively with recent measurements. The decrease below T_c is seen in measurement of the static, uniform bulk susceptibility [25, 75] and also in the Knight shift measurements [47, 48]. Moreover, in agreement with our results, a slight enhancement of in-plane anisotropy is observed [47].

In summary, we have studied the uniform magnetic susceptibility for a model of FeSe and FeSe_1−xS_x compounds with particular attention on the consequences of non-local d_xy-nematicity. We associate the corresponding Lifshitz transition of a Y-electron pocket with a sharp decrease of the spin component of the magnetic susceptibility, whereas large in-plane anisotropy of the magnetic susceptibility is linked to the orbital susceptibility. The hierarchy of the anisotropy depend on orbital structure of the electronic bands at and away from the Fermi level where the orbital selective quasiparticle weights could be only one potential factor affecting the anisotropy.

We further note that the nematicity also affects the anisotropy of the spin fluctuations at the antiferromagnetic momentum near (π, 0) or (0, π) wavevectors. This anisotropy we also found in our calculations by computing the spin response at large momenta (not shown). This behavior is quite similar in both scenarios of nematicity, while we expect a different temperature dependence of the uniform magnetic susceptibility at q = 0 in both cases.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author/s.

Author Contributions

SB made the analytical and numercial calculations under the supervision of IE, both discussed the obtained results and wrote the manuscript.

Funding

This work was supported by a joint NSFC-DFG grant (ER 463/14-1).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We are thankful to Jakob Böker and Luke Rhodes for fruitful discussions. We also acknowledge support by the Open Access Publication Funds of the Ruhr-Universität Bochum.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.919784/full#supplementary-material

References

1. Kastner MA, Birgeneau RJ, Shirane G, Endoh Y. Magnetic, Transport, and Optical Properties of Monolayer Copper Oxides. Rev Mod Phys (1998) 70:897–928. doi:10.1103/RevModPhys.70.897

CrossRef Full Text | Google Scholar

2. Tranquada JM, Xu G, Zaliznyak IA. Superconductivity, Antiferromagnetism, and Neutron Scattering. J magnetism Magn Mater (2014) 350:148–60. doi:10.1016/j.jmmm.2013.09.029

CrossRef Full Text | Google Scholar

3. Fernandes RM, Chubukov AV, Schmalian J. What Drives Nematic Order in Iron-Based Superconductors? Nat Phys (2014) 10:97–104. doi:10.1038/nphys2877

CrossRef Full Text | Google Scholar

4. Böhmer AE, Kreisel A. Nematicity, Magnetism and Superconductivity in Fese. J Phys Condensed Matter (2017) 30:023001.

Google Scholar

5. Dai P. Antiferromagnetic Order and Spin Dynamics in Iron-Based Superconductors. Rev Mod Phys (2015) 87:855–96. doi:10.1103/revmodphys.87.855

CrossRef Full Text | Google Scholar

6. Fernandes RM, Schmalian J. Manifestations of Nematic Degrees of freedom in the Magnetic, Elastic, and Superconducting Properties of the Iron Pnictides. Supercond Sci Technol (2012) 25:084005. doi:10.1088/0953-2048/25/8/084005

CrossRef Full Text | Google Scholar

7. Fanfarillo L, Cortijo A, Valenzuela B. Spin-orbital Interplay and Topology in the Nematic Phase of Iron Pnictides. Phys Rev B (2015) 91:214515. doi:10.1103/PhysRevB.91.214515

CrossRef Full Text | Google Scholar

8. Fanfarillo L, Mansart J, Toulemonde P, Cercellier H, Le Fèvre P, Bertran F, et al. Orbital-dependent Fermi Surface Shrinking as a Fingerprint of Nematicity in Fese. Phys Rev B (2016) 94:155138. doi:10.1103/PhysRevB.94.155138

CrossRef Full Text | Google Scholar

9. Fanfarillo L, Benfatto L, Valenzuela B. Orbital Mismatch Boosting Nematic Instability in Iron-Based Superconductors. Phys Rev B (2018) 97:121109. doi:10.1103/PhysRevB.97.121109

CrossRef Full Text | Google Scholar

10. Hsu FC, Luo JY, Yeh KW, Chen TK, Huang TW, Wu PM, et al. Superconductivity in the Pbo-type Structure α-fese. Proc Natl Acad Sci (2008) 105:14262–4. doi:10.1073/pnas.0807325105

PubMed Abstract | CrossRef Full Text | Google Scholar

11. McQueen T, Williams A, Stephens P, Tao J, Zhu Y, Ksenofontov V, et al. Tetragonal-to-orthorhombic Structural Phase Transition at 90 K in the Superconductor Fe 1.01 Se. Phys Rev Lett (2009) 103:057002. doi:10.1103/PhysRevLett.103.057002

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Bendele M, Amato A, Conder K, Elender M, Keller H, Klauss HH, et al. Pressure Induced Static Magnetic Order in Superconducting Fese_1−x. Phys Rev Lett (2010) 104:087003. doi:10.1103/PhysRevLett.104.087003

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Gallais Y, Paul I. Charge Nematicity and Electronic Raman Scattering in Iron-Based Superconductors. Comptes Rendus Physique (2016) 17:113–39. Iron-based superconductors /Supraconducteurs à base de fer. doi:10.1016/j.crhy.2015.10.001

CrossRef Full Text | Google Scholar

14. Coldea AI, Watson MD. The Key Ingredients of the Electronic Structure of Fese. Annu Rev Condensed Matter Phys (2018) 9:125–46. doi:10.1146/annurev-conmatphys-033117-054137

CrossRef Full Text | Google Scholar

15. Shibauchi T, Hanaguri T, Matsuda Y. Exotic Superconducting States in Fese-Based Materials. J Phys Soc Jpn (2020) 89:102002. doi:10.7566/jpsj.89.102002

CrossRef Full Text | Google Scholar

16. Baek SH, Efremov D, Ok J, Kim J, Van Den Brink J, Büchner B. Orbital-driven Nematicity in Fese. Nat Mater (2015) 14:210–4. doi:10.1038/nmat4138

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Su Y, Liao H, Li T. The Form and Origin of Orbital Ordering in the Electronic Nematic Phase of Iron-Based Superconductors. J Phys Condensed Matter (2015) 27:105702. doi:10.1088/0953-8984/27/10/105702

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Mukherjee S, Kreisel A, Hirschfeld PJ, Andersen BM. Model of Electronic Structure and Superconductivity in Orbitally Ordered Fese. Phys Rev Lett (2015) 115:026402. doi:10.1103/PhysRevLett.115.026402

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Jiang K, Hu J, Ding H, Wang Z. Interatomic Coulomb Interaction and Electron Nematic Bond Order in Fese. Phys Rev B (2016) 93:115138. doi:10.1103/PhysRevB.93.115138

CrossRef Full Text | Google Scholar

20. Yamakawa Y, Onari S, Kontani H. Nematicity and Magnetism in Fese and Other Families of Fe-Based Superconductors. Phys Rev X (2016) 6:021032. doi:10.1103/physrevx.6.021032

CrossRef Full Text | Google Scholar

21. Böhmer A, Arai T, Hardy F, Hattori T, Iye T, Wolf T, et al. Origin of the Tetragonal-To-Orthorhombic Phase Transition in Fese: A Combined Thermodynamic and Nmr Study of Nematicity. Phys Rev Lett (2015) 114:027001. doi:10.1103/PhysRevLett.114.027001

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Xing RQ, Classen L, Khodas M, Chubukov AV. Competing Instabilities, Orbital Ordering, and Splitting of Band Degeneracies from a Parquet Renormalization Group Analysis of a Four-Pocket Model for Iron-Based Superconductors: Application to Fese. Phys Rev B (2017) 95:085108. doi:10.1103/PhysRevB.95.085108

CrossRef Full Text | Google Scholar

23. Margadonna S, Takabayashi Y, McDonald MT, Kasperkiewicz K, Mizuguchi Y, Takano Y, et al. Crystal Structure of the New Fese 1- X Superconductor. Chem Commun (2008) 5607–9. doi:10.1039/b813076k

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Tanatar MA, Böhmer AE, Timmons EI, Schütt M, Drachuck G, Taufour V, et al. Origin of the Resistivity Anisotropy in the Nematic Phase of Fese. Phys Rev Lett (2016) 117:127001. doi:10.1103/physrevlett.117.127001

PubMed Abstract | CrossRef Full Text | Google Scholar

25. He M, Wang L, Hardy F, Xu L, Wolf T, Adelmann P, et al. Evidence for Short-Range Magnetic Order in the Nematic Phase of Fese from Anisotropic In-Plane Magnetostriction and Susceptibility Measurements. Phys Rev B (2018) 97:104107. doi:10.1103/physrevb.97.104107

CrossRef Full Text | Google Scholar

26. Chen T, Chen Y, Kreisel A, Lu X, Schneidewind A, Qiu Y, et al. Anisotropic Spin Fluctuations in Detwinned Fese. Nat Mater (2019) 18:709–16. doi:10.1038/s41563-019-0369-5

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Lu X, Zhang W, Tseng Y, Liu R, Tao Z, Paris E, et al. Spin-excitation Anisotropy in the Nematic State of Detwinned Fese (2021). arXiv preprint arXiv:2108.04484.

Google Scholar

28. Coldea AI, Watson MD. The Key Ingredients of the Electronic Structure of Fese. Annu Rev Condensed Matter Phys (2018) 9:125–46. doi:10.1146/annurev-conmatphys-033117-054137

CrossRef Full Text | Google Scholar

29. Xu H, Niu X, Xu D, Jiang J, Yao Q, Chen Q, et al. Highly Anisotropic and Twofold Symmetric Superconducting gap in Nematically Ordered Fese 0.93 S 0.07. Phys Rev Lett (2016) 117:157003. doi:10.1103/physrevlett.117.157003

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Sprau PO, Kostin A, Kreisel A, Böhmer AE, Taufour V, Canfield PC, et al. Discovery of Orbital-Selective cooper Pairing in Fese. Science (2017) 357:75–80. doi:10.1126/science.aal1575

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Rhodes LC, Watson MD, Haghighirad AA, Evtushinsky DV, Eschrig M, Kim TK. Scaling of the Superconducting gap with Orbital Character in Fese. Phys Rev B (2018) 98:180503. doi:10.1103/physrevb.98.180503

CrossRef Full Text | Google Scholar

32. Kushnirenko Y, Fedorov A, Haubold E, Thirupathaiah S, Wolf T, Aswartham S, et al. Three-dimensional Superconducting gap in Fese from Angle-Resolved Photoemission Spectroscopy. Phys Rev B (2018) 97:180501. doi:10.1103/physrevb.97.180501

CrossRef Full Text | Google Scholar

33. Liu D, Li C, Huang J, Lei B, Wang L, Wu X, et al. Orbital Origin of Extremely Anisotropic Superconducting gap in Nematic Phase of Fese Superconductor. Phys Rev X (2018) 8:031033. doi:10.1103/physrevx.8.031033

CrossRef Full Text | Google Scholar

34. Hashimoto T, Ota Y, Yamamoto HQ, Suzuki Y, Shimojima T, Watanabe S, et al. Superconducting gap Anisotropy Sensitive to Nematic Domains in Fese. Nat Commun (2018) 9:1–7. doi:10.1038/s41467-017-02739-y

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Huh S, Lu Z, Kim YS, Kim D, Liu S, Ma M, et al. Cu Doping Effects on the Electronic Structure of Fe1-Xcuxse (2021). arXiv preprint arXiv:2110.14463.

Google Scholar

36. Mizuguchi Y, Tomioka F, Tsuda S, Yamaguchi T, Takano Y. Substitution Effects on Fese Superconductor. J Phys Soc Jpn (2009) 78:074712. doi:10.1143/jpsj.78.074712

CrossRef Full Text | Google Scholar

37. Schoop LM, Medvedev SA, Ksenofontov V, Williams A, Palasyuk T, Troyan IA, et al. Pressure-restored Superconductivity in Cu-Substituted Fese. Phys Rev B (2011) 84:174505. doi:10.1103/physrevb.84.174505

CrossRef Full Text | Google Scholar

38. Medvedev S, McQueen T, Troyan I, Palasyuk T, Eremets M, Cava R, et al. Electronic and Magnetic Phase Diagram of β-fe1. 01se with Superconductivity at 36.7 K under Pressure. Nat Mater (2009) 8:630–3. doi:10.1038/nmat2491

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Shimojima T, Suzuki Y, Sonobe T, Nakamura A, Sakano M, Omachi J, et al. Lifting of Xz/yz Orbital Degeneracy at the Structural Transition in Detwinned Fese. Phys Rev B (2014) 90:121111. doi:10.1103/PhysRevB.90.121111

CrossRef Full Text | Google Scholar

40. Watson MD, Haghighirad AA, Rhodes LC, Hoesch M, Kim TK. Electronic Anisotropies Revealed by Detwinned Angle-Resolved Photo-Emission Spectroscopy Measurements of Fese. New J Phys (2017) 19:103021. doi:10.1088/1367-2630/aa8a04

CrossRef Full Text | Google Scholar

41. Yi M, Pfau H, Zhang Y, He Y, Wu H, Chen T, et al. Nematic Energy Scale and the Missing Electron Pocket in Fese. Phys Rev X (2019) 9:041049. doi:10.1103/physrevx.9.041049

CrossRef Full Text | Google Scholar

42. Huh S, Seo J, Kim B, Cho S, Jung JK, Kim S, et al. Absence of Y-Pocket in 1-fe Brillouin Zone and Reversed Orbital Occupation Imbalance in Fese. Commun Phys (2020) 3:1–7.

CrossRef Full Text | Google Scholar

43. Pfau H, Yi M, Hashimoto M, Chen T, Dai PC, Shen ZX, et al. Quasiparticle Coherence in the Nematic State of Fese. Phys Rev B (2021) 104:L241101. doi:10.1103/physrevb.104.l241101

CrossRef Full Text | Google Scholar

44. Zhou R, Scherer DD, Mayaffre H, Toulemonde P, Ma M, Li Y, et al. Singular Magnetic Anisotropy in the Nematic Phase of Fese. npj Quan Mater (2020) 5:1–9. doi:10.1038/s41535-020-00295-1

CrossRef Full Text | Google Scholar

45. Watson MD, Kim TK, Haghighirad AA, Davies NR, McCollam A, Narayanan A, et al. Emergence of the Nematic Electronic State in Fese. Phys Rev B (2015) 91:155106. doi:10.1103/PhysRevB.91.155106

CrossRef Full Text | Google Scholar

46. Chu JH, Analytis JG, De Greve K, McMahon PL, Islam Z, Yamamoto Y, et al. In-plane Resistivity Anisotropy in an Underdoped Iron Arsenide Superconductor. Science (2010) 329:824–6. doi:10.1126/science.1190482

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Vinograd I, Edwards S, Wang Z, Kissikov T, Byland J, Badger J, et al. Inhomogeneous Knight Shift in Vortex Cores of Superconducting Fese. Phys Rev B (2021) 104:014502. doi:10.1103/physrevb.104.014502

CrossRef Full Text | Google Scholar

48. Li J, Kang B, Zhao D, Lei B, Zhou Y, Song D, et al. Se 77-nmr Evidence for Spin-Singlet Superconductivity with Exotic Superconducting Fluctuations in Fese. Phys Rev B (2022) 105:054514. doi:10.1103/physrevb.105.054514

CrossRef Full Text | Google Scholar

49. Pustogow A, Luo Y, Chronister A, Su YS, Sokolov D, Jerzembeck F, et al. Constraints on the Superconducting Order Parameter in Sr2ruo4 from Oxygen-17 Nuclear Magnetic Resonance. Nature (2019) 574:72–5. doi:10.1038/s41586-019-1596-2

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Zhang P, Qian T, Richard P, Wang XP, Miao H, Lv BQ, et al. Observation of Two Distinct D_xz/d_yz Band Splittings in Fese. Phys Rev B (2015) 91:214503. doi:10.1103/PhysRevB.91.214503

CrossRef Full Text | Google Scholar

51. Suzuki Y, Shimojima T, Sonobe T, Nakamura A, Sakano M, Tsuji H, et al. Momentum-dependent Sign Inversion of Orbital Order in Superconducting Fese. Phys Rev B (2015) 92:205117. doi:10.1103/PhysRevB.92.205117

CrossRef Full Text | Google Scholar

52. Zhang Y, Yi M, Liu ZK, Li W, Lee JJ, Moore RG, et al. Distinctive Orbital Anisotropy Observed in the Nematic State of a Fese Thin Film. Phys Rev B (2016) 94:115153. doi:10.1103/PhysRevB.94.115153

CrossRef Full Text | Google Scholar

53. Watson MD, Haghighirad AA, Takita H, Mansuer W, Iwasawa H, Schwier EF, et al. Shifts and Splittings of the Hole Bands in the Nematic Phase of Fese. J Phys Soc Jpn (2017) 86:053703. doi:10.7566/JPSJ.86.053703

CrossRef Full Text | Google Scholar

54. Kreisel A, Andersen BM, Sprau PO, Kostin A, Davis JS, Hirschfeld P. Orbital Selective Pairing and gap Structures of Iron-Based Superconductors. Phys Rev B (2017) 95:174504. doi:10.1103/physrevb.95.174504

CrossRef Full Text | Google Scholar

55. Hu H, Yu R, Nica EM, Zhu JX, Si Q. Orbital-selective Superconductivity in the Nematic Phase of Fese. Phys Rev B (2018) 98:220503. doi:10.1103/physrevb.98.220503

CrossRef Full Text | Google Scholar

56. Rhodes LC, Böker J, Müller MA, Eschrig M, Eremin IM. Non-local D Xy Nematicity and the Missing Electron Pocket in Fese. npj Quan Mater (2021) 6:1–14. doi:10.1038/s41535-021-00341-6

CrossRef Full Text | Google Scholar

57. Islam KR, Böker J, Eremin IM, Chubukov AV. Specific Heat and gap Structure of a Nematic Superconductor: Application to Fese. Phys Rev B (2021) 104:094522. doi:10.1103/physrevb.104.094522

CrossRef Full Text | Google Scholar

58. Marciani M, Benfatto L. Resistivity Anisotropy from Multiorbital Boltzmann Equation in Nematic Fese (2022). arXiv preprint arXiv:2202.12070.

Google Scholar

59. Rhodes LC, Eschrig M, Kim TK, Watson MD. Fese and the Missing Electron Pocket Problem. Frontiers in Physics (2022) 10:859017. doi:10.3389/fphy.2022.859017

CrossRef Full Text | Google Scholar

60. Fernandes RM, Vafek O. Distinguishing Spin-Orbit Coupling and Nematic Order in the Electronic Spectrum of Iron-Based Superconductors. Phys Rev B (2014) 90:214514. doi:10.1103/PhysRevB.90.214514

CrossRef Full Text | Google Scholar

61. Classen L, Xing RQ, Khodas M, Chubukov AV. Interplay between Magnetism, Superconductivity, and Orbital Order in 5-pocket Model for Iron-Based Superconductors: Parquet Renormalization Group Study. Phys Rev Lett (2017) 118:037001. doi:10.1103/PhysRevLett.118.037001

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Christensen MH, Fernandes RM, Chubukov AV. Orbital Transmutation and the Electronic Spectrum of Fese in the Nematic Phase. Phys Rev Res (2020) 2:013015. doi:10.1103/PhysRevResearch.2.013015

CrossRef Full Text | Google Scholar

63. Li J, Lei B, Zhao D, Nie LP, Song DW, Zheng LX, et al. Spin-orbital-intertwined Nematic State in Fese. Phys Rev X (2020) 10:011034. doi:10.1103/PhysRevX.10.011034

CrossRef Full Text | Google Scholar

64. Watson M, Kim T, Haghighirad A, Davies N, McCollam A, Narayanan A, et al. Emergence of the Nematic Electronic State in Fese. Phys Rev B (2015) 91:155106. doi:10.1103/physrevb.91.155106

CrossRef Full Text | Google Scholar

65. Cvetkovic V, Vafek O. Space Group Symmetry, Spin-Orbit Coupling, and the Low-Energy Effective Hamiltonian for Iron-Based Superconductors. Phys Rev B (2013) 88:134510. doi:10.1103/physrevb.88.134510

CrossRef Full Text | Google Scholar

66. Scherer DD, Jacko A, Friedrich C, Şaşıoğlu E, Blügel S, Valentí R, et al. Interplay of Nematic and Magnetic Orders in Fese under Pressure. Phys Rev B (2017) 95:094504. doi:10.1103/physrevb.95.094504

CrossRef Full Text | Google Scholar

67. Borisenko S, Evtushinsky DV, Liu ZH, Morozov I, Kappenberger R, Wurmehl S, et al. Direct Observation of Spin–Orbit Coupling in Iron-Based Superconductors. Nat Phys (2015) 12:311. doi:10.1038/nphys3594

CrossRef Full Text | Google Scholar

68. Day RP, Levy G, Michiardi M, Zwartsenberg B, Zonno M, Ji F, et al. Influence of Spin-Orbit Coupling in Iron-Based Superconductors. Phys Rev Lett (2018) 121:076401. doi:10.1103/PhysRevLett.121.076401

PubMed Abstract | CrossRef Full Text | Google Scholar

69. Kostin A, Sprau PO, Kreisel A, Chong YX, Böhmer AE, Canfield PC, et al. Imaging Orbital-Selective Quasiparticles in the Hund’s Metal State of Fese. Nat Mater (2018) 17:869. doi:10.1038/s41563-018-0151-0

PubMed Abstract | CrossRef Full Text | Google Scholar

70. Kreisel A, Hirschfeld PJ, Andersen BM. On the Remarkable Superconductivity of Fese and its Close Cousins. Symmetry (2020) 12. doi:10.3390/sym12091402

CrossRef Full Text | Google Scholar

71. Yin ZP, Haule K, Kotliar G. Kinetic Frustration and the Nature of the Magnetic and Paramagnetic States in Iron Pnictides and Ironchalcogenide. Nat Mater (2018) 10:932. doi:10.1038/nmat3120

PubMed Abstract | CrossRef Full Text | Google Scholar

72. Maier T, Graser S, Scalapino D, Hirschfeld P. Neutron Scattering Resonance and the Iron-Pnictide Superconducting gap. Phys Rev B (2009) 79:134520. doi:10.1103/physrevb.79.134520

CrossRef Full Text | Google Scholar

73. Graser S, Maier T, Hirschfeld P, Scalapino D. Near-degeneracy of Several Pairing Channels in Multiorbital Models for the Fe Pnictides. New J Phys (2009) 11:025016. doi:10.1088/1367-2630/11/2/025016

CrossRef Full Text | Google Scholar

74. Kemper AF, Maier TA, Graser S, Cheng HP, Hirschfeld P, Scalapino D. Sensitivity of the Superconducting State and Magnetic Susceptibility to Key Aspects of Electronic Structure in Ferropnictides. New J Phys (2010) 12:073030. doi:10.1088/1367-2630/12/7/073030

CrossRef Full Text | Google Scholar

75. Li J, Lei B, Zhao D, Nie L, Song D, Zheng L, et al. Spin-orbital-intertwined Nematic State in Fese. Phys Rev X (2020) 10:011034. doi:10.1103/physrevx.10.011034

CrossRef Full Text | Google Scholar

76. He M, Wang L, Ahn F, Hardy F, Wolf T, Adelmann P, et al. Dichotomy between In-Plane Magnetic Susceptibility and Resistivity Anisotropies in Extremely Strained Bafe₂as₂. Nat Commun (2017) 8. doi:10.1038/s41467-017-00712-3

PubMed Abstract | CrossRef Full Text | Google Scholar

77. Coldea AI, Blake SF, Kasahara S, Haghighirad AA, Watson MD, Knafo W, et al. Evolution of the Low-Temperature Fermi Surface of Superconducting Fese1- Xsx across a Nematic Phase Transition. npj Quan Mater (2019) 4:1–7. doi:10.1038/s41535-018-0141-0

CrossRef Full Text | Google Scholar