Estimating the stopping power distribution during proton therapy: A proof of concept

Objective: We introduce a new treatment verification technique to estimate the primary particle’s stopping power from prompt gamma timing measurements in proton therapy.

Approach: The starting point is the Spatio-temporal Emission Recostruction technique, which provides the time-depth distribution of the emitted prompt photons with a multiple Prompt-Gamma Timing detector setup based on Lanthanum Bromide crystals. A dedicated formalism based on an analytical approximation of the stopping power is developed to obtain the desired information. Its performance is evaluated in a proof of concept configuration via Monte Carlo simulations of monochromatic proton beams impinging on a homogeneous PMMA phantom.

Main Results: Results indicate stopping power estimations as good as 3.8% with respect to NIST values, and range estimations within 0.3 cm (standard deviation), when considering 250 ps FWHM timing resolution.

Significance: The current study shows, for the first time, the feasibility of evaluating the stopping power of primary beams with a technique that can be performed in-vivo, opening up new possibilities in the field of treatment verification and therapy optimization.

1 Introduction

Many efforts have been made to fully exploit charged particles’ specific features to deliver the most possible optimal dose. Although the characteristic dose maximum, defined by the Bragg peak, can be well characterized in materials of known composition and physical properties, uncertainties in its determination are encountered in the clinical practice [1, 2]. Several groups have tackled this issue, developing different techniques for treatment verification based on the detection of secondary particles [3–8]. Despite the efforts made in the treatment verification field, a clinical device completely integrated in the patient routine is yet to be available. In this paper we present, for the first time, a new approach to treatment verification, based on the evaluation of the primary beam’s electronic stopping power.

As the electronic stopping power is the main component of the delivered dose and it defines the Bragg peak position, it is a critical parameter for treatment optimization. Current measurements of the stopping power rely on assumptions—i.e., conversion from photon attenuation measured via X-ray Computed Tomography (CT), which is a major source of uncertainty [9]—or require beam line adaptations and additional beam time (proton CT) [10, 11]. These measurements are mainly deployed in treatment planning and cannot be used directly as a treatment verification tool during proton therapy. In this study, the stopping power of proton beams is estimated from the measurement of prompt photons.

Prompt photon radiation is produced from the nuclear de-excitation of nuclei left in an excited state after nuclear interaction. As prompt photons are emitted along the beam track almost synchronously with the irradiation, they offer a quasi real-time way of monitoring the treatment. Different techniques based on the detection of prompt photons have been developed for range verification [12]. Focusing on the Prompt-Gamma-Timing (PGT) technique, the measurement of the Time-Of-Flight (TOF), i.e. the difference between the detection time of prompt photons and the delivery time of primary protons, is exploited to gain information about the beam [13–16]. The TOF distribution depends on the prompt photon emission points and emission times, whose cumulative distribution is related to the average motion of the primary particles inside the target. The shape of the TOF distribution changes with the particle range, and can be used for treatment verification, as it depends on the target position and stopping power, beam energy, and detector position with respect to the target [17, 18].

In an attempt to propose a solution to the long-standing issue of how to reach an optimized, fast patient-tailored treatment planning, we recently introduced a reconstruction procedure with which to assess the primary particle range from PGT measurements [16]. The procedure, called Spatio-temporal Emission Reconstruction (SER-PGT), outputs a 2D-distribution of the emission of prompt photons in the space-time domain. It relies on the Maximum Likelihood Expectation Maximization (MLEM) algorithm followed by dedicated post-processing, and has the significant feature of not requiring any information about the target composition. The most interesting innovation of SER-PGT is that, it not only provides information about the range of the particles, but it is also useful to study the motion of the protons inside the target. In the current study, we expand the premises of SER-PGT, previously used to assess the particle range only, to estimate the stopping power of proton beams. In particular, an analytical function based on the Bortfeld approximation of the stopping power [19] is developed and used to fit the SER-PGT reconstruction output to obtain the desired information. To prove the concept of this technique, Monte Carlo simulations [20, 21] of monochromatic proton beams incident on homogeneous polymethyl methacrylate (PMMA) targets were used.

The proposed approach introduces a new way to perform treatment verification. Moreover, the approach outcomes could be directly compared to the stopping power maps obtained from the patient CT conversion, so as to better understand the particle beam properties and potentially reduce uncertainties given by stoichiometric approximations.

2 Materials and methods

2.1 Monte Carlo simulations

Simulations were carried out with the FLUKA Monte Carlo tool, 2020 version [20, 21]. The simulated setup comprises monolithic Cesium-doped Lanthanum bromide (LaBr₃:Ce) crystals arranged in a multi-detector configuration. This setup is based on the INFN MERLINO project, in which LaBr₃:Ce crystals coupled to either silicon photomultipliers (SiPM) or photomultiplier tubes (PMT) will be used to measure the prompt photon arrival time, whereas the primary proton time will be provided by Ultra-Fast Silicon Detectors (UFSDs), which have shown a timing resolution of the order of 10 ps for a 50 μm-thick sensor [22, 23]. As UFSDs are able to measure single protons with excellent timing performances, they were not modelled in the simulation. LaBr₃:Ce have excellent energy resolution (reaching ∼4% FWHM at 662 keV [24]), and have been found to be suitable for PGT applications [14, 17]. We simulated 110 LaBr₃:Ce detectors. Each detector has a cylindrical shape, with 3.81 cm diameter and 3.81 cm height. The chosen detector size represents a compromise between energy deposition within the energy range of interest and needed timing performances. Bigger crystals are better suited for higher energies, whereas smaller crystals lead to better timing performance.

The setup is shown in Figure 1. Note that the detectors are placed asymmetrically: for the considered scenario, with the beam at the isocenter, a symmetrical configuration would only contribute to improve the statistics, without adding any additional information. Instead, we have here different information coming from the TOF of detectors placed at different angles and positions.

FIGURE 1

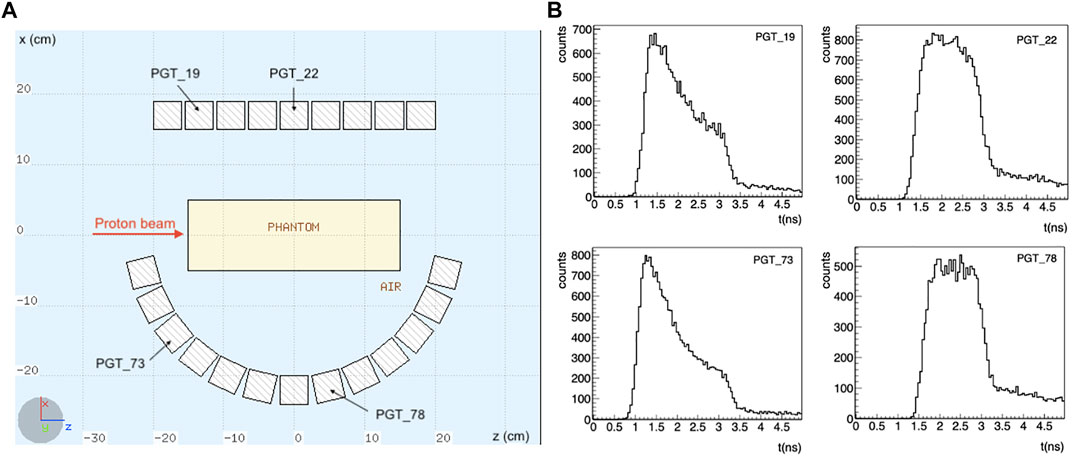
FIGURE 1. (A) Schematics of the simulated setup. A total of 110 LaBr₃:Ce detectors is considered, placed asymmetrically around the target, in 5 rows along the y axis. Only the central section of the setup is shown. The proton beam is impinging towards the positive z direction in a homogeneous PMMA phantom. (B) Some exemplary TOF distributions for a 200 MeV proton beam are shown. The TOF shape changes depending on the detector position with respect to the target. A timing resolution of 250 ps FWHM was considered.

Being this a proof of concept, we considered a homogeneous 10 × 10 × 30 cm³ PMMA phantom as target. Six monoenergetic proton beams ranging from 110 to 219 MeV were simulated at the isocenter (i.e. x = 0, y = 0), with a null initial transverse size along the z axis (beam axis). Still, particles are transported according to the physics model implemented in FLUKA, which produces lateral scattering and energy straggling [25]. For each energy, a total of 10⁷ protons was simulated, and 50 independent simulation runs were performed to increase the statistical significance of the result: 40 realizations were used for the method optimization and 10 for its validation.

The energy and interaction time of the detected events were smeared with a Gaussian distribution, considering 10% ΔE/E and 250 ps FWHM timing resolutions, respectively. Preliminary experimental investigation with the LaBr₃:Ce detector coupled to either the Hamamatsu R13089-11 PMT or an in-house SiPM tile showed energy resolutions ranging from 3 to 10% in the energy range of interest. The timing resolution, on the other hand, is consistent with previous experimental findings [17]. Therefore, the characteristics of the simulated detector represent a compromise to model both the scintillation crystals and electronics features, staying on a conservative side.

An energy window between 1 and 6 MeV was also applied to discard most uncorrelated events [15, 17]. The contribution of false proton-photons coincidences, which mainly depend on the accelerator and the fine time structure of the beam, was here not taken into account. This approximation is reasonable for this proof of concept since the approach can be tested experimentally with the accelerator operating at tens of MHz or less, where the false coincidence rate is negligible.

2.2 The SER-PGT model: A quick recap

SER-PGT is able to provide an estimation of the prompt photon emission inside the target in the spatio-temporal domain (z, t), provided that several TOF distributions are given as input. In this way, the information coming from a given set of detectors placed at different positions is integrated by means of MLEM. The reconstructed 2D-histogram of the prompt photon emission positions and times reflects the collective behavior of the protons. After reconstruction, pixels below a certain threshold T with respect to the maximum reconstructed intensity are excluded to mitigate artifacts and background noise. Both the number of iterations k and the post-reconstruction threshold T need to be optimized (see Section 2.4). To estimate the proton range inside the target, the center of gravity of the positions corresponding to the last reconstructed emission time is identified as the reconstructed range R₀. All spatio-temporal emission distributions were reconstructed here with a binning of 50 ps (0–5 ns) and 0.25 cm (−20–20 cm). For a full description of the algorithm, refer to [16].

2.3 Formulation of the problem

SER-PGT provides the prompt photons spatio-temporal distribution, but how do we get to a stopping power distribution from here?

Let’s first take a look at an analytical approximation of the stopping power. While the energy loss per unit distance was first described by Bethe in 1930 [26], the direct implementation of its equation is a non-trivial task. A relatively straightforward approximation can be found in Bortfeld’s description, which relies on the assumption that the Bragg curve resulting from Bethe’s equation can be described in closed form by a combination of a Gaussian and a parabolic cylindrical function [19]. Bortfeld assumes that the range inside a target R₀ is related to the particle’s initial kinetic energy E₀, so that $R_0=\alpha E_0^p$, with α and p being target material- and proton energy-dependent parameters [9, 19, 27]. In particular, α is inversely proportional to the target mass density [cmMeV^−p], whereas p is a number. In [19], Bortfeld describes the corresponding energy profile over distance in a target

$E\left(\widehat{z}\right)=\sqrt[p]{\frac{R_0-\widehat{z}}{\alpha }}(1)$

with $\widehat{z}=z-z_0$ representing the distance from the target entry. The two parameters α and p are also used in the description of the stopping power:

$S\left(\widehat{z}\right)=-\frac{dE}{dz}=\frac{1}{p\sqrt[p]{\alpha }}{\left(R_0-\widehat{z}\right)}^{1/p-1}.(2)$

Next we obtain a parametrization of (z, t) that depends on these two parameters, which can then be used to analyze the distribution in the emission space-time reconstructed by SER-PGT. The relativistic speed v of the primary proton is thus derived using the description introduced by Bortfeld:

$v\left(E\left(\widehat{z}\right)\right)=c\sqrt{1-{\left(\frac{m_0{c}^2}{E\left(\widehat{z}\right)+m_0{c}^2}\right)}^2}=c\sqrt{1-{\left(\frac{m_0{c}^2}{\sqrt[p]{\frac{R_0-\widehat{z}}{\alpha }}+m_0{c}^2}\right)}^2}(3)$

with m₀ the rest mass of the particle and c the speed of light. Integrating the inverse of the speed over the distance travelled inside the material yields the time t for each position z:

$t\left(z\right)={\int }_{z_0}^z\frac{d{z}^{\prime }}{v\left(E\left(z^{\prime }-z_0\right)\right)}+t_0={\int }_0^{z-z_0}\frac{d{\widehat{z}}^{\prime }}{v\left(E\left({\widehat{z}}^{\prime }\right)\right)}+t_0.(4)$

To solve this integral, we have obtained a closed solution for the undefined integral

$\begin{array}{c}\hfill \int \frac{d\widehat{z}}{v\left(E\left(\widehat{z}\right)\right)}=\frac{-p\left(R_0-\widehat{z}\right)}{c\left(4p^2-1\right)\sqrt{\frac{2m_0{c}^2}{E\left(\widehat{z}\right)}+1}}.\left(\left(p-1\right)\sqrt{\frac{2E\left(\widehat{z}\right)}{m_0{c}^2}+4}{}_2{F}_1\left(\frac{1}{2},p+\frac{1}{2};p+\frac{3}{2};-\frac{E\left(\widehat{z}\right)}{2m_0{c}^2}\right)+\left(\frac{2m_0{c}^2}{E\left(\widehat{z}\right)}+1\right)\left(2p+1\right)\right),\end{array}(5)$

where the term ₂F₁ is a realization of the generalized hypergeometric function [28]. The formulae implementation is done in C++ using the GNU scientific library¹, and its execution times are negligible with respect to the SER-PGT reconstruction times.

As the particle range R₀ can be expressed in terms of the initial particle energy, we see that the only dependence lays in E₀, in the particle mass at rest m₀ (which are both known values), and in the two unknown parameters α and p. Rearranging $R_0=\alpha E_0^p$ to $\alpha =\frac{R_0}{E_0^p}$ and using the range estimate obtained from SER-PGT allows us to have only p as a free parameter of t(z).

The reconstructed (z, t) distribution given py SER-PGT is converted to pairs of z and t by calculating the center of gravity of the positions of each temporal bin. The resulting data points are fitted to Eq. 5 using the ROOT 6.26/00 MINUIT implementation². An exemplary reconstructed emission is shown in Figure 2A for a 200 MeV beam impinging on PMMA. Its corresponding stopping power distribution (Eq. 2), obtained with the described fitting procedure, is reported in Figure 2B. The theoretical stopping power values, obtained from NIST³, are shown as reference.

FIGURE 2

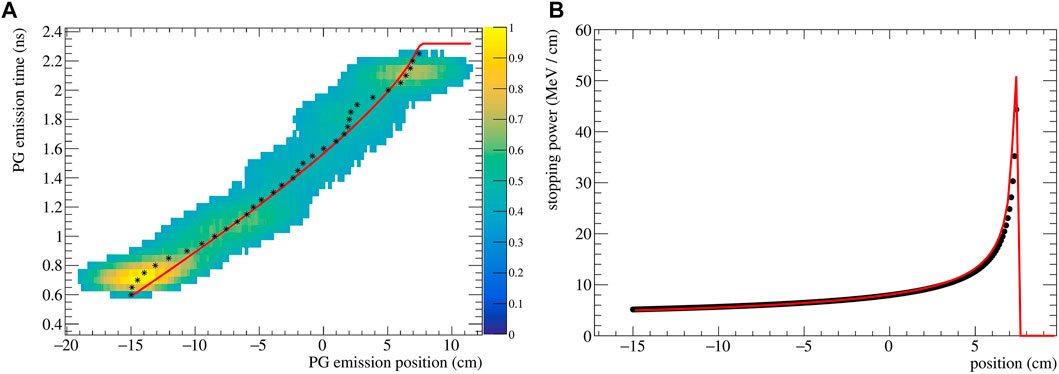
FIGURE 2. (A) Spatio-temporal emission reconstructed with the SER-PGT algorithm for a 200 MeV proton beam (10⁷ primary protons) impinging on a PMMA phantom. The reconstruction is made with 24 iterations, and a post-reconstruction threshold equal to 0.38. The black stars represent the mean value of each position at a fixed emission time. The distribution is fitted with an analytical function (red line) based on the Bortfeld approximation. (B) Corresponding stopping power distribution (red curve) and values from NIST (black points).

2.4 Optimization of the SER-PGT parameters

As seen in [16], the reconstructed spatio-temporal emission distribution depends on both the number of iterations k and the threshold T applied after reconstruction. We carried out a joint optimization of these two parameters by changing the values of k (from 1 to 100 with steps of 1) and T (from 0.025 to 0.8 with steps of 0.025). For each (k, T) combination, the resulting range R₀ and stopping power distribution were evaluated starting from the corresponding spatio-temporal emission. We repeated this evaluation for all simulated energies, using 40 realizations per energy.

To assess the accuracy of the technique, the stopping power estimation S_E was then compared to the NIST electronic stopping power S_NIST by calculating their Mean Relative Error (MRE) averaged for all spatial bins i and 40 realizations:

$MRE\left(S_E,S_{\mathit{NIST}}\right)=\frac{1}{I}\sum _{i=1}^I\left|\frac{S_{\text{E,i}}-S_{\text{NIST},i}}{S_{\text{NIST},i}}\right|(6)$

where a bin width of 0.1 cm was considered. Calculations after the NIST particle range were not performed, leading I to range from 80 to 265 bins per realization, depending on E₀. We used the MRE to assess which (k, T) combination provided the best results. As an example, the MRE distribution is reported in Figure 3A for the 200 MeV case.

FIGURE 3

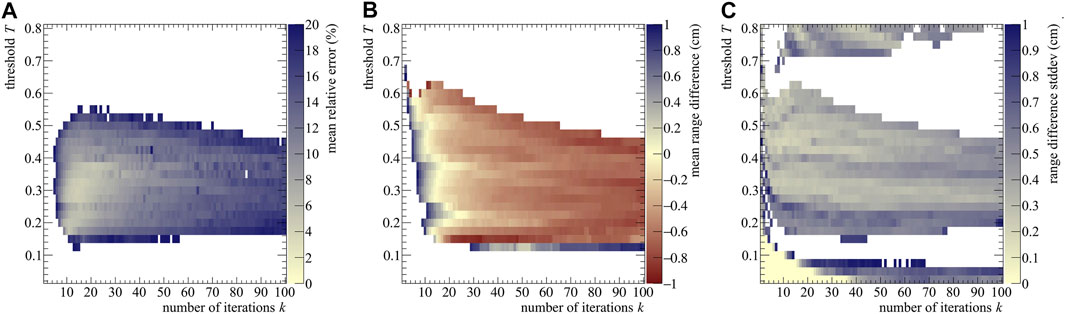
FIGURE 3. (A) Stopping power mean relative error (B) range difference averaged over 40 realizations, (C) and range standard deviation as a function of the number of iterations k and post-processing threshold T for a proton beam of 200 MeV impinging on a PMMA phantom. The color bars were set to have in the same color both the best stopping power assessment (i.e., the pale yellow area with MRE values below 2%) and the best range assessment (again pale yellow, with $\mathrm{\Delta }\bar{R}$ within ±0.2 cm). White areas correspond either to values outside the respective color bars or to (k, T) combinations where the fit failed.

An assessment of the range was also carried out by calculating the range difference ΔR between the estimated value R₀ and the NIST expected one. We report the mean $\mathrm{\Delta }\bar{R}$ and standard deviation σ_ΔR of the calculated range from the considered simulation realizations, which respectively give insight into the systematic and statistical error of the range estimation. The mean $\mathrm{\Delta }\bar{R}$ is shown for the 200 MeV case in Figure 3B.

The MRE, $\mathrm{\Delta }\bar{R}$, and σ_ΔR plots of all simulated energies can be found in the Supplementary Materials. The visualization of MRE and $\mathrm{\Delta }\bar{R}$ are restricted from 0 % to 20% and ±1 cm respectively, since errors outside these ranges are not acceptable for clinical practice. Pairs of k and T producing errors beyond the defined ranges are painted white. The same goes for the combinations where the fit failed to converge to a valid solution.

As seen from Figure 3, the best range estimation does not necessarily correspond to the best stopping power estimation. Pixel-wise, the two plots do not follow exactly the same pattern and the two distributions have different shapes: this is due to the fact that the range estimation only relies on the last point of the distribution (e.g, see for reference Figure 2A), which identifies the value of R₀. Instead, the stopping power depends on the whole shape of the (t, z) curve, making it more sensitive to the reconstruction result. Moreover, both estimations also depend on the initial energy, with higher energies needing less iterations, probably due to the higher number of secondaries produced and therefore detected. Further discussion on the estimation trend can be found in the Supplementary Materials.

The k and T parameters were chosen first by considering a region in the MRE distribution with consistently low values, then by locating which parameter combination minimized the $\mathrm{\Delta }\bar{R}$ and the σ_ΔR in the corresponding range difference plot.

3 Results

To evaluate the performance of the stopping power estimation, we used 10 simulation runs. These realizations are independent of the ones used in the optimization process, so the MRE and $\mathrm{\Delta }\bar{R}$ calculations were repeated. The chosen optimization parameters and the corresponding results are reported in Figure 4A. In addition to the MRE and $\mathrm{\Delta }\bar{R}$, the standard deviation of the range difference σ_ΔR is also reported as a way to evaluate the range resolution.

FIGURE 4

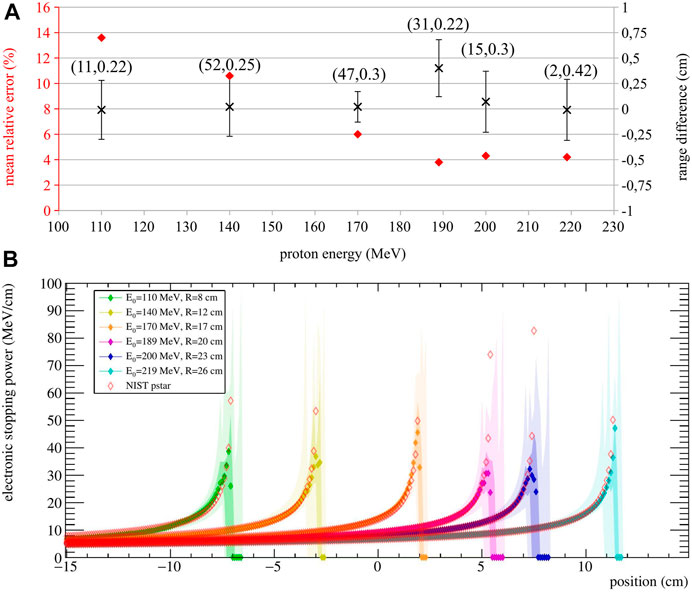
FIGURE 4. (A) Stopping power MRE (red diamond) and range difference $\mathrm{\Delta }\bar{R}$ (black cross, averaged over 10 realizations) for each simulated energy. The chosen iteration and threshold, optimized for the stopping power estimation, are reported as (k, T). The range standard deviation σ_ΔR is displayed as error bars. (B) Median of stopping power estimations for 10 realizations per energy. Their quartiles (0%, 25%, 75% and 100%) are reported in different color shades. The NIST reference stopping power for each energy averaged over 1 mm bins is also reported (empty diamonds). The expected ranges for the considered energies are stated in the legend.

Results show that the calculated range is very accurate for all energies, with $\mathrm{\Delta }\bar{R}$ below 0.07 cm, except the 189 MeV case, with $\mathrm{\Delta }\bar{R}$ equal to 0.4 cm. The standard deviation of the range difference also shows that a range resolution within 0.3 cm can be reached. As for the stopping power, MRE values show that an agreement between 13.6% and 3.8% is reached between the estimation and the NIST values, with the higher agreement reached at higher energies. This can be explained by the fact that SER-PGT is very sensitive to the number of detected events used for reconstruction. The higher the energy, the more secondary radiation is produced along the path and therefore more detected events are available for reconstruction. For example, the number of detected events was about 0.4 times lower for the 110 MeV beam with respect to the 219 MeV beam.

For visualization purposes, the obtained stopping power estimation are shown in Figure 4B. Here, the median and the estimation quartiles of the 10 validation runs are reported in different color shades.

4 Discussion

A proof of concept to directly evaluate the electronic stopping power of proton beams from PGT measurements is presented. Currently, stopping power measurements include techniques such as photon CT, Dual Energy CT, or proton CT. These techniques are generally used in treatment planning, and require additional ionizing radiation to the patient and additional time. Therefore, they cannot be repeated for every fraction of the treatment. Most importantly, they cannot be performed while the treatment is being delivered, while the proposed approach could be indeed used as a real-time verification method.

Most treatment verification methods rely on the detection of secondaries to evaluate the particle range, which is a quantity indirectly correlated to the radiation dose distribution. The presented approach is based on kinematic considerations regarding the primary particle motion inside the target and should therefore represent a more direct way to perform treatment verification with respect to the state of the art. Moreover, the approach gives information about the whole beam path, instead of the integrated information given by range estimations.

The approach is promising for both treatment verification purposes, and treatment optimization strategies, as its output could be directly compared to the stopping power maps used for treatment planning. Monte Carlo simulations with homogeneous targets show that the stopping power is estimated with a mean relative error ranging from 3.8% to 13% with respect to the expected value, with slightly worse agreement found in the Bragg Peak region with respect to the plateau region (Figure 4B). In fact, the stopping power estimation becomes most sensitive at the end of the range, because of the inherent steep gradient in that region. However, in a real treatment, different beam energies are delivered in the same spot—hence, the information coming from higher energies could be used to improve the estimate of the Bragg Peak for lower energies. On the other hand, a correct estimation of the particle path up to the end of the range is most desirable, since any deviations will affect the energy profile for all the subsequent positions. Future work will include the expansion of the model to fit multiple energies together, so as to improve the overall stopping power calculation.

Better agreement is found at higher energies, probably due to an increase of the number of events used for reconstruction. Still, it should be kept in mind that the presented results highly depend on the reconstruction parameters k and T (i.e, the number of iteration and threshold), which were chosen looking at a different dataset, as described in Section 2.4. This adds robustness and allows to keep a more generalized approach that is also applicable to experimental data. Interestingly, the 189 MeV case yielded the highest stopping power agreement but also the highest systematic error in the range calculation (i.e. mean range difference), underlining the fact that the two estimations (i.e., range and stopping power) do not have the same dependency on the SER-PGT parameters. Still, it is important to keep in mind that the range resolution is consistent for all simulated energies, with standard deviations within 0.3 cm. The execution time of the stopping power estimation is dominated by the SER-PGT algorithm reconstruction times (around 6 min for 100 iterations on a personal workstation using 1 thread), with the fitting procedure taking a negligible computing time.

The SER-PGT reconstruction algorithm used in the current paper was first introduced in [16]. There, we specifically optimized the k and T parameters for the particle range evaluation, reaching a range resolution of about 0.5 cm when using 10⁷ protons with energies between 110 and 229 MeV. The setup comprised 9 PET detector modules based on Lutetium Fine Silicate (LFS) scintillating crystals, to show the feasibility of using the same detectors to measure both β⁺-decaying isotopes and prompt photons. Therefore, the application of SER-PGT to different detector setups (i.e., LaBr₃:Ce and LFS) demonstrates its versatility.

One of the main simplifications that we made was that Eq. 5 describes the average behavior of a group of particles undergoing only electromagnetic interactions. While this is true for many primary particles, other interactions like nuclear reactions and multiple Coulomb scattering occur, changing the path and kinetic energy of the protons. Still, the nuclear stopping power becomes significant mainly towards the end of the particle range. Therefore, focusing on the electronic stopping power alone is a reasonable approximation for the presented methodology. Even though an analytical solution was presented, its base model $R_0=\alpha E_0^p$ is very simplistic compared to the complete description contained in the Bethe-Bloch equation. On a macroscopic scale, it still proved to be a good approximation of the proton motion and its dependence on only two free parameters is advantageous for fitting numerical data. The presented solution is valid between the target entry and the estimated particle range (see Supplementary Material).

An extremely important feature that strengthens the robustness of the approach is the complete absence of any a-priori information about the target chemical composition in both the reconstruction algorithm and the evaluation of the stopping power. Therefore, the approach does not rely on nuclear interactions, or excitation/de-excitation models implemented in the Monte Carlo tool. This is a very important point, since the need for treatment verification arises from possible mismatches between the patient CT used for treatment planning and the real anatomy during the treatment, and the inclusion of target information might lead to biased results.

Other fitting procedures, all starting from Bortfeld’s approximation, were investigated, but yielded worse results. The other procedures involved, for example, leaving both α and p as free parameters, or were based on multiple fits (i.e., the reconstructed spatio-temporal emission t(z) was first fitted with a polynomial, non-physical function, and the resulting v(z) was then fitted with Bortfeld’s description of the speed). Moreover, a numerical calculation based on the kinematic description of the energy was investigated starting from the position and time pairs, but it showed non-physical features (i.e., speeding up of the particles at the end of the range).

The selected fitting procedure was, among the investigated ones, the most consistent, showing the best accuracy. Still, for certain combinations of k and T, the fitting procedure does not converge to a valid solution. In most cases, this is due to unstable reconstruction outputs because of too few iterations or a threshold value that leaves too much background noise or removes significant parts of the distribution. Another limitation of the current procedure is the fact that the stopping power evaluation depends on the accuracy of the calculated range. A range resolution within 0.3 cm standard deviation was obtained, but how the algorithm performs with non-homogeneous targets is yet to be verified. Still, a preliminary investigation on an anthropomorphic phantom showed the capability of assessing the range with SER-PGT with an accuracy of 0.7 cm [16]. However, before approaching a more complex target with the proposed technique and assess the stopping power, careful studies must be carried out. Piece-wise homogeneous targets will be explored, to understand the contribution of α and p as a function of the homogeneous region under consideration. The current study represents the starting point towards a full understanding of the proposed approach before aiming for more complex scenarios. Extensive studies will be done in the near future to expand the approach to non-homogeneous targets and treatment plans, which might involve the use of different fitting procedures or the investigations of new algorithms altogether.

Presently, the simulation did not include false proton-photon coincidences. This allows better identification of the intrinsic resolution of the proposed method. The effect of these false coincidences will be addressed in the future by taking into account the beam time structure. The same goes for the initial transverse beam shape, which was point-like in this study. The behaviour of UFSD was not modelled in the simulation. These detectors have excellent time resolution - hence, the timing resolution of the TOF measurement is dominated by the secondary particle detectors. Currently, our UFSD is a small sensor (eight strips of about 2.2 mm² of active area each), reaching a detection efficiency up to 24%, depending on the beam initial energy. Taking into consideration this efficiency could result in a situation in which the primary particle is not detected, but its eventual secondary photon is, adding to the random contribution. However, since the initial transverse beam width was neglected in this study, the primary particles detection efficiency was also not modelled. In any case, the total random contribution due to false coincidences can be properly included in the simulation only after a thorough characterization of the beam time structure, which depends on the particular accelerator and experimental facility used.

Since this is a proof of concept, a large number of detectors was used for reconstruction. Future work will also include the selection of a subset of detectors to understand where the most meaningful information comes from, so as to optimize and build the detector setup of the MERLINO project. In order to reach the desired timing resolution of the system (i.e. 250 ps FWHM), careful R&D will be carried out with the LaBr₃:Ce detectors coupled to either PMT or SiPMs. The MERLINO setup will then be tested with proton beams in order to validate the proposed theoretical approach in a clinical environment.

5 Conclusion

We have introduced a new approach to estimate the stopping power with the SER-PGT technique, first presented in [16], as the starting point. The approach was tested by Monte Carlo simulations, providing excellent results in both stopping power (with estimations as good as 3.8%) and range evaluations (range resolution within 0.3 cm standard deviation), when considering energies between 100 and 219 MeV, with a 250 ps FWHM timing resolution. Further studies about how to improve the technique, especially in view of non-homogeneous phantoms, are mandatory. Nonetheless, the presented approach offers a new way to perform treatment monitoring and optimization, opening up new possibilities to study the stopping power distribution with a technique that can be performed in-vivo.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

VF, EF, FP, and MR developed the initial idea. VF, EF, and FP developed the Monte Carlo simulations and programmed the SER-PGT reconstruction. VF, FP, MR, and JW designed the stopping power estimation analysis. JW programmed the stopping power analysis. VF and JW performed the data analysis and wrote the manuscript. PC, EF, FP, MR, and AV reviewed the manuscript. All authors read and approved the submitted version.

Funding

This work is supported by the INFN Group 5 Young Investigators Grant MERLINO and partly by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)—Grant no. 383681334.

Acknowledgments

We are grateful to Andreas Bolke and Jona Kasprzak (Institute of Medical Engineering, University of Lübeck) for their advice.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.971767/full#supplementary-material

Footnotes

¹https://www.gnu.org/software/gsl/

²https://doi.org/10.5281/zenodo.848818

³https://physics.nist.gov/PhysRefData/Star/Text/PSTAR.html

References

1. Paganetti H. Range uncertainties in proton therapy and the role of Monte Carlo simulations. Phys Med Biol (2012) 57:R99–R117. doi:10.1088/0031-9155/57/11/r99

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Placidi L, Bolsi A, Lomax AJ, Schneider RA, Malyapa R, Weber DC, et al. Effect of anatomic changes on pencil beam scanned proton dose distributions for cranial and extracranial tumors. Int J Radiat Oncol Biol Phys (2017) 97:616–23. doi:10.1016/j.ijrobp.2016.11.013

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Parodi K, Paganetti H, Shih HA, Michaud S, Loeffler JS, DeLaney TF, et al. Patient study of in vivo verification of beam delivery and range, using positron emission tomography and computed tomography imaging after proton therapy. Int J Radiat Oncol Biol Phys 68 (2007) 920–34. doi:10.1016/j.ijrobp.2007.01.063

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Nischwitz SP, Bauer J, Welzel T, Rief H, Jäkel O, Haberer T, et al. Clinical implementation and range evaluation of in vivo PET dosimetry for particle irradiation in patients with primary glioma. Radiother Oncol (2015) 115:179–85. doi:10.1016/j.radonc.2015.03.022

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Fiorina E, Ferrero V, Baroni G, Battistoni G, Belcari N, Camarlinghi N, et al. Detection of inter-fractional morphological changes in proton therapy: a simulation and in-vivo study with the inside in-beam pet. Front Phys (2020) 8:660. doi:10.3389/fphy.2020.578388

CrossRef Full Text | Google Scholar

6. Fischetti M, Baroni G, Battistoni G, Bisogni G, Cerello P, Ciocca M, et al. Inter-fractional monitoring of 12 C ions treatments: Results from a clinical trial at the CNAO facility. Sci Rep (2020) 10:1–11.

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Verburg J, Hueso-Gonzalez F, Tattenberg S, Wohlfahrt P, Ruggieri T, Bortfeld T. First-in-human use of prompt gamma-ray spectroscopy for proton range verification. In: Joint AAPM and COMP Meeting; July 12-16 (2020) (2020). p. 12.

Google Scholar

8. Berthold J, Khamfongkhruea C, Petzoldt J, Thiele J, Hölscher T, Wohlfahrt P, et al. First-in-human validation of ct-based proton range prediction using prompt gamma imaging in prostate cancer treatments. Int J Radiat Oncol Biol Phys (2021) 111:1033–43. doi:10.1016/j.ijrobp.2021.06.036

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Durante M, Paganetti H. Nuclear physics in particle therapy: a review. Rep Prog Phys (2016) 79:096702. doi:10.1088/0034-4885/79/9/096702

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Johnson RP. Review of medical radiography and tomography with proton beams. Rep Prog Phys (2017) 81:016701. doi:10.1088/1361-6633/aa8b1d

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Meyer S, Kamp F, Tessonnier T, Mairani A, Belka C, Carlson DJ, et al. Dosimetric accuracy and radiobiological implications of ion computed tomography for proton therapy treatment planning. Phys Med Biol (2019) 64:125008. doi:10.1088/1361-6560/ab0fdf

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Krimmer J, Dauvergne D, Létang J, Testa É. Prompt-gamma monitoring in hadrontherapy: a review. Nucl Instr Methods Phys Res Sect A: Acc Spect Detect Assoc Equip (2018) 878:58–73. doi:10.1016/j.nima.2017.07.063

CrossRef Full Text | Google Scholar

13. Golnik C, Hueso-González F, Müller A, Dendooven P, Enghardt W, Fiedler F, et al. Range assessment in particle therapy based on prompt γ-ray timing measurements. Phys Med Biol (2014) 59:5399–422. doi:10.1088/0031-9155/59/18/5399

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Hueso-González F, Enghardt W, Fiedler F, Golnik C, Janssens G, Petzoldt J, et al. First test of the prompt gamma ray timing method with heterogeneous targets at a clinical proton therapy facility. Phys Med Biol (2015) 60:6247–72. doi:10.1088/0031-9155/60/16/6247

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Werner T, Berthold J, Hueso-González F, Koegler T, Petzoldt J, Roemer K, et al. Processing of prompt gamma-ray timing data for proton range measurements at a clinical beam delivery. Phys Med Biol (2019) 64:105023. doi:10.1088/1361-6560/ab176d

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Pennazio F, Ferrero V, D’Onghia G, Garbolino S, Fiorina E, Villarreal OAM, et al. Proton therapy monitoring: Spatiotemporal emission reconstruction with prompt gamma timing and implementation with PET detectors. Phys Med Biol (2022) 67:065005. doi:10.1088/1361-6560/ac5765

CrossRef Full Text | Google Scholar

17. Marcatili S, Collot J, Curtoni S, Dauvergne D, Hostachy J, Koumeir C, et al. Ultra-fast prompt gamma detection in single proton counting regime for range monitoring in particle therapy. Phys Med Biol (2020) 65:245033. doi:10.1088/1361-6560/ab7a6c

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Jacquet M, Marcatili S, Gallin-Martel ML, Bouly JL, Boursier Y, Dauvergne D, et al. A time-of-flight-based reconstruction for real-time prompt-gamma imaging in proton therapy. Phys Med Biol (2021) 66:135003. doi:10.1088/1361-6560/ac03ca

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Bortfeld T. An analytical approximation of the Bragg curve for therapeutic proton beams. Med Phys (1997) 24:2024–33. doi:10.1118/1.598116

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Ferrari A, Sala PR, Fassò A, Ranft J. Fluka: a multi-particle transport code. Geneva, Switzerland: CERN. doi:10.5170/CERN-2005-010Tech. rep. (2005). Citeseer

CrossRef Full Text | Google Scholar

21. Böhlen T, Cerutti F, Chin M, Fassò A, Ferrari A, Ortega PG, et al. The fluka code: developments and challenges for high energy and medical applications. Nucl Data sheets (2014) 120:211–4. doi:10.1016/j.nds.2014.07.049

CrossRef Full Text | Google Scholar

22. Vignati A, Giordanengo S, Milian FM, Ganjeh ZA, Donetti M, Fausti F, et al. A new detector for the beam energy measurement in proton therapy: a feasibility study. Phys Med Biol (2020) 65:215030. doi:10.1088/1361-6560/abab58

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Siviero F, Arcidiacono R, Borghi G, Boscardin M, Cartiglia N, Vignali MC, et al. Optimization of the gain layer design of ultra-fast silicon detectors. Nucl Instr Methods Phys Res Sect A: Acc Spect Detect Assoc Equip (2022) 1033:166739. doi:10.1016/j.nima.2022.166739

CrossRef Full Text | Google Scholar

24. Owens A, Bos A, Brandenburg S, Dathy C, Dorenbos P, Kraft S, et al. γ-ray performance of a 1242cm3 LaCl3:Ce scintillation spectrometer. Nucl Instr Methods Phys Res Sect A: Acc Spect Detect Assoc Equip (2007) 574:110–4. doi:10.1016/j.nima.2007.01.091

CrossRef Full Text | Google Scholar

25. Battistoni G, Boehlen T, Cerutti F, Chin PW, Esposito LS, Fassò A, et al. Overview of the fluka code. Ann Nucl Energ (2015) 82:10–8. doi:10.1016/j.anucene.2014.11.007

CrossRef Full Text | Google Scholar

26. Bethe HZ. Theorie des durchgrangs schneller korpuskularstrahlen durch materie. Ann Phys (1930) 397:325–400. doi:10.1002/andp.19303970303

CrossRef Full Text | Google Scholar

27. Evans RD. The atomic nucleus. New York, NY. McGraw-Hill (1955). p. 647–54. chap. 22.

Google Scholar

28. Nørlund NE. Hypergeometric functions. Acta Math (1955) 94:289–349. doi:10.1007/bf02392494

CrossRef Full Text | Google Scholar