- 1Department of Statistics and Data Science, Yonsei University, Seoul, Republic of Korea
- 2Department of Applied Statistics, Yonsei University, Seoul, Republic of Korea
Clustering is a fundamental task in data science that aims to group data based on their similarities. However, defining similarity is often ambiguous, making it challenging to determine the most appropriate objective function for a given dataset. Traditional clustering methods, such as the
1 Introduction
Quantum machine learning (QML) offers new possibilities and approaches to address various challenges in data science, pushing the boundaries of existing methods. Among its potential applications, clustering is a widely used technique in numerous domains of pattern recognition and data mining, such as image recognition, social network analysis, customer segmentation, and anomaly detection [1–8]. In addition, clustering has found increasing applications in drug discovery, aiding in the selection of potential leads, mapping protein binding sites, and designing targeted therapies [9–11].
Despite its broad applicability and importance, clustering encounters several challenges from an optimization perspective [12–14]. A primary issue is the ambiguity in defining the objective function for clustering. As there is no ground truth, it is often unclear which criteria should be used to group the target dataset, requiring the analyst to make subjective decisions about what constitutes similarity. A common approach involves using distance measures to quantify similarity. However, this approach still requires determining whether to rely on local information, such as the pairwise distance between individual data points, or global information, such as the distance between a data point and the centroid of a cluster. When using local information, clustering can be formulated as combinatorial optimization and approached by solving the maximum
To address these challenges, we develop a unified framework that incorporates multiple data characteristics—such as local and global information—into the optimization objective, with the flexibility to assign arbitrary weights to specify their relative importance in clustering. Our approach begins by decomposing the problem of finding
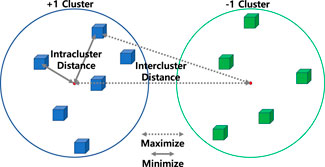
Figure 1. Illustration of the intracluster distance and the intercluster distance. Unlike supervised learning, unsupervised learning cannot utilize a loss function with exact labels. In a clustering approach, the loss function can be created based on how well the hypothesis separates data points into their appropriate groups. We customized and combined intracluster distance, which measures how tightly data points are clustered together within a cluster, and intercluster distance, which measures how far apart different cluster centers are, as weighted criteria in QUBO formula. By optimizing this loss function, we were able to solve the clustering problem.
We benchmark the effectiveness of our approach and the proposed Hamiltonian formulations (i.e., the combinatorial optimization problems) using several datasets: Iris, Wine, a subset of MNIST, and a synthetic Gaussian overlapping dataset. To evaluate performance, we employed the Silhouette Score (SS) [27] and the Rand Index (RI) [28] as metrics, conducting comparative analysis with the
2 Related work
In this section, we review prior research efforts that framed centroid-based clustering as a combinatorial optimization problem. Several studies have approached this with a particular focus on Quadratic Unconstrained Binary Optimization (QUBO) formulations. Ref. [31] and Ref. [32] explored the representation of cluster centroids in QUBO under the assumption of equal cluster sizes, typically in the context of
These works illustrate that centroid-based clustering algorithms, like
In contrast to previous approaches, our method does not require predefined cluster sizes or rely on computationally intensive iterative processes. It directly incorporates the number of data points in each cluster as a variable in the objective function, eliminating the assumption of fixed cluster sizes. This enables greater flexibility and adaptability to a wider range of data distributions.
3 Methodology
We begin by discussing the process of mapping clustering problems to combinatorial optimization problems. To represent the assignment of
In the Hamiltonian formulation, we introduce
In the context of clustering,
where
Existing QUBO-based clustering algorithms typically rely solely on pairwise distances between data points. In this case,
where
This optimization problem is also known as the weighted max-cut problem on a graph. However, this formulation of clustering neglects global information, such as centroids, in the optimization process. This limitation is primarily due to the computational complexities and challenges involved in representing centroids within the combinatorial optimization framework, unless there is prior knowledge that the dataset is evenly distributed among clusters [32, 35, 36] as noted in Section 2.
To incorporate the centroid information into the combinatorial optimization (e.g., QUBO) framework, we introduce the variables
These variables serve as the building blocks for constructing the desired objective function, along with any necessary constraints. The centroids of the two clusters can then be expressed as
Moreover, for a given dataset
Here,
To construct a clustering objective function that incorporates centroid information, one can take a linear combination of the distance functions
3.1 Intracluster distance
We start by setting up the optimization problem aimed at minimizing intracluster distances. This is achieved by linearly combining
This formulation encourages clusters to concentrate around their centroids by minimizing intracluster variance, which is conceptually equivalent to the objective of the well-known
However, the minimum of the objective function in Equation 5 can be achieved by setting either
Notably, in each intracluster distance term, either
3.2 Intercluster distance
To achieve well-separated clusters, it is beneficial to consider intercluster distance, which aims to maximize the separation between different clusters. While minimizing intracluster distance enhances cohesion within each cluster, it may introduce ambiguity near adjacent clusters, especially when boundaries are unclear. By focusing on intercluster separation, we can better distinguish data points near ambiguous or overlapping boundaries, thereby improving the overall clustering performance. Following a similar approach to that used for intracluster distances, the objective function is constructed by linearly combining
In this formulation, we maximize the squared distance of each data point to the centroid of the opposite cluster, encouraging the data points to be as far as possible from the other cluster. We observe that this approach enhances clustering performance, particularly in cases where cluster boundaries are not clearly defined (see Section 4).
3.3 Combining intra and intercluster distances
Now, we can integrate both intracluster and intercluster distances within a unified framework. By simultaneously optimizing these distances, we aim to strengthen the compactness within clusters while enhancing the separation between different clusters. This can be achieved by linearly combining Equation 5 and Equation 7, with the multiplicative factor
The optimization aims to assign each data point
By rearranging Equation 8 (see Supplementary Appendix 1.3), the combined objective function can also be expressed as:
This expression reveals that optimizing the combined intracluster and intercluster distances is equivalent to maximizing the squared distance between the cluster centroids. Therefore, by optimizing the combined objective function in Equation 8, we inherently maximize the separation between the centroids of the two clusters.
3.4 Constrained clustering
In practice, analysts often need to perform clustering under constraints, which are dictated by task requirements or the available information. These constraints ensure that clustering not only groups data effectively but also adheres to the underlying structure and expert knowledge specific to the domain. According to Ref. [37], these constraints typically fall into three main categories: labeling constraints, cluster constraints and comparison constraints.
Labeling constraints are based on preassigned labels from domain knowledge, guiding the clustering algorithm to ensure that labeled objects are assigned to the correct groups. Cluster constraints focus on the characteristics of the clusters, such as the desired number of clusters or restrictions on cluster size or density. Comparison constraints include Must-Link (ML) and Cannot-Link (CL) relations, which specify whether certain objects should or should not be placed in the same cluster based on their inherent relationships. This approach allows users to specify relationships between data points even in the absence of class labels. In our framework, these constraints can be incorporated by augmenting the objective function with penalty terms that increase the objective value when the constraints are violated.
To implement labeling constraints, we modify the objective function to penalize incorrect cluster assignments. If the
Here,
Comparison constraints, such as Must-Link (ML) and Cannot-Link (CL), can also be incorporated. Using the penalty term described in Ref. [38], where
The second term ensures that the objective value increases when Must-Link or Cannot-Link constraints are violated, thereby seeking a solution that satisfies these pairwise relationships.
Note that the constraints are incorporated via the penalty method, where the hyperparameter
3.5
Building upon the work of Ref. [35], we briefly discuss a
4 Experiments
To assess the effectiveness of our array of customized Hamiltonians, we conducted experimental analyses using the Silhouette Score (SS) and the Rand Index (RI) as primary performance metrics, with comparisons to the
4.1 Exact solutions
To establish a baseline for evaluating the performance of our proposed Hamiltonian methods, we employed a brute-force algorithm to exhaustively search the solution space on small datasets. Although this approach is computationally expensive and infeasible for large datasets, it allows us to find exact solutions and precisely evaluate the performance of our proposed methods. For this reason, we selected the Iris and Wine datasets for our experiments due to their widespread usage as standard benchmarks in clustering and classification tasks, as well as their suitability for exhaustive search given their size. The Iris dataset consists of 150 samples with four features categorized into three classes, while the Wine dataset contains 178 samples with thirteen features also categorized into three classes. To focus on binary clustering, we excluded the Setosa class (50 samples) from the Iris dataset and class 1 (59 samples) from the Wine dataset. For each dataset, we randomly sampled 16 data points and repeated the experiment 150 times. We applied normalization to scale the features of the Iris dataset to a range between 0 and 1. For the Wine dataset, we applied standard scaling to transform the features to have zero mean and unit variance.
Figure 2 summarizes the performance of different methods on the Iris and Wine dataset. For the Silhouette Score, the
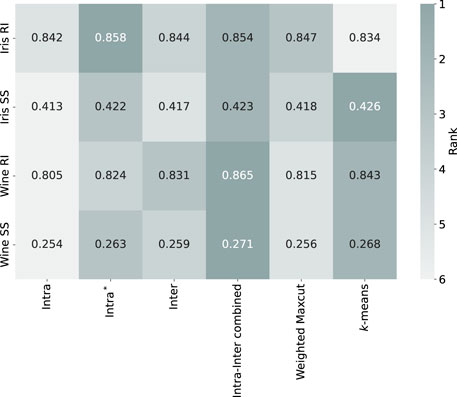
Figure 2. The heatmap illustrates exact search results, showing the performance of Hamiltonian methods on the Iris and Wine datasets. The values represent the means of performance metrics (RI: Rand Index, SS: Silhouette Score), with darker shades indicating higher rank (better performance). White text indicates the best results for each evaluation metric.
4.2 Simulated annealing
Although the brute-force algorithm guarantees exact solutions, its high computational complexity restricts its application to small datasets. To validate the scalability of our method, we employ the simulated annealing algorithm. This approach enables testing on larger datasets, including not only the Iris and Wine datasets but also Gaussian-distributed synthetic dataset and 0–1 MNIST dataset. The synthetic dataset follows Gaussian distributions with overlapping ranges (see Supplementary Figure S1 in Supplementary Appendix 2), and the 0–1 MNIST dataset contains handwritten images of digits 0 and 1 in a
Figure 3 presents the performance of different methods across these dataset. For the synthetic dataset, the
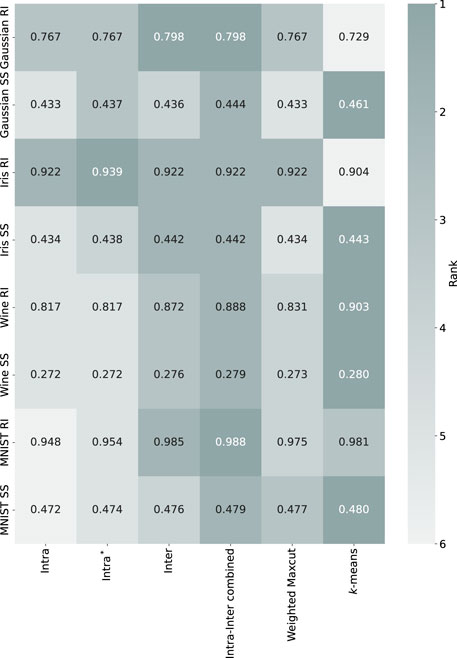
Figure 3. The heatmap illustrates simulated annealing results, showing the performance of Hamiltonian methods on the Gaussian synthetic, Iris, Wine and MNIST 0–1 datasets. The values represent the means of performance metrics (RI: Rand Index, SS: Silhouette Score), with darker shades indicating higher rank (better performance). White text highlights the best results for each evaluation metric.
4.3 Quantum annealing
To verify that our method can operate on a current quantum device, we performed quantum annealing using the D-Wave Advantage System 6.4, which employs the Pegasus topology (see Figure 4B). Our clustering problem inherently involves a fully connected (complete) graph, as depicted in Figure 4A. This connectivity poses challenges for current quantum devices, which often have limited qubit connectivity. We utilized the clique sampler from the D-Wave Ocean SDK [42], which is designed to optimally embed fully connected problems onto the hardware. In graph theory, a clique is a subset of vertices in which every pair of distinct vertices is connected by an edge, forming a complete subgraph. The term clique size refers to the number of vertices in such a fully connected subgraph. Notably, the maximum clique size for the D-Wave Advantage System 6.4 is 175, meaning that it can embed fully connected problems involving up to 175 logical qubits (representing data points). This capability allowed us to process the entire Iris and Wine datasets—each containing fewer than 175 data points—in a single trial. However, the 0–1 MNIST dataset exceeds the limited qubit connectivity of the system, necessitating the random selection of subsets of 175 data points. To ensure statistical robustness, we repeated this sampling process ten times. Our intercluster method demands additional qubits beyond those representing the data points due to the inclusion of higher-order terms (see Supplementary Equation S21 in Supplementary Appendix 1.2) and hence the slack variables necessary for formulating it as a Binary Quadratic Model (BQM). This extra qubit requirement exceeds the hardware’s maximum clique size when handling larger datasets, leading us to exclude the intercluster method from our quantum annealing experiments given the current hardware constraints.
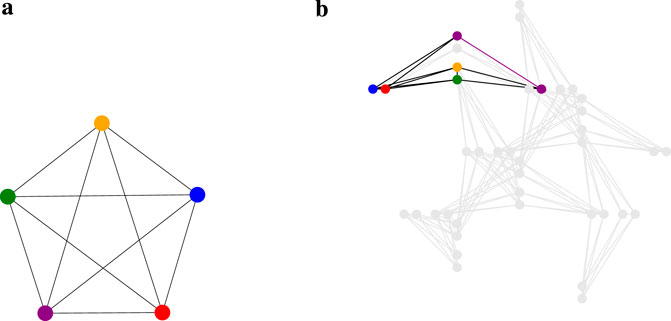
Figure 4. (a) A visualization of a complete graph with 5 vertices, denoted as
In this analysis, the Intra-Inter combined method achieved higher Rand Index values while maintaining similar Silhouette Scores compared to the
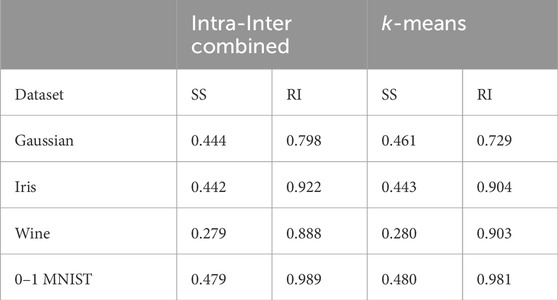
Table 1. Comparison of quantum annealing results: Silhouette Score and Rand Index between Intra-Inter combined method and
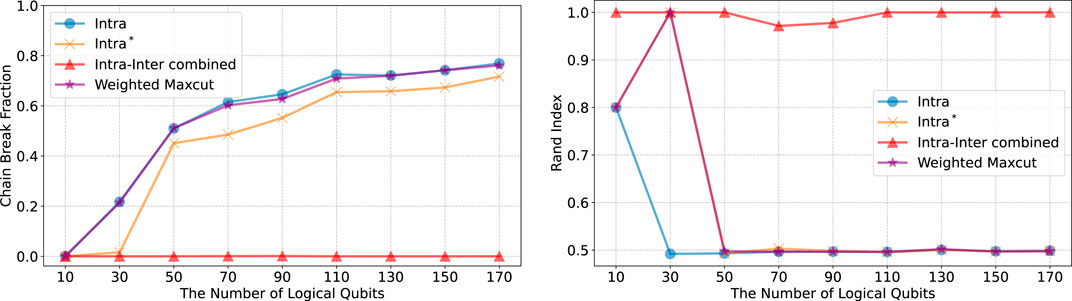
Figure 5. Chain break fraction for four different Hamiltonians using the D-Wave Advantage System 6.4. We conducted 200 samplings on a single quantum machine instruction on a QPU, setting the annealing time to the maximum possible duration of 2000
4.4 Constrained clustering
We performed constrained clustering on the Iris and Wine datasets using Must-Link (ML) and Cannot-Link (CL) constraints, implemented through simulated annealing. Labels of randomly selected data points were revealed according to specified proportions from the entire dataset. Based on these revealed labels, we generated constraints whether pairs of data points should be grouped together (ML) or separated (CL). The proportion of data points with revealed labels ranged from 0% to 100% in 10% increments, resulting in 11 distinct levels. A 0% ratio reflects a standard clustering scenario without any constraint information, whereas a 100% ratio indicates that all labels are fully known. For each ratio, we conducted 50 trials using different random samples to calculate average performance metrics. This choice balances statistical robustness and computational efficiency.
Figure 6 presents the outcomes of constrained clustering with ML and CL constraints. In both datasets, the Rand Index initially declined when only 10%–30% of label information was provided, but progressively improved as more information available. In the case of Wine dataset, the Intra-Inter combined method quickly converged to the true labels. In contrast, the Inter method showed no consistent trend and exhibited considerable variability. This suggests that the solution values are sensitive to the hyperparameter
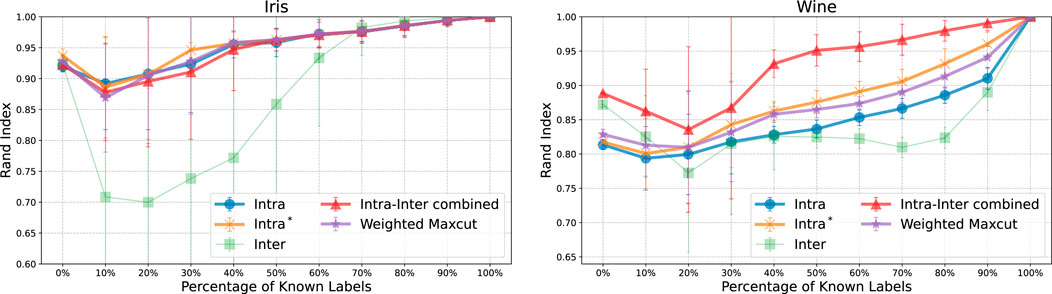
Figure 6. The plots display the Rand Index as a function of the percentage of known labels for the Iris (left) and Wine (right) datasets, under constrained clustering with Must-Link (ML) and Cannot-Link (CL) constraints. Where the proportion of revealed labels ranges from 0% to 100% in 10% increments. The performance improves as more label information is revealed, with the both dataset showing a recovery in performance after an initial decline between 10% and 30%. The variability in the Inter method suggests sensitivity to the hyperparameter
Subsequently, we implemented cardinality constraints to assign a specific number of data points to each cluster on the Iris and Wine datasets using simulated annealing. For each experiment, we selected a total of 50 data points from the Iris dataset and 48 data points from the Wine dataset, drawn from labels 1 and 2 according to predetermined ratios. The proportions of data points from label 1 and label 2 varied as follows: (10%, 90%), (20%, 80%), (30%, 70%), (40%, 60%), (50%, 50%), (60%, 40%), (70%, 30%), (80%, 20%), and (90%, 10%). This means we started with 10% data points from label 1% and 90% from label 2, gradually adjusting the proportions until we reached 90% from label 1% and 10% from label 2.
Figure 7 illustrates the performance of our methods with cardinality constraints. The

Figure 7. The top plots show the Rand Index across various methods with cardinality constraints applied to the Iris (left) and Wine (right) datasets. The bottom plots depict the difference between the given cardinality
5 Conclusions and discussion
In this work, we formulated the clustering problem as finding the ground state of a Hamiltonian and developed methods to integrate centroid information directly into the objective function. We defined a distance function
The significance of our research lies in developing a flexible and unified clustering strategy capable of addressing complex clustering challenges. By enabling the integration of various clustering objectives, our approach effectively manages data points clustered around their mean and handles overlapping clusters, as evidenced by our experimental results. Application to real datasets further highlights the practical utility of the Hamiltonian formulation. A key benefit of our method is its compatibility with quantum simulation techniques. In particular, our quantum annealing experiments on the D-Wave Systems showed that the Intra-Inter combined method operates effectively on current quantum device, demonstrating its applicability to real-world problems.
Potential directions for future research include expanding the Hamiltonian-based clustering framework to develop data-driven, automated methods for determining the optimal number of clusters. The intracluster distance formulation in our Hamiltonian approach can be leveraged to enforce density constraints. Additionally, refining the Intra-Inter combined method by applying dynamic weights to the linear combination of distances could allow adaptation to context-specific requirements. Extending this Hamiltonian formulation to address more complex clustering scenarios, such as time series and high-dimensional datasets, also presents a promising direction. Exploring alternative quantum hardware platforms, such as Rydberg atom arrays [48–53], could further expand the utility of our approach. While large-scale all-to-all qubit connectivity is not naturally available, ongoing advances in high-fidelity control [54], highly tunable interactions [55], and long coherence times [56, 57] open a path for scaling our method to larger problem instances. These advancements have the potential to enable new applications in fields like finance, drug discovery, and social network analysis.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
MS: Data curation, Formal Analysis, Investigation, Methodology, Software, Validation, Visualization, Writing–original draft, Writing–review and editing. DP: Conceptualization, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Supervision, Validation, Writing–original draft, Writing–review and editing.
Funding
The author(s) declare that financial support was received for the research and/or publication of this article. This work was supported by Korea Research Institute for Defense Technology Planning and Advancement---grant funded by Defense Acquisition Program Administration (DAPA) (KRIT-CT-23–031). This work was also supported by Institute of Information and communications Technology Planning and evaluation (IITP) grant funded by the Korea government (No. 2019-0-00003, Research and Development of Core technologies for Programming, Running, Implementing and Validating of Fault-Tolerant Quantum Computing System), the Yonsei University Research Fund of 2024 (2024-22-0147), the National Research Foundation of Korea (2023M3K5A1094813 and RS-2023-NR119931), and the KIST Institutional Program (2E32941-24-008). Access to the D-Wave system was supported by the `Quantum Information Science R&D Ecosystem Creation’ through the National Research Foundation of Korea (NRF) funded by the Korean government (Ministry of Science and ICT) (2020M3H3A1110365).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The author(s) declare that no Generative AI was used in the creation of this manuscript.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2025.1544623/full#supplementary-material
References
1. Coleman GB, Andrews HC. Image segmentation by clustering. Proc IEEE (1979) 67:773–85. doi:10.1109/proc.1979.11327
2. Baraldi A, Blonda P. A survey of fuzzy clustering algorithms for pattern recognition. i. IEEE Trans Syst Man, Cybernetics, B (Cybernetics) (1999) 29:778–85. doi:10.1109/3477.809032
3. Jain AK, Murty MN, Flynn PJ. Data clustering: a review. ACM Comput Surv (Csur) (1999) 31:264–323. doi:10.1145/331499.331504
4. Madeira SC, Oliveira AL. Biclustering algorithms for biological data analysis: a survey. IEEE/ACM Trans Comput Biol Bioinformatics (2004) 1:24–45. doi:10.1109/tcbb.2004.2
5. Wu J, Lin Z. Research on customer segmentation model by clustering. In: Proceedings of the 7th international conference on Electronic commerce China, August 15 - 17, 2005, (2005). p. 316–8.
6. Handcock MS, Raftery AE, Tantrum JM. Model-based clustering for social networks. J R Stat Soc Ser A (Statistics Society) (2007) 170:301–54. doi:10.1111/j.1467-985x.2007.00471.x
7. Agrawal S, Agrawal J. Survey on anomaly detection using data mining techniques. Proced Computer Sci (2015) 60:708–13. doi:10.1016/j.procs.2015.08.220
8. Saxena A, Prasad M, Gupta A, Bharill N, Patel OP, Tiwari A, et al. A review of clustering techniques and developments. Neurocomputing (2017) 267:664–81. doi:10.1016/j.neucom.2017.06.053
9. Voicu A, Duteanu N, Voicu M, Vlad D, Dumitrascu V. The rcdk and cluster r packages applied to drug candidate selection. J Cheminformatics (2020) 12:3–8. doi:10.1186/s13321-019-0405-0
10. Dara S, Dhamercherla S, Jadav SS, Babu CM, Ahsan MJ. Machine learning in drug discovery: a review. Artif Intelligence Rev (2022) 55:1947–99. doi:10.1007/s10462-021-10058-4
11. Mak KK, Wong YH, Pichika MR. Artificial intelligence in drug discovery and development. Drug Discov Eval Saf Pharmacokinetic Assays (2023) 1–38. doi:10.1007/978-3-030-73317-9_92-1
12. Jain AK. Data clustering: 50 years beyond k-means. Pattern recognition Lett (2010) 31:651–66. doi:10.1016/j.patrec.2009.09.011
13. Xu D, Tian Y. A comprehensive survey of clustering algorithms. Ann Data Sci (2015) 2:165–93. doi:10.1007/s40745-015-0040-1
14. Ezugwu AE, Ikotun AM, Oyelade OO, Abualigah L, Agushaka JO, Eke CI, et al. A comprehensive survey of clustering algorithms: state-of-the-art machine learning applications, taxonomy, challenges, and future research prospects. Eng Appl Artif Intelligence (2022) 110:104743. doi:10.1016/j.engappai.2022.104743
15. Lucas A. Ising formulations of many np problems. Front Phys (2014) 2. doi:10.3389/fphy.2014.00005
16. Dong Y, Lin L, Tong Y. Ground state preparation and energy estimation on early fault-tolerant quantum computers via quantum eigenvalue transformation of unitary matrices. arXiv preprint arXiv:2204.05955 (2022) 3:040305. doi:10.1103/prxquantum.3.040305
17. Poulin D, Wocjan P. Preparing ground states of quantum many-body systems on a quantum computer. Phys Rev Lett (2009) 102:130503. doi:10.1103/physrevlett.102.130503
18. Ge Y, Tura J, Cirac JI. Faster ground state preparation and high-precision ground energy estimation with fewer qubits. J Math Phys (2019) 60:022202. doi:10.1063/1.5027484
19. Lin L, Tong Y. Near-optimal ground state preparation. Quantum (2020) 4:372. doi:10.22331/q-2020-12-14-372
20. Zeng P, Sun J, Yuan X. Universal quantum algorithmic cooling on a quantum computer. arXiv preprint arXiv:2109.15304 (2023).
21. Peruzzo A, McClean J, Shadbolt P, Yung MH, Zhou XQ, Love PJ, et al. A variational eigenvalue solver on a photonic quantum processor. Nat Commun (2014) 5:4213. doi:10.1038/ncomms5213
22. McClean JR, Romero J, Babbush R, Aspuru-Guzik A. The theory of variational hybrid quantum-classical algorithms. New J Phys (2016) 18:023023. doi:10.1088/1367-2630/18/2/023023
23. Cerezo M, Arrasmith A, Babbush R, Benjamin SC, Endo S, Fujii K, et al. Variational quantum algorithms. Nat Rev Phys (2021) 3:625–44. doi:10.1038/s42254-021-00348-9
24. Farhi E, Goldstone J, Gutmann S. A quantum approximate optimization algorithm. arXiv preprint arXiv:1411.4028 (2014).
25. Johnson MW, Amin MH, Gildert S, Lanting T, Hamze F, Dickson N, et al. Quantum annealing with manufactured spins. Nature (2011) 473:194–8. doi:10.1038/nature10012
26. Jiang M, Shan K, He C, Li C. Efficient combinatorial optimization by quantum-inspired parallel annealing in analogue memristor crossbar. Nat Commun (2023) 14:5927. doi:10.1038/s41467-023-41647-2
27. Rousseeuw PJ. Silhouettes: a graphical aid to the interpretation and validation of cluster analysis. J Comput Appl Math (1987) 20:53–65. doi:10.1016/0377-0427(87)90125-7
28. Rand WM. Objective criteria for the evaluation of clustering methods. J Am Stat Assoc (1971) 66:846–50. doi:10.1080/01621459.1971.10482356
29. Pedregosa F, Varoquaux G, Gramfort A, Michel V, Thirion B, Grisel O, et al. Scikit-learn: machine learning in python. J machine Learn Res (2011) 12:2825–30. doi:10.48550/arXiv.1201.0490
31. Bauckhage C, Brito E, Cvejoski K, Ojeda C, Sifa R, Wrobel S. Ising models for binary clustering via adiabatic quantum computing. In: Energy minimization methods in computer vision and pattern recognition: 11th international conference, EMMCVPR 2017, venice, Italy, october 30–november 1, 2017, revised selected papers 11. Springer (2018). p. 3–17.
32. Arthur D, Date P. Balanced k-means clustering on an adiabatic quantum computer. Quan Inf Process (2021) 20:294–30. doi:10.1007/s11128-021-03240-8
33. Bauckhage C, Piatkowski N, Sifa R, Hecker D, Wrobel S. “A QUBO formulation of the k-medoids problem,” in Lernen, Wissen, Daten, Analysen, Berlin, Germany, CEUR Workshop Proceedings. Aachen, Germany: LWDA (2019) 2454:54–63. Available from at: https://ceur-ws.org/Vol-2454/paper_39.pdf
34. Matsumoto N, Hamakawa Y, Tatsumura K, Kudo K. Distance-based clustering using qubo formulations. Scientific Rep (2022) 12:2669. doi:10.1038/s41598-022-06559-z
35. Kumar V, Bass G, Tomlin C, Dulny J. Quantum annealing for combinatorial clustering. Quan Inf Process (2018) 17:39. doi:10.1007/s11128-017-1809-2
36. Date P, Arthur D, Pusey-Nazzaro L. Qubo formulations for training machine learning models. Scientific Rep (2021) 11:10029. doi:10.1038/s41598-021-89461-4
37. Gançarski P, Dao TBH, Crémilleux B, Forestier G, Lampert T. Constrained clustering: current and new trends. In: A guided tour of artificial intelligence research: volume II: AI algorithms (2020). p. 447–84.
38. Wang X, Davidson I. Flexible constrained spectral clustering. In: Proceedings of the 16th ACM SIGKDD international conference on Knowledge discovery and data mining (2010). p. 563–72.
39. Bergstra J, Bengio Y. Random search for hyper-parameter optimization. J Mach Learn Res (2012) 13:281–305. doi:10.5555/2188385.2188395
40. Snoek J, Larochelle H, Adams RP. Practical bayesian optimization of machine learning algorithms. In: F Pereira, C Burges, L Bottou, and K Weinberger, editors. Advances in neural information processing systems, 25. Red Hook, New York, United States: Curran Associates, Inc (2012).
41. Boothby K, Bunyk P, Raymond J, Roy A. Next-generation topology of d-wave quantum processors (2020).
42. Boothby T, King AD, Roy A. Fast clique minor generation in Chimera qubit connectivity graphs. Quant Inf Proc (2016) 15:495–508. doi:10.1007/s11128-015-1150-6
43. Hamerly R, Inagaki T, McMahon PL, Venturelli D, Marandi A, Onodera T, et al. Experimental investigation of performance differences between coherent ising machines and a quantum annealer. Sci Adv (2019) 5:eaau0823. doi:10.1126/sciadv.aau0823
44. Grant E, Humble TS. Benchmarking embedded chain breaking in quantum annealing. Quan Sci Technology (2022) 7:025029. doi:10.1088/2058-9565/ac26d2
45. Le TV, Nguyen MV, Nguyen TN, Dinh TN, Djordjevic I, Zhang ZL. Benchmarking chain strength: an optimal approach for quantum annealing, 1. IEEE international conference on quantum computing and engineering (QCE). IEEE (2023). p. 397–406. doi:10.1109/qce57702.2023.00052
46. Pelofske E. Comparing three generations of d-wave quantum annealers for minor embedded combinatorial optimization problems. Quantu Sci Technolog (2023) 10 (2):025025. doi:10.1088/2058-9565/adb029
47. Gilbert V, Louise S. Quantum annealers chain strengths: a simple heuristic to set them all. In: L Franco, C de Mulatier, M Paszynski, VV Krzhizhanovskaya, JJ Dongarra, and PMA Sloot, editors. Computational science – ICCS 2024. Cham: Springer Nature Switzerland (2024). p. 292–306.
48. Qiu X, Zoller P, Li X. Programmable quantum annealing architectures with ising quantum wires. PRX Quan (2020) 1:020311. doi:10.1103/PRXQuantum.1.020311
49. Kim M, Kim K, Hwang J, Moon EG, Ahn J. Rydberg quantum wires for maximum independent set problems. Nat Phys (2022) 18:755–9. doi:10.1038/s41567-022-01629-5
50. Ebadi S, Keesling A, Cain M, Wang TT, Levine H, Bluvstein D, et al. Quantum optimization of maximum independent set using rydberg atom arrays. Science (2022) 376:1209–15. doi:10.1126/science.abo6587
51. Lanthaler M, Dlaska C, Ender K, Lechner W. Rydberg-blockade-based parity quantum optimization. Phys Rev Lett (2023) 130:220601. doi:10.1103/PhysRevLett.130.220601
52. Nguyen MT, Liu JG, Wurtz J, Lukin MD, Wang ST, Pichler H. Quantum optimization with arbitrary connectivity using rydberg atom arrays. PRX Quan (2023) 4:010316. doi:10.1103/PRXQuantum.4.010316
53. Wurtz J, Bylinskii A, Braverman B, Amato-Grill J, Cantu SH, Huber F, et al. Aquila: quera’s 256-qubit neutral-atom quantum computer (2023).
54. Evered SJ, Bluvstein D, Kalinowski M, Ebadi S, Manovitz T, Zhou H, et al. High-fidelity parallel entangling gates on a neutral-atom quantum computer. Nature (2023) 622:268–72. doi:10.1038/s41586-023-06481-y
55. Shi XF. Quantum logic and entanglement by neutral rydberg atoms: methods and fidelity. Quan Sci Technology (2022) 7:023002. doi:10.1088/2058-9565/ac18b8
56. Barnes K, Battaglino P, Bloom BJ, Cassella K, Coxe R, Crisosto N, et al. Assembly and coherent control of a register of nuclear spin qubits. Nat Commun (2022) 13:2779. doi:10.1038/s41467-022-29977-z
Keywords: clustering, quantum machine learning, quantum computing, combinatorial optimization, quantum algorithms, unsupervised learning
Citation: Seong M and Park DK (2025) Hamiltonian formulations of centroid-based clustering. Front. Phys. 13:1544623. doi: 10.3389/fphy.2025.1544623
Received: 13 December 2024; Accepted: 28 February 2025;
Published: 22 April 2025.
Edited by:
Jaewoo Joo, University of Portsmouth, United KingdomReviewed by:
Saravana Prakash Thirumuruganandham, SIT Health, EcuadorXiao-Feng Shi, Hainan University, China
Robson Christie, University of Portsmouth, United Kingdom
Copyright © 2025 Seong and Park. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Daniel Kyungdeock Park, ZGtkLnBhcmtAeW9uc2VpLmFjLmty
 Myeonghwan Seong
Myeonghwan Seong Daniel Kyungdeock Park
Daniel Kyungdeock Park