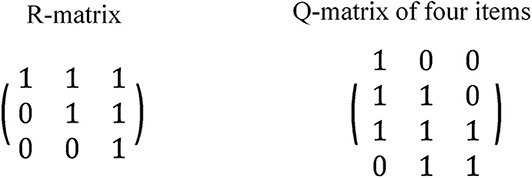- Collaborative Innovation Center of Assessment for Basic Education Quality, Beijing Normal University, Beijing, China
Longitudinal diagnostic classification models (DCMs) with hierarchical attributes can characterize learning trajectories in terms of the transition between attribute profiles for formative assessment. A longitudinal DCM for hierarchical attributes was proposed by imposing model constraints on the transition DCM. To facilitate the applications of longitudinal DCMs, this paper explored the critical topic of the Q-matrix design with a simulation study. The results suggest that including the transpose of the R-matrix in the Q-matrix improved the classification accuracy. Moreover, 10-item tests measuring three linear attributes across three time points provided satisfactory classification accuracy for low-stakes assessment; lower classification rates were observed with independent or divergent attributes. Q-matrix design recommendations were provided for the short-test situation. Implications and future directions were discussed.
Introduction
Diagnostic cognitive models (DCMs; or cognitive diagnostic models, CDMs) have received increasing attention because the latent variable modeling approach to diagnostic assessment can shed light on the learning process (Rupp et al., 2010). A variety of latent variable models have been proposed in recent decades including specific models (e.g., the Deterministic Input, Noisy “and” Gate, DINA; Junker and Sijtsma, 2001) and generalized frameworks (e.g., the log-linear cognitive diagnostic model, LCDM; Henson et al., 2009). Two recent directions aim to address hierarchical attributes (Gierl et al., 2010; Templin and Bradshaw, 2014) and the mastery of attributes in longitudinal data (Li et al., 2016; Kaya and Leite, 2017; Wang et al., 2017; Madison and Bradshaw, 2018a,b), respectively.
The transition DCM (TDCM), proposed by Madison and Bradshaw (2018a,b), is a longitudinal model combining the LCDM and the latent transition analysis (LTA). The TDCM have been used on tests measuring independent attributes (Madison and Bradshaw, 2018a,b). However, empirical studies have suggested the presence of interdependencies among attributes in many educational cases (e.g., Gierl et al., 2010; Templin and Bradshaw, 2014). The incorporation of attribute hierarchy into the Q-matrix and the model parameterization has become important research topics in recent years. One of the approaches to modeling the attribute relationships is to impose a hierarchical structure in which mastering an attribute could be a prerequisite to mastering another attribute (Tatsuoka, 1983; Leighton et al., 2004; Templin and Bradshaw, 2014). Taking this approach, Templin and Bradshaw (2014) extended LCDM to its hierarchical form—hierarchical diagnostic classification model (HDCM). Similarly, the longitudinal model TDCM can be constrained to incorporate hierarchical attributes. Following this line of thinking, we proposed the hierarchical transition DCM (H-TDCM) and explored the effects of Q-matrix designs on its classifications in this study.
The Q-matrix design, as a core element of the DCM-based test design, has not been adequately addressed in the context of longitudinal DCMs, since existing research focuses on model development and applications of longitudinal DCMs (e.g., Kaya and Leite, 2017; Madison and Bradshaw, 2018a,b). The Q-matrix links the items and the latent constructs to be measured (i.e., attributes) (Tatsuoka, 1983). Rows of the Q-matrix correspond to items, columns correspond to attributes, and its binary elements indicate whether an item measures an attribute (to put it differently, whether mastery of an attribute is required to succeed on an item). The row vectors of the Q-matrix are also called q-vectors. The Q-matrix plays important roles, both theoretically and statistically. From a theoretical perspective, cognitive theories could have a real impact on testing practice through the Q-matrix. This is especially true when the attributes are related to each other according to the cognitive theory. From a statistical perspective, the Q-matrix plays a significant role in model identification (Xu and Zhang, 2016; Xu, 2017; Köhn and Chiu, 2018; Gu and Xu, 2019a, forthcoming) and classification accuracy (DeCarlo, 2011; Madison and Bradshaw, 2015; Liu et al., 2017; Tu et al., 2019).
The identifiability conditions need to be satisfied for consistent estimation of the model parameters. Gu and Xu (2019a) identified the sufficient and necessary condition for identification of DINA and DINO. It requires that each attribute is measured by at least three items with a Q-matrix in the form (T denotes transpose), in which any two different columns of the submatrix Q′ are distinct (Gu and Xu, 2019a). The indentifiability issue is more complicated for saturated models (e.g., GDINA) and details on strict or generic identification can be found in Gu and Xu (forthcoming). The identification condition for hierarchical DCMs has also been discussed (Gu and Xu, forthcoming).
However, the Q-matrices that lead to identification may provide varying classification accuracy rates (DeCarlo, 2011; Madison and Bradshaw, 2015). To provide guidance for test construction practices based on DCMs, researchers explored the effects of different Q-matrix designs on the classification accuracy. For example, on the effects of Q-matrix designs with independent attributes, DeCarlo (2011) and Madison and Bradshaw (2015) have found that including more items measuring each attributes in isolation could help increase classification accuracy for DINA and LCDM.
When attribute hierarchies are involved, there has not been a consensus on the Q-matrix design regarding whether all q-vectors are eligible (Templin and Bradshaw, 2014; Tu et al., 2019). When a test involves K independent attributes, there are 2K − 1 distinct q-vectors. Consider a linear hierarchy with three attributes: α1 → α2 → α3. Attribute α2 has direct relationships with the other two attributes while Attribute α1 and α3 have an indirect relationship. The reachability matrix or R-matrix can be used to capture both direct and indirect relationships (Tatsuoka, 1983; Gierl et al., 2000; Leighton et al., 2004). The R-matrix for three attributes under a linear hierarchy is presented in Figure 1. Some researchers argued that an item cannot measure a higher-level attribute without measuring its prerequisite(s) (Leighton et al., 2004; Köhn and Chiu, 2018; Tu et al., 2019), referred to as the restricted Q-matrix approach. According to the restricted Q-matrix approach, only three q-vectors are allowed in the Q-matrix in the case of three linear attributes, which correspond to the three column vectors of the R-matrix. In contrast, some studies use all 2K − 1 = 7 q-vectors in the Q-matrix as in an independent-attribute situation (Liu and Huggins-Manley, 2016; Liu et al., 2017), referred to as the unstructured Q-matrix approach.
Tu et al. (2019) took the restricted Q-matrix approach in a simulation study and emphasized the importance of containing the transpose of the R-matrix in the Q-matrix. Figure 1 provided an example Q-matrix containing the transpose of the R-matrix, RT. Liu et al. (2017), taking the unstructured Q-matrix approach, proposed different approaches to generate Q-matrices with linear, divergent, convergent, or unstructured attributes under the hierarchical diagnostic classification model (HDCM; Templin and Bradshaw, 2014). The adjacent approach (allowing each item to measure at most two attributes with direct relationships) was found to lead to higher classification accuracy in a shorter test (Liu et al., 2017).
To sum up, the purposes of the current study are 2-fold: First, the H-TDCM was defined to incorporate hierarchical attributes in the longitudinal DCM. Second, different Q-matrix designs were explored for TDCM and H-TDCM with a Monte Carlo simulation study. Both longitudinal models are based on LCDM, which is a general framework without limitations of the model fit assumptions. The rest of the paper is organized as follows. The next section briefly introduces LCDM, HDCM, and TDCM before defining the H-TDCM. Then, previous studies on the Q-matrix design are reviewed, followed by a simulation study on Q-matrix designs for TDCM and H-TDCM. The paper is concluded with a discussion of the limitations and educational implications.
Models
LCDM, HDCM, and TDCM
The LCDM (Henson et al., 2009) is a general diagnostic model that parameterizes the effects of the attributes measured by the item on the probability of a correct response given examinee attribute profile. The LCDM subsumes many specific DCMs, including the DINA model (Junker and Sijtsma, 2001) and the DINO model (Templin and Henson, 2006).
Examinee attribute profiles are denoted by vectors αc = (αc1, …αck, …, αcK), where c = 1, …, C and αck takes the value of 0 or 1, indicating the non-mastery or mastery, respectively, of the kth attribute. The LCDM classifies examinees into one of the C = 2K attribute profiles assuming independent attributes. The number of attribute profiles decreases accordingly with hierarchical attributes.
For each item measured on a test, the LCDM item response function models the attributes mastery effects on the item response in terms of an intercept, the main effect for each attribute measured by the item, and the interaction term(s) that correspond to each possible combination of multiple attributes measured by the item. The general form of the LCDM item response function can be expressed as
where λi,0 is the intercept parameter of item i, λi contains all other item parameters including the main effects and interaction terms for item i, qi denotes the q-vector of item i, the superscript T denotes transpose, and the function h results in a linear combination of αc and qi.
Templin and Bradshaw (2014) proposed the hierarchical diagnostic classification models (HDCM) to address hierarchical attributes. Specifically, two changes are made to LCDM. First, the attribute profile space is limited and αc in Equations (1) and (2) is replaced by for notation. When a linear hierarchy is assumed, the number of mastery profiles is reduced from the original C = 2K to C = K + 1. The second change is that model constraints are imposed on LCDM. Specifically, some model parameters of the measurement model are fixed as zero.
Madison and Bradshaw (2018a,b) combined LCDM with latent transition analysis (LTA) to produce TDCM. LTA is a longitudinal latent class model that classifies examinees into latent classes and captures the latent class transitions over time (Collins and Lanza, 2010). As a conventional latent class analysis, it consists of the structural model and the measurement model. It is also a special case of the latent or hidden Markov model (HMM; Baum and Petrie, 1966). LTA parameterizes the probabilities of each latent class transitioning from one latent class to another between each time point in addition to latent class proportions and item parameters (i.e., the parameters estimated in conventional latent class analysis. LCDM serves as the measurement model of LTA. The LTA-DINA (Li et al., 2016) and LTA-DINO (Kaya et al., 2016) can be seen as special cases of the TDCM.
H-TDCM
The proposed H-TDCM combined the features of HDCM and TDCM to deal with hierarchical attributes in longitudinal data. The attribute hierarchy is imposed on TDCM by constraining corresponding item parameters in the measurement model as in HDCM and the structural parameters that are specific to TDCM. Specifically, model parameters for the main effects of nested attributes and some interaction terms are constrained as zero in light of the prerequisite relationships among them. Also, similar constraints are set on the transition parameters and prevalence parameters.
Given the expression of LTA (Collins and Lanza, 2010, p. 198), the probability of an examinee's response vector on I items over T time points is given by
where i = 1, 2, …, I; item i has Ri response categories; yi, t is the examinee's response to item i at time point t and I(yi, t = ri, t) is an indicator function that is equal to 1 when the response is ri, t, and equal to 0 otherwise; each sum ranges over each of the C attribute profiles at each time point, the first product is over the T time points, and the second product is over the I items; if the test measures K attributes with a certain hierarchical structure, the attribute profile at Time Point t is , for simplicity, Ct = C.
There are three types of parameters to be estimated (similar to the case of TDCM) in Equation (3). The first type includes HDCM item parameters λi,0 and λi. The second type is the probability of membership in attribute profile c at time point 1, denoted as δαc1; and the third is the probability of transitioning between different attribute profiles (from αct−1 to αct) between time point t−1 to time point t, denoted as ταct|αct−1, usually expressed as a multinomial regression model (e.g., Reboussin et al., 1998; Nylund, 2007):
We take for example a test measuring three linear attributes (α1 → α2 → α3). The C = 4 attribute profiles are the rows in
Four item parameters are to be estimated including the intercept effect λi,0, the main effect λi,1,(1), the second-order interaction effect λi,2,(2(1)), and the third-order interaction effect λi,3,(3(2,1)):
Note that Equation (3) is a general form of the H-TDCM. The combination of LTA and any other specific hierarchical CDM can be realized by imposing parameter constraints. The H-TDCM, in turn, can be seen as a special case of TDCM, and the two models can be compared with a likelihood-ratio difference test (Collins and Lanza, 2010). When the attribute hierarchy exists, H-TDCM is supposed to provide a more succinct model with a better fit than TDCM (Templin and Bradshaw, 2014).
Simulation Study
Design
The simulation study aimed to explore the effects of different Q-matrices on the classifications of TDCM with or without an attribute hierarchy. There has been a need for short tests that measure a couple of fine-grained attributes in the classroom setting. The simulation conditions approximated a practical formative assessment over a learning period of 2–4 weeks. A limited number of attributes would be focused on within such a short period, and time for testing is also very limited so short sessions are preferred. This short test is supposed to be administered three times: at the beginning, in the middle, and approaching the end of the learning period. Therefore, the simulations only consider three-attribute tests administered over three time points. Three attribute hierarchies (independent, divergent, and linear) are considered. The three attribute hierarchies with three attributes and the associated R-matrices are presented in Figure 2.
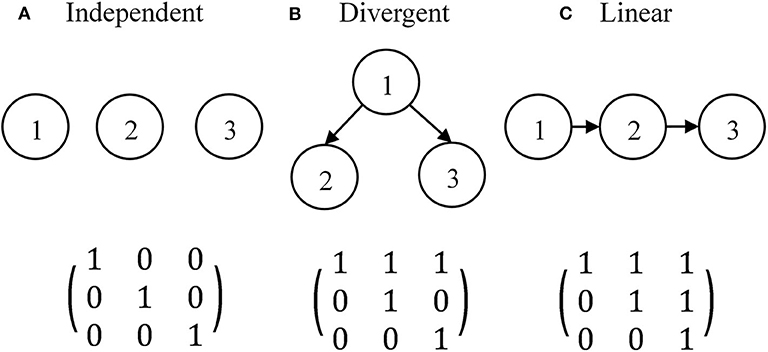
Figure 2. Three attribute hierarchies with three attributes and their R-matrix. (A) Independent. (B) Divergent. (C) Linear.
As mentioned earlier, there are two general approaches to Q-matrix design with hierarchical attributes—the restricted and the unstructured Q-matrix approaches. The restricted Q-matrix approach only allows q-vectors in the transpose of the R-matrix, denoted as RT (Leighton et al., 2004; Köhn and Chiu, 2018; Tu et al., 2019), and the general guideline is to contain several RTs in the Q-matrix to obtain acceptable classification accuracy (Tu et al., 2019). We took the unstructured Q-matrix approach, which means an item can measure all possible combinations of attributes as in an independent-attribute situation (Liu and Huggins-Manley, 2016; Liu et al., 2017), because there exists no empirical evidence against the possibility of items measuring a higher-level attribute without measuring its prerequisite(s). With three attributes in a test, there are seven q-vectors corresponding to seven item types. However, it remains an open question whether it is still beneficial to contain RTs in the Q-matrix even though the unstructured approach was adopted. For each attribute hierarchy, three Q-matrix designs were used. The first Q-matrix design does not contain RT, denoted as Q1. The second and third Q-matrix designs include one or two RTs, which are denoted as Q2 and Q3, respectively. Crossing two factors (i.e., attribute hierarchy and Q-matrix design) led to a total of 9 conditions. The simulation study focused on the Q-matrix design; thus, all Q-matrices were assumed to be correctly specified.
The item parameters are assumed to be time-invariant for the attribute profiles to retain the same meaning over time. Previous studies have shown that the examinee sample size barely has an impact on the classification rates of DCMs (de la Torre et al., 2010; Kaya and Leite, 2017). The effect of sample sizes was explored in Madison and Bradshaw (2018a) with TDCM. Therefore, the sample size was not manipulated but set to be 1,000 in each condition. The attribute profile of examinees followed a uniform distribution. Ten-item tests were generated under each condition.
To avoid the effects of item quality, we fixed the item parameters over all conditions: The intercept effect was −1, the main effect was 2, and the interaction effect was 1. As a result, P(X = 1|α = 0) ranged from 0.1 to 0.3, and P(X = 1|α = 1) was between 0.7 and 1.0. There are 8, 5, and 4 attribute profiles under independent, divergent, and linear hierarchies, respectively. With three independent attributes, there were 23 attribute profiles: c1 (0, 0, 0), c2 (0, 0, 1), c3 (0, 1, 0), c4 (0, 1, 1), c5 (1, 0, 0), c6 (1, 0, 1), c7 (1, 1, 0), and c8 (1, 1, 1). The divergent hierarchy condition had c1 (0, 0, 0), c5 (1, 0, 0), c6 (1, 0, 1), c7 (1, 1, 0), and c8 (1, 1, 1). Three linear attributes led to four attribute profiles: c1 (0, 0, 0), c5 (1, 0, 0), c7 (1, 1, 0), and c8 (1, 1, 1).
Mplus 7.4 (Muthén and Muthén, 1998–2015) was used to generate and analyze the response data of three time points based on TDCM or H-TCDM via maximum likelihood estimation. We include the Mplus syntax for estimation as an Supplementary Material. Evaluation criteria include the marginal correct classification rates (MCCRs) for each attribute and the correct classification rates (CCRs) for each attribute profile. Each simulation condition was replicated 100 times.
Results
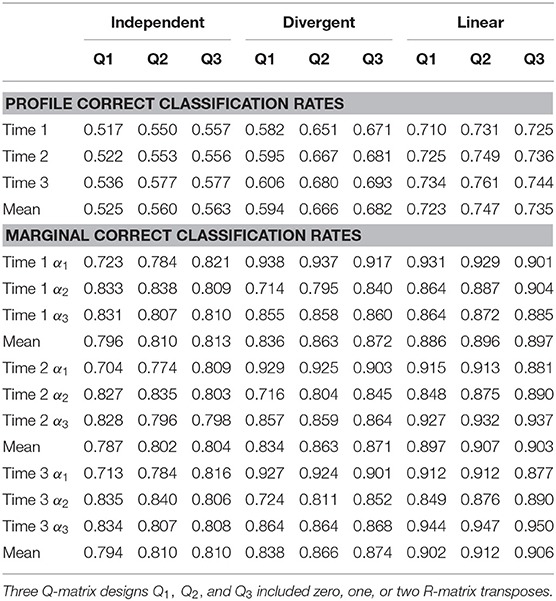
The correct classification rates are presented in Table 1. The results suggested that including the transpose of the R-matrix in the Q-matrix (i.e., Q2) increased the profile CCRs and marginal CCRs at each time point for independent, divergent, and linear hierarchies. Including one more transpose of the R-matrix (i.e., Q3) further slightly increased the CCRs except for the linear hierarchy. Another interesting finding is that the profile CCRs tended to increase with time. The CCRs at Time 3 were the highest. This trend was found under each combination of attribute hierarchy and Q-matrix design. The increase with time was not found in the marginal CCRs for independent attributes. Within the divergent or linear hierarchy, the marginal CCRs of the highest-level attribute (i.e., α2 and α3 under the divergent hierarchy and α3 under the linear hierarchy) increased with time while the lowest-level attribute (i.e., α1) had decreasing CCRs with time.
Comparing the three attribute hierarchies revealed that the CCRs generally increased as the relationship between attributes became stronger, and meanwhile, the number of attribute profiles became smaller. The profile CCRs were above 0.7, and the marginal CCRs were above 0.85 under the linear hierarchy with 10-item tests. The classifications for the independent attributes were the most difficult.
Discussion
This paper proposed H-TDCM for hierarchical attributes in the longitudinal DCM by imposing model constraints on TDCM. The simulation study explored Q-matrix designs with different numbers of R-matrices. The CCRs generally increased with stronger dependencies between attributes, which is consistent with the findings of Templin and Bradshaw (2014) with LCDM. Ten-item tests for three linear attributes lead to profile CCRs above 0.7 and marginal CCRs above 0.85 at each time point, which might to acceptable for low-stakes classroom assessment. However, longer tests are needed for independent or divergent attributes to obtain acceptable classification rates. The profile CCRs increased with time, which means the attribute profile estimate from the final test would be the most accurate among several tests. The final attribute profile estimation may benefit from information from all the previous tests and provides a relatively accurate picture of the learning outcome, which is a desirable property for the longitudinal model.
Regarding the Q-matrix design, we took the unstructured Q-matrix approach (Liu and Huggins-Manley, 2016; Liu et al., 2017) by allowing all possible q-vectors, but explored Q-matrix designs containing different numbers of RT. Simulation results showed that including one R-matrix transpose in the Q-matrix increased the CCRs in the case of independent attributes. Note that although the identification issue of CDMs and the Q-matrix design are usually treated as two separate research areas, the identification requirement may not always be satisfied in the Q-matrix design studies, especially for more complicated models and shorter tests.
First, we looked at the results for independent attributes. A closer look at the Q-matrices revealed that the first Q-matrix design (Q1) did not measure α1 in isolation; the second Q-matrix design (Q2) contained only one identity matrix and measured α1 in isolation only once. This explained the much lower classification rates for α1 compared with other attributes. This finding with the TDCM agrees with the results of conventional DCMs (DeCarlo, 2011; Madison and Bradshaw, 2015). From the identification perspective, it has been proven that including two identity matrices in the Q-matrix is necessary for a saturated DCM such as LCDM with independent attributes (Gu and Xu, forthcoming). Under Q1 and Q2 for independent attributes, the model parameters suffered from the non-identifiability issue and the consequence was reflected in the lower profile CCRs with Q1 and Q2 than with Q3 in Table 1. It also explains why the marginal CCRs of α1 under Q1 and Q2 were substantially lower than those under Q3, while the marginal CCRs of the other two attributes did not differ much between Q-matrix designs.
Including RT in the Q-matrix also increases the classification rates for the hierarchical cases in this study, which is consistent with the empirical findings from Tu et al. (2019). The results for hierarchical attributes can also be explained from the identification perspective as discussed in Gu and Xu (forthcoming). For a generalized multi-parameter DCM such as LCDM or HDCM, the concept of a separable Γ -matrix was introduced (Gu and Xu, forthcoming). The rows and columns of the Γ -matrix is indexed by the items and the attribute profiles, respectively. An entry of the Γ -matrix equals to 1 if an attribute profile has the highest correct response probability on an item and 0 otherwise. A Γ -matrix is said to be separable if any two column vectors of are distinct. The separability of the Γ -matrix is necessary for strict identification. We show that RT as a submatrix in the Q-matrix ensures a separable Γ -matrix in Table 2. It can be further shown that the matrix of RT is in the form of
after some row permutation, in which * takes the value of 0 or 1 and K is the number of attributes. Two RTs were contained in Q3, which led to a separable Γ -matrix. As a result, Q3 always ensures the identification of the model, while the first design may lead to non-identification issues (Gu and Xu, forthcoming). In contrast, Q2 contained one RT and at least one identity matrix instead of two RTs, which does not affect the model identification. Therefore, Q2 and Q3 showed similar classification rates. One major difference between the two designs is that Q2 contains more single-attribute items and fewer multiple-attribute items. Under the linear hierarchy, for example, Q3 has at least two items with q=(111), which has seven item parameters to be estimated. The parameter recovery of such items may be more difficult than single-attribute items, and the classification rate may suffer. As a result, the performance of Q2 turned out to be better than Q3 for the linear hierarchy.
This study aimed to demonstrate the classification performance of the H-TDCM with a short test and provide practical guidelines for the applications of this longitudinal model for formative classroom assessment. For the current setting of short tests and only a few attributes, we recommend that the Q-matrix contains (1) two identity matrices for independent attributes, (2) two RTs for a divergent hierarchy, and (3) one RT and one identity matrix for a linear hierarchy. Besides, each attribute should be probed by at least three items. However, it should be noted that the current simulation study assumes that it is possible to develop items of all types of q-vectors with equal easiness, which may not be true for certain subject areas. For example, it may be more difficult to develop items that measure each attribute in isolation.
The formative classroom assessment has received renewed attention recently with the development of curriculum reform. The fusion of curriculum, instruction, and the assessment requires timely and constructive feedback that is closely connected to a curriculum and are based on students' learning history (e.g., Bennett, 2015; Gotwals, 2018; Shepard et al., 2018). Such feedback can be obtained from a diagnostic model that portrays the progression of attribute profiles. To establish the learning progression in terms of attribute profiles, however, is not an easy task. A possible solution could be collecting longitudinal assessment data from multiple classrooms and applying H-TDCM. The model parameters and classification results from H-TDCM can be used to understand the learning process better and to give teachers and students prior information before the learning begins. The current study focused on short tests for classroom applications where the attribute hierarchy is prespecified. Future simulation research can extend to longer tests for the purpose of exploring the learning process by estimating the attribute hierarchy. Those who are interested may refer to the requirement on the Q-matrix design (Gu and Xu, 2019b).
Data Availability Statement
The datasets generated for this study are available on request to the corresponding author.
Author Contributions
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
Funding
This study is supported by the National Education Sciences Planning Projects Multilevel cognitive diagnostic model: individual and group diagnosis in large-scale educational assessment (CCA150160).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fpsyg.2020.01694/full#supplementary-material
References
Baum, L., and Petrie, T. (1966). Statistical inference for probabilistic functions of finite state Markov chains. Ann. Math. Stat. 37, 1554–1563. doi: 10.1214/aoms/1177699147
Bennett, R. E. (2015). The changing nature of educational assessment. Rev. Res. Educ. 39, 370–407. doi: 10.3102/0091732X14554179
Collins, L. M., and Lanza, S. T. (2010). Latent Class and Latent Transition Analysis: With Applications in the Social, Behavioral, and Health Sciences. Hoboken, NJ: John Wiley and Sons.
de la Torre, J., Hong, Y., and Deng, W. (2010). Factors affecting the item parameter estimation and classification accuracy of the DINA model. J. Educ. Measure. 47, 227–249. doi: 10.1111/j.1745-3984.2010.00110.x
DeCarlo, L. T. (2011). On the analysis of fraction subtraction data: The DINA model, classification, latent class sizes, and the Q-matrix. Appl. Psychol. Measure. 35, 8–26. doi: 10.1177/0146621610377081
Gierl, M. J., Alves, C., and Majeau, R. T. (2010). Using the attribute hierarchy method to make diagnostic inferences about examinees' knowledge and skills in mathematics: An operational implementation of cognitive diagnostic assessment. Int. J. Test. 10, 318–341. doi: 10.1080/15305058.2010.509554
Gierl, M. J., Leighton, J. P., and Hunka, S. (2000). Exploring the logic of Tatsuoka's rule-space model for test development and analysis. Educ. Measure. Issues Prac. 19, 34–44. doi: 10.1111/j.1745-3992.2000.tb00036.x
Gotwals, A. W. (2018). Where are we now? Learning progressions and formative assessment. Appl. Measure. Educ. 31, 157–164. doi: 10.1080/08957347.2017.1408626
Gu, Y., and Xu, G. (2019a). The sufficient and necessary condition for the identifiability and estimability of the DINA model. Psychometrika 84, 468–483. doi: 10.1007/s11336-018-9619-8
Gu, Y., and Xu, G. (2019b). Identification and estimation of hierarchical latent attribute models. arXiv:1906.07869.
Gu, Y., and Xu, G. (forthcoming). Partial identifiability of restricted latent class models. Ann. Stat.
Henson, R. A., Templin, J. L., and Willse, J. T. (2009). Defining a family of cognitive diagnosis models using log-linear models with latent variables. Psychometrika 74, 191–210. doi: 10.1007/s11336-008-9089-5
Junker, B. W., and Sijtsma, K. (2001). Cognitive assessment models with few assumptions, and connections with nonparametric item response theory. Appl. Psychol. Measure. 25, 258–272. doi: 10.1177/01466210122032064
Kaya, Y., and Leite, W. L. (2017). Assessing change in latent skills across time with longitudinal cognitive diagnosis modeling: an evaluation of model performance. Educ. Psychol. Measure. 77, 369–388. doi: 10.1177/0013164416659314
Kaya, Y., Leite, W. L., and Miller, M. D. (2016). A comparison of logistic regression models for DIF detection in polytomous items: the effect of small sample sizes and non-normality of ability distributions. Int. J. Assessment Tools Educ. 2, 22–39. doi: 10.21449/ijate.239563
Köhn, H. F., and Chiu, C. Y. (2018). How to build a complete Q-matrix for a cognitively diagnostic test. J. Classification 35, 273–299. doi: 10.1007/s00357-018-9255-0
Leighton, J. P., Gierl, M. J., and Hunka, S. M. (2004). The attribute hierarchy method for cognitive assessment: a variation on Tatsuoka's Rule-Space approach. J. Educ. Measure. 41, 205–237. doi: 10.1111/j.1745-3984.2004.tb01163.x
Li, F., Cohen, A., Bottge, B., and Templin, J. (2016). A latent transition analysis model for assessing change in cognitive skills. Educ. Psychol. Measure. 76, 181–204. doi: 10.1177/0013164415588946
Liu, R., and Huggins-Manley, A. C. (2016). The specification of attribute structures and its effects on classification accuracy in diagnostic test design. In: Quantitative Psychology Research, eds L. A. van der Ark, D. M. Bolt, W.-C. Wang, J. A. Douglas, and M. Wiberg (New York, NY: Springer), 243–254.
Liu, R., Huggins-Manley, A. C., and Bradshaw, L. (2017). The impact of Q-matrix designs on diagnostic classification accuracy in the presence of attribute hierarchies. Educ. Psychol. Measure. 77, 220–240. doi: 10.1177/0013164416645636
Madison, M. J., and Bradshaw, L. P. (2015). The effects of Q-matrix design on classification accuracy in the log-linear cognitive diagnosis model. Educ. Psychol. Measure. 75, 491–511. doi: 10.1177/0013164414539162
Madison, M. J., and Bradshaw, L. P. (2018a). Assessing growth in a diagnostic classification model framework. Psychometrika 83, 963–990. doi: 10.1007/s11336-018-9638-5
Madison, M. J., and Bradshaw, L. P. (2018b). Evaluating intervention effects in a diagnostic classification model framework. J. Educ. Measure. 55, 32–51. doi: 10.1111/jedm.12162
Nylund, K. L. (2007). Latent transition analysis: Modeling extensions and an application to peer victimization (doctoral dissertation). University of California, Los Angeles, CA, United States.
Reboussin, B. A., Reboussin, D. M., Liang, K.-Y., and Anthony, J. C. (1998). Latent transition modeling of progression of health-risk behavior. Multivariate Behav. Res. 33, 457–478. doi: 10.1207/s15327906mbr3304_2
Rupp, A., Templin, J., and Henson, R. (2010). Diagnostic Measurement: Theory, Methods, and Applications. New York, NY: Guilford Press.
Shepard, L. A., Penuel, W. R., and Pellegrino, J. W. (2018). Classroom assessment principles to support learning and avoid the harms of testing. Educ. Measure. Issues Pract. 37, 52–57. doi: 10.1111/emip.12195
Tatsuoka, K. K. (1983). Rule space: an approach for dealing with misconceptions based on item response theory. J. Educ. Measure. 20, 345–354. doi: 10.1111/j.1745-3984.1983.tb00212.x
Templin, J., and Bradshaw, L. (2014). Hierarchical diagnostic classification models: a family of models for estimating and testing attribute hierarchies. Psychometrika 79, 317–339. doi: 10.1007/s11336-013-9362-0
Templin, J. L., and Henson, R. A. (2006). Measurement of psychological disorders using cognitive diagnosis models. Psychol. Methods 11, 287–305. doi: 10.1037/1082-989X.11.3.287
Tu, D., Wang, S., Cai, Y., Douglas, J., and Chang, H. (2019). Cognitive diagnostic models with attribute hierarchies: model estimation with a restricted Q-matrix design. Appl. Psychol. Measure. 43, 255–271. doi: 10.1177/0146621618765721
Wang, S., Yang, Y., Culpepper, S. A., and Douglas, J. A. (2017). Tracking skill acquisition with cognitive diagnosis models: a higher-order, hidden markov model with covariates. J. Educ. Behav. Stat. 43, 57–87. doi: 10.3102/1076998617719727
Xu, G. (2017). Identifiability of restricted latent class models with binary responses. Ann. Stat. 45, 675–707. doi: 10.1214/16-AOS1464
Keywords: Q-matrix, longitudinal DCMs, hierarchical attributes, TDCM, HDCM
Citation: Tian W, Zhang J, Peng Q and Yang X (2020) Q-Matrix Designs of Longitudinal Diagnostic Classification Models With Hierarchical Attributes for Formative Assessment. Front. Psychol. 11:1694. doi: 10.3389/fpsyg.2020.01694
Received: 02 February 2020; Accepted: 22 June 2020;
Published: 30 July 2020.
Edited by:
Hong Jiao, University of Maryland, College Park, United StatesReviewed by:
Lietta Marie Scott, Arizona Department of Education, United StatesGongjun Xu, University of Michigan, United States
Copyright © 2020 Tian, Zhang, Peng and Yang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jiahui Zhang, bmVsbHlraW1AMTI2LmNvbQ==
 Wei Tian
Wei Tian Jiahui Zhang
Jiahui Zhang Qian Peng
Qian Peng Xiaoguang Yang
Xiaoguang Yang