- 1Department of Biological Systems Engineering, University of Nebraska–Lincoln, Lincoln, NE, United States
- 2Department of Food Science and Technology, Nebraska Food for Health Center, University of Nebraska–Lincoln, Lincoln, NE, United States
Prevention of the growth of harmful microorganisms in food products is an important requirement for ensuring food safety and quality. Mathematical models to predict the quantitative changes in microbial populations in food to the variations of environmental conditions are useful tools in this regard. While equations for microbial inactivation have typically been formulated based on polynomial functions, empirical choice of the model order and terms not only results in over- or underfitting, but also makes it difficult to identify key factors governing the target variable. To address this issue, we present a data-driven modeling pipeline that enables 1) automatic discovery of model equations through parsimonious selection of relevant terms from a pre-built library and 2) subsequent evaluation of the impacts of individual terms on the model output. Through case studies using literature data, we evaluated the effectiveness of our pipeline in predicting the D-value (i.e., the time taken to reduce microbial population to 10% of the initial level) as a function of multiple factors including temperature, pH, water activity, NaCl content, and phosphate level. In doing this, we determined basic functional forms of input and output variables based on their pre-known relationships, e.g., by accounting for the Arrhenius dependence of D-value on temperature. Incorporation of such theoretical knowledge into the pipeline improved model accuracy. Using the Akaike information criterion, we optimally determined hyperparameters that control a trade-off between model accuracy and sparsity. We found the literature models benchmarked in this study to be over- or under-determined and consequently proposed better structured and more accurate equations. The subsequent global sensitivity analysis allowed us to evaluate the context-dependent impacts of key factors on the D-value. The pipeline presented in this work is readily applicable to many other related non-linear systems without being limited to microbial inactivation datasets.
1 Introduction
Food is vulnerable to contamination by pathogens and spoilers. Pathogens in contaminated food induce foodborne diseases, while spoilers deteriorate the quality of food by changing the biochemical properties of food materials (Lianou et al., 2016). The invasion of those harmful microorganisms can take place anytime throughout the lifecycle of food including production, processing, distribution, storing, and preservation (Lianou et al., 2016). Treatment of food with extreme conditions is known to render microbes inert, which is however not an ideal solution due to adverse effects on texture, taste, and flavor, denaturation of nutrients (e.g., vitamin A), as well as excessive energy demand (Amit et al., 2017). As complete removal of pathogens and spoilers from food is often infeasible as such, their suppression to a safe low level by refining treatment methods and conditions is essential for ensuring food safety and quality. Therefore, determination of optimal conditions to control the growth of harmful microorganisms requires meeting multiple objectives that are often contradictory (Madoumier et al., 2019). While many alternative microbial inactivation technologies with temperate processing conditions have emerged, such as high-pressure processing (Podolak et al., 2020), pulsed light inactivation (Artíguez et al., 2011), and various non-thermal methods (Mañas and Pagán, 2005), accurate evaluation of the relative influences of the associated process factors remains challenging due to the lack of a tractable and generalizable approach to analyze the process mechanics.
Mathematical models are indispensable tools for predicting and optimizing microbial inactivation processes in food. Accurate modeling of microbial growth or inactivation is a difficult task due its complex dependence on numerous internal (such as water activity, pH, composition, and preservatives) and external food conditions (e.g., temperature and humidity) (Akkermans et al., 2020). Appropriate consideration of the functional relationships between microbial populations and such intrinsic and extrinsic parameters is critical for model performance. Microbial inactivation models are often built on fitted polynomial equations, while other forms such as Arrhenius or square root relationships have also been considered (Whiting, 1995; Ross and Dalgaard, 2003). Typical modeling efforts using the polynomial equations have focused on determining optimal parameter values (i.e., coefficients of pre-chosen terms) through data fit. However, this approach cannot ensure robust development of microbial inactivation models because inadequate representation of equations can lead to poor performance in data fit and prediction due to intrinsic structural error that cannot be compensated through parameter estimation (Kaplan, 2002). Moreover, empirical determination of governing terms often lacks expandability with increasing number of process variables, necessitating a more systematic, rational approach.
Sparse Identification of Nonlinear Dynamics (SINDy) (Brunton et al., 2016) is a promising approach that enables automatic discovery of model equations without having to assume model structure a priori, making it distinct from typical approaches that focus on estimating optimal values of the parameters through data fit in a pre-defined function. SINDy allows the use of a library of input variables (that potentially affect the output variables of interest) to identify the model structure by linear combinations of the terms in the library. Following the Occam’s razor principle postulating that the simplest explanation generally tends to be the correct representation (Blumer et al., 1987; Song et al., 2013), SINDy promotes parsimony in model identification based on a minimal subset of terms.
In this work, we present a data-driven modeling pipeline utilizing SINDy for robust development of microbial inactivation models for application in food safety and quality. While the original goal of SINDy is to identify sparse models of nonlinear dynamical systems, we apply it to non-dynamical systems through appropriate reformulation (see Methods). For demonstration, we considered case studies of modeling the change in D-values—the time taken for a 90% reduction in microbial population—under the variations of multiple factors including temperature, pH, water activity, NaCl content, and phosphate level. Built on SINDy, our modeling pipeline has three major additional features: 1) Incorporation of theoretical knowledge on the relationships between basic input and output variables, e.g., by accounting for the temperature dependence of D-value following the Arrhenius equation; 2) rational determination of hyperparameters (such as the polynomial order and sparsity-controlling parameter) based on information-theoretic metric for an optimal balance between model accuracy and sparsity, and 3) integration with global sensitivity analysis to evaluate the effects of key factors on model outputs. Our analysis showed that the benchmark models in the literature considered in this work are mostly over- or underfitted. Using our approach, therefore, we were able to propose better structured models with improved accuracy and less complexity.
2 Materials and methods
Identification of model structure (i.e., functional forms of the relationship between input and output variables) is challenging as there are many possible solutions to formulate a specific model from a given dataset. In this section, we describe how systematic identification of model equations and key variables/terms governing microbial inactivation can be enabled by an advanced data-driven approach called SINDy (Brunton et al., 2016) in conjunction with global sensitivity analysis, respectively.
2.1 Essence of sparse identification of nonlinear dynamics
The original motivation of SINDy is to discover governing equations for nonlinear dynamical systems, which is reconfigured here to apply to non-dynamical systems as follows:
where
where
where
SINDy seeks a parsimonious model composed with minimal number of terms as possible without compromising model accuracy. Sparse regression methods such as Sequentially Thresholded Least Squares (STLS) and Least Absolute Shrinkage and Selection Operator (LASSO) are useful algorithms that can be used in SINDy for this purpose (Brunton et al., 2016). In this work, we employ STLS where
2.2 Application of SINDy to microbial inactivation modeling
We use SINDy to formulate microbial inactivation as functions of various process variables including temperature (
While SINDy offers flexibility to pick any nonlinear terms for input and output variables, we determine the inclusion of their specific functional forms following the known mechanistic knowledge and characteristics of the system. Therefore, we used a vector of
2.3 Tuning model sparsity and accuracy based on an information-theoretic criterion
We tune the order of combination of primitive process variables and the sparsity index,
where MSE denotes mean squared error,
2.4 Density-based global sensitivity analysis
We perform sensitivity analyses on our models as an alternative to arduous assessment of the relative effects of the process variables on microbial inactivation directly from highly distributed experimental data. As the models are linear combinations of nonlinear terms and the datasets used in this work span over a wide parameter space, the possibility of model forming stiff parameter dependency is high. Therefore, we employ a density-based global sensitivity analysis approach called PAWN (Pianosi and Wagener, 2015), instead of local sensitivity approach. Based on this approach, absolute deviation is calculated between an unconditional cumulative density function of model output,
Here,
2.5 Experimental datasets
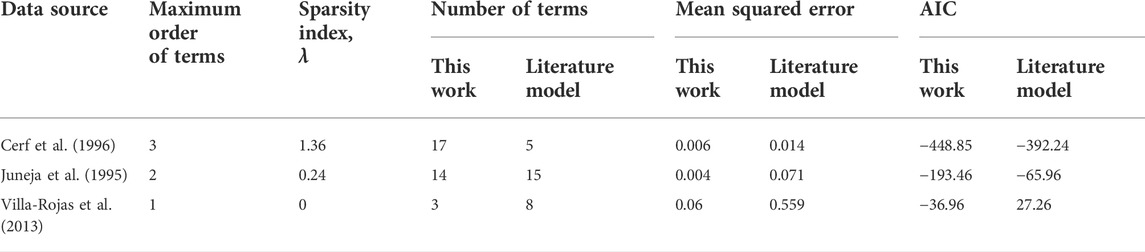
The experimental datasets used for microbial inactivation modeling in this work are collated in Table 1. We chose datasets that are predominantly distinct in terms of microorganisms, media, process variables, and parameter space to demonstrate the tractability of our knowledge-informed data-driven pipeline for model development. We also found that the structure of the literature models developed from these datasets was under- or over-determined, rather than optimally determined. Consequently, the datasets and benchmark models we chose serve as an ideal testbed for evaluating the robustness of our approach.
2.6 Computational implementation
Numerical codes were developed using MATLAB® R2021a by adapting the prototype codes of SINDy provided in Brunton and Kutz (2019) and PAWN global sensitivity analysis given in Pianosi and Wagener (2015) and Pianosi et al. (2015).
3 Results
3.1 Development of a knowledge-informed data-driven modeling pipeline
Our data-driven modeling approach combines SINDy and global sensitivity analysis to identify model equations and key factors that govern microbial inactivation in food. As a main feature, users can define any functional forms of input variables (
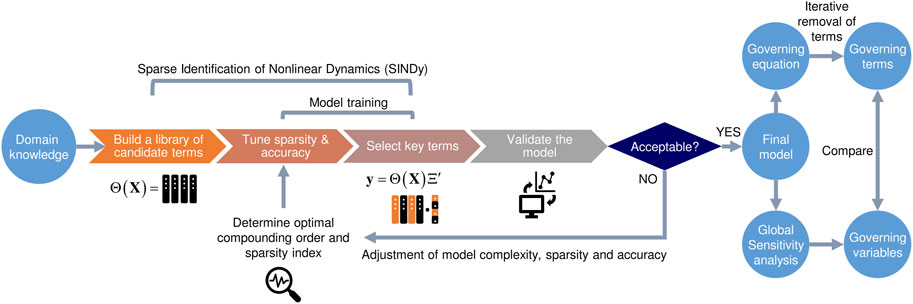
FIGURE 1. Flowchart depicting our knowledge-informed data-driven model development pipeline. The weights assigned to the columns of experimental input variables curated to the functional forms of candidate terms in the library instruct the choice of terms to be included in the final model structure through Sequentially Thresholded Least Squares (STLS) regression (more details in main texts).
The development of data-driven microbial inactivation model can be facilitated by known characteristics of the system. While first-order representation is a typical choice for input and output variables, it is possible to improve model performance by a more appropriate choice of their functional forms. For this purpose, we leverage mechanistic microbial growth models (Whiting, 1995) to inform our choice of functional forms for microbial inactivation dynamics as follows:
where
By definition, the population density is
Therefore, D-value is simply:
Subsequently, applying logarithm to the equation above yields:
where
Consequently, the functional forms of output variable and input variables provided for SINDy implementations are
3.2 Optimization of model complexity: Setting polynomial order and model sparsity
To substantiate our choice of functional forms for input and output variables in the preceding section, we compare the model performance per our approach (orange lines in Figure 2) against another base case with non-logarithmic D-values and non-reciprocal temperature and other process variables (blue lines in Figure 2). Here, complete non-parsimonious models are used to ensure fair comparison of the models without the influence of sparse regression. Our approach consistently performed better in terms of MSE calculated based on logarithmic D-values for both cases across different datasets and orders of polynomial combinations of input variables. For all the results that follow henceforth, our choice of the functional forms (i.e., orange lines in Figure 2) are adopted.
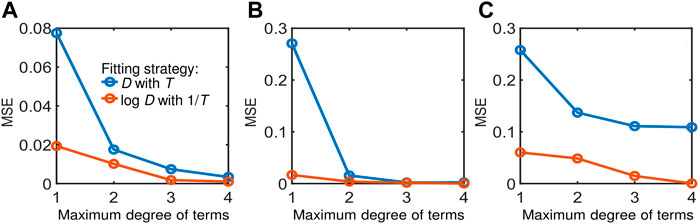
FIGURE 2. Comparison of model performance between different choices of functional forms for input and output variables using datasets from: (A) Cerf et al. (1996), (B) Juneja et al. (1995), and (C) Villa-Rojas et al. (2013). The blue line represents a model with D (chosen as the target variable) and
With
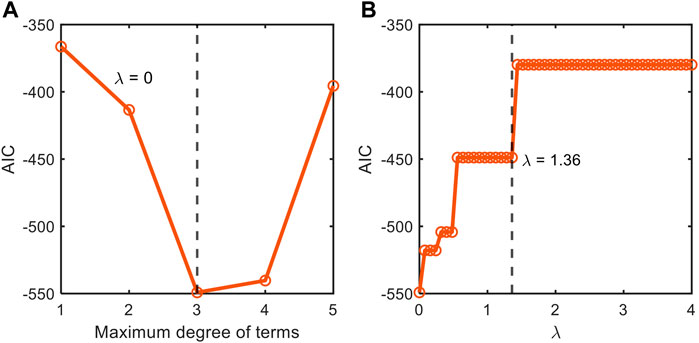
FIGURE 3. Stepwise tuning of model accuracy and sparsity through the comparison of information-theoretic metric (AIC) by first (A) fixing the order of polynomial combinations of input variables for non-parsimonious model (
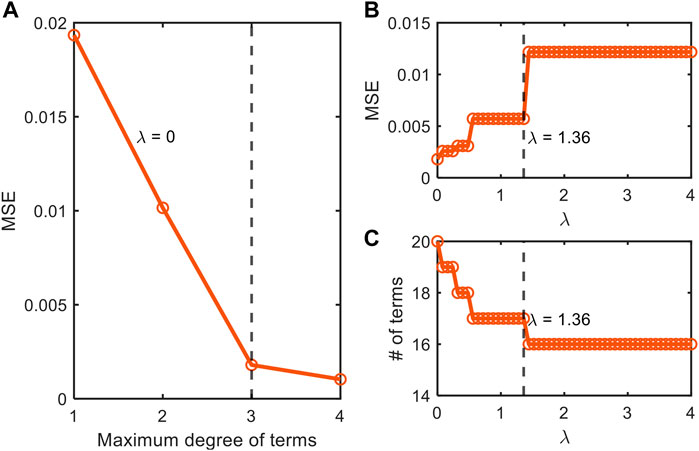
FIGURE 4. Depiction of our stepwise model tuning approach that minimizes model overfitting through the optimization of (A) the order of polynomial combinations of input variables for non-parsimonious model (
We also applied this stepwise model construction approach to the datasets from Juneja et al. (1995) (Supplementary Figures S1, S2) and Villa-Rojas et al. (2013) (Supplementary Figures S3, S4). The analysis for the dataset from Juneja et al. (1995) showed that AIC values have two local minima at the polynomial orders 2 and 4 (Supplementary Figure S1A). Through further checking with MSE and the number of terms, we chose the second-order model for better interpretability. After determining the polynomial order, we subsequently determined the optimal value of
3.3 Data-driven identification of governing equations for enhanced accuracy and expandability
Following the guidelines outlined in the preceding and Methods sections, we developed models for all experimental datasets considered in this work. The resulting model equations are summarized in Table 2. The individual models consist of varying number and degree of monomial terms as identified through our data-driven model development pipeline which are optimal to represent the output variable within the parameter space of the respective datasets. The identification of the optimal terms (especially higher-order terms) would not be possible with the previous approaches that rely on empirical choices of equation terms. The issues of model overfitting and uncertainties are also minimized with our stepwise approach in model design.

Table 2. Governing model equations identified by leveraging our knowledge-informed data-driven modeling pipeline.
We compare the performance of our models with existing models from the literature in Figure 5. Our models consistently perform better than the literature models across all datasets, particularly for the dataset from Juneja et al. (1995) that has considered additional process variables, i.e.,
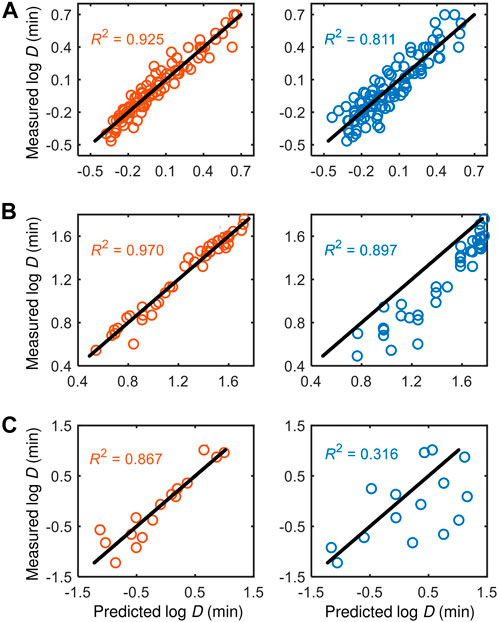
FIGURE 5. Comparison of the performance of our knowledge-informed data-driven models (left panels) against literature models (right panels) across different datasets: (A) Cerf et al. (1996), (B) Juneja et al. (1995), and (C) Villa-Rojas et al. (2013).
3.4 Integration of data-driven approach and sensitivity analysis for determining key governing process variables and model terms
While our model governing equations offer good representations of experimental data, the individual effects of process variables remain elusive. In addition to data-driven modeling, we leverage global sensitivity analysis (Pianosi and Wagener, 2015) using the model-derived governing equations to identify key governing process variables and possibly divulge the interactions between them. Here, the sensitivities are evaluated for the entire parameter space encompassed by the respective datasets (Table 1). Our results demonstrate highly disparate sensitivity measures for the process variables across datasets as shown in Figure 6, positing that the relative effects of the process variables may be highly environment dependent. For example,
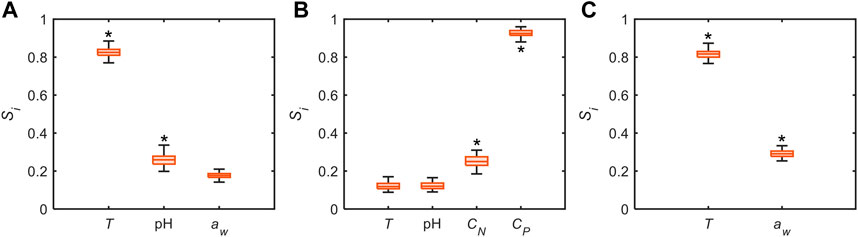
FIGURE 6. Distribution of global sensitivities of process variables on output variable, i.e.,
To resolve this issue, we implement the combined use of data-driven approach and global sensitivity analysis that enables elucidation of the factors influencing the process dynamics from the contexts of governing equations, key process variables and critical model monomial terms. To this effect, we iteratively removed each term in the governing equations, and subsequently refitted the models with new MSEs as shown in Figure 7, whereby considerable increase in MSE (as compared to the original complete model, represented by horizontal dashed lines) indicates that the respective terms are essential to represent the output variable. In the model for data from Cerf et al. (1996), removal of terms containing
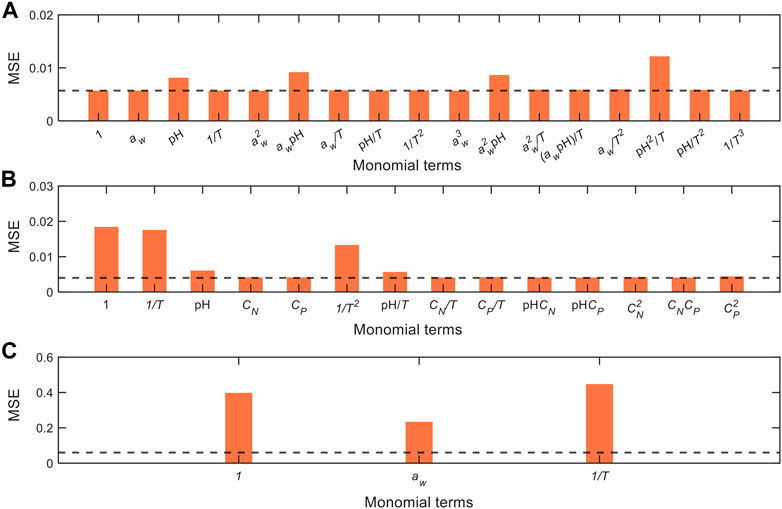
FIGURE 7. Comparison of model performance with iterative removal of terms from the model equations generated from different datasets: (A) Cerf et al. (1996), (B) Juneja et al. (1995), and (C) Villa-Rojas et al. (2013). MSEs are recalculated after refitting the model with the removal of each term, whereby a large increase in MSEs indicates that the respective terms are highly critical to represent the output data. The MSEs of the original complete model are denoted by the horizontal dashed lines (cf. MSEs in Table 3).
Conversely, in the model for data from Juneja et al. (1995), removal of terms with
4 Discussion
Conventional modeling approaches that empirically ascertain model structures and parameter functional forms are forceful approximations as there exists an overwhelmingly large number of possible solutions. Using a systematic data-driven model development pipeline guided by knowledge-informed choices of parameter functional forms and methodical tuning of model sparsity and accuracy, we developed microbial inactivation models that outperformed existing models from the literature. Our approach not only ensures identifying the most plausible model structure by leveraging on domain knowledge of the system, but also elucidates the factors affecting the process dynamics through the combined use of global sensitivity analysis.
The sound choice of functional forms for input and output target variables as informed by mechanistic formulation (e.g., Arrhenius equation in this work) can be integral in optimizing model structure and performance. The inclusion of the reciprocal functional form for temperature is fitting as it resembles the inverse relationship between logarithmic rate and temperature in linear Arrhenius equation. We could not make such consideration for other variables in the absence of any literary basis or improvements to model fits with reciprocal terms. The choice of logarithmic output variable is also apt for several reasons: 1) Logarithmic D-values form linear relationships with temperature and other process variables that may assume the classical power-law form, which is realized through the linear combinations of monomial terms of various degrees through SINDy, and 2) training the model on logarithmic D-values ensure that the resulting model is sensitive and operates optimally in the small D-value regions which are especially critical for microbial inactivation dynamics. Although even empirical formulation may bear structural similarity to our models to a degree, we highlight that our choice of final terms to represent the output variable is guided by systematic sparse identification as described in Section 2.
The use of information-theoretic criterion such as AIC guided us to determine optimal levels of model complexity, while the literature models were inappropriately structured. Therefore, our approach allowed us to propose more accurate models with fewer number of terms as demonstrated through the cases with Juneja et al. (1995) and Villa-Rojas et al. (2013) in Table 3. In contrast, in the case of underfitted models such as the one from Cerf et al. (1996), we showed how to further reduce the error by adding extra terms. The inclusion of higher-order terms (polynomial combinations of individual process variables) in the model is critical to account for mixed effects between the process variables. For example, a lower temperature is generally observed to increase the effects of pH but the effects on water activity are contradictory in the literature (Villa-Rojas et al., 2013). Despite potential importance, those mixed effects have been overlooked in microbial inactivation studies except the well-known interaction between temperature and pH. Even in the case of accounting for combinatorial effects of multiple process variables, determination of their functional forms remains largely elusive. In contrast, our pipeline evaluates interaction effects through the higher-order terms, which are subsequently compared with individual effects through global sensitivity analysis to divulge complex associations between the process variables. Our approach is particularly useful to handle systems with many process variables as all possible interactions are simultaneously handled in the library matrix, which otherwise would be inefficient in conventional approaches. As highlighted here and above, therefore, our approach complements SINDy by providing additional guidance towards selection of basic functional forms for input and output variables and determination of the optimal level of model complexity, ensuring the robust performance across different cases.
While our knowledge-informed data-driven modeling pipeline worked well for all the datasets considered in this work, user may further tweak the model design to their desired complexity, sparsity, and accuracy through the feedback loop in Figure 1. For example, one may employ a larger
Beyond achieving enhanced performance of data fit compared to existing models, our approach provides a systematic and generalizable pipeline for high-throughput development of microbial growth and inactivation models applicable to various types of datasets. This capability should prove useful for food manufacturers and researchers to assess the efficacy of their existing food production stratagem and to identify new necessary conditions for effective microbial inactivation in a yet unexamined food. Further, our approach also serves as a future basis to model new microbial inactivation processing technologies that steer away from conventional processing conditions to more intricate parameters such as pressure, light pulses and degree of exposure, and various non-thermal variables (Mañas and Pagán, 2005; Artíguez et al., 2011; Podolak et al., 2020). Moreover, our approach can be readily extended to develop primary (dynamic) inactivation models when appropriate and adequate time-series microbial inactivation data becomes available to render the model reasonably identifiable. Lastly, the combined use of data-driven modeling and global sensitivity analysis in the pipeline is also useful for rational model-based optimization of operating conditions and design of control systems, not only for microbial inactivation processes but any non-linear systems for a wide range of applications.
Data availability statement
The MATLAB codes and literature data used in this study can be found in the GitHub repository at https://github.com/hyunseobsong/sindy4inactivation. Further inquiries can be directed to the corresponding author for additional information.
Author contributions
H-SS conceptualized the data-driven modeling pipeline and designed the study. FA contributed to the formulation of the framework and performed global sensitivity analysis. SZ built SINDy models to compare with literature results. SZ and FA drafted the manuscript, which was edited by H-SS to its final version. All authors contributed to the interpretation and analysis of the results.
Funding
This work was supported by Nebraska Tobacco Settlement Biomedical Research Enhancement Funds to H-SS.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frfst.2022.996399/full#supplementary-material
References
Akaike, H. (1998). Information theory and an extension of the maximum likelihood principle, 199–213. doi:10.1007/978-1-4612-1694-0_15
Akkermans, S., Smet, C., Valdramidis, V., and Van Impe, J. (2020). Microbial inactivation models for thermal processes. Food Eng. Ser., 399–420. doi:10.1007/978-3-030-42660-6_15
Amit, S. K., Uddin, M. M., Rahman, R., Islam, S. M. R., and Khan, M. S. (2017). A review on mechanisms and commercial aspects of food preservation and processing. Agric. Food Secur. 6, 1–22. doi:10.1186/s40066-017-0130-8
Artíguez, M. L., Lasagabaster, A., and Marañón, I. M. de (2011). Factors affecting microbial inactivation by Pulsed Light in a continuous flow-through unit for liquid products treatment. Procedia Food Sci. 1, 786–791. doi:10.1016/j.profoo.2011.09.119
Blumer, A., Ehrenfeucht, A., Haussler, D., and Warmuth, M. K. (1987). Occam’s Razor. Inf. Process. Lett. 24, 377–380. doi:10.1016/0020-0190(87)90114-1
Brunton, S. L., and Kutz, J. N. (2019). Data-Driven Sci. Eng. Cambridge University Press, Cambridge, UK, doi:10.1017/9781108380690
Brunton, S. L., Proctor, J. L., Kutz, J. N., and Bialek, W. (2016). Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proc. Natl. Acad. Sci. U. S. A. 113, 3932–3937. doi:10.1073/pnas.1517384113
Burnham, K. P., and Anderson, D. R. (2002). Model selection and multimodel inference: A practical information-theoretic approach. Springer Science & Business Media, Berlin/Heidelberg, Germany, 2nd ed. doi:10.1016/j.ecolmodel.2003.11.004
Cerf, O., Davey, K. R., and Sadoudi, A. K. (1996). Thermal inactivation of bacteria - a new predictive model for the combined effect of three environmental factors: Temperature, pH and water activity. Food Res. Int. doi:10.1016/0963-9969(96)00039-7
Juneja, V. K., Marmer, B. S., Phillips, J. G., and Miller, A. J. (1995). Influence of the intrinsic properties of food on thermal inactivation of spores of nonproteolytic Clostridium botulinum: Development of a predictive model. J. Food Saf. doi:10.1111/j.1745-4565.1995.tb00145.x
Kaplan, D. (2002). Structural equation modeling. Int. Encycl. Soc. Behav. Sci., 15215–15222. doi:10.1016/B0-08-043076-7/00776-2
Lianou, A., Panagou, E. Z., and Nychas, G. J. E. (2016). Microbiological spoilage of foods and beverages. Elsevier. Amsterdam, Netherlands, doi:10.1016/B978-0-08-100435-7.00001-0
Madoumier, M., Trystram, G., Sébastian, P., and Collignan, A. (2019). Towards a holistic approach for multi-objective optimization of food processes: A critical review. Trends Food Sci. Technol. 86, 1–15. doi:10.1016/j.tifs.2019.02.002
Mañas, P., and Pagán, R. (2005). Microbial inactivation by new technologies of food preservation. J. Appl. Microbiol. 98, 1387–1399. doi:10.1111/j.1365-2672.2005.02561.x
Pianosi, F., Sarrazin, F., and Wagener, T. (2015). A matlab toolbox for global sensitivity analysis. Environ. Model. Softw. 70, 80–85. doi:10.1016/j.envsoft.2015.04.009
Pianosi, F., and Wagener, T. (2015). A simple and efficient method for global sensitivity analysis based on cumulative distribution functions. Environ. Model. Softw. 67. doi:10.1016/j.envsoft.2015.01.004
Podolak, R., Whitman, D., and Black, D. G. (2020). Factors affecting microbial inactivation during high pressure processing in juices and beverages: A review. J. Food Prot. 83, 1561–1575. doi:10.4315/JFP-20-096
Ross, T., and Dalgaard, P. (2003). Secondary models. Model. Microb. Responses Food, 63–150. doi:10.1201/9780203503942.ch3
Song, H.-S., DeVilbiss, F., and Ramkrishna, D. (2013). Modeling metabolic systems: The need for dynamics. Curr. Opin. Chem. Eng. 2, 373–382. doi:10.1016/j.coche.2013.08.004
Villa-Rojas, R., Tang, J., Wang, S., Gao, M., Kang, D. H., and Mah, J. H., (2013). Thermal inactivation of salmonella enteritidis PT 30 in almond kernels as influenced by water activity. J. Food Prot. doi:10.4315/0362-028X.JFP-11-509
Keywords: food safety and security, data-driven modeling, microbial inactivation, global sensitivity analysis, information-theoretic criteria
Citation: Zhang S, Ahamed F and Song H-S (2022) Knowledge-informed data-driven modeling for sparse identification of governing equations for microbial inactivation processes in food. Front. Food. Sci. Technol. 2:996399. doi: 10.3389/frfst.2022.996399
Received: 17 July 2022; Accepted: 15 September 2022;
Published: 07 October 2022.
Edited by:
Muhammad Sajid Arshad, Government College University, Faisalabad, PakistanReviewed by:
Jiajia Chen, The University of Tennessee, Knoxville, United StatesQingli Dong, University of Shanghai for Science and Technology, China
Copyright © 2022 Zhang, Ahamed and Song. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Hyun-Seob Song, aHNvbmc1QHVubC5lZHU=
†These authors have contributed equally to this work and share first authorship
 Steve Zhang
Steve Zhang Firnaaz Ahamed
Firnaaz Ahamed Hyun-Seob Song
Hyun-Seob Song