- 1Laboratory of Bio-Inspired, Bionic, Nano, Meta, Materials & Mechanics, Department of Civil, Environmental and Mechanical Engineering, University of Trento, Trento, Italy
- 2Department of Biological Sciences, Macquarie University, Sydney, NSW, Australia
- 3Queen Mary University of London, London, United Kingdom
Spiders are able to produce different types of silk with different mechanical and biological properties. Piriform silk is produced to secure spiders and their webs to surfaces by using a nano-fibril network embedded in a cement-like matrix. Despite their fundamental role, the mechanical properties and function of these anchorages are still poorly understood due to the practical difficulties in nano-fibril sample preparation, the complexity of the system, and the high variation of attachment disc structures. Here we estimated the mechanical properties of this nano-fibril silk and those of the whole silk membrane in the large wandering spider Cupiennius salei through a combination of nanoindentation and nanotensile techniques and with the support of a simple analytical model. The results highlight the mechanical properties of the piriform silk, facilitating the modeling of silk composite mechanics. This could inspire the design of more efficient bio-inspired adhesives and fabrics.
Introduction
Silk is produced by spiders to fulfill various functions such as for hunting, for locomotion, and to build robust cocoons and webs (Foelix, 2011). In 400 million years of evolution, the optimization of the properties of the spider silk has been achieved through the diversification of this protein-based material (Brunetta and Craig, 2010). Each of the different silk types is equipped with a unique combination of physical, chemical, and biological properties (Brunetta and Craig, 2010). In particular, the outstanding mechanical and biological properties of the dragline (Agnarsson et al., 2010; Lepore et al., 2017) (mainly produced by the ampullate glands) have been intensely studied in the last two decades, inspiring and developing novel technologies (Eisoldt et al., 2011; Wolff et al., 2017a; Dellaquila et al., 2019).
Although the dragline silk is in the main focus of the applied silk science, it is only one representative of the silk family among the huge variety of silk types that exist. If the number of species of spiders on Earth (more than 48,000, Foelix, 2011) and the fact that each one of them is able to spin from two to seven types of silk (Vollrath and Knight, 2001) are considered, there might be more than 150,000 different types of spider silk, each one with different properties tailored for a specific need (Basu, 2015). Among them, the silk produced by the piriform gland has been one of the least studied, although it is one of the most common types of spider silk with a fundamental function: the attachment of silk threads to substrates.
The first studies that reported a histological analysis of the piriform glands were conducted by Kovoor and Zylberberg (1980) and Kovoor and Zylberberg (1982). They informed about the shapes and the dimensions of these glands and highlighted their position close to the spinnerets that also host the duct of the major ampullate gland. In comparison to the latter, the piriform glands are much smaller and numerous.
Blasingame et al. (2009) associated the protein of the piriform gland to the silk family due to the revealed conservation of the C-terminal region. The predicted aminoacidic composition of the piriform silk (the fibrous component) revealed a high amount of alanine in comparison to the other types of silk produced by the same spider (Blasingame et al., 2009; Geurts et al., 2010). Alanine can be associated with crystal-forming polyalanine chains, which contribute to a high Young's modulus and strength of the silk material (Yarger et al., 2018). Moreover, a recent study (Chaw et al., 2017) predicted the molecular weight of the PySp1 (the main protein of the piriform fibers) to be 578 kDa, which is larger than that of the dragline (between 200 and 300 kDa Vollrath and Knight, 2001). The molecular weight has been demonstrated to be directly correlated with the strength of fibers both in native and artificial silks (Xia et al., 2010; Bowen et al., 2018).
Piriform silk is used by spiders to create robust and efficient anchorages and adhesive systems that have been optimized during the evolution of spiders (Wolff et al., 2019). These affix the dragline to a surface, securing the arachnid in the event of a fall (Foelix, 2011; Asakura and Miller, 2014) (Figures 1A–C). Moreover, they are used to anchor the supporting threads of a cobweb to a surface or to join ampullate silk threads inside a web (Foelix, 2011; Asakura and Miller, 2014; Basu, 2015; Greco et al., 2019). The attachment discs are spun very fast and create a durable, efficient adhesive anchorage (Wolff and Gorb, 2016).

Figure 1. (A) Schematic of a spider that spins its dragline, anchored to the substrate by means of an attachment disc. (B) The initial part of the dragline is composed of more threads than the (C) distal part of the dragline. (D) Scanning electron microscopy (SEM) picture of the median part of the attachment disc, (E) the lateral part, and (F) an enlargement of the lateral part, which shows fibrils attached to the surface.
The adhesive membrane (“attachment disc”) is composed of a multi-fibril system embedded in a cement-like matrix (Figures 1D–F) that creates a structure able to bear high loads (Blasingame et al., 2009; Cranford et al., 2012). Spiders can adjust the morphology of the attachment disc and thus its overall mechanical behavior. For example, the attachment discs used to secure the supporting lines of cobwebs are different from the ones used in pre-stressed trapping lines (Sahni et al., 2012). Moreover, it has been demonstrated that spiders spin larger attachment discs if their weight is experimentally increased (Wolff et al., 2018).
The sectioning of attachment discs revealed that the relative proportion of the cement-like glue and the fiber content of the attachment discs differs between spiders of different ecology and evolutionary history; and that the piriform fibers and the dragline are not in contact with the substrate (Denny, 1976; Wirth et al., 2019). Accordingly, the fibers are not directly involved in the attachment disc's adhesion, yet they may modulate the mechanical properties of the surrounding glue layer. Whereas the ultrastructure of the piriform fibers is rather constant across species, the ultrastructure of the glue is very different (Wirth et al., 2019).
In order to understand the mechanical behavior of attachment discs under load, several approaches have been used. The multiple peeling theory (Pugno, 2011) has been used as a key model in order to explain the relationship between structure, material properties, and adhesive performance of the attachment discs and anchorages by means of multiple contacts points (Pugno et al., 2013; Brely et al., 2015; Liprandi et al., 2019; Greco et al., 2020). From the experimental point of view, the load to detach these membranes from surfaces has been measured by varying the surface's conditions, demonstrating a strong dependence on the type of used substrate (Grawe et al., 2014).
All these aspects, together with the structural hierarchical analysis that has been done on the piriform attachment discs (Wolff et al., 2015; Wirth et al., 2019), could be used for the development and the design of bio-inspired adhesives with superior mechanical performances (Jain et al., 2014).
However, several knowledge gaps have to be filled in the modeling and characterization of the piriform silk and the attachment discs before achieving possible bio-inspired solutions. Among these, there is the need for an understanding of the effects of attachment disc geometry on its load-bearing capabilities (Wolff et al., 2017b). Moreover, the understanding of the mechanical properties of the piriform silk is crucial in order to model the mechanical behavior of attachment discs. The first tensile tests of piriform silk have been performed on isolated piriform silk fibers (including their glue layer) of a hunting spider (Drassodex sp.) that were carefully peeled off an anti-adhesive polymer substrate (Wolff et al., 2017c). In this work, an extensibility of 0.5 mm/mm, a strength of 511 MPa, a toughness modulus of 141 MPa, and a Young's modulus of 5.6 GPa were measured. However, in attachment discs, single piriform fibers are not used in isolation, but it is their assembly into a multi-fiber compound material that makes up its full-scale properties. It is therefore indispensable to generate a model to understand the mechanical properties of attachment discs on multiple hierarchical levels.
In this work, we empirically determined the mechanical properties of the single piriform silk fiber and of the whole attachment disc of the species Cupiennius salei through nanoindentation and nanotensile techniques. We developed a simple model in order to explain the overall mechanical behavior of the membrane under traction composed of piriform silk and the dragline. With this work, we aim to create a comprehensive understanding of the mechanical properties of piriform silk and its spinning product (the attachment disc), with the potential to inspire the design of novel bio-inspired adhesives and fabrics with superior properties.
Analytical Model
Evaluation of the Spacing Among Fibrils
Determining the mechanical properties of piriform silk from attachment disc membranes creates difficulties due to the chaotic distribution of the fibers in the membrane-like silk film (Figure 2). Based on the observation that piriform fibers form a layered network in the attachment disc (Figures 1, 2), we model the silk membrane as a lattice of a glue–fiber material (Figure 3).

Figure 2. Scanning electron microscopy (SEM) images of an attachment disc of Cupiennius salei. (A) The structure is composed of a dragline thread that is suspended in a network of glue-coated fibrils. (B–F) Different details of the piriform silk network in the attachment disc.

Figure 3. (A) Scanning electron microscopy (SEM) picture of an attachment disc. (B–D) Schematic model in the three directions used to compute the mechanical properties of the membrane and composing fibrils.
As modeling the complexity of natural attachment discs is analytically unfeasible, for the purpose to calculate the tensile properties of piriform silk, we simplify the structure as a parallelepiped lattice. The spacing between the fibers (i.e., the porosity of the membrane) was estimated by determining the mean mass and dimension of the membranes through precise measurements.
Based on the observation of Wirth et al. (2019) that in C. salei the glue fraction of piriform silk is much smaller (i.e., mean thickness of ~20 nm) than the fiber fraction (thickness of ~0.5–1.5 μm), we neglected the presence of the glue (third phase) in the calculation of the volume. We assume that the density of the piriform silk is similar to that of major ampullate silk (). The nominal volume of the membrane Vn (= w·l·t) multiplied by the mean density of the membrane (ρm) is equal to the mass m of the membrane:
from which we can obtain the mean density of the membrane. The membrane mass is also given by the real density of the silk multiplied by the real volume of the silk fibrils in the membrane. By following the schematic in Figure 3, we can thus write:
where Ad is the cross-sectional area of the dragline fiber of length l, and Ap is the cross-sectional area of the piriform fibril network with fibrils of length l and spacing s (Figure 3).
Equation (1) can then be used to compute the mean spacing between the fibers in the piriform membrane.
Evaluation of the Stress in the Fibrils in Tensile Tests
In order to evaluate the mechanical properties of the whole membranes through tensile tests, the engineering stress needs to be determined. By referring to Figure 3, we can estimate it through the measurement of the applied load and section involved. In this approach, we homogenize the layered structure of piriform silk integrating across its glue and fiber fraction.
Along the y direction (Figure 3B), we have:
On the other hand, along the x direction (Figure 3D), we have:
It is thus possible to compute the engineering stress on the anisotropic membrane according to Equations (2) and (3).
Interestingly, if we consider the force applied to the membrane in one of the two directions, we find in the y direction that:
whereas in the x direction that:
This means that according with our scheme the stress computed along the x direction gives exactly the stress on the piriform silk (since the perpendicular dragline silk does not support any load).
Equation (4) represents also a relation between the strength of the dragline (σd), the strength of the piriform silk (σp), and the strength of the whole membrane (in this case σy). Thus, knowing the strength of the piriform silk measured along x via Equation (5), there is the possibility to check the strength value of the dragline measuring the strength along y with Equation (4) as a control.
Evaluation of the Young's Modulus of the Fibrils in Tensile Tests
In order to estimate the effective Young's modulus of the whole membrane under traction, the topology expressed in Figure 3 can be applied again.
The membrane is composed of piriform fibrils with the Young's modulus Ep.
The relation between the Young's modulus (E) and the spring constant (k) of a fiber under tensile longitudinal load is in general given by:
where A is the section of the fiber and L its length.
During loading parallel to the orientation of the dragline thread (y direction), we have n fibrils in series, N and N′ in parallel (x and z direction) that can be obtained by:
where lp is the mean length of the fibril.
Thus, the stiffness of the piriform fibrils along y is predicted to be:
where kp = EpAp/lp is the spring constant of the piriform fibril. Moreover, in the y direction, we also have to consider the contribution of the dragline, which is longitudinally attached to the membrane. The total membrane stiffness is thus predicted to be:
where Ed is the Young's modulus of the dragline and ld its length.
We then can estimate the Young's modulus of the whole membrane through Equation (6) and by assuming l ≈ ld as:
where dp is the diameter of the piriform fibers, and dd is the diameter of the dragline.
On the other hand, if we consider the membrane pulled along the x direction, we have n′ fibrils in series along the x direction, N and N″ in parallel (y and z direction), namely:
The equivalent membrane stiffness along the x direction is thus:
and from this, we can estimate the Young's modulus of the whole membrane along the x direction by using Equation (6), i.e.,:
It is possible to notice that Equations (7) and (8) differ only for the contribution of the dragline, which increases the equivalent Young's modulus of the membrane along y with respect to x.
Finally, Equations (7) and (8) are used to estimate the Young's modulus of the single piriform fibers from the mechanical properties of the whole membrane obtained through experimental tensile testing.
Materials and Methods
Spiders
The spiders under study were adult females of C. salei (Keyserling, 1877) from a captive bred lab stock. They were kept in different plastic boxes and fed with a weekly diet of Blaptica dubia or Acheta domestica (feed with carrots and fish food). All the plastic boxes were set in a room with controlled environmental parameters. Windows provided natural light, and temperature was about 22°C in the night and 25°C during the day; the humidity rate was controlled in each terrarium to be around 80% with the support of a hygrometer. Each terrarium was provided with a refuge considering the needs of the spider to feel protected and live without stress, according to the Italian regulation on animal protection and EU Directive 2010/63/EU for animal experiments.
Scanning Electron Microscopy
Samples of attachment discs were air-dried and sputter coated with 80:20 Pt/Pd for 5 min in a Q150T.
Scanning electron microscopy (SEM) imaging was performed using a Zeiss−40 Supra.
Measurement of Attachment Disc Mass
The mass of the membranes was measured with a TGA ANALYSIS TA Q5000. We measured the mass of 13 membranes and then the mass of 14 membranes for 3 min (to get stable values). The difference between obtained values represents the average mass of a membrane, of about 5 μg.
Measurement of Attachment Disc Length
We used microphotographs obtained with an optical microscope (Zeiss Axiotech and Axiovert) and analyzed in the ImageJ (Schneider et al., 2012) software. We measured the mean length and the width of the membranes. The thickness was measured through a caliper by sandwiching five membranes between its jaws, this procedure was repeated 100 times. An optical microscope was used to confirm that this procedure was reflecting the native profile of the samples. In particular, by looking laterally at the attachment discs that were produced directly on a quartz substrate, it was possible to get the idea of the profile. For each measurement, 100 samples were measured.
Nanoindentation
The tested samples were prepared by letting the spider walk on a quartz substrate and letting it spin the attachment discs. This quartz substrate was then mounted into an iNano®Nanoindenter (Nanomechanics Inc.). The declared sensitivity of the machine is 3nN for the load and 0.001 nm for the displacement.
The used mapping method (Nanoblitz 3d, Nanomechanics Inc.) involved a 200 μm × 200 μm square with 400 indentation points inside (each for a maximum of 0.05 mN loads for the piriform and 5 mN for the dragline, which resulted in a below 10% indentation depth). We used a Berkovich tip with a tip radius of about 20 nm for the experiments.
Tensile Testing
Dragline samples were prepared by cutting pieces of the dragline from the attachment disc and sticking them on a paper holder with a window of 1 × 1 cm using double-sided tape. The diameters of the fibers that compose the dragline were measured with an optical microscope (Zeiss Axiotech and Axiovert).
Membrane samples were obtained by detaching attachment discs from the substrate (commercial braplast plastic box, www.braplast.com). The test samples of piriform silk were prepared by fixing the attachment discs (per intended pulling direction, e.g., x or y) on a paper frame provided with a rectangular window with 1 mm height. The sample was fixed to the paper frame with a double-sided tape and by using Loctite super glue (Blackledge et al., 2005). For the y direction, the dragline was included in the membrane.
The tests were performed with the support of the nanotensile machine Agilent UTM T150 (Keysight technology) with a cell load of 500 mN. The displacement speed was 1% of the gauge length per second. The declared sensitivity of the machine is 10nN for the load and 1 Ȧ for the displacement in the dynamic configuration. The tests were recorded with a Sony Camera.
The anchorage samples for peeling tests were produced by letting the spider walk on a black paper surface. Once the spider spun the anchorages, we cut the dragline at a length of about 5 mm and stuck the piece of paper (containing the dragline) on a wood block of about 2 cm3 × 0.5 cm3 × 0.5 cm3. This was fixed on the paper frame (1 cm square window) and then fixed on the machine. The testing speed was 6 mm/min.
ANOVA Analysis
Analysis of variance was performed to compare the mean values of the strain at break, strength, Young's modulus, and toughness modulus from x- and y-stress tests (i.e., attachment discs pulled along or perpendicular the dragline direction).
The parameters used to verify the null hypothesis, i.e., all the data sets come from the same distribution and have the same mean value, were:
where G is the number of different samples under consideration, ng is the number of tests of the same sample, mu is the mean value of all the data, mg is the mean value within the group (i.e., sample), and x is the single force value. These sums of squares were used to compute the T value:
that has been compared with the ideal value of the Fisher function F with a significance level of 5%. If T > F, we reject the null hypothesis, and thus, we can consider the difference among the data set as significant (i.e., the difference is due to intrinsic differences among the samples and not a consequence of internal variance). The p-value was computed in MatLab®.
Weibull Statistics
In order to analyze the fracture strength distribution, we used Weibull statistics (by following Yang et al., 2020). Weibull cumulative density function is defined by the following relation (we omit the scaling effects here):
where x is the fracture strength, c is the shape parameter, and x0 is the scale parameter. F represents the probability that the sample breaks at the strength lower than x.
In order to obtain the relative probability density distributions of the different samples (i.e., ), we obtained the Weibull shape and scale parameters by using the linear regression method. By applying the double logarithm to Equation (9), we obtain the following equation:
where F could be estimated through the median rank estimator
where n is the number of the tested specimens, and i is the order of the considered one (after the organization of the samples from the weakest until the strongest). Kolmogorov–Smirnov and R square tests were performed to each set of data to verify (under the 95% of acceptance, MatLab®) that Weibull statistics could be applied to the data set.
Results
When a spider walks, it produces attachment discs where it secures the dragline (Figure 1A). Close to the attachment disc, the dragline is composed of more fibers (Figure 1B) than in its distal portion (i.e., close to the spinnerets; Figure 1C). The attachment discs are complex structures composed of multiple fibers with a mean diameter of 1.2 ± 0.5 μm and coated with a glue (Figures 1, 2). The thickness, the width, and the length of the membranes are, respectively, 5 ± 1 μm, 1.8 ± 0.4 mm, and 3.3 ± 0.6 mm (Figure S1). The mass of the membranes (Figure S2) has been measured as about 5 μg, which gives us by Equation (1) the mean fibril spacing of about 4.6 μm (Table S1).
Nanoindentation Tests
In order to measure the mechanical properties of the piriform silk, we used nanoindentation and nanotensile tests.
We performed a series of experiments to compare the Young's modulus obtained by both nanoindentation and tensile tests (Denny, 1976; Das et al., 2017).
The tests on the dragline attached to the membranes revealed consistent values between the two techniques. With nanoindentation (Figure S3, Table S2), we measured a Young's modulus of 4.2 ± 0.8 GPa, which was also found with the mapping method (Figure S4). In the tensile tests (Table S3), we measured a Young modulus of 5.2 ± 4.8 GPa (computed by taking the slope of the fitting regression line in the initial and steepest part of the stress–strain curve), a strain at break of 0.27 ± 0.09 mm/mm, a mean strength of 365 ± 290 MPa, and a mean toughness modulus of 61 ± 47 MJ/m3. From nanoindentation, we obtained a hardness of 0.33 ± 0.10 GPa for the dragline.
The investigation of the piriform silk through nanoindentation was performed by using both the single indentation method and the mapping method. The single indentation method was performed on different positions along the membrane (Figure S5). The obtained Young's modulus of the single fiber was 3.9 ± 1.4 GPa (Table S4), and the hardness was 0.09 ± 0.05 GPa. These observations were confirmed by the mapping method (Figure 4, Figures S6, S7). The results were consistent with the indentation depth (Figure S8), which was kept >10% of the thickness of the fibers (Hay et al., 1998; Fischer-Cripps, 2011).
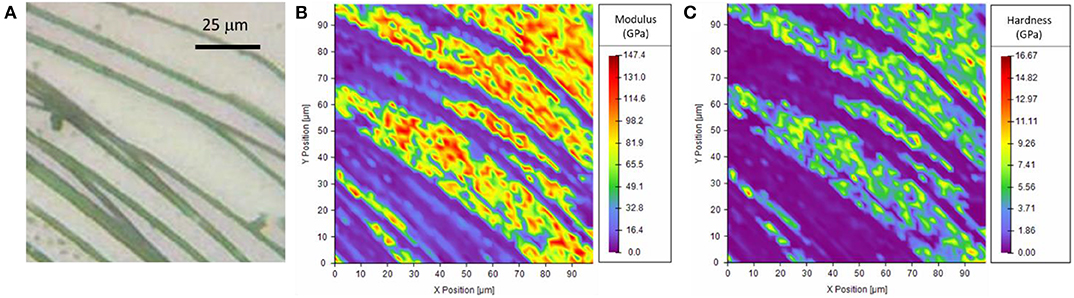
Figure 4. (A) Optical microscopy image of the sample, (B,C) Nanoindentation mapping of the mechanical properties of the piriform silk on the border of the attachment disc. Note that high values result from measurements of the quartz substrate exposed between the (softer) silk fibrils.
Tensile Tests
In order to measure the overall mechanical properties of the different silk composites, we performed the following nanotensile tests: test of the dragline, the whole membrane pulled along the y direction (Figure 3B, Supplementary Video SV1), and the whole membrane pulled along the x direction (Figure 3D, Supplementary Video SV2). The obtained stress–strain and load displacement (for the last type of test) curves are depicted in Figure 5. The stress on the membrane was computed by using Equations (2) and (3), and related extracted values are reported in Table S1.
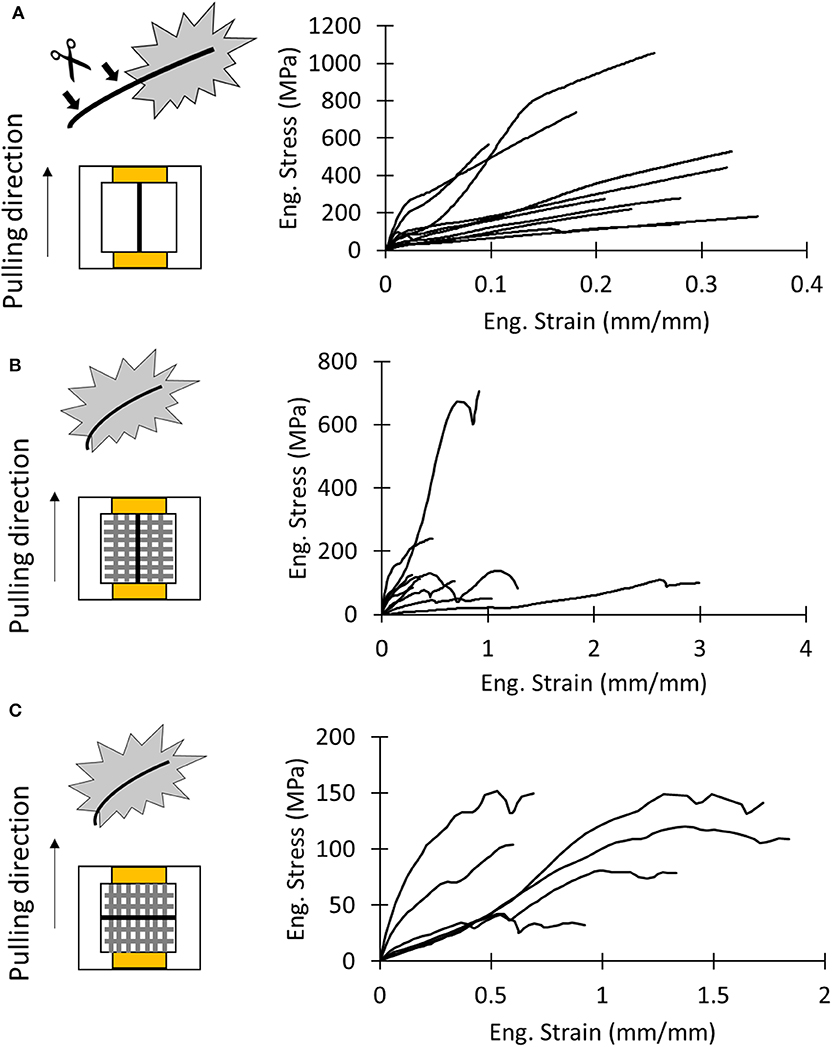
Figure 5. (A) Schematics of test sample and stress–strain curves of dragline samples. (B) Schematics of test sample and stress–strain curves of the attachment disc pulled in the dragline direction (y direction). (C) Schematics of test sample and stress–strain curves of the attachment disc pulled in the pure fibrils direction (x direction).
There was no significant difference in mechanical properties between the x- and y-mounting of attachment disc samples (Tables S5, S6). For the x and y direction, respectively, we found a strain at break of 1.18 ± 0.53 and 0.93 ± 0.85, a strength of 106 ± 42 MPa and 190 ± 180 MPa, a Young's modulus of 0.19 ± 0.10 MPa and 0.33 ± 0.18 MPa, and a toughness modulus of 87 ± 53 MJ/m3 and 97 ± 90 MJ/m3.
In order to evaluate the difference of the mechanical properties between attachment discs and the dragline, we performed a one-way ANOVA test (Table S7). Only the strength of the dragline and the membrane pulled along the x direction resulted to be statistically different (p = 0.00487, all post hoc pairwise comparisons p < 0.05). This suggests that the dragline is stronger than the piriform silk membrane.
A better understanding of the difference between the strength of the analyzed samples can be given by looking at Weibull statistics. In this case, the linear regression method was used to compute the Weibull parameters (Figure 6A, Table S8), and these were used to plot the strength's probability density distributions of the tested samples (Figure 6B). The narrower shape of the strength probability distribution of the membranes relative to the dragline indicated their more homogeneous fracture behavior.
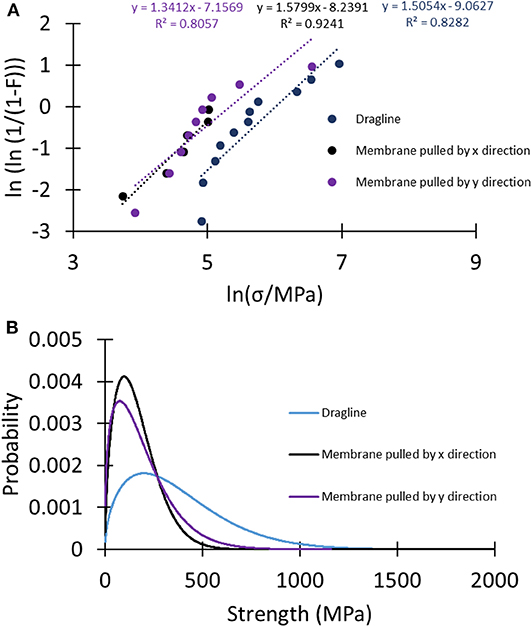
Figure 6. (A) Linear regression plots of the different sets of samples to compute the Weibull parameters used to plot (B) the Weibull probability density distributions of the strength of the tested samples.
Comparison With the Model
Table 1 reports mechanical properties of silk fibers and membranes determined in this work and their comparison with values reported in the literature. The Young's modulus estimated with Equations (7) and (8) (i.e., Young's modulus of the whole membrane under traction relative to the Young's modulus of the single fibers) is similar to the one measured by nanoindentation. The values we obtained for single piriform silk fibers are comparable to those previously measured in isolated piriform silk fibers (Wolff et al., 2017c). Equation (7) was also used as a control for estimating the Young's modulus of the dragline, which was found to be comparable to the one directly measured by the dragline tensile test.
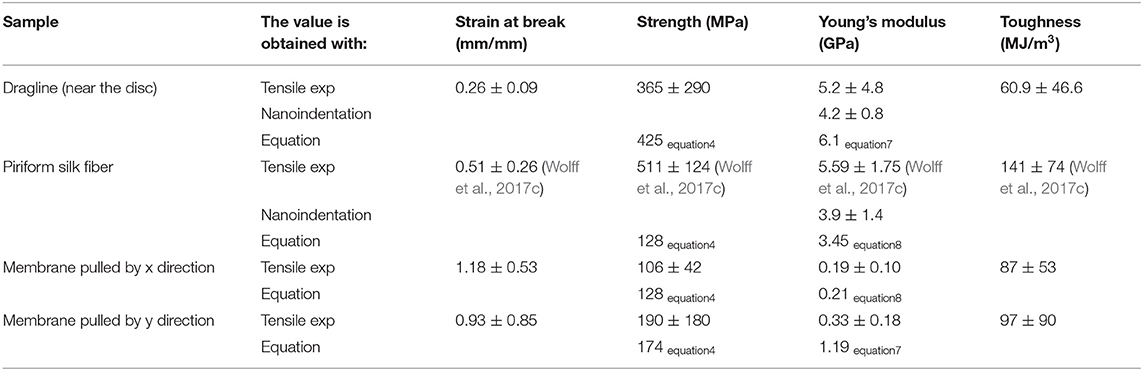
Table 1. Values of the mechanical properties of tested silk products obtained in the experimental (tensile tests of the whole membrane and dragline threads and nanoindentation on single fibers) and analytical model compared with literature values (from other species).
Equation (4) gives us the possibility to estimate the strength of the dragline by knowing the measured strength of the membrane along the x and y directions and the strength of the piriform silk. The obtained value is very similar to the one measured in tensile tests, confirming the validity of our simple model.
It is important to understand how the spacing distance s can affect the results. We thus plotted the theoretical values obtained with Equations (4), (7), and (8) as functions of the spacing distance s in the measured range (Figure S7). This confirmed that our results fit well with respect to the obtained s values.
Peeling Experiments
In order to quantify the attachment of the whole membrane to the substrate, we performed pull-off tests (Figure S10). We found that detachment occurred at displacements of 2.9 ± 1.2 mm, with peak force of 18 ± 10 mN and a membrane stiffness of 6.8 ± 5.8 N/m (Table S9). These numbers are comparable to the ones reported in literature (Grawe et al., 2014; Wolff et al., 2015, 2017b,c; Wolff and Gorb, 2016; Wolff and Herberstein, 2017). We found that the failure of the attachment discs occurs mainly at the level of the piriform silk (Figure S10C) in our setup, instead of at the dragline's level [see Grawe et al. (2014) for a detailed discussion of the different failure modes resulting from the hierarchical structure of attachment discs]. This was indicated by the observation that detached attachment discs remained almost intact (Figure S10D). This supports that the adhesion was measured and not the fracture of the attachment disc.
Discussion
Due to the adhesive nature of piriform silk, it is difficult to obtain native fiber samples for tensile tests. Here, we used a whole-membrane approach, in combination with an analytical model to determine the mechanical properties of piriform silk. When collecting samples, the detachment of the attachment discs from the carrier substrate may create damage or induce a pre-stress that could affect the measurements (Garrido et al., 2002; Perez-Rigueiro, 2005). We therefore backed up our test results by a nanoindentation approach that has been proven a good solution in order to measure the mechanical properties of native attachment discs in loco without the requirement of sample manipulation (Das et al., 2017). The combined results from these different approaches are consistent.
The nanoindentation tests revealed that the piriform silk of C. salei has a Young's modulus comparable to its dragline. The fact that, in this species, the amount of glue is low if compared to other species (Wirth et al., 2019) partially justifies our approach that neglects the presence of the third phase.
The theoretical model was developed to justify the mechanical properties of the single fibers, obtained by means of nanoindentation, to the mechanical properties of the whole membrane (under tensile tests). Overall, we found consistency in the values obtained from our nanoidentation and tensile test approaches and those reported in the literature (Wolff et al., 2017c). This highlights that anisotropy plays a negligible role in the mechanics of piriform silk. The effect of variation in the spacing parameter s was investigated (Figure S9). We note that obtained values for the spacing parameter represent an average of the naturally variable spacing across the lattice.
Another important aspect to consider about the strength of materials is their dimensions. Increasing the size of a material (or in general its dimension) usually leads to a decrease of strength (Carpinteri and Pugno, 2005). This is also valid for spider silk (Greco et al., submitted). Piriform silk is composed of numerous small fibers. This could increase the strength of each fiber and then the strength of the whole membrane.
Regarding the overall mechanical behavior of the membrane, the complexity of the structure and its random shape could be an important cause for the remarkable mechanical properties of attachment discs, as randomization in a system could improve its toughness and ductility (Cranford, 2013).
The parameters determined in this work enable the improvement of numerical models that describe the peeling mechanics and adhesion of composite membranes, which is an important goal in the study of the mechanical function and biomimetics of biological adhesive systems (Liprandi et al., 2019; Wolff et al., 2019).
Conclusion
Hundreds of million years have selected attachment systems of spiders to bear high loads (Wolff et al., 2019). Despite their fundamental role, these anchorages are still poorly understood due to the practical difficulties in sample preparation, the complexity of the system, and the high variation of attachment disc structures.
In order to understand the overall mechanical behavior of the whole membrane, knowledge of the mechanical properties of the attachment disc material (piriform silk) is essential.
With this work we delivered some useful information regarding piriform silk mechanical properties. This in our opinion will facilitate the enhancement of numerical models of peeling dynamics for a better understanding of the adhesion function of attachment discs and stimulate the design of new bio-inspired strong adhesives and micro-composite materials.
Data Availability Statement
All datasets generated for this study are included in the article/Supplementary Material.
Ethics Statement
Ethical review and approval was not required for the animal study because, according to the Italian regulation on animal protection and EU Directive 2010/63/EU for animal experiments, no special requirements are necessary for spiders.
Author Contributions
GG performed the experiments, acquired the data, and wrote the first draft of the manuscript. JW contributed to the interpretation of the results and the manuscript writing. NP supervised the study, suggested the model and the data analyses, and finalized the paper. All authors were involved in revising manuscript drafts and viewed and approved the final manuscript.
Funding
JW is supported by a Discovery Early Career Researcher Award of the Australian Research Council (DE190101338). NP is supported by the European Commission under the FET Proactive (Neurofibres) grant No. 732344, the FET Open (Boheme) grant No. 863179, as well as by the Italian Ministry of Education, University and Research (MIUR) under the Departments of Excellence grant L. 232/2016.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We would like to thank Lorenzo Moschini, Antonella Motta, Devid Maniglio, and Claudio Migliaresi (Biotech–Mattarello, University of Trento) for their support.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2020.00138/full#supplementary-material
References
Agnarsson, I., Kuntner, M., and Blackledge, T. A. (2010). Bioprospecting finds the toughest biological material: extraordinary silk from a giant riverine orb spider. PLoS ONE 5, 1–8. doi: 10.1371/journal.pone.0011234
Blackledge, T. A., Cardullo, R. A., and Hayashi, C. Y. (2005). Polarized light microscopy, variability in spider silk diameters, and the mechanical characterization of spider silk. Invertebr. Biol. 124, 165–173. doi: 10.1111/j.1744-7410.2005.00016.x
Blasingame, E., Tuton-Blasingame, T., Larkin, L., Falick, A. M., Zhao, L., Fong, J., et al. (2009). Pyriform spidroin 1, a novel member of the silk gene family that anchors dragline silk fibers in attachment discs of the black widow spider, Latrodectus hesperus. J. Biol. Chem. 284, 29097–29108. doi: 10.1074/jbc.M109.021378
Bowen, C. H., Dai, B., Sargent, C. J., Bai, W., Ladiwala, P., Feng, H., et al. (2018). Recombinant spidroins fully replicate primary mechanical properties of natural spider silk. Biomacromolecules 19, 3853–3860. doi: 10.1021/acs.biomac.8b00980
Brely, L., Bosia, F., and Pugno, N. M. (2015). Numerical implementation of multiple peeling theory and its application to spider web anchorages. Interface Focus 5:20140051. doi: 10.1098/rsfs.2014.0051
Brunetta, L., and Craig, C. L. (2010). Spider Silk: Evolution and 400 Million Years of Spinning, Waiting, Snagging, and Mating. Yale University Press.
Carpinteri, A., and Pugno, N. (2005). Are scaling laws on strength of solids related to mechanics or to geometry? Nat. Mater. 4, 421–423. doi: 10.1038/nmat1408
Chaw, R. C., Saski, C. A., and Hayashi, C. Y. (2017). Complete gene sequence of spider attachment silk protein (PySp1) reveals novel linker regions and extreme repeat homogenization. Insect Biochem. Mol. Biol. 81, 80–90. doi: 10.1016/j.ibmb.2017.01.002
Cranford, S. W. (2013). Increasing silk fibre strength through heterogeneity of bundled fibrils. J. R. Soc. Interface 10:20130148. doi: 10.1098/rsif.2013.0148
Cranford, S. W., Tarakanova, A., Pugno, N. M., and Buehler, M. J. (2012). Nonlinear material behaviour of spider silk yields robust webs. Nature 482, 72–76. doi: 10.1038/nature10739
Das, R., Kumar, A., Patel, A., Vijay, S., Saurabh, S., Kuma, N., et al. (2017). Biomechanical characterization of spider webs. J. Mech. Behav. Biomed. Mater. 67, 101–109. doi: 10.1016/j.jmbbm.2016.12.008
Dellaquila, A., Greco, G., Campodoni, E., Mazzocchi, M., Mazzolai, B., Tampieri, A., et al. (2019). Optimized production of a high-performance hybrid biomaterial : biomineralized spider silk for bone tissue engineering. J. Appl. Polym. Sci. 48739, 1–9. doi: 10.1002/app.48739
Denny, M. W. (1976). The physical properties of spider's silk and their role in the design of orb-webs. J. Exp. Biol. 65, 483–506.
Eisoldt, L., Smith, A., and Scheibel, T. (2011). Decoding the secrets of spider silk. Mater. Today 14, 80–86. doi: 10.1016/S1369-7021(11)70057-8
Garrido, M. A., Elices, M., Viney, C., and Pérez-Rigueiro, J. (2002). The variability and interdependence of spider drag line tensile properties. Polymer (Guildf). 43, 4495–4502. doi: 10.1016/S0032-3861(02)00254-9
Geurts, P., Zhao, L., Hsia, Y., Gnesa, E., Tang, S., Jeffery, F., et al. (2010). Synthetic spider silk fibers spun from pyriform spidroin 2, a glue silk protein discovered in orb-weaving spider attachment discs. Biomacromolecules 11, 3495–3503. doi: 10.1021/bm101002w
Grawe, I., Wolff, J. O., and Gorb, S. N. (2014). Composition and substrate-dependent strength of the silken attachment discs in spiders. J. R. Soc. Interface 11:20140477. doi: 10.1098/rsif.2014.0477
Greco, G., Bosia, F., Tramacere, F., Mazzolai, B., and Pugno, N. M. (2020). The role of hairs in the adhesion of octopus suckers: a hierarchical peeling approach. Bioinspir. Biomim. 15:035006. doi: 10.1088/1748-3190/ab72da
Greco, G., Pantano, M. F., Mazzolai, B., and Pugno, N. M. (2019). Imaging, and mechanical characterization of different junctions in spider orb webs. Sci. Rep. 9:5776. doi: 10.1038/s41598-019-42070-8
Hay, J. L., O'Hern, M. E., and Oliver, W. (1998). The importance of contact radius for substrate independent property measurement of thin films. Mat. Res. Soc. Symp. Proc. 522, 27–32. doi: 10.1557/PROC-522-27
Jain, D., Sahni, V., and Dhinojwala, A. (2014). Synthetic adhesive attachment discs inspired by spider's pyriform silk architecture. J. Polym. Sci. Part B Polym. Phys. 52, 553–560. doi: 10.1002/polb.23453
Keyserling, E. (1877). Ueber amerikanische Spinnenarten der Unterordnung Citigradae. Verhandlungen der Kaiserlich-Königlichen Zoologisch-Botanischen Gesellschaft in Wien 26, 609–708.
Kovoor, J., and Zylberberg, L. (1980). Fine structural aspects of silk secretion dladematus. IN THE. Tissue Cell 12, 547–556. doi: 10.1016/0040-8166(80)90044-0
Kovoor, J., and Zylberberg, L. (1982). Fine structural aspects of silk secretion in a spider. Tissue Cell 14, 519–530. doi: 10.1016/0040-8166(82)90044-1
Lepore, E., Bosia, F., Bonaccorso, F., Bruna, M., Taioli, S., Garberoglio, G., et al. (2017). Spider silk reinforced by graphene or carbon nanotubes. 2D Materials 4:031013.
Liprandi, D., Bosia, F., and Pugno, N. M. (2019). A theoretical-numerical model for the peeling of elastic membranes. J. Mech. Phys. Solids 136:103733. doi: 10.1016/j.jmps.2019.103733
Perez-Rigueiro, J. (2005). The effect of spinning forces on spider silk properties. J. Exp. Biol. 208, 2633–2639. doi: 10.1242/jeb.01701
Pugno, N. M. (2011). The theory of multiple peeling. Int. J. Fract. 171, 185–193. doi: 10.1007/s10704-011-9638-2
Pugno, N. M., Cranford, S. W., and Buehler, M. J. (2013). Synergetic material and structure optimization yields robust spider web anchorages. Small 9, 2747–2756. doi: 10.1002/smll.201201343
Sahni, V., Harris, J., Blackledge, T. A., and Dhinojwala, A. (2012). Cobweb-weaving spiders produce different attachment discs for locomotion and prey capture. Nat. Commun. 3, 1106–1107. doi: 10.1038/ncomms2099
Schneider, C. A., Rasband, W. S., and Eliceri, K. W. (2012). NIH Image to ImageJ: 25 years of image analysis. Nat. Methods 9, 671–675. doi: 10.1038/nmeth.2089
Vollrath, F., and Knight, D. P. (2001). Liquid crystal spinning of spider silk. Nature 410, 541–548. doi: 10.1038/35069000
Wirth, M., Wolff, J. O., Appel, E., and Gorb, S. N. (2019). Ultrastructure of spider thread anchorages. J. Morphol. 280, 534–543. doi: 10.1002/jmor.20962
Wolff, J. O., and Gorb, S. N. (2016). Attachment Structures and Adhesive Secretions in Arachnids. Cham: Springer, 184.
Wolff, J. O., Grawe, I., Wirth, M., Karstedt, A., and Gorb, S. N. (2015). Spider's super-glue: thread anchors are composite adhesives with synergistic hierarchical organization. Soft Matter 11, 2394–2403. doi: 10.1039/C4SM02130D
Wolff, J. O., and Herberstein, M. E. (2017). Three-dimensional printing spiders: back-and-forth glue application yields silk anchorages with high pull-off resistance under varying loading situations. J. R. Soc. Interface 14:20160783. doi: 10.1098/rsif.2016.0783
Wolff, J. O., Jones, B., and Herberstein, M. E. (2018). Plastic material investment in load-bearing silk attachments in spiders. Zoology 131, 45–47. doi: 10.1016/j.zool.2018.05.002
Wolff, J. O., Paterno, G. B., Liprandi, D., Ramírez, M. J., Bosia, F., van der Meijden, A., et al. (2019). Evolution of aerial spider webs coincided with repeated structural optimization of silk anchorages. Evolution 73, 2122–2134. doi: 10.1111/evo.13834
Wolff, J. O., Rez,áč, M., Krejčí, T., and Gorb, S. N. (2017c). Hunting with sticky tape: functional shift in silk glands of araneophagous ground spiders (Gnaphosidae). J. Exp. Biol. 220, 2250–2259. doi: 10.1242/jeb.154682
Wolff, J. O., Van der Meijden, A., and Herberstein, M. E. (2017b). Distinct spinning patterns gain differentiated loading tolerance of silk thread anchorages in spiders with different ecology. Proc. R. Soc. B Biol. Sci. 284:20171124. doi: 10.1098/rspb.2017.1124
Wolff, J. O., Wells, D., Reid, C. R., and Blamires, S. J. (2017a). Clarity of objectives and working principles enhances the success of biomimetic programs Clarity of objectives and working principles enhances the success of biomimetic programs. Bioinspir. Biomim. 12:051001. doi: 10.1088/1748-3190/aa86ff
Xia, X.-X., Qian, Z.-G., Ki, C. S., Park, Y. H., Kaplan, D. L., and Lee, S. Y. (2010). Native-sized recombinant spider silk protein produced in metabolically engineered Escherichia coli results in a strong fiber. Proc. Natl. Acad. Sci. 107, 14059–14063. doi: 10.1073/pnas.1003366107
Yang, Y., Greco, G., Maniglio, D., Mazzolai, B., Migliaresi, C., Pugno, N., et al. (2020). Spider (Linothele megatheloides) and silkworm (Bombyx mori) silks: Comparative physical and biological evaluation. Mater. Sci. Eng. C 107:110197. doi: 10.1016/j.msec.2019.110197
Keywords: spider silk, piriform silk, attachment disc, mechanical properties, nanoindentation
Citation: Greco G, Wolff JO and Pugno NM (2020) Strong and Tough Silk for Resilient Attachment Discs: The Mechanical Properties of Piriform Silk in the Spider Cupiennius salei (Keyserling, 1877). Front. Mater. 7:138. doi: 10.3389/fmats.2020.00138
Received: 30 January 2020; Accepted: 21 April 2020;
Published: 11 June 2020.
Edited by:
Giuseppe Saccomandi, University of Perugia, ItalyReviewed by:
Giuseppe Puglisi, Politecnico di Bari, ItalyGaetano Napoli, University of Salento, Italy
Copyright © 2020 Greco, Wolff and Pugno. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Nicola M. Pugno, bmljb2xhLnB1Z25vQHVuaXRuLml0
 Gabriele Greco
Gabriele Greco Jonas O. Wolff
Jonas O. Wolff Nicola M. Pugno
Nicola M. Pugno