Mechanical properties of 3D-Printed aluminum, nickel, and titanium using a hybrid machine learning and computational mechanics approach

This study presents a hybrid computational framework designed to accurately predict the mechanical properties of essential 3D printing materials, namely, Aluminum (Al), Titanium (Ti), and Nickel (Ni). By integrating first-principles simulations via the CASTEP code—grounded in Density Functional Theory (DFT)—with machine learning techniques, specifically Ridge regression, the approach aims to enhance prediction accuracy while minimizing computational costs. The analysis focuses on key elastic properties, including Bulk Modulus, Young’s Modulus, and Shear Modulus. Initial simulations using CASTEP provide benchmark mechanical values, which are subsequently used to train and validate the Ridge regression model. The results reveal outstanding predictive accuracy, with R² values surpassing 0.999 across all properties and minimal mean squared errors. A close correlation between DFT-derived and AI-predicted values confirms the robustness of the approach. This methodology significantly reduces reliance on physical experimentation and heavy simulations, making it a powerful tool for material design and optimization. Moreover, the findings emphasize Aluminum’s potential for lightweight structures, Titanium’s superior stiffness suited for biomedical and aerospace applications, and Nickel’s strong resistance to compression, making it ideal for demanding industrial settings. Such insights contribute to faster and more efficient materials selection and customization in additive manufacturing.

1 Introduction

Additive manufacturing (AM), commonly known as 3D printing, has experienced remarkable growth in demanding industrial sectors such as aeronautics, automotive, and biomedical industries (Ngo et al., 2018; Gibson et al., 2021). This technology stands out from traditional manufacturing processes due to its ability to produce complex geometries with high precision while reducing material waste and production lead times (Fraz and ier, 2014; Gibson, 2015). These advantages make it a preferred solution for creating lightweight, strong, and customized parts, such as aerospace structural components or tailored medical implants (Ngo et al., 2018; Perdew et al., 1996; Murr et al., 2010).

However, despite these benefits, the widespread adoption of AM faces persistent challenges, particularly in material selection and optimization. Mechanical properties, such as Young’s modulus, shear modulus, and tensile strength, play a crucial role in the performance and durability of printed parts, especially under intense mechanical stress or corrosive environments (Abe, 2019; Segall et al., 2002). Traditionally, the evaluation of these properties relies on experimental testing, which is costly, time-consuming, and requires significant material resources (Butler et al., 2018; Saharudin et al., 2025).

To overcome these limitations, computational methods have emerged as a promising alternative. Among these, Density Functional Theory (DFT) has become a reference tool for predicting material properties at the atomic scale. Implemented in software such as CASTEP (Zhang and Ling, 2018; Grimme et al., 2010; Karouchi et al., 2024a), DFT enables accurate modeling of electronic structure and mechanical characteristics of materials (Curtin and Miller, 2003; Grimme, 2004). However, although this approach provides reliable results, it is still associated with prohibitive computational times, limiting its use for large-scale screening (Soler et al., 2002; Curtarolo et al., 2012).

To address these challenges, the integration of machine learning (ML) with DFT simulations has recently gained popularity. This synergy combines the accuracy of quantum calculations with the speed of predictive models, paving the way for accelerated material characterization. Several studies have already validated the potential of this hybrid approach, particularly for metallic alloys (Samine et al., 2022; Deng et al., 2020), titanium-based materials (Bhesania et al., 2022),and nickel superalloys (Xu et al., 2022; Schütt et al., 2017). For instance, advanced techniques such as graph neural networks (Xie and Grossman, 2018; Samine et al., 2023)and deep learning (Schütt et al., 2017; Kibrete et al., 2023) have demonstrated remarkable ability to predict mechanical properties from structural data. In the specific field of AM, recent research has highlighted the critical influence of printing parameters, such as infill density and layer orientation, on the final performance of printed parts (Rooney et al., 2024).

Studies have investigated the influence of process parameters on the microstructure and mechanical properties of Ti-6Al-4V alloys, highlighting the significant effect of build orientation (Andreacola et al., 2023). Similarly, research on aluminum AM components has demonstrated notable variations in mechanical performance depending on post-process heat treatment conditions (Ponnusamy et al., 2017).

The fatigue behavior of AM materials has also been examined, with findings emphasizing the critical role of surface roughness (Andreacola et al., 2021). Additionally, annealing treatments applied to 316L stainless steel produced by selective laser melting (SLM) have been shown to enhance ductility at the expense of strength (Eskandari et al., 2022). Comparative studies on titanium and aluminum alloys have confirmed the decisive impact of laser parameters on final mechanical properties (Brando et al., 2023).

The challenges associated with AM of complex metal parts—including residual stresses and deformations have been comprehensively reviewed (Rashid et al., 2017). A detailed assessment of material science principles in metal 3D printing has provided insights into process modeling (Aboulkhair et al., 2019). Furthermore, investigations into microcellular structures in lightweight AM alloys have revealed their influence on mechanical performance (Brandl et al., 2012). Finally, studies on maraging steel M300 have quantified the effect of build orientation on fracture toughness, underscoring its potential for demanding industrial applications (Komarasamy et al., 2019). In this context, our study proposes an innovative methodology that combines DFT simulations performed with CASTEP with Ridge regression models to predict the mechanical properties of three strategic AM materials: aluminum (Al), titanium (Ti), and nickel (Ni). The selection of these materials is motivated by their industrial importance and complementary mechanical characteristics. Our approach aims to establish a predictive framework that is both accurate and efficient, significantly reducing the time and costs associated with the development of new materials for AM.

Ultimately, this research aligns with a multidisciplinary perspective aimed at accelerating the design of high-performance materials for critical applications. The results obtained could have major implications in sectors such as aeronautics, where reducing component weight without compromising mechanical strength is a key challenge, or in the biomedical field, where implant customization requires precise control of mechanical properties.

In this study, we focused on pure metallic materials, namely, aluminum, titanium, and nickel. These materials are frequently used in metal additive manufacturing, particularly in the Selective Laser Melting (SLM) technique. This method involves locally fusing successive layers of metal powder using a laser to produce solid parts.

Although the study is based solely on theoretical calculations using Density Functional Theory (DFT) with the CASTEP code, it is important to note that the mechanical properties of printed parts can be significantly influenced by printing process parameters, such as laser power, scan speed, or layer thickness. The evaluation of these effects will be the subject of future work.

2 Computational methods

The mechanical properties of aluminum (Al), nickel (Ni), and titanium (Ti) were calculated using density functional theory (DFT) as implemented in the CASTEP code. Both Al and Ni possess face-centered cubic (FCC) crystal structures, while Ti was considered in a body-centered cubic (BCC) form. The exchange-correlation effects were treated using the generalized gradient approximation (GGA) in the Perdew–Burke–Ernzerhof (PBE) formulation. For the electronic structure calculations, a plane-wave basis set was employed with an energy cutoff of 500 eV. The Brillouin zone was sampled using a Monkhorst-Pack grid with a k-point mesh of 4 × 4 × 4 to ensure sufficient accuracy. Prior to calculating the mechanical properties, geometry optimization was performed for each material, ensuring that the atomic positions and cell parameters were relaxed until the forces on the atoms were minimized.

In this study, we used artificial intelligence (AI) to predict the mechanical properties of Aluminum, Titanium, and Nickel. The approach relies on a machine learning model, specifically Ridge regression, which is a variant of traditional linear regression with a regularization term.

Ridge regression is particularly suited to problems where the explanatory variables are correlated, as is often the case in materials science applications involving properties such as elastic constants and mechanical moduli. This model introduces a penalty to the classical linear regression equation, which prevents the inflation of coefficients and reduces the risk of overfitting.

This approach is particularly relevant in the field of 3D printing, where the ability to accurately predict the mechanical properties of materials allows for optimized material selection, the design of stronger parts, and a reduction in the number of experimental tests required.

3 Results and discussion

3.1 Structural propriety

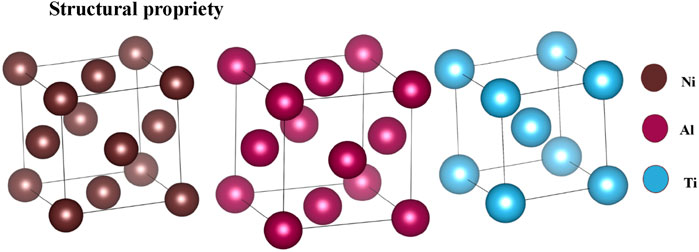
The crystal structures of the studied materials (Al, Ni, and Ti) are shown in Figure 1. Aluminum and nickel adopt a face-centered cubic (FCC) structure, while titanium is represented in its body-centered cubic (BCC) phase. The FCC structure, as shown in the center, features atoms at the corners and at the centers of each cube face, resulting in a densely packed arrangement. The BCC structure of titanium, depicted on the left, has an atom located at the center of the cube with additional atoms at the cube corners.

Figure 1

Figure 1. Crystal structures of the studied materials.

These structural configurations play a critical role in determining the mechanical and electronic properties of the materials.

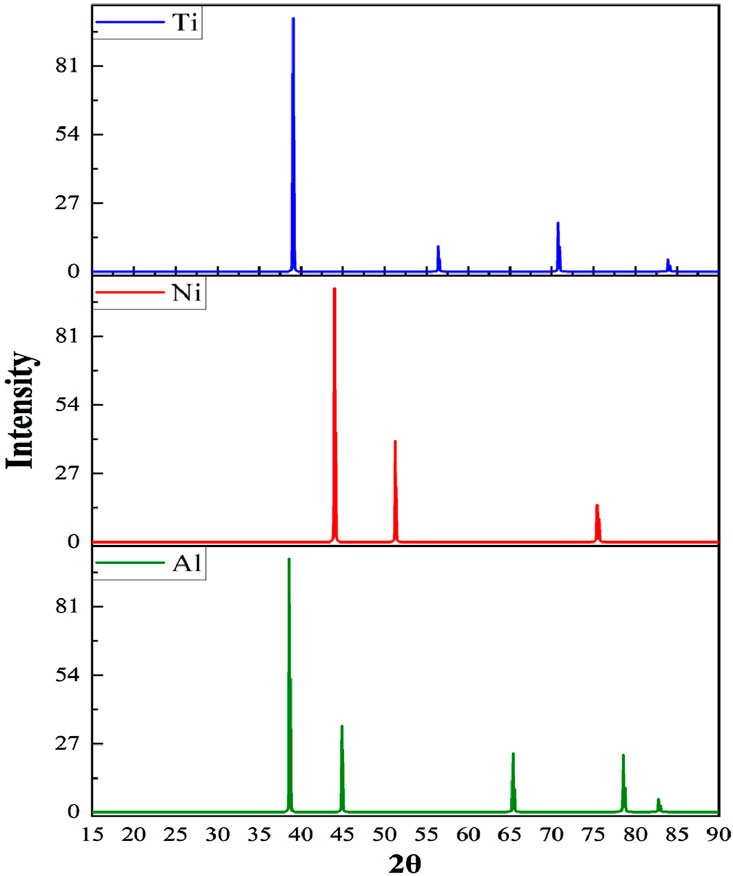
Analysis of the material’s structure using VESTA software revealed the presence of three distinct phases: titanium (Ti), nickel (Ni), and aluminum (Al). The diffraction patterns of the Ti, Ni, and Al phases obtained from VASP simulations are shown in Figure 2.

Figure 2

Figure 2. Diffraction patterns of Ti, Ni, and Al phases from VASP simulations.

The Ti phase exhibits a sharp peak in the calculated diffraction pattern, indicative of high crystallinity and suggesting a relatively pure phase. The Ni phase also displays strong crystallinity, characterized by two prominent peaks consistent with the expected diffraction pattern for Ni. The Al phase, in contrast, shows a less pronounced crystalline structure compared to Ti and Ni, with multiple peaks exhibiting broader profiles. This broadening suggests a potential polycrystalline nature of the Al phase or the presence of internal strain within the Al lattice. The co-existence of these three phases within the simulation could indicate a mixture of Ti, Ni, and Al powders or, alternatively, a composite material composed of these elements. The relative intensities of the peaks can be utilized to estimate the relative proportions of each phase.

3.2 Mechanical properties

This section focuses on the evaluation of the mechanical behavior of the selected materials Aluminum, Titanium, and Nickel using DFT simulations. Key mechanical parameters such as elastic constants, bulk modulus, shear modulus, and Young’s modulus are discussed in detail. The objective is to analyze and compare their suitability for additive manufacturing based on their resistance to stress, deformation, and compression.

The mechanical properties of materials, including the elastic constants of the crystal, result from the response to external forces. These constants describe the mechanical behavior of the material under stress and deformation (Hoeun et al., 2023; Mouhat and Coudert, 2014). Based on Hook’s law of elasticity, there are six components of tensile strength, as well as six other stress-related components in the three dimensions (3D) of the crystal. This framework allows for the description of interactions between applied stresses (or compressions) and the resulting deformations in a crystalline material (Ledbetter and Migliori, 2006).

Hook’s law can be expressed by the following formulas (Muhammad et al., 2014; Mavko et al., 2009; Mouhat and Coudert, 2014):

$\begin{array}{rr}{\sigma }_i& =C_{ij}{ϵ}_j\\ {ϵ}_i& =S_{ij}{\sigma }_j\end{array}$

Where $i,j=1,2,3$, with:

• Elasticity constant (Cij), which represents the rigidity of the material.

• Compliance, or softness (inverse of), which describes how the material deforms under stress.

• Stress applied to the material.

• Resulting strain.

Hooke’s law for elasticity, which involves a (6 × 6) matrix on the surface of the material, can be expressed in the following form:

$\left(\begin{array}{c}{\sigma }_1\\ {\sigma }_2\\ {\sigma }_3\\ {\sigma }_4\\ {\sigma }_5\\ {\sigma }_6\end{array}\right)=\left(\begin{array}{cccccc}{C}_{11}& C_{12}& C_{13}& 0& 0& 0\\ C_{12}& C_{22}& C_{23}& 0& 0& 0\\ C_{13}& C_{23}& C_{33}& 0& 0& 0\\ 0& 0& 0& C_{44}& 0& 0\\ 0& 0& 0& 0& C_{55}& 0\\ 0& 0& 0& 0& 0& C_{66}\end{array}\right)\left(\begin{array}{c}{ϵ}_1\\ {ϵ}_2\\ {ϵ}_3\\ {ϵ}_4\\ {ϵ}_5\\ {ϵ}_6\end{array}\right)$

And the elastic matrix ${\mathrm{C}}_{\text{ij}}$ can be written as (Karouchi et al., 2024b; Yoshida and Pappalettera, 2023):

${\mathrm{C}}_{\text{ij}}=\left[\begin{array}{llllll}C11& C12& C13& C14& C15& C16\\ C21& C22& C23& C24& C25& C26\\ C31& C32& C33& C34& C35& C36\\ C41& C42& C43& C44& C45& C46\\ C51& C52& C53& C54& C55& C56\\ C61& C62& C63& C64& C65& C66\end{array}\right]$

These equations represent a linear system between stress and strain in an elastic material. For anisotropic materials such as crystals, these equations can be generalized in the form of a $6\times 6$ elasticity tensor that relates the six components of stress to the six components of strain. Each material (Al, Ni, Ti) possesses a unique set of elastic constants $C_{ij}$ obtained from CASTEP simulations.

3.3 Elastic constants

The calculated elastic stiffness matrices (Cij) for Aluminum (Al), Titanium (Ti), and Nickel (Ni), derived using CASTEP simulations. Each matrix provides crucial insights into the mechanical properties of these materials, including Young’s modulus, Poisson’s ratio, and bulk modulus. An interpretation of the results follows, focusing on the values of C11, C22, C33, and off-diagonal components like C12, C13, etc. for each material (Ejjabli et al., 2024; Karouchi et al., 2023).

3.3.1 Aluminum (Al)

The matrix of elastic constants for Aluminum is shown below:

$\left(\begin{array}{cccccc}133.71085& 50.71550& 50.71550& 0& 0& 0\\ 50.71550& 133.71085& 50.71550& 0& 0& 0\\ 50.71550& 50.71550& 133.71085& 0& 0& 0\\ 0& 0& 0& 29.41765& 0& 0\\ 0& 0& 0& 0& 29.41765& 0\\ 0& 0& 0& 0& 0& 29.41765\end{array}\right)\text{GPa}$

The values of the elastic constants $C_{11},C_{22}$, and $C_{33}$ are all equal to 133.71 GPa. This indicates that aluminum exhibits isotropic mechanical behavior. Where the mechanical response is the same in all principal directions of the crystal. The values of the off-diagonal elements, such as $C_{12},C_{13}$, and $C_{23}$, are all equal to 50.72 GPa. These values confirm the uniform response of aluminum to mechanical stress applied in different directions, further reinforcing the isotropic nature of the material.

The values of the shear modulus $C_{44},C_{55,}$ and $C_{66}$ are all equal to 29.42 GP. This suggests that aluminum has moderate resistance to shear deformation. The shear modulus measures the material’s ability to resist forces that tend to cause sliding, and these moderate values show that aluminum can deform under shear while remaining relatively rigid. The bulk modulus of aluminum is 78.38 GPa. This modulus measures the material’s resistance to uniform compression. A value of 78.38 GPa indicates that aluminum is moderately compressible, in line with the known properties of this metal. The Young’s modulus of aluminum, is 88.59 GPa. This modulus measures the stiffness of the material in response to tensile or compressive stress along an axis. A value of 88.59 GPa means that aluminum has moderate stiffness, making it suitable for applications requiring a balance between lightness and mechanical strength.

3.3.2 Titanium (Ti)

The matrix of elastic constants for Titanium is shown below:

$\left(\begin{array}{cccccc}72.21045& 116.94895& 116.94895& 0& 0& 0\\ 116.94895& 72.21045& 116.94895& 0& 0& 0\\ 116.94895& 116.94895& 72.21045& 0& 0& 0\\ 0& 0& 0& 30.92695& 0& 0\\ 0& 0& 0& 0& 30.92695& 0\\ 0& 0& 0& 0& 0& 30.92695\end{array}\right)\text{GPa}$

The values of the elastic constants $C_{11},C_{22}$, and $C_{33}$ for titanium are 72.21 GPa. This indicates that titanium exhibits anisotropic mechanical behavior, where the mechanical response differs along different principal directions of the crystal. This anisotropy is typical of materials with a hexagonal close-packed $\left(\text{HCP}\right)$ crystal structure, such as titanium. The values of the off-diagonal elements, including $C_{12}$ and $C_{13}$, are significantly larger at 116.95 GPa. These values confirm titanium’s enhanced response to mechanical stress applied in various directions, further reinforcing the directional dependence of the material’s stiffness.

The shear modulus $C_{44},C_{55}$, and $C_{66}$ are all equal to 30.93 GPa. This suggests that titanium has a higher resistance to shear deformation compared to aluminum. The shear modulus measures the material’s ability to resist forces that tend to cause sliding, and these values indicate that titanium can deform under shear while maintaining considerable rigidity. The bulk modulus of titanium is 102.04 GPa. This modulus measures the material’s resistance to uniform compression. A value of 102.04 GPa indicates that titanium is moderately compressible, consistent with the known properties of this metal. The Young’s modulus of titanium, calculated using the Voigt average, is 27.95 GPa, while the Hill average gives a higher value of 479.17 GPa. These moduli measure the stiffness of the material in response to tensile or compressive stress along an axis. The higher Hill average reflects titanium’s considerable stiffness, making it suitable for applications that require exceptional strength-to-weight ratios, such as in aerospace and automotive industries.

3.3.3 Nickel (Ni)

The matrix of elastic constants for Nickel is shown below:

$\left(\begin{array}{cccccc}132.86275& 137.71295& 137.71295& 0& 0& 0\\ 137.71295& 132.86275& 137.71295& 0& 0& 0\\ 137.71295& 137.71295& 132.86275& 0& 0& 0\\ 0& 0& 0& 74.66560& 0& 0\\ 0& 0& 0& 0& 74.66560& 0\\ 0& 0& 0& 0& 0& 74.66560\end{array}\right)\text{\hspace{0.17em}GPa}$

The values of the elastic constants $C_{11},C_{22}$, and $C_{33}$ for nickel are all equal to 132.86 GPa. This indicates that nickel exhibits isotropic mechanical behavior, where the mechanical response is the same in all principal directions of the crystal. This isotropy is characteristic of materials with a face-centered cubic (FCC) crystal structure, similar to that of aluminum.

The values of the off-diagonal elements, such as $C_{12},C_{13}$, and $C_{23}$, are all equal to 137.71 GPa. These higher values confirm the uniform response of nickel to mechanical stress applied in different directions, further reinforcing the isotropic nature of the material.

The values of the shear modulus $C_{44},C_{55}$, and $C_{66}$ are approximately 74.67 GPa. This suggests that nickel has a moderate resistance to shear deformation, which is typical for FCC metals. The shear modulus measures the material’s ability to resist forces that tend to cause sliding, and these moderate values indicate that nickel can deform under shear while maintaining considerable rigidity. The bulk modulus of nickel is 136.10 GPa. This modulus measures the material’s resistance to uniform compression. A value of 136.10 GPa indicates that nickel is less compressible, which aligns with the known properties of this metal. The Young’s modulus of nickel, is approximately 118.74 GPa. This modulus measures the stiffness of the material in response to tensile or compressive stress along an axis. A value of 118.74 GPa means that nickel has moderate stiffness, making it suitable for applications that require a balance between strength and ductility.

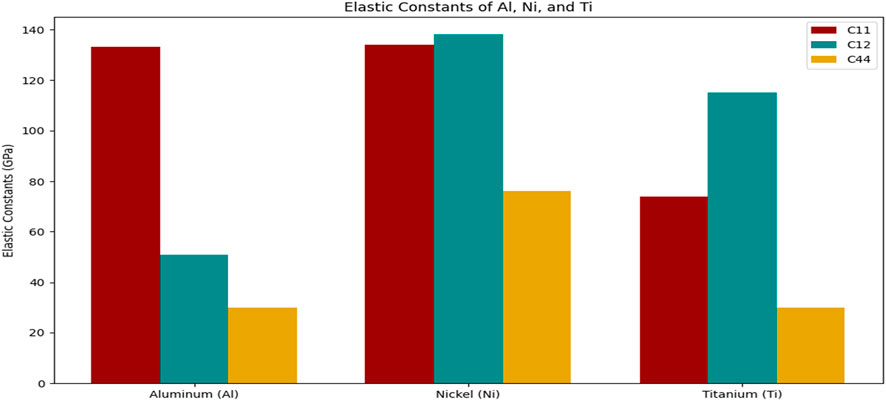
The elastic constants of aluminum (Al), titanium (Ti), and nickel (Ni) reveal important insights into their mechanical properties and potential applications. Aluminum, with its isotropic cubic structure, shows uniform stiffness in all directions (C11 = C22 = C33 = 133.71 GPa) and moderate shear resistance (C44 = 29.42 GPa), making it ideal for lightweight applications such as in aerospace and automotive industries. Titanium, exhibiting anisotropy due to its hexagonal structure, has lower axial stiffness (C11 = 72.21 GPa) but higher shear stiffness (C12 = 116.95 GPa), indicating its suitability for high-strength applications like medical implants and aerospace components. Nickel, with its FCC structure, demonstrates high stiffness in both normal and shear directions (C11 = 132.86 GPa, C44 = 74.67 GPa), making it excellent for corrosion-resistant and high-durability applications, such as in turbines and superalloys. These results highlight the materials’ varied mechanical properties, offering guidance for their use in specific industrial applications, and suggest that further doping or alloying could improve performance for targeted technologies.

3.3.4 Discussion

Figure 3 compares three fundamental elastic constants: C11, C12, and C44. C11 measures stiffness along the principal crystallographic directions, C12 represents the interaction between different directions within the crystal structure, and C44 relates to the material’s shear resistance.

• C11 represents the material’s stiffness along a given direction. Nickel has the highest value, indicating greater stiffness compared to aluminum and titanium. Titanium shows the lowest stiffness in this direction.

• C12 shows the interaction between different directions. Nickel has a much higher value, indicating stronger interaction between directions, while aluminum has a significantly lower interaction.

• C44 measures shear stiffness. Nickel shows moderate shear rigidity, aluminum has the lowest value, and titanium lies in between, reflecting better shear resistance.

Figure 3

Figure 3. Comparison of elastic constants (C11, C12, C44) for aluminum, nickel, and titanium.

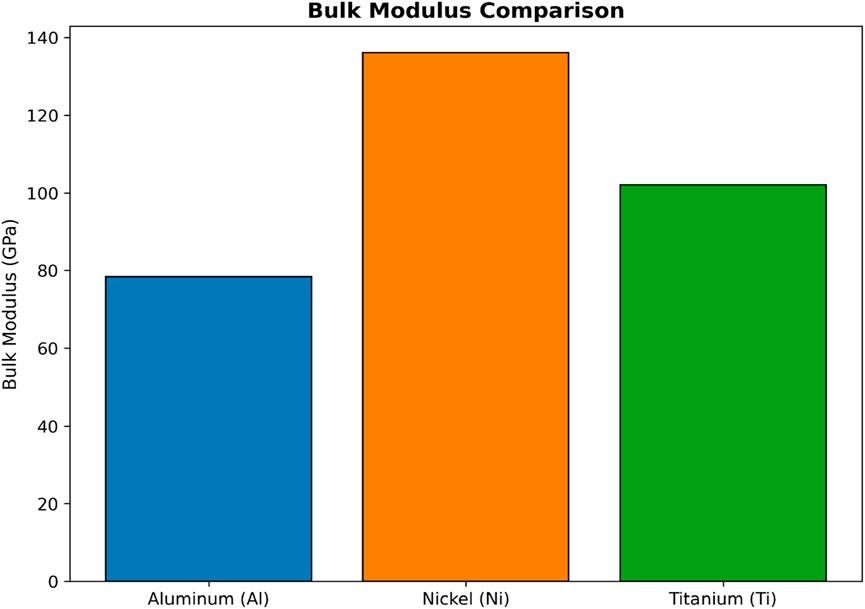
The bulk modulus, also called the volume modulus, evaluates a material’s ability to resist uniform compression. This graph (Figure 4) highlights the differences between aluminum, nickel, and titanium in terms of compression resistance.

• Nickel has the highest bulk modulus, indicating it is the most difficult to compress, making it suitable for applications requiring high pressure resistance.

• Titanium follows with a slightly lower but still high bulk modulus, reflecting its capacity to resist compression while maintaining some flexibility.

• Aluminum, with the lowest bulk modulus, is easier to compress, which is advantageous in applications where a lighter and more flexible material is needed.

Figure 4

Figure 4. Bulk modulus comparison for aluminum, nickel, and titanium.

In 3D printing, materials with high Bulk Modulus like Nickel are essential for producing parts that will endure heavy loads and compression. This predictive modeling can help streamline the material selection process, enabling manufacturers to optimize materials for specific applications with minimal experimental effort.

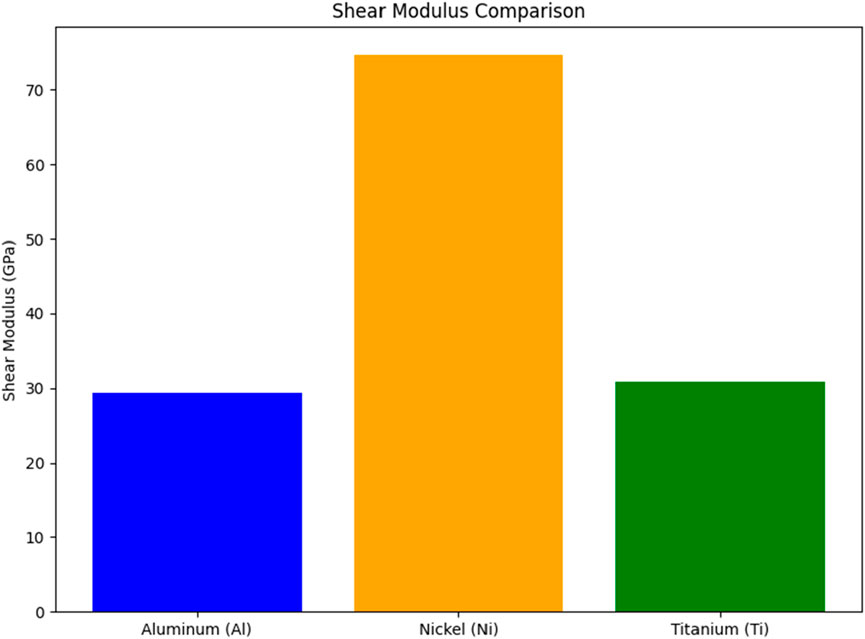
The shear modulus measures a material’s resistance to forces that tend to slide one part of the material over another. This graph (Figure 5) compares the ability of the three materials used in 3D printing to resist angular deformation:

• Nickel displays an exceptionally high shear modulus, indicating strong resistance to shear deformation. This makes it an optimal choice for 3D printing applications where parts require high resistance to torsion or angular forces, especially in environments subjected to high mechanical stresses.

• Titanium and Aluminum show much lower shear moduli, making them more prone to angular deformation compared to nickel. However, in the context of 3D printing, these materials offer advantages for fabricating parts where greater flexibility is needed or where lightweight materials are essential, such as in aerospace and automotive sectors.

Figure 5

Figure 5. Shear modulus comparison for aluminum, nickel, and titanium.

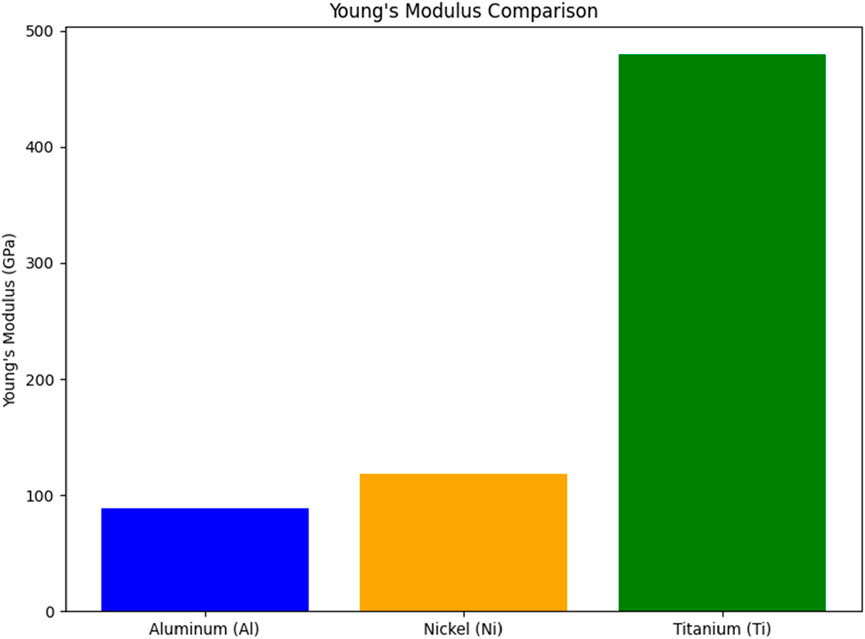
Young’s modulus measures the stiffness of a material, indicating its ability to resist elastic deformation under tension or compression. Figure 6 shows the differences in stiffness between aluminum, nickel, and titanium.

• Titanium has the highest Young’s modulus, reaching nearly 500 GPa, indicating excellent rigidity. This makes it suitable for applications that require high strength and minimal deformation under load, such as biomedical implants or critical structural components.

• Aluminum and Nickel have much lower Young’s moduli, meaning they deform more easily under stress. This flexibility makes them ideal for applications like prototypes or lightweight parts used in the aerospace and automotive industries.

Figure 6

Figure 6. Young’s modulus comparison for aluminum, nickel, and titanium.

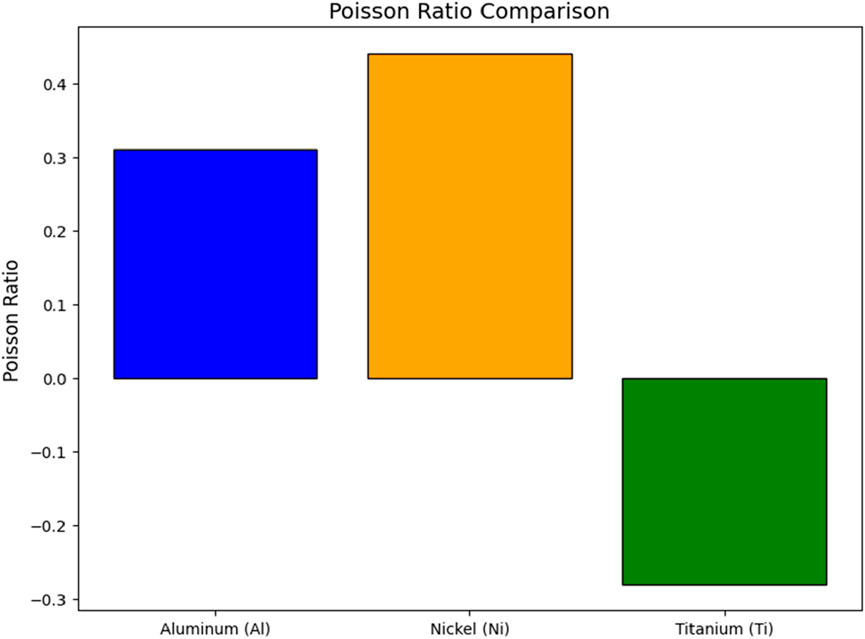
The Poisson ratio (Figure 7) describes the ratio between transverse contraction and longitudinal extension when a material is stretched or compressed. It reflects how a material contracts or expands when subjected to tension.

• Nickel shows the highest Poisson ratio, indicating a significant tendency to expand laterally when stretched. This property is advantageous for applications requiring ductility or stress absorption.

• Aluminum has a moderate Poisson ratio, providing a good balance between deformation and stability.

• Titanium has a negative Poisson ratio, which is unusual. This suggests it could exhibit auxetic behavior (expanding laterally when stretched). Such behavior could be beneficial in advanced 3D printing applications or for designing auxetic structures.

Figure 7

Figure 7. Poisson ratio comparison for aluminum, nickel, and titanium.

In 3D printing, understanding a material’s lateral deformation is key to ensuring that parts maintain their structural integrity under load. For flexible parts, Nickel’s behavior could be advantageous, while Titanium’s unique behavior can be leveraged in niche applications requiring materials with counterintuitive deformation characteristics. The predictive modeling of Poisson’s Ratio ensures that manufacturers can anticipate and mitigate deformation issues before production.

3.4 Analysis of mechanical properties predictions with AI

In this study, we present the mechanical properties of three materials “Aluminum, Titanium, and Nickel” obtained through computational methods (CASTEP Code) and predictions made using a machine learning approach based on Ridge regression. The primary focus is on the Bulk Modulus, Young’s Modulus, and Shear Modulus, which are critical for evaluating the performance of materials in various applications, including 3D printing. The results from the CASTEP calculations provided actual values for the mechanical properties of each material, which were then compared to the predicted values obtained from the Ridge regression model. The following sections detail the findings for each property:

• Bulk Modulus

The Bulk Modulus measures a material’s resistance to uniform compression. For Aluminum, the actual Bulk Modulus was 78.38 GPa, while the predicted value was 79.37 GPa. Similarly, for Titanium, the actual value was 102.04 GPa, with a predicted value of 101.65 GPa. Nickel exhibited an actual Bulk Modulus of 136.10 GPa, with a predicted value of 135.50 GPa. The mean squared error (MSE) for the predictions was 0.4957, and the R-squared (R²) value was 0.9991, indicating an excellent fit between the predicted and actual values.

• Young’s Modulus

Young’s Modulus reflects the stiffness of a material under elastic deformation. The actual Young’s Modulus for Aluminum was 88.59 GPa, while the predicted value was 88.02 GPa. Titanium’s actual value was 27.94 GPa, and the predicted value was 28.74 GPa. Nickel demonstrated an actual Young’s Modulus of 118.74 GPa, with a predicted value of 118.51 GPa. The predictions achieved an MSE of 0.3377 and an R-squared (R²) value of 0.9998, further supporting the model’s reliability.

• Shear Modulus

The Shear Modulus indicates a material’s response to shear stress. For Aluminum, the actual Shear Modulus was 29.42 GPa, compared to a predicted value of 29.94 GPa. Titanium’s actual Shear Modulus was 30.93 GPa, with a predicted value of 30.86 GPa. Nickel exhibited an actual value of 74.67 GPa, and the predicted value was 74.22 GPa. The MSE for the Shear Modulus predictions was 0.1606, and the R-squared (R²) value reached 0.9996, indicating exceptional accuracy.

The results obtained from the regression model demonstrate a high level of accuracy in predicting the mechanical properties of Aluminum, Titanium, and Nickel. The low MSE values and high R-squared scores suggest that the model is highly effective for these materials. These findings highlight the potential of using artificial intelligence techniques to predict material properties, which can aid in the design and optimization of materials for various engineering applications, including 3D printing.

3.4.1 Comparison table of CASTEP results and AI predictions

Table 1 provides a detailed comparison between the actual mechanical properties obtained through CASTEP simulations and the predictions generated by the AI model using Ridge regression. The table highlights the consistency between the two sets of results, as demonstrated by the low Mean Squared Error (MSE) values and the high R-squared (R²) scores, which exceed 0.999 for all properties. This high level of agreement underscores the reliability of the hybrid approach in accurately predicting critical mechanical properties such as Bulk Modulus, Young’s Modulus, and Shear Modulus. By enabling precise predictions, this method significantly reduces the need for extensive computational and experimental resources, making it a valuable tool for material optimization in 3D printing applications.

Table 1

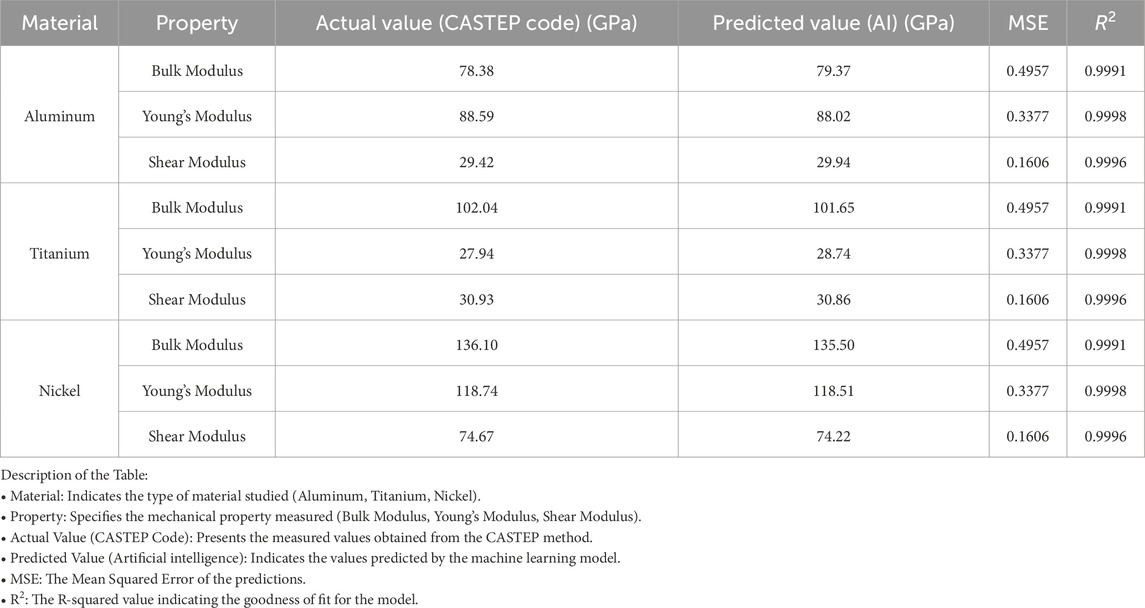
Table 1. Comparison of actual and AI-Predicted mechanical properties with performance metrics (MSE and R²).

3.4.2 Comparison of CASTEP code and IA results

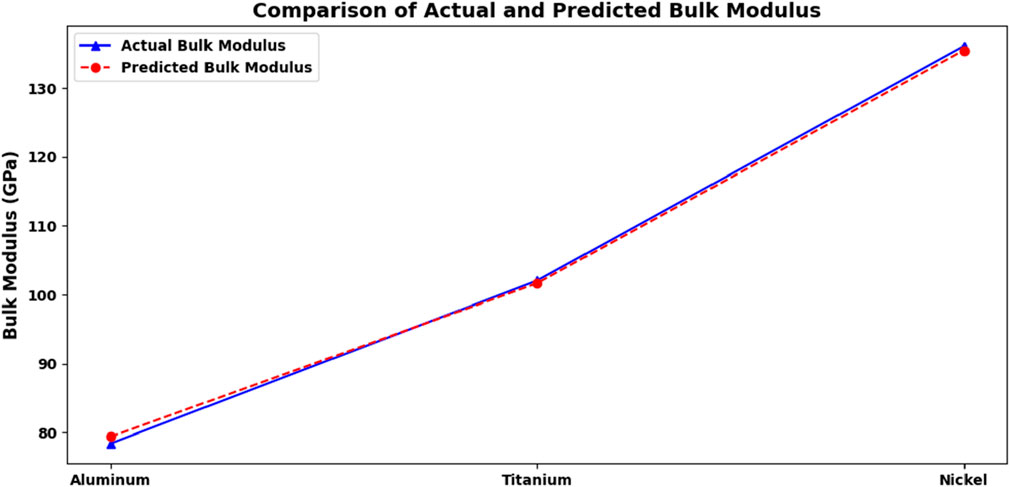
Figure 8 illustrates the comparison between the bulk modulus values derived from CASTEP Code simulations (solid blue line) and those predicted by AI models (red dashed line) for the three materials: aluminum, titanium, and nickel. Both lines show a close overlap, signifying a high degree of accuracy in the AI model’s predictions.

Figure 8

Figure 8. Comparison of actual and AI-predicted bulk modulus.

From the graph, a clear trend is observed in the bulk modulus values. Both actual and predicted values increase progressively from aluminum to titanium, and finally to nickel. This suggests that nickel has the highest resistance to uniform compression, followed by titanium, with aluminum having the lowest resistance. These insights are valuable for materials selection, especially when resistance to compressive forces is a key factor in design applications.

The close agreement between the actual and predicted bulk modulus values, as reflected by the nearly identical curves, highlights the exceptional performance of the AI model. This high correlation is further supported by the R² value of approximately 0.9991, indicating a near-perfect match between the predicted and actual data. The model’s accuracy makes it a reliable tool for predicting the mechanical properties of materials, providing valuable assistance in the design and optimization of components for applications such as 3D printing.

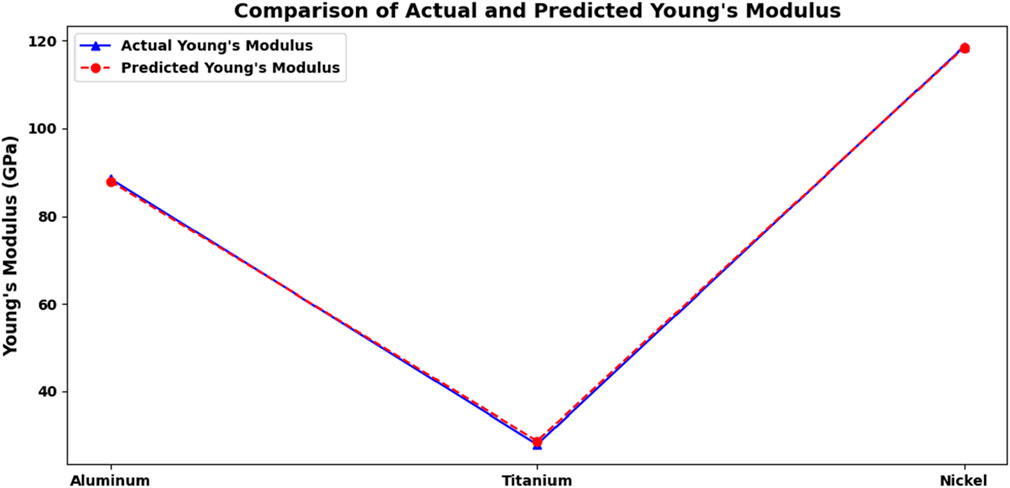
Figure 9 illustrates the comparison between the values of Young’s modulus derived from CASTEP Code simulations and those predicted by AI models for aluminum, titanium, and nickel. The predicted values, represented by the red dashed line, align closely with the actual values indicated by the solid blue line. This close correspondence suggests that the AI model can provide reliable estimates of Young’s modulus for the materials analyzed.

Figure 9

Figure 9. Comparison of actual and predicted Young’s modulus.

The high R² values, close to 0.9998, further support the close alignment of the curves. This consistency reinforces the credibility of the AI model’s predictions and its utility in estimating Young’s modulus for these materials.

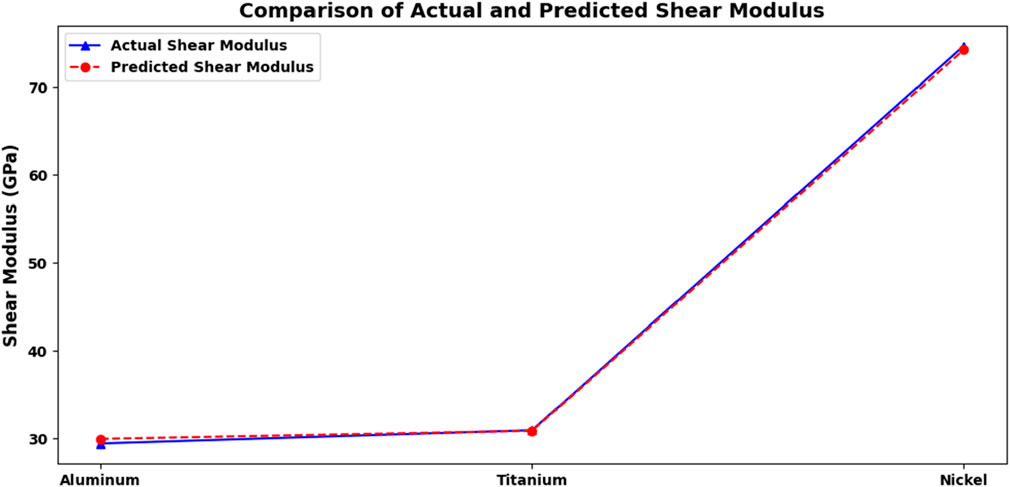
Figure 10 compares the shear modulus values obtained from CASTEP Code simulations with those predicted by AI models for aluminum, titanium, and nickel. The predicted values, depicted by the red dashed line, align almost perfectly with the actual values represented by the blue solid line. This remarkable alignment demonstrates the excellent accuracy of the AI model’s predictions for the shear modulus.

Figure 10

Figure 10. Comparison of actual and predicted shear modulus.

The shear modulus trend indicates an increase from aluminum to titanium and finally to nickel. This trend signifies that nickel possesses the highest resistance to angular deformation, followed by titanium, while aluminum exhibits the lowest shear modulus among the three materials. Understanding these properties is essential for applications where shear resistance is critical.

The close correspondence of the curves, combined with high R² values near 0.9996, corroborates the reliability of the AI model’s predictions. This affirmation suggests that the model can be trusted to evaluate the mechanical properties of materials effectively, providing valuable insights for engineering and material selection.

3.4.3 Discussion

The results of this study demonstrate the effectiveness of integrating computational methods such as CASTEP Code with machine learning models, specifically Ridge regression, to predict the mechanical properties of materials used in 3D printing. The high R-squared values (exceeding 0.999) and the low Mean Squared Errors (MSE) across all predicted properties (Bulk Modulus, Young’s Modulus, and Shear Modulus) validate the reliability of this hybrid approach in predicting material behavior with great accuracy. These findings emphasize the potential of machine learning techniques to significantly reduce the time and computational resources typically required for material testing and optimization.

3.4.3.1 Material-specific findings

Aluminum: The results highlight Aluminum’s balanced mechanical properties, particularly its moderate Bulk Modulus and Young’s Modulus, which make it suitable for lightweight applications requiring a balance between strength and flexibility. Its relatively low Shear Modulus compared to Titanium suggests that Aluminum may be more appropriate for structures that prioritize lightness over extreme shear resistance. This makes Aluminum highly useful in sectors such as aerospace, where weight reduction is essential but material strength must not be compromised.

In 3D printing, Aluminum is widely used in various domains:

• Aerospace and aviation: Lightweight components for fuselages, satellites, and drones.

• Automotive industry: Manufacturing of lightweight parts such as engine mounts and housings.

• Rapid prototyping: Development of functional prototypes requiring both strength and lightness.

• Electronics: Enclosures for electronic devices where reduced weight is essential.

Titanium: Titanium’s exceptional mechanical performance, particularly its high Young’s Modulus and Shear Modulus, makes it the stiffest and most rigid of the three materials tested. This positions Titanium as an ideal candidate for applications that demand high mechanical strength and resistance to deformation, such as biomedical implants and aerospace components. However, the unique negative Poisson’s Ratio of Titanium introduces complexities in terms of its deformation behavior, which may pose challenges in specific 3D printing processes. Despite these challenges, the material’s high performance under stress and resistance to corrosion make it indispensable for high-end engineering applications.

In 3D printing, Titanium is utilized in the following areas:

• Medical: Biomedical implants (bone and dental prostheses) due to its biocompatibility and corrosion resistance.

• Aerospace: Critical engine parts and structural components under high stress.

• Sports equipment: High-performance products like bicycle frames and golf clubs.

• Luxury goods: Watches and jewelry requiring both lightness and robustness.

Nickel: Nickel stands out for its superior resistance to compression, as indicated by its highest Bulk Modulus, and its good overall mechanical properties, making it a strong contender for industrial applications where parts are subjected to high compressive forces. Although Nickel is heavier and more rigid compared to Aluminum, it offers a robust option for environments that require durability and compression resistance, such as in machinery components. However, its lower flexibility compared to Aluminum suggests it may be less suited for lightweight applications.

3D printing applications for Nickel include:

• Energy industry: Manufacturing of turbines and components for power plants.

• Petrochemical industry: Production of heat exchangers and corrosion-resistant tanks.

• Aerospace: Components for jet engines exposed to high temperatures.

• Machinery: Durable machine parts subjected to heavy compression forces.

3.4.3.2 Advantages of the hybrid approach

This study demonstrates the power of combining machine learning models with traditional computational methods. The strong alignment between the predicted values and actual values shows that the Ridge regression model is not only capable of capturing the complex relationships between material properties but can do so with minimal computational cost compared to purely simulation-based approaches. This offers significant advantages for industries using 3D printing, allowing for faster prototyping, cost-efficient material testing, and the optimization of material properties before committing to costly physical trials.

The hybrid approach also shows great promise for future applications in materials science, particularly in the development of novel materials for additive manufacturing. By leveraging machine learning to predict mechanical properties with high accuracy, researchers and manufacturers can significantly reduce the time required to bring new materials to market, driving innovation in industries where performance, customization, and efficiency are critical.

4 Conclusion

In this study, a hybrid methodology integrating Density Functional Theory (DFT) simulations via CASTEP with machine learning algorithms was successfully developed to predict the mechanical properties of 3D-printed aluminum, titanium, and nickel. The DFT-generated data served as a high-fidelity dataset for training and validating predictive models.

Among the tested algorithms, the Ridge regression model exhibited outstanding predictive capabilities, achieving R-squared values consistently above 0.999 for Young’s modulus, bulk modulus, and shear modulus. This level of precision confirms the effectiveness and reliability of the proposed machine learning approach in replicating computational results with negligible error.

Beyond numerical performance, the study also provided material-specific insights relevant to additive manufacturing. Aluminum was confirmed as optimal for lightweight, ductile structures; nickel demonstrated high compressive strength, ideal for robust components; and titanium, while offering superior strength and stiffness, requires careful process control due to its complex deformation behavior during printing.

This hybrid approach not only reduces the computational burden associated with DFT simulations but also accelerates the process of material selection and design optimization in 3D printing. The integration of quantum mechanical simulations with artificial intelligence establishes a powerful framework for the intelligent development of next-generation materials tailored for additive manufacturing.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

SS: Methodology, Software, Supervision, Validation, Writing – original draft. MK: Methodology, Software, Writing – review and editing. MZ: Supervision, Validation, Writing – review and editing. NH: Supervision, Writing – review and editing. SB: Methodology, Validation, Writing – review and editing.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abe, K. (2019). Ab initio study of metallic aluminum hydrides at high pressures. Phys. Rev. B 100 (17), 174105. doi:10.1103/PhysRevB.100.174105

CrossRef Full Text | Google Scholar

Aboulkhair, N. T., Simonelli, M., Parry, L., Ashcroft, I., Tuck, C., and Hague, R. (2019). 3D printing of Aluminium alloys: additive Manufacturing of Aluminium alloys using selective laser melting. Prog. Mater Sci. 106, 100578. doi:10.1016/j.pmatsci.2019.100578

CrossRef Full Text | Google Scholar

Andreacola, F. R., Capasso, I., Langella, A., and Brando, G. (2023). 3D-printed metals: process parameters effects on mechanical properties of 17-4 P H stainless steel. Heliyon 9 (7), e17698. doi:10.1016/j.heliyon.2023.e17698

PubMed Abstract | CrossRef Full Text | Google Scholar

Andreacola, F. R., Capasso, I., Pilotti, L., and Brando, G. (2021). Influence of 3d-printing parameters on the mechanical properties of 17-4PH stainless steel produced through Selective Laser Melting. Frat. Ed. Integrità Strutt. 15 (58), 282–295. doi:10.3221/IGF-ESIS.58.21

CrossRef Full Text | Google Scholar

Bhesania, A. S., Kamboj, P., Peddakotla, S. A., and Kumar, R. (2022). In-depth analysis of reaction kinetics parameters of phenolic resin using molecular dynamics and unsupervised machine learning approach. Comput. Mater Sci. 206, 111215. doi:10.1016/j.commatsci.2022.111215

CrossRef Full Text | Google Scholar

Brandl, E., Heckenberger, U., Holzinger, V., and Buchbinder, D. (2012). Additive manufactured AlSi10Mg samples using Selective Laser Melting (SLM): microstructure, high cycle fatigue, and fracture behavior. Mater Des. 34, 159–169. doi:10.1016/j.matdes.2011.07.067

CrossRef Full Text | Google Scholar

Brando, G., Romana Andreacola, F., Capasso, I., Forni, D., and Cadoni, E. (2023). Strain-rate response of 3D printed 17-4PH stainless steel manufactured via selective laser melting. Constr. Build. Mater 409, 133971. doi:10.1016/j.conbuildmat.2023.133971

CrossRef Full Text | Google Scholar

Butler, K. T., Davies, D. W., Cartwright, H., Isayev, O., and Walsh, A. (2018). Machine learning for molecular and materials science. Nature 559 (7715), 547–555. doi:10.1038/s41586-018-0337-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Curtarolo, S., Setyawan, W., Hart, G. L., Jahnatek, M., Chepulskii, R. V., Taylor, R. H., et al. (2012). AFLOW: an automatic framework for high-throughput materials discovery. Comput. Mater Sci. 58, 218–226. doi:10.1016/j.commatsci.2012.02.005

CrossRef Full Text | Google Scholar

Curtin, W. A., and Miller, R. E. (2003). Atomistic/continuum coupling in computational materials science. Model Simul. Mat. Sci. Eng. 11 (3), R33–R68. doi:10.1088/0965-0393/11/3/201

CrossRef Full Text | Google Scholar

Deng, Z., Yin, H. Q., Jiang, X., Zhang, C., Zhang, G. F., Xu, B., et al. (2020). Machine-learning-assisted prediction of the mechanical properties of Cu-Al alloy. Int. J. Minerals, Metallurgy Mater. 27 (3), 362–373. doi:10.1007/s12613-019-1894-6

CrossRef Full Text | Google Scholar

Ejjabli, A., Karouchi, M., Al-Hattab, M., Bajjou, O., Rahmani, K., and Lachtioui, Y. (2024). Investigation of lead-free halide K2AgSbBr6 double Perovskite’s structural, electronic, and optical properties using DFT functionals. Chem. Phys. Impact 9, 100656. doi:10.1016/j.chphi.2024.100656

CrossRef Full Text | Google Scholar

Eskandari, H., Lashgari, H. R., Ye, L., Eizadjou, M., and Wang, H. (2022). Microstructural characterization and mechanical properties of additively manufactured 17–4PH stainless steel. Mater Today Commun. 30, 103075. doi:10.1016/j.mtcomm.2021.103075

CrossRef Full Text | Google Scholar

Frazier, W. E. (2014). Metal additive manufacturing: a review. J. Mater Eng. Perform. 23 (6), 1917–1928. doi:10.1007/s11665-014-0958-z

CrossRef Full Text | Google Scholar

Gibson, I. (2015). Additive manufacturing technologies: 3D printing, Rapid prototyping, and direct digital manufacturing. Johns. Matthey Technol. Rev. (3), 193–198. doi:10.1595/205651315X68840659

CrossRef Full Text | Google Scholar

Gibson, I., Rosen, D., Stucker, B., and Khorasani, M. (2021). Additive manufacturing technologies. Cham: Springer International Publishing. doi:10.1007/978-3-030-56127-7

CrossRef Full Text | Google Scholar

Grimme, S., Antony, J., Ehrlich, S., and Krieg, H. (2010). A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 132 (15), 154104. doi:10.1063/1.3382344

PubMed Abstract | CrossRef Full Text | Google Scholar

Grimme, S. (2004). Accurate description of van der Waals complexes by density functional theory including empirical corrections. J. Comput. Chem. 25 (12), 1463–1473. doi:10.1002/jcc.20078

PubMed Abstract | CrossRef Full Text | Google Scholar

Hoeun, S., Bernard, F., Grondin, F., Kamali-Bernard, S., and Alam, S. Y. (2023). Elastic constants of nano-scale hydrated cement paste composites using reactive molecular dynamics simulations to homogenization of hardened cement paste mechanical properties. Mater Today Commun. 36, 106671. doi:10.1016/j.mtcomm.2023.106671

CrossRef Full Text | Google Scholar

Karouchi, M., Ejjabli, A., Bajjou, O., Guerroum, J., Al-Hattab, M., Basyooni-M. Kabatas, M. A., et al. (2024a). Investigating the structural, electronic, and optical properties of the novel double perovskite K2AgBiI6 using DFT. Front. Mater 11 (Sep). doi:10.3389/fmats.2024.1448400

CrossRef Full Text | Google Scholar

Karouchi, M., Bajjou, O., Jabraoui, H., Ejjabli, A., Archi, M., Moulaoui, L., et al. (2023). “Increasing electro-optical properties of perovskite FAPbI 3 under the effect of doping by Sn,” in 2023 3rd international conference on innovative research in applied science, engineering and technology (IRASET) (IEEE), 1–7. doi:10.1109/IRASET57153.2023.10152963

CrossRef Full Text | Google Scholar

Karouchi, M., Ejjabli, A., Samine, S., Bajjou, O., and Lachtioui, Y. (2024b). Enhancing the optoelectronic properties of TiPbO3 perovskite through lanthanum doping. Sol. Energy Sustain. Dev. J., 142–155. doi:10.51646/jsesd.v14iSI_MSMS2E.397

CrossRef Full Text | Google Scholar

Kibrete, F., Trzepieciński, T., Gebremedhen, H. S., and Woldemichael, D. E. (2023). Artificial intelligence in predicting mechanical properties of composite materials. J. Compos. Sci. 7, 364. doi:10.3390/jcs7090364

CrossRef Full Text | Google Scholar

Komarasamy, M., Shukla, S., Williams, S., Kandasamy, K., Kelly, S., and Mishra, R. S. (2019). Microstructure, fatigue, and impact toughness properties of additively manufactured nickel alloy 718. Addit. Manuf. 28, 661–675. doi:10.1016/j.addma.2019.06.009

CrossRef Full Text | Google Scholar

Ledbetter, H., and Migliori, A. (2006). A general elastic-anisotropy measure. J. Appl. Phys. 100 (6). doi:10.1063/1.2338835

CrossRef Full Text | Google Scholar

Mavko, G., Mukerji, T., and Dvorkin, J. (2009). The rock physics handbook. Cambridge University Press. doi:10.1017/CBO9780511626753

CrossRef Full Text | Google Scholar

Mouhat, F., and Coudert, F.-X. (2014). Necessary and sufficient elastic stability conditions in various crystal systems. Phys. Rev. B 90 (22), 224104. doi:10.1103/PhysRevB.90.224104

CrossRef Full Text | Google Scholar

Muhammad, I. D., Awang, M., Mamat, O., and Shaari, Z. B. (2014). First-principles calculations of the structural, mechanical and thermodynamics properties of cubic zirconia. World J. Nano Sci. Eng. 04 (02), 97–103. doi:10.4236/wjnse.2014.42013

CrossRef Full Text | Google Scholar

Murr, L. E., Gaytan, S. M., Medina, F., Lopez, H., Martinez, E., Machado, B. I., et al. (2010). Next-generation biomedical implants using additive manufacturing of complex, cellular and functional mesh arrays. Philosophical Trans. R. Soc. A Math. Phys. Eng. Sci. 368 (1917), 1999–2032. doi:10.1098/rsta.2010.0010

PubMed Abstract | CrossRef Full Text | Google Scholar

Ngo, T. D., Kashani, A., Imbalzano, G., Nguyen, K. T. Q., and Hui, D. (2018). Additive manufacturing (3D printing): a review of materials, methods, applications and challenges. Compos B Eng. 143, 172–196. doi:10.1016/j.compositesb.2018.02.012

CrossRef Full Text | Google Scholar

Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized gradient approximation made simple. Phys. Rev. Lett. 77 (18), 3865–3868. doi:10.1103/PhysRevLett.77.3865

PubMed Abstract | CrossRef Full Text | Google Scholar

Ponnusamy, P., Masood, S. H., Palanisamy, S., Rahman Rashid, R. A., and Ruan, D. (2017). Characterization of 17-4PH alloy processed by selective laser melting. Mater Today Proc. 4 (8), 8498–8506. doi:10.1016/j.matpr.2017.07.196

CrossRef Full Text | Google Scholar

Rashid, R., Masood, S. H., Ruan, D., Palanisamy, S., Rahman Rashid, R. A., and Brandt, M. (2017). Effect of scan strategy on density and metallurgical properties of 17-4PH parts printed by Selective Laser Melting (SLM). J. Mater Process Technol. 249, 502–511. doi:10.1016/j.jmatprotec.2017.06.023

CrossRef Full Text | Google Scholar

Rooney, K., Dong, Y., Basak, A. K., and Pramanik, A. (2024). Prediction of mechanical properties of 3D printed particle-reinforced resin composites. J. Compos. Sci. 8 (10), 416. doi:10.3390/jcs8100416

CrossRef Full Text | Google Scholar

Saharudin, M. S., Ullah, A., and Younas, M. (2025). Innovative and sustainable advances in polymer composites for additive manufacturing: processing, microstructure, and mechanical properties. J. Manuf. Mater. Process. 9 (2), 51. doi:10.3390/jmmp9020051

CrossRef Full Text | Google Scholar

Samine, S., Zemzami, M., Hmina, N., Lagache, M., and Belhouideg, S. (2022). “Towards the use of artificial intelligence and machine learning in material scientist field,” in 2022 8th international conference on optimization and applications (ICOA) (IEEE), 1–5. doi:10.1109/ICOA55659.2022.9934559

CrossRef Full Text | Google Scholar

Samine, S., Zemzami, M., Hmina, N., Lagache, M., and Belhouideg, S. (2023). “Using machine learning and deep learning in additive manufacturing,” in 2023 9th international conference on optimization and applications (ICOA) (IEEE), 1–5. doi:10.1109/ICOA58279.2023.10308810

CrossRef Full Text | Google Scholar

Schütt, K. T., Arbabzadah, F., Chmiela, S., Müller, K. R., and Tkatchenko, A. (2017). Quantum-chemical insights from deep tensor neural networks. Nat. Commun. 8 (1), 13890. doi:10.1038/ncomms13890

PubMed Abstract | CrossRef Full Text | Google Scholar

Segall, M. D., Lindan, P. J. D., Probert, M. J., Pickard, C. J., Hasnip, P. J., Clark, S. J., et al. (2002). First-principles simulation: ideas, illustrations and the CASTEP code. J. Phys. Condens. Matter 14 (11), 2717–2744. doi:10.1088/0953-8984/14/11/301

CrossRef Full Text | Google Scholar

Soler, J. M., Artacho, E., Gale, J. D., García, A., Junquera, J., Ordejón, P., et al. (2002). The SIESTA method for ab initio order- N materials simulation. J. Phys. Condens. Matter 14 (11), 2745–2779. doi:10.1088/0953-8984/14/11/302

CrossRef Full Text | Google Scholar

Xie, T., and Grossman, J. C. (2018). Crystal graph convolutional neural networks for an accurate and interpretable prediction of material properties. Phys. Rev. Lett. 120 (14), 145301. doi:10.1103/PhysRevLett.120.145301

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, Y., Cui, L., and Xu, X. (2022). A prediction method of fracture toughness of nickel-based superalloys. Comput. Syst. Sci. Eng. 42 (1), 121–132. doi:10.32604/csse.2022.022758

CrossRef Full Text | Google Scholar

Yoshida, S., and Pappalettera, G. (2023). Mechanics and analysis of advanced materials and structures. Materials 16 (5), 2123. doi:10.3390/ma16052123

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Y., and Ling, C. (2018). A strategy to apply machine learning to small datasets in materials science. NPJ Comput. Mater 4 (1), 25. doi:10.1038/s41524-018-0081-z

CrossRef Full Text | Google Scholar