TiAlNb alloy interatomic potentials: comparing passive and active machine learning techniques with MTP and DeePMD

Intermetallic titanium aluminides are interesting for aerospace and automotive applications due to their superior high-temperature mechanical properties. In particular, $\gamma$-TiAl-based alloys containing 5–10 at.% Niobium (Nb) have attracted significant attention. Molecular dynamics (MD) simulations can elucidate and optimize these materials, provided that accurate interatomic potentials are available. In this work, we compare active and passive machine learning approaches for developing TiAlNb interatomic potentials using both deep potential molecular dynamics (DeePMD) and the moment tensor potential (MTP) methods. Our comprehensive evaluation encompasses elastic constants, equilibrium volume, lattice parameters, and finite-temperature behavior, as well as simulated tension tests and generalized stacking fault energy calculations to assess the impact of Nb on the thermo-mechanical properties of $\gamma$-TiAl and ${\alpha }_2$-Ti₃Al phases. Active learning consistently outperformed passive learning for both methods while requiring only a fraction of the training samples. Notably, active learning with DeePMD yielded a single potential capable of predicting the properties of both phases, whereas MTP exhibited limitations that necessitated separate training for each phase. Although active learning potentials excelled in predicting high-temperature behavior, their room-temperature property predictions were less accurate due to a sample selection bias toward higher temperatures. Overall, our thermomechanical analysis demonstrates that Nb incorporation enhances ductility while simultaneously reducing strength.

1 Introduction

Intermetallic alloys based on $\gamma$-titanium aluminide ($\gamma$-TiAl) have emerged as superior lightweight materials for aerospace and automotive applications. Their unique combination of low density, excellent oxidation resistance, and strong creep resistance at elevated temperatures makes them particularly attractive (Appel et al., 2011). Typically, these alloys consist of two intermetallic phases: the $\gamma$-TiAl phase, which adopts an ordered face-centered tetragonal structure (L1₀, P4/mmm), and the ${\alpha }_2$-Ti₃Al phase, characterized by an ordered hexagonal structure (D0₁₉, P6₃/mmc). Significant progress has been made in developing $\gamma$-TiAl alloys for high-temperature applications, notably within the TNM (TiAl-Nb-Mo) and TNB (TiAl-Nb-B) systems (Appel et al., 2011; Zhang et al., 2016; Li et al., 2014; Clemens and Mayer, 2012; Klein et al., 2016). These systems generally contain 5–10 at.% Nb along with minor additions of elements such as Mo, B, C, Si, W, Cr, and Ta. Although Nb is known to enhance mechanical performance by improving both strength and ductility (Zhu et al., 2018; Chen and Zhang, 2002; Cheng et al., 2016; Liu et al., 2022; Song et al., 2020; Zhang et al., 2023; Appel et al., 2011, Appel et al., 2006; Clemens and Mayer, 2012; Appel et al., 2000; Liu et al., 2002), its precise role in these alloys remains somewhat ambiguous.

In our previous work Chandran et al. (2024a), we investigated the effect of Nb on the thermo-mechanical properties of TiAl-based alloys using atomistic simulations with Farkas’ ternary interatomic potential (Farkas and Jones, 1996). We examined a range of models—from single-phase structures and lamellar interfaces to complex microstructure-informed atomistic models (MIAMs) featuring nano-polycolonies. Our study revealed that Farkas’ potential (Farkas and Jones, 1996) is limited in handling Nb concentrations above 1 at.% in MIAMs and above 2 at.% in certain lamellar interfaces, a significant drawback given that Nb levels of 5–10 at.% are most promising for enhancing strength and ductility. To overcome this limitation, our subsequent work Chandran et al. (2024b) focused on developing machine learning (ML)-based interatomic potentials for TiAlNb in molecular dynamics (MD) simulations. We employed moment tensor potential (MTP) and deep potential molecular dynamics (DeePMD) methods, performing a comparative evaluation based on error analysis, performance metrics, and calculations of key material properties such as elastic constants, equilibrium volume, and lattice parameters. Finite temperature properties, including specific heat capacity and thermal expansion, were also computed, and mechanical properties were assessed through simulated uniaxial tension tests and generalized stacking fault energy calculations. However, these approaches required extensive datasets (333,340 configurations for DeePMD and 40,000 for MTP) and struggled to accurately capture the ${\alpha }_2$-Ti₃Al phase characteristics. In the current work, we implement an advanced active learning strategy to develop a robust interatomic potential with reduced reliance on large datasets. We also compare active and passive learning procedures to determine the effective approach for developing the interatomic potentials for TiAlNb alloys.

The development of such an effective potential is a crucial step, as it provides the foundation for bridging the gap between atomistic mechanisms and macroscopic mechanical behavior. The ultimate failure of polycrystalline materials is mainly governed by processes initiated at the atomic and microstructural scales, such as dislocation activity and nano-void formation (Maruschak et al., 2023). Key properties calculated from atomistic models, including the generalized stacking fault energy (GSFE) and elastic constants, directly inform these fundamental deformation mechanisms. Therefore, an accurate potential is an essential first step toward building predictive, multi-scale models of the structural integrity and service life of Ti-Al-Nb components.

Various ML techniques have been developed for generating interatomic potentials. Among these, the deep potential (DP) and MTP methods have distinguished themselves through their success in modeling both ordered and disordered systems. DP-based potentials have been effectively applied to diverse systems, including ${\text{MgCl}}_2$-NaCl and ${\text{MgCl}}_2$-KCI (Xu et al., 2023), LiF and FLiBe (Rodriguez et al., 2021), AlN (Li et al., 2024) and Cu (Du et al., 2022). Similarly, MTP has been utilized in studies on Ti_0.5Al_0.5N (Tasnádi et al., 2021). In addition, the work by Lu et al. (2023) is particularly noteworthy, as it developed a DeePMD potential for TiAlNb that not only validates the bulk material properties of TiAl-based alloys but also provides accurate evaluations of the stacking fault energy and tensile properties of $\gamma$-TiAl. Notably, Zhao et al. (2024) applied the neuroevolution potential (NEP) method to train a general-purpose Ti-Al-Nb potential that both explains the high-temperature mechanical properties of TiAl-based alloys and reproduces their fundamental material properties.

Active learning is a sophisticated approach that initiates the training process with a small dataset. As learning proceeds, the algorithm selectively incorporates the most informative data points, thereby incrementally enhancing the model’s performance. This strategy facilitates the development of high-quality interatomic potentials without the need for extensive datasets, substantially reducing computational costs—especially considering that dataset generation often relies on numerous computationally intensive ab initio molecular dynamics (AIMD) calculations. AIMD integrates the atomic equations of motion in real time using forces derived from first-principles, thereby capturing the dynamic evolution of a system at finite temperatures. In contrast, density functional theory (DFT) is a static approach that calculates the ground-state electronic structure for a fixed atomic configuration, yielding highly accurate energies and forces. Thus, while AIMD utilizes DFT to generate realistic dynamical trajectories, DFT itself provides precise, time-independent property evaluations. Active learning has been successfully implemented within the MTP framework for various materials, including Rosenbrock et al. (2021), Ta-V-Cr-W alloys (Gubaev et al., 2023), Cu-Ni-Si-Cr alloys (Ángel et al., 2023; Attarian et al., 2022), Mo–Nb–Ta systems (Novikov et al., 2021), as well as Cu-Pd, Co-Nb-V, and Al-Ni-Ti systems (Gubaev et al., 2019), along with Zr (Luo et al., 2023) and U (Chen et al., 2023). Similarly, active learning in DeePMD has been applied to materials such as Ag₂S (Balyakin and Sadovnikov, 2022), B₄C (Ghaffari et al., 2024; Du et al., 2022), HfO₃ (Wu et al., 2021), AI (Cheng et al., 2021), MgAlSi (Zhu et al., 2024), MgCl₂-NaCl-KCl (Feng and Lu, 2024), SnSe (Guo et al., 2021), and SrTiO₃ (He et al., 2022).

In this paper, we compare passive and active learning strategies using the MTP and DeePMD methods. Section 2.1 describes the generation of the dataset for potential training. Here, the term “dataset” refers to the collection of atomic configurations, along with their corresponding energies and forces derived from AIMD simulations, which serve as the input for training the interatomic potentials. We also introduce the formulations of the MTP (Section 2.2) and DeePMD (Section 2.3) active learning strategies, as well as the methodology for simulated tension tests (Section 2.4). In Section 3.1, we present a detailed analysis of active learning performance—illustrated through root mean square error (RMSE) energy/atom and force curves—and compare these metrics with those obtained via passive learning. Finally, MD simulations were conducted to evaluate the predictive accuracy of the developed potentials, as demonstrated by equilibrium lattice parameters, equilibrium volume and elastic constants (Section 3.2.1), finite-temperature properties (Section 3.2.2), and thermo-mechanical behavior under uniaxial tension, including GSFE calculations (Section 3.2.3). Figure 1 depicts a comprehensive workflow that outlines both the active learning strategy employed in our study and the approach used to compare passive and active learning potentials.

Figure 1

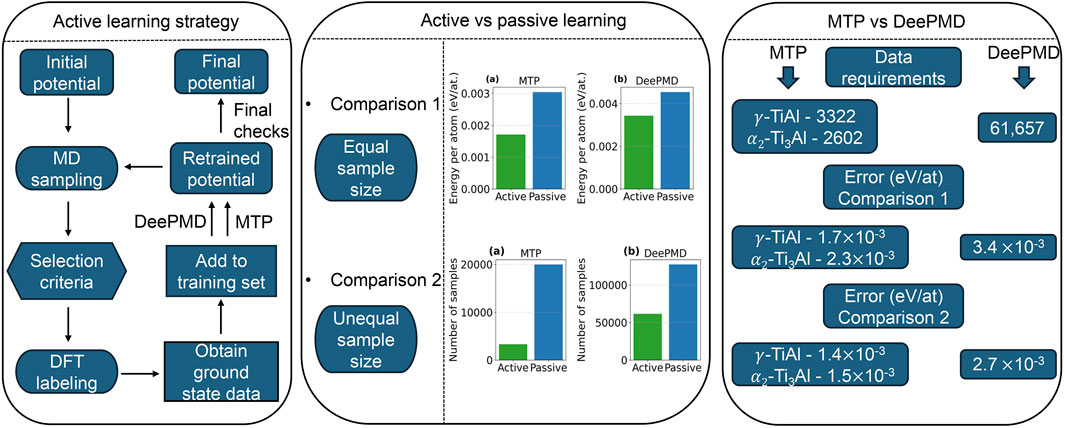
Figure 1. Graphical workflow of the study. The diagram outlines the active learning strategy implemented for both MTP and DeePMD and it illustrates the two levels of comparison between active and passive learning potentials. Sampling (MD simulations, Section 2.2, Section 2.3) generates diverse atomic configurations at the target thermodynamic conditions, while labeling (DFT calculations, Section 2.2, Section 2.3) assigns accurate energies and forces to those configurations. In Comparison 1, both potentials are trained using the same number of samples to directly evaluate their relative performance, while in Comparison 2, different sample sizes are used to achieve comparable error levels. The conclusion summarizes the comparisons in terms of data requirements and prediction accuracy of active learning potential for both methods.

2 Materials and methods

2.1 Dataset generation

The dataset generation began by constructing a series of unique structural configurations for $\gamma$-TiAl and ${\alpha }_2$-Ti₃Al alloys with varying Nb concentrations. These concentrations spanned from 1 at.% to 14 at.%, resulting in 28 unique structural configurations. Each configuration consisted of 108 atoms for $\gamma$-TiAl and 128 atoms for ${\alpha }_2$-Ti₃Al. Here, a configuration refers to a distinct atomic arrangement within the simulation cell, defined by the specific positions and chemical identities of the atoms. While the primary focus was on Nb concentrations between 1 and 10 at.%, additional configurations with concentrations up to 14 at.% were included to strengthen the dataset for training. The introduction of Nb atoms into titanium lattice sites was carefully executed, accounting for the preferential site occupancy of Nb in these materials. The methodology for generating these configurations is detailed in our prior work Chandran et al. (2024a), as well as in other related studies (Holec et al., 2016; Ouadah et al., 2020; Ouadah et al., 2021; Song et al., 2000; Wei et al., 2012). Precise structural configurations were generated using the Atomsk tool (Hirel, 2015).

To generate the dataset, AIMD simulations were performed on these configurations using the Vienna ab-initio simulation (VASP). The AIMD calculations employed projector augmented wave (PAW) potentials (Blöchl, 1994) to accurately model electron-ion interactions, while exchange-correlation effects were treated via the generalized gradient approximation (GGA) using the Perdew–Burke–Ernzerhof (PBE) functional (Perdew et al., 1996; Perdew et al., 1997). An energy cutoff of 510 eV was adopted, with the Brillouin zone sampled by a $\mathrm{\Gamma }$-centered $1\times 1\times 1$ k-point mesh and a time step of 0.5 femtoseconds to ensure temporal precision.

For active learning, short AIMD simulations were conducted at 300 K using the NVT ensemble (constant particle number, volume, and temperature) for 2.5 ps. These runs provided the initial training set for the DeePMD and MTP active learning models. The dataset containing the training and testing data for both MTP and DeePMD are available under the link: Active learning dataset. In contrast, the passive learning models were trained on the TiAlNb dataset from our previous work Chandran et al. (2024b), which comprises additional AIMD simulations carried out with both the NVT ensemble and the NPT (which maintains constant particle number, pressure, and temperature while allowing volume fluctuations) ensemble for approximately 10 ps across all configurations. For further details on the TiAlNb dataset, please refer to Chandran et al. (2024b).

For DeePMD potential training, the DeePMD-kit (Wang et al., 2018) was employed in conjunction with the LAMMPS package (Thompson et al., 2022) for MD simulations. Similarly, MTP potentials were trained using the MLIP package (Novikov et al., 2021), integrated with LAMMPS (Thompson et al., 2022) to streamline MD simulations. These tools facilitated efficient and accurate training for both DeePMD and MTP models.

2.2 Moment tensor potential (MTP) and active learning strategy

The theoretical foundation of MTP and its associated moment tensor descriptors has been extensively discussed in our previous work Chandran et al. (2024b) and in other publications Novikov et al. (2021), Podryabinkin et al. (2023). We refer the reader to these resources for a detailed understanding of these concepts. This section will concentrate on the active learning formulations concerning MTP.

Traditional methods for constructing interatomic potential training sets often involve manual trial-and-error. However, by defining extrapolation mathematically, this process can be automated. The D-optimality criterion (Novikov et al., 2021), which maximizes the information matrix, introduces an extrapolation grade, denoted as $\gamma (\text{cfg})$. This grade correlates with prediction errors without requiring ab initio data. In active learning simulations, configurations exceeding a specified $\gamma$ threshold are computed using an ab initio method and then added to the training set, thus reducing extrapolation.

The D-optimality criterion is particularly straightforward for linear regression, where MTP is parameterized by linear variables $\xi =\{{\xi }_1,\dots ,{\xi }_m\}$. For a given configuration, the energy can be expressed as Novikov et al. (2021):

$E^{\text{mtp}}\left(\text{cfg};\xi \right)={\displaystyle \sum _i}{\displaystyle \sum _{\alpha =1}^m}{\xi }_{\alpha }{B}_{\alpha }\left({\eta }_i\right)={\displaystyle \sum _{\alpha =1}^m}{\xi }_{\alpha }{\displaystyle \sum _i}{B}_{\alpha }\left({\eta }_i\right)={\displaystyle \sum _{\alpha =1}^m}{\xi }_{\alpha }{\displaystyle \underset{b_{\alpha }\left(\mathrm{c}\mathrm{f}\mathrm{g}\right)}{{\displaystyle \underbrace{{\displaystyle \sum _i}{B}_{\alpha }\left({\eta }_i\right)}}}}.(1)$

Here $B_{\alpha }$ represents the basis functions and $\eta$_i corresponds to local atomic neighborhood of i^th atom. When fitting to energy values, an overdetermined system of $K$ linear equations for $\xi$ is solved, which can be represented in the following matrix form:

$\mathbf{B}=\left(\begin{array}{ccc}\hfill b_1\left({\text{cfg}}_1\right)\hfill & \hfill \cdots \hfill & \hfill b_m\left({\text{cfg}}_1\right)\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill b_1\left({\text{cfg}}_K\right)\hfill & \hfill \cdots \hfill & \hfill b_m\left({\text{cfg}}_K\right)\hfill \end{array}\right).(2)$

Each equation corresponds to a specific configuration. The D-optimality criterion selects $m$ configurations that form the most linearly independent system of equations. This is equivalent to finding an $m\times m$ submatrix $A$ with the largest determinant, $|\text{det}(A)|$, which corresponds to the maximum volume. These configurations constitute the active set. Within the MLIP code, the active learning state is characterized by this active set, along with $A$ and its inverse, $A^{-1}$. From the MTP perspective, this D-optimal active set contains the most “extreme” and diverse configurations. The Maxvol algorithm efficiently constructs this active set by choosing the submatrix with the greatest volume from a pool of configurations.

The extrapolation grade $\gamma (\text{cfg})$ for a given configuration is computed as:

$\gamma \left(\text{cfg}\right)=\underset{1\le j\le m}{\max }|c_j|,(3)$

where

$\left(c_1\dots c_m\right)=\left(b_1\dots b_m\right)A^{-1}.(4)$

If $\gamma (\text{cfg})>1$, this indicates that $|\det (A)|$ could be increased. In such cases, the Maxvol algorithm replaces the row in $A$ indexed by

$k=\arg \underset{1\le j\le m}{\max }|c_j|,(5)$

with the corresponding row from $(b_1\dots b_m)$, and the active set is updated accordingly.

When the active set and the training set are the same, the parameters $\xi$ can be determined by solving the system:

$\xi =\left(E^{\text{qm}}\left({\text{cfg}}_1\right)\dots E^{\text{qm}}\left({\text{cfg}}_m\right)\right)A^{-1}.(6)$

Therefore, the energy of any configuration can be written as:

$E^{\text{mtp}}\left(\text{cfg}\right)={\displaystyle \sum _{j=1}^m}{c}_j{E}^{\text{qm}}\left({\text{cfg}}_j\right).(7)$

This mathematical formulation shows that MTP is extrapolating if $\gamma (\text{cfg})>1$, and interpolating otherwise. Here $E^{\text{qm}}$ corresponds to the quantum mechanical energy of configurations obtained using AIMD calculations. Thus, $\gamma$ effectively serves as the extrapolation grade.

To extend the D-optimality criterion to MTP with nonlinear parameters, energies $E^{\text{mtp}}$ are linearized with respect to the parameters $\bar{\theta }$, assuming these are close to their optimal values. In this scenario, the matrix $\mathbf{B}$ becomes a tall Jacobi matrix:

$\mathbf{B}=\left(\begin{array}{ccc}\hfill \frac{\partial }{\partial {\theta }_1}{E}^{\text{mtp}}\left({\text{cfg}}_1;\bar{\theta }\right)\hfill & \hfill \cdots \hfill & \hfill \frac{\partial }{\partial {\theta }_m}{E}^{\text{mtp}}\left({\text{cfg}}_1;\bar{\theta }\right)\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill \frac{\partial }{\partial {\theta }_1}{E}^{\text{mtp}}\left({\text{cfg}}_K;\bar{\theta }\right)\hfill & \hfill \cdots \hfill & \hfill \frac{\partial }{\partial {\theta }_m}{E}^{\text{mtp}}\left({\text{cfg}}_K;\bar{\theta }\right)\hfill \end{array}\right).(8)$

Each row of this matrix corresponds to a specific configuration in the training set, while the matrix $\mathbf{A}$ has a similar structure. The rest of the active learning algorithm remains the same as in the linear case. Equations 1–8 pertain to the active learning strategy of MTP.

To assess the effectiveness of our active learning strategy, we conducted two types of comparisons. In Comparison 1, we evaluated the performance of active versus passive learning using an identical number of training configurations, thereby isolating the impact of the learning strategy on model accuracy. In Comparison 2, we varied the dataset sizes to determine the number of configurations required by each approach to achieve comparable RMSEs. While working with MTP, we found that attempting to train a single active learning model for both $\gamma$-TiAl and ${\alpha }_2$-Ti₃Al phases yielded unsatisfactory results. Consequently, we opted to perform active learning separately for each phase to better fine-tune the models.

For each phase, we employed a consistent active learning workflow that comprises two main phases: sampling and labeling. During the sampling phase, MD simulations are performed using the initial potential (trained on a limited sample size) to explore the configuration space—the set of possible atomic arrangements and states of the system. Configurations where the model fails to accurately predict energies or forces are identified. In the labeling phase, these selected configurations are accurately annotated using DFT simulations, and the new data is incorporated into the training set, thereby refining the potential.

The initial training set comprised 170 configurations extracted from short NVT simulations of 2.5 ps at 300 K. We initiated the training with a 10.mtp (potential model with level 10) model and divided the active learning process into four steps. Steps 1, 2, and 3 corresponded to Comparison 1, using an equal number of samples for both learning strategies, while Step 4 extended the process for Comparison 2 by incorporating datasets of varying sizes. In step 1, MD simulations were conducted using the NVT ensemble at 300 K across different Nb concentrations, with iterations continuing until no new configurations were added to the training set. In Step 2, the exploration temperature range was expanded to 300 K, 500 K, 700 K, and 900 K, and the iterative process was repeated until no new configurations were chosen. In Step 3, we upgraded the model to 20.mtp, refined the k-point mesh to $2\times 2\times 2$ for DFT labeling, and pruned half of the configurations obtained with a coarser k-point mesh during the previous steps. This procedure follows the methodology outlined in Luo et al. (2023), Novikov et al. (2021), Bock et al. (2024). The iterations continued until no new configurations were selected. Finally, in Step 4, we further upgraded the model to 24.mtp and repeated the active learning iterations across the full temperature spectrum (300 K–900 K), again until the training set stabilized.

For MD exploration, we utilized LAMMPS (Thompson et al., 2022), while VASP (Kresse and Furthmüller, 1996b; Kresse and Furthmüller, 199a) was employed for the ab initio calculations.

2.3 DeePMD and active learning strategy

The theoretical foundations of DeePMD have been discussed extensively in our previous work Chandran et al. (2024b) and elsewhere Zhang et al. (2019). Here, we focus on the active learning aspects. As with MTP, we performed two types of comparisons: in Comparison 1, we evaluated the performance of active versus passive learning using an identical number of training configurations; in Comparison 2, we varied the dataset sizes to determine how many configurations each approach requires to achieve comparable RMSEs. Unlike the MTP approach—where separate active learning processes were conducted for $\gamma$-TiAl and ${\alpha }_2$-Ti₃Al—the DeePMD method incorporated both phases together.

For DeePMD, we began with a larger initial dataset of 40,000 configurations (20,000 for $\gamma$-TiAl and 20,000 for ${\alpha }_2$-Ti₃Al), since deep neural networks typically require more training data than linear regression-based models. This dataset was assembled from snapshots of short AIMD simulations (2.5 ps at 300 K using the NVT ensemble), which provided the initial training data for the active learning procedure.

During the sampling phase, MD simulations were conducted at 300 K, 500 K, 700 K, and 900 K using both the NVT and NPT ensembles for all Nb concentration cases across both phases. For Comparison 1, active learning iterations were performed over 80 cycles. The process began with 300 K NVT simulations, then transitioned to 300 K NPT simulations, with the number of simulation steps increasing as the iterations progressed, and eventually extending to higher temperatures. The production model of potential for Comparison 1 was obtained with a training run of 2$\times$ 10⁶ steps. By the end of these iterations, the RMSEs for energy/atom and force were within acceptable limits. For Comparison 2, the exploration was extended by an additional 20 iterations, focusing on high-temperature configurations until the potential error was further reduced. As with Comparison 1, the production model of potential for Comparison 2 was obtained using a training run of 2$\times$ 10⁶ steps.

To assess the reliability of atomic force predictions, we used the concept of model deviation (Zhang et al., 2019), denoted as $\mathcal{E}$ (Equation 9), which is defined as the maximum standard deviation of the predicted atomic forces across multiple models initialized with different parameters:

$\mathcal{E}=\underset{i}{\max }\sqrt{{‖{\mathbf{f}}_i-{\widehat{\mathbf{f}}}_i‖}^2},{\mathbf{f}}_i=⟨{\widehat{\mathbf{f}}}_i⟩.(9)$

Here, ${\mathbf{f}}_i$ represents the atomic force prediction for atom $i$ from a specific model, and ${\widehat{\mathbf{f}}}_i$ is the average prediction over all models. The notation $⟨\cdot \cdot \cdot ⟩$ represents the ensemble average, which is computed across the set of models in the ensemble. Using the maximum standard deviation rather than an average is crucial because atomic forces are highly sensitive to local variations, making this metric more effective at identifying localized prediction failures that might be overlooked by global energy evaluations (Zhang et al., 2019).

Selected configurations exhibiting high model deviation were subsequently labeled using DFT simulations. These DFT calculations employed projector augmented wave (PAW) potentials (Blöchl, 1994) to accurately model electron–ion interactions, along with the generalized gradient approximation (GGA) (Perdew et al., 1996; Perdew et al., 1997) using the Perdew–Burke–Ernzerhof (PBE) functional. A cutoff energy of 510 eV and a k-spacing of 0.2 ${\mathring{A}}^{-1}$ were used to ensure precision.

The DeePMD model architecture comprised radial and angular embedded-atom neural networks, each with three hidden layers containing 25, 50, and 100 nodes, respectively, to effectively capture complex interatomic interactions. Additionally, the fitting networks were constructed with three hidden layers of 240 nodes each. The training process began with an initial learning rate of 0.001, which was gradually reduced to $3.51\times 10^{-8}$ to allow for fine adjustments and improved predictions. Weighting factors were also carefully calibrated: energy weights were initially set at 0.02 and increased to 1, while force weights started at 1,000 and were reduced to 1, thereby prioritizing force accuracy in the early stages before shifting focus toward energy accuracy.

2.4 Simulated tension tests

To investigate the influence of Nb on the thermomechanical properties of the alloy, we performed uniaxial tension tests using MD models of both the $\gamma$-TiAl and ${\alpha }_2$-Ti₃Al phases at varying Nb concentrations. In these simulations, periodic boundary conditions were imposed in all directions, and uniaxial tension was applied along the Z-axis at a strain rate of $10^9{\text{s}}^{-1}$. Prior to loading, each system was equilibrated at 300 K using an NVT ensemble, after which the uniaxial stress was applied along the Z-direction.

3 Results and discussion

3.1 Error analysis

This section presents the error analysis for the machine learning potentials developed for $\gamma$-TiAl and ${\alpha }_2$-Ti₃Al, comparing their performance against passive learning approaches.

3.1.1 MTP

Figures 2a–h presents the detailed error analysis for the active learning performed using MTP. Panels a, b, c, and d show the RMSEs for energy/atom and force for Comparison 1 and Comparison 2 in the $\gamma$-TiAl phase, while panels e, f, g, and h display the corresponding RMSEs for the ${\alpha }_2$-Ti₃Al phase using MTP. The learning curves for MTP in both phases are shown in Supplementary Figure S1 in the supplementary section.

Figure 2

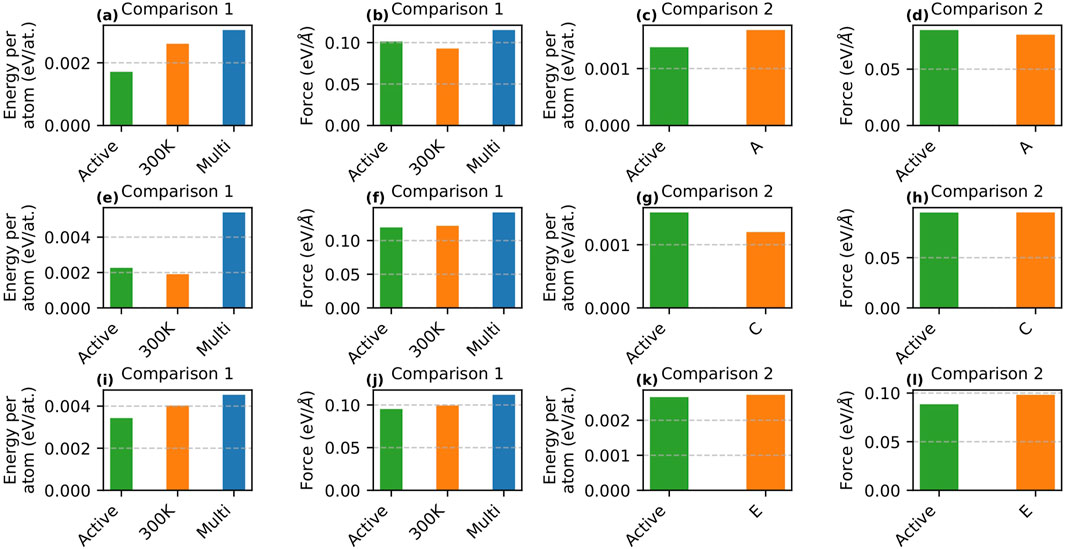
Figure 2. Comparison of RMSE energy/atom and force on the testing dataset during active learning using MTP and DeePMD. Panels (a–d) show MTP results for the $\gamma$-TiAl phase, and panels (e–h) for the ${\alpha }_2$-Ti₃Al phase; panels (i–l) display DeePMD results. “Active” refers to the active learning approach. In Comparison 1, the active learning potential is evaluated against two passive learning potentials trained with the same number of samples: one at 300 K (labeled 300 K) and one with multi-temperature data (300 K, 500 K, 700 K, and 900 K, labeled Multi). For Comparison 1, MTP used 3,094 samples for $\gamma$-TiAl and 1,665 for ${\alpha }_2$-Ti₃Al, while DeePMD used 57,180 samples. Comparison 2 examines the effect of dataset size by comparing the active learning potential with passive learning potentials trained on Dataset-A and Dataset-C (20,000 samples) for MTP, and on Dataset-E (127,212 samples) for DeePMD. For Comparison 2, active learning for MTP used 3,322 samples for $\gamma$-TiAl and 2,602 for ${\alpha }_2$-Ti₃Al, while DeePMD required 61,657 samples.

For the $\gamma$-TiAl phase, we began with a simple 10.mtp model and performed MD sampling up to 15 iterations. During iterations 1–5, only NVT simulations at 300 K were employed. From iteration 6, NVT simulations covering a temperature range of 300–900 K were included. At iteration 15, no additional configurations were added to the training set. Starting from iteration 16, we transitioned to a more complex 20.mtp model and continued exploring configuration space with NVT simulations at various temperature ranges. A finer k-point mesh of $2\times 2\times 2$ was used for DFT labeling. Iterations up to 33 were considered for Comparison 1. Subsequently, from iteration 34, we switched to a 24.mtp model (Comparison 2) and continued until iteration 36, where no new configurations were selected. The transition to 20.mtp and the finer k-point mesh led to a noticeable drop in RMSE for energy and force values of $\gamma$-TiAl, as shown in Supplementary Figure S1 in the supplementary section. By iteration 33, the training set contained 3,094 configurations, which increased to 3,322 configurations by iteration 36.

To evaluate the effectiveness of the active learning strategy, we performed passive learning for Comparison 1 using 3,094 configurations under two scenarios. In the first scenario, only 300 K configurations were included in the training set to replicate the initial conditions of active learning. In the second scenario, configurations spanning a range of temperatures (300 K–900 K) were used. The RMSEs for energy/atom and force for all three cases (active learning, passive learning with 300 K configurations, and passive learning with multi-temperature configurations) are shown in Figures 2a,b. The results indicate that active learning achieved the lowest RMSE for energy/atom ($1.71\times 10^{-3}$ eV/atom), followed by passive learning with 300 K configurations ($2.61\times 10^{-3}$ eV/atom) and passive learning with multi-temperature configurations ($3.04\times 10^{-3}$ eV/atom). In contrast, the RMSE for force from active learning ($101.35\times 10^{-3}$ eV/Å) was slightly higher than that from passive learning with 300 K configurations ($92.83\times 10^{-3}$ eV/Å), but lower than that from passive learning with multi-temperature configurations ($115.18\times 10^{-3}$ eV/Å). The higher RMSE for passive learning with multi-temperature configurations is attributed to thermodynamic noise from high-temperature frames.

For Comparison 2, we examined whether a passive learning model trained on a larger dataset could match or exceed the predictive accuracy (in terms of RMSE) of active learning. At this stage, the active learning model was trained using 3,322 samples. Initially, passive learning was performed using Dataset-A (20,000 samples). Although the errors obtained from Dataset-A were comparable to those from active learning, we further investigated whether increasing the sample size with Dataset-B (80,000 samples) could reduce the error. Figures 2c,d compare the performance of active learning and passive learning using Dataset-A, while the RMSE values for Dataset-B are provided in Supplementary Table S1 in the supplementary section. Note that the passive learning models for Comparison 2 utilized a 24.mtp model. As shown in Figures 2c,d, active learning produced a lower RMSE for energy/atom ($1.37\times 10^{-3}$ eV/atom) than passive learning with Dataset-A ($1.67\times 10^{-3}$ eV/atom). However, the force RMSE from active learning ($84.72\times 10^{-3}$ eV/Å) was slightly higher than that from passive learning ($80.59\times 10^{-3}$ eV/Å). Furthermore, passive learning with Dataset-B resulted in errors similar to those of both active learning and passive learning with Dataset-A, yielding RMSE values of $1.32\times 10^{-3}$ eV/atom for energy/atom and $80.14\times 10^{-3}$ eV/Å for force, indicating that expanding the sample size to 80,000 did not significantly reduce the error values.

For the ${\alpha }_2$-Ti₃Al phase, a similar active learning strategy as that of $\gamma$-TiAl was applied. The learning curves for Comparison 1 and Comparison 2 are shown in Supplementary Figure S1 in the supplementary section. Initial training involved 300 K samples starting with a 10.mtp model up to iteration 18. From iteration 19 onward, configurations from a broader temperature range (300 K–900 K) were included, continuing until iteration 48 when no new configurations were selected. At this point, we transitioned to a 20.mtp model, applied a finer k-point mesh $(2\times 2\times 2)$, and resumed exploration. A significant drop in RMSE for energy/atom was observed, although the decrease in RMSE for force was less pronounced. At iteration 61, the training set contained 1,665 configurations, which were used for Comparison 1. From iteration 62 onward, we adopted a 24.mtp model and concluded at iteration 65 with 2,602 configurations in the training set, used for Comparison 2.

For Comparison 1, we compared active learning with passive learning using 1,665 configurations. The passive learning scenarios included both 300 K-only and multi-temperature samples. As shown in Figures 2e,f, active learning yielded a slightly higher RMSE for energy/atom ($2.26\times 10^{-3}$ eV/atom) than passive learning with 300 K samples ($1.91\times 10^{-3}$ eV/atom), yet a markedly lower RMSE compared to multi-temperature samples ($5.39\times 10^{-3}$ eV/atom). Similarly, active learning produced a lower RMSE for force ($119.56\times 10^{-3}$ eV/Å) than both passive learning with 300 K samples ($121.90\times 10^{-3}$ eV/Å) and multi-temperature samples ($141.81\times 10^{-3}$ eV/Å). The higher RMSE observed for passive learning with multi-temperature configurations is beacuse of the thermodynamic noise from high-temperature frames.

For Comparison 2, passive learning was conducted using Dataset-C (comprising 20,000 samples), while active learning was performed with 2,602 samples. Similar to the $\gamma$-TiAl case, although Dataset-C produced errors comparable to those obtained from active learning, Dataset-D (comprising 80,000 samples) was also employed to assess how the errors change with an increased sample size. The RMSE comparisons between active learning and passive learning using Dataset-C are presented in Figures 2g,h, while the errors from Dataset-D are tabulated in Supplementary Table S1 in the supplementary section. As illustrated in Figures 2g,h, active learning resulted in a slightly higher RMSE for energy/atom ($1.51\times 10^{-3}$ eV/atom) compared to passive learning using Dataset-C ($1.20\times 10^{-3}$ eV/atom). However, for force, active learning ($94.94\times 10^{-3}$ eV/Å) achieved a slightly lower RMSE than passive learning using Dataset-C ($95.06\times 10^{-3}$ eV/Å). Furthermore, Dataset-D produced errors similar to those of both active learning and passive learning with Dataset-C (energy/atom: $1.23\times 10^{-3}$ eV/atom; force: $94.44\times 10^{-3}$ eV/Å), indicating that increasing the sample size to 80,000 did not substantially improve the error values.

3.1.2 DeePMD

Here, we explore the comparison between active learning of DeePMD and passive learning using Comparison 1 and Comparison 2. The learning curves are presented in Supplementary Figure S2 in the supplementary section. Initially, we used 20,000 samples each from the $\gamma$-TiAl and ${\alpha }_2$-Ti₃Al phases. Exploration began with NVT simulations for both phases at 300 K for 10 iterations, followed by NPT simulations at 300 K for another 10 iterations. Subsequently, higher temperature simulations were introduced, combining NVT and NPT simulations for MD exploration every 20 iterations. By the end of 80 iterations, the potential exhibited sufficiently low RMSE for energy/atom and force, was selected for Comparison 1. At this stage, the training data contained 57,180 samples. We continued with 20 more iterations using higher-temperature NVT and NPT simulations to ensure the potentials were adequately trained on high-temperature samples until the error values of the potential becomes significantly lower than that in Comparison 1. The training data then contained 61,657 samples.

Figures 2i–l show the RMSEs for energy/atom and force for active learning potentials and their passive learning counterparts for Comparison 1 and Comparison 2, respectively. Similar to the case of MTP, for Comparison 1, we performed passive learning with the same number of samples as active learning (57,180 samples). Two scenarios were considered: one with only 300 K samples (matching the starting conditions of active learning) and the other with multi-temperature samples. The RMSE values for the active learning potential (RMSE energy/atom = $3.43\times 10^{-3}$ eV/atom, RMSE force = $95.27\times 10^{-3}$ eV/Å) were lower than those for both passive learning cases (300 K samples: RMSE energy/atom = $4.03\times 10^{-3}$ eV/atom, RMSE force = $99.41\times 10^{-3}$ eV/Å; multi-temperature samples: RMSE energy/atom = $4.54\times 10^{-3}$ eV/atom, RMSE force = $111.89\times 10^{-3}$ eV/Å. Similar to the MTP case, the increased RMSE observed in passive learning with multi-temperature configurations can be due to thermodynamic noise arising from high-temperature frames.

For Comparison 2, we conducted passive learning using Dataset-E, which comprises 127,212 samples. As in the MTP approach, although Dataset-E produced errors similar to those from active learning, we increased the sample size to create Dataset-F (333,340 samples) to examine whether a larger dataset would yield further error reduction. Note that active learning was performed using 61,657 samples. The RMSE comparisons are presented in Figures 2k,l, while the errors for Dataset-F are provided in Supplementary Table S1 in the supplementary section. The RMSE energy/atom values for active learning ($2.66\times 10^{-3}$ eV/atom) and passive learning with Dataset-E ($2.73\times 10^{-3}$ eV/atom) are nearly identical, whereas the RMSE force for active learning ($88.53\times 10^{-3}$ eV/Å) is slightly lower than that for passive learning with Dataset-E ($98.22\times 10^{-3}$ eV/Å). In contrast, passive learning with Dataset-F clearly outperforms both active learning and passive learning with Dataset-E, achieving an RMSE energy/atom of $1.07\times 10^{-3}$ eV/atom and an RMSE force of $93.14\times 10^{-3}$ eV/Å. In the case of DeePMD, further increasing the sample size results in an additional decrease in the error.

3.2 MD results

In this section, we summarize the results of MD simulations performed using the potentials derived from both active and passive learning. In Section 3.1, we assessed the RMSEs of the active and passive learning potentials under two scenarios—Comparison 1 and Comparison 2. Here, we present the MD simulation results obtained with these potentials to evaluate their effectiveness in predicting the fundamental material and thermo-mechanical properties of the two phases.

For Comparison 1, we utilized the passive learning potential trained on multi-temperature samples, which provides a fair comparison with active learning when exploring high-temperature properties. For Comparison 2, we selected the active learning cases using Dataset-A ($\gamma$-TiAl) and Dataset-C (${\alpha }_2$-Ti₃Al) in MTP, as well as Dataset-E in DeePMD, all of which achieved performance comparable to that of active learning in terms of RMSE for energy/atom and force.

3.2.1 Energy volume curve and elastic constants

In this section, we evaluate the energy-volume (EV) curves obtained via the Murnaghan fit to compare the performance of passive and active learning. Figures 3, 4 display the EV curves for Comparison 1 and Comparison 2, respectively, alongside the corresponding DFT curves for MTP and DeePMD.

Figure 3

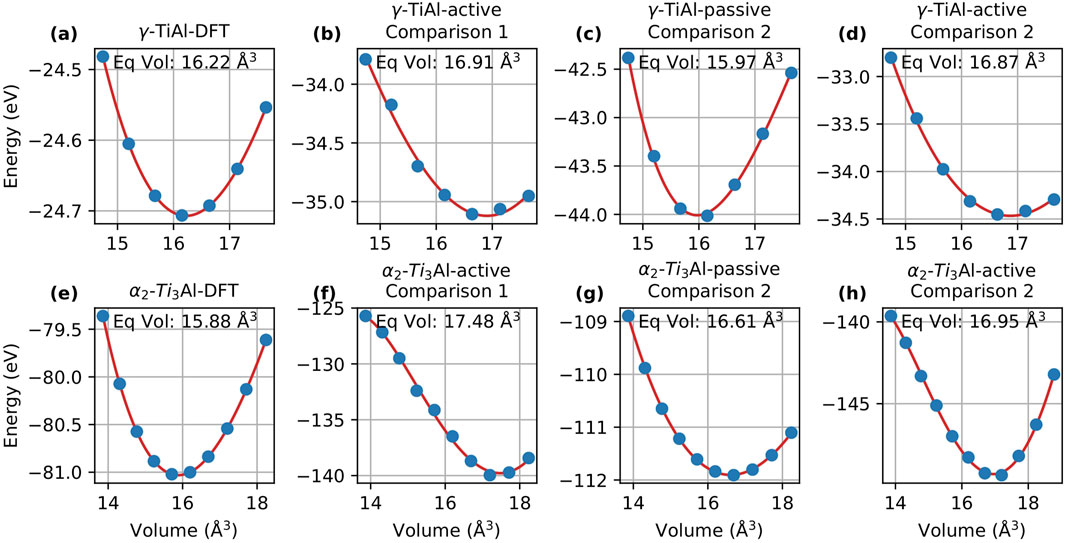
Figure 3. Energy-volume curves for $\gamma$-TiAl (a–d) and ${\alpha }_2$-Ti₃Al (e–h) obtained using DFT, an active learning potential, and a passive learning potential developed with MTP. The curves correspond to Comparison 1 and Comparison 2. In Comparison 1, both potentials were trained with the same number of samples to enable a direct performance comparison, whereas in Comparison 2, different training dataset sizes were employed to achieve comparable error levels.

Figure 4

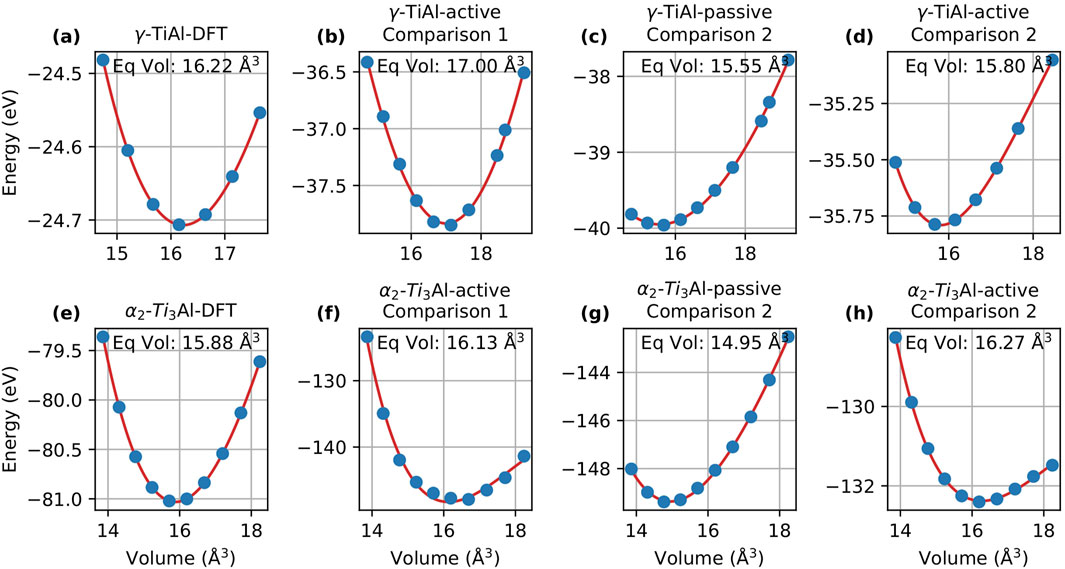
Figure 4. Energy-volume curves for $\gamma$-TiAl (a–d) and ${\alpha }_2$-Ti₃Al (e–h) obtained using DFT, an active learning potential, and a passive learning potential developed with DeePMD. The curves correspond to Comparison 1 and Comparison 2. In Comparison 1, both potentials were trained with the same number of samples to enable a direct performance comparison, whereas in Comparison 2, different training dataset sizes were employed to achieve comparable error levels.

Here we focus on MTP. For Comparison 1, the passive learning potential failed to find a minimum volume, and therefore, the results for passive learning are not included here. For $\gamma$-TiAl, the equilibrium volume predicted by the active learning potential was 16.91 $\mathring{\mathrm{A}}$³, compared to 16.22 $\mathring{\mathrm{A}}$³ obtained from DFT. The equilibrium lattice parameters were $a=3.99\mathring{\mathrm{A}}$ and $c=4.18\mathring{\mathrm{A}}$ for the active learning potential, while the DFT values were $a=3.95\mathring{\mathrm{A}}$ and $c=4.14\mathring{\mathrm{A}}$. For ${\alpha }_2$-Ti₃Al, the equilibrium volume predicted by the active learning potential (17.48 $\mathring{\mathrm{A}}$³) deviated more from the DFT value (15.88 $\mathring{\mathrm{A}}$³). The predicted lattice parameters were $a=5.79\mathring{\mathrm{A}}$ and $c=4.73\mathring{\mathrm{A}}$, whereas DFT values were $a=5.62\mathring{\mathrm{A}}$ and $c=4.59\mathring{\mathrm{A}}$.

For Comparison 2, the equilibrium volume for $\gamma$-TiAl for active learning, though over-predicted, remained the same as in Comparison 1, while the passive learning potential predicted 15.97 $\mathring{\mathrm{A}}$³, which under-predicted the DFT value. For ${\alpha }_2$-Ti₃Al, the equilibrium volume predicted by active learning was 16.95 $\mathring{\mathrm{A}}$³, while passive learning predicted 16.61 $\mathring{\mathrm{A}}$³, which was closer to the DFT value. The equilibrium lattice parameters predicted by active learning for $\gamma$-TiAl were $a=3.99\mathring{\mathrm{A}}$ and $c=4.18\mathring{\mathrm{A}}$, while passive learning predicted $a=3.95\mathring{\mathrm{A}}$ and $c=4.14\mathring{\mathrm{A}}$. For ${\alpha }_2$-Ti₃Al, the predicted lattice parameters were $a=5.79\mathring{\mathrm{A}}$ and $c=4.73\mathring{\mathrm{A}}$ for active learning, and $a=5.74\mathring{\mathrm{A}}$ and $c=4.68\mathring{\mathrm{A}}$ for passive learning.

When analyzing DeePMD, Figure 4 compares the EV curves for active and passive learning for both Comparison 1 and Comparison 2. Similar to the case of $\gamma$-TiAl the passive learning potential failed to accurately find a minimum volume. For $\gamma$-TiAl, the equilibrium volume predicted by the active learning potential was 17 $\mathring{\mathrm{A}}$³, and the equilibrium lattice parameters were $a=4.03\mathring{\mathrm{A}}$ and $c=4.22\mathring{\mathrm{A}}$. These values are farther from the DFT predictions compared to the MTP case. For ${\alpha }_2$-Ti₃Al, the equilibrium volume predicted by active learning (16.13 $\mathring{\mathrm{A}}$³) was closer to the DFT value (15.88 $\mathring{\mathrm{A}}$³) than in the MTP case, with lattice parameters $a=5.68\mathring{\mathrm{A}}$ and $c=4.63\mathring{\mathrm{A}}$.

In Comparison 2, the equilibrium volume predicted for $\gamma$-TiAl by active learning was 15.80 $\mathring{\mathrm{A}}$³, and that by passive learning was 15.55 $\mathring{\mathrm{A}}$³. Active learning was closer to the DFT prediction. The equilibrium lattice parameters for $\gamma$-TiAl predicted by active learning were $a=3.91\mathring{\mathrm{A}}$ and $c=4.10\mathring{\mathrm{A}}$, matching passive learning predictions. For ${\alpha }_2$-Ti₃Al, the equilibrium volume predicted by active learning was 16.27 $\mathring{\mathrm{A}}$³, closer to DFT than the passive learning value of 14.95 $\mathring{\mathrm{A}}$³. The lattice parameters predicted by active learning were $a=5.68\mathring{\mathrm{A}}$ and $c=4.63\mathring{\mathrm{A}}$, while those predicted by passive learning were $a=5.51\mathring{\mathrm{A}}$ and $c=4.49\mathring{\mathrm{A}}$, which are closer to DFT values than the active learning predictions.

Along with evaluating equilibrium volume and lattice parameters, a comparative analysis of elastic constants was performed for both $\gamma$-TiAl and ${\alpha }_2$-Ti₃Al using DFT, active learning, and passive learning potentials at 300 K. These analyses were carried out with both MTP and DeePMD (refer Figure 5) models. For reference the additional plots showing the absolute differences between the elastic constants predicted by the passive and active learning potentials with respect to those predicted by DFT are included in Supplementary Figure S3 in the supplementary section.

Figure 5

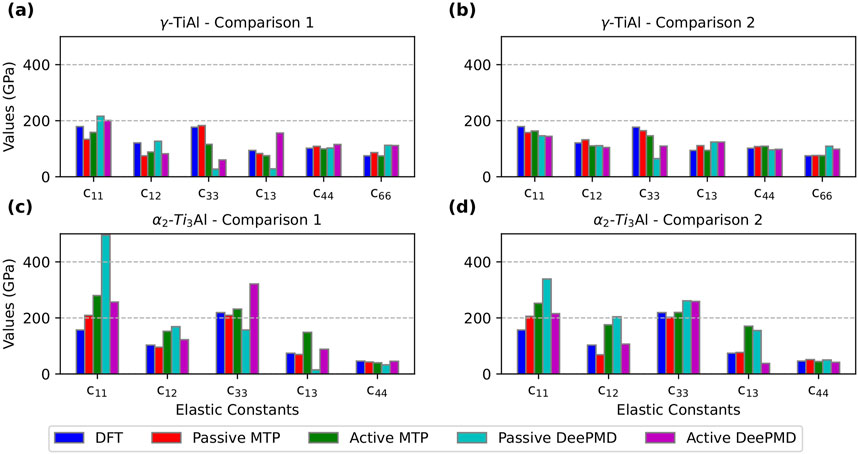
Figure 5. Comparison of elastic constants calculated using DFT, passive learning, and active learning potentials developed with MTP and DeePMD. (a,b) correspond to $\gamma$-TiAl, while (c,d) correspond to ${\alpha }_2$-Ti₃Al. In Comparison 1, both active and passive learning potentials were trained with the same number of samples to enable a direct performance evaluation. In Comparison 2, the training dataset sizes were adjusted to achieve comparable error levels. Note that the unit for elastic constants is GigaPascal (GPa) and they are computed at 300 K.

For MTP, in the case of $\gamma$-TiAl, active learning outperformed passive learning in predicting higher elastic constants such as $C_{11}$, $C_{12}$ and and $C_{66}$, with values closer to those from DFT in both Comparison 1 (where both learning methods were trained on the same number of samples) and Comparison 2 (where different dataset sizes were used to achieve comparable errors). However, passive learning showed better agreement for constants like $C_{33}$ especially in Comparison 1. In Comparison 2, while both methods improved their alignment with DFT (see Supplementary Figure S3 in the supplementary section), active learning provided more balanced performance across all constants, even though passive learning occasionally achieved closer predictions for $C_{33}$. For ${\alpha }_2$-Ti₃Al, active learning generally predicted elastic constants further from DFT values compared to passive learning, as highlighted in Supplementary Figures S3c, d in the supplementary section. Nevertheless, active learning and passive learning results aligned with DFT in the case of $C_{33}$ and $C_{44}$.

For DeePMD, in the case of $\gamma$-TiAl, passive learning exhibited significant deviations from DFT in Comparison 1—most notably, $C_{11}$ was overpredicted and active learning struggled with elastic constants such as $C_{13}$ and $C_{33}$. In Comparison 2, both learning approaches showed improved agreement with DFT; active learning was more consistent for $C_{33}$ and $C_{13}$. For ${\alpha }_2$-Ti₃Al, active learning outperformed passive learning in Comparison 1 for elastic constants such as $C_{12}$ and $C_{13}$, whereas passive learning overpredicted higher constants like $C_{11}$. Moreover, compared to the MTP results, the active learning potentials developed with DeePMD provided predictions for ${\alpha }_2$-Ti₃Al that were closer to DFT (see Supplementary Figure S3 in supplementary section). In Comparison 2, both active and passive learning approaches exhibited improved accuracy. Active learning achieved superior predictions for $C_{12}$, while for $C_{44}$ both methods demonstrated marginally better agreement.

Overall, active learning consistently demonstrated robust predictive capability for fundamental material properties—including lattice parameters, equilibrium volume, and elastic constants—compared to passive learning. However, passive learning exhibited greater variability and a tendency to overpredict, particularly in Comparison 1. It is also noteworthy that active learning produced some outliers, especially for the MTP active learning potential in ${\alpha }_2$-Ti₃Al elastic constants and for certain equilibrium volume and lattice parameter predictions. This may be attributed to the fact that these basic properties were not the primary focus during the active learning sample selection process, leading to a bias towards higher temperature configurations that deviate from the base state, thus affecting the overall prediction accuracy.

3.2.2 Finite temperature results

To evaluate the finite-temperature properties and compare the performance of active and passive learning for MTP and DeePMD, we computed the radial distribution functions (RDFs) and compared them with AIMD results. The RDFs were evaluated for both $\gamma$-TiAl and ${\alpha }_2$-Ti₃Al using configurations that were not included in the training set. The RDF comparisons for $\gamma$-TiAl obtained with MTP and DeePMD (Comparison 1) are shown in Figure 6, while Figure 7 presents the corresponding comparisons for ${\alpha }_2$-Ti₃Al. Similarly, the RDF comparisons for Comparison 2 are provided in the Supplementary Material (see Supplementary Figure S4; Supplementary Figure S5).

Figure 6

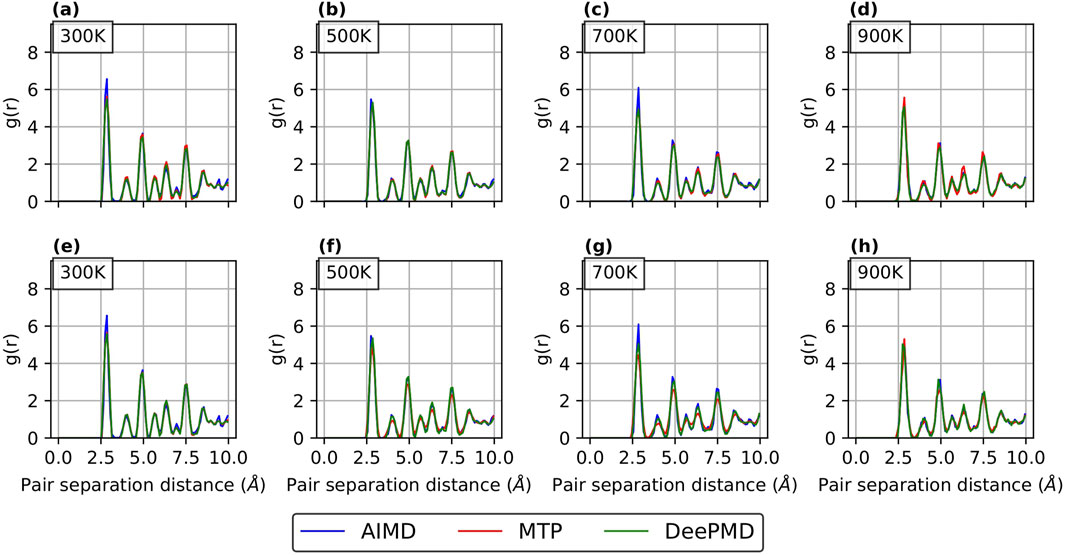
Figure 6. RDF curves for $\gamma$-TiAl with a 5.6 at.% Nb configuration obtained from passive and active learning potentials, compared with AIMD results at 300 K, 500 K, 700 K, and 900 K for both MTP and DeePMD. The top row (a–d) shows the AIMD and active learning potential results, while the bottom row (e–h) presents the curves from the passive learning potential. These results correspond to Comparison 1, where both active and passive learning potentials were trained using the same number of samples, allowing for a direct evaluation of their relative performance.

Figure 7

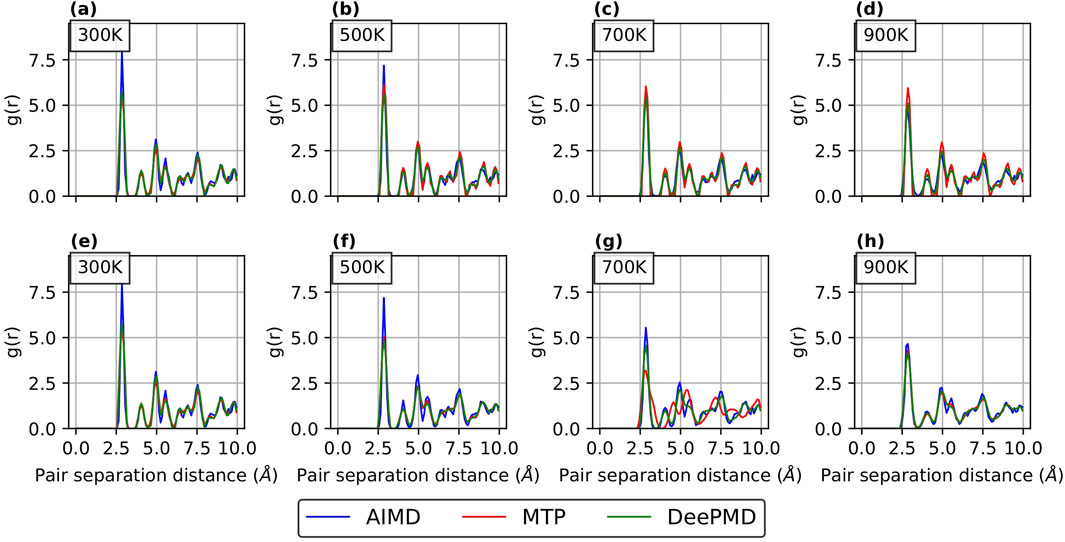
Figure 7. RDF curves for ${\alpha }_2$-Ti₃Al with a 2.3 at.% Nb configuration obtained from passive and active learning potentials, compared with AIMD results at 300 K, 500 K, 700 K, and 900 K for both MTP and DeePMD. The top row (a–d) shows the AIMD and active learning potential results, while the bottom row (e–h) presents the curves from the passive learning potential. These results correspond to Comparison 1, where both active and passive learning potentials were trained using the same number of samples, allowing for a direct evaluation of their relative performance.

RDFs provide a quantitative measure of how accurately a potential predicts the atomic arrangement in a material. In this study, RDFs were computed over a range of temperatures to evaluate the performance of the potentials from low to high temperatures. As shown in Figure 6 for $\gamma$-TiAl, the RDFs predicted by both passive and active learning using MTP and DeePMD are nearly identical, which is expected since $\gamma$-TiAl is relatively straightforward for the potentials to model. In contrast, Figure 7 indicates that ${\alpha }_2$-Ti₃Al poses a greater challenge for accurate prediction, particularly for passively trained potentials. This is most evident in the noticeable discrepancies that appear at 700 K (Figure 7g). This intermediate temperature allows the system to access complex, high-energy atomic configurations that may be statistically underrepresented in a randomly sampled passive learning dataset. The failure of the passively trained MTP potential to maintain the correct structure suggests it is extrapolating poorly into these unlearned regions. In contrast, the comparatively good performance of the active learning potentials (Figure 7c) demonstrates their ability to identify and specifically learn from these challenging configurations, resulting in a more stable and physically accurate model across the wider temperature range.

For Comparison 2 (refer Supplementary Figure S4; Supplementary Figure S5 in the supplementary section), the RDF curves show a good match with AIMD results for both passive and active learning. This is in line with our expectations, as our primary aim in Comparison 2 was to employ different sample sizes for active and passive learning while achieving comparable errors.

3.2.3 Tension tests and generalized stacking fault energy

In this study, we evaluated the performance of MTP and DeePMD potentials in capturing the thermo-mechanical behavior of our target phases ($\gamma$-TiAl and ${\alpha }_2$-Ti₃Al). To this end, we simulated uniaxial tension tests on selected samples at a strain rate of $10^9{\text{s}}^{-1}$. The detailed method is already discussed in Section 2.4. The stress-strain curves obtained via active learning for both the $\gamma$-TiAl and ${\alpha }_2$-Ti₃Al phases for Comparison 1 and Comparison 2 are illustrated in Figures 8, 9. Our analysis focused primarily on ultimate tensile strength (UTS) to evaluate the accuracy of the mechanical property predictions. For the MTP potentials, a consistent decrease in UTS with increasing Nb concentration was observed in both Comparison 1 and Comparison 2, a trend evident for both $\gamma$-TiAl and ${\alpha }_2$-Ti₃Al phases using MTP and DeePMD potentials. Notably, under active learning in Comparison 1 for MTP, the UTS values for $\gamma$-TiAl at 3.7 at.% Nb, 5.6 at.% Nb, and 7.4 at.% Nb were very similar (Figure 8d), and a similar pattern was observed in Comparison 2 (Figure 8f) for 1.9 at.% Nb, 3.7 at.% Nb, and 5.6 at.% Nb. Overall, a significant reduction in UTS with increasing Nb concentration was found for both phases, and this trend was consistent across active and passive learning cases. These observations align with our earlier findings Chandran et al. (2024a) and with results reported in other studies Dumitraschkewitz et al. (2017), Lu et al. (2023), Qi et al. (2023). The stress-strain curves of DeePMD (Figure 9) reveal that the ${\alpha }_2$-Ti₃Al phase at high Nb concentrations is particularly challenging to model accurately. The unphysical fluctuations seen in Figure 9a and c are the most severe for the highest Nb content. This suggests that the combination of the complex D0₁₉ lattice and the significant local distortions introduced by a high concentration of Nb atoms creates unique, high-energy configurations under strain. The relative stability of the $\gamma$-TiAl phase across all concentrations underscores the difficulty of modeling the ${\alpha }_2$-Ti₃Al phase with high Nb concentration.

Figure 8

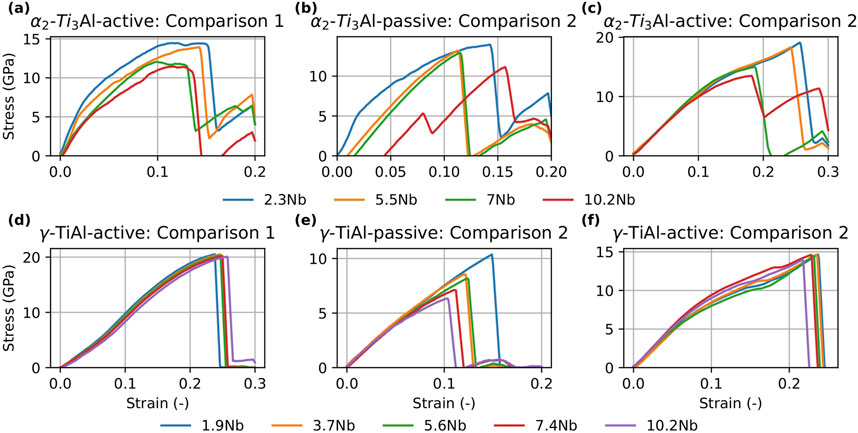
Figure 8. Stress-strain curves for ${\alpha }_2$-${\mathrm{T}\mathrm{i}}_3$Al (a–c) and $\gamma$-TiAl (d–f) at varying Nb concentrations, obtained using active and passive learning potentials developed with MTP. All simulations were conducted at a strain rate of $10^9{\text{s}}^{-1}$. Results are shown for both Comparison 1 and Comparison 2. In Comparison 1, both potentials were trained with the same number of samples to enable a direct performance evaluation, while in Comparison 2 the training dataset sizes were adjusted to achieve comparable error levels.

Figure 9

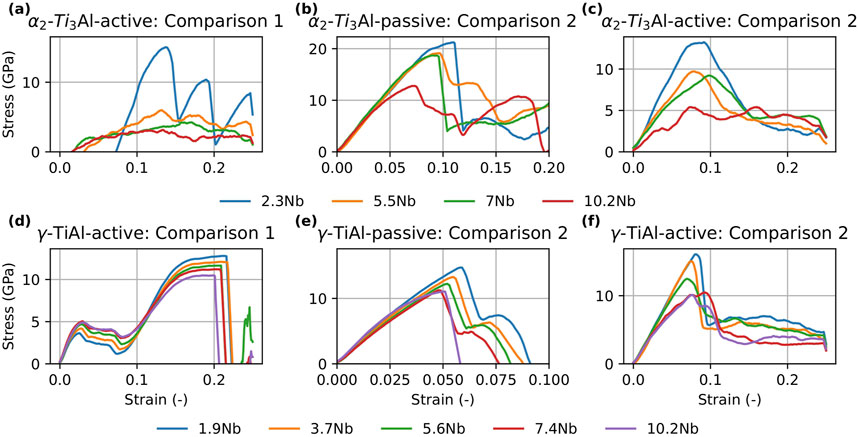
Figure 9. Stress-strain curves for ${\alpha }_2$-${\mathrm{T}\mathrm{i}}_3$Al (a–c) and $\gamma$-TiAl (d–f) at varying Nb concentrations, obtained using active and passive learning potentials developed with DeePMD. All simulations were conducted at a strain rate of $10^9{\text{s}}^{-1}$. Results are shown for both Comparison 1 and Comparison 2. In Comparison 1, both potentials were trained with the same number of samples to enable a direct performance evaluation, while in Comparison 2 the training dataset sizes were adjusted to achieve comparable error levels.

In addition to the tension tests, we computed the generalized stacking fault energy (GSFE) for both $\gamma$-TiAl and ${\alpha }_2$-Ti₃Al using active learning potentials. For the MTP approach, the active learning GSFE results were compared with those reported in Qi et al. (2023), where MTP was employed to calculate the stacking fault energies for these phases, and were further benchmarked against the corresponding DFT values from the same study. In the case of DeePMD, due to the absence of previous GSFE studies using this method, our results were compared solely with the DFT values reported in Qi et al. (2023).

For $\gamma$-TiAl, dislocation glide occurs on the {111} close-packed planes. Here, the complex stacking fault (CSF) is associated with ordinary $⟨\bar{1}10⟩/2$ dislocations, while the antiphase boundary (APB) is linked to $⟨11\bar{2}⟩/2$ super-dislocations. (Note that we did not compute the intrinsic stacking fault (SISF) for $\gamma$-TiAl.) The GSFE values obtained from active learning using both MTP and DeePMD, at two stages (Comparison 1 and Comparison 2), are provided in Tables 1, 2. It is evident that the energy values from Comparison 2 are closer to the reference and DFT values. This improvement in accuracy can be attributed to the lower energy/atom and force RMSEs of the active learning potential in Comparison 2 versus Comparison 1, as shown in Figure 2. Moreover, an increase in Nb concentration leads to a noticeable reduction in the energies for both CSF and APB, consistent with the findings of Dumitraschkewitz et al. (2017). Generally, a higher GSFE indicates greater resistance to dislocation motion and reduced dislocation mobility, which directly enhances the strengthening behavior in nanomaterials. Conversely, a lower GSFE implies increased dislocation mobility and improved ductility.

Table 1

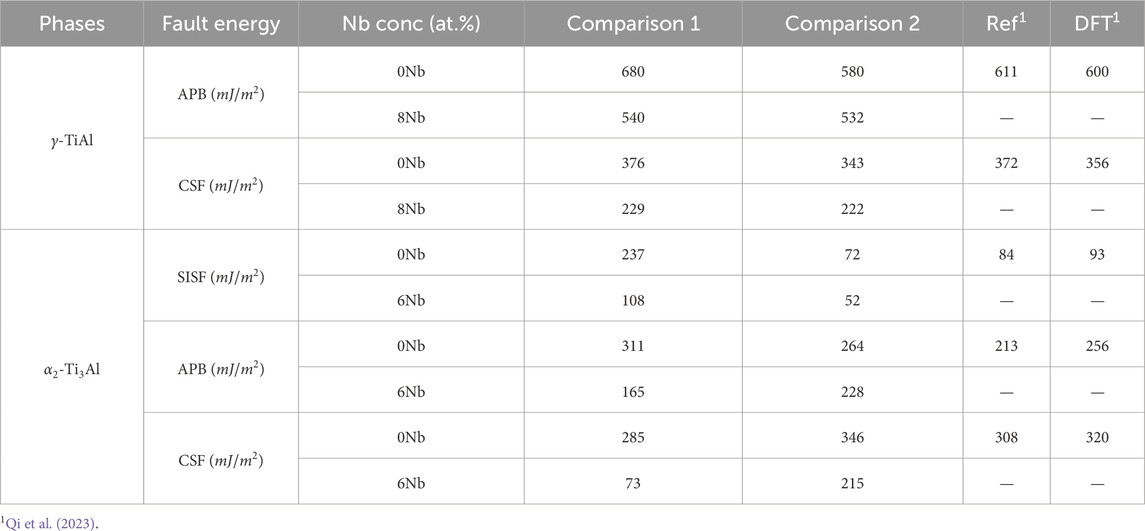
Table 1. Comparison of generalized stacking fault energy values for $\gamma$-TiAl and ${\alpha }_2$-${\mathrm{T}\mathrm{i}}_3$Al using MTP. The figure compares two scenarios: (i) Comparison 1, where both active and passive learning potentials were trained on the same number of samples for a direct performance evaluation, and (ii) Comparison 2, where training dataset sizes were varied to achieve comparable error levels.

Table 2

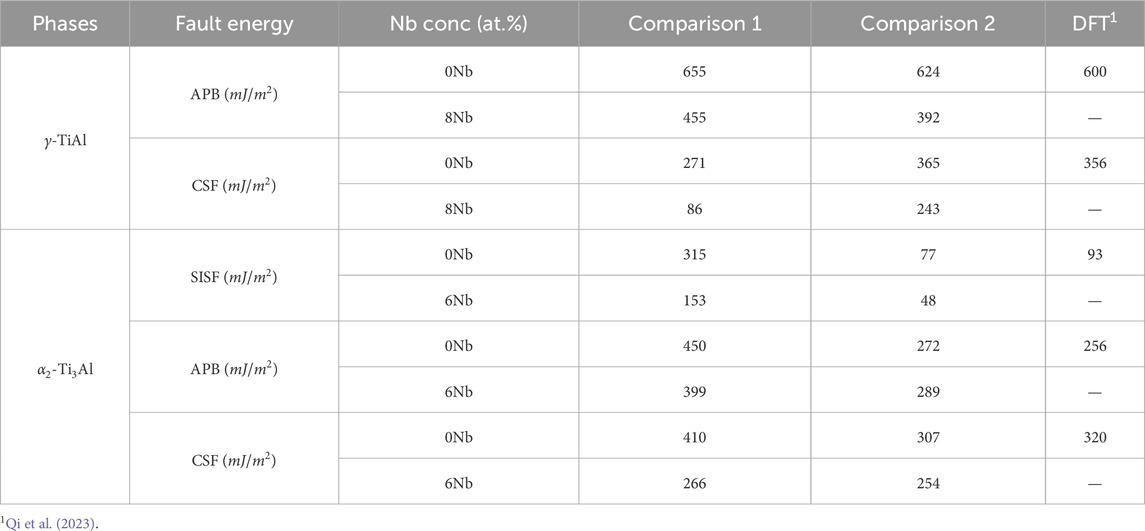
Table 2. Comparison of generalized stacking fault energy values for $\gamma$-TiAl and ${\alpha }_2$-${\mathrm{T}\mathrm{i}}_3$Al using DeePMD. The figure compares two scenarios: (i) Comparison 1, where both active and passive learning potentials were trained on the same number of samples for a direct performance evaluation, and (ii) Comparison 2, where training dataset sizes were varied to achieve comparable error levels.

Turning to the ${\alpha }_2$-Ti₃Al phase, which is characterized by hexagonal symmetry and multiple slip systems, our analysis primarily focused on the fundamental {0001} plane. Here we computed CSF, APB and SISF. As shown in Tables 1, 2, the GSFE values obtained from Comparison 2 for this phase also align more closely with the DFT benchmarks. Additionally, similar to $\gamma$-TiAl, an increase in Nb concentration results in a decrease in stacking fault energies, indicating that Nb alloying enhances the ductility of the ${\alpha }_2$-Ti₃Al phase.

In summary, the combined results of the tension tests and GSFE calculations suggest that Nb addition generally decreases the strength of both phases while simultaneously increasing ductility. These findings are in agreement with our previous work Chandran et al. (2024a), which demonstrated that Nb alloying enhances dislocation density and ductility at the cost of reduced strength.

4 Conclusion

In our study, we performed a comprehensive evaluation of passive and active learning strategies for developing interatomic potentials using both MTP and DeePMD methods. The analysis was structured into two stages. In Comparison 1, both approaches were trained on the same number of samples, allowing for a direct assessment of their performance on a fixed dataset. In Comparison 2, the number of training configurations was varied to determine how many samples are required to achieve comparable RMSE values for energy/atom and force. Under Comparison 1, the active learning potential outperformed the passive learning potential. In Comparison 2, where the primary goal was to achieve comparable accuracies for passive and active learning potentials, the active learning potentials required significantly fewer samples. Specifically, for MTP, the active learning potential used only 3,322 samples for $\gamma$-TiAl and 2,602 samples for ${\alpha }_2$-Ti₃Al, compared to 20,000 samples for passive learning in both phases. Similarly, for DeePMD, the active learning potential was trained on 61,657 samples, whereas the passive learning approach required 127,212 samples.

The MTP approach required separate potentials for $\gamma$-TiAl and ${\alpha }_2$-Ti₃Al, while DeePMD enabled the training of a single potential for both phases. Both methods commenced with relatively small datasets—170 samples for MTP and 40,000 samples for DeePMD—generated solely at 300 K, which substantially reduced the need for computationally expensive AIMD simulations. In contrast, our passive learning work relied on 180 AIMD simulations of 10 ps each (Chandran et al., 2024b), whereas the active learning approach required only 32 AIMD simulations of 2.5 ps duration.

The predictive accuracy of the active learning potentials was further verified by comparing key material properties—such as elastic constants, equilibrium volume, and lattice parameters—against DFT results for both $\gamma$-TiAl and ${\alpha }_2$-Ti₃Al. Although active learning generally produced predictions close to DFT, some outliers were observed, particularly for the elastic constants of the ${\alpha }_2$-Ti₃Al phase (in Comparison 1) and in certain equilibrium volume estimates. These discrepancies likely arise because these basic material properties were not the primary targets during the active learning sample selection, leading to a bias toward higher temperature configurations that deviate from the base state.

Finite-temperature properties, as assessed using radial distribution functions, showed good agreement with AIMD for both phases, with slightly better results for $\gamma$-TiAl. Moreover, simulated tension tests and generalized stacking fault energy calculations provided insights into the thermomechanical behavior of the alloy. Analysis of the stress–strain curves revealed a consistent decrease in UTS with increasing Nb concentration. Similarly, the GSFE analysis indicated that higher Nb content reduces stacking fault energies, which correlates with enhanced ductility. Overall, these findings confirm that Nb incorporation improves ductility at the expense of reduced strength, in agreement with our previous work Chandran et al. (2024a) and other studies Dumitraschkewitz et al. (2017).

The accuracy and reliability of the developed potentials were validated through a comprehensive procedure. Accuracy was established by achieving low RMSEs on an independent test set and by good agreement of key physical properties like equilibrium volume, elastic constants, and GSFEs with reference DFT data. The potential’s reliability was confirmed by its ability to maintain thermal stability up to 900 K and to produce physically realistic stress-strain responses under large deformation. While some instabilities were observed, they were confined to the most demanding conditions: the ${\alpha }_2$-Ti₃Al phase with high Nb content. This demonstrated success under both thermal and mechanical extremes confirms that these potentials are accurate and reliable tools for future large-scale simulations.

Finally, we acknowledge that the scope of this study was intentionally limited to defect free, single crystal models to isolate the properties of the $\gamma$-TiAl and ${\alpha }_2$-Ti₃All phases. While this approach was necessary to isolate the intrinsic effect of Nb on the thermomechanical properties of these alloys, it consequently excludes the complex influence of microstructural features like grain boundaries and phase interfaces, which are crucial to the behavior of real-world alloys.

In summary, our study demonstrates that active learning provides a more efficient and accurate approach for interatomic potential development, significantly reducing data requirements and computational cost while maintaining robust predictive performance across various material properties and thermomechanical behaviors.

Data availability statement

The original contributions presented in the study are publicly available. This data can be found here: Zenodo under the link: https://zenodo.org/uploads/14990265

Author contributions

AC: Conceptualization, Data curation, Investigation, Methodology, Software, Writing – original draft, Resources. AS: Validation, Writing – review and editing. CP: Validation, Writing – review and editing. PJ: Validation, Writing – review and editing. RA: Investigation, Project administration, Supervision, Writing – review and editing, Validation. CC: Funding acquisition, Investigation, Project administration, Supervision, Writing – review and editing, Validation.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. The authors gratefully acknowledge funding by the ${\text{I}}^2$B project MetalMD at Helmholtz-Zentrum Hereon, Germany.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that Generative AI was used in the creation of this manuscript. During the preparation of this work the author(s) used ChatGpt (ChatGpt 4o-mini) in order to improve the language and readability of the text. After using this tool/service, the author(s) reviewed and edited the content as needed and take(s) full responsibility for the content of the publication.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2025.1591955/full#supplementary-material

References

Ángel, D. C., Xu, X., Gravelle, S., YazdanYar, A., Schmauder, S., and Fyta, M. (2023). Stability of binary precipitates in cu-ni-si-cr alloys investigated through active learning. Mater. Chem. Phys. 306, 128053. doi:10.1016/j.matchemphys.2023.128053

CrossRef Full Text | Google Scholar

Appel, F., Oehring, M., and Paul, J. (2006). Nano-scale design of tial alloys based on β-phase decomposition. Adv. Eng. Mater. 8, 371–376. doi:10.1002/adem.200600013

CrossRef Full Text | Google Scholar

Appel, F., Oehring, M., and Wagner, R. (2000). Novel design concepts for gamma-base titanium aluminide alloys. Intermetallics 8, 1283–1312. doi:10.1016/s0966-9795(00)00036-4

CrossRef Full Text | Google Scholar

Appel, F., Paul, J. D. H., and Oehring, M. (2011). Gamma titanium aluminide alloys: science and Technology. John Wiley and Sons.

Google Scholar

Attarian, S., Morgan, D., and Szlufarska, I. (2022). Thermophysical properties of flibe using moment tensor potentials. J. Mol. Liq. 368, 120803. doi:10.1016/j.molliq.2022.120803

CrossRef Full Text | Google Scholar

Balyakin, I., and Sadovnikov, S. (2022). Deep learning potential for superionic phase of ag2s. Comput. Mater. Sci. 202, 110963. doi:10.1016/j.commatsci.2021.110963

CrossRef Full Text | Google Scholar

Blöchl, P. E. (1994). Projector augmented-wave method. Phys. Rev. B 50, 17953–17979. doi:10.1103/physrevb.50.17953

PubMed Abstract | CrossRef Full Text | Google Scholar

Bock, F., Tasnádi, F., and Abrikosov, I. A. (2024). Active learning with moment tensor potentials to predict material properties: Ti0.5al0.5n at elevated temperature. J. Vac. Sci. and Technol. A, 42. doi:10.1116/6.0003260

CrossRef Full Text | Google Scholar

Chandran, A., Ganesan, H., and Cyron, C. J. (2024a). Studying the effects of nb on high-temperature deformation in tial alloys using atomistic simulations. Mater. and Des. 237, 112596. doi:10.1016/j.matdes.2023.112596

CrossRef Full Text | Google Scholar

Chandran, A., Santhosh, A., Pistidda, C., Jerabek, P., Aydin, R. C., and Cyron, C. J. (2024b). Comparative analysis of ternary tialnb interatomic potentials: moment tensor vs. deep learning approaches. Front. Mater. 11. doi:10.3389/fmats.2024.1466793

CrossRef Full Text | Google Scholar

Chen, G., and Zhang, L. (2002). Deformation mechanism at large strains in a high-nb-containing tial at room temperature. Mater. Sci. Eng. A 329 (331), 163–170. doi:10.1016/s0921-5093(01)01554-4

CrossRef Full Text | Google Scholar

Chen, H., Yuan, D., Geng, H., Hu, W., and Huang, B. (2023). Development of a machine-learning interatomic potential for uranium under the moment tensor potential framework. Comput. Mater. Sci. 229, 112376. doi:10.1016/j.commatsci.2023.112376

CrossRef Full Text | Google Scholar

Cheng, L., Li, J., Xue, X., Tang, B., Kou, H., and Bouzy, E. (2016). Superplastic deformation mechanisms of high nb containing tial alloy with (α₂ + γ) microstructure. Intermetallics 75, 62–71. doi:10.1016/j.intermet.2016.06.003

CrossRef Full Text | Google Scholar

Cheng, Y., Wang, H., Wang, S., Gao, X., Li, Q., Fang, J., et al. (2021). Deep-learning potential method to simulate shear viscosity of liquid aluminum at high temperature and high pressure by molecular dynamics. AIP Adv. 11. doi:10.1063/5.0036298

CrossRef Full Text | Google Scholar

Clemens, H., and Mayer, S. (2012). Design, processing, microstructure, properties, and applications of advanced intermetallic tial alloys. Adv. Eng. Mater. 15, 191–215. doi:10.1002/adem.201200231

CrossRef Full Text | Google Scholar

Du, Y., Meng, Z., Yan, Q., Wang, C., Tian, Y., Duan, W., et al. (2022). Deep potential for a face-centered cubic cu system at finite temperatures. Phys. Chem. Chem. Phys. 24, 18361–18369. doi:10.1039/d2cp02758e

PubMed Abstract | CrossRef Full Text | Google Scholar

Dumitraschkewitz, P., Clemens, H., Mayer, S., and Holec, D. (2017). Impact of alloying on stacking fault energies in γ-tial. Appl. Sci. 7, 1193. doi:10.3390/app7111193

CrossRef Full Text | Google Scholar

Farkas, D., and Jones, C. (1996). Interatomic potentials for ternary Nb - Ti - Al alloys. Model. Simul. Mater. Sci. Eng. 4, 23–32. doi:10.1088/0965-0393/4/1/004

CrossRef Full Text | Google Scholar

Feng, T., and Lu, G. (2024). Hydration mgcl2-nacl-kcl molten salt using a novel approach for training machine learning potential. J. Mol. Liq. 394, 123533. doi:10.1016/j.molliq.2023.123533

CrossRef Full Text | Google Scholar

Ghaffari, K., Bavdekar, S., Spearot, D. E., and Subhash, G. (2024). Validation workflow for machine learning interatomic potentials for complex ceramics. Comput. Mater. Sci. 239, 112983. doi:10.1016/j.commatsci.2024.112983

CrossRef Full Text | Google Scholar

Gubaev, K., Podryabinkin, E. V., Hart, G. L., and Shapeev, A. V. (2019). Accelerating high-throughput searches for new alloys with active learning of interatomic potentials. Comput. Mater. Sci. 156, 148–156. doi:10.1016/j.commatsci.2018.09.031

CrossRef Full Text | Google Scholar

Gubaev, K., Zaverkin, V., Srinivasan, P., Duff, A. I., Kästner, J., and Grabowski, B. (2023). Performance of two complementary machine-learned potentials in modelling chemically complex systems. npj Comput. Mater. 9, 129. doi:10.1038/s41524-023-01073-w

CrossRef Full Text | Google Scholar

Guo, D., Li, C., Li, K., Shao, B., Chen, D., Ma, Y., et al. (2021). The thermoelectric performance of new structure snse studied by quotient graph and deep learning potential. Mater. Today Energy 20, 100665. doi:10.1016/j.mtener.2021.100665

CrossRef Full Text | Google Scholar

He, R., Wu, H., Zhang, L., Wang, X., Fu, F., Liu, S., et al. (2022). Structural phase transitions in SrTio₃ from deep potential molecular dynamics. Phys. Rev. B 105, 064104. doi:10.1103/physrevb.105.064104

CrossRef Full Text | Google Scholar

Hirel, P. (2015). Atomsk: a tool for manipulating and converting atomic data files. Comput. Phys. Commun. 197, 212–219. doi:10.1016/j.cpc.2015.07.012

CrossRef Full Text | Google Scholar

Holec, D., Reddy, R. K., Klein, T., and Clemens, H. (2016). Preferential site occupancy of alloying elements in tial-based phases. J. Appl. Phys. 119. doi:10.1063/1.4951009

CrossRef Full Text | Google Scholar

Klein, T., Clemens, H., and Mayer, S. (2016). Advancement of compositional and microstructural design of intermetallic γ-tial based alloys determined by atom probe tomography. Materials 9, 755. doi:10.3390/ma9090755

PubMed Abstract | CrossRef Full Text | Google Scholar

Kresse, G., and Furthmüller, J. (1996a). Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50. doi:10.1016/0927-0256(96)00008-0

CrossRef Full Text | Google Scholar

Kresse, G., and Furthmüller, J. (1996b). Efficient iterative schemes forab initiototal-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186. doi:10.1103/physrevb.54.11169

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, J., Liu, Y., Liu, B., Wang, Y., Zhao, K., and He, Y. (2014). Effect of nb particles on the flow behavior of tial alloy. Intermetallics 46, 22–28. doi:10.1016/j.intermet.2013.10.004

CrossRef Full Text | Google Scholar

Li, T., Hou, Q., Cui, J.-c., Yang, J.-h., Xu, B., Li, M., et al. (2024). Deep learning interatomic potential for thermal and defect behaviour of aluminum nitride with quantum accuracy. Comput. Mater. Sci. 232, 112656. doi:10.1016/j.commatsci.2023.112656

CrossRef Full Text | Google Scholar

Liu, P., Hou, B., Wang, A., Xie, J., and Wang, Z. (2022). Balancing the strength and ductility of ti2alc/tial composite with a bioinspired micro-nano laminated architecture. Mater. and Des. 220, 110851. doi:10.1016/j.matdes.2022.110851

CrossRef Full Text | Google Scholar

Liu, Z., Lin, J., Li, S., and Chen, G. (2002). Effects of nb and al on the microstructures and mechanical properties of high nb containing tial base alloys. Intermetallics 10, 653–659. doi:10.1016/s0966-9795(02)00037-7

CrossRef Full Text | Google Scholar

Lu, J., Wang, J., Wan, K., Chen, Y., Wang, H., and Shi, X. (2023). An accurate interatomic potential for the tialnb ternary alloy developed by deep neural network learning method. J. Chem. Phys. 158, 204702. doi:10.1063/5.0147720

PubMed Abstract | CrossRef Full Text | Google Scholar

Luo, Y., Meziere, J. A., Samolyuk, G. D., Hart, G. L. W., Daymond, M. R., and Béland, L. K. (2023). A set of moment tensor potentials for zirconium with increasing complexity. J. Chem. Theory Comput. 19, 6848–6856. doi:10.1021/acs.jctc.3c00488

PubMed Abstract | CrossRef Full Text | Google Scholar

Maruschak, P., Konovalenko, I., and Sorochak, A. (2023). Methods for evaluating fracture patterns of polycrystalline materials based on the parameter analysis of ductile separation dimples: a review. Eng. Fail. Anal. 153, 107587. doi:10.1016/j.engfailanal.2023.107587

CrossRef Full Text | Google Scholar

Novikov, I. S., Gubaev, K., Podryabinkin, E. V., and Shapeev, A. V. (2021). The mlip package: moment tensor potentials with mpi and active learning. Mach. Learn. Sci. Technol. 2, 025002. doi:10.1088/2632-2153/abc9fe

CrossRef Full Text | Google Scholar

Ouadah, O., Merad, G., and Abdelkader, H. S. (2021). Atomistic modelling of the γ-tial/α₂-ti3al interfacial properties affected by solutes. Mater. Chem. Phys. 257, 123434. doi:10.1016/j.matchemphys.2020.123434

CrossRef Full Text | Google Scholar

Ouadah, O., Merad, G., Saidi, F., Mendi, S., and Dergal, M. (2020). Influence of alloying transition metals on structural, elastic, electronic and optical behaviors of γ-tial based alloys: a comparative dft study combined with data mining technique. Mater. Chem. Phys. 242, 122455. doi:10.1016/j.matchemphys.2019.122455

CrossRef Full Text | Google Scholar

Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868. doi:10.1103/physrevlett.77.3865

PubMed Abstract | CrossRef Full Text | Google Scholar

Perdew, J. P., Burke, K., and Ernzerhof, M. (1997). Generalized gradient approximation made simple [phys. rev. lett. 77, 3865 (1996)]. Phys. Rev. Lett. 78, 1396. doi:10.1103/physrevlett.78.1396

CrossRef Full Text | Google Scholar

Podryabinkin, E., Garifullin, K., Shapeev, A., and Novikov, I. (2023). Mlip-3: active learning on atomic environments with moment tensor potentials. J. Chem. Phys. 159, 084112. doi:10.1063/5.0155887

PubMed Abstract | CrossRef Full Text | Google Scholar

Qi, J., Aitken, Z. H., Pei, Q., Tan, A. M. Z., Zuo, Y., Jhon, M. H., et al. (2023). Machine learning moment tensor potential for modeling dislocation and fracture in l1₀-TiAl and d0₁₉-ti₃Al alloys. Phys. Rev. Mater. 7, 103602. doi:10.1103/physrevmaterials.7.103602

CrossRef Full Text | Google Scholar

Rodriguez, A., Lam, S., and Hu, M. (2021). Thermodynamic and transport properties of lif and flibe molten salts with deep learning potentials. ACS Appl. Mater. and Interfaces 13, 55367–55379. doi:10.1021/acsami.1c17942

PubMed Abstract | CrossRef Full Text | Google Scholar

Rosenbrock, C. W., Gubaev, K., Shapeev, A. V., Pártay, L. B., Bernstein, N., Csányi, G., et al. (2021). Machine-learned interatomic potentials for alloys and alloy phase diagrams. npj Comput. Mater. 7, 24. doi:10.1038/s41524-020-00477-2

CrossRef Full Text | Google Scholar

Song, L., Appel, F., Wang, L., Oehring, M., Hu, X., Stark, A., et al. (2020). New insights into high-temperature deformation and phase transformation mechanisms of lamellar structures in high nb-containing tial alloys. Acta Mater. 186, 575–586. doi:10.1016/j.actamat.2020.01.021

CrossRef Full Text | Google Scholar

Song, Y., Yang, R., Li, D., Hu, Z., and Guo, Z. (2000). A first principles study of the influence of alloying elements on tial: site preference. Intermetallics 8, 563–568. doi:10.1016/s0966-9795(99)00164-8

CrossRef Full Text | Google Scholar

Tasnádi, F., Bock, F., Tidholm, J., Shapeev, A. V., and Abrikosov, I. A. (2021). Efficient prediction of elastic properties of ti0.5al0.5n at elevated temperature using machine learning interatomic potential. Thin Solid Films 737, 138927. doi:10.1016/j.tsf.2021.138927

CrossRef Full Text | Google Scholar

Thompson, A. P., Aktulga, H. M., Berger, R., Bolintineanu, D. S., Brown, W. M., Crozier, P. S., et al. (2022). Lammps - a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comput. Phys. Commun. 271, 108171. doi:10.1016/j.cpc.2021.108171

CrossRef Full Text | Google Scholar

Wang, H., Zhang, L., Han, J., and E, W. (2018). Deepmd-kit: a deep learning package for many-body potential energy representation and molecular dynamics. Comput. Phys. Commun. 228, 178–184. doi:10.1016/j.cpc.2018.03.016

CrossRef Full Text | Google Scholar

Wei, Y., Zhang, Y., Lu, G.-H., and Xu, H. (2012). Effects of transition metals in a binary-phase tial–ti3al alloy: from site occupancy, interfacial energetics to mechanical properties. Intermetallics 31, 105–113. doi:10.1016/j.intermet.2012.06.012

CrossRef Full Text | Google Scholar

Wu, J., Zhang, Y., Zhang, L., and Liu, S. (2021). Deep learning of accurate force field of ferroelectric hfo₂. Phys. Rev. B 103, 024108. doi:10.1103/physrevb.103.024108

CrossRef Full Text | Google Scholar

Xu, T., Li, X., Wang, Y., and Tang, Z. (2023). Development of deep potentials of molten mgcl2–nacl and mgcl2–kcl salts driven by machine learning. ACS Appl. Mater. and Interfaces. doi:10.1021/acsami.2c19272

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, H., Lu, D., Pei, Y., Chen, T., Zou, T., Wang, T., et al. (2023). Tensile behavior, microstructural evolution, and deformation mechanisms of a high nb-tial alloy additively manufactured by electron beam melting. Mater. and Des. 225, 111503. doi:10.1016/j.matdes.2022.111503

CrossRef Full Text | Google Scholar

Zhang, L., Lin, D.-Y., Wang, H., Car, R., and E, W. (2019). Active learning of uniformly accurate interatomic potentials for materials simulation. Phys. Rev. Mater. 3, 023804. doi:10.1103/physrevmaterials.3.023804

CrossRef Full Text | Google Scholar

Zhang, S., Zhang, C., Du, Z., Hou, Z., Lin, P., Kong, F., et al. (2016). Deformation behavior of high nb containing tial based alloy in α + γ two phase field region. Mater. and Des. 90, 225–229. doi:10.1016/j.matdes.2015.10.080

CrossRef Full Text | Google Scholar

Zhao, Z., Yi, M., Guo, W., and Zhang, Z. (2024). General-purpose neural network potential for ti-al-nb alloys towards large-scale molecular dynamics with ab initio accuracy. Phys. Rev. B 110, 184115. doi:10.1103/PhysRevB.110.184115

CrossRef Full Text | Google Scholar

Zhu, B., Xue, X., Kou, H., Li, X., and Li, J. (2018). Effect of microstructure on the fracture toughness of multi-phase high nb-containing tial alloys. Intermetallics 100, 142–150. doi:10.1016/j.intermet.2018.06.014

CrossRef Full Text | Google Scholar

Zhu, C.-s., Dong, W.-j., Gao, Z.-h., Wang, L.-j., and Li, G.-z. (2024). Deep potential fitting and mechanical properties study of mgalsi alloy. Comput. Mater. Sci. 239, 112966. doi:10.1016/j.commatsci.2024.112966

CrossRef Full Text | Google Scholar