Energy dissipation properties of backfill materials under compaction in solid waste backfill mining

The compaction of backfill materials is critical in Solid Waste Backfill Mining (SWBM) systems, as it can reduce the chance of dynamic hazards effectively. Despite its importance, the compaction and energy dissipation properties of backfill materials are still not fully understood. In this research, a series of laboratory tests were conducted to explore the deformation, particle morphology, and energy dissipation properties of gangue particles. The results indicated that the process of axial strain increase encompassed three stages: rapid increase (0∼2 MPa) stage, slow increase (2∼8 MPa) stage, and slight increase (8∼16 MPa) stage. For the specimen (n = 0.4), the particle flatness ranges from 1.38 to 1.75 and decreases gradually with some fluctuations. The total surface area and particle crushing energy exhibit a similar trend, both increasing monotonically with the increase of axial stress, varying within 0.688∼2.092 m² and 4.81∼14.35 kJ/m³, respectively. The relationship between particle crushing energy and axial strain is approximated by a linear function. The energy consumed by particle breakage constitutes a small proportion (0.7%∼7.8%) of the total energy consumption for specimen deformation, while the majority of energy consumption is attributed to inter-particle friction, especially in the later compaction stage. However, the initial particle size distribution has negligible influence on the total surface area and particle crushing energy.

1 Introduction

With the development of underground mining, the complexity and depth of underground mining operations has led to an increasing risk of dynamic hazards, including rock bursts, coal and gas outbursts, and shockwaves (Zhou et al., 2016; Wu et al., 2020; Wu et al., 2022; Shi et al., 2023a; Wu et al., 2024; Zhang et al., 2025). These events may have devastating consequences for mine safety and productivity. Therefore, it is critical to develop effective measures to control and mitigate these dynamic hazards.

In recent years, solid waste backfill mining (SWBM) technology, which is the core technology to realize green mining, has been widely applied in more than 20 mining areas in China (Zhang et al., 2022; Shi et al., 2023b). The basic principle of strata movement control in SWBM is achieved by an independent backfilling system. Solid waste backfill materials (e.g., gangue, fly ash, and other solid wastes on the ground) are pre-treated, transported to underground, and then backfilled into the goaf to replace the original coal seam supporting the roof, thus restrict overlying strata movement. As the working face advances, the backfill materials are further compacted and effectively support the overlying strata. Simultaneously, during the compaction process, the energy released from the deformation and failure of the roof is absorbed. SWBM has demonstrated its potential to not only reduce the chance of dynamic hazards effectively (Zhang et al., 2019a; Li et al., 2021), but also provide an environmental-friendly method for the dispose of gangue or other solid wastes (Huang et al., 2011). As SWBM continues to gain attention in the mining industry, it is essential to understand the compaction characteristics and energy dissipation properties of backfill materials. These two factors play important roles in understanding the effectiveness of SWBM to mitigate dynamic hazards and ensure safe mining operations.

The compaction properties of backfill materials are affected by many factors, such as particle morphology, particle size, and particle type (Hamdani, 1983; Day et al., 2000; Cho et al., 2006; Ma et al., 2014; Yu et al., 2020; Li et al., 2023; Shi et al., 2024; Zhang et al., 2023; Yang et al., 2024; Xu et al., 2024). The particles can be crushed during the loading (Hardin, 1985; Coop et al., 2004; Guerrero and Vallejo, 2005; Casini et al., 2013; De and Mcdowell, 2016), which may be influenced by various factors including applied stress, the initial grading of the tested specimens (Coop et al., 2004), the change in particle mixture (Ma et al., 2015), the geological framework (Aydin et al., 2006) and the complex shape in physics and geometry.

Studies have been conducted broadly to investigate the energy dissipation properties of rocks (Liu et al., 2014; Meng et al., 2016; Zhou et al., 2020; Han et al., 2022; Yan et al., 2024; Deng et al., 2023; Reches and Wetzler, 2025). In the process of rock failure, energy dissipation always exists, which is an irreversible process (Rezaei et al., 2015; Sangkyu et al., 2019; Zhang et al., 2019b; Yu et al., 2020). The energy dissipation properties are closely related to the types of rocks, water content, and loading methods (Hou et al., 2021; Jin et al., 2022).

This study is motivated by understanding the significance of the compaction and energy dissipation properties of backfill materials in SWBM. Specifically, this study aims to (1.) design a compacting device that can be installed on the electro-hydraulic servo-controlled test system to simulate the compaction of backfill materials in SWBM; (2.) test specimens of gangue particles with different size distributions to characterize the deformation, particle morphology evolution, and energy dissipation properties during compaction; and (3.) investigate the correlation between particle crushing energy and axial stress.

2 Materials and methods

2.1 Testing system

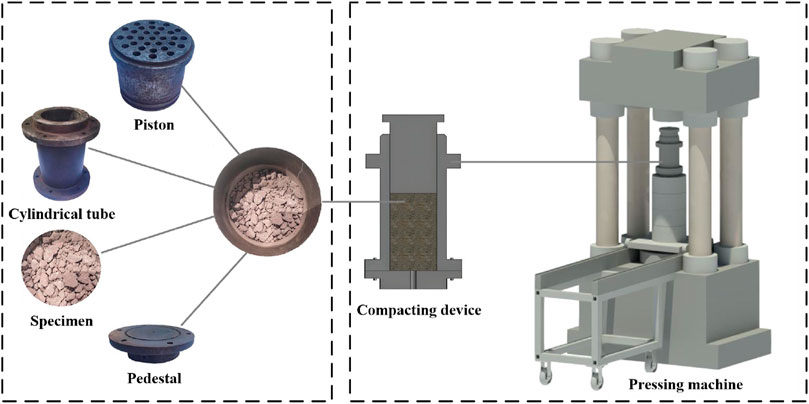
Backfill materials in working faces of SWBM are confined horizontally by sidewalls and the internal friction between themselves. A compacting device was designed to simulate the compaction of backfill materials in SWBM and characterize their energy dissipation properties. As shown in Figure 1, the compacting device consisted of three main parts: a piston, a cylinder tube, and a pedestal. The piston was employed to apply axial load to the test backfill materials. The cylinder tube was fabricated from fully quenched 45# steel, of which the elastic modulus was 210 GPa. The inner diameter and the wall thickness of this steel cylinder were 100 and 10 mm, respectively. The test accuracy of the pressing machine were axial force 20 N and axial stress 0.001 mm.

Figure 1

Figure 1. Compacting device.

2.2 Experimental materials and specimen preparation

The gangue specimens used as backfill materials in this research were collected from the −592 m deep strata of Xiaojihan coal mine in Shanxi province of China. The main mineral composition of the tested gangue was determined through experimental analysis, showing that the gaugue specimens consist of 32% feldspar, 28% quartz, 12% kaolinite, 9% illite, 7% chlorite, 4% calcite, 3% siderite, and 5% other minerals. The average dry density was 2,562 kg/m³. The uniaxial compressive strength, tensile strength, cohesion, internal friction angle, elasticity modulus, and fracture toughness were 58.61 MPa, 7.65 MPa, 10.32 MPa, 34.08°, 30.40 GPa and 0.44 MPa m^1/2, respectively.

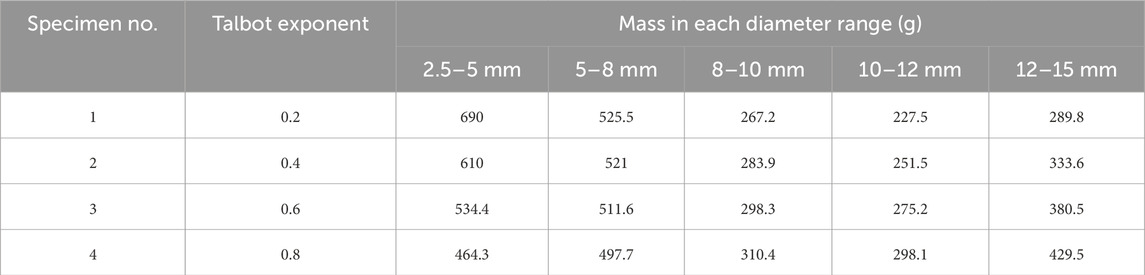
The test specimens were prepared in the laboratory following the procedure below: (1.) The gangue blocks were initially crushed into particles; (2.) The particles were separated by separation screens into five groups by their sizes, with diameters ranging from 2.5 to 5 mm (group A), 5∼8 mm (group B), 8∼10 mm (group C), 10–12 mm (group D), and 12∼15 mm (group E), as shown in Figure 2; and (3.) Specimens were prepared by mixing particles from groups A∼E, with a total mass of 2000 g. To account for the diverse size distribution of backfill materials and overcome the dimension disaster, each specimen was created using a combination of particles from different diameter ranges, according to Talbot theory (Yu et al., 2020). The Talbot formula is written in the following form

$P={\left(\frac{d}{d_{\max }}\right)}^n\times 100\%(1)$

where $P$ is the passing rate of each diameter size in gangue particles, $d$ is the particle diameter, $d_{\max }$ is the maximum particle diameter, and $n$ is the Talbot exponent. Based on Equation 1, the mass amount in each diameter range of the gangue specimens for four different cases (n = 0.2, n = 0.4, n = 0.6, and n = 0.8) are provided in Table 1.

Figure 2

Figure 2. Gangue particles in different diameter ranges.

Table 1

Table 1. The mass amount in each diameter range of each specimen.

2.3 Testing procedure

Due to the movement of the overlying strata, the backfill materials in the working face are subjected to varying levels of loading over time. The compaction level increases gradually from beginning to end. Therefore, the impact of the compaction level (axial stress) on the energy dissipation of the backfill materials need to be considered. Given the working face depth (−592 m) and the in-situ strata stress (average bulk density of 0.024 MN/m³), a maximum axial stress of 16 MPa was prescribed for the compacting test. In this test, the axial stress was set to five different levels (2, 4, 8, 12, and 16 MPa). Thus, the energy dissipation properties of the four specimens were tested under six different conditions (including the initial state). A total of 24 sets of experiments were conducted.

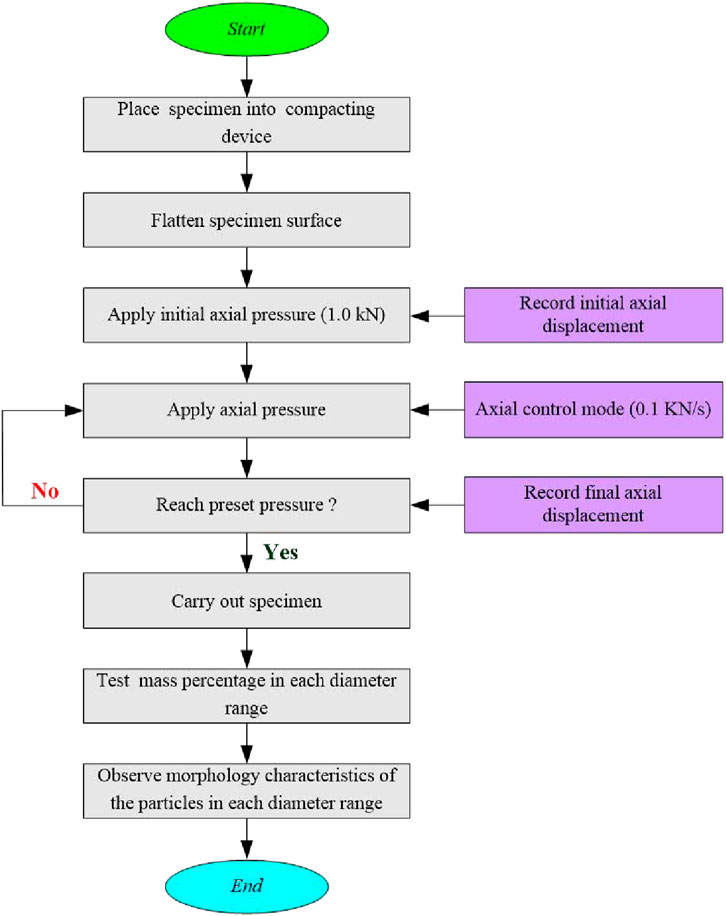
To obtain the energy dissipation properties under different axial stresses, an axial force control mode was applied and the specimens were separated after the test. Each set of experiments was repeated three times, and the average test results were used in the analysis. Figure 3 illustrates the testing procedure.

Figure 3

Figure 3. Testing procedure.

2.4 Particle flatness calculation

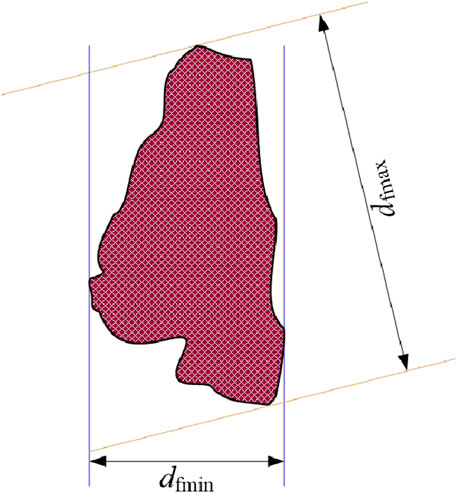
In this research, particle flatness, $f$, was employed to quantify the evolution of particle morphology. It was expressed by the following equation.

$f=d_{f\max }/d_{f\min }(2)$

where $d_{f\max }$ and $d_{f\min }$ are the maximum and minimum Feret’s diameters of the particles, respectively. The specific notation for the two diameters is shown in Figure 4. Based on Equation 2, this value is always greater than or equal to 1. Particle flatness characterizes the elongation of particles; the closer a particle is to a spherical shape, the closer this value is to 1. Conversely, the more flattened and elongated the particle, the higher the value.

Figure 4

Figure 4. Feret’s diameters of the particle.

2.5 Energy dissipation parameters calculation

Strain energy density is used to express the energy consumed by the deformation of specimens per unit volume under compaction. In this test, the elastic deformation of testing equipment (e.g., dowel bar, compacting head, piston, cylindrical tube, and pedestal) played a negligible role, and the work done by the pressure machine was mainly consumed by the deformation of specimens and friction between the gangue particles and cylindrical tube inner wall. The work done by compaction per unit volume of specimen $W$ can be calculated by

$W={\int }_0^{\epsilon }{\sigma }_{1}d\epsilon (3)$

Based on Equation 3, the unit energy dissipation of the friction between the gangue particles and the cylindrical tube’s inner wall $W_m$ can be calculated by

$W_m=\frac{{\int }_0^{\epsilon }\left[\mu \lambda \sigma 2\pi r{h}_0\left(1-\epsilon \right)\right]\frac{h_0}{2}d\epsilon }{\pi r^2{h}_0\left(1-\epsilon \right)}=\frac{\lambda \mu h_0}{r}W(4)$

where $\mu$, $\lambda$, $r$ and $h_0$ are the friction coefficient, lateral pressure coefficient, radius of the cylindrical tube inner wall, and initial height of specimen, respectively. In Equation 4, the friction coefficient and lateral pressure coefficient were set at 0.25 and 0.43, respectively (Zhou et al., 2016).

Therefore, the strain energy density ${\nu }_{\epsilon }$ of the specimen can be expressed as

${\nu }_{\epsilon }=W-W_m=\left(1-0.1075\frac{h_0}{r}\right)W(5)$

Based on Equation 5, the energy consumption during the compaction process of a unit volume specimen includes particle crushing energy, ${\nu }_{\mathrm{b}}$, frictional energy dissipation, ${\nu }_{\mathrm{f}}$, between particles, particle deformation energy, ${\nu }_{\mathrm{d}}$, and other forms of energy dissipation, ${\nu }_{\mathrm{e}}$, which can be expressed by Equation 6

${\nu }_{\epsilon }={\nu }_{\mathrm{b}}+{\nu }_{\mathrm{f}}+{\nu }_{\mathrm{d}}+{\nu }_{\mathrm{e}}(6)$

According to Griffith’s fracture mechanics theory, the energy consumption $W_b$ associated with the formation of new fracture surfaces during particle breakage can be expressed (Lawn, 1993)

$W_b=2K_{IC}^2\Delta A/E(7)$

where $K_{IC}$ is the fracture toughness of the particle material, $\Delta A$ is the area of the new fracture surfaces generated by particle breakage, and $E$ is the elastic modulus of the particle material.

The relationship between the surface area, $A_S$, of an individual gangue particle and its particle size, $d_s$, can be expressed by Equation 8

$A_s\propto d_s^2(8)$

In this test, gangue particles of different size ranges were sieved using circular perforated sieves. Considering that gangue particles are irregular polyhedra and that their particle circularity decreases during compaction (Yu et al., 2020), in this research, spherical shapes were used to simulate gangue particles for volume calculation. For a single spherical particle with a diameter of $d_s$, its volume, $V_s$, is calculated as follows

$V_s=\pi {d_s}^3/6(9)$

For gangue particles within a certain size range, considering their irregular shape, the average of the upper and lower sieve apertures $D_i$ and $D_{i+1}$ was taken as the characteristic value, $d_{\mathrm{i}}$, of the particle size for that range, which can be expressed as

$d_i=\left(D_i+D_{i+1}\right)/2(10)$

By substituting $d_{\mathrm{i}}$ in Equation 10 into Equation 9 instead of $d_s$, Equation 9 can be rewritten as Equation 11.

$V_s=\pi {d_i}^3/6(11)$

Assuming the number of particles within this size range is $N_i$, the total surface area, $A_i$, of all particles can be expressed as

$A_i=N_i\pi {d_i}^2(12)$

Thus, the total mass, $m_i$, of particles within this size range can be expressed as

$m_i=\rho N_i\pi {d_i}^3/6(13)$

where $\rho$ is the density of the gangue particles.

By combining Equations 12, 13, we obtain

$A_i=6m_i/\rho d_i(14)$

During the compaction process of the specimens, under a certain axial stress, ${\sigma }_1^{\mathrm{j}}$, the mass, $m_i$, of gangue particles in each size range can be obtained through sieving and weighing. Substituting these values into Equation 14, we obtain the total surface area, $A_i$, of gangue particles for that size range. Summing the values calculated for each size range provides the total surface area of gangue particles, $A_j$, in the entire specimen, which can be expressed by Equation 15.

$A_j={\displaystyle \sum _1^6}{A}_i(15)$

Using the data from the previous axial stress, ${\sigma }_1^{\mathrm{j}-1}$, the increment, $\Delta A_j$, in the surface area of gangue particles can be obtained.

$\Delta A_j=A_j-A_{j-1}(16)$

Substituting Equation 16 into Equation 7, the energy required to generate new surfaces during gangue particle breakage, $W_{\mathrm{b}}^j$, can be calculated.

Therefore, under axial stress, ${\sigma }_1^{\mathrm{j}}$, the particle crushing energy consumption, ${\nu }_{\mathrm{b}}^j$, per unit volume of the specimen can be expressed by Equation 17

${\nu }_{bj}=\left({\displaystyle \sum _1^j}{W}_b^j\right)/V_j(17)$

where $V_j$ is the volume of the specimen under axial stress.

3 Results

3.1 Deformation properties

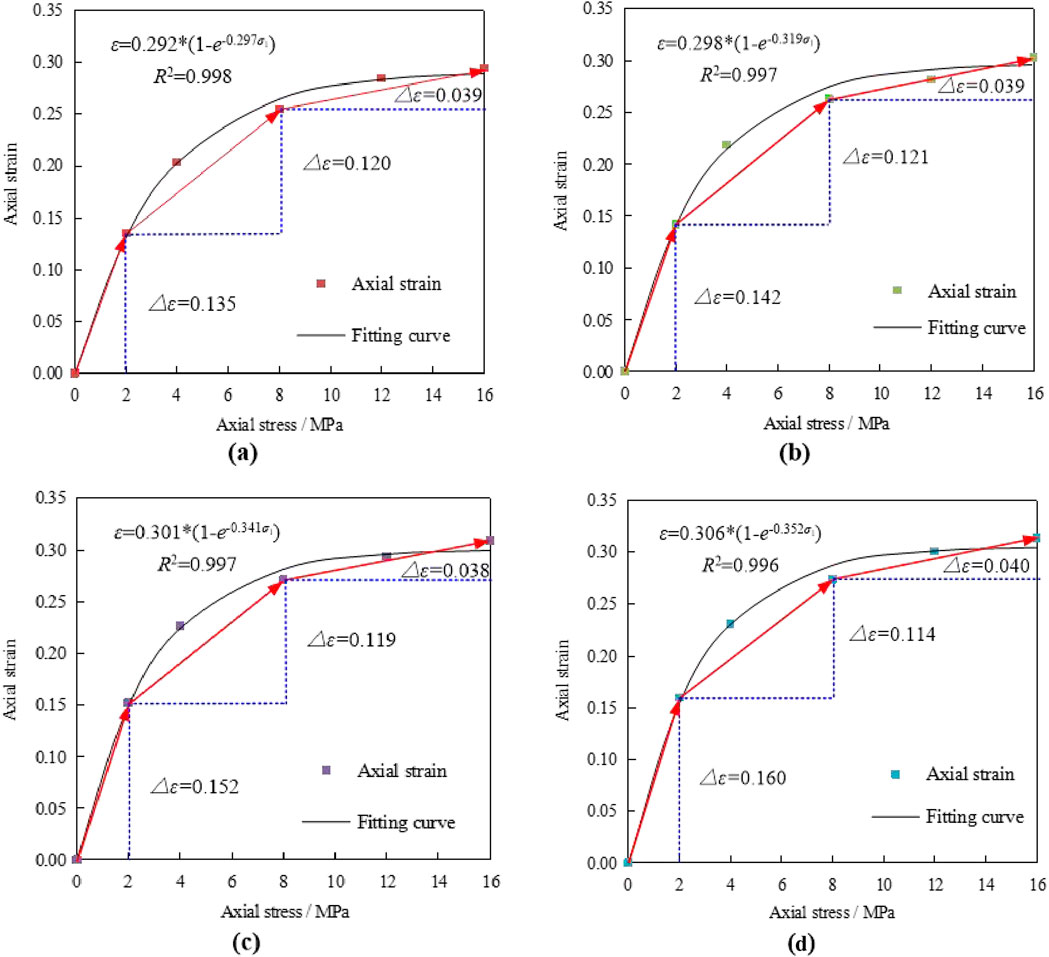
Based on the test data of axial stress and axial strain, the relationship between axial strain and axial stress was investigated (Figure 5). As observed, the axial strain increased with the increase in axial stress. The increase in axial strain consisted of three stages: the rapid increase (0∼2 MPa) stage, the slow increase (2∼8 MPa) stage, and the slight increase (8∼16 MPa) stage. During the rapid increase stage, the axial strain increased quickly by 45.87%–50.97% of the total increment (0∼16 MPa). During the slight increase stage, the axial strain increased slightly by 12.43%–13.51% of the total increment and tended to become stable.

Figure 5

Figure 5. Axial strain vs. axial stress curves. (a) n = 0.2 (b) n = 0.4 (c) n = 0.6 (d) n = 0.8.

The relationship between axial strain and axial stress was approximated by a negative exponential function, and the correlation coefficients were all above 0.99. The axial strain was expressed by Equation 18

$\epsilon =a\left(1-e^{-b{\sigma }_1}\right)(18)$

where $\epsilon$ is the axial strain, ${\sigma }_1$ is the axial stress, and $a$ and $b$ are fitting parameters.

3.2 Particle morphology evolution

To investigate the evolution of particle morphology, the particle morphology and size measurement method proposed by Yu et al. was applied (Yu et al., 2020). The “Analyze Particles” function of ImageJ was employed in this research to calculate the maximum and minimum Feret’s diameters of each particle. The particle flatness was then calculated using Equation 2.

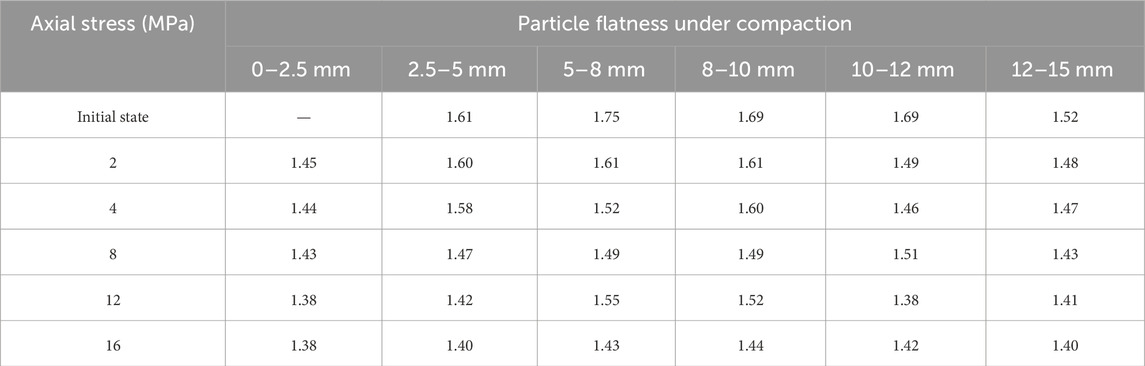
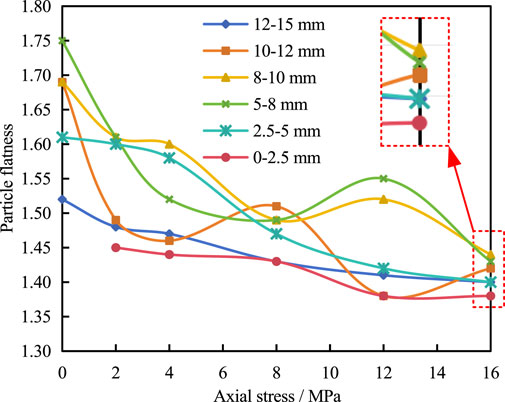
Table 2 exhibits the calculated particle flatness (n = 0.4), and Figure 6 shows the relationship between particle flatness and axial stress. As seen, the particle flatness varied from 1.38 to 1.75 across different axial stress levels. With the increase of axial stress, the particle flatness decreased gradually with some fluctuations. This can be mainly explained by the constant particle breakage during compaction, leading to the detachment of particle edges and corners. Hence, the gangue particles became more and more regular in shape. Interestingly, the particle flatness of gangue particles in the 0∼2.5 mm range was relatively low and stable as compared to larger particles, ranging from 1.38 to 1.45. This is mainly because smaller particles are more regular in shape and less likely to break again. In contrast, for the gangue particles with diameters of 5∼8 mm, 8∼10 mm, and 10∼12 mm ranges, the particle flatness values fluctuated significantly, mainly due to random breakage of larger particles during compaction. Under 16 MPa axial stress, the particle flatness values ranged from 1.39 to 1.42. The flatness values of particles in the 0∼2.5 mm, 2.5∼5 mm, and 12∼15 mm ranges were relatively lower, while those in the 5∼8 mm, 8∼10 mm, and 10∼12 mm ranges were relatively higher.

Table 2

Table 2. Particle flatness of the specimen under compaction (n = 0.4).

Figure 6

Figure 6. Particle flatness vs. axial stress curves.

3.3 Energy dissipation properties

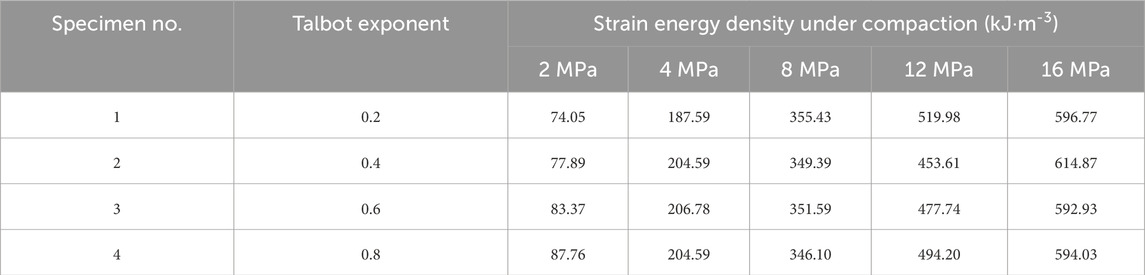
Table 3 exhibits the calculated strain energy density values, which varied from 74.05 kJ/m³ to 614.87 kJ/m³. When the compaction started, the specimen structure was loose, with many voids, low friction between gangue particles, and many particle edges, making them prone to breakage. Consequently, the energy consumption for specimen deformation was low. Thus, the specimen was easily deformed, and the strain energy density increased slowly. During the 0∼4 MPa process, axial strain accounted for 69.41%∼73.48% of the total strain, while strain energy density accounted for only 31.43%∼34.88% of the total increment. As the compaction progressed, the specimen structure became dense, featuring close contact among gangue particles, higher friction, and reduced particle movement and breakage. As a result, significant energy was required for the specimen to deform.

Table 3

Table 3. Strain energy density of the specimens under compaction.

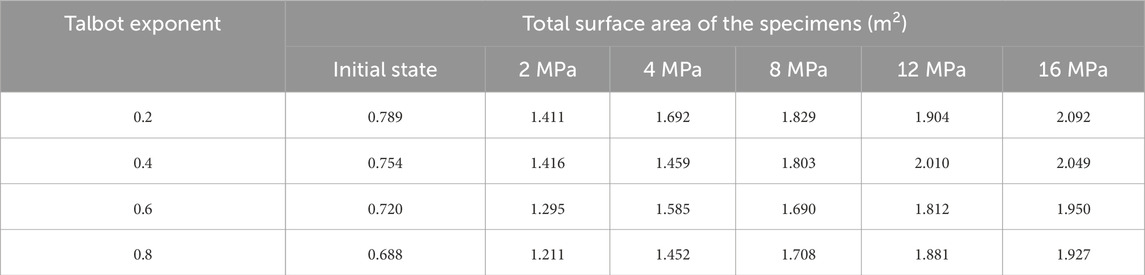
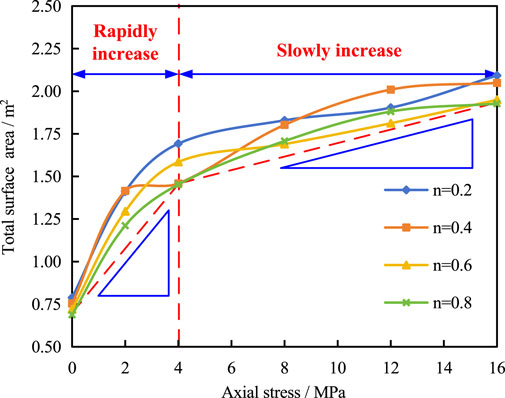
Table 4 exhibits the calculated total surface area, and Figure 7 shows the relationship between total surface area and axial stress. As indicated in Figure 7, the total surface area varied from 0.688 m² to 2.092 m² and increased monotonically with the increase of the axial stress. When the axial stress was lower than 4 MPa, the total surface area increased rapidly, accounting for 54.44%–70.33% of the total increment. This was observed primarily due to the particle morphology in the initial stage of compaction, during which particles had numerous edges, and some were slender. When the specimen was compressed, stress concentration easily occurred, forming large new fracture surfaces. The total surface area increased slowly between 4 MPa and 16 MPa. However, the initial particle size distribution (Talbot exponent) had negligible influence on the total surface area.

Table 4

Table 4. Total surface area of the specimens under compaction.

Figure 7

Figure 7. Total surface area vs. axial stress curves.

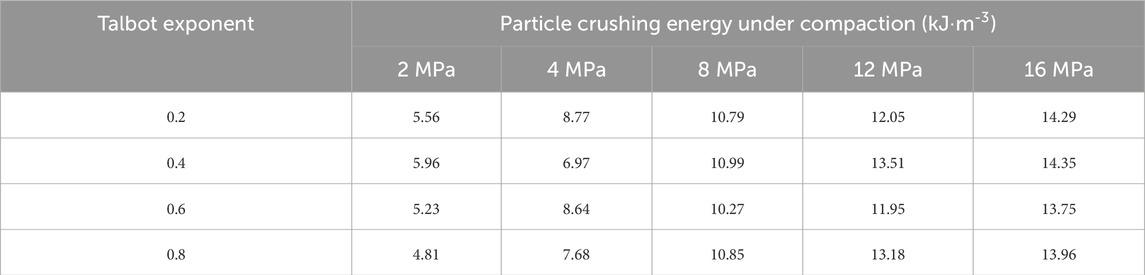
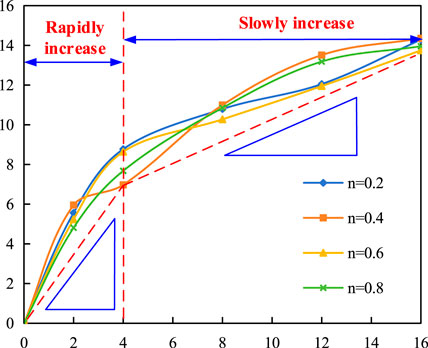
Table 5 exhibits the calculated particle crushing energy, and Figure 8 shows how the particle crushing energy vary with axial stress. As illustrated in Figure 8, the particle crushing energy varied from 4.81 kJ/m³ to 14.35 kJ/m³ and increased monotonically with the increase of the axial stress. The trend in strain energy density is similar to that of the total surface area and can be divided into two stages, with 4 MPa as the inflection point: a rapid increase stage below 4 MPa and a slow increase stage above 4 MPa.

Table 5

Table 5. Particle crushing energy of the specimens under compaction.

Figure 8

Figure 8. The particle crushing energy vs. axial stress curves.

Figure 9

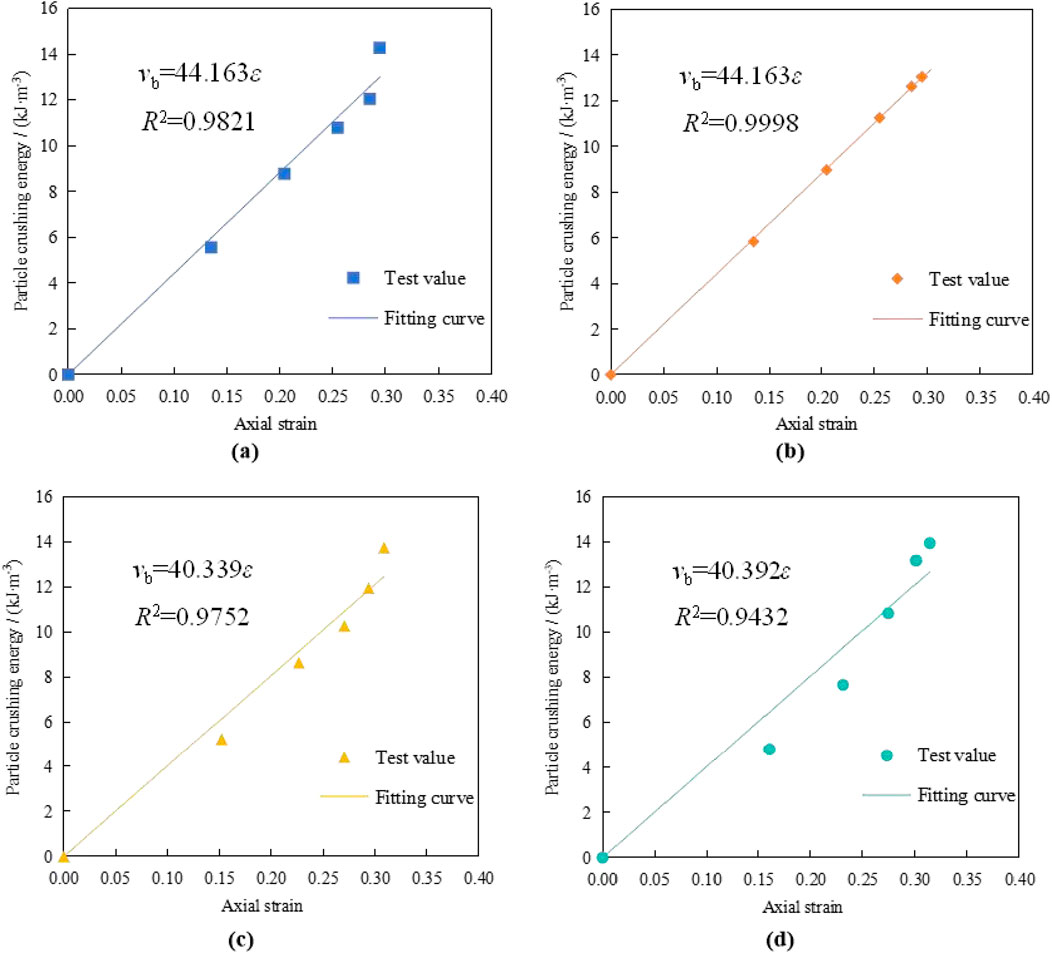
Figure 9. The relationship between the particle crushing energy and axial strain. (a) n = 0.2 (b) n = 0.4 (c) n = 0.6 (d) n = 0.8.

4 Discussion

As illustrated in Figure 9, the relationship between particle crushing energy ${\nu }_{\mathrm{b}}$, and axial strain $\epsilon$, was approximated by a linear function, and the correlation coefficients were all above 0.94. The particle crushing energy was expressed by Equation 19.

${\nu }_{\mathrm{b}}=a_2\epsilon (19)$

where $a_2$ is a fitting parameter.

The energy consumption during the compaction of a unit volume specimen includes particle crushing energy ${\nu }_{\mathrm{b}}$, frictional energy dissipation ${\nu }_{\mathrm{f}}$ between particles, particle deformation energy ${\nu }_{\mathrm{d}}$, and other forms of energy dissipation ${\nu }_{\mathrm{e}}$. Considering the mutual filling of large and small gangue particles in the specimen and the absence of significant elastic deformation observed during the test, ${\nu }_{\mathrm{d}}$ and ${\nu }_{\mathrm{e}}$ can be neglected. The energy consumption during the compaction process mainly includes ${\nu }_{\mathrm{b}}$ and ${\nu }_{\mathrm{f}}$ between particles. Based on the test data, the relationship between the increment in particle crushing energy and the increment in strain energy density can be established, as shown in Figure 10. As indicated in Figure 10, with the increase of the axial stress, the ratio of particle crushing energy to strain energy density decreased overall, varying from 0.7% to 7.8%. Within the 0∼2 MPa range, the increment in particle crushing energy was 5.88%∼7.81% of the increment in strain energy density. Within the 12∼16 MPa range, the increment in particle crushing energy was 1.45%∼2.34% of the strain energy density. This trend suggests that throughout the entire compaction process, the energy consumed by particle breakage accounted for a small proportion of the total energy consumption for specimen deformation. The majority of energy consumption was contributed by inter-particle friction. In particular, during the later stages of compaction, particles became more regular in shape and breakage primarily occurred in the form of grinding, which requires less energy.

Figure 10

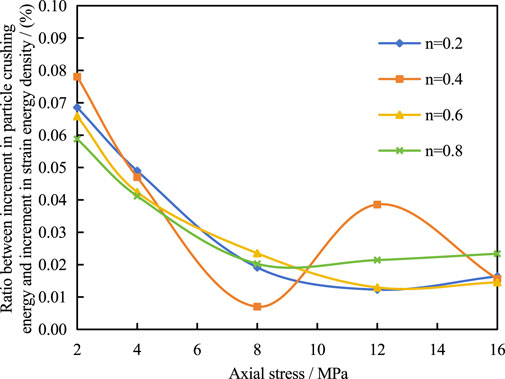
Figure 10. The ratio between increment in particle crushing energy and increment in strain energy density.

As mentioned above, the deformation, particle morphology, and energy dissipation properties of gangue particles were obtained, and the change rules of particle flatness and particle crushing energy were analyzed. Our results can provide some theory and information for the further research on materials and technologies to reduce dynamic hazards in underground mining, such as selection of backfill materials, optimization of particle gradation, prediction of surface subsidence and mine pressure hazards.

However, it should be pointed out that in this research, due to the limitations of test equipment and test scheme, gangue particles were simplified into spherical particles when calculating the particle morphology characteristics, and the surface roughness of gangue particles was not considered. Therefore, the data such as surface area, volume and crushing energy dissipation were different from the facts to some extent. In the following research, high-precision 3D scanner will be used to accurately scan the morphology parameters of particles, and the energy dissipation properties during compaction will be obtained.

5 Conclusion

This research aimed to investigate the compaction behavior of gangue particles in SWBM using a custom-designed testing system. Specifically, this study characterized the deformation, particle morphology, and energy dissipation of gangue particles under various axial stresses. The key findings of this study are as follows:

1) The relationship between axial strain and axial stress was approximated by a negative exponential function, with three stages of axial strain increase: rapid increase (0∼2 MPa), slow increase (2∼8 MPa), and slight increase (8∼16 MPa).

2) For the specimen (n = 0.4), the particle flatness ranged from 1.38 to 1.75. With the increase of axial stress, the particle flatness decreased gradually with some fluctuations. Among them, the flatness of gangue particles in the 0∼2.5 mm range was relatively small and stable, ranging from 1.38 to 1.45.

3) The total surface area varied from 0.688 m² to 2.092 m², increasing monotonically with the increase of the axial stress. When the axial stress was lower than 4 MPa, the total surface area increased rapidly, while the total surface area increased slowly between 4 MPa and 16 MPa. Besides, the initial particle size distribution (Talbot exponent) had a negligible impact on the total surface.

4) The particle crushing energy increased monotonically from 4.81 kJ/m³ to 14.35 kJ/m³ with the increase of the axial stress, following a similar trend to that of the total surface area and could be divided into two stages with 4 MPa as the inflection point. The relationship between particle crushing energy and axial strain was approximated by a linear function.

5) The ratio between increment in particle crushing energy and increment in strain energy density ranged from 0.7% to 7.8% and tended to decrease on the whole. Throughout the compaction process, particle breakage accounted for a small proportion of the total energy consumption for specimen deformation, while inter-particle friction dominated the energy dissipation process, especially during the later compaction stages.

The findings of this study highlight the importance of understanding the compaction behavior of gangue particles in SWBM, as it can help prevent dynamic hazards and ensure safety in mining operations. By understanding the importance of the compaction and energy dissipation properties of backfill materials, effective measures can be taken to minimize the risk of dynamic hazards. Ultimately, this knowledge can contribute to a safer and more sustainable mining industry.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

BY: Writing – original draft, Writing – review and editing. XH: Data curation, Writing – review and editing. YZ: Investigation, Resources, Writing – review and editing. JJ: Data curation, Writing – review and editing. AL: Formal Analysis, Software, Writing – review and editing. ZL: Funding acquisition, Methodology, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work was funded by the Science and Technology Project of Changzhou (Grant no. CE20235011), the QingLan Project (Grant no.30320190222002), the Changzhou Longcheng Talent Program - Young Science and Technology Talent Lifting Project (Grant no.30520190722002).

Conflict of interest

Authors BY and ZL were employed by Wuxi RL Precision Machinery Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The authors declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aydin, A., Borja, R. I., and Eichhubl, P. (2006). Geological and mathematical framework for failure modes in granular rock. J. Struct. Geol. 28, 83–98. doi:10.1016/j.jsg.2005.07.008

CrossRef Full Text | Google Scholar

Casini, F., Viggiani, G. M. B., and Springman, S. M. (2013). Breakage of an artificial crushable material under loading. Granul. Matter 15, 661–673. doi:10.1007/s10035-013-0432-x

CrossRef Full Text | Google Scholar

Cho, G. C., Dodds, J., and Santamarina, J. C. (2006). Particle shape effects on packing density, stiffness, and strength: natural and crushed sands. J. Geotechnical & Geoenvironmental Eng. 132, 591–602. doi:10.1061/(asce)1090-0241(2006)132:5(591)

CrossRef Full Text | Google Scholar

Coop, M. R., Sorensen, K. K., Bodas Freitas, T., and Georgoutsos, G. (2004). Particle breakage during shearing of a carbonate sand. Geotechnique 54, 157–163. doi:10.1680/geot.54.3.157.36347

CrossRef Full Text | Google Scholar

Day, R. W., Boutwell, G. P., Benson, C. H., and Blotz, L. R. (2000). Estimating optimum water content and maximum dry unit weight for compacted clays. J. Geotechnical & Geoenvironmental Eng. 126, 195–197. doi:10.1061/(asce)1090-0241(2000)126:2(195)

CrossRef Full Text | Google Scholar

De, B. J. P., and Mcdowell, G. R. (2016). Particle breakage criteria in discrete-element modelling. Geotechnique 66, 1014–1027. doi:10.1680/jgeot.15.p.280

CrossRef Full Text | Google Scholar

Deng, S., Xiong, F., Liu, Y., and Jiang, Q. (2023). Temperature-dependent permeability model of granite after thermal treatment based on energy dissipation theory and fractal theory. Rock Mech. Rock Eng. 56, 6321–6335. doi:10.1007/s00603-023-03382-4

CrossRef Full Text | Google Scholar

Guerrero, S. L., and Vallejo, L. E. (2005). Discrete element method evaluation of granular crushing under direct shear test conditions. J. Geotechnical & Geoenvironmental Eng. 131, 1295–1300. doi:10.1061/(ASCE)1090-0241(2005)131:10(1295)

CrossRef Full Text | Google Scholar

Hamdani, I. H. (1983). Optimum moisture content for compacting soils one-point method. J. Irrigation & Drainage Eng. 109, 232–237. doi:10.1061/(asce)0733-9437(1983)109:2(232)

CrossRef Full Text | Google Scholar

Han, Z. Y., Li, D. Y., and Li, X. B. (2022). Dynamic mechanical properties and wave propagation of composite rock-mortar specimens based on SHPB tests. Int. J. Min. Sci. Technol. 32, 793–806. doi:10.1016/j.ijmst.2022.05.008

CrossRef Full Text | Google Scholar

Hardin, B. O. (1985). Crushing of soil particles. J. Geotechnical Eng. 111, 1177–1192. doi:10.1061/(asce)0733-9410(1985)111:10(1177)

CrossRef Full Text | Google Scholar

Hou, Y. Q., Yin, S. H., Yang, S. X., Zhang, M. Z., and Cao, Y. (2021). Energy consumption characteristics and damage characteristics of full tailings cemented backfill under impact loading. Chin. J. Nonferrous Metals 31, 1661–1671. doi:10.11817/j.ysxb.1004.0609.2021-37755

CrossRef Full Text | Google Scholar

Huang, Y. L., Zhang, J. X., Zhang, Q., and Nie, S. (2011). Backfilling technology of substituting waste and fly ash for coal underground in China coal mining area. Environ. Eng. & Manag. J. 10, 769–775. doi:10.30638/eemj.2011.104

CrossRef Full Text | Google Scholar

Jin, J. F., Xu, H., Yu, X., and Liao, Z. X. (2022). Effect of dynamic load and water content on failure and energy dissipation characteristics of red sandstone. Rock Soil Mech. 43, 3231–3240. doi:10.16285/j.rsm.2021.2128

CrossRef Full Text | Google Scholar

Lawn, B. (1993). Fracture of brittle solids. Cambridge University Press, Cambridge, United Kingdom.

Google Scholar

Li, M., Zhang, J. X., Huang, P., Sun, Q., and Yan, H. (2021). Deformation behaviour of crushed waste rock under lateral cyclic loading. Rock Mech. Rock Eng. 54, 6665–6672. doi:10.1007/s00603-021-02607-8

CrossRef Full Text | Google Scholar

Li, Z., Yang, X., Yang, P., Feng, G., Liu, J., Zhu, C., et al. (2023). Layered re-breaking behavior of gangue backfilling materials and inspirations for protecting mined ecological environments. Constr. Build. Mater. 368, 130477. doi:10.1016/j.conbuildmat.2023.130477

CrossRef Full Text | Google Scholar

Liu, J. F., Xie, H. P., Hou, Z. M., Yang, C., and Chen, L. (2014). Damage evolution of rock salt under cyclic loading in unixial tests. Acta Geotech. 9, 153–160. doi:10.1007/s11440-013-0236-5

CrossRef Full Text | Google Scholar

Ma, D., Bai, H. B., Chen, Z. Q., and Pu, H. (2015). Effect of particle mixture on seepage properties of crushed mudstones. Transp. Porous Media 108, 257–277. doi:10.1007/s11242-015-0473-1

CrossRef Full Text | Google Scholar

Ma, Z. G., Gu, R. X., Huang, Z. M., Peng, G., Zhang, L., and Ma, D. (2014). Experimental study on creep behavior of saturated disaggregated sandstone. Int. J. Rock Mech. & Min. Sci. 66, 76–83. doi:10.1016/j.ijrmms.2014.01.004

CrossRef Full Text | Google Scholar

Meng, Q. B., Zhang, M. W., Han, L. J., Pu, H., and Nie, T. (2016). Effects of acoustic emission and energy evolution of rock specimens under the uniaxial cyclic loading and unloading compression. Rock Mech. Rock Eng. 49, 3873–3886. doi:10.1007/s00603-016-1077-y

CrossRef Full Text | Google Scholar

Reches, Z., and Wetzler, N. (2025). Energy dissipation and fault dilation during intact-rock faulting. J. Struct. Geol. 191, 105325. doi:10.1016/j.jsg.2024.105325

CrossRef Full Text | Google Scholar

Rezaei, M., Hossaini, M. F., and Majdi, A. (2015). Determination of longwall mining-induced stress using the strain energy method. Rock Mech. Rock Eng. 48, 2421–2433. doi:10.1007/s00603-014-0704-8

CrossRef Full Text | Google Scholar

Sangkyu, K., Young, J. A., and Yong, H. J. (2019). Frictional energy dissipation for coupled systems subjected to harmonically varying loads. Tribol. Int. 134, 205–210. doi:10.1016/j.triboint.2019.01.021

CrossRef Full Text | Google Scholar

Shi, H., Chen, W. L., Zhang, H. Q., and Song, L. (2023b). A novel obtaining method and mesoscopic mechanism of pseudo-shear strength parameter evolution of sandstone. Environ. Earth Sci. 82, 60. doi:10.1007/s12665-023-10748-y

CrossRef Full Text | Google Scholar

Shi, H., Chen, W. L., Zhang, H. Q., Song, L., Li, M., Wang, M., et al. (2023a). Dynamic strength characteristics of fractured rock mass. Eng. Fract. Mech. 292, 109678. doi:10.1016/j.engfracmech.2023.109678

CrossRef Full Text | Google Scholar

Shi, H., Zhang, H. Q., Chen, W. L., Song, L., and Li, M. (2024). Pull-out debonding characteristics of rockbolt with prefabricated cracks in rock: a numerical study based on particle flow code. Comput. Part. Mech. 11, 29–53. doi:10.1007/s40571-023-00607-9

CrossRef Full Text | Google Scholar

Wu, J. Y., Jing, H. W., Gao, Y., Meng, Q., Yin, Q., and Du, Y. (2022). Effects of carbon nanotube dosage and aggregate size distribution on mechanical property and microstructure of cemented rockfill. Cem. Concr. Compos. 127, 104408–104421. doi:10.1016/j.cemconcomp.2022.104408

CrossRef Full Text | Google Scholar

Wu, J. Y., Jing, H. W., Yin, Q., Yu, L. Y., Meng, B., and Li, S. C. (2020). Strength prediction model considering material, ultrasonic and stress of cemented waste rock backfill for recycling gangue. J. Clean. Prod. 276, 123189. doi:10.1016/j.jclepro.2020.123189

CrossRef Full Text | Google Scholar

Wu, J. Y., Wong, H. S., Zhang, H., Yin, Q., Jing, H. W., and Ma, D. (2024). Improvement of cemented rockfill by premixing low-alkalinity activator and fly ash for recycling gangue and partially replacing cement. Cem. Concr. Compos. 145, 105345. doi:10.1016/j.cemconcomp.2023.105345

CrossRef Full Text | Google Scholar

Xu, J., Liu, S., Wang, H., Zhou, N., and Zhang, Y. (2024). Experimental study on permeability characteristics of compacted backfill Body after gangue grouting and backfilling in the mining space. Appl. Sci. 14, 6045. doi:10.3390/app14146045

CrossRef Full Text | Google Scholar

Yan, B., Kang, H., Zuo, J., Wang, P., Li, X., Cai, M., et al. (2024). Study on damage anisotropy and energy evolution mechanism of jointed rock mass based on energy dissipation theory. Bull. Eng. Geol. Environ. 82, 294. doi:10.1007/s10064-023-03278-1

CrossRef Full Text | Google Scholar

Yang, K., Fang, J. J., Zhang, J. X., Aslani, F., He, X., Zhang, L. F., et al. (2024). Compression load-bearing characteristics and consolidation mechanism of grout-modified solid backfill materials. J. China Uni. Mining Technol., 53, 456–468. doi:10.13247/j.cnki.jcumt.20230438

CrossRef Full Text | Google Scholar

Yu, B. Y., Pan, S. C., and Xu, K. S. (2020). Particle crushing and morphology evolution of saturated crushed gangue under compaction. Adv. Civ. Eng. 2020, 1–10. doi:10.1155/2020/8839302

CrossRef Full Text | Google Scholar

Zhang, J. X., Feng, J. V., Li, M., Ma, D., and Zhang, Q. (2025). Research progress of strata control theory and method in deep backfilling mining. Bull. Natl. Nat. Sci. Found. China 38, 1043–1051. doi:10.16262/j.cnki.1000-8217.2024.06.011

CrossRef Full Text | Google Scholar

Zhang, J. X., Zhang, Q., Jv, F., Zhou, N., and Li, M. (2019a). Practice and technique of green mining with integration of mining, dressing, backfilling and X in coal resources. J. China Coal Soc. 44, 64–73. doi:10.13225/j.cnki.jccs.2018.5045

CrossRef Full Text | Google Scholar

Zhang, J. X., Zhang, Q., Zhou, N., Li, M., and Huang, P. (2022). Research progress and prospect of coal based solid waste backfilling mining technology. J. China Coal Soc. 47, 4167–4181. doi:10.13225/j.cnki.jccs.2022.1053

CrossRef Full Text | Google Scholar

Zhang, S., Liu, W., and Lv, H. (2019b). Creep energy damage model of rock graded loading. Results Phys. 12, 1119–1125. doi:10.1016/j.rinp.2018.12.081

CrossRef Full Text | Google Scholar

Zhang, T. J., Wang, X. J., Pang, M. K., Zhang, S., and Wang, F. (2023). Study on compaction and re-crushing of crushed gangue considering intermittent grading. J. Central South Univ. Sci. Technol. 54, 314–326. doi:10.11817/j.issn.1672-7207.2023.01.029

CrossRef Full Text | Google Scholar

Zhou, C. T., Zhang, K., Wang, H. B., and Xu, Y. X. (2020). A plastic strain based statistical damage model for brittle to ductile behaviour of rocks. Geomechanics Eng. 21, 349–356. doi:10.12989/gae.2020.21.4.349

CrossRef Full Text | Google Scholar

Zhou, N., Han, X. L., Zhang, J. X., and Li, M. (2016). Compressive deformation and energy dissipation of crushed coal gangue. Powder Technol. 297, 220–228. doi:10.1016/j.powtec.2016.04.026

CrossRef Full Text | Google Scholar