- College of Aerospace Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing, China
Free vibration calculations of Sandwich plates with curvilinear fiber variable stiffness composite face sheets usually require a significant computing effort to obtain a high computational accuracy. An improved approach integrating the differential quadrature method (DQM) and first-order shear deformation theory (FSDT) is introduced in this work. The skins of sandwich plates are composed of one or several layers of variable stiffness composite laminates (VSCL) with fiber paths assumed to follow a specific linear pattern. The FSDT and von Kármán strain–displacement relationship were used to derive the governing equations of the sandwich plate, and DQM was applied to discretize such governing equations and solve for the fundamental frequency of the sandwich plate. The computational results were verified and compared with other FSDT–based computational results, and there was good agreement with the suggested model. Also, the variation patterns of the natural frequency under different parameters such as fiber orientation angles, boundary conditions, number of layers, and core/skin thickness were investigated. The novelty of this study lies in the first application of an integrated DQM-FSDT approach to the free vibration analysis of sandwich plates with variable-stiffness curvilinear fiber composites. Notably, this method attains accuracy comparable to higher-order models (<5% error) with merely a 19 × 19 mesh. Key results demonstrate that optimizing the fiber path can enhance the fundamental frequency of VSCL sandwich plates by up to 32.7% (CFFF boundary), providing an efficient design tool for vibration control of aerospace lightweight structures.
1 Introduction
The high stiffness-to-weight ratio property of VSCL sandwich plates holds significant promise for their application in lightweight structures, such as aircraft wings, satellite fairings, and wind turbine blades. Typically, a sandwich construction has three sections: a top, middle, and bottom segment with a core located in the center and skins at the top and bottom (Vinson, 1999), where the skins have the same material and thickness while the core can be made of almost any material or architecture. The face sheets require high strength (Carrera and Brischetto, 2009) and the core requires light weight. Noor et al. (1996) first systematically demonstrated that sandwich plates have very high stiffness-to-weight ratio and strength-to-weight ratio properties, and Noor et al. (1996) further verified the advantages of the mechanical properties of sandwich plates through computational modelling. Based on these properties, sandwich plates are widely used in aerospace, automotive and other engineering applications (Siriruk et al., 2009). Langdon et al. (2012) specifically investigated the blast resistance of sandwich plates in marine structures. Osa-uwagboe et al. (2023), on the other hand, explored the innovative application of sandwich plates in large structures such as wind turbine blades. Sandwich structures offer significant advantages, such as high strength-to-weight ratios. These benefits, coupled with ongoing discoveries of new materials (Vinson, 2001), drive their continued use in structural design. The conventional skins of constant stiffness composite laminates (CSCL) consist of straight fibers whose stiffness, such as elasticity and flexibility, remains uniform or constant in all directions in the plane of the material. While VSCL are typically made by carefully designing and arranging layers of different materials or by altering the path of reinforcing fibers (curvilinear fiber) in the construction. Advanced technologies (e.g., automated layup) enable curved fiber placement by controlling fiber orientation. This results in continuous variation of fiber angles, as illustrated in Figure 1. As a result, the variable stiffness composite plate and shell with curvilinear fiber can be fabricated, as shown in Figure 2. (Yaman and Önal, 2016) It is obvious that a more flexible method of increasing a plate’s rigidity can be achieved by using VSCL. (Setoodeh et al., 2009) Researchers (Akhavan and Ribeiro, 2018) have recently used theoretical analysis, empirical and semi-empirical modelling, numerical simulations, and experimental testing to examine the mechanical properties of sandwich constructions. Experimental data is typically used to verify the modelling, (Yazdani and Ribeiro, 2015), while numerical simulations (Antunes et al., 2020) are preferred for their computational efficiency and rapid turnaround time.
The foundation for VSCL has been laid by numerous academics using the statics analysis of CSCL sandwich plates. Kant and Swaminathan. (2001) have analyzed the fundamental frequency of CSCL laminates and sandwich plates and the solution method used is finite element. They used a higher–order refined theory as the basis for their modelling and as parametric inputs, they systematically changed the plate thickness, the ratio of core to skin thickness, and the boundary conditions. Furthermore, their investigation included a rigorous comparative analysis with established methods to demonstrate the precision and robustness of their chosen theory. Yuan and Dawe. (2002) looked at the vibration properties of conventional sandwich plates that are rectangular in shape, including the natural frequencies and modes, using the spline finite strip method and it was concluded that the techniques of single-plate analysis were not applicable to the structural analysis of most plate structures. To lower the computational cost in the fundamental frequency prediction of sandwich plates and composite laminates, Mantari and Ore. (2015) presented a simplified FSDT. Reducing the amount of unknowns in the modelling computations allows for the reduction of the number of degrees of freedom. Comparing the computational results with those of other computational models serves as verification of the method’s accuracy. Rezaiee-Pajand and Masoodi. (2019) developed a mixed-interpolated triangular shell element using MITC theory and total Lagrangian formulation, effectively mitigating shear/membrane locking in buckling/post-buckling analysis of plates/shells, with novel benchmarks validating accuracy for complex curved structures.
The advent of advanced technologies ushered in a new era of VSCL plates and revolutionized the design landscape of composite plates. By manipulating the fiber orientation, VSCL plates offer improved mechanical properties by altering the stiffness distribution. Gürdal and Olmedo, (1993) used a numerical model to solve static problems such as displacement field and overall stiffness of VSCL symmetric laminates. They pointed out that by choosing an appropriate starting and ending angle, the given loading conditions can be better considered and a certain stiffness can be achieved or possibly the buckling behavior can be improved. Lopes et al. (2008) predicted various failure modes of VSCL plates in compression and simulated the first layer failure in post-buckling. Finite element modelling was used to predict the physical failure criteria for different modes of failure of the VSCL plates. Khani et al. (2011) applied a new solution to incorporate the failure criteria for strength into the parameter space of the laminates. The numerical results showed an increase in strength compared with the quasi–isotropic construction. Akhavan and Ribeiro. (2011) analyzed the law of variation of fundamental frequencies and mode shapes with fiber orientation angles for VSCL laminates, third-order shear deformation theory (TSDT) was the modelling technique applied, and p-version finite elements were employed in the solution. Through data comparison, they explored some connections that exist between fiber orientation angles and fundamental frequencies.
Existing research on VSCL plates focuses on statics and has only investigated their dynamics to a limited extent, which warrants further research into their dynamics in future studies. Houmat. (2020) and Hachemi. (2020); Hachemi. (2022) are among the few scholars who have performed free vibration analysis of VSCL sandwich plates. The modelling theory used by Houmat is three-dimensional elasticity theory, while the analysis of Hachemi is grounded in both layer-wise theory and HSDT. They both chose p-version finite elements as the solution method. By adjusting factors including fiber orientation angles, boundary conditions, and skin-to-core thickness ratios, the variation patterns of fundamental frequencies as well as other dynamic responses were examined, highlighting the benefits of VSCL sandwich plates in structural investigations.
Systems of partial differential equations that typically have difficult-to-find closed-form solutions characterize engineering challenges. (Civalek, 2008) Consequently, engineers and researchers frequently turn to approximative numerical techniques to solve such systems. These methods include the finite element, the p-version finite element, the Rayleigh–Ritz methods, the finite volume method and so on. Pany. (2022) developed a PS-FEM model using triangular shell elements to estimate wave propagation constants in line-supported periodic plates, enabling efficient prediction of bandgap characteristics and multi-span panel frequencies through propagation surface discretization. Pany and Li. (2023) combined periodic structure theory with FEM to model wave propagation in metamaterials and pressurized frames, enabling non-reciprocal transmission and prestress simulation. Bellman and Casti. (1971) developed the differential quadrature technique (DQM) for solving partial differential equations. DQM has the advantage of having a smaller number of discrete points with higher computational accuracy. Liu. (2001) utilized Mindlin plate theory as the modelling theory and applied DQM to the investigation of rectangular plate buckling. Liew et al. (1996) used DQM to conduct a static study of a rectangular plate on Winkler’s basis, utilizing FSDT as the modelling theory. This is the first successful application of DQM to thick–plate problems. Based on previous work, Liew et al. (2003) applied the moving least squares differential quadrature (MLSDQ) to calculate and study the fundamental frequency of symmetric laminates of medium thickness and the modelling theory is FSDT. The free vibration problem of sandwich plates with functional grades on an elastic foundation was investigated by Fu et al. (2020). They employed DQM, and the modelling theory is NSDT. Ghandehari et al. (2025) modeled temp-dependent CNT-reinforced nested conical shells via FSDT/GDQM, introducing elastic interlayers and arbitrary BCs for vibration analysis under thermal loads. Mottaghi et al. (2025) employed FSDT and Hamilton’s principle for modelling and GDQM for solving, investigating the free vibration of CNT-reinforced polymer composite rings, analyzing agglomeration, porosity, and elastic coupling effects. Innovatively, they developed a novel CBR model, unraveling multifactor coupling mechanisms. To the best of our knowledge, no studies have yet applied the DQM to the free vibration analysis of VSCL sandwich plates modelling by FSDT.
This work proposes an FSDT-based DQM approach to give a reasonably accurate and computationally cheap computer model for the free vibration analysis of VSCL sandwich structures. The plate consists of two VSCL skins and an isotropic core. Based on the FSDT, the governing equations were derived using the von Kármán strain–displacement relationship and Hamilton’s principle. By applying the DQM, the fundamental frequencies of the sandwich plates were determined numerically, and the impacts of several parameters on the plate’s vibration behaviour were examined. Distinguishing from existing studies that mostly use the finite element method to analyze VSCL structures, this study is the first to apply the combination of DQM and FSDT to the free vibration analysis of VSCL sandwich plates with curvilinear fiber. The method significantly reduces the computational cost by reducing the number of grid points (only 19 × 19 grids are required) while maintaining comparable accuracy to higher-order models (see Tables 2, 3), providing a new way for efficient dynamic modelling under complex boundary conditions.
This is how the remainder of the paper is structured. The modelling procedure and analytical method employed are stated in the second section. In the third section, numerical applications and discussion, encompassing both CSCL and VSCL sandwich plates, are presented. The last section summarizes the conclusions.
2 Theoretical formulation
2.1 Geometric description
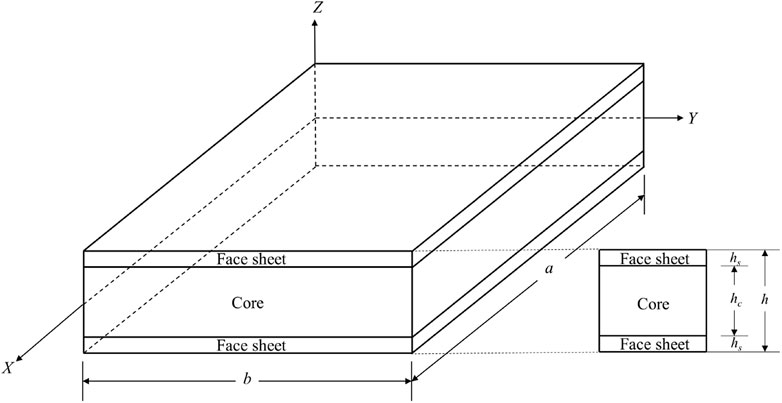
The geometrical design and parameterization of a sandwich plate with variable stiffness skins are displayed in Figure 3. The upper and lower composite skins, every stratum of the skin consisting of single or laminated composite layers with curvilinear fibers, with a soft core in the centre, make up the entire plate, assume that the dimensions of the plate are a, b, and h, respectively, for length, breadth, and thickness. The total thickness h can be decomposed into upper and lower skins
To simplify the definition, the point of central symmetry of the reference path is typically specified to be at the center of each individual layer of the skin, as illustrated in Figure 3, and the Cartesian coordinate system is defined as
where,
Integrating the above equation gives the reference path for the curvilinear fiber placement as Equation 2:
2.2 Modelling theory
Between the skin and core materials of sandwich plates, there are significant differences in stiffness and material properties, making the performance analysis of the sandwich structure quite intricate. As a result, the calculation model selected has a significant impact on how accurately the sandwich structure is calculated. (Pandey and Pradyumna, 2015). Transverse shear deformation is not taken into account by the classical laminated plate theory (CLPT), which is predicated on Kirchhoff’s assumptions. Therefore, for plates of moderate thickness, CLPT’s estimates on both static and dynamic analysis are biased. (Abrate, 2008; Zare et al., 2015; Pushparaj and Suresha, 2016; Belarbi et al., 2017). For the purpose of this study’s free vibration analysis of sandwich plates, the author employed the FSDT modelling theory, (Reddy, 2004), which accounts for the impact of shear deformation.
In this study, the FSDT theory and the linear part of the von Kármán strain-displacement relationship [the nonlinear term is neglected in Equation 4] are used, which is suitable for the linear analysis of free vibration under small deformations. Based on the first two assumptions of Kirchhoff (the normal remains straight and perpendicular to the midplane), this study ignores the third assumption (ignoring the positive strain in the thickness direction), and adopts the FSDT theory to consider the transverse shear deformation. In case a symmetric sandwich plate is used, the vibrations in the transverse and in-plane directions are separated by the symmetry in the z direction, and the in-plane deformation at
where the displacements along the three coordinate axes are denoted by u, v, and w, and the midplane of the plate rotates about the x and y axes at angles
Per the von Kármán strain-displacement relationship, linear strain components are:
Applying Hooke’s law and assuming plane stress, the stress components of the plate areas are obtained in the following way:
where
where
where
Hamilton’s principle can be used to generate the moving equations in the following way: (Reddy, 2004):
where U is the strain form and T is the kinetic form of energy, respectively.
The strain energy can be shown in the following way:
The kinetic energy can be shown in the following way:
The moving equations for the sandwich plate’s free vibration may be acquired by substituting Equations 4,–7,9,10 into Equation 8:
where
2.3 Equation of motion
The stress resultants Mij and transverse shear force Qij can be determined by integrating the stresses in each single layer along the direction of thickness.
Equation 11 can be substituted with Equation 12 to assemble the following formulations for the governing equations of the sandwich plate’s free vibration.
where Aij and Dij are the stretching and bending stiffnesses, respectively, and the expressions are given in Equation 16.
Aij are stiffness coefficients related to internal forces and midplane strains only, collectively referred to as stretching stiffness. Dij are stiffness coefficients related to internal moments with respect to curvature and twist rate, collectively referred to as bending stiffness.
2.4 Differential quadrature method
DQM is essentially a differential equation in the function at each node of the derivative with the calculation of the region of all nodes at the function value of the weighted sum to replace. (Bellman and Casti, 1971). The required differential equation’s numerical solution can be found in the resultant system of equations. This is how DQM transforms the differential equation solution problem into the linear equation system solving problem. (Shu et al., 2002; 2004; Thai et al., 2014; Malikan and Far, 2018). Supplementary Appendix SI provides the specific implementation of this technique.
To simplify the calculation, for the DQM discretization of the moving equations, the expressions for the weighting coefficients were obtained:
The separating variables for the displacement terms (w,
where
To facilitate subsequent calculations and comparisons, the data are dimensionless as follows:
where
Substituting Equations 17–19 into Equations 13–15 and performing a DQM discretization, the governing equations can be shown as follows:
where
To simplify the calculation, Equations 20–22 can be stated more succinctly as Equations 24 or 25:
or
Similarly, the boundary conditions can be derived by discretization using the DQM
The solution of the specific matrix
To find the basic frequencies, or eigenvalues, and the accompanying eigenvectors, all mesh points were divided into two groups: internal domain points and boundary points. The boundary points, indicated by {b} in vector form, are situated at the plate’s four edges. The domain points are the set of all remaining interior points and are denoted by {d}. Boundary conditions are substituted into the governing equations. The resulting system is then divided and rearranged into the following matrix equation:
By eliminating the non–zero element
where
2.5 Boundary conditions
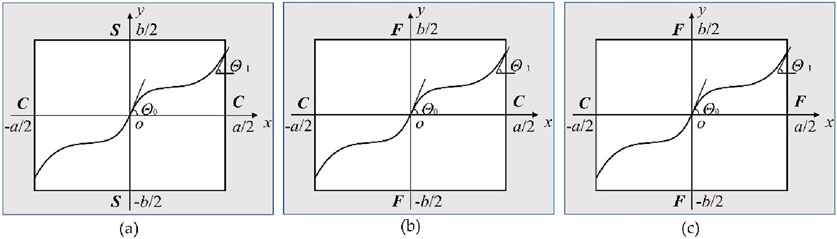
This study covers five types of boundary conditions: four-side clamped support (CCCC), four-side simply support (SSSS), opposite-side clamped support-simply support (CSCS), opposite-side clamped support-free (CFCF), and three-side clamped support-free on one side (CFFF), whose mathematical expressions are presented in Equations 29–31. Figure 5 Illustrates the constraint schematics of CSCS, CFCF and CFFF.
The following are the boundary condition phrases for each edge.
(a) Clamped (C)
(b) Simply supported (S)
(c) Free (F)
Substituting Equation 12 into Equation 31, gives the following Equation 32:
Equations 29–31 can be combined to express the boundary conditions for a sandwich plate with hybrid boundary conditions.
After applying the DQM to discretize the above equations, the following Equations 33–35 can be got.
(a) Clamped
(b) Simply supported
(c) Free
In this way, the specific matrix
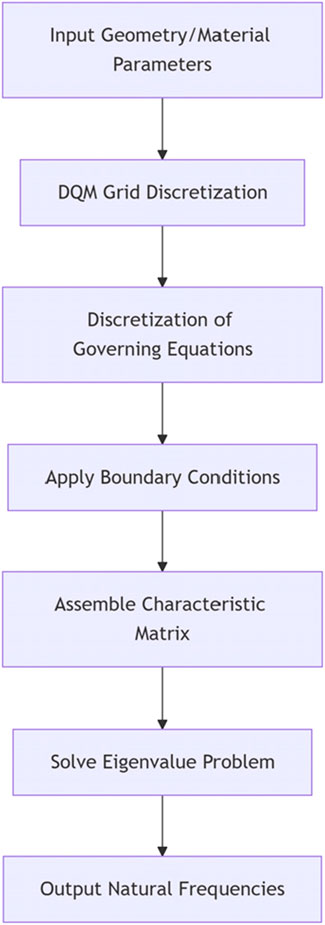
Figure 6 illustrates the solution procedure of the Differential Quadrature Method (DQM). The core concept involves replacing differential operations with a weighted summation of grid points (see Supplementary Appendix SI), significantly reducing computational dimensionality. By implementing the flowchart in MATLAB, the natural frequencies of sandwich plates can be effectively determined.
3 Results and discussion
3.1 Validation and convergence studies
The validation and convergence investigations of the free vibration for VSCL sandwich plates using the DQM solution method are provided in this part. By comparing the results with other FSDT-based numerical solution solutions for currently available CSCL sandwich plates, the quantity of DQM grid points was ascertained.
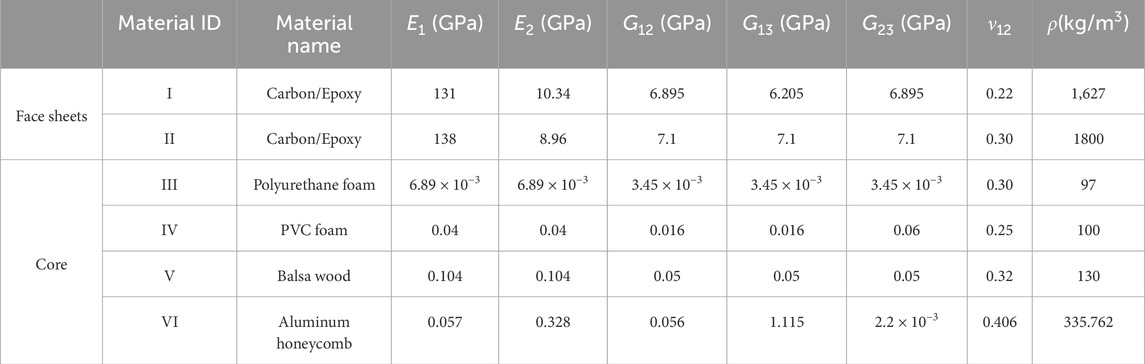
Since the skins of a sandwich structure provides the main load-carrying capacity, the core transfers the load between the skins. Therefore, in terms of material selection, skins are usually made of high-strength and lightweight materials, while the core is selected as a flexible layer with low density and good energy absorption capability. In the selection of skins and cores for aircraft and spacecraft, aluminum alloys, carbon fibers, and glass fibers are usually chosen as skin materials, while the core can be made of solid low-density materials, honeycomb-like expanded high-density materials, and corrugated expanded high-density materials. Based on the above requirements, the Mechanical properties of the materials selected for this work are listed in Table 1. In the study, material I and material III in Table 1 were used as the skins and the core, respectively.
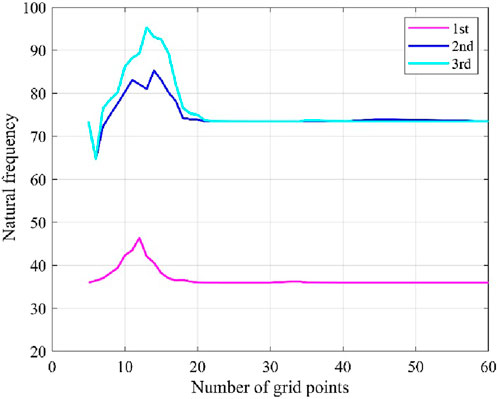
First, the quantity of grid points at which the natural frequency generated by this method might be stabilized is determined by selecting an anti–symmetric sandwich plate of [0/90/core/0/90] with the geometric parameters
The quantity of grid points in this investigation was selected as
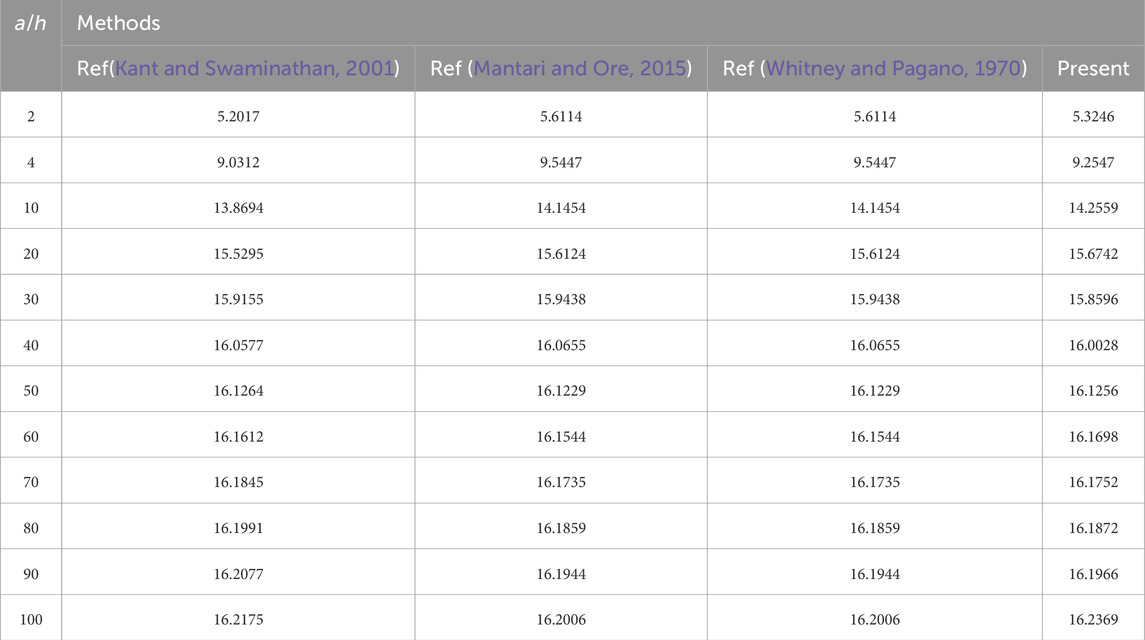
Table 2. The dimensionless fundamental frequency of anti–symmetric
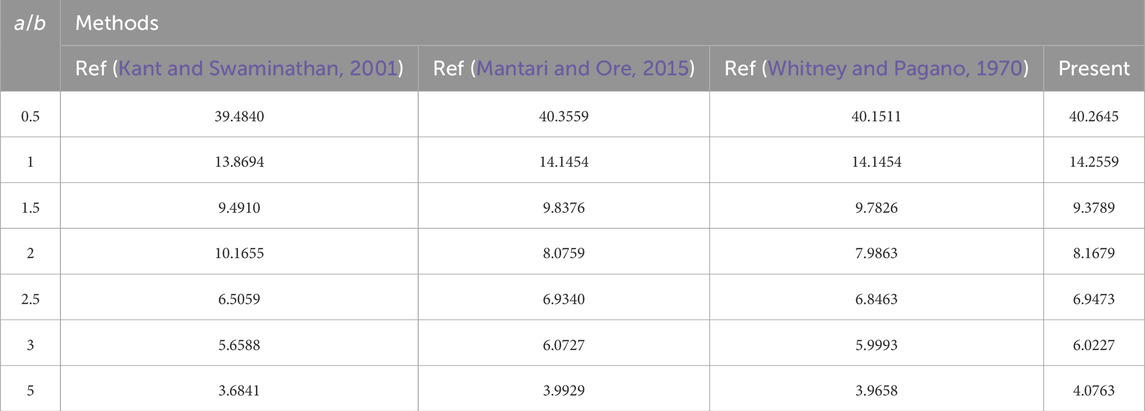
Table 3. The dimensionless fundamental frequency of anti–symmetric
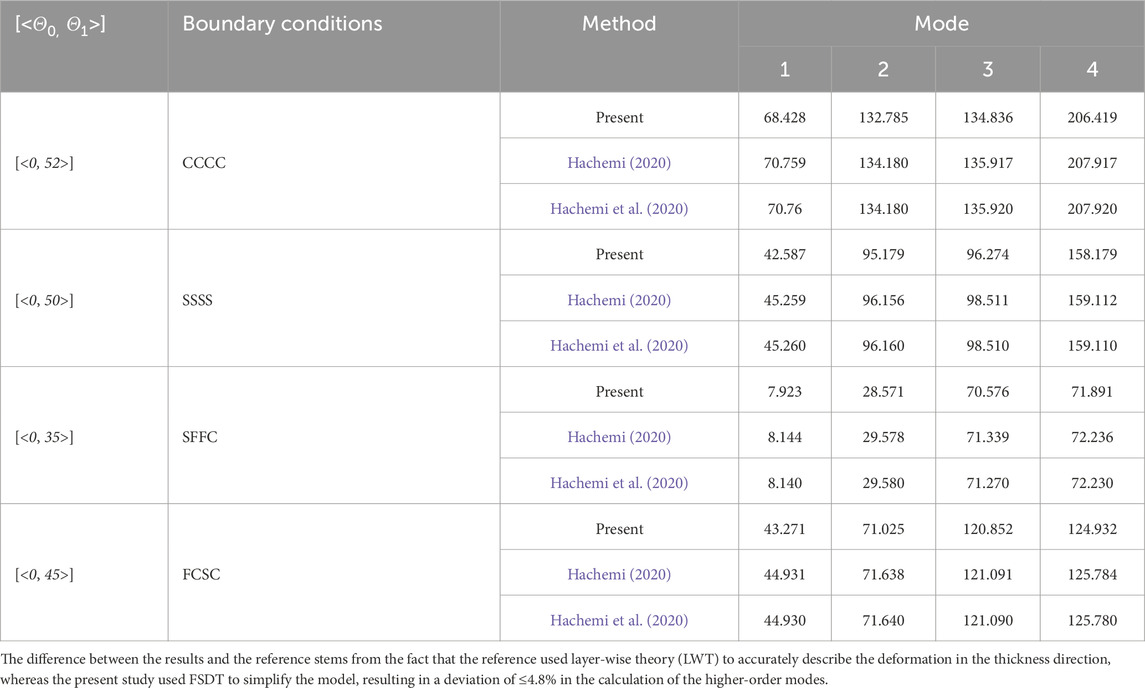
As is evident from Tables 2 and 3, the results of the DQM used in this study to calculate the composite sandwich plates are only slightly different from those of the references, indicating that the mechanical model and calculation method used in this study are correct. At the same time, only 19 × 19 grid points are used in this study, which enables high accuracy of the results. Regarding computation effectiveness, the current paper’s approach is better.
The free vibration analysis of VSCL plate is carried out in the next step. The first four orders of the natural frequency of the single layer plate are investigated for different starting angle Θ0 and termination angle Θ1. The first four orders of the natural frequency of the single layer plate are investigated. Different boundary conditions are selected. The material was chosen as material II in Table 1 and the ratio of width to thickness a/h was chosen as 0.001. The results of the calculations are listed in Table 4. When the number of mesh points was selected as 19, the computed results were compared with the existing solutions of FSDT and p-version finite elements. The computational results are in very good agreement, verifying the reliability of the present method for VSCL plate computation.
3.2 Parameter study
A parameter research of the free vibrations was carried out to enhance the vibratory behavior of the VSCL sandwich plates. The fundamental frequency of the sandwich plate was examined in relation to the fiber orientation angles, boundary conditions, number of layers, and core/skin thickness.
3.3 Fiber orientation angles
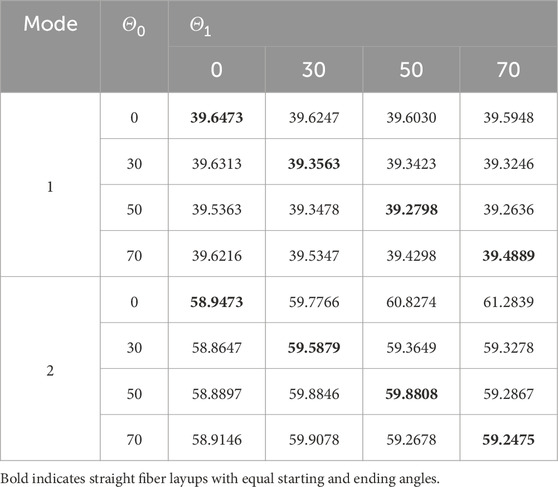
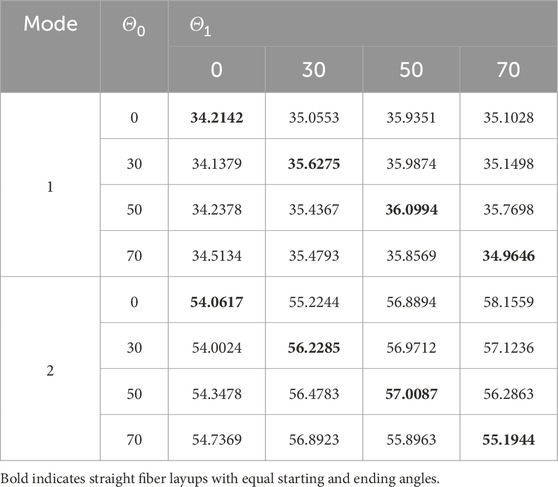
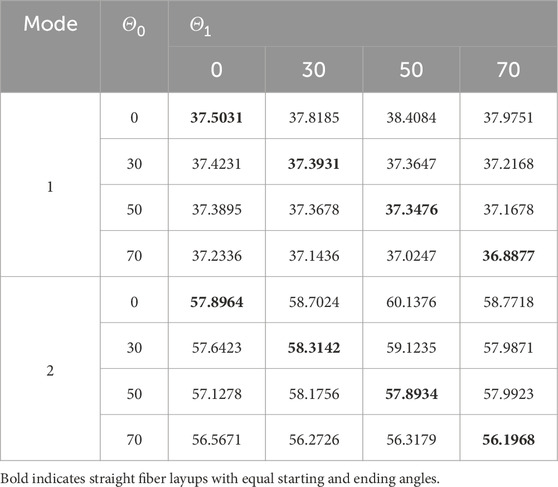
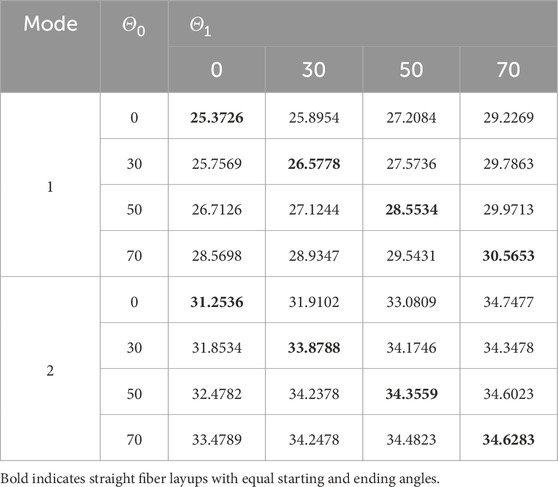
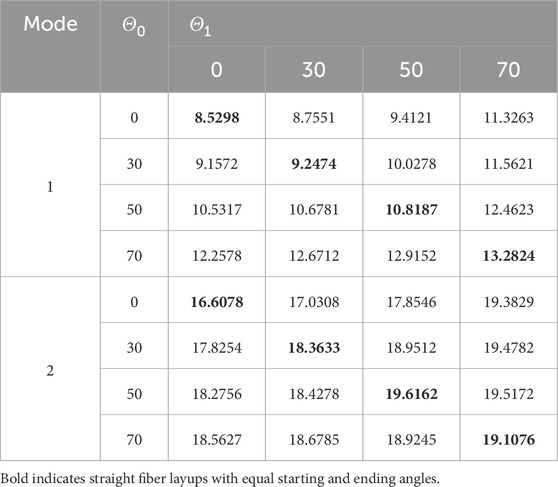
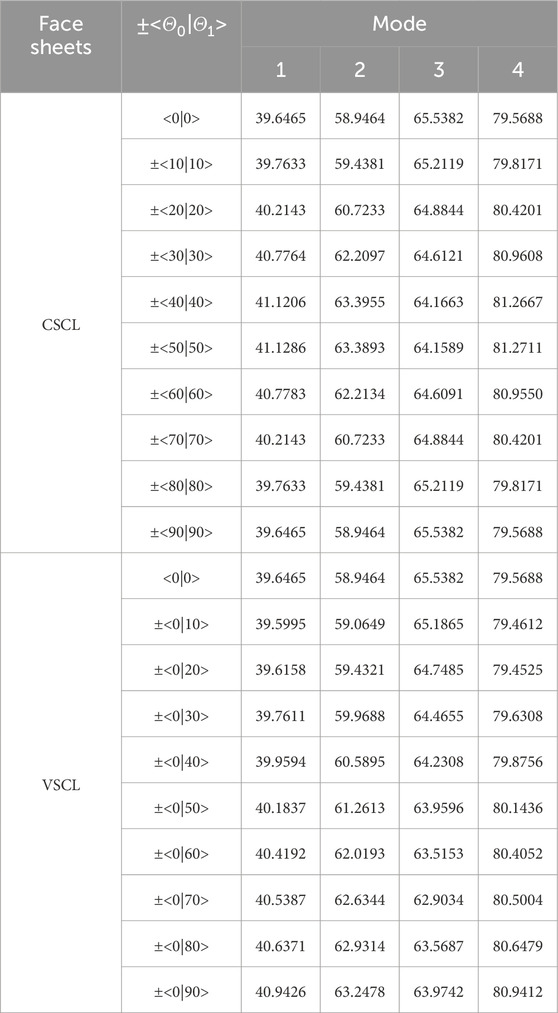
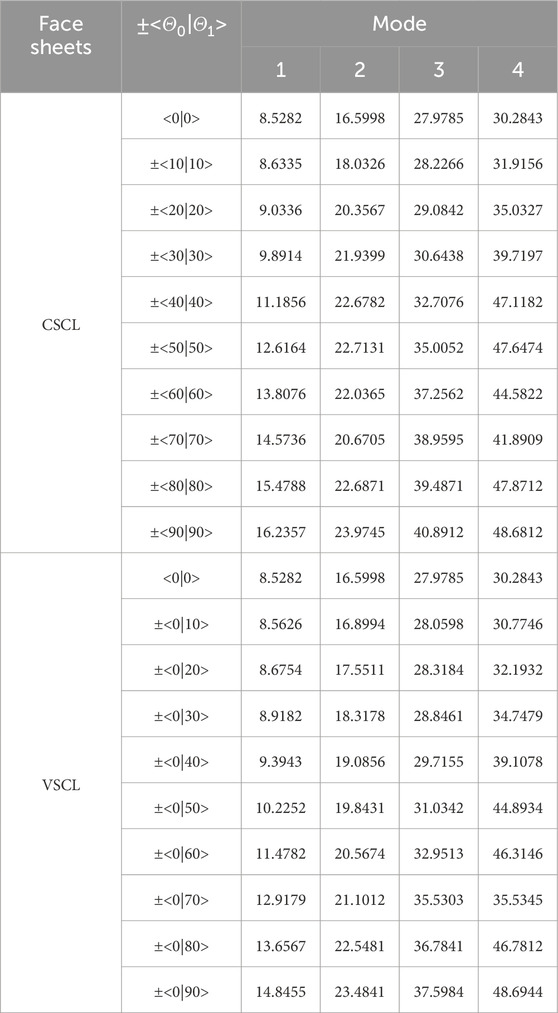
First, the effect of changes in the start and termination angles was investigated. In this section, a VSCL sandwich plate with four symmetric skins
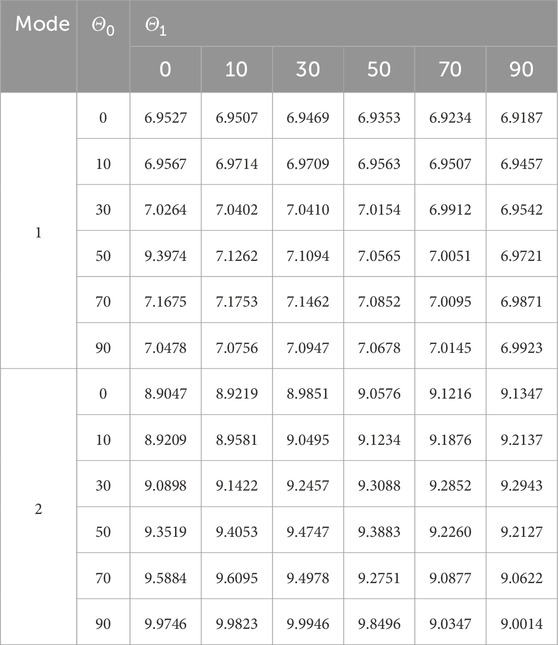
Table 5. First and second natural frequencies of the VSCL sandwich square plate
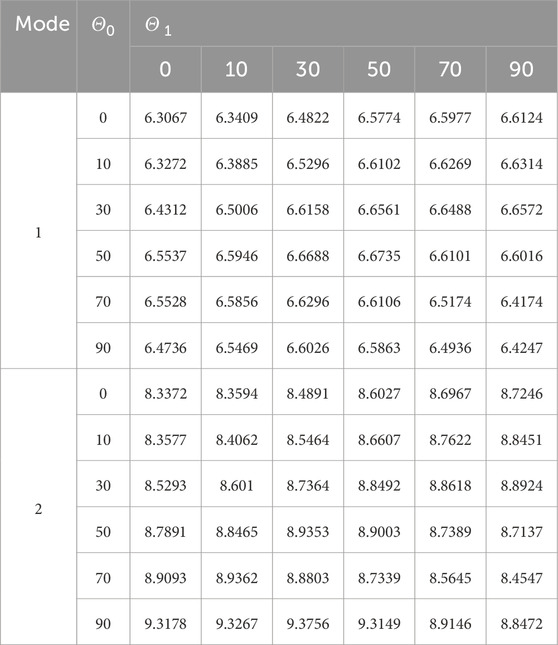
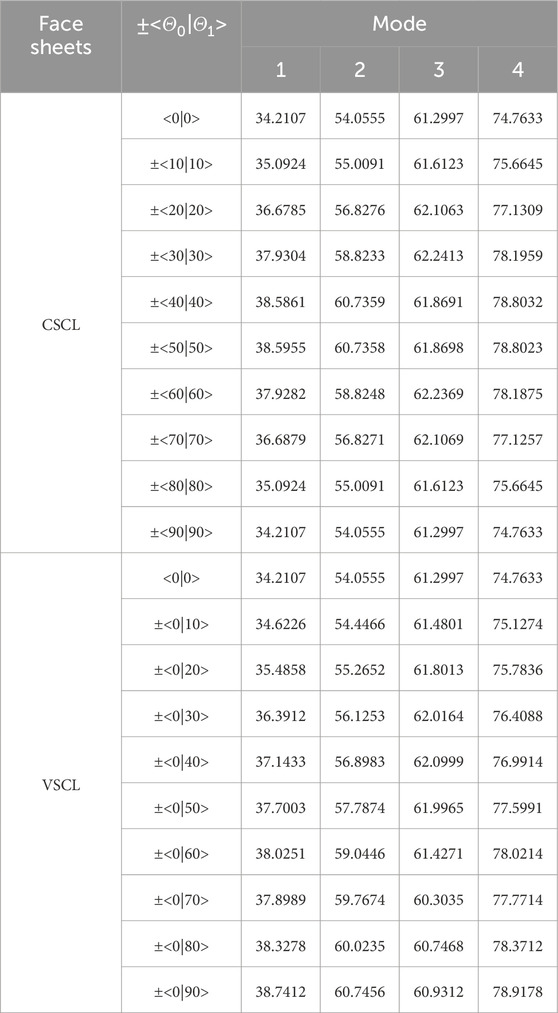
Table 6. First and second natural frequencies of the VSCL sandwich square plate
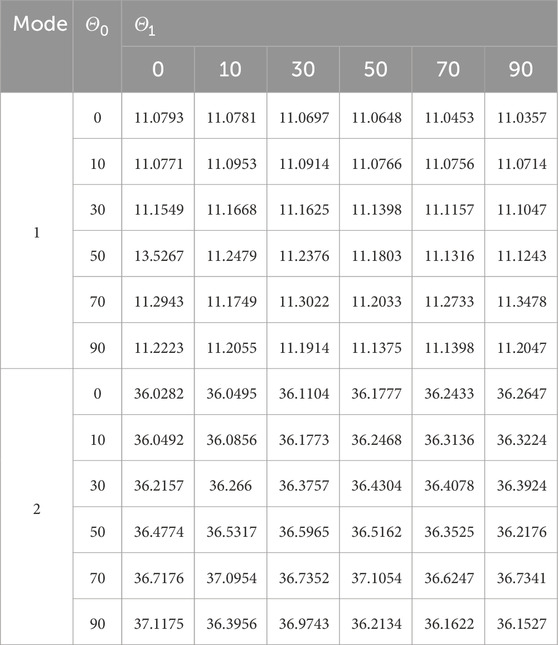
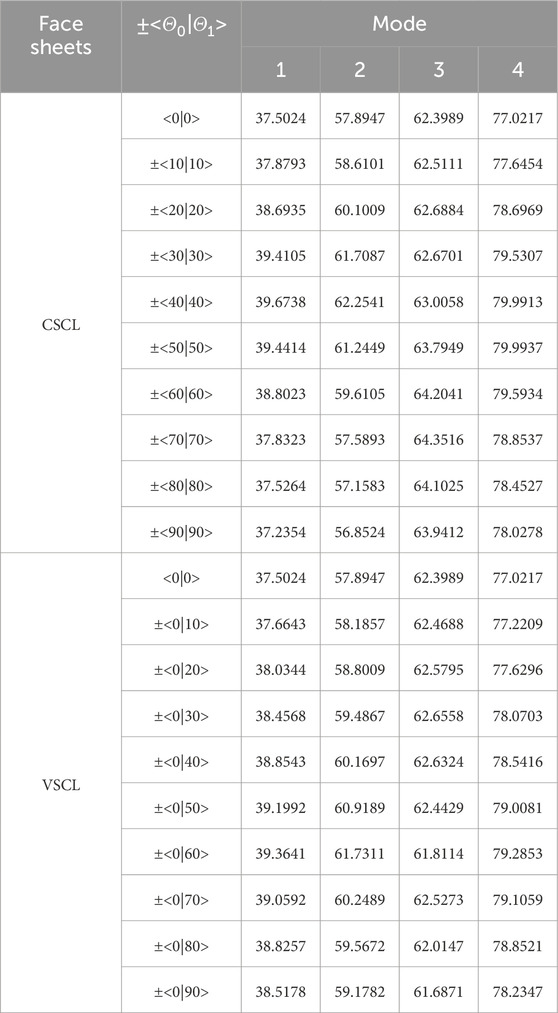
Table 7. First and second natural frequencies of the VSCL sandwich square plate
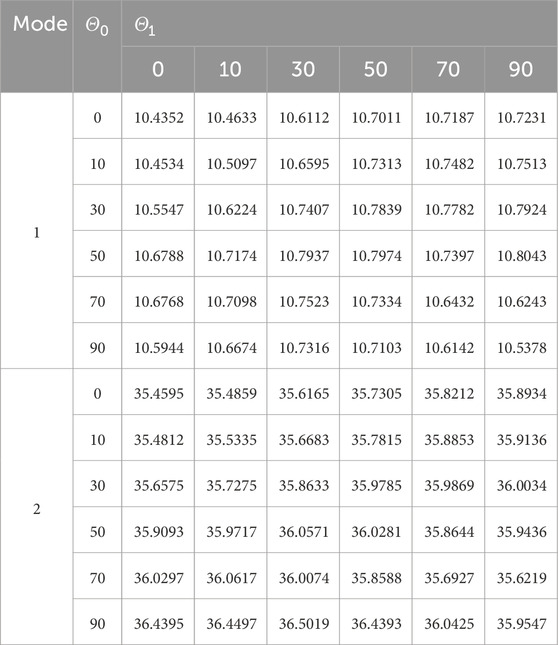
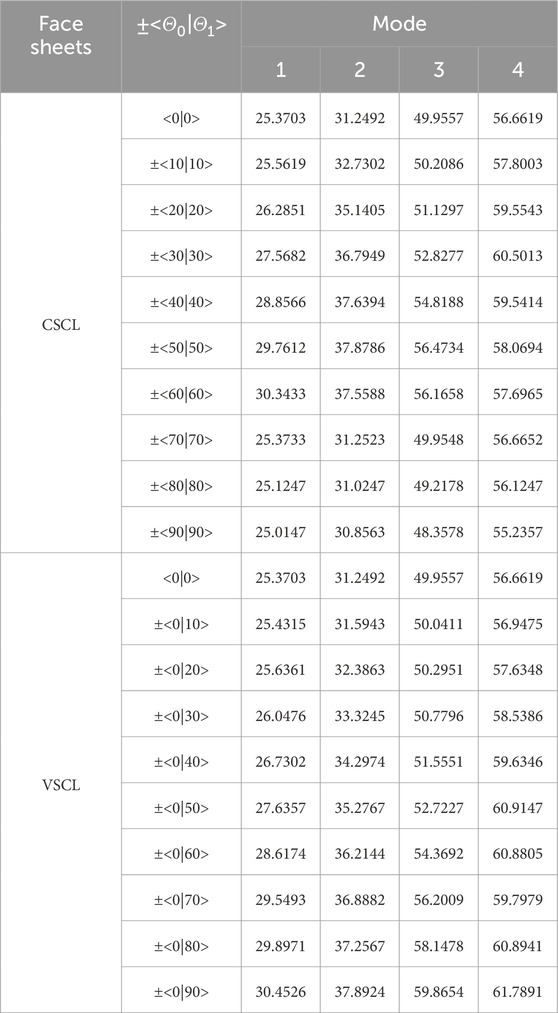
Table 8. First and second natural frequencies of the VSCL sandwich square plate
Tables 5–8 reveal that the majority of fundamental frequencies typically rise with the increase of fiber orientation angle. A corresponding decrease in the natural frequency was observed when the fiber orientation angle reached the maximum value. Therefore, sandwich plates can be made stiffer by using curvilinear fibers with low curvatures. In order to avoid fiber kinking, the curved fibers must have a maximum value of curvature on each skin of less than 3.28 m-1. The curvature k is given by Equation 36. In the case of curved fibers with curvature values less than 3.28 m-1, the use of lower curvature leads to higher stiffness. In certain instances, industry designers must alter the fundamental frequency to a greater or lesser value for the purpose of preventing resonance. This can be accomplished by using VSCL, sandwich plates without having to change the size of the plate or constituent materials. The reason for this is that the natural frequency is sensitive to changes in fiber orientation in each layer.
3.4 Boundary conditions
In order to investigate the first two fundamental frequencies at various fiber orientation angles, five boundary conditions were taken into consideration in this section. A comparative study between the CSCL and VSCL sandwich plates was also conducted. In this section, sandwich plates with single-ply skins
Tables 9–13 demonstrate that for the SSSS, CSCS, CFCF, and CFFF boundary conditions, the VSCL sandwich plate’s natural frequency tends to grow when the ending angle
3.5 Limited layer impact (≤5)
This section looks into how the number of layers affects sandwich plate’s fundamental frequency. Based on sandwich plates with single-ply skins
From Tables 14–18, it is clear that when
Under CCCC and CSCS boundary conditions, VSCL sandwich plates exhibit 6%–12% higher fundamental frequencies than CSCL counterparts. This was determined by comparing the fundamental frequencies of the two sandwich plates. Sandwich plate vibration properties can be considerably altered by the application of curvilinear fiber. For instance, when comparing
3.6 Core/skin thickness
Sandwich plates that are symmetric and anti-symmetric are used in this part to investigate the relation between the fundamental frequency and the ratio of the core to skin. The skins and core were selected with the same thickness and mechanical characteristics as those in the preceding section, except for the plate thickness
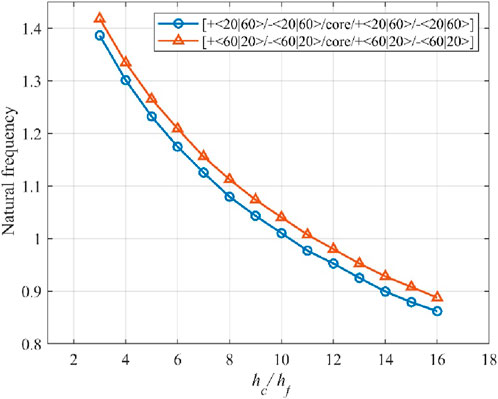
![Graph showing the natural frequency versus the ratio of \( h_c / h_f \). A blue line with circles represents one data set, while an orange line with triangles represents another. Both lines depict a decreasing trend. The legend explains the layering sequences: [+<20|60>/-<20|60>/core/-<20|60>/+<20|60>] and [+<60|20>/-<60|20>/core/-<60|20>/+<60|20>].](https://www.frontiersin.org/files/Articles/1601813/fmats-12-1601813-HTML/image_m/fmats-12-1601813-g008.jpg)
Figure 8. Natural frequency (non-dimensional) to core/skin ratio hc/hs effect of the symmetric VSCL sandwich plate [+<20|60>/-<20|60>/core/-<20|60>/+<20|60>] and [+<60|20>/-<60|20>/core/-<60|20>/+<60|20>], CSCS.
 /-<20|60>/core/+<20|60>/-<20|60>]" and another with red triangles labeled "[+<60|20>/-<60|20>/core/+<60|20>/-<60|20>]". Both lines decrease as the \(h_c/h_f\) ratio increases." id="F9" loading="lazy">
/-<20|60>/core/+<20|60>/-<20|60>]" and another with red triangles labeled "[+<60|20>/-<60|20>/core/+<60|20>/-<60|20>]". Both lines decrease as the \(h_c/h_f\) ratio increases." id="F9" loading="lazy">
Figure 9. Natural frequency (non-dimensional) to core/skin ratio hc/hs effect of the anti-symmetric VSCL sandwich plate [+<20|60>/-<20|60>/core/+<20|60>/-<20|60>] and [+<60|20>/-<60|20>/core/+<60|20>/-<60|20>], CSCS.
As shown in Figures 8, 9, the VSCL sandwich plates exhibit the highest natural frequency at the lowest core/skin thickness ratio. The average decline in fundamental frequency from the greatest to the lowest point was 67%.
The findings of the aforementioned parametric study suggest that VSCL sandwich plates hold promise for aircraft panel design applications. By manipulating the starting and ending angles along with the curvature of the fiber reference path, these plates can potentially exhibit reduced lateral deformation, increased stiffness, and higher natural frequencies. Moreover, lower structural mass can be achieved under certain mechanical and environmental loading circumstances by using VSCL sandwich plates.
4 Conclusion
This study used FSDT in conjunction with DQM to examine the free vibration of sandwich plates with curvilinear fiber variable stiffness skins. In this study, the x-coordinate was supposed to fluctuate linearly with the fiber orientation angle. Compared with other numerical solution methods, the DQM is computationally inexpensive, converges quickly, and it is capable of precisely forecasting sandwich plate fundamental frequencies. The reduction or increase in the natural frequency when using VSCL face sheets was investigated and compared with that of CSCL face sheets. The impacts of fiber orientation angles, boundary conditions, number of layers, and core/skin thickness were investigated parametrically. Notably, the integration of higher-order theory and layer theory can enhance the accuracy of sandwich plate analysis, particularly when investigating thick plates. The computations used in this study allow for the following deductions.
(1) In the vast majority of cases, as the fiber orientation angle increases, the fundamental frequency rises as well. Optimizing the curved fiber path improves the fundamental frequency of the CFFF boundary condition by 32.7% and the CFCF boundary condition by 15.2%, outperforming the constant stiffness design (CSCL). The use of curvilinear fibers leads to VSCL sandwich plates with lower lateral deformations and higher natural frequencies.
(2) The sandwich plate’s natural frequency was impacted by the fiber orientation angle as the curvilinear fibers’ curvature grew. The larger the angle of the center fiber was, the more rigid the curvilinear fiber became, until the curvature threshold is reached (3.28 m-1). The plate’s rigidity can be raised by using low-curvature curvilinear fibers.
(3) With an increase in layers came a rise in the sandwich plate’s fundamental frequency. Anti-symmetric stacking (±<Θ0|Θ1>) improves frequency by 6%–12% compared to single-layer skins. This also indicates that the fundamental frequency increases with rising plate thickness.
(4) The VSCL sandwich plates exhibited greater natural frequencies in comparison to the CSCL sandwich plates when subjected to the CCCC and CSCS boundary conditions. As boundary restrictions get tighter, the frequency rises. Tighter boundaries (CCCC, CSCS) amplify the benefits of VSCL by more than 10%. Due to their increased ability to adapt to complex boundary circumstances, curvilinear fibers have higher fundamental frequencies than parallel fibers.
(5) The frequency response was strongly impacted by the ratio of skin to core thickness. Frequencies peak at minimal hc/hs (3:1) and decline by 67% as ratios increase to 16:1. The natural frequency of the sandwich plate reached its maximum value at the lowest core–to-skin thickness ratio. The effect of adding more layers was in line with this trend.
(6) The FSDT accuracy decreases for core-to-mask ratios hc/hs > 16 (see Table 2 for a/h = 2 error of 5.2%), and it is recommended that the HSDT model be used for thick plates.
The method proposed in this paper provides theoretical support for the vibration control design of lightweight structures in the aerospace field, such as enabling the adjustment of natural frequencies under specific operational conditions through fiber path optimization. Additionally, the precise insights obtained from this study guide researchers seeking viable solutions and can serve as a foundation for further exploration into panel flutter in VSCL sandwich plates. The current model does not consider interlayer delamination damage, and in the future, the Reissner interlayer continuity condition will be introduced to simulate the debonding effect and improve the damage tolerance prediction of VSCL sandwich plates.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
ZZ: Writing – review and editing, Software, Writing – original draft, Validation, Investigation, Conceptualization, Supervision, Methodology.
Funding
The author(s) declare that no financial support was received for the research and/or publication of this article.
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The author(s) declare that no Generative AI was used in the creation of this manuscript.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2025.1601813/full#supplementary-material
References
Abrate, S. (2008). Functionally graded plates behave like homogeneous plates. Compos. B. Eng. 39, 151–158. doi:10.1016/j.compositesb.2007.02.026
Akhavan, H., and Ribeiro, P. (2011). Natural modes of vibration of variable stiffness composite laminates with curvilinear fibers. Compos. Struct. 93, 3040–3047. doi:10.1016/j.compstruct.2011.04.027
Akhavan, H., and Ribeiro, P. (2018). Aeroelasticity of composite plates with curvilinear fibres in supersonic flow. Compos. Struct. 194, 335–344. doi:10.1016/j.compstruct.2018.03.101
Antunes, A. M., Ribeiro, P., Dias Rodrigues, J., and Akhavan, H. (2020). Modal analysis of a variable stiffness composite laminated plate with diverse boundary conditions: experiments and modelling. Compos. Struct. 239, 111974. doi:10.1016/j.compstruct.2020.111974
Belarbi, M. O., Tati, A., Ounis, H., and Khechai, A. (2017). On the free vibration analysis of laminated composite and sandwich plates: a layerwise finite element formulation. Lat. Am. J. Solids Struct. 14, 2265–2290. doi:10.1590/1679-78253222
Bellman, R., and Casti, J. (1971). Differential quadrature and long-term integration. J. Math. Anal. Appl. 34, 235–238. doi:10.1016/0022-247X(71)90110-7
Birman, V., and Bert, C. W. (2002). On the choice of shear correction factor in sandwich structures. J. Sandw. Struct. Mater. 4, 83–95. doi:10.1177/1099636202004001180
Carrera, E., and Brischetto, S. (2009). A survey with numerical assessment of classical and refined theories for the analysis of sandwich plates. Appl. Mech. Rev. 62, 1–17. doi:10.1115/1.3013824
Civalek, Ö. (2008). Free vibration analysis of symmetrically laminated composite plates with first-order shear deformation theory (FSDT) by discrete singular convolution method. Finite Elem. Anal. Des. 44, 725–731. doi:10.1016/j.finel.2008.04.001
Fu, T., Chen, Z., Yu, H., Wang, Z., and Liu, X. (2020). Free vibration of functionally graded sandwich plates based on nth-order shear deformation theory via differential quadrature method. J. Sandw. Struct. Mater. 22, 1660–1680. doi:10.1177/1099636218809451
Ghandehari, M. A., Masoodi, A. R., and Hosseininia, E. S. (2025). Temperature-dependency and boundary condition impacts on the multiscale vibrational behavior of laminated nested dual conical shell structure semi-AUV applications. Appl. Ocean. Res. 154, 104425. doi:10.1016/j.apor.2025.104425
Gürdal, Z., and Olmedo, R. (1993). In-plane response of laminates with spatially varying fiber orientations: variable stiffness concept. AIAA J. 31, 751–758. doi:10.2514/3.11613
Hachemi, M. (2020). Vibration analysis of variable stiffness laminated composite sandwich plates. Mech. Adv. Mater. Struct. 27, 1687–1700. doi:10.1080/15376494.2018.1524951
Hachemi, M. (2022). Layer-wise solutions for variable stiffness composite laminated sandwich plate using curvilinear fibers. Mech. Adv. Mater. Struct. 29, 5460–5477. doi:10.1080/15376494.2021.1956028
Hachemi, M., Hamza-Cherif, S. M., and Houmat, A. (2020). Free vibration analysis of variable stiffness composite laminate plate with circular cutout. Aust. J. Mech. Eng. 18, 63–79. doi:10.1080/14484846.2017.1385694
Houmat, A. (2020). Three-dimensional solutions for free vibration of variable stiffness laminated sandwich plates with curvilinear fibers. J. Sandw. Struct. Mater. 22, 896–925. doi:10.1177/1099636218778731
Kant, T., and Swaminathan, K. (2001). Analytical solutions for free vibration of laminated composite and sandwich plates based on a higher-order refined theory. Compos. Struct. 53, 73–85. doi:10.1016/S0263-8223(00)00180-X
Khani, A., Ijsselmuiden, S. T., Abdalla, M. M., and Gürdal, Z. (2011). Design of variable stiffness panels for maximum strength using lamination parameters. Compos. Part B Eng. 42, 546–552. doi:10.1016/j.compositesb.2010.11.005
Langdon, G. S., von Klemperer, C. J., Rowland, B. K., and Nurick, G. N. (2012). The response of sandwich structures with composite face sheets and polymer foam cores to air-blast loading: preliminary experiments. Eng. Struct. 36, 104–112. doi:10.1016/j.engstruct.2011.11.023
Liew, K. M., Han, J. B., Xiao, Z. M., and Du, H. (1996). Differential quadrature method for Mindlin plates on Winkler foundations. Int. J. Mech. Sci. 38, 405–421. doi:10.1016/0020-7403(95)00062-3
Liew, K. M., Huang, Y. Q., and Reddy, J. N. (2003). Vibration analysis of symmetrically laminated plates based on FSDT using the moving least squares differential quadrature method. Comput. Methods Appl. Mech. Eng. 192, 2203–2222. doi:10.1016/S0045-7825(03)00238-X
Liu, F. L. (2001). Differential quadrature element method for buckling analysis of rectangular mindlin plates having discontinuities. Int. J. Solids Struct. 38, 2305–2321. doi:10.1016/S0020-7683(00)00120-7
Lopes, C. S., Gürdal, Z., and Camanho, P. P. (2008). Variable-stiffness composite panels: buckling and first-ply failure improvements over straight-fibre laminates. Comput. Struct. 86, 897–907. doi:10.1016/j.compstruc.2007.04.016
Malikan, M., and Far, M. N. S. (2018). Differential Quadrature method for dynamic buckling of graphene sheet coupled by a viscoelastic medium using Neperian Frequency based on nonlocal elasticity theory. J. Appl. Comput. Mech. 4, 147–160. doi:10.22055/JACM.2017.22661.1138
Mantari, J. L., and Ore, M. (2015). Free vibration of single and sandwich laminated composite plates by using a simplified FSDT. Compos. Struct. 132, 952–959. doi:10.1016/j.compstruct.2015.06.035
Mindlin, R. D. (1951). Influence of rotatory inertia and shear on flexural motions of isotropic, elastic plates. J. Appl. Mech. 18, 31–38. doi:10.1115/1.4010217
Mottaghi, T. H., Ghandehari, M. A., and Masoodi, A. R. (2025). Dynamic behavior of carbon nanotube-reinforced polymer composite ring-like structures: unraveling the effects of agglomeration, porosity, and elastic coupling. Polym. (Basel) 17, 696. doi:10.3390/polym17050696
Noor, A. K., Burton, W. S., and Bert, C. W. (1996). Computational models for sandwich panels and shells. Appl. Mech. Rev. 49, 155–199. doi:10.1115/1.3101923
Osa-uwagboe, N., Silberschimdt Vadim, V., Aremi, A., and Demirci, E. (2023). Mechanical behaviour of fabric-reinforced plastic sandwich structures: a state-of-the-art review. J. Sandw. Struct. Mater. 25, 591–622. doi:10.1177/10996362231170405
Pandey, S., and Pradyumna, S. (2015). A new C0 higher-order layerwise finite element formulation for the analysis of laminated and sandwich plates. Compos. Struct. 131, 1–16. doi:10.1016/j.compstruct.2015.04.034
Pany, C. (2022). An insight on the estimation of wave propagation constants in an orthogonal grid of a simple line-supported periodic plate using a finite element mathematical model. Front. Mech. Eng. 8, 1–13. doi:10.3389/fmech.2022.926559
Pany, C., and Li, G. Q. (2023). Editorial: application of periodic structure theory with finite element approach. Front. Mech. Eng. 9, 2022–2024. doi:10.3389/fmech.2023.1192657
Pushparaj, P., and Suresha, B. (2016). Free vibration analysis of laminated composite plates using finite element method. Polym. Polym. Compos. 24, 529–538. doi:10.1177/096739111602400712
Reddy, J. N. (2004). Mechanics of laminated composite plates and shells; theory and analysis. Boca Raton, FL: CRC Press.
Rezaiee-Pajand, M., and Masoodi, A. R. (2019). Shell instability analysis by using mixed interpolation. J. Braz. Soc. Mech. Sci. Eng. 41, 419–18. doi:10.1007/s40430-019-1937-y
Setoodeh, S., Abdalla, M. M., Ijsselmuiden, S. T., and Gürdal, Z. (2009). Design of variable-stiffness composite panels for maximum buckling load. Compos. Struct. 87, 109–117. doi:10.1016/j.compstruct.2008.01.008
Shu, C., Ding, H., and Yeo, K. S. (2004). Solution of partial differential equations by a global radial basis function-based differential quadrature method. Eng. Anal. Bound. Elem. 28, 1217–1226. doi:10.1016/j.enganabound.2003.02.001
Shu, C., Yao, Q., Yeo, K. S., and Zhu, Y. D. (2002). Numerical analysis of flow and thermal fields in arbitrary eccentric annulus by differential quadrature method. Heat Mass Transf. Stoffuebertragung 38, 597–608. doi:10.1007/s002310100193
Siriruk, A., Jack Weitsman, Y., and Penumadu, D. (2009). Polymeric foams and sandwich composites: material properties, environmental effects, and shear-lag modeling. Compos. Sci. Technol. 69, 814–820. doi:10.1016/j.compscitech.2008.02.034
Thai, H.-T., Nguyen, T.-K., Vo, T. P., and Lee, J. (2014). Analysis of functionally graded sandwich plates using a new first-order shear deformation theory. Eur. J. Mech. - A/Solids 45, 211–225. doi:10.1016/j.euromechsol.2013.12.008
Torabi, K., Afshari, H., and Aboutalebi, F. H. (2019). Vibration and flutter analyses of cantilever trapezoidal honeycomb sandwich plates. J. Sandw. Struct. Mater. 21, 2887–2920. doi:10.1177/1099636217728746
Vinson, J. R. (1999). The behavior of sandwich structures of isotropic and composite materials. Lancaster, PA: Technomic.
Whitney, J. M., and Pagano, N. J. (1970). Shear deformation in heterogeneous anisotropic plates. J. Compos. Mater. 37, 1031–1036. doi:10.1115/1.3408654
Yaman, M., and Önal, T. (2016). Investigation of dynamic properties of natural material-based sandwich composites: experimental test and numerical simulation. J. Sandw. Struct. Mater. 18, 397–414. doi:10.1177/1099636215582216
Yazdani, S., and Ribeiro, P. (2015). A layerwise p-version finite element formulation for free vibration analysis of thick composite laminates with curvilinear fibres. Compos. Struct. 120, 531–542. doi:10.1016/j.compstruct.2014.10.030
Yuan, W. X., and Dawe, D. J. (2002). Free vibration of sandwich plates with laminated faces. Int. J. Numer. Methods Eng. 54, 195–217. doi:10.1002/nme.411
Keywords: free vibration, sandwich plate, variable stiffness composite laminates, curvilinear fibers, differential quadrature method
Citation: Zhou Z (2025) Differential quadrature free vibration analysis of sandwich plates with curvilinear fiber variable stiffness composite face sheets. Front. Mater. 12:1601813. doi: 10.3389/fmats.2025.1601813
Received: 28 March 2025; Accepted: 03 July 2025;
Published: 30 July 2025.
Edited by:
Geoffrey Robert Mitchell, Polytechnic Institute of Leiria, PortugalReviewed by:
Amir R. Masoodi, Ferdowsi University of Mashhad, IranChitaranjan Pany, Vikram Sarabhai Space Centre, India
Copyright © 2025 Zhou. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zhenyu Zhou, enp5NjYwOTA5QDEyNi5jb20=
 Zhenyu Zhou
Zhenyu Zhou