Absorbent material composition prediction based on multi-objective regression with value stacking and selection

Introduction: Electromagnetic wave absorption materials reduce incoming wave energy, with machine learning focusing on data-driven design methods. Traditional multi-objective regression methods often fail to provide accurate component predictions, limiting their performance.

Method: We propose a multi-objective predictive model for absorbent compositions. Using single-variable predictions as cumulative features in a regression chain improves feature representation. Performance metrics identify the optimal predictor variables for material composition, aiding in the classification of carbon nanotubes based on required performance and predicted values.

Result and discussion: Experimental results indicate that the model achieves better ${\text{R}}^2$ and mean squared error for carbon nanotubes, carbon black, and carbon fiber than other methods, with optimal Accuracy and Matthews Correlation Coefficient in classifying carbon nanotubes, validating the method for material composition design.

1 Introduction

Electromagnetic wave absorption (EWA) materials have become widely used in various applications Zeng et al. (2020); Lv et al. (2022); Lv et al. (2024). EWA materials capture electromagnetic waves, converting them into heat energy and reducing the negative effects of electromagnetic radiation Zeng et al. (2020). The absorbing material is made by combining a substrate with an absorbing agent, and a fixed thickness of a single layer of absorbing material will only provide effective absorption in certain frequency bands Li et al. (2023). Due to the low density and tunable conductivity of EWA materials, how to effectively predict the properties and compositions using data-driven methods is a key research focus in materials science and artificial intelligence Pollice et al. (2021).

Machine learning has progressed in material design. Wang et al. (2019) developed a machine learning system for discovering new copper alloys, utilizing error feedback to enable bidirectional design of properties and components to meet specific tensile strength and electrical conductivity requirements. Tayyebi et al. (2024) suggested using interpretable techniques for thin film preparation and SHAP analysis to identify units that influence water permeability positively and negatively. Machine learning has made strides in crystal graph networks and lens images, but it mainly depends on rich features. Predicting the property-composition of carbon-related EWA materials requires finite characteristic dimensions for designing associated variables. The traditional multi-objective regression method for predicting material composition and properties encounters the following challenges.

Feature Limitation. The prediction of EWA materials is constrained by limited features, typically thickness, mass fraction, and operating frequency. It is crucial to utilize data analysis or model prediction to expand the range of potential features to improve model predictions.

Chain Sequence. The order of the prediction chain impacts results. Two main methods for constructing prediction chains are the dependent correlation coefficient Melki et al. (2017) and exhaustive link averaging Masmoudi et al. (2020). Applying the prediction performance to obtain effective values during linking can improve composition design accuracy.

To solve the above two problems, a performance-based multi-object method (GBDT Performanced-guided Cumulative Chain, GPCC) was proposed to achieve numerical and categorical component prediction of EWA materials. To enhance the data features, we introduce the predicted value of a single feature within a multi-object framework, thereby reducing the impact of accumulated prediction errors. For the prediction chain of composition, we evaluated each variable in the training set and averaged the top $N$ variables to predict thickness, mass fraction, and working frequency. GPCC also utilizes these predicted variables to classify carbon nanotube materials. The contributions are as follows.

• A predictive accumulation strategy optimizes input features in a multi-objective framework. Due to limitations on available features in the data, results from a single model are used to improve the framework and reduce cumulative errors.

•The regression chain construction method for the numerical component of absorbent material has been implemented. The proposed method uses measured data to create a multi-objective regression framework, and identify optimal prediction indicators with the training data performance.

•A classification prediction method for carbon nanotube materials has been developed, using numerical predictions as input to validate the regression chain’s effectiveness.

This paper validates the proposed method through experiments on carbon EWA materials. The structure includes: Section 2 on intelligence material design and multi-objective prediction methods. Section 3 on the proposed method. Section 4 on the dataset and experimental setting. Section 5 on experimental results. Section 6 summarizes the conclusion.

2 Related Work

2.1 Intelligent material design

Intelligent material design technology has significantly improved the efficiency of new material research and development, from the microscopic to the production level. Noh et al. (2020) proposed reverse design to accelerate traditional material design by leveraging hidden knowledge in material data to predict properties, and developed an image-based generator framework named iMatGen Zeng et al. (2020). Han et al. (2023) created a generative model using a crystal diffusion variational auto-encoder to customize crystal structures based on desired compositions. The model employs a deep neural network to extract global features from the crystal’s physical properties and optimizes structures using density functional theory. Hu et al. (2022) added a formation energy predictor to improve the model’s potential space, ensuring that the generated structures are morphologically reasonable and energetically stable. These approaches highlight the potential of machine learning in designing and reverse engineering stable crystalline materials. The above methods highlight the potential of machine learning in designing stable new crystalline materials, especially for prediction and design.

Data-driven technology in absorber design improves performance prediction and the discovery of efficient absorbers. Nadell et al. (2019) used deep learning to predict transmittance spectra for all-dielectric surfaces based on ADM parameters. Hou et al. (2020) developed a deep neural network for on-demand meta-material design, calculating split ring resonator parameters from reflectivity. On et al. (2024) created an electromagnetic absorber using deep learning, integrating a variational auto-encoder with CMA-ES optimization for efficient meta-structure design in a specific frequency band.

2.2 Multi-objective regression

Multi-objective regression is a key area of machine learning that predicts multiple output variables from given input variables. The challenges of multi-objective regression can be addressed through algorithm-level and ensemble-level methods.

At the algorithmic level, single-objective regression methods are optimized for multi-objective scenarios. M-SVR Tuia et al. (2011) and MLS-SVR Xu et al. (2013) enhance support vector machine (SVM) techniques to optimize multiple outputs while considering their interrelationships and nonlinear correlations. Tran et al. (2024) found that SVM methods like ELS-SVR are ineffective for target component issues and suggested using artificial neural networks. They proposed a multi-output regression technique with gradient boosting and deep neural networks, training each layer on the residuals of the previous iteration’s squared loss function. Zheng et al. (2023) introduced a multi-objective prediction method using an adaptive dynamic genetic algorithm and adaptive moment estimation (ADGA-AM-ANN), which adds noise to the output and globally optimizes ANN.

At the ensemble level, regression chains sequentially concatenate multiple regression problems to predict target variables. Spyromitros-Xioufis et al. (2016) introduced the ensemble regression chain method, which incorporates previous target predictions as additional inputs. The maximum correlation chain model (SVRCC) Melki et al. (2017) builds on this concept, leveraging target correlations to enhance prediction performance and reduce computational complexity. Geiß et al. (2022) developed a regression chain ensemble method using repeated permutations to address insufficient multi-task objectives. This approach enhances the model’s ability to learn inter-task dependencies by propagating each target variable’s predicted values to subsequent models, thereby improving the accuracy of multi-variable predictions. The regression chain enhances prediction accuracy through multi-task concatenation and task relevance, and is widely used in energy materials estimation Yu et al. (2023), production process design Turetskyy et al. (2021), and material surface design Akhtar et al. (2024) in intelligent material design.

3 Methodology

3.1 Problem definition

We selected EWA materials from 1 GHz to 18 GHz working frequency and acquired the performance. By varying the components in carbon materials, we tested their dielectric constant and permeability. The sample preparation process is shown in Figure 1.

Figure 1

Figure 1. Prepare coaxial ring material using paraffin as the matrix material and carbon tube powder. Using mass fraction, thickness and operating frequency, the real part, imaginary part and tangent values of dielectric constant and permeability are obtained.

Permittivity and permeability as input $X$ to predict the values and categories of carbon materials. The properties of absorbing agents like carbon nanotubes, carbon black, and carbon fiber vary with different thicknesses and mass fractions at specific operating frequencies. We denote the predicted numerical variables as $y_1$, $y_2$, and $y_3$. Carbon nanotubes are categorized into two types, which differ in outer diameter, pile density, and other characteristics. This is treated as a binary classification problem with variable value $y_4$.

3.2 Base learner

There is a complex nonlinear relationship between properties and composition. Figure 2 shows the dielectric constant and permeability changes of $TNIM8$ carbon nanotubes at mass fractions of $1\%$ and $7.7\%$ across different operating frequencies. Gradient Boosting Decision Trees (GBDT) effectively capture this complexity by integrating multiple decision tree models, and managing feature interactions to improve material composition predictions. The performance in Figure 2 shows significant fluctuations in several local frequency ranges, and GBDT is robust against noise and outliers from experimental data. Thus, we apply GBDT as the base learner to enhance prediction performance based on local features and fitting errors.

Figure 2

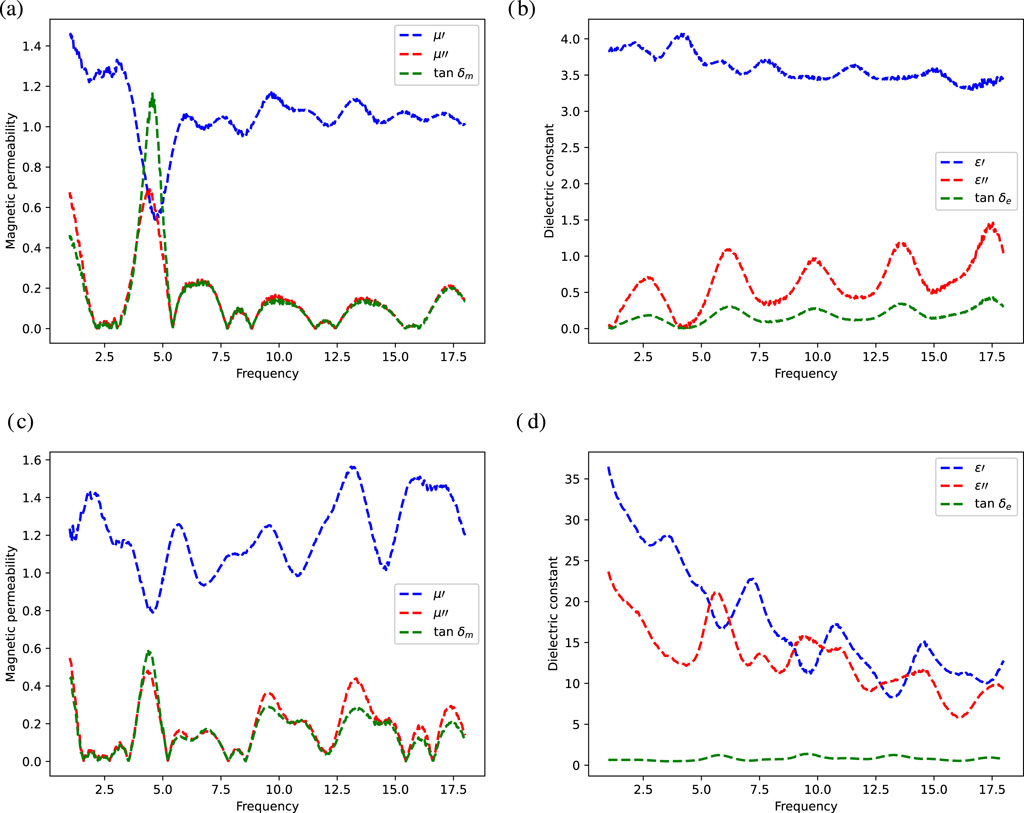
Figure 2. The variation trend of dielectric constant and permeability under different mass fraction, (a,c) describe the curves of magnetic permeanbility versus frequency, (b,d) describe the curves of dielectric constant versus frequency.

GBDT employs classification and regression trees as weak learners, where errors from each learner optimize subsequent predictions of EWA materials. Taking the composition of the EWA material as an example, the data composition is as follows: ${\{(x_i,y_i)\}}^n,i=\mathrm{1,2},\dots ,n$, where $n$ represents the number of samples, $x_i$ represents the material performance of the $i$-th sample, while $y_i$ denotes the material component to be predicted. The loss function is denoted as $L(y,F_m(x))$, which can be defined as the mean squared error in regression and exponential loss in classification. Additionally, $F_m(x)$ represents the $m$-th weak classifier. During the initialization phase, $c$ can be set as the mean of the material indicators from the training set, and is expressed as Equation 1:

$F_0\left(x\right)=\underset{\gamma }{\mathrm{arg\; min}}{\displaystyle \sum _{i=1}^n}L\left(y_i,c\right),(1)$

where $\gamma$ minimize the loss function and can be the mean or majority vote in the first iteration. In the $M$ iteration stage, for $m=\mathrm{1,2},\dots ,M$, the input optimization of the tree is performed. For the $i$-th sample, the negative gradient of the $m$-th tree is expressed as Equation 2:

${\gamma }_{m,i}=-{\left[\frac{\partial L\left(y_i,F\left(x_i\right)\right)}{\partial F\left(x_i\right)}\right]}_{F\left(x\right)=F_{m-1}\left(x\right)}.(2)$

The current decision tree $h_m(x)$ utilizes to train the weak classifier, thereby obtaining the corresponding leaf stage area $R_{m,j}$, where $j=\mathrm{1,2},\dots ,J_m$, $J_m$ represents the number of child nodes of the $m$-th regression leaf. For each leaf node, its fitted value is calculated as Equation 3:

$c_{m,j}=\underset{c}{\mathrm{arg\; min}}{\displaystyle \sum _{x_i\in R_{m,j}}}L\left(y_i,F_{m-1}\left(x_i\right)+c\right).(3)$

Obtain the expression for the strong learner $F_M(x)$:

$F_M\left(x\right)=F_0\left(x\right)+{\displaystyle \sum _{m=1}^M}{\displaystyle \sum _{j=1}^J}{c}_{m,j}I\left(x\in R_{m,j}\right).(4)$

Among them, $I$ represents the indicator function, which indicates whether the sample $x$ is at the leaf node $j$. The attenuation coefficient can be added to the last term of Equation 4 to gradually increase the influence of subsequent tree models.

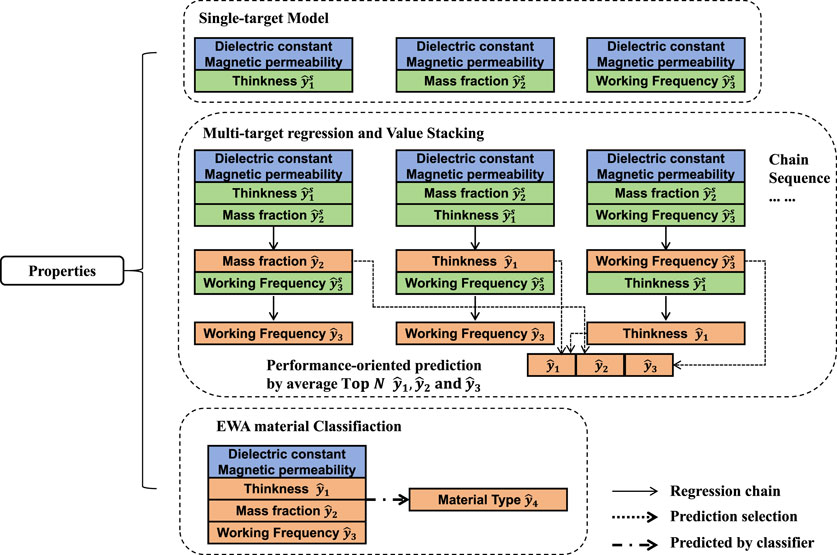
3.3 Multi-target regression and value stacking

The cumulative strategy is a relearning procedure that increases data dimensions linearly with each iteration in the regression chain. According to Geiß et al. (2022), both non-cumulative and cumulative enhancements of the feature vector yield competitive predictions. Our accumulation strategy employs single variable prediction as the data dimension, with the $q$-th dimension’s prediction depending on the arrangement of the $(q-1)$ dimensions and the prediction result of the single variable $\widehat{y}$. While assuming ${\widehat{y}}_{q-1}$ that represents the prediction from the $(q-1)$-th dimension regression chain, and ${\widehat{y}}_{q-1}^s$ denotes the prediction result of this variable that solely depends on $x$, then the $q$-th dimension predictor variable is:

${\widehat{y}}_q=f_q\left(x_0,\dots ,x_d,{\widehat{y}}_0^s,{\widehat{y}}_1^s,{\widehat{y}}_1,\dots ,{\widehat{y}}_{q-1}^s,{\widehat{y}}_{q-1}\right),(5)$

where $f_q$ identifies the GBDT in the $q$ dimension and $d$ is the dimension of $x$. Due to limitations in absorbent data acquisition, we use a separate model to predict results in the cumulative regression chain. This method is also widely utilized in the field of computer vision, particularly in image pyramids, which employ feature maps of varying scales. These maps are integrated into the model system to enhance data dimensionality, allowing the model to focus on different perspectives. The cumulative design identifies the relationship between $y_q$ and $y_{q-1}$ and analyzes the predicted value based on the independent variable $x$. As learning progresses, the target variable’s estimation is added to subsequent models as features, enhancing the training dataset in the regression chain order.

Various strategies exist for constructing regression chains. Geiß et al. (2022) expanded single-variable regression to multiple variables, creating chains that were alternately combined to find the optimal link. Wahid et al. (2023) utilized three different regression links for combined predictions, while Melki et al. (2017) based link ordering on the correlation coefficient between variables. However, correlation links may not align with regression performance, and accumulating errors can reduce the accuracy of subsequent predictors. For example, our tests showed that the predicted result for $\widehat{y_1}-\widehat{y_2}-\widehat{y_3}$ was lower than that for $\widehat{y_1}-\widehat{y_3}-\widehat{y_2}$. To achieve the optimal regression link, we predict variables based on performance. For instance, after constructing a link with Equation 5, we calculate and store the coefficient of determination $(R^2)$ for certain sequence in the training set. If $R^2$ exceeds a preset top $N$, we record the predicted results from the test set, averaging these for the composition prediction. The same approach applies when using an indicator like mean squared error (MSE) to predict the smallest top $N$ values. The pseudocode is shown in Algorithm 1.

Algorithm 1

Algorithm 1.EWA Material Multi-object Regression.

3.4 EWA material classification

In material composition design, we analyze the training set’s performance and composition to derive numerical compositions and material types. We use observed material properties with $y_1$, $y_2$, and $y_3$ as input to predict carbon nanotube types with a classifier. $X$ is constructed from the required material properties and numerical composition, enabling the trained model to predict $y_4$. This method optimizes the use of existing numerical components and meets practical needs for numerical components and types based on material properties. The pseudocode is shown in Algorithm 2.

Algorithm 2

Algorithm 2.EWA material Classification.

The overall process flow is illustrated in Figure 3.

Figure 3

Figure 3. Material component prediction based on multi-target sequence and value stacking.

4 Experimental design

We analyzed two research questions through experiment.

Research question (RQ) 1: The effect of variable accumulation and result screening methods in Section 3.3 on material design.

RQ 2: The impact of GPCC on the prediction of material classification.

The experimental setup for the two problems is explained in Section 4, with analysis in Section 5.

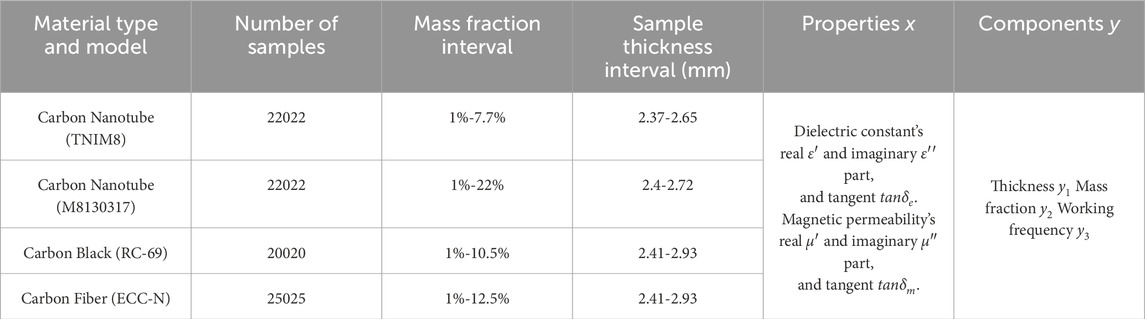
4.1 Dataset description

Data for EWA material batches were collected: carbon nanotube $TNIM8$ and $M8130317$ were 22022, carbon black was 20020, and carbon fiber was 25025. Split the training set and the test set in a 4:1. The detail of the material dataset with components and properties is shown in Table 1.

Table 1

Table 1. Datail of Dataset.

Variations in feature dimensions and numerical ranges can affect their influence during model training, impacting performance and accuracy. Thus, data normalization for the experimental data, as shown in Equation 6.

$X_{\text{norm}}=\frac{X-X_{\text{min}}}{X_{\text{max}}-X_{\text{min}}}(6)$

In addition, the regression values $y_1,y_2,y_3$ can also be normalized from Equation 6 to accurately evaluate the changes in MSE corresponding to different dimensions of the dependent variable.

4.2 Comparison method and evaluation performance

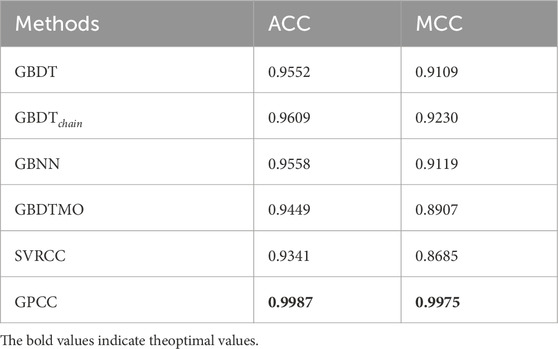
The experiment aims to analyze the impact of chain sorting and compare it with other five GBDT-based or multi-regression methods.

• GPCC: Our proposed method, the parameters for the base leaner keep the same with GBDT.

•GBDT: Applying 300 trees with a maximum depth of 3. A minimum of 5 samples is required for splitting, with a learning rate of 0.05 and squared error as the loss function.

•${\text{GBDT}}_{\mathit{chain}}$: Utilizing a GBDT to assess the prediction results of the multi-objective regression chain and verify chain sequence. Maintaining the same parameter settings as GBDT.

•GBNN Emami and Martínez-Muñoz (2023): Gradient boosted neural network is an additive model that approximates the objective function by sequential training and combining multiple sub-models into a multi-objective regression model. Using 300 neural networks, updating one at each step. It has a learning rate of 0.05 and employs the L-BFGS optimizer with a logistic activation function.

•GBDTMO Zhang and Jung (2020): GBDT for multiple outputs regression. Construct predictions for all variables or selected subsets at each leaf node by summing the target gains of all output variables. Sharing parameter settings with GBDT.

•SVRCC Melki et al. (2017): Finding the direction of maximum correlation among the targets and uses that order as the only chain.

We use $R^2$ and MSE as evaluation metrics for the RQ1. The calculation equations are shown in Equations 7, 8:

$R^2=1-\frac{S{S}_{\mathit{res}}}{S{S}_{\mathit{tol}}},(7)$

$MSE=\frac{1}{n}{\displaystyle \sum _{i=1}^n}{\left(y_i-{\widehat{y}}_i\right)}^2.(8)$

$S{S}_{\mathit{res}}$ is the sum of squares of the residuals, which is the sum of the squares of the differences between the predicted values and the actual values. The total sum of squares $S{S}_{\mathit{tol}}$ is the sum of the squares of the differences between the actual values and the mean of those values. A higher $R^2$ value, closer to 1, indicates a stronger explanatory power of the model. MSE is the average of the squares of the differences between predicted values and actual values.

For RQ 2, we used GBDT as a classifier and used Accuracy (ACC) and Matthews Correlation Coefficient (MCC) to evaluate the test set. The calculation equations are shown in Equations 9, 10:

$ACC=\frac{TP+TN}{TP+TN+FP+FN},(9)$

$MCC=\frac{TP\ast TN+FP\ast FN}{\sqrt{\left(TP+FP\right)\ast \left(TP+FN\right)\ast \left(TN+FP\right)\ast \left(TN+FN\right)}},(10)$

where TP indicates true positives, FN denotes false negatives, FP represents false positives, and TN signifies true negatives. ACC measures the proportion of correct predictions, while the MCC evaluates misclassifications, reducing the impact of sample imbalance on performance metrics.

5 Results and discussion

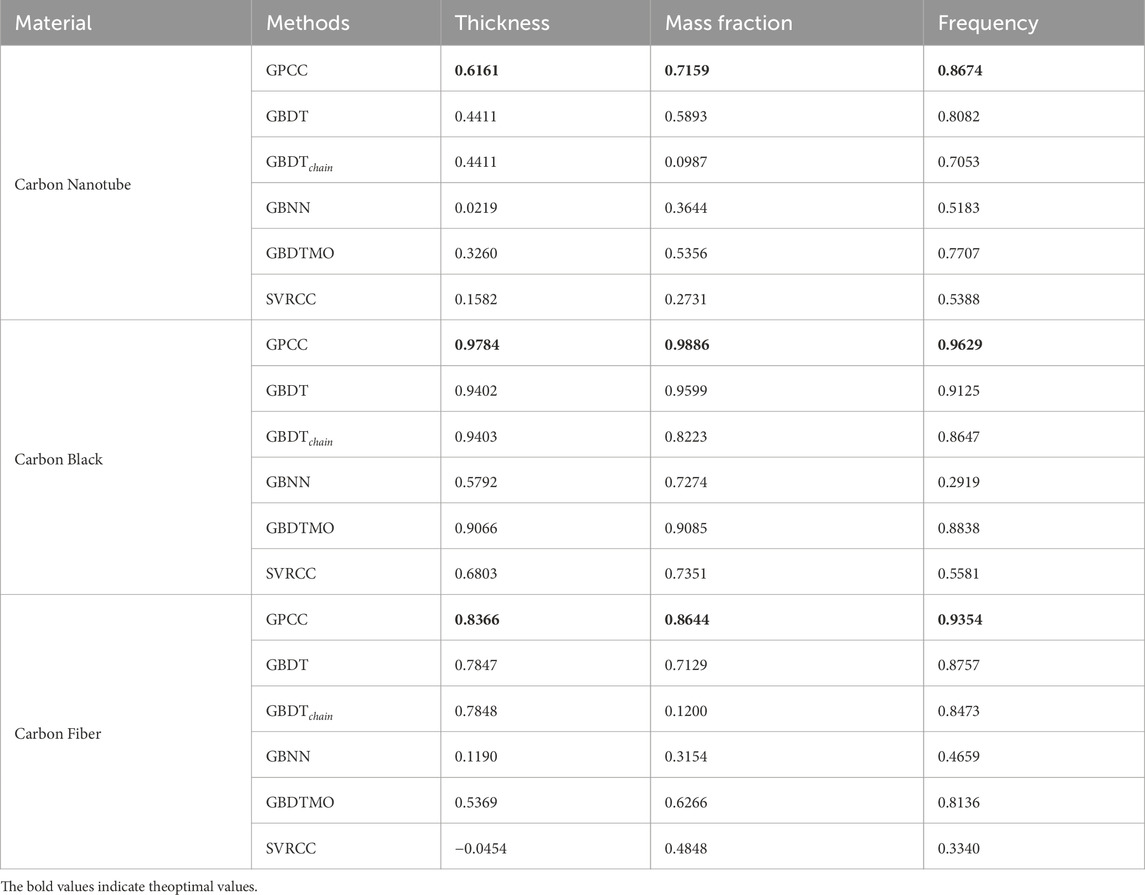
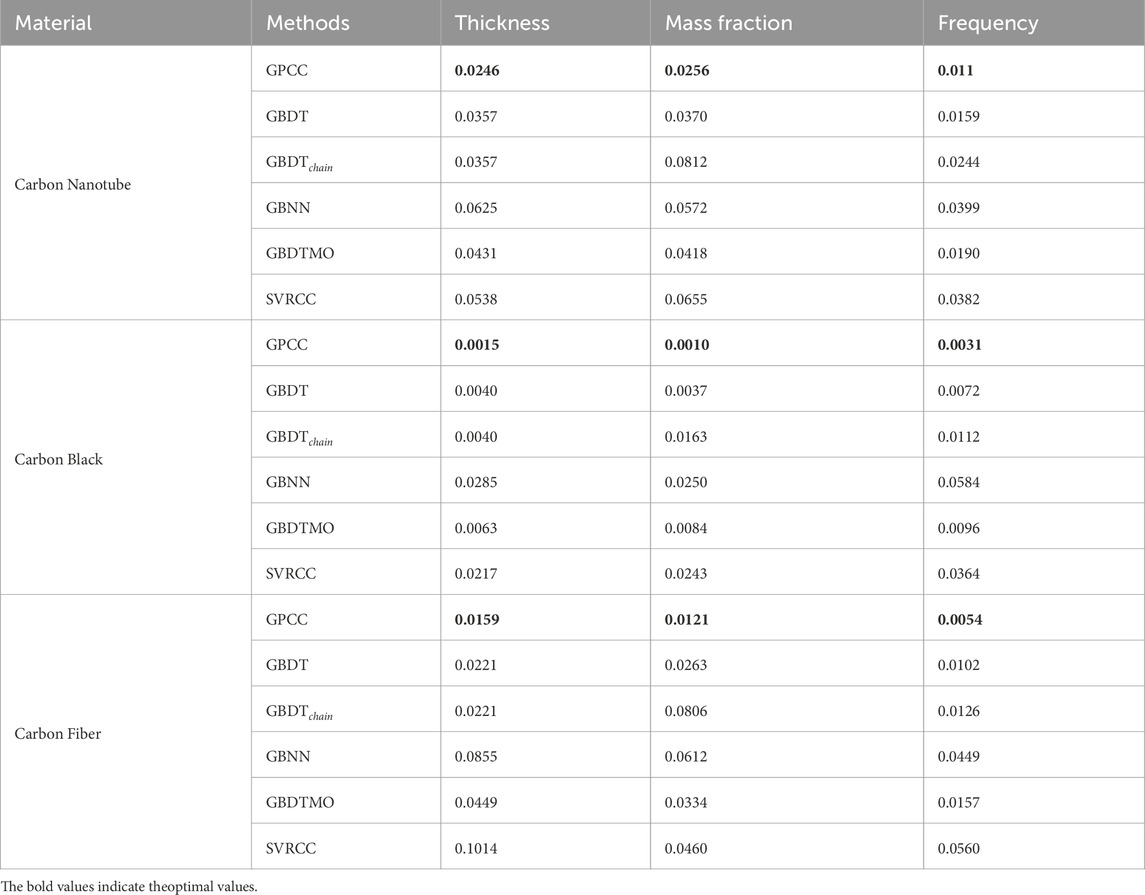
5.1 Performance of multi-regression

We use $R^2$ and MSE corresponding to three types of EWA materials, as shown in Table 1, 2.

Table 2

Table 2. $R^2$ in compared methods.

Table 3

Table 3. MSE in compared methods.

The proposed GPCC demonstrates a significant improvement over alternative methodologies, achieving an average increase in $R^2$ of 0.1 and a reduction in MSE of 0.008 when compared to GBDT. The consistent predictive performance of GPCC suggests that our optimal link search methodology effectively identifies the most accurate predicted values. Furthermore, we observed that the link mining sequence that yields the highest $R^2$ and the lowest MSE remains consistent, indicating the reusability of the optimal link and predicted location. In contrast, ${\text{GBDT}}_{\mathit{chain}}$ exhibits comparable thickness and operating frequency to GBDT but experiences an average decrease in $R^2$ of 0.4. This observation implies that, despite the correlation among variables, errors tend to accumulate following the construction of links, thereby diminishing predictive performance. Although certain studies, such as those by Melki et al (2017), have introduced correlation coefficients, these do not directly correlate with performance outcomes, as evidenced by the results of SVRCC. Additionally, GBNN exhibits instability in predictions, particularly with significant errors in the operating frequency of carbon black. When predicting the properties of EWA materials, models that utilize extensive feature sets, such as neural networks, perform less effectively than GPCC, further highlighting the latter’s efficacy.

We examine the predictive capabilities of various methodologies for assessing the absorption characteristics of materials, specifically focusing on carbon black, carbon nanotubes, and carbon fibers. The performance of carbon black stabilizes at a mass fraction of $18\%$, exhibiting negligible variations beyond this threshold. The GPCC demonstrates the most effective regression performance for carbon nanotubes, yielding $R^2$ and MSE of 65.26$\%$ and 0.0223, respectively. Conversely, the ${\text{GBDT}}_{\mathit{chain}}$ reveals a decline in predictive accuracy for both carbon nanotubes and carbon fibers, suggesting a lack of stability in its predictions. Notably, carbon nanotubes and fibers outperform carbon black in predicting operational frequency, although carbon black is associated with a higher MSE. Therefore, a thorough analysis during the design of compositions necessitates an evaluation of the predicted properties of various components across different material types.

5.2 Performance of classification

Numerical predictions from five comparison algorithms were used to predict carbon nanotube types by combining material performance data. ACC and MCC evaluated their performance, with $M8130317$ as the positive class and $TNIM8$ as the negative. Performance is shown in Table 4.

Table 4

Table 4. ACC and MCC in compared methods, the best results are in bold.

Table 4 shows the ACC and MCC results from the five-fold cross-validation to improve the stability of the prediction. In the parameter search, we use actual properties and components as the training set and those predicted in Section 5.2 as the test set. We apply five-fold cross-validation to find optimal parameters and evaluate them with the test set. The parameter search candidates are: number of trees 10, 20, 30, learning rate 0.01, 0.1, 0.2, and maximum depth 3, 5, 7. Unlike other methods, GPCC does not have more misjudgments for positive classes. SVRCC is ineffective for regression but achieves about 0.93 accuracy in classification, emphasizing its performance importance. GPCC improved ACC and MCC by $6.46\%$ and $12.9\%$, respectively, compared to SVRCC, while maintaining high accuracy. By combining regression and classification for EWA materials, GPCC proved its superiority and practicality in the test set against various related algorithms.

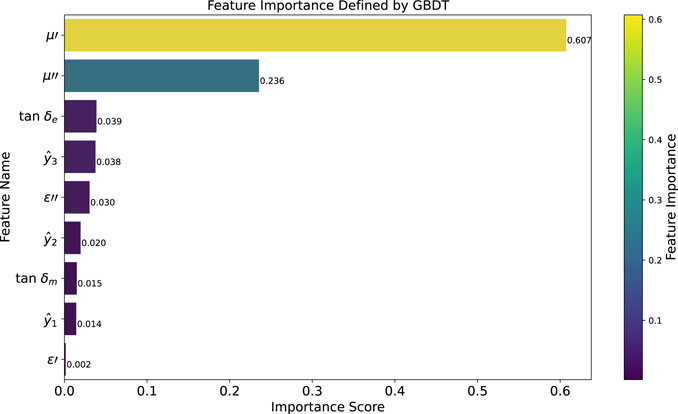
In Figure 4, we list the importance of each feature when GBDT is used as a classifier. It can be seen that the features related to magnetic permeability are of relatively high importance for the classification of carbon nanotubes. The predicted values of ${\widehat{y}}_3$ and ${\widehat{y}}_2$ by the regression method corresponding to the GPCC that we proposed also play a significant role in the classification, which is greater than the importance of the corresponding dielectric constant. This indicates that the prediction results of the regression chain we proposed contribute well to the classification performance.

Figure 4

Figure 4. Feature importance in classification using GBDT.

5.3 Ablation experiment

To verify the influence of cumulative strategy on the prediction ability, we used ${\text{GPCC}}_{\mathit{nonC}}$, which represents the method without using single prediction as a feature, and used the regression index of 5.1 for comparison. The prediction ability of GPCC in materials was compared, as shown in Figures 5, 6.

Figure 5

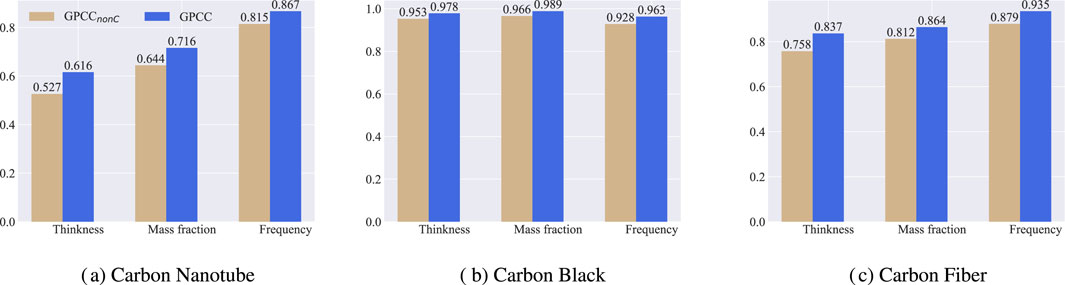
Figure 5. Effect of model complexity on $R^2$. (a–c) compare the prediction results of carbon nanotube,carbon black and carbon fiber for three component indexes.

Figure 6

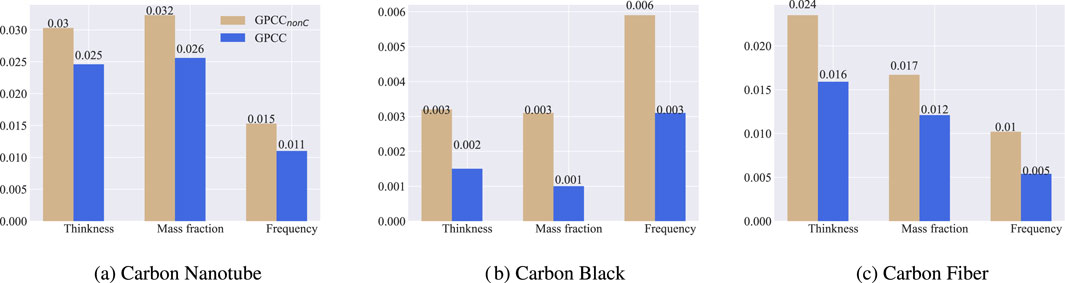
Figure 6. Effect of stacking prediction on MSE. (a–c) compare the prediction results of carbon nanotube,carbon black and carbon fiber for three component indexes.

The mean $R^2$ of ${\text{GPCC}}_{\mathit{nonC}}$ was 5.38$\%$ lower than GPCC, which optimizes ${\text{GPCC}}_{\mathit{nonC}}$’s MSE by 38$\%$. ${\mathrm{G}\mathrm{P}\mathrm{C}\mathrm{C}}_{\mathit{nonC}}$ outperforms other methods, only lagging behind GPCC in carbon nanotubes and carbon black, underscoring the effectiveness of indicators for link selection. Carbon fiber also shows strong results in mass fraction and operating frequency, and the performance can be improved from ${\text{GPCC}}_{\mathit{nonC}}$ using cumulative features.

To verify the influence of model parameters on the fitting effect, we used ${\text{GPCC}}_1$, ${\text{GPCC}}_2$ and ${\text{GPCC}}_3$ to represent the increase of the number of individual trees by 300–500, respectively, and the results were shown in Figures 7, 8. Overall, the complexity of the model is increased, and the performance is improved in each component. The degree of enhancement is inconsistent in different materials. MSE decreases significantly in carbon black at operating frequency, but MSE optimization is low in carbon nanotubes and fibers. In the process of model construction, there is no overfitting phenomenon, indicating the robustness of our GBDT as a base learner. In practical applications, it is necessary to balance model complexity and evaluation metrics to complete the prediction within the inference time.

Figure 7

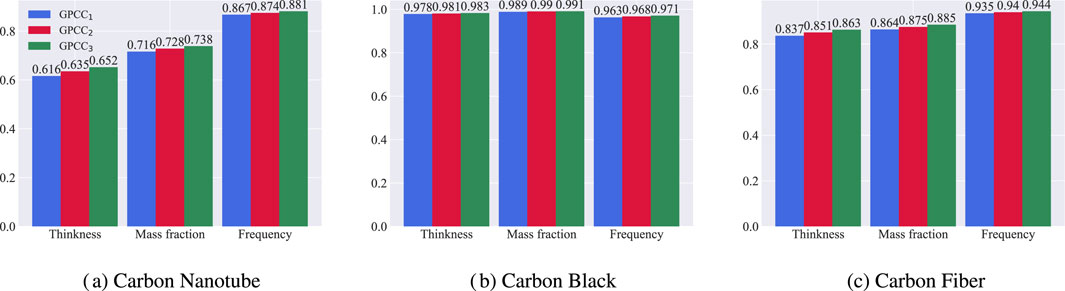
Figure 7. Effect of model complexity on $R^2$. (a–c) compare the prediction results of carbon nanotube,carbon black and carbon fiber for three component indexes.

Figure 8

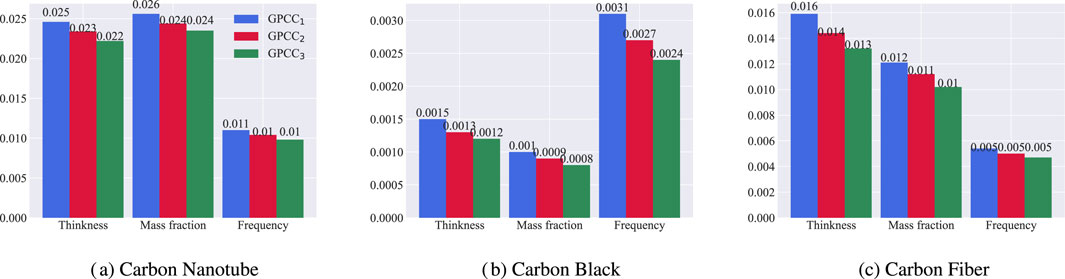
Figure 8. Effect of model complexity on MSE. (a–c) compare the prediction results of carbon nanotube,carbon black and carbon fiber for three component indexes.

6 Conclusion

We present a method for predicting the composition and category of absorbing materials using the GBDT model. A multi-objective regression framework enhances the accuracy of predictions regarding the composition and operational frequency of materials, such as carbon nanotubes. The amalgamation of regression outcomes with material properties enables a comprehensive analysis and prediction of material types.

To assess the efficacy of the proposed methodology, we performed experimental training on various datasets of absorbent materials. The regression model demonstrated a high level of precision in its predictions when compared to established algorithms. The GPCC model effectively captures intricate relationships among target variables and substantiates the feature-enhanced cumulative strategy for multi-objective regression. The prediction of material categories, derived from regression data, yielded elevated ACC and MCC scores, thereby improving material classification by eliminating irrelevant features. Future research may leverage semi-supervised data to advance the design of material compositions and facilitate the mixed predictions of multiple materials.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

SH: Methodology, Software, Writing – original draft. JC: Software, Validation, Writing – original draft. KH: Methodology, Validation, Writing – original draft. JM: Data curation, Resources, Writing – review and editing. KL: Data curation, Resources, Writing – review and editing. TL: Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. Kai Huang reports financial support was provided by Natural Science Foundation (2024J08197) of Fujian Province of China and the Startup Fund (ZQ2024001) of Jimei University. Kexun Li reports financial support from the National Key Laboratory on Electromagnetic Environment Effects (6142205230404) of China.

Acknowledgments

The authors would like to express our sincere gratitude and appreciation for the contributions throughout the course of this research paper.

Conflict of interest

Authors KL and TL were employed by China Electronics Technology Group Corporation 33th Research Institute.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Akhtar, S., Ali, R., and Ameen, S. M. (2024). “Predicting the surface elastic parameters of soft solids using multi-output decision tree regressor,” in AIP conference proceedings, 3168. Melville, NY: AIP Publishing, 020024. doi:10.1063/5.0219700AIP Conf. Proc.

CrossRef Full Text | Google Scholar

Emami, S., and Martínez-Muñoz, G. (2023). Sequential training of neural networks with gradient boosting. IEEE Access 11, 42738–42750. doi:10.1109/access.2023.3271515

CrossRef Full Text | Google Scholar

Geiß, C., Brzoska, E., Pelizari, P. A., Lautenbach, S., and Taubenböck, H. (2022). Multi-target regressor chains with repetitive permutation scheme for characterization of built environments with remote sensing. Int. J. Appl. Earth Observation Geoinformation 106, 102657. doi:10.1016/j.jag.2021.102657

CrossRef Full Text | Google Scholar

Han, S., Lee, J., Han, S., Moosavi, S. M., Kim, J., and Park, C. (2023). Design of new inorganic crystals with the desired composition using deep learning. J. Chem. Inf. Model. 63, 5755–5763. doi:10.1021/acs.jcim.3c00935

PubMed Abstract | CrossRef Full Text | Google Scholar

Hou, Z., Tang, T., Shen, J., Li, C., and Li, F. (2020). Prediction network of metamaterial with split ring resonator based on deep learning. Nanoscale Res. Lett. 15, 83–88. doi:10.1186/s11671-020-03319-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, P., Ge, B., Liu, Y., and Huang, W. (2022). “Energy-constrained crystals wasserstein gan for the inverse design of crystal structures,” in Proceedings of the 8th international conference on computing and artificial intelligence, 24–31.

Google Scholar

Li, H., Cao, Z., Xia, Y., Yao, G., Miao, L., and Jiang, J. (2023). Dispersion manipulation method for ultrahigh frequency band reconfigurable absorbers. IEEE Trans. Antennas Propag. 72, 1983–1988. doi:10.1109/tap.2023.3330635

CrossRef Full Text | Google Scholar

Lv, H., Cui, J., Li, B., Yuan, M., Liu, J., and Che, R. (2024). Insights into civilian electromagnetic absorption materials: challenges and innovative solutions. Adv. Funct. Mater. 35, 2315722. doi:10.1002/adfm.202315722

CrossRef Full Text | Google Scholar

Lv, H., Yang, Z., Pan, H., and Wu, R. (2022). Electromagnetic absorption materials: current progress and new frontiers. Prog. Mater. Sci. 127, 100946. doi:10.1016/j.pmatsci.2022.100946

CrossRef Full Text | Google Scholar

Masmoudi, S., Elghazel, H., Taieb, D., Yazar, O., and Kallel, A. (2020). A machine-learning framework for predicting multiple air pollutants’ concentrations via multi-target regression and feature selection. Sci. Total Environ. 715, 136991. doi:10.1016/j.scitotenv.2020.136991

PubMed Abstract | CrossRef Full Text | Google Scholar

Melki, G., Cano, A., Kecman, V., and Ventura, S. (2017). Multi-target support vector regression via correlation regressor chains. Inf. Sci. 415, 53–69. doi:10.1016/j.ins.2017.06.017

CrossRef Full Text | Google Scholar

Nadell, C. C., Huang, B., Malof, J. M., and Padilla, W. J. (2019). Deep learning for accelerated all-dielectric metasurface design. Opt. express 27, 27523–27535. doi:10.1364/oe.27.027523

PubMed Abstract | CrossRef Full Text | Google Scholar

Noh, J., Gu, G. H., Kim, S., and Jung, Y. (2020). Machine-enabled inverse design of inorganic solid materials: promises and challenges. Chem. Sci. 11, 4871–4881. doi:10.1039/d0sc00594k

PubMed Abstract | CrossRef Full Text | Google Scholar

On, H.-I., Jeong, L., Seo, T.-M., Jo, Y., Choi, W., Kang, D.-J., et al. (2024). Novel method of performance-optimized metastructure design for electromagnetic wave absorption in specific band using deep learning. Eng. Appl. Artif. Intell. 137, 109274. doi:10.1016/j.engappai.2024.109274

CrossRef Full Text | Google Scholar

Pollice, R., dos Passos Gomes, G., Aldeghi, M., Hickman, R. J., Krenn, M., Lavigne, C., et al. (2021). Data-driven strategies for accelerated materials design. Accounts Chem. Res. 54, 849–860. doi:10.1021/acs.accounts.0c00785

PubMed Abstract | CrossRef Full Text | Google Scholar

Spyromitros-Xioufis, E., Tsoumakas, G., Groves, W., and Vlahavas, I. (2016). Multi-target regression via input space expansion: treating targets as inputs. Mach. Learn. 104, 55–98. doi:10.1007/s10994-016-5546-z

CrossRef Full Text | Google Scholar

Tayyebi, A., Alshami, A. S., Tayyebi, E., Buelke, C., Talukder, M. J., Ismail, N., et al. (2024). Machine learning–driven surface grafting of thin-film composite reverse osmosis (tfc-ro) membrane. Desalination 579, 117502. doi:10.1016/j.desal.2024.117502

CrossRef Full Text | Google Scholar

Tran, N. K., Kühle, L. C., and Klau, G. W. (2024). A critical review of multi-output support vector regression. Pattern Recognit. Lett. 178, 69–75. doi:10.1016/j.patrec.2023.12.007

CrossRef Full Text | Google Scholar

Tuia, D., Verrelst, J., Alonso, L., Pérez-Cruz, F., and Camps-Valls, G. (2011). Multioutput support vector regression for remote sensing biophysical parameter estimation. IEEE Geoscience Remote Sens. Lett. 8, 804–808. doi:10.1109/lgrs.2011.2109934

CrossRef Full Text | Google Scholar

Turetskyy, A., Wessel, J., Herrmann, C., and Thiede, S. (2021). Battery production design using multi-output machine learning models. Energy Storage Mater. 38, 93–112. doi:10.1016/j.ensm.2021.03.002

CrossRef Full Text | Google Scholar

Wahid, M. F., Tafreshi, R., Khan, Z., and Retnanto, A. (2023). Multiphase flow rate prediction using chained multi-output regression models. Geoenergy Sci. Eng. 231, 212403. doi:10.1016/j.geoen.2023.212403

CrossRef Full Text | Google Scholar

Wang, C., Fu, H., Jiang, L., Xue, D., and Xie, J. (2019). A property-oriented design strategy for high performance copper alloys via machine learning. npj Comput. Mater. 5, 87. doi:10.1038/s41524-019-0227-7

CrossRef Full Text | Google Scholar

Xu, S., An, X., Qiao, X., Zhu, L., and Li, L. (2013). Multi-output least-squares support vector regression machines. Pattern Recognit. Lett. 34, 1078–1084. doi:10.1016/j.patrec.2013.01.015

CrossRef Full Text | Google Scholar

Yu, H., Yang, K., Zhang, L., Wang, W., Ouyang, M., Ma, B., et al. (2023). Multi-output ensemble deep learning: a framework for simultaneous prediction of multiple electrode material properties. Chem. Eng. J. 475, 146280. doi:10.1016/j.cej.2023.146280

CrossRef Full Text | Google Scholar

Zeng, X., Cheng, X., Yu, R., and Stucky, G. D. (2020). Electromagnetic microwave absorption theory and recent achievements in microwave absorbers. Carbon 168, 606–623. doi:10.1016/j.carbon.2020.07.028

CrossRef Full Text | Google Scholar

Zhang, Z., and Jung, C. (2020). Gbdt-mo: gradient-boosted decision trees for multiple outputs. IEEE Trans. neural Netw. Learn. Syst. 32, 3156–3167. doi:10.1109/tnnls.2020.3009776

PubMed Abstract | CrossRef Full Text | Google Scholar

Zheng, J., Liu, C., Huang, S., and He, Y. (2023). A novel adaptive dynamic ga combined with am to optimize ann for multi-output prediction: small samples enhanced in industrial processing. Inf. Sci. 644, 119285. doi:10.1016/j.ins.2023.119285

CrossRef Full Text | Google Scholar