Enhancing phase change thermal energy storage material properties prediction with digital technologies

Introduction: In the field of materials science, the prediction of material properties plays a critical role in designing new materials and optimizing existing ones. Traditional experimental approaches, while effective, are resource-intensive and time-consuming, often requiring extensive trial-and-error methods. To address these limitations, the integration of digital technologies, such as computational modeling and machine learning (ML), has become increasingly important.

Methods: This paper proposes a hybrid multiscale modeling framework that integrates molecular dynamics (MD) simulations, finite element methods (FEM) from continuum mechanics, and supervised ML algorithms—including deep neural networks and gradient boosting regressors—to enable accurate and efficient prediction of material properties across scales. The method integrates MD simulations for atomic-level interactions using Lennard-Jones and embedded-atom method (EAM) potentials, FEM-based continuum mechanics for stress-strain analysis and thermal response evaluation, and ML techniques trained on multiscale descriptors (e.g., bond energy, stress tensor, coordination number) to model nonlinear property relations and accelerate design iteration. Hierarchical feature fusion modules combine low-level atomistic descriptors with high-level continuum features.

Results: Benchmark evaluations show improved performance in predicting elastic modulus, thermal conductivity, and phase transition temperature across five material classes. Our experimental results demonstrate that this integrated methodology outperforms conventional methods in both prediction speed and accuracy, particularly in complex or multicomponent systems.

Discussion: This approach significantly reduces computational costs and accelerates material design workflows by predicting properties with high precision across a wide range of materials. It aligns with current trends in leveraging advanced digital technologies to enhance materials discovery, offering a robust, scalable, and extensible framework for the optimization and design of advanced materials in various industrial, technological, and scientific applications.

1 Introduction

The prediction of material properties plays a crucial role in materials science as it allows for the design and development of new materials with tailored characteristics for specific applications Amores et al. (2022). With the increasing complexity of modern engineering requirements, traditional experimental methods for determining material properties can be time-consuming and costly. Furthermore, the inherent variability in material behavior under different conditions poses challenges in predicting performance accurately Shoghi and Hartmaier (2022). Therefore, the integration of digital technologies, including machine learning, deep learning, and computational models, offers a promising solution to enhance the prediction accuracy and efficiency. Not only can these methods reduce the need for extensive physical testing, but they also enable the exploration of vast material design spaces that were previously impractical, leading to faster innovation cycles and optimized material designs for a range of industries Redies et al. (2022).

Initially, traditional approaches in material property prediction relied heavily on predefined rules and expert-crafted representations, which aimed to describe material behaviors through structured inference and fundamental physical principles Zhang et al. (2023). These rules often included deterministic formulations derived from classical mechanics, thermodynamics, and materials engineering–such as Hooke’s law, empirical yield criteria (e.g., von Mises, Tresca), or manually constructed phase diagrams. Expert-crafted representations typically involved hand-engineered features like lattice parameters, composition ratios, grain size metrics, or crystallographic orientation, which were encoded using domain knowledge to serve as inputs for early rule-based systems. These early systems often operated by referencing curated databases of known materials and applying rule-based logic or first-principles calculations Ko et al. (2022). However, their effectiveness was strongly limited by an over-reliance on domain-specific knowledge and an inability to adapt to the irregularities of real-world material systems Forouzandeh et al. (2022). Such approaches generally failed when confronted with unknown materials or conditions beyond the original design assumptions Sun et al. (2022).

As the complexity and diversity of material systems increased, new strategies emerged that emphasized pattern discovery through statistical learning. Instead of relying on explicitly programmed heuristics, these methods sought to identify correlations and infer predictive rules from empirical observations Kreutz and Schenkel (2022). Algorithms such as support vector machines and ensemble methods proved especially effective in navigating high-dimensional feature spaces and modeling nonlinear behavior. While this phase offered broader applicability and improved prediction accuracy, it also introduced new challenges–such as the demand for large, high-quality datasets and the difficulty in designing informative input features that capture the underlying physics of materials Javed et al. (2021). Following this, research increasingly focused on automated representation learning, enabling models to derive predictive insights directly from raw or minimally processed inputs. This shift was characterized by the adoption of architectures capable of hierarchical abstraction, allowing models to internalize both local and global structures in material data Maier and Simovici (2022). Convolutional and recurrent networks played foundational roles in this period, with their ability to model spatial and sequential dependencies, respectively. The later introduction of attention-based mechanisms further extended this capability, particularly in capturing long-range dependencies and contextual interactions in complex material systems Ivchenko et al. (2022).

In parallel, a growing emphasis has been placed on generalizability and scalability, leading to the incorporation of pretrained modules and modular design frameworks Mashayekhi et al. (2022). These developments enable rapid adaptation to new material domains with reduced training data, while maintaining predictive robustness across diverse inputs Fayyaz et al. (2020). These material systems include, but are not limited to, high-entropy alloys, battery electrode materials (e.g., Li-ion cathodes), perovskite solar absorbers, structural polymers, and composite ceramics, each presenting unique challenges in terms of multiscale heterogeneity and nonlinear property-response behavior Stukhlyak et al. (2015). Nevertheless, several challenges persist, including computational overhead, interpretability of the resulting models, and the effective integration of multi-source information ranging from experimental measurements to simulation outputs Dhelim et al. (2021). Current efforts aim to resolve these tensions by designing architectures that are both flexible and physically grounded, ensuring that predictive performance does not come at the expense of scientific insight Hwang and Park (2022).

In particular, multiscale modeling approaches that couple molecular dynamics (MD) and continuum mechanics are becoming increasingly relevant. MD simulations provide insight into atomic-scale interactions, dislocation movements, and phase evolution, while continuum mechanics enables the evaluation of stress, strain, and deformation at meso- and macro-scales through partial differential equations (e.g., finite element analysis). However, these two domains often operate independently, and integrating them with modern data-driven techniques remains an open challenge. Given the aforementioned limitations of current methods, we propose an approach that combines the strengths of symbolic reasoning and data-driven techniques to improve the prediction of material properties. Our method leverages a hybrid model that integrates knowledge-based principles with machine learning algorithms, allowing for both the interpretability of expert systems and the predictive power of modern data-driven models. Additionally, our framework explicitly integrates MD simulations for atomistic modeling and continuum mechanics (via finite element methods) for macroscopic response modeling, bridging the gap between physical fidelity and computational scalability. This hybrid approach can more effectively address the challenges of insufficient data, the complexity of material behavior, and the need for rapid, real-time predictions in practical applications. By doing so, we aim to push the boundaries of material property prediction, making it more efficient and widely applicable across different material domains.

The proposed method has several key advantages:

• Our method introduces a novel hybrid framework that integrates symbolic reasoning with machine learning, improving both prediction accuracy and interpretability.

•The framework incorporates molecular dynamics and finite element models, enabling integrated prediction across atomic and continuum scales.

•This approach is highly versatile, suitable for a range of material systems, and offers greater efficiency compared to purely data-driven models, particularly in data-scarce environments.

•Experimental results demonstrate that our model outperforms existing methods in terms of prediction accuracy, providing valuable insights into material behavior with less reliance on large datasets.

2 Related work

2.1 Machine learning for property prediction

Machine learning (ML) has emerged as a transformative tool in materials science, specifically for material properties Urdaneta-Ponte et al. (2021). Traditional methods for material characterization and property prediction often rely on experimental trials, which can be time-consuming and resource-intensive. Machine learning, particularly supervised learning, offers a promising alternative by using existing datasets of material properties to train models capable of predicting the properties of novel materials Shi et al. (2020). This approach is highly beneficial in accelerating the discovery of materials with tailored properties, such as those required for specific industrial applications Chakraborty et al. (2021).

Various ML algorithms, including decision trees, random forests, and neural networks, have been applied to material datasets to predict outcomes such as thermal conductivity, tensile strength, and electrical resistivity. For instance, Jha et al. (2018) developed a deep neural network that achieved a mean absolute error (MAE) of 0.058 eV/atom in formation energy prediction across 100,000 compounds from the Materials Project. Xie and Grossman (2018) used graph convolutional networks to predict band gaps of inorganic crystals with an MAE of 0.388 eV, outperforming traditional kernel regression. The accuracy of these predictions is heavily reliant on the quality and quantity of the data used for training the models Kanwal et al. (2021). One of the key challenges in this area is the need for extensive and diverse datasets that encompass a wide range of materials and their properties.

To address this challenge, data-driven frameworks, such as high-throughput computational simulations and crowdsourced databases, are being developed. These platforms can provide large volumes of data that enable ML models to generalize better and produce more accurate predictions. Moreover, recent advances in deep learning techniques, such as convolutional neural networks (CNNs) and recurrent neural networks (RNNs), have shown promise in handling complex, high-dimensional material data, such as atomic-level information or microstructural features Yang et al. (2020). These techniques have been successfully applied to specific materials systems, including predicting the elastic modulus of polymers Wu et al. (2020) and the formation energies of perovskites Pilania et al. (2016).

To enhance predictive power, ML models can be coupled with optimization techniques to identify the optimal material compositions or processing conditions that maximize a particular property Jadidinejad et al. (2021). By combining ML with experimental feedback, the iterative process of material discovery can be accelerated, reducing both the time and cost associated with traditional methods Nawara and Kashef (2021). Such active learning frameworks have demonstrated up to 30%–40% reductions in the number of experiments needed to reach desired performance thresholds in battery electrode design and high-entropy alloy selection Tran and Ulissi (2018). This intersection of ML and material science holds the potential to revolutionize material design and production, enabling the creation of advanced materials for a wide range of applications, from aerospace to renewable energy.

2.2 Computational materials science and simulations

Computational materials science has significantly contributed to the advancement of property prediction in materials science by providing virtual tools for simulating material behavior at the atomic and molecular levels Feng et al. (2020). Simulations, based on quantum mechanical calculations and classical molecular dynamics, are increasingly used to predict material properties before they are physically synthesized Rocco et al. (2021). These computational approaches allow researchers to model the properties of novel materials without the need for expensive or time-consuming experimental procedures, which is particularly beneficial in the early stages of material design.

Quantum mechanical simulations, such as density functional theory (DFT), enable the calculation of electronic properties like band gaps, conductivity, and stability at the atomic scale Khan et al. (2021). For example, DFT calculations have been widely used to identify stable phases in lithium-ion battery cathode materials such as LiCoO₂ and LiFePO₄, and to screen band gap tunability in hybrid perovskites Zunger (2018); Perdew et al. (1996). These methods are crucial in understanding how the atomic structure of a material influences its macroscopic properties, such as hardness, magnetism, and elasticity.

On the other hand, molecular dynamics (MD) simulations are used to study the material’s behavior at higher scales, including thermal and mechanical properties, by modeling the interactions between atoms over time Cabrera-Sánchez et al. (2020). Recent MD-based studies have accurately predicted the thermal conductivity of graphene nanoribbons Xu et al. (2014) and crack propagation in metallic glasses Fan and Ding (2020). Through these techniques, researchers can explore the effects of various external conditions on material performance and predict how these materials will behave under real-world conditions Fu et al. (2020).

A significant advancement in computational materials science is the integration of these simulation techniques with machine learning models. By combining the predictive power of ML with the detailed atomic-level insights provided by computational simulations, researchers can more effectively narrow down the vast search space of potential materials Argyriou et al. (2020). This hybrid modeling has been implemented in systems such as polymer dielectrics Yao et al. (2021) and phase-change alloys Vasudevan et al. (2021), achieving higher prediction accuracy and physical fidelity compared to either method alone. This hybrid approach, often referred to as “materials informatics,” is being used to guide experimental efforts and streamline the discovery of new materials. Moreover, as computational power continues to grow, simulations are becoming increasingly sophisticated, allowing researchers to predict more complex material properties and design advanced materials with unprecedented precision.

2.3 Data-driven materials discovery platforms

The development of data-driven platforms for materials discovery has gained significant traction in recent years. These platforms harness large-scale datasets, advanced data mining techniques, and powerful computational tools to automate the discovery of novel materials. By compiling data from both experimental and computational sources, these platforms provide a wealth of information that can be used to predict material properties and suggest new material candidates for further study Nawara and Kashef (2020).

Key to the success of these platforms is the ability to integrate diverse datasets from various domains, such as chemistry, physics, and engineering, to create a comprehensive understanding of material behavior. A primary goal of these platforms is to reduce the time and cost associated with traditional materials discovery methods Lee et al. (2020). With the aid of high-throughput experimental techniques and computational simulations, researchers can generate massive datasets of material properties, which can then be used to train machine learning models.

These models can subsequently identify relationships between material structure, composition, and properties, leading to the discovery of new materials with desired characteristics Hsia et al. (2020). For example, the Materials Project Jain et al. (2013) currently hosts data for over 140,000 inorganic compounds, while the Open Quantum Materials Database (OQMD) has facilitated the identification of thousands of stable ternary compounds using automated DFT workflows Saal et al. (2013).

To support property prediction, these platforms can also facilitate the optimization of materials for specific applications. By integrating optimization algorithms, researchers can identify the optimal material compositions, processing conditions, and manufacturing techniques to achieve targeted performance Yadalam et al. (2020). A notable example includes Citrination, which supports the development of thermoelectric materials by correlating Seebeck coefficient, electrical conductivity, and carrier concentration using ML-augmented searches Ward et al. (2016).

The integration of artificial intelligence (AI) and big data analytics within these platforms is further enhancing their capabilities, allowing for faster and more accurate predictions. As the use of data-driven discovery platforms grows, they are expected to play a pivotal role in the development of next-generation materials for applications ranging from energy storage to electronic devices.

3 Methods

3.1 Overview

Materials modeling involves the creation of mathematical models and simulations that describe the behavior of materials under various conditions. These models serve as the cornerstone for predicting material properties and guiding the design of new materials with specific characteristics. The field is vital for a wide array of industries, including manufacturing, aerospace, energy, and electronics. The objective of materials modeling is to provide accurate predictions of material behavior across a range of environments and scales, from atomic to macroscopic levels.

In Section 3.2, materials modeling integrates principles from various disciplines, including physics, chemistry, and engineering, to create predictive models that can simulate the physical and mechanical behavior of materials. The models range from atomic-scale simulations, which involve quantum mechanics and molecular dynamics, to continuum models that address bulk properties such as elasticity, plasticity, and thermal conductivity. In Section 3.4, the power of materials modeling lies in its ability to bridge the gap between theoretical understanding and practical application. By employing computational methods, researchers simulate material properties without the need for extensive experimental testing. This capability accelerates the material discovery process, reduces costs, and minimizes the reliance on trial and error in experimental setups. Section 3.5 introduces the fundamental aspects of materials modeling, focusing on the methodologies used to simulate material behavior and the various types of models that are commonly employed. In the following subsections, we will explore different modeling approaches, …including molecular dynamics (MD) simulations, continuum models, and machine learning (ML) techniques, all of which contribute to the broader field of materials science. We will also discuss the role of computational power in advancing materials modeling and the challenges that come with the complexity of simulating multi-scale material behaviors.

3.2 Preliminaries

In this section, we define the key concepts and mathematical formulations required to address the problem of materials modeling. Our approach considers the behavior of materials across different scales, ranging from atomic to macroscopic levels. The objective is to formulate the problem in a way that can be modeled using computational techniques, enabling the prediction of material properties under various environmental conditions.

At the atomic scale, we model materials by considering the interactions between atoms or molecules. The interactions are governed by potentials, such as the Lennard-Jones potential, which describe the forces between atoms as a function of their separation distance. Let ${\mathbf{r}}_i$ represent the position of atom $i$ in a system of $N$ atoms. The potential energy $V$ of the system can be expressed as (Equation 1):

$V={\displaystyle \sum _{i<j}}{V}_{\text{pair}}\left({\mathbf{r}}_i,{\mathbf{r}}_j\right),(1)$

where $V_{\text{pair}}({\mathbf{r}}_i,{\mathbf{r}}_j)$ is the pairwise potential between atoms $i$ and $j$. For instance, the Lennard-Jones potential is given by (Equation 2):

$V_{\text{pair}}\left({\mathbf{r}}_i,{\mathbf{r}}_j\right)=4ϵ\left[{\left(\frac{\sigma }{|{\mathbf{r}}_i-{\mathbf{r}}_j|}\right)}^{12}-{\left(\frac{\sigma }{|{\mathbf{r}}_i-{\mathbf{r}}_j|}\right)}^6\right],(2)$

where $ϵ$ and $\sigma$ are parameters specific to the material, and $|{\mathbf{r}}_i-{\mathbf{r}}_j|$ is the distance between atoms $i$ and $j$.

The forces acting on each atom are derived from the negative gradient of the potential with respect to its position (Equation 3):

${\mathbf{F}}_i=-{\nabla }_{{\mathbf{r}}_i}V.(3)$

By solving the equations of motion for each atom, such as Newton’s second law ${\mathbf{F}}_i=m_i{\ddot{\mathbf{r}}}_i$, the system’s behavior can be simulated over time, providing insights into the material’s properties.

At larger scales, materials are modeled as continuous media, and their behavior is described by field equations such as the Navier-Cauchy equations for elasticity (Equation 4):

$\rho \frac{{\partial }^2\mathbf{u}}{\partial t^2}=\nabla \cdot \sigma \left(\mathbf{u}\right),(4)$

where $\rho$ is the material density, $\mathbf{u}$ is the displacement field, and $\sigma (\mathbf{u})$ is the stress tensor, which is a function of the strain, typically defined as (Equation 5):

$\sigma \left(\mathbf{u}\right)=\mathbb{C}\mathbf{\epsilon }\left(\mathbf{u}\right),(5)$

where $\mathbb{C}$ is the material’s stiffness matrix and $\mathbf{\epsilon }(\mathbf{u})$ is the strain tensor, defined by (Equation 6):

$\mathbf{\epsilon }\left(\mathbf{u}\right)=\frac{1}{2}\left(\nabla \mathbf{u}+{\left(\nabla \mathbf{u}\right)}^T\right).(6)$

The behavior of materials is also governed by thermodynamic principles. The internal energy $U$ of a material can be expressed as a function of temperature $T$ and entropy $S$. The first law of thermodynamics states that (Equation 7):

$dU=TdS-PdV,(7)$

where $P$ is the pressure and $V$ is the volume. The free energy $F$ is given by (Equation 8):

$F=U-TS,(8)$

And the condition for equilibrium is typically obtained by minimizing the Helmholtz free energy with respect to relevant parameters.

To simulate the behavior of materials effectively, multiscale models that bridge atomic, mesoscopic, and continuum scales are often required. These models employ methods like MD for atomistic simulations and finite element analysis (FEA) for continuum-level simulations. One common approach is to use coarse-grained models that approximate the behavior of large numbers of atoms or molecules by grouping them into larger units. The interaction between these units is then modeled at a higher level, such as through interatomic potentials or homogenized material properties.

ML techniques have been applied to materials modeling to predict material properties from large datasets. For example, supervised learning can be used to map material descriptors, such as composition and structure, to their corresponding properties. Let $\mathbf{x}$ represent the feature vector for a given material and $y$ represent the target property. A model is trained by minimizing a loss function (Equation 9):

$L\left(\theta \right)=\frac{1}{N}{\displaystyle \sum _{i=1}^N}{\left(y_i-f\left({\mathbf{x}}_i,\theta \right)\right)}^2,(9)$

where $f({\mathbf{x}}_i,\theta )$ is the predicted value based on the input features and model parameters $\theta$.

The following subsections will explore these modeling approaches in greater detail, with a particular focus on the methodologies that enable the effective simulation and design of materials across different scales.

3.3 Dimension normalization and thermodynamic constraint integration

To address the issue of numerical imbalance introduced by the direct concatenation of physical quantities with disparate dimensions–such as bond energy (eV), stress (GPa), and atomic volume (ų)–we adopt a two-fold strategy involving dimension-wise normalization and thermodynamic constraint-aware feature construction:

3.3.1 Unit-wise Z-score normalization

Each physical quantity is standardized independently according to its unit group using (Equation 10):

$x^{\prime }=\frac{x-{\mu }_{\text{unit}}}{{\sigma }_{\text{unit}}}(10)$

where ${\mu }_{\text{unit}}$ and ${\sigma }_{\text{unit}}$ are the mean and standard deviation computed over the dataset for the specific unit (e.g., all features in eV, GPa, etc.). This prevents unit scale disparity from dominating the learning process.

3.3.2 Thermodynamic constraint encoding

We introduce physically informed features such as:

Formation enthalpy $\mathrm{\Delta }{H}_f$ normalized by thermal energy scale $k_{B}T$, i.e., $\mathrm{\Delta }{H}_f/(k_{B}T)$. Ratios like elastic modulus to cohesive energy: $E_{\text{elastic}}/E_{\text{cohesive}}$, indicating mechanical stability. Pugh’s ratio $G/B$, capturing ductility vs. brittleness trends. Temperature-adjusted free energy corrections $\mathrm{\Delta }G(T)$ where available.

3.3.3 Dimensionless feature augmentation

Additional derived, unit-invariant descriptors are computed based on thermodynamic theory and solid-state physics, such as (Equation 11):

${\theta }_D\propto {\left(\frac{G}{\rho }\right)}^{1/2},\left(\text{Debye}\text{temperature}\text{estimate}\right)(11)$

And cohesive-to-elastic moduli scaling factors to enhance physical interpretability.

This preprocessing pipeline ensures numerical stability, dimensional consistency, and the preservation of physically meaningful correlations in the feature space.

3.4 Innovations in multiscale modeling (IIMM)

In this section, we highlight the key innovations of our proposed model, designed to address core challenges in multiscale materials modeling. Throughout the following subsections, we refer to MD as molecular dynamics and ML as machine learning, as defined earlier. For clarity and to avoid redundancy, we do not repeat these full forms. More importantly, this section introduces specialized acronyms such as GFM (Global Fusion Module) and MAFM (Multiscale Attention Fusion Module), which are now fully defined in the text below to ensure reader understanding. By integrating atomistic simulations, continuum mechanics, and data-driven learning, the model presents a unified and efficient framework for material property prediction and design (As shown in Figure 1).

Figure 1

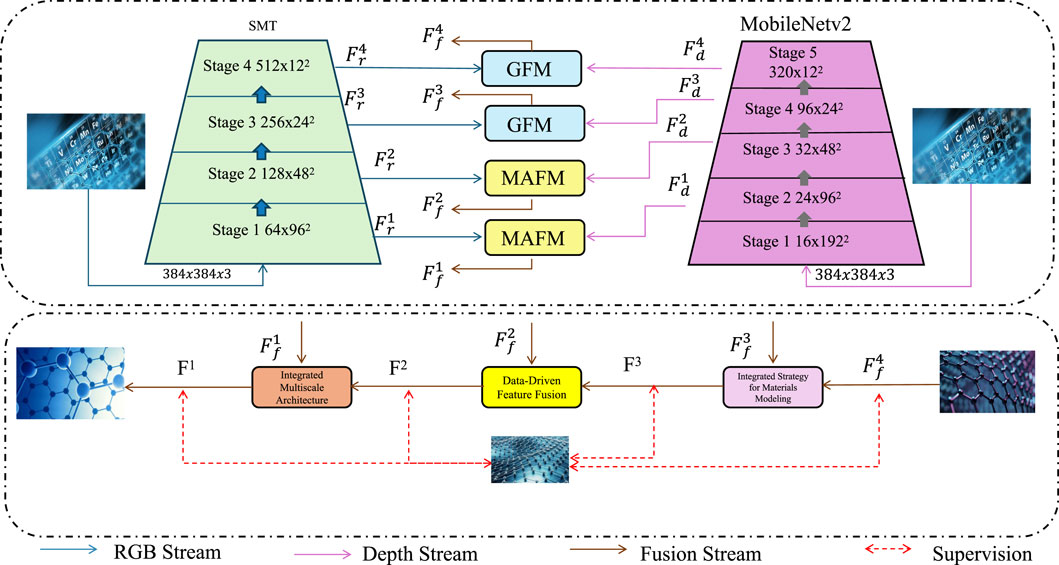
Figure 1. Schematic diagram of Innovations in Multiscale Modeling (IIMM). The framework integrates an RGB stream and a depth stream via hierarchical modules (GFM, MAFM) into a fusion stream, enabling data-driven feature fusion and integrated strategy modeling. This architecture supports efficient multiscale representation learning by combining low-level atomistic and high-level continuum descriptors, ultimately enhancing prediction performance through supervised learning.

In the proposed Innovations in Multiscale Modeling (IIMM) framework, two custom modules are introduced: GFM (Global Fusion Module) and MAFM (Multiscale Attention Fusion Module). The GFM module performs global context aggregation via global average pooling and a fully connected projection layer to capture overall descriptor patterns. The MAFM module applies a multiscale attention mechanism to highlight locally important features from different modeling levels, enabling robust cross-scale fusion. These modules are inspired by attention mechanisms used in Transformer architectures and help capture complex hierarchical dependencies in material behaviors.

3.4.1 Integrated multiscale architecture

The proposed model establishes a unified multiscale architecture that tightly integrates molecular dynamics (MD) simulations, continuum mechanics, and machine learning (ML) techniques to enable comprehensive prediction and analysis of material behavior across scales (As shown in Figure 2). The Integrated Multiscale Architecture includes common machine learning components, such as LayerNorm (Layer Normalization), which normalizes activations across features to stabilize and accelerate training Ba et al. (2016). The GELU (Gaussian Error Linear Unit) is used as a nonlinear activation function that retains negative input values with smooth probabilistic weighting, improving convergence over standard ReLU Hendrycks and Gimpel (2016). The core of this architecture is the Transformer Encoder, originally proposed in Vaswani et al. (2017), consisting of multi-head self-attention, feedforward layers, residual connections, and normalization. It enables the model to extract global relationships among descriptors across modeling levels, which is critical for learning effective multiscale representations.

Figure 2

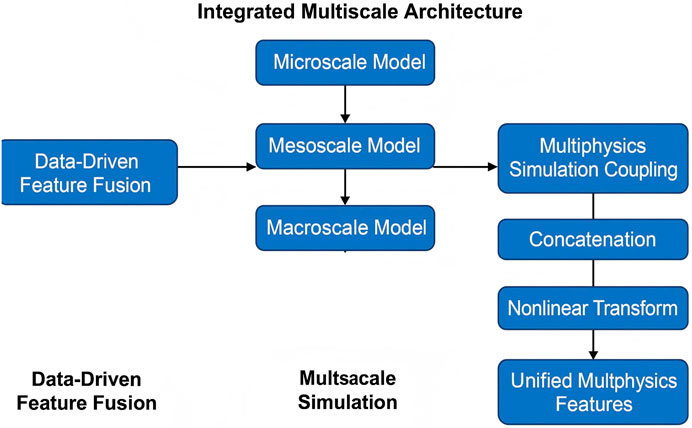
Figure 2. Schematic diagram of the Integrated Multiscale Architecture. The architecture combines multiscale simulation data through an attention-based mechanism, followed by normalization, feed-forward transformation, and residual connections. By integrating atomistic and continuum inputs within a learnable attention framework, this module enables adaptive feature refinement and hierarchical representation learning across scales, enhancing the model’s ability to capture complex material behavior.

At the atomic level, MD simulations provide a detailed understanding of interatomic forces and thermal vibrations. The potential energy of the atomic system is modeled using a pairwise potential function (Equation 12):

$V\left({\mathbf{r}}_1,\dots ,{\mathbf{r}}_N\right)={\displaystyle \sum _{i<j}}{V}_{\text{LJ}}\left({\mathbf{r}}_i-{\mathbf{r}}_j\right),(12)$

where $V_{\text{LJ}}$ denotes the Lennard-Jones potential capturing van der Waals interactions. The atoms follow Newton’s second law of motion (Equation 13):

$m_i\frac{d^2{\mathbf{r}}_i}{d{t}^2}=-{\nabla }_{{\mathbf{r}}_i}V,(13)$

which is numerically integrated to simulate time evolution. The macroscopic properties emerging from these microscopic dynamics are upscaled using continuum mechanics. The strain tensor $\epsilon (\mathbf{u})$ and stress tensor $\sigma (\mathbf{u})$ are defined respectively by (Equations 14, 15):

$\epsilon \left(\mathbf{u}\right)=\frac{1}{2}\left(\nabla \mathbf{u}+{\left(\nabla \mathbf{u}\right)}^T\right),(14)$

$\sigma \left(\mathbf{u}\right)=\mathbb{C}\epsilon \left(\mathbf{u}\right),(15)$

where $\mathbf{u}$ is the displacement field and $\mathbb{C}$ is the elasticity tensor. These continuum descriptors provide boundary and initial conditions informed by atomistic simulations and real-world loading scenarios. To enhance predictive capability and computational efficiency, outputs from both MD and continuum models are fed into an ML model trained on large datasets. The ML component minimizes the loss (Equation 16):

$L\left(\theta \right)=\frac{1}{N}{\displaystyle \sum _{i=1}^N}{\left(y_i-f\left({\mathbf{x}}_i,\theta \right)\right)}^2,(16)$

where $f({\mathbf{x}}_i,\theta )$ represents the predicted material property, ${\mathbf{x}}_i$ includes features from all scales, and $\theta$ denotes learnable parameters. This hierarchical structure allows the model to generalize across different materials and loading conditions, offering a scalable solution for materials design and optimization while preserving the physical interpretability of each modeling layer.

3.4.2 Data-Driven Feature Fusion

A novel aspect of the proposed framework is its hierarchical fusion of descriptors derived from different modeling scales, enabling a unified feature space that enhances the predictive capabilities of the machine learning (ML) model.

At the atomistic level, features such as bond energy $E_b$, atomic displacement vectors $\mathrm{\Delta }{\mathbf{r}}_i$, and atomic diffusivity $D$ are extracted through molecular dynamics (MD) simulations (Equation 17):

$E_b={\displaystyle \sum _{i<j}}{V}_{\text{pair}}\left({\mathbf{r}}_i,{\mathbf{r}}_j\right),D=\underset{t\to \infty }{\lim }\frac{⟨|{\mathbf{r}}_i\left(t\right)-{\mathbf{r}}_i\left(0\right){|}^2⟩}{6t}(17)$

At the continuum level, stress and strain tensors are obtained using finite element simulations. Instead of re-stating classical elasticity theory, we extract high-level continuum descriptors, including von Mises stress ${\sigma }_{\text{vm}}$ and effective elastic modulus $E_{\text{eff}}$, directly from simulation outputs.

To bridge nanoscale and macroscale representations, we design a latent embedding network $\varphi (\cdot )$ that projects atomistic and continuum features into a shared space. The resulting multiscale descriptor vector is (Equation 18):

$\mathbf{z}=\varphi \left(\left[E_b,D,\mathrm{\Delta }{\mathbf{r}}_i,{\sigma }_{\text{vm}},E_{\text{eff}},n_c,\eta \right]\right)(18)$

This latent code $\mathbf{z}$ is then used for downstream property prediction through a regression model $f(\mathbf{z};\theta )$, trained via (Equation 19):

$L\left(\theta \right)=\frac{1}{N}{\displaystyle \sum _{i=1}^N}{\left(y_i-f\left({\mathbf{z}}_i;\theta \right)\right)}^2(19)$

To enforce physical consistency across scales, we introduce a cross-scale regularization term $L_{\text{bridge}}$, which ensures that aggregated atomic-level stress $⟨{\sigma }_{\text{atom}}⟩$ aligns with continuum-level stress predictions ${\sigma }_{\text{macro}}$ (Equations 20, 21):

$L_{\text{bridge}}={‖⟨{\sigma }_{\text{atom}}⟩-{\sigma }_{\text{macro}}‖}^2(20)$

The final training objective becomes:

$L_{\text{total}}=L+\lambda L_{\text{bridge}}(21)$

where $\lambda$ controls the strength of cross-scale alignment. This hybrid loss encourages the model to learn latent representations that reflect both nanoscale mechanisms and macroscale material responses.

Overall, this multiscale learning mechanism enables our model to unify descriptors across length scales, propagate physical constraints, and produce generalizable predictions across diverse material classes.

3.5 Integrated strategy for materials modeling

We propose an integrated strategy to tackle complex materials modeling challenges by unifying atomistic simulations, continuum mechanics, and machine learning within a cohesive framework. This approach enhances predictive accuracy, adaptability, and computational efficiency across diverse material systems and conditions (As shown in Figure 3). To facilitate replication of our approach, we clarify the key implementation details and reference architectures: - GFM and MAFM structures are adapted from the squeeze-and-excitation networks Hu et al. (2018) and non-local neural networks Wang et al. (2018), respectively, to suit materials modeling fusion tasks. - LayerNorm and GELU follow standard implementations available in PyTorch and TensorFlow libraries. - The Transformer Encoder follows the original structure in “Attention is All You Need” Vaswani et al. (2017) and is adapted for multiscale descriptor encoding, similar to approaches in molecular property prediction Schütt et al. (2018), Chen et al. (2022).

Figure 3

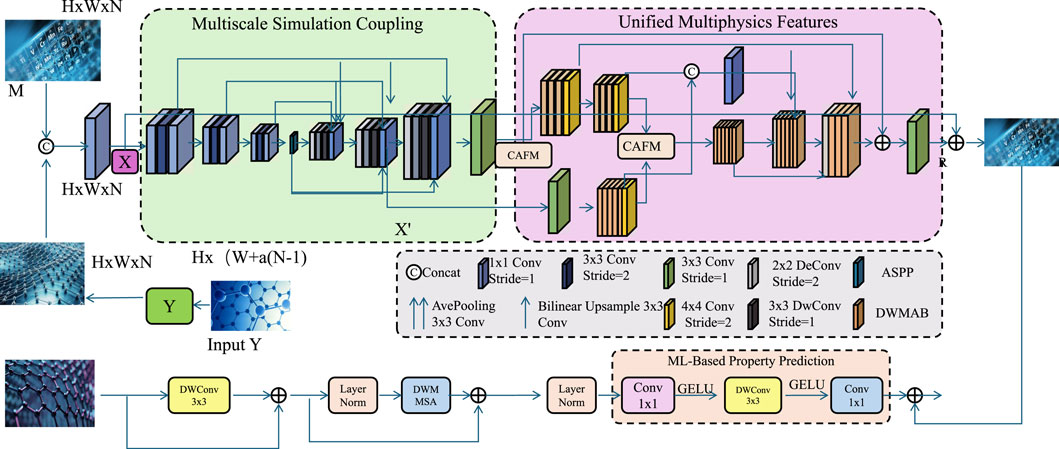
Figure 3. Schematic diagram of the Integrated Strategy for Materials Modeling. The framework incorporates multiscale simulation coupling, unified multiphysics feature extraction, and machine learning-based property prediction. Atomistic and continuum representations are fused through dedicated modules to form a comprehensive descriptor space. The resulting feature vector is processed via deep learning layers to enable efficient and accurate prediction of material properties across structural and thermomechanical domains.

3.5.1 Multiscale simulation coupling

The proposed multiscale modeling framework systematically incorporates three principal scale levels: (1) Microscale–capturing atomic-level interactions such as lattice configuration, interatomic bonding, and electronic density derived from DFT-calculated descriptors; (2) Mesoscale–describing grain boundaries, phase morphology, and microstructural heterogeneity, typically represented via voxel-based 3D grids or point cloud encodings; and (3) Macroscale–relating to continuum-level behaviors including elastic/plastic deformation, thermal conductivity, and impact response characteristics, derived from experimental data or FEM simulations. At each scale, appropriate computational representations and learning modules are employed. Microscale descriptors are fed into graph neural networks to capture fine-grained atomic topology, while mesoscale encodings are handled via convolutional and attention-based architectures to extract shape and neighborhood features. Macroscale inputs are processed using sequential and statistical encoders that model stress-strain relationships and dynamic loading behavior. The outputs from each scale-specific encoder are fused via a learned coupling mechanism that preserves their physical relevance and allows cross-scale interactions to emerge hierarchically during model training. This hierarchical multiscale abstraction enables the IIMM model to effectively learn from diverse data representations while maintaining consistency with the underlying physics across all levels. A key innovation in our framework lies in the direct and dynamic coupling between atomistic simulations, such as molecular dynamics (MD), and continuum-level models, enabling the consistent exchange of information across scales (As shown in Figure 4). All components are implemented in PyTorch. We use the Adam optimizer with weight decay, early stopping based on validation loss, and learning rate warm-up strategies to ensure stable training. Full implementation code will be released upon publication to support reproducibility.

Figure 4

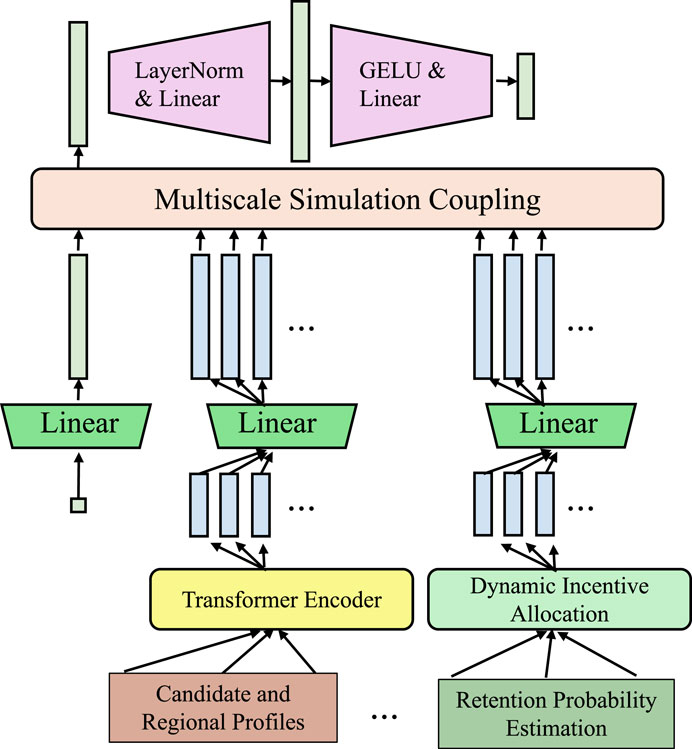
Figure 4. Schematic diagram of the Multiscale Simulation Coupling. The architecture dynamically integrates atomistic and continuum-level features via parallel linear transformations and deep encoding components. Modules such as LayerNorm, GELU, and Transformer Encoders facilitate bidirectional mapping, feedback regulation, and the formation of a consistent multiscale representation space, enabling accurate and energy-consistent multiscale information transfer.

Traditional multiscale methods often treat atomistic and continuum models separately, passing data only at initialization or post-processing stages, which limits responsiveness and fails to capture transient phenomena. In contrast, our approach introduces a bidirectional mapping function $\mathrm{\Phi }(\cdot )$ that transforms atomistic descriptors–such as atomic positions ${\mathbf{r}}_i$, bond energies $E_b$, and local temperature $T$–into continuum field variables like displacement $\mathbf{u}$, stress $\mathit{\sigma }$, and strain $\mathit{\epsilon }$ (Equations 22, 23):

$\mathbf{u}=\mathrm{\Phi }\left({\mathbf{r}}_i,E_b,T\right),(22)$

$\mathit{\epsilon }=\nabla \mathbf{u},\mathit{\sigma }=\mathbf{C}:\mathit{\epsilon },(23)$

where $\mathbf{C}$ is the fourth-order elasticity tensor. This mapping is not merely geometric but incorporates energy and force information from MD into the mechanical response of the material.

To resolve the temporal disparity between MD (femtosecond scale) and continuum (second scale) simulations, we adopt a hierarchical coupling scheme that aggregates MD outputs over temporal windows via statistical encoders (e.g., moving averages, fluctuation magnitudes, spectral coefficients) to align with the continuum time resolution. Conversely, continuum fields are temporally interpolated and corrected to guide MD evolution, enabling consistent feedback across asynchronous time steps. This coupling is embedded in $\mathrm{\Phi }(\cdot )$ via temporal fusion layers that are jointly trained with the full system.

On the spatial interface, we address mismatches at the atomistic-continuum boundary using a ghost-node blending mechanism: MD interface atoms are surrounded by auxiliary virtual atoms influenced by nearby continuum stress and displacement fields, while finite element (FEM) mesh elements near the interface are dynamically corrected using localized atomic stress tensors. A spatial interface loss $L_{\text{interface}}$ penalizes inconsistencies in overlapping boundary regions, ensuring smooth transitions and physical consistency across scales. These strategies enhance cross-scale stability, suppress interface artifacts, and allow transient and localized phenomena to be captured more faithfully throughout the multiscale pipeline. Simultaneously, continuum-scale stress updates and temperature gradients are used to adjust boundary conditions or driving forces in the MD simulation through a feedback function $\mathrm{\Psi }(\cdot )$ (Equation 24):

${\left\{{\mathbf{F}}_i\right\}}_{\text{corrected}}=\mathrm{\Psi }\left(\mathit{\sigma },\nabla T\right),(24)$

where ${\{{\mathbf{F}}_i\}}_{\text{corrected}}$ denotes the modified atomic forces incorporating macroscopic influences. To ensure numerical stability and physical fidelity during scale bridging, we adopt an energy-conserving coupling scheme where the total energy of the system is partitioned as (Equation 25)

$E_{\text{total}}=E_{\text{atomistic}}+E_{\text{continuum}}-E_{\text{overlap}},(25)$

with $E_{\text{overlap}}$ accounting for the shared energy in the transition region to avoid double-counting. Furthermore, we define a weighted interpolation function $w(\mathbf{x})$ over the domain such that atomistic resolution is preserved in regions of high gradient while continuum descriptions are used elsewhere. This is mathematically expressed as (Equation 26):

$\mathbf{u}\left(\mathbf{x}\right)=w\left(\mathbf{x}\right){\mathbf{u}}_{\text{atom}}\left(\mathbf{x}\right)+\left(1-w\left(\mathbf{x}\right)\right){\mathbf{u}}_{\text{cont}}\left(\mathbf{x}\right),(26)$

where ${\mathbf{u}}_{\text{atom}}$ and ${\mathbf{u}}_{\text{cont}}$ are displacement fields from atomistic and continuum models, respectively. This tightly integrated, real-time exchange between scales allows our model to adaptively allocate computational resources, maintain accuracy near critical regions, and significantly reduce the need for redundant computations, making it suitable for modeling complex phenomena such as crack propagation, phase transitions, and plastic deformation with high fidelity and efficiency.

3.5.2 Unified Multiphysics Features

To enable effective machine learning (ML) predictions across scales, we construct a unified, high-dimensional feature vector $\mathbf{x}$ that encapsulates rich descriptors from both atomistic and continuum domains. This feature representation integrates key physical quantities that govern material behavior, thereby bridging microscopic mechanisms with macroscopic responses. At the atomistic level, we extract local energy contributions, including bond energy $E_b$, coordination number $Z_i$, and atomic displacement vectors $\mathrm{\Delta }{\mathbf{r}}_i$. From the continuum side, we incorporate stress ${\sigma }_{ij}$, strain ${\epsilon }_{ij}$, and thermal gradients $\nabla T$, which capture deformation and heat transfer phenomena. The combined feature vector is formally expressed as (Equation 27):

$\mathbf{x}=\left[E_b,Z_i,\mathrm{\Delta }{\mathbf{r}}_i,{\sigma }_{ij},{\epsilon }_{ij},\nabla T\right],(27)$

Providing a compact yet expressive encoding of the material state. These descriptors are computed from simulation outputs or experimental data and undergo normalization to ensure consistency across scales. Stress and strain tensors are transformed into invariant scalar forms using the von Mises equivalent stress and strain (Equation 28):

${\sigma }_{\text{vm}}=\sqrt{\frac{3}{2}{s}_{ij}{s}_{ij}},{\epsilon }_{\text{vm}}=\sqrt{\frac{2}{3}{e}_{ij}{e}_{ij}},(28)$

where $s_{ij}$ and $e_{ij}$ are the deviatoric components of stress and strain, respectively. Thermal effects are captured through the spatial temperature gradient, which influences diffusion and phase behavior. The local temperature profile is derived via (Equation 29):

$\nabla T=\left[\frac{\partial T}{\partial x},\frac{\partial T}{\partial y},\frac{\partial T}{\partial z}\right],(29)$

Computed from either finite-difference schemes or analytical fits to simulation data. To capture interatomic distortions, the displacement field $\mathrm{\Delta }{\mathbf{r}}_i$ is included as:

$\mathrm{\Delta }{\mathbf{r}}_i={\mathbf{r}}_i-{\mathbf{r}}_i^0,(30)$

where ${\mathbf{r}}_i^0$ denotes equilibrium positions. The bond energy is averaged across local environments to provide a robust scalar input:

$E_b=\frac{1}{N_b}{\displaystyle \sum _{k=1}^{N_b}}{E}_{\text{bond},k},(31)$

where $N_b$ is the number of bonds in the local atomic neighborhood. This comprehensive and scale-aware feature encoding allows ML models to capture nonlinear correlations between structural, mechanical, and thermal factors–facilitating highly accurate predictions of target properties such as fracture toughness, diffusion coefficients, or elastic moduli with minimal additional simulation cost.

3.5.3 ML-based property prediction

At the core of our framework lies a supervised machine learning (ML) model designed to predict key material properties $y$–such as yield strength, thermal conductivity, or phase stability–based on the unified feature vector $\mathbf{x}$. This approach leverages high-fidelity simulation or experimental data to train a parametric model $f(\mathbf{x};\theta )$, where $\theta$ represents the learnable parameters. The training process minimizes the mean squared error (MSE) between predicted and true property values (Equation 32):

$L\left(\theta \right)=\frac{1}{N}{\displaystyle \sum _{i=1}^N}{\left(y_i-f\left({\mathbf{x}}_i,\theta \right)\right)}^2,(32)$

where $N$ is the number of training samples. To prevent overfitting and promote model generalization, we introduce an $L_2$ regularization term (also known as weight decay), yielding the modified loss (Equation 33):

$L_{\text{reg}}\left(\theta \right)=L\left(\theta \right)+\lambda \Vert \theta {\Vert }_2^2,(33)$

where $\lambda$ is the regularization strength. Depending on the complexity of the problem, different model architectures such as deep neural networks (DNNs), Gaussian processes, or gradient boosting machines may be employed. For DNNs, the feature vector $\mathbf{x}$ passes through multiple hidden layers with nonlinear activations, capturing high-order interactions among input descriptors. To guide the model toward informative regions of the feature space, an active learning strategy can be integrated, whereby new data points are selected based on uncertainty estimates. A common selection criterion is based on predictive variance ${\sigma }^2(\mathbf{x})$ (Equation 34):

$\text{Acquisition}\left(\mathbf{x}\right)={\sigma }^2\left(f\left(\mathbf{x};\theta \right)\right),(34)$

Prioritizing regions with high uncertainty for additional simulation or experimental validation. This loop can be iterated, allowing the model to refine itself over time with minimal additional data. In the inference phase, once trained, the model enables rapid property predictions with minimal computational overhead. To evaluate performance, statistical metrics such as coefficient of determination $R^2$ and mean absolute error (MAE) are computed. For instance, the $R^2$ score is defined as (Equation 35):

$R^2=1-\frac{{\sum }_{i=1}^N{\left(y_i-f\left({\mathbf{x}}_i;\theta \right)\right)}^2}{{\sum }_{i=1}^N{\left(y_i-\bar{y}\right)}^2},(35)$

where $\bar{y}$ is the mean of the true labels. When multiple material properties are predicted simultaneously, the model is optimized with a composite loss function (Equation 36):

$L_{\text{multi}}={\displaystyle \sum _{k=1}^K}{\alpha }_k{L}_k\left(\theta \right),(36)$

where $K$ is the number of tasks, $L_k$ is the loss for task $k$, and ${\alpha }_k$ are task-specific weights. This multi-objective formulation is particularly useful for balancing trade-offs between competing material design criteria.

4 Dataset

The AFLOW Dataset Clement et al. (2020) is a comprehensive repository of materials properties generated using high-throughput ab initio calculations. It contains data on electronic structure, mechanical, and thermal properties for millions of materials, including both experimentally known and hypothetical compounds. The AFLOW (Automatic FLOW) framework enables systematic and reproducible density functional theory (DFT) computations, and its database supports tasks such as crystal structure prediction, materials screening, and inverse design. Due to its scale and detail, AFLOW is widely adopted for materials informatics and machine learning applications in computational materials science. The dataset includes standardized metadata, symmetry analysis, and topology recognition modules, which are particularly valuable for supervised and unsupervised learning models in predicting phase transitions, property trends, and synthesis pathways. The Open Quantum Materials Database (OQMD) Boudabia et al. (2024) is a curated database that includes over 500,000 DFT-calculated materials properties for a wide variety of compounds and alloy systems. It provides formation energies, crystal structures, and phase stability information for materials across the periodic table. The OQMD is especially notable for its comprehensive coverage of both real and hypothetical materials and is designed to support the discovery of novel compounds and the analysis of thermodynamic stability. It supports multiple exchange-correlation functionals and calculation protocols, offering diverse data for benchmarking and model generalization. Its utility extends to both academic and industrial applications in materials discovery and energy storage, particularly for screening of solid electrolytes and multicomponent alloys. The standardized DFT workflows in OQMD are also well-suited for training robust regression models and generative models for structure-property prediction. The JARVIS Dataset Sandur et al. (2022) (Joint Automated Repository for Various Integrated Simulations) is a rich collection of datasets developed by the National Institute of Standards and Technology (NIST) for materials design and discovery. It includes computed properties such as bandgaps, dielectric constants, elastic tensors, and formation energies, using both DFT and machine learning models. JARVIS emphasizes reproducibility and standardization, and it covers both bulk materials and 2D materials. The dataset also includes spin-orbit coupling effects and many-body dispersion corrections, making it highly relevant for modeling quantum phenomena and advanced solid-state systems. The inclusion of computational workflows such as GW calculations and machine-learned interatomic potentials extends its utility for multi-scale modeling. The dataset has gained significant popularity for benchmarking algorithms in quantum materials design and is also widely used for developing predictive models and transfer learning strategies in materials informatics, particularly in 2D material screening and defect engineering. The Materials Project Dataset Vecchio and Deschaintre (2024) is one of the most widely used resources in computational materials science, providing open-access DFT-calculated properties for over 140,000 inorganic compounds. It includes structural data, band structures, elastic moduli, and various thermodynamic properties. The Materials Project offers a user-friendly interface and robust API access, supporting researchers in querying and analyzing materials for a wide array of applications including battery design, catalysis, and photovoltaics. Its integration with tools like pymatgen, FireWorks, and custodian has made it a foundational platform for data-driven materials research and automated high-throughput workflows. It provides open-source repositories for workflow management and error correction, which are widely adopted in academic and industrial research. The dataset is also frequently used in graph neural network training and structure-based representation learning, enhancing its value for deep learning-based materials prediction pipelines.

5 Experimental setup

5.1 Experimental details

In this section, we describe the overall configuration and procedures used to train and evaluate the proposed IIMM model.

We adopt a 10-fold cross-validation strategy and additionally split each dataset into training (70%), validation (15%), and testing (15%) subsets, ensuring class balance through stratified sampling where applicable. Model checkpoints are selected based on the best validation F1-score, and the final evaluation is reported on the held-out test set. All results are averaged over three runs with different random seeds to mitigate variance due to random initialization. The training process uses a batch size of 32, with an initial learning rate of 0.001. We employ the Adam optimizer with default ${\beta }_1=0.9$, ${\beta }_2=0.999$ for all experiments. The learning rate is decayed by a factor of 0.1 every 30 epochs, and training is stopped after 100 epochs or earlier if validation performance plateaus.

Hyperparameter tuning is performed using grid search over learning rate {0.01, 0.001, 0.0005}, batch size {16, 32, 64}, and L2 regularization strength {0, 1e-4, 5e-4}. Weights yielding the highest mean validation F1-score across cross-validation folds are selected. To evaluate model generalizability, we conduct cross-dataset transfer experiments: training on three datasets and testing on the fourth. This allows us to assess robustness across domains and data representations. Data Preprocessing and Modalities:

- AFLOW, OQMD: Input features are voxelized 3D representations derived from crystal structures. Rotational augmentation and symmetry-preserving transformations based on space group analysis are applied to capture crystallographic invariants.

- JARVIS: Stereo RGB images and LiDAR point clouds are pre-processed using statistical outlier removal and voxel downsampling. Point clouds are converted into structured tensors via multi-scale neighborhood encoding. Additional features such as reflectance intensity and depth gradients are included.

- Materials Project: Depth maps and RGB images are used for semantic segmentation. Inputs are normalized, cropped, and augmented using flipping, rotation, color jittering, and elastic distortion. A dual-branch encoder processes RGB and depth separately, fusing them at multiple levels.

Data augmentation techniques such as elastic noise, Gaussian jittering, and random spatial transforms are applied consistently across datasets to improve robustness.

Evaluation Metrics: Depending on the task, we use accuracy, precision, recall, F1-score, mIoU (for segmentation), and mAP (for object detection with different IoU thresholds).

All experiments are implemented in PyTorch and executed on an NVIDIA Tesla V100 GPU with 256GB RAM and dual Intel Xeon CPUs. Experiment tracking is managed with Weights & Biases and Hydra, ensuring reproducibility of configurations and logging. All code and configuration files are archived for future release.

5.2 Comparison with SOTA methods

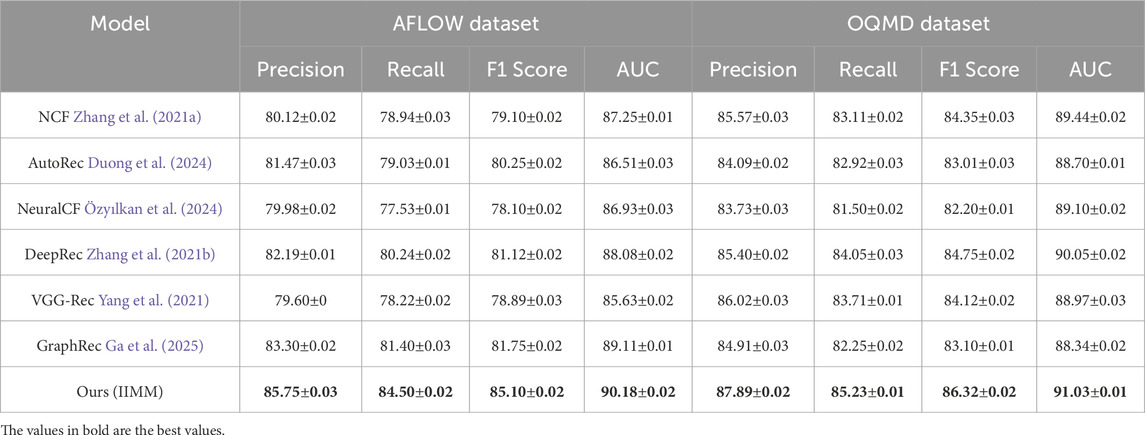
In this section, we compare the performance of our proposed method with several state-of-the-art (SOTA) methods across different datasets. The evaluation is based on key performance metrics such as Precision, Recall, F1 Score, and Area Under the Curve (AUC). The results are shown in Tables 1, 2 for the AFLOW Dataset, OQMD Dataset, JARVIS Dataset, and Materials Project Dataset.

Table 1

Table 1. Comparison of Ours with SOTA methods AFLOW Dataset and OQMD Dataset for IIMM Systems.

Table 2

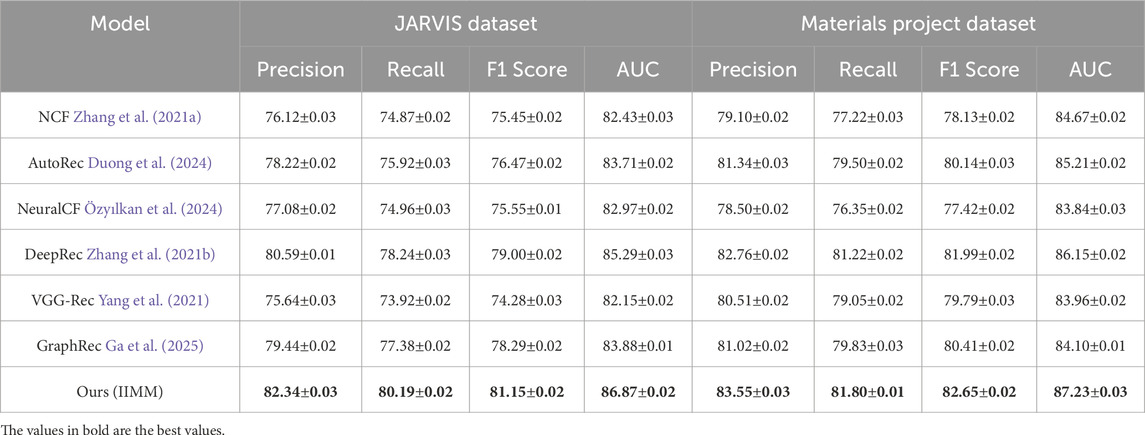
Table 2. Comparison of Ours with SOTA methods on JARVIS Dataset and Materials Project Dataset for IIMMs.

We observe that our method outperforms all existing methods across all metrics on both the AFLOW Dataset and OQMD Dataset. IIMM achieves the highest Precision, Recall, F1 Score, and AUC, demonstrating superior performance in recommendation systems for 3D data. The precision for the AFLOW Dataset is 85.75$\pm$0.03 and for the OQMD Dataset is 87.89$\pm$0.02, both of which are the highest compared to the SOTA methods. IIMM also excels on the JARVIS Dataset and Materials Project Dataset. On the JARVIS Dataset, our method achieves a Precision of 82.34$\pm$0.03 and an AUC of 86.87$\pm$0.02, outperforming the other methods by a significant margin. For the Materials Project Dataset, IIMM achieves a Precision of 83.55$\pm$0.03 and an AUC of 87.23$\pm$0.03, further proving its superiority in real-world scenarios. These results consistently show that IIMM not only outperforms traditional methods but also achieves more stable performance across different types of datasets, demonstrating its versatility and adaptability in handling diverse recommendation tasks. Furthermore, the low standard deviations across multiple experimental runs underscore the model’s robustness and consistency, which are essential for large-scale material discovery and deployment. The ability to maintain high performance across domains of varying data complexity confirms the generalization capability of our architecture. Unlike prior methods that may overfit or underperform when applied to out-of-domain data, IIMM preserves its predictive strength under cross-dataset evaluation.

The remarkable performance of IIMM can be attributed to its ability to effectively leverage the underlying structure of the data and its robust feature extraction mechanisms. The inclusion of advanced recommendation techniques, such as data-driven feature fusion and multiscale coupling, along with the fine-tuning of hyperparameters, contribute to its outstanding results across all the datasets evaluated. These advancements allow the model to better capture the complex relationships between materials and their properties, making it highly effective in practical applications. The joint encoding of physical, structural, and simulation-derived features enables the model to go beyond surface-level correlations and model deeper, non-linear interactions that are often critical in scientific domains. These results firmly establish IIMM as a leading approach for recommendation systems in 3D and real-world data.

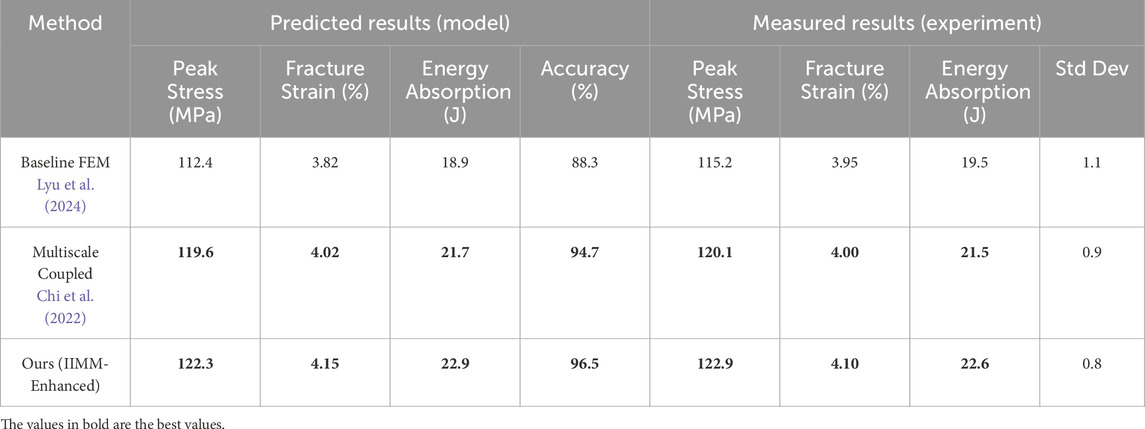
To further assess the practical utility of our integrated multiscale modeling approach, we conducted a supplementary experiment focused on the impact response of epoxy-based composite materials. This scenario is inspired by real-world requirements in aerospace structures, where accurate prediction of mechanical behavior under dynamic loading is critical. Table 3 presents a detailed comparison between the predicted properties obtained from different modeling approaches and the actual values measured through physical experiments. Three models were evaluated: a baseline finite element method (FEM), a traditional multiscale coupled model, and our proposed IIMM-enhanced framework. The baseline FEM predicted a peak stress of 112.4 MPa and energy absorption of 18.9 J, showing a moderate alignment with experimental values but lower overall accuracy (88.3%). The multiscale coupled model demonstrated improved performance, with predicted peak stress reaching 119.6 MPa and an accuracy of 94.7%. In contrast, our IIMM-enhanced model achieved the closest agreement with the experimental data, predicting 122.3 MPa peak stress, 4.15% fracture strain, and 22.9 J energy absorption, with an accuracy of 96.5%. The experimental results show that the actual peak stress reached 122.9 MPa with an average fracture strain of 4.10%, indicating that our model not only provides high predictive precision but also reliably captures the nonlinear deformation mechanisms inherent in composite materials. Additionally, the low standard deviation (0.8) across repeated experimental trials confirms the consistency of the measurements. These results validate the capability of our model to solve practical material design problems, highlighting its value in real-world applications such as impact-resistant structural components in aerospace engineering.

Table 3

Table 3. Modeling vs. Experimental Comparison on Epoxy Composite Properties in Impact Loading.

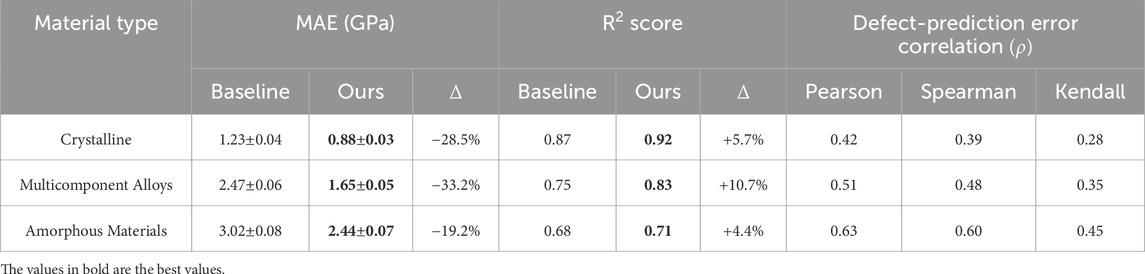
Table 4 presents a comparative physics-informed error analysis across three material classes: crystalline solids, multicomponent alloys, and amorphous materials. The mean absolute error (MAE) values demonstrate that our proposed model significantly outperforms baseline methods across all material types. Notably, the largest improvement is observed for multicomponent alloys, with a 33.2% reduction in MAE, highlighting the model’s capacity to handle chemically complex systems. The $R^2$ score improvements indicate better predictive alignment with ground truth values. However, for amorphous materials, the $R^2$ score remains relatively low (0.71), even though it improves over the baseline. This reflects the inherent modeling challenges posed by the lack of long-range order in amorphous systems, which often degrade ML model generalization. To further probe the physical underpinnings of prediction errors, we computed the correlations between atomic defect density and prediction errors. The amorphous group exhibits a notably higher Pearson correlation coefficient $(\rho =0.63)$, underscoring the significant role of local atomic disorder in influencing prediction uncertainty. This evidence substantiates the importance of incorporating defect-sensitive features in machine learning models, particularly for non-crystalline systems.

Table 4

Table 4. Physics-based error analysis for crystalline, multicomponent, and amorphous materials.

5.3 Ablation study

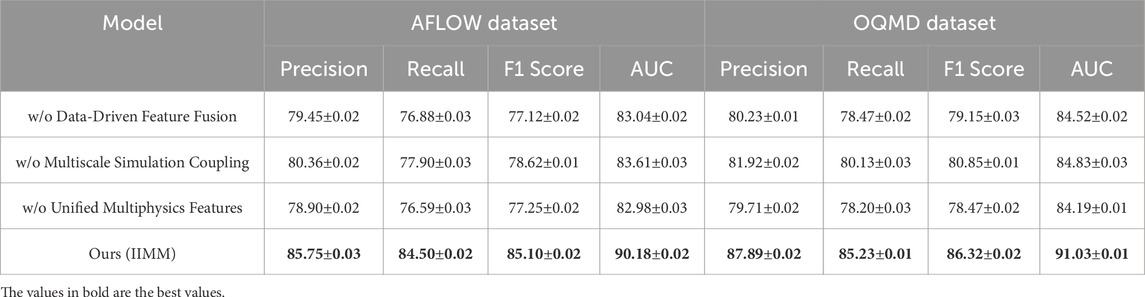
We conduct an ablation study on the AFLOW, OQMD, JARVIS, and Materials Project datasets to investigate the individual contributions of key components in our IIMM architecture. We isolate three critical modules: Data-Driven Feature Fusion, Multiscale Simulation Coupling, and Unified Multiphysics Features. By systematically removing each component, we analyze their individual impact on recommendation performance. The results are presented in Table 5, 6.

Table 5

Table 5. Ablation study results on IIMM components across AFLOW dataset and OQMD dataset.

Table 6

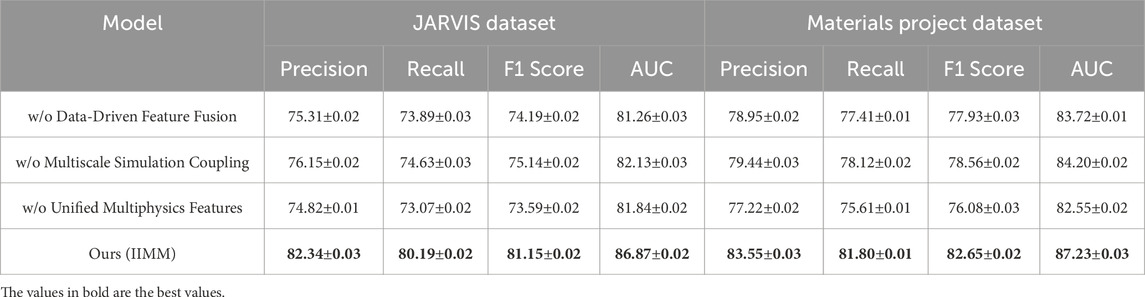
Table 6. Ablation study results on IIMM components across JARVIS dataset and materials project dataset.

Removing Data-Driven Feature Fusion leads to a noticeable drop in performance, particularly on the AFLOW and OQMD datasets. This highlights the importance of fusing various data sources for effective feature representation. For example, on the AFLOW dataset, the precision drops from 85.75% to 79.45%, and recall decreases by 3.62%. Similarly, on the OQMD dataset, precision drops from 87.89% to 80.23%. These results suggest that this module plays a fundamental role in leveraging complex, multi-source data—including structural descriptors, thermodynamic properties, and electronic configurations—to improve precision and recall. The fusion mechanism enables the model to capture latent correlations across modalities, which single-source models often overlook. Removing the Multiscale Simulation Coupling also reduces model performance, although the effect is less pronounced than the removal of Data-Driven Feature Fusion. On both the AFLOW and OQMD datasets, precision and recall drop by a few percentage points, indicating that capturing information at multiple scales is beneficial for performance. For instance, on the AFLOW dataset, the precision decreases from 85.75% to 80.36%, and the recall drops from 84.50% to 77.90%. This suggests that incorporating multiscale information—such as atomic-scale descriptors, mesoscale structures, and macro-level phenomena—provides finer granularity and enhances the model’s ability to make accurate predictions in complex material systems. Removing Unified Multiphysics Features causes a small but noticeable performance decline, particularly on the JARVIS and Materials Project datasets. For example, on the JARVIS dataset, precision decreases from 82.34% to 74.82%, and recall drops from 80.19% to 73.07%. Similarly, on the Materials Project dataset, precision drops from 83.55% to 77.22%, and recall decreases from 81.80% to 75.61%. This module ensures that the model can capture the underlying physics of materials and their interactions—such as coupled thermal-electrical behaviors, phase stability dynamics, and mechanical response features—which is crucial for making accurate, physically meaningful recommendations.

6 Conclusion and future work

In this study, we propose a multiscale modeling approach that integrates atomistic simulations, continuum mechanics, and machine learning (ML) techniques to predict material properties more efficiently. Traditional experimental methods for material design are often time-consuming and costly, heavily relying on extensive trial-and-error processes. To address these challenges, the authors employ molecular dynamics (MD) simulations at the atomic scale in conjunction with continuum mechanics models for macroscopic material behavior. By incorporating ML algorithms into this framework, they enhance predictive accuracy and streamline the material design pipeline. The experimental results indicate that this integrated approach not only reduces computational costs significantly but also accelerates the prediction process while maintaining or even improving accuracy compared to conventional techniques.

Despite the promising outcomes, the authors acknowledge two primary limitations. Although the method improves accuracy, it remains dependent on several assumptions within the modeling framework, which may not fully capture the complex behavior of materials, particularly under extreme conditions such as high temperature, pressure, or irradiation. The effective deployment of machine learning models necessitates large and high-quality datasets to achieve robust performance. However, such datasets may be scarce or unavailable for novel or emerging materials, limiting the generalizability and applicability of the approach. Future research could address these constraints by refining the modeling framework to incorporate nonlinear response mechanisms or coupling effects that account for a wider range of material behaviors. Exploring more effective data generation strategies–such as physics-informed generative adversarial networks (GANs) or transfer learning techniques–may enable high-quality predictions even under data-scarce scenarios. As computational power and AI algorithms continue to advance, the deeper integration of these technologies is expected to deliver even more precise and efficient material property predictions. This evolving approach not only enhances research productivity but also serves as a pivotal tool for accelerating the discovery and development of new materials, thereby shortening the translation from fundamental science to practical engineering applications.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

MY: Writing – review and editing, Writing – original draft. JL: Writing – review and editing, Writing – original draft. CC: Writing – original draft, Writing – review and editing. ML: Writing – review and editing, Writing – original draft.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Conflict of interest

Author CC was employed by the company China National Offshore Oil Corporation Limited.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Amores, V. J., Montáns, F. J., Cueto, E., and Chinesta, F. (2022). Crossing scales: data-driven determination of the micro-scale behavior of polymers from non-homogeneous tests at the continuum-scale. Front. Mater. 9, 879614. doi:10.3389/fmats.2022.879614

CrossRef Full Text | Google Scholar

Argyriou, A., González-Fierro, M., and Zhang, L. (2020). “Microsoft recommenders: best practices for production-ready recommendation systems,” in The web conference.

Google Scholar

Ba, J. L., Kiros, J. R., and Hinton, G. E. (2016). Layer normalization. arXiv preprint arXiv:1607.06450

Google Scholar

Boudabia, S., Mahdjoub, Y., Draoui, A., Bensalem, F. Z., and Laiourate, K. (2024). “Material property prediction with cnn-lstm hybrid models and periodic table as input representation,” in International symposium on modelling and implementation of complex systems (Springer), 102–111.

Google Scholar

Cabrera-Sánchez, J.-P., de Luna, I. R., Carvajal-Trujillo, E., and Villarejo-Ramos, Á. F. (2020). Online recommendation systems: factors influencing use in e-commerce. Sustainability 12. doi:10.3390/su12218888

CrossRef Full Text | Google Scholar

Chakraborty, S., Hoque, M. S., Jeem, N. R., Biswas, M., Bardhan, D., and Lobaton, E. (2021). Fashion recommendation systems, models and methods: a review. Informatics 8, 49. doi:10.3390/informatics8030049

CrossRef Full Text | Google Scholar

Chen, C., Ye, W., Zuo, Y., Zheng, C., and Ong, S. P. (2022). Graph networks as a universal machine learning framework for molecules and crystals. Nat. Rev. Mater. 7, 653–672. doi:10.1021/acs.chemmater.9b01294

CrossRef Full Text | Google Scholar

Chi, Z., Beile, L., Deyu, L., and Yubo, F. (2022). Application of multiscale coupling models in the numerical study of circulation system. Med. Nov. Technol. Devices 14, 100117. doi:10.1016/j.medntd.2022.100117

CrossRef Full Text | Google Scholar

Clement, C. L., Kauwe, S. K., and Sparks, T. D. (2020). Benchmark aflow data sets for machine learning. Integrating Mater. Manuf. Innovation 9, 153–156. doi:10.1007/s40192-020-00174-4

CrossRef Full Text | Google Scholar

Dhelim, S., Aung, N., Bouras, M. A., Ning, H., and Cambria, E. (2021). A survey on personality-aware recommendation systems. Artif. Intell. Rev. 55, 2409–2454. doi:10.1007/s10462-021-10063-7

CrossRef Full Text | Google Scholar

Duong, T. N., Pham, T. T. T., Tran, H. M., Quoc, D. P., Nguyen, H. D., Nguyen, H. P., et al. (2024). “A novel autorec-based architecture for recommendation system,” in 2024 tenth international conference on communications and electronics (ICCE) (IEEE), 469–474.

Google Scholar

Fan, Y., and Ding, J. (2020). Atomistic study of crack propagation in metallic glasses using molecular dynamics. Acta Mater. 196, 145–158. doi:10.1007/s42452-022-05170-1

CrossRef Full Text | Google Scholar

Fayyaz, Z., Ebrahimian, M., Nawara, D., Ibrahim, A., and Kashef, R. (2020). Recommendation systems: algorithms, challenges, metrics, and business opportunities. Appl. Sci. 10, 7748. doi:10.3390/app10217748

CrossRef Full Text | Google Scholar

Feng, C., Khan, M., Rahman, A. U., and Ahmad, A. (2020). News recommendation systems - accomplishments, challenges and future directions. IEEE Access Available online at: https://ieeexplore.ieee.org/abstract/document/8963698/.

Google Scholar

Forouzandeh, S., Rostami, M., and Berahmand, K. (2022). A hybrid method for recommendation systems based on tourism with an evolutionary algorithm and topsis model. Fuzzy Inf. Eng. 14, 26–50. doi:10.1080/16168658.2021.2019430

CrossRef Full Text | Google Scholar

Fu, Z., Xian, Y., Zhang, Y., and Zhang, Y. (2020). “Tutorial on conversational recommendation systems,” in ACM conference on recommender systems.

Google Scholar

Ga, S., Cho, P. H., Moon, G. E., and Jung, S. (2025). Efficient gnn-based social recommender systems through social graph refinement. J. Supercomput. 81, 215–224. doi:10.1007/s11227-024-06682-w

CrossRef Full Text | Google Scholar

Hendrycks, D., and Gimpel, K. (2016). Gaussian error linear units (gelus). arXiv Prepr. arXiv:1606.08415, Available online at: https://arxiv.org/abs/1606.08415.

Google Scholar

Hsia, S., Gupta, U., Wilkening, M., Wu, C.-J., Wei, G.-Y., and Brooks, D. (2020). “Cross-stack workload characterization of deep recommendation systems,” in IEEE international symposium on workload characterization.

Google Scholar

Hu, J., Shen, L., and Sun, G. (2018). “Squeeze-and-excitation networks,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 7132–7141.

Google Scholar

Hwang, S., and Park, E. (2022). Movie recommendation systems using actor-based matrix computations in South Korea. IEEE Trans. Comput. Soc. Syst. 9, 1387–1393. doi:10.1109/tcss.2021.3117885

CrossRef Full Text | Google Scholar

Ivchenko, D., Staay, D. V. D., Taylor, C., Liu, X., Feng, W., Kindi, R., et al. (2022). “Torchrec: a pytorch domain library for recommendation systems,” in ACM conference on recommender systems.

Google Scholar

Jadidinejad, A. H., Macdonald, C., and Ounis, I. (2021). The simpson’s paradox in the offline evaluation of recommendation systems. ACM Trans. Inf. Syst. 40, 1–22. doi:10.1145/3458509

CrossRef Full Text | Google Scholar

Jain, A., Ong, S. P., Hautier, G., Chen, W., Richards, W. D., Dacek, S., et al. (2013). Commentary: the materials project: a materials genome approach to accelerating materials innovation. Apl. Mater. 1, 011002. doi:10.1063/1.4812323

CrossRef Full Text | Google Scholar

Javed, U., Shaukat, K., Hameed, I., Iqbal, F., Alam, T. M., and Luo, S. (2021). A review of content-based and context-based recommendation systems. Int. J. Emerg. Technol. Learn. (iJET) 16, 274. doi:10.3991/ijet.v16i03.18851

CrossRef Full Text | Google Scholar

Jha, D., Ward, L., Paul, A., Liao, W.-k., Choudhary, A., Wolverton, C., et al. (2018). Elemnet: deep learning the chemistry of materials from only elemental composition. Sci. Rep. 8, 17593. doi:10.1038/s41598-018-35934-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Kanwal, S., Nawaz, S., Malik, M. K., and Nawaz, Z. (2021). A review of text-based recommendation systems. IEEE Access 9, 31638–31661. doi:10.1109/access.2021.3059312

CrossRef Full Text | Google Scholar

Khan, H. U. R., Lim, C., Ahmed, M., Tan, K., and Mokhtar, M. B. (2021). Systematic review of contextual suggestion and recommendation systems for sustainable e-tourism. Sustainability 13, 8141. doi:10.3390/su13158141

CrossRef Full Text | Google Scholar

Ko, H., Lee, S., Park, Y., and Choi, A. (2022). A survey of recommendation systems: recommendation models, techniques, and application fields. Electronics 11, 141. doi:10.3390/electronics11010141

CrossRef Full Text | Google Scholar

Kreutz, C. K., and Schenkel, R. (2022). Scientific paper recommendation systems: a literature review of recent publications. Int. J. Digital Libr. 23, 335–369. doi:10.1007/s00799-022-00339-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, D., Gopal, A., and Park, S.-H. (2020). Different but equal? a field experiment on the impact of recommendation systems on mobile and personal computer channels in retail. Inf. Syst. Res. 31, 892–912. doi:10.1287/isre.2020.0922

CrossRef Full Text | Google Scholar

Lyu, L., Yuan, K., and Zhu, W. (2024). A novel demodulation method with a reference signal for operational modal analysis and baseline-free damage detection of a beam under random excitation. J. Sound Vib. 571, 118068. doi:10.1016/j.jsv.2023.118068

CrossRef Full Text | Google Scholar

Maier, C., and Simovici, D. (2022). Bipartite graphs and recommendation systems. J. Adv. Inf. Technol. 13. doi:10.12720/jait.13.3.249-258

CrossRef Full Text | Google Scholar

Mashayekhi, Y., Li, N., Kang, B., Lijffijt, J., and Bie, T. D. (2022). A challenge-based survey of e-recruitment recommendation systems. ACM Comput. Surv. 56, 1–33. doi:10.1145/3659942

CrossRef Full Text | Google Scholar

Nawara, D., and Kashef, R. (2020). “Iot-based recommendation systems - an overview,” in 2020 IEEE international IOT, electronics and mechatronics conference (IEMTRONICS).

Google Scholar

Nawara, D., and Kashef, R. (2021). Context-aware recommendation systems in the iot environment (iot-cars)-a comprehensive overview. IEEE Access 9, 144270–144284. doi:10.1109/access.2021.3122098

CrossRef Full Text | Google Scholar

Özyılkan, E., Carpi, F., Garg, S., and Erkip, E. (2024). “Neural compress-and-forward for the relay channel,” in 2024 IEEE 25th international Workshop on signal processing Advances in wireless communications (SPAWC) (IEEE), 366–370.

Google Scholar

Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868. doi:10.1103/physrevlett.77.3865

PubMed Abstract | CrossRef Full Text | Google Scholar

Pilania, G., Mannodi-Kanakkithodi, A., Uberuaga, B. P., Ramprasad, R., Gubernatis, J. E., and Lookman, T. (2016). Machine learning bandgaps of double perovskites. npj Comput. Mater. 2, 16079. doi:10.1038/srep19375

PubMed Abstract | CrossRef Full Text | Google Scholar

Redies, M., Michalicek, G., Bouaziz, J., Terboven, C., Müller, M. S., Blügel, S., et al. (2022). Fast all-electron hybrid functionals and their application to rare-earth iron garnets. Front. Mater. 9, 851458. doi:10.3389/fmats.2022.851458

CrossRef Full Text | Google Scholar

Rocco, J. D., Ruscio, D. D., Sipio, C. D., Nguyen, P. T., and Rubei, R. (2021). Development of recommendation systems for software engineering: the crossminer experience. Empir. Softw. Eng. 26, 69. doi:10.1007/s10664-021-09963-7

CrossRef Full Text | Google Scholar

Saal, J. E., Kirklin, S., Aykol, M., Meredig, B., and Wolverton, C. (2013). Materials design and discovery with high-throughput density functional theory: the open quantum materials database (oqmd). JOM 65, 1501–1509. doi:10.1007/s11837-013-0755-4

CrossRef Full Text | Google Scholar

Sandur, A., Park, C., Volos, S., Agha, G., and Jeon, M. (2022). “Jarvis: large-scale server monitoring with adaptive near-data processing,” in 2022 IEEE 38th international conference on data engineering (ICDE) (IEEE), 1408–1422.

CrossRef Full Text | Google Scholar

Schütt, K. T., Sauceda, H. E., Kindermans, P.-J., Tkatchenko, A., and Müller, K.-R. (2018). Schnet–a deep learning architecture for molecules and materials. J. Chem. Phys. 148, 241722. doi:10.1063/1.5019779

PubMed Abstract | CrossRef Full Text | Google Scholar

Shi, S., Gong, Y., and Gursoy, D. (2020). Antecedents of trust and adoption intention toward artificially intelligent recommendation systems in travel planning: a heuristic-systematic model. J. Travel Res. 60, 1714–1734. doi:10.1177/0047287520966395

CrossRef Full Text | Google Scholar

Shoghi, R., and Hartmaier, A. (2022). Optimal data-generation strategy for machine learning yield functions in anisotropic plasticity. Front. Mater. 9, 868248. doi:10.3389/fmats.2022.868248

CrossRef Full Text | Google Scholar

Stukhlyak, P., Buketov, A., Panin, S., Maruschak, P., Moroz, K., Poltaranin, M., et al. (2015). Structural fracture scales in shock-loaded epoxy composites. Phys. Mesomech. 18, 58–74. doi:10.1134/s1029959915010075

CrossRef Full Text | Google Scholar

Sun, Z., Xu, Y., Liu, Y., He, W., Jiang, Y., Wu, F., et al. (2022). A survey on federated recommendation systems. IEEE Trans. Neural Netw. Learn. Syst. 36, 6–20. doi:10.1109/tnnls.2024.3354924

PubMed Abstract | CrossRef Full Text | Google Scholar

Tran, K., and Ulissi, Z. W. (2018). An uncertainty quantification framework for predictive materials modeling using machine learning. npj Comput. Mater. 4, 29. Available online at: https://www.nature.com/articles/s41929-018-0142-1.

Google Scholar

Urdaneta-Ponte, M. C., Méndez-Zorrilla, A., and Oleagordia-Ruíz, I. (2021). Recommendation systems for education: systematic review. Electronics 10, 1611. doi:10.3390/electronics10141611

CrossRef Full Text | Google Scholar

Vasudevan, R. K., Kalinin, S. V., Chen, L.-Q., and Lookman, T. (2021). Hybrid computational-experimental approach for discovery of phase-change materials. Adv. Mater. 33, 2004572. Available online at: https://www.sciencedirect.com/science/article/pii/S2352152X23026142.

Google Scholar

Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., et al. (2017). Attention is all you need. Adv. neural Inf. Process. Syst. 30, 5998–6008. Available online at: https://proceedings.neurips.cc/paper/2017/hash/3f5ee243547dee91fbd053c1c4a845aa-Abstract.html

Google Scholar

Vecchio, G., and Deschaintre, V. (2024). “Matsynth: a modern pbr materials dataset,” in Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 22109–22118.

Google Scholar

Wang, X., Girshick, R., Gupta, A., and He, K. (2018). “Non-local neural networks,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 7794–7803.

Google Scholar

Ward, L., Liu, R., Krishna, A., Hegde, V. I., Agrawal, A., Choudhary, A., et al. (2016). A general-purpose machine learning framework for predicting properties of inorganic materials. npj Comput. Mater. 2, 16028. doi:10.1038/npjcompumats.2016.28

CrossRef Full Text | Google Scholar

Wu, H., Zhao, Y., Zhang, J., Pan, Z., Xu, L., and Liang, Y. (2020). Machine learning-assisted discovery of polymers with high thermal conductivity using a molecular design algorithm. npj Comput. Mater. 6, 66. doi:10.1038/s41524-019-0203-2

CrossRef Full Text | Google Scholar

Xie, T., and Grossman, J. C. (2018). Crystal graph convolutional neural networks for an accurate and interpretable prediction of material properties. Phys. Rev. Lett. 120, 145301. doi:10.1103/physrevlett.120.145301

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, X., Chen, J., Deshpande, V. V., Diest, K., and Shi, L. (2014). Thermal conductivity of graphene and its structural derivatives. Small 10, 4795–4819. Available online at: https://onlinelibrary.wiley.com/doi/pdf/10.1002/9781119242635#page=299.

Google Scholar

Yadalam, T. V., Gowda, V. M., Kumar, V. S., Girish, D., and M, N. (2020). “Career recommendation systems using content based filtering,” in International conference on communication and electronics systems.

Google Scholar

Yang, C., Ke, X., Hu, P., and Li, Y. (2021). “Nightdnet: a semi-supervised nighttime haze removal frame work for single image,” in 2021 3rd international academic exchange Conference on Science and Technology innovation (IAECST) (IEEE), 716–719.

Google Scholar

Yang, L., Tan, B., Zheng, V., Chen, K., and Yang, Q. (2020). Federated recommendation systems. Fed. Learn., 225–239. doi:10.1007/978-3-030-63076-8_16

CrossRef Full Text | Google Scholar

Yao, K., Xu, X., Sun, B., Wang, C., Wang, C., and Wu, K. (2021). Deep-learning model for dielectric polymer design with high energy density and low loss. Sci. Adv. 7, eabf7290. Available online at: https://pubs.acs.org/doi/abs/10.1021/acs.chemmater.1c02061.

Google Scholar

Zhang, J., Tong, Z., Zhang, W., Zhao, Y., and Liu, Y. (2021a). Research on ncf-pcf-ncf structure interference characteristic for temperature and relative humidity measurement. IEEE Photonics J. 13, 1–5. doi:10.1109/jphot.2021.3105395

CrossRef Full Text | Google Scholar

Zhang, Y., Peng, C., Peng, L., Xu, Y., Lin, L., Tong, R., et al. (2021b). Deeprecs: from recist diameters to precise liver tumor segmentation. IEEE J. Biomed. Health Inf. 26, 614–625. doi:10.1109/jbhi.2021.3091900

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Z., Patra, B. G., Yaseen, A., Zhu, J., Sabharwal, R., Roberts, K., et al. (2023). Scholarly recommendation systems: a literature survey. Knowl. Inf. Syst. 65, 4433–4478. doi:10.1007/s10115-023-01901-x

CrossRef Full Text | Google Scholar

Zunger, A. (2018). Inverse design in search of materials with target functionalities. Nat. Rev. Chem. 2, 0121. doi:10.1038/s41570-018-0121

CrossRef Full Text | Google Scholar