Influence of soil parameters on dynamic compaction: numerical analysis and predictive modeling using GA-optimized BP neural networks

This study analyses the effect of soil parameters (angle of internal friction, cohesion, modulus of elasticity, Poisson’s ratio, density) on the amount of ramming settlement of rammed reinforced foundations and proposes a prediction model for the depth of ramming reinforcement based on GA-BP neural network. Based on the finite element method, a numerical model of dynamic consolidation foundation is established, and the model is verified by field test results. Orthogonal experimental design and single factor analysis were used to quantify the influence of each parameter on the compaction volume. In order to improve the prediction accuracy, this paper introduces genetic algorithm (GA) to optimize the BP neural network model, constructs a multi-factor dynamic compaction prediction model, and compares it with the traditional BP model. The results show that the compaction rate is most sensitive to the internal friction Angle and cohesive force. Compared with the traditional BP model, GA-BP model has better prediction accuracy and generalization ability, and the fitting accuracy reaches 0.974. GA optimization improves the convergence speed of the model and the ability to solve the global optimal solution. The GA-BP model used in this paper provides a high-precision tool for the prediction of dynamic compaction foundation treatment and has important engineering application value.

1 Introduction

Ramming method is widely used in foundation treatment in various engineering fields because of its high efficiency and economic characteristic (Chow et al., 1992; Scott et al., 2021). The tamping parameters are the key factors that determine the effective reinforcement effect of foundation treatment by ramming, and most of the existing studies focus on the influence of tamping parameters on foundation treatment effect, such as tamping energy level, number of tamping strokes, tamping shape, tamping distance, and other parameter (Yang et al., 2024; Scott et al., 2021; Jia et al., 2018; Freire de Souza and Pasqual, 2021). This study aims to investigate the effects of tamping parameters on the reinforcement depth achieved by dynamic compaction, and to develop a predictive model for reinforcement depth using neural network tools, thereby providing a powerful and convenient tool for related practical engineering applications. This research base analyses in detail the influence of relevant parameters on the effect of ramming reinforcement by numerical simulation and field test, and proposes a prediction model for the depth of ramming reinforcement based on GA-BP neural network.

In existing studies, many researchers have analyzed the compaction mechanisms of dynamic compaction. Miao et al., 2006 based on dynamic-compaction trials con-ducted on an expressway, reported a marked improvement in the liquefaction resistance of the treated soil layers; Feng et al. (2015) through deformation tests on collapsible loess after compaction, demonstrated that dynamic compaction substantially enhances the bearing capacity of poor-quality foundations; Hu et al. (2017) using plate-load and permeability tests on various soil samples, identified the effective improvement depth of dynamic compaction and its controlling factors. Several researchers have also examined the mechanics of the tamping action (Li et al., 2023), concluding that “heavy-hammer, low-drop” schemes outperform “light-hammer, high-drop” approaches; Salah et al. (2023) applied the Analytic Hierarchy Process (AHP) to rank the factors influencing dynamic-compaction efficacy and recommended that dynamic compaction be confined to areas at least 30 m from buildings and 15 m from sub-surface utilities for safety. Wei et al. (2019) conducted an in-depth study of the com-paction mechanism, dividing the process into an improvement-development stage and an improvement-attenuation stage. Because field tests are time-consuming and labor-intensive, most scholars have routinely relied on simulation software to model dynamic compaction. Ghorbani et al. (2020) developed a finite-element model to analyze the dynamic compaction process, proposed a generalized form of viscous boundaries, and elucidated the role of soil plasticity parameters in dynamic compaction. Jim et al. (2023) using a macro–micro coupled approach to analyze the evolution of dynamic stresses, showed that increasing drop energy beyond a certain threshold yields diminishing returns in settlement reduction; Lopez-Querol et al. (2008) investigated constitutive models for sand in dynamic-compaction consolidation and assessed their applicability; Sun et al. (2024) built a three-dimensional fluid–solid coupling model for high-energy dynamic compaction based on FDM-DEM and proposed that pre-drainage and preload (i.e., staged dewatering and surcharge) can further enhance compaction effectiveness.

However, in real-world projects the geological conditions vary greatly from site to site, so under identical hammer parameters the effectiveness of dynamic compaction can differ markedly for foundations composed of crushed-stone fill, sands, low-saturation silts and clays, collapsible loess, natural fill or miscellaneous fill (Kufre Etim et al., 2021; Yusoff et al., 2017). Hence, it is of great practical importance to analyze how different soil parameters influence compaction performance. Wang et al. (2023) conducted field monitoring on high-embankment red soil subjected to dynamic compaction at various energy levels and confirmed that the method not only enhances the reuse potential of the soil but also increases the bearing capacity of otherwise poor-quality soils. However, there remains a paucity of mechanistic studies on how dynamic compaction performance varies with soil parameters (Hu et al., 2024; Mayne et al., 1984). Therefore, it is essential to investigate the effects of those parameters on compaction outcomes, perform sensitivity analyses, and identify the key factors that govern the success of dynamic compaction.

With the advancement of artificial intelligence, neural networks—owing to their powerful nonlinear modeling, self-learning capabilities, and aptitude for high-dimensional data—have increasingly attracted researchers’ attention (Koohsari et al., 2023; Zhou et al., 2020). Ziaee et al. (2015) employed an artificial neural network to predict foundation bearing capacity, per-forming sensitivity analyses with field-measured data to develop their prediction model; Teramoto et al. (2024) developed a deep learning based compaction settlement prediction model, providing a pertinent reference for subsequent neural-network models of compaction behavior. The GA-BP method uniquely combines a genetic algorithm (GA) with a back-propagation neural network (BP) to optimise the initial weights and network structure, addressing limitations such as slow BP convergence and local minima traps (Wang et al., 2016).

Therefore, this paper introduces a Genetic Algorithm (GA) to optimize the BP neural network and establishes a GA-BP model to predict the dynamic compaction settlement of foundation soils under different parameters, including internal friction angle, cohesion, elastic modulus, Poisson’s ratio, and density. As the first application of dynamic compaction reinforcement prediction, it outperforms traditional BP, PSO-BP, and other models by providing customized global optimization, reducing RMSE by 10%, and achieving faster convergence (Wu et al., 2020). This model aims to offer effective references for evaluating the reinforcement effect of dynamic compaction.

2 Model building and validation

2.1 Numerical model for ground improvement by dynamic compaction

2.1.1 Basic assumptions

In this study, explicit dynamics is used to implement the complex dynamics of the rammed reinforcement finite element simulation process. In this paper, without violating the principle of ramming reinforcement, the finite element model of ramming reinforcement is established and the following basic assumptions are made to simplify the calculations and make the model more consistent with the actual working conditions (Sun et al., 2023):

(1) Given that the stiffness of the tamping hammer far exceeds that of the foundation soil, its deformation during dynamic compaction is negligible, and it can therefore be treated as a rigid body.

(2) The effect of groundwater on the ramming process is not considered.

(3) The energy loss due to friction between the rammer and the soil is not considered.

2.1.2 Parameterisation

2.1.2.1 Loading Regime

Field measurements of contact stress during dynamic compaction indicate that, upon impact of the tamper on the ground, the contact stress rapidly rises to a peak and then de-cays just as quickly. A triangular load-time history closely approximates this actual stress variation, reflecting the generation and dissipation characteristics of the tamping force and thereby rendering the simulation more realistic. Moreover, the triangular load form is computationally simple and readily implemented in finite-element analyses, enhancing computational efficiency while effectively capturing the propagation of stress waves through the soil induced by the tamping action.

2.1.2.2 Initial Velocity

Dynamic compaction is modeled herein as an explicit-dynamic problem, due to its inherently large deformations and high loading rates. By directly prescribing an initial velocity to the tamper, the hammer impacts the soil at the specified speed, and the resulting stresses and deformations are propagated through the soil via an explicit integration scheme. This approach accurately simulates the incremental transfer of impact energy in-to the ground and yields results that closely mirror the actual compaction process. In the present study, the compaction energy level is 4,000 kN·m, the tamper density is 7,850 kg/m³, and the prescribed initial velocity corresponds to an acceleration of 20 m/s². Throughout the tamping event, the tamper motion is constrained strictly to the vertical axis, with no lateral displacement.

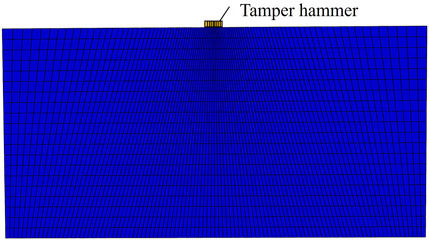
The C3D8R cell is selected to meet the demand of displaying dynamic analysis, and the effective area of ramming reinforcement is mainly near the ramming hammer, so in order to reduce the intensity of the model calculation work, the grid is divided in a way that the middle is dense and the two ends are sparse.

2.1.2.3 Soil constitutive model:

The Drucker-Prager principal model (D-P model) can effectively capture the shear damage characteristics of the soil body, especially the yielding behaviour of the soil body in compression and shear. The D-P model can effectively simulate the yielding, plastic deformation and local damage of the soil body during ramming, especially the compression and plastic flow of the soil body under the impact of the rammer. The D-P model performs well under dynamic loading (e.g., ramming impact) and its parameters are easily obtainable, which is suitable for simulating the performance of the soil body in different stress states and simulating the transient response of the soil body under the impact action. Therefore, this study adopts the Drucker–Prager (D–P) constitutive model, whose elastic response is given by Equation 1, yield function by Equation 2. The soil parameters are selected from the geological investigation report of the actual project, and the density of the foundation soil is 1800 kg/m³, the cohesion is 21 kPa, the internal friction angle is 18°, the shear angle is 0.1°, the modulus of elasticity is 2.8 MPa, and the Poisson’s ratio is 0.35.

The elastic response is shown in Equation 1.

${\sigma }_{ij}=D_{ijkl}\left({\epsilon }_{kl}-{\epsilon }_{kl}^p\right)(1)$

where D_ijkl is the isotropic stiffness tensor defined by Young’s modulus E and Poisson’s ratio ν.

The Drucker–Prager yield function is Equation 2.

$F\left({\sigma }_{ij}\right)=\sqrt{J_2}+\alpha I_1-k\le 0(2)$

I₁ and J₂ are calculated from Equation 3.

$I_1={\sigma }_{kk},J_2=\frac{1}{2}{S}_{ij}{S}_{ij},S_{ij}={\sigma }_{ij}-\frac{1}{3}{I}_1{\sigma }_{ij}(3)$

The parameters α and k are related to cohesion c and friction angle ϕ by Equation 4.

$\alpha =\frac{2\mathit{sin}\phi }{\sqrt{3}\left(3-\mathit{sin}\phi \right)},k=\frac{6ccos\phi }{\sqrt{3}\left(3-\mathit{sin}\phi \right)}(4)$

2.1.2.4 Damping:

The role and implementation of damping have a significant impact on the accuracy and stability of a dynamic compaction simulation. Damping primarily serves to repro-duce the energy-dissipation behavior of the soil during impact, thereby more realistically modeling both the propagation and attenuation of stress waves generated by tamping. In Abaqus, Rayleigh damping—a combination of mass-proportional and stiffness-proportional terms—is commonly employed. The damping matrix C is defined by Equation 5.

$\mathit{C}=\mathbf{\alpha }\mathit{M}+\mathit{\beta }(5)$

Where, C is the total damping matrix; α is the mass proportional damping coefficient, related to low frequency vibration; β is the stiffness proportional damping coefficient, related to high frequency vibration; M is the mass matrix; K is the stiffness matrix.

The impact load of the rammer on the soil during the dynamic compaction is applied as the first tamping by directly giving the rammer a certain speed and the foundation sur-face for contact impact load. The schematic diagram of the finite element model is shown in Figure 1.

Figure 1

Figure 1. Finite element model of dynamic consolidation.

2.2 Field trials

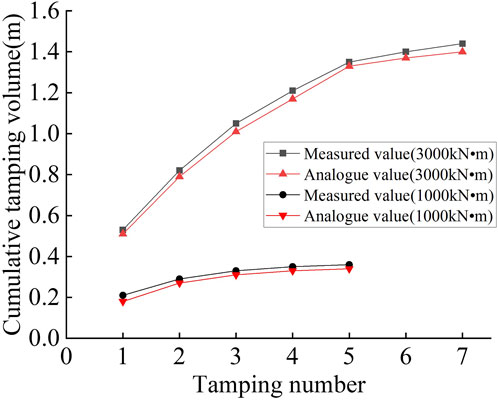
Based on the properties of the foundation soil, a typical test area is selected. The test site has an area of 1,200 m² (30 m × 40 m), with a compaction point spacing of 5.0 m. The number of hammer strikes at each compaction point should be determined according to the relationship curve between the number of strikes and the settlement obtained from the field trial compaction. During the test, 2 to 4 passes of point compaction are carried out, with a hammer energy of 3,000 kN m for each strike. Afterward, a hammer energy of 1,000 kN m is used for two full compaction passes. The hammer should have a circular cross-section, and the compaction points should be arranged in a rectangular pattern. For the first pass, the spacing between compaction points should be 2.5 times the diameter of the hammer. For the second pass, the compaction points should be located between the points of the first pass, as shown in Figure 2a. During full compaction, the overlap of the hammer imprints should be 1/4 of the hammer diameter, as shown in Figure 2b.

Figure 2

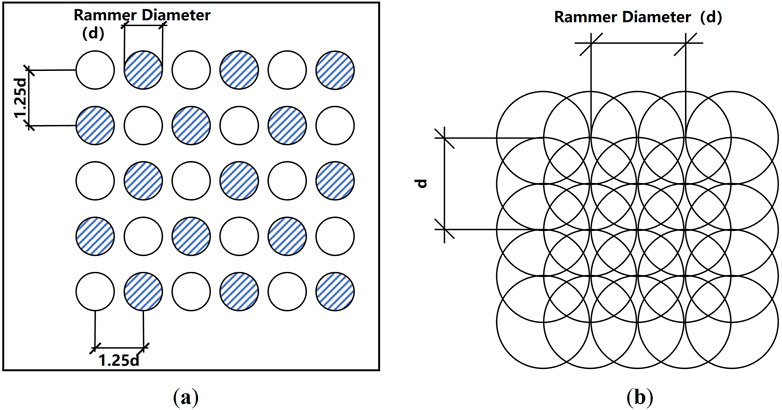
Figure 2. Layout diagram of tamping point. (a) Schematic layout of the first and second ramming points. (b) Schematic layout of full tamping points.

The field test used a crawler crane with automatic decoupling device, hammer weight 21 t, rammer diameter 2.4 m, and according to the weight and ramming energy calculated lifting height, strong ramming strictly according to the calculated lifting height set up automatic decoupling device. The construction process is as follows: levelling the site - measuring the elevation - setting up points for positioning - the first point tamping - pushing the tamping pit, levelling the site - the second point tamping - pushing the tamping pit, levelling the site -Full tamping - repair the site - delivery surface measurement - testing - provide a test tamping report (Pan et al., 2024).

The site construction plan is shown in Figure 3.

Figure 3

Figure 3. Site construction drawing.

2.3 Validation of numerical calculation results

In the tamping reinforcement numerical simulation calculation, through the initial ground stress equilibrium so that the foundation soil he reached a stable state, the first tamping directly endowed rammer with v0 velocity and the foundation surface for contact impact load, the bottom of the rammer and the foundation in the normal direction of the hard contact relationship in the tangential direction to meet the conditions of frictionless, the subsequent several ramming for the tamping hammer to lift to a specified height after the free fall generated. The nonlinear geometry (NLGEOM) option is set to ON, which activates the Updated Lagrangian large-deformation algorithm, automatically accounting for corrections to the geometric stiffness matrix and updating the stress tensor at each increment.

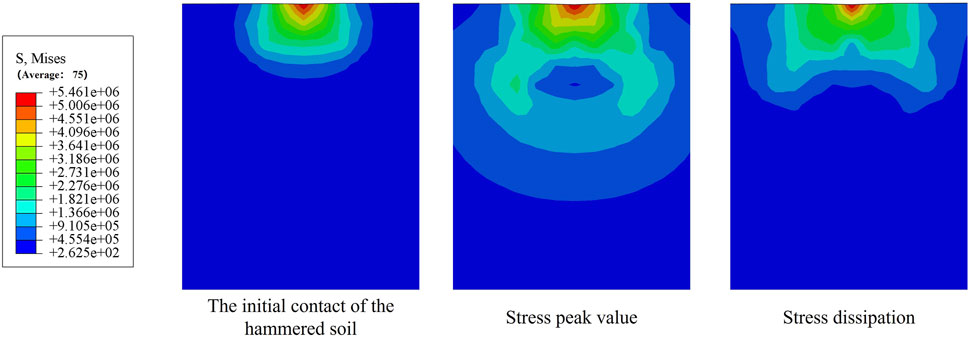
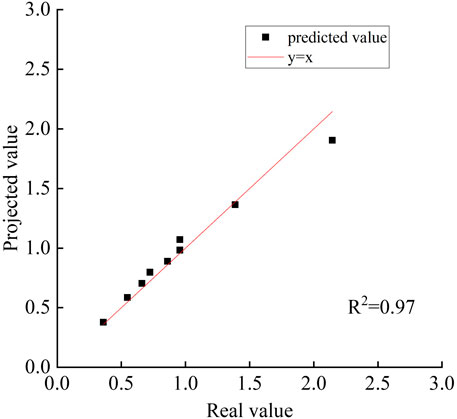
In order to verify the reliability of the numerical model, the results of the model were compared with the results of the on-site inspection. The comparison between the rammer consolidation depth results obtained from the model and the field test results is shown in Figure 4. From the test results, it can be seen that the tamping volume gradually increases with the number of tamping and the single tamping volume is getting smaller and small-er, and finally the cumulative tamping volume tends to be stable; the larger the tamping energy is, the higher the cumulative tamping volume is, which is in line with the previous studies. Comparing the simulation results with the field settlement monitoring, the curve fit R2 reaches more than 97%, which meets the requirement of simulation accuracy. After simulating with literature data, the stress contour map of dynamic compaction (as shown in Figure 5) was obtained. Comparing it with the original data (Mei et al., 2021), the relative error in the stress calculation was found to be 8.25%. It is evident that the trend of the simulated load closely matches the calculated values, further confirming the feasibility of the hammer-soil contact setup and load application method presented in this study.

Figure 4

Figure 4. Comparison between field compaction and simulation result.

Figure 5

Figure 5. Variation of stress at tamping point.

3 Strong tamping reinforcement depth law based on orthogonal test

3.1 Orthogonal test programme design

The effectiveness of dynamic compaction is governed by various geotechnical parameters of the soil, each exerting a different influence on the magnitude of settlement. An orthogonal experimental design systematically varies combinations of these parameters to quantify the contribution of each factor to the observed settlement. This approach identifies the parameters with the greatest impact on settlement and evaluates their interactions, revealing any synergistic or inhibitory effects. Such insight enables practitioners to prioritize control of the most critical parameters in field applications. By employing an orthogonal testing matrix in the analysis of soil properties for dynamic compaction, one can comprehensively elucidate the influence patterns of all factors on settlement, thereby providing data-driven, scientific guidance for both design optimization and construction practice. Consequently, orthogonal experiments serve as a vital engineering tool in dynamic compaction research.

In this paper, orthogonal test and numerical simulation are used to study the sensitivity of soil parameters and analyse the sensitivity magnitude.

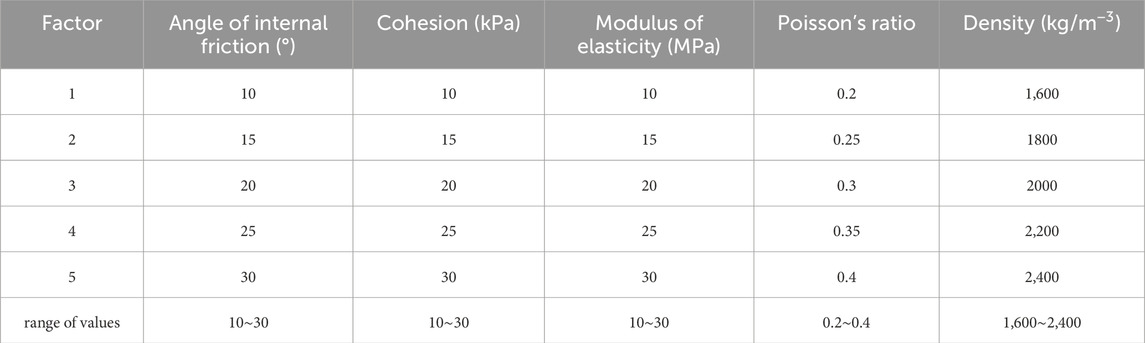
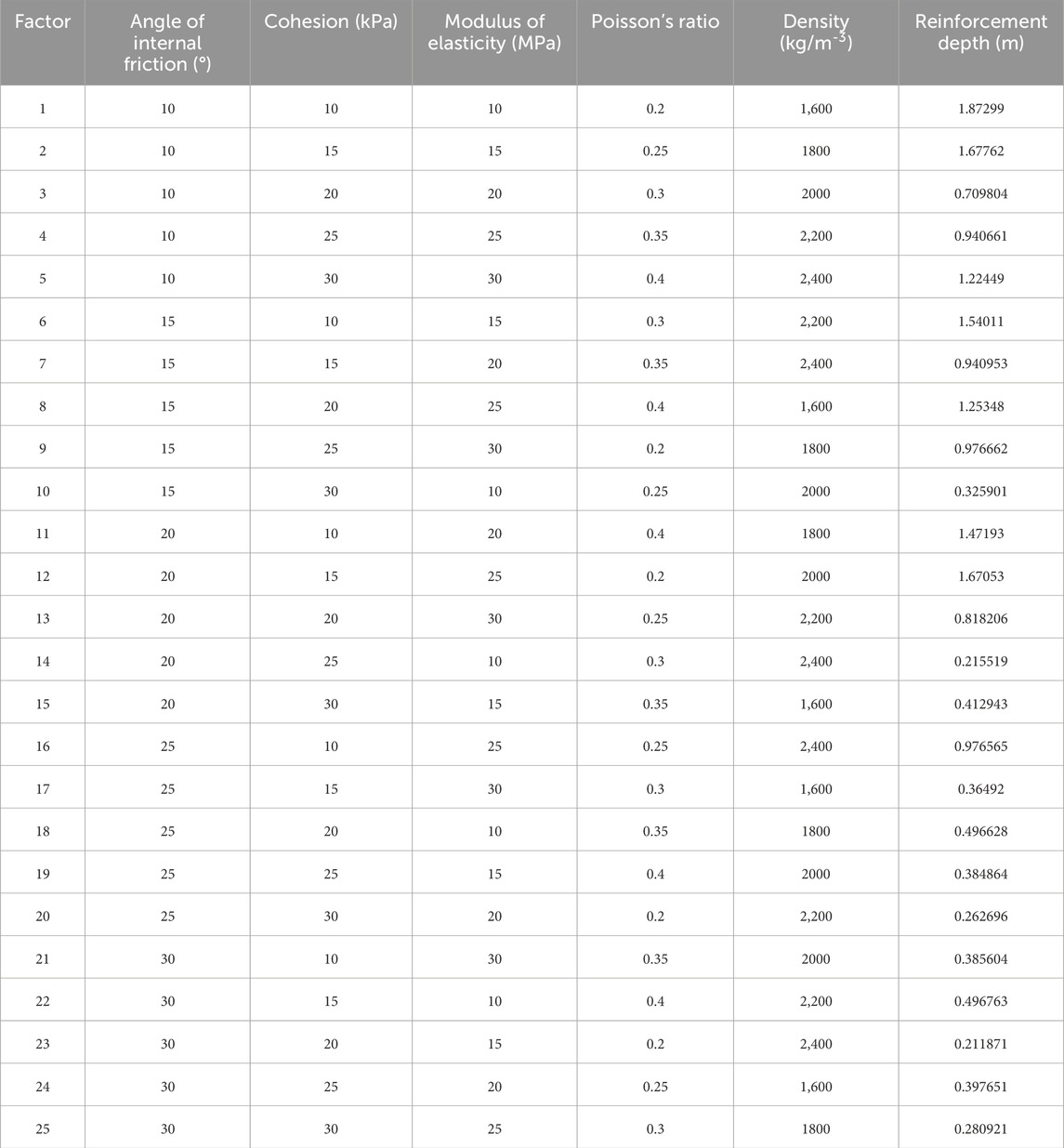
According to the Mohr’s and Coulomb’s strength criterion, there are five main mechanical parameters of soil body: modulus of elasticity, Poisson’s ratio, cohesion, angle of internal friction, and density, which are taken as the five factors of orthogonal test, and each factor is taken as five levels. The specific design is shown in Table 1 (Khaboushan et al., 2018; Pan et al., 2024). The selection of the range of parameter values is based on the experience in engineering practice and the physical properties of the soil.

Table 1

Table 1. The value range and level of each parameter.

3.2 Analysis of simulation results

According to the calculation results of ABAQUS, the reinforcement depth of soil under the action of 4000 kN·m energy level strong tamping under each condition of orthogonal test was obtained. The results are shown in Table 2.

Table 2

Table 2. Orthogonal test table.

In order to determine the influence of each factor on the dynamic water pressure of the travelling car, according to the above orthogonal test obtained by the dynamic water pressure calculation results, the polar deviation and variance analysis.

The intuitive analysis method determines the influence of each factor on the experimental results by calculating the range of the average effect values of each factor at different levels. This range reflects the degree to which the variation in the factor’s levels affects the indicators. A larger range indicates that the changes in the factor’s different levels have a more significant impact on the indicators. Polar deviation analysis can screen out the soil parameters that have a significant effect on the amount of tamping, and then provide a scientific basis for the optimisation of design and construction.

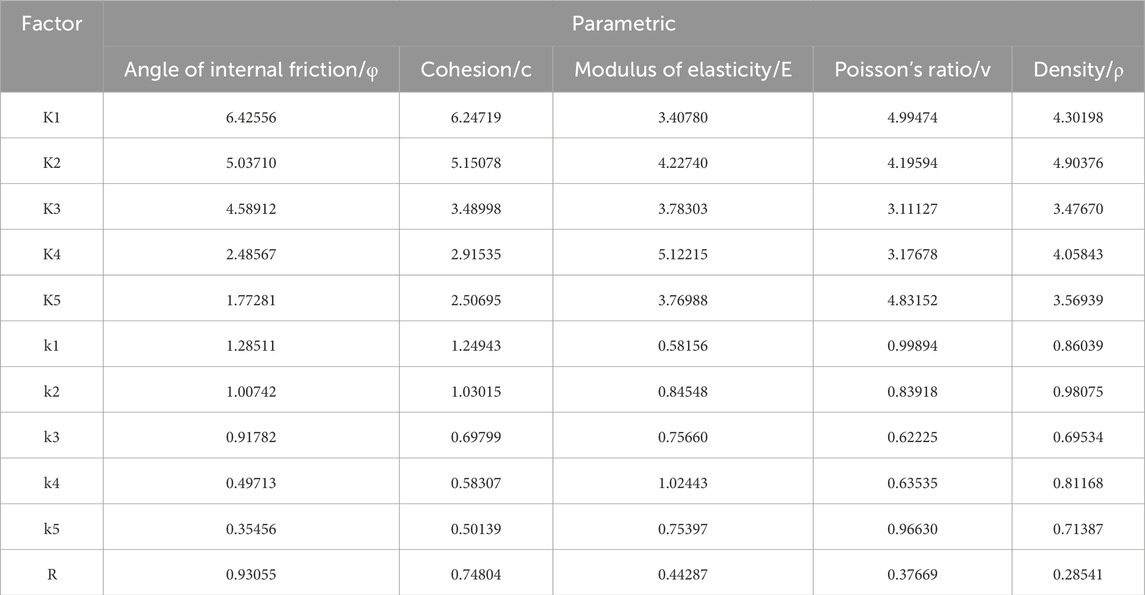
The mean and extreme difference of each level of each factor are shown in Table 3. According to the data in the extreme difference column of Table 3, it can be seen that the extreme difference corresponding to the internal friction angle is the largest, the cohesion is relatively second, the elastic modulus and Poisson’s ratio correspond to the smallest, and the order of the parameter sensitivities is as follows: the internal friction angle, the cohesion, the elastic modulus, Poisson’s ratio, and the density. The internal friction angle exerts the greatest influence on the efficacy of dynamic compaction, while the elastic modulus and cohesion have a moderate effect, and Poisson’s ratio and density contribute relatively little. This hierarchy arises because the primary objective of dynamic compaction is to enhance the soil’s shear-resistance strength, thereby increasing the bearing capacity and overall stability of the foundation. As parameters that quantify a soil’s resistance to shear failure, the internal friction angle and cohesion directly govern its ability to withstand externally applied loads without slipping. Higher values of friction angle and cohesion result in a post-treatment soil mass that is significantly more resistant to shear failure, thus minimizing deformation and reducing the risk of instability. Accordingly, the core goal of dynamic compaction is to improve these two strength parameters to elevate the soil’s overall stability.

Table 3

Table 3. Parameter range analysis.

By contrast, deformation parameters—such as the elastic modulus and Poisson’s ratio—primarily influence the soil’s stiffness and deformation response (for example, by reducing settlement and increasing deformation rigidity), but do not, by themselves, substantially increase shear strength. Consequently, modifications to these deformation parameters yield only secondary benefits in terms of overall compaction performance. Density likewise has a comparatively minor role, affecting mass and inertial properties more than shear capacity. In practice, then, optimizing dynamic-compaction design and execution hinges on maximizing the improvement in internal friction angle and cohesion, with adjustments to stiffness and density playing a supporting rather than leading role.

3.3 Strong tamping reinforcement single factor analysis

According to the results of orthogonal test analysis, the internal friction angle and cohesion are the two most significant factors. In the following, the influence of internal friction angle and cohesive force on the depth of soil reinforcement under ramming is further investigated.

3.3.1 Analysis of the role of angle of internal friction on the depth of reinforcement

In the single-factor computational analysis of the reinforcement depth of the soil under dynamic compaction, the energy level of dynamic compaction was set to 4,000 kN m, the cohesion to 20 kPa, the elastic modulus to 30 MPa, the Poisson’s ratio to 0.35, and the soil density to 1800 kg/m³. The simulation calculations were conducted for the reinforcement depths under dynamic compaction at internal friction angles of 10°, 15°, 20°, 25°, 30°, 35°, and 40°. The calculation results are shown in Figure 6; Table 4.

Figure 6

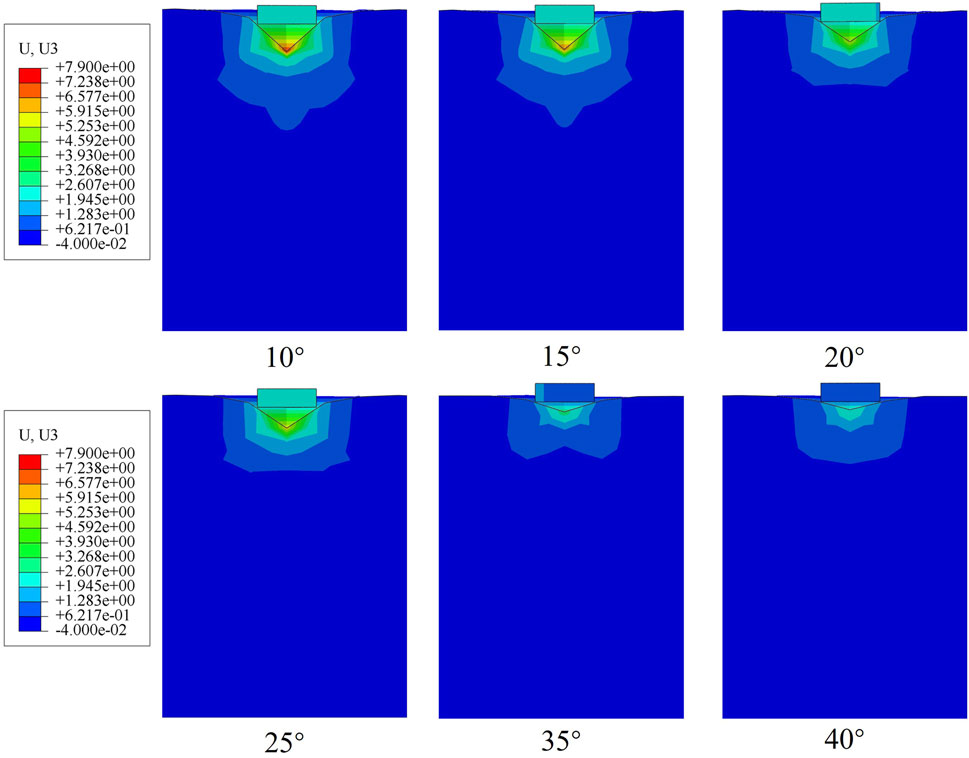
Figure 6. Cloud picture of strengthening effect of dynamic compaction under different internal friction angles. (5°, 15°, 20°, 25°, 35°, 40°).

Table 4

Table 4. Internal friction Angle and tamping capacity.

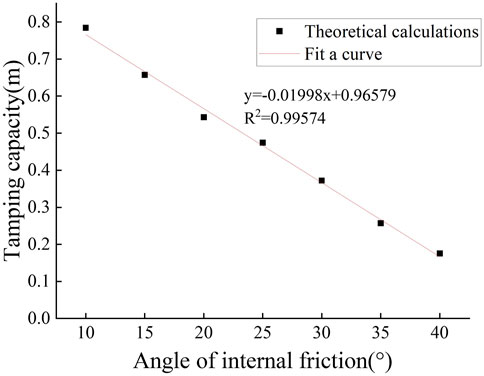
From Figure 6, it can be seen that when the soil’s internal friction angle is relatively large, the reinforced zone typically assumes a more stable configuration, with stresses distributed more uniformly. Under these conditions, the soil’s shear strength increases and its resistance to external loading is enhanced. Although the settlement at the tamping point is relatively small, the reinforced zone’s area of influence is substantial, and the bearing-capacity distribution within the reinforced zone tends toward uniformity, making the formation of localized “soft spots” or “voids” unlikely. Conversely, when the soil’s internal friction angle is low, the reinforced zone’s geometry tends to develop more vertically, concentrating stresses within a smaller area; in this scenario, the reinforced zone may become steeper and more confined, exhibiting reduced stability and increasing the likelihood of local sliding or failure. In the D-P model, the yield surface is conical, the larger the angle of internal friction, the larger the slope of the cone, and the increased shear capacity of the soil. Shear expansion may occur at high internal friction angles and densification is reduced, but the depth of reinforcement may be deeper due to stress transfer. According to Figure 7, it can be seen that there is a good correlation between the angle of internal friction and the amount of tamping settlement, and the fitting accuracy reaches 0.995.

Figure 7

Figure 7. Internal friction angle and tamping capacity.

From the Figure 7, it can be seen that the soil tamping sedimentation decreases substantially with the increase of φ value in the case of other soil parameters being the same. For example, when the φ value of the foundation increases from 10° to 15°, 25°, and 35°, the soil tamping settlement decreases by 16.2%, 39.5%, and 67.2%, respectively. This behavior arises because dynamic compaction densifies the soil through the impact energy of the tamper, thereby increasing its density and strength. The role of the angle of internal friction (φ) in the soil is to enhance the shear capacity of the soil by increasing the friction between the particles. The larger φ is, the stronger the friction between the particles is, and the easier it is for the soil to resist the action of the external force, which in turn affects the depth and scope of the reinforcement. When the angle of internal friction of the soil body is small, the frictional resistance between particles is low, and the soil body is more likely to slip and be displaced under external forces. This makes it easier for the soil to compress during dynamic compaction, resulting in a larger tamping settlement.

3.3.2 Analysis of the role of cohesion on the depth of reinforcement

In the analysis of single factor calculation of cohesion on the depth of soil reinforcement under dynamic compaction, the energy level of dynamic compaction is set to 4,000 kN·m, the angle of internal friction is 20°, the modulus of elasticity is 30 MPa, Poisson’s ratio is 0.35, and the density of the soil is 2000 kg/m^-3, and the simulation calculations of the depth of soil reinforcement under dynamic compaction under the conditions of cohesion 10 kPa, 15 kPa, 20 kPa, 25 kPa, 30 kPa, 35 kPa and 40 kPa, were made. 35 kPa, 40 kPa case of strong tamping under the action of soil reinforcement depth simulation calculation, the calculation results are shown in Figure 8.

Figure 8

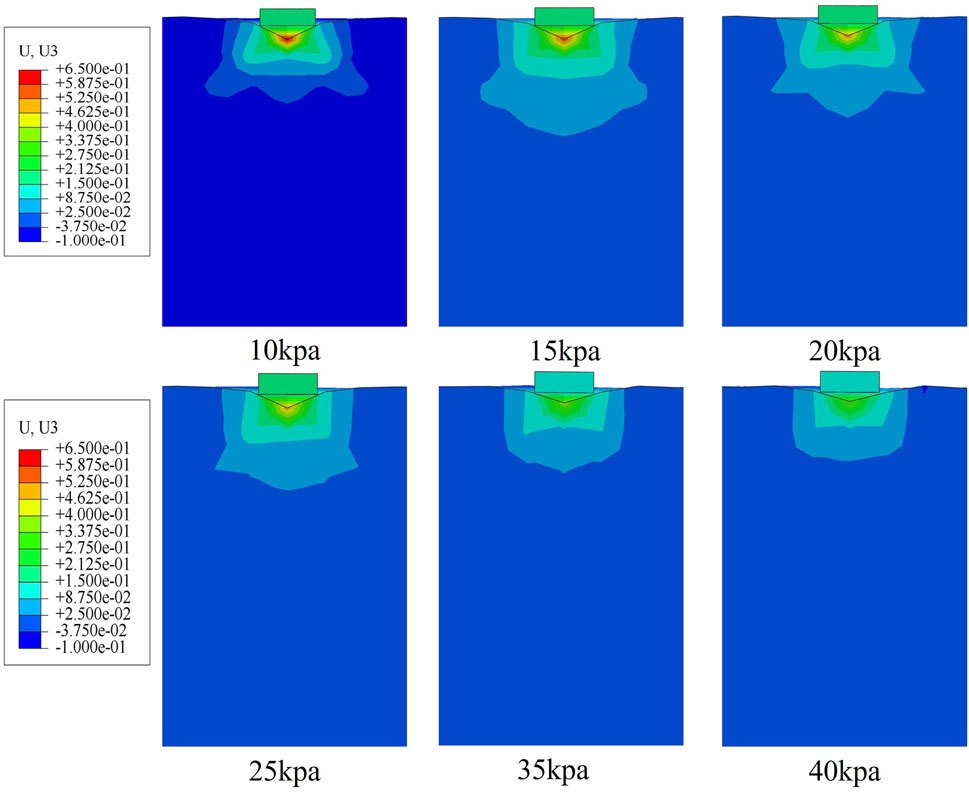
Figure 8. Cloud picture of strengthening effect of dynamic compaction under different cohesive forces. (10kpa, 15kpa, 20kpa, 25kpa, 35kpa, 40kpa).

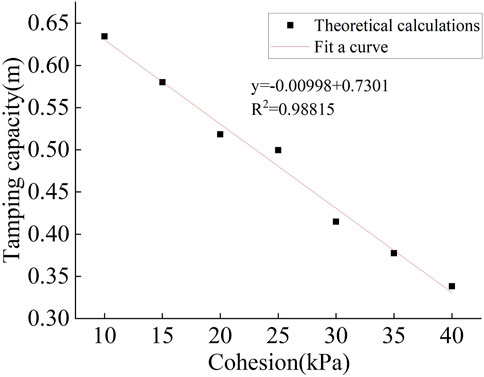
The model calculation results in Table 5 are plotted in Figure 9. It can be seen that in the case of other soil parameters are the same, there is a good linear correlation between soil cohesion and tamping volume, the fitting accuracy is high, and the overall trend of the tamping volume with the increase of soil cohesion and the continuous attenuation of the tamping volume, for example, when the soil cohesion of the subgrade soil is gradually increased from 10 kPa to 15 kPa, 25 kPa, and 35 kPa, the tamping volume of the soil was attenuated by 8.5%, respectively, 21.2%, and 39.6% respectively. Fitting accuracy of 0.988. This is due to the fact that the increase of soil cohesion leads to an increase in the attraction between soil particles, and the particles are more tightly bound to each other. This makes the soil less susceptible to particle displacement and compression when subjected to dynamic compaction, resulting in a reduction in the amount of dynamic compaction. Also, high cohesion is usually accompanied by higher initial densities (Mendez et al., 2011). This means that the energy applied by dynamic compaction is used more to improve the intrinsic strength and overall stability of the soil body, rather than causing particle rearrangement or significant compression, which improves the overall strength and deformation resistance of the soil body.

Table 5

Table 5. Cohesion and tamping capacity.

Figure 9

Figure 9. Cohesion and tamping capacity.

4 GA-BP neural network based prediction

The use of traditional simulation calculation is too time-consuming and labour-intensive, in contrast, the emergence of neural network agent method can be a good solution to this problem, to achieve the depth prediction of strong tamping reinforcement conveniently and quickly in the actual project. Neural network, as a powerful data-driven method, is particularly suitable for the task of predicting the mechanical properties of complex soils and engineering requirements due to its ability to effectively process multi-dimensional complex data and capture potential non-linear patterns, so this paper adopts the GA-BP neural network based method to predict the compaction settlement of soils with different parameters under the action of strong tamping method.

4.1 Artificial neural network–based prediction method for dynamic compaction improvement depth

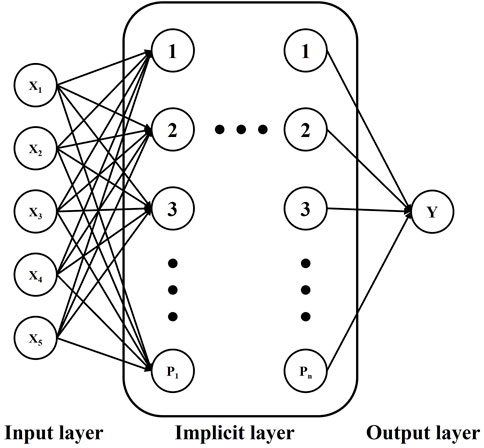
BP algorithm is a widely used supervised learning algorithm in neural networks. BP (Backpropagation) neural network is a type of multi-layer feed-forward neural network, which is composed of an input layer, a hidden layer (there can be more than one), and an output layer. The core of the BP neural network is to adjust the weight and bias of the network through the back-propagation algorithm, and it can be used between inputs and outputs to establish a mapping relationship. Through training, the network can automatically learn the features from the data, thus improving the generalisation ability and prediction accuracy (Ding et al., 2011). The BP neural network architecture is shown in Figure 10.

Figure 10

Figure 10. BP neural network structure diagram.

Considering the slow training speed of BP neural networks, especially in deeper networks, the gradient descent method is slower to converge and may suffer from the problem of gradient vanishing; it is prone to overfitting, if there is no means of preventing overfitting, such as regularisation or early stopping (Xing and Li, 2020; Liang et al., 2019), the model may remember the noise in the training set and fail to generalise well to new data; the complexity of the parameter tuning, the BP neural network needs to adjust several hyper-parameters (such as the learning rate, number of neurons in the hidden layer, etc.), and different parameter set-tings are required under different tasks (Zhang et al., 2018). The RF Deep Neural Network leverages the principle of ensemble learning, which mitigates overfitting; however, its relatively high model complexity renders the interpretation of deeper nonlinear relationships difficult (Ombres et al., 2024; Pistolesi et al., 2025). In this paper, several optimisations are done on the basis of traditional BP neural network to improve its deficiencies. The Leven-berg-Marquardt algorithm accelerates the training speed and solves the problem of slow convergence of traditional gradient descent. The use of a regularisation term prevents model overfitting and enhances the generalisation ability of the model. The use of early stopping provides an effective mechanism to avoid model overfitting during training.

BP neural networks are highly sensitive to their initial weights and biases; varying these initial values can lead the network to converge on different local optima. Traditional genetic algorithms (GA), on the oth er hand, offer strong global search capabilities and do not require gradient information, making them less prone to becoming trapped in local minima. However, GA typically exhibit slow convergence rates, limited precision, and lack the ability to perform fine-grained local adjustments, which often results in relatively high values of mean squared error (MSE), mean absolute error (MAE), and maximum error. Dynamic compaction data often contain measurement errors, environmental disturbances, and other noise. The population evolution and selection mechanisms of the GA provide a certain “smoothing” effect, preventing extreme weight updates caused by isolated noise. BP fine-tuning can still focus on capturing the overall trend, and their combination exhibits more robust performance in noisy environments. By employing a GA to optimize the conventional BP model, one can identify solutions that closely approximate the global optimum within fewer iterations, thereby reducing the number of training epochs required for the BP neural network and enhancing both its convergence speed and accuracy. The GA-optimized BP network is better tailored to the training data and demonstrates improved generalization performance. This improvement arises because, during the optimization process, the genetic algorithm’s selection, crossover, and mutation operators enable a more comprehensive exploration of the solution space, yielding optimized weights and biases that enhance predictive performance on novel data. Furthermore, due to the GA’s global search characteristics, more suitable initial parameters can be obtained even with relatively small datasets, thereby diminishing the network’s dependence on data volume.

When predicting the depth of dynamic compaction reinforcement, the data typically display pronounced non-linearity, intricate interactions among geotechnical parameters (e.g., soil type, moisture content, and compaction energy), and a limited sample size owing to the high cost of field testing. Support Vector Regression (SVR) underperforms in such settings because it is sensitive to high-dimensional, non-linear feature spaces and demands extensive kernel tuning, which becomes computationally expensive for small, noisy datasets. Although Random Forests and XGBoost are robust for tabular data, they struggle to capture the inherently complex, continuous non-linear relationships in deep dynamic compaction depth prediction; their reliance on discrete splits can lead to overfitting or underfitting when samples are scarce. By contrast, a GA-BP model leverages the global optimization capability of genetic algorithms to dynamically adjust the weights and architecture of the BP neural network, effectively modeling the complex geotechnical dynamic characteristics while enhancing convergence and generalization performance.

Five factors, namely, internal friction angle, cohesion, modulus of elasticity, Poisson’s ratio and density of the soil were used as the input nodes of the GA-BP neural network; and the amount of tamping settlement of the rammed reinforcement was used as the out-put of the model. The empirical Formula 6 was used to determine the number of neurons in the hidden layer (You and Zhang, 2022):

$l=\sqrt{m+n}+a(6)$

Where: l is the number of neurons in the hidden layer, n is the dimension of the input layer, m the dimension of the output layer, and a takes a constant between 1 and 10.

The relationship between the input and output variables of the neuron is shown in Equation 7:

$y_i=f\left({\displaystyle \sum _{i=1}^n}{w}_{ji}{x}_i\right)+b_j(7)$

where f is the activation function, typically a sigmoid, tanh or relu function is used; y_i is the output value; w_ji is the weight, x_i is the normalised input variable; b_j is the bias, b_j = - threshold.

For the training samples, this paper, on the basis of the orthogonal test mentioned above, carries out Latin hypercubic sampling through the Ihsdesign function in MATLAB for the sample variables of five factors and five levels, randomly generates 100 groups of five-factor data, and simulates and calculates the different combinations of the five factors to obtain 100 groups of test results as the learning samples of data for training by ABAQUS, and divides the learning samples into training sets and test sets in the ratio of 7:3 respectively. The learning samples were divided into training set and testing set in the ratio of 7:3 respectively.

4.2 Analysis of model results

Use the soil’s internal friction angle, cohesion, elastic modulus, Poisson’s ratio, and density as input variables. Treat the dynamic-compaction settlement as the target output. Employ MATLAB to build a GA-BP neural-network model that predicts the settlement produced by dynamic-compaction reinforcement. The hidden layer used tansig activation function, and the output layer used purelin activation function. The population size of GA is set to 140, the crossover probability is 0.7, the variation probability is 0.35, the maximum number of generations is 350, the elite retention ratio is 0.2, and the optimal number of nodes in the hidden layer is determined to be 5 according to the principle of trial and error method. It used the bootstrap method to estimate the uncertainty by resampling the training data (70% of the dataset, coded) 100 times in order to calculate 95% confidence intervals for the depth of pre-strengthened reinforcement. The results show an average confidence interval width of ±0.08 m, reflecting the reliability of the prediction. The prediction results are shown in Figure 11.

Figure 11

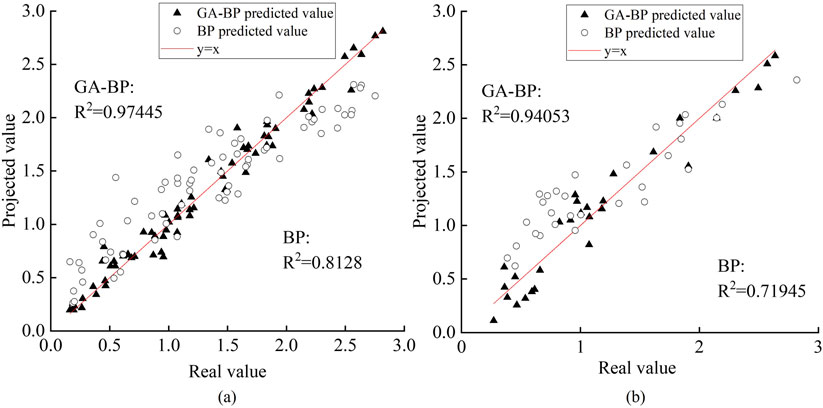
Figure 11. Comparison between GA-BP and traditional BP neural network. (a) Predicted versus measured values for the training set. (b) Comparison of predicted and measured values for the test set.

Figure 12

Figure 12. Comparison of model prediction and field test results.

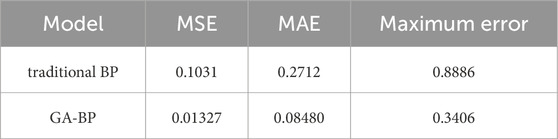
Figure 11 show the prediction results of GA-BP neural network, traditional BP neural network for strong tamping reinforcement tamping settlement under different foundation parameters, respectively. From the figure, it is obvious that the traditional BP neural network has poor accuracy in predicting the tamping settlement of strong tamping reinforcement, and the difference of coefficient of determination R² between the training set and the test set is 0.8128 and 0.71745, which indicates that the model is not well generalised to the test set, and exhibits the phenomenon of overfitting, which results in the model not being able to deal with the data of the test set very well. The GA-BP neural network model constructed in this paper predicts the results with high accuracy, and the highest error between its predicted and actual values is only 12.9%, and the coefficients of determination R2 of the training set and the test set are 0.97445 and 0.94053, which indicates that the GA-BP model is more accurate than the traditional BP neural network model for the prediction of the amount of tamping and dynamic compaction of the strong rammer reinforcement.

The conventional BP neural network tends to underestimate the measured values and exhibits poor predictive accuracy. A comparison of the MSE, MAE, and maximum error in Table 6 shows that the GA-optimized BP neural network fits the training data more effectively, improves generalization, and enhances network stability. Consequently, the tamping-settlement predictions produced by the GA-BP model can better guide on-site construction and provide a superior reference for using dynamic compaction to treat various foundation types.

Table 6

Table 6. Comparison of MSE, MAE and Maximum Error of traditional BP and GABP.

The GA-BP model, while highly effective for this study, has certain limitations. Its high model capacity may lead to overfitting on small or noisy datasets, though regularization techniques like dropout and early stopping can mitigate this issue. Additionally, the model’s performance depends on sufficient, representative training data, with reduced effectiveness under data scarcity or distribution shifts. The finite element method (FEM) simplifies boundary conditions, and the Drucker-Prager (D-P) model assumes isotropic material behavior, limiting its ability to capture anisotropic or time-dependent soil responses, which may impact prediction accuracy.

5 Conclusion

The geotechnical properties of the foundation soil exert a major influence on the effectiveness of dynamic compaction; therefore, when evaluating compaction performance, one must comprehensively account for the effects of the soil’s internal friction angle, cohesion, elastic modulus, Poisson’s ratio, and density on the resulting settlement.

(1) 3,000 kN·m and 1,000 kN·m tamping model test and field test results of the cumulative tamping volume curve of the fit R2 have reached more than 97%, and tamping law in line with the tamping volume with the increase in tamping energy increases with the increase in the number of times of tamping and gradually tends to stabilise, indicating that this paper’s method of establishing numerical models It shows that the numerical model established by the method in this paper has a certain degree of reliability.

(2) The core objective of tamping reinforcement is to improve the shear strength parameter to enhance the overall stability of the soil body, while the deformation parameters (elastic modulus and Poisson’s ratio) have a relatively small impact on the reinforcement effect.

(3) The GA-BP neural-network model developed for predicting settlement under dynamic compaction achieves high accuracy. Soil parameters (including internal friction angle, cohesion, elastic modulus, Poisson’s ratio, and density) substantially affect the predicted settlement. As the first time the GA-BP model is applied to the prediction of strong tamping reinforcement, the database can continue to be enriched by combining with field tests in order to further improve the prediction accuracy of the model.

(4) The creep and consolidation behavior of the soil under dynamic loading is a key aspect for improvement. In the future, elastic models can be combined with viscoelastic models to characterize the time-dependent mechanical properties of the soil during dynamic compaction, thereby enabling more accurate predictions of long-term deformations and delayed effects. Subsequent studies could further optimise the model by reconsidering the effect of groundwater and the friction between the rammer and the soil.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

YZ: Data curation, Validation, Writing – original draft. XC: Investigation, Writing – review and editing. HG: Conceptualization, Software, Writing – review and editing. ZG: Conceptualization, Supervision, Writing – review and editing. XL: Writing – original draft, Visualization.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This research was supported by the National Natural Science Foundation of China (52408460), the Hunan Provincial Natural Science Foundation (2024JJ6055).

Conflict of interest

Authors YZ, XC, HG, and ZG were employed by Shenzhen Municipal Group Co.

The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Chow, Y. K., Yong, D. M., Yong, K. Y., and Lee, S. L. (1992). Dynamic compaction analysis. J. Geotechnical Eng. 118 (8), 1141–1157. doi:10.1061/(asce)0733-9410(1992)118:8(1141)

CrossRef Full Text | Google Scholar

Ding, S., Su, C., and Yu, J. (2011). An optimizing BP neural network algorithm based on genetic algorithm. Artif. Intell. Rev. 36, 153–162. doi:10.1007/s10462-011-9208-z

CrossRef Full Text | Google Scholar

Feng, S. J., Du, F. L., Shi, Z. M., Shui, W. H., and Tan, K. (2015). Field study on the reinforcement of collapsible loess using dynamic compaction. Eng. Geol. 185, 105–115. doi:10.1016/j.enggeo.2014.12.006

CrossRef Full Text | Google Scholar

Freire de Souza, T., and Pasqual, R. P. S. (2021). New method to predict crater depth obtained in dynamic compaction. Geotechnical Geol. Eng. 39, 3981–3993. doi:10.1007/s10706-021-01726-x

CrossRef Full Text | Google Scholar

Ghorbani, J., Nazem, M., and Carter, J. P. (2020). Dynamic compaction of clays: numerical study based on the mechanics of unsaturated soils. Int. J. Geomechanics 20 (10), 04020195. doi:10.1061/(asce)gm.1943-5622.0001840

CrossRef Full Text | Google Scholar

Hu, R., Shi, W., Shui, W., and Zhang, Y. (2017). Study on the effective depth of improvement and influential factors by high energy dynamic compaction for backfilled soil.

Google Scholar

Hu, Z., Zhang, J., Tan, X., and Yang, H. (2024). Modeling of the particle abrasion process and a discrete element method study of its shape effect. Materials 17 (16), 3947. doi:10.3390/ma17163947

PubMed Abstract | CrossRef Full Text | Google Scholar

Jia, M., Yang, Y., Liu, Bo, and Wu, S. (2018). PFC/FLAC coupled simulation of dynamic compaction in granular soils. Granul. Matter 20 (4), 76–0. doi:10.1007/s10035-018-0841-y

CrossRef Full Text | Google Scholar

Khaboushan, E. A., Emami, H., Mosaddeghi, M. R., and Astaraei, A. R. (2018). Estimation of unsaturated shear strength parameters using easily-available soil properties. Soil Tillage Res. 184, 118–127. doi:10.1016/j.still.2018.07.006

CrossRef Full Text | Google Scholar

Koohsari, H., Alielahi, H., Najafi, A., and Adampira, M. (2023). The application of artificial intelligence methods on the optimizing improvement depth of dynamic compaction.

Google Scholar

Kufre Etim, R., Ufot Ekpo, D., Attah, I. C., and Chibuzor Onyelowe, K. (2021). Effect of micro sized quarry dust particle on the compaction and strength properties of cement stabilized lateritic soil. Clean. Mater. 2 (0), 100023. doi:10.1016/j.clema.2021.100023

CrossRef Full Text | Google Scholar

Li, P., Sun, J., Ge, X., Zhang, M., and Wang, J. (2023). Parameters of dynamic compaction based on model test. Soil Dyn. Earthq. Eng. 168, 107853. doi:10.1016/j.soildyn.2023.107853

CrossRef Full Text | Google Scholar

Liang, Y., Ren, C., Wang, H., Huang, Y. b., and Zheng, Z. t. (2019). Research on soil moisture inversion method based on GA-BP neural network model. Int. J. remote Sens. 40 (5-6), 2087–2103. doi:10.1080/01431161.2018.1484961

CrossRef Full Text | Google Scholar

López-Querol, S., Fernández-Merodo, J. A., Mira, P., and Pastor, M. (2008). Numerical modelling of dynamic consolidation on granular soils. Int. J. Numer. Anal. methods geomechanics 32 (12), 1431–1457. doi:10.1002/nag.676

CrossRef Full Text | Google Scholar

Mayne, P. W., Jones, Jr J. S., and Dumas, J. C. (1984). Ground response to dynamic compaction. J. Geotechnical Eng. 110 (6), 757–774. doi:10.1061/(asce)0733-9410(1984)110:6(757)

CrossRef Full Text | Google Scholar

Mei, Y., Zhang, S., Hu, C., Wang, X., Yuan, Y., Zhao, L., et al. (2021). Field test study on dynamic compaction in treatment of a deep collapsible loess foundation. Bull. Eng. Geol. Environ. 80 (10), 8059–8073. doi:10.1007/s10064-021-02343-x

CrossRef Full Text | Google Scholar

Mendez, R., Romanski, F. S., and Tomassone, M. S. (2011). Density behavior of cohesive granular materials. Powder Technol. 211 (2-3), 189–198. doi:10.1016/j.powtec.2010.11.024

CrossRef Full Text | Google Scholar

Miao, L., Chen, G., and Hong, Z. (2006). Application of dynamic compaction in highway: a case study. Geotechnical and Geol. Eng. 24, 91–99. doi:10.1007/s10706-004-2002-9

CrossRef Full Text | Google Scholar

Ombres, L., Aiello, M. A., Cascardi, A., and Verre, S. (2024). Modeling of steel-reinforced grout composite system-to-concrete bond capacity using artificial neural networks. J. Compos. Constr. 28 (5), 04024034. doi:10.1061/jccof2.cceng-4453

CrossRef Full Text | Google Scholar

Pan, Z., Han, W., Wang, Z., Jun Cao, J. C., and Lin, Z. (2024). “Numerical simulation study on the effect of solid ramming on self-weight wet sinking loess foundation,” in Proceedings of the 2024 International Conference on Smart City and Information System, 5–10. doi:10.1145/3685088.3685090

CrossRef Full Text | Google Scholar

Pistolesi, F., Baldassini, M., Volpe, E., Focacci, F., and Cattoni, E. (2025). Fast and interpretable prediction of seismic kinematics of flexible retaining walls in sand through explainable artificial intelligence. Comput. Geotechnics 179, 107007. doi:10.1016/j.compgeo.2024.107007

CrossRef Full Text | Google Scholar

Salah, A., Sodangi, M., Derdas, E. S., Al Nasser, J. N., Alshehri, A. A., et al. (2023). Analysis of factors affecting the performance of dynamic compaction technique: a study of coastal area of eastern province in Saudi arabia, 496, 504. doi:10.29117/cic.2023.0067

CrossRef Full Text | Google Scholar

Scott, B., Jaksa, M., and Mitchell, P. (2021). Depth of influence of rolling dynamic compaction. Proc. institution Civ. engineers-ground Improv. 174 (2), 85–94. doi:10.1680/jgrim.18.00117

CrossRef Full Text | Google Scholar

Sun, Y., Huang, K., Chen, X., Zhang, D., Lou, X., Huang, Z., et al. (2023). Study on the reinforcement mechanism of high-energy-level dynamic compaction based on FDM–DEM coupling. Mathematics 11 (13), 2807. doi:10.3390/math11132807

CrossRef Full Text | Google Scholar

Sun, Y. (2024). Vertical additional dynamic stress transfer characteristics of silt soil foundation reinforced by dynamic compaction. J. Transp. Sci. Eng. 40 (1), 16–27. doi:10.16544/j.cnki.cn43-1494/u.2023020324021997

CrossRef Full Text | Google Scholar

Teramoto, S., Ito, S., and Kobayashi, T. (2024). Deep learning-based soil compaction monitoring: a proof-of-concept study. J. Terramechanics 111, 65–72. doi:10.1016/j.jterra.2023.10.001

CrossRef Full Text | Google Scholar

Wang, L., Du, F., Liang, Y., Gao, W., Zhang, G., Sheng, Z., et al. (2023). A comprehensive in situ investigation on the reinforcement of high-filled red soil using the dynamic compaction method. Sustainability 15 (6), 4756. doi:10.3390/su15064756

CrossRef Full Text | Google Scholar

Wang, S., Zhang, N., Wu, L., and Wang, Y. (2016). Wind speed forecasting based on the hybrid ensemble empirical mode decomposition and GA-BP neural network method. Renew. energy 94, 629–636. doi:10.1016/j.renene.2016.03.103

CrossRef Full Text | Google Scholar

Wei, Y. -q., Cai, H., Wu, S. -f., Xiao, J. -z., and Song, J. -z. (2019). Vibration response and reinforcement mechanism of high-fill soil-stone mixtures by dynamic compaction. Chin. J. Geotechnical Eng. 41 (Z1), 237–240. doi:10.11779/CJGE2019S1060

CrossRef Full Text | Google Scholar

Wu, L., Zhou, J., and Li, Z. (2020). Applying of GA-BP neural network in the land ecological security evaluation. IAENG Int. J. Comput. Sci. 47 (1), 11–18.

Google Scholar

Xing, Y., and Li, F. (2020). Research on the influence of hidden layers on the prediction accuracy of GA-BP neural network. J. Phys. Conf. Ser. IOP Publ. 1486 (2), 022010. doi:10.1088/1742-6596/1486/2/022010

CrossRef Full Text | Google Scholar

Yang, H., Li, X., Zhang, J., Hu, Z., and Li, S. (2024). The distributions and dependences of 3D particle morphology characteristics for crushed and natural sands by X-ray uCT investigations. Materials 17 (23), 5805. doi:10.3390/ma17235805

PubMed Abstract | CrossRef Full Text | Google Scholar

You, Y., and Zhang, L. (2022). Application of bayesian regularized BP neural network in air quality index prediction. J. Chongqing Univ. Sci. Technol. Nat. Sci. Ed. 24 (01), 78–32. doi:10.19406/j.cnki.cqkjxyxbzkb.2022.01.011

CrossRef Full Text | Google Scholar

Yusoff, S. A. N. M., Bakar, I., Wijeyesekera, D. C., Zainorabidin, A., Azmi, M., and Ramli, H. (2017). “The effects of different compaction energy on geotechnical properties of kaolin and laterite,” in AIP conference proceedings. AIP Publishing, 030009. doi:10.1063/1.4998380

CrossRef Full Text | Google Scholar

Zhang, L., Wang, F., Sun, T., and Xu, B. (2018). A constrained optimization method based on BP neural network. Neural Comput. Appl. 29, 413–421. doi:10.1007/s00521-016-2455-9

CrossRef Full Text | Google Scholar

Zhan, X., Li, W., Yang, S., Zhu, Q., Xu, X., and Huang, H. (2023). Model tests on landslide dam materials improved by dynamic compaction. Chin. J. Geotechnical Eng. 45 (5), 953–963. doi:10.11779/CJGE20220198

CrossRef Full Text | Google Scholar

Zhou, C., Jiang, H., Yao, Z., Li, H., Yang, C., Chen, L., et al. (2020). Evaluation of dynamic compaction to improve saturated foundation based on the fluid-solid coupled method with soil cap model. Comput. Geotechnics 125, 103686. doi:10.1016/j.compgeo.2020.103686

CrossRef Full Text | Google Scholar

Ziaee, S. A., Sadrossadat, E., Alavi, A. H., and Mohammadzadeh Shadmehri, D. (2015). Explicit formulation of bearing capacity of shallow foundations on rock masses using artificial neural networks: application and supplementary studies. Environ. earth Sci. 73, 3417–3431. doi:10.1007/s12665-014-3630-x

CrossRef Full Text | Google Scholar